Deep Learning with Gaussian Differential Privacy

Abstract

Deep learning models are often trained on datasets that contain sensitive information such as individuals’ shopping transactions, personal contacts, and medical records. An increasingly important line of work therefore has sought to train neural networks subject to privacy constraints that are specified by differential privacy or its divergence-based relaxations. These privacy definitions, however, have weaknesses in handling certain important primitives (composition and subsampling), thereby giving loose or complicated privacy analyses of training neural networks. In this paper, we consider a recently proposed privacy definition termed f-differential privacy [18] for a refined privacy analysis of training neural networks. Leveraging the appealing properties of f-differential privacy in handling composition and subsampling, this paper derives analytically tractable expressions for the privacy guarantees of both stochastic gradient descent and Adam used in training deep neural networks, without the need of developing sophisticated techniques as [3] did. Our results demonstrate that the f-differential privacy framework allows for a new privacy analysis that improves on the prior analysis [3], which in turn suggests tuning certain parameters of neural networks for a better prediction accuracy without violating the privacy budget. These theoretically derived improvements are confirmed by our experiments in a range of tasks in image classification, text classification, and recommender systems. Python code to calculate the privacy cost for these experiments is publicly available in the TensorFlow Privacy library.

1. Introduction

In many applications of machine learning, the datasets contain sensitive information about individuals such as location, personal contacts, media consumption, and medical records. Exploiting the output of the machine learning algorithm, an adversary may be able to identify some individuals in the dataset, thus presenting serious privacy concerns. This reality gave rise to a broad and pressing call for developing privacy-preserving data analysis methodologies. Accordingly, there have been numerous investigations in the scholarly literature of many fields—statistics, cryptography, machine learning, and law—for the protection of privacy in data analysis.

Along this line, research efforts have repeatedly suggested the necessity of a rigorous and versatile definition of privacy. Among other things, researchers have questioned whether the use of a privacy definition gives interpretable privacy guarantees, and if so, whether this privacy definition allows for high accuracy of the private model among alternative definitions. In particular, anonymization as a syntactic and ad-hoc privacy concept has been shown to generally fail to guarantee privacy. Examples include the identification of a homophobic individual in the anonymized Netflix Challenge dataset [45] and the identification of the health records of the then Massachusetts governor in public anonymized medical datasets [56].

In this context, (ε, δ)-differential privacy (DP) arose as a mathematically rigorous definition of privacy [23]. Today, this definition has developed into a firm foundation of private data analysis, with its applications deployed by Google [26], Apple [5], Microsoft [16], and the US Census Bureau [4]. Despite its impressive popularity in both the scholarly literature and the industry, (ε, δ)-DP is not versatile enough to handle composition, which is perhaps the most fundamental primitive in statistical privacy. For example, the training process of deep neural networks is in effect the composition of many primitive building blocks known as stochastic gradient descent (SGD). Under a modest privacy budget in the (ε, δ)-DP sense, however, it was not clear how to maintain a high prediction accuracy of deep learning. This requires a tight privacy analysis of composition in the (ε, δ)-DP framework. Indeed, the analysis of the privacy costs in deep learning was refined only recently using a sophisticated technique called the moments accountant [3].

Ideally, we hope to have a privacy definition that allows for refined privacy analyses of various algorithms in a principled manner, without resorting to sophisticated techniques. Having a refined privacy analysis not only enhances the trustworthiness of the models but can also be leveraged to improve the prediction accuracy by trading off privacy for utility. One possible candidate is f-differential privacy, a relaxation of (ε, δ)-DP that was recently proposed by Dong, Roth, and Su [18]. This new privacy definition faithfully retains the hypothesis testing interpretation of differential privacy and can losslessly reason about common primitives associated with differential privacy, including composition, privacy amplification by subsampling, and group privacy. In addition, f-DP includes a canonical single-parameter family that is referred to as Gaussian differential privacy (GDP). Notably, GDP is the focal privacy definition due to a central limit theorem that states that the privacy guarantees of the composition of private algorithms are approximately equivalent to telling apart two shifted normal distributions.

The main results of this paper show that f-DP offers a rigorous and versatile framework for developing private deep learning methodologies¹. Our guarantee provides protection against an attacker with knowledge of the network architecture as well as the model parameters, which is in the same spirit as [53, 3]. In short, this paper delivers the following messages concerning f-DP:

Closed-form privacy bounds.

In the f-DP framework, the overall privacy loss incurred in training neural networks admits an amenable closed-form expression. In contrast, the privacy analysis via the moments accountant must be done by numerical computation [3], and the implicit nature of this earlier approach can hinder our understanding of how the tuning parameters affect the privacy bound. This is discussed in Section 3.1.

Stronger privacy guarantees.

The f-DP approach gives stronger privacy guarantees than the earlier approach [3], even in terms of (ε, δ)-DP. This improvement is due to the use of the central limit theorem for f-DP, which accurately captures the privacy loss incurred at each iteration in training the deep learning models. This is presented in Section 3.2 and illustrated with numerical experiments in Section 4.1.

Improved prediction accuracy.

Leveraging the stronger privacy guarantees provided by f-DP, we can trade a certain amount of privacy for an improvement in prediction performance. This can be realized, for example, by appropriately reducing the amount of noise added during the training process of neural networks so as to match the target privacy level in terms of (ε, δ)-DP. See Section 3.2 and Section 4.2 for the development of this utility improvement.

The remainder of the paper is structured as follows. In Section 1.1 we provide a brief review of related literature. Section 2 introduces f-DP and its basic properties at a minimal level. Next, in Section 3 we analyze the privacy cost of training deep neural networks in terms of f-DP and compare it to the privacy analysis using the moments accountant. In Section 4, we present numerical experiments to showcase the superiority of the f-DP approach to private deep learning in terms of test accuracy and privacy guarantees. The paper concludes with a discussion in Section 5.

1.1. Related Work

There are continued efforts to understand how privacy degrades under composition. Developments along this line include the basic composition theorem and the advanced composition theorem [22, 24]. In a pioneering work, [32] obtained an optimal composition theorem for (ε, δ)-DP, which in fact served as one of the motivations for the f-DP work [18]. However, it is #P hard to compute the privacy bounds from their composition theorem [44]. More recently, [17] derived sharp composition bounds on the overall privacy loss for exponential mechanisms.

From a different angle, a substantial recent effort has been devoted to relaxing differential privacy using divergences of probability distributions to overcome the weakness of (ε, δ)-DP in handling composition [21, 11, 43, 12]. Unfortunately, these relaxations either lack a privacy amplification by subsampling argument or present a quite complex argument that is difficult to use [8, 57]. As subsampling is inherently used in training neural networks, therefore, it is difficult to directly apply these relaxations to the privacy analysis of deep learning.

To circumvent these technical difficulties associated with (ε, δ)-DP and its divergence-based relaxations, Abadi et al. [3] invented a technique termed the moments accountant to track detailed information of the privacy loss in the training process of deep neural networks. Using the moments accountant, their analysis significantly improves on earlier privacy analysis of SGD [14, 55, 10, 53, 61] and allows for meaningful privacy guarantees for deep learning trained on realistically sized datasets. This technique has been extended to a variety of situations by follow-up work [41, 48]. In contrast, our approach to private deep learning in the f-DP framework leverages some powerful tools of this new privacy definition, nevertheless providing a sharper privacy analysis, as seen both theoretically and empirically in Sections 3 and 4.

For completeness, we remark that different approaches have been put forward to incorporate privacy considerations into deep learning, without leveraging the iterative and subsampling natures of training deep learning models. This line of work includes training a private model by an ensemble of “teacher” models [47, 46], the development of noised federated averaging algorithms [42], and analyzing privacy costs through the lens of the optimization landscape of neural networks [59].

2. Preliminaries

2.1. f-Differential Privacy

In the differential privacy framework, we envision an adversary that is well-informed about the dataset except for a single individual, and the adversary seeks to determine whether this individual is in the dataset on the basis of the output of an algorithm. Roughly speaking, the algorithm is considered private if the adversary finds it hard to determine the presence or absence of any individual.

Informally, a dataset can be thought of as a matrix, whose rows each contain one individual’s data. Two datasets are said to be neighbors if one can be derived by discarding an individual from the other. As such, the sizes of neighboring datasets differ by one². Let S and S′ be neighboring datasets, and ε ⩾ 0, 0 ⩽ δ ⩽ 1 be two numbers, and denote by M a (randomized) algorithm that takes as input a dataset.

Definition 2.1 ([23, 22]).

A (randomized) algorithm M gives (ε, δ)-differential privacy if for any pair of neighboring datasets S, S′ and any event E,

$$\mathbb{P}\left(M(S)\in E\right)⩽{\text{e}}^{\epsilon }\mathbb{P}\left(M\left(S^{\prime }\right)\in E\right)+\delta .$$

To achieve privacy, the algorithm M is necessarily randomized, whereas the two datasets in Definition 2.1 are deterministic. This privacy definition ensures that, based on the output of the algorithm, the adversary has a limited (depending on how small ε, δ are) ability to identify the presence or absence of any individual, regardless of whether any individual opts in to or opts out of the dataset.

In essence, the adversary seeks to tell apart the two probability distributions M(S) and M(S′) using a single draw. In light of this observation, it is natural to interpret what the adversary does as testing two simple hypotheses:

$$H_0:\text{ the true dataset is }S\text{ versus }{H}_1:\text{ the true dataset is }{S}^{\prime }.$$

The connection between differential privacy and hypothesis testing was, to our knowledge, first noted in [58], and was later developed in [32, 39, 9]. Intuitively, privacy is well guaranteed if the hypothesis testing problem is hard. Following this intuition, the definition of (ε, δ)-DP essentially uses the worst-case likelihood ratio of the distributions M(S) and M(S′) to measure the hardness of testing the two simple hypotheses.

Is there a more informative measure of the hardness? In [18], the authors propose to use the trade-off between type I error (the probability of erroneously rejecting H₀ when H₀ is true) and type II error (the probability of erroneously accepting H₀ when H₁ is true) in place of a few privacy parameters in (ε, δ)-DP or divergence-based DP definitions. To formally define this new privacy definition, let P and Q denote the distributions of M(S) and M(S′), respectively, and let ϕ be any (possibly randomized) rejection rule for testing H₀ : P against H₁ : Q. With these in place, [18] defines the trade-off function of P and Q as

$$\begin{gathered} T\left(P,Q\right):[0,1]\mapsto [0,1] \\ \alpha \mapsto \underset{\varphi }{\text{inf}}\left\{1-{\mathbb{E}}_Q[\varphi ]:{\mathbb{E}}_P[\varphi ]⩽\alpha \right\}. \end{gathered}$$

Above, ${\mathbb{E}}_P[\varphi ]$ and $1-{\mathbb{E}}_Q[\varphi ]$ are type I and type II errors of the rejection rule ϕ, respectively. Writing f = T(P, Q), the definition says that f(α) is the minimum type II error among all tests at significance level α. Note that the minimum can be achieved by taking the likelihood ratio test, according to the Neymann–Pearson lemma. As is self-evident, the larger the trade-off function is, the more difficult the hypothesis testing problem is (hence more privacy). This motivates the following privacy definition.

Definition 2.2 ([18]).

A (randomized) algorithm M is f-differentially private if

$$T\left(M(S),M\left(S^{\prime }\right)\right)⩾f$$

for all neighboring datasets S and S′.

In this definition, both T and f are functions that take α ∈ [0, 1] as input and the inequality holds pointwise for all 0 ⩽ α ⩽ 1, and we abuse notation by identifying M(S) and M(S′) with their associated distributions. This privacy definition is easily interpretable due to its inherent connection with the hypothesis testing problem. By adapting a result due to Wasserman and Zhou [58], (ε, δ)-DP is a special instance of f-DP in the sense that an algorithm is (ε, δ)-DP if and only if it is f_ε,δ-DP with

$$f_{\epsilon ,\delta }(\alpha )=\text{max}\left\{0,1-\delta -{\text{e}}^{\epsilon }\alpha ,{\text{e}}^{-\epsilon }(1-\delta -\alpha )\right\}.$$ (1)

The more intimate relationship between the two privacy definitions is that they are dual to each other: briefly speaking, f-DP ensures (ε, δ(ε))-DP with δ(ε) = 1 + f*(−e^ε) for every ε ⩾ 0³.

Next, we define a single-parameter family of privacy definitions within the f-DP class for a reason that will be apparent later. Let $G_{\mu }≔T(\mathcal{N}(0,1),\mathcal{N}(\mu ,1))$ for μ ⩾ 0. Note that this tradeoff function admits a closed-form expression G_μ(α) = Φ(Φ⁻¹(1−α)−μ), where Φ is the cumulative distribution function of the standard normal distribution.

Definition 2.3 ([18]).

A (randomized) algorithm M is μ-Gaussian differentially private (GDP) if

$$T\left(M(S),M\left(S^{\prime }\right)\right)⩾G_{\mu }$$

for all neighboring datasets S and S′.

In words, μ-GDP says that determining whether any individual is in the dataset is at least as difficult as telling apart the two normal distributions $\mathcal{N}(0,1)$ and $\mathcal{N}(\mu ,1)$ based on one draw. The Gaussian mechanism serves as a template to achieve GDP. Consider the problem of privately releasing a univariate statistic θ(S). The Gaussian mechanism adds $\mathcal{N}\left(0,{\sigma }^2\right)$ noise to the statistic θ, which gives μ-GDP if σ = sens(θ)/μ. Here the sensitivity of θ is defined as sens(θ) = sup_S,S′ |θ(S)− θ(S′)|, where the supremum is over all neighboring datasets.

2.2. Properties of f-Differential Privacy

Composition.

Deep learning models are trained using the composition of many SGD updates. Broadly speaking, composition is concerned with a sequence of analyses on the same dataset where each analysis is informed by the explorations of prior analyses. A central question that every privacy definition is faced with is to pinpoint how the overall privacy guarantee degrades under composition. Formally, letting M₁ be the first algorithm and M₂ be the second, we define their composition algorithm M as M(S) = (M₁(S), M₂(S, M₁(S))). Roughly speaking, the composition is to “release all information that is learned by the algorithms.” Notably, the second algorithm M₂ can take as input the output of M₁ in addition to the dataset S. In general, the composition of more than two algorithms follows recursively.

To introduce the composition theorem for f-DP, [18] defines a binary operation ⊗ on trade-off functions. Given trade-off functions f = T(P, Q) and g = T(P′, Q′), let f ⊗ g = T(P × P′, Q × Q′). This definition depends on the distributions P, Q, P′, Q′ only through f and g. Moreover, ⊗ is commutative and associative. Now the composition theorem can be readily stated as follows. Let M_t be f_t-DP conditionally on any output of the prior algorithms for t = 1, …, T. Then their T-fold composition algorithm is f₁ ⊗ ⋯ ⊗ f_T-DP. This result shows that the composition of algorithms in the f-DP framework is reduced to performing the ⊗ operation on the associated trade-off functions. As an important fact, the privacy bound f₁ ⊗ ⋯ ⊗ f_T in general cannot be improved. Put more precisely, one can find an f_t-DP mechanism M_t for t = 1, …, T such that their composition is precisely f₁ ⊗ ⋯ ⊗ f_T-DP (see the discussion following Theorem 4 in [18]).

More profoundly, a central limit theorem phenomenon arises in the composition of many “very private” f-DP algorithms in the following sense: the trade-off functions of small privacy leakage accumulate to G_μ for some μ under composition. Informally, assuming each f_t is very close to Id(α) = 1 − α, which corresponds to perfect privacy, then we have

$$f_1\otimes f_2\otimes \cdots \otimes f_T\text{ is approximately }{G}_{\mu }$$ (2)

if the number of iterations T is sufficiently large⁴. This central limit theorem approximation is especially suitable for the privacy analysis of deep learning, where the training process typically takes at least tens of thousands of iterations. The privacy parameter μ depends on some functionals such as the Kullback–Leibler divergence of the trade-off functions. The central limit theorem yields a very accurate approximation in the settings considered in Section 4 (see numerical confirmation in Appendix A). For a rigorous account of this central limit theorem for differential privacy, see Theorem 6 in [18]. We remark that a conceptually related article [54] developed a central limit theorem for privacy loss random variables.

At a high level, this convergence-to-GDP result brings GDP to the focal point of the family of f-DP guarantees, implying that GDP is to f-DP as normal random variables to general random variables. Furthermore, this result serves as an effective approximation tool for approximating the privacy guarantees of composition algorithms. In contrast, privacy loss cannot be losslessly tracked under composition in the (ε, δ)-DP framework.

Subsampling.

In training neural networks, the gradient at each iteration is computed from a mini-batch that is subsampled from the training examples. Intuitively, an algorithm applied to a subsample gives stronger privacy guarantees than applied to the full sample. Looking closely, this privacy amplification is due to the fact that an individual enjoys perfect privacy if not selected in the subsample. A concrete and pressing question is, therefore, to precisely characterize how much privacy is amplified by subsampling in the f-DP framework.

Consider the following sampling scheme: for each individual in the dataset S, include his or her datum in the subsample independently with probability p, which is sometimes referred to as the Poisson subsampling [57]. The resulting subsample is denoted by Sample_p(S). For the purpose of clearing up any confusion, we remark that the subsample Sample_p(S) has a random size and as an intermediate step is not released. Given any algorithm M, denote by M ◦ Sample_p the subsampled algorithm.

The subsampling theorem for f-DP states as follows. Let M be f-DP, write f_p for pf+(1−p)Id, and denote by $f_p^{-1}$ the inverse⁵ of f_p. It is proved in Appendix A that the subsampled algorithm M ◦ Sample_p satisfies

$$T\left(M\circ {\text{Sample}}_p(S),M\circ {\text{Sample}}_p\left(S^{\prime }\right)\right)⩾f_p$$ (3)

if S can be obtained by removing one individual from S′. Likewise,

$$T\left(M\circ {\text{Sample}}_p\left(S^{\prime }\right),M\circ {\text{Sample}}_p(S)\right)⩾f_p^{-1}.$$

As such, the two displays above say that the trade-off function of M ◦ Sample_p on any neighboring datasets is lower bounded by $\text{min}\left\{f_p,f_p^{-1}\right\}$, which however is in general non-convex and thus is not a trade-off function. This suggests that we can boost the privacy bound by replacing $\text{min}\left\{f_p,f_p^{-1}\right\}$ with its double conjugate $\text{min}{\left\{f_p,f_p^{-1}\right\}}^{**}$, which is the greatest convex lower bound of $\text{min}\left\{f_p,f_p^{-1}\right\}$ and is indeed a trade-off function. Taken together, all the pieces show that the subsampled algorithm M ◦ Sample_p is $\text{min}{\left\{f_p,f_p^{-1}\right\}}^{**}-\text{DP}$.

Notably, the privacy bound $\text{min}{\left\{f_p,f_p^{-1}\right\}}^{**}$ is larger than f and cannot be improved in general. In light of the above, the f-DP framework is flexible enough to nicely handle the analysis of privacy amplification by subsampling. In the case where the original algorithm M is (ε, δ)-DP, this privacy bound strictly improves on the subsampling theorem for (ε, δ)-DP [38].

3. Algorithms and Their Privacy Analyses

3.1. NoisySGD and NoisyAdam

SGD and Adam [33] are among the most popular optimizers in deep learning. Here we introduce a new privacy analysis of a private variant of SGD in the f-DP framework and then extend the study to a private version of Adam.

Letting S = {x₁, …, x_n} denote the dataset, we consider minimizing the empirical risk

$$L(\theta )=\frac{1}{n}\sum _{i=1}^n\mathcal{l}\left(\theta ,x_i\right),$$

where θ denotes the weights of the neural networks and ℓ(θ, x_i) is a loss function. At iteration t, a mini-batch I_t is selected from {1, 2, …, n} with subsampling probability p, thereby having an approximate size of pn. Taking learning rate η_t and initial weights θ₀, the vanilla SGD updates the weights according to

$${\theta }_{t+1}={\theta }_t-{\eta }_t\cdot \frac{1}{|I_t|}\sum _{i\in I_t}{\nabla }_{\theta }\mathcal{l}\left({\theta }_t,x_i\right).$$

To preserve privacy, [14, 55, 10, 3] introduce two modifications to the vanilla SGD. First, a clip step is applied to the gradient so that the gradient is in effect bounded. This step is necessary to have a finite sensitivity. The second modification is to add Gaussian noise to the clipped gradient, which is equivalent to applying the Gaussian mechanism to the updated iterates. Formally, the private SGD algorithm is described in Algorithm 1. Herein I is the identity matrix and ∥ · ∥₂ denotes the ℓ₂ norm. Formally, we present this in Algorithm 1, which we henceforth refer to as NoisySGD. As a contribution of the present paper, NoisySGD uses the Poisson subsampling, as opposed to the uniform sampling used in [18]. For completeness, we remark that there is another possible subsampling method: shuffling (randomly permuting and dividing data into folds at each epoch). We emphasize that different subsampling mechanisms produce different privacy guarantees.

The analysis of the overall privacy guarantee of NoisySGD makes heavy use of the compositional and subsampling properties of f-DP. We first focus on the privacy analysis of the step that computes θ_t+1 from θ_t. Let M denote the gradient update and write Sample_p(S) for the mini-batch I_t (we drop the subscript t for simplicity). This allows us to use M ◦ Sample_p(S) to represent what NoisySGD does at each iteration. Next, note that adding or removing one individual would change the value of ${\sum }_{i\in I_t}{\overline{v}}_t^{(i)}$ by at most R in the ℓ₂ norm due to the clipping operation, that is, ${\sum }_{i\in I_t}{\overline{v}}_t^{(i)}$ has sensitivity R. Consequently, the Gaussian mechanism with noise standard deviation σR ensures that M is $\frac{1}{\sigma }-\text{GDP}$. With a few additional arguments, in Appendix B we show that NoisySGD is min{f, f⁻¹}**-DP with f = (pG_1/σ + (1 − p)Id)^⊗T. As a remark, it has been empirically observed in [3, 6] that the performance of the private neural networks is not sensitive to the choice of the clipping norm bound R (see more discussion in [48, 60]).

To facilitate the use of this privacy bound, we now derive an analytically tractable approximation of min{f, f⁻¹}** using the privacy central limit theorem in a certain asymptotic regime, which further demonstrates the mathematical coherence and versatility of the f-DP framework. The central limit theorem shows that, in the asymptotic regime where $p\sqrt{T}\to \nu$ for a constant ν > 0 as T → ∞,

$$f={\left(p{G}_{1/\sigma }+(1-p)\text{Id}\right)}^{\otimes T}\to G_{\mu },$$

where $\mu =\nu \sqrt{{\text{e}}^{1/{\sigma }^2}-1}$. Thus, the overall privacy loss in the form of the double conjugate satisfies

$$\text{min}{\left\{f,f^{-1}\right\}}^{**}\approx \text{min}{\left\{G_{\mu },G_{\mu }^{-1}\right\}}^{**}=G_{\mu }^{**}=G_{\mu }.$$ (4)

As such, the central limit theorem demonstrates that NoisySGD is approximately $p\sqrt{T\left({\text{e}}^{1/{\sigma }^2}-1\right)}-\text{GDP}$. Denoting by B = pn the mini-batch size, the privacy parameter $p\sqrt{T\left({\text{e}}^{1/{\sigma }^2}-1\right)}$ equals $\frac{B}{n}\sqrt{T\left({\text{e}}^{1/{\sigma }^2}-1\right)}$. Intuitively, this reveals that NoisySGD gives good privacy guarantees if $B\sqrt{T}/n$ is small and σ is not too small.

As an aside, we remark that this new privacy analysis is different from the one performed in Section 5 of [18]. Therein, the authors consider Algorithm 1 with uniform subsampling and obtain a privacy bound that is different from the one in the present paper.

Next, we present a private version of Adam [33] in Algorithm 2, which we refer to as NoisyAdam and can be found in [2]. This algorithm has the same privacy bound as NoisySGD in the f-DP framework. In short, this is because the momentum m_t and u_t are deterministic functions of the noisy gradients and no additional privacy cost is incurred due to the post-processing property of differential privacy. In passing, we remark that the same argument applies to AdaGrad [20] and therefore it is also asymptotically GDP in the same asymptotic regime.

3.2. Comparisons with the Moments Accountant

It is instructive to compare the moments accountant with our privacy analysis performed in Section 3.1 using the f-DP framework. Developed in [3], the moments accountant gives a tight one-to-one mapping between ε and δ for specifying the overall privacy loss in terms of (ε, δ)-DP under composition, which is beyond the reach of the advanced composition theorem [24]. In slightly more detail, the moments accountant uses the moment generating function of the privacy loss random variable to track the privacy loss under composition. As abuse of notation, this paper uses functions δ_MA = δ_MA(ε) and ε_MA = ε_MA(δ) to denote the mapping induced by the moments accountant in both directions⁶. For self-containedness, the appendix includes a formal description of the two functions.

Although NoisySGD and NoisyAdam are our primary focus, our following discussion applies to general iterative algorithms where composition must be addressed in the privacy analysis. Let algorithm M_t be f_t-DP for t = 1, …, T and write M for their composition. On the one hand, the moments accountant technique ensures that M is (ε, δ_MA(ε))-DP for any ε or, put equivalently, is (ε_MA, δ)-DP⁷. On the other hand, the composition algorithm is f₁ ⊗ ⋯ ⊗ f_T-DP from the f-DP viewpoint and, following from the central limit theorem (2), this composition can be shown to be approximately GDP in a certain asymptotic regime. For example, both NoisySGD and NoisyAdam presented in Algorithm 1 and Algorithm 2, respectively, asymptotically satisfy μ_CLT-GDP with privacy parameter

$${\mu }_{\text{CLT}}=p\sqrt{T\left({\text{e}}^{1/{\sigma }^2}-1\right)}.$$ (5)

In light of the above, it is tempting to ask which of the two approaches yields a sharper privacy analysis. In terms of f-DP guarantees, it must be the latter, which we refer to as the CLT approach, because the composition theorem of f-DP is tight and, more importantly, the privacy central limit theorem is asymptotic exact. To formally state the result, note that the moments accountant asserts that the private optimizer is (ε, δ_MA(ε))-DP for all ε ⩾ 0, which is equivalent to ${\text{sup}}_{\epsilon ⩾0}{f}_{\epsilon ,{\delta }_{\text{MA}}(\epsilon )}-\text{DP}$ by recognizing (1) (see also Proposition 2.11 in [18]). Roughly speaking, the following theorem says that ${\text{sup}}_{\epsilon ⩾0}{f}_{\epsilon ,{\delta }_{\text{MA}}(\epsilon )}-\text{DP}$ asymptotically) promises no more privacy guarantees than the bound of μ_CLT-GDP given by the CLT approach. This simple result is summarized by the following theorem and see Appendix B for a formal proof of this result.

Theorem 1 (Comparison in f-DP).

Assume that $p\sqrt{T}$ converges to a positive constant as T → ∞. Then, both NoisySGD and NoisyAdam satisfy

$$\underset{T\to \infty }{\text{lim sup }}\left(\underset{\epsilon ⩾0}{\text{sup }}{f}_{\epsilon ,{\delta }_{\text{MA}}(\epsilon )}(\alpha )-G_{{\mu }_{\text{CLT}}}(\alpha )\right)⩽0$$

for every 0 ⩽ α ⩽ 1.

Remark 1.

For ease of reading, we point out that, in the (ε, δ)-DP framework, the smaller ε, δ are, the more privacy is guaranteed. In contrast, in the f-DP framework, the smaller f is, the less privacy is guaranteed.

From the (ε, δ)-DP viewpoint, however, the question is presently unclear. Explicitly, the duality between f-DP and (ε, δ)-DP shows that μ-GDP implies (ε, δ(ε; μ))-DP for all ε ⩾ 0, where⁸

$$\delta (\epsilon ;\mu )=1+G_{\mu }^{*}\left(-{\text{e}}^{\epsilon }\right)=\Phi \left(-\frac{\epsilon }{\mu }+\frac{\mu }{2}\right)-{\text{e}}^{\epsilon }\Phi \left(-\frac{\epsilon }{\mu }-\frac{\mu }{2}\right).$$ (6)

The question is, therefore, reduced to the comparison between δ_MA(ε) and δ_CLT(ε) ≔ δ(ε; μ_CLT) or, equivalently, between ε_MA(δ) and ε_CLT(δ) ≔ ε(δ; μ_CLT)⁹.

Theorem 2 (Comparison in (ε, δ)-DP).

Under the assumptions of Theorem 1, the f-DP framework gives an asymptotically sharper privacy analysis of both NoisySGD and NoisyAdam than the moments accountant in terms of (ε, δ)-DP. That is,

$$\underset{T\to \infty }{\text{lim sup }}\left({\delta }_{\text{CLT}}(\epsilon )-{\delta }_{\text{MA}}(\epsilon )\right)<0$$

for all 7 ε ⩾ 0.

In words, the CLT approach in the f-DP framework allows for an asymptotically smaller δ than the moments accountant at the same ε. It is worthwhile mentioning that the inequality in this theorem holds for any finite T if δ is derived by directly applying the duality to the (exact) privacy bound f₁ ⊗ ⋯ ⊗ f_T. Equivalently, the theorem says that lim sup_T→∞ (ε_CLT(δ) − ε_MA(δ)) < 0 for any δ¹⁰. As such, by setting the same δ in both approaches, say δ = 10⁻⁵, the f-DP based CLT approach shall give a smaller value of ε.

From a practical viewpoint, this refined privacy analysis allows us to trade privacy guarantees for improvement in utility. More precisely, recognizing the aforementioned conclusion that δ(ε; μ_CLT) ≡ δ_CLT(ε) < δ_MA(ε) (for sufficiently large T) and that δ(ε; μ) increases as μ increases, one can find ${\tilde{\mu }}_{\text{CLT}}>{\mu }_{\text{CLT}}$ such that

$$\delta \left(\epsilon ;{\tilde{\mu }}_{\text{CLT}}\right)={\delta }_{\text{MA}}(\epsilon ).$$ (7)

Put differently, we can carefully adjust some parameters in Algorithm 1 and Algorithm 2 in order to let the algorithms be ${\tilde{\mu }}_{\text{CLT}}-\text{GDP}$. For example, we can reduce the scale of the added noise from σ to a certain $\tilde{\sigma }<\sigma$, which can be solved from (7) and

$${\tilde{\mu }}_{\text{CLT}}=p\sqrt{T\left({\text{e}}^{1/{\tilde{\sigma }}^2}-1\right)}.$$ (8)

Note that this is adapted from (5).

Figure 1 shows the flowchart of the privacy analyses using the two approaches and their relationship. In addition, numerical comparisons are presented in Figure 2, consistently demonstrating the superiority of the CLT approach.

Figure 1:

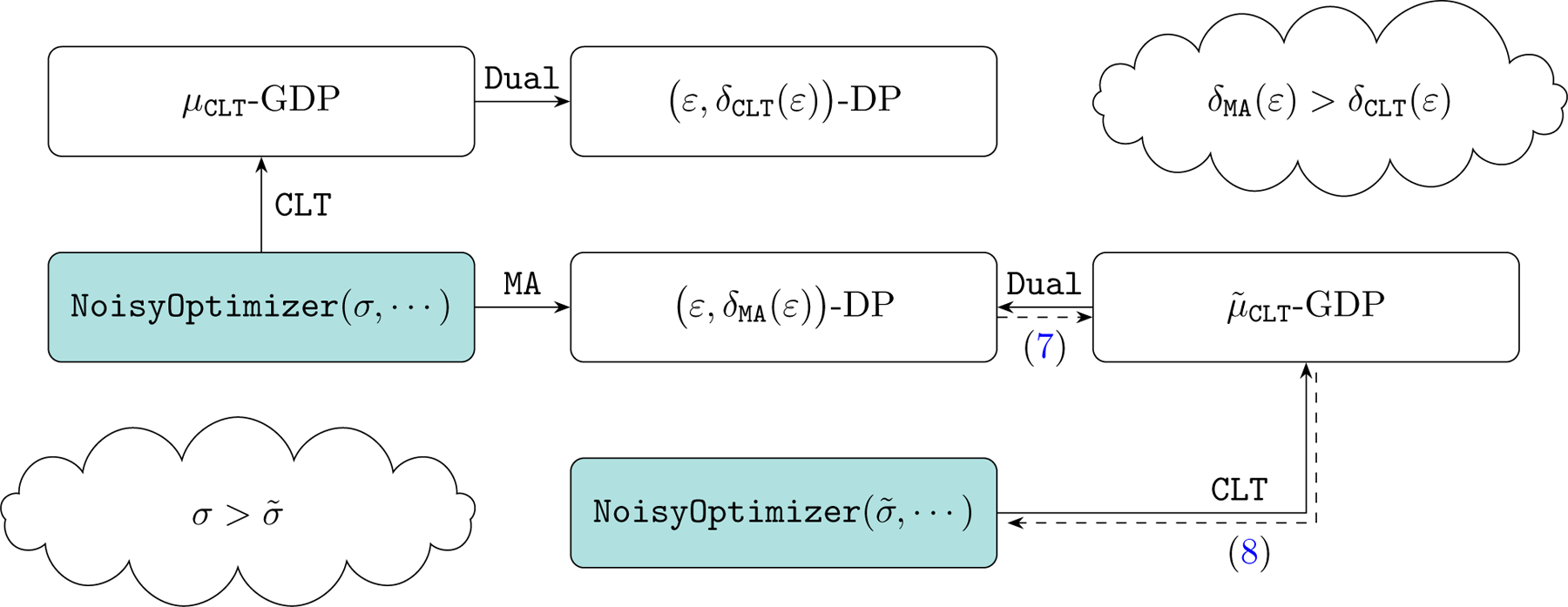
An illustration of the CLT approach in the f-DP framework and the moments accountant in the (ε, δ)-DP framework. NoisyOptimizer(σ, …) using the moments accountant gives the same privacy guarantees in terms of (ε, δ)-DP as $\text{NoisyOptimizer}(\tilde{\sigma },\dots )$ using the CLT approach (the ellipses denote omitted parameters). Note that the duality formula (6) is used in solving ${\tilde{\mu }}_{\text{CLT}}$ from (7).

Figure 2:

Tradeoffs between ε and δ for both CLT and MA, which henceforth denotes the moments accountant. The settings follows the MNIST experiment in Section 4 with σ = 0.7, p = 256/60000. The bottom two plots assume δ = 10⁻⁵. Note ε and δ in the CLT are related via (6) with μ = μ_CLT. The bottom right plot is consistent with the conclusion $\sigma >\tilde{\sigma }$ shown in the cloud icon of Figure 1.

4. Results

In this section, we use NoisySGD and NoisyAdam to train private deep learning models on datasets for tasks ranging from image classification (MNIST), text classification (IMDb movie review), recommender systems (MovieLens movie rating), to regular binary classification (Adult income). Note that these datasets all contain sensitive information about individuals, and this fact necessitates privacy consideration in the training process. Code to reproduce the results using the TensorFlow Privacy library is available at https://github.com/tensorflow/privacy/tree/master/research/GDP_2019.

4.1. The f-DP Perspective

This section demonstrates the utility and practicality of the private deep learning methodologies with associated privacy guarantees in terms of f-DP. In Section 4.2, we extend the empirical study to the (ε, δ)-DP framework. Throughout the experiments, the parameter δ we use always satisfies δ < 1/n, where n is the number of training examples.

MNIST.

The MNIST dataset [35] contains 60,000 training images and 10,000 test images. Each image is in 28 × 28 gray-scale representing a handwritten digit ranging from 0 to 9. We train neural networks with the same architecture (two convolutional layers followed by one dense layer) as in [2, 3] on this dataset. Throughout the experiment, we set the subsampling probability to p = 256/60000 and use a constant learning rate η.

Table 1 displays the test accuracy of the neural networks trained by NoisySGD as well as the associated privacy analyses. The privacy parameters ε in the last two columns are both with respect to δ = 10⁻⁵. Over all six sets of experiments with different tuning parameters, the CLT approach gives a significantly smaller value of ε than the moments accountant, which is consistent with our discussion in Section 3.2. The point we wish to emphasize, however, is that f-DP offers a much more comprehensive interpretation of the privacy guarantees than (ε, δ)-DP. For instance, the model from the third row preserves a decent amount of privacy since it is not always easy to tell apart $\mathcal{N}(0,1)$ and $\mathcal{N}(1.13,1)$. In stark contrast, the (ε, δ)-DP viewpoint is too conservative, suggesting that for the same model not much privacy is left, due to a very large “likelihood ratio” e^ε in Definition 2.1: it equals e^7.10 = 1212.0 or e^5.07 = 159.1 depending on which approach is chosen. This shortcoming of (ε, δ)-DP cannot be overcome by taking a larger δ, which, although gives rise to a smaller ε, would undermine the privacy guarantee from a different perspective.

Table 1:

Experimental results for NoisySGD and their privacy analyses on MNIST. The accuracy is averaged over 10 independent runs. The hyperparameters in the first three rows are the same as in [2]. The μ in the 6th row is calculated using (5), which carries over to the 7th row via (6) with δ = 10⁻⁵. The number of epochs is equal to T × mini-batch size/n = pT.

η	R	σ	Epochs	Test accuracy (%)	CLT μ	CLT ε	MA ε
0.25	1.5	1.3	15	95.0	0.23	0.83	1.19
0.15	1.0	1.1	60	96.6	0.57	2.32	3.01
0.25	1.5	0.7	45	97.0	1.13	5.07	7.10
0.25	1.5	0.6	62	97.6	2.00	9.98	13.27
0.25	1.5	0.55	68	97.8	2.76	14.98	18.72
0.25	1.5	0.5	100	98.0	4.78	31.12	32.40

For all experiments described in Table 1, Figure 3 illustrates the privacy bounds given by the CLT approach and the moments accountant both in terms of trade-off functions. The six plots in the first and third rows are with respect to δ = 10⁻⁵, from which the f-DP framework is seen to provide an analyst with substantial improvements in the privacy bounds. Note that the first row in Figure 3 corresponds to the first three rows in Table 1, and the third row in Figure 3 corresponds to the last three rows in Table 1. For the model corresponding to 96.6% test accuracy, concretely, the minimum sum of type I and type II errors in the sense of hypothesis testing is (at least) 77.6% by the CLT approach, whereas it is merely (at least) 9.4% by the moments accountant. For completeness, we show the optimal trade-off functions over all pairs of ε, δ given by the moments accountant in the middle row. The gaps between the two approaches exist, as predicted by Theorem 1, and remain significant.

Figure 3:

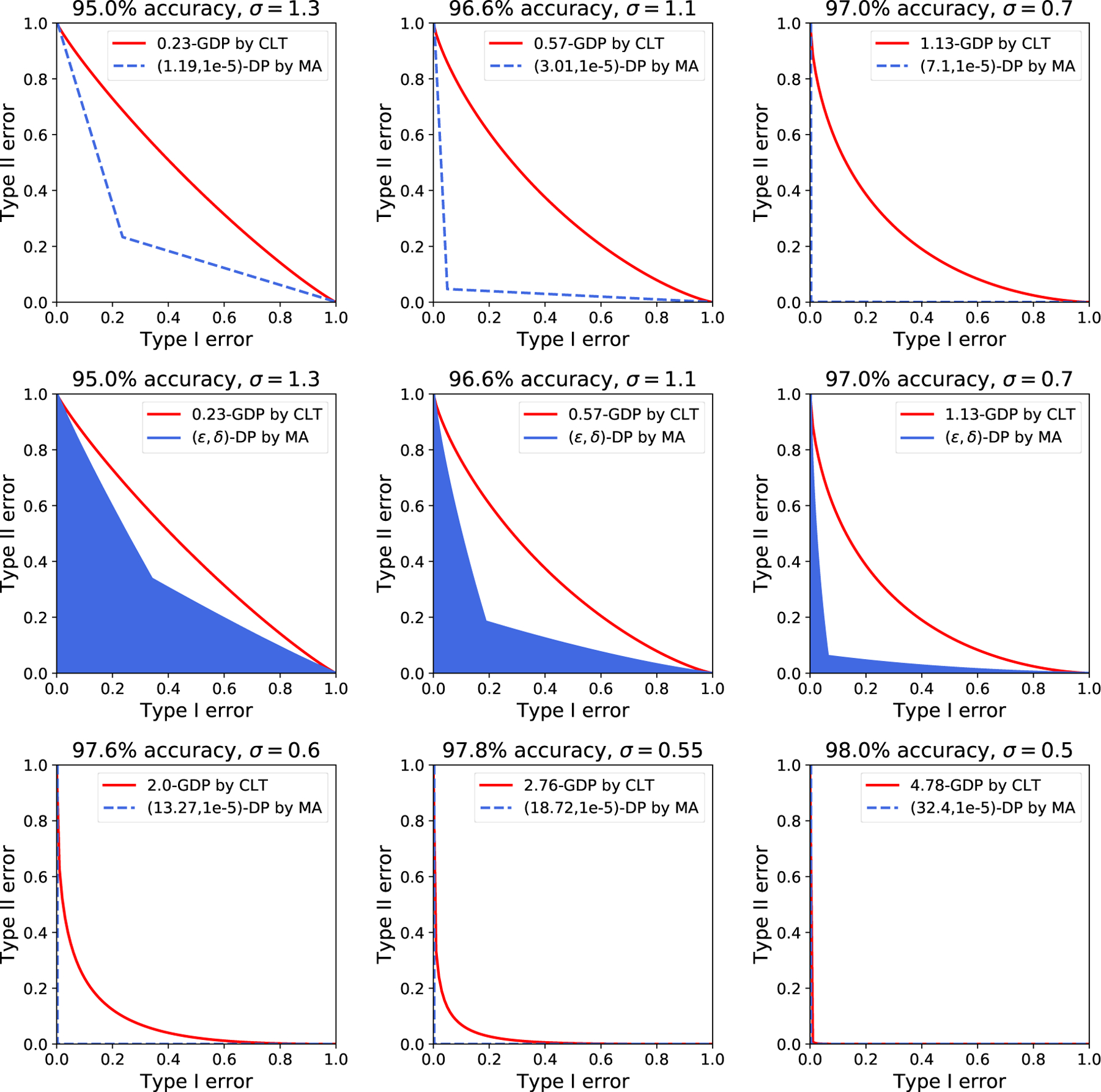
Comparisons between the two ways of privacy analysis on MNIST in terms of the tradeoff between type I and type II errors, in the same setting as Table 1. The plots are different from Figure 7 in [18]. The (ε, δ)-DP guarantees are plotted according to (1). The blue regions in the plots from the second row correspond to all pairs of (ε, δ) computed by MA. The blue regions are not noticeable in the third row.

Next, we extend our experiments to other datasets to further test f-DP for training private neural networks. The experiments compare private models under the privacy budget μ ≤ 2 to their non-private counterparts and some popular baseline methods. For simplicity, we focus on shallow neural networks and leave the investigation of complex architectures for future research.

Adult income.

Originally from the UCI repository [19], the Adult income dataset has been preprocessed into the LIBSVM format [13]. This dataset contains 32,561 examples, each of which has 123 features and a label indicating whether the individual’s annual income is more than $50,000 or not. We randomly choose 10% of the examples as the test set (3,256 examples) and use the remaining 29,305 examples as the training set.

Our model is a single-layer multi-perceptron with 16 neurons and the ReLU activation. We set σ = 0.55, p = 256/29305, η = 0.15, R = 1, and use NoisySGD as our optimizer. The results displayed in Table 2 show that our private model achieves comparable performance to the baselines in the MLC++ library [34] in terms of test accuracy.

Table 2:

Results for NoisySGD on the Adult income dataset. The ε parameters are with respect to δ = 10⁻⁵.

Models	Epochs	Test accuracy (%)	CLT μ	CLT ε	MA ε
private networks	18	84.0	2.03	10.20	14.70
non-private networks	20	84.5	—	—	—
kNN [15]	—	79.7	—	—	—
naive Bayes	—	83.9	—	—	—
voted ID3 [49]	—	84.4	—	—	—
C4.5 [50]	—	84.5	—	—	—

IMDb.

We use the IMDb movie review dataset [40] for binary sentiment classification (positive or negative reviews). The dataset contains 25,000 training and 25,000 test examples. In our experiments, we prepocess the dataset by only including the top 10,000 frequently used words and discard the rest. Next, we set every example to have 256 words by truncating the length or filling with zeros if necessary.

In our neural networks, the input is first embedded into 16 units and then is passed through a global average pooling. The intermediate output is fed to a fully-connected layer with 16 neurons, followed by a ReLU layer. We set σ = 0.56, p = 512/25000, η = 0.02, R = 1, and use NoisyAdam as our optimizer, which is observed to converge much faster than NoisySGD in this training task. We use the (non-private) two-layer LSTM RNN model in the Tensorflow tutorials [1] as a baseline model. Table 3 reports the experimental results. Notably, the private neural networks perform comparably to the baseline model, at the cost of only one percent drop in test accuracy compared to the non-private counterpart.

Table 3:

Results for NoisyAdam on the IMDB dataset, with δ = 10⁻⁵ used in the privacy analyses.

Models	Epochs	Test accuracy (%)	CLT μ	CLT ε	MA ε
private networks	9	83.8	2.07	10.43	15.24
non-private networks	20	84.7	—	—	—
LSTM-RNN [30]	10	85.4	—	—	—

MovieLens.

The MovieLens movie rating dataset [28] is a benchmark dataset for recommendation tasks. Our experiments consider the MovieLens 1M dataset, which contains 1,000,209 movie ratings from 1 star to 5 stars. In total, there are 6,040 users who rated 3,706 different movies. For this multi-class classification problem, the root mean squared error (RMSE) is chosen as the performance measure. It is worthwhile to mention that, as each user only watched a small fraction of all the movies, most (user, movie) pairs correspond to missing ratings. We randomly sample 20% of the examples as the test set and take the remainder as the training set.

Our model is a simplified version of the neural collaborative filtering in [29]. The network architecture consists of two branches. The left branch applies generalized matrix factorization to embed the users and movies using five latent factors. The output of the user embedding is multiplied by the item embedding. In the right branch, we use 10 latent factors for embedding. The embedding from both branches are then concatenated, which is fed to a fully-connected output layer. We set σ = 0.6, p = 1/80, η = 0.01, and R = 5 in NoisyAdam.

Table 4 presents the numerical results of our neural networks as well as baseline models in the Suprise library [31] in their default settings. The difference in RMSE between the non-private networks and the private one is relatively large for the MovieLens 1M dataset. Nevertheless, the private model still outperforms many popular non-private models, including the user-based collaborative filtering and nonnegative matrix factorization.

Table 4:

Results for NoisyAdam on the MovieLens 1M dataset, with δ = 10⁻⁶ used in the privacy analyses. CF stands for collaborative filtering.

Models	Epochs	RMSE	CLT μ	CLT ε	MA ε
private networks	20	0.915	1.94	10.61	15.39
non-private networks	20	0.893	—	—	—
SVD	—	0.873	—	—	—
NMF	—	0.916	—	—	—
user-based CF [52]	—	0.923	—	—	—
global average	—	1.117	—	—	—

4.2. The (ε, δ)-DP Perspective

While we hope that the f-DP perspective has been conclusively demonstrated to be advantageous, this section shows that the CLT approach continues to bring considerable benefits even in terms of (ε, δ)-DP. Specifically, by making use of the comparisons between the CLT approach and the moments accountant in Section 3.2, we can add less noise to the gradients in NoisySGD and NoisyAdam while achieving the same (ε, δ)-DP guarantees provided by the moments accountant. With less added noise, conceivably, an optimizer would have a higher prediction accuracy.

Figure 4 illustrates the experimental results on MNIST. In the top two plots, we set the noise scales to σ = 1.3, $\tilde{\sigma }=1.06$, which are both shown to give (1.34, 10⁻⁵)-DP at epoch 20 using the moments accountant and the CLT approach, respectively. The test accuracy associated with the CLT approach is almost always higher than that associated with the moments accountant. In addition, another benefit of taking the CLT approach is that it gives rise to stronger privacy protection before reaching epoch 20, as shown by the right plot. For the bottom plots, although the improvement in test accuracy at the end of training is less significant, the CLT approach leads to much faster convergence at early epochs. To be concrete, the numbers of epochs needed to achieve 95%, 96%, and 97% test accuracy are 18, 26, and 45, respectively, for the neural networks with less noise, whereas the numbers of epochs are 23, 33, and 64, respectively, using noise level that is computed by the moments accountant. In a similar vein, the moments accountant gives a test accuracy of 92% for the first time when ε = 4 and the CLT approach achieves 96% under the same privacy budget.

Figure 4:

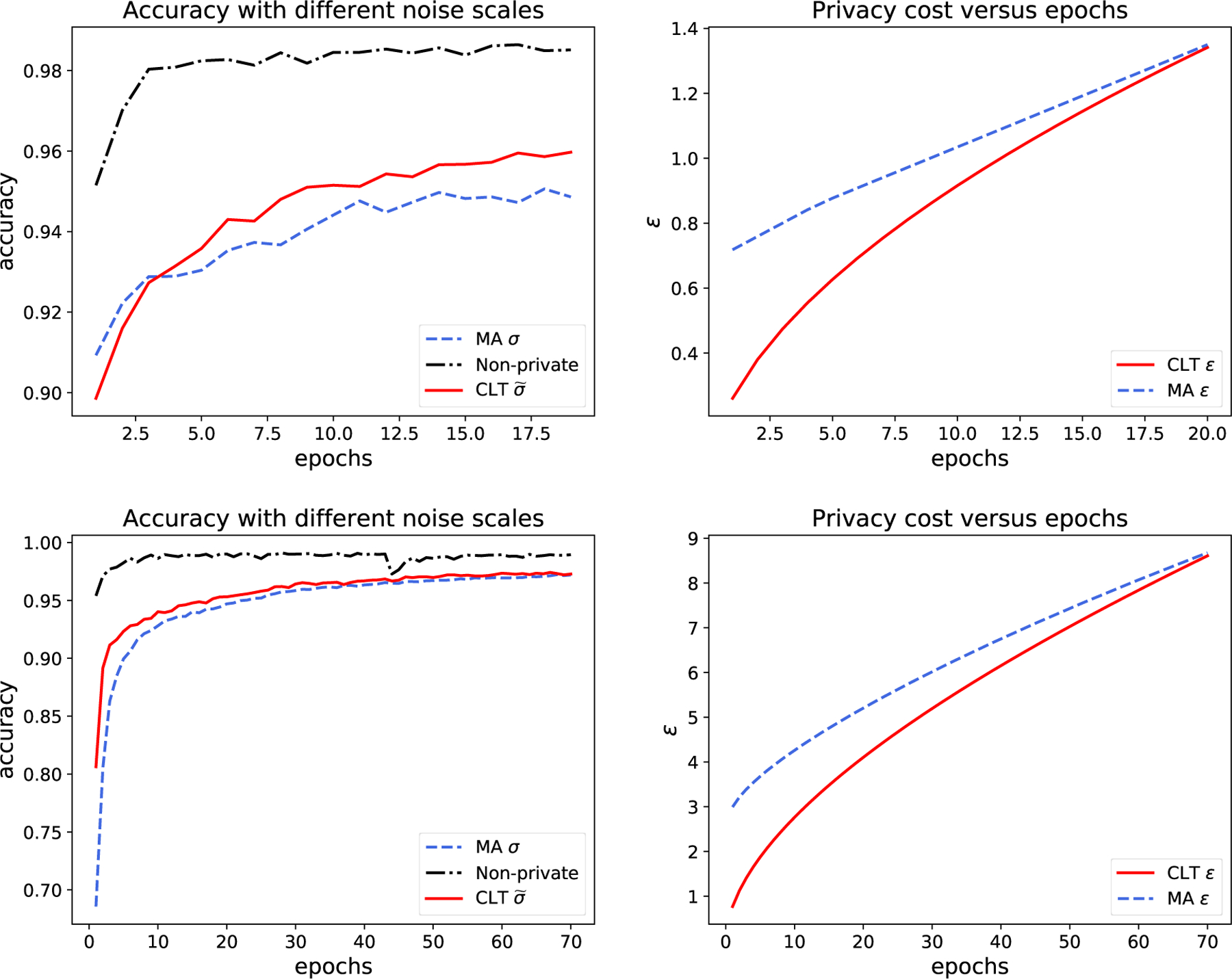
Experimental results from one run of NoisySGD on MNIST with different noise scales but the same (ε, δ)-DP guarantees. The top plots use p = 256/60000, η = 0.15, R = 1.5, and σ = 1.3, $\tilde{\sigma }=1.06$. The CLT approach with $\tilde{\sigma }=1.06$ and the moments accountant with σ = 1.3 give (1.34, 10⁻⁵)-DP at the 20th epoch (μ_CLT = 0.35). The bottom plots use the same parameters except for σ = 0.7, $\tilde{\sigma }=0.638$, and η = 0.15. Both approaches give (8.68, 10⁻⁵)-DP at epoch 70 (μ_CLT = 1.78). The right plots show the privacy loss during the training process in terms of the ε spending with respect to δ = 10⁻⁵.

5. Discussion

In this paper, we have showcased the use of f-DP, a very recently proposed privacy definition, for training private deep learning models using SGD or Adam. Owing to its strength in handling composition and subsampling and the powerful privacy central limit theorem, the f-DP framework allows for a closed-form privacy bound that is sharper than the one given by the moments accountant in the (ε, δ)-DP framework. By numerical experiments, we show that the trained neural networks can be quite private from the f-DP viewpoint (for instance, 1.13-GDP¹¹) but are not in the (ε, δ)-DP sense due to over conservative privacy bounds (for instance, (7.10, 10⁻⁵)-DP) computed in the (ε, δ)-DP framework. This in turn suggests that one can add less noise during the training process while having the same privacy guarantees as using the moments accountant, thereby improving model utility.

We conclude this paper by offering several directions for future research. As the first direction, we may consider using time-dependent noise scales and learning rates in NoisySGD and NoisyAdam for a better tradeoff between privacy loss and utility in the f-DP framework. Note that [37] has made considerable progress using concentrated differential privacy along this line. More generally, a straightforward but interesting problem is to extend this work to complex neural network architectures with a variety of optimization strategies. For example, can we develop some guidelines for choosing an optimizer among NoisySGD, NoisyAdam, and others for a given classification problem under some privacy constraint? Empirically, deep learning models are very sensitive to hyperparameters such as mini-batch size in terms of test accuracy. Therefore, from a practical standpoint, it would be of great importance to incorporate hyperparameter tuning into the f-DP framework [27]. Inspired by [36], another interesting direction is to explore the possible relationship between f-DP guarantees and adversarial robustness of neural networks. Given f-DP’s good interpretability and powerful toolbox, it is worthwhile investigating whether, from a broad perspective, its superiority over earlier differential privacy relaxations would hold in general private statistical and machine learning tasks. We look forward to more research efforts to further the theory and extend the use of f-DP.

Figure 5:

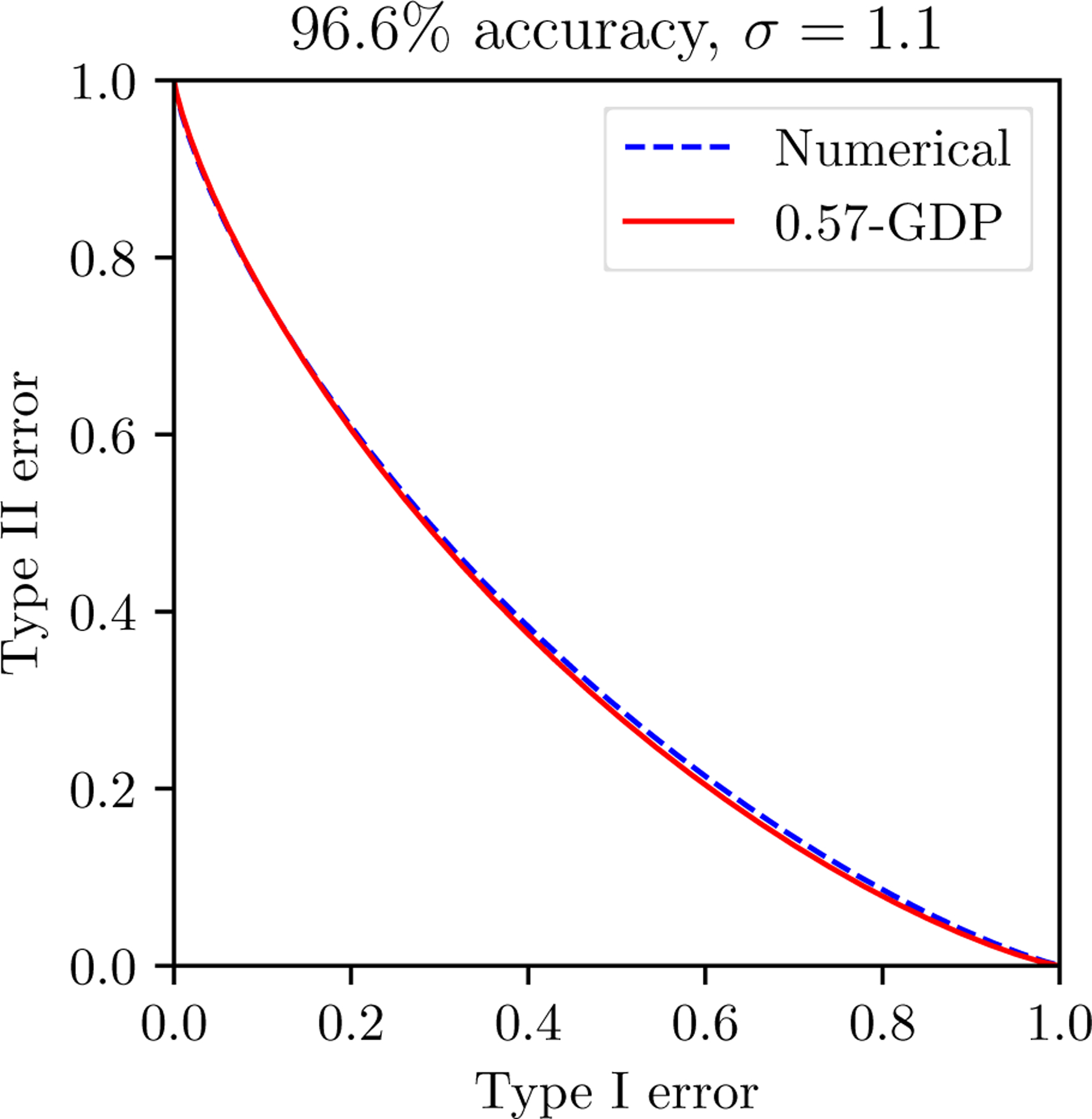
(pG_1/σ + (1 − p)Id)^⊗T (blue dashed) is numerically computed and compared with the GDP limit (red solid) predicted by CLT. The two are almost identical at merely epoch one.

A. Omitted Details in Section 2

We present Equation (3) as the following proposition, which is given in Section 2 but not in the foundational work [18].

Proposition A.1.

If M is f-DP, and S′ = S ∪ {x₀}, then

$$T\left(M\circ {\text{Sample}}_p(S),M\circ {\text{Sample}}_p\left(S^{\prime }\right)\right)⩾pf+(1-p)\text{Id}.$$

Proof.

We first write the two distributions M ◦ Sample_p(S) and M ◦ Sample_p(S′) as mixtures.

Without loss of generality, we can assume S = {x₁, …, x_n} and S′ = {x₀, x₁, …, x_n}. An outcome of the process Sample_p when applied to S is a bit string $\overrightarrow{b}=\left(b_1,\dots ,b_n\right)\in {\left\{0,1\right\}}^n$. Bit b_i dependes on whether x_i is selected into the subsample. We use $S_{\overrightarrow{b}}\subseteq S$ to denote the subsample determined by $\overrightarrow{b}$. When each b_i is sampled from a Bernoulli(p) distribution independently, $S_{\overrightarrow{b}}$ can be identified with Sample_p(S). Let ${\theta }_{\overrightarrow{b}}$ be the probability that $\overrightarrow{b}$ appears. More specifically, if k out of n entries of $\overrightarrow{b}$ is one, then ${\theta }_{\overrightarrow{b}}=p^k{(1-p)}^{n-k}$. With this notation, M ◦Sample_p(S) can be written as the following mixture:

$$M\circ {\text{Sample}}_p(S)=\sum _{\overrightarrow{b}\in {\{0,1\}}^n}{\theta }_{\overrightarrow{b}}\cdot M\left(S_{\overrightarrow{b}}\right).$$

Similarly, M ◦ Sample_p(S) can also be written as a mixture, with an additional bit indicating the presence of x₀. Alternatively, we can divide the components into two groups: one with x₀ present, and the other with x₀ absent. Namely,

$$M\circ {\text{Sample}}_p\left(S^{\prime }\right)=\sum _{\overrightarrow{b}\in {\{0,1\}}^n}p\cdot {\theta }_{\overrightarrow{b}}\cdot M\left(S_{\overrightarrow{b}}\cup \left\{x_0\right\}\right)+\sum _{\overrightarrow{b}\in {\{0,1\}}^n}(1-p)\cdot {\theta }_{\overrightarrow{b}}\cdot M\left(S_{\overrightarrow{b}}\right).$$

Note that $S_{\overrightarrow{b}}\cup \left\{x_0\right\}$ and $S_{\overrightarrow{b}}$ are neighbors, i.e. M ◦ Sample_p(S′) is the mixture of neighboring distributions. The following lemma is the perfect tool to deal with it.

Lemma A.2.

Let I be an index set. For all i ∈ I, P_i and Q_i are distributions that reside on a common sample space. (θ_i)_i∈I is a collection of non-negative numbers that sums to 1. If f is a trade-off function and T(P_i, Q_i) ⩾ f for all i, then

$$T\left(\sum {\theta }_i{P}_i,(1-p)\sum {\theta }_i{P}_i+p\sum {\theta }_i{Q}_i\right)⩾pf+(1-p)\text{Id}.$$

To apply the lemma, let the index be $\overrightarrow{b}\in {\left\{0,1\right\}}^n$, P_i be $M\left(S_{\overrightarrow{b}}\right)$ and Q_i be $M\left(S_{\overrightarrow{b}}\cup \left\{x_0\right\}\right)$. Condition T(P_i, Q_i) ⩾ f is the consequence of M being f-DP. The conclusion simply translates to

$$T\left(M\circ {\text{Sample}}_p(S),M\circ {\text{Sample}}_p\left(S^{\prime }\right)\right)⩾pf+(1-p)\text{Id},$$

which is what we want. The proof is complete. □

Proof of Lemma A.2.

Let P = ∑θ_iP_i and Q = (1 − p)∑θ_iP_i + p∑θ_iQ_i. Suppose ϕ satisfies ${\mathbb{E}}_P\varphi =\alpha$. That is,

$$\sum {\theta }_i{\mathbb{E}}_{P_i}\varphi =\alpha .$$

It is easy to see that

$${\mathbb{E}}_Q\varphi =(1-p)\alpha +p\sum {\theta }_i{\mathbb{E}}_{Q_i}\varphi .$$

We know that T(P_i, Q_i) ⩾ f. Hence ${\mathbb{E}}_{Q_i}\varphi ⩽1-f\left({\mathbb{E}}_{P_i}\varphi \right)$. So

$$\sum {\theta }_i{\mathbb{E}}_{Q_i}\varphi ⩽1-\sum {\theta }_{i}f\left({\mathbb{E}}_{P_i}\varphi \right).$$

Since f is convex, Jensen’s inequality implies

$$\sum {\theta }_{i}f\left({\mathbb{E}}_{P_i}\varphi \right)⩾f(\sum {\theta }_i{\mathbb{E}}_{P_i}\varphi )=f(\alpha ).$$

Next we use a figure to justify the claim we made in Section 2.2 that “CLT approximation works well for SGD”. Recall that we argued in Section 3 that Algorithms 1 and 2 are min{f, f⁻¹}**-DP where

$$f={\left(p{G}_{1/\sigma }+(1-p)\text{Id}\right)}^{\otimes T}.$$

This function converges to G_μ with $\mu =\nu \sqrt{{\text{e}}^{1/{\sigma }^2}-1}$ as T → ∞ provided $p\sqrt{T}\to \nu$. In the following figure, we numerically compute f (blue dashed) and compare it with the predicted limit G_μ (red solid). More specifically, the configuration is designed to illustrate the fast convergence in the setting of the second line of Table 1, i.e. noise scale σ = 1.1, final GDP parameter μ = 0.57 and test accuracy 96.6%. Originally the algorithm runs 60 epochs, i.e. ≈ 14k iterations. To best illustrate that convergence appears in early stage, the numerical evaluation uses a much smaller T_numeric = 234, i.e. only one epoch. In order to make the final limit consistent, we also enlarge the sample probability to p_numeric so that $p_{\text{numeric}}\cdot \sqrt{T_{\text{numeric }}}$ remain the same.

We have to remark that when σ is small, $\mu =\nu \sqrt{{\text{e}}^{1/{\sigma }^2}-1}$ gets large and yields challenges in the numerical computation of (pG_1/σ + (1 − p)Id)^⊗T. We leave rigorous and complete study to future work.

B. Omitted Details in Section 3

B.1. Privacy Property of Algorithms 1 and 2

Theorem 3.

Algorithms 1 and 2 are both min{f, f⁻¹}**-DP with f = (pG_1/σ + (1 − p)Id)^⊗T.

Proof.

The proof is mostly done in the main text, except the composition step. Let V be the vector space that all θ_t live in and $\tilde{M}=M\circ {\text{Sample}}_p:X^n\times V\to V$ be the gradient update. We have already proved (using Proposition A.1) that for both Algorithms 1 and 2, if S′ = S∪{x₀}, then $\tilde{M}$ satisfies

$$T\left(M(S),M\left(S^{\prime }\right)\right)⩾f_p≔p{G}_{1/\sigma }+(1-p)\text{Id}.$$

Note that we cannot say M is f_p-DP because T(M(S′), M(S)) is not necessarily lower bounded by f_p. So we need a more specific composition theorem than stated in [18].

Theorem 4 (Refined Composition).

Suppose M₁ : X → Y, M₂ : X × Y → Z satisfy the following conditions for any S, S′ such that S′ = S ∪ {x₀}:

1. T(M₁(S), M(S′)) ⩾ f;

2. T(M₂(S, y), M₂(S′, y)) ⩾ g for any y ∈ Y.

Then the composition M₂ ◦ M₁ : X → Y × Z satisfies

$$T\left(M_2\circ M_1(S),M_2\circ M_1\left(S^{\prime }\right)\right)⩾f\otimes g$$

for any S, S′ such that S′ = S ∪ {x₀}.

• The theorem can be identically proved as Theorem 3.2 in [18].

• Taking Algorithm 1 as an example, since

$$\begin{gathered} \text{NoisySGD : }{X}^n\to V\times V\times \cdots \times V \\ S\mapsto \left({\theta }_1,{\theta }_2,\dots ,{\theta }_T\right) \end{gathered}$$

is simply the composition of T copies of $\tilde{M}$, the above composition theorem implies that

$$T\left(\text{NoisySGD}(S),\text{NoisySGD}\left(S^{\prime }\right)\right)⩾{\left(p{G}_{1/\sigma }+(1-p)\text{Id}\right)}^{\otimes T}=f.$$

Moreover, T(NoisySGD(S), NoisySGD(S′)) ⩾ f⁻¹. The two inequality let us conclude that any trade-off function of neighboring distributions must be lower bounded by at least one of f and f⁻¹, hence min{f, f⁻¹}, hence min{f, f⁻¹}**. In other words, NoisySGD is min{f, f⁻¹}**-DP.

For NoisyAdam, we argued that its privacy property is the same as NoisySGD in each iteration, so the above argument also applies, and we have the same conclusion. □

B.2. Justifying CLT for Algorithms 1 and 2

The main purpose of this section is to show the following theorem

Theorem 5.

Suppose p depends on T and $p\sqrt{T}\to \nu$. Then we have the following uniform convergence as T → ∞

$${\left(p{G}_{1/\sigma }+(1-p)\text{Id}\right)}^{\otimes T}=G_{\mu },$$

where $\mu =\nu \cdot \sqrt{T\left({\text{e}}^{1/{\sigma }^2}-1\right)}$.

This theorem is the corollary of the following more general CLT on composition of subsample mechanisms and Lemma B.1 below.

Theorem 6.

Suppose f is a trade-off function such that (1) f(0) = 1, (2) f(x) > 0, for all x < 1 and (3) ${\int }_0^1{\left(f^{\prime }(x)+1\right)}^4\text{ d}x<+\infty$. Let f_p = pf+(1−p)Id as usual. Furthermore, assume $p\sqrt{T}\to \nu$ as T → ∞ for some constant ν > 0. Then we have the uniform convergence

$$f_p^{\otimes T}\to G_{\nu \sqrt{{\chi }^2(f)}}$$

as T → ∞, where ${\chi }^2(f)={\int }_0^1{\left(f^{\prime }(x)\right)}^2\text{ d}x-1$.

Lemma B.1.

We have

$${\chi }^2\left(G_{1/\sigma }\right)={\text{e}}^{1/{\sigma }^2}-1.$$

In order to prove Theorem 6, we need an even more general CLT. The first privacy CLT was introduced in [18]. However, that version is valid only when each component trade-off function is symmetric, which is not true for pG_1/σ + (1 − p)Id. In order to state the general CLT that applies to asymmetric trade-off functions, we need to introduce the following functionals:

$$\text{kl}(f)≔-{\int }_0^1\text{log}|f^{\prime }(x)|\text{d}x$$

$$\widetilde{\text{kl}}(f)≔{\int }_0^1|f^{\prime }(x)|\text{ log}|f^{\prime }(x)|\text{d}x$$

$${\kappa }_2(f)≔{\int }_0^1{\text{log}}^2|f^{\prime }(x)|\text{d}x$$

$${\tilde{\kappa }}_2(f)≔{\int }_0^1|f^{\prime }(x)|{\text{log}}^2|f^{\prime }(x)|\text{d}x$$

$${\kappa }_3(f)≔{\int }_0^1{|\text{log}|f^{\prime }(x)||}^3 \text{d}x$$

$${\tilde{\kappa }}_3(f)≔{\int }_0^1|f^{\prime }(x)|\cdot {|\text{log}|f^{\prime }(x)||}^3 \text{d}x.$$

Theorem 7.

Let ${\left\{f_{ni}:1⩽i⩽n\right\}}_{n=1}^{\infty }$ be a triangular array of (possibly asymmetric) trade-off functions and assume the following limits for some constants K ⩾ 0 and s > 0 as n → ∞:

1. ${\sum }_{i=1}^n\text{kl}\left(f_{ni}\right)+\widetilde{\text{kl}}\left(f_{ni}\right)\to K$;

2. max_1⩽i⩽n kl(f_ni) → 0, ${\text{max}}_{1⩽i⩽n}\widetilde{\text{kl}}\left(f_{ni}\right)\to 0$;

3. ${\sum }_{i=1}^n{\kappa }_2\left(f_{ni}\right)\to s^2$, ${\sum }_{i=1}^n{\tilde{\kappa }}_2\left(f_{ni}\right)\to s^2$;

4. ${\sum }_{i=1}^n{\kappa }_3\left(f_{ni}\right)\to 0$, ${\sum }_{i=1}^n{\tilde{\kappa }}_3\left(f_{ni}\right)\to 0$.

Then, we have

$$\underset{n\to \infty }{\text{lim}}{f}_{n1}\otimes f_{n2}\otimes \cdots \otimes f_{nn}(\alpha )=G_{K/s}(\alpha )$$

uniformly for all α ∈ [0, 1].

Proof of this theorem exactly mimics that of Theorem 3.5 in [18], which we omit here for its length and tediousness.

Next, we apply the asymmetric CLT to (pf + (1 − p))^⊗T and prove Theorem 6. We start by collecting the necessary expressions into the following lemma. All of them are straightforward.

Lemma B.2.

Let g(x) = −f′(x) − 1 = |f′(x)| − 1. Then

$$\text{kl}\left(f_p\right)=-{\int }_0^1\text{log}(1+pg(x))\text{ d}x$$

$$\widetilde{\text{kl}}\left(f_p\right)={\int }_0^1(1+pg(x))\text{ log}(1+pg(x))\text{ d}x$$

$${\kappa }_2\left(f_p\right)={\int }_0^1{[\text{log}(1+pg(x))]}^2\text{ d}x$$

$${\tilde{\kappa }}_2\left(f_p\right)={\int }_0^1(1+pg(x)){[\text{log}(1+pg(x))]}^2\text{ d}x$$

$${\kappa }_3\left(f_p\right)={\int }_0^1{[\text{log}(1+pg(x))]}^3\text{ d}x$$

$${\tilde{\kappa }}_3\left(f_p\right)={\int }_0^1(1+pg(x)){[\text{log}(1+pg(x))]}^3\text{ d}x.$$

Proof of Theorem 6.

It suffices to compute the limits in the asymmetric Central Limit Theorem 7, namely

$$T\cdot \left(\text{kl}\left(f_p\right)+\widetilde{\text{kl}}\left(f_p\right)\right),T\cdot {\kappa }_2\left(f_p\right),T\cdot {\tilde{\kappa }}_2\left(f_p\right),T\cdot {\kappa }_3\left(f_p\right)\text{ and }T\cdot {\tilde{\kappa }}_3\left(f_p\right).$$

Since T ~ p⁻², we can consider $p^{-2}\left(\text{kl}\left(f_p\right)+\widetilde{\text{kl}}\left(f_p\right)\right)$ and so on.

As in Lemma B.2, let g(x) = −f′(x)−1 = |f′(x)|−1. The assumption expressed in terms of g is simply

$${\int }_0^{1}g{(x)}^4\text{ d}x<+\infty .$$

In particular, it implies |g(x)|^k is integrable in [0, 1] for k = 2, 3, 4. In addition, by Lemma B.2,

$${\chi }^2(f)={\int }_0^1{\left(f^{\prime }(x)\right)}^2\text{ d}x-1={\int }_0^1{\left(f^{\prime }(x)+1\right)}^2\text{ d}x={\int }_0^{1}g{(x)}^2\text{ d}x.$$

For the functional kl, by Lemma B.2,

$$\begin{gathered} \underset{p\to 0^{+}}{\text{lim}}\frac{1}{p^2}\left(\text{kl}\left(f_p\right)+\widetilde{\text{kl}}\left(f_p\right)\right)=\underset{p\to 0^{+}}{\text{lim}}{\int }_0^{1}g(x)\cdot \frac{1}{p}\text{log}(1+pg(x))\text{d}x \\ ={\int }_0^{1}g(x)\cdot \underset{p\to 0^{+}}{\text{lim}}\frac{1}{p}\text{log}(1+pg(x))\text{d}x \\ ={\int }_0^{1}g{(x)}^2 \text{d}x={\chi }^2(f) \end{gathered}$$ (9)

Changing the order of the limit and the integral in (9) is approved by the dominated convergence theorem. To see this, notice that log(1 + x) ⩽ x. The integrand in (9) satisfies

$$0⩽g(x)\cdot \frac{1}{p}\text{log}(1+pg(x))⩽g{(x)}^2.$$

We already argued that g(x)² is integrable, so it works as a dominating function and the limit is justified. When $p\sqrt{T}\to \nu$, we have

$$T\cdot \text{kl}\left(f_p\right)\to {\nu }^2\cdot {\chi }^2(f).$$

So the constant K in Theorem 7 is ν² · χ²(f).

For the functional κ₂ we have

$$\frac{1}{p^2}{\kappa }_2\left(f_p\right)={\int }_0^1{\left[\frac{1}{p}\text{log}(1+pg(x))\right]}^2\text{ d}x.$$

By a similar dominating function argument,

$$\underset{p\to 0^{+}}{\text{lim}}\frac{1}{p^2}{\kappa }_2\left(f_p\right)=\underset{p\to 0^{+}}{\text{lim}}\frac{1}{p^2}{\tilde{\kappa }}_2\left(f_p\right)={\int }_0^{1}g{(x)}^2\text{ d}x={\chi }^2(f).$$

Adding in the limit $p\sqrt{T}\to \nu$, we know s² in Theorem 7 is ν² · χ²(f).

The same argument involving |g(x)|³ and g(x)⁴ applies to the functional κ₃ and ${\tilde{\kappa }}_3$ respectively and yields

$$\underset{p\to 0^{+}}{\text{lim}}\frac{1}{p^3}{\kappa }_3\left(f_p\right)=\underset{p\to 0^{+}}{\text{lim}}\frac{1}{p^3}{\tilde{\kappa }}_3\left(f_p\right)={\int }_0^{1}g{(x)}^3\text{ d}x.$$

Note the different power in p in the denominator. It means κ₃(f_p) = o(p²) and hence T·κ₃(f_p) → 0 when $p\sqrt{T}\to \nu$.

Hence all the limits in Theorem 7 check and we have a G_μ limit where

$$\mu =K/s=s=\sqrt{{\nu }^2\cdot {\chi }^2(f)}=\nu \cdot \sqrt{{\chi }^2(f)}.$$

This completes the proof. □

We finish the section by proving the formula in Lemma B.1.

Proof of Lemma B.1.

The best calculation is done via better understanding. We point out that the functional χ² is doing nothing more than computing the famous χ²-divergence. Recall that Neyman χ²-divergence (reverse Pearson) of P, Q is defined as

$${\chi }^2(P\Vert Q)≔{\mathbb{E}}_P\left[{\left(\frac{\text{d}Q}{\text{ d}P}-1\right)}^2\right]$$

Lemma B.3.

If f = T(P, Q) and f(0) = 1, f(x) > 0, for all x < 1, then χ²(f) = χ²(P∥Q).

This lemma is a straightforward corollary of Proposition B.4 in [18], which gives expressions for all F-divergence¹². In particular, if f = T(P, Q) and f(0) = 1, f(x) > 0, ∀x < 1, then F-divergence of P, Q can be computed from their trade-off function as follows:

$$D_F(P\Vert Q)={\int }_0^{1}F\left({|f^{\prime }(x)|}^{-1}\right)\cdot |f^{\prime }(x)|\text{d}x.$$

Neyman χ²-divergence corresponds to $F(t)=\frac{1}{t}-1$, so

$$\begin{gathered} {\chi }^2(P\Vert Q)={\int }_0^1\left(\frac{1}{{|f^{\prime }(x)|}^{-1}}-1\right)\cdot |f^{\prime }(x)|\text{ d}x \\ ={\int }_0^1{\left(f^{\prime }(x)\right)}^2\text{ d}x-{\int }_0^1|f^{\prime }(x)|\text{ d}x \\ ={\int }_0^1{\left(f^{\prime }(x)\right)}^2\text{ d}x-1. \end{gathered}$$

With this formula, computing χ²(G_1/σ) is straightforward:

$${\chi }^2\left(G_{1/\sigma }\right)={\chi }^2\left(\mathcal{N}\left(\frac{1}{\sigma },1\right)\Vert \mathcal{N}(0,1)\right)={\text{e}}^{1/{\sigma }^2}-1.$$

B.3. Proof of Theorems 1 and 2

Recall that Theorems 1 and 2 compare our CLT approach to moments accountant (MA) from two different perspectives: f-DP perspective in Theorem 1 and (ε, δ)-DP perspective in Theorem 2. We first show that Theorem 1 can be derived from Theorem 2. Then we prove a refined version of Theorem 2. To be more precise about the statement, let us first expand the notations used in the main text.

Let δ_MA(ε; σ, p, T) be the δ value computed by moment accountant method (described in detail below) for NoisySGD algorithm with subsampling probability p, iteration T and noise scale σ. Similarly, δ_CLT(ε; σ, ν) denotes the δ value computed for the same algorithm using central limit theorem assuming $p\sqrt{T}\to \nu$.

Let $f_T(\alpha )={\text{sup}}_{\epsilon ⩾0}{f}_{\epsilon ,{\delta }_{\text{MA}}(\epsilon )}(\alpha )$. It is supported by $f_{{\epsilon }_T,{\delta }_{\text{MA}}}\left({\epsilon }_T\right)$ at α. Theorem 2 says this supporting function is smaller than that of $G_{{\mu }_{\text{CLT}}}$ at α by a strict gap. Taking the limit, lim sup_T→∞ f_T (α) has at least that much gap from $G_{{\mu }_{\text{CLT}}}\left(\alpha \right)$, which proves Theorem 1.

Theorem 2 is a straightforward corollary of the following proposition. Note that the inequality is reversed compared to the statement of Theorem 2 so that the gap is positive, which also turns lim sup into lim inf.

Proposition B.4.

$$\underset{T\to \infty }{\text{lim inf }}{\delta }_{\text{MA}}\left(\epsilon ;\sigma ,\frac{\nu }{\sqrt{T}},T\right)-{\delta }_{\text{CLT}}(\epsilon ;\sigma ,\nu )⩾{\text{e}}^{\epsilon }\cdot \Phi \left(-\frac{\epsilon }{\mu }-\frac{\mu }{2}\right)$$

where $\mu =\nu \cdot \sqrt{{\text{e}}^{1/{\sigma }^2}-1}$.

Let us first describe how the two methods compute δ from ε.

$$\begin{gathered} {\delta }_{\text{nMA}}(\epsilon ;\sigma ,p,T)≔\underset{\lambda \in \text{orders}}{\text{inf}}\text{exp }\left(T\cdot {\alpha }_{\text{GM}}(\lambda ;\sigma ,p)-\lambda \epsilon \right) \\ {\delta }_{\text{MA}}(\epsilon ;\sigma ,p,T)≔\underset{\lambda >0}{\text{inf}}\text{exp }\left(T\cdot {\alpha }_{\text{GM}}(\lambda ;\sigma ,p)-\lambda \epsilon \right) \end{gathered}$$

where α_GM(λ; σ, p) is a scaled version of the Rényi divergence of Gaussian mixtures. More specifically, let $P=\mathcal{N}(0,1)$ and $Q=\mathcal{N}\left(\frac{1}{\sigma },1\right)$. We further denote the Gaussian mixture pQ + (1 − p)P by GM_p,σ. The

$${\alpha }_{\text{GM}}(\lambda ;\sigma ,p)=\text{max}\left\{\lambda D_{\lambda +1}\left({\text{GM}}_{p,\sigma }\Vert P\right),\lambda D_{\lambda +1}\left(P\Vert {\text{GM}}_{p,\sigma }\right)\right\}.$$

In [3], it has been shown that Algorithm 1 (hence also the Adam variant, Algorithm 2) with subsampling probability p, iteration T and noise scale σ is (ε, δ)-DP for each ε ⩾ 0 if δ = δ_MA(ε; σ, p, T). To evaluate the infimum, the domain is discretized¹³. This results in the numerical moment accountant method that is actually implemented. Since δ_nMA(ε; σ, p, T) ⩾ δ_MA(ε; σ, p, T), Algorithm 1 is also (ε, δ)-DP with δ = δ_nMA(ε; σ, p, T).

On the other hand, δ_CLT(ε; σ, ν) is obtained by first observing Algorithm 1 is asymptotically μ_CLT-GDP with ${\mu }_{\text{CLT}}=\nu \cdot \sqrt{{\text{e}}^{1/{\sigma }^2}-1}$ and then convert GDP to (ε, δ)-DP via Equation (6), i.e. Algorithm 1 asymptotically satisfies (ε, δ)-DP where

$$\delta ={\delta }_{\text{CLT}}(\epsilon ;\sigma ,\nu )=1+G_{{\mu }_{\text{CLT}}}^{*}\left(-{\text{e}}^{\epsilon }\right).$$

We have just explained how MA and CLT works. Next we prove Proposition B.4

Proof of Proposition B.4.

Let f_T = (pG_μ+(1−p)Id)^⊗T. We need a lemma (whose proof is provided later) that relates the Rényi divergence to the trade-off function f_T.

Lemma B.5.

$$T\cdot {\alpha }_{\text{GM}}(\lambda ;\sigma ,p)⩾\text{log}{\int }_0^1{|f_T^{\prime }(x)|}^{\lambda +1}\text{ d}x.$$

Let x_T ∈ (0, 1) be the point such that $f_T^{\prime }\left(x_T\right)=-{\text{e}}^{\epsilon }$ (or $x_T\in \partial f_T^{*}\left(-{\text{e}}^{\epsilon }\right)$ if readers worry about diffesrentiability). We have

$$1+f_T^{*}\left(-{\text{e}}^{\epsilon }\right)=\underset{0⩽x⩽1}{\text{sup}}\left\{1-f_T(x)-{\text{e}}^{\epsilon }x\right\}=1-f_T\left(x_T\right)-{\text{e}}^{\epsilon }{x}_T$$

It is clear that $|f_T^{\prime }(x)|⩾{\text{e}}^{\epsilon }$ for 0 ⩽ x ⩽ x_T.

On the other hand, using Lemma B.5, we get

$$\begin{gathered} {\delta }_{\text{MA}}(\epsilon ;\sigma ,p,T)=\underset{\lambda >0}{\text{inf}}\text{exp }\left(T\cdot {\alpha }_{\text{GM}}(\lambda ;\sigma ,p)-\lambda \epsilon \right) \\ ⩾\underset{\lambda >0}{\text{inf}}{\text{e}}^{-\lambda \epsilon }{\int }_0^1{|f_T^{\prime }(x)|}^{\lambda +1}\text{ d}x \\ >\underset{\lambda >0}{\text{inf}}{\int }_0^{x_T}{|f_T^{\prime }(x)|}^{\lambda +1}{\text{e}}^{-\lambda \epsilon }\text{ d}x \\ =\underset{\lambda >0}{\text{inf}}{\int }_0^{x_T}|f_T^{\prime }(x)|\cdot {|f_T^{\prime }(x)|}^{\lambda }{\text{e}}^{-\lambda \epsilon }\text{ d}x \\ ⩾\underset{\lambda >0}{\text{inf}}{\int }_0^{x_T}|f_T^{\prime }(x)|\cdot {\left({\text{e}}^{\epsilon }\right)}^{\lambda }{\text{e}}^{-\lambda \epsilon }\text{ d}x \\ =f_T(0)-f_T\left(x_T\right) \\ =1-f_T\left(x_T\right) \\ =\left(1-f_T\left(x_T\right)-{\text{e}}^{\epsilon }{x}_T\right)+{\text{e}}^{\epsilon }{x}_T \\ =1+f_T^{*}\left(-{\text{e}}^{\epsilon }\right)+{\text{e}}^{\epsilon }{x}_T. \end{gathered}$$

In summary, we have

$${\delta }_{\text{MA}}(\epsilon ;\sigma ,p,T)>1+f_T^{*}\left(-{\text{e}}^{\epsilon }\right)+{\text{e}}^{\epsilon }{x}_T.$$ (10)

Setting $p=\frac{\nu }{\sqrt{T}}$, we would like to take limit on both sides of (10). First notice that f_T converge pointwise to $G_{{\mu }_{\text{CLT}}}$, which we have already proven in Appendix B.2. The limit of x_T is taken care of in the following lemma:

Lemma B.6.

$$\underset{T\to \infty }{\text{lim}}{x}_T=x^{*}≔\Phi \left(-\frac{\epsilon }{{\mu }_{\text{CLT}}}-\frac{{\mu }_{\text{CLT}}}{2}\right).$$

Combining these results, we can take limits on both sides of (10):

$$\begin{gathered} \underset{T\to \infty }{\text{lim inf }}{\delta }_{\text{MA}}(\epsilon ;\sigma ,p,T)⩾\underset{T\to \infty }{\text{lim}}1+f_T^{*}\left(-{\text{e}}^{\epsilon }\right)+{\text{e}}^{\epsilon }{x}_T \\ =1+G_{{\mu }_{\text{CLT}}}^{*}\left(-{\text{e}}^{\epsilon }\right)+{\text{e}}^{\epsilon }{x}^{*} \\ ={\delta }_{\text{CLT}}(\epsilon ;\sigma ,\nu )+{\text{e}}^{\epsilon }\cdot \Phi \left(-\frac{\epsilon }{{\mu }_{\text{CLT}}}-\frac{{\mu }_{\text{CLT}}}{2}\right). \end{gathered}$$

This finishes the proof. □

Proof of Lemma B.5.

The Rényi divergence can also be computed from the trade-off function, just like the χ²-divergence. In fact, under the same assumptions as in Lemma B.1, we have

$$D_{\alpha }(Q\Vert P)=\frac{1}{\alpha -1}\text{log}{\int }_0^1{|f^{\prime }(x)|}^{\alpha -1}\text{ d}x.$$

Alternatively,

$$\lambda D_{\lambda +1}(Q\Vert P)=\text{log}{\int }_0^1{|f^{\prime }(x)|}^{\lambda }\text{ d}x.$$ (11)

This identity will be the bridge between α_GM and f_T.

On one hand, α_GM(λ; σ, p) is the maximum of two Rényi divergences, so

$${\alpha }_{\text{GM}}(\lambda ;\sigma ,p)⩾\lambda D_{\lambda +1}(pQ+(1-p)P\Vert P)$$

Consequently,

$$\begin{gathered} T\cdot {\alpha }_{\text{GM}}(\lambda ;\sigma ,p)⩾T\lambda D_{\lambda +1}(pQ+(1-p)P\Vert P) \\ =\lambda D_{\lambda +1}\left({(pQ+(1-p)P)}^T\Vert P^T\right). \end{gathered}$$

The last step is the tensorization identity of Rényi divergence.

On the other hand, notice that pG_μ + (1 − p)Id = T(P, GM_p,σ) where we continue the use of notations $P=\mathcal{N}(0,1)$, $Q=\mathcal{N}\left(\frac{1}{\sigma },1\right)$ and GM_p,σ = pQ + (1 − p)P. We have

$$f_T={\left(p{G}_{\mu }+(1-p)\text{Id}\right)}^{\otimes T}=T{(P,(pQ+(1-p)P))}^{\otimes T}=T\left(P^T,{(pQ+(1-p)P)}^T\right)$$

Using (11), we have

$$\begin{gathered} T\cdot {\alpha }_{\text{GM}}(\lambda ;\sigma ,p)⩾\lambda D_{\lambda +1}\left({(pQ+(1-p)P)}^T\Vert P^T\right) \\ =\text{log}{\int }_0^1{|f_T^{\prime }(x)|}^{\lambda }\text{ d}x. \end{gathered}$$

Proof of Lemma B.6.

By definition, $f_T^{\prime }\left(x_T\right)=-{\text{e}}^{\epsilon }$. The convexity of f_T implies $\nabla f_T^{*}\left(-{\text{e}}^{\epsilon }\right)=x_T$.

Since f_T converges uniformly to $G_{{\mu }_{\text{CLT}}}$ in [0, 1], we have uniform convergence $f_T^{*}\to G_{{\mu }_{\text{CLT}}}^{*}$. By convexity of these functions, the convergence also implies the convergence of derivatives (See Theorem 25.7 of [51]), namely,

$$\nabla f_T^{*}\to \nabla G_{{\mu }_{\text{CLT}}}^{*}.$$

Therefore,

$$x_T=\nabla f_T^{*}\left(-{\text{e}}^{\epsilon }\right)\to \nabla G_{{\mu }_{\text{CLT}}}^{*}\left(-{\text{e}}^{\epsilon }\right).$$

Let $x^{*}=\nabla G_{{\mu }_{\text{CLT}}}^{*}\left(-{\text{e}}^{\epsilon }\right)$ be the limit. Using the convexity again, we have

$$-{\text{e}}^{\epsilon }=G_{{\mu }_{\text{CLT}}}^{\prime }\left(x^{*}\right).$$

We can solve for x* using the expression of G_μ (6). After some algebra, we have

$$x^{*}=\Phi \left(-\frac{\epsilon }{{\mu }_{\text{CLT}}}-\frac{{\mu }_{\text{CLT}}}{2}\right).$$

The proof is complete. □