Significance
Sequential activity is a prominent feature of many neural systems, in multiple behavioral contexts. Here, we investigate how Hebbian rules lead to storage and recall of random sequences of inputs in both rate and spiking recurrent networks. In the case of the simplest (bilinear) rule, we characterize extensively the regions in parameter space that allow sequence retrieval and compute analytically the storage capacity of the network. We show that nonlinearities in the learning rule can lead to sparse sequences and find that sequences maintain robust decoding but display highly labile dynamics to continuous changes in the connectivity matrix, similar to recent observations in hippocampus and parietal cortex.
Keywords: sequences, recurrent networks, Hebbian plasticity
Abstract
Sequential activity has been observed in multiple neuronal circuits across species, neural structures, and behaviors. It has been hypothesized that sequences could arise from learning processes. However, it is still unclear whether biologically plausible synaptic plasticity rules can organize neuronal activity to form sequences whose statistics match experimental observations. Here, we investigate temporally asymmetric Hebbian rules in sparsely connected recurrent rate networks and develop a theory of the transient sequential activity observed after learning. These rules transform a sequence of random input patterns into synaptic weight updates. After learning, recalled sequential activity is reflected in the transient correlation of network activity with each of the stored input patterns. Using mean-field theory, we derive a low-dimensional description of the network dynamics and compute the storage capacity of these networks. Multiple temporal characteristics of the recalled sequential activity are consistent with experimental observations. We find that the degree of sparseness of the recalled sequences can be controlled by nonlinearities in the learning rule. Furthermore, sequences maintain robust decoding, but display highly labile dynamics, when synaptic connectivity is continuously modified due to noise or storage of other patterns, similar to recent observations in hippocampus and parietal cortex. Finally, we demonstrate that our results also hold in recurrent networks of spiking neurons with separate excitatory and inhibitory populations.
Sequential activity has been reported across a wide range of neural systems and behavioral contexts, where it plays a critical role in temporal information encoding. Sequences can encode choice-selective information (1), the timing of motor actions (2), planned or recalled trajectories through the environment (3), and elapsed time (4–6). This diversity in function is also reflected at the level of neuronal activity. Sequences occur at varying timescales, from those lasting tens of milliseconds during hippocampal sharp-wave ripples, to those spanning several seconds in the striatum (7, 8). Sequential activity also varies in temporal sparsity. In nucleus HVC of zebra finch, highly precise sequential activity is present during song production, where many neurons fire only a single short burst during a syllable (9). In primate motor cortex, single neurons are typically active throughout a whole reach movement, but with heterogeneous and rich dynamics (10).
Numerous models have explored how networks with specific synaptic connectivity can generate sequential activity (11–20). These models span a wide range of single neuron models, from binary to spiking, and a wide range of synaptic connectivities. A large class of models employs temporally asymmetric Hebbian (TAH) learning rules to generate a synaptic connectivity necessary for sequence retrieval. In these models, a sequence of random input patterns are presented to the network, and a Hebbian learning rule transforms the resulting patterns of activity into synaptic weight updates. In networks of binary neurons, TAH learning together with synchronous update dynamics lead to sequence storage and retrieval (21). With asynchronous dynamics, additional mechanisms such as delays are needed to generate robust sequence retrieval (13).
Another longstanding and influential class of model has centered on the “synfire chain” architecture (22) in networks of spiking neurons, in which discrete pools of neurons are connected in a chain-like, feedforward fashion, and a barrage of synchronous activity in the first pool propagates down connected pools, separated in time by synaptic delays (22, 23). Theoretical studies have shown that synfire chains can self-organize from initially unstructured connectivity through an appropriate choice of plasticity rule and stimulus (16, 19). Other studies have shown that these chains produce sequential activity when embedded into recurrent networks if appropriate recurrent and feedback connections are introduced among pools (24–26).
Despite decades of research on this topic, the relationships between network parameters and experimentally observed features of sequential activity are still poorly understood. In particular, few models account for the temporal statistics of sequential activity during retrieval and across multiple recording sessions. In many sequences, a greater proportion of neurons encode for earlier times, and the tuning width of recruited neurons increases in time (5, 27, 28). Neural sequences are also not static, but change over the timescales of days, even when controlling for the same environment and task constraints (29, 30). TAH learning provides an appealing framework for how sequences of neuronal activity are embedded in the connectivity matrix. While TAH learning has been extensively explored in binary neuron network models, it remains an open question as to whether these learning rules can produce sequential activity in more realistic network models and also reproduce the observed temporal statistics of this activity. It is also unclear whether a theory can be developed to understand the resulting activity, as has been done with networks of binary neurons. Rate networks provide a useful framework for investigating these questions, as they balance analytical tractability and biological realism.
We start by constructing a theory of transient activity that can be used to predict the sequence capacity of these networks and focus on two features of sequences that have been described in the experimental literature: temporal sparsity and the selectivity of single-unit activity. We find that several temporal characteristics of sequential activity are reproduced by the network model, including the temporal distribution of firing-rate peak widths and times. Introduction of a nonlinearity to the learning rule allows for the generation of temporally sparse sequences. We also find that storing multiple sequences yields selective single-unit activity resembling that found during two-alternative forced-choice tasks (1). Consistent with experiment, we find that the population activity of these sequences changes over time in the face of ongoing synaptic changes, while decoding performance is preserved (29, 30). Finally, we demonstrate that our findings also hold in networks of excitatory and inhibitory leaky-integrate and fire (LIF) neurons, where learning takes place only in excitatory-to-excitatory connections.
Results
We have studied the ability of large networks of sparsely connected rate units to learn sequential activity from random, unstructured input, using analytical and numerical methods. We focus initially on a network model composed of neurons, each described by a firing rate () that evolves according to standard rate equations (31)
| [1] |
where is the time constant of rate dynamics, is the total synaptic input to neuron , and is the connectivity matrix. is a sigmoidal neuronal transfer function,
| [2] |
which is described by three parameters: , the maximal firing rate (set to one in most of the following); , the input at which the firing rate is half its maximal value; and , a parameter which is inversely proportional to the slope (gain) of the transfer function. Note that when , the transfer function becomes a step function: for , 0 otherwise. Note also that the specific shape of the transfer function (Eq. 2) was chosen for the sake of analytical tractability, but our results are robust to other choices of transfer function (see Fig. 7).
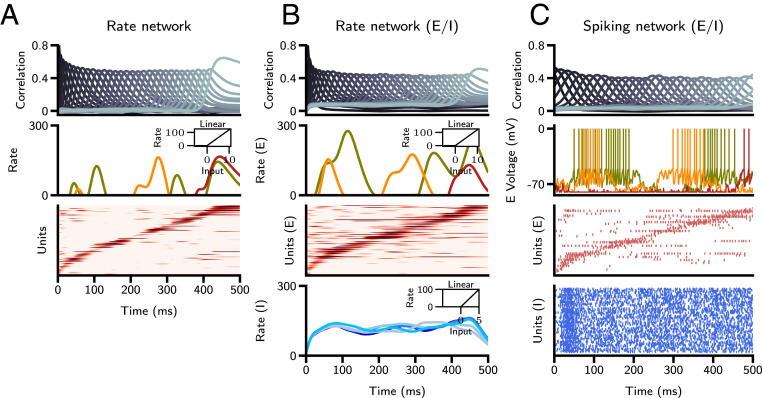
Fig. 7.
Sequence retrieval in excitatory–inhibitory (E-I) networks. (A) Single-population rate network with threshold-linear transfer function. (A, Top) Correlation of network activity with stored patterns. (A, Middle) Firing rates of three representative units, where color corresponds to unit identity. A, Middle, Inset displays transfer function. (A, Bottom) Raster plot of units, sorted by time of peak firing rate. (B) Two-population rate network; panels are as in A. The lowermost graph in B shows the firing rate of representative inhibitory units. (C) Two-population LIF spiking network. (C, Top) As in A and B. (C, Middle) Voltage traces of three representative excitatory units. (C, Bottom) Raster plots of excitatory (sorted) and inhibitory units. Note that the same realizations of random sequences are stored in the three networks, and parameters of the E-I networks are computed so as to match the characteristics of sequences in the single-population rate network. In A and B, every 100th neuron is plotted in the raster plots for clarity, and silent neurons ( of the population) are excluded. In C, every 200th neuron is plotted in the excitatory raster, and every 50th neuron in the inhibitory raster.
Learning Rule.
We assume that the synaptic connectivity matrix is the result of a learning process through which a set of sequences of random inputs presented to the network has been stored using a TAH learning rule. Specifically, we consider two different types of input, corresponding to a continuous and discretized sequence. In the continuous-input scenario, input sequences of duration are defined as realizations of independent Ornstein–Uhlenbeck (OU) processes, with zero mean, SD , and correlation time constant , where is the neuronal index and where is the sequence index. The strength of a synaptic connection from neuron to neuron is modified according to a TAH learning rule, that associates presynaptic inputs at time with postsynaptic inputs at time , , where the functions and describe how postsynaptic and presynaptic inputs affect synaptic strength, respectively, and is a temporal offset. After presentation of all sequences, the connectivity matrix is given by
| [3] |
where is a matrix of independent and identically distributed (i.i.d.) Bernoulli random variables ( with probabilities , ), describing the “structural” connectivity matrix (i.e., whether a connection from neuron to neuron exists or not), represents the average in-degree of a neuron, and controls the strength of the recurrent connectivity.
In the case , , , if we discretize the OU process with a timestep of , then Eq. 3 becomes:
| [4] |
where memorized sequences are now composed of random i.i.d. Gaussian input patterns (, ). This procedure is equivalent to a continuous-time learning process where each input is active for a duration , and in Eq. 3, corresponds to random uncorrelated inputs , where (Fig. 1A). For simplicity, when investigating discretized input, we only explore the case in which the discretization timestep of the input matches the temporal offset of the learning rule, .
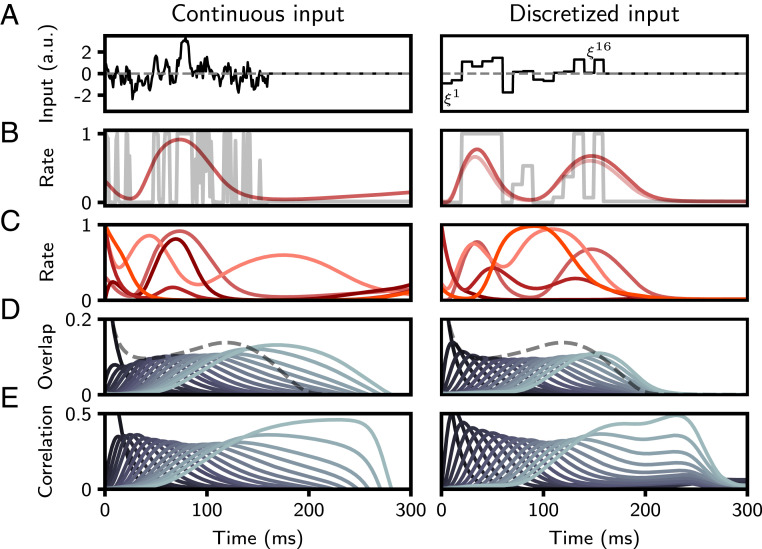
Fig. 1.
Retrieval of a stored sequence in the continuous (Left) and discrete (Right) cases. (A, Left) Continuous input to a single neuron, drawn from an OU process with = 4 ms and . (A, Right) Sequence of 16 discrete input patterns presented to a particular neuron . A.u., arbitrary units. (B) Dark red line: dynamics of the firing rate of the neuron during recall of the sequence, following initialization to the first pattern, (Left) or (Right). Gray line: input patterns passed through the neuronal nonlinearity. Note that the dynamics during recall produces a smooth approximation of the sequence. Light red line: dynamics following initialization to a noisy version of the first pattern. (C) Dynamics of four additional representative neurons, showing the diversity of temporal profiles of activity. (D) Overlap of network activity with each stored pattern (solid lines). In the continuous case, pattern values were sampled every 10 ms. Dashed gray line: average squared rates, . (E) Correlation of network activity with each stored pattern (or pattern sampled every 10 ms in the continuous case). Parameters: N = 40,000, c = 0.005, = 10 ms, , (Left) or (Right).
Note that this learning rule makes a number of simplifications, for the sake of analytical tractability: 1) Plasticity is assumed to depend only on external inputs to the network, and recurrent synaptic inputs are neglected during the learning phase. 2) Inputs are assumed to be discrete in time, and the learning rule is assumed to associate a presynaptic input at a given time, with postsynaptic input at the next time step. In other words, the temporal structure in the input should be matched with the prepost delay maximizing synaptic potentiation. Continuous-time sequences in which inputs change on faster timescales than this delay can also be successfully stored and retrieved (Fig. 1, Left). We note that the temporal asymmetry is consistent with both spike-timing dependent plasticity (STDP), that operates on timescales of tens of milliseconds (32), and behavioral timescale synaptic plasticity that operates on timescales of seconds (33).
Retrieval of Stored Sequences.
We first ask the question of whether such a network can recall the stored sequences and characterize the phenomenology of the retrieved sequences. We start by considering a network that stores a single sequence of length (corresponding to continuous input), or i.i.d. Gaussian patterns, for all , (corresponding to discretized input), using a bilinear learning rule ( and ). Without loss of generality, we choose , as this parameter can be absorbed into the transfer function by defining new parameters and . The Gaussian assumption can be justified for a network in which neurons receive a large number of weakly correlated inputs, since the sum of such inputs is expected to be close to Gaussian due to the central-limit theorem. The bilinearity assumption is made for the sake of analytical tractability and will be relaxed below.
In Fig. 1B, we show the retrieval of a single sequence of 16 input patterns from the perspective of a single unit. The gray line corresponds to the sequence of firing rates driven by input patterns for this particular neuron (i.e., , or , for ). The solid red line displays the unit’s activity following initialization to the first pattern in that sequence, after learning has taken place. Note that for this learning rule, the network dynamics do not reproduce exactly the stored input sequence, but, rather, produce a dynamical trajectory that is correlated with that input sequence. In Fig. 1B, we have specifically selected a unit whose activity transits close to the stored patterns during recall. In Fig. 1C, the activity of several random units is displayed during sequence retrieval. As each unit experiences an uncorrelated random sequence of inputs during learning, activity is highly heterogeneous, and units differ in the degree to which they are correlated with input patterns (SI Appendix, Fig. S1). The distribution of firing rates during recall depends on the parameters of the neural transfer function, . If the threshold is large, then the distribution of rates is unimodal, with a peak around zero, and few neurons firing at high rates. If the threshold is zero, the distribution of firing rates is bimodal, with increasing density at the minimal and maximal rates as the inverse gain parameter is decreased (SI Appendix, Fig. S11). Retrieval is also highly robust to noise—a random perturbation of the initial conditions of magnitude 75% of the pattern itself leads to sequence retrieval, as shown in Fig. 1B (compare the two solid lines, corresponding to unperturbed and perturbed initial conditions, respectively—see also SI Appendix for more details about noise robustness).
A natural quantity to measure sequence retrieval at the population level is the overlap (dot product) of the instantaneous firing rates with a given stored pattern in the sequence. For discretized input, this quantity is given by . To measure overlaps in networks storing continuous input, we sampled pattern values every from the continuous input (Fig. 1 D and E, Left; SI Appendix). Overlaps can be thought of as linear decoders of the activity of the network. Another quantity is the (Pearson) correlation between network activity and the stored pattern, which for the bilinear rule corresponds to the overlap divided by the SD of the firing rates across the population. In the general case, we consider the correlation between the transformed presynaptic input and network activity (SI Appendix). Overlaps and correlations are shown in Fig. 1 D and E, respectively, showing that all patterns in the sequence are successively retrieved, with an approximately constant peak overlap () and correlation (). Note that the maximum achievable overlap and correlation for the bilinear rule are 0.388 and 0.825, respectively, following retrieval from initialization to the first pattern (SI Appendix). In the remainder of the paper, we investigate the dynamics of sequential activity arising from stored discretized input.
Temporal Characteristics of the Retrieved Sequence.
We next consider the temporal characteristics of retrieved sequences. The speed of retrieval of a sequence is defined as the inverse of the interval between the peaks in the overlaps with successive patterns in the sequence. We find that the network retrieves the sequence at a speed of approximately one pattern retrieved per time constant . For instance, in Fig. 1, in which the time constant of the units is 10 ms, the whole sequence of 16 patterns is retrieved in approximately 150 ms (the first pattern was retrieved at time 0). Empirically, we find that the time it takes to retrieve the whole sequence is approximately invariant to the number of sequences stored and the parameters of the rate-transfer function, and is well predicted by (SI Appendix, Fig. S2). When storing discretized input, the retrieval time (and connectivity in Eq. 4) does not depend on the temporal offset of the learning rule , as the discretization timestep of the stored input is matched to this interval. For continuous sequences of duration , the time to retrieve stored sequences is proportional to —i.e., the retrieval time is again proportional to the time constant of the rate dynamics , but is inversely proportional to the temporal offset of the learning rule .
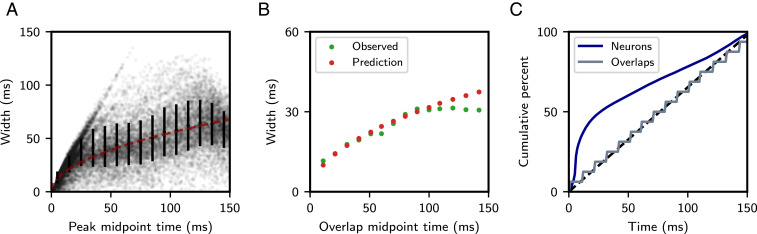
While the sequence is retrieved at an approximately constant speed, several other features of retrieval depend strongly on the time within the sequence. In particular, the peak overlap magnitudes decay as a function of time within the sequence, but the width increases as , where denotes the index of the overlap (Fig. 2B and SI Appendix). Similarly, neurons at the beginning of a sequence are sharply tuned, and those toward the end have broader profiles (Fig. 2A). This is consistent with experimental findings in rat CA3 (5), medial prefrontal cortex (27) and monkey lateral prefrontal cortex (28). Another commonly reported experimental observation involves the temporal ordering of these peaks. Across these same areas and species, a larger number of neurons appear to encode for earlier parts of the sequence than for later segments, resulting in sequences that are not uniformly represented in time by neuronal activity (5, 27, 28). A similar pattern of overrepresentation is found in the model. The cumulative density of firing-rate peak times deviates from a uniform distribution, while the density of the overlap peak times are roughly uniform in time (Fig. 2C). This is due to a combination of two factors: Both initial overlaps and average activity are larger initially, leading to a larger probability that neurons with large values of s for the initial patterns in the sequence will develop a peak.
Fig. 2.
Temporal characteristics of a retrieved sequence. (A) Distribution of single-neuron peak widths, defined as continuous firing intervals occurring one SD above the single-neuron time-averaged firing rate. Black error bars denote mean and SD of widths within each 10-ms interval. Dashed red curve is best-fit trend using scaled square root function (SI Appendix). (B) Green dots correspond to observed overlap widths, defined as the weighted sample SD of (SI Appendix). Red dots display the analytically predicted overlap width of , where = 10 ms and (SI Appendix). (C) Cumulative percentage of peak times for single neurons (blue) and overlaps (gray). The dashed black line represents a uniform distribution. All parameters are as in Fig. 1.
A Low-Dimensional Description of Dynamics.
To better understand the properties of these networks, we employed mean-field theory to analyze how the overlaps in a typical network realization evolve in time. To this end, we defined several “order parameters.” The first set of order parameters measures the typical overlap of network activity in time with the -th pattern: , where the average is taken over the statistics of the patterns. Note that these are distinct from the previously defined overlaps , which are empirically measured values for a particular realization of sequential activity patterns. However, for the large, sparse networks considered here, these quantities describe any typical realization of random input patterns and connectivity (SI Appendix). We also define the average squared rate , the two time autocorrelation function , and the network memory load as the number of patterns stored per average synaptic in-degree—i.e., .
Framing the network in these terms yields a low-dimensional description in which the time-dependent evolution of the overlaps can be written as an effective delay line system (SI Appendix). In this formulation, the activation level of each overlap is driven by a gain-modulated version of the previous one in the sequence, where the gain depends on the sequential load, rate variability, and norm of the overlaps
| [5] |
and the gain function is given by
| [6] |
The dynamics of and are given by coupled integro-differential equations (SI Appendix). With a constant gain below one, recall of a sequence would decay to zero, as each overlap would become increasingly less effective at driving the next one in the sequence. Conversely, a constant gain above one would eventually result in runaway growth (SI Appendix). In Eq. 5, the gain changes in time due to its dependence on the norm of and . During successful retrieval, the gain transiently rises to a value that is slightly larger than one, allowing for overlap peaks to maintain an approximately constant value (SI Appendix, Fig. S3B). We find that there are two different regimes for successful retrieval that depend on the shape of G (and, therefore, the transfer-function parameters): One in which sequences of arbitrarily small initial overlap are retrieved and another in which a finite initial overlap is required (SI Appendix, Fig. S3 A and C).
The predictions from mean-field theory agree closely with the full network simulations. Fig. 3A shows the dynamics of a network in which two sequences of identical length are stored. At time 0, we initialize to the first pattern of the first sequence (corresponding overlaps shown in red). At 250 ms, we present an input lasting 10 ms corresponding to the first pattern of the second (blue) sequence. The solid lines show the overlap of the full network activity with each of the stored input patterns. The predicted overlaps from simulating mean-field equations are shown in dashed lines. The average squared rate is also predicted well by the theory, as is the two time autocorrelation function (SI Appendix, Fig. S4).
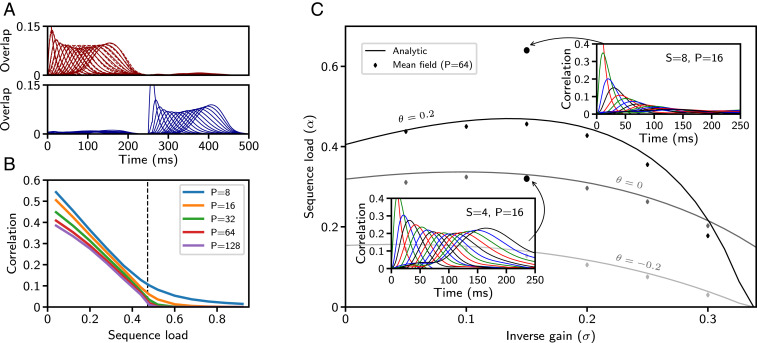
Fig. 3.
Sequence capacity for Gaussian patterns. (A) Overlaps of two discrete sequences. Solid lines are full network simulations; dashed lines are simulations of the mean-field equations. (B) The maximal correlation with the final pattern in the stored sequence obtained from simulating mean-field equations, as a function of sequence load, for parameters corresponding to Fig. 1 ( and ). The vertical dashed line marks the predicted capacity for and . (C) Storage capacity as a function of the gain of the neural transfer function for three values of (all other parameters fixed). Solid curves: storage capacity computed from SI Appendix, Eqs. 39 and 40. Symbols: storage capacity, computed from simulations of mean-field equations (SI Appendix). C, Insets display representative overlap dynamics for network parameters above and below the capacity curve corresponding to = 0.2 (solid lines within Insets are full network simulations). Parameters for A are as in Fig. 1, except .
Storage Capacity of the Network.
We next asked how the properties of retrieved sequences depend on the memory load and what is the maximal storage capacity of the network, defined as the largest value of for which sequences can be retrieved successfully. Fig. 3B shows the peak correlation value that the network attained with the final pattern in a sequence as a function of the sequence load, obtained by using the mean-field equations. It shows that the correlation with the last pattern decreases with until it reaches, for long enough sequences, a value close to zero at . We calculated analytically this sequence capacity and found that it is implicitly determined by solving the relation for , where is the average squared firing rate at capacity (SI Appendix). At capacity, for a fixed number of incoming connections , the network can store one long patterned sequence of length , or any number of sequences that collectively sum to this length (SI Appendix, Fig. S6).
In Fig. 3C, the analytically computed capacity curve is shown as a function of the inverse gain parameter of the rate-transfer function and for three values of (solid lines). Below a specified capacity curve, a sequence can be retrieved, and above it decays to zero. A small inverse gain corresponds to a transfer function with a very steep slope, whereas a large inverse gain produces a more shallow slope. The parameter determines the threshold of input required to drive a unit to half its maximum firing rate , where a larger corresponds to a higher threshold. The storage capacity obtained from simulating the mean-field equations (symbols) agrees well with the analytical result (solid lines).
For Gaussian patterns, we find that capacity is maximal for transfer functions with a positive threshold (SI Appendix, Figs. S3A and 5). The capacity decreases smoothly for , but drops abruptly to zero above . This abrupt drop is due to the behavior of the gain function as parameters and are varied (SI Appendix, Fig. S3C). For (SI Appendix, Fig. S3 A, region F), has a region of stability (range of values of such that ) that is bounded away from zero. For , and for appropriate initial conditions, the gain eventually stabilizes around one: Either an initially large gain will decrease or an initially small gain will grow. As crosses , however, this region of stability disappears, resulting in zero capacity . Capacity decreases continuously in other parameter directions. In particular, as approaches its lower bound , and as approaches its upper bound , the capacity continuously decreases to zero.
Nonlinear Learning Rules Produce Sparse Sequences.
We have explored so far the storage of Gaussian sequences and found that the stored sequences can be robustly retrieved. Activity at the population level is heterogeneous in time (Fig. 1B), with many units maintaining high levels of activity throughout recall. However, many neural systems exhibit more temporally sparse sequential activity (9). While the average activity level of the network can be controlled to some degree by the neuronal threshold , retrieved sequences are nonsparse, even for the largest values of , for which the capacity is nonzero. Altering the statistics of the stored patterns will, in turn, change the statistics of neuronal activity during retrieval, which could lead to more sparse activity.
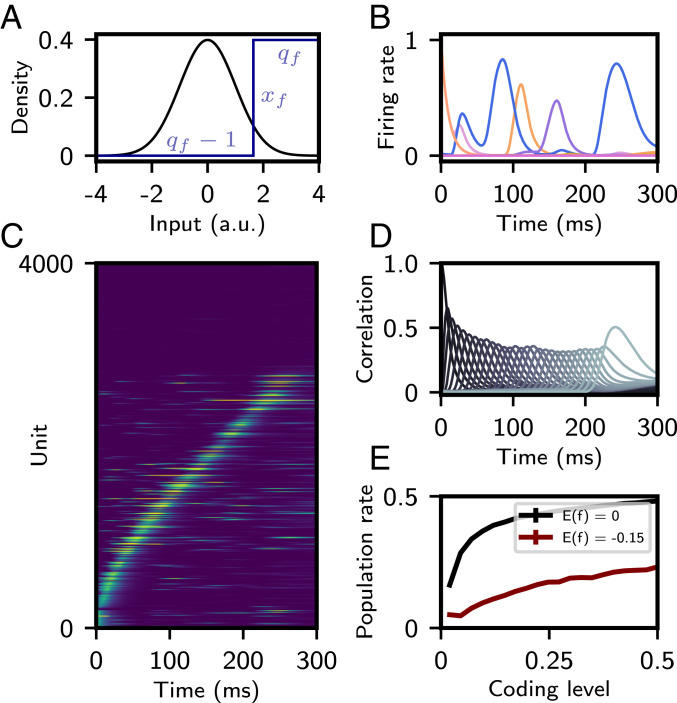
We therefore revisited Eq. 4 and explored nonlinear presynaptic and postsynaptic transformations ( and , respectively). We focus on a simplified functional form, similar to one shown to fit learning rules inferred from in vivo cortical data (34) and shown to maximize storage capacity in networks storing fixed-point attractors (35). For each synaptic terminal (pre and post), we apply a transformation that binarizes the activity patterns into high and low values according to a threshold (Fig. 4A):
| [7] |
| [8] |
In the following, we choose and set such that . This fixes the mean connection strength to zero, thereby preventing the mean total synaptic input from growing with the number of patterns stored, as was also the case with the bilinear learning rule. The parameter is chosen such that (34, 35).
Fig. 4.
Sparse sequences with a nonlinear learning rule. (A) Probability density of Gaussian input pattern (black). Step function binarizing the input patterns prior to storage in the connectivity matrix (blue) is shown. (B) Firing rate of several representative units as a function of time. (C) Firing rates of 4,000 neurons (out of 40,000) as a function of time, with “silent” neurons shown on top and active neurons on the bottom, sorted by time of peak firing rate. (D) Correlation of network activity with each stored pattern. (E) Average population rate as a function of “coding level” (probability that input pattern is above ). The average of is maintained by varying with . In red, the average of is constrained to , the value in A–D. In black, the average of is fixed to zero. All other parameters are as in A–D. For A–D, parameters of the learning rule were , , , and . , .
High thresholds (, ) lead to a low “coding level” (the probability that an input pattern is above ) of the binarized representation of the patterns stored in the connectivity matrix. We find that storage of such patterns leads to sparse sequential activity at a population level (Fig. 4 B and C) and strong transient correlations with these patterns during retrieval (Fig. 4D). Quantitative analysis of this activity reveals that both single-neuron peak and overlap widths are largely constant in time, unlike retrieval following a bilinear learning rule. Single-neuron peak times are still biased toward the start of the sequence, but to a lesser degree than with the bilinear rule (SI Appendix, Fig. S7). As a result of this sparse activity, overlap values are smaller than those resulting from the bilinear rule, but correlations are of similar magnitude, due to smaller pattern and firing rate variance.
This sparse activity is reflected in the average population firing rate, which is in Fig. 4 B–D, compared to Fig. 1, where it was . Compared to networks storing Gaussian patterned sequences, this is a consequence of fewer neurons firing, and not due to a uniform decrease of single-unit activity. As the coding level decreases, the average population firing rate decreases (Fig. 4E). The magnitude of this decrease is dependent on the average of (holding all other parameters equal) and becomes smaller as this average becomes more negative. Given a low coding level, we expect many neurons to be silent during recall. As can be seen in Fig. 4C, for this choice of parameters, roughly 25% of neurons display no activity. The sequence capacity of these networks is larger than those resulting from the bilinear rule and increases as the coding level decreases (SI Appendix, Fig. S9).
Diverse Selectivity Properties Emerge from Learning Random Sequences.
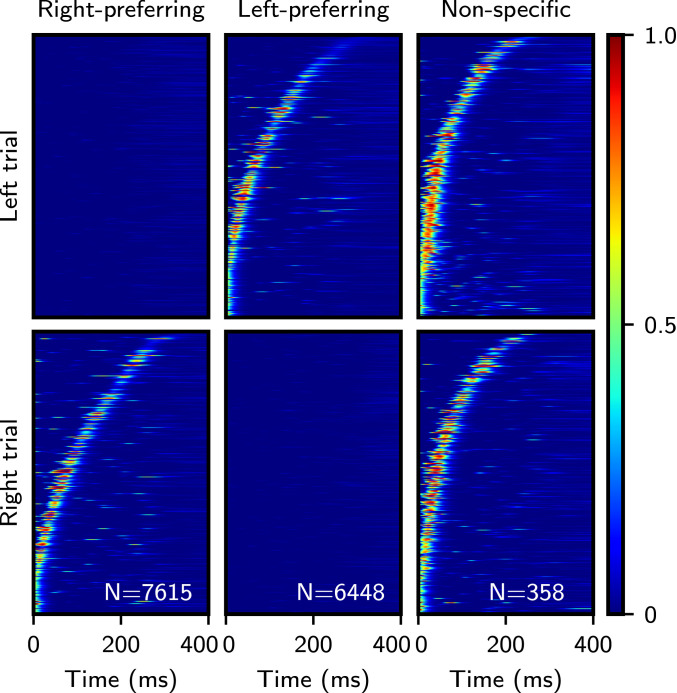
Experimentally observed sequential activity often displays some degree of diversity in selectivity properties. For instance, in posterior parietal cortex (PPC), mice show choice-selective sequential activity during two-alternative force-choice T-maze tasks. In the task, mice are briefly cued at the start of a trial before running down a virtual track that is identical across trial contexts. At the end of the track, they must turn either left or right according to the remembered cue to receive reward (1). Within a single recording session and across trials, many neurons display a preference for firing at a specific location during a single-choice context and are silent or weakly active otherwise. Other neurons fire at the same interval during both choice contexts, at different intervals, or are not modulated by the task (1). Similar activity has been described in rat CA1 hippocampal neurons during the short delay period preceding a different two-alternative figure-eight maze (4). It is an open question as to whether these different types of selectivity are a signature of task-specific mechanisms or simply the expected by-product of storing uncorrelated random inputs. To investigate this question, we stored two random uncorrelated sequences, each corresponding to the “left” and “right” target decisions in the T-maze task. The patterns in these sequences were transformed according to the nonlinear learning rule described in the previous section. We find that the same qualitative heterogeneity of response type exists in our network model. In Fig. 5, subpopulations of identified right-preferring, left-preferring, and nonspecific units (i.e., units that fire at similar times in both sequences) are plotted during a single recall trial of each sequence. Note that while the model reproduces qualitatively the diversity of selectivity properties seen in the data, quantitatively, the fraction of nonspecific neurons found in the model () is much smaller than that found in experiment ( of putative imaged cells in ref. 1). This discrepancy might be due to different levels of sparsity or to correlations in the two sequences stored in mouse PPC.
Fig. 5.
Diverse selectivity properties emerge after learning two random input sequences. Single-trial raster plots display units that are active only during the right trial (Left), left trial (Center), and at similar times during both trials (Right). Activity is sorted by the time of maximal activity, and this sorting is fixed across rows. Numbers indicate amount of neurons passing selection criteria (total neuron count is 40,000). , and all other parameters are as in Fig. 4.
Changes in Synaptic Connectivity Preserve Collective Sequence Retrieval while Profoundly Changing Single-Neuron Dynamics.
While sequential activity in PPC is stereotyped across multiple trials in a single recording session, it changes significantly across multiday recordings (30). In a single recording session, many neurons display a strong peak of activity at one point in time during the task. Across consecutive days of recordings, however, a substantial fraction of these peaks are either gained or lost. Critically, information about trial type is not lost over multiple recording sessions, as reflected by above chance decoding performance of trial type (left vs. right) in subsets of cells (30). Similarly, place cells in CA1 of hippocampus form stable sequences within a single recording session, but exhibit large changes in single neuron place fields across days, even in the same environment (29). As in PPC, a total remapping is not observed, and information about the position of the animal is preserved at the population level across time (29).
We explored the possibility that these changes in single neuron selectivity might be due to ongoing changes in synaptic connectivity, consistent with spine dynamics observed in cortex and hippocampus (36, 37). To probe whether dynamic reorganization of sequential activity is consistent with such ongoing synaptic dynamics, we introduced random weight perturbations to the synaptic connectivity. We simulated the network over multiple days, where the weights on day are defined as a sum of a fixed, sequential component () as in Eq. 4, and a random dynamic component ():
| [9] |
| [10] |
| [11] |
| [12] |
where controls the decay of random perturbations, controls their amplitude, and are i.i.d. random Gaussian variables of zero mean and unit variance.
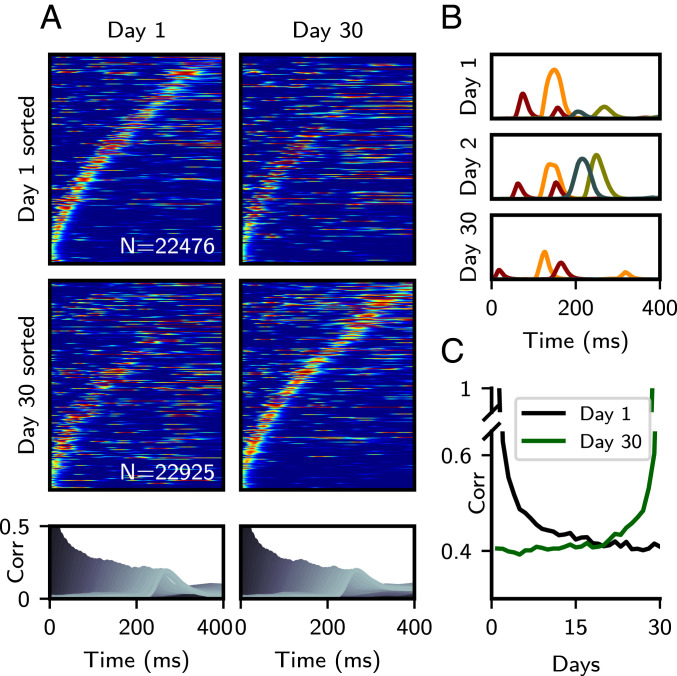
In Fig. 6, we examine the reorganization of activity during a 30-d period, for parameters such that the activity strongly decorrelates over the time course of a few days. In Fig. 6A, sorted sequential activity is plotted for retrieval on day 1, followed by that during the 30-d mark. We find that sequential activity shows progressive reorganization, with the sequence on day 30 being only weakly, but significantly correlated (with a Pearson correlation coefficient of ) with the sequence on day 1. Critically, the underlying stored sequence can be read out equally well on both days, as shown by the pattern-correlation values plotted below. In Fig. 6B, representative single-unit activity is shown on the first, second, and final simulated day for four neurons, showing the emergence and disappearance of localized activity peaks in multiple neurons. To measure how quickly sequential activity decorrelated across time, for each day we plotted the average correlation of single-unit activity profiles with those on day 1 or 30 (Fig. 6C). For the parameters chosen here, sequences decorrelate in a few days, such that by day 15, the correlation has reached a stable baseline. This qualitatively matches the ensemble activity correlation times reported in mouse CA1 (38). The dependence of the timescale and degree of decorrelation on and is shown in SI Appendix, Fig. S8.
Fig. 6.
Changes in synaptic connectivity preserve retrieval while changing single-neuron dynamics. (A) Sorted raster plots at the start and end of a 30-d simulation. (A, Top) Sorted to activity on day 1. (A, Middle) Sorted to activity on day 30. (A, Bottom) Pattern correlations computed on day 1 and 30. (B) Representative single-unit activity profiles of four neurons across days 1, 2, and 30. Color corresponds to unit identity. (C) Average correlation of activity profiles between day n, and either day 1 (black) or 30 (green). , , and all other parameters as in Fig. 4. Note that the SD of the “noise” term in the connectivity matrix is larger than the SD of the fixed sequential component . The colormap scale for days 1 and 30 in A are the same as in Fig. 5.
Sequence Retrieval in Excitatory–Inhibitory Spiking Networks.
For simplicity, we had previously chosen to neglect two key features of neuronal circuits: the separation of excitation and inhibition, and action-potential generation. To investigate whether our results are valid in more realistic networks, we developed a procedure to map the dynamics of a single-population rate network onto a network of current-based LIF neurons with separate populations of excitatory and inhibitory units. To implement sequence learning in two population networks, we made the following assumptions: 1) Learning takes place only between excitatory-to-excitatory recurrent connections; 2) to implement the sign constraint in those connections, we apply to the Hebbian connectivity matrix (Eq. 4) a nonlinear synaptic transfer function that imposes a nonnegativity constraint—specifically, we use a simple rectification (SI Appendix); and 3) inhibition is faster than excitation. Under these assumptions, we reformulate the two-population network into an equivalent single-population network with two sets of connections: one representing the excitatory-to-excitatory inputs, and the other representing the inhibitory feedback. We compute the effective inhibitory drive that balances the average positive excitatory recurrent drive arising from rectification, and, in turn, excitatory-to-inhibitory and inhibitory-to-excitatory connection strengths in the original two-population model that achieve this balance.
Fig. 7 shows the results of applying this procedure in two steps (from a one-population to two-population rate model, and then from a two-population rate model to a two-population LIF network—see SI Appendix for details). In Fig. 7A, sequential activity is shown from a single-population rate network of size N = 20,000 with a rectified linear rate-transfer function. In Fig. 7B, we transform this population into excitatory units by rectifying their synaptic weights and add an additional population of N = 5,000 inhibitory units, with random sparse connections to and from the excitatory units. Finally, in Fig. 7C, we construct a current-based spiking network using parameters derived from LIF transfer functions. These LIF transfer functions were fit to a bounded region of the rectified linear transfer functions in Fig. 7B (SI Appendix). Connectivity matrices are identical for Fig. 7 B and C up to a constant scaling factor. Raster plots of excitatory neurons reveal that activity is sparse, with individual neurons firing strongly for short periods of time. Inhibitory neurons fire at rates that are much less temporally modulated than those of excitatory neurons and inherit their fluctuations in activity from random connections from the excitatory neurons. Retrieval in the spiking network is robust to perturbations of the inhibitory feedback (SI Appendix, Fig. S12). Increasing by 5% or decreasing by 20% the strength of excitatory-to-inhibitory connections () results in diminished or elevated global firing activity, respectively, but the sequence is retrieved with the same fidelity, as measured by pattern correlations.
Discussion
We have investigated a simple TAH learning rule in rate and spiking networks models and developed a theory of the transient activity observed in these networks. Using this theory, we have computed analytically the storage capacity for sequences in the case of a bilinear learning rule and derived parameters of the neuronal transfer function (threshold and gain) that maximize capacity.
We have found that a variety of temporal features of population activity in the network model match experimental observations, including those made from single trials of activity and across multiday recording sessions. A bilinear learning rule produces sequences that qualitatively match recorded distributions of single-neuron preferred times and tuning widths in cortical and hippocampal areas. Tuning widths increase over the course of retrieval, and activity peaks are more concentrated at earlier segments of retrieval (5, 27, 28). With a nonlinear learning rule, sequential activity is temporally sparse and more uniform in time, consistent with findings in nucleus HVC of zebra finch (39, 40). To mimic the effects of synaptic turnover and ongoing learning across multiday recording sessions, we continually perturbed synaptic connectivity across repeated trials of activity. We show that single-unit activity can dramatically reorganize over this time period while maintaining a stable readout of sequential activity at the population level, consistent with recent experimental findings (29, 30). Finally, we have developed a procedure to map the sequential activity in simple rate networks to excitatory–inhibitory spiking networks.
Comparison with Previous Models.
A large body of work has explored the generation and development of sequential activity in network models (11–19, 41. The storage and retrieval of binary activity patterns using TAH learning rules has been studied in networks of both binary and rate units. In networks of binary neurons, with asymmetric connectivity and parallel updating, the activity transitions instantaneously from one pattern to the next at each time step. With asynchronous updating, synaptic currents induced by the asymmetric component in the connectivity need to be endowed with delays in order to stabilize pattern transitions (13, 42). In contrast to previously studied rate and binary models, the present rate network neither transitions immediately between patterns nor dwells in pure pattern states for fixed periods of time. Instead, network activity during retrieval smoothly evolves in time in such a way as to become transiently correlated successively with each of the patterns in the sequence.
Previous studies of network of spiking neurons have heavily focused on the reproduction of temporally sparse synfire chain activity (15, 16, 44). However, a growing number of observations indicate that, outside specialized neural systems such as nucleus HVC, sequences are rarely consistent with such a simplified description. Contrary to previous work, our approach seeks to provide a unified framework to account for the diversity of observed dynamics. Recent modeling efforts to reproduce quantitatively experimentally observed dynamics have used supervised learning algorithms, in which initially randomly connected networks are trained to reproduce exactly activity patterns observed in experiment (18, 44). However, these learning rules are nonlocal, and there are currently no known biophysical mechanisms that would allow them to be implemented in brain networks. Here, we have shown that a simpler and more biophysically realistic learning rule is sufficient to reproduce many experimentally observed features of sequential activity.
Storage Capacity.
The analytical methods used in this paper are generalizations of mean-field methods used extensively both in networks of binary neurons (48–51) and in networks of rate units (35, 52). Using these methods, we were able to compute analytically the storage capacity of sequences of independent Gaussian-distributed patterns of activity in rate models using a TAH learning rule. This allowed us to characterize how the storage capacity depends on the parameters of the transfer function and to obtain the threshold and gain of the transfer function that optimizes this storage capacity. We found, as in fixed-point attractor networks (35, 48, 53), and networks of binary neurons storing sequences (49, 50), that capacity scales linearly with the mean number of connections per neuron. The storage capacity of our model for the bilinear rule is of the same order of magnitude as storage capacities previously computed in networks of binary neurons, both in sparsely connected (49) and fully connected networks (50). While our results are derived in the large limit, we have shown that it predicts well the measured capacity for finite-size networks. We also computed numerically the capacity for networks with nonlinear learning rules and found that the capacity increases when sequences become sparser, similar to what is found in networks storing fixed-point attractor states (35, 54, 55).
Storage and Retrieval.
In the present work, we have used a simplified version of a TAH rule in which only nearest-neighbor pairs in the sequence of uncorrelated patterns modify the weights. This learning rule assumes that network activity is “clamped” during learning by external inputs, and that recurrent inputs do not interfere with such learning. The temporally discrete input considered here can be seen as an approximation of a continuous input sequence (Fig. 1A). Alternatively, it can describe situations in which the inputs are discrete in time and/or learning in the presence of a strong global oscillation, where the time difference between consecutive input patterns would correspond to the period of the oscillation. We found for the bilinear rule that, following learning, the speed of retrieval (i.e., the inverse time between recall of consecutive patterns) matches the time constant of the rate dynamics. Moreover, we showed empirically that this speed does not depend on the number of stored patterns, nor on the particulars of the neural transfer function. This suggests that if patterns are presented during learning at this same timescale (i.e., ), one that is consistent with STDP, then they can be retrieved at the same speed as they were presented, without any additional mechanisms (56). If patterns are presented on slower timescales, then retrieval of input patterns could proceed on a faster speed than in which they were originally presented. Such a mechanism could underlie the phenomenon of hippocampal replay during sharp-wave ripple events, in which previously experienced sequences of place cell-activity can reactivate on significantly temporally compressed timescales (57). Whether additional cell-intrinsic or network mechanisms allow for dynamic control of retrieval speed remains an open question.
Retrieval in the present network model bears similarities to that of the functionally feedforward linear-rate networks analyzed by Goldman (58), in which recurrent connectivity was constructed by using an orthogonal random matrix to rotate a feedforward chain of unity synaptic weights. Retrieval was initiated by briefly stimulating an input corresponding to the first orthogonal pattern in the chain. The retrieval dynamics in those networks correspond exactly to those of the overlap dynamics for the bilinear rule in the presently studied network if a constant gain of is assumed (SI Appendix). The key difference in our model is that the gain is dynamic (Eq. 6), as it depends on network activity and overlaps with the stored patterns (Eq. 5). When retrieval is successful, network dynamics ensure that it maintains a value slightly above one throughout retrieval of the full sequence (see SI Appendix for detailed discussion), without any need for fine tuning.
We also found that retrieval is highly robust to initial Gaussian perturbations. Contrary to expectation, storage of additional nonretrieved patterns/sequences confers significantly increased robustness against a perturbation of the same magnitude (SI Appendix, Fig. S10). This can be understood by examining the mean-field equations and noticing that a larger provides a greater range of convergence in initial overlap values to a gain that reaches an equilibrium value around one (see SI Appendix for detailed discussion).
While we have made several simplifying assumptions in the interest of analytical tractability, many of these assumptions do not hold in real neural networks. Biological neurons receive spatially and temporally correlated input. Plasticity rules also operate over a range of temporal offsets, and not at a single discrete time interval, as was assumed here (59). The learning rule we considered here operates on external inputs and does not account for the recurrent inputs arising from pattern presentations during learning. Feedback from these inputs could dramatically alter firing rates during learning and require additional mechanisms to stabilize learning. However, we note that the learning rule described here could potentially be a good approximation of a firing-rate-based rule, in a scenario in which learning is gated by neuromodulators. In such a scenario, plasticity would be gated by neuromodulators that would also act to weaken recurrent inputs, ensuring that external inputs are the primary drivers of neuronal activity. During the retrieval phase, recurrent inputs would be strong enough to sustain retrieval without ongoing additional external inputs (see, e.g., ref. 60). Understanding how each of these properties impact the findings presented will be the subject of future work.
Temporal Characteristics of Activity.
We have found two emergent features of retrieval with a bilinear learning rule that are consistent with experiment: a broadening of single-unit activity profiles with time and an overrepresentation of peaks at earlier times of the sequence. These features have been reported in hippocampal area CA3 (5), medial prefrontal cortex (27) and lateral prefrontal cortex (28). Our theory provides a simple explanation for both of these features. Mean-field theory analysis shows that the temporal profile of the overlaps control, to a large extent, the profiles of single units. Specifically, the mean input current of a single unit is a linear combination of overlaps, with coefficients equal to the pattern values shown during learning. For Gaussian patterns, the overlaps rise transiently through an effective delay-line system, where the activation of each overlap is fed as input to drive the next. As the overlaps decay on the same timescale that they rise, the effective decay time grows for inputs later in the sequence, resulting in more broadly tuned profiles. This is also reflected in the longer decay time in the two time autocorrelation function at later times (SI Appendix, Fig. S4B). The overrepresentation of peaks at earlier times can be accounted for by a decrease in overlap magnitude throughout recall, as fluctuations in activity earlier in recall are more likely to rise above threshold and establish a peak.
We have also investigated the effects of storing sparse patterns using a nonlinear learning rule. The form of this rule bears similarities to that inferred from electrophysiological data in inferior temporal cortex (34) and has been shown to be optimal for storing fixed-point attractors in the space of separable, sigmoidal learning rules (35). Sparse patterns lead to sequence statistics that are consistent, instead, with song-specific sequential activity in nucleus HVC of zebra finch (39, 40).
Effects of Random Synaptic Fluctuations on Sequence Retrieval.
We showed that simulating the effects of random fluctuations of synaptic weights by adding random weight perturbations can account for sequences that are unstable at the single-unit level, but which still maintain information as a population, consistent with experiment (29, 30, 38). We assumed that synaptic connectivity has both a stable component (storing the memory of sequences) and an unstable component that decays over timescales of days. The fluctuations of synaptic connectivity described by Eqs. 9–12 are roughly consistent with observations of spine dynamics over long timescales (e.g., ref. 61). When both components are of similar magnitude, the unstable component interferes with recall, producing noise that causes the input current to a single neuron to fluctuate strongly from day to day. While this noise is of sufficient strength to produce temporally sparse sequential activity with activity peaks that depends on its realization, it is not strong enough to disrupt recall driven by the stable sequential weight component.
If synaptic weights had no stable component and performed an unbiased random walk starting from their initial values, then decoded sequential activity representing task variables would unsurprisingly be expected to dissipate after some period of elapsed time. Experimentally, sequential activity after several weeks still exhibits a significant correlation with the initial pattern of activity. It is still an open question whether this correlation decays to zero on longer timescales. Here, we assumed that there exists a stable component to the synaptic connectivity (perhaps due to repeated exposure, and consequent relearning, of the animal to the same sensory environment), while fluctuations, described by a simple OU process, either represent purely stochastic synaptic fluctuations or are due to learning of other information unrelated to the specific task under which sequential activity is measured.
From Rate to Spiking Network Model.
While our initial results were derived in rate models that do not respect Dale’s law, we have shown that it is possible to build a network of spiking excitatory and inhibitory neurons that stores and retrieves sequences in a qualitatively similar way as in the rate model. In the spiking network, the Hebbian rule operates in excitatory-to-excitatory connections only, while all connections involving inhibitory neurons are fixed. With this architecture, most excitatory neurons show strong temporal modulations in their firing rate, while inhibitory neurons show much smaller temporal modulations around an average firing rate. These firing patterns are consistent with observations in multiple neural systems of smaller temporal modulations in the firing of inhibitory neurons, compared to excitatory cells (9, 62, 63).
Overall, our paper demonstrates that a simple Hebbian learning rule leads to storage and retrieval of sequences in large networks, with a phenomenology that mimics multiple experimental observations in multiple neural systems. The next step will be to investigate how the connectivity matrix used in this study can be obtained through biophysically realistic online learning dynamics.
Materials and Methods
Details of the numerical and analytical methods can be found in SI Appendix, including the mean-field theory for the bilinear rule, construction of the excitatory–inhibitory rate network, and details of the LIF spiking network. Simulation and analysis details for all figures are documented in SI Appendix, Supplemental Procedures. Parameters for all simulations can be found in SI Appendix, Parameter Tables.
Software.
Rate and spiking network simulations were performed by using custom C++ and Python routines with the aid of NumPy (64), SciPy (65), Numba (66), Cython (67), Ray (68), and Jupyter (69). Graphics were generated by using Matplotlib (70).
Supplementary Material
Acknowledgments
This work was supported by NIH Grant R01 EB022891 and Office of Naval Research Grant N00014-16-1-2327. We thank Henry Greenside and Harel Shouval for their comments on a previous version of the manuscript, and all members of the N.B. group for discussions.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1918674117/-/DCSupplemental.
Data Availability.
Code to generate the figures is available at GitHub, https://www.github.com/maxgillett/hebbian_sequence_learning.
References
- 1.Harvey C. D., Coen P., Tank D. W., Choice-specific sequences in parietal cortex during a virtual-navigation decision task. Nature 484, 62–68 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wang J., Narain D., Hosseini E. A., Jazayeri M., Flexible timing by temporal scaling of cortical responses. Nat. Neurosci. 21, 102–110 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Lee A. K., Wilson M. A., Memory of sequential experience in the hippocampus during slow wave sleep. Neuron 36, 1183–1194 (2002). [DOI] [PubMed] [Google Scholar]
- 4.Pastalkova E., Itskov V., Amarasingham A., Buzsaki G., Internally generated cell assembly sequences in the rat hippocampus. Science 321, 1322–1327 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Salz D. M., et al. , Time cells in hippocampal area CA3. J. Neurosci. 36, 7476–7484 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Heys J. G., Dombeck D. A., Evidence for a subcircuit in medial entorhinal cortex representing elapsed time during immobility. Nat. Neurosci. 21, 1574–1582 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Buzsaki G., Hippocampal sharp waves: Their origin and significance. Brain Res. 398, 242–252 (1986). [DOI] [PubMed] [Google Scholar]
- 8.Akhlaghpour H., et al. , Dissociated sequential activity and stimulus encoding in the dorsomedial striatum during spatial working memory. eLife 5, e19507 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hahnloser R. H., Kozhevnikov A. A., Fee M. S., An ultra-sparse code underlies the generation of neural sequences in a songbird. Nature 419, 65–70 (2002). [DOI] [PubMed] [Google Scholar]
- 10.Churchland M. M., Shenoy K. V., Temporal complexity and heterogeneity of single-neuron activity in premotor and motor cortex. J. Neurophysiol. 97, 4235–4257 (2007). [DOI] [PubMed] [Google Scholar]
- 11.Amari S.-I., Learning patterns and pattern sequences by self-organizing nets of threshold elements. IEEE Trans. Comput. C-21, 1197–1206 (1972). [Google Scholar]
- 12.Herz A., Sulzer B., Kühn R., van Hemmen J. L., The Hebb rule: Storing static and dynamic objects in an associative neural network. Europhys. Lett. 7, 663–669 (1988). [Google Scholar]
- 13.Kuhn R., Van Hemmen J. L., “Temporal association” in Models of Neural Networks I, Domany E., Van Hemmen J. L., Schulten K., Eds. (Springer, Berlin, 1995), pp. 221–288. [Google Scholar]
- 14.Rabinovich M., et al. , Dynamical encoding by networks of competing neuron groups: Winnerless competition. Phys. Rev. Lett. 87, 068102 (2001). [DOI] [PubMed] [Google Scholar]
- 15.Long M. A., Jin D. Z., Fee M. S., Support for a synaptic chain model of neuronal sequence generation. Nature 468, 394–399 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fiete I. R., Senn W., Wang C. Z., Hahnloser R. H., Spike-time-dependent plasticity and heterosynaptic competition organize networks to produce long scale-free sequences of neural activity. Neuron 65, 563–576 (2010). [DOI] [PubMed] [Google Scholar]
- 17.Cannon J., Kopell N., Gardner T., Markowitz J., Neural sequence generation using spatiotemporal patterns of inhibition. PLoS Comput. Biol. 11, e1004581 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rajan K., Harvey C. D., Tank D. W., Recurrent network models of sequence generation and memory. Neuron 90, 128–142 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Tannenbaum N. R., Burak Y., Shaping neural circuits by high order synaptic interactions. PLoS Comput. Biol. 12, e1005056 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Murray J. M., Escola G. S., Learning multiple variable-speed sequences in striatum via cortical tutoring. eLife 6, e26084 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Herrmann M., Hertz J. A., Prugel-Bennet A., Analysis of synfire chains. Netw. Comput. Neural Syst. 6, 403–414 (1995). [Google Scholar]
- 22.Abeles M., Corticonics (Cambridge University Press, New York, NY, 1991). [Google Scholar]
- 23.Diesmann M., Gewaltig M. O., Aertsen A., Stable propagation of synchronous spiking in cortical neural networks. Nature 402, 529–533 (1999). [DOI] [PubMed] [Google Scholar]
- 24.Aviel Y., Pavlov E., Abeles M., Horn D., Synfire chain in a balanced network. Neurocomputing 44, 285–292 (2002). [Google Scholar]
- 25.Kumar A., Rotter S., Aertsen A., Conditions for propagating synchronous spiking and asynchronous firing rates in a cortical network model. J. Neurosci. 28, 5268–5280 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chenkov N., Sprekeler H., Kempter R., Memory replay in balanced recurrent networks. PLoS Comput. Biol. 13, e1005359 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tiganj Z., Jung M. W., Kim J., Howard M. W., Sequential firing codes for time in rodent medial prefrontal cortex. Cerebr. Cortex 27, 5663–5671 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tiganj Z., Cromer J. A., Roy J. E., Miller E. K., Howard M. W., Compressed timeline of recent experience in monkey lateral prefrontal cortex. J. Cognit. Neurosci. 30, 935–950 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ziv Y., et al. , Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Driscoll L. N., Pettit N. L., Minderer M., Chettih S. N., Harvey C. D., Dynamic reorganization of neuronal activity patterns in parietal cortex. Cell 170, 986–999 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hopfield J. J., Neurons with graded response have collective computational properties like those of two-state neurons. Proc. Natl. Acad. Sci. U.S.A. 81, 3088–3092 (1984). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Markram H., Lubke J., Frotscher M., Sakmann B., Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science 275, 213–215 (1997). [DOI] [PubMed] [Google Scholar]
- 33.Bittner K. C., Milstein A. D., Grienberger C., Romani S., Magee J. C., Behavioral time scale synaptic plasticity underlies CA1 place fields. Science 357, 1033–1036 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lim S., et al. , Inferring learning rules from distributions of firing rates in cortical neurons. Nat. Neurosci. 18, 1804–1810 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pereira U., Brunel N., Attractor dynamics in networks with learning rules inferred from in vivo data. Neuron 99, 227–238 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Holtmaat A., Svoboda K., Experience-dependent structural synaptic plasticity in the mammalian brain. Nat. Rev. Neurosci. 10, 647–658 (2009). [DOI] [PubMed] [Google Scholar]
- 37.Pfeiffer T., et al. , Chronic 2P-STED imaging reveals high turnover of dendritic spines in the hippocampus in vivo. eLife 7, e34700 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Rubin A., Geva N., Sheintuch L., Ziv Y., Hippocampal ensemble dynamics timestamp events in long-term memory. eLife 4, e12247 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Lynch G. F., Okubo T. S., Hanuschkin A., Hahnloser R. H., Fee M. S., Rhythmic continuous-time coding in the songbird analog of vocal motor cortex. Neuron 90, 877–892 (2016). [DOI] [PubMed] [Google Scholar]
- 40.Picardo M. A., et al. , Population-level representation of a temporal sequence underlying song production in the zebra finch. Neuron 90, 866–876 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kleinfeld D., Sequential state generation by model neural networks. Proc. Natl. Acad. Sci. U.S.A. 83, 9469–9473 (1986). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sompolinsky H., Kanter I., Temporal association in asymmetric neural networks. Phys. Rev. Lett. 57, 2861–2864 (1986). [DOI] [PubMed] [Google Scholar]
- 43.Kleinfeld D., Sompolinsky H., Associative neural network model for the generation of temporal patterns. Theory and application to central pattern generators. Biophys. J. 54, 1039–1051 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Memmesheimer R. M., Rubin R., Olveczky B. P., Sompolinsky H., Learning precisely timed spikes. Neuron 82, 925–938 (2014). [DOI] [PubMed] [Google Scholar]
- 45.Veliz-Cuba A., Shouval H. Z., Josić K., Kilpatrick Z. P., Networks that learn the precise timing of event sequences. J. Comput. Neurosci. 39, 235–254 (2015). [DOI] [PubMed] [Google Scholar]
- 46.Tully P. J., Linden H., Hennig M. H., Lansner A., Spike-based Bayesian-Hebbian learning of temporal sequences. PLoS Comput. Biol. 12, e1004954 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Murray J. D., et al. , Stable population coding for working memory coexists with heterogeneous neural dynamics in prefrontal cortex. Proc. Natl. Acad. Sci. U.S.A. 114, 394–399 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Derrida B., Gardner E., Zippelius A., An exactly solvable asymmetric neural network model. Europhys. Lett. 4, 167–173 (1987). [Google Scholar]
- 49.Gutfreund H., Mezard M., Processing of temporal sequences in neural networks. Phys. Rev. Lett. 61, 235–238 (1988). [DOI] [PubMed] [Google Scholar]
- 50.During A., Coolen A. C. C., Sherrington D., Phase diagram and storage capacity of sequence processing neural networks. J. Phys. Math. Gen. 31, 8607–8621 (1998). [Google Scholar]
- 51.Kawamura M., Okada M., Transient dynamics for sequence processing neural networks. J. Phys. Math. Gen. 35, 253–266 (2002). [Google Scholar]
- 52.Tirozzi B., Tsodyks M., Chaos in highly diluted neural networks. Europhys. Lett. 14, 727–732 (1991). [Google Scholar]
- 53.Amit D. J., Gutfreund H., Sompolinsky H., Storing infinite numbers of patterns in a spin-glass model of neural networks. Phys. Rev. Lett. 55, 1530–1531 (1985). [DOI] [PubMed] [Google Scholar]
- 54.Tsodyks M., Feigel’man M. V., The enhanced storage capacity in neural networks with low activity level. Europhys. Lett. 6, 101–105 (1988). [Google Scholar]
- 55.Tsodyks M. V., Associative memory in asymmetric diluted network with low level of activity. Europhys. Lett. 7, 203–208 (1988). [Google Scholar]
- 56.Gerstner W., Ritz R., van Hemmen J. L., Why spikes? Hebbian learning and retrieval of time-resolved excitation patterns. Biol. Cybern. 69, 503–515 (1993). [PubMed] [Google Scholar]
- 57.Nadasdy Z., Hirase H., Czurko A., Csicsvari J., Buzsaki G., Replay and time compression of recurring spike sequences in the hippocampus. J. Neurosci. 19, 9497–9507 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Goldman M. S., Memory without feedback in a neural network. Neuron 61, 621–634 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Abbott L. F., Nelson S. B., Synaptic plasticity: Taming the beast. Nat. Neurosci. 3, 1178–1183 (2000). [DOI] [PubMed] [Google Scholar]
- 60.Hasselmo M. E., The role of acetylcholine in learning and memory. Curr. Opin. Neurobiol. 16, 710–715 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Trachtenberg J. T., et al. , Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex. Nature 420, 788–794 (2002). [DOI] [PubMed] [Google Scholar]
- 62.Kosche G., Vallentin D., Long M. A., Interplay of inhibition and excitation shapes a premotor neural sequence. J. Neurosci. 35, 1217–1227 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Grienberger C., Milstein A. D., Bittner K. C., Romani S., Magee J. C., Inhibitory suppression of heterogeneously tuned excitation enhances spatial coding in CA1 place cells. Nat. Neurosci. 20, 417–426 (2017). [DOI] [PubMed] [Google Scholar]
- 64.van der Walt S., Colbert S. C., Varoquaux G., The NumPy array: A structure for efficient numerical computation. Comput. Sci. Eng. 13, 22–30 (2011). [Google Scholar]
- 65.Virtanen P., et al. , SciPy 1.0: Fundamental algorithms for scientific computing in python. Nat. Methods 17, 261–272 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Lam S. K., Pitrou A., Seibert S., “Numba: A LLVM-based python JIT compiler” in Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, LLVM’15 (Association for Computing Machinery, New York, NY, 2015), pp. 1–6. [Google Scholar]
- 67.Behnel S., et al. , Cython: The best of both worlds. Comput. Sci. Eng. 13, 31–39 (2011). [Google Scholar]
- 68.Moritz P., et al. , “A distributed framework for emerging AI applications” in Proceedings of the 13th USENIX Conference on Operating Systems Design and Implementation (USENIX Association, 2018), pp. 561–577. [Google Scholar]
- 69.Thomas K., et al. , “Jupyter Notebooks – A publishing format for reproducible computational workflows” in Positioning and Power in Academic Publishing: Players, Agents, and Agendas, F. Loizides, B. Scmidt, eds. (IOS Press, Amsterdam, Netherlands, 2016), pp. 87–90.
- 70.Hunter J. D., Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 9, 90–95 (2007). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Code to generate the figures is available at GitHub, https://www.github.com/maxgillett/hebbian_sequence_learning.