Abstract
Complex behaviors are often driven by an internal model, which integrates sensory information over time and facilitates long-term planning to reach subjective goals. A fundamental challenge in neuroscience is, How can we use behavior and neural activity to understand this internal model and its dynamic latent variables? Here we interpret behavioral data by assuming an agent behaves rationally—that is, it takes actions that optimize its subjective reward according to its understanding of the task and its relevant causal variables. We apply a method, inverse rational control (IRC), to learn an agent’s internal model and reward function by maximizing the likelihood of its measured sensory observations and actions. This thereby extracts rational and interpretable thoughts of the agent from its behavior. We also provide a framework for interpreting encoding, recoding, and decoding of neural data in light of this rational model for behavior. When applied to behavioral and neural data from simulated agents performing suboptimally on a naturalistic foraging task, this method successfully recovers their internal model and reward function, as well as the Markovian computational dynamics within the neural manifold that represent the task. This work lays a foundation for discovering how the brain represents and computes with dynamic latent variables.
Keywords: cognition, neuroscience, computation, rational, neural coding
Understanding how the brain works requires interpreting neural activity. The behaviorist tradition aims to understand the brain as a black box solely from its inputs and outputs. Modern neuroscience has been able to gain major insights by looking inside the black box, but still largely relates measurements of neural activity to the brain’s inputs and outputs. While this is the basis of both sensory neuroscience and motor neuroscience, most neural activity supports computations and cognitive functions that are left unexplained—we might call these functions “thoughts.” To understand brain computations, we should relate neural activity to thoughts. The trouble is, how does one measure a thought?
We propose to model thoughts as dynamic beliefs that we impute to an animal by combining explainable artificial intelligence (XAI) cognitive models for naturalistic tasks with measurements of the animal’s sensory inputs and behavioral outputs. We define an animal’s task by the relevant dynamics of its world, observations it can make, actions it can take, and the goals it aims to achieve. The XAI models that solve these tasks generate beliefs, their dynamics, and actions that reflect the essential computations needed to solve the task and generate behavior like the animal. With these estimated thoughts in hand, we propose an analysis of brain activity to find neural representations and transformations that potentially implement these thoughts.
Our approach combines the flexibility of complex neural network models while maintaining the interpretability of cognitive models. It goes beyond black-box neural network models that solve one particular task and find representational similarity with the brain (1–3). Instead, we solve a whole family of tasks and then find the task whose solution best describes an animal’s behavior. We then associate properties of this best-matched task with the animal’s mental model of the world and call it “rational” since it is the right thing to do under this internal model of the world. Our method explains behavior and neural activity based on underlying latent variable dynamics, but it improves upon the usual latent variable methods for neural activity that just compress data without regard to tasks or computation (4–6). In contrast, our latent variables inherit meaning from the task itself and from the animal’s beliefs according to its internal model. This provides interpretability to both our behavioral and neural models.
We also want to ensure we can explain crucial neural computations that underlie ecological behavior in natural tasks. We can accomplish this by using tasks with key properties that ensure our model solutions implement these neural computations. First, a natural task should include latent or hidden variables: Animals do not act directly upon their sensory data, as the data are merely an indirect observation of a hidden real world (7). Second, the task should involve uncertainty, since real-world sense data are fundamentally ambiguous and behavior improves when weighing evidence according to its reliability. Third, relationships between latent variables and sensory evidence should be nonlinear in the task, since if linear computation were sufficient, then animals would not need a brain: They could just wire sensors to muscles and compute the same result in one step. Fourth, the task should have relevant temporal dynamics, since actions affect the future; animals must account for this.
While natural tasks that animals perform every day do have these properties, most neuroscience studies isolate a subset of them for simplicity, such as two-alternative forced-choice tasks, multiarmed bandits, or object classification. These have revealed important aspects of neural computation, but miss some fundamental structure of brain computation. Recent progress warrants increasing the naturalism and complexity of the tasks and models.
This paper makes progress toward understanding how the brain produces complex behavior by providing methods to estimate thoughts and interpret neural activity. We first describe a model-based technique we call inverse rational control for inferring latent dynamics which could underlie rational thoughts. Then we offer a theoretical framework about neural coding that shows how to use these imputed rational thoughts to construct an interpretable description of neural dynamics.
We illustrate these contributions by analyzing a task performed by an artificial brain, showing how to test the hypothesis that a neural network has an implicit representation of task-relevant variables that can be used to interpret neural computation. As a case study, we choose a simple but ecologically critical task—foraging—whose solution requires an agent to account for the four crucial properties mentioned above: latent variables, partial observability, nonlinearities, and dynamics. Our general approaches should serve as valuable tools for interpreting behavior and brain activity for real agents performing naturalistic tasks.
Results I: Modeling Behavior as Rational
In an uncertain and partially observable environment, animals learn to plan and act based on limited sensory information and subjective values. To better understand these natural behaviors and interpret their neural mechanisms, it would be beneficial to estimate the internal model and reward function that explains animals’ behavioral strategies. In this paper, we model animals as rational agents acting optimally to maximize their own subjective rewards, but under a family of possibly incorrect assumptions about the world. We then invert this model to infer the agent’s internal assumptions and rewards and estimate the dynamics of internal beliefs. We call this approach inverse rational control (IRC), because we infer the reasons that explain an agent’s suboptimal behavior to control its environment.
This method creates a probabilistic model for an agent’s trajectory of observations and actions and selects model parameters that maximize the likelihood of this trajectory. We make assumptions about the agent’s internal model, namely that it believes that it gets unreliable sensory observations about a world that evolves according to known stochastic dynamics. We assume that the agent’s actions are chosen to maximize its own subjectively expected long-term utility. This utility includes both benefits, such as food rewards, and costs, such as energy consumed by actions; it should also account for internal states describing motivation, like hunger or fatigue, that modulate the subjective utility. Finally, we assume that the agent follows a stationary policy based upon its mental model. This means that we cannot model learning with our method, although we can study adaptation and context dependence as long as our model represents these variables and their dynamics. We use the agent’s sequence of observations and actions to learn the parameters of this internal model for the world. Without a model, inferring both the rewards and latent dynamics is an underdetermined problem leading to many degenerate solutions. However, under reasonable model constraints, we demonstrate that the agent’s reward functions and assumed dynamics can be identified. Our learned parameters include the agent’s assumed stochastic dynamics of the world variables, the reliability of sensory observations about those world states, and subjective weights on action-dependent costs and state-dependent rewards.
Partially Observable Markov Decision Process.
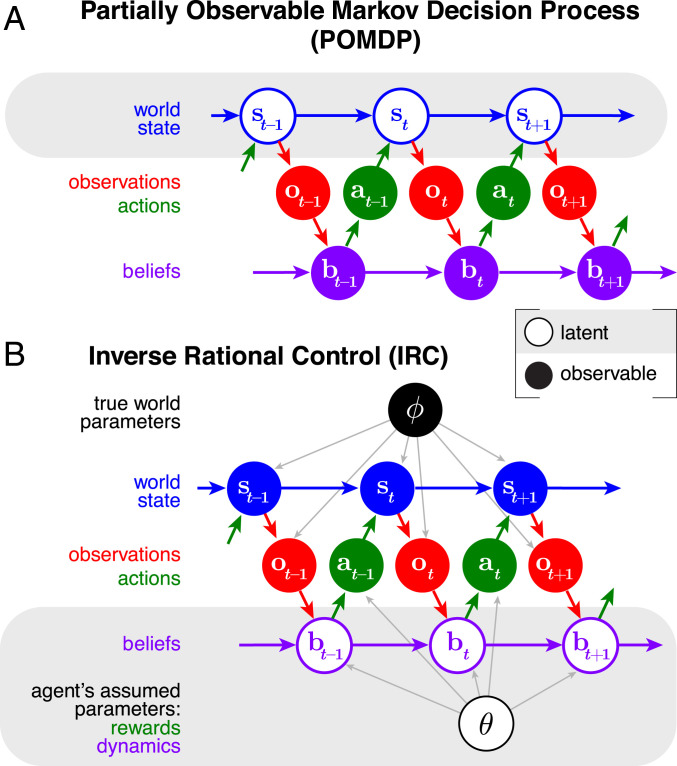
To define the inverse rational control problem, we first formalize the agent’s task as a partially observable Markov decision process (POMDP) (Fig. 1A) (8), a powerful framework for modeling agent behavior under uncertainty. A Markov chain is a temporal sequence of states for which the transition probability to the next state depends only on the current state, not on any earlier ones: . A Markov decision process (MDP) is a Markov chain where an agent can influence the world state transitions by deciding to take an action , changing the transitions to be . At each time step the agent receives a reward or incurs a cost (negative reward) that depends on the world state and action, . The agent aims to choose actions that maximize its value , measured by total expected future reward (negative cost) with a temporal discount factor , so that , where the angle brackets denote an average with respect to the subscripted distribution. Actions are drawn from a state-dependent probability distribution called a policy, , which may be concentrated entirely on one action. In a normal MDP, the agent can fully observe the current world state, but must plan for an unknown future. In a POMDP, the agent again does not know the future, but does not even know the current world state exactly. Instead the agent gets only unreliable observations about it, drawn from the distribution . The agent’s goal is still to maximize the total expected temporally discounted future reward. A POMDP is a tuple of all of these mathematical objects: . Different tuples reflect different tasks.
Fig. 1.
(A and B) Graphical model of a POMDP (A) and the IRC problem (B). Open circles denote latent variables, and solid circles denote observable variables. For the POMDP, the agent knows its beliefs but must infer the world state. For IRC, the scientist knows the world state but must infer the beliefs. The real-world dynamics depend on parameters , while the belief dynamics and actions of the agent depend on parameters , which include both its assumptions about the stochastic world dynamics and observations and its own subjective rewards and costs.
Optimal solution of a POMDP requires the agent to compute a time-dependent posterior probability over the world state , given its history of observations and actions. Knowledge of all of that history can be summarized concisely in a single distribution, the posterior . We consider this to reflect the belief of the agent about its current world state. It is useful to define a more compact belief state as a set of sufficient statistics that completely summarize the posterior, so we can write . This belief state can be expressed recursively using the Markov property as a function of its previous value (SI Appendix, Eq. 1).
We can express the entire partially observed MDP as a fully observed MDP called a belief MDP, where the relevant fully observed state is not the world state but instead the agent’s own belief state (9). To do so, we must reexpress the transitions and rewards as a function of these belief states (SI Appendix, Eqs. 5 and 7). The optimal agent then determines a value function over this belief space and allowed actions, based on its own subjective rewards and costs. This value can be computed recursively through the Bellman equation (10) (SI Appendix, Eq. 8). The optimal policy deterministically selects actions maximizing the state-action value function. An alternative stochastic policy samples actions from a softmax function on value, with a temperature parameter and normalization constant , giving the agent some chance of choosing a suboptimal action. In the limit of a low temperature we recover the optimal policy, but a real agent may be better described by a stochastic policy with some controlled exploration. Similarly, we can introduce stochasticity on top of the belief dynamics dictated by Bayes’ rule, allowing for lapses, gradual forgetting, or bounded rationality.
Inverse Rational Control.
Despite the appeal of optimality, animals rarely appear optimal in experimental tasks and not just by exhibiting more randomness. Short of optimality, what principled guidance can we have about an animal’s actions that would help us understand its brain? One possibility is that an animal is rational—that is, optimal for different circumstances than those being tested. Here we show how to analyze behavior assuming that agents are rational in this sense. The core idea is to parameterize possible strategies of an agent by those tasks under which each one is optimal and find which of those best explains the behavioral data.
We specify a family of POMDPs where each member has its own task dynamics, observation probabilities, and subjective rewards, together constituting a parameter vector . These different tasks yield a corresponding family of optimal agents, rather than a single optimized agent. We then define a log-likelihood over the tasks in this family, given the experimentally observed data and marginalized over the agent’s latent beliefs (Fig. 1B):
| [1] |
In other words, we find a likelihood over which tasks an agent solves optimally. In [1], and are known quantities in the experimental setup that determine the world dynamics. Since they affect only other observed quantities in the graphical model, they do not affect the model likelihood over (SI Appendix).
This mathematical structure connects interpretable models directly to experimentally observable data, allowing us to formalize important scientific problems in behavioral neuroscience. For example, we can maximize the likelihood to find the best interpretable explanation of an animal’s behavior as rational within a model class, as we show below. We can also compare categorically different model classes that attribute to the agent different reward structures or assumptions about the task.
The log-likelihood 1 seems complicated, as it depends on the entire sequence of observations and actions and requires marginalization over latent beliefs. Nonetheless it can be calculated using the Markov property of the POMDP: The actions and observations constitute a Markov chain where the agent’s belief state is a hidden variable. We show that it is possible to exploit this structure to compute this likelihood efficiently (SI Appendix).
Challenges and Solutions for Rationalizing Behavior.
To solve the IRC problem, we need to parameterize the task, beliefs, and policies, and then we need to optimize the parameterized log-likelihood to find the best explanation of the data. This raises practical challenges that we need to address.
Our core idea for interpreting behavior is to parameterize everything in terms of tasks. All other elements of our models are ultimately referred back to these tasks. Consequently, the beliefs and transitions are distributions over latent task variables, the policy is expressed as a function of task parameters and preferences, and the log-likelihood is a function of the task parameters that we assume the agent assumes.
Thus, whatever representations we use for the belief space or policy, we need to be able to propagate our optimization over the task parameters through those representations. This is one requirement for practical solutions of IRC. A second requirement is that we can actually compute the optimal policies.
Efficient representation of general beliefs and transitions is hard since the space of probabilities is much larger than the state space it measures. The belief state is a probability distribution and thus takes on continuous values even for discrete world states. For continuous variables the space of probabilities is potentially infinite-dimensional. This poses a substantial challenge both for machine learning and for the brain, and finding neurally plausible representations of uncertainty is an active topic of research (11–16). We consider two simple methods to solve IRC using lossy compression of the beliefs: discretization or distributional approximation. We then provide a concrete example application in the discrete case.
Discrete beliefs and actions.
If we have a discrete state space, then we can use conventional solution strategies for MDPs. For a small enough world space, we can exhaustively discretize the belief space and then solve the belief MDP problem with standard MDP algorithms (10, 17). In particular, the state-action value function under a softmax policy can be expressed recursively by a Bellman equation, which we solve using value iteration (9, 10). The resultant value function then determines the softmax policy and thereby determines the policy-dependent term in the log-likelihood 1. To solve the IRC problem we can directly optimize this log-likelihood, for example by greedy line search (SI Appendix). An alternative in higher-dimensional problems is to use expectation–maximization to find a local optimum, with a gradient ascent M step (18, 19) that we compute exactly (SI Appendix).
Continuous beliefs and actions.
The computational expense of the discrete solution grows rapidly with problem size and becomes intractable for continuous state spaces and continuous controls. One practical choice is to continually update a finite set of summary statistics as for an extended Kalman filter. Alternatively, it may be tractable to learn and use a more general set of statistics (16). Rational control with continuous actions also requires us to implement a flexible family of continuous policies that map from beliefs to actions. We use deep neural networks to implement these policies (20). Deep-learning methods are commonly used in reinforcement learning to provide flexibility, but they lack interpretability: Information about the policy is distributed across the weights and biases of the network. Crucially, to maintain interpretability, we parameterize this family by the task. Specifically, we provide the model parameters as additional inputs to a policy network, , and train its weights to approximate a family of optimal policies simultaneously over a prior distribution on task parameters (20). This allows the network to generalize its optimal strategies across POMDPs in the task family and allows us to easily maximize the likelihood (Eq. 1) by gradient ascent using autodifferentiation (20).*
Application to Foraging.
We applied our analyses to understand the workings of a neural network performing a foraging task. The task requires an agent to combine unreliable sensory data with an internal memory to infer when and where rewards are available and how to best acquire them. We train an artificial recurrent neural network to solve this task in a suboptimal but rational way and use IRC to infer its assumptions, subjective preferences, and beliefs.
Task description.
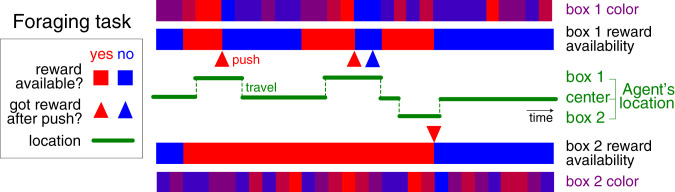
Two locations (“feeding boxes”) have hidden food rewards that appear and disappear according to independent telegraph processes with specified transition probabilities (Fig. 2) (21). The boxes provide unreliable color cues about the current reward availability, ranging from blue (probably unavailable) to red (probably available). There are three possible locations for the agent: the locations of boxes 1 and 2 and a middle location 0. We include a small “grooming” reward for staying at the middle location, to allow the agent to stop and rest. A few discrete actions are available to the agent: It can push a button to open a box to either get the reward or observe its absence, it can move toward a new location, or it can do nothing. Traveling and pushing a button to open the box each have a cost, so the agent does not benefit from repeating fruitless actions. When a button-press action is taken to open a box, any available reward there is acquired. Afterward, the animal knows there is no more food available in the box (since it was either unavailable or consumed) and the belief about food availability in that box is reset to zero. The specific values of these parameters used in our experiments are described in SI Appendix.
Fig. 2.
Illustration of foraging task with latent dynamics and partially observable sensory data. The reward availability in each of the two boxes evolves according to a telegraph process, switching between available (red) and unavailable (blue), and colors give the animal an ambiguous sensory cue about the reward availability. The agent may travel between the locations of the two boxes. When a button is pushed to open a box, the agent receives any available reward.
Neural network agent.
To test the IRC algorithm and our subsequent neural coding analyses, we wanted a synthetic brain for which we could assess the ground truth. We therefore used imitation learning to train a recurrent neural network to reproduce the policy of one rational agent. However, to favor representations that generalize well and are thereby more likely to represent beliefs, we actually trained the network to reproduce optimal policies on a family of tasks. The inputs to this network included not only the sensory observations of location, color cues, and rewards, but also the task parameters (SI Appendix, Fig. S1A). For each task we trained the network output to match the policy of a corresponding “teacher” that optimally solves that POMDP problem (Materials and Methods). After training, the outputs of the neural network closely matched the teachers’ policies (SI Appendix, Fig. S1B). Any task-relevant beliefs that emerge automatically through training (22) are encoded implicitly only in the large population of neurons.
Finally, to impose suboptimality upon our neural network agent, we misled it by providing inputs that specified the wrong set of task parameters : These did not match the parameters of the true test task. When we challenged this simulated rational brain with a foraging task, we obtained a time series of observations , actions , and neural activity . Together these constituted the experimental measurements for our suboptimal agent.
Inverse rational control for foraging.
In our target applications, we do not know the agent’s assumed world parameters, their subjective costs, or the amount of randomness (softmax policy temperature). Our goal is to estimate a simulated agent’s internal model and belief dynamics from its chosen actions in response to its sensory observations. We infer all of these using IRC.
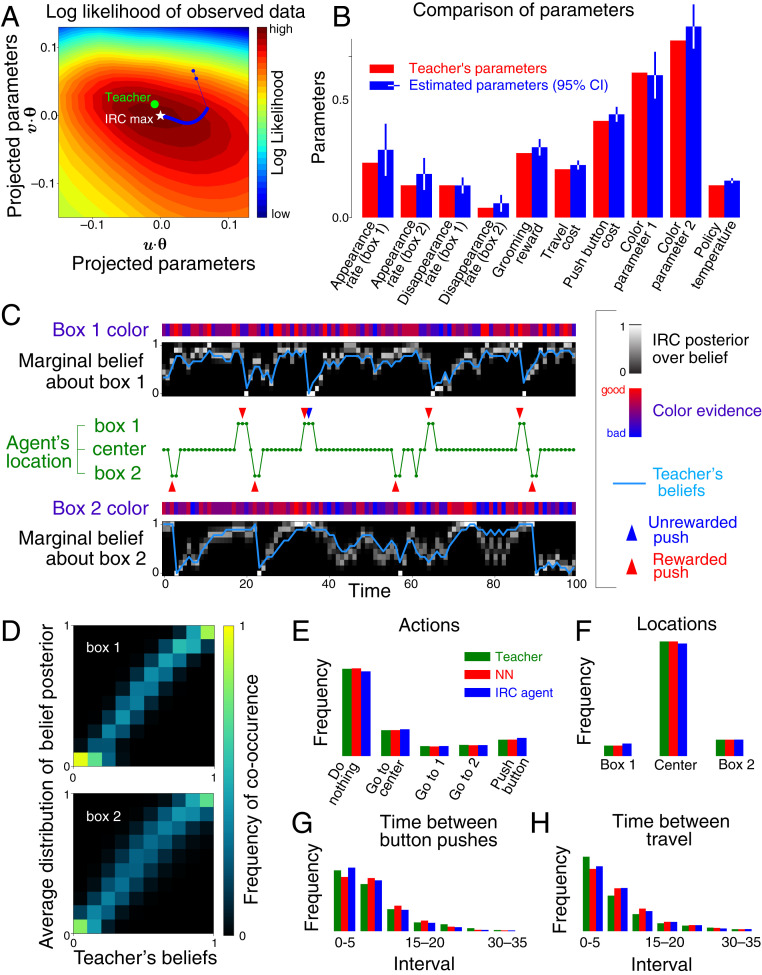
The actions and sensory evidence (color cues, locations, and rewards) obtained by the agent all constitute observations for the experimenter’s learning of the agent’s internal model. Based on 5,000 color observations, 1,595 movements, and 566 button presses, IRC infers the parameters of the internal model that best explain the behavioral data (Fig. 3A). Fig. 3B shows that IRC correctly imputes a rational model to the neural network, whose parameters closely match those of its teacher.
Fig. 3.
Successful recovery of agent model by inverse rational control. The agent was a neural network trained to imitate a suboptimal but rational teacher and tested on a novel task. (A) The estimated parameters converge to the optimal point of the observed data log-likelihood (white star). Since the parameter space is high-dimensional, we project it onto the first two principal components of the learning trajectory for (blue). The estimated parameters differ slightly from the teacher’s parameters (green dot) due to data limitations. (B) Comparison of the teacher’s parameters and the estimated parameters. Error bars show 95% confidence intervals (CI) based on the Hessian of log-likelihood (SI Appendix, Fig. S2). (C) Estimated and the teacher’s true marginal belief dynamics over latent reward availability. These estimates are informed by the noisy color data at each box and the times and locations of the agent’s actions. The posteriors over beliefs are consistent with the dynamics of the teacher’s beliefs (blue line). (D) Teacher’s beliefs versus IRC belief posteriors averaged over all times when the teacher had the same beliefs, . These mean posteriors concentrate around the true beliefs of the teacher. (E–H) Inferred distributions of (E) actions, (F) residence times, (G) intervals between consecutive button-presses, and (H) intervals between movements.
Data limitations imply some discrepancy between the teacher’s true parameters and the estimated parameters which can be reduced with more data. With the estimated parameters, we are able to infer a posterior over the dynamic beliefs (Fig. 3C). (Note that this is an experimenter’s posterior over the agent’s subjective posterior!) Although we do not know what the neural network believes, the inferred posterior is consistent with the imitated teacher’s subjective probabilities of food availability in each box. The inferred distributions over beliefs reveal strong correlations between the belief states of the teacher and the belief states imputed to the neural network (Fig. 3D).
Fig. 3 E–H shows that the teacher, the artificial brain, and the inferred agent choose actions with similar frequencies, occupy the three locations for the same fraction of time, and wait similar amounts of time between pushing buttons or traveling. This demonstrates that the IRC-derived agent generates behaviors that are consistent with behaviors of the agent from which it learned.
Results II: Neural Coding
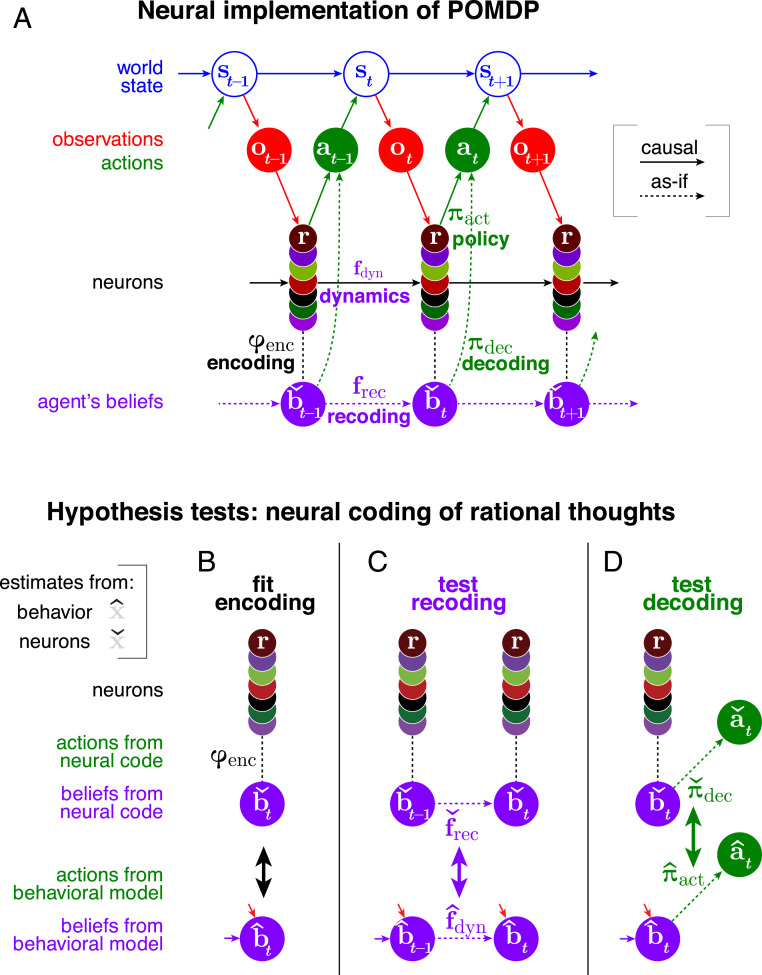
We do not presume that any real brain explicitly calculates a solution to the Bellman equation, but rather learns a policy by combining experience and mental modeling. We assume that, with enough training, the result is an agent that behaves “as if” it were solving the POMDP (Fig. 4A). Next, we present a framework for understanding brain computations that could implement such behaviors.
Fig. 4.
Schematic for analyzing a dynamic neural code. (A) Graphical model of a POMDP problem with a solution implemented by neurons implicitly encoding beliefs. (B) We find how behaviorally relevant variables (here, beliefs) are encoded in measured neural activity through the function . (C) We then test our hypothesis that the brain recodes its beliefs rationally by testing whether the dynamics of the behaviorally estimated belief match the dynamics of the neurally estimated beliefs , as expressed through the update dynamics and recoding function . (D) Similarly, we test whether the brain decodes its beliefs rationally by comparing the behaviorally and neurally derived policies and . Quantities estimated from behavior or from neurons are denoted by up-pointing or down-pointing hats, and , respectively (SI Appendix, Table S1).
To move toward more interpretable computations, our analysis does not focus on neural responses, but rather on the task-relevant information encoded in those responses. Targeted dimensionality reduction abstracts away the fine details of the neural signals in favor of an algorithmic- or representational-level description. This decreases how many parameters characterize the dynamics, substantially reducing overfitting. More importantly, it can avoid the massive degeneracies inherent in neuron-level mechanisms: Different neural networks could have entirely different neural dynamics but could share the task-relevant computations. This indicates how a deeper, more invariant understanding of neural computations is more possible at the algorithmic level than at the mechanistic level (23).
Analysis of the linked processes of encoding, recoding, and decoding can help interpret task-relevant computations. These processes correspond to representation, dynamics, and action. The brain’s “encoding” specifies the task-relevant and -irrelevant coordinates of neural activity (Fig. 4B). “Recoding” describes how that encoding is transformed over time and space by neural processing (Fig. 4C). “Decoding” describes how those estimates predict future actions (Fig. 4D).†
The neural coding framework makes one crucial assumption: The neural data must be sufficient to capture the task-relevant neural processes. The important aspects are different for encoding, recoding, and decoding. To describe the encoding, we need to measure the right neurons at the right resolution to be sensitive to the task-relevant properties, which may include nonlinear statistics (24, 25) and will certainly exhibit some variability (26). To describe the recoding accurately, all measured changes in neural state must depend only on the current state. In other words, the measured neural dynamics should be Markovian. Markovian dynamics are an essential property of any causal system. To describe decoding accurately, we must measure the neural signals that eventually drive the behavior. If the chosen state space lacks any of this relevant information due to missing neurons, slow measurements, lossy postprocessing, etc., then we will see unexplainable variability in the encoded variables, recoding dynamics, and decoded actions.
As long as we do measure the right signals, our neural coding framework applies equally well to spiking, multiunit activity, calcium concentration, neurotransmitter concentration, local field potentials, conventional frequency bands, or any other signals hypothesized to contain task-relevant information. For example, if distinct neural frequency bands encode distinct information or interactions, then slow firing rates alone will not be sufficient to capture dynamics. Nonetheless, in such cases we may be able to construct a sufficient state space by augmenting the neural states, for example by explicitly including multiple frequency bands or the recent firing-rate history.
Once we fit a neural encoding, we subsequently concentrate only on the task-relevant coordinates specified by that encoding. By construction, this level of explanation need not capture every facet of neural responses nor the physical mechanism by which they evolve. Nonetheless, it would be great progress if we can account for stimulus- and action-dependent neural dynamics within task-relevant coordinates (27) that explain how temporal sequences of sensory signals interact in the brain and predict behavior. Although this “as if” description cannot legitimately claim to be causal, it can be promoted to a causal description since it does provide useful predictions for causal tests about what neural features should influence computation and action (28, 29).
Just as a complete description of neural mechanisms requires those dynamics to be Markovian, a complete lower-dimensional description of task-relevant computations also requires that the dynamics are Markovian. In other words, we seek task-relevant coordinates whose updates depend only on those coordinates. Otherwise we will again find unexplained variability in the task-relevant dynamics (SI Appendix, Fig. S3) or actions.
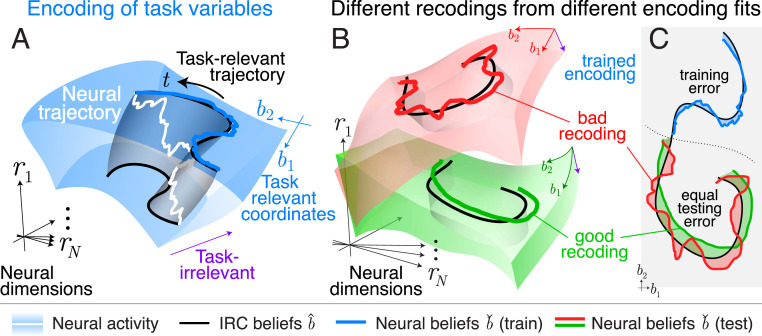
Fig. 5 provides a conceptual illustration of the geometry of task-relevant and -irrelevant coordinates in neural activity space and the types of errors that can occur when measuring task-relevant neural computation. Neural activity occupies a manifold of much lower dimension than the ambient space of all possible neural responses (30). Within that manifold there is further structure, with task-relevant variables tracing out submanifolds related to each other by task-irrelevant neural variations.
Fig. 5.
Conceptual illustration of encoding and recoding. (A) Neural responses inhabit a manifold (blue volume, here three-dimensional) embedded in the high-dimensional space of all possible neural responses. A neural encoding model divides this manifold into task-relevant and -irrelevant coordinates (blue and purple axes). We must estimate these coordinates from training data, given some inferred task-relevant targets . According to this encoding, many activity patterns can correspond to the same vector of task variables . Any particular neural trajectory (white curve) is just one of many that would trace out the same task-relevant projection (black curves). The set of all neural activities consistent with one task-relevant trajectory therefore spans a manifold (gray ribbon). (B) After fitting an estimator of the task variables using training data, we can measure how well the encoding describes the task variables in a new testing dataset. Different encodings (red and green volumes) divide the same neural manifold differently into relevant and irrelevant coordinates, and the task variables estimated from these neural encodings (red and green curves) will deviate in different ways from the variables inferred from behavior (black). (C) The testing error of these neurally derived task variables (red, green) will be larger than the training error (blue). Task-relevant variables derived from different encoding models may have the same total errors, but may nonetheless have different recoding dynamics. Here the smoother green dynamics are closer to the behaviorally inferred dynamics than the rougher red dynamics, which implies that these task-relevant dimensions better capture the computations implied by inverse rational control. SI Appendix, Fig. S3 provides more detail of good and bad recodings.
In principle, this framework can apply to many different tasks and computations. For concreteness, here we present our analysis using the computations and variables inferred by inverse rational control. The inferred internal model allows us to impute the agent’s time-dependent beliefs about the partially observed world state . Such a belief vector might include the full posterior over the world state, as we used for the discrete IRC above, or a point estimate of the world state and a measure of uncertainty about it, say a covariance , as in the Gaussian approximation we have used for continuous IRC (20). To us, as scientists, the agent’s beliefs are latent variables, so our algorithm can at best create a posterior over those beliefs or a point estimate indicating the most probable belief. Here we base our analyses on a point estimate over beliefs. Below we describe our general analysis approach and apply it to understand the neural computations implemented during foraging by the simulated brain.
Encoding.
Given beliefs imputed by IRC, we can estimate how they are encoded in the neural responses . An encoding defines a response distribution , which determines both task-relevant and -irrelevant coordinates (Fig. 5A). To find what is encoded by this probabilistic mapping, we use a (potentially nonlinear) readout function fitted to minimize the discrepancy between the behavioral target belief and the neural estimate (Fig. 4B).‡After training to match the behavioral targets and ignore task-irrelevant aspects of the neural responses, we can then cross-validate it on new estimates from fresh neural data. Since data are finite and noisy, the models invariably have some errors caused by deviations between the estimated task-relevant coordinates and the true ones. These errors are smaller for the training data and larger for fresh testing data. Fits from different encoding models partition the neural manifold differently and will thus generally have different testing errors (Fig. 5B).
Recoding.
Recoding describes the changes in a neural encoding. While neural dynamics may affect every dimension of neural activity, we focus only on the low-dimensional, interpretable dynamics within the neural manifold. By construction, those dynamics reflect the changes in the agent’s beliefs.
The rational control model predicts that beliefs are updated by sensory observations and past beliefs, with interactions that are determined by the internal model according to a function , where and reflect the task-relevant and -irrelevant parts of the dynamics (the latter absorbs stochastic components as well as deterministic components that depend on uncontrolled task-irrelevant dimensions; Fig. 5 and SI Appendix, Fig. S3). If our neural analysis correctly identifies dynamics responsible for behavior, then the beliefs estimated from the neural encoding should be recoded over time following those same update rules. We estimate this neural recoding function directly from the sequence of neurally estimated beliefs by minimizing differences between the actual and predicted future neural beliefs. We then compare to the update dynamics posited by the behavioral model (Fig. 4C). (Note that we should compare these only over the distribution of experienced beliefs, i.e., those beliefs for which the recoding function matters in practice.) Agreement between the behavioral belief dynamics and the neurally derived belief dynamics implies that we have successfully understood the recoding process. Even for good encoding models this is not guaranteed, since activity outside the encoding coordinates could influence the neural dynamics: Two different fitted encoding models could provide equal reconstruction errors, and yet because of limited data or model mismatch only one has neural dynamics that match the behaviorally derived dynamics (Fig. 5 B and C).
Decoding.
These encodings and recodings do not matter if the brain never decodes that information into behavior. We can evaluate how the brain uses its information by fitting a policy to predict observed actions directly from the neurally encoded beliefs. We then test the hypothesis that the brain decodes neurally encoded rational thoughts by comparing that neutrally derived policy against the behavioral policy, (Fig. 4D).
Application to Simulated Foraging Agent.
Fig. 6 presents the results of applying this neural coding framework to look inside the brain of our simulated agent while it forages.
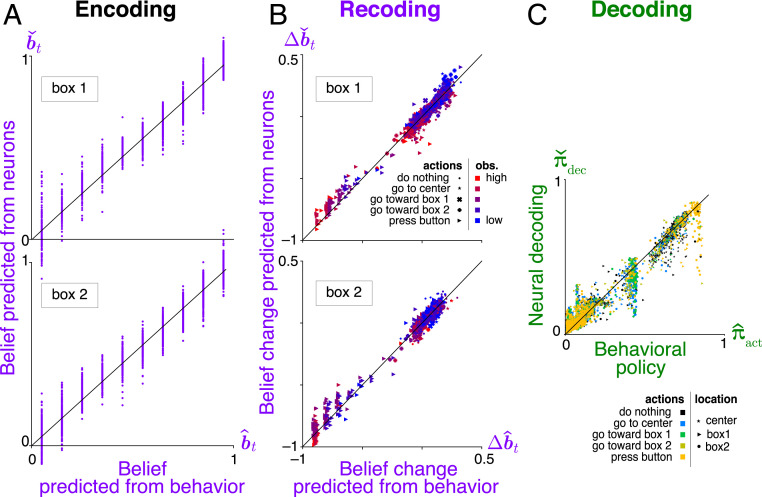
Fig. 6.
Analysis of neural coding of rational thoughts. (A) Encoding: Neurally derived beliefs match behaviorally derived beliefs based on IRC. Cross-validated neural beliefs are estimated from testing neural responses using a linear estimator, , with the weight matrix fitted from separate training data. (B) Recoding: Belief updates from the neural recoding function match the corresponding belief updates from the task dynamics . Neural updates are estimated using nonlinear regression with radial basis functions (Materials and Methods). (C) Decoding: The policy predicted by decoding neural beliefs approximately matches the policy estimated from behavior by IRC. Neural policy is estimated from actions and neural beliefs using nonlinear multinomial regression (Materials and Methods).
To evaluate the encoding for our synthetic brain, we assume that beliefs are linearly encoded instantaneously in neural activity . After performing linear regression of behaviorally derived beliefs against neural activity , we can estimate other beliefs from previously unseen neural data. Fig. 6A shows that these beliefs estimated from neural data are accurate.
Fig. 6B shows that the recoding dynamics obtained from the neural belief dynamics also match the dynamics described by the rational model. We characterize these neural dynamics using kernel ridge regression between and (Materials and Methods). The resultant temporal changes in the neutrally derived beliefs agree with the corresponding changes in the behavioral model beliefs, . Although some of these changes are driven directly by the sensory observations (colors), that only explains part of the belief updates: Even conditioned on a given sensory input at one time, the updates agree between the neurons and the behavioral model. This provides evidence that we understand the internal model that governs recoding at the algorithmic level.
To account for the discrete actions space, our example analysis of neural decoding uses nonlinear multinomial regression to fit the probabilities of allowed actions as a function of neurally derived beliefs (Materials and Methods). The resultant decoding function and the rational policy match well (Fig. 6C), providing evidence that we understand the decoding process by which task-relevant neural activity generates behavior.
Discussion
This paper presents an explainable AI paradigm to infer an internal model, latent beliefs, and subjective preferences of a rational agent that solves a complex dynamic task described as a partially observable Markov decision process. We fitted the model by maximizing the likelihood of the agent’s sensory observations and actions over a family of tasks. We then described a neural coding framework for testing whether the imputed latent beliefs encoded in a low-dimensional manifold of neural responses are recoded and decoded in a manner consistent with this behavioral model. We demonstrated these two contributions by analyzing the neural coding of an implicit computational model by an artificial neural network trained to solve a simple foraging task requiring memory, evidence integration, and planning. Our method successfully recovered the agent’s internal model and subjective preferences and found neural computations consistent with that rational model.
Related Work.
Our approach generalizes previous work in artificial intelligence on the inverse problem of learning agents by observing behavior. Methodologically, other studies of inverse problems address parts of inverse rational control, typically with the goal of getting artificial agents to solve tasks by learning from demonstrations of expert behavior. Inverse reinforcement learning (IRL) tackles the problem of learning how an agent judges rewards and costs based on observed actions (31), but assumes a known dynamics model (19, 32). This approach has even been applied to learn the computational goal of a recurrent network (33). Conversely, inverse optimal control (IOC) learns the agent’s internal model for the world dynamics (34) and observations (35), but assumes the reward functions. In refs. 36 and 37 both reward function and dynamics were learned, but only the fully observed MDP case is explored. We solve the natural but more difficult partially observed setting and ensure these solutions provide a scientific basis for interpreting animal behavior.
As a cognitive theory, by positing a rational but possibly mistaken agent, our approach resembles Bayesian theory of mind (BToM) (38–43). Previous work in BToM has considered tasks with uncertainty about static latent variables that were unknown until fully observed (43) or tasks with partially observed variables but simpler trial-based structure (38, 39). Here we allow for a more natural world, with dynamic latent variables and partial observability, and we infer models where agents make long-term plans and choose sequences of actions. Where prior work in BToM learned subjective rewards (43) or internal models (41), our inverse rational control infers both internal models and subjective preferences in a partially observable world.
BToM studies have focused on models of behavior, whereas we aim to connect dynamic model computations to brain dynamics. Some work has posited a POMDP model for behavior and hypothesized how specific brain regions might implement the relevant computations (44). Here we demonstrate an analysis framework to test such connections, by examining neural representations of latent variables and showing how computational functions could be embodied by low-dimensional neural dynamics.
While low-dimensional neural dynamics are an important topic for studies of large-scale neural activity (1, 5, 6, 30), few have been able to relate these dynamic activity patterns to interpretable latent model variables. Far more commonly, these low-dimensional manifolds are attributed to an intrinsically generated manifold (27, 45) or are related to measurable quantities like sensory inputs or behavioral outputs (1, 46, 47). Population activity in the visual system is known to relate to latent representations of deep networks (2, 3). While this shows that many task-relevant features extracted by machine-learning solutions are also task relevant for the visual system, these features account for neither temporal dynamics nor uncertainty, nor are they readily interpretable (48). Our model-based analysis of population activity is currently our best bet for finding interpretable computational principles.
Limitations and Generalizations.
We demonstrated our approach to understanding cognition and neural computation by applying it to a task involving multiple important features, namely partially observable latent variables with structured dynamics requiring nonlinear computation. However, this foraging task is still fairly simple. Our conceptual framework is much more general and should be able to scale to more complex tasks. As we showed, it can model common errors of cognitive systems, such as inferring false beliefs derived from incorrect or incomplete knowledge of task parameters. But it can also be used to infer incorrect structure within a given model class. For example, it is natural for animals to assume that some aspects of the world, such as reward rates at different locations, are not fixed, even if an experiment actually uses fixed rates (49). Similarly, an agent may have a superstition that different reward sources are correlated even when they are independent in reality. Given a model class that includes such counterfactual relationships between task variables, our method can test whether an agent holds these incorrect assumptions. Our framework can also be generalized to cases of bounded rationality (50) by incorporating additional internal representational or computational constraints, such as metabolic costs (51) or architectural constraints (52). However, our approach does use model-based reinforcement learning and thus does require a model. Like any model-based algorithm, it can explain only behaviors we can represent by states and policies that the model can generate. Moreover, even if the model can express some policies in principle, it must be able to learn that family of policies in practice. This can pose challenges that modern reinforcement learning methods are making rapid progress in overcoming.
When there are insufficient data to distinguish possible rational models, we may recover a sloppy model (53, 54) for which multiple combinations of parameters have nearly the same likelihood (Eq. 1). The curvatures of the observed data log-likelihood (SI Appendix, Fig. S2) show that our models were sufficiently constrained that all parameters were identifiable, although some combinations produced more optimistic beliefs compensated by higher action costs to generate similar action sequences.
Our core assumption for the behavioral model is that animals assume the world is Markovian, which leads them to use stationary policies. What if they do not, due to a changing task or motivation? By including additional latent states, such as slow context variables or an internal motivation state, we may recover a stationary policy, and then our approach is again applicable. That said, this will be a poor model while the animal is learning something for the first time, and a higher-level rational learning model will be required.
Our approach to creating interpretable rational models requires that the policy receives inputs that are themselves interpretable and rational, regardless of whether the policy is implemented as an explicit POMDP solution or as a neural network trained to optimality on the task family. Here our inputs were belief states that fully summarize the posterior over the current world state. While maintaining interpretability we could also deliberately allow worse probabilistic representations, as long as we choose a model class that specifies their structure. For instance, we could permit hypotheses of factorized posteriors, tractable variational families (39, 55), random statistics (16, 56, 57), or limited sampling (12, 58, 59). In addition, we could hypothesize approximate inference algorithms associated with these belief representations (60, 61). Among these hypotheses, IRC could be used to find and compare the likelihoods of observed action trajectories given rational agents with those structured assumptions.
In more complex tasks, simplifying assumptions are likely to be as crucial for the brain as they are for any algorithm: As the number of task-relevant variables grows, the dimensionality of the full belief space grows prohibitively. In addition to the structured approximations mentioned above, representation learning (62) can provide compressed representations of sensory histories that are useful for performing tasks. In good cases it can learn to represent sufficient statistics over world states that are needed to guide actions and obtain rewards. Large-scale tasks are now being solved with expressive neural networks (63, 64) that provide rich state representations, but may not permit interpretation. This may be an unavoidable limitation in a world of complex structure (65, 66). Or, near any solution found by machine-learning optimization, there may be other solutions that perform similarly while retaining interpretability (67). Additionally, solutions that match the causal structure of the environment are naturally more interpretable and tend to generalize better (68, 69) and thus may be favored by biological learning. It may be that the uninterpretable representations found by brute-force model-free machine learning are insufficiently constrained and that richer tasks, multitask training, and priors favoring sparse causal interactions may bias networks toward more human-interpretable representations (67, 69–71) that relate more closely to actionable latent variables.
Conclusion.
The success of our methods on simulated agents suggests they could be fruitfully applied to experimental data from real animals performing such foraging tasks (21, 72) or to richer tasks requiring even more sophisticated computations. XAI models help construct belief states and dynamics needed to solve interesting tasks. This will provide useful targets for interpreting dynamic neural activity patterns, which in turn could help identify the neural substrates of thought.
Materials and Methods
Inverse Rational Control.
Full mathematical details for IRC, the foraging task, and neural network training are available in SI Appendix. Parameters were selected to expose interesting behaviors, such as balancing the relevance of predictable dynamics with sensory cues. Code for the discrete case is available at https://github.com/XaqLab/IRC_TwoSiteForaging.
Neural Coding Analysis.
Encoding.
We find an encoding matrix by regressing against . This produces neural estimates of task-relevant variables for new data.
Recoding.
We find dynamics by regressing against with kernel ridge regression. The kernel functions are radial basis functions with centers on discretized target beliefs and a width at half-max equal to the spacing between discrete beliefs. This yields the recoding function representing the nonlinear dynamics of the neural beliefs. We compare the belief updates from the recoding function and the corresponding belief updates from the task dynamics .
Decoding.
We compute the brain’s decoding function, i.e., an approximate policy , using nonlinear multinomial regression of against with the same radial basis functions as used in recoding. We use a feature space of radial basis functions with centers on a grid over beliefs, with width equal to the center spacing, and an outer product space over locations.
Supplementary Material
Acknowledgments
We thank Dora Angelaki, Baptiste Caziot, Valentin Dragoi, Krešimir Josić, Zhe Li, Rajkumar Raju, and Neda Shahidi for useful discussions. Z.W., P.S., and X.P. were supported in part by BRAIN Initiative National Institutes of Health Grant 5U01NS094368. Z.W. and X.P. were supported in part by an award from the McNair Foundation. S.D. and X.P. were supported in part by the Simons Collaboration on the Global Brain Award 324143 and National Science Foundation (NSF) 1450923 BRAIN 43092. X.P. and M.K. were supported in part by NSF CAREER Award IOS-1552868.
Footnotes
The authors declare no competing interest.
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “Brain Produces Mind by Modeling,” held May 1–3, 2019, at the Arnold and Mabel Beckman Center of the National Academies of Sciences and Engineering in Irvine, CA. NAS colloquia began in 1991 and have been published in PNAS since 1995. From February 2001 through May 2019, colloquia were supported by a generous gift from The Dame Jillian and Dr. Arthur M. Sackler Foundation for the Arts, Sciences, & Humanities, in memory of Dame Sackler’s husband, Arthur M. Sackler. The complete program and video recordings of most presentations are available on the NAS website at http://www.nasonline.org/brain-produces-mind-by.
This article is a PNAS Direct Submission.
Data deposition: Code for the discrete case in this paper is available in Github at https://github.com/XaqLab/IRC_TwoSiteForaging.
*Even when the policy is implemented by a neural network, there is no need for that network architecture to match the architecture of the brain it aims to interpret, as long as it can be trained to match an optimal input–output function from beliefs to actions for the relevant task family.
†In our use of the term decoding, we are taking the brain’s perspective. The term more often reflects the scientist’s perspective, where the scientist decodes brain activity to estimate encoding quality. Instead, we reserve the term decoding to describe how neural activity affects actions: We say that the brain decodes its own activity to generate behavior.
‡Estimates based on the behavioral model are consistently denoted by an up-pointing hat, , as distinguished from estimates based on the neural responses denoted by a down-pointing hat, , as indicated in SI Appendix, Table S1.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.1912336117/-/DCSupplemental.
Data Availability.
No data are associated with this paper.
References
- 1.Mante V., Sussillo D., Shenoy K. V., Newsome W. T., Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kriegeskorte N., Deep neural networks: A new framework for modeling biological vision and brain information processing. Annu. Rev. Vision Sci. 1, 417–446 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Yamins D. L. K., et al. , Performance-optimized hierarchical models predict neural responses in higher visual cortex. Proc. Natl. Acad. Sci. U.S.A. 111, 8619–8624 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Gao Y., Archer E. W., Paninski L., Cunningham J. P., “Linear dynamical neural population models through nonlinear embeddings” in NeurIPS, Lee D. D., Sugiyama M., Luxburg U. V., Guyon I., Garnett R., Eds. (Curran Associates, Inc., 2016), pp. 163–171. [Google Scholar]
- 5.Chaudhuri R., Gercek B., Pandey B., Peyrache A., Fiete I., The population dynamics of a canonical cognitive circuit. bioRxiv:516021 (9 January 2019). [DOI] [PubMed]
- 6.Whiteway M. R., Butts D. A., The quest for interpretable models of neural population activity. Curr. Opin. Neurobiol. 58, 86–93 (2019). [DOI] [PubMed] [Google Scholar]
- 7.Plato A. B., Adam K., The Republic (Basic Books, 2016). [Google Scholar]
- 8.Sutton R. S., Barto A. G., Reinforcement Learning: An Introduction (MIT Press, 2018). [Google Scholar]
- 9.Pack Kaelbling L., Littman M. L., Moore A. W., Reinforcement learning: A survey. J. Artif. Intell. Res. 4, 237–285 (1996). [Google Scholar]
- 10.Bellman R., Dynamic Programming (Princeton University Press, 1957). [Google Scholar]
- 11.Lee T. S., Mumford D., Hierarchical Bayesian inference in the visual cortex. J. Opt. Soc. Am. A 20, 1434–1448 (2003). [DOI] [PubMed] [Google Scholar]
- 12.Berkes P., Orban G., Lengyel M., Fiser J., Spontaneous cortical activity reveals hallmarks of an optimal internal model of the environment. Science 331, 83–87 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ma W. J., Beck J. M., Latham P. E., Pouget A., Bayesian inference with probabilistic population codes. Nat. Neurosci. 9, 1432–1438 (2006). [DOI] [PubMed] [Google Scholar]
- 14.Savin C., Deneve S., “Spatio-temporal representations of uncertainty in spiking neural networks” in NeurIPS, Ghahramani Z., Welling M., Cortes C., Lawrence N. D., Weinberger K. Q., Eds. (Curran Associates, Inc., 2014), pp. 2024–2032. [Google Scholar]
- 15.Raju R. V., Pitkow Z., “Inference by reparameterization in neural population codes” in NeurIPS, Lee D. D., Sugiyama M., Luxburg U. V., Guyon I., Garnett R., Eds. (Curran Associates, Inc., 2016), pp. 2029–2037. [Google Scholar]
- 16.Vértes E., Sahani M., “Flexible and accurate inference and learning for deep generative models” in NeurIPS, Bengio S., Wallach H., Larochelle H., Grauman K., Cesa-Bianchi N., Garnett R., Eds. (Curran Associates, Inc., 2018), pp. 4166–4175. [Google Scholar]
- 17.Howard R. A., Dynamic Programming and Markov Processes (Wiley for The Massachusetts Institute of Technology, 1964). [Google Scholar]
- 18.Dempster A. P., Laird N. M., Rubin D. B., Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. B 39, 1–38 (1977). [Google Scholar]
- 19.Babes M., Marivate V., Subramanian K., Littman M. L., “Apprenticeship learning about multiple intentions” in Proceedings of the 28th International Conference on Machine Learning (ICML-11), Getoor L., Scheffer T., Eds. (ACM, 2011), pp. 897–904. [Google Scholar]
- 20.Daptardar S., Paul S., Pitkow X., Inverse rational control with partially observable nonlinear dynamics. arXiv:1908.04696 (13 August 2019). [PMC free article] [PubMed]
- 21.Sugrue L. P., Corrado G. S., Newsome W. T., Matching behavior and the representation of value in the parietal cortex. Science 304, 1782–1787 (2004). [DOI] [PubMed] [Google Scholar]
- 22.Orhan A. E., Ma W. J., Efficient probabilistic inference in generic neural networks trained with non-probabilistic feedback. Nat. Commun. 8, 138 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Marr D., Vision: A Computational Investigation into the Human Representation and Processing of Visual Information (MIT Press, 1982). [Google Scholar]
- 24.Shamir M., Sompolinsky H., Nonlinear population codes. Neural Comput. 16, 1105–1136 (2004). [DOI] [PubMed] [Google Scholar]
- 25.Yang Q., Pitkow X. S., Revealing nonlinear neural decoding by analyzing choices. bioRxiv:332353 (28 May 2018). [DOI] [PMC free article] [PubMed]
- 26.Moreno-Bote R., et al. , Information-limiting correlations. Nat. Neurosci. 17, 1410–1417 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chaudhuri R., Gerçek B., Pandey B., Peyrache A., Fiete I., The intrinsic attractor manifold and population dynamics of a canonical cognitive circuit across waking and sleep. Nat. Neurosci. 22, 1512–1520 (2019). [DOI] [PubMed] [Google Scholar]
- 28.Sadtler P. T., et al. , Neural constraints on learning. Nature 512, 423–426 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Semedo J. D., Zandvakili A., Machens C. K., Byron M. Y., Kohn A., Cortical areas interact through a communication subspace. Neuron 102, 249–259 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Stringer C., Pachitariu M., Steinmetz N., Carandini M., Harris K. D., High-dimensional geometry of population responses in visual cortex. Nature 571, 361–365 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Russell S., “Learning agents for uncertain environments” in Proceedings of the Eleventh Annual Conference on Computational Learning Theory, Bartlett P. L., Mansour Y., Eds. (ACM, 1998), pp. 101–103. [Google Scholar]
- 32.Choi J., Kim K.-E., Inverse reinforcement learning in partially observable environments. J. Mach. Learn. Res. 12, 691–730 (2011). [Google Scholar]
- 33.Chalk M., Tkačik G., Marre O., Inferring the function performed by a recurrent neural network. bioRxiv:598086 (5 April 2019). [DOI] [PMC free article] [PubMed]
- 34.Dvijotham K., Todorov E., “Inverse optimal control with linearly-solvable MDPs” in Proceedings of the 27th International Conference on Machine Learning (ICML-10), Fürnkranz J., Joachims T., Eds. (Omnipress, 2010), pp. 335–342. [Google Scholar]
- 35.Schmitt F., Bieg H.-J., Herman M., Rothkopf C. A., “I see what you see: Inferring sensor and policy models of human real-world motor behavior” in Thirty-First AAAI Conference on Artificial Intelligence, Singh S., Markovitch S., Eds. (Association for the Advancement of Artificial Intelligence, 2017), pp. 3797–3803. [Google Scholar]
- 36.Herman M., Gindele T., Wagner J., Schmitt F., Burgard W., “Inverse reinforcement learning with simultaneous estimation of rewards and dynamics” in Artificial Intelligence and Statistics, Gretton A., Robert C. C., Eds. (Proceedings of Machine Learning Research, 2016), pp. 102–110. [Google Scholar]
- 37.Reddy S., Dragan A. D., Levine S., Where do you think you’re going? Inferring beliefs about dynamics from behavior. arxiv:1805.08010 (21 May 2018).
- 38.Daunizeau J., et al. , Observing the observer (I): Meta-Bayesian models of learning and decision-making. PLoS One 5, e15554 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Houlsby N. M. T., et al. , Cognitive tomography reveals complex, task-independent mental representations. Curr. Biol. 23, 2169–2175 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Baker C., Saxe R., Tenenbaum J., “Bayesian theory of mind: Modeling joint belief-desire attribution” in Proceedings of the Annual Meeting of the Cognitive Science Society, Carlson L. A., Hoelscher C., Shipley T. F., Eds. (Cognitive Science Society, 2011), vol. 33. [Google Scholar]
- 41.Rafferty A. N., LaMar M. M., Griffiths T. L., Inferring learners’ knowledge from their actions. Cognit. Sci. 39, 584–618 (2015). [DOI] [PubMed] [Google Scholar]
- 42.Khalvati K., Rao R. P., “A Bayesian framework for modeling confidence in perceptual decision making” in NeurIPS, Cortes C., Lawrence N. D., Lee D. D., Sugiyama M., Garnett R., Eds. (Curran Associates, Inc., 2015), pp. 2413–2421. [Google Scholar]
- 43.Baker C. L., Jara-Ettinger J., Saxe R., Tenenbaum J. B., Rational quantitative attribution of beliefs, desires and percepts in human mentalizing. Nat. Hum. Behav. 1, 0064 (2017). [Google Scholar]
- 44.Rao R. P. N., Decision making under uncertainty: A neural model based on partially observable Markov decision processes. Front. Comput. Neurosci. 4, 146 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tsodyks M., Kenet T., Grinvald A., Arieli A., Linking spontaneous activity of single cortical neurons and the underlying functional architecture. Science 286, 1943–1946 (1999). [DOI] [PubMed] [Google Scholar]
- 46.Churchland M. M., et al. , Neural population dynamics during reaching. Nature 487, 51–56 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Musall S., Kaufman M. T., Juavinett A. L., Gluf S., Churchland A. K., Single-trial neural dynamics are dominated by richly varied movements. bioRxiv:308288 (18 April 2019). [DOI] [PMC free article] [PubMed]
- 48.Zeiler M. D., Fergus R., “Visualizing and understanding convolutional networks” in European Conference on Computer Vision, Fleet D. J., Pajdla T., Schiele B., Tuytelaars T., Eds. (Springer, 2014), pp. 818–833. [Google Scholar]
- 49.Glaze C. M., Filipowicz A. L. S., Kable J. W., Balasubramanian V., Gold Joshua I., A bias–variance trade-off governs individual differences in on-line learning in an unpredictable environment. Nat. Hum. Behav. 2, 213–224 (2018). [Google Scholar]
- 50.Simon H. A. “Bounded rationality” in Utility and Probability, Eatwell J., Milgate M., Newman P., Eds. (Springer, 1990), pp. 15–18. [Google Scholar]
- 51.Laughlin S. B., Energy as a constraint on the coding and processing of sensory information. Curr. Opin. Neurobiol. 11, 475–480 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Bullmore E., Sporns O., The economy of brain network organization. Nat. Rev. Neurosci. 13, 336–349 (2012). [DOI] [PubMed] [Google Scholar]
- 53.Prinz A. A., Bucher D., Marder E., Similar network activity from disparate circuit parameters. Nat. Neurosci. 7, 1345–1352 (2004). [DOI] [PubMed] [Google Scholar]
- 54.Gutenkunst R. N., et al. , Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 3, e189 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Parr T., Markovic D., Kiebel S. J., Friston K. J., Neuronal message passing using mean-field, Bethe, and marginal approximations. Sci. Rep. 9, 1–18 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Pitkow X., “Compressive neural representation of sparse, high-dimensional probabilities” in NeurIPS, Pereira F., Burges C. J. C., Bottou L., Weinberger K. Q., Eds. (Curran Associates, Inc., 2012), pp. 1349–1357. [Google Scholar]
- 57.Maoz O., Saleh Esteki M., Tkacik G., Kiani R., Schneidman E., Learning probabilistic representations with randomly connected neural circuits. bioRxiv:478545 (27 November 2018). [DOI] [PMC free article] [PubMed]
- 58.Vul E., Goodman N., Griffiths T. L., Tenenbaum J. B., One and done? Optimal decisions from very few samples. Cognit. Sci. 38, 599–637 (2014). [DOI] [PubMed] [Google Scholar]
- 59.Haefner R. M., Berkes P., Fiser J., Perceptual decision-making as probabilistic inference by neural sampling. Neuron 90, 649–660 (2016). [DOI] [PubMed] [Google Scholar]
- 60.Gershman S. J., Horvitz E. J., Tenenbaum J. B., Computational rationality: A converging paradigm for intelligence in brains, minds, and machines. Science 349, 273–278 (2015). [DOI] [PubMed] [Google Scholar]
- 61.Pitkow X., Angelaki D. E., Inference in the brain: Statistics flowing in redundant population codes. Neuron 94, 943–953 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Bengio Y., Courville A., Vincent P., Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 35, 1798–1828 (2013). [DOI] [PubMed] [Google Scholar]
- 63.Mnih V., et al. , Playing Atari with deep reinforcement learning. arXiv:1312.5602 (19 December 2013).
- 64.Silver D., et al. , Mastering the game of go with deep neural networks and tree search. Nature 529, 484–489 (2016). [DOI] [PubMed] [Google Scholar]
- 65.Sutton R., The bitter lesson. Incomplete Ideas (2019). http://www.incompleteideas.net/IncIdeas/BitterLesson.html. Accessed 16 June 2020.
- 66.Lillicrap T. P., Kording K. P., What does it mean to understand a neural network? arXiv:1907.06374 (15 July 2019).
- 67.Rudin C., Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 1, 206–215 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Schölkopf B., Causality for machine learning. arXiv:1911.10500 (24 November 2019).
- 69.Goyal A., et al. , Recurrent independent mechanisms. arXiv:1909.10893 (24 September 2019).
- 70.Gatys L., Ecker A. S., Bethge M., “Texture synthesis using convolutional neural networks” in NeurIPS, Cortes C., Lawrence N. D., Lee D. D., Sugiyama M., Garnett R., Eds. (Curran Associates, Inc., 2015), pp. 262–270. [Google Scholar]
- 71.Sinz F. H., Pitkow X., Reimer J., Bethge M., Tolias A. S., Engineering a less artificial intelligence. Neuron 103, 967–979 (2019). [DOI] [PubMed] [Google Scholar]
- 72.Odoemene O., Pisupati S., Nguyen H., Churchland A. K., Visual evidence accumulation guides decision-making in unrestrained mice. J. Neurosci. 38, 10143–10155 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
No data are associated with this paper.