Abstract
PREMISE
Measuring plant productivity is critical to understanding complex community interactions. Many traditional methods for estimating productivity, such as direct measurements of biomass and cover, are resource intensive, and remote sensing techniques are emerging as viable alternatives.
METHODS
We explore drone‐based remote sensing tools to estimate productivity in a tallgrass prairie restoration experiment and evaluate their ability to predict direct measures of productivity. We apply these various productivity measures to trace the evolution of plant productivity and the traits underlying it.
RESULTS
The correlation between remote sensing data and direct measurements of productivity varies depending on vegetation diversity, but the volume of vegetation estimated from drone‐based photogrammetry is among the best predictors of biomass and cover regardless of community composition. The commonly used normalized difference vegetation index (NDVI) is a less accurate predictor of biomass and cover than other equally accessible vegetation indices. We found that the traits most strongly correlated with productivity have lower phylogenetic signal, reflecting the fact that high productivity is convergent across the phylogeny of prairie species. This history of trait convergence connects phylogenetic diversity to plant community assembly and succession.
DISCUSSION
Our study demonstrates (1) the importance of considering phylogenetic diversity when setting management goals in a threatened North American grassland ecosystem and (2) the utility of remote sensing as a complement to ground measurements of grassland productivity for both applied and fundamental questions.
Keywords: biomass, phylogenetic diversity, phylogeny, prairie, productivity, remote sensing
Plant productivity shapes how species compete and respond to stressors (Mahaut et al., 2020) and consequently how species are distributed in space, thereby shaping the assembly of plant communities. Productivity is traditionally estimated directly by measuring aboveground biomass and cover, but remote sensing is emerging as a less time‐ and resource‐intensive tool (Heinsch et al., 2006; Yu et al., 2018). Estimating vegetation cover requires relatively little time and resources but considers growth in only two dimensions, ignoring vegetation height and density. Biomass estimates more directly measure total plant growth; however, collecting, drying, and weighing biomass are both resource intensive and destructive, limiting the practicality of biomass studies at large spatial and temporal scales.
Recent developments in remote multispectral imagery and vegetation structure mapping have improved our ability to estimate plant productivity (Cerasoli et al., 2018; Fischer et al., 2019). Multispectral vegetation indices (VIs) are a collection of ratios and transformations of light reflectance intensities detected in certain spectral bands. They are based on the light that is reflected by vegetation, which is influenced by leaf health, density, and photosynthetic activity (Xue and Su, 2017); thus, VIs have emerged as an important tool for estimating plant community productivity (Wang et al., 2010; Cavender‐Bares et al., 2017). Many VIs use the ratio of red to near‐infrared reflectance because of the correlation between the contrast in the absorption of these bands and leaf health (Myneni et al., 1995). The normalized difference vegetation index (NDVI; Tucker, 1979) is the most commonly used VI. NDVI is based on the ratio of red and near infrared reflectance and is often applied in ecological studies (Pettorelli et al., 2005), where it has been shown to be correlated with productivity in trees (Wang et al., 2004) and biomass in prairie (Wang et al., 2016) and tundra habitats (Goswami et al., 2015). Furthermore, variation in reflectance across spectra may be phylogenetically conserved (Cavender‐Bares et al., 2016, 2017), suggesting that multispectral analyses can potentially be used to remotely estimate the community phylogenetic composition and diversity.
Remote sensing techniques can also estimate productivity by providing data to model the physical structure of vegetation. Photogrammetry uses overlapping photographs to reconstruct 3D structures, producing models of the outermost layer of vegetation visible in the photographs (Baltsavias, 1999). It can accurately capture the structure of large and complex vegetation forms, both as individuals (Scher et al., 2019) and as blocks of vegetation. Light detection and ranging (LiDAR) yields a more nuanced view of the layers of vegetation that comprise a community or individual plant (Baltsavias, 1999; Dubayah and Drake, 2000), enabling the estimation of both vegetation volume and density. While LiDAR provides more detail than photogrammetry, both techniques can accurately estimate biomass from volume over small areas (Wallace et al., 2017). Furthermore, photogrammetry requires only red‐green‐blue (RGB) photographs, whereas LiDAR requires more expensive equipment (Solazzo et al., 2018).
High‐resolution satellite imagery remains prohibitively expensive for many ecology applications (Wang et al., 2010). By contrast, the cost of quality drone imagery is decreasing rapidly, making it an exciting tool for the investigation of individual plants and local landscapes (Cannon et al., 2018). Precision agriculture regularly uses high‐resolution drone‐based imagery (Zhang and Kovacs, 2012), and the decreasing costs of drone imagery are making this technology equally accessible to ecologists.
In this study, we first investigate how high‐resolution (<1.5 cm) drone‐based multispectral imagery and volume estimates correlate with field‐based estimates of grassland productivity. We compare four productivity proxies: two measured from field observations (aboveground biomass and percent vegetation cover) and two measured via drone‐based photography (individual light spectra and VIs [Table 1] and photogrammetry‐derived vegetation volume). We then use the productivity proxies to illuminate how the evolution of functional traits that influence plant productivity and competitive interactions shape the phylogenetic distribution of grassland productivity. Our study demonstrates the utility of remote sensing to address fine‐scale ecological questions efficiently and economically. Furthermore, it advances our understanding of how the evolution of plant traits and lineage diversity shape grassland ecosystem processes.
TABLE 1.
Spectral bands and vegetation indices used in analyses.
| Index | Name | Reference | Wavelength range or formula |
|---|---|---|---|
| GRE | Green | 530–570 nm | |
| RED | Red | 640–680 nm | |
| REG | Red edge | 730–740 nm | |
| NIR | Near infrared | 770–810 nm | |
| NDVI | Normalized difference vegetation index | Tucker (1979) | (NIR − R)/(NIR + R) |
| GNDVI | Green normalized difference vegetation index | Gitelson et al. (1996) | (NIR − G)/(NIR + G) |
| GDVI2 | Generalized difference vegetation index | Wu (2014) | (NIR2 − R2)/(NIR2 + R2) |
METHODS
Site
Our study system is a tallgrass prairie restoration experiment located at The Morton Arboretum in northeastern Illinois, USA. The soils (Markham series, fine, illitic, mesic, mollic oxyaquic Hapludalfs) on the site are deep and moderately well drained, forming in a thin layer of silt loam loess overlying silty clay loam till (USDA‐NRCS, 2019). Our experiment manipulates phylogenetic and trait diversity in mixed species plots drawn from 127 tallgrass prairie plants, all of which essentially reached maximum productivity at the time the biomass and remote sensing data were collected (Hipp et al., 2018). The site is divided into 437 4‐m2 plots, which were partitioned based on measurements of their soil traits into two superblocks (west and east), each containing three blocks (A–C in the west superblock, D–F in the east superblock; Fig. 1). Of the 437 plots, our analysis used 326 plots of two types, monoculture and multispecies, all planted from plugs in August–September 2016, with follow‐up planting of failed or initially unavailable plants in summer 2017. For each of the 127 species used, we planted one monoculture plot in each superblock, for a total of 254 monoculture plots. Each multispecies plot was planted with one of 36 combinations of 15‐species mixes, and the 15‐species planting order was randomized within each quarter plot. Multispecies plots were also duplicated in both superblocks for a total of 72 multispecies plots. Complete details of the experimental design are described by Hipp et al. (2018).
FIGURE 1.
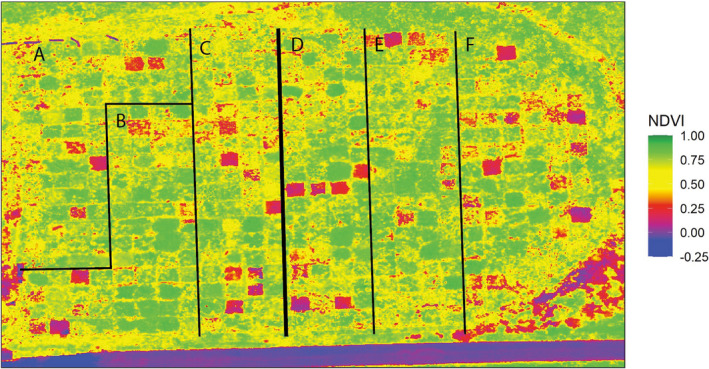
An NDVI map of the experimental prairie with blocks labeled. The thin lines mark blocks, and the thick line separates the superblocks.
Soil analysis
We measured the A horizon in each plot and interpolated the gravimetric soil moisture, loss on ignition soil organic matter, pH, electrical conductivity, wet aggregate stability, and phosphorus from measurements of a subset of the plots. We used a principal component analysis to identify groups of plots that differed in these soil characteristics and thus partitioned the site into blocks. See Appendix S1 for details.
Photo capture and orthomosaic construction
A DJI Phantom 4 drone (Shenzhen DJI Sciences and Technologies Ltd., Shenzhen, China) carrying a Parrot Sequoia (Parrot Drones SAS, Paris, France) was flown over the experimental prairie on 1 August 2017, during the peak of its first full growing season following establishment. The drone captured 598 RGB photos and single‐band images of the red, green, near‐infrared, and red edge bands. For details, see Appendix S1.
Seven orthomosaics were produced by merging 598 photos of the site into a single image; each orthomosaic shows one of the three VIs measured (Table 1) or one of the four wavelength bands (Table 1, Appendix S2). Values of each VI range from −1 to 1, with high values representing dense vegetation and values close to and below 0 representing non‐vegetative surfaces. Each VI, however, captures differences in vegetation density at varying levels; for example, NDVI saturates at high levels of chlorophyll concentration, and therefore does not capture variation in high vegetation densities. The green normalized difference vegetation index (GNDVI) uses green reflectance instead of red and has a larger dynamic range at high vegetation densities (Gitelson et al., 1996); GDVI2, a form of the generalized difference vegetation index (GDVI), is derived from NDVI and increases the dynamic range at low vegetation densities (Wu, 2014). The orthomosaics were exported from Agisoft Photoscan (Agisoft, St. Petersburg, Russia) in the tagged image file format (TIFF).
Biomass
Vegetative material was collected between 9 October and 20 November 2017, before the first major frost, to avoid leaf disintegration. In the multispecies plots, all vegetative material in the southwest quadrant was collected. In the monoculture plots, material was collected only from the central 0.25 m2 of the southwest quadrant. All individuals of the planted species rooted inside the given area were clipped at ground level. The vegetation was dried in paper bags at 50°C for at least 48 h and weighed immediately after removal from the oven. We calculated the biomass of each species and the total biomass for the multispecies plots, which was converted to a dry weight of grams per square meter.
Vegetation collected early in the season from some multispecies plots in blocks A, B, C, and F was not dried sufficiently before its biomass was measured. Biomass measurements in these plots were biased upward in the preliminary analyses, so multispecies plots that were affected are excluded from all biomass analyses.
Vegetation cover
Vegetation cover was evaluated using two methods: cover of only planted species (“planted cover”) and cover of all species (“total cover”). The planted cover was estimated by observers in the field (29 August 2017 to 1 September 2017) for all plots, using the midpoints of 14 cover classes (producing 0%, 0.5%, 3%, 7.5%, 15%, 25%, 35%, 45%, 55%, 65%, 75%, 85%, 92.5%, 97%, and 99.5% classes). Subsequently, two different observers estimated the total cover by examining the RGB orthomosaic. Each independently assessed the total percentage of each plot covered by vegetation, and their estimates were then averaged.
Spectral imagery
All spectral band and VI orthomosaics (Table 1) were processed as rasters using the raster package (Hijmans and van Etten, 2012) in R (R Core Team, 2019). The outer 0.25 m of each plot was removed to avoid counting turf species encroaching from the paths, which were also excluded from the manual field‐based productivity estimates. For each of the seven rasters, all pixels within the resulting 1.5 × 1.5‐m squares were averaged. These values represent all vegetation in the plot at the time when the aerial images were taken, but because only the biomass of the planted species was measured after being collected later in the growing season, we used a correction factor to adjust the orthomosaics for a more consistent comparison. The adjustment was used to correct for weeds that were present in the drone images but whose biomass was not measured, as well as growth that occurred between the photo capture and biomass measurement. For details on the correction, see Appendix S1. This procedure produced 14 spectral values for each plot, representing the raw and corrected values from each of the seven rasters.
Estimation of vegetation volume
The vegetation volume of each plot was estimated using a vegetation height model (VHM) produced by subtracting a digital terrain model (DTM) from a digital surface model (DSM). The DSM and DTM were built in Agisoft Photoscan using all points in the dense cloud and only ground‐level points, respectively. The DSM does not distinguish vegetation height from changes in ground level, so plants on higher ground appear taller, whereas the DTM interpolates the ground level below the vegetation from ground‐level points. Subtracting the DTM from the DSM produced a VHM containing the height of vegetation after correcting for ground level. We then calculated the vegetation volume as the average height of the plot multiplied by the length and width of the plot. To minimize the effects of very slight variations in plot size, the resulting volume was then standardized to a 1.5 × 1.5‐m plot. Standardizing in this way has the effect of transforming volume estimates into average vegetation heights, as estimated in the VHM. In either case, the estimate is fundamentally different from cover estimates (which estimate the area covered by a shadow cast by the vegetation) or the VIs (based on reflectance of discrete spectra).
Predicting productivity using models
We used a linear regression to estimate how well the remote sensing metrics predict biomass and cover using base R (R Core Team, 2019) and the lme4 package (Bates et al., 2015). We also use the MuMIn (Barton, 2009), lmer4Test (Kuznetsova et al., 2017), and qpcR (Spiess, 2018) packages to evaluate the models. Each model predicting biomass uses covariates from three groups: (1) a VI or single band, (2) total or planted cover, and (3) photogrammetry‐modeled volume (hereafter, “volume”). Because the remote sensing metrics were calculated based on all the vegetation in each plot, we modeled total cover, not planted cover, using (1) a VI or single band and (2) volume. Covariates and responses were scaled to unit variance and a mean of zero prior to model fitting. Each combination of variables was run as a multiple linear regression and a mixed‐effects model using block as a random effect. All regressions were fitted using all plots, only monoculture plots, and only multispecies plots. For the multispecies plots, we modeled total biomass and cover, not partitioned by species. While there is an expected collinearity between VIs, cover, and volume, all are maintained as covariates in the models to estimate partial correlation coefficients. Although a case can be made for eliminating predictors that covary to a great extent, the retention of the relatively small number of covariates in this study is key to assessing whether there is variance in the biomass left to explain after the other potential predictors have been factored out (Legendre and Legendre, 1998).
To test whether the presence of non‐photosynthetic flowers that could alter VI values (Shen et al., 2010) affects the model fit, linear regressions were also conducted using only plots that did not have open flowers at the time of photo capture. We ran models on all nonflowering plots and on only nonflowering monoculture plots; there were only three nonflowering multispecies plots, so we did not run separate models on them.
We used R 2 to evaluate the model fit and Akaike’s information criterion (AIC) to estimate the predictive value of the models (Sober, 2002). The AIC weight (AICw) of each model was calculated as its relative likelihood as a proportion of the summed relative likelihoods of all models evaluated (following Burnham and Anderson, 2002, 2004). We then quantified the importance of each covariate by summing the AICw of all models in which the covariate was used (Burnham and Anderson, 2002) to obtain a cumulative AICw for each covariate across all models. A high cumulative AICw for a covariate indicates that the covariate is present in models that carry higher predictive weight. Unlike the AIC, the absolute value of the cumulative AICw is meaningful: a cumulative AICw near 1.0 implies that the covariate has high predictive weight relative to the population of models evaluated. In evaluating the support for individual models, we also report ΔAIC, the difference between the AIC of the best model evaluated for that test and the model being reported. While there are no hard rules about ΔAIC values, models with ΔAIC < 2 are generally considered to be practically indistinguishable in evidentiary support from the best model considered and thus to contribute significantly to our understanding of variance in the system we are studying, while those with ΔAIC > 10 have “essentially no support” (Burnham and Anderson, 2004).
Trait data
Quantitative and qualitative trait data for each species were gathered from published sources (Iverson et al., 1999; Amatangelo et al., 2014; Sonnier et al., 2014; Ash et al., 2015; Hipp et al., 2018; Clark et al., 2019) or collected as described in Appendix S1, using the species classification described by Bai et al. (2012). Nitrogen fixation and root types (adventitious, primary, bulb, corm, fibrous, rhizome, stolon, and tuber) were coded as binary traits. Quantitative traits included the genome size, petiole length, leaf length, leaf width, leaf thickness, vegetative height, seed mass, leaf dry‐matter content, specific leaf area, leaf nitrogen content, leaf carbon content, leaf phosphorus content, stem dry‐matter content, and circularity.
Phylogenetic and trait analyses
To assess how trait evolution shapes the phylogenetic structure of species‐level productivity estimates in the monoculture plots, a phylogeny synthesized from published phylogenies and taxonomic knowledge of unsampled species (a “synthesis phylogeny” sensu Li et al., 2019; Fig. 2) was developed using Zanne et al. (2014) as a framework, followed by the pruning and splicing of taxa of interest in this study, as detailed by Hipp et al. (2018). We estimated the phylogenetic signal in species’ traits, biomass, and corrected VI measures from monoculture plots (see methods above) using Blomberg’s K (Blomberg et al., 2003) and Pagel’s λ (Pagel, 1999) in geiger version 2.0.6.2 (Harmon et al., 2008). The correlation (Pearson’s r) of plant traits with NDVI was plotted against their correlation with biomass, and the point size was scaled by the phylogenetic heritability to explore how the phylogenetic heritability of traits correlates with their influence on productivity. We then used Mantel tests of pairwise species comparisons of NDVI and phylogenetic distance, closely mirroring analyses conducted by Schweiger et al. (2018) that assessed the plant‐level correlation between the species’ mean spectral profiles and phylogenetic distance, to evaluate whether VIs at the plot level (from our study) show comparable phylogenetic heritability to the hyperspectral data at the plant level (from Schweiger et al., 2018).
FIGURE 2.
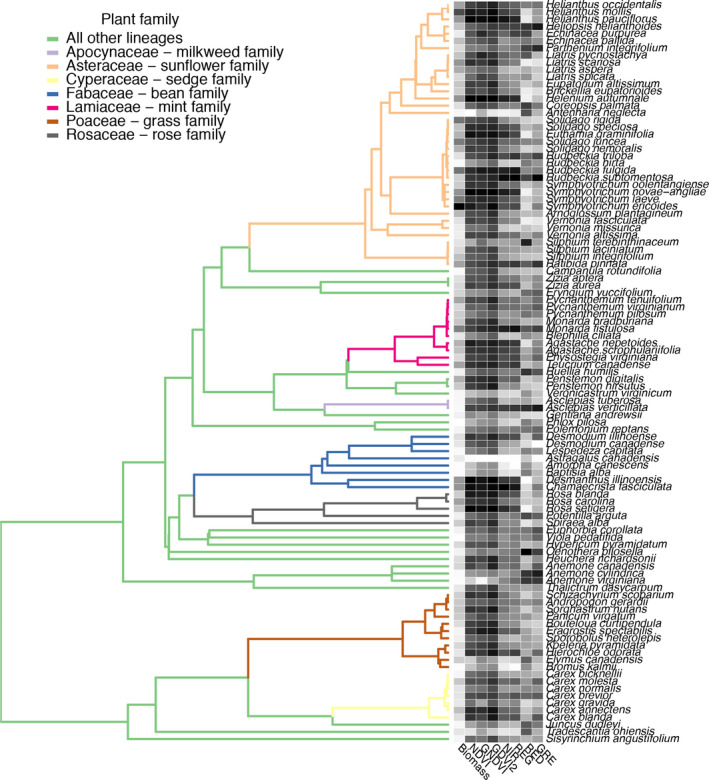
A 127‐species phylogeny with corresponding biomass measurements and spectra mapped. Trait and productivity metrics are all rescaled from 0 (white) to 1 (black); raw measurements can be found in the data sets provided in GitHub (https://github.com/lanescher/prairie-remote-sensing-2020/tree/master/DATA). Colored branches indicate dominant plant families. GRE, green; RED, red; REG, red edge; NIR, near infrared; NDVI, normalized difference vegetation index; GNDVI, green normalized difference vegetation index; GDVI2, generalized difference vegetation index.
We used non‐metric multidimensional scaling (Kruskal, 1964) to visualize individual species positions in the trait and productivity space, using monoMDS in the R package vegan (Oksanen et al., 2019) on a Gower’s distance matrix estimated from seven functional traits (stem dry‐matter content, leaf dry‐matter content, leaf circularity, vegetative height, leaf carbon content, leaf length, leaf thickness) along with biomass, NDVI, and GNDVI. The productivity response and trait variables were fit to the ordination in vegan using the envfit function.
The reader may note that we did not estimate partitioned biodiversity effects (sensu Loreau and Hector, 2001). The biomass sampling size in the monocultures (0.25 m2) in our study did not equal the sampling size in the multispecies plots (1 m2), and multispecies plot samples consequently included a greater proportion of plot edges than the monocultures. As the null expectation that diversity effects will equal zero is not met in the current sample, we leave these analyses to future studies.
RESULTS
Soil types
The first two axes of the soil principal component analysis explained 49.2% and 19.6% of the variance, respectively (available as Supplement 3 on GitHub and Zenodo [Scher et al., 2020], see Data Availability statement). The depth of the A horizon was responsible for 48.06% of the variance observed on the first axis and 23.88% of the second axis. Soils differ significantly among blocks, primarily distinguishing block A (μ = 38.5 ± 0.6 cm [SEM]) from blocks B–F (μ = 26.2 ± 0.2 cm; Kruskal–Wallis test, k = 172.44, P = 2.19 × 10−35; Fig. 1). Block type was consequently retained as a random effect in biomass and cover regressions to account for differences in soil.
Biomass
The biomass of the monoculture plots ranged from 0 to 3977 g per 4‐m2 plot, with a mean of 399.0 g and a standard error of 29.1 g (Table 2, Fig. 3). There was no effect of soil blocking on the biomass (Kruskal–Wallis test, k = 6.15, P = 0.292). We did not analyze these patterns in the multispecies plots, because the multispecies plots that were measured incorrectly were concentrated in a few blocks, the removal of which might introduce bias from block conditions. We do, however, show summaries of correctly measured multispecies plots in Fig. 3. All biomass measurements for the monoculture and multispecies plots are listed in Supplements 4 and 5 (available on GitHub and Zenodo, see Data Availability statement), respectively.
TABLE 2.
Summary statistics for the productivity proxies measured.
| All | Monocultures | Multispecies | ||||||
|---|---|---|---|---|---|---|---|---|
| Productivity proxies | Mean | Min, max | Mean | Min, max | Mean | Min, max | Plot type P value | Block P value |
| Biomass | 410.88 | 0.00, 3977.62 | 398.97 | 0.00, 3977.62 | 479.62 | 78.80, 981.00 | 0.0016 | 0.4001 |
| Planted cover | 62.81 | 0.00, 99.50 | 62.77 | 0.00, 99.50 | 73.98 | 45.00, 97.00 | 0.003 | 0.2748 |
| Total cover | 74.14 | 0.00, 100.00 | 74 | 0.00, 100.00 | 83.68 | 47.50, 100.00 | 0.143 | 0.0026 |
| NDVI | 0.65 | 0.08, 0.88 | 0.65 | 0.08, 0.88 | 0.72 | 0.34, 0.85 | 0.0025 | 0.026 |
| GNDVI | 0.66 | 0.39, 0.82 | 0.67 | 0.39, 0.82 | 0.7 | 0.49, 0.79 | 0.0015 | 0.0037 |
| GDVI2 | 0.85 | 0.15, 0.99 | 0.86 | 0.15, 0.99 | 0.92 | 0.53, 0.98 | 0.0086 | 0.0187 |
| VOL | 0.96 | −0.31, 3.55 | 0.87 | −0.31, 3.55 | 1.29 | 0.06, 2.73 | 0.0000 | 0.0076 |
GDVI2 = generalized difference vegetation index; GNDVI = green normalized difference vegetation index; NDVI = normalized difference vegetation index; VOL = vegetation volume.
FIGURE 3.
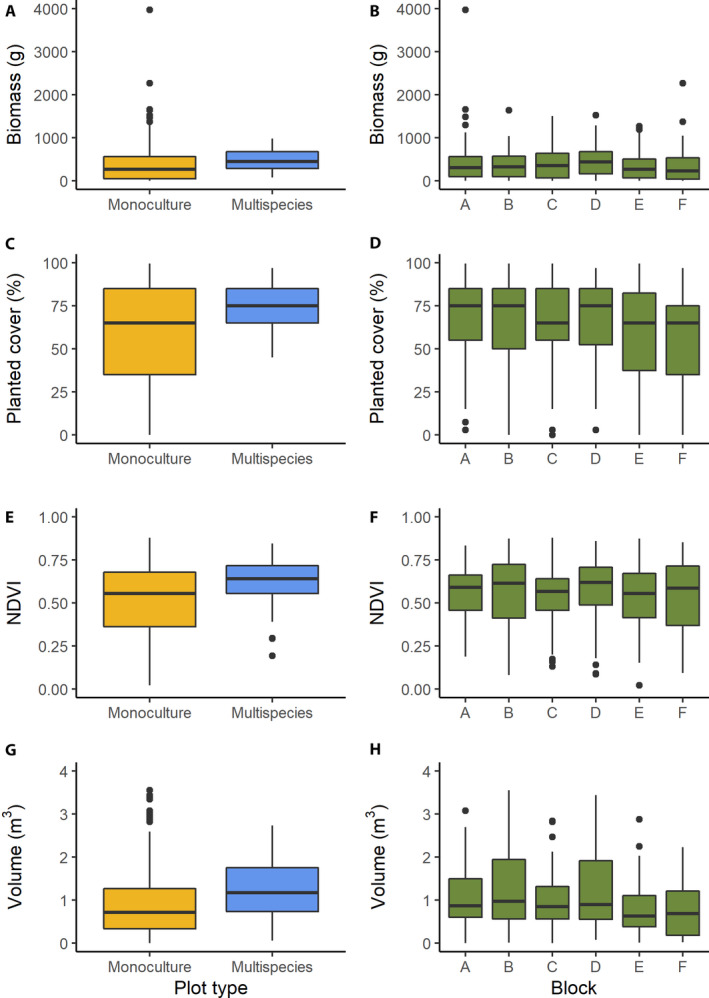
Boxplots of biomass (A, B), planted cover (C, D), NDVI (E, F), and volume (G, H), separated by plot type (A, C, E, G) and block (B, D, F, H).
Vegetation cover
The planted cover ranged from 0% to 99.5%, with a mean of 62.8% (Table 2, Fig. 3). The planted cover was significantly higher in the multispecies plots (74.0% ± 1.48% [SEM]) than the monoculture plots (62.8% ± 1.87%; two‐sided Mann–Whitney test: w = 11,005, P = 0.003). There was no effect of the block type on the planted cover (Kruskal–Wallis test, k = 6.34, P = 0.275).
The total cover ranged from 0% to 100%, with a mean of 74.1% and standard error of 1.4%. There was no effect of diversity on the total cover (μMonoculture = 74.0 ± 1.8, μMultispecies = 83.7 ± 1.1; two‐sided Mann–Whitney test: w = 10,176, P = 0.143), but there was a significant block effect (Kruskal–Wallis test, k = 18.33, P = 0.003).
Vegetation indices
The 598 photo sets were used to build multispectral orthomosaics at a resolution of 1.15 cm/pix (Fig. 1). A 2‐m scale bar measured 1.99 m in the orthomosaic, indicating that the scaling of the orthomosaic had a precision of >99%. The mean GDVI2 (0.85 ± 0.01) was higher than NDVI (0.65 ± 0.01) and GNDVI (0.66 ± 0.01; Table 2; Kruskal–Wallis test: k = 355.78, P < 0.0001). Furthermore, NDVI, GNDVI, and GDVI2 were all significantly higher in the multispecies plots (μNDVI = 0.72 ± 0.01, μGNDVI = 0.70 ± 0.01, μGDVI2 = 0.92 ± 0.01) than in the monoculture plots (μNDVI = 0.65 ± 0.01, μGNDVI = 0.67 ± 0.01, μGDVI2 = 0.86 ± 0.01; two‐sided Mann–Whitney test, NDVI: w = 11,279, P = 0.003; GNDVI: w = 11,379, P = 0.002; GDVI2: w = 10,999, P = 0.009, Fig. 3) and varied among blocks (Kruskal–Wallis test, NDVI: k = 12.73, P = 0.026; GNDVI: k = 17.47, P = 0.004; GDVI2: k = 13.55, P = 0.019).
Volume
The mean volume across all plots was 0.96 m3 and ranged from –0.31 m3 to 3.55 m3. The 17 negative volume estimates suggest there was little vegetation within those plots and that the ground may slope. The volume was higher in multispecies plots (1.29 ± 0.08 m3) than in monoculture plots (0.87 ± 0.05 m3; Table 2; Kruskal–Wallis test: w = 12,705, P < 0.0001) and varied among blocks (two‐sided Mann–Whitney test, k = 15.74, P = 0.008).
Evaluation of biomass models
We evaluated models predicting biomass with combinations of covariates from three groups (a VI or single band, total or planted cover, volume), for a total of 89 models with between one and three covariates each. Including block as a random effect resulted in negligible improvement in model likelihood and consequently the AIC increased (poorer model fit) for all models (available as Supplements 6–8 on GitHub and Zenodo, see Data Availability statement). We therefore only discuss models without block as a random effect. Moreover, the rank order of models based on AIC using plots with and without flowers was similar to that of models using only plots without flowers (available as Supplement 9 on GitHub and Zenodo, see Data Availability statement), so we do not discuss the results of the analyses conducted solely on plots without flowers. Models predicting the biomass of monoculture (Table 3 and Supplement 10 [available on GitHub and Zenodo, see Data Availability statement]) and multispecies plots (Table 4 and Supplement 11 [available on GitHub and Zenodo, see Data Availability statement]) separately produced very different results. Because of the difference in the number of monoculture plots (n = 254) and multispecies plots (n = 72) used here, the models evaluating all plot types together (see Supplement 12 on GitHub and Zenodo, see Data Availability statement) were dominated by the monoculture plots, and were almost identical to the models of monoculture plots alone. We therefore report the results for monoculture and multispecies plots separately.
TABLE 3.
Models of biomass in monoculture plots. Only models using planted cover and those using uncorrected VIs are shown, as well as models mentioned in the text. See Supplement 10 (available on GitHub and Zenodo, see Data Availability statement) for all models.
| VI used | Cover used | VI | Cover | Volume | R 2 | AIC | ∆AIC |
|---|---|---|---|---|---|---|---|
| GDVI2 | Planted | −0.14, P = 0.0351 | 0.49, P < 0.0001 | 0.36, P < 0.0001 | 0.461 | 591.37 | 0 |
| NDVI | Planted | −0.11, P = 0.0997 | 0.47, P < 0.0001 | 0.37, P < 0.0001 | 0.457 | 593.14 | 1.77 |
| GNDVI | Planted | −0.11, P = 0.1502 | 0.47, P < 0.0001 | 0.37, P < 0.0001 | 0.456 | 593.79 | 2.42 |
| — | Planted | — | 0.43, P < 0.0001 | 0.33, P < 0.0001 | 0.451 | 593.9 | 2.53 |
| REG | Planted | −0.09, P = 0.2236 | 0.46, P < 0.0001 | 0.37, P < 0.0001 | 0.454 | 594.39 | 3.02 |
| NIR | Planted | −0.09, P = 0.2552 | 0.46, P < 0.0001 | 0.38, P < 0.0001 | 0.454 | 594.58 | 3.21 |
| RED | Planted | 0.05, P = 0.4077 | 0.44, P < 0.0001 | 0.34, P < 0.0001 | 0.452 | 595.2 | 3.83 |
| GRE | Planted | −0.02, P = 0.6753 | 0.43, P < 0.0001 | 0.33, P < 0.0001 | 0.451 | 595.72 | 4.35 |
| NIR | Planted | 0.15, P = 0.0257 | 0.53, P < 0.0001 | — | 0.395 | 617.94 | 26.57 |
| REG | Planted | 0.11, P = 0.0985 | 0.56, P < 0.0001 | — | 0.39 | 620.22 | 28.85 |
| — | Planted | — | 0.62, P < 0.0001 | — | 0.383 | 620.99 | 29.62 |
| GNDVI | Planted | 0.07, P = 0.3183 | 0.58, P < 0.0001 | — | 0.385 | 621.98 | 30.61 |
| GDVI2 | Planted | −0.04, P = 0.5205 | 0.65, P < 0.0001 | — | 0.384 | 622.57 | 31.2 |
| NDVI | Planted | 0.03, P = 0.6771 | 0.61, P < 0.0001 | — | 0.383 | 622.81 | 31.44 |
| GRE | Planted | 0.01, P = 0.7781 | 0.62, P < 0.0001 | — | 0.383 | 622.91 | 31.54 |
| RED | Planted | 0.01, P = 0.8138 | 0.63, P < 0.0001 | — | 0.383 | 622.93 | 31.56 |
| GDVI2 | Total | −0.16, P = 0.0626 | 0.33, P = 1e‐04 | 0.50, P < 0.0001 | 0.384 | 635.55 | 44.18 |
| GNDVI | — | 0.14, P = 0.0443 | — | 0.50, P < 0.0001 | 0.353 | 645.99 | 54.62 |
| NIR | — | 0.13, P = 0.0880 | — | 0.49, P < 0.0001 | 0.35 | 647.14 | 55.77 |
| REG | — | 0.11, P = 0.1202 | — | 0.52, P < 0.0001 | 0.349 | 647.64 | 56.27 |
| NDVI | — | 0.10, P = 0.1272 | — | 0.54, P < 0.0001 | 0.349 | 647.73 | 56.36 |
| — | — | — | — | 0.60, P < 0.0001 | 0.343 | 648.09 | 56.72 |
| GDVI2 | — | 0.08, P = 0.1890 | — | 0.55, P < 0.0001 | 0.347 | 648.34 | 56.97 |
| RED | — | −0.06, P = 0.2922 | — | 0.58, P < 0.0001 | 0.346 | 648.96 | 57.59 |
| GRE | — | −0.04, P = 0.4989 | — | 0.60, P < 0.0001 | 0.344 | 649.63 | 58.26 |
| NIR | — | 0.50, P < 0.0001 | — | — | 0.248 | 682.11 | 90.74 |
| REG | — | 0.46, P < 0.0001 | — | — | 0.216 | 692.91 | 101.54 |
| GNDVI | — | 0.46, P < 0.0001 | — | — | 0.215 | 693.21 | 101.84 |
| NDVI | — | 0.42, P < 0.0001 | — | — | 0.173 | 706.41 | 115.04 |
| GDVI2 | — | 0.37, P < 0.0001 | — | — | 0.135 | 717.85 | 126.48 |
| RED | — | −0.24, P = 1e‐04 | — | — | 0.058 | 739.42 | 148.05 |
| GRE | — | 0.03, P = 0.6113 | — | — | 0.001 | 754.38 | 163.01 |
— = no covariate was used; AIC = Akaike’s information criterion; ∆AIC = the difference between the AIC of the best model evaluated for that test and the model being reported; GDVI2 = generalized difference vegetation index; GNDVI = green normalized difference vegetation index; GRE = green; NDVI = normalized difference vegetation index; NIR = near infrared; REG = red edge; VI = vegetation index.
TABLE 4.
Models of biomass in multispecies plots. Only models using planted cover and those using uncorrected VIs are shown. See Supplement 11 (available on GitHub and Zenodo, see Data Availability statement) for all models.
| VI used | Cover used | VI | Cover | Volume | R 2 | AIC | ∆AIC |
|---|---|---|---|---|---|---|---|
| REG | — | −0.26, P = 0.1203 | — | 0.67, P < 0.0001 | 0.498 | 46.52 | 0 |
| — | — | — | — | 0.55, P < 0.0001 | 0.468 | 47.14 | 0.62 |
| GRE | — | −0.12, P = 0.2221 | — | 0.56, P < 0.0001 | 0.487 | 47.52 | 1 |
| NIR | — | −0.18, P = 0.2333 | — | 0.64, P < 0.0001 | 0.486 | 47.6 | 1.08 |
| REG | Total | −0.30, P = 0.1014 | 0.11, P = 0.5656 | 0.66, P < 0.0001 | 0.502 | 48.15 | 1.63 |
| RED | — | −0.12, P = 0.4167 | — | 0.52, P < 0.0001 | 0.476 | 48.43 | 1.91 |
| REG | Planted | −0.27, P = 0.1239 | 0.03, P = 0.8134 | 0.67, P < 0.0001 | 0.499 | 48.46 | 1.94 |
| GDVI2 | — | −0.09, P = 0.6474 | — | 0.57, P < 0.0001 | 0.47 | 48.92 | 2.4 |
| — | Planted | — | −0.03, P = 0.8335 | 0.55, P < 0.0001 | 0.468 | 49.09 | 2.57 |
| NDVI | — | −0.02, P = 0.9047 | — | 0.55, P < 0.0001 | 0.468 | 49.13 | 2.61 |
| GNDVI | — | −0.02, P = 0.9171 | — | 0.56, P = 1e‐04 | 0.468 | 49.13 | 2.61 |
| GRE | Planted | −0.12, P = 0.2343 | 0.01, P = 0.9497 | 0.55, P < 0.0001 | 0.487 | 49.52 | 3 |
| NIR | Planted | −0.19, P = 0.2429 | 0.02, P = 0.8837 | 0.64, P < 0.0001 | 0.486 | 49.58 | 3.06 |
| RED | Planted | −0.13, P = 0.4029 | −0.04, P = 0.7525 | 0.54, P < 0.0001 | 0.477 | 50.32 | 3.8 |
| GDVI2 | Planted | −0.08, P = 0.6652 | −0.02, P = 0.8714 | 0.58, P < 0.0001 | 0.471 | 50.89 | 4.37 |
| NDVI | Planted | −0.01, P = 0.9333 | −0.03, P = 0.8493 | 0.56, P < 0.0001 | 0.468 | 51.09 | 4.57 |
| GNDVI | Planted | −0.02, P = 0.9311 | −0.03, P = 0.8415 | 0.56, P = 2e‐04 | 0.468 | 51.09 | 4.57 |
| GNDVI | — | 0.56, P = 0.0010 | — | — | 0.229 | 63.45 | 16.93 |
| GNDVI | Planted | 0.52, P = 0.0043 | 0.12, P = 0.4476 | — | 0.24 | 64.82 | 18.3 |
| NDVI | — | 0.45, P = 0.0068 | — | — | 0.162 | 67.1 | 20.58 |
| NDVI | Planted | 0.39, P = 0.0264 | 0.14, P = 0.3947 | — | 0.177 | 68.31 | 21.79 |
| NIR | — | 0.36, P = 0.0159 | — | — | 0.131 | 68.7 | 22.18 |
| REG | — | 0.36, P = 0.0313 | — | — | 0.106 | 69.96 | 23.44 |
| NIR | Planted | 0.30, P = 0.0723 | 0.13, p = 0.4762 | — | 0.142 | 70.15 | 23.63 |
| GDVI2 | — | 0.44, P = 0.0375 | — | — | 0.099 | 70.28 | 23.76 |
| GDVI2 | Planted | 0.36, P = 0.0984 | 0.20, P = 0.2262 | — | 0.131 | 70.69 | 24.17 |
| REG | Planted | 0.28, P = 0.1289 | 0.15, P = 0.3901 | — | 0.122 | 71.16 | 24.64 |
| RED | Planted | −0.29, P = 0.1315 | 0.23, P = 0.1659 | — | 0.121 | 71.19 | 24.67 |
| RED | — | −0.35, P = 0.0655 | — | — | 0.078 | 71.27 | 24.75 |
| — | Planted | — | 0.28, P = 0.0818 | — | 0.07 | 71.66 | 25.14 |
| GRE | Planted | −0.12, P = 0.3611 | 0.32, P = 0.0578 | — | 0.089 | 72.75 | 26.23 |
| GRE | — | −0.06, P = 0.6590 | — | — | 0.005 | 74.66 | 28.14 |
— = no covariate was used; AIC = Akaike’s information criterion; ∆AIC = the difference between the AIC of the best model evaluated for that test and the model being reported; GDVI2 = generalized difference vegetation index; GNDVI = green normalized difference vegetation index; GRE = green; NDVI = normalized difference vegetation index; NIR = near infrared; REG = red edge; VI = vegetation index.
Planted cover (30/89 models; cumulative AICw = 0.999) and volume (45/89 models; cumulative AICw = 0.999) held by far the most predictive power, followed distantly by GDVI2 (6/89 models; cumulative AICw = 0.252). The cumulative AICw of all other predictors was less than 0.104. The best model for predicting biomass in monoculture plots used GDVI2, volume, and planted cover as predictors, and accounts for 46% of the variation in biomass. All models incorporating planted cover and volume account for approximately 45% of the variation in biomass and have ΔAIC values <4.6. All models without both planted cover and volume have ΔAIC > 26.57 and R 2 < 0.42. The best model for predicting monoculture plots using only metrics from remote sensing imagery is similar to the best overall, but uses total cover, estimated by a visual inspection of aerial imagery, instead of planted cover, estimated by a visual inspection at ground level (R 2 = 0.38, P < 2.2 × 10−16).
The most important predictors of multispecies plots were volume (45/89 models, AICw = 0.999), total cover (30/89 models, AICw = 0.217), and planted cover (30/89 models, AICw = 0.215). Models incorporating volume have ΔAIC < 4.62 and account for at least 47% of the variance in biomass, whereas models that do not include volume have ΔAIC > 16.9 and account for less than 23% of the variance in biomass. The best model for predicting multispecies plots using only remotely sensed variables uses the red edge band, total cover, and volume (R 2 = 0.50).
Across all models, the residuals were nonlinear and heteroskedastic, suggesting the covariates we used did not account for all the variation in the response.
Cover models
We evaluated models predicting cover with combinations of covariates produced by selecting one variable from each of two groups (VI or single band and volume), for a total of 15 models with one or two covariates each. Models including all plots were dominated by monocultures (see Supplement 13 on GitHub and Zenodo, see Data Availability statement), and models predicting including and excluding flowers were very similar (see Supplement 14 on GitHub and Zenodo, see Data Availability statement). Similar to the models predicting biomass, including block as a random effect increased the AIC in all models (see Supplements 15–17 on GitHub and Zenodo, see Data Availability statement).
The best model for predicting cover in monoculture plots uses GDVI2 and volume and accounts for 67% of the variance in biomass. The AIC and R 2 scores are similar for models using only a VI and models using the same VI with volume (ΔAIC < 2), except in the case of GDVI2, for which the model using volume is better (ΔAIC = 10.3). The ΔAIC is >105.99 for the models using single bands instead of VIs (Table 5). Volume (8/15 models) and GDVI2 (2/15 models) are the most important covariates for predicting cover in monoculture plots (cumulative AICw = 0.999 and 0.994, respectively), with the AICw of all other covariates less than 1.5 × 10−6.
TABLE 5.
Models of total cover in monoculture plots.
| VI used | VI | Volume | R 2 | AIC | ∆AIC |
|---|---|---|---|---|---|
| GDVI2 | 0.72, P < 0.0001 | 0.16, P = 5e‐04 | 0.661 | 483.05 | 0 |
| GDVI2 | 0.80, P < 0.0001 | — | 0.644 | 493.35 | 10.3 |
| NDVI | 0.73, P < 0.0001 | 0.10, P = 0.0497 | 0.622 | 510.61 | 27.56 |
| NDVI | 0.79, P < 0.0001 | — | 0.616 | 512.52 | 29.47 |
| GNDVI | 0.78, P < 0.0001 | — | 0.607 | 518.76 | 35.71 |
| GNDVI | 0.76, P < 0.0001 | 0.04, P = 0.4758 | 0.607 | 520.24 | 37.19 |
| NIR | 0.69, P < 0.0001 | — | 0.481 | 589.04 | 105.99 |
| NIR | 0.67, P < 0.0001 | 0.03, P = 0.6723 | 0.481 | 590.86 | 107.81 |
| REG | 0.58, P < 0.0001 | 0.13, P = 0.0481 | 0.463 | 599.7 | 116.65 |
| REG | 0.67, P < 0.0001 | — | 0.455 | 601.67 | 118.62 |
| RED | −0.43, P < 0.0001 | 0.40, P < 0.0001 | 0.45 | 605.63 | 122.58 |
| RED | −0.56, P < 0.0001 | — | 0.31 | 661.45 | 178.4 |
| — | — | 0.55, P < 0.0001 | 0.287 | 669.88 | 186.83 |
| GRE | −0.04, P = 0.4078 | 0.55, P < 0.0001 | 0.289 | 671.18 | 188.13 |
| GRE | 0.02, P = 0.7886 | — | 0 | 755.59 | 272.54 |
— = no covariate was used; AIC = Akaike’s information criterion; ∆AIC = the difference between the AIC of the best model evaluated for that test and the model being reported; GDVI2 = generalized difference vegetation index; GNDVI = green normalized difference vegetation index; GRE = green; NDVI = normalized difference vegetation index; NIR = near infrared; REG = red edge; VI = vegetation index.
All multispecies‐plot models (Table 6) have lower R 2 values than models predicting monoculture cover. The best model for multispecies plots uses only GNDVI and accounts for 29% of the variation in cover. Volume (8/15 models), GNDVI (2/15 models), and red edge (2/15 models) are the most important predictors of cover in multispecies plots (AICw = 0.384, 0.358, and 0.232, respectively).
TABLE 6.
Models of total cover in multispecies plots.
| VI used | VI | Volume | R 2 | AIC | ∆AIC |
|---|---|---|---|---|---|
| GNDVI | 0.46, P = 1e‐04 | — | 0.293 | 29.89 | 0 |
| REG | 0.41, P = 3e‐04 | — | 0.275 | 31.01 | 1.12 |
| GNDVI | 0.42, P = 0.0106 | 0.03, P = 0.7565 | 0.295 | 31.79 | 1.9 |
| NIR | 0.36, P = 4e‐04 | — | 0.258 | 32.05 | 2.16 |
| NDVI | 0.41, P = 4e‐04 | — | 0.257 | 32.07 | 2.18 |
| REG | 0.35, P = 0.0158 | 0.07, P = 0.5169 | 0.282 | 32.55 | 2.66 |
| NDVI | 0.32, P = 0.0198 | 0.10, P = 0.3165 | 0.275 | 32.98 | 3.09 |
| RED | −0.28, P = 0.0256 | 0.18, P = 0.0250 | 0.267 | 33.47 | 3.58 |
| NIR | 0.30, P = 0.0259 | 0.07, P = 0.4732 | 0.267 | 33.49 | 3.6 |
| GDVI2 | 0.28, P = 0.0892 | 0.15, P = 0.1058 | 0.228 | 35.74 | 5.85 |
| GDVI2 | 0.42, P = 0.0045 | — | 0.177 | 36.58 | 6.69 |
| — | — | 0.24, P = 0.0052 | 0.171 | 36.88 | 6.99 |
| RED | −0.36, P = 0.0053 | — | 0.171 | 36.92 | 7.03 |
| GRE | 0.01, P = 0.9353 | 0.23, P = 0.0061 | 0.172 | 38.87 | 8.98 |
| GRE | 0.03, P = 0.7293 | — | 0.003 | 45.03 | 15.14 |
— = no covariate was used; AIC = Akaike’s information criterion; ∆AIC = the difference between the AIC of the best model evaluated for that test and the model being reported; GDVI2 = generalized difference vegetation index; GNDVI = green normalized difference vegetation index; GRE = green; NDVI = normalized difference vegetation index; NIR = near infrared; REG = red edge; VI = vegetation index.
Phylogenetic signal of functional traits correlated with biomass and NDVI
Traits exhibit high variation in phylogenetic heritability (see Supplement 18 on GitHub and Zenodo, see Data Availability statement), but overall the multivariate trait space is moderately predicted by phylogeny, with plants largely intermixed in trait space by family, although the Fabaceae and Poaceae stand out as distinct (Fig. 4). Stem dry‐matter content and vegetative height, two of the traits most strongly correlated with productivity, show low phylogenetic heritability (stem dry‐matter content: λ < 0.00001, K = 0.00263; vegetative height: λ < 0.00001, K = 0.00651) (Fig. 5, Supplement 18 [available on GitHub and Zenodo, see Data Availability statement]). Leaf thickness and circularity are also strongly correlated with biomass and have moderate estimates of phylogenetic heritability (λ = 0.43687 and 0.33924, respectively). Seed mass is weakly positively correlated with productivity and has moderate phylogenetic heritability (λ = 0.0771). The three traits with particularly strong phylogenetic heritability (genome size, λ = 0.88188; leaf nitrogen content, λ = 0.80715; leaf length, λ = 0.5112; and leaf width, λ = 0.40038) were weakly correlated with biomass and NDVI (Fig. 5). All measures of Blomberg’s K were significantly less than 1, suggesting that the variance for each trait measured is relatively high within the sampled clades vs. among clades. Genome size, leaf nitrogen content, and specific leaf area had the highest measures (K = 0.02821, 0.01307, and 0.01013, respectively).
FIGURE 4.
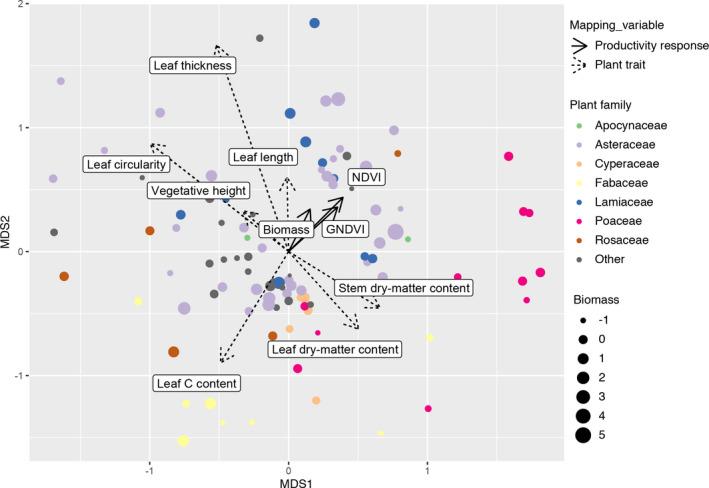
Non‐metric multidimensional scaling ordination of all 127 species, given their functional traits. Point size shows biomass centered and scaled to have a mean of 0 and standard deviation of 1.
FIGURE 5.
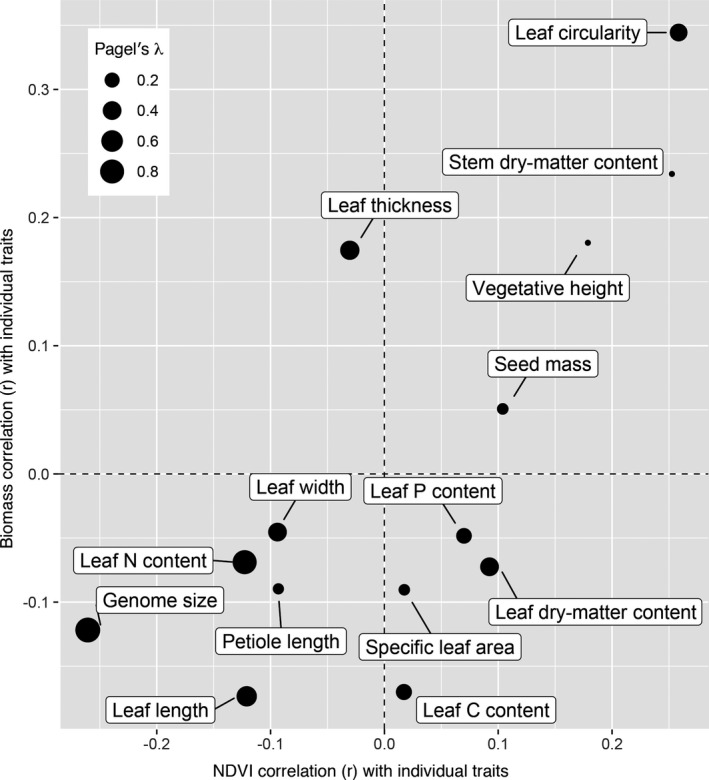
Correlation of biomass and NDVI with individual traits. Size of dots represent phylogenetic heritability, as estimated using Pagel’s λ. The traits with greatest heritability (lower left; i.e., leaf nitrogen [N] content and genome size) are weakly correlated with biomass and NDVI, whereas traits with a high correlation have low heritability (upper right; i.e., stem dry‐matter content, vegetative height).
The correlation between the pairwise VI dissimilarity and phylogenetic distance was not statistically significant (see Supplement 19 on GitHub and Zenodo, see Data Availability statement), but biomass was significantly correlated with phylogeny using the same Mantel tests (r = 0.4476, P < 0.001). Our pairwise species‐level VIs were also not significantly correlated with the pairwise VIs described by Schweiger et al. (2018) (r = 0.0089, P = 0.468), likely because our VIs were collected at the plot level instead of the leaf level and thus less closely tied to individual species.
DISCUSSION
Predictive ability depends on vegetation diversity
Our study demonstrates that the predictive ability of all remote sensing metrics varies depending on diversity, but indicates that the drone‐based quantification of vegetation volume is a useful estimator in both monoculture and multispecies plots, explaining 34% and 47% of the variation in biomass, respectively. Of the predictors we tested for biomass, we found that volume is the most important for multispecies plots (cumulative AICw = 0.999) and second‐most important (after planted cover) for monoculture plots (cumulative AICw = 0.999). Only one combination of covariates (volume and red edge) estimates biomass in multispecies plots better than volume alone (R 2 = 0.50, ΔAIC = 0.62). Conversely, volume is less effective at predicting biomass in monoculture plots than 58/89 combinations of covariates based on ΔAIC (volume and total or planted cover with or without any VI or single band; planted cover with or without any VI or single band; planted cover alone; volume and corrected or uncorrected NDVI, GNDVI, red edge, or near‐infrared, or corrected green or red), which explain up to 46% of the variation in biomass (see Supplement 10 on GitHub and Zenodo, see Data Availability statement). This finding is particularly interesting because the variance in biomass among monoculture plots is higher than the variance among multispecies plots (Fig. 3). This is what we would expect, as the monoculture plots contain the extremes of growth form whereas multispecies plots are weighted averages of these extremes; consequently, it is hard to see how the variance of mixture plot variance could not be less than the variance of the monoculture plot variance.
Volume may explain more of the variance in multispecies biomass than monoculture biomass if high‐diversity plots have greater vertical niche partitioning and thus show a tighter correlation between volume and biomass due to a more complete filling of the volume estimated by photogrammetry. Vertical niche partitioning may result in more efficient space filling in the multispecies plots: species with different growth forms may exploit vertical layers more efficiently, mirroring canopy packing in diverse forests (Jucker et al., 2015). In monocultures, individuals of the same species are more likely to occupy the same level, leading to empty space under the highest vegetation layer. Because volume is estimated from the outermost layer of vegetation only, empty space will result in lower measured biomass but will have no effect on estimated volume. Therefore, monocultures will likely have a looser relationship between biomass and volume. Because of the limitations of our sampling that make it impossible to tease apart complementarity from selection effects in the multispecies plots (see discussion above), we cannot directly test the hypothesis here. To further investigate this relationship, LiDAR metrics that identify the density of vegetation at different heights could be useful, as would future analyses in which monoculture biomass and multispecies plot biomass were measured in the same way.
Surprisingly, although NDVI is one of the most commonly used VIs (Pettorelli et al., 2005), it was not the best VI predictor of biomass or vegetation cover in either plot type in our experimental prairie. Based on AICw, GDVI2 was more important in predicting both biomass and cover (cumulative AICw = 0.252 and 0.999, respectively) than NDVI (cumulative AICw = 0.104 and 1.43 × 10−6, respectively) in monoculture plots. In multispecies plots, red edge was the most important spectral predictor of biomass (cumulative AICw = 0.160) and GNDVI was the most important spectral predictor of cover (cumulative AICw = 0.385); by contrast, NDVI was the least important spectral predictor of biomass (cumulative AICw = 0.042) and the third‐most important spectral predictor of cover (cumulative AICw = 0.152). The difference in the best spectral predictors of biomass is likely related to the difference in vegetation density between monoculture and multispecies plots: GDVI2 is more dynamic for less‐dense vegetation (Wu, 2014), whereas red edge is a good indicator of biomass at higher vegetation densities (Cao et al., 2016). Similarly, GDVI2 and GNDVI likely predict cover in monocultures and multispecies plots best because they are more sensitive to variation at low and high vegetation densities, respectively (Gitelson et al., 1996; Wu, 2014). We expect that the patterns we describe here will be generalizable to other grassland community types that are similar in diversity, density, and stratification.
Prairie productivity is driven by phylogenetically labile traits
The traits most strongly correlated with productivity in our study are also traits with low phylogenetic heritability (Fig. 5). Although traits evolving without constraint or selection are expected to track phylogeny (Felsenstein, 1985), natural selection dampens the effect of phylogenetic heritage on trait variation if it is uniform across taxa (e.g., in stabilizing selection) (Hansen, 1997), and even more dramatically when there is convergence between clades in ecologically significant traits (e.g., Cavender‐Bares et al., 2004). Our results suggest that traits responsible for productivity—estimated in our study as biomass and VIs—are more variable within clades than between clades, either due to convergence, stabilizing selection, or pleiotropy on other selected traits. This is not true of all traits; in multivariate space, some plant families segregated based on functional traits (Fig. 4). This is expected if traits in general tend to track phylogeny; while individual traits diverge even under neutral expectations, even a wide range of traits that all fail to track phylogeny closely may track it in aggregate (Givnish and Sytsma, 1997; Cadotte et al., 2017). The mint family (Lamiaceae) and sunflower family (Asteraceae) are particular exceptions in our study as they cover a relatively broad range of trait space, suggesting that trait variance within these lineages may be driving the observed patterns.
These results suggest that additional unmeasured traits associated with phylogeny may drive aboveground productivity. Alternatively, we may be observing a biodiversity effect (Duffy et al., 2017) that correlates with phylogeny, even if individual traits do not. Trait correlations with both productivity and phylogeny may be more complex than our metrics suggest; leaf dry matter content, for example, has been shown to be correlated with productivity (Smart et al., 2017), but is inconsistently correlated with productivity metrics in the current study and exhibits moderate phylogenetic conservatism (Fig. 5). Furthermore, we also assessed whether measures of productivity were correlated with traits that influence productivity, such as leaf carbon content. Although NDVI has been used as a predictive tool for measures of biomass and leaf nitrogen content (Cabrera‐Bosquet et al., 2011), we did not find such a correlation with leaf carbon content, likely because the spectra involved in distinguishing the levels of carbon are different from those involved in detecting nitrogen levels.
Application of high‐resolution imagery in ecological studies
Remote sensing metrics are often used to detect productivity (Wang et al., 2004), as well as species richness and diversity (Gould, 2000); however, few studies examine these three features together (Wang et al., 2016). Here, we find that these three features are interrelated: vegetation diversity affects the relationship between remote sensing metrics and productivity. Specifically, these results suggest that when using metrics derived from imagery to estimate productivity, diversity needs to be considered. We focus on only two levels of diversity (monoculture and multispecies), but future studies using more levels could examine this relationship in more detail.
Our finding that volume is more useful than NDVI in estimating biomass has two important implications: (1) a traditional camera can capture adequate RGB images for volume reconstruction, reducing costs compared to techniques requiring a multispectral sensor; and (2) LiDAR approaches may prove even more accurate, given the informative vegetation structure data. The VIs, particularly NDVI, have been the focus of most previous biomass estimations (Das and Singh, 2012; Goswami et al., 2015), but our results support recent research suggesting that high‐resolution volume data are also a good estimate of biomass (Wallace et al., 2017).
We demonstrate the use of high‐resolution remote sensing imagery to address an ecological question. We find that volume is a good predictor of biomass regardless of diversity. Because structural metrics such as volume are the least expensive remote sensing proxy to obtain, this technique could be used much more widely than those requiring a multispectral sensor. Finally, we find that the relationship between remote sensing proxies of productivity depends on the diversity of the vegetation. The variation in this relationship is likely due to differences in vegetation structure and warrants further investigation.
AUTHOR CONTRIBUTIONS
C.L.S., A.L.H., M.C.G., and B.C.S. designed the experiment. C.L.S., M.C.G., A.T., A.L.H., and B.C.S. conducted the experiment and collected data. C.L.S., N.K., and A.L.H. analyzed the data. C.L.S., A.L.H., N.K., C.H.C., A.T., and B.C.S. wrote and revised the manuscript. All authors approved the final version.
Supporting information
APPENDIX S1. Detailed methods used in this study.
APPENDIX S2. Parameters used for photo processing and orthomosaic production.
ACKNOWLEDGMENTS
The authors thank the dedicated Morton Arboretum weekly prairie volunteers (K. Thomas, R. Czuprynski, P. Tota, J. Knight, and J. Field), as well as all the other adult and youth volunteers who have helped us plant and maintain this experiment. We thank R. Barak (Chicago Botanic Garden), D. Larkin (University of Minnesota), and E. Williams (Chicago Botanic Garden) for collecting data. This work was supported by the National Science Foundation (award #1354551 to A.L.H.) and The Morton Arboretum’s Center for Tree Science. We thank the three anonymous reviewers for their insightful comments and feedback.
Scher, C. L. , Karimi N., Glasenhardt M.‐C., Tuffin A., Cannon C. H., Scharenbroch B. C., and Hipp A. L.. 2020. Application of remote sensing technology to estimate productivity and assess phylogenetic heritability. Applications in Plant Sciences 8(11): e11401.
DATA AVAILABILITY
Scripts and data used in these analyses, as well as all supplements referenced in this article, are available on GitHub (https://github.com/lanescher/prairie‐remote‐sensing‐2020) and on Zenodo (https://doi.org/10.5281/zenodo.3981500; Scher et al., 2020).
LITERATURE CITED
- Amatangelo, K. L. , Johnson S. E., Rogers D. A., and Waller D. M.. 2014. Trait–environment relationships remain strong despite 50 years of trait compositional change in temperate forests. Ecology 95(7): 1780–1791. [DOI] [PubMed] [Google Scholar]
- Ash, J. , Li D., Johnson S., Rogers D. A., and Waller D. M.. 2015. Predicting species‐environment relationships with functional traits for the understory flora of Wisconsin. American Geophysical Union Fall Meeting 2015: B41E–0479. [Google Scholar]
- Bai, C. , Alverson W. S., Follansbee A., and Waller D. M.. 2012. New reports of nuclear DNA content for 407 vascular plant taxa from the United States. Annals of Botany 110: 1623–1629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baltsavias, E. P. 1999. A comparison between photogrammetry and laser scanning. ISPRS Journal of Photogrammetry and Remote Sensing 54(2–3): 83–94. [Google Scholar]
- Barton, K. 2009. Mu‐MIn: Multi‐model inference. R Package Version 0.12.2/r18. Website http://R‐Forge.R‐project.org/projects/mumin/ [accessed 3 November 2020].
- Bates, D. , Mächler M., Bolker B., and Walker S.. 2015. Fitting linear mixed‐effects models using lme4. Journal of Statistical Software 67(1): 1–48. 10.18637/jss.v067.i01. [DOI] [Google Scholar]
- Blomberg, S. P. , Garland T., and Ives A. R.. 2003. Testing for phylogenetic signal in comparative data: Behavioral traits are more labile. Evolution 57(4): 717–745. [DOI] [PubMed] [Google Scholar]
- Burnham, K. P. , and Anderson D. R.. 2002. Model selection and multimodel inference: A practical information‐theoretic approach. Springer, New York, New York, USA. [Google Scholar]
- Burnham, K. P. , and Anderson D. R.. 2004. Multimodel inference. Sociological Methods & Research 33: 261–304. [Google Scholar]
- Cabrera‐Bosquet, L. , Molero G., Stellacci A., Bort J., Nogués S., and Araus J.. 2011. NDVI as a potential tool for predicting biomass, plant nitrogen content and growth in wheat genotypes subjected to different water and nitrogen conditions. Cereal Research Communications 39(1): 147–159. [Google Scholar]
- Cadotte, M. W. , Davies T. J., and Peres‐Neto P. R.. 2017. Why phylogenies do not always predict ecological differences. Ecological Monographs 87(4): 535–551. [Google Scholar]
- Cannon, C. H. , Scher C. L., Gao A., Khan T., and Kua C. S.. 2018. Building a tree observatory. Acta Horticulturae 1222: 85–92. [Google Scholar]
- Cao, Q. , Miao Y., Shen J., Yu W., Yuan F., Cheng S., Huang S., et al. 2016. Improving in‐season estimation of rice yield potential and responsiveness to topdressing nitrogen application with Crop Circle active crop canopy sensor. Precision Agriculture 17(2): 136–154. [Google Scholar]
- Cavender‐Bares, J. , Ackerly D. D., Baum D. A., and Bazzaz F. A.. 2004. Phylogenetic overdispersion in Floridian oak communities. American Naturalist 163(6): 823–843. [DOI] [PubMed] [Google Scholar]
- Cavender‐Bares, J. , Meireles J., Couture J., Kaproth M., Kingdon C., Singh A., Serbin S., et al. 2016. Associations of leaf spectra with genetic and phylogenetic variation in oaks: Prospects for remote detection of biodiversity. Remote Sensing 8(3): 221. [Google Scholar]
- Cavender‐Bares, J. , Gamon J. A., Hobbie S. E., Madritch M. D., Meireles J. E., Schweiger A. K., and Townsend P. A.. 2017. Harnessing plant spectra to integrate the biodiversity sciences across biological and spatial scales. American Journal of Botany 104(7): 966–969. [DOI] [PubMed] [Google Scholar]
- Cerasoli, S. , Campagnolo M., Faria J., Nogueira C., and da Conceição Caldeira M.. 2018. On estimating the gross primary productivity of Mediterranean grasslands under different fertilization regimes using vegetation indices and hyperspectral reflectance. Biogeosciences 15(17): 5455–5471. [Google Scholar]
- Clark, C. M. , Simkin S. M., Allen E. B., Bowman W. D., Belnap J., Brooks M. L., Collins S. L., et al. 2019. Potential vulnerability of 348 herbaceous species to atmospheric deposition of nitrogen and sulfur in the United States. Nature Plants 5(7): 697–705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das, S. , and Singh T. P.. 2012. Correlation analysis between biomass and spectral vegetation indices of forest ecosystem. International Journal Engineering Research and Technology 1(5): IJERTV1IS5369. [Google Scholar]
- Dubayah, R. O. , and Drake J. B.. 2000. Lidar remote sensing for forestry. Journal of Forestry 98(6): 44–46. [Google Scholar]
- Duffy, J. E. , Godwin C. M., and Cardinale B. J.. 2017. Biodiversity effects in the wild are common and as strong as key drivers of productivity. Nature 549: 261–264. [DOI] [PubMed] [Google Scholar]
- Felsenstein, J. 1985. Phylogenies and the comparative method. American Naturalist 125: 1–15. [DOI] [PubMed] [Google Scholar]
- Fischer, R. , Knapp N., Bohn F., Shugart H. H., and Huth A.. 2019. The relevance of forest structure for biomass and productivity in temperate forests: New perspectives for remote sensing. Surveys in Geophysics 40(4): 709–734. [Google Scholar]
- Gitelson, A. A. , Kaufman Y. J., and Merzlyak M. N.. 1996. Use of a green channel in remote sensing of global vegetation from EOS‐ MODIS. Remote Sensing of Environment 58(3): 289–298. [Google Scholar]
- Givnish, T. J. , and Sytsma K. J.. 1997. Consistency, characters, and the likelihood of correct phylogenetic inference. Molecular Phylogenetics and Evolution 7(3): 320–330. [DOI] [PubMed] [Google Scholar]
- Goswami, S. , Gamon J., Vargas S., and Tweedie C.. 2015. Relationships of NDVI, biomass, and leaf area index (LAI) for six key plant species in Barrow, Alaska. PeerJ PrePrints e1127. Published 19 March 2015 [accessed 17 September 2020]. Available from: https://peerj.com/preprints/913/.
- Gould, W. 2000. Remote sensing of vegetation, plant species richness, and regional biodiversity hotspots. Ecological Applications 10(6): 1861–1870. [Google Scholar]
- Hansen, T. F. 1997. Stabilizing selection and the comparative analysis of adaptation. Evolution 51(5): 1341–1351. [DOI] [PubMed] [Google Scholar]
- Harmon, L. J. , Weir J. T., Brock C. D., Glor R. E., and Challenger W.. 2008. GEIGER: Investigating evolutionary radiations. Bioinformatics 24: 129–131. [DOI] [PubMed] [Google Scholar]
- Heinsch, F. A. , Zhao M., Running S. W., Kimball J. S., Nemani R. R., Davis K. J., Bolstad P. V., et al. 2006. Evaluation of remote sensing based terrestrial productivity from MODIS using regional tower eddy flux network observations. IEEE Transactions on Geoscience and Remote Sensing 44(7): 1908–1923. [Google Scholar]
- Hijmans, R. J. , and van Etten J.. 2012. raster: Geographic data analysis and modeling. R package version 2.0‐12. Website https://CRAN.R‐project.org/package=raster [accessed 13 October 2020].
- Hipp, A. L. , Glasenhardt M. C., Bowles M. L., Garner M., Scharenbroch B. C., Williams E. W., Barak R. S., et al. 2018. Effects of phylogenetic diversity and phylogenetic identity in a restoration ecology experiment In Scherson R. A. and Faith D. P. [eds.], Phylogenetic diversity: Applications and challenges in biodiversity science, 189–210. Springer, Cham, Switzerland. [Google Scholar]
- Iverson, L. R. , Ketzner D., and Karnes J.. 1999. Illinois Plant Information Network. Available at https://www.nrs.fs.fed.us/data/il/ilpin/ [accessed 17 September 2020].
- Jucker, T. , Bouriaud O., and Coomes D. A.. 2015. Crown plasticity enables trees to optimize canopy packing in mixed‐species forests. Functional Ecology 29(8): 1078–1086. [Google Scholar]
- Kruskal, J. B. 1964. Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis. Psychometrika 29: 1–27. [Google Scholar]
- Kuznetsova, A. , Brockhoff P. B., and Christensen R. H. B.. 2017. lmerTest Package: Tests in linear mixed effects models. Journal of Statistical Software 82(13): 1–26. 10.18637/jss.v082.i13. [DOI] [Google Scholar]
- Legendre, P. , and Legendre L.. 1998. Numerical ecology, 2nd English edition. Elsevier, Amsterdam, the Netherlands. [Google Scholar]
- Li, D. , Trotta L., Marx H. E., Allen J. M., Sun M., Soltis D. E., Soltis P. S., et al. 2019. For common community phylogenetic analyses, go ahead and use synthesis phylogenies. Ecology 100: e02788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loreau, M. , and Hector A.. 2001. Partitioning selection and complementarity in biodiversity experiments. Nature 412: 72–76. [DOI] [PubMed] [Google Scholar]
- Mahaut, L. , Fort F., Violle C., and Freschet G. T.. 2020. Multiple facets of diversity effects on plant productivity: Species richness, functional diversity, species identity and intraspecific competition. Functional Ecology 34(1): 287–298. [Google Scholar]
- Myneni, R. B. , Hall F. G., Sellers P. J., and Marshak A. L.. 1995. The interpretation of spectral vegetation indexes. IEEE Transactions on Geoscience Remote Sensing 33: 481–486. [Google Scholar]
- Oksanen, J. , Blanchet F. G., Friendly M., Kindt R., Legendre P., McGlinn D., Minchin P. R., et al. 2019. vegan: Community Ecology Package. R package version 2.5‐5. Website https://CRAN.R‐project.org/package=vegan [accessed 13 October 2020].
- Pagel, M. 1999. Inferring the historical patterns of biological evolution. Nature 401: 877–884. [DOI] [PubMed] [Google Scholar]
- Pettorelli, N. , Vik J. O., Mysterud A., Gaillard J. M., Tucker C. J., and Stenseth N. C.. 2005. Using the satellite‐derived NDVI to assess ecological responses to environmental change. Trends in Ecology and Evolution 20(9): 503–510. [DOI] [PubMed] [Google Scholar]
- R Core Team . 2019. R: A language and environment for statistical computing. The R Foundation for Statistical Computing, Vienna, Austria: Website https://www.r‐project.org/ [accessed 13 October 2020]. [Google Scholar]
- Scher, C. L. , Griffoul E., and Cannon C. H.. 2019. Drone‐based photogrammetry for the construction of high‐resolution models of individual trees. Trees ‐ Structure and Function 33(5): 1385–1397. [Google Scholar]
- Scher, C. L. , Karimi N., Tuffin A., and Hipp A.. 2020. lanescher/prairie‐remote‐sensing‐2020: First release (version 1.0.0) [published 12 August 2020]. Available at Zenodo repository: 10.5281/zenodo.3981500 [accessed 13 October 2020]. [DOI]
- Schweiger, A. K. , Cavender‐Bares J., Townsend P. A., Hobbie S. E., Madritch M. D., Wang R., Tilman D., and Gamon J. A.. 2018. Plant spectral diversity integrates functional and phylogenetic components of biodiversity and predicts ecosystem function. Nature Ecology and Evolution 2(6): 976–982. [DOI] [PubMed] [Google Scholar]
- Shen, M. , Chen J., Zhu X., Tang Y., and Chen X.. 2010. Do flowers affect biomass estimate accuracy from NDVI and EVI? International Journal of Remote Sensing 31(8): 2139–2149. [Google Scholar]
- Smart, S. M. , Glanville H. C., del Carmen Blanes M., Mercado L. M., Emmett B. A., Jones D. L., Cosby B. J., et al. 2017. Leaf dry matter content is better at predicting above‐ground net primary production than specific leaf area. Functional Ecology 31(6): 1336–1344. [Google Scholar]
- Sober, E. 2002. Instrumentalism, parsimony, and the Akaike framework. Philosophy of Science 69: S112–S123. [Google Scholar]
- Solazzo, D. , Sankey J. B., Sankey T. T., and Munson S. M.. 2018. Mapping and measuring aeolian sand dunes with photogrammetry and LiDAR from unmanned aerial vehicles (UAV) and multispectral satellite imagery on the Paria Plateau, AZ, USA. Geomorphology 319: 174–185. [Google Scholar]
- Sonnier, G. , Johnson S. E., Amatangelo K. L., Rogers D. A., and Waller D. M.. 2014. Is taxonomic homogenization linked to functional homogenization in temperate forests? Global Ecology and Biogeography 23(8): 894–902. [Google Scholar]
- Spiess, A.‐N. 2018. qpcR: Modelling and analysis of real‐time PCR data. Package version 1.4‐1. Website https://CRAN.R‐project.org/package=qpcR [accessed 3 November 2020].
- Tucker, C. J. 1979. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sensing of Environment 8(2): 127–150. [Google Scholar]
- USDA‐NRCS . 2019. Web soil survey. Website http://websoilsurvey.sc.egov.usda.gov/ [accessed 3 November 2020].
- Wallace, L. , Hillman S., Reinke K., and Hally B.. 2017. Non‐destructive estimation of above‐ground surface and near‐surface biomass using 3D terrestrial remote sensing techniques. Methods in Ecology and Evolution 8(11): 1607–1616. [Google Scholar]
- Wang, J. , Rich P. M., Price K. P., and Kettle W. D.. 2004. Relations between NDVI and tree productivity in the central Great Plains. International Journal of Remote Sensing 25(16): 3127–3138. [Google Scholar]
- Wang, K. , Franklin S. E., Guo X., and Cattet M.. 2010. Remote sensing of ecology, biodiversity and conservation: A review from the perspective of remote sensing specialists. Sensors 10(11): 9647–9667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, R. , Gamon J., Montgomery R., Townsend P., Zygielbaum A., Bitan K., Tilman D., and Cavender‐Bares J.. 2016. Seasonal variation in the NDVI–species richness relationship in a prairie grassland experiment (Cedar Creek). Remote Sensing 8(2): 128. [Google Scholar]
- Wu, W. 2014. The Generalized Difference Vegetation Index (GDVI) for dryland characterization. Remote Sensing 6(2): 1211–1233. [Google Scholar]
- Xue, J. , and Su B.. 2017. Significant remote sensing vegetation indices: A review of developments and applications. Journal of Sensors 2017: 1353691. [Google Scholar]
- Yu, T. , Sun R., Xiao Z., Zhang Q., Liu G., Cui T., and Wang J.. 2018. Estimation of global vegetation productivity from global land surface satellite data. Remote Sensing 10(2): 327. [Google Scholar]
- Zanne, A. E. , Tank D. C., Cornwell W. K., Eastman J. M., Smith S. A., Fitzjohn R. G., McGlinn D. J., et al. 2014. Three keys to the radiation of angiosperms into freezing environments. Nature 506: 89–92. [DOI] [PubMed] [Google Scholar]
- Zhang, C. , and Kovacs J. M.. 2012. The application of small unmanned aerial systems for precision agriculture: A review. Precision Agriculture 13(6): 693–712. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
APPENDIX S1. Detailed methods used in this study.
APPENDIX S2. Parameters used for photo processing and orthomosaic production.
Data Availability Statement
Scripts and data used in these analyses, as well as all supplements referenced in this article, are available on GitHub (https://github.com/lanescher/prairie‐remote‐sensing‐2020) and on Zenodo (https://doi.org/10.5281/zenodo.3981500; Scher et al., 2020).


