Electronic Control of Spin-Crossover Properties in Four-Coordinate Bis(formazanate) Iron(II) Complexes

Abstract

The transition between spin states in d-block metal complexes has important ramifications for their structure and reactivity, with applications ranging from information storage materials to understanding catalytic activity of metalloenzymes. Tuning the ligand field (Δ_O) by steric and/or electronic effects has provided spin-crossover compounds for several transition metals in the periodic table, but this has mostly been limited to coordinatively saturated metal centers in octahedral ligand environments. Spin-crossover complexes with low coordination numbers are much rarer. Here we report a series of four-coordinate, (pseudo)tetrahedral Fe(II) complexes with formazanate ligands and demonstrate how electronic substituent effects can be used to modulate the thermally induced transition between S = 0 and S = 2 spin states in solution. All six compounds undergo spin-crossover in solution with T_1/2 above room temperature (300–368 K). While structural analysis by X-ray crystallography shows that the majority of these compounds are low-spin in the solid state (and remain unchanged upon heating), we find that packing effects can override this preference and give rise to either rigorously high-spin (6) or gradual spin-crossover behavior (5) also in the solid state. Density functional theory calculations are used to delineate the empirical trends in solution spin-crossover thermodynamics. In all cases, the stabilization of the low-spin state is due to the π-acceptor properties of the formazanate ligand, resulting in an “inverted” ligand field, with an approximate “two-over-three” splitting of the d-orbitals and a high degree of metal–ligand covalency due to metal → ligand π-backdonation. The computational data indicate that the electronic nature of the para-substituent has a different influence depending on whether it is present at the C–Ar or N–Ar rings, which is ascribed to the opposing effect on metal–ligand σ- and π-bonding.

Introduction

Molecular materials that can be switched between two (or more) spin states are of interest for their potential application in electronic devices such as sensors and data storage. In addition to materials applications, compounds in different spin state have vastly different reactivity, and this has implications in catalytic reactions both in biology and in synthetic chemistry.¹ Although initial observations of spin-crossover behavior were described by Cambi and co-workers as early as 1931,² it took more than 50 years before a more general understanding of the phenomenon was developed and its relevance more widely appreciated.³ Despite the advances in the past decades, it is still not straightforward to rationally design spin-crossover compounds. This is a reflection of the small energy difference that is associated with a change in spin state. The vast majority of compounds that show spin-crossover behavior is based on six-coordinate transition metal complexes.⁴ The energies within the d-orbital manifold (e.g., the ligand-field splitting energy, Δ_O, in an octahedral complex) can be manipulated by exploiting ligand effects, which allows tuning of the relative stability of the various spin states.⁵ Complexes based on a d⁶ Fe(II) ion coordinated by six nitrogen-based ligands (FeN₆) are arguably the most well-studied examples of spin-crossover compounds due to the large change in magnetism that results from transitions between the low-spin, diamagnetic (S = 0) state to a high-spin (S = 2) state.⁶ Changes in the steric and/or electronic properties of the ligands bound to the metal center are known to alter the spin-crossover behavior, which can most concisely be described by the so-called spin-crossover temperature (T_1/2), that is, the temperature at which both spin states are equally populated. At this temperature, the difference in enthalpy (ΔH) between the low- and high-spin states is equal to the difference in the entropic contribution to the Gibbs free energy (TΔS).

In addition to the influence exerted on spin-crossover properties by ligands that are directly attached to the metal center, the importance of packing effects (in the solid state), the influence of the (noncoordinating) counterions, and intermolecular interactions (e.g., hydrogen bonding) can be of similar magnitude as (or even more important than) intrinsic molecular properties, and these effects can lead to interesting cooperative behavior.^4,7,8

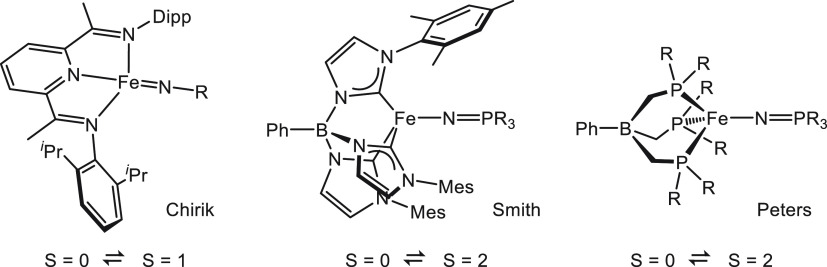
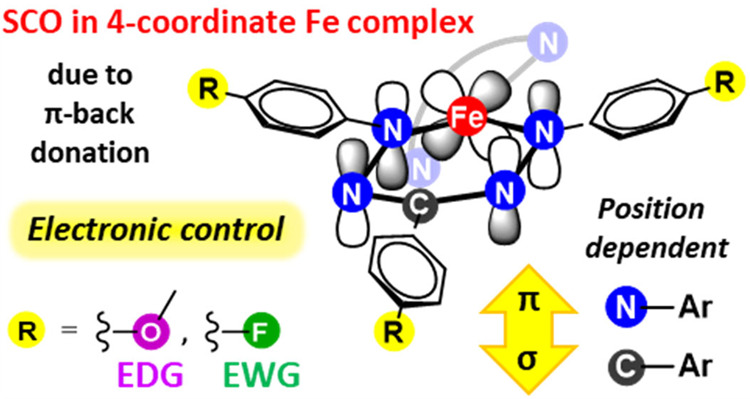
In contrast to the established class of octahedral compounds, four-coordinate 3d transition metal complexes have much smaller splitting energies and are therefore in general high-spin. For Fe(II) compounds, a few notable exceptions are known: Chirik’s square-planar (PDI)Fe imido complexes (PDI = pyrridinediimine),⁹ and complexes with tris(carbene)- or tris(phosphine)borate ligands in the presence of phosphoraniminato coligands by Smith¹⁰ and Peters,¹¹ respectively, have been reported to show spin-crossover (Chart 1). The latter compounds are unique in the sense that the geometrical constraints in the ligand enforce a trigonal symmetry (“umbrella” distortion) that leads to a d-orbital energy splitting diagram resembling that of an octahedron.^12,13 In combination with a strong π-donor as the fourth ligand this has been shown to result in spin-crossover behavior that may be tuned via steric and electronic substituent effects.^10b In 2016, we reported a four-coordinate Fe(II) spin-crossover complex with formazanate ligands.¹⁴ The unusual stability of the low-spin state in this compound was shown to originate from an “inverted” ligand field that is due to the π-acceptor properties of the ligand which stabilizes one of the d-orbitals that is antibonding in a “classical” tetrahedral complex and gives rise to a “two-over-three” splitting pattern reminiscent of an octahedral ligand field. Metal complexes in low-coordinate environments are important from the perspective of reactivity/catalysis, and thus an understanding of the ways in which the spin state of such compounds can be modulated is highly desirable. In this contribution we evaluate the influence of electronic substituent effects on spin-crossover properties in triarylformazanate iron(II) complexes. Combining solid-state structural analysis from X-ray crystallography, spin-crossover thermodynamics in solution (NMR, UV/vis), and computational studies, we delineate the factors that govern spin-crossover in this class of compounds. The data indicate that para-substituents on the ligand N–Ar or C–Ar rings have an opposite effect on solution thermodynamics, which can be ascribed to competing influences on metal–ligand σ- and π-bonding.

Chart 1.

Results and Discussion

Synthesis of Bis(formazanate) Iron(II) Complexes

Treatment of Fe[N(SiMe₃)₂]₂ with 2 equiv of formazan L1H on the NMR scale in THF-d₈ resulted in complete conversion of the starting materials and appearance of the signals of the known bis(formazanate) iron complex 1,¹⁴ with concomitant formation of HN(SiMe₃)₂. Performing the reaction on a preparative scale, followed by crystallization from hot hexane, gave compound 1 in a good isolated yield of 84%. This synthetic protocol was subsequently performed with a variety of formazanate ligands (L2H–L6H) that differ in their substitution patterns, which in all cases led to straightforward, clean formation of the new homoleptic bis(formazanate) iron complexes 2–6 with minimal work-up involved (Scheme 1). Compounds 1–6 all have symmetric triaryl formazanate ligands differing from each other from the substituents in the para-position of the aromatic rings, which allows us to investigate electronic effects on spin-crossover in these compounds without structural perturbations due to changes in steric properties. Specifically, we focus on a comparison between electron-withdrawing (R = F) and electron-donating (R = OMe) substituents on the aromatic groups (−C₆H₄-p-R) on either the C or N atoms of the formazanate backbone (R^C and R^N, see Scheme 1).

Scheme 1. Synthesis of Compounds 1–6.

X-ray Crystallography

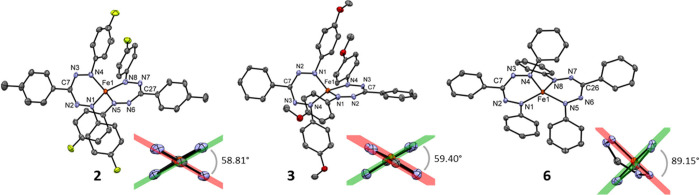
The solid-state structures of compounds 2–6 were established by using X-ray crystallography at 100 K (the structure of 1 was communicated previously¹⁴). As anticipated, the structure determination shows a pseudotetrahedral coordination geometry in which the central Fe ion is coordinated by the terminal nitrogen atoms of two bidentate formazanate ligands. The molecular structures of three selected examples (complexes 2, 3, and 6) are shown in Figure 1; a comparison of pertinent metrical parameters is given in Table S1. Similar to the X-ray structure of 1 measured at 100 K,¹⁴ all compounds (with the exception of 6, vide infra) feature short Fe–N bond lengths in the range 1.809–1.847 Å that are indicative of a low-spin state for the complexes 2–5. Structurally related high-spin Fe(II) complexes have been reported to have significantly larger Fe–N distances (e.g., 1.98 Å in [(1)FeX₂][NBu₄],¹⁵ 2.02 Å in a bis(β-diketiminate)iron complex¹⁶). In addition, the intraligand N–N bonds in 1–5 are slightly elongated (1.32–1.33 Å) compared to the typical bond lengths found in complexes with triarylformazanate ligands (1.29–1.31 Å). These features can be attributed to π-backdonation from a filled Fe d-orbital into the empty π*-orbital of the formazanate ligand.¹⁴ In agreement with this notion, complexes 1–5 show a flattening of the tetrahedral geometry, with dihedral angles ∠(N–Fe–N)/(N–Fe–N) between the ligand coordination planes of around 60° for 1–4 and ca. 70° for 5. The substantial distortion from 90° allows maximizing of the π-backbonding interaction without causing prohibitive steric pressure between adjacent N–Ar groups.

Figure 1.

Molecular structure of compounds 2, 3, and 6 showing 50% probability ellipsoids; hydrogen atoms are omitted for clarity. The inset for each shows the Fe(NNCNN)₂ core of the structure with the N–Fe–N planes and their dihedral angle.

Even though compound 1 was shown to undergo spin-crossover in the solid state at 428 K,¹⁴ differential scanning calorimetry (DSC) for compounds 2–4 does not indicate changes to these compounds up to the decomposition temperature, indicating that in the solid state no spin-crossover occurs.

To our surprise, the molecular structure (determined by X-ray crystallography at 100 K) of the closely related compound 6, which differs only from 1 by the absence of the p-tolyl R^C = Me groups in the C–Ar position, is markedly different (Figure 1). Instead of the “flattened” tetrahedral structure observed for 1–5, the formazanate ligands in 6 are virtually perpendicular to each other, with a dihedral angle between the ligand coordination planes of 89.15(9)°. Moreover, the Fe–N distances in the solid-state structure of 6 are long (1.9532(15)–1.9812(15) Å), suggesting that 6 is high-spin. The result that 1 and 6 are distinctly different in the solid state is unexpected: analysis of close contacts in the solid-state structures does not provide evidence for differences in intermolecular interactions, and it thus appears that subtle effects (e.g., packing in the solid state) can be sufficient to override any electronic preference for either geometry (and, by extension, spin state). The importance of solid-state packing effects is well-established in six-coordinate Fe(II) spin-crossover compounds, where factors such as crystal density (polymorphs), π–π stacking interactions, or the incorporation of different (noncoordinating) anions can have significant effects on spin-crossover.^7a

For compound 5, the observation of an endothermic peak at 448 K in the DSC curve (see the Supporting Information) suggested that this compound could show spin-crossover in the solid state. Moreover, the interligand dihedral angle in compound 5 of 69.38(7)° is closer to the high-spin value than that in 1–4. A variable temperature X-ray crystallography study for 5 indeed provided evidence for a (gradual) spin transition in the solid. Analysis of the data between 100 K and room temperature suggests little change, with consistently short Fe–N distances (average 1.830–1.838 Å) and dihedral angles between ligand coordination planes of 69.4(1)°–70.6(1)°. Upon going to higher temperatures, a steady increase in both metrical parameters is observed, reaching an average Fe–N bond length of 1.930 Å at 425 K and an NFeN/NFeN angle of 77.8(4)° (Figure 2). Attempts to determine the structure at even higher temperature (450 K) resulted in reasonable diffraction images (given the high temperature), but indexing of the spots was problematic. From the time evolution of the diffraction images at 450 K it appeared that the crystal gradually underwent a single-crystal-to-single crystal transformation during data acquisition. Subsequent cooling and data collection at room temperature allowed determination of the newly formed crystal structure. Although the crystal still shows a monoclinic setting (space group P2₁/n), there are slight changes to the unit cell parameters which result in a volume that is noticeably smaller (3673.0(4) and 3564.9(6) ų before and after heating to 450 K, respectively). The structure determination before heating showed the presence of smeared-out electron density (attributed to a disordered THF solvate molecule) and a high degree of rotational disorder in one of the ligand N–Ph rings. After heating to 450 K, the solvent molecule is lost, and no disorder is observed anymore. The thermally induced loss of solvent from the crystal lattice has been reported to be associated with differences in magnetic properties for many spin-crossover compounds,¹⁷ but for compound 5 that does not appear to be the case: both before and after heating the structures measured at 293 K show virtually identical (short) Fe–N distances and “flattened” tetrahedral coordination geometries (see the Supporting Information for details). It should be noted that the gradual changes in the metrical parameters for 5 stand in marked contrast to the VT crystallography for 1: in the latter compound, the structure is unchanged between 100 and 400 K, but an abrupt transition is observed to take place at 428 K which results in a 7% increase in cell volume in response to the increase in Fe–N distances due to spin-crossover.¹⁴ A recent variable-temperature X-ray diffraction study of a six-coordinate Fe(II) spin-crossover compound showed gradual changes as a function of temperature, which were deconvoluted into purely thermal and spin-transition effects by comparison to the Zn(II) analogue.¹⁸ This analysis suggests that during the gradual transition a random distribution of low- and high-spin molecules occurs rather than the formation of discrete domains.¹⁹ A similar situation is likely the case for 5, since no discrete Braggs peaks are observed for low- and high-spin domains.²⁰

Figure 2.

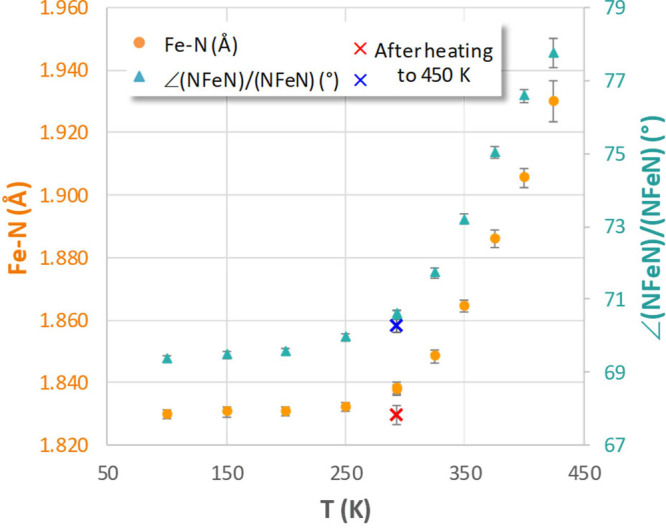
Average Fe–N bond lengths (orange circles) and dihedral angle between ligand coordination planes (blue triangles) as a function of temperature in a single crystal of compound 5. The crosses correspond to the structure after heating to 450 K and loss of the solvent molecule. Error bars show the estimated standard deviations obtained from the X-ray analysis.

Mössbauer Spectroscopy and SQUID Magnetometry Studies in the Solid State

Complexes 1–6 were further characterized by Mössbauer spectroscopy, which provides information about the charge density at the Fe nucleus (via the isomer shift, δ) and the asymmetry of the charge distribution (via the quadrupole splitting, |ΔE_q|). Compounds 2–5 show low isomer shifts of 0.01–0.05 mm/s (Table 1), similar to that of 1 reported previously (0.03 mm/s).¹⁴ Despite the fact that the molecular structure of 6 is distinct from the others, its Mössbauer spectrum (of a powder sample) showed similar parameters as the others (δ = 0.03 mm/s; |ΔE_q| = 1.82 mm/s). Although this is surprising, we demonstrate below that it can be explained by packing effects in the crystalline state.

Table 1. Mössbauer Parameters (δ = Isomer Shift in mm s^–1; |ΔE_q| = Quadrupole Splitting in mm s^–1) for 1–6^a.

	1	2	3	4b	5	6
δexp	0.03	0.01	0.02	0.03	0.05	0.03 (LS)
						0.60 (HS)
δcalcc	–0.03	–0.05	–0.02	–0.04	0.01	0.47 (LS)
						0.51 (HS)
δcalcd	–0.01	–0.01	–0.01	–0.01	–0.01	–0.01 (LS)
						0.55 (HS)
|ΔEq|exp	2.05	2.19	2.19	1.99	1.56	1.82 (LS)
						0.91 (HS)
ΔEq,calcc	–1.93	–1.97	–2.17	–1.79	–1.40	2.85 (LS)
						1.25 (HS)
ΔEq,calcd	–1.46	–1.49	–1.51	–1.47	–1.45	–1.47 (LS)
						1.34 (HS)

^aMeasured in the solid state at 80 K unless noted otherwise.

^bMeasured at 7 K.

^cCalculated by using the crystallographic coordinates; values for 1–5 are for the LS state, except for 6 (LS/HS).

^dCalculated at the optimized geometry for 1–5 (LS, OPBE/def2-TZVP). Values for 6 are given for both spin states (LS/HS).

The Mössbauer parameters for 2–6 were calculated by using the method reported by Neese and co-workers,²¹ using either the crystallographic coordinates or those that result from geometry optimization (Table 1). On the singlet surface, compounds 2–5 converge on minima that closely reproduce the X-ray structures with “flattened” tetrahedral structures and short Fe–N distances (a more detailed discussion of the DFT geometries/energies is provided below), and the calculated Mössbauer isomer shifts (δ = −0.01 mm/s) are in good agreement with those measured experimentally (δ = 0.01–0.05 mm/s). For compound 6, on the other hand, the optimized singlet geometry resembles the other low-spin compounds but is distinctly different from the structure determined by X-ray crystallography. The Mössbauer isomer shift calculations are sensitive to these differences in geometry: at the optimized geometry for LS 6 the computed isomer shift is the same as the others (−0.01 mm/s), whereas using the crystallographic coordinates results in δ = 0.47 mm/s. Geometry optimization of the S = 2 state for 1–6 leads to minima with much longer Fe–N distances (1.99 Å) and dihedral angles between the ligand planes close to 90°; these metrical parameters are similar to those of the X-ray crystal structure of 6. The Mössbauer isomer shift at those geometries is δ = 0.55 mm/s, which may be taken as reference value for the high-spin state in this series of compounds.

Therefore, we hypothesized that the difference in the data for 6 (low-spin according to Mössbauer spectroscopy vs high-spin based on the X-ray crystal structure) may be due to a discrepancy between the properties of 6 in the crystalline state or as a powder. This was evaluated by comparison of the powder X-ray diffraction pattern of a bulk sample of 6 with the simulated pattern based on the single-crystal data. Indeed, the experimental powder diffraction pattern is very different (see Figure S4), confirming that the single-crystal X-ray structure is not representative of the bulk and that packing forces in crystalline 6 are responsible for its structure and spin-state being different from the rest of the series.

Additional support for this notion comes from the observation of a mixture of two Fe-containing species in a different batch of 6: in addition to the low-spin form (15%, δ = 0.03 mm/s, and |ΔE_q| = 1.82 mm/s), the major species (85%) in this sample shows a quadrupole doublet with δ = 0.60 mm/s and |ΔE_q| = 0.91 mm/s. SQUID magnetization data for this sample of 6 gave χ_MT = 2.55 cm³ mol^–1 K in the temperature range 50–300 K, which is consistent with the expected value for a 15:85 mixture of low- and high-spin complex. It should be noted that the Mössbauer parameters for this major species are also in good agreement with the data calculated for high-spin 6 using either the crystallographic coordinates or the optimized quintet geometry. At higher temperature (ca. 390 K), the SQUID magnetization increases to χ_MT = 3.2 cm³ mol^–1 K, in agreement with transition to a fully high-spin sample. This is also observed in the DSC of 6 (Figure S8), which in the first heating cycle shows an endothermic peak at 397 K. After this transition, subsequent cycling indicates exothermic and endothermic peaks at ca. 333 and 348 K, respectively. Because the SQUID data do not indicate a change in magnetization upon cooling, we ascribe these additional features to a phase transition that does not involve a spin-state change. It should be noted that the temperature of the first transition (LS to HS) is again dependent on crystallinity, and grinding the sample of 6 shifts the transition temperature to 421 K.

Whereas compounds 1–4 are low-spin in the solid state over the temperature range that is accessible for SQUID measurements (up to 400 K), the X-ray data for 5 suggest that its magnetic properties are temperature-dependent. As shown in Figure 3, the SQUID data confirm that this is the case: the magnetic susceptibility increases slowly above ca. 250 K. At 400 K, it reaches a value that corresponds to ca. 40% population of the S = 2 state at 400 K, and the process is reversible upon cooling.

Figure 3.

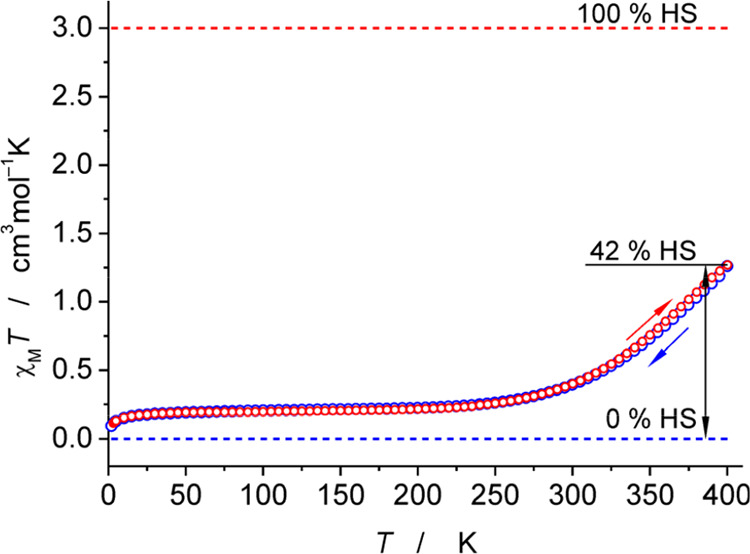
Magnetic susceptibility data for 5 in the solid state. The dashed red and blue lines show spin-only values for S = 2 and S = 0 spin states, respectively.

Variable-Temperature NMR and UV/Vis Spectroscopy in Solution

To study the spin-crossover behavior in the absence of intermolecular interactions and packing effects in the solid state, we turned our attention to solution-phase studies. ¹H NMR spectroscopy at room temperature of compounds 2–6 in THF-d₈ solution showed the expected number of resonances for a symmetrical bischelate structure in the range between δ −10 and +20 ppm. For all compounds, decreasing the temperature led to a shift of the resonances toward the diamagnetic region (between δ −2 and +14 ppm), while at high temperature the signals broaden and are dispersed over a larger chemical shift range (see the Supporting Information). These observations are contrary to the typical Curie behavior expected of a paramagnetic compound but, instead, are in agreement with a temperature-dependent equilibrium between a LS (S = 0) diamagnetic state at low temperature and a HS (S = 2) paramagnet at high temperature.

Monitoring the changes in the ¹H NMR spectrum as a function of temperature allows determination of the thermodynamic parameters for the spin-state equilibrium via eq 1.^10b,22

1

In our analysis, the Curie constant (C) and the changes in enthalpy (ΔH) and entropy (ΔS) are fitting parameters, whereas the chemical shift in the low-spin extreme are either constrained to the value from the lowest temperature NMR data (when the data indicate the low-spin fraction to be close to 1) or estimated from the curve fitting. Excellent fits of the experimental data points are obtained for all compounds (see the Supporting Information), allowing accurate thermodynamic parameters to be extracted (Table 2).

Table 2. Thermodynamic Parameters for the Equilibrium between S = 0 and S = 2 Spin States in THF-d₈ Solution for Compounds 1–6.

	1a	1	2	3	4	5	6
ΔH (kJ mol–1)	22.2 ± 0.3	18.8 ± 0.1	27.2 ± 0.5	8.6 ± 0.2	17.4 ± 0.2	20.6 ± 0.2	17.9 ± 0.1
ΔS (J mol–1 K–1)	64 ± 1	54 ± 1	75 ± 2	29 ± 1	50 ± 1	56 ± 1	54 ± 1
T1/2b (K)	345 ± 7	346 ± 3	361 ± 12	300 ± 15	345 ± 13	368 ± 5	329 ± 4

^aData reproduced from ref (14), measured in toluene-d₈.

^bThe uncertainty in T_1/2 is obtained by using error propagation from ΔH and ΔS.

Solution NMR data for 1 were previously reported in toluene-d₈, but because the solubility of some of the other compounds was significantly better in THF-d₈, we report here measurements of the entire series in the latter solvent. The difference in enthalpy between the low- and high-spin state of 1 is smaller in THF-d₈ (ΔH = 18.8(1) kJ mol^–1) than it is in toluene-d₈ (22.2(3) kJ mol^–1), but at the same time also the entropy change is lower (ΔS = 54.1(4) and 64(1) J mol^–1 K^–1 in THF-d₈ and toluene-d₈, respectively). Coordination of THF is considered unlikely in these compounds, and we conclude that the (small) variation is due to a difference in dielectric constant of the medium, which leads to changes between solvation of the diamagnetic and paramagnetic states.²³ Overall, the thermodynamic parameters that describe the equilibrium lead in both solvents to a spin-crossover temperature that is the same within experimental error (T_1/2 = 345 and 346 K). Despite the distinctly different structural features of 1 and 6 in the solid state (vide supra), their characterization data in solution are very similar, with 6 having a marginally smaller value for ΔH (17.9(1) kJ mol^–1) resulting in a spin-crossover temperature of 329 K. Thus, the effect of the p-tolyl group (R^C = Me) on spin-crossover thermodynamics is small.

A comparison of compounds 1–3 allows electronic effects of the N–Ar groups (Ar = C₆H₄-p-R, with R^N = H (1), F (2), and OMe (3)) to be evaluated.²⁴ An increase in both ΔH and ΔS is observed for the fluoro-substituted compound 2 (ΔH = 27.2(5) kJ mol^–1; ΔS = 75(2) J mol^–1 K^–1). Conversely, the electron-donating methoxy group in 3 results in a significant drop of these values to ΔH = 8.6(2) kJ mol^–1 and ΔS = 29(1) J mol^–1 K^–1. As a consequence of these changes, the spin-crossover temperature is lower in 3 (T_1/2 = 300 K) than it is in 2 (T_1/2 = 361 K).

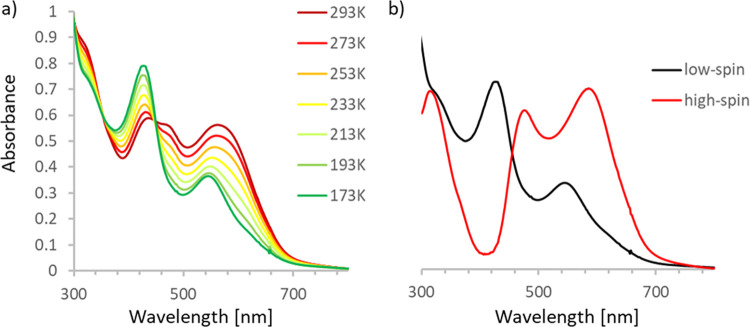
To further probe spin-crossover in solution, the temperature dependence of the UV/vis absorption spectra for 2–6 was evaluated in THF (Figure 4 for 3; for others see the Supporting Information). At 173 K, all compounds show two absorption maxima in the visible range: a low-energy feature is observed between 525 and 550 nm, and an additional absorption occurs at around 405–425 nm. These bands are attributed to the low-spin complexes, as this is the predominant form present at this temperature. The high intensity of both bands and the observation that their position does not significantly change with solvent polarity (see Figure S22 for a comparison of UV/vis spectra in toluene, THF, and 1,2-dichloroethane) are indicative of ligand-based π–π* transitions. Upon warming the UV/vis solutions, the signals broaden due to the appearance of additional spectral features indicating population of the high-spin state. Although at room temperature the spin-crossover is incomplete (<50%), difference spectra indicate that the high-spin state has two new absorption maxima that are shifted to lower energy (around 450–475 and 580–590 nm, respectively). For these dilute solutions, further increasing the temperature results in the appearance of decomposition products (loss of isosbestic points) which is likely due to reaction with adventitious air/moisture. Analysis of the changes in the UV/vis data between 173 and 293 K gives equilibrium parameters that are in good agreement with those from NMR data, corroborating the trends discussed above (see the Supporting Information for details).

Figure 4.

(a) UV/vis spectra for 3 collected in THF solution between 173 and 293 K. (b) Comparison of (normalized) spectral data for the low-spin state (173 K) and high-spin state (from scaled subtraction of the data at 293 and 173 K).

On the basis of these solution characterization data, the following general features emerge. The thermodynamic parameters (ΔH and ΔS) that describe the spin equilibrium in this series vary in a manner that is correlated to the nature of the substituent in the para-position (in particular for the N–Ar groups). Despite this variation, the spin-crossover temperatures are found in a relatively narrow range (T_1/2 = 300–368 K). This is due to a linear relationship between ΔH and ΔS, which leads to a “compensation” effect between enthalpic and entropic contributions to the change in Gibbs free energy (Figure 5).²⁵ Literature reports on electronic substituent effects in spin-crossover compounds have shown contradictory results in different series of pseudo-octahedral compounds, depending on whether inductive effects (i.e., on σ-type metal–ligand interactions)^10b,26 or π-bonding effects²⁷ are most important. A recent report on six-coordinate Fe(II) spin-crossover compounds with di(pyrazol-1-yl)pyridine ligands resolved some of these ambiguities by careful consideration of the position of the substituent in the molecule and the relative impact on metal–ligand σ- or π-bonding interactions.²⁸ In the compounds discussed here, the largest difference in thermodynamic parameters is between compounds that differ in the N–Ar substituent (i.e., 2 and 3), with the fluorinated derivative 2 having the largest values for ΔH and ΔS. The opposite trend is found for the C–Ar substituents: the fluorinated derivative 4 has a relatively low ΔH/ΔS. These empirical trends are in agreement with arguments based on a qualitative analysis of the MO interactions in these compounds, which indicate that the “flattened” structure of the low-spin state is stabilized due to metal-to-ligand (d → π*) backdonation (Figure 6).¹⁴ The π-backbonding interaction lowers one of the d-orbitals (the d_yz orbital that belongs to the t₂ set in a tetrahedral complex) in the low-spin state, while this π-bonding component is reduced in the quintet state. The para-substituents on the N–Ar rings influence the energy of the π*-acceptor orbital of the formazanate backbone, and as a consequence the N–Ar substituents affect the extent of π-backbonding and thus the stabilization of the low-spin state (Figure 6). On the other hand, the C–Ar substituent lies in the nodal plane of the π*-orbital, resulting in a much smaller inductive effect that primarily affects the σ-donor strength.

Figure 5.

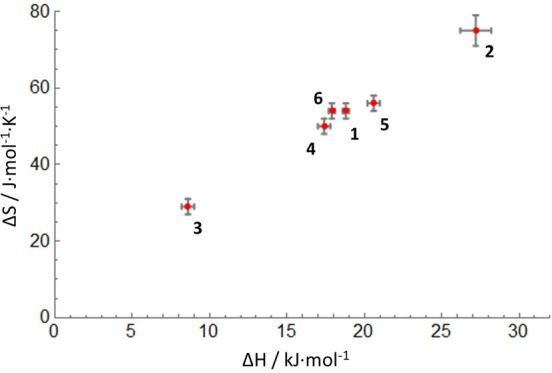
Correlation between ΔH and ΔS in compounds 1–6. Error bars are shown as 2σ in ΔH and ΔS.

Figure 6.

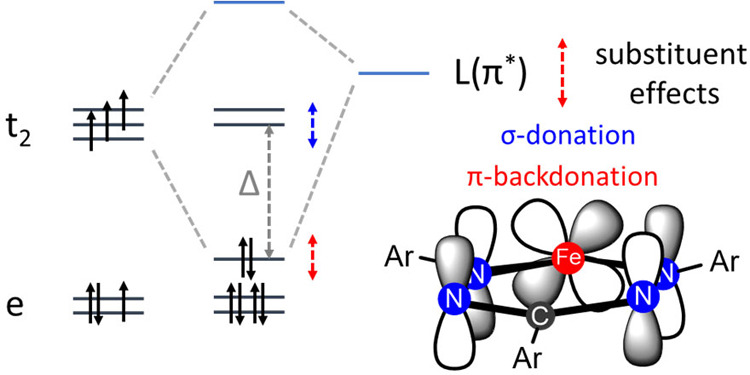
Qualitative MO diagram, showing the d_yz → π* backbonding interaction that stabilizes the low-spin state (only one ligand is shown for clarity).

Computational Studies

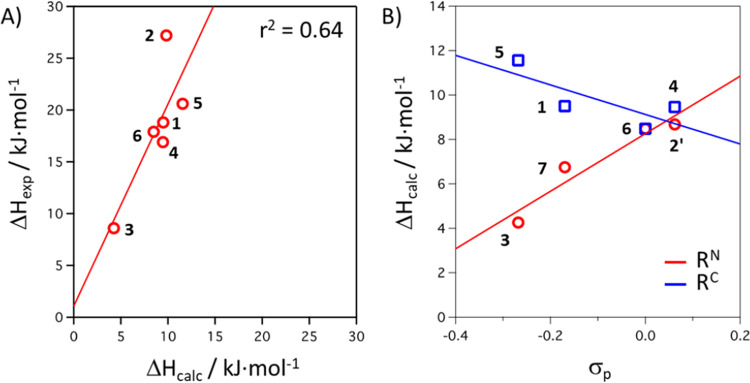
To gain insight into the experimentally observed trends for compounds 1–6, electronic structure calculations at the density functional theory (DFT) level were performed by using Gaussian09.²⁹ Using the OPBE functional³⁰ with a triple-ζ basis set with polarization functions³¹ on all atoms, we fully optimized the structures of compounds 1–6 in both spin states (S = 0 and S = 2). A good agreement for the Fe–N bond lengths is observed between the low-spin minima and the crystallographic data for compounds 1_calc–5_calc, while the high-spin DFT geometry of 6_calc matches closely with the X-ray structure of 6. Similarly, the N–N bond lengths are properly reproduced in the calculations (see Tables S9 and S10). The optimized geometries show an increase of 0.17 Å in the Fe–N bonds associated with the S = 0 → S = 2 transition, which is accompanied by a smaller decrease of the N–N bond lengths. The dihedral angles between the NFeN coordination planes in the low-spin compounds 1–5 are somewhat larger in the DFT-optimized structures than those determined by X-ray crystallography, but the computed structures do show the “flattened” tetrahedral coordination environments typical for these compounds in the low-spin state. The metrical parameters are virtually identical within the series 1_calc–5_calc, which confirms that the para-substituents only lead to small (electronic) perturbations. We subsequently focused on the thermochemistry for spin-crossover calculated at the DFT level. The computed enthalpy changes (ΔH_calc) for the spin-crossover are systematically lower than the empirical data but follow the experimental trends (Figure 7A). An estimation of the corresponding T_1/2 for systems 1–6 can be done by using the thermochemical quantities, and although the computed values are below the experimental ones, also here the experimental trend is properly reproduced (see Table S13). A scan of the potential energy surface with variation of the dihedral angle between the NFeN coordination planes shows that in both spin states the PES is relatively flat around the minima, with changes in the dihedral angle of ±10° only associated with a <5 kJ mol^–1 increase in the electronic energy. The two energy curves show that at the low-spin minimum the energy of the high-spin state lies ca. 45 kJ mol^–1 above, and the two spin states intersect at an interplanar angle of ca. 90° (Figure S58).

Figure 7.

(A) Plot of DFT-calculated vs experimental ΔH values for the equilibrium between low- and high-spin states in 1–6. (B) Plot of ΔH_calc vs the Hammett parameter σ_p for para-substituents at either the N–Ar (R^N) or the C–Ar (R^C) position.

To explain the trends in spin-crossover thermodynamics, we subsequently focused on identifying the origin of substituent effects (R^N and R^C) on the enthalpy differences (ΔH) in the series. If the spin-crossover properties in these complexes are governed by stabilization of the d_yz orbital due to π-backdonation,¹⁴ a correlation is expected between the Hammett parameter σ_p of the N–Ar substituent (R^N) and the enthalpy term ΔH for the spin-state equilibrium. We modeled the C–Ar and N–Ar substitution independently; that is, 2 is replaced with 2′ (R^N = F, R^C = H) and 7 (R^N = Me, R^C = H) is added to the series. A plot of ΔH_calc vs σ_p for complexes with different R^N substituents shows that increasing its electron-withdrawing ability indeed leads to larger values for ΔH_calc, while the opposite effect is seen for the C–Ar para-substituent (R^C, Figure 7B). Although the calculated LS–HS energy differences are small in this series (on the order of a few kJ/mol), the results are in qualitative agreement with basic ligand field arguments: the R^N substituent primarily influences M–L π-bonding whereas R^C has an inductive effect on the M–L σ-bonds.

A comparison of the frontier orbitals shows that the R^N group has the expected effect on the absolute energies of all frontier orbitals via electron-donation/withdrawal, but the relative energies are similar and the orbital splitting changes only slightly. Although the low symmetry in these compounds does not result in the familiar, (near-)degenerate t + e splitting of the d-orbitals, the DFT calculations show a “two-over-three” pattern that is very similar across the series, with a relatively small HOMO–LUMO gap that varies between 9672 cm^–1 (R^N = OMe) and 9936 cm^–1 (R^N = F). In contrast to typical octahedral Fe(II) spin-crossover compounds, as well as the four-coordinate Fe(II) complexes of Smith et al. (>26000 cm^–1),³² these energy gaps are very small and would not normally be associated with spin-crossover behavior. However, the large degree of covalency in the Fe–N bonds in bis(formazanate) iron complexes apparently leads to low interelectronic repulsion through the nephelauxetic effect, favoring the low-spin state. This is further corroborated by intrinsic bond orbital (IBO) analysis. IBOs allow interpretation of the wave function in terms of localized orbitals that provide a chemically intuitive connection with classical (Lewis-type) bonding.³³ Analysis of the IBOs at the iron center in low-spin 6_calc reveals three occupied orbitals that have d-character. Two of these are π-bonding with the ligand as shown by substantial delocalization onto the formazanate N atoms, reflected in the relative charge contributions of the Fe and N centers to the overall orbital occupation (Figure 8). The IBOs are insensitive to substituent effects (both for R^N and R^C), which implies that covalent Fe–N π-bonding causes the unusual d-orbital splitting pattern but is not modulated significantly by the R^N or R^C substituents.

Figure 8.

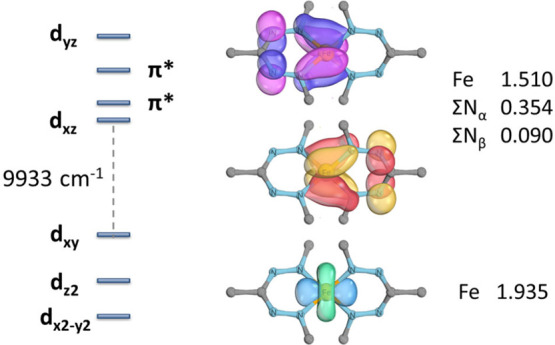
Energy diagram of the frontier orbitals in low-spin bis(formazanate) iron complexes (left) and IBOs with major contribution from the Fe d-orbitals (right; Ar groups omitted for clarity). Values given are the charge contributions of the relevant atoms.

Focusing on the compounds that are shown experimentally to differ the most, i.e., 2 and 3, it is clear that a simplistic explanation based on substituent effects to the ligand-field strength is insufficient to explain the difference in ΔH of 18.6 kJ/mol: there is only a difference of ∼250 cm^–1 in the orbital splitting energies between the two at the DFT level. However, this discrepancy is perhaps not surprising because there are multiple additional contributions that determine spin-crossover thermochemistry (e.g., geometry relaxation and vibrational entropy terms).^25b Regardless, the DFT calculations can capture the trends for the compounds studied here in a qualitatively correct manner. Similar to iron(II) complexes with 2,6-di(pyrazol-1-yl)pyridine ligands,²⁸ the different influence of R^C and R^N substituents suggests that both Fe–L σ- and π-bonding effects are involved, which have an opposing influence on spin-crossover properties.

Conclusions

We have demonstrated that spin-crossover in bis(formazanate) iron(II) complexes is a general feature of this class of compounds. Characterization in the solid state shows that changes in ligand substituents can affect packing forces such that the preference for a more compact low-spin state can be overridden in favor of high-spin, which can be extended to include an example (complex 5) that has sufficient plasticity in the solid state to undergo a gradual, reversible spin transition. In the absence of packing effects, the spin-crossover behavior in solution shows that the thermodynamic values are sensitive to substituent effects, but the high degree of correlation between ΔH and ΔS results in transition temperatures (T_1/2) that are between 300 and 368 K. The most significant differences are observed for compounds 2 and 3, which can be ascribed to the electronic nature of the para-substituent at the N–Ar ring (R^N). The effect of the R^N and R^C substituents on spin-crossover thermodynamics is found to be in the opposite direction, which is related to the competing influence of the substituents R^N/R^C on metal–ligand σ- and π-bonding. More generally, this study provides insight into how the enthalpy and entropy contributions to the spin-state energetics can be manipulated in this class of compounds, but the observed correlation between ΔH and ΔS results in spin-crossover temperatures that are remarkably similar. Extension of this work to break this correlation and obtain a wider range of spin-crossover temperatures will likely require more extensive ligand modifications, for instance through steric effects. Overall, this work provides general access to a novel class of low-coordinate Fe(II) complexes that reliably yield spin-crossover behavior by virtue of the metal–ligand π-covalency. This feature may be more generally applicable to the stabilization of first-row metal complexes in their low-spin state, which we anticipate to be useful in understanding the influence of spin state on reactivity.

Experimental Section

Synthesis of Fe[(C₆H₄(p-F))NNC(p-Tol)NN(C₆H₄(p-F))]₂ (2)

A red THF (15 mL) solution of L2H (439.4 mg, 1.26 mmol) was added to a green solution of Fe[N(SiMe₃)₂]₂ (236.3 mg, 0.63 mmol) in 10 mL of THF. The reaction mixture was stirred for 1 day at room temperature, leading to a dark red solution. The volatiles were removed under vacuum. The product was extracted into THF, and slow diffusion of hexane into the THF solution afforded 2 as dark crystalline material (419.9 mg, 0.52 mmol, 83%). ¹H NMR (400 MHz, THF-d₈, 25 °C): δ 9.08 (4H, C₆H₄(p-F) m-CH), 8.88 (2H, p-Tol m-CH), 6.67 (2H, p-Tol o-CH), 5.50 (3H, p-Tol CH₃), 3.71 (m, THF)* 3.85 (br, 4H, C₆H₄(p-F) o-CH), 1.87 (m, THF)* ppm. ¹H NMR (500 MHz, THF-d₈, −70 °C): δ 8.29 (2H, p-Tol o-CH), 7.35 (2H, p-Tol m-CH), 7.02 (4H C₆H₄(p-F) m-CH), 6.52 (4H, C₆H₄(p-F) o-CH), 3.62 (m, THF)* 2. 41 (3H, p-Tol CH₃), 1.79 (m, THF)* ppm. ¹⁹F NMR (470 MHz, THF-d₈, −70 °C): δ −115.40 ppm. ¹³C NMR (126 MHz, THF-d₈, −70 °C): δ 163.7 (d, ¹J_C–F = 247 Hz, C₆H₄(p-F) ipso C–F), 162.5 (br^‡, C₆H₄(p-F) ipso C–C), 147.7 (ipso N–C = N), 140.3 (p-Tol ipso C–CH₃), 135.9 (p-Tol ipso C–C), 130.3 (p-Tol m-CH), 128.3 (p-Tol o-CH), 127.0 (d, ³J_C–F = 6 Hz, C₆H₄(p-F) o-CH), 115.8 (d, ²J_C–F = 23 Hz, C₆H₄(p-F) m-CH), 21.6 (p-Tol CH₃) ppm. *Crystals of 2 contain 1.5 THF per iron complex based on the SQUEEZE results (120 electrons per unit cell). Based on integration of the ¹H NMR spectrum of 2 in C₆D₆, the bulk sample contains ca. 0.75 THF per iron complex. ^‡The peak is broad due to ⁴J_C–F. Anal. Calcd for C₄₃H₃₆N₈F₄O_0.75Fe: C, 63.87; H, 4.49; N, 13.86. Found: C, 64.14; H 4.33; N, 14.00.

Synthesis of Fe[(p-An)NNC(Ph)NN(p-An)]₂ (3)

A fuchsia THF (15 mL) solution of L3H (421.8 mg, 1.17 mmol) was added to a green solution of Fe[N(SiMe₃)₂]₂ (220.4 mg, 0.59 mmol) in 10 mL of THF. The reaction mixture was stirred for 1 day at room temperature, leading to a dark plum-colored solution. The volatiles were removed under vacuum. The product was extracted into THF, and slow diffusion of hexane into the THF solution afforded 3 as dark powder (322.9 mg, 0.42 mmol, 71%). Single crystals suitable for X-ray analysis were obtained by slow diffusion of hexane into a THF solution. ¹H NMR (500 MHz, THF-d₈, 25 °C): δ 19.31 (4H, p-An m-CH), 17.06 (2H, Ph m-CH), 3.88 (m, THF)*, 3.76 (6H, p-An OCH₃), 2.51 (1H, Ph p-CH), −1.52 (2H, Ph o-CH), 2.01 (m, THF)*, −6.80 (2H p-An o-CH^A), −8.20 (2H p-An o-CH^B) ppm. ¹H NMR (500 MHz, THF-d₈, −70 °C): 12.97 (4H, p-An m-CH), 12.52 (2H, Ph m-CH), 4.40 (2H, Ph o-CH), 3.51 (6H, p-An OCH₃), 3.07 (1H, Ph p-CH), 0.74 (2H p-An o-CH^A), −0.08 (2H p-An o-CH^B) ppm. Attempts to obtain ¹³C NMR data were unsuccessful due to the presence of the high-spin form at −70 °C. *The integration of the peaks of the solvate molecules in the ¹H NMR spectrum of 3 in C₆D₆ indicates 0.25 THF per iron complex. Anal. Calcd for C₄₄H₄₂N₈O_4.5Fe: C, 65.19; H, 5.22; N, 13.82. Found: C, 64.74; H 5.10; N, 13.30.

Synthesis of Fe[PhNNC(C₆H₄(p-F))NNPh]₂ (4)

A red THF (15 mL) solution of L4H (401.7 mg, 1.26 mmol) was added to a green solution of Fe[N(SiMe₃)₂]₂ (237.6 mg, 0.63 mmol) in 10 mL of THF. The reaction mixture was stirred overnight at room temperature, leading to a dark red solution. The volatiles were removed under vacuum. The product was extracted into THF, and slow diffusion of hexane into the THF solution afforded 4 as dark red powder (333.7 mg, 0.48 mmol, 77%). Single crystals suitable for X-ray analysis were obtained by slow diffusion at room temperature of hexane into a THF solution. ¹H NMR (500 MHz, THF-d₈, 25 °C): δ 15.53 (4H, Ph m-CH), 12.46 (2H, C₆H₄(p-F) m-CH), 3.43 (2H C₆H₄(p-F) o-CH), 0.99 (2H, Ph p-CH), −0.97 (br, Ph o-CH) ppm. ¹H NMR (500 MHz, THF-d₈, −65 °C): δ 7.98 (4H, C₆H₄(p-F) m-CH and p-CH), 7.89 (4H, Ph m-CH), 6.66 (2H, Ph p-CH), 5.60 (4H, Ph o-CH) ppm. ¹⁹F NMR (470 MHz, THF-d₈, −65 °C): δ −111.30 ppm. ¹³C NMR (126 MHz, THF-d₈, −65 °C): δ 205.6 (ipso) 170.9 (d, ¹J_C–F = 247 Hz, C₆H₄(p-F) ipso C–F), 147.3 (Ph o-CH), 139.8 (br^‡, C₆H₄(p-F) o-CH), 136.0 (Ph p-CH), 128.16 (Ph m-CH), 125.9 (ipso), 112.5 (d, ²J_C–F = 23 Hz, C₆H₄(p-F) m-CH) ppm. ^‡The peak is broad due to ³J_C–F. Anal. Calcd for C₃₈H₂₈N₈F₂Fe: C, 66.10; H, 4.09; N, 16,23. Found: C, 65.18; H 4.04; N, 15.36.

Synthesis of Fe[PhNNC(p-An)NNPh]₂ (5)

A fuchsia THF (15 mL) solution of L5H (643.4 mg, 2.0 mmol) was added to a green solution of Fe[N(SiMe₃)₂]₂ (376.5 mg, 1.0 mmol) in 10 mL of THF. The reaction mixture was stirred overnight at room temperature, leading to a wine-colored solution. The volatiles were removed under vacuum. The product was extracted into THF, and slow diffusion of pentane into the THF solution afforded dark red crystals of 5 (571.5 mg, 0.8 mmol, 80%). ¹H NMR (500 MHz, THF-d₈, 25 °C): δ 10.61 (4H, Ph m-CH), 9.77 (2H, p-An m-CH), 5.53 (2H p-An o-CH), 4.92 (3H, p-An OCH₃), 3.81 (m, THF)*, 3.47 (2H, Ph p-CH), 2.5–1.5 (br, Ph o-CH), 1.97 (m, THF)* ppm. ¹H NMR (500 MHz, THF-d₈, −70 °C): 8.27 (2H, p-An o-CH), 7.36 (4H, Ph m-CH), 7.29 (2H, p-An m-CH), 7.16 (2H, Ph p-CH), 6.24 (4H, Ph o-CH), 3.98 (3H, p-An OCH₃), 3.69 (m, THF)*, 1.86 (m, THF)*. ¹³C NMR (126 MHz, THF-d₈, −70 °C): δ 185.7 (ipso), 164.3 (ipso), 163.3 (p-An ipso C–OCH₃), 132.2 (p-An o-CH), 131.5 (Ph o-CH), 130.6 (Ph p-CH), 128.6 (Ph m-CH),113.6 (p-An m-CH), 55.7 (p-An OCH₃) ppm. *Crystals of 5 contain 0.5 THF per iron complex. The integration of the peaks of the solvate molecules in the ¹H NMR spectrum of 5 in C₆D₆ indicates 0.4 THF per iron complex. Anal. Calcd for C₄₂H₃₈N₈O_2.5Fe: C, 67.20; H, 5.10; N, 14.93. Found: C, 66.85; H 5.03; N, 14.69.

Synthesis of Fe[(Ph)NNC(Ph)NN(Ph)]₂ (6)

A red THF (15 mL) solution of L6H (454.0 mg, 1.51 mmol) was added to a green solution of Fe[N(SiMe₃)₂]₂ (283.9 mg, 0.75 mmol) in 10 mL of THF. The reaction mixture was stirred for 1 day at room temperature, leading to a dark red solution. The solution was filtered, and the volatiles were removed under vacuum. The solid was washed with cold hexane to afford 6 as dark red powder (422.1 mg, 0.65 mmol, 86% yield). Single crystal suitable for X-ray analysis were obtained by slow diffusion of hexane into a THF solution at −30 °C. ¹H NMR (500 MHz, THF-d₈, 25 °C): δ 14.09 (4H, N-Ph m-CH), 13.16, (2H, C-Ph m-CH), 3.09 (2H, C-Ph o-CH), 0.26 (2H, N-Ph p-CH), 0.15 (1H, C-Ph p-CH), −1.78 (br, 4H, N-Ph o-CH) ppm. ¹H NMR (500 MHz, THF-d₈, −65 °C): δ 8.30 (2H, C-Ph m-CH), 8.02 (4H, N-Ph m-CH), 7.91 (2H, C-Ph o-CH), 6.60 (1H, C-Ph p-CH), 6.54 (2H, N-Ph p-CH), 5.48 (br, 4H, N-Ph o-CH) ppm. ¹³C NMR (126 MHz, THF-d₈, −65 °C): δ 150.9 (N-Ph o-CH), 139.3 (C-Ph o-CH), 137.0 (C-Ph p-CH and N-Ph p-CH), 129.0 (N-Ph m-CH), 125.1 (C-Ph m-CH) ppm. *The integration of the peaks of the solvate molecules in the ¹H NMR spectrum of 6 in C₆D₆ indicates 0.3 THF per iron complex. Anal. Calcd for C_39.2H_32.4N₈O_0.3Fe: C, 69.63; H, 4.83; N, 16.57. Found: C, 68.92; H 4.48; N, 15.29.

X-ray Crystallography

Single crystals of compounds 2–6 (directly obtained from the mother liquor) were mounted on top of a cryoloop and transferred into the cold nitrogen stream (100 K) of a Bruker-AXS D8 Venture diffractometer. Data collection and reduction were done by using the Bruker software suite APEX3.³⁴ The final unit cell was obtained from the xyz centroids of 9985 (2), 4635 (3), 9252 (4), 9634 (5), and 9855 (6) reflections after integration. A multiscan absorption correction was applied based on the intensities of symmetry-related reflections measured at different angular settings (SADABS). The structures were solved by direct methods using SHELXS,³⁵ and refinement of the structure was performed by using SHLELXL.³⁶ For compound 2, refinement was frustrated by the presence of disordered solvent molecules located in two different voids. Attempts to model the electron density allowed identification of THF as the most likely solvate, but the extent of disorder was such that the contribution from these parts of the structure were removed by using the PLATON/SQUEEZE routine.³⁷ For compounds 3 and 4, inspection of the diffraction images and attempts to index the spots indicated it to be twinned. The two orientation matrices of the unit cell were determined by using CELL_NOW.³⁸ After integration of the data with these two unit cell orientations, an absorption correction was performed with TWINABS.³⁹ Initial structure solution was performed with the HKLF4 file; subsequent refinement used the HKLF5 file. For compound 5, refinement indicated the presence of a THF molecule that was disordered over an inversion center. The contribution of this solvate molecule was removed by the PLATON/SQUEEZE routine.³⁷ An additional disorder was indicated by the highly anisotropic displacement parameters of four carbon atoms in one of the N–C₆H₅ rings in the ligand. A three-site disorder model was applied to describe the rotational disorder of this group. The site-occupancy factors of these three components refined to 0.42, 0.38, and 0.20. RIGU instructions were used for the disordered phenyl ring to prevent some atoms from obtaining nonpositive definite displacement parameters. For all structures, the hydrogen atoms were generated by geometrical considerations, constrained to idealized geometries and allowed to ride on their carrier atoms with an isotropic displacement parameter related to the equivalent displacement parameter of their carrier atoms. Crystal data and details on data collection and refinement are presented in Tables S2 and S4.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c10010.

• Full experimental and characterization data, computational details (PDF)

• Crystallographic data for compounds 2−6 (CIF)

• Crystallographic data for the variable-temperature study of compound 5 (CIF)

The authors declare no competing financial interest.