Identifying chromosomal subpopulations based on their recombination histories advances the study of the genetic basis of phenotypic traits

Abstract

Recombination is a main source of genetic variability. However, the potential role of the variation generated by recombination in phenotypic traits, including diseases, remains unexplored because there is currently no method to infer chromosomal subpopulations based on recombination pattern differences. We developed recombClust, a method that uses SNP-phased data to detect differences in historic recombination in a chromosome population. We validated our method by performing simulations and by using real data to accurately predict the alleles of well-known recombination modifiers, including common inversions in Drosophila melanogaster and human, and the chromosomes under selective pressure at the lactase locus in humans. We then applied recombClust to the complex human 1q21.1 region, where nonallelic homologous recombination produces deleterious phenotypes. We discovered and validated the presence of two different recombination histories in these regions that significantly associated with the differential expression of ANKRD35 in whole blood and that were in high linkage with variants previously associated with hypertension. By detecting differences in historic recombination, our method opens a way to assess the influence of recombination variation in phenotypic traits.

Recombination plays a central role in adaptation and evolution, and its influence in human disease is becoming increasingly clear (Alves et al. 2017). During the last decade, our understanding of genome-wide recombination rates and landscape has been greatly increased by the resolution and power of high-throughput data and analysis methods on population samples. Methods that extract recombination signals using linkage between SNPs have been instrumental (Stumpf and McVean 2003; McVean et al. 2004; Kong et al. 2010; Auton and McVean 2012; Alves et al. 2014). However, despite these great advances, the outstanding question on how recombination variability influences phenotypes has lagged behind because there has not been a method to measure recombination variation among individuals in large association studies. A large body of theoretical work, initiated by Nei (1967), has explored the conditions under which the variability of general recombination modifiers evolve (Feldman et al. 1996; Kirkpatrick and Barton 2006), yet empirical studies that link recombination variability in a genomic region with phenotypic traits and fitness are restricted to already known specific modifiers, such as inversions or specific polymorphisms (Stefansson et al. 2005; Hussin et al. 2013; Puig et al. 2015). In this context, we developed recombClust, a pioneering method to detect recombination variability between chromosomes by inferring the differences in recombination histories within a genomic region.

Recombination produces offspring chromosomes with new combinations of maternal and paternal DNA material at each side of a recombination event (Thacker and Keeney 2016). As such, recombination is a main source of novel genetic diversity. At the population level, when multiple recombination events have occurred between two genomic markers, the linkage between them decreases and a random association is then observed. Historic recombination patterns were thus successfully extracted from the linkage between dense SNP markers, strongly matching direct observations on recombination events in sperm samples (Myers et al. 2005). Because linkage methods are population-based estimates, they have been intensely used to compute accurate recombination rates and landscapes in large population samples but, at the same time, have also been disregarded in their ability to detect recombination variation among individuals (Coop and Przeworski 2007), that is, used to infer groups of chromosomes with different recombination histories in a genomic region. However, latent variable mixture models can be incorporated to linkage methods to detect the underlying mixture of chromosome subpopulations, characterized by different recombination patterns. We therefore hypothesized that in a genomic region where the recombination frequency and location are modified in a subpopulation of chromosomes, the chromosomes can be grouped according to consistent recombination histories within that region. The detected chromosome groups could then be tested for association with phenotypes, allowing the use of large cohorts to study the phenotypic effects of recombination variability in a given genomic region.

Here, we propose a method that leverages chromosomal differences in linkage patterns in a target genomic region to classify the chromosomes of a population into groups with different recombination histories. The method, named recombClust, comprises three steps. First, it classifies chromosomes into those with a history of high recombination or with a history of high linkage at a recombination point. The classification is based on the linkage structure between two SNP-blocks flanking the recombination point. A SNP-block is a combination of two contiguous SNPs. Several recombination points are then used to cover the targeted genomic region, each of them flanked by a SNP-block pair producing a chromosome classification. Second, recombClust searches for groups of chromosomes with consistent classifications across all the recombination points, further clustering the chromosomes into subpopulations with common histories of recombination across the region. And third, recombClust reconstructs the spatial recombination pattern for each chromosome subpopulation.

We tested the performance and adequacy of the method using numerous simulated scenarios and showed its ability to detect the correct recombination patterns of known recombination modifiers using real data for Drosophila melanogaster and humans. Finally, we used the method to (1) detect and validate chromosome subpopulations with different historic recombination at 1q21.1, a genomic region at risk of deleterious rearrangements leading to the thrombocytopenia-absent radius (TAR) syndrome (Mefford et al. 2008; Rosenfeld et al. 2012); and (2) to associate the obtained chromosome groups with changes in gene expression in blood. The method is implemented in a computationally efficient tool, compatible with Bioconductor's packages and the Variant Call Format (VCF).

Results

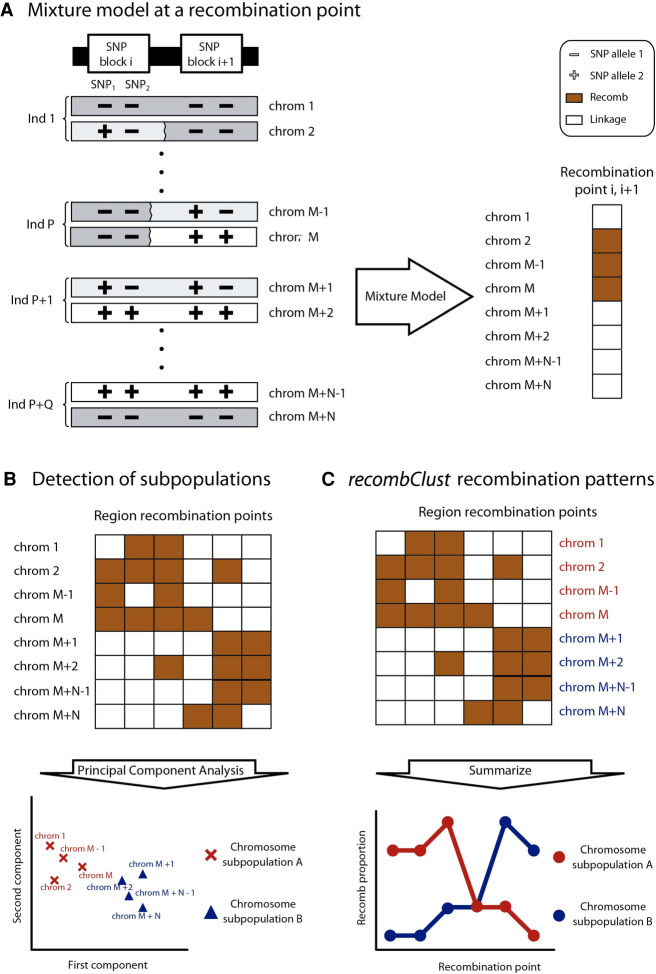
We propose recombClust, a method to classify chromosomes into groups with different recombination histories across a predefined target region (Fig. 1). The method is based on phased SNP data; therefore, it classifies chromosomes. The target region is tiled by SNP-blocks made of multiple contiguous SNPs. The classification of chromosomes into different recombination histories along the target region is performed in two clustering steps. In the first step, the method fits a mixture model of two chromosome groups (recomb/linkage) on a SNP-block pair, flanking one recombination point in the region. In chromosomes of the recomb group, SNP-blocks display random association at the recombination point, whereas in chromosomes of the linkage group, SNP-blocks are in complete association (Fig. 1A). Several classifications are then obtained from fitting the mixture model at recombination points covering the region. In the second step, recombClust classifies chromosomes into subpopulations (A/B) based on a consensus clustering across all the mixture models fitted along the target region (Fig. 1B). The chromosome groups A/B are the subpopulations associated with different historical recombination patterns across the region. This underlying chromosome substructure (A/B) can be used in downstream analysis, such as transcription and methylation profiling or association with phenotypes. Finally, the spatial recombination patterns are reconstructed from the proportion of chromosomes in the recomb group at each recombination point (Fig. 1C).

Figure 1.

recombClust scheme. recombClust is a method to classify chromosomes into underlying recombination patterns using SNP data, which comprises three steps. (A) Mixture model fitting at a recombination point, flanked by a pair of SNP-blocks. A mixture model classifies the chromosomes into recomb (orange) and linkage (white) groups at a recombination point. For simplicity, SNP-blocks are represented with two alleles. Historical recombination between the SNP-blocks is represented by a broken vertical line between the SNP-blocks. Notice that haplotypes in linkage are those that maximize the likelihood of the mixture model and are not the ancestral haplotypes of the population. (B) Chromosome classification into subpopulations A and B. The mixture models provide a recomb/linkage classification at different recombination points across the target region. In the figure, the orange cells of the classification matrix represent chromosomes classified in the recomb population across recombination points (columns). A principal component (PC) analysis is performed on this matrix. The first PCs reveal clusters of chromosomes for which their recomb/linkage classifications are consistent along the target region and therefore share similar recombination patterns. Each chromosome is assigned to a recombination subpopulation (A: red; B: blue), with chromosomes from 1 to M classified as subpopulation A and chromosomes from M + 1 to M + N as subpopulation B. (C) The recombination pattern for each chromosome subpopulation is reconstructed from the proportion of chromosomes in the recomb group at each point in the genomic region.

Modeling the mixture of chromosomes under recombination and linkage

We developed a mixture model to split the chromosomes of a population into those showing high recombination and those showing high linkage history between two SNP-blocks (Methods). Figure 1A illustrates an instance in which the mixture model is fitted between two SNP-blocks. For illustration purposes, only two alleles are shown at each SNP-block (+,−). The mixture model classifies chromosomes in linkage and recomb groups at this recombination point, maximizing the likelihood of the model. Haplotypes in the linkage group are defined in a probabilistic manner. Thus, haplotypes in the linkage group cannot be considered the ancestral haplotypes in the population, but the haplotypes that maximize the likelihood of the model.

Our mixture modeling is applicable to a wide range of theoretical scenarios. To assess its feasibility, we used multiple data sets to determine the characteristics of the mixtures that could affect its performance. These data sets are composed of SNP-block pairs that flanked one recombination point for a group of chromosomes (recomb) but remained in linkage for a second group (linkage) (Methods). In addition, notice that these data sets do not assume realistic linkage disequilibrium within or between the blocks. At this stage, we thus tested the theoretical robustness of our modeling approach, using a wide range of generative mixture models. Relevant biological scenarios were considered in latter simulations.

We first evaluated how the proportion between recomb and linkage populations affected the accuracy of the model to correctly classify the chromosomes, varying the proportion between 0.1 and 0.9. We observed that the mixture model had high accuracy (>80%) across all the proportions range, being optimal, as expected, when the mixture was small, that is, the mixture frequency approached 1 or 0 (Supplemental Fig. S1A). We also observed that the model was robust under different initializations of the mixture frequency (Supplemental Fig. S1B). Overall, our simulations showed that the mixture model was able to robustly split the chromosomes into two groups, one with null LD (recomb) and other with full LD (linkage) between a pair of SNP-blocks.

We then evaluated the accuracy of the model under different within and between SNP-block variabilities, using a fixed scenario with a 0.5 proportion of mixture between the recomb and linkage groups. To test SNP-block variability, we simulated multiple SNP-block pairs, flanking a recombination point, and determined the haplotypes across the blocks. We varied the number of SNP alleles that were different between the most frequent recomb and linkage haplotypes. We thus assessed the extent to which the accuracy of the model was affected by increasing mutation divergence between the groups. We observed that the mixture model had an accuracy of 75% when most frequent haplotypes were shared between groups and topped to 90% when the difference between the haplotypes was given by only one SNP allele (Supplemental Fig. S1C). This suggests a substantial gain in accuracy when the differences in mutation divergence between the groups are small, which, in addition, can be boosted by the presence of one SNP allele that associates with one of the groups. We then assessed the influence of intra-block linkage disequilibrium (i.e., linkage disequilibrium between the SNPs of a SNP-block) on model accuracy. For a scenario of full linkage of the SNPs within all blocks, which reduces to having blocks of 1 SNP, the accuracy dropped to ∼60% (Supplemental Fig. S1D).

Classifying chromosomes into different recombination histories within a genomic region

The second step of recombClust is a consensus clustering of mixture model classifications at numerous points to group chromosomes into consistent recombining groups (A/B) along a targeted genomic region (Fig. 1B). Within the region, all possible SNP-block pairs are tested such that they do not overlap. To speed up the computation, we only considered SNP-block pairs with a distance shorter than 10 kb. Using data from human inv8p23.1, we observed that, above this distance, most SNPs do not show differences in linkage disequilibrium (LD) between inverted and standard subpopulations (Supplemental Fig. S2). For each SNP-block pair, a mixture model is fitted and the chromosomes are classified into the recomb and linkage groups. Because chromosomes can be in recomb at one point of the region and in linkage at another point, a consistent classification over the mixture model predictions was considered. For this step, we applied a clustering method (k-means) on the first two PCA components of the mixture model classification matrix across all recombination points along the region (Fig. 1B). By default, recombClust identifies two clusters based on the first two PCs, although the implementation allows the definition of additional clusters and PCs. The clusters identified were then considered as chromosomes with similar recombination patterns across the region. The mixture model classification matrix was used to reconstruct the spatial recombination pattern of each subpopulation, given by their proportion of recomb classifications at each point (Fig. 1C). This pattern was then compared with the recombination patterns obtained by other linkage-based methods, which are applicable only when the chromosome subpopulation A/B is initially known.

Calibration was then required to test how the number of chromosomes and the number of recombination points affected the overall performance of recombClust modeling. At this stage, we tested whether the method performed as expected in the theoretical scenarios for which it was designed. We thus simulated data sets representing SNP-block pairs that flanked multiple recombination points. We simulated two kinds of idealized scenarios: (1) a mixture population, in which one subpopulation (A) belonged to the recomb group in half of the points and to the linkage group in the other half while a second subpopulation (B) belonged to the linkage and recomb groups, respectively; and (2) a single population in which all chromosomes belonged to the same recombination groups across all recombination points. After the calibration, we considered testing recombClust in more realistic scenarios, because these theoretical situations are unlikely to arise in natural conditions.

First, to assess false discovery rate and statistical power, we selected several calibrating scenarios changing the number of chromosomes per population (from 20 to 60) and the number of recombination points (from 10 to 100). In all cases, we performed a PCA on the mixture model classification matrix (Fig. 1B). Then, using k-means, we clustered the first two PC components in two groups and considered that recombClust detected differences in recombination patterns when the average silhouette value of the clustering was higher than 0.7 (Supplemental Fig. S3; Kaufman and Rousseeuw 1990). We observed that under single population simulations at equilibrium, recombClust had a false discovery rate less than 0.05 for recombination points greater than 70 and for all the number of chromosomes considered (more than 20). In addition, the power to detect different recombination patterns for simulations of chromosomes with two different recombination histories achieved 80% for more than 25 chromosomes and for differences in historical recombination in more than 16 points (Supplemental Fig. S4).

Second, to confirm that the model detected differences in recombination histories rather than allele differences, we compared recombClust classification with that of a PCA on the simulated genotypes. For a simulation with chromosome mixture, we observed a neat separation of the chromosome subpopulations (Supplemental Fig. S5A) with recombClust, which we did not observe for allele differences.

recombClust accurately classifies inversion status based on differences in historic recombination

The alleles of polymorphic inversions differ in the recombination histories inside the inverted region because recombination is suppressed in heterokaryotypes (Alves et al. 2014). As such, inversions offer realistic scenarios to test recombClust. We, therefore, asked the extent to which the inversion alleles, being strong recombination modifiers, could be inferred by recombination differences using recombClust. We first evaluated the method's performance to predict human simulated inversions from the forward-time simulator invertFREGENE. Using real genomic data, we then tested its accuracy to classify validated human and Drosophila melanogaster inversions (Supplemental Table S1). Using invertFREGENE (O'Reilly et al. 2010), we simulated inversions with different lengths (from 50 kb to 1 Mb) and frequencies (from 0.1 to 0.9) and tested the prediction accuracy of chromosome classification into their inversion alleles. We observed an accuracy >90% for inversions larger than 250 kb (Supplemental Fig. S5B). As expected, the accuracy for short inversions was lower as they presented fewer recombination points. recombClust’s mean accuracy was higher (95%) for inversion frequencies between 0.2 and 0.8 (Supplemental Fig. S6) but did not correlate with the inversion's age (r = 0.02, P-value = 0.19) (Supplemental Fig. S7). Finally, we explored the potential effect of population expansion on recombClust accuracy, by simulating 100 inversions with frequency 0.5 and 500 kb length, where the population doubled just before the inversion appeared. In this scenario, recombClust classification perfectly matched inversion status in 99% of the simulations.

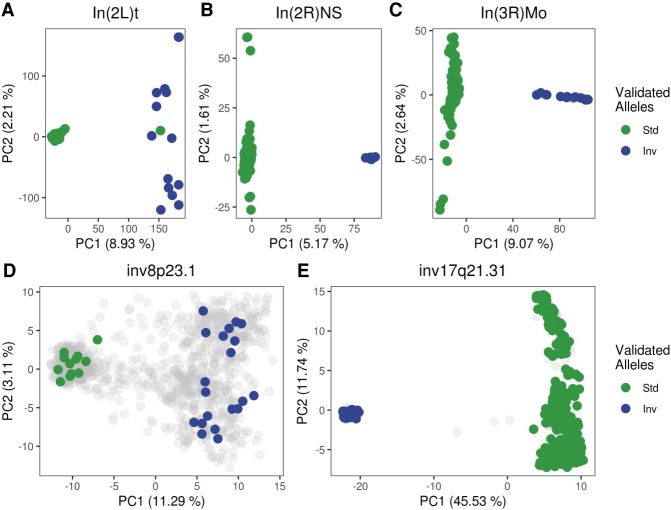
We then used recombClust to determine whether the alleles of three common polymorphic chromosomal inversions in Drosophila melanogaster [In(2L)t, In(2R)NS, and In(3R)Mo] could be identified based on their recombination histories. We ran recombClust on genome-wide SNP data from 205 lines derived from the Raleigh, North Carolina, population, comprised in the Drosophila melanogaster Genetics Reference Panel (DGRP2) (Mackay et al. 2012; Huang et al. 2014) and compared the inferred recombining subpopulations with the experimental inversion alleles of the lines. For all the inversions, we observed clear clustering in the first two PC components of the mixture classification matrix (Fig. 2A–C) that resulted in a 98% match with the inversion alleles when a k-means clustering was applied. Likewise, we compared the recombClust calling of human inversions at 8p23.1 and 17q21.31 with the experimental inversion genotypes, as obtained from the invFEST repository (Martínez-Fundichely et al. 2014) for the European subjects of The 1000 Genomes Project. Using SNP-phased data, we found that recombClust neatly separated inverted and standard chromosomes (Fig. 2D,E) in the first PC component of the mixture model classification matrix. The k-means clustering of the first PC accurately matched the experimental inversion alleles (8p23.1: 100%; 17q21.31: 99.3%). Overall, these results showed that the recombination substructure can reliably identify the inversion alleles of some common inversions in two different species.

Figure 2.

PCAs of recombClust probabilities for chromosomal inversions in Drosophila melanogaster and human. First two principal components of chromosomes, derived from the recombination classification at multiple recombination points along different inverted regions. Each point is a chromosome. Clusters mapping the inversion status in both Drosophila and human inversions are observed. Chromosomes with known inversion genotypes are colored (green: standard, blue: inverted). (A–C) Drosophila inversions in DGRP lines. (D,E) Human inversions in the European individuals of The 1000 Genomes Project. Gray points represent chromosomes either from individuals without experimentally defined inversion status or heterozygous individuals for the inversion.

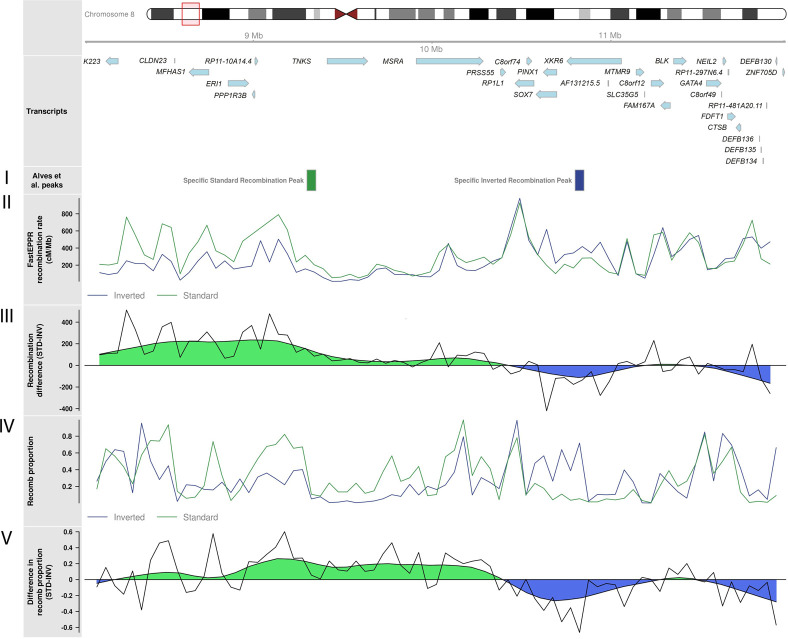
To validate the ability of recombClust to extract underlying groups with different historical recombination patterns, we compared recombClust inferred patterns underlying the 8p23.1 inversion region with the recombination rates independently estimated for chromosomes with known inversion alleles using FastEPRR (Fig. 3, II and IV; Gao et al. 2016). We observed that the inferred proportion of chromosomes in the recomb population across the genomic region (Fig. 1C) accurately captured the underlying recombination patterns obtained by FastEPRR for each of the 8p23.1 inversion alleles. We also observed that the largest differences in recombination proportions were obtained near the recombination peaks described by Alves et al. (2014) (Fig. 3, I). These results confirmed that the chromosome subpopulations identified by recombClust are mapped to different recombination histories.

Figure 3.

Underlying recombination patterns in human inversions 8p23.1 for the European individuals of The 1000 Genomes Project. Ideogram for the 8p23.1 inverted region showing the transcripts in the region. (I) Approximate location of recombination peaks for standard or inverted chromosomes identified by Alves and colleagues (Alves et al. 2014). (II) Recombination rate obtained from FastEPRR independently for standard and inverted chromosomes. (III) Raw and smoothed difference (moving average) in recombination rates between standard and inverted chromosomes as computed from FastEPRR. (IV) The proportion of chromosomes belonging to recomb population in the chromosome subpopulations inferred by recombClust, which accurately predicted inversion status. (V) Raw and smoothed difference (moving average) in the proportion of chromosomes belonging to the recomb population in inverted and standard chromosomes, as predicted by recombClust.

recombClust detects recombination histories associated with ancestral differences

Modifiers of historical recombination patterns include numerous processes other than inversions that can act simultaneously on the same genomic region. In particular, differences in historical recombination patterns between ancestries can derive from random differences in the occurrence of recombination events or from the emergence of hotspot differences regulated by ancestry-specific alleles (Jeffreys and Neumann 2009). As such, we asked to which extent differences between human populations could also be detected in loci already under the influence of inversion alleles. We, therefore, used recombClust to detect underlying recombination modifier alleles corresponding to the human inversions at 8p23.1 and 17q21.31 for all the individuals in The 1000 Genomes Project, covering four different continental populations (Sudmant et al. 2015). We inspected the first two PC components of the mixture model predictions for inv-8p23.1 (Supplemental Fig. S8) and observed multiple clusters, in which chromosomes segregated both by inversion status and ancestry. However, for inv-17q21.31, the additional clusters observed in the standard allele did not map to ancestral differences. The observations on both human inversions confirmed that clusters identified in the first PCs of the mixture model predictions can be interpreted as non-recombining chromosome groups that differ in inversion status, ancestry, or other unobserved factors that suppress recombination between the groups, such as copy number variants likely segregating the chromosomes at 17q21.31 (Steinberg et al. 2012).

recombClust detects recombination histories associated with selection

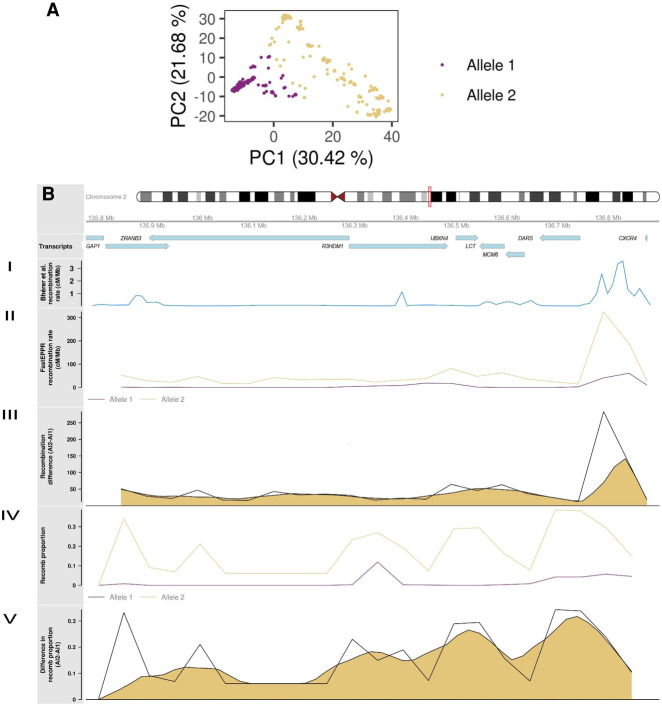
Chromosomes with advantageous alleles show a decrease in recombination around the locus under selection. Although selection, like demography, does not have a direct influence on the biological process of recombination, they modulate the historical recombination patterns (Stumpf and McVean 2003). Therefore, we asked whether recombClust was able to detect chromosomes under selection and recover their recombination patterns. We studied the LCT locus, a human locus known to be under positive selection for lactase tolerance, as defined in PopHumanScan (Chr 2: 135,770,000–136,900,000, hg19) (Murga-Moreno et al. 2019). We aimed to detect the underlying chromosomes under selection and their recombination pattern in the LCT locus, for the European individuals of The 1000 Genomes Project. We observed two chromosomes subpopulations (allele 1/allele 2) by clustering the first PC components of the mixture classification matrix (allele 1: 60.8%; allele 2: 39.2%) (Fig. 4A). Chromosome allele 1 was the most frequent except for the Tuscany population (TSI) (Supplemental Table S2), the only European population which does not show marks of selection in the LCT locus, as reported in PopHumanScan (Murga-Moreno et al. 2019). We also observed a strong correlation between rs4988235 [C/T(-13910)], a SNP linked to lactose persistence, and the inferred subpopulation groups (r² = 0.64), where the allele conferring lactose persistence (T) was very frequent in chromosome allele 1 (83%) and almost absent in chromosome allele 2 (<1%). The ability of recombClust to detect chromosomes under selection was further confirmed by the spatial recombination patterns in the locus. We observed a low and homogenous recombination pattern in group A (lactose persistence group) across the LTC locus, possibly owing to a recent selective sweep (Fig. 4B, II). We also recovered the recombination patterns independently obtained with FastEPRR, for each chromosome subpopulation (Fig. 4B, IV). Recombination peaks for chromosome allele 2 were found between genes R3HDM1 and DARS genes, matching previously reported recombination peaks (Fig. 4B, I; Bhérer et al. 2017).

Figure 4.

Underlying recombination patterns in the LCT locus. (A) First two principal components of chromosomes, derived from the recombination classification at multiple recombination points along the LCT locus. (B) Ideogram for the LCT locus under selection showing the genes in the region. (I) Recombination rates reported by Bhérer and colleagues (Bhérer et al. 2017). (II) Recombination rate obtained from FastEPRR independently for chromosomes with alleles 1 and 2 detected by recombClust. (III) Raw and smoothed difference (moving average) in recombination rates between alleles 1 and 2 as computed from FastEPRR. (IV) The proportion of chromosomes belonging to recomb population in the chromosome subpopulations with alleles 1 and 2, correctly predicting a flat pattern for the allele 1 that is under selection. (V) Raw and smoothed difference (moving average) in the proportion of chromosomes belonging to recomb population in alleles 1 and 2.

recombClust detects recombination differences in complex genomic regions

The region at 1q21.1 between Chr 1: 145,399,075–145,594,214 (hg19) (Albers et al. 2012) is prone to various deleterious rearrangements by nonallelic homologous recombination (NAHR) at the numerous segmental duplications (SD) in the region (Rosenfeld et al. 2012). The rearrangements include microdeletions leading to the thrombocytopenia-absent radius (TAR) syndrome and a range of multiple neurodevelopmental phenotypes caused by duplications and deletions distal to the TAR region (Rosenfeld et al. 2012). Because strong control of recombination is expected in regions at risk of NAHR during meiosis (Sasaki et al. 2010), we hypothesized that different recombination histories would be detectable in this region and aimed to determine their functional correlates.

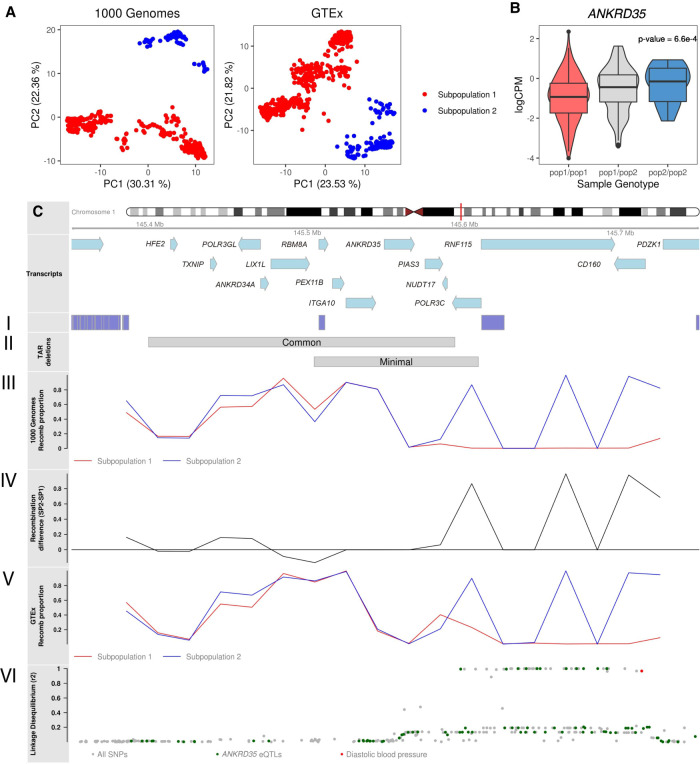
We ran recombClust across the region Chr 1: 145.35–145.75 Mb characterized by four blocks of segmental duplications. The most common deletion for the TAR syndrome is observed between the first and third block (Klopocki et al. 2007), whereas the smallest reported deletion was found between the second and third block (Fig. 5C, I and II; Rosenfeld et al. 2012). We first analyzed the European individuals of The 1000 Genomes Project and observed two clear clusters in the first two PCs of the mixture model classification matrix (Fig. 5A). We defined two chromosome subpopulations (subpopulation 1: 80.9%; subpopulation 2: 19.1%) that were in Hardy-Weinberg equilibrium (P = 1) and thus confirmed our hypothesis for the presence of different recombination histories in the region. We also analyzed a randomly selected region (Chr 1: 14.6–15 Mb) of the same length of the TAR region, but where we did not expect any recombClust signal. We confirmed that no clusters could be clearly defined (Supplemental Fig. S9) and that the first two principal components explained much less variance than those for the TAR or LCT regions.

Figure 5.

Underlying recombination patterns in the TAR syndrome locus. (A) Chromosome subpopulations with different recombination patterns between the coordinates Chr 1: 145.35–145.75 (hg19), as detected in the genomic data of The 1000 Genomes and GTEx projects. (B) Transcriptomic analyses for the genes in the region identified that ANKRD35 transcription is significantly associated with the chromosome population substructure. Individuals are grouped by their chromosome subpopulations (pop1/pop1, pop1/pop2, pop2/pop2). (C) Ideogram for the TAR region showing the genes in the region. (I) Segmental duplications. (II) Location of common and minimal deletions. (III) Proportion of recomb chromosomes in each subpopulation in the 1000 Genomes data. (IV) Difference between the proportion of recomb chromosomes in subpopulation 2 and subpopulation 1 in the 1000 Genomes data. (V) Proportion of recomb chromosomes in each subpopulation in GTEx data. (VI) Linkage disequilibrium (r2) between region SNPs and recombClust subpopulation. (Green) eQTLs for ANKRD35 in whole blood; (red) GWAS hits for diastolic blood pressure.

For each group, we estimated the recombination pattern given by the proportion of chromosomes in recomb (Fig. 5, III), observing important differences between the groups. Chromosomes in subpopulation 2 had higher recombination proportion than those in subpopulation 1 along the region except for the small interval containing the genes LIX1L and RBM8A, the causative gene of TAR syndrome (Albers et al. 2012). However, the highest differences in recombination proportions were observed between the third and fourth SD blocks, where subpopulation 1 showed null recombination. We fully validated the chromosome subpopulations and their recombination patterns using whole-genome sequencing data of 287 European individuals from the Genotype-Tissue Expression (GTEx) project (Fig. 5A,C, V). We thus obtained strong evidence for the existence of two recombination histories in the region.

We further asked whether the recombination histories could have a functional role. We tested, using RNA sequencing data in blood from the GTEx project, if the expression levels of the genes in 1q21.1 were associated with the two different recombination histories. We found a significant differential expression of ANKRD35 (Fig. 5B) (log fold change = 0.18, P = 6.7 × 10⁻⁴) and noted that the SNP rs10910843, an eQLTs of ANKRD35 in blood (Westra et al. 2013), was in high linkage with the chromosome subpopulations (Fig. 5C, VI). We additionally found that the SNP rs72704264, a risk factor for hypertension (Evangelou et al. 2018), was also in high linkage with the subpopulations, showing likely functional links associated with the different recombination histories.

recombClust classification correlates with mutation-based population structure

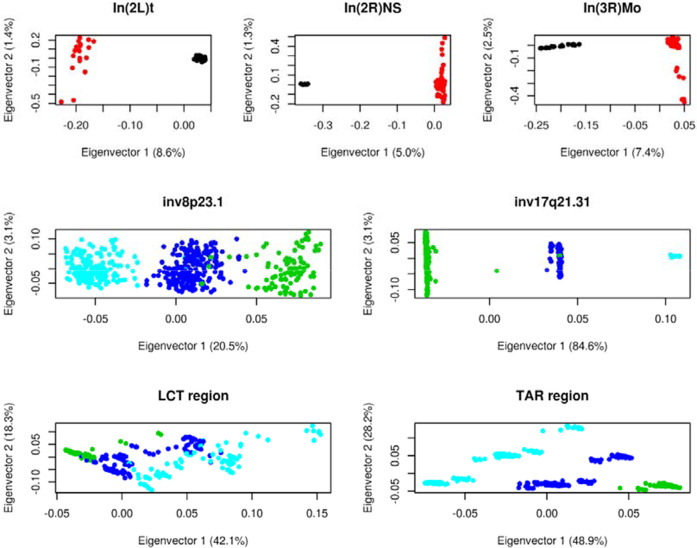
We observed that recombClust classification strongly correlated with mutation-based population structure. The mutation-based substructure was detected in all the regions analyzed with recombClust (three Drosophila melanogaster inversions, two human inversions, the LCT and the TAR regions), using PCAs of the SNPs within the regions (Fig. 6). In all cases, the first two principal components revealed population clusters that overlapped with recombClust subpopulations (Fig. 6). For inversions in D. melanogaster and humans, mutation-based population substructure and recombClust classification mapped to inversion genotypes of the individuals, homozygous for D. melanogaster inbreds. Although mutation-based substructures for the LCT and TAR regions were more complex, they mapped to recombClust subpopulations. Therefore, recombClust not only detects population substructure, as mutation-based methods, but also deepens into the substructure as it additionally computes divergent recombination histories, which naturally account for the accumulation of specific mutations.

Figure 6.

recombClust classification recovers the population structure detected by principal component analysis (PCA) of SNP data. In D. melanogaster inversions [In(2L)t, In(2R)NS, and In(3R)Mo], each point represents the first two principal components of an inbred line, colored by recombClust classification: (black) subpopulation 1; (red) subpopulation 2. In humans, each point represents the first two PCs of a diploid individual colored by the recombClust classification: (green) subpop1/subpop1; (blue) subpop1/subpop2; (cyan) subpop2/subpop2.

Discussion

recombClust is the first method to classify chromosomes into different subpopulations based on the inference of the recombination histories along genomic regions. Linkage methods for detecting historic recombination patterns have been important to characterize the distribution of recombination hotspots between species and ancestries (Winckler et al. 2005; Laayouni et al. 2011; Smukowski and Noor 2011). Although current methods aim to robustly estimate the recombination rate between markers by coalescent modeling, accounting for selection and demographic effects, they do not detect recombination variation between individuals. recombClust fills this gap, further allowing to test the association between differences in recombination histories with phenotypes.

recombClust assumes that there is an inverse relationship between recombination and linkage between SNP-blocks. However, the similarity of the recombination patterns obtained with recombClust with those obtained with FastEPRR shows that this assumption is accurate. This is because recombClust is also the first method to incorporate the spatial correlation of the recombination signal along a genomic region, which other linkage methods do not. Consequently, demographic and selection signals, which induce spatial correlation, are directly extracted from the data (Figs. 4, 5). Additional analyses are, however, required to identify the nature of different recombination histories and to determine whether they are due to ancestry, selection, or the presence of chromosomal rearrangements affecting the recombination patterns within the region. In particular, the method successfully split the groups of chromosomes being selected in the LCT locus from those which are not, giving a flat recombination pattern, with the group under selection likely produced by a recent selective sweep. This is an added advantage with respect to methods like FastEPRR in the computation of recombination patterns because recombClust explicitly extracts the selection signal from the data by identifying the chromosomes under selection as those with a flat recombination pattern in the locus. Our analyses showed that at the LCT locus, the pattern differences between chromosomes groups were large, further suggesting a novel approach in the detection of selection signals.

We have shown that when recombination modifiers are expected to affect a genomic region, such as inversions, recombClust can be reliably used to infer its alleles in large population samples. recombClust can, for instance, be added to other methods that genotype inversion from SNP data, offering an additional signal derived from recombination patterns (Cáceres and González 2015). However, we expect that the limitations of these methods also apply to recombClust, such as being best suited to identify ancient and nonrecurrent inversions. Thus, recombClust is likely to improve performance when substantial differences in recombination histories accumulate. Recombination modifiers acting on small targeted sequences that are not expected to show a spatial-extended historic pattern require further methodological developments, like merging the mixture model with a coalescent modeling. In general, recombination modifiers whose effects cannot be observed in historical recombination patterns are beyond linkage methods.

We also showed that recombClust can detect differences in recombination histories in complex regions prone to nonallelic homologous recombination (NAHR) and, therefore, likely subjected to tight regulation of recombination (Sasaki et al. 2010). We discovered and validated the existence or two recombination histories in the 1q21.1 locus at risk of deleterious syndromes. Detailed analyses are needed to disentangle the nature of the recombination modifiers acting on the region, which can be, for instance, a mixture of genomic rearrangements, epigenetic marks, or functional mechanisms regulating double-strand breaks that avoid NAHR (Sasaki et al. 2010). In addition, the question arises over whether the recombination between the chromosome subpopulations confers specific risks to deletions and duplications in the offspring. As for the subpopulations’ relation with more common phenotypes, we observed a strong linkage with a risk factor for hypertension showing probable implications of recombination variation with this trait within 1q21.1. We, therefore, showed an approach to measure the impact of different recombination histories on phenotypes, opening a way to study how recombination variation influences traits.

In this study, we have shown that recombClust can detect two different recombination histories in a target region. However, there is a clear possibility that more histories along a candidate region can be detected, even if the mixture models at a point are binary classifiers. In these cases, more clusters will appear in the consensus PCA determining the chromosomal subpopulations. The application of recombClust to the human inversion inv8p23.1 when samples from multiple ancestries are included (Supplemental Fig. S8) revealed that chromosomes were differentiated by inversion status (inverted vs. standard) and ancestries (African vs. other) comprising four main clusters, each with a combination of inversion status and ancestry and revealing different recombination histories. The implementation of recombClust enables the detection of more clusters with additional PCA dimensions. Nonetheless, further evaluation of those scenarios is needed. In addition, the examples provided here are based on the human and the D. melanogaster genomes, but recombClust could be applied to other organisms as well. To this end, different parameters (such as the maximum distance between SNP-blocks) can be adapted to the genome features of the target organism.

Methods

recombClust description

We proposed a method to classify chromosomes into different groups based on recombination histories in a target region. Consider a situation in which two different recombination histories are latent, generating two chromosome subpopulations in a given genomic region (Supplemental Fig. S10). A first subpopulation of chromosomes comprises those whose ancestral chromosomes have recombined at a given point within the region, and a second subpopulation comprises those with a history of recombination at other points. In this work, we proposed the method recombClust that clusters the individuals into recombination histories in a target genomic region, using two steps. First, at each selected point within the region, it fits a mixture model to classify chromosomes into those that have recombined between two SNP-blocks and those that have not. Second, it computes a consensus classification of chromosomes across all selected points, separating the population of chromosomes according to different recombination patterns along the segment.

Mixture model to classify chromosomes into recombining groups

The first step of recombClust is to draw multiple classifications of a sample of chromosomes at various recombination points covering a target genomic region. At a given point, the method classifies the chromosomes with a history of recombination between two SNP-blocks flanking the point and those without it. SNP-blocks are made of L contiguous SNPs. We propose to model the likelihood that a chromosome in the sample was drawn from a mixture of chromosomes that highly recombined at that point (recomb) and that remained in complete LD (linkage) (Fig. 1A). The likelihood is therefore given by a mixture of two latent chromosome groups (recomb/linkage). We model the recombination at a point that lies in the sequence interval between a pair of SNP-blocks (i = 1, 2), each of length L. Phased SNP alleles are encoded by 0 or 1, the haplotype of a chromosome at block i is a random variable denoted X_i ∈ {0, 1}^L, and the haplotype of the joint blocks is the random variable given by the concatenation of the block variables X₁₂ = X₁ ○ X₂. Under our model, the recombination completely breaks the LD between the SNP-blocks (r² = 0) in the recomb subpopulation and therefore X₁ and X₂ are statistically independent. Therefore, the probability that a chromosome is observed with haplotype x₁₂ in a chromosome group under recombination is

$$P_{\mathrm{recomb}}\left(X_{12}=x_{12}|n_1,n_2\right)=P\left(X_1=x_1|n_1\right)\times P\left(X_2=x_2|n_2\right),$$

given the haplotype frequencies n₁ and n₂.

For the second chromosome group, we consider that there is no recombination, and we model the SNP-blocks to be in complete LD (r² = 1). For the chromosomes in the linkage group, X₁ and X₂ are completely linked. X₂ can be unambiguously mapped to X₁ (f:X₂ → X₁). Under this model, the probability of observing haplotype x₁₂ is

$$P_{\mathrm{linkage}}\left(X_{12}=x_{12}|d,f\right)=\left\{P\left(X_1=x_1|d\right),x_1=f\left(x_2\right);0,\mathrm{otherwise}\right\},$$

where the frequencies of X₁ are denoted by d.

We define the mixture model with two components, following Equations (1) and (2). The model represents a chromosome population with a mixture of recomb and linkage groups with proportion π. We therefore assume that the probability of observing a chromosome with haplotype x₁₂ is

$$P_{\mathrm{mixture}}\left(X_{12}=x_{12}|r_{1,}{r}_{2,}{l}_{1,}g,\pi \right)=\pi P_{\mathrm{recomb}}\left(X_{12}=x_{12}|r_1,r_2\right)+\left(1-\pi \right)P_{\mathrm{linkage}}\left(X_{12}=x_{12}|l_1,g\right)$$

where r₁ and r₂ are the frequencies of haplotypes X₁ and X₂ in recomb; l₁ is the haplotype frequencies of X₁ in linkage; and g is the function linking X₂ to X₁.

Given a set of m independent chromosomes ($k=1,\dots ,m$), we denote the random variable for the joint blocks over all chromosomes as $Y_{12}=\left(X_{12}^1,X_{12}^2,\dots ,X_{12}^m\right)$ and therefore the likelihoods of observing the data y₁₂ under the mixture model is

$$L_{\mathrm{mixture}}\left(y_{12}\right)=\prod _{k=1}^m{P}_{\mathrm{mixture}}\left(X_{12}^k=x_{12}^k|r_1,r_{2,}{l}_1,g,\pi \right).$$

The mixture model parameters are determined using an expectation-maximization (EM) algorithm. For each chromosome, we define a hidden variable z_kε{0, 1}. This variable indicates if the chromosome belongs to the recomb or the linkage groups. The EM algorithm updates the model parameters iteratively maximizing the expectation of the data. Given the parameters of the model ω, ω = (r₁, r₂, l₁, g, π), we define the probability that chromosome k belongs to the linkage group, $s_{0,k}\left(\omega \right)=P\left(z_k=0|x_{12}^k,\omega \right)$. Similarly, the probability that individual k belongs to the recomb group given ω is $s_{1,k}\left(\omega \right)=P\left(z_k=1|x_{12}^k,\omega \right)$. For each k, the probability of belonging to any group is 1 and, therefore, s_0,k(ω) + s_1,k(ω) = 1. In each step of the EM algorithm, we find the value of ω′ that maximizes

$$\begin{array}{rl}{\omega }^{\mathrm{\prime }}=& \mathrm{argma}{\mathrm{x}}_{\omega }\sum _{k=1}^m[\log \left(\left(1-{\pi }^{\mathrm{\prime }}\right)\times P_{\mathrm{link}}\left(x_{12}^k|l_1^{\mathrm{\prime }},g^{\mathrm{\prime }}\right)\right)\times s_{0,k}\left(\omega \right)\\ & +\log \left({\pi }^{\mathrm{\prime }}{P}_{\mathrm{rec}}\left(x_{12}^k|r_1^{\mathrm{\prime }},r_2^{\mathrm{\prime }}\right)\right)\times s_{1,k}\left(\omega \right)]\end{array}$$

We, therefore, update the mixture likelihood by ω′ given by

$${\pi }^{\mathrm{\prime }}=\mathrm{argma}{\mathrm{x}}_{\pi }[\log \left(\left(1-\pi \right)x{s}_0\left(\omega \right)\right)+\log \left(\pi x{s}_1\left(\omega \right)\right)],$$

$$r_1^{\mathrm{\prime }}=\mathrm{argma}{\mathrm{x}}_{r_1}\sum _{k=1}^m\log [P\left(x_{12}^k|r_1\right)]\times s_{1,k}\left(\omega \right),$$

$$r_2^{\mathrm{\prime }}=\mathrm{argma}{\mathrm{x}}_{r_2}\sum _{k=1}^m\log [P\left(x_{12}^k|r_2\right)]\times s_{1,k}\left(\omega \right),$$

$$l_1^{\mathrm{\prime }}=\mathrm{argma}{\mathrm{x}}_{l_1}\sum _{k=1}^m\log [P\left(x_{12}^k|l_1\right)]\times s_{0,k}\left(\omega \right).$$

We estimate haplotype frequencies r₁, r₂, and l₁ in close form using Lagrange multipliers (Sindi and Raphael 2010). In particular, we obtain

$$\pi =\frac{s_1\left(\omega \right)}{s_0\left(\omega \right)+s_1\left(\omega \right)},$$

where s₀(ω) and s₁(ω) are the probabilities that a chromosome in the population belongs to the linkage or the recomb groups [$s_0\left(\omega \right)={\sum }_{k=1}^m{s}_{0,k}\left(\omega \right)$; $s_1\left(\omega \right)={\sum }_{k=1}^m{s}_{1,k}\left(\omega \right)$]. We consider that a chromosome k belongs to recomb if s_1,k > 0.5. The function g′ is defined using a greedy algorithm. It sequentially pairs each observed r₂, in decreasing order by their frequency, with the x₁ for which the observed frequency of x₁₂ is maximum and has not been previously paired. The final ω′ is such that its square root difference with the previous estimate is lower than machine precision. In addition, for numerical stability, we set the zero in Equation (2) to 10⁻⁵.

Clustering of chromosomes into different recombination histories

Chromosomes belonging to the same recombination history are those with consistent recombination or linkage across the different selected points along the target region. In the second step of recombClust, a consensus clustering is performed on all the recombination points tested over the target region to determine whether individual chromosomes can be consistently classified into groups with common historical recombination patterns. Therefore, to detect a subpopulation of chromosomes across the target region based on their recombination patterns, recombClust first extensively fits the mixture model between numerous pairs of nonoverlapping blocks of two SNPs each (L = 2 in the mixture model), covering the region. For each model, the method computes the probability that the chromosomes belong to the recomb group. Finally, recombClust produces a consensus classification of the chromosomes by clustering the first principal component of the recomb probabilities matrix across all mixture models fitted in the genomic region (Fig. 1B).

Extraction of spatial patterns of historic recombination along a genomic region

For each subpopulation, we defined its recombClust recombination pattern as the proportion of chromosomes that belonged to the recomb group at different points along the target region (Fig. 1C). Windows were defined as predetermined regular partitions of the target region to summarize the results of each subpopulation in terms of the recomb and linkage clustering. In particular, for a given subpopulation, we computed the proportion of chromosomes that were classified in the recomb group across all the models contained in each window. A chromosome was classified as recomb if it had a recomb probability above 0.5 in more than half of the models in a window. We then showed that the proportion of recomb classification along the region recapitulated the recombination pattern for the subpopulation, as determined by other methods such as FastEPRR. We defined a partition in regular windows of 50 kb for the human ∼4 Mb inversion 8p23.1 and the ∼1 Mb LCT region, to compare with FastEPRR recombination patterns. We defined nonoverlapping windows of size 20 kb in the 0.4 Mb 1q21.1 region to increase the resolution of the recombination patterns.

Simulated data sets to calibrate the mixture model

We simulated various scenarios to calibrate our mixture model. Two hundred instances of a reference scenario were generated and compared with the 200 instances of multiple scenarios featuring different SNP-blocks and between chromosome group variabilities. For one instance of the reference scenario, we simulated 1000 chromosomes in the recomb and the linkage groups each, given by the random and full linkage association between a pair of SNP-blocks, respectively. For the recomb group, the chromosome alleles at each SNP were drawn from a binomial distribution whose frequency was independently sampled from a uniform distribution [unif(0.55, 0.95)], assuming no LD within the blocks and between blocks. For the linkage group, SNPs within the blocks were independent but the pair of blocks, flanking the recombination point, was in maximum LD. We then considered that the most frequent haplotype for the joint SNP-blocks was the same in both subpopulations and given by the SNP alleles with maximum frequency, so the overall linkage in the total population was of D′ = 1. Different scenarios were obtained by changing the parameters of these simulations, in which we assessed the performance of the mixture model, given by the accuracy to correctly classify chromosomes into the recomb/linkage groups. We first assessed the extent to which the accuracy of the model was affected by the nucleotide divergence between the populations, by considering that the differences between the most frequent block-pair haplotypes in each chromosome group were increasingly higher. We did this by changing the number of SNP alleles that were different between the most frequent haplotypes in each group.

We also assessed the influence of intra-block linkage disequilibrium on model accuracy, by taking blocks where the linkage between the SNPs in the block was maximum. This scenario reduces to having blocks of 1 SNP. Finally, we evaluated how the proportion between recomb and linkage populations affected the mixture model performance. We simulated different scenarios in which the proportion of the recomb population ranged between 0.1 and 0.9. We tested the model in the reference scenario using different initializations for the mixture frequency.

Performance of recombClust to detect chromosomes with different recombination histories

We also evaluated the performance of classifying the chromosomes under different recombination patterns using simulated inversions. Because inversion polymorphisms produce chromosomal subpopulations that differ in their historical recombination patterns along with the inversion, we tested the ability of recombClust to detect inversion status in simulated inversions. We simulated inversions using invertFREGENE (O'Reilly et al. 2010) with different lengths (from 50 kb to 1 Mb) and inversion frequencies (from 0.1 to 0.9). Each combination of frequency and length was run 100 times. In all simulations, we used Ne = 1000, a recombination rate = 1.25 × 10⁻⁷ and a mutation rate = 2.3 × 10⁻⁷, as suggested in invertFREGENE manual to speed up the execution time. Our simulated inversions represent potential scenarios in which there are no selective pressures and the subpopulations recently diverged.

D. melanogaster and human inversions

We tested whether recombClust could characterize real chromosomal inversions by inferring different historical recombination patterns in D. melanogaster and in humans (Supplemental Table S1). We used recombClust to infer the inversion status of chromosomes for three well-known inversions: In(2L)t (2L:2225744–13154180, dm6), In(2R)NS (2R:11278659–16163839, dm6), and In(3R)Mo (3R:17232639–24857019). We used SNP data from DGRP2 lines (Mackay et al. 2012; Huang et al. 2014), excluding individuals with call rate <95% and SNPs having any missing or a minor allele frequencies (MAF) <5%, classified the lines into the underlying recombination patterns computed by recombClust, and compared the classification with experimental inversion genotypes (Huang et al. 2014).

We used recombClust to classify phased chromosomes into underlying recombination patterns within human inversions at 8p23.1 (Chr 8: 8,055,789–11,980,649, hg19) and 17q21.31 (Chr 17: 43,661,775–44,372,665, hg19). We used SNP-phased data from The 1000 Genomes Project (Sudmant et al. 2015). We inferred underlying chromosomal subpopulations with different recombination histories using recombClust and compared them with the experimental inversion genotypes available in the invFEST repository (Martínez-Fundichely et al. 2014).

Recombination substructure in the susceptibility region of TAR syndrome

We ran recombClust across the region Chr 1: 145.35–145.75 Mb characterized by four blocks of segmental duplications. This region is prone to deleterious rearrangements by nonallelic homologous recombination (NAHR), which can lead to the thrombocytopenia-absent radius (TAR) syndrome. We analyzed the 503 European individuals from The 1000 Genomes Project and the 528 European individuals of Genotype-Tissue Expression (GTEx) project (The GTEx Consortium 2013). We obtained GTEx data from the NCBI database of Genotypes and Phenotypes (dbGaP; https://www.ncbi.nlm.nih.gov/gap/) (accession code: phs000424.v7.p2), we phased it with SHAPEIT (Delaneau et al. 2013), and we selected those individuals classified as European by peddy (Pedersen and Quinlan 2017) with a probability higher than 0.9. In the recombClust analysis, we included SNPs with a MAF > 0.05 and performed the consensus clustering across the tested points with a hierarchical clustering. For the GTEx data, we used the first two PCs of the mixture model classification probabilities, but for the 1000 Genomes data we used the second PC. We tested Hardy-Weinberg equilibrium using SNPassoc (González et al. 2007).

We studied whether the chromosome genotypes, derived from the chromosome subpopulations, were associated with gene expression and phenotype differences between individuals. We evaluated the association with gene expression in whole blood using GTEx data, using the gene raw counts from recount2 (Collado-Torres et al. 2017). For each tissue, we removed genes with fewer than 10 counts in >90% of the samples. We tested the association between the chromosome alleles and gene expression, applying a robust linear regression with limma (Ritchie et al. 2015) to log₂ CPM values obtained with voom (Law et al. 2014). We included sex, platform, top three genome-wide principal components, and variables from PEER as covariates.

Software availability

Development and release versions of recombClust are available at GitHub (https://github.com/isglobal-brge/recombClust). The version used to run the analysis of this manuscript (v1.0.0) is available in our Supplementary Code repository (https://github.com/isglobal-brge/Supplementary-Material/tree/master/Ruiz-Arenas_2020) as a source package. Finally, a vignette exemplifying how to apply recombClust to a new data set can be found at GitHub (https://github.com/isglobal-brge/recombClust/blob/master/vignettes/Overview.pdf). The code used to create figures, tables, and perform simulation studies is available at GitHub (https://github.com/isglobal-brge/Supplementary-Material/tree/master/Ruiz-Arenas_2020) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.