Abstract
Learning dependence relationships among variables of mixed types provides insights in a variety of scientific settings and is a well-studied problem in statistics. Existing methods, however, typically rely on copious, high quality data to accurately learn associations. In this paper, we develop a method for scientific settings where learning dependence structure is essential, but data are sparse and have a high fraction of missing values. Specifically, our work is motivated by survey-based cause of death assessments known as verbal autopsies (VAs). We propose a Bayesian approach to characterize dependence relationships using a latent Gaussian graphical model that incorporates informative priors on the marginal distributions of the variables. We demonstrate such information can improve estimation of the dependence structure, especially in settings with little training data. We show that our method can be integrated into existing probabilistic cause-of-death assignment algorithms and improves model performance while recovering dependence patterns between symptoms that can inform efficient questionnaire design in future data collection.
Keywords: cause of death, mixed data, high dimensional, spike-and-slab, parameter expansion
1. Introduction
In many parts of the world, deaths are not systematically recorded, meaning that there is massive uncertainty about the distribution of deaths by cause (Horton, 2007; Jha, 2014). Knowing why individuals are dying is essential for both rapid, acute public health actions (e.g. responding to an infectious disease outbreak) and for longer term monitoring (e.g. encouraging behavior change to head off an obesity epidemic). In many such areas, a survey-based tool called Verbal Autopsy (VA) are routinely used to collect information about the causes of death when medical autopsies cannot be performed. VAs consist of an interview with a caregiver or relative of the decedent and contain questions about the decedent’s medical history and the circumstances surrounding the death. Collecting VA surveys is a time-consuming and resource intensive enterprise. A community informant alerts a health official of a recent death and then, after a period of months, a survey team returns to administer the VA survey with the relative or caregiver. VA surveys are taxing for the relative or caregiver both because they typically consist of over a hundred questions and because they require a person recall a traumatic time in depth. What’s more, VA surveys themselves do not reveal the cause of death, but only the circumstances and symptoms. Assigning cause of death requires either coding directly by a clinician or using one of several statistical and machine learning algorithms.
The majority of the existing statistical or algorithmic methods to assign cause of death using VA surveys make the assumption that VA symptoms are independent from one another conditional on cause of death (Byass et al., 2003; James et al., 2011; Miasnikof et al., 2015; McCormick et al., 2016). This assumption simplifies computation and is efficient in settings with limited training data. The ignored associations, however, provide valuable information that could be used to improve cause of death classification. Knowing that a person lives in a Malaria-prone area and had a fever before dying, for example, gives substantially more information than knowing only that the person presented with a fever before dying. One previous method by King and Lu (2008) does account for associations using a regression model on stochastic samples of combinations of symptoms taken from a gold-standard training dataset. This computation, however, is extensive for even moderately large symptom sets. Moreover, in order to account for symptom dependence, both the classic regression method (King and Lu, 2008) and the recently developed latent factor approach by Kunihama et al. (2018) relies on the existence of high-quality training data, which is typically unavailable in practice.
In this paper, we propose a latent Gaussian graphical model to infer associations between symptoms in VA data. In developing our model for associations between symptoms on VA surveys, we must address three statistical challenges that arise from the VA data. First, the VA data are of mixed types. That is, survey questions are a mixture of binary (e.g. Was the decedent in an auto accident?), continuous (e.g. How long did the decedent have a fever?), and count (e.g. How many times did the decedent vomit blood?) outcomes. The data are then usually pre-processed into a standard set of binary indicators for which many methods have been proposed to automatically assign cause(s) of death. Instead of dichotomize the many continuous variables, we develop a (latent) Gaussian graphical model and introduce new spike-and-slab prior for inverse correlation matrices to mitigate the risk of inferring spurious associations. We also develop an efficient Markov chain Monte Carlo algorithm to sample from the resulting posterior distribution.
A second challenge is that we want to not only learn the dependence structures among the symptoms given causes of death, but also to use them to improve prediction for unknown cause of death. As shown by a numerical example in the supplementary material (Li et al., 2019b), violations of the conditional independence assumption can substantially bias the prediction of the cause of death. In practice, researchers are typically interested in both the accuracy of the method in assigning cause of death for a specific individual as well as the overall fraction of deaths due to each cause in the sample, in order to understand disease epidemiology and inform public policies. We address this challenge by extending the latent Gaussian model to a Gaussian mixture models framework so that it can be integrated into existing VA methods for both cause-of-death assignment and estimation of population cause-specific mortality fractions.
Lastly, a fundamental challenge we face in building such predictive model is that there is typically very limited training data available. “Gold standard” training data typically consists of physical autopsies with pathology reports. Obtaining such data is very expensive in low resource settings where they are not common practice, requires physicians commit time to performing autopsies rather than treating patients, and is generally only possible for the selected set of deaths that happen in a hospital. To date there is only one single “gold standard” dataset that is widely available to train VA algorithms (Murray et al., 2011a). This dataset, described in further detail in subsequent sections, contains cases from six different geographic areas. Using the binary symptoms from this dataset, Clark et al. (2018) show that the empirical marginal probabilities (or conditional probabilities given a cause-of-death) of observing a symptom can vary significantly across training sites. The lack of reliable training data in the VA context limits the applicability of currently available statistical approaches. A standard approach to joint modeling of mixed variables, for example, is through characterizing the vector of observed variables by latent variables that follow some parametric models. However, when the data contains only a small number of observations and a high proportion of missing values, sometimes even the marginal distribution of the variables cannot be reliably estimated and thus it may lead to erroneous inference of the joint distribution of variables.
We address this challenge by incorporating expert knowledge, a common strategy in VA cause of death classification. In the VA context, expert knowledge consists of information about the marginal likelihood of seeing symptom given that the person died of a particular cause. This type of information is widely used in the VA literature (Byass et al., 2003) and is substantially less costly to obtain than in person autopsies. Only marginal propensities can be obtained since asking experts about all possible symptom combinations would be laborious and time consuming. A small number of joint probabilities could be solicited from experts, but there is currently no means available to guide researchers about which combinations are most influential. Our work provides one such approach for choosing combinations to elicit.
We incorporate information about the marginal propensity of seeing each symptom by decoupling the correlation matrix from the marginal variances and allow researchers to incorporate marginal informative priors through hierarchical models. This differs from many existing work on Gaussian copula models. Gaussian copula graphical models typically proceed by estimating the latent precision matrix while treating the marginal distributions as nuisance parameters (e.g., Hoff, 2007; Dobra et al., 2011). Since only the ranks of the observations within the same variable enter the likelihood, any available prior information on the marginal distributions of different variables is not straightforward to incorporate. Our approach also contributes to the literature on inference of correlation matrices from mixed data, where several related ideas have been explored previously in other context. For instance, Talhouk et al. (2012) proposed a Bayesian framework for latent graphical models with decomposable graphs. Our shrinkage prior provides a more flexible approach to allow also non-decomposable graphs with a rejection-free sampling strategy. The recent work from Fan et al. (2016) studied semiparametric approaches for structure learning and provided a two-step procedure to obtain sparse graph structures. Our approach also yields improved estimation of the latent correlation matrices and is more robust to missing data, as illustrated in Section 5. Our work also incorporates a different kind of expert knowledge, the marginal distribution of variables, rather than the interactions between variables, such as reference network structure among variables (Peterson et al., 2013) or distance metrics measuring ‘closeness’ of variables (Bu and Lederer, 2017).
The rest of the paper is structured as follows. In Section 2 we describe the proposed latent Gaussian graphical model to characterize the dependence structure in mixed data and present two different prior choices of the latent correlation matrix, reflecting different types of prior beliefs. In Section 3 we describe the details of the posterior sampling algorithms. In Section 4 we show how the latent Gaussian model could be extended to Gaussian mixture models and integrated into existing VA methods for cause-of-death assignment. Section 5 examines the performance of correlation matrix estimation, structure learning, and prediction performance with extensive numerical simulation. In Section 6 we apply our methods to a gold standard dataset and data from a health and demographic surveillance system (HDSS) site where only physician coded causes are available. Finally, in Section 7 we discuss the remaining limitations of the approach and some future directions for improvement.
2. Latent Gaussian graphical model for mixed data
We begin by considering the characterization and estimation of dependence structures in mixed data. Let X = (X1, . . . , Xn)T denote the data with n observations of p-dimensional random variables. In survey data, for example, Xij may represent the response of respondent i on question j. We use a latent Gaussian representation to encode the dependence between the variables by assuming that the observed data matrix X can be represented by a set of multivariate Gaussian random variables Z under some monotone transformation:
where R is a correlation matrix, and fj(·)’s are non-decreasing functions. When the marginal transformation functions are unknown, this formulation is usually referred to as the Gaussian copula model (e.g., Xue et al., 2012). For continuous variables, a popular strategy to deal with the marginal transformation fj is to first estimate it by , where is typically taken to be the empirical marginal cumulative distribution function of the j-th variable (e.g. Klaassen and Wellner, 1997; Liu et al., 2009). Inference on R is then performed with pseudo-data . However, this strategy is problematic for discrete data, since directly applying monotonic marginal transformations changes only the sample space instead of the distribution of the observed data (Hoff, 2007). Therefore, for data with mixed variable types, it is common to adopt the semi-parametric marginal likelihood approach (Hoff, 2007). Inference on the correlation matrix is then carried out based on the marginal likelihood of the observed ordering of the variables, with the marginal transformation functions considered as nuisance parameters.
Moving now to binary variables, the marginal distribution can be characterized by the marginal probability, a single parameter. Thus direct estimation of the transformation functions can be reduced to estimating cutoffs of the latent Gaussian variables (Fan et al., 2016). Conceptually, we can fix the marginal transformation, and estimate only the latent mean variable μ. That is, we can write the data generating process as
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where Λ is a diagonal matrix that contains marginal standard deviations for the continuous variables and fixed at 1 for the binary variables, and R is a correlation matrix. The marginal prior probabilities for binary variables pj = Pr(Xij = 1) are specified though the priors for μ, since the expectation of Xij given μ is Pr(Xij = 1) = Pr(Zij > 0) = 1 − Φ(−μj) = Φ(μj).
For simplicity, throughout this paper we assume the continuous variables are marginally Gaussian, similar to the scenario considered in Fan et al. (2016). The extension to the case where the continuous variables exhibit non-Gaussian marginal patterns is straightforward by first preprocessing the raw continuous variables into pseudo-data using their marginal prior distributions (Liu et al., 2009), , so that . Specifying priors on their marginal variances, i.e., Λ, usually depends on the context. In this paper we adopt the improper prior on the marginal standard deviations suggested in Gelman (2006), so that Λjj ∝ 1.
The latent Gaussian distribution provides a simplistic description of the conditional independence relationship for Z. Zeros in off-diagonal elements of the inverse correlation matrix, R−1, correspond to pairs of latent variables that are conditionally independent given other latent variables. Thus for high-dimensional problems, we typically favor priors on R where elements in R−1 are shrunk to zero. The conditional independence relationships among latent variables do not imply conditional independence of the observed binary variables (Fan et al., 2016; Bhadra et al., 2018). Thus the adoption of this latent Gaussian strategy should be done with care when the dichotomous variables cannot be easily interpreted as binary manifestations of some continuous latent process. In our case, modeling symptoms collected from verbal autopsy surveys, many symptoms are natural truncations of some continuous variables (e.g. durations, frequencies, and severity of symptoms). While the latent Gaussian model does not aim to recover the actual continuous variables as if they were collected, the dependence between the latent variables more provide some insights into the relationship among such underlying processes.
The transformation of the marginal prior probabilities to μ0 in the proposed model requires to have unit variance for the binary variables, or equivalently, the submatrix of corresponding to binary variables to be a correlation matrix. This complication prohibits standard graphical model problem to apply since posterior sampling on the space of the correlation matrices is generally more difficult than from the covariance matrices due to the constraint of unit diagonal elements. Next, we propose new class of priors and describe a parameter expansion (PX) scheme (Liu and Wu, 1999; Meng and Van Dyk, 1999) where the correlation matrix R is first expanded to a covariance matrix and updated, and then projected back to the space of correlation matrices.
2.1. Prior specification for the correlation matrix
We discuss two classes of priors for that lead to efficient posterior inference: one with the standard conjugate priors for the covariance matrix and uniform marginal priors for R, and one with a sparse structure in R−1. Similar priors for marginally uniform R were proposed in Talhouk et al. (2012) for the multivariate probit model. Their direct generalization to sparse R−1 uses a Metropolis-Hasting algorithm that is computationally expensive and imposes an additional decomposability constraint on the graph structure. A major advantage of the proposed model, summarized in Section 3, is the computational simplicity of posterior sampling, as well as the removal of the decomposability constraint.
Marginally uniform prior for the correlation matrix
First, we review a marginally uniform prior on the correlation matrix, and the corresponding parameter expansion scheme. Without any additional knowledge about the structure of the latent correlation matrix, the marginal uniform prior on all the elements of R (Barnard et al., 2000) is
For the model Zi ~ Normal(μ, R), sampling from the posterior distribution p(R∣Z, μ) is not straightforward. However, with parameter expansion, we can expand the correlation matrix into the covariance matrix by Σ = DRD, where D = diag(d1, . . . , dp), and the observed data model into DZi ~ Normal(Dμ, Σ). By carefully constructing the augmentation of the expansion parameters, the expanded covariance or precision matrix can be much easier to sample from. Following Talhouk et al. (2012), we put an inverse gamma prior on the expansion parameters,
that induces an inverse Wishart prior on the expanded precision matrix Ω = Σ−1 ~ Wishart(p+1, Ip). The conjugacy allows easy posterior updating of Σ. This marginally uniform prior does not directly impose any sparsity constraints on the precision matrix. To summarize the conditional independence structure in a more concise manner, one option would be to estimate a sparse representation of using a two-stage procedure similar to Fan et al. (2016) with the posterior mean as input. Alternatively, we could incorporate sparsity directly into the prior, which we describe in the next section.
Spike-and-slab prior for the inverse correlation matrix
The marginally uniform prior for R is sometimes inappropriate for settings where sparse structure in is strongly suspected a priori. For example, we may expect only small groups of symptoms in a VA survey, say, all pregnancy-related symptoms, would be correlated but are conditionally independent of other clusters of symptoms. Several priors for sparse precision matrices have been proposed. The G-Wishart prior (Roverato, 2002) extends the Wishart distribution by restricting cells in the precision matrix that correspond to non-edges in a graph to be exact zeros, and has been extensively studied in existing literature (Jones et al., 2005; Lenkoski and Dobra, 2011; Mohammadi et al., 2017). More recently shrinkage priors have become more popular, in part due to their computational simplicity. Bayesian analogies to penalized precision matrix estimators have been proposed for lasso (Wang et al., 2012; Peterson et al., 2013), horseshoe (Li et al., 2017) and spike-and-slab mixture penalties (Wang, 2015; Li and McCormick, 2019; Deshpande et al., 2017). In this work we adapt the spike-and-slab prior idea proposed in Wang (2015) and propose a mixture prior for the inverse correlation matrix. The supplement material contains a brief introduction to Wang’s original proposal and its relationship to Wishart priors. The spike-and-slab framework is appealing because it performs graph selection and parameter inference simultaneously, in contrast to other shrinkage priors that require a further thresholding step after shrinkage. We put Gaussian priors on each off-diagonal element of the inverse correlation matrix, R−1, i.e.
where R+ denotes the space of correlation matrices, and δjk is the binary indicator for the (j, k)-th element in R−1 being drawn from the slab distribution. The prior distribution of δ is parameterized by πδ ∈ (0, 1). We show in the supplementary material that this joint distribution can be factored into two conditional distributions with a finite normalizing constant that cancels out, similar to the prior used in Wang (2015). The proposed setup differs from current literature on shrinkage priors in two ways. First, we restrict the support of R to the space of the correlation matrix, so that working with latent variables that cannot be normalized does not create identifiability issues. In the next section we show that this additional restriction does not increase computational cost by much. Second, we add a ∣R∣−(p+1) term to ensure that the prior assigns no weight to degenerate R−1. This term also allows the marginal distribution of Ω after parameter expansion to be in a form similar to the spike-and-slab prior defined in Wang (2015). Finally, we complete the parameter expansion scheme by defining the expansion parameter D such that ~ InvGamma((p+1)/2, 1/2). The expanded precision matrix Ω = (DRD)−1 has the following marginal prior distribution:
| (6) |
where is the j-th diagonal element of Ω−1. This expanded prior can be derived with a standard change of variables, as described in more detail in the supplementary material. The dependence between Ω and makes the posterior sampling seem complicated. However, it turns out that it can be efficiently sampled with a block update. We fully describe our sampling scheme in detail in Section 3.1.
Choosing the shrinkage parameters
The proposed prior for R has several hyperparameters, v0, v1, λ, and πδ, that jointly determine the prior scales and sparsity of R−1. The relationship between the implied prior sparsity, i.e., p(δ = 1) and the hyperparameters, however, cannot be easily obtained, because of the constrained space of R+ and the intractable normalizing constant Cδ. We follow a similar practice to Wang (2015) in choosing the hyperparameters by simulating the implied prior edge probabilities from different combination of hyperparameters. We use the sampler in Section 3 and choose the values that lead to the desired prior sparsity.
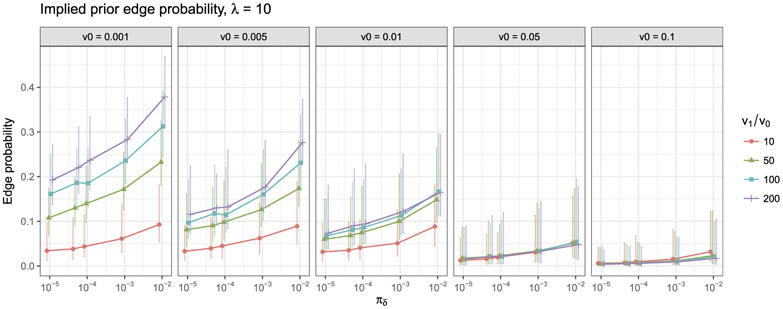
Generally, v1/v0 needs to be large so that it gives enough separation between the spike-and-slab densities. The choice of v0 also needs to be carefully considered: an extremely small v0 leads to a density that approaches the point-mass and thus can slow the mixing of the Markov chain, while a larger v0 may absorb many elements of R−1 and assigns a heavy portion of prior mass on the ‘sparse’ models with many small values. The choice of v0 may be roughly guided by comparing the marginal distributions implied by the prior to a pre-specified threshold for practical significance. We let v0 = 0.01 in our experiments, as it can be seen from the prior simulation in Figure 1 that it assigns reasonable weights to graphs with edge probability between 0.05 to 0.2 under various choices of v1 and πδ. Because of the linear constraints on the elements of R−1 imposed by the space of R+, the hyperparameter πδ typically differs from the implied marginal edge probability significantly, and also needs to be determined from numerical simulation. From Figure 1, the prior sparsity is relatively consistent for v0 = 0.01 when v1/v0 > 50 and πδ < 0.001 We chose v1/v0 = 100 and πδ = 0.0001 in our experiments.
Figure 1: Implied prior edge probability with λ = 10 for p = 100 graph.
The dots represent the median prior probabilities and the error bars represent the 0.025 and 0.975 quantiles. The densities are derived from sampling 1,000 draws using MCMC from the prior distribution after 1,000 iterations of burn-in.
It is also worth noting that λ also contributes to the prior sparsity directly, as it regularizes the diagonal elements of R−1. Since the support of diagonal elements of R−1 are (1, ∞), large λ restricts rjj to be closer to 1, leading the correlation between the j-th variable and other variables to be closer to 0, and thus sparser models. From our prior simulation, we found the choice of λ = 10 usually leads to reasonable prior sparsity. We include more discussion of the relationships between the proposed prior and that of Wang (2015) in the supplementary material.
3. Sampling from the posterior
Inference using the full model can be performed using Markov Chain Monte Carlo with mostly Gibbs steps and elliptical slice sampling (ESS), a rejection-free MCMC technique (Murray et al., 2010). We first describe in detail the sampling procedure with the spike-and-slab prior, and then describe how this step fits into the full inference procedure in Section 3.2.
3.1. Posterior sampling with the spike-and-slab prior
We begin by describing sampling with the spike-and-slab prior. We update Ω with the prior defined in (6) in a column-wise fashion. Consider the j-th row and column of Ω, if we denote u = Ω[j,−j] and the Schur complement , then given the expanded sample covariance matrix, , and the variance specified by the latent indicators, , the joint distribution of u and v can be calculated as
where . Notice that , and for all k ≠ j, depends on both u and v, rendering the block Gibbs update scheme in Wang (2015) inapplicable. However, the full conditional distribution for u and v can both be written as the product of a standard distribution and an additional correction term. We let
then we have the full conditional distributions
where . To sample from p(u∣·), we use elliptical slice sampling (ESS) (Murray et al., 2010) to sample from both distributions by treating the normal distribution part as “prior” and the later term as “likelihood.” For u, ESS first generates an elliptical locus from the normal prior and then searches for acceptable points for slice sampling. ESS typically sticks to the same posterior region when strong signals are provided in the “prior” Gaussian distribution, as is the case here. Additionally when Ω−1 is sparse, and should be close to each other, and thus the signal from the “prior” part is typically much stronger. The sampling of v can be performed using the generalized ESS (Nishihara et al., 2014) or other techniques as it does not involve a Gaussian part in the likelihood. However, since sjj is typically much smaller than n because the expansion parameters are drawn from invGamma((p + 1)/2, 1/2), placing much of its prior mass close to 0. We can, therefore, reasonably approximate the Gamma likelihood in p(v∣·) by Normal, which again allows easy use of ESS. The effect of this approximation on the posterior distributions are evaluated in the supplementary material. Furthermore, the added computational burden of ESS over the block Gibbs sampler in Wang (2015) is minimal, as the ’s can be easily calculated by the fact that , and , without any additional computation of a matrix inversion. It is also worth noting that at each iteration of the update, the sampled precision matrix maintains to be positive definite because det(Ω) = vdet(Ω[−j,−j]) > 0.
Finally, each time a block update is performed, all latent indicators can be updated with the corresponding conditional posterior inclusion probabilities,
3.2. Full posterior sampling steps
Given suitable initial values, the full sampling scheme updates each parameter in turn.
Update Z The conditional posterior distributions of the latent variables conditional on the observed data are truncated Normal distributions with the truncation defined by domain Iij where Iij = (−∞, 0) if Xij binary and Xij = 0, (0, +∞) if Xij binary and Xij = 1, and (−∞, +∞) if Xij is missing or continuous. To sample from the multivariate truncated normal posterior, we draw approximate samples by iteratively sampling Zij∣Zi,−j by
where , , and the truncated domain Iij is defined above.
Update Λ We perform the conditional update of Λ by sampling from iteratively. The improper uniform prior on Λjj is equivalent to , leading to the conditional posterior distribution
where the constant terms are
These conditional distributions can be efficiently sampled with ESS (Murray et al., 2010).
Update μ The conditional posterior distribution for the mean parameters is also multivariate normal,
Update R To update the latent correlation matrix, we first draw the working expansion parameter with ~ InvGamma((p+1)/2, β), where β = rii/2 for the marginally uniform prior, and β = 1/2 for the spike-and-slab prior. The inverse Gamma distribution is parameterized with shape and scale. We then construct the expanded observation W = ZD, where D = diag(d1, d2, . . . , dp), and compute the sample covariance matrix . For the marginally uniform prior, the posterior conditional distribution of the expanded precision matrix Ω takes the conjugate form, Ω∣W,μ ~ Wishart(Ip + S, n + p + 2). For the spike-and-slab prior, we sample the expanded precision matrix Ω∣W, γ using ESS as described in Section 3.1.
After a new Ω is sampled, we can then compute the induced expansion parameter and the induced correlation matrix R = D−1Ω−1D−1. For problems with very large p, it may also be sometimes useful to perform the posterior sampling in two stages, where the first stage updates all the parameters, while in the second stage, δ is fixed to be the posterior median graph estimated from the first stage. The two-stage procedure may improve the mixing of the chain by reducing the dimension of discrete parameters in the second stage, especially in the mixture model case discussed in the next section. For all the numerical examples used in this paper, adding an extra post-selection stage does not change the posterior mean estimators of interest by much and thus all results are reported using MCMC with a single stage.
4. Cause-of-death assignment using latent Gaussian mixture model
In this section we extend the latent Gaussian graphical models to model data from a mixture of underlying distributions. This extension allows us to complete our model to simultaneously estimate the latent correlation matrix and assign causes of death using VA data. Before we describe our model, it is worth noting that for many existing automated VA methods such as InSilicoVA (McCormick et al., 2016), InterVA (Byass et al., 2003), and the Naive Bayes Classifier (Miasnikof et al., 2015), the classification rule is closely related to the naive Bayes classifier under the assumption of (conditional) independence between symptoms, i.e.
For algorithms using this conditional independence assumption, the information provided by training data (aside from a prior guess of πc) can be summarized by the conditional relationships between a single sign/symptom and causes. In contexts without training data, expert clinicians provide the same information in the form of informative prior beliefs (e.g. Byass et al., 2003; McCormick et al., 2016). Thus to extend the latent Gaussian graphical model to the context of cause-of-death assignment, we hope to incorporate such conditional relationships as well, in order to make full use of the existing information. This can be achieved similarly as before. We let yi denote the categorical indicator from a set of C causes of death for person i. A key goal of VA analysis is to associate unlabeled data with cause-of-death assignments. With a generative model similar to Section 2, we let the mean of the latent variable Zi depend on the class of the i-th observation. The complete data generating mechanism can be written as
where the priors for μ and are the same as in Section 2. Following the setup presented in McCormick et al. (2016), we treat the causes of death for unlabeled observations as missing data, and the relationship between symptoms and causes are iteratively re-estimated until the distributions of individual cause-of-death probabilities are compatible with the population cause-specific mortality fractions (CSMF). We model the distribution of the class assignment indicator given the CSMF with a multinomial distribution and adopt an over-parameterized normal prior for the CSMF introduced in McCormick et al. (2016). Specifically, we let yi∣π ~ Multi(π) and πc = expθc/∑cθc with θ ~ Normal. We put diffuse uniform prior on μθ and .
To account for the different strength of prior information for each mixture, we can also put an additional hyper-prior on . In our experiments with unspecified , we use weak independent priors such that ~ InvGamma(0.001, 0.001), for c = 1, . . . , C. Although not presented here, if marginal information on the continuous variable distributions is available in practice, we may also let Xij∣yi = c to be , where is the fixed marginal distribution function, and inference can be similarly carried out with one additional step to update the observed continuous variables each time an assignment changes.
The mixture model approach allows the joint distribution of symptoms in the data to further guide the estimation of the latent correlation matrix. The proposed model is ideally suited for settings with some, but not extensive, training data. In verbal autopsy this typically happens when a small subset of deaths is assigned a cause either by a traditional medical autopsy or, more commonly, when clinicians review the verbal autopsy data and assign a cause of death, so-called ‘physician-coded’ VAs. In most settings physician-coded VAs are comparatively (very) rare because physician coding is costly in terms of physician time and opportunity costs, e.g. physicians not seeing living patients. The informative prior setup we propose allows researchers to combine prior or clinician-derived expert information with training data. Conceptually, in the extreme case when no training data exist, the latent Gaussian mixture model can still be estimated given strong informative priors on μ, i.e. the conditional probabilities of symptoms, and the latent correlation matrix will be estimated dynamically based on cause assignments in each iteration. In the following sections we show the advantages of combining both strong priors and limited training data using both simulated and observed data.
Finally, if the labeled and unlabeled deaths come from different populations (e.g. the labeled deaths occur in a high Malaria region whereas the unlabeled deaths do not), then one could let the labeled and unlabeled deaths follow two multinomial distributions with different π, or further include additional subpopulation-specific π. Posterior inference of π, μ and R can be similarly carried out as in Section 3.2 with minor modifications. The posterior assignment distribution for each death can then be obtained by averaging over B draws from the MCMC, i.e., . We leave the detailed algorithms in the supplementary material.
5. Simulation evidence
In this section we conduct simulation experiments to characterize the performance of the proposed method for both the estimation of R under the latent Gaussian framework and classification under the mixture framework. We describe our data generation process and provide results for correlation matrix estimation and graph recovery. Additional simulation results for classification accuracy are included in the supplementary material.
To examine the performance of our method in recovering the latent correlation matrix under different scenarios, we follow a data generating procedure similar to those in Liu et al. (2012) and Fan et al. (2016). In all our simulations, we generate the sparse precision matrix Ω so that ωjj = 1, and ωjk = tajk, where ajk ~ Bernoulli((2π)−0.5 exp(∥zj − zk∥2)/(2c)) and zj’s are independent bivariate uniform random variables sampled from [0, 1]2. We set c = 0.2 so that on average each node has 6.4 edges in the graph, and set t so that the precision matrix is positive definite. In all our examples we further rescale Ω so that its inverse is a correlation matrix. We consider the following two scenarios using the assumed generative model:
Assume X contains 10% continuous Gaussian variables and the marginal means for the latent variables μj ~ Unif[−1, 1], and let the marginal prior mean μ0 be the true μ.
Same as before, except the marginal prior μ0j is misspecified to be sign(μ0j) * , and we further generate continuous variables from the misspecified marginal distribution so that is marginally Gaussian.
The misspecified case reflects the practical scenario where more extreme marginal probabilities are relatively easier to solicit but may be provided on a different scale compared to the truth. In all our simulations we set n = 200, p = 50, and randomly remove m% of the entries in the data matrix to represent m% missing data. We repeat the simulation under each scenario 100 times. The results are similar for synthetic data with only binary variables and thus are omitted from reporting here. For both proposed models, we run the MCMC 3,000 iterations and report the mean estimator for R from the second half of the posterior draws. In this simulation study, we found 3,000 iterations is sufficient for the chain to converge, which takes our Java implementation about 5 minutes to compute on a MacBook Pro with 2.6 GHz Intel Core i7 processor.
To benchmark the performance of our method in recovering the true correlation matrix, we compare our method with the semi-parametric estimator proposed in Fan et al. (2016). To obtain a fair comparison with our method that uses marginal priors, we calculate the rank-based estimator with the prior marginal probabilities, instead of the empirical marginal probabilities calculated from data. In our experiments described above, this approach leads to better estimation of R. We note that this substitution may harm the estimator performance when marginal priors are misspecified significantly. We also compare our methods with other Bayesian Gaussian copula graphical models with the G-Wishart prior, estimated using the birth-death MCMC (Mohammadi et al., 2017) and reversible jump MCMC (Dobra et al., 2011). Marginal priors cannot be used in these two approaches since they are treated as nuisance parameters and do not enter the likelihood. Both sampling methods were implemented with the BDgraph package (Mohammadi and Wit, 2017). We drew 10,000 samples with the first half discarded, and calculated the induced correlation matrix from the posterior mean of the latent precision matrix. We compare the estimated correlation matrix error in terms of the matrix element-wise maximum norm, spectral norm, and Frobenius norm. The results are shown in Table 1. The posterior mean estimator from the proposed approach consistently outperforms the rank-based estimator for all three norms and is more robust to missing data and model misspecification.
Table 1: Simulation results under different scenarios.
The proposed latent Gaussian graphical model approach (Spike-and-Slab prior) outperforms the semi-parametric alternatives, the marginal uniform prior (Uniform prior), and G-Wishart Gaussian copula graphical models, sampled using birth-death MCMC (G-Wishart BD) and reversible jump MCMC (G-Wishart RJ), in almost all scenarios.
| Bias: | Structure: | ||||||
|---|---|---|---|---|---|---|---|
| Case | Missing | Estimator | M norm | S norm | F norm | AUC | max F1 |
| (i) | 0% | Semi-parametric | 0.45 | 6.13 | 6.35 | 0.70 | 0.70 |
| Uniform prior | 0.32 | 4.39 | 4.63 | – | – | ||
| G-Wishart RJ | 0.30 | 3.74 | 3.94 | 0.48 | 0.66 | ||
| G-Wishart BD | 0.30 | 3.70 | 3.93 | 0.61 | 0.67 | ||
| Spike-and-Slab prior | 0.27 | 3.30 | 3.57 | 0.74 | 0.70 | ||
| 20% | Semi-parametric | 0.53 | 7.11 | 7.33 | 0.61 | 0.67 | |
| Uniform prior | 0.35 | 4.93 | 5.25 | – | – | ||
| G-Wishart RJ | 0.31 | 4.04 | 4.36 | 0.44 | 0.65 | ||
| G-Wishart BD | 0.32 | 4.06 | 4.39 | 0.56 | 0.67 | ||
| Spike-and-Slab prior | 0.29 | 3.64 | 3.96 | 0.67 | 0.68 | ||
| 50% | Semi-parametric | 0.64 | 9.35 | 9.45 | 0.44 | 0.65 | |
| Uniform prior | 0.46 | 6.49 | 7.04 | – | – | ||
| G-Wishart RJ | 0.34 | 4.37 | 4.81 | 0.38 | 0.64 | ||
| G-Wishart BD | 0.34 | 4.43 | 4.90 | 0.51 | 0.67 | ||
| Spike-and-Slab prior | 0.35 | 4.63 | 5.09 | 0.56 | 0.67 | ||
| (ii) | 0% | Semi-parametric | 0.42 | 5.61 | 5.90 | 0.72 | 0.70 |
| Uniform prior | 0.32 | 4.39 | 4.62 | – | – | ||
| G-Wishart RJ | 0.30 | 3.75 | 3.96 | 0.47 | 0.66 | ||
| G-Wishart BD | 0.30 | 3.70 | 3.92 | 0.61 | 0.67 | ||
| Spike-and-Slab prior | 0.26 | 3.36 | 3.76 | 0.73 | 0.70 | ||
| 20% | Semi-parametric | 0.49 | 6.59 | 6.87 | 0.63 | 0.67 | |
| Uniform prior | 0.35 | 4.92 | 5.25 | – | – | ||
| G-Wishart RJ | 0.31 | 4.04 | 4.37 | 0.44 | 0.65 | ||
| G-Wishart BD | 0.32 | 4.04 | 4.42 | 0.56 | 0.67 | ||
| Spike-and-Slab prior | 0.27 | 3.58 | 4.05 | 0.66 | 0.68 | ||
| 50% | Semi-parametric | 0.61 | 8.79 | 8.95 | 0.46 | 0.65 | |
| Uniform prior | 0.46 | 6.46 | 7.01 | – | – | ||
| G-Wishart RJ | 0.34 | 4.36 | 4.81 | 0.38 | 0.63 | ||
| G-Wishart BD | 0.34 | 4.43 | 4.85 | 0.51 | 0.67 | ||
| Spike-and-Slab prior | 0.29 | 3.92 | 4.54 | 0.55 | 0.67 | ||
To evaluate performance for graph recovery under the spike-and-slab prior and the G-Wishart models, we can directly threshold the marginal posterior inclusion probabilities, , calculated by the proportion of iterations where an edge is selected. We define the false positive rate and true positive rate by
where E is the number of edges in the graph. Table 1 shows the comparison of the receiver operating characteristic (ROC) curve using Area Under Curve (AUC) and maximum F1 score. Under all scenarios our estimator yields better AUC and F1 scores, especially when the fraction of missing data is high.
6. Analysis of verbal autopsy data
In this section we present results comparing the proposed model and all of the widely adopted algorithms for cause-of-death assignment using VA data in two contexts. First, in Section 6.1, we compare the different methods using a set of gold standard data. In this scenario, we have sufficient labeled data to obtain good estimates of the conditional distribution of each symptom given each cause. This setting mimics a scenario where informative prior information is available and of high quality, which is common but not ubiquitous in practice. In Section 6.2, we evaluate our methods using data from health and demographic surveillance system (HDSS) sites where the missing data proportion is much higher and the sample sizes are smaller. We compare different methods with physician-coded causes of death and show that the proposed approach is able to improve classification accuracy compared to both InterVA and the Naive Bayes classifier with noisy marginal priors that are poorly specified, in the scenarios where no or little labeled data are available. In both scenarios, we also explore the possibility of supplementing the model with labeled data that potentially come from a different cause-of-death distributions, in order to improve the estimation of the latent dependence structures. However, in all experiments, we do not assume the labeled data follow the same cause-of-death distribution in order to achieve fair comparisons with other methods.
6.1. PHMRC gold standard data
We first evaluate the performance of the proposed methods using the Population Health Metrics Research Consortium (PHMRC) ‘gold standard’ VA dataset (Murray et al., 2011a). The PHMRC dataset consists of about 7,000 deaths recorded in six sites across four countries (Andhra Pradesh, India; Bohol, Philippines; Dar es Salaam, Tanzania; Mexico City, Mexico; Pemba Island, Tanzania; and Uttar Pradesh, India). Gold standard causes are assigned using a set of specific diagnostic criteria that use laboratory, pathology, and medical imaging findings. All deaths occurred in a health facility. For each death, a blinded verbal autopsy was also conducted. We removed all deaths due to external causes, e.g., homicide, road traffic, etc., since the conditional probabilities of many symptom given an external cause is less meaningful, and external causes are also much easier to identify with a deterministic screening procedure in practice. For the rest of the deaths from 26 causes, we randomly selected 1,000 deaths as testing data, additional 1,000 deaths as labeled data, and used the rest of the dataset to calculate the conditional probability matrix of each symptom given each cause as the informative prior. Several VA algorithms can be fit using this conditional probability matrix only, including InterVA (Byass et al., 2003), Naive Bayes Classifier (Miasnikof et al., 2015), and InSilicoVA (McCormick et al., 2016). For InterVA and InSilicoVA, we use the exact same conditional probability matrix described above, without truncating them into discrete levels or reestimating them in InSilicoVA. We also compared the performance with the Tariff method (James et al., 2011; Serina et al., 2015) implemented in the openVA package (Li et al., 2019a). The Tariff method is fitted with the labeled deaths as training data as it does not directly utilize the conditional probabilities as the other methods above. We fit the proposed model with both the unlabeled and the labeled data, assuming that the cause distributions are independent between the two datasets. In this way, the additional information provided by the labeled data is restricted to only the conditional distribution of symptoms given causes. The comparison is implemented in the R statistical programming environment (R Core Team, 2018). For InSilicoVA, we drew 10,000 posterior samples with the first half discarded.
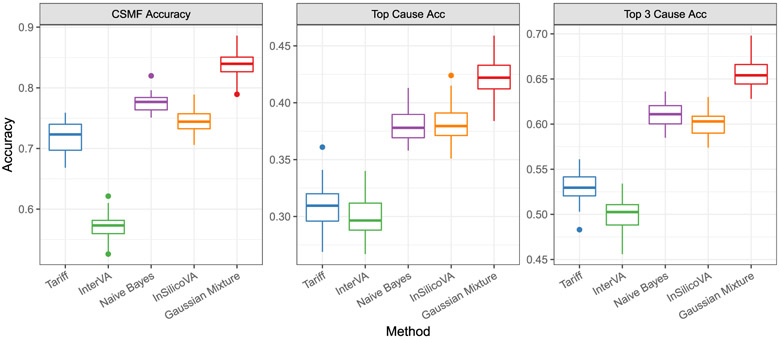
We repeated this experiment 50 times. For the proposed model, we ran the MCMC chains for 20,000 iterations with the first half discarded as a burn-in period, and every 10th sample was saved. To assess the performance in estimating class probability, as is a main goal in VA analysis, we also compared the estimation of π with the truth using ‘CSMF accuracy’ (Murray et al., 2011b) defined as . We put the hyper-prior described in Section 4 on σ2. We compared with the truth in terms of the accuracy of most likely cause, top three most likely causes, and CSMF accuracy. Figure 2 shows clear improvements of the proposed method over alternatives that assume conditional independence.
Figure 2: CSMF and classification accuracy for PHMRC cross-validation study.
The metrics are evaluated on 1,000 randomly selected deaths for Tariff, InterVA, Naive Bayes classifier, InSilicoVA, and the proposed Gaussian mixture model. An additional 1,000 randomly selected labeled death is used as input in the proposed model, but are not assumed to have the same distribution of causes.
6.2. HDSS sites
In this section, we apply our method to a dataset from the Karonga HDSS (Crampin et al., 2012). The Karonga site monitors a population of about 35,000 in northern Malawi near the port village of Chilumba. The current system began with a baseline census from 2002–2004 and has maintained continuous demographic surveillance with verbal autopsy on all deaths since 2002. To validate the proposed method, we use 1,900 adult deaths from Karonga that occurred to people of both sexes from 2002–2014. All deaths have both a VA interview and a physician-assigned causes of death. The distribution of the deaths by cause and year can be found in the supplementary material.
The Karonga VA data were first coded by two physicians, and if they disagreed, a third physician adjudicated and determined the final cause assignment. These assignments were originally coded into 88 cause categories. We removed the small fraction of deaths due to external causes (such as traffic accident and suicide) from this dataset since they are in practice easy to classify and may be conditionally independent from most of the symptoms. Given the limited sample size, we further aggregated the remaining causes into broader groups. We aggregated the assignments into 16 subcategories. We remove the symptoms that are missing for over 90% of the data which reduces the size of the symptom list to 92. Finally, we formed a “prior” dataset by taking all the deaths (VA symptoms and the physician-assigned causes) during 2002–2007 – about 50% of the entire dataset. Because the physician-provided conditional probabilities, P(symptom∣cause), used in InterVA and InSilicoVA are defined with respect to a different cause list, we calculated the empirical P(symptom∣cause) matrix from the training data so that P(symptom s∣cause c) = (number of s = 1 occurring with c)/(number of c), and replace 0 and 1 in the prior probabilities with 0.5pmin and 1 − 0.5(1 − pmax).
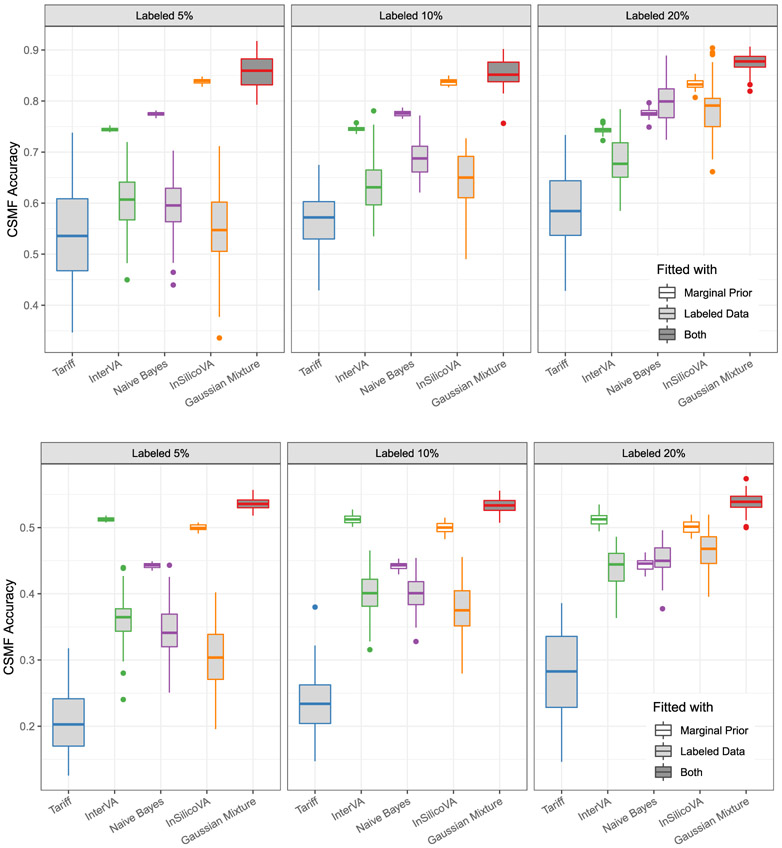
We first explore the performance of the proposed method with only a small number of labeled data. We randomly selected α% of the data after 2007 and reveal their labels, for α = 5, 10, 20. Unlike the random split in the previous example, now we use the smaller fraction of labeled data that are from the same period as the testing data; thus, we may have more accurate estimates of P(symptom s∣cause c). However, models trained on the labeled data ignoring prior information may suffer from high variance due to the small size of the labeled data that determine the classification rule. Figure 3 illustrates the comparison of various methods using either the prior information or the labeled data, based on the accuracy of the top-cause assignment and CSMF accuracy. As more labeled data are available, models trained on the labeled data show similar performance to models trained on less relevant prior information. However, the proposed methods, by combining both sources of information, consistently outperform models using only one source of information.
Figure 3: CSMF accuracy (Top row) and Classification accuracy (Bottom rule) for Karonga physician coded data from cross-validation.
The five different methods are plotted with different colors. Except the proposed Gaussian mixture approach, results using only the prior information are filled in white, and results trained on only the labeled data on filled in light gray. Tariff can only be fitted with labeled data. The proposed method uses both information. Methods using the prior information typically show higher accuracy in this experiment, as the size of the labeled data is small. The proposed method consistently outperforms alternative methods.
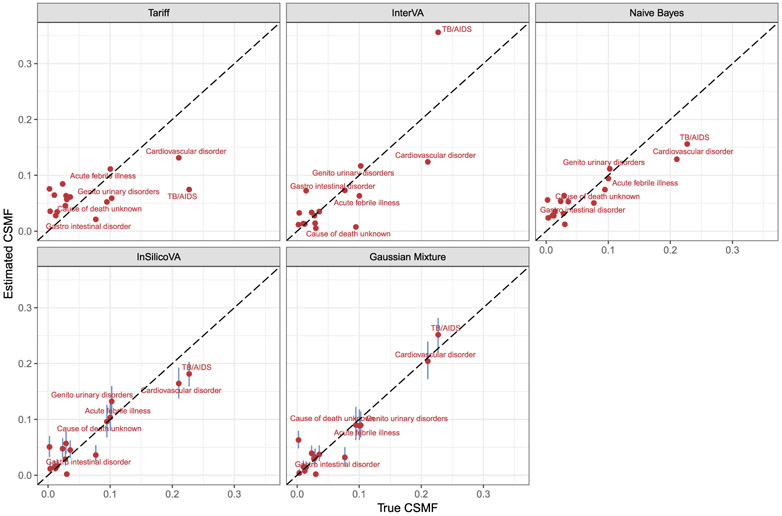
Finally, we fit the model on all the data from 2008–2014 using this empirical conditional probability matrix. We used the same hyperparameter setup as the previous subsection. In the VA questionnaires, there are several groups of questions probing different aspects of the same symptom, for example “fever of any kind” and “fever lasting less than 2 weeks”, or “male” and any pregnancy-related symptoms. Such questions are expected to be conditional dependent due to the structure of the questionnaire, and thus we fix the corresponding selection indices to be 1 in the inverse correlation matrix. We compare our method with the other methods using the same “prior” information. Table 2 summarizes the performance of each algorithm, and Figure 4 shows the estimated CSMF compared to the truth.
Table 2: CSMF accuracy, Top 1 to 3 cause assignment accuracy for Karonga physician coded data.
The marginal probabilities are calculated with data from 2002 to 2007. The training data consist of all the data from 2002 to 2007. The testing data are the rest of the data from 2008 to 2014. The proposed Gaussian mixture model achieves the highest CSMF and Top 1 cause assignment accuracy and also high Top 2 and 3 cause assignment accuracy.
| CSMF | Top1 | Top2 | Top3 | |
|---|---|---|---|---|
| Tariff | 0.626 | 0.375 | 0.538 | 0.695 |
| InterVA | 0.744 | 0.512 | 0.625 | 0.703 |
| Naive Bayes | 0.774 | 0.442 | 0.641 | 0.733 |
| InSilicoVA | 0.839 | 0.501 | 0.689 | 0.767 |
| Gaussian Mixture | 0.887 | 0.533 | 0.674 | 0.745 |
Figure 4: Scatter plot of the estimated CSMF against true CSMF for Karonga data from 2008 to 2014 using different methods.
Causes with true fractions larger than 0.05 are labeled in the plot. The vertical bars correspond to the 95% posterior credible intervals estimated for InSilicoVA and the proposed method. The proposed Gaussian mixture model shows smaller bias.
In addition to the structure induced by the questionnaire, we also recover interesting symptom pairs with conditionally dependent latent factors. For example, the latent variable underlying history of high blood pressure is strongly positively associated with that of paralysis of one side of the body, which is expected given the relatively high prevalence of cardiovascular diseases in the data. In our experiment, there are 3874 potential edges excluding the ones known from the survey. Table 3 summarizes the list of symptom pairs with posterior inclusion probability, , greater than 0.5.
Table 3: List of symptom pairs with conditional dependent latent factors.
The non-zero elements in the inverse correlation matrix are selected by the estimated median probability graph.
| Prob | Symptom | Symptom | Partial Corr |
|---|---|---|---|
| 1.00 | Swelling of the face (puffiness of face) | Both feet or ankles swollen | 0.5 |
| 0.91 | History of mental confusion | Unconscious for at least 24 hours before death | 0.49 |
| 0.87 | Sores or white patches in the mouth or tongue | Difficulty or pain while swallowing liquids | 0.43 |
| 0.87 | History of high blood pressure | Paralysis of one side of the body | 0.38 |
| 0.87 | Age 15-49 years | History of high blood pressure | −0.16 |
| 0.86 | Abdominal distension | Any skin rash (non-measles) | 0.29 |
| 0.84 | Abdominal distension lasting 2 weeks or more | Both feet or ankles swollen | 0.16 |
| 0.80 | Diarrhoea lasting 4 weeks or more | Weight loss | 0.22 |
| 0.68 | Mental confusion for more than 3 months | Unconscious for at least 24 hours before death | 0.27 |
| 0.66 | Weight loss | Sores or white patches in the mouth or tongue | 0.15 |
| 0.65 | Abdominal distension lasting 2 weeks or more | Any skin rash (non-measles) | 0.17 |
| 0.65 | Fever of any kind | Headache | 0.1 |
| 0.64 | Fever lasting 2 weeks or more | Breathlessness lasting 2 weeks or more | 0.07 |
| 0.61 | Sores or white patches in the mouth or tongue | Lumps/swellings | 0.12 |
| 0.59 | Swelling of the face (puffiness of face) | Pale (thinning of blood) or pale palms/soles or nail beds | 0.18 |
| 0.58 | Fever lasting 2 weeks or more | Diarrhoea lasting 4 weeks or more | 0.11 |
| 0.55 | History of asthma | Mental confusion for more than 3 months | 0.17 |
| 0.53 | Breathlessness lasting 2 weeks or more | Paralysis of one side of the body | −0.08 |
| 0.52 | Weight loss | Pale (thinning of blood) or pale palms/soles or nail beds | 0.07 |
| 0.51 | History of asthma | Unconscious for at least 24 hours before death | 0.19 |
| 0.50 | Headache | Stiff or painful neck | 0.12 |
7. Discussion
Understanding the correlation structure among high dimensional mixed data in the presence of missing data is a challenging task. In this work we propose a method that models the joint distribution of variables of mixed types and leverages marginal prior information. Using both simulation, gold-standard, and physician-coded VA data, we demonstrate that our new framework can significantly improve estimation of the latent correlation structure, graph recovery, and classification performance. The estimation of sparse inverse correlation matrices proposed in this paper allows us to decouple the parameterization of the marginal distributions of variables from their dependence structures. It is, however, important to notice that the dependence structures the model learns are between the latent variables rather than the binary observations. In understanding VA data, the interpretation of conditional dependence of underlying latent processes driving the presence of symptoms are usually of more interest than the binary symptoms themselves, since the latter are sometimes subject to somewhat arbitrary cutoffs. In future research, it may also be interesting to explore other parsimonious representations (e.g. Murray et al., 2013; Gruhl et al., 2013; Jin and Matteson, 2018) in the context of analyzing VA data. In particular, Bhadra et al. (2018) recently proposed a conditionally Gaussian density formulation in which the joint distribution of the observed mixed variables can be represented as a scale mixture of multivariate normals. This formulation may provide another useful direction in characterizing the conditional independence relationship of the observed binary and continuous indicators more explicitly, without relying on the latent representation of copula models.
The proposed model can be extended in a few different ways. First, estimating the mixture model using MCMC may suffer from slow mixing when the sampler gets trapped in local modes. This is especially problematic with strong prior information on the extreme values, i.e. conditional probabilities close to 0 and 1. An alternative approach would be to target the posterior modes directly with deterministic EM-type algorithms (e.g. Ročková and George, 2014; Li and McCormick, 2019; Gan et al., 2018). Second, symptom reduction in VA analysis is of key interest as a shorter set of symptoms can both reduce the cost as well as improve the quality of data collection. There has been active research on variable selection in Gaussian mixture models (Andrews and McNicholas, 2014), and consequently the proposed framework may also be extended to perform symptom selection in a data-driven way. Third, the model presented in this paper focuses mostly on binary and continuous data. Extensions to ordinal data are also possible by specifying priors on additional cut-off points. With a normal prior on the logscale differences between consecutive cutoffs, the proposed model can easily incorporate prior information on marginal probabilities of more than two levels. Finally, in this paper we only consider the case where all mixtures follow the same correlation matrix. Direct extension to group-specific correlation matrices would be straightforward, but estimating several correlation matrices independently in the context of VA can be problematic since mixture probabilities are highly unbalanced. Priors on joint distribution of multiple correlation matrix that allow them to borrow information needs to be developed.
Finally, we would like to draw attention to the fact that using marginal information to guide the modeling of joint associations is strongly related to stratified sampling. If we consider cause of death as an unknown stratification variable, the marginal informative prior helps smooth the potentially noisy estimates of the stratum effects from small samples. Thus the proposed approach might also be extended to improve inference with disproportionate samples, e.g. VA data collected from an HIV study site might have better samples of HIV deaths compared to deaths from other causes.
Supplementary Material
Acknowledgments
This work was supported by grants K01HD078452, R01HD086227, and R21HD095451 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD). The authors thank the Karonga health and demographic surveillance system site in Malawi and its director Amelia C. Crampin for helpful inputs and discussion. The authors are also grateful to Adrian Dobra, Jon Wakefield, Johannes Lederer, and Laura Hatfield for helpful comments.
Footnotes
Supplementary Material
Supplementary Material to “Using Bayesian Latent Gaussian Graphical Models to Infer Symptom Associations in Verbal Autopsies” (DOI: 10.1214/19-BA1172SUPP; .pdf). PDF document of supplementary material. The replication R and Java codes to implement the proposed method can be found in the repository at https://github.com/richardli/LGGM.
References
- Andrews JL and McNicholas PD (2014). “Variable selection for clustering and classification.” Journal of Classification, 31(2): 136–153. MR3232592. doi: 10.1007/s00357-013-9139-2. [DOI] [Google Scholar]
- Barnard J, McCulloch R, and Meng X-L (2000). “Modeling Covariance Matrices in Terms of Standard Deviations and Correlations, With Application To Shrinkage.” Statistica Simca, 10(4): 1281–1311. MR1804544. [Google Scholar]
- Bhadra A, Rao A, and Baladandayuthapani V (2018). “Inferring network structure in non-normal and mixed discrete-continuous genomic data.” Biometrics, 74(1): 185–195. MR3777939. doi: 10.1111/biom.12711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bu Y and Lederer J (2017). “Integrating Additional Knowledge Into Estimation of Graphical Models.” arXiv preprint arXiv:1704.02739. [DOI] [PubMed] [Google Scholar]
- Byass P, Huong DL, and Van Minh H (2003). “A probabilistic approach to interpreting verbal autopsies: methodology and preliminary validation in Vietnam.” Scandinavian Journal of Public Health, 31(62 suppl): 32–37. [DOI] [PubMed] [Google Scholar]
- Clark SJ, Li ZR, and McCormick TH (2018). “Quantifying the contributions of training data and algorithm logic to the performance of automated cause-assignment algorithms for Verbal Autopsy.” arXiv preprint arXiv:1803.07141. [Google Scholar]
- Crampin AC, Dube A, Mboma S, Price A, Chihana M, Jahn A, Baschieri A, Molesworth A, Mwaiyeghele E, Branson K, et al. (2012). “Profile: the Karonga health and demographic surveillance system.” International Journal of Epidemiology, 41(3): 676–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshpande SK, Rockova V, and George EI (2017). “Simultaneous Variable and Covariance Selection with the Multivariate Spike-and-Slab Lasso.” arXiv preprint arXiv:1708.08911. [Google Scholar]
- Dobra A, Lenkoski A, et al. (2011). “Copula Gaussian graphical models and their application to modeling functional disability data.” The Annals of Applied Statistics, 5(2A): 969–993. MR2840183. doi: 10.1214/10-AOAS397. [DOI] [Google Scholar]
- Fan J, Liu H, Ning Y, and Zou H (2016). “High dimensional semiparametric latent graphical model for mixed data.” Journal of the Royal Statistical Society: Series B (Statistical Methodology). MR3611752. doi: 10.1111/rssb.12168. [DOI] [Google Scholar]
- Gan L, Narisetty NN, and Liang F (2018). “Bayesian regularization for graphical models with unequal shrinkage.” Journal of the American Statistical Association, 1–14.30034060 [Google Scholar]
- Gelman A (2006). “Prior distributions for variance parameters in hierarchical models (comment on article by Browne and Draper).” Bayesian analysis, 1(3): 515–534. MR2221284. doi: 10.1214/06-BA117A. [DOI] [Google Scholar]
- Gruhl J, Erosheva EA, and Crane PK (2013). “A semiparametric approach to mixed outcome latent variable models: Estimating the association between cognition and regional brain volumes.” The Annals of Applied Statistics, 2361–2383. MR3161726. doi: 10.1214/13-AOAS675. [DOI] [Google Scholar]
- Hoff PD (2007). “Extending the rank likelihood for semiparametric copula estimation.” The Annals of Applied Statistics, 265–283. MR2393851. doi: 10.1214/07-AOAS107. [DOI] [Google Scholar]
- Horton R (2007). “Counting for health.” Lancet, 370(9598): 1526. [DOI] [PubMed] [Google Scholar]
- James SL, Flaxman AD, Murray CJ, and Consortium Population Health Metrics Research (2011). “Performance of the Tariff Method: validation of a simple additive algorithm for analysis of verbal autopsies.” Population Health Metrics, 9(31). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jha P (2014). “Reliable direct measurement of causes of death in low-and middle-income countries.” BMC medicine, 12(1): 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin Z and Matteson DS (2018). “Independent Component Analysis via Energy-based and Kernel-based Mutual Dependence Measures.” arXiv preprint arXiv:1805.06639. MR3671757. doi: 10.1080/01621459.2016.1150851. [DOI] [Google Scholar]
- Jones B, Carvalho C, Dobra A, Hans C, Carter C, and West M (2005). “Experiments in stochastic computation for high-dimensional graphical models.” Statistical Science, 388–400. MR2210226. doi: 10.1214/088342305000000304. [DOI] [Google Scholar]
- King G and Lu Y (2008). “Verbal autopsy methods with multiple causes of death.” Statistical Science, 100(469). MR2523943. doi: 10.1214/07-STS247. [DOI] [Google Scholar]
- Klaassen CA and Wellner JA (1997). “Efficient estimation in the bivariate normal copula model: normal margins are least favourable.” Bernoulli, 3(1): 55–77. MR1466545. doi: 10.2307/3318652. [DOI] [Google Scholar]
- Kunihama T, Li ZR, Clark SJ, and McCormick TH (2018). “Bayesian factor models for probabilistic cause of death assessment with verbal autopsies.” arXiv preprint arXiv:1803.01327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenkoski A and Dobra A (2011). “Computational aspects related to inference in Gaussian graphical models with the G-Wishart prior.” Journal of Computational and Graphical Statistics, 20(1): 140–157. MR2816542. doi: 10.1198/jcgs.2010.08181. [DOI] [Google Scholar]
- Li Y, Craig BA, and Bhadra A (2017). “The Graphical Horseshoe Estimator for Inverse Covariance Matrices.” arXiv preprint arXiv:1707.06661. [Google Scholar]
- Li Z and McCormick TH (2019). “An Expectation Conditional Maximization approach for Gaussian graphical models.” Journal of Computational and Graphical Statistics, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li ZR, McCormick T, and Clark S (2019a). openVA: Automated Method for Verbal Autopsy. R package version 1.0.8. URL http://CRAN.R-project.org/package=openVA. [Google Scholar]
- Li ZR, McCormick T, and Clark S (2019b). “Supplementary Material to “Using Bayesian latent Gaussian graphical models to infer symptom associations in verbal autopsies”.” Bayesian Analysis. doi: 10.1214/19-BA1172SUPP. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Han F, Yuan M, Lafferty J, Wasserman L, et al. (2012). “High-dimensional semiparametric Gaussian copula graphical models.” The Annals of Statistics, 40(4): 2293–2326. MR3059084. doi: 10.1214/12-AOS1037. [DOI] [Google Scholar]
- Liu H, Lafferty J, and Wasserman L (2009). “The nonparanormal: Semiparametric estimation of high dimensional undirected graphs.” Journal of Machine Learning Research, 10(October): 2295–2328. MR2563983. [PMC free article] [PubMed] [Google Scholar]
- Liu JS and Wu YN (1999). “Parameter Expansion for Data Augmentation.” Journal of the American Statistical Association, 94(448): 1264–1274. MR1731488. doi: 10.2307/2669940. [DOI] [Google Scholar]
- McCormick TH, Li ZR, Calvert C, Crampin AC, Kahn K, and Clark SJ (2016). “Probabilistic cause-of-death assignment using verbal autopsies.” Journal of the American Statistical Association, 111(515): 1036–1049. MR3561927. doi: 10.1080/01621459.2016.1152191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng X-L and Van Dyk DA (1999). “Seeking efficient data augmentation schemes via conditional and marginal augmentation.” Biometrika, 86(2): 301–320. MR1705351. doi: 10.1093/biomet/86.2.301. [DOI] [Google Scholar]
- Miasnikof P, Giannakeas V, Gomes M, Aleksandrowicz L, Shestopaloff AY, Alam D, Tollman S, Samarikhalaj A, and Jha P (2015). “Naive Bayes classifiers for verbal autopsies: comparison to physician-based classification for 21,000 child and adult deaths.” BMC medicine, 13(1): 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mohammadi A, Abegaz F, van den Heuvel E, and Wit EC (2017). “Bayesian modelling of Dupuytren disease by using Gaussian copula graphical models.” Journal of the Royal Statistical Society: Series C (Applied Statistics), 66(3): 629–645. MR3632345. doi: 10.1111/rssc.12171. [DOI] [Google Scholar]
- Mohammadi R and Wit EC (2017). “BDgraph: An R Package for Bayesian Structure Learning in Graphical Models.” arXiv preprint arXiv:1501.05108. MR3420899. doi: 10.1214/14-BA889. [DOI] [Google Scholar]
- Murray CJ, Lopez AD, Black R, Ahuja R, Ali SM, Baqui A, Dandona L, Dantzer E, Das V, Dhingra U, et al. (2011a). “Population Health Metrics Research Consortium gold standard verbal autopsy validation study: design, implementation, and development of analysis datasets.” Population health metrics, 9(1): 27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray CJ, Lozano R, Flaxman AD, Vahdatpour A, and Lopez AD (2011b). “Robust metrics for assessing the performance of different verbal autopsy cause assignment methods in validation studies.” , 9(1): 28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray I, Adams R, and MacKay D (2010). “Elliptical slice sampling.” In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, 541–548. [Google Scholar]
- Murray JS, Dunson DB, Carin L, and Lucas JE (2013). “Bayesian Gaussian copula factor models for mixed data.” Journal of the American Statistical Association , 108(502): 656–665. MR3174649. doi: 10.1080/01621459.2012.762328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishihara R, Murray I, and Adams RP (2014). “Parallel MCMC with generalized elliptical slice sampling.” The Journal of Machine Learning Research, 15(1): 2087–2112. MR3231603. [Google Scholar]
- Peterson C, Vannucci M, Karakas C, Choi W, Ma L, and Meletić-Savatić M (2013). “Inferring metabolic networks using the Bayesian adaptive graphical lasso with informative priors.” Statistics and its Interface, 6(4): 547. MR3164658. doi: 10.4310/SII.2013.v6.n4.a12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team (2018). R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: URL https://www.R-project.org/. [Google Scholar]
- Ročková V and George EI (2014). “EMVS: The EM approach to Bayesian variable selection.” Journal of the American Statistical Association, 109(506): 828–846. MR3223753. doi: 10.1080/01621459.2013.869223. [DOI] [Google Scholar]
- Roverato A (2002). “Hyper Inverse Wishart Distribution for Non-decomposable Graphs and its Application to Bayesian Inference for Gaussian Graphical Models.” Scandinavian Journal of Statistics, 29(3): 391–411. MR1925566. doi: 10.1111/1467-9469.00297. [DOI] [Google Scholar]
- Serina P, Riley I, Stewart A, James SL, Flaxman AD, Lozano R, Hernandez B, Mooney MD, Luning R, Black R, et al. (2015). “Improving performance of the Tariff Method for assigning causes of death to verbal autopsies.” BMC medicine, 13(1): 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Talhouk A, Doucet A, and Murphy K (2012). “Efficient Bayesian Inference for Multivariate Probit Models With Sparse Inverse Correlation Matrices.” Journal of Computational and Graphical Statistics, 21(February 2015): 739–757. MR2970917. doi: 10.1080/10618600.2012.679239. [DOI] [Google Scholar]
- Wang H (2015). “Scaling it up: Stochastic search structure learning in graphical models.” Bayesian Analysis, 10(2): 351–377. MR3420886. doi: 10.1214/14-BA916. [DOI] [Google Scholar]
- Wang H et al. (2012). “Bayesian graphical lasso models and efficient posterior computation.” Bayesian Analysis, 7(4): 867–886. MR3000017. doi: 10.1214/12-BA729. [DOI] [Google Scholar]
- Xue L, Zou H, et al. (2012). “Regularized rank-based estimation of high-dimensional nonparanormal graphical models.” The Annals of Statistics, 40(5): 2541–2571. MR3097612. doi: 10.1214/12-AOS1041. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.