Predicting Missing Values in Medical Data Via XGBoost Regression

Abstract

The data in a patient’s laboratory test result is a notable resource to support clinical investigation and enhance medical research. However, for a variety of reasons, this type of data often contains a non-trivial number of missing values. For example, physicians may neglect to order tests or document the results. Such a phenomenon reduces the degree to which this data can be utilized to learn efficient and effective predictive models. To address this problem, various approaches have been developed to impute missing laboratory values; however, their performance has been limited. This is due, in part, to the fact no approaches effectively leverage the contextual information (1) in individual or (2) between laboratory test variables. We introduce an approach to combine an unsupervised prefilling strategy with a supervised machine learning approach, in the form of extreme gradient boosting (XGBoost), to leverage both types of context for imputation purposes. We evaluated the methodology through a series of experiments on approximately 8200 patients’ records in the MIMIC-III dataset. The results demonstrate that the new model outperforms baseline and state-of-the-art models on 13 commonly collected laboratory test variables. In terms of the normalized root mean square derivation (nRMSD), our model exhibits an imputation improvement by over 20%, on average. Missing data imputation on the temporal variables can be largely improved via prefilling strategy and the supervised training technique, which leverages both the longitudinal and cross-sectional context simultaneously.

Introduction

In the healthcare domain, electronic health records (EHR) are often used to make a clinical investigation and develop models for outcome prediction [1]. However, poor data quality can substantially influence the fidelity of the models learned from such data, leading to weakened correlations and incorrect findings. Data completeness is critical to ensuring its quality [2], and yet, EHR data is plagued by completeness issues, especially for continuous variables, which usually document changes in their values over time and, thus, require repeated testing or monitoring. A typical example is a laboratory test result (e.g., blood glucose or potassium level) or vital signs (e.g., heart rate or body temperature) [3]. For a variety of reasons, it is not uncommon for such variables to contain missing values at certain time points [4]. First, some missing values are artifacts of human factors; for example, clinicians may neglect to order certain laboratory tests or forget to document the results [5]. Second, some types of missing values are realized because certain variables follow distinct patterns of collection frequency (e.g., every 5 min vs. every 5 h), which are influenced by specific clinical ordering requirements. For example, in the inpatient setting, the time between orders for a patient’s white blood cell count is often longer than a blood pressure reading simply because it is expected to change at a slower rate [6]. Third, missing values can arise when patients transfer between healthcare systems, resulting in information gaps [7].

The missing value problem impedes researchers from learning accurate models and, subsequently, making reasonable decisions [3, 8]. This is because it is challenging to accommodate missing data in machine learning algorithms [9]. Simply removing the instances with a missing value is a simple solution, but it risks biasing the learned models and reducing the amount of available data [7]. To address this problem, some studies attempted to design and subsequently apply missing data imputation techniques to improve the accuracy and reproducibility of machine learning models. Among various proposed models for imputing missing values of the clinical dataset, methods that rely on multivariate imputation via chained equations, such as MICE [10] and 3D-MICE [11], have shown great promise. These methods invoke the context between the investigated variable and other measurements (i.e., cross-sectional contextual pattern) and/or the context within the investigated variable to predict the missing values. However, these models are limited because they learn the two aforementioned contextual patterns independently and then combine them through a static weighting strategy. Specifically, such an approach can (1) make the prediction of missing data highly dependent on the predefined weights, which are usually not optimized, and (2) neglect the features from the cross-sectional context with neighboring timestamps (e.g., laboratory test values taken within a certain period of time).

To address these limitations, we introduce a hybrid imputation framework that integrates three components: (1) an unsupervised imputation strategy to prefill the dataset with missing points, (2) a feature extraction based on window size strategy, and (3) a supervised machine learning approach, in the form of extreme gradient boosting (XGBoost), to predict the missing values. We refer to our framework as xgbooSt MIssing vaLues In timE Series, or SMILES. We hypothesized that the XGBoost algorithm can identify an efficient way to combine the local and global contextual patterns. We further hypothesized that unsupervised prefilling methods can improve the performance of machine learning models for imputation. To test these hypotheses, we performed a series of experiments on 16,534 patient records in the Medical Information Mart for Intensive Care III (MIMIC-III) dataset [12], each of which contains a time series of 13 commonly collected laboratory tests.

Related Research

Numerous imputation models have been developed to solve the missing medical data problem [9, 13–16]. Mean imputation is one of the easiest and most commonly adopted unsupervised imputation strategies [17, 18]. This type of approach considers the contextual information within a variable [17]. Weighted K-nearest neighbors (KNNimpute) improves mean imputation by leveraging the information of neighbors [17]. Based on the nearest neighbor algorithm, KNNimpute imputes the missing value with the weighted mean of its neighboring values [9, 19]. However, neither mean imputation nor KNNimpute utilizes the correlation between different variables, leading to subpar performance [17].

Rather than relying solely on local clues to predict missing values, more advanced approaches leverage contextual variables [20–23]. Multivariable imputation by chained equations (MICE) is a regression-based conditional model that uses the information of other variables to predict the missing values for a variable of interest [10, 24]. When compared with methods that focus on the prediction of missing continuous values, the missForest imputation algorithm is a highly flexible model that can impute multivariate data that consists of both continuous and categorical variables [25]. This algorithm creates a random forest model for each variable and uses the remainder of the dataset to predict the missing values of the investigated variable [9]. MissForest outperforms KNNimpute and MICE on multiple biological and medical datasets [25]; however, it is computationally expensive because it calculates a separate forest for each variable and runs until convergence [26].

Still, none of the abovementioned approaches efficiently incorporates the contextual signal within the investigated variable or between variables.

Materials and Methods

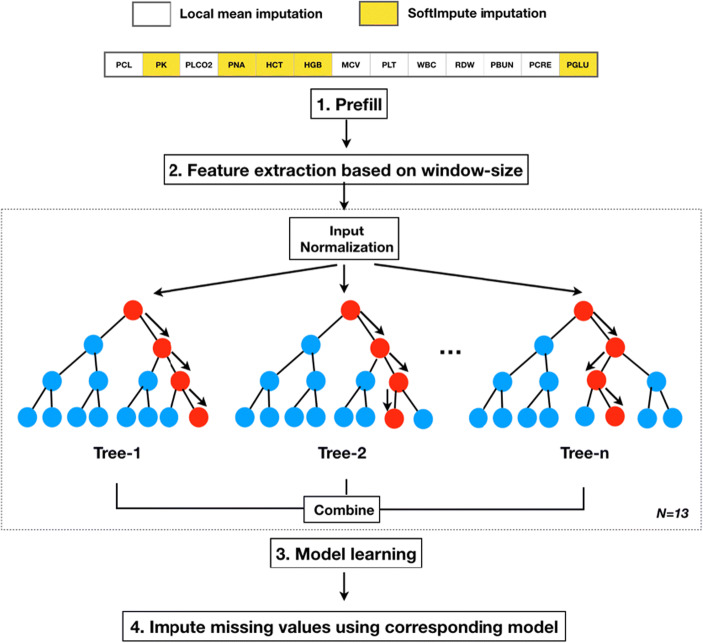
In this section, we describe our imputation framework. The workflow of the imputation framework includes the following: (1) unsupervised learning to prefill missing values, (2) feature extraction based on window size to create feature spaces for an XGBoost model, (3) training and validation of an XGBoost model for each laboratory test variable, and (4) applying the learned models to impute missing values for each laboratory test variable. Figure 1 depicts the workflow, where n represents the number of regression trees in a boosting model, and N denotes the total number of boosting models, which, in this case, corresponds to laboratory test variables. Before providing the details of the framework, we introduce the dataset that will be used to evaluate methods.

Fig. 1.

The four steps of the SMILES imputation workflow

Dataset

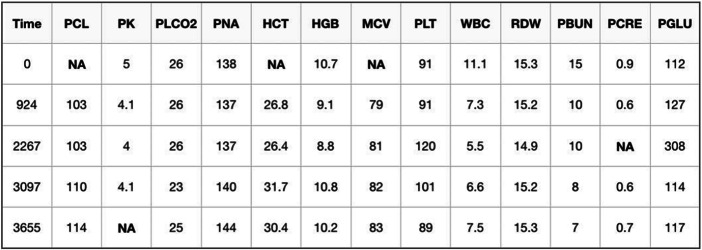
We evaluated our model using data from the Data Analytics Challenge on Missing data Imputation (DACMI)1 at the 2019 IEEE International Conference on Healthcare Informatics. The goal of this challenge is based on a general imputation scenario. Specifically, the goal is to impute missing values in a clinical dataset of longitudinal multivariable laboratory test results. Figure 2 shows an example of a patient’s laboratory test results, which is in a timestamped tabular structure. As can be seen, each patient visit is affiliated with 13 commonly measured laboratory variables, including chloride (PCL), potassium (PK), bicarbonate (PLCO2), sodium (PNA), hematocrit (HCT), hemoglobin (HGB), mean corpuscular volume (MCV), platelets (PLT), white blood cell (WBC) count, red cell distribution width (RDW), blood urea nitrogen (PBUN), creatinine (PCRE), and glucose (PGLU) [11]. “NA” indicates a missing value. The unit for time is reported in seconds from the first test time point in the dataset.

Fig. 2.

Example data for one patient

A dataset, which consists of 8267 patients (each of which has a single intensive care unit visit record), was provided for the training stage to develop the models. A second dataset, also containing 8267 patient visits, was provided for the testing stage to evaluate performance. This dataset was sampled from MIMIC-III, which is a large, freely available database comprising de-identified health-related data associated with over forty thousand patients who stayed in critical care units of Beth Israel Deaconess Medical Center between 2001 and 2012 [12].

There are two types of missing values: (1) real, which lack ground truth, and (2) simulated, which correspond to test results that were nulled (at random) by the challenge committee. In the training set, 6.9% (193,405) of the missing values are real and 3.8% (107,471) are simulated. In the test set, 6.9% are real and 3.9% are simulated.

Prefill

The first step of SMILES prefills the missing values in each time series. Here, prefilling is applied for preparing a larger usable dataset for the downstream training of machine learning models. To determine an appropriate strategy for each laboratory variable, we assessed four prefilling strategies: (1) global mean, which uses the mean of a single variable across all patients. This approach considers each laboratory variable across all patients; (2) local mean, which uses the mean of the values at neighboring timestamps of the missing value within each patient. This approach considers each patient and each laboratory variable independently; (3) Iterative Singular Value Decomposition (SVD), in which missing values are imputed by an iterative low-rank SVD decomposition [27]; and (4) soft impute, which repeatedly fills in missing values with the current prediction, and then solves an optimization problem on the complete matrix using a soft-thresholded SVD [28]. The latter two strategies are performed at the patient level and are widely used in general matrix completion tasks. By comparing their imputation performance, we fix the best prefilling strategy for each laboratory variable as its final strategy to apply.

Feature Extractions Based on Window Size

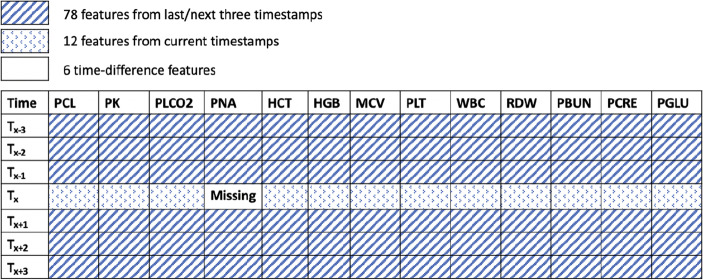
3D-MICE utilizes the benefits of integrating both longitudinal and cross-sectional information into the imputation model [11]; however, it considered both contexts independently and then combined them in an ad hoc manner. To simultaneously capture longitudinal and cross-sectional correlations of a single cell value of a laboratory test variable, we developed a feature extraction strategy based on a sliding window, a strategy that has been effective at improving imputation performance [29]. Specifically, we extracted features based on how close they are to the investigated cell (missing value). As shown in Fig. 3, for an investigated cell (missing value), setting the window size to 7 yields 6 × 13 + 12 + 6 = 96 features, including the 78 values from the previous and following 3 timestamps of the laboratory test variable, the 12 values affiliated with the current timestamp, and 6 time differences between each row. We used the minute as the unit for time difference features instead of the second in the provided dataset. We normalized the laboratory variable features using global mean and standard derivation of each variable to mitigate the feature dominance issue. We then built the dataset by applying the window-based extraction strategy from patients’ records. In doing so, we generated 146,124 training instances by selecting only the timestamps that have no missing laboratory test values in the original data (before prefilling).

Fig. 3.

An example of feature extractions based on window size for a window size of 7

Prediction Model

We used a supervised learning approach, XGBoost, to train missing laboratory test value prediction models. XGBoost is an optimized distributed gradient boosting library [30]. It applies a recursive binary splitting approach to select the best split at each step to reach the best model. The tree-based nature of XGBoost is insensitive to outliers and, like many boosting methods, is robust against overfitting, which largely facilitates the model selection. Equation 1 shows the regularized objective of the XGBoost model at the t^th training step [30], where l(y^(t)_pred, y_truth) represents the loss, which corresponds to measuring the difference between the prediction of the simulated missing value y^(t)_pred and the corresponding ground truth y_truth.

$$L^{\left(t\right)}=\sum _{i}l\left({y^{\left(t\right)}}_{\text{pred}},y_{\text{truth}}\right)+\sum _k\mathrm{\Omega }\left(f_k\right)$$ 1

Here, $\mathrm{\Omega }\left(f_k\right)=\mathit{\gamma T}+\frac{1}{2}\lambda {‖\omega ‖}^2$ is a regularizer representing the complexity of the k^th tree, where T denotes the number of leaves and ‖ω‖² denotes the L2 norm of all leaf scores for training instances. The parameters γ and λ control the degree of conservatism when searching the tree.

We train one XGBoost model for each laboratory test variable, which takes the constructed features (as shown in Section 3.3) as the input and yields the predicted value of the laboratory variable.

Evaluation of Performance

The performance of the prefilling strategies and prediction models is measured using the normalized root mean square derivation (nRMSD) [11]. This measure calculates the difference between values predicted by a model and the ground truth-value. Let X_p,a represents predictions for variable a of patient p and Y_p,a represents the ground truth-value. Let i represents the time index corresponding to X and Y, and let I_p,a,i represents whether the value for patient p, variable a is missing (I = 1) or not (I = 0). Then, the nRMSD is defined as follows:

$$\mathit{\text{nRMSD}}\left(a\right)=\sqrt{\frac{{\sum }_{p,i}{I}_{p,a,i}{\left(\frac{\left|X_{p,a,i}-\left(Y_{p,a,i}\right|\right)}{max\left(Y_{p,a}\right)-min\left(Y_{p,a}\right)}\right)}^2}{{\sum }_{p,i}{I}_{p,a,i}}}$$ 2

Experimental Setting

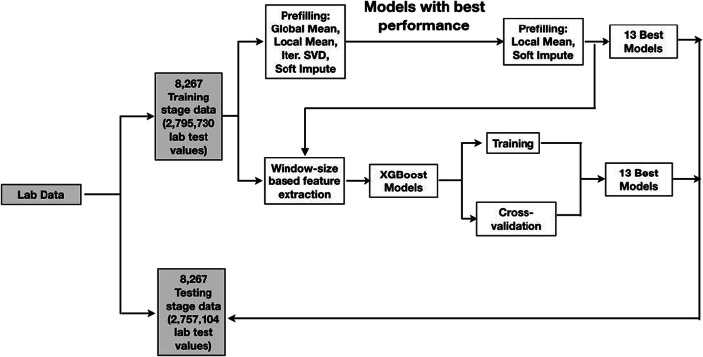
Figure 4 shows that data is partitioned into training, validation, and testing sets. We use 8267 patient visits in the training stage dataset to train and validate the XGBoost models. We applied an 8-fold cross-validation to avoid overfitting. We then used 8267 patient visits from the testing stage dataset to evaluate their performances.

Fig. 4.

Dataset construction for training, cross-validation, and evaluation

Prefilling does not require a training process. As such, we selected 10% of the visits in the training stage dataset as a validation set to determine which method is the best to supplement the feature extraction based on window size and XGBoost models. To test the performance of prefilling models that exhibited the best performance in the validation set, we used another 8267 patient visits in the testing stage dataset.

Since we are unable to distinguish real from simulated missing values, we imputed both types during training and validation; however, we evaluate the performance of the models using only the simulated missing values in the test set. We performed our experiments with the 13 XGBoost models learned using the GridSearchCV [31] and determined the optimized number of trees to fit f, the maximum tree depth for the base learners d, and the minimum sum of instance weight (Hessian) needed in a child s for each laboratory variable. We set the window size w = (5, 7, 9), the learning rate l = 0.1, f = (500, 1000, 1500), d = (3, 5, 6), and s = (1, 3, 5) for each model based on the optimized values.

Experimental Results

Prefill

Table 1 summarizes the performance of the prefilling methods with the validation dataset [11]. It can be seen that the local mean and soft impute strategies are more effective than the others. In particular, local mean yields better imputations for MCV, PBUN, PCL, PCRE, PLCO2, PLT, RDW, and WBC, while soft impute yields better performance in HCT, HGB, PGLU, PK, and PNA. Thus, we chose to apply the local mean strategy to impute the missing values belonging to the former set of variables and apply the soft impute strategy to the latter set of variables. We further assessed the performance of the two prefilling methods on the test set. It was found that the prefilling strategy achieved an average performance of 0.2116, which is 5.32% lower (better) than 3D-MICE, the state-of-the-art method. This suggests that the prefilling strategy may enhance the prediction capability of the SMILES model. We applied the strategy before the prediction model training stage by performing an initial imputation on the missing values.

Table 1.

nRMSD of the prefilling strategies on the validation set, where a smaller score indicates better performance

	Global mean	Local mean	Iter SVD	Soft impute
HCT	0.5247	0.2238	0.1838	0.1727
HGB	0.5509	0.2266	0.1843	0.1748
MCV	1.4799	0.2571	0.3460	0.2628
PBUN	1.4516	0.1549	0.3058	0.2232
PCL	0.5038	0.2006	0.2533	0.2022
PCRE	2.2009	0.2136	0.3126	0.2340
PGLU	0.3970	0.2765	0.3579	0.2672
PK	0.3396	0.2554	0.3394	0.2497
PLCO2	0.5052	0.2159	0.2955	0.2333
PLT	1.4507	0.1771	0.3327	0.2367
PNA	0.4485	0.2235	0.2679	0.2125
RDW	2.0197	0.2098	0.3490	0.2507
WBC	1.2387	0.2182	0.3498	0.2499
Average	1.0086	0.2195	0.2983	0.2284

Prediction Models

Table 2 displays the results with respect to the test set and the cross-validation results. We compared SMILES with 3D-MICE, as well as the prefilling results in terms of nRMSD [11]. The average performance of SMILES with respect to nRMSD on the 13 laboratory tests was 0.1797, 0.1788, and 0.1783 for a window size of 5, 7, and 9, respectively. These results are 20.0% lower (better) than 3D-MICE (0.2235). The cross-validation resulted in an nRMSD of 0.1767 (± 0.0018). The performance for HCT, HGB, PBUN, PCL, PLT, and PNA is between 26.06 and 34.41% better than those of 3D-MICE, while the performance for MCV, PCRE, PK, PLCO2, RDW, and WBC is between 10.83 and 12.92% better. It should be noted that the prefilling strategy influences the final results. The average performance of SMILES using the simplest prefilling strategy, global mean, is 0.8151, which is 78.1% higher (worse) than SMILES (0.1788) using local mean or soft impute strategies.

Table 2.

rRMSD of prefill, 3D-MICE and SMILES on the test set, and SMILES cross-validation (CV)

Variable	3D-MICE	Prefill	SMILES
			Global mean	w = 5	w = 7	w = 9	CV
HCT	0.1505	0.1799	0.5495	0.1060	0.1092	0.1059	0.1050
HGB	0.1488	0.1798	0.3291	0.0986	0.1024	0.0976	0.0943
MCV	0.2713	0.2644	0.2945	0.2421	0.2405	0.2359	0.2378
PBUN	0.1846	0.1583	0.2307	0.1337	0.1338	0.1346	0.1322
PCL	0.2000	0.2034	0.2983	0.1406	0.1413	0.1407	0.1367
PCRE	0.2338	0.2128	0.2345	0.1856	0.1842	0.1851	0.1834
PGLU	0.2769	0.2675	0.3511	0.2816	0.2641	0.2726	0.2525
PK	0.2632	0.2551	0.2729	0.2284	0.2288	0.2292	0.2334
PLCO2	0.2314	0.2109	0.2202	0.1818	0.1831	0.1831	0.1868
PLT	0.2294	0.1796	0.2012	0.1597	0.1598	0.1612	0.1627
PNA	0.2145	0.2129	0.2933	0.1600	0.1592	0.1586	0.1580
RDW	0.2458	0.2059	3.1691	0.2158	0.2136	0.2105	0.2110
WBC	0.2560	0.2208	4.1516	0.2026	0.2047	0.2037	0.2036
Average	0.2235	0.2116	0.8151	0.1797	0.1788	0.1783	0.1767

It should be noted that by expanding the window size from 5 to 7, the SMILE’s performance over PGLU improves from 0.2816 to 0.2641 and outperforms 3D-MICE (0.2769) by 4.8%. This suggests that PGLU requires a more longitudinal context from neighboring time points to support a more accurate prediction.

We further expanded the window size from 7 to 9; the average performance of SMILES improves from 0.1788 to 0.1783 (only 0.28% improvement). The results show that using a larger window size does not noticeably improve imputation, but it did increase the number of engineered features. As a consequence, we halted our experiments into larger window sizes.

Discussion

This investigation suggests that prefilling approaches based on expected values can provide evidence that assists XGBoost regressions through better initialization. This enables a faster convergence and, thus, better performance in imputation. Additionally, the feature extraction based on window size method can find an effective way to combine the contextual information of a single variable and across variables.

This work indicates that researchers may benefit by combining unsupervised and supervised learning methods for the imputation of missing laboratory values. However, it should be recognized that this is a pilot study and there are some limitations that could be addressed through further investigation. First, the reproducibility of the framework has not been validated. The framework is built upon MIMIC-III data only and it is unclear what the performance of these models will be with data collected from other healthcare organizations. Second, the scalability and generalizability of our framework require further investigation. Notably, when the number of variables is substantially larger than what is encountered in the MIMIC-III, the feature extraction based on window size method is likely to generate a high-dimensional feature space that influences model performance. In such a scenario, a straightforward way to address this issue would be to apply a feature selection strategy to drop highly correlated features. Third, we observed that the proposed framework does not sufficiently predict missing values for variables that exhibit sudden change points, such as PGLU (glucose).

Conclusions

In this paper, we introduced the SMILES model to impute the missing values of laboratory test variables. The model integrates prefilling, feature extraction based on window size, and machine learning. While each laboratory test variable has unique features (in terms of sensitivity to time and correlation with other variables), the feature extraction based on window size, along with the prefilling approach, appears to sufficiently handle such idiosyncrasies. SMILES addresses limitations in earlier models (e.g., independent pattern learning and ad hoc weighting schemas) and also accounts for longitudinal and cross-sectional features simultaneously. The empirical analysis with data from MIMIC-III demonstrated that SMILES can achieve an improvement of 20%, on average, over the state-of-the-art approaches.

Funding Information

This research was supported, in part, by the National Library of Medicine of the National Institutes of Health under Award Number R01LM012854. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Data Availability

The dataset is sampled from Medical Information Mart for Intensive Care III. (MIMIC-III) (https://mimic.physionet.org/).

Compliance with Ethical Standards

Conflict of Interest

The authors declare that they have no conflict of interest.

Code Availability

Source code at https://github.com/yanchao0222/SMILES.