Abstract
Purpose:
Chemical exchange saturation transfer (CEST) MRI experiments of mobile macromolecules, e.g. proteins, carbohydrates and phospholipids, often show signals due to saturation transfer from aliphatic protons to water. Currently, the mechanism of this nuclear Overhauser effect (NOE) based transfer pathway is not completely understood and could be due either to NOEs directly to bound water or NOEs relayed intramolecularly via exchangeable protons. We used glycogen as a model system to investigate this saturation transfer pathway in sugar polymer solution.
Theory and Methods:
To determine whether proton exchange affected saturation transfer, saturation spectra (Z-spectra) were measured for glycogen solutions of different pH, D2O/H2O ratio, and glycogen particle size. A theoretical model was derived to analytically describe the NOE-based signals in these spectra. Numerical simulations were performed to verify this theory, which was further tested by fitting experimental data for different exchange regimes.
Results:
Signal intensities of aliphatic NOEs in Z-spectra of glycogen (glycoNOEs) in D2O solution were influenced by hydroxyl proton exchange rates, while those in H2O were not. This indicates that the primary transfer pathway is an exchange-relayed NOE (rNOE) from these aliphatic protons to neighboring hydroxyl protons, followed by the exchange to water protons. Experimental data for glycogen solutions in D2O and H2O could be analyzed successfully using an analytical theory derived for such rNOE transfer, which was further validated using numerical simulations with the Bloch equations.
Conclusions:
The predominant mechanism underlying aliphatic signals in Z-spectra of mobile carbohydrate polymers is intramolecular relayed NOE (rNOE) transfer followed by proton exchange.
Keywords: MRI, relayed NOE, dipolar relaxation, glucose, D2O, carbohydrate
Introduction
In the CEST MRI method, a radiofrequency (RF) pulse is applied to saturate the protons of targeted molecules, and the change in water signal due to saturation transfer is quantified as a function of saturation frequency in the Z-spectrum (1-5). Magnetization transfer (MT) between protons may occur via several mechanisms: (I) through-space cross-relaxation (or nuclear Overhauser effect, NOE); (II) exchange processes, including conformational exchange (6,7), ligand binding (8,9), protein hydration (10) and labile (hydroxyl, amide or amine) proton exchange with water (2). Due to the abundance of proton magnetization transfer processes in vivo, multiple signals appear in the output Z-spectrum. Typically, chemical exchange peaks from labile protons appear on the positive side of the Z-spectrum (referenced to water at 0 ppm), NOEs from macromolecular aliphatic protons primarily but not exclusively appear on the negative side (2), while NOEs from solid-like materials appear over a broad range on both sides of the Z-spectrum (conventional magnetization transfer contrast, MTC).
Previous CEST MRI studies (11-14) on carbohydrate polymers such as glycogen and glycosaminoglycans (GAGs) reported “strong magnetic connections” between the aliphatic protons in these macromolecules and water protons. For CEST experiments on macromolecular carbohydrates (12,14), the MT from an aliphatic proton to water can be achieved via two mechanisms (2,3,14,15): (a) relayed NOE (rNOE), in which the NOE between an aliphatic proton and a neighboring labile (hydroxyl or amino) proton is relayed to water via chemical exchange; (b) direct NOE between aliphatic protons and long-lived (>1 ns) bound water, which has been shown to exist in DNA (16), RNA (17) and protein interior space (18). For both solid-like proteins (19) and large mobile proteins (2,20,21), previous evidence in vitro and in vivo shows that the magnetization transfer to water under physiological conditions is dominated by the rNOE mechanism. However, for carbohydrate polymers, the transfer pathway is not yet fully understood.
We recently developed an MRI method for the water-based detection of glycogen utilizing nuclear Overhauser effects (glycoNOE) from its aliphatic protons to water (14). Here we use glycogen (Fig. 1) as a model system to investigate the MT mechanism in carbohydrates and report direct evidence that the glycoNOEs occur primarily via the rNOE exchange mechanism (a). The rNOE signal in glycogen is shown to depend on pH, water solvent D2O/H2O ratio (and thus hydroxyl proton exchange) and particle size (and thus molecular motion that affects intramolecular cross-relaxation). We also show that the rNOE process can be described analytically by a simplified two-step magnetization transfer model, which agrees with the experimental evidence and numerical simulations based on the Bloch equations. This study provides insight into the origin of Z-spectra of carbohydrate polymers as well as a theoretical basis for CEST MRI effects related to carbohydrate polymers.
Figure 1.
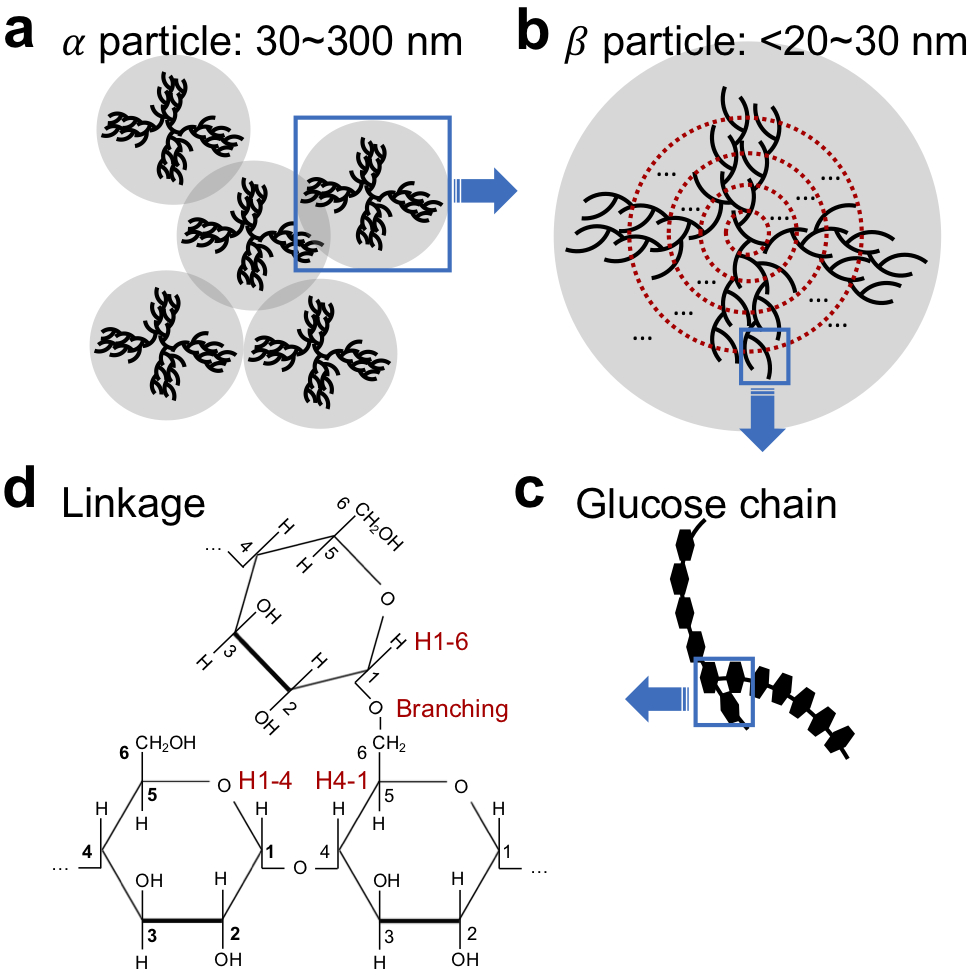
Spatial and chemical glycogen structures. (a) Rosette-like α particles (30~300 nm) consist of aggregates of smaller spherical β particles. (b) Tiered model (31) for glucose chain arrangement in β particles. (c) Spatial structure of a glucose chain fragment (d) Chemical structure of three glucose units in the boxed in chain branch of (c), showing α(1-4) linkage and α(1-6) branching points.
Methods
Theory
Based on experimental evidence to be presented in the Results section and using the glucose unit structure (22), a relayed NOE network that describes the magnetization transfer pathways between glycogen aliphatic protons and water (Fig. 2) is proposed, and simplified to a 3-pool model as:
where Ha, He and Hw represent a glycogen aliphatic proton pool, a neighboring exchangeable (hydroxyl) proton pool and the free water proton pool, respectively; σae and σea are the “effective” NOE cross-relaxation rates, which would be equal between two pools of equal size (e.g. in the simplified 3-pool approach); kew and kwe are the exchange rates of the neighboring hydroxyl and the water protons, respectively. As kew and kwe are highly sensitive to solvent pH, the glycoNOE signal is also expected to be pH-dependent in some exchange regimes.
Figure 2.
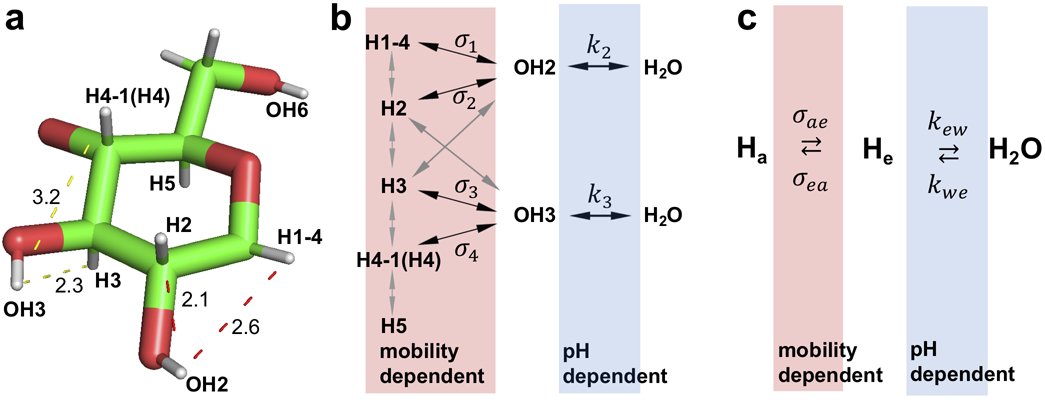
Schematic of the magnetization transfer pathways for the glycoNOE effect. (a) 3D structure for a glucose unit in glycogen (Protein data bank ID: 1c58 (20)). Dashed lines with a corresponding number indicate the distance in Å between proton pairs. (b) Magnetization transfer network involving multiple NOEs and hydroxyl proton chemical exchange. (c) A simplified 3-pool representation of the magnetization transfer pathway from a glycogen aliphatic proton to water (Ha = H1-4, H2, H3, H4-1(H4), or H5) that applies when selectively saturating a proton pool.
In the 3-pool model, the z-magnetization evolutions under a continuous RF saturation pulse (ω1 = γB1, assumed to be selective for Ha) are described by a set of modified Bloch equations,
| [1] |
| [2] |
| [3] |
where ρa, ρe and ρw are the longitudinal relaxation rates (without chemical exchange contributions) for the glycogen aliphatic (Ha) and hydroxyl protons (He), and free water protons (Hw), respectively. The analytical solution for steady-state saturation transfer experiments can be derived to be (see details in Supporting Information):
| [4] |
Here “e” is the “enhancement factor”, . , is the “saturation efficiency”. . For a solvent with 100% H2O, . Let’s define the water proton fraction as P (P = 1 for H2O and 0.05 for 95% D2O). In the case of 95% D2O, 95% of the glycogen hydroxyl positions are taken by deuterons (OD) and only 5% are OH. During an experiment, the Ha protons are continuously saturated but only the proton hydroxyl (OH) residues will efficiently couple to the Ha protons and transfer the saturation to water and contributed to the detected proton signal (Hw). Looking at 1 Ha/He pair, we have: [Ha]effective = [He] = P*[hydroxyl] and [Hw] = P*2*[water]; So the ratio [He]/ [Hw] does not change with the enrichment. And . So f also does not change with the proton enrichment.
Obtaining an analytical solution for α would require solving the full set of 3-pool Bloch equations (Supporting Information Eqs. S1-S5). For simplification, we here assume the evolution of the Ha magnetization (in the 3-pool model) can be described as that of a 1-pool system during the continuous application of ω1 irradiation (23) to Ha. That is, (T1a and T2a are the “effective” relaxation rates of Ha in the single-spin system, different from the terms λa and ρa in the 3-pool model, Ωa is the chemical shift offset relative to the water frequency) (23).
In the case of glycogen in H2O, where the hydroxyl proton exchange rate is much faster than the NOE rate, the expression for the enhancement factor in Eq. 4 can be simplified. Assuming the slow tumbling limit,
| [5] |
then,
| [6] |
and (with f equal to ),
| [7] |
Eq. 7 resembles the analytical solution for the proton transfer enhancement factor in the 2-pool CEST model (24), but now with the NOE transfer as the determining rate instead of kew. Eqs. 4-7 indicate that the relative values of the NOE rate and the hydroxyl proton exchange rate are important in determining the glycoNOE signals at different pH values. When kew >> ∣σae∣, the rNOE signal in the Z-spectrum is expected to be pH independent, which will be expected for glycogen under physiological conditions. Such a situation is thus not by definition incompatible with the rNOE mechanism, just a special situation. The presence of the rNOE mechanism then needs to be proven by going to a slower exchange regime, such as in some D2O solutions.
In the case where NOE transfer is the rate determining step, the two-step model is equivalent to a single-step model (see Supporting Information) and Eq. 7 can be further simplified for macromolecules at low concentration:
| [8] |
then,
| [9] |
where T1w = 1/ρw, is the water solvent T1 (without chemical exchange, i.e. solvent only).
Saturation Transfer Experiments at 17.6T
Three types of glycogen, from bovine liver, rabbit liver, and oyster (Sigma, St. Louis, USA), were dissolved in phosphate-buffered saline (PBS) prepared with either 95% H2O/5% D2O or 95% D2O/5% H2O (increased D2O content to slow down hydroxyl exchange (19)) and pH-adjusted (25) using concentrated (>1 M) NaOH or HCl solutions. pD = pH-meter reading + 0.4. Based on using minute amounts of highly concentrated NaOH and HCl, we assumed that the D2O/H2O ratio of solvent was not affected by the pH titration procedures. NMR experiments were conducted using a 17.6T Bruker Avance III (Bruker, Ettlingen, Germany) scanner at 20 °C. In each scan repetition, the pre-scan delay was set to be 10s (in 95% H2O/5% D2O) or 50 s (95% D2O/5% H2O), and magnetic labeling of protons was achieved with a continuous pre-saturation period of 0.5-8s (95% H2O/5% D2O) or 2-40s (95% D2O/5% H2O), with B1 values ranging from 0.12 to 1 μT. T1 values of water in the two PBS solutions (95% D2O/5% H2O and 95% H2O/5% D2O) were measured using inversion recovery pulse sequences. For 95% D2O/5% H2O solution, the pre-scan delay was 50s and variable delay list was 0.01-60s. For 95% H2O/5% D2O solution, the pre-scan delay was 15s and variable delay list was 0.01-12s. In both cases a small gradient was applied during the inversion delay to remove effects of radiation damping.
Glycogen Particle Size Measurements and glycoNOE MRI
Rabbit liver glycogen (100 mM glucose units) and oyster glycogen (100 mM) were dissolved into PBS (100% H2O) separately and the pH was adjusted to 3.0. To obtain glycogen samples of varied particle size, the glycogen solutions were heated to 80 °C for hydrolysis for between 0 and 25 days. The average particle sizes were determined by taking the weighted average of the size distribution curves measured using dynamic light scattering (DLS, Zetasizer Nano ZS90, Malvern Instruments). In addition to 17.6T studies, Z-spectra for these samples with varied particle size were also acquired at 11.7 T (Bruker Biospec, Ettlingen, Germany) using an ultra-short echo time saturation transfer (UTE-ST) MRI sequence described previously (14) with a B1 of 1.0 μT.
Data Analysis
The Z-spectra for glycogen were fit to 4 Lorentzian line shapes (26) centered at +1.2, +0.6, 0.0 and −1.0 ppm) (14,24) to estimate the peak intensities of NOEs (at −1.0 ppm and +0.6 ppm), OH-CEST (at +1.2 ppm) and water. To quantify the cross-relaxation rates, the H1-4 NOE peak (+0.6 ppm) intensities from Z-spectra of glycogen at pH of 9.6 were fit as a function of B1 (see supporting theory). To quantify the signal intensities in the 1D NMR spectra of glycogen, each spectrum was divided into three regions: OH2 + OH3 region (>0.8 ppm), H1-4 + OH6 region (0.4 to 0.8 ppm), and the “other peaks” region (<0.4 ppm). Each region was fit to multiple Lorentzian line shapes to separate out the background from the peaks of interest. The hydroxyl exchange rates of glycogen at different pH were estimated using either line-width analysis or selective inversion recovery experiments on OH2 + OH3 (+1.2 ppm) NMR signals (see details in Supporting Information).
Results
Numerical Simulations
To validate the steady-state analytical solution of Eq. 4, numerically simulated Z-spectra data were created and analyzed for different exchange regimes ranging from kew ≈ ∣σae∣ to kew >> ∣σae∣. This was done both for solutions in D2O (Figs. 3a-c, with water T1 = 12s) and H2O (Figs. 3d-f, water T1 = 2.8s). Figures 3a and 3d show the Z-spectra for different hydroxyl exchange rates from numerical simulations (parameters in Table 1) in H2O and D2O, respectively. At the intermediate exchange regime, kew ≈ ∣σae∣, the rNOE signal (Ha peak at −1 ppm, Figs. 3a, d) increases with the exchange rate kew, while when kew >> ∣σae∣, the rNOE signal is mostly independent of exchange rates kew. Simulations of glycoNOE intensities as a function of B1 for kew = 4000 s−1 confirm that the saturation factor α can be described analytically by Supporting Information Eq. S19 (Figs. 3b, e). Finally, signal enhancement factors (e) for the simulated glycoNOE peaks show exact correspondence with analytical calculations for a range of NOE rates at kew = 4000 s−1 (Figs. 3c, f).
Figure 3.
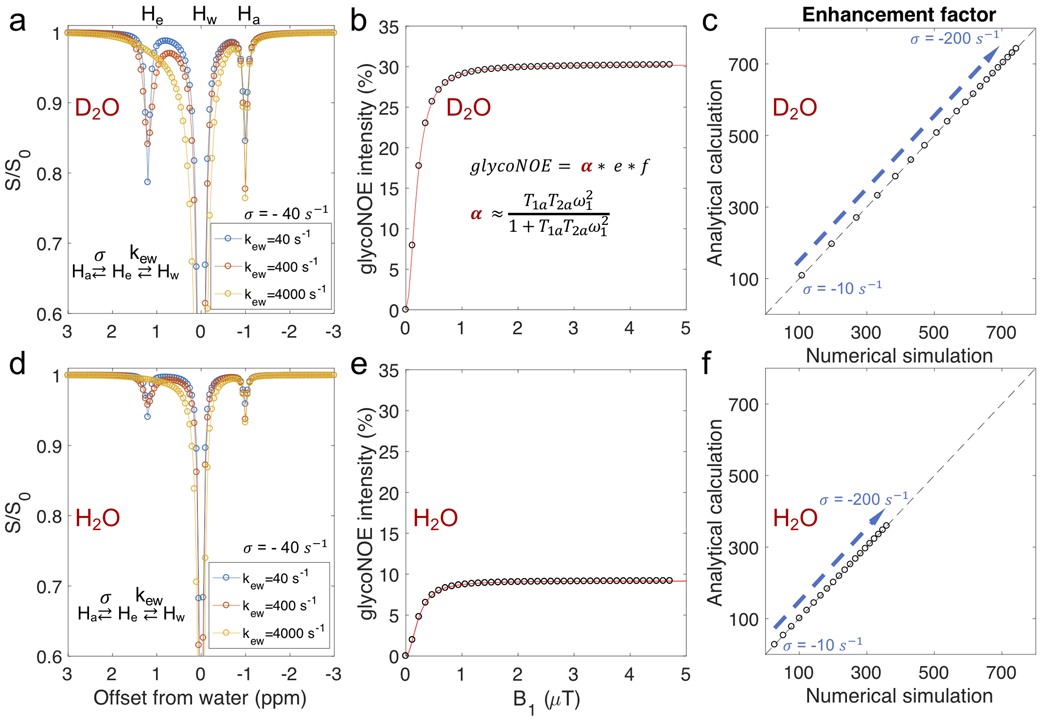
Numerical simulations (Supporting Information Eqs. S1-S5) for the three-pool model agree with the steady state analytical results (Eq. 4). (a, d) Numerically simulated Z-spectra for different hydroxyl exchange rates. For exchange rates (kew) that are much faster than the NOE transfer rate (σ = σae = σea = −40 s−1), changes in kew cause negligible changes in the Ha (glycoNOE, −1 ppm) peak intensity in the Z-spectrum. (b, d) The dependence of the numerically simulated glycoNOE (black circles) intensities on B1 field strength is in agreement with that using the analytical solution (red line, using Eq. 4 and Supporting Information Eq. S19). (c, f) Values for the enhancement factor (e) for numerically and analytically simulated data are the same. The exchange rate (kew) was set to 4000 s−1, and the NOE rate varied (−10 to −200 s−1). To avoid direct water saturation, the chemical shift of Ha peak was set to be −20 ppm in the simulations. The water proton longitudinal relaxation time (T1w) was set to be 12s for D2O (a, b, c) and 2.8s for H2O (d, e, f).
Table 1.
Values of the parameters as set in numerical simulations.
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| 1/ρa (ms) | 1/σae | [Ha] (M)3 | 0.2 |
| 1/ρe (ms) | 1/σae | [He] (M) | 0.2 |
| 1/ρw (ms) | 12000, 2800 | [Hw] (M) | 110 |
| 1/λa (ms)1 | 10 | μ (s−1)4 | 40 |
| 1/λe (ms) | 10 | σae, σea (s−1) | −10 to −200 |
| 1/λw (ms) | 750 | kew (s−1) | 40 to 4000 |
| Ωa (ppm)2 | −1, −20 | ω1 (rad/s)5 | 30 to 1260 |
| Ωe (ppm) | +1.2 | t (s) | 100 |
| Ωw (ppm) | 0 | B0 (T) | 17.6 |
Transverse relaxation rate (without chemical exchange contributions) of Ha;
chemical shift offset of Ha relative to water protons;
concentration of Ha;
transverse cross-relaxation rate between Ha and He;
B1 field strength. For more details on numerical simulations, see Supporting Information.
Phantom Experiments
The hydroxyl proton exchange rate with water is known to be affected by solvent pH (15), buffer concentration, and the H2O/D2O ratio (19). First, the effect of different glycogen hydroxyl exchange rates on the glycoNOE signal was evaluated by varying pH and solvent composition. Figure 4a and Supporting Information Figure S1 show 1D NMR spectra for oyster glycogen dissolved in 95% D2O/5% H2O as a function of pH. Linewidth and exchange rate analysis for the combined glycogen hydroxyl proton (OH2 + OH3) signal at an offset of +1.2 ppm from water (Fig. 4a) show that the hydroxyl exchange rate is relatively slow (~102 s−1) in the pH range from 6 to 7 in D2O and increases by an order of magnitude (>103 s−1) at lower and higher pH (Supporting Information Table S1). In the Z-spectra (Fig. 4b and Supporting Information Figure S2) for glycogen in 95% D2O/5% H2O, a pH dependence (Fig. 4c) is observed for the intensity of peaks at +1.2 ppm (hydroxyl protons OH2 + OH3 CEST) (24), +0.6 ppm (H1-4 NOE + OH6 CEST) (11,24,27), and −1 ppm (glycoNOE) (14). Importantly, the glycoNOE (−1 ppm) signal intensity is lowest in the pH range 5.7 to ~7 and increases at lower and higher pH (Fig. 4c), the same pattern as observed in the dependence of hydroxyl exchange rates on pH (Supporting Information Table S1). Fig. 4d shows the B1 dependence of the glycoNOE effects fitted using Eq. 4 of our analytical equations, indicating excellent agreement between theory and experiment.
Figure 4.
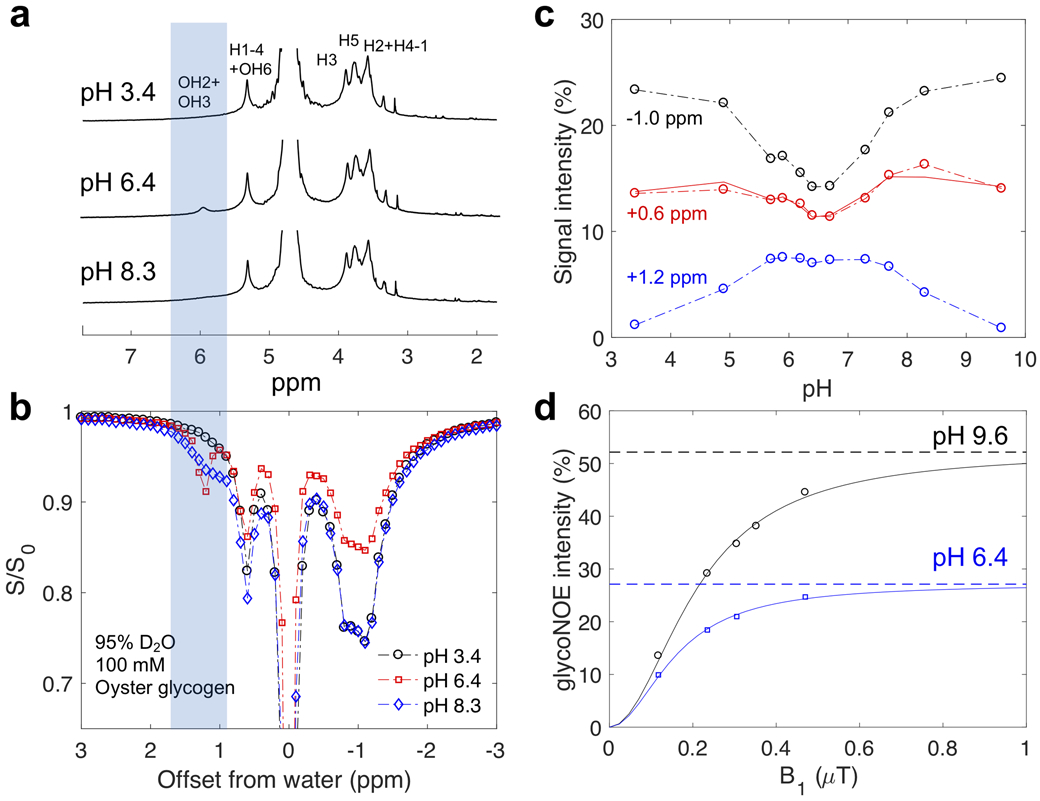
The pH dependence of NMR and Z-spectral intensities for oyster glycogen (100 mM glucose units) in PBS buffer prepared using 95% D2O/5% H2O at 17.6T and 20°C. (a) 1D NMR spectra at different pH (see Supporting Information Figure S1 for full range). The aliphatic and hydroxyl proton peak assignments are based on previous studies (24,27). (b) Z-spectra at three pH values (4s continuous RF irradiation, B1 = 0.4 μT). (c) Lorentzian fitted peak intensities (S/S0) at +1.2, +0.6 and −1.0 ppm as a function of pH. The solid red line is [0.57*S(−1.0 ppm)+0.48*S(+1.2 ppm)]/S0, using the signal for OH3 + OH2 as an estimate for OH6 to confirm that both CEST (OH6) and NOE (H1-4) contribute to the +0.6 ppm peak in the Z-spectra. (d) GlycoNOE (−1 ppm) intensity as a function of B1 (16s continuous RF) at two pH values. The curve was fitted using Eq. 4 with α from Eq. S19. At pH 6.4 (intermediate exchange regime), glycoNOE intensities become about 50% of the maximum intensity at pH 9.6, when kew >> ∣σae∣ (fast exchange regime).
We next performed saturation transfer experiments in which 1D NMR spectra were acquired as a function of saturation frequency (Fig. 5a). At each saturation frequency, Lorentzian fitting was applied to determine the spectral intensities for each proton pool in the 1D NMR spectrum (Fig. 5a). These fitted peak intensities were then plotted as a function of saturation frequency (Fig. 5b), giving Z-spectra for each proton pool. These were subsequently analyzed to learn about the NOE networks between the glycogen protons. The data show that saturation of one proton pool causes a signal reduction in the others (Fig. 5b), demonstrating that each proton pool is connected with the rest via NOE or/and rNOE (water). For instance, when saturating around the −1.1 ppm aliphatic resonances, the signals of H2O, H1-4 + OH6 and OH2 + OH3 are affected, indicating coupling of these pools. Importantly, when the OH2 + OH3 frequency is saturated, effects are clearly visible for aliphatic pools H2 + H4-1, H5 and H3. Notice also that the Lorentzian shape of the direct saturation of OH2 + OH3 is not well defined, because the exchange is still faster than the saturation.
Figure 5.
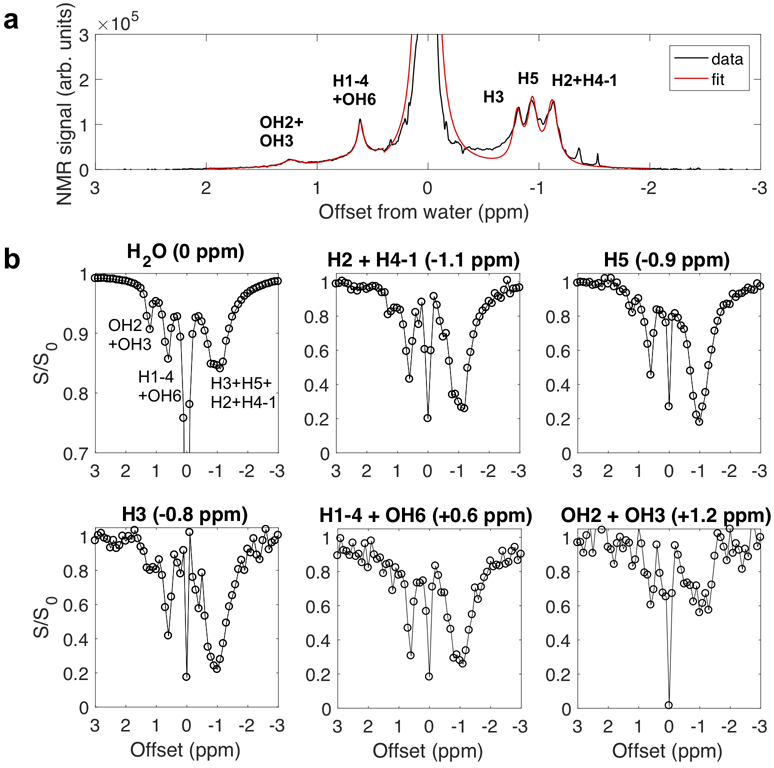
Coupling of different proton groups in oyster glycogen (100 mM) in 95% D2O/5% H2O at pH 6.4. (a) A representative proton NMR spectrum with Lorentzian line-shape fitting to quantify the peak intensities of the six pools. (b) Z-spectra for the six proton pools assigned in (a), i.e. a plot of intensities relative to the full signal of the particular proton group plotted as a function of saturation frequency. In the absence of coupling between pools, only the direct saturation peak for a particular pool would be visible.
When the hydroxyl exchange rate is in the fast exchange regime (kew >> ∣σae∣), i.e., at high or low pH, the OH2 + OH3 (+1.2 ppm) and OH6 (+0.6 ppm) CEST signals become negligible in the Z-spectra at low B1 (Fig. 6) and the H1-4 NOE rate (σ1) can be quantified from the +0.6 ppm peak in the Z-spectra (using Eq. 7). Table 2 shows the σ1 values for different glycogen samples (pH of 9.6) in D2O and H2O. The NOE rates are found to be slightly faster in D2O than those in H2O, in agreement with the expectation that molecular motion is slower in D2O due to its higher solvent viscosity. In contrast to the small increases in NOE rates when replacing H2O with D2O, the glycoNOE signals (and CEST signal) increased up to ~3 fold (Fig. 6), due to an increase in water T1 (2.8s in 95% H2O and 10.2s in 95% D2O). (Eq. 7 and Fig. 3)
Figure 6.
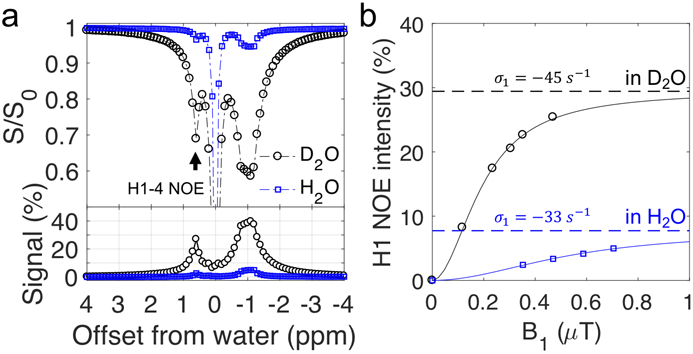
Oyster glycogen (pH 9.6) in H2O and D2O. (a) The Z-spectra (B1 = 0.4 μT) of glycogen (100 mM, pH 9.6) in H2O (95% H2O/5% D2O) and D2O (95% D2O/5% H2O). The bottom panel shows the magnetization transfer difference signal of these Z-spectra after removing the direct water saturation background. (b) The H1-4 NOE peak (+0.6 ppm) intensity as a function of B1 saturation power. The H1-4 NOE rates (σ1) were fitted according to Eqs. 4 and 7 and assuming the slow tumbling limit ().
Table 2.
Glycogen particle size and the H1-4 NOE rates (σ1, at 750 MHz, 20 °C, pH 9.6)
| Glycogen type | bovine liver | rabbit liver | oyster |
|---|---|---|---|
| particle size (nm) | 7 | 52 | 30 |
| σ1 (s−1) in D2O | −5(±0.4a) | −36(±4) | −45(±3) |
| σ1 (s−1) in H2O | −2.4(±4) | −28(±7) | −33(±4) |
SD values were calculated from fitting with 95% confidence bounds.
It is known that molecules with larger molecular weights tend to have slower molecular motions and hence larger NOE rates. Interestingly, among the three types of glycogen samples measured, oyster glycogen was found to have the largest NOE rates, which cannot be fully explained by particle size, as rabbit liver glycogen is the largest in average particle size (Table 2 and Supporting Information Figure S3). The signal dependence on glycogen particle size was further evaluated in detail for oyster glycogen and rabbit liver glycogen in H2O (Fig. 7). For glycogen particles smaller than ~30 nm, glycoNOE signal increased with particle size, while glycoNOE signal was independent of measured particle size for rabbit liver glycogen over ~30 nm. Oyster glycogen has a stronger signal than rabbit liver glycogen of similar size, indicating particle size is not the only factor determining the NOE rate (or molecular motions) in glycogen (Fig. 7 and Table. 2).
Figure 7.
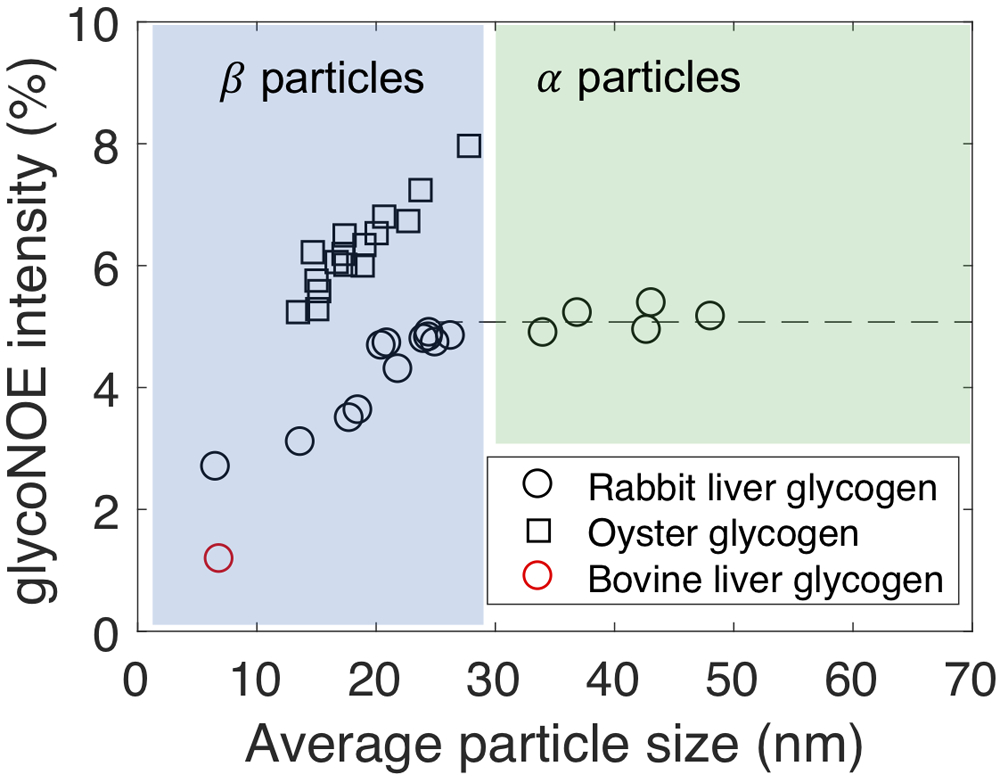
The dependence of measured glycoNOE signal (at a magnetic field of 11.7T, 20 °C) intensities (at −1 ppm) on average particle size for three types of glycogen particles (100 mM). Based on the measured particle sizes, glycogen belongs to either α particle or β particle.
Discussion
We recently reported that glycoNOE signals can be used to image glycogen using the water signal in MRI (14). However, the detailed mechanism of saturation transfer, a direct or relayed NOE (rNOE) process to water, remained unclear. The results in the current study provide strong experimental evidence that the glycoNOE signal occurs via a relayed exchange pathway. Direct NOE transfer from glycogen aliphatic protons to water protons would occur to bound water and the rate of water-binding is not expected to depend on pH. On the other hand, rNOE transfer should in principle depend on the hydroxyl proton exchange rate and factors that affect this rate, such as pH, temperature, salt concentration and H2O/D2O ratio. The reported lack of a pH dependence for the in vitro experiments in H2O (14) appears to be evidence that the mechanism is based on direct NOEs. However, this is counterintuitive based on the knowledge that direct NOEs are generally small to negligible in mobile macromolecules (18,21). We therefore performed an in-depth investigation of the pH dependence of the glycoNOE effect in D2O solution, where the hydroxyl exchange rates slow down.
The data in Fig. 4 and Supporting Information Figures S2 and S3 show that the glycoNOE signal in the Z-spectra are pH independent in H2O (14), but become pH dependent in D2O. This interesting phenomenon can be explained in terms of the relative magnitude of the hydroxyl exchange rates and NOE transfer rates at different pH and in different solvents, i.e., in terms of different exchange regimes. In H2O, the hydroxyl exchange rates are always much faster than the NOE rates (Table 2 and Supporting Information Table S1) regardless of pH (fast exchange regime), and the glycoNOEs appear to be pH-independent. This is the case under physiological conditions, and, as a consequence, factors affecting hydroxyl exchange rates (e.g. pH, temperature) therefore have a negligible influence on glycoNOE signal in vivo. At lower pH in D2O, on the other hand, the hydroxyl exchange rates decrease to a level that is comparable to NOE rates (intermediate exchange regime, see Supporting Information Table S1 at pH 6.4), and the glycoNOEs become pH-dependent (Eq. 4).
In principle, both rNOE and direct NOE mechanisms may contribute. In order to investigate the mechanism further, we derived an analytical solution of the glycogen rNOE signal in Z-spectra and validated this simple model by numerical simulations with the full Bloch equations. We then tested whether this rNOE model could describe the experimental glycoNOE signal dependence on solvent pH, H2O/D2O ratio and glycogen particle sizes. The data in Fig. 4d show that for the pH range of 6.2-6.7 in D2O, the glycoNOE intensities are about 50% of the maximum signal (measured at pH of 9.6), which is in agreement with the predicted intensity of about 60% of the maximum signal using the measured hydroxyl exchange rates for this range (kew ≈ ∣σ1∣). This suggests that rNOE mechanism alone is sufficient to explain the predominance of the data, and that the contribution from direct NOE mechanism may be minimal.
Effect of Molecular Motions
The NOE rates in glycogen (and thus the glycoNOE signal intensity) are known to be determined more by glycogen intramolecular motions than the overall molecular tumbling of the glycogen particle (11,28-30). The pattern of glycoNOE dependence on glycogen particle size (Fig. 7) falls in line with this. Glycogen is known to consist of linear chains of 10 to 18 glucosyl units. Each glucose chain has about two branching points, where new chains are added and organized into a multiple tiered tree-like structure, the β particle (Figs. 1b, c) (31). This well-accepted “tiered” model of glycogen structure (31,32) indicates that the number of glucose chains in a tier is 2n and that 50% of glucose chains are always at the outermost tier of the β particle (Fig. 1b). The diameter of β particles varies from several nanometers (nm) to about 30 nm (33). As the glycogen β particle increases in size, the outermost tier becomes increasingly dense and the internal motion of glucose chains on average becomes increasingly restricted, causing average glycogen NOE rates to increase. The β particle size reaches a maximum around 20-30 nm. Multiple β particles can adhere to form large molecular complexes known as α particles, whose diameter can reach up to 200 nm (Fig. 1). During this process, the internal motion of glucose chain within a β particle is unlikely to be altered. As a result, the glycoNOE signal stays relatively constant above a size of 25 nm, i.e., during the formation of α particles. Importantly, this observation suggests that for a large proportion of glycogen in vivo, glycoNOE is independent of particle size. Considering that the average liver glycogen particle size fluctuates over a small range (15 to 30 nm) in vivo (34), it is not surprising to explain the recent finding of measured glycoNOEs being linearly dependent on glycogen concentration in vivo, allowing the glycoNOE signal to be used to map liver glycogen levels in vivo (14). It is also interesting to see that the glycoNOE is larger in oyster glycogen than in rabbit liver glycogen, even when the particle sizes of these two types are similar (Fig. 7). We attribute this difference to a larger NOE rate due to slower internal motions in oyster glycogen, as the hydroxyl exchange rate is not a factor affecting glycoNOE signal under physiological conditions in H2O. Such slower internal motions of oyster glycogen chains compared with those of rabbit liver glycogen might be due to an increase in branching (35) that might restrict chain motions.
Implications for Carbohydrate Polymer Studies
Carbohydrate polymers play vital roles in the function and structure of organisms (36) and are also applied for biomedical use (37,38). For instance, glycogen is the primary form of glucose (or short-term energy) storage in mammals (39). Glycosaminoglycans (GAGs) are essential for the musculoskeletal function, cell regulation, and spinal function (12). Quantifying the concentrations of sugar polymers in vivo is desirable for evaluating cellular metabolism and functions (12,40-43). These sugar polymers have been previously detected in vivo with signal enhancement using CEST MRI method (11,12,14,24), opening up opportunities to study carbohydrate polymer metabolism at high spatial and temporal resolutions in vivo. Another carbohydrate polymer, dextran, has been assessed with CEST MRI to study tumor based blood brain barrier permeability (44,45) and even tumor receptor binding (46). The presence of strong magnetic coupling between aliphatic protons in macromolecular carbohydrates and water suggests that rNOE MRI can be a good alternative strategy to detect carbohydrate polymers in vivo. (12,14) The chemical structure of the glucose unit (Fig. 2) and other sugars (such as fructose, ribose) shows that most of the aliphatic protons have multiple hydroxyl protons in close vicinity (2 ~ 4 Å), an important prerequisite for efficient NOE cross-relaxation. Besides, the hydroxyl proton exchange rate is fast in H2O and thus any NOEs to hydroxyl protons can be efficiently relayed to water protons, making hydroxyl protons ideal relaying sites for magnetization transfer. (15) Such water-detected relayed NOEs have been observed in glycosaminoglycans (GAGs) (12) and glycogen (14), they are expected to exist in many other sugar polymer systems as long as the motion of sugar units (in polymeric forms) are on slow (>1 ns) time scales. For instance, we were already able to detect an NOE signal in 2000 kD dextran (Supporting Information Figure S4).
Sugar polymers often have excellent bio-safety and bio-degradable properties, and have already been suggested as a new category of CEST MRI contrast agents. The ability for detection using the water-based rNOE method in addition to CEST, extends the applicability of these agents as well as the ability to detect such polymers in situ in tissue. While both chemical exchange and rNOE in saturation transfer experiments are effective signal enhancement mechanisms (2) for low-concentration molecules, they have different characteristics. First, the CEST signal is highly dependent on kew and thus on pH and temperature. While rNOEs are also pH dependent, the rNOE signal appears pH-independent due to kew of hydroxyl protons in H2O solution being fast compared to the NOE rate (fast exchange regime, Eq. 7), leading to the NOE transfer rate being rate-determining for the rNOE transfer. The rNOE in tissue is also temperature independent (14). Second, because the NOE rate σ is the rate-limiting step, the measured rNOE often increases with reduced molecular motion. For proteins, this results in stronger NOEs with increased molecular weight. For carbohydrate polymers on the other hand, due to a high degree of internal motion that is not necessarily dependent on particle size, the rNOE signals are more dependent on internal chain motions than molecular weight (Fig. 7). Compared to CEST detection of carbohydrate polymers, rNOE may have the advantage that low B1 can be used to reach a high level of saturation in the aliphatic proton pool, providing a constant source of saturation to be transferred to newly-arrived OH protons. This is somewhat analogous to the IMMOBILISE mechanism (9) where the ligand proton pool remains fully saturated and saturation is transferred rapidly upon binding to a macromolecule. Also, the effect will not be influenced by pH in H2O as kew > 400 s−1 at all pH values, which simplifies the interpretation of any signal changes.
In summary, the rNOE model provides a good explanation for the dependence of water NOE signals in glycogen on solvent pH, temperature, H2O/D2O ratio and particle sizes. The rNOE mechanism should exist in sugar polymers that have slow molecular motions.
Conclusion
The current study demonstrates that the magnetization transfer from aliphatic protons in glycogen to water protons can be explained by the relayed NOE (rNOE) transfer mechanism, despite its apparent independence on pH in vivo. The proposed theoretical model and the experimental validation of the presence of rNOEs in glycogen is expected to be useful in understanding the aliphatic components of Z-spectra of sugar polymers as well as of other macromolecules such as proteins and lipids.
Supplementary Material
Supporting Information Figure S1. The visibility of glycogen hydroxyl protons in the proton NMR spectrum at different pH (100 mM in PBS buffer prepared with 95% D2O/5% H2O, 17.6T, 20°C).
Supporting Information Figure S2. The 17.6T Z-spectra for oyster glycogen (100 mM in PBS buffer prepared with 95% D2O/5% H2O, 20 °C) at different pH, using a continuous RF B1 field, B1 = 0.35 μT and tsat = 4s.
Supporting Information Figure S3. Particle size distribution of bovine liver glycogen, oyster glycogen and rabbit liver glycogen samples. Sizes of the commercial samples (Sigma) in PBS were measured using dynamic light scattering (DLS) based zetasizer (Zetasizer Nano ZS90, Malvern Instruments).
Supporting Information Figure S4. UTE-CEST scan (47) on dextran (~ 2000 kD) solution (200 mM glucose unit, pH 7.4, 20 °C) at 11.7 T.
Supporting Information Table S1. Estimated oyster glycogen (100 mM, 20 °C) hydroxyl exchange rates in D2O (95%) and H2O (95%) based on NMR linewidth analysisa and selective inversion recoveryb analysis of the composite OH2+OH3 peak (+1.2 ppm).
Acknowledgments
This research was supported by NIH grants EB015032 and EB025295.
Data Availability Statement
The MR data and processing code used in this study are available on Open Science Framework at https://osf.io/esdh7/
References
- 1.Ward K, Balaban R. Determination of pH using water protons and chemical exchange dependent saturation transfer (CEST). Magnetic Resonance in Medicine 2000;44(5):799–802. [DOI] [PubMed] [Google Scholar]
- 2.van Zijl PC, Yadav NN. Chemical exchange saturation transfer (CEST): what is in a name and what isn't? Magnetic Resonance in Medicine 2011;65(4):927–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.van Zijl PC, Lam WW, Xu J, Knutsson L, Stanisz GJ. Magnetization transfer contrast and chemical exchange saturation transfer MRI. Features and analysis of the field-dependent saturation spectrum. Neuroimage 2018;168:222–241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jones KM, Pollard AC, Pagel MD. Clinical applications of chemical exchange saturation transfer (CEST) MRI. Journal of Magnetic Resonance Imaging 2018;47(1):11–27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Zaiss M, Bachert P. Chemical exchange saturation transfer (CEST) and MR Z-spectroscopy in vivo: a review of theoretical approaches and methods. Physics in Medicine & Biology 2013;58(22):R221. [DOI] [PubMed] [Google Scholar]
- 6.Zhou Y, Yang D. Effects of J couplings and unobservable minor states on kinetics parameters extracted from CEST data. Journal of Magnetic Resonance 2014;249:118–125. [DOI] [PubMed] [Google Scholar]
- 7.Zhou Y, Yang D. Equilibrium folding dynamics of meACP in water, heavy water, and low concentration of urea. Scientific reports 2017;7(1):16156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Xiao T, Fan Js, Zhou H, Lin Q, Yang D. Local unfolding of fatty acid binding protein to allow ligand entry for binding. Angewandte Chemie International Edition 2016;55(24):6869–6872. [DOI] [PubMed] [Google Scholar]
- 9.Yadav NN, Yang X, Li Y, Li W, Liu G, van Zijl PC. Detection of dynamic substrate binding using MRI. Scientific reports 2017;7(1):10138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Otting G, Liepinsh E, Wuthrich K. Protein hydration in aqueous solution. Science 1991;254(5034):974–980. [DOI] [PubMed] [Google Scholar]
- 11.Chen W, Avison MJ, Zhu XH, Shulman RG. NMR studies of proton NOEs in glycogen. Biochemistry 1993;32(43):11483–11487. [DOI] [PubMed] [Google Scholar]
- 12.Ling W, Regatte RR, Navon G, Jerschow A. Assessment of glycosaminoglycan concentration in vivo by chemical exchange-dependent saturation transfer (gagCEST). Proceedings of the National Academy of Sciences 2008;105(7):2266–2270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sayers EW, Weaver JL, Prestegard JH. Hydrogen bonding geometry of a protein-bound carbohydrate from water exchange-mediated cross-relaxation. Journal of biomolecular NMR 1998;12(2):209–222. [DOI] [PubMed] [Google Scholar]
- 14.Zhou Y, van Zijl PCM, Xu X, Xu J, Li Y, Chen L, Yadav NN. Magnetic resonance imaging of glycogen using its magnetic coupling with water. Proceedings of the National Academy of Sciences 2020;117(6):3144–3149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Liepinsh E, Otting G. Proton exchange rates from amino acid side chains—implications for image contrast. Magnetic Resonance in Medicine 1996;35(1):30–42. [DOI] [PubMed] [Google Scholar]
- 16.Johannesson H, Halle B. Minor groove hydration of DNA in solution: dependence on base composition and sequence. Journal of the American Chemical Society 1998;120(28):6859–6870. [Google Scholar]
- 17.Newby MI, Greenbaum NL. Investigation of Overhauser effects between pseudouridine and water protons in RNA helices. Proceedings of the National Academy of Sciences 2002;99(20):12697–12702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Otting G, Liepinsh E, Wuethrich K. Proton exchange with internal water molecules in the protein BPTI in aqueous solution. Journal of the American Chemical Society 1991;113(11):4363–4364. [Google Scholar]
- 19.Eliav U, Navon G. Multiple quantum filtered NMR studies of the interaction between collagen and water in the tendon. Journal of the American Chemical Society 2002;124(12):3125–3132. [DOI] [PubMed] [Google Scholar]
- 20.van Zijl PC, Zhou J, Mori N, Payen JF, Wilson D, Mori S. Mechanism of magnetization transfer during on-resonance water saturation. A new approach to detect mobile proteins, peptides, and lipids. Magnetic Resonance in Medicine 2003;49(3):440–449. [DOI] [PubMed] [Google Scholar]
- 21.Hwang T-L, van Zijl PC, Mori S. Accurate quantitation of water-amide proton exchange rates using the phase-modulated CLEAN chemical EXchange (CLEANEX-PM) approach with a Fast-HSQC (FHSQC) detection scheme. Journal of biomolecular NMR 1998;11(2):221–226. [DOI] [PubMed] [Google Scholar]
- 22.Gessler K, Usón I, Takaha T, Krauss N, Smith SM, Okada S, Sheldrick GM, Saenger W. V-Amylose at atomic resolution: X-ray structure of a cycloamylose with 26 glucose residues (cyclomaltohexaicosaose). Proceedings of the National Academy of Sciences 1999;96(8):4246–4251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bloch F. Nuclear induction. Physical review 1946;70(7-8):460. [Google Scholar]
- 24.van Zijl PC, Jones CK, Ren J, Malloy CR, Sherry AD. MRI detection of glycogen in vivo by using chemical exchange saturation transfer imaging (glycoCEST). Proceedings of the National Academy of Sciences 2007;104(11):4359–4364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Krȩżel A, Bal W. A formula for correlating pKa values determined in D2O and H2O. Journal of inorganic biochemistry 2004;98(1):161–166. [DOI] [PubMed] [Google Scholar]
- 26.Desmond KL, Moosvi F, Stanisz GJ. Mapping of amide, amine, and aliphatic peaks in the CEST spectra of murine xenografts at 7 T. Magnetic Resonance in Medicine 2014;71(5):1841–1853. [DOI] [PubMed] [Google Scholar]
- 27.Zang L-H, Howseman AM, Shulman RG. Assignment of the 1H chemical shifts of glycogen. Carbohydrate research 1991;220:1–9. [DOI] [PubMed] [Google Scholar]
- 28.Zang LH, Laughlin MR, Rothman DL, Shulman RG. Carbon-13 NMR relaxation times of hepatic glycogen in vitro and in vivo. Biochemistry 1990;29(29):6815–6820. [DOI] [PubMed] [Google Scholar]
- 29.Zang L-H, Rothman DL, Shulman RG. 1H NMR visibility of mammalian glycogen in solution. Proceedings of the National Academy of Sciences 1990;87(5):1678–1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sillerud LO, Shulman RG. Structure and metabolism of mammalian liver glycogen monitored by carbon-13 nuclear magnetic resonance. Biochemistry 1983;22(5):1087–1094. [DOI] [PubMed] [Google Scholar]
- 31.Goldsmith E, Sprang S, Fletterick R. Structure of maltoheptaose by difference Fourier methods and a model for glycogen. Journal of molecular biology 1982;156(2):411–427. [DOI] [PubMed] [Google Scholar]
- 32.Gunja-Smith Z, Marshall J, Mercier C, Smith E, Whelan WJ. A revision of the Meyer-Bernfeld model of glycogen and amylopectin. FEBS letters 1970;12(2):101–104. [DOI] [PubMed] [Google Scholar]
- 33.Ryu J-H, Drain J, Kim JH, McGee S, Gray-Weale A, Waddington L, Parker GJ, Hargreaves M, Yoo S-H, Stapleton D. Comparative structural analyses of purified glycogen particles from rat liver, human skeletal muscle and commercial preparations. International journal of biological macromolecules 2009;45(5):478–482. [DOI] [PubMed] [Google Scholar]
- 34.Sullivan MA, Aroney ST, Li S, Warren FJ, Joo JS, Mak KS, Stapleton DI, Bell-Anderson KS, Gilbert RG. Changes in glycogen structure over feeding cycle sheds new light on blood-glucose control. Biomacromolecules 2014;15(2):660–665. [DOI] [PubMed] [Google Scholar]
- 35.Matsui M, Kakut M, Misaki A. Fine structural features of oyster glycogen: mode of multiple branching. Carbohydrate polymers 1996;31(4):227–235. [Google Scholar]
- 36.Ferreira SS, Passos CP, Madureira P, Vilanova M, Coimbra MA. Structure–function relationships of immunostimulatory polysaccharides: A review. Carbohydrate polymers 2015;132:378–396. [DOI] [PubMed] [Google Scholar]
- 37.Banerjee A, Bandopadhyay R. Use of dextran nanoparticle: a paradigm shift in bacterial exopolysaccharide based biomedical applications. International journal of biological macromolecules 2016;87:295–301. [DOI] [PubMed] [Google Scholar]
- 38.Gopinath V, Saravanan S, Al-Maleki A, Ramesh M, Vadivelu J. A review of natural polysaccharides for drug delivery applications: Special focus on cellulose, starch and glycogen. Biomedicine & Pharmacotherapy 2018;107:96–108. [DOI] [PubMed] [Google Scholar]
- 39.Adeva-Andany MM, González-Lucán M, Donapetry-García C, Fernández-Fernández C, Ameneiros-Rodríguez E. Glycogen metabolism in humans. BBA clinical 2016;5:85–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Price T, Rothman D, Avison M, Buonamico P, Shulman R. 13C-NMR measurements of muscle glycogen during low-intensity exercise. Journal of Applied Physiology 1991;70(4):1836–1844. [DOI] [PubMed] [Google Scholar]
- 41.Magnusson I, Rothman D, Katz L, Shulman R, Shulman G. Increased rate of gluconeogenesis in type II diabetes mellitus. A 13C nuclear magnetic resonance study. The Journal of clinical investigation 1992;90(4):1323–1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gruetter R, Magnusson I, Rothman DL, Avison MJ, Shulman RG, Shulman GI. Validation of 13C NMR measurements of liver glycogen in vivo. Magnetic Resonance in Medicine 1994;31(6):583–588. [DOI] [PubMed] [Google Scholar]
- 43.Brown AM, Ransom BR. Astrocyte glycogen and brain energy metabolism. Glia 2007;55(12):1263–1271. [DOI] [PubMed] [Google Scholar]
- 44.Li Y, Qiao Y, Chen H, Bai R, Staedtke V, Han Z, Xu J, Chan KW, Yadav N, Bulte JW. Characterization of tumor vascular permeability using natural dextrans and CEST MRI. Magnetic Resonance in Medicine 2018;79(2):1001–1009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Chen H, Liu D, Li Y, Xu X, Xu J, Yadav NN, Zhou S, van Zijl PC, Liu G. CEST MRI monitoring of tumor response to vascular disrupting therapy using high molecular weight dextrans. Magnetic Resonance in Medicine 2019;82(4):1471–1479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Liu G, Banerjee SR, Yang X, Yadav N, Lisok A, Jablonska A, Xu J, Li Y, Pomper MG, van Zijl P. A dextran-based probe for the targeted magnetic resonance imaging of tumours expressing prostate-specific membrane antigen. Nature biomedical engineering 2017;1(12):977–982. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen L, Wei Z, Chan KW, Cai S, Liu G, Lu H, Wong PC, van Zijl PC, Li T, Xu J. Protein aggregation linked to Alzheimer's disease revealed by saturation transfer MRI. NeuroImage 2019;188:380–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Figure S1. The visibility of glycogen hydroxyl protons in the proton NMR spectrum at different pH (100 mM in PBS buffer prepared with 95% D2O/5% H2O, 17.6T, 20°C).
Supporting Information Figure S2. The 17.6T Z-spectra for oyster glycogen (100 mM in PBS buffer prepared with 95% D2O/5% H2O, 20 °C) at different pH, using a continuous RF B1 field, B1 = 0.35 μT and tsat = 4s.
Supporting Information Figure S3. Particle size distribution of bovine liver glycogen, oyster glycogen and rabbit liver glycogen samples. Sizes of the commercial samples (Sigma) in PBS were measured using dynamic light scattering (DLS) based zetasizer (Zetasizer Nano ZS90, Malvern Instruments).
Supporting Information Figure S4. UTE-CEST scan (47) on dextran (~ 2000 kD) solution (200 mM glucose unit, pH 7.4, 20 °C) at 11.7 T.
Supporting Information Table S1. Estimated oyster glycogen (100 mM, 20 °C) hydroxyl exchange rates in D2O (95%) and H2O (95%) based on NMR linewidth analysisa and selective inversion recoveryb analysis of the composite OH2+OH3 peak (+1.2 ppm).
Data Availability Statement
The MR data and processing code used in this study are available on Open Science Framework at https://osf.io/esdh7/


