Persistent spectral graph

Abstract

Persistent homology is constrained to purely topological persistence while multiscale graphs account only for geometric information. This work introduces persistent spectral theory to create a unified low-dimensional multiscale paradigm for revealing topological persistence and extracting geometric shapes from high-dimensional datasets. For a point-cloud dataset, a filtration procedure is used to generate a sequence of chain complexes and associated families of simplicial complexes and chains, from which we construct persistent combinatorial Laplacian matrices. We show that a full set of topological persistence can be completely recovered from the harmonic persistent spectra, i.e., the spectra that have zero eigenvalues, of the persistent combinatorial Laplacian matrices. However, non-harmonic spectra of the Laplacian matrices induced by the filtration offer another powerful tool for data analysis, modeling, and prediction. In this work, fullerenes stability is predicted by using both harmonic and non-harmonic persistent spectra. While non-harmonic persistent spectra are successfully devised to analyze the structure of fullerenes and model protein flexibility, which cannot be straightforwardly extracted from the current persistent homology. The proposed method is found to provide excellent predictions of the protein B-factors for which current popular biophysical models break down.

1. Introduction

Graph theory, a branch of discrete mathematics, concerns the relationship between objects. These objects can be either simple vertices, i.e., nodes and/or points (zero simplexes), or high-dimensional simplexes. Here, the relationship refers to connectivity with possible orientations. Graph theory has many branches, such as geometric graph theory, algebraic graph theory, and topological graph theory. The study of graph theory draws on many other areas of mathematics, including algebraic topology, knot theory, algebra, geometry, group theory, combinatorics, etc. For example, algebraic graph theory can be investigated by using either linear algebra, group theory, or graph invariants. Among them, the use of learning algebra in graph study leads to spectral graph theory.

Precursors of the spectral theory have often had a geometric flavor. An interesting spectral geometry question asked by Mark Kac was “Can one hear the shape of a drum?” [1]. The Laplace-Beltrami operator on a closed Riemannian manifold has been intensively studied [2]. Additionally, eigenvalues and isoperimetric properties of graphs are the foundation of the explicit constructions of expander graphs [3]. Moreover, the study of random walks and rapidly mixing Markov chains utilized the discrete analog of the Cheeger inequality [4]. The interaction between spectral theory and differential geometry became one of the critical developments [5]. For example, the spectral theory of the Laplacian on a compact Riemannian manifold is a central object of de Rham-Hodge theory [2]. Note that the Hodge Laplacian spectrum contains the topological information of the underlying manifold. Specifically, the harmonic part of the Hodge Laplacian spectrum corresponds to topological cycles. Connections between topology and spectral graph theory also play a central role in understanding the connectivity properties of graphs [6–9]. Similarly, as the topological invariants revealing the connectivity of a topological space, the multiplicity of 0 eigenvalues of a 0-combinatorial Laplacian matrix is the number of connected components of a graph. Indeed, the number of q-dimensional holes can also be unveiled from the number of 0 eigenvalues of the q-combinatorial Laplacian [10–13]. Nonetheless, spectral graph theory offers additional non-harmonic spectral information beyond topological invariants.

The traditional topology and homology are independent of metrics and coordinates and thus, retain little geometric information. This obstacle hinders their practical applicability in data analysis. Recently, persistent homology has been introduced to overcome this difficulty by creating low-dimensional multiscale representations of a given object of interest [14–19]. Specifically, a filtration parameter is devised to induce a family of geometric shapes for a given initial data. Consequently, the study of the underlying topologies or homology groups of these geometric shapes leads to the so-called topological persistence. Like the de Rham-Hodge theory which bridges differential geometry and algebraic topology, persistent homology bridges multiscale analysis and algebraic topology. Topological persistence is the most important aspect of the popular topological data analysis (TDA) [20–23] and has had tremendous success in computational biology [24, 25] and worldwide competitions in computer-aided drug design [26].

Graph theory has been applied in various fields [27]. For example, spectral graph theory is applied to the quantum calculation of π-delocalized systems. The Hückel method, or Hückel molecular orbital theory, describes the quantum molecular orbitals of π-electrons in π-delocalized systems in terms of a kind of adjacency matrix that contains atomic connectivity information [28, 29]. Additionally, the Gaussian network model (GNM) [30] and anisotropic network model (ANM) [31] represent protein C_α atoms as an elastic mass-and-spring network by graph Laplacians. These approaches were influenced by the Flory theory of elasticity and the Rouse model [32]. Like traditional topology, traditional graph theory extracts very limited information from data. In our earlier work, we have proposed multiscale graphs, called multiscale flexibility rigidity index (mFRI), to describe the multiscale nature of biomolecular interactions [33], such as hydrogen bonds, electrostatic effects, van der Waals interactions, hydrophilicity, and hydrophobicity. A multiscale spectral graph method has also been proposed as generalized GNM and generalized ANM [34]. Our essential idea is to create a family of graphs with different characteristic length scales for a given dataset. We have demonstrated that our multiscale weighted colored graph (MWCG) significantly outperforms traditional spectral graph methods in protein flexibility analysis [35]. More recently, we demonstrate that our MWCG outperforms other existing approaches in protein-ligand binding scoring, ranking, docking, and screening [36].

The objective of the present work is to introduce persistent spectral graph as a new paradigm for the multiscale analysis of the topological invariants and geometric shapes of high-dimensional datasets. Motivated by the success of persistent homology [25] and multiscale graphs [36] in dealing with complex biomolecular data, we construct a family of spectral graphs induced by a filtration parameter. In the present work, we consider the radius filtration via the Vietoris-Rips complex while other filtration methods can be implemented as well. As the filtration radius is increased, a family of persistent q-combinatorial Laplacians are constructed for a given point-cloud dataset. The diagonalization of these persistent q-combinatorial Laplacian matrices gives rise to persistent spectra. It is noted that our harmonic persistent spectra of 0-eigenvalues fully recover the persistent barcode or persistent diagram of persistent homology. Additional information is generated from non-harmonic persistent spectra, namely, the non-zero eigenvalues and associated eigenvectors. In a combination with a simple machine learning algorithm, this additional spectral information is found to provide a powerful new tool for the quantitative analysis of molecular data, including the prediction of a set of protein B-factors for which existing standard predictors fail to work.

2. Theories and methods

In this section, we give a brief review of spectral graph theory and simplicial complex to establish notations and provide essential background. Subsequently, we introduce persistent spectral analysis.

2.1. Spectral graph theory

Graph structure encodes inter-dependencies among constituents and provides low-dimensional representations of high-dimensional datasets. One of the representations frequently used in spectral graph theory (SGT) is to associate graphs with matrices, such as the Laplacian matrix and adjacency matrix. Analyzing the spectra from such matrices leads to the understanding of the topological and spectral properties of the graph.

Let V be the vertex set, and E be the edge set. For a given simple graph G(V, E) (A simple graph can be either connected or disconnected), the degree of the vertex v ∈ V is the number of edges that are adjacent to v, denoted deg(v). The adjacency matrix $\mathcal{A}$ is defined by

$$\mathcal{A}(G)=\{\begin{array}{ll}1\hfill & \text{ if }{v}_i\text{ and }{v}_j\text{ are adjacent,}\hfill \\ 0\hfill & \text{ otherwise}.\hfill \end{array}$$ (1)

and the Laplacian matrix $\mathcal{L}$ is given by

$$\mathcal{L}(G)=\{\begin{array}{ll}\text{deg}\left(v_i\right)\hfill & \text{ if }{v}_i=v_j,\hfill \\ -1\hfill & \text{ if }{v}_j\text{ and }{v}_j\text{ are adjacent,}\hfill \\ 0\hfill & \text{ otherwise}.\hfill \end{array}$$ (2)

Obviously, the adjacency matrix characterizes the graph connectivity. The above two matrices are related through diagonal matrix $\mathcal{D}$

$$\mathcal{L}=\mathcal{D}-\mathcal{A}$$

Assuming G(V, E) has N nodes, then adjacency matrix A and Laplacian matrix $\mathcal{L}$ are both real symmetric N × N matrices. The eigenvalues of adjacency and Laplacian matrices are denoted and ordered as

$$\begin{gathered} {\alpha }_{\text{min}}={\alpha }_N\le \cdots \le {\alpha }_2\le {\alpha }_1={\alpha }_{\text{max}} \\ {\lambda }_{\text{min}}={\lambda }_1\le {\lambda }_2\le \cdots \le {\lambda }_N={\lambda }_{\text{max}}. \end{gathered}$$ (3)

The spectra of $\mathcal{A}$ and $\mathcal{L}$ have several interesting proprieties. To understand the robustness and connectivity of a graph, the algebraic connectivity λ₂ and the multiplicity of 0 eigenvalues are taken into consideration which will be illustrated in the Theorem 2.1 and Remark 2.1. For more detailed theorems and proofs, we refer the interested reader to a survey on Laplacian eigenvalues of graphs [8]. Furthermore, some interesting properties and examples can be found in the Supporting Material: S1 as well.

Theorem 2.1. Let G(V, E) be a simple graph of order N, then the multiplicity of 0 eigenvalue for Laplacian matrix is the number of connected components of G(V, E). The vertex degree is the value of the diagonal entry.

Remark 2.1. In this section, the Laplacian spectrum of simple graph G(V, E) is concerned. For

$$G(V,E)=G_1\left(V_1,E_1\right)\cup \cdots \cup G_m\left(V_m,E_m\right),m\ge 1,m\in \mathbb{Z},$$

where G_i(V_i, E_i) ⊂ G(V, E), i = 1, ⋯ , m is a connected simple graph. If m ≥ 2, the zero eigenvalue of $\mathcal{L}(G)$ has multiplicity m, which results in algebraic connectivity λ₂ = 0. However, λ₂ = 0 cannot give any information about the G_i(V_i, E_i). Therefore, we study the smallest non-zero eigenvalue of $\mathcal{L}(G)$, which is actually the smallest algebraic connectivity of $\mathcal{L}(G_i)$, i = 1, ⋯ , m. In subsection 2.3 and section 3, we analyze the smallest non-zero eigenvalue of the Laplacian matrix. To make the expression more concise, we still use ${\tilde{\lambda }}_2$ as the smallest non-zero eigenvalue. If G(V, E) is a connected simple graph, i.e., m = 1, one has ${\lambda }_2={\tilde{\lambda }}_2$.

2.2. Simplicial complex

A simplicial complex is a powerful algebraic topology tool that has wide applications in graph theory, topological data analysis [17], and many physical fields [25]. We briefly review simplicial complexes to generate notation and provide essential preparation for introducing persistent spectral graph.

2.2.1. Simplex

Let {v₀, v₁, ⋯ , v_q} be a set of points in ${ℝ}^n$. A point $v=\sum _{i=0}^q{\lambda }_i{v}_i,{\lambda }_i\in ℝ$ is an affine combination of v_i if $\sum _{i=0}^q{\lambda }_i=1$. An affine hull is the set of affine combinations. Here, q + 1 points v₀, v₁, ⋯ , v_q are affinely independent if v₁ − v₀, v₂ −v₀, ⋯ , v_q − v₀ are linearly independent. A q-plane is well-defined if the q + 1 points are affinely independent. In ${ℝ}^n$, one can have at most n linearly independent vectors. Therefore, there are at most n + 1 affinely independent points. An affine combination $v=\sum _{i=0}^q{\lambda }_i{v}_i$ is a convex combination if all λ_i are non-negative. The convex hull is the set of convex combinations.

A (geometric) q-simplex denoted as σ_q is the convex hull of q + 1 affinely independent points in ${ℝ}^n(n\ge q)$ with dimension dim(σ_q) = q. A 0-simplex is a vertex, a 1-simplex is an edge, a 2-simplex is a triangle, and a 3-simplex is a tetrahedron, as shown in Figure 1. The convex hull of each nonempty subset of q + 1 points forms a subsimplex and is regarded as a face of σ_q denoted τ. The p + 1-vertices of a q-simplex is the subset {v_i1, ⋯ , v_ip} of the q-simplex.

Figure 1:

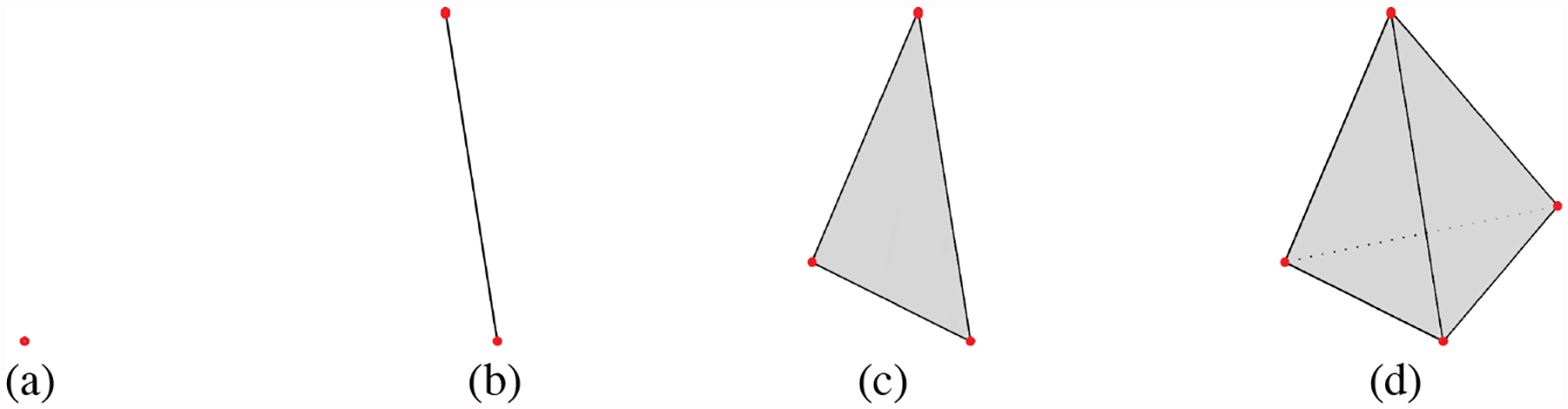
Illustration of simplices. (a) 0-simplex (a vertex), (b) 1-simplex (an edge), (c) 2-simplex (a triangle), and (d) 3-simplex (a tetrahedron)

2.2.2. Simplicial complex

A (finite) simplicial complex K is a (finite) collection of simplices in ${ℝ}^n$ satisfying the following conditions

1. If σ_q ∈ K and σ_p is a face of σ_q, then σ_p ∈ K.

2. The non-empty intersection of any two simplices σ_q, σ_p ∈ K is a face of both of σ_q and σ_p.

Each element σ_q ∈ K is a q-simplex. The dimension of K is defined as dim(K) = max{dim(σ_q) : σ_q ∈ K}. To distinguish topological spaces based on the connectivity of simplicial complexes, one uses Betti numbers. The k-th Betti number, β_k, counts the number of k-dimensional holes on a topological surface. The geometric meaning of Betti numbers in ${ℝ}^3$ is the following: β₀ represents the number of connected components, β₁ counts the number of one-dimensional loops or circles, and β₂ describes the number of two-dimensional voids or holes. In a nutshell, the Betti number sequence {β₀, β₁, β₂, ⋯} reveals the intrinsic topological property of the system.

Recall that in graph theory, the degree of a vertex (0-simplex) v is the number of edges that are adjacent to the vertex, denoted as deg(v). However, once we generalize this notion to q-simplex, problem aroused since q-simplex can have (q − 1)-simplices and (q + 1)-simplices adjacent to it at the same time. Therefore, the upper adjacency and lower adjacency are required to define the degree of a q-simplex for q > 0 [10, 12].

Defination 2.1. Two q-simplices ${\sigma }_q^i$ and ${\sigma }_q^j$ of a simplicial complex K are lower adjacent if they share a common (q − 1)-face, denoted ${\sigma }_q^i\stackrel{L}{~}{\sigma }_q^j$. The lower degree of q-simplex, denoted deg_L(σ_q), is the number of nonempty (q − 1)-simplices in K that are faces of σ_q, which is always q + 1.

Defination 2.2. Two q-simplices ${\sigma }_q^i$ and ${\sigma }_q^j$ of a simplicial complex K are upper adjacent if they share a common (q + 1)-face, denoted ${\sigma }_q^i\stackrel{U}{~}{\sigma }_q^j$. The upper degree of q-simplex, denoted deg_U(σ_q), is the number of (q + 1)-simplices in K of which σ_q is a face.

Then, the degree of a q-simplex (q > 0) is defined as:

$$\text{deg}\left({\sigma }_q\right)={\text{deg}}_L\left({\sigma }_q\right)+{\text{deg}}_U\left({\sigma }_q\right)={\text{deg}}_U\left({\sigma }_q\right)+q+1.$$ (4)

A supplemental example which illustrate the relation between simplicial complex and its corresponding Betti number can be found in the Supporting Material: S2.

2.2.3. Chain complex

Chain complex is an important concept in topology, geometry, and algebra. Let K be a simplicial complex of dimension q. A q-chain is a formal sum of q-simplices in K with ${\mathbb{Z}}_2$ field of the coefficients for the sum. Under the addition operation of ${\mathbb{Z}}_2$, a set of all q-chains is called a chain group and denoted C_q(K). To relate these chain groups, we denote boundary operator by ∂_q : C_q(K) → C_q−1(K). The boundary operator maps a q-chain which is a linear combination of q-simplices to the same linear combination of the boundaries of the q-simplices. Denoting σ_q = [v₀, v₁, ⋯ , v_q] for the q-simplex spanned by its vertices, its boundary operator can be defined as:

$${\partial }_q{\sigma }_q=\sum _{i=0}^q{(-1)}^i{\sigma }_{q-1}^i,$$ (5)

with σ_q = [v₀, ⋯ , v_q] being the q-simplex. Here, ${\sigma }_{q-1}^i=\left[v_0,\cdots ,{\widehat{v}}_i,\cdots ,v_q\right]$ is the (q − 1)-simplex with v_i being omitted. A q-chain is called q-cycle if its boundary is zero. A chain complex is the sequence of chain groups connected by boundary operators

$$\cdots \stackrel{{\partial }_{q+2}}{\to }{C}_{q+1}(K)\stackrel{{\partial }_{q+1}}{\to }{C}_q(K)\stackrel{{\partial }_q}{\to }{C}_{q-1}(K)\stackrel{{\partial }_{q-1}}{\to }\cdots$$ (6)

2.3. Persistent spectral analysis

In this section, we introduce persistent spectral theory (PST) to extract rich topological and spectral information of simplicial complexes via a filtration process. We briefly review preliminary concepts about the oriented simplicial complex and q-combinatorial Laplacian, while more detail information can be found elsewhere [11–13, 37]. Then, we discuss the properties of the q-combinatorial Laplacian matrix together with its spectrum. Moreover, we employ the q-combinatorial Laplacian to establish the PST. Finally, we discuss some variants of the persistent q-combinatorial Laplacian matrix and illustrate their formulation on simple geometry, i.e., a benzene molecule.

2.3.1. Oriented simplicial complex and q-combinatorial Laplacian

An oriented simplicial complex is the one in which all of the simplices in the simplicial complex, except for vertices and ∅, are oriented. A q-combinatorial Laplacian is defined based on oriented simplicial complexes, and its lower- and higher-dimensional simplexes can be employed to study a specifically oriented simplicial complex.

We first introduce oriented simplex complexes. Let σ_q be a q-simplex, we can define the ordering of its vertex set. If two orderings defined on σ_q differ from each other by an even permutation, we say that they are equivalent, and each of them is called an orientation of σ_q. An oriented q-simplex is a simplex σ_q with the orientation of σ_q. An oriented simplicial complex K is defined if all of its simplices are oriented. Suppose ${\sigma }_q^i$ and ${\sigma }_q^j\in K$ with K being an oriented simplicial complex. If ${\sigma }_q^i$ and ${\sigma }_q^j$ are upper adjacent with a common upper (q + 1)-simplex τ_q+1, we say they are similarly oriented if both have the same sign in ∂_q+1(τ_q+1) and dissimilarly oriented if the signs are opposite. Additionally, if ${\sigma }_q^i$ and ${\sigma }_q^j$ are lower adjacent with a common lower (q − 1)-simplex η_q−1, we say they are similarly oriented if η_q−1 has the same sign in ${\partial }_q\left({\sigma }_q^i\right)$ and ${\partial }_q\left({\sigma }_q^j\right)$, and dissimilarly oriented if the signs are opposite.

Similarly, we can define q-chains based on an oriented simplicial complex K. The q-chain C_q(K) is also defined as the linear combinations of the basis, with the basis being the set of oriented q-simplices of K. The q-boundary operator ∂_q : C_q(K) → C_q−1(K) is

$${\partial }_q{\sigma }_q=\sum _{i=0}^q{(-1)}^i{\sigma }_{q-1}^i,$$ (7)

with σ_q = [v₀, ⋯ , v_q] to be the oriented q-simplex, and ${\sigma }_{q-1}^i=\left[v_0,\cdots ,{\widehat{v}}_i,\cdots ,v_q\right]$ the oriented (q − 1)-simplex with its vertex v_i being removed. Let ${\mathcal{B}}_q$ be the matrix representation of a q-boundary operator with respect to the standard basis for C_q(K) and C_q−1(K) with some assigned orderings. Then, the number of rows in ${\mathcal{B}}_q$ corresponds to the number of (q−1)-simplices and the number of columns shows the number of q-simplices in K, respectively. Associated with the q-boundary operator is the adjoint operator denoted q-adjoint boundary operator, defined as

$${\partial }_q^{*}:C_{q-1}(K)\to C_q(K),$$ (8)

and the transpose of ${\mathcal{B}}_q$, denoted ${\mathcal{B}}_q^T$, is the matrix representation of ${\partial }_q^{*}$ relative to the same ordered orthonormal basis as ∂_q [38].

Let K be an oriented simplicial complex, for integer q ≥ 0, the q-combinatorial Laplacian is a linear operator Δ_q : C_q(K) → C_q(K)

$${\Delta }_q≔{\partial }_{q+1}{\partial }_{q+1}^{*}+{\partial }_q^{*}{\partial }_q$$ (9)

with ∂_q∂_q+1 = 0, which implies Im(∂_q+1) ⊂ ker(∂_q). The q-combinatorial Laplacian matrix, denoted ${\mathcal{L}}_q$, is the matrix representation¹.

$${\mathcal{L}}_q={\mathcal{B}}_{q+1}{\mathcal{B}}_{q+1}^T+{\mathcal{B}}_q^T{\mathcal{B}}_q$$ (10)

of operator Δ_q, with ${\mathcal{B}}_q$ and ${\mathcal{B}}_{q+1}$ being the matrices of dimension q and q + 1. Additionally, we denote upper and lower q-combinatorial Laplacian matrices by ${\mathcal{L}}_q^U={\mathcal{B}}_{q+1}{\mathcal{B}}_{q+1}^T$ and ${\mathcal{L}}_q^L={\mathcal{B}}_q^T{\mathcal{B}}_q$, respectively. Note that ∂₀ is the zero map which leads to ${\mathcal{B}}_0$ being a zero matrix. Therefore, ${\mathcal{L}}_0(K)={\mathcal{B}}_1{\mathcal{B}}_1^T+{\mathcal{B}}_0^T{\mathcal{B}}_0$, with K the (oriented) simplicial complex of dimension 1, which is actually a simple graph. Especially, 0-combinatorial Laplacian matrix ${\mathcal{L}}_0(K)$ is actually the Laplacian matrix defined in the spectral graph theory. In fact, Eq. (2) is exactly the same as Eq. (14) given below.

Given an oriented simplicial complex K with 0 ≤ q ≤ dim(K), one can obtain the entries of its corresponding upper and lower q-combinatorial Laplacian matrices explicitly [13]

$${\left({\mathcal{L}}_q^U\right)}_{ij}=\{\begin{array}{ll}{\text{deg}}_U\left({\sigma }_q^i\right),\hfill & \text{ if }i=j,\hfill \\ 1,\hfill & \text{ if }i\ne j,{\sigma }_q^i\stackrel{U}{~}{\sigma }_q^j\text{ with similar orientation},\hfill \\ -1,\hfill & \text{ if }i\ne j,{\sigma }_q^i\stackrel{U}{~}{\sigma }_q^j\text{ with dissimilar orientation},\hfill \\ 0,\hfill & \text{ otherwise}.\hfill \end{array}$$ (11)

$${\left({\mathcal{L}}_q^L\right)}_{ij}=\{\begin{array}{ll}{\text{deg}}_L\left({\sigma }_q^i\right)=q+1,\hfill & \text{ if }i=j,\hfill \\ 1,\hfill & \text{ if }i\ne j,{\sigma }_q^i\stackrel{L}{~}{\sigma }_q^j\text{ with similar orientation},\hfill \\ -1,\hfill & \text{ if }i\ne j,{\sigma }_q^i\stackrel{L}{~}{\sigma }_q^j\text{ with dissimilar orientation},\hfill \\ 0,\hfill & \text{ otherwise}.\hfill \end{array}$$ (12)

The entries of q-combinatorial Laplacian matrices are

$$q>0,{\left({\mathcal{L}}_q\right)}_{ij}=\{\begin{array}{ll}\text{deg}\left({\sigma }_q^i\right)+q+1,\hfill & \text{ if }i=j.\hfill \\ 1,\hfill & \text{ if }i\ne j,{\sigma }_q^i\stackrel{U}{\nsim }{\sigma }_q^j\text{ and }{\sigma }_q^i\stackrel{L}{~}{\sigma }_q^j\text{ with similar orientation}.\hfill \\ -1,\hfill & \text{ if }i\ne j,{\sigma }_q^i\stackrel{U}{\nsim }{\sigma }_q^j\text{ and }{\sigma }_q^i\stackrel{L}{~}{\sigma }_q^j\text{ with dissimilar orientation}.\hfill \\ 0,\hfill & \text{ if }i\ne j\text{ and either },{\sigma }_q^i\stackrel{U}{~}{\sigma }_q^j\text{ or }{\sigma }_q^i\stackrel{L}{\nsim }{\sigma }_q^j.\hfill \end{array}$$ (13)

$$q=0,{\left({\mathcal{L}}_q\right)}_{ij}=\{\begin{array}{ll}\text{deg}\left({\sigma }_0^i\right),\hfill & \text{ if }i=j.\hfill \\ -1,\hfill & \text{ if }{\sigma }_0^i\stackrel{U}{~}{\sigma }_0^j.\hfill \\ 0,\hfill & \text{ otherwise}.\hfill \end{array}$$ (14)

2.3.2. Spectral analysis of q-combinatorial Laplacian matrices

A q-combinatorial Laplacian matrix for oriented simplicial complexes is a generalization of the Laplacian matrix in graph theory. The spectra of a Laplacian matrix play an essential role in understanding the connectivity and robustness of simple graphs (simplicial complexes of dimension 1). They can also distinguish different topological structures. Inspired by the capability of the Laplacian spectra of analyzing topological structures, we study the spectral properties of q-combinatorial Laplacian matrices to reveal topological and spectral information of simplicial complexes with dimension 0 ≤ q ≤ dim(K).

We clarify that for a given finite simplicial complex K, the spectra of its q-combinatorial Laplacian matrix is independent of the choice of the orientation for the q-simplices of K. The proof can be found in Ref. [13]. Figure 2 provides a simple example to illustrate this property. In Figure 2, we have two oriented simplicial complexes, K₁ and K₂, with the same geometric structure but different orientations. For the sake of brevity, we use 1, 2, 3, 4, and 5 to represent 0-simplices (vertices), 12, 23, 34, 24, and 45 to describe 1-simplices (edges), and 234 to stand for the 2-simplex (triangle). Then the 0-combinatorial Laplacian matrix of K₁ and K₂ is

$${\mathcal{L}}_0\left(K_1\right)={\mathcal{L}}_0\left(K_2\right)=\left[\begin{array}{ccccc}1& -1& 0& 0& 0\\ -1& 3& -1& -1& 0\\ 0& -1& 2& -1& 0\\ 0& -1& -1& 3& -1\\ 0& 0& 0& -1& 1\end{array}\right].$$

Figure 2:

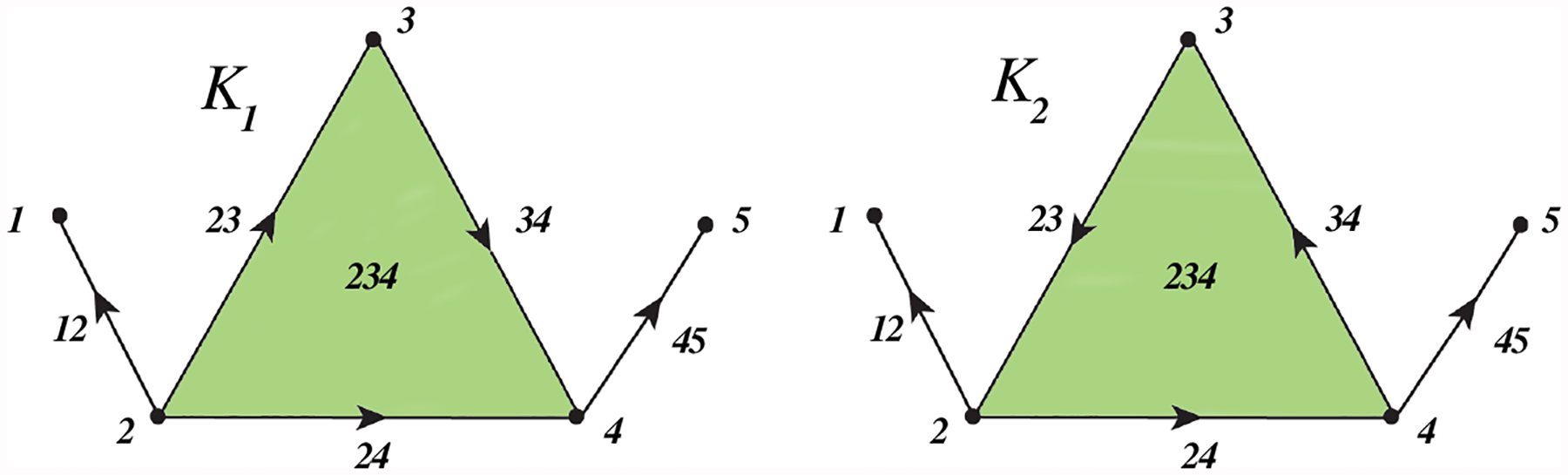
Illustration of two oriented simplicial complexes with the same geometric structure but having different orientations. Here, we denote the vertices by 1, 2, 3, 4, and 5, edges by 12, 23, 34, 24, and 45, and the triangle by 234.

Obviously, ${\mathcal{L}}_0\left(K_1\right)$ and ${\mathcal{L}}_0\left(K_2\right)$ have the same spectra. For q = 1, there are five 1-simplices in K₁ and K₂, while 1-combinatorial Laplacian matrices have dimension 5×5. Using K₁ as an example, since 12 and 23 are lower adjacent with similar orientation, the element of ${\mathcal{L}}_1\left(K_1\right)$ addressed at first row and second column is 1 according to Eq. (13). Since 34 and 45 are lower adjacent with dissimilar orientation, ${\left({\mathcal{L}}_1\left(K_1\right)\right)}_{35}=-1$. Moreover, 23 and 34 are upper adjacent which results in ${\left({\mathcal{L}}_1\left(K_1\right)\right)}_{23}=0$. For the diagonal parts, 12 and 45 are not the faces of any 2-simplex, while 23, 34, and 24 are the faces of 2-simplex 234. Therefore, deg_U(12) = deg_U(12) = 0, and deg_U(23) = deg_U(34) = deg_U(34) = 1, so the diagonal terms of ${\mathcal{L}}_0\left(K_1\right)$ are 2, 3, 3, 3, and 2.

$${\mathcal{L}}_1\left(K_1\right)=\left[\begin{array}{ccccc}2& 1& 0& 1& 0\\ 1& 3& 0& 0& 0\\ 0& 0& 3& 0& -1\\ 1& 0& 0& 3& -1\\ 0& 0& -1& -1& 2\end{array}\right],{\mathcal{L}}_1\left(K_2\right)=\left[\begin{array}{ccccc}2& -1& 0& 1& 0\\ -1& 3& 0& 0& 0\\ 0& 0& 3& 0& 1\\ 1& 0& 0& 3& -1\\ 0& 0& 1& -1& 2\end{array}\right].$$

The spectra of ${\mathcal{L}}_1\left(K_1\right)$ and ${\mathcal{L}}_1\left(K_2\right)$ have the same eigenvalues: $\left\{3,\frac{5\pm \sqrt{5}}{2},\frac{5\pm \sqrt{13}}{2}\right\}$. Since K₁ and K₂ do not have 3-simplices, ${\mathcal{L}}_q$ is a zero matrix when q ≥ 3.

A q-combinatorial Laplacian matrix is symmetric and positive semi-definite. Therefore, its eigenvalues are all real and non-negative. An analogy to the property that the number of zero eigenvalues of ${\mathcal{L}}_0$ represents the number of connected components (β₀) in the simple graph (simplicial complex with dimension 1), the number of zero eigenvalues of ${\mathcal{L}}_q$ can also reveal the topological information. More specifically, for a given finite oriented simplicial complex, the Betti number β_q of K satisfy

$${\beta }_q=\text{dim}\left({\mathcal{L}}_q(K)\right)-\text{rank}\left({\mathcal{L}}_q(K)\right)=\text{ nullity }\left({\mathcal{L}}_q(K)\right)=\#\text{ of zero eigenvalues of }{\mathcal{L}}_q(K)$$ (15)

In the Supporting material: S3, we illustrate the connection between Betti number and the dimension of the rank of q-combinatorial Laplacian matrix.

2.3.3. Persistent spectral theory

Instead of using the aforementioned spectral analysis for q-combinatorial Laplacian matrix to describe a single configuration, we propose a persistent spectral theory to create a sequence of simplicial complexes induced by varying a filtration parameter, which is inspired by persistent homology and our earlier work in multiscale graphs [34, 35]. We provide a brief introduction to persistent homology in the Supporting Material: S4.

A filtration of an oriented simplicial complex K is a sequence of sub-complexes ${\left(K_t\right)}_{t=0}^m$ of K

$$\varnothing =K_0\subseteq K_1\subseteq K_2\subseteq \cdots \subseteq K_m=K.$$ (16)

It induces a sequence of chain complexes

$$\begin{array}{cccccccccccccc}\cdots & C_{q+1}^1& \underset{{\partial }_{q+1}^{1*}}{\overset{{\partial }_{q+1}^1}{\rightleftharpoons }}& C_q^1& \underset{{\partial }_q^{1*}}{\overset{{\partial }_q^1}{\rightleftharpoons }}& \cdots & \underset{{\partial }_3^{1*}}{\overset{{\partial }_3^1}{\rightleftharpoons }}& C_2^1& \underset{{\partial }_2^{1*}}{\overset{{\partial }_2^1}{\rightleftharpoons }}& C_1^1& \underset{{\partial }_1^{1*}}{\overset{{\partial }_1^1}{\rightleftharpoons }}& C_0^1& \underset{{\partial }_0^{1*}}{\overset{{\partial }_0^1}{\rightleftharpoons }}& C_{-1}^1\\ \cdots & \stackrel{|\cap }{C_{q+1}^2}& \underset{{\partial }_{q+1}^{2*}}{\overset{{\partial }_{q+1}^2}{\rightleftharpoons }}& \stackrel{|\cap }{C_q^2}& \underset{{\partial }_q^{2*}}{\overset{{\partial }_q^2}{\rightleftharpoons }}& \cdots & \underset{{\partial }_3^{2*}}{\overset{{\partial }_3^2}{\rightleftharpoons }}& \stackrel{|\cap }{C_2^2}& \underset{{\partial }_2^{2*}}{\overset{{\partial }_2^2}{\rightleftharpoons }}& \stackrel{|\cap }{C_1^2}& \underset{{\partial }_1^{2*}}{\overset{{\partial }_1^2}{\rightleftharpoons }}& \stackrel{|\cap }{C_0^2}& \underset{{\partial }_0^{2*}}{\overset{{\partial }_0^2}{\rightleftharpoons }}& C_{-1}^1\\ \cdots & \stackrel{|\cap }{C_{q+1}^m}& \underset{{\partial }_{q+1}^{m*}}{\overset{{\partial }_{q+1}^m}{\rightleftharpoons }}& \stackrel{|\cap }{C_q^m}& \underset{{\partial }_q^{m*}}{\overset{{\partial }_q^m}{\rightleftharpoons }}& \cdots & \underset{{\partial }_3^{m*}}{\overset{{\partial }_3^m}{\rightleftharpoons }}& \stackrel{|\cap }{C_2^m}& \underset{{\partial }_2^{m*}}{\overset{{\partial }_2^m}{\rightleftharpoons }}& \stackrel{|\cap }{C_1^m}& \underset{{\partial }_1^{m*}}{\overset{{\partial }_1^m}{\rightleftharpoons }}& \stackrel{|\cap }{C_0^m}& \underset{{\partial }_0^{m*}}{\overset{{\partial }_0^m}{\rightleftharpoons }}& C_{-1}^1\end{array}$$ (17)

where $C_q^t≔C_q\left(K_t\right)$ and ${\partial }_q^t:C_q\left(K_t\right)\to C_{q-1}\left(K_t\right)$. Each K_t itself is an oriented simplicial complex which has dimension denoted by dim(K_t). If q < 0, then C_q(K_t) = {∅} and ${\partial }_q^t$ is actually a zero map.² For a general case of 0 < q ≤ dim(K_t), if σ_q is an oriented q-simplex of K_t, then

$${\partial }_q^t\left({\sigma }_q\right)=\sum _i^q{(-1)}^i{\sigma }_{q-1}^i,{\sigma }_q\in K_t,$$

with σ_q = [v₀, ⋯ , v_q] being the oriented q-simplex, and ${\sigma }_{q-1}^i=\left[v_0,\cdots ,{\widehat{v}}_i,\cdots ,v_q\right]$ being the oriented (q − 1)-simplex for which its vertex v_i is removed.

Let ${ℂ}_q^{t+p}$ be the subset of $C_q^{t+p}$ whose boundary is in $C_{q-1}^t$:

$${ℂ}_q^{t+p}:=\left\{\alpha \in C_q^{t+p}\mid {\partial }_q^{t+p}(\alpha )\in C_{q-1}^t\right\}.$$ (18)

We define

$${ð}_q^{t+p}:{ℂ}_q^{t+p}\to C_{q-1}^t$$ (19)

Based on the q-combinatorial Laplacian operator, the p-persistent q-combinatorial Laplacian operator ${\Delta }_q^{t+p}:C_q\left(K_t\right)\to C_q\left(K_t\right)$ defined along the filtration can be expressed as

$${\Delta }_q^{t+p}={ð}_{q+1}^{t+p}{\left({ð}_{q+1}^{t+p}\right)}^{*}+{\partial }_q^{t^{*}}{\partial }_q^t.$$ (20)

We denote the matrix representations of boundary operator ${ð}_{q+1}^{t+p}$ and ${\partial }_q^t$ by ${\mathcal{B}}_{q+1}^{t+p}$ and ${\mathcal{B}}_q^t$, respectively. It is clear that the number of rows in ${\mathcal{B}}_{q+1}^{t+p}$ is the number of oriented q-simplices in K_t, and the number of columns is the number of oriented (q+1)-simplices in $K_{t+p}\cap {ℂ}_{q+1}^{t+p}$. The transpose of the matrices ${\mathcal{B}}_{q+1}^{t+p}$ and ${\mathcal{B}}_q^t$, are the matrix representations of the adjoint boundary operator ${\left({\partial }_{q+1}^{t+p}\right)}^{*}$ and ${\partial }_q^{t*}$, respectively. Therefore, the p-persistent q-combinatorial Laplacian matrix, ${\mathcal{L}}_q^{t+p}$, is

$${\mathcal{L}}_q^{t+p}={\mathcal{B}}_{q+1}^{t+p}{\left({\mathcal{B}}_{q+1}^{t+p}\right)}^T+{\left({\mathcal{B}}_q^t\right)}^T{\mathcal{B}}_q^t.$$ (21)

Intuitively, for a non-empty set $C_q^t$, the p-persistent q-combinatorial Laplacian matrix ${\mathcal{L}}_q^{t+p}$ is a square matrix with dimension to be the number of q-simplices in K_t. Moreover, ${\mathcal{L}}_q^{t+p}$ is symmetric and positive semidefined and thus, all the spectra of ${\mathcal{L}}_q^{t+p}$ are real and non-negative. If p = 0, then ${\mathcal{L}}_q^{t+0}$ is exactly the q-combinatorial Laplacian matrix defined in Eq. (10).

We are interested in the difference between ${\mathcal{L}}_q^{t+0}$ and ${\mathcal{L}}_q^{t+p}$. Suppose we have an oriented simplicial complex K_t, and also an oriented simplicial complex K_t+p constructed by adding different dimensions simplices (”outer” topological structures) to K_t with dim(K_t+p) = q + 1. Since K_t ⊂ K_t+p, we have

$${\mathcal{L}}_q^{t+0}={\mathcal{B}}_{q+1}^{t+0}{\left({\mathcal{B}}_{q+1}^{t+0}\right)}^T+{\left({\mathcal{B}}_q^t\right)}^T{\mathcal{B}}_q^t$$

$${\mathcal{L}}_q^{t+p}={\mathcal{B}}_{q+1}^{t+p}{\left({\mathcal{B}}_{q+1}^{t+p}\right)}^T+{\left({\mathcal{B}}_q^t\right)}^T{\mathcal{B}}_q^t.$$

Case 1. If $\left(\text{Im}\left({ð}_{q+1}^{t+p}\right)\cap \left(K_{t+p}\backslash K_t\right)\right)\cap C_q^t=\varnothing$ for all possible q, then the ”outer” topological structures are disconnected with K_t. Therefore, the boundary matrix ${\mathcal{B}}_{q+1}^{t+p}$ is exactly the same with ${\mathcal{B}}_{q+1}^t$. In this situation, the spectra of ${\mathcal{L}}_q^{t+0}$ and ${\mathcal{L}}_q^{t+p}$ are the same, which reveals the fact that the topological structure K_t does not change under the filtration process.

Case 2. If $\left(\text{Im}\left({ð}_{q+1}^{t+p}\right)\cap \left(K_{t+p}\backslash K_t\right)\right)\cap C_q^t\ne \varnothing$ for at least one q, then the boundary matrix ${\mathcal{B}}_{q+1}^{t+p}$ will be changed by adding additional non-zero columns. Therefore, ${\mathcal{L}}_q^{t+p}$ is no longer the same as ${\mathcal{L}}_q^{t+0}$, but the structure information in K_t will still be preserved in ${\mathcal{L}}_q^{t+p}$. In this case, the topological structure K_t builds connection with “outer” topological structures. By calculating the spectra of ${\mathcal{L}}_q^{t+p}$, the disappeared and preserved structure information of K_t under the filtration process can be revealed.

Based on the fact that the topological and spectral information of K_t can also be analyzed from ${\mathcal{L}}_q\left(K_t\right)$ along with the filtration parameter by diagonalizing the q-combinatorial Laplacian matrix, we focus on the spectra information calculated from ${\mathcal{L}}_q^{t+p}$. Denote the set of spectra of ${\mathcal{L}}_q^{t+p}$ by

$$\text{Spectra }\left({\mathcal{L}}_q^{t+p}\right)=\left\{{\left({\lambda }_1\right)}_q^{t+p},{\left({\lambda }_2\right)}_q^{t+p},\cdots ,{\left({\lambda }_N\right)}_q^{t+p}\right\},$$

where ${\mathcal{L}}_q^{t+p}$ has dimension N × N and spectra are arranged in ascending order. The smallest non-zero eigenvalue of ${\mathcal{L}}_q^{t+p}$ is defined as ${\left({\tilde{\lambda }}_2\right)}_q^{t+p}$. In the previous section, we have seen that Betti numbers (i.e # of zero eigenvalues) can reveal q-cycle information. Similarly, we define the number of zero eigenvalues of p-persistent q-combinatorial Laplacian matrix ${\mathcal{L}}_q^{t+p}$ to be the p-persistent qth Betti numbers

$${\beta }_q^{t+p}=\text{dim}\left({\mathcal{L}}_q^{t+p}\right)-\text{rank}\left({\mathcal{L}}_q^{t+p}\right)=\text{ nullity }\left({\mathcal{L}}_q^{t+p}\right)=\#\text{ of zero eigenvalues of }{\mathcal{L}}_q^{t+p}.$$ (22)

In fact, ${\beta }_q^{t+p}$ counts the number of q-cycles in K_t that are still alive in K_t+p, which exactly provides the same topological information as persistent homology does. However, persistent spectral theory offers additional geometric information from the spectra of persistent combinatorial Laplacian matrix beyond topological persistence. In general, the topological changes can be read off from persistent Betti numbers (harmonic persistent spectra) and the geometric changes can be derived from the non-harmonic persistent spectra.

Figure 3 demonstrates an example of a standard filtration process. Here the initial setup K₁ consists of five 0-simplices (vertices). We construct Vietoris-Rips complexes by using an ever-growing circle centered at each vertex with radius r. Once two circles overlapped with each other, an 1-simplex (edge) is formed. A 2-simplex (triangle) will be created when 3 circles contact with one another, and a 3-simplex will be generated once 4 circles get overlapped one another. As Figure 3 shows, we can attain a series of simplicial complexes from K₁ to K₆ with the radius of circles increasing. Table 1 lists the number of q-cycles of simplicial complex To fully illustrate how to construct p-persistent q-combinatorial Laplacian matrices by the boundary operator and determine persistent Betti numbers, we analyze 6 p-persistent q-combinatorial Laplacian matrices and their corresponding harmonic persistent spectra (i.e., persistent Betti numbers) and non-harmonic persistent spectra. An supplementary example to distinguish different topological structures by implementing PST is provided in the Supporting Material: S5. Moreover, additional matrices are analyzed in the Supporting Material: S6.

Figure 3:

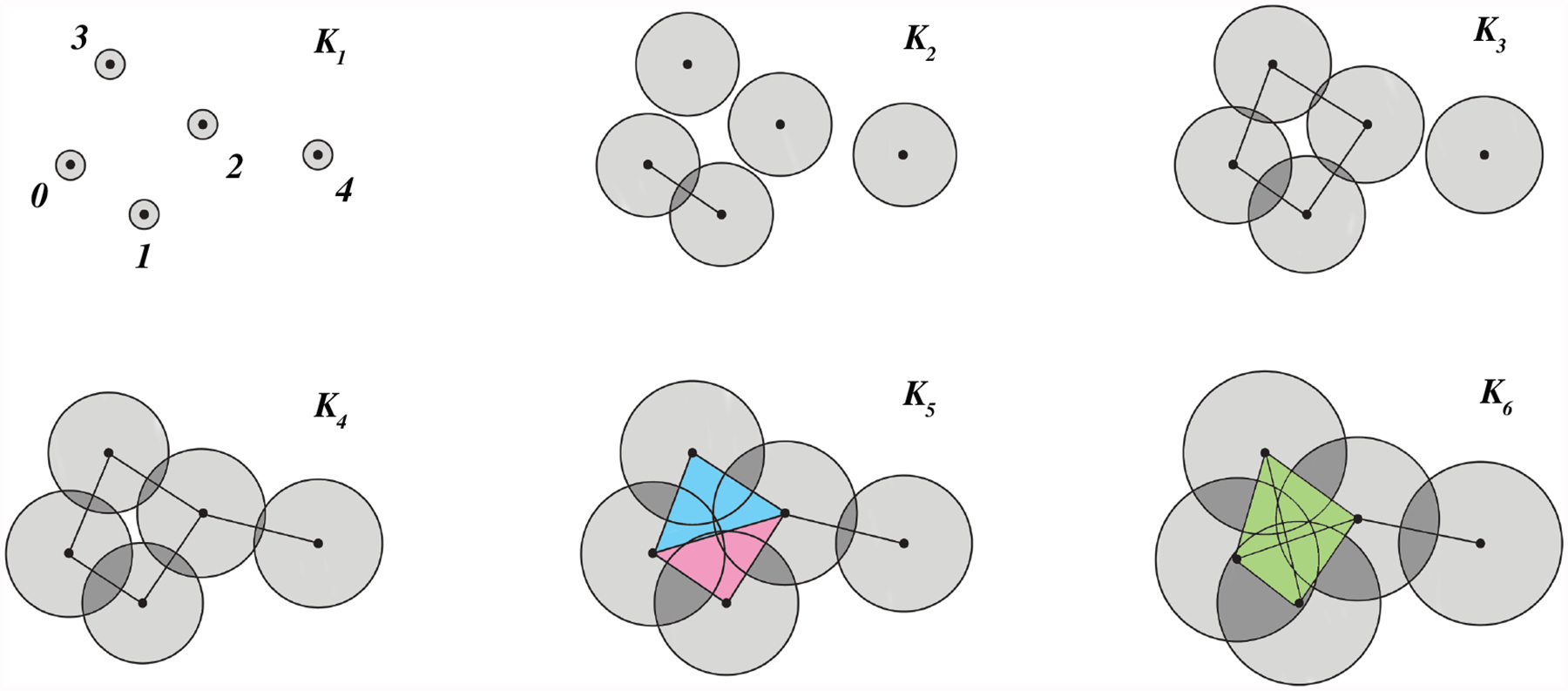
Illustration of filtration. We use 0, 1, 2, 3, and 4 to stand for 0-simplices, 01, 12, 23, 03, 24, 02, and 13 for 1simplices, 012, 023, 013, and 123 for 2-simplices, and 0123 for the 3-simplex. Here, K₁ has five 0-cycles, K₂ has four 0-cycles, K₃ has two 0-cycles and a 1-cycle, K₄ has a 0-cycle and a 1-cycle, K₅ has one 0-cycle, and K₆ has a 0-cycle.

Table 1:

The number of q-cycles of simplicial complexes demonstrated in Figure 3.

# of q-cycles	K1	K2	K3	K4	K5	K6
q = 0	5	4	2	1	1	1
q = 1	0	0	1	1	0	0
q = 2	0	0	0	0	0	0

Case 1. The initial setup is K₃ and the end status is K₄. The 1-persistent 0, 1, 2-combinatorial Laplacian operators are

$${\Delta }_0^{3+1}={ð}_1^{3+1}{\left({ð}_1^{3+1}\right)}^{*}+{\partial }_0^{3^{*}}{\partial }_0^3,$$

$${\Delta }_1^{3+1}={ð}_2^{3+1}{\left({ð}_2^{3+1}\right)}^{*}+{\partial }_1^{3^{*}}\partial 1^3,$$

$${\Delta }_2^{3+1}={ð}_3^{3+1}{\left({ð}_3^{3+1}\right)}^{*}+{\partial }_2^{3^{*}}{\partial }_2^3,$$

Since 2-simplex and 3-simplex do not exist in K₄, ${\partial }_2^3$, ${\partial }_2^{3+1}$, and ${\partial }_2^3$ do not exist, then

$${\mathcal{L}}_0^{3+1}={\mathcal{B}}_1^{3+1}{\left({\mathcal{B}}_1^{3+1}\right)}^T+{\left({\mathcal{B}}_0^3\right)}^T{\mathcal{B}}_0^3,$$

$${\mathcal{L}}_1^{3+1}={\left({\mathcal{B}}_1^3\right)}^T{\mathcal{B}}_1^3.$$

From Table 2, one can see that ${\beta }_0^{3+1}=0$ and ${\beta }_1^{3+1}=1$, which reveals only one 0-cycle and one 1-cycle in K₃ are still alive in K₄.

Table 2:

K₃ → K₄

q	q = 0	q = 1	q = 2
${\mathcal{B}}_{q+1}^{3+1}$	$\begin{array}{ll}\hfill & \begin{array}{ccccc}01& 12& 23& 03& 24\end{array}\hfill \\ \begin{array}{c}0\\ 1\\ 2\\ 3\\ 4\end{array}\hfill & \left[\begin{array}{ccccc}-1& 0& 0& -1& 0\\ 1& -1& 0& 0& 0\\ 0& 1& -1& 0& -1\\ 0& 0& 1& 1& 0\\ 0& 0& 0& 0& 1\end{array}\right]\hfill \end{array}$	/	/
${\mathcal{B}}_q^3$	$\begin{array}{c}\begin{array}{ccccc}0& 1& 2& 3& 4\end{array}\\ \left[\begin{array}{ccccc}0& 0& 0& 0& 0\end{array}\right]\end{array}$	$\begin{array}{cc}& \begin{array}{cccc}01& 12& 23& 03\end{array}\\ \begin{array}{c}0\\ 1\\ 2\\ 3\\ 4\end{array}& \left[\begin{array}{cccc}-1& 0& 0& -1\\ 1& -1& 0& 0\\ 0& 1& -1& 0\\ 0& 0& 1& 1\\ 0& 0& 0& 0\end{array}\right]\end{array}$	/
${\mathcal{L}}_q^{3+1}$	$\left[\begin{array}{ccccc}2& -1& 0& -1& 0\\ -1& 2& -1& 0& 0\\ 0& -1& 3& -1& -1\\ -1& 0& -1& 2& 0\\ 0& 0& -1& 0& 1\end{array}\right]$	$\left[\begin{array}{cccc}2& -1& 0& 1\\ -1& 2& -1& 0\\ 0& -1& 2& 1\\ 1& 0& 1& 2\end{array}\right]$	/
${\beta }_q^{3+1}$	1	1	/
$\text{dim}\left({\mathcal{L}}_q^{3+1}\right)$	5	4	/
$\text{rank}\left({\mathcal{L}}_q^{3+1}\right)$	4	3	/
$\text{nullity }\left({\mathcal{L}}_q^{3+1}\right)$	1	1	/
$\text{Spectra }\left({\mathcal{L}}_q^{3+1}\right)$	{0, 0.8299, 2, 2.6889, 4.4812}	{0, 2, 2, 4}	/

Case 2. The initial setup is K₆ and the end status is K₆. The 0-persistent 0, 1, 2-combinatorial Laplacian operators are

$${\mathcal{L}}_0^{6+0}={\mathcal{B}}_1^{6+0}{\left({\mathcal{B}}_1^{6+0}\right)}^T+{\left({\mathcal{B}}_0^6\right)}^T{\mathcal{B}}_0^6,$$

$${\mathcal{L}}_1^{6+0}={\mathcal{B}}_2^{6+0}{\left({\mathcal{B}}_2^{6+0}\right)}^T+{\left({\mathcal{B}}_1^6\right)}^T{\mathcal{B}}_1^6,$$

$${\mathcal{L}}_2^{6+0}={\mathcal{B}}_3^{6+0}{\left({\mathcal{B}}_3^{6+0}\right)}^T+{\left({\mathcal{B}}_2^6\right)}^T{\mathcal{B}}_2^6,$$

From Table 3, ${\beta }_0^{6+0}=1$, ${\beta }_1^{6+0}=0$, and ${\beta }_2^{6+0}=0$ imply that only one 0-cycle (connected component) exists in K₆.

Table 3:

K₆ → K₆

q	q = 0	q = 1	q = 2
${\mathcal{B}}_{q+1}^{6+0}$	$\begin{array}{cc}& \begin{array}{ccccccc}01& 12& 23& 03& 24& 02& 13\end{array}\\ \begin{array}{c}0\\ 1\\ 2\\ 3\\ 4\end{array}& \left[\begin{array}{ccccccc}-1& 0& 0& -1& 0& -1& 0\\ 1& -1& 0& 0& 0& 0& -1\\ 0& 1& -1& 0& -1& 1& 0\\ 0& 0& 1& 1& 0& 0& 1\\ 0& 0& 0& 0& 1& 0& 0\end{array}\right]\end{array}$	$\begin{array}{cc}& \begin{array}{cccc}012& 023& 013& 123\end{array}\\ \begin{array}{c}01\\ 12\\ 23\\ 03\\ 24\\ 02\\ 13\end{array}& \left[\begin{array}{cccc}1& 0& 1& 0\\ 1& 0& 0& 1\\ 0& 1& 0& 1\\ 0& -1& -1& 0\\ 0& 0& 0& 0\\ -1& 1& 0& 0\\ 0& 0& 1& -1\end{array}\right]\end{array}$	${\mathcal{B}}_3^{6+0}$
${\mathcal{B}}_q^6$	$\begin{array}{cc}& \begin{array}{ccccc}0& 1& 2& 3& 4\end{array}\\ /& \left[\begin{array}{ccccc}0& 0& 0& 0& 0\end{array}\right]\end{array}$	$\begin{array}{cc}& \begin{array}{ccccccc}01& 12& 23& 03& 24& 02& 13\end{array}\\ \begin{array}{c}0\\ 1\\ 2\\ 3\\ 4\end{array}& \left[\begin{array}{ccccccc}-1& 0& 0& -1& 0& -1& 0\\ 1& -1& 0& 0& 0& 0& -1\\ 0& 1& -1& 0& -1& 1& 0\\ 0& 0& 1& 1& 0& 0& 1\\ 0& 0& 0& 0& 1& 0& 0\end{array}\right]\end{array}$	${\mathcal{B}}_2^6$
${\mathcal{L}}_q^{6+0}$	$\left[\begin{array}{ccccc}3& -1& -1& -1& 0\\ -1& 2& -1& 0& 0\\ -1& -1& 4& -1& -1\\ -1& 0& -1& 2& 0\\ 0& 0& -1& 0& 1\end{array}\right]$	$\left[\begin{array}{ccccccc}4& 0& 0& 0& 0& 0& 0\\ 0& 4& 0& 0& -1& 0& 0\\ 0& 0& 4& 0& 1& 0& 0\\ 0& 0& 0& 4& 0& 0& 0\\ 0& -1& 1& 0& 2& -1& 0\\ 0& 0& 0& 0& -1& 4& 0\\ 0& 0& 0& 0& 0& 0& 4\end{array}\right]$	${\mathcal{L}}_3^{6+0}$
${\beta }_q^{6+0}$	1	0	0
$\text{dim}\left({\mathcal{L}}_q^{6+0}\right)$	5	7	4
$\text{rank}\left({\mathcal{L}}_q^{6+0}\right)$	4	7	4
$\text{ nullity }\left({\mathcal{L}}_q^{6+0}\right)$	1	0	0
$\text{ Spectra }\left({\mathcal{L}}_q^{6+0}\right)$	{0, 1, 4, 4, 5}	{1, 4, 4, 4, 4, 4, 5}	{4, 4, 4, 4}

with

$${\mathcal{B}}_3^{6+0}=\begin{array}{cc}& 0123\\ \begin{array}{c}012\\ 023\\ 013\\ 123\end{array}& \left[\begin{array}{c}-1\\ -1\\ 1\\ 1\end{array}\right]\end{array},{\mathcal{B}}_2^6=\begin{array}{cc}& \begin{array}{cccc}012& 023& 013& 123\end{array}\\ \begin{array}{c}01\\ 12\\ 23\\ 03\\ 24\\ 02\\ 13\end{array}& \left[\begin{array}{cccc}1& 0& 1& 0\\ 1& 0& 0& 1\\ 0& 1& 0& 1\\ 0& -1& -1& 0\\ 0& 0& 0& 0\\ -1& 1& 0& 0\\ 0& 0& 1& -1\end{array}\right]\end{array},{\mathcal{L}}_3^{6+0}=\left[\begin{array}{cccc}4& 0& 0& 0\\ 0& 4& 0& 0\\ 0& 0& 4& 0\\ 0& 0& 0& 4\end{array}\right].$$

We have constructed a family of persistent spectral graphs induced by a filtration parameter. For the sake of simplicity, we focus on the analysis of high-dimensional spectra with p = 0 in the rest of this section. As clarified before, the 0-persistent q-combinatorial Laplacian matrix is the q-combinatorial Laplacian matrix. A graph structure encodes inter-dependencies among constituents and provides a convenient representation of the high-dimensional data. Naturally, the same idea can be applied to higher-dimensional spaces. For a set of points $V\subset {ℝ}^n$ without additional structures, we consider growing an (n − 1)-sphere centered at each point with an ever-increasing radius r. Therefore, a family of 0-persistent q-combinatorial Laplacian matrices as well as spectra can be generated as the radius r increases, which provides topological and spectral features to distinguish individual entries of the dataset.

2.3.4. Variants of p-persistent q-combinatorial Laplacian matrices

The traditional approach in defining the q-boundary operator ∂_q : C_q(K) → C_q−1(K) can be expressed as:

$${\partial }_q{\sigma }_q=\sum _{i=0}^q{(-1)}^i{\sigma }_{q-1}^i,$$

which leads to the corresponding elements in the boundary matrices being either 1 or −1. However, to encode more geometric information into the Laplacian operator, we add volume information of q-simplex σ_q to the expression of q-boundary operator.

Given a vertex set V = {v₀, v₁, ⋯ , v_q} with q + 1 isolated points (0-simplices) randomly arranged in the n-dimensional Euclidean space ${ℝ}^n$, often with n ≥ q. Set d_ij to be the distances between v_i and v_j with 0 ≤ i ≤ j ≤ q and obviously, d_ij = d_ji. The Cayley-Menger determinant can be expressed as [39]

$${\text{Det}}_{\text{CM}}\left(v_0,v_1,\cdots ,v_q\right)=\left|\begin{array}{cccccc}0& d_{01}^2& d_{02}^2& \cdots & d_{0q}^2& 1\\ d_{10}^2& 0& d_{12}^2& \cdots & d_{1q}^2& 1\\ d_{20}^2& d_{21}^2& 0& \cdots & d_{2q}^2& 1\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮\\ d_{q0}^2& d_{q1}^2& d_{q2}^2& \cdots & 0& 1\\ 1& 1& 1& 1& 1& 0\end{array}\right|$$ (23)

The q-dimensional volume of q-simplex σ_q with vertices {v₀, v₁, ⋯ , v_q} is defined by

$$\text{Vol}\left({\sigma }_q\right)=\sqrt{\frac{{(-1)}^{q+1}}{{(q!)}^2{2}^q}{\text{Det}}_{\text{CM}}\left(v_0,v_1,\cdots ,v_q\right)}.$$ (24)

In trivial cases, Vol(σ₀) = 1, meaning the 0-dimensional volume of 0-simplex is 1, i.e., there is only 1 vertex in a 0-simplex. Also, the 1-dimensional volume of 1-simplex σ₁ = [v_i, v_j] is the distance between v_i and v_j, and the 2-dimensional volume of 2-simplex is the area of a triangle [v_i, v_j, v_k].

In applications, it is often useful to replace the characteristic number “1” with some other descriptive quantities [40]. Therefore, we define weighted boundary operator equipped with volume, denoted ${\widehat{\partial }}_q$,

$${\widehat{\partial }}_q{\sigma }_q=\sum _{i=0}^q{(-1)}^i\text{Vol}\left({\sigma }_q^i\right){\sigma }_{q-1}^i.$$ (25)

Employing the same concept to the persistent spectral theory, we have the volume-weighted p-persistent q-combinatorial Laplacian operator. We also define

$${\widehat{ð}}_q^{t+p}:{ℂ}_q^{t+p}\to C_{q-1}^t$$ (26)

with

$${ℂ}_q^{t+p}:=\left\{\alpha \in C_q^{t+p}\mid {\widehat{\partial }}_q^{t+p}(\alpha )\in C_{q-1}^t\right\}.$$

Similarly, an inverse-volume weighted boundary operator, denoted ${\check{\partial }}_q$, is given by

$${\check{\partial }}_q{\sigma }_q=\sum _{i=0}^q{(-1)}^i\frac{1}{\text{Vol}\left({\sigma }_q^i\right)}{\sigma }_{q-1}^i.$$ (27)

To define an inverse-volume weighted p-persistent q-combinatorial Laplacian operator. We define

$${\check{ð}}_q^{t+p}:{ℂ}_q^{t+p}\to C_{q-1}^t$$ (28)

with

$${ℂ}_q^{t+p}:=\left\{\alpha \in C_q^{t+p}\mid {\check{\partial }}_q^{t+p}(\alpha )\in C_{q-1}^t\right\}$$

Then volume-weighted and inverse-volume-weighted p-persistent q-combinatorial Laplacian operators defined along the filtration can be expressed as

$$\begin{array}{l}{\widehat{\Delta }}_q^{t+p}={\widehat{ð}}_{q+1}^{t+p}{\left({\widehat{ð}}_{q+1}^{t+p}\right)}^{*}+{\widehat{\partial }}_q^{t^{*}}{\widehat{\partial }}_q^t,\hfill \\ {\check{\Delta }}_q^{t+p}={\check{ð}}_{q+1}^{t+p}{\left({\check{ð}}_{q+1}^{t+p}\right)}^{*}+{\check{\partial }}_q^{t^{*}}{\check{\partial }}_q^t.\hfill \end{array}$$ (29)

The corresponding weighted matrix representations of boundary operators ${\widehat{ð}}_{q+1}^{t+p}$, ${\widehat{ð}}_q^t$, ${\check{ð}}_{q+1}^{t+p}$, and ${\check{ð}}_q^t$ are denoted ${\widehat{\mathcal{B}}}_{q+1}^{t+p}$, ${\widehat{\mathcal{B}}}_q^t$, ${\check{\mathcal{B}}}_{q+1}^{t+p}$, and ${\check{\mathcal{B}}}_q^t$, respectively. Therefore, volume-weighted and inverse-volume-weighted p-persistent q-combinatorial Laplacian matrices can be expressed as

$$\begin{array}{l}{\widehat{\mathcal{L}}}_q^{t+p}={\widehat{\mathcal{B}}}_{q+1}^{t+p}{\left({\widehat{\mathcal{B}}}_{q+1}^{t+p}\right)}^T+{\left({\widehat{\mathcal{B}}}_q^t\right)}^T\left({\widehat{\mathcal{B}}}_q^t\right),\hfill \\ {\check{\mathcal{L}}}_q^{t+p}={\check{\mathcal{B}}}_{q+1}^{t+p}{\left({\check{\mathcal{B}}}_{q+1}^{t+p}\right)}^T+{\left({\check{\mathcal{B}}}_q^t\right)}^T\left({\check{\mathcal{B}}}_q^t\right).\hfill \end{array}$$ (30)

Although the expressions of the weighted persistent Laplacian matrices are different from the original persistent Laplacian matrices, some properties of ${\mathcal{L}}_q^{t+p}$ are preserved. The weighted persistent Laplacian operators are still symmetric and positive semi-defined. Additionally, their ranks are the same as ${\mathcal{L}}_q^{t+p}$. With the embedded volume information, weighted PSGs can provide richer topological and geometric information through the associated persistent Betti numbers and non-harmonic spectra (i.e., non-zero eigenvalues). In real applications, we are more interested in the 0, 1, 2-combinatorial Laplacian matrices because its more intuitive to depict the relation among vertex, edges, and faces. Given a set of vertices V = {v₀, v₂, ⋯ , v_N} with N + 1 isolated points (0-simplices) randomly arranged in ${ℝ}^n$. By varying the radius r of the (n − 1)-sphere centered at each vertex, a variety of simplicial complexes is created. We denote the simplicial complex generated at radius r to be K_r, then the 0-persistent q-combinatorial Laplacian operator and matrix at initial set up K_r is

$${\mathcal{L}}_q^{r+0}={\mathcal{B}}_{q+1}^{r+0}{\left({\mathcal{B}}_{q+1}^{r+0}\right)}^T+{\left({\mathcal{B}}_q^r\right)}^T{\mathcal{B}}_q^r.$$ (31)

The volume of any 1-simplex σ₁ = [v_i, v_j] is Vol(σ₁) is actually the distance between v_i and v_j denoted d_ij. Then the 0-persistent 0-combinatorial Laplacian matrix based on filtration r can be expressed explicitly as

$${\left({\mathcal{L}}_0^{r+0}\right)}_{ij}=\{\begin{array}{ll}-\sum _j{\left({\mathcal{L}}_0^{r+0}\right)}_{ij},\hfill & \text{ if }i=j\hfill \\ -1,\hfill & \text{ if }i\ne j\text{ and }{d}_{ij}-2r<0\hfill \\ 0,\hfill & \text{ otherwise}.\hfill \end{array}$$ (32)

Correspondingly, we can denote the 0-persistent 1-combinatorial Laplacian matrix based on filtration r by ${\mathcal{L}}_1^{r+0}$, and the 0-persistent 2-combinatorial Laplacian matrix based on filtration ${\mathcal{L}}_2^{r+0}$.

Alternatively, variants of persistent 0-combinatorial Laplacian matrices can be defined by adding the Euclidean distance information. The distance-weight persistent 0-combinatorial Laplacian matrix based on filtration r can be expressed explicitly as

$${\left({\widehat{\mathcal{L}}}_0^{r+0}\right)}_{ij}=\{\begin{array}{ll}-\sum _j{\left({\widehat{\mathcal{L}}}_0^{r+0}\right)}_{ij},\hfill & \text{ if }i=j\hfill \\ -d_{ij},\hfill & \text{ if }i\ne j\text{ and }{d}_{ij}-2r<0\hfill \\ 0,\hfill & \text{ otherwise}.\hfill \end{array}$$ (33)

Moreover, the inverse-distance-weight persistent 0-combinatorial Laplacian matrix based on filtration r can also be implemented:

$${\left({\check{\mathcal{L}}}_0^{r+0}\right)}_{ij}=\{\begin{array}{ll}-\sum _j{\left({\check{\mathcal{L}}}_0^{r+0}\right)}_{ij},\hfill & \text{ if }i=j\hfill \\ -\frac{1}{d_{ij}},\hfill & \text{ if }i\ne j\text{ and }{d}_{ij}-2r<0\hfill \\ 0,\hfill & \text{ otherwise}.\hfill \end{array}$$ (34)

The spectra of the aforementioned 0-persistent 0-combinatorial Laplacian matrices based on filtration are given by

$$\text{Spectra }\left({\mathcal{L}}_0^{r+0}\right)=\left\{{\left({\lambda }_1\right)}_0^{r+0},{\left({\lambda }_2\right)}_0^{r+0},\cdots ,{\left({\lambda }_N\right)}_0^{r+0}\right\},$$

$$\text{Spectra }\left({\widehat{\mathcal{L}}}_0^{r+0}\right)=\left\{{\left({\widehat{\lambda }}_1\right)}_0^{r+0},{\left({\widehat{\lambda }}_2\right)}_0^{r+0},\cdots ,{\left({\widehat{\lambda }}_N\right)}_0^{r+0}\right\},$$

$$\text{Spectra }\left({\check{\mathcal{L}}}_0^{r+0}\right)=\left\{{\left({\check{\lambda }}_1\right)}_0^{r+0},{\left({\check{\lambda }}_2\right)}_0^{r+0},\cdots ,{\left({\check{\lambda }}_N\right)}_0^{r+0}\right\},$$

where N is the dimension of persistent Laplacian matrices, ${\left({\widehat{\lambda }}_j\right)}_0^{r+0}$ and ${\left({\check{\lambda }}_j\right)}_0^{r+0}$ are the j-th eigenvalues of ${\widehat{\mathcal{L}}}_0^{r+0}$ and ${\check{\mathcal{L}}}_0^{r+0}$, respectively. We denote ${\widehat{\beta }}_q^{r+0}$ and ${\check{\beta }}_q^{r+0}$ the qth Betti for ${\widehat{\mathcal{L}}}_q^{r+0}$ and ${\check{\mathcal{L}}}_q^{r+0}$, respectively.

The smallest non-zero eigenvalue of ${\mathcal{L}}_0^{r+0}$, denoted ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$, is particularly useful in many applications. Similarly, the smallest non-zero eigenvalues of ${\widehat{\mathcal{L}}}_0^{r+0}$ and ${\check{\mathcal{L}}}_0^{r+0}$ are denoted as ${\left({\tilde{\widehat{\lambda }}}_2\right)}_0^{r+0}$ and ${\left({\tilde{\widehat{\lambda }}}_2\right)}_0^{r+0}$, respectively.

Finally, it is mentioned that using the present procedure, more general weights, such as the radial basis function of the Euclidean distance, can be employed to construct weighted boundary operators and associated persistent combinatorial Laplacian matrices.

2.3.5. Multiscale spectral analysis

In the past few years, we have developed a multiscale spectral graph method such as generalized GNM and generalized ANM [33, 34], to create a family of spectral graphs with different characteristic length scales for a given dataset. Similarly, in our persistent spectral theory, we can construct a family of spectral graphs induced by a filtration parameter. Moreover, we can sum over all the multiscale spectral graphs as an accumulated spectral graph. Specifically, a family of ${\mathcal{L}}_0^{r+0}$ matrices, as well as the accumulated combinatorial Laplacian matrices, can be generated via the filtration. By analyzing the persistent spectra of these matrices, the topological invariants and geometric shapes can be revealed from the given input point-cloud data. The spectra of ${\mathcal{L}}_0^{r+0}$, ${\widehat{\mathcal{L}}}_0^{r+0}$, and ${\check{\mathcal{L}}}_0^{r+0}$ mentioned above carry similar information on how the topological structures of a graph are changed during the filtration. Benzene molecule (C₆H₆), a typical aromatic hydrocarbon which is composed of six carbon atoms bonded in a planar regular hexagon ring with one hydrogen joined with each carbon atom. It provides a good example to demonstrate the proposed PST. Figure 4 illustrates the filtration of the benzene molecule. Here, we label 6 hydrogen atoms by H₁, H₂, H₃, H₄, H₅, and H₆, and the carbon adjacent to the labeled hydrogen atoms are labeled by C₁, C₂, C₃, C₄, C₅, and C₆, respectively. Figure 5(b) depicts that when the radius of the solid sphere reaches 0.54 Å, each carbon atom in the benzene ring is overlapped with its joined hydrogen atom, resulting in the reduction of ${\beta }_0^{r+0}$ to 6. Moreover, once the radius of solid spheres is larger than 0.70 Å, all the atoms in the benzene molecule will connect and constitute a single component which gives rise ${\beta }_0^{r+0}=1$. Furthermore, we can deduce that the C-C bond length of the benzene ring is about 1.40 Å, and the C-H bond length is around 1.08 Å, which are the real bond lengths in benzene molecule. Figure 5(c) shows that a 1-dimensional hole (1-cycle) is born when the filtration parameter r increase to 0.70 Å and dead when r = 1.21 Å. In Figures 5(b) and 5(c), it can be seen that variants of 0-persistent 0-combinatorial Laplacian and 1 -combinatorial Laplacian matrices based on filtration give us the identical ${\beta }_0^{r+0}$ and ${\beta }_1^{r+0}$ information respectively.

Figure 4:

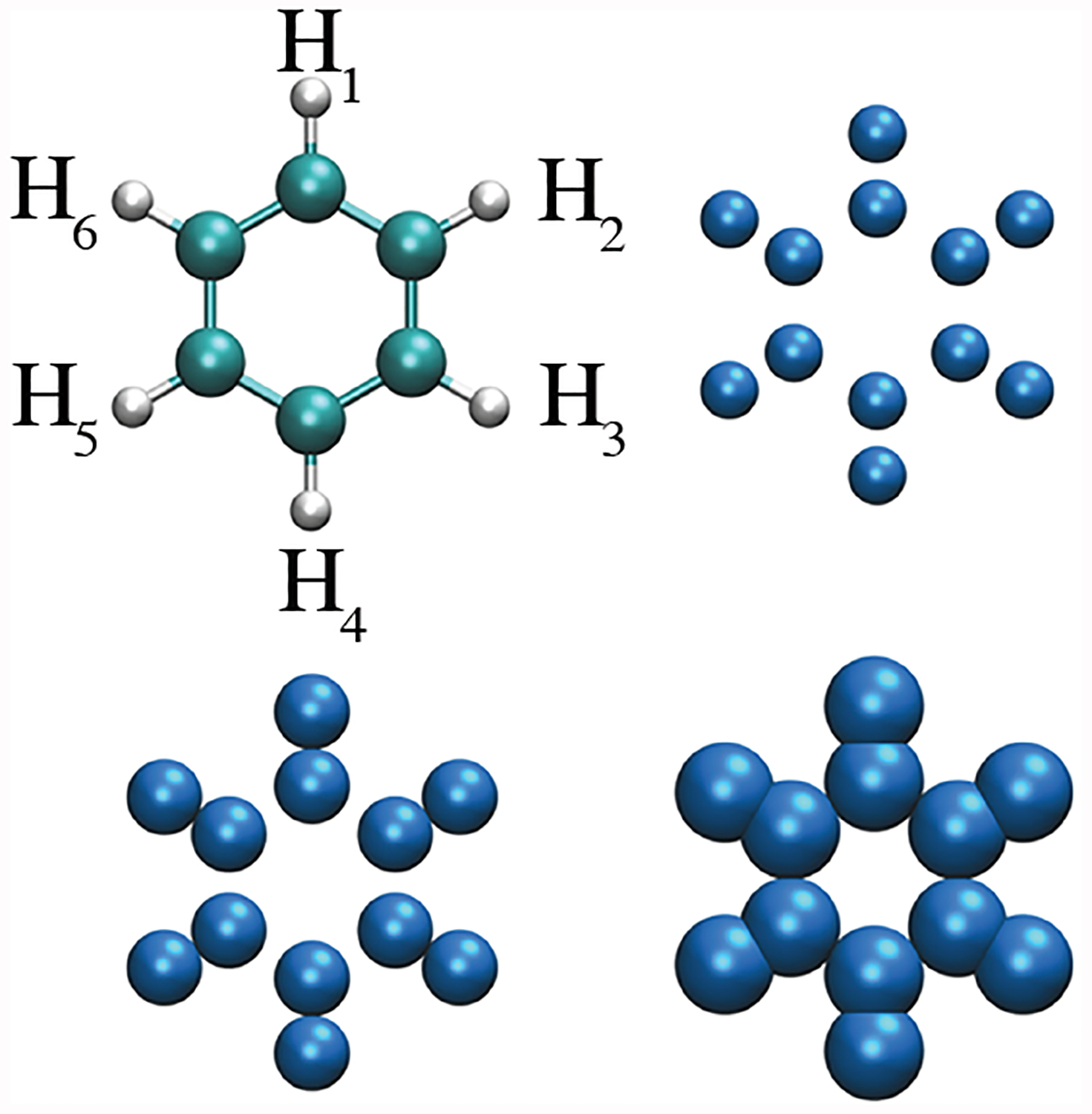
Benzene molecule and its topological changes during the filtration process.

Figure 5:

Persistent spectral analysis of the benzene molecule induced by filtration parameter r. Blue line, orange line, and green line represent ${\mathcal{L}}_0^{r+0}$, ${\widehat{\mathcal{L}}}_0^{r+0}$, and ${\check{\mathcal{L}}}_0^{r+0}$ respectively. (a) Plot of the smallest non-zero eigenvalues with radius filtration under ${\mathcal{L}}_0^{r+0}$ (blue line), ${\widehat{\mathcal{L}}}_0^{r+0}$ (red line), and ${\check{\mathcal{L}}}_0^{r+0}$ (green line). Total 10 jumps observed in this plot which represent 10 possible distances between atoms. (b) Plot of the number of zero eigenvalues (${\beta }_0^{r+0}$) with radius filtration under ${\mathcal{L}}_0^{r+0}$, ${\widehat{\mathcal{L}}}_0^{r+0}$, and ${\check{\mathcal{L}}}_0^{r+0}$ (three spectra are superimposed). When r = 0.00 Å, 12 atoms are disconnected with each other. After r = 0.54 Å, H atoms and their adjacent C atoms are connected with one another resulting in ${\beta }_0^{r+0}=6$. With r keeps growing, all of the atoms are connected with one another and then ${\beta }_0^{r+0}=1$. (c) Plot of the number of zero eigenvalues (${\beta }_1^{r+0}$) with radius filtration under ${\mathcal{L}}_1^{r+0}$. When r = 0.70 Å, a 1-cycle created since all of the C atoms are connected and form a hexagon, resulting in ${\beta }_1^{r+0}=1$. After the radius reached 1.21 Å, the hexagon disappears and ${\beta }_1^{r+0}=0$.

The C-C bond length of benzene is 1.39 Å, and the C-H bond length is 1.09 Å. Due to the perfect hexagon structure of the benzene ring, we can calculate all of the distances between atoms. The shortest and longest distances between carbons and the hydrogen atoms are 1.09 Å and 3.87 Å. In Figure 5(a), a total of 10 changes of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ values is observed at various radii. Table 4 lists all the distances between atoms and the values of radii when the changes of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ occur. It can be seen that the distance between atoms approximately equals twice of the radius value when a jump of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ occurs. Therefore, we can detect all the possible distances between atoms with the nonzero spectral information. Moreover, in Figure 5(b), the values of the smallest nonzero eigenvalues of ${\mathcal{L}}_0^{r+0}$, ${\widehat{\mathcal{L}}}_0^{r+0}$, and ${\check{\mathcal{L}}}_0^{r+0}$ change concurrently.

Table 4:

Distances between atoms in the benzene molecule and the radii when the changes of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ occur (Values increase from left to right).

Type	C1-H1	C1-C2	C2-H1	C1-C3	H1-H2	C1-C4	C3-H1	C4-H1	H1-H3	H1-H4
Distance (Å)	1.09	1.39	2.15	2.41	2.48	2.78	3.39	3.87	4.30	4.96
r (Å)	0.54	0.70	1.08	1.21	1.24	1.40	1.70	1.94	2.15	2.49

3. Applications

In this section, we apply the proposed persistent spectral theory to the study of two important systems, fullerenes and proteins. All three different types of persistent combinatorial Laplacian matrices are employed in our investigation. The resulting persistent spectra contain not only the full set of topological persistence from the harmonic spectra, which is identical to that from a persistent homology analysis, but also non-harmonic eigenvalues and eigenvectors. Since the power of topological persistence has been fully explored and exploited in the past decade [20–23], to demonstrate the additional utility of our persistent spectral analysis, we mainly emphasize the non-harmonic spectra in the present applications. In particular, we demonstrate that persistent spectral theory is able to accurately predict the B-factors of a set of proteins for which the current biophysical models break down.

3.1. Fullerene analysis and prediction

In 1985 Kroto et all discovered the first structure of C₆₀ [41], which was confirmed by Kratschmer et al in 1990 [42]. Since then, the quantitative analysis of fullerene molecules has become an interesting research topic. The understanding of the fullerene structure-function relationship is important for nanoscience and nanotechnology. Fullerene molecules are only made of carbon atoms that have various topological shapes, such as the hollow spheres, ellipsoids, tubes, or rings. Due to the monotony of the atom type and the variety of geometric shapes, the minor heterogeneity of fullerene structures can be ignored. The fullerene system offers a moderately large dataset with relatively simple structures. Therefore, it is suitable for validating new computational methods because every single change in the spectra is interpretable. The proposed persistent spectral theory, i.e., persistent spectral analysis, is applied to characterize fullerene structures and predict their stability.

All the structural data can be downloaded from CCL.NET Webpage. This dataset gives the coordinates of fullerene carbon atoms. In this section, we will analyze fullerene structures and predict the heat of formation energy.

3.1.1. Fullerene structure analysis

The smallest member of the fullerene family is C₂₀ molecule with a dodecahedral cage structure. Note that 12 pentagons are required to form a closed fullerene structure. Following the Euler’s formula, the number of vertices, edges, and faces on a polygon have the relationship V − E + F = 2. Therefore, the 20 carbon atoms in the dodecahedral cage form 30 bonds with the same bond length. The C₂₀ is the only fullerene smaller than C₆₀ that has the molecular symmetry of the full icosahedral point group I_h. C₆₀ is a molecule that consists of 60 carbon atoms arranged as 12 pentagon rings and 20 hexagon rings. Unlike C₂₀, C₆₀ has two types of bonds: 6 : 6 bonds and 6 : 5 bonds. The 6 : 6 bonds are shorter than 6 : 5 bonds, which can also be considered as “double bond” [43]. C₆₀ is the most well-know fullerene with geometric symmetry I_h. Since C₂₀ and C₆₀ are highly symmetrical, they are ideal systems for illustrating the persistent spectral analysis.

Figure 6 (a) illustrates the radius filtration process built on C₂₀. As the radius increases, the solid balls corresponding to carbon atoms grow, and a sequence of ${\mathcal{L}}_0^{r+0}$ matrices can be defined through the overlap relations among the set of balls. At the initial state (r = 0.00 Å), all of the atoms are isolated from one another. Therefore, ${\mathcal{L}}_0^{r+0}$ is a zero matrix with dimension 20×20. Since the C₂₀ molecule has the same bond length which can be denoted as l(C₂₀), once the radius of solid balls is greater than l(C₂₀), all of the balls are overlapped, which makes the system a singly connected component. Figure 6 (b) depicts the accumulated ${\mathcal{L}}_0^{r+0}$ for C₂₀. For C₆₀, the accumulated ${\mathcal{L}}_0^{r+0}$ is described in Figure 7 (a). Figure 7s (b)-(f) are the plots of ${\mathcal{L}}_0^{r+0}$ under different filtration r values. The blue cell located at the ith row and jth column means the balls centered at atom i and atom j connected with each other, i.e., a 1-simplex formed with its vertex to be i and j. When the radius filtration increases, more and more bluer cells are created. In Figure 7 (f), the color of cells, except the cells located in the diagonal, turns to blue, which means all of the carbon atoms are connected with one another at r = 3.6 Å. For clarity, we set the diagonal terms to 0.

Figure 6:

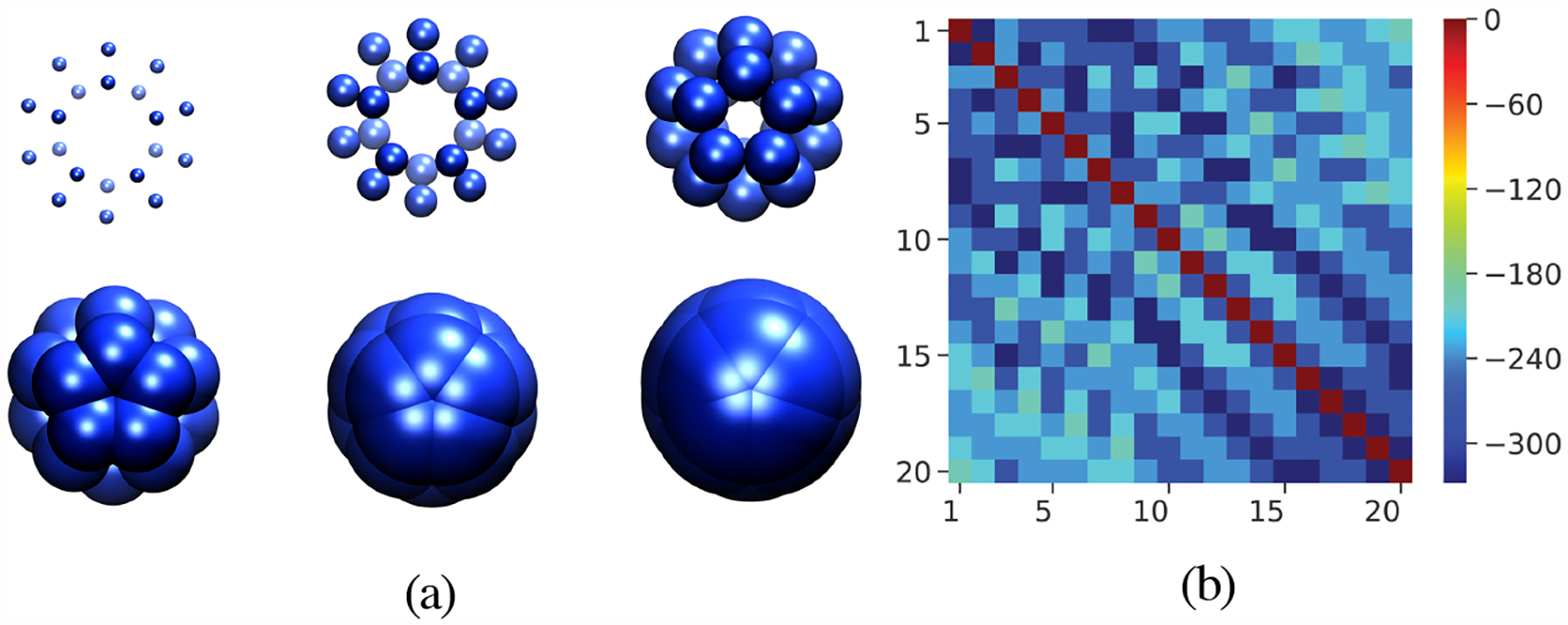
(a) Illustration of filtration built on fullerene C₂₀. Each carbon atom of C₂₀ is plotted by its given coordinates, which are associated with an ever-increasing radius r. The solid balls centered at given coordinates keep growing along with the radius filtration parameter. (b) The accumulated ${\mathcal{L}}_0^{r+0}$ matrix for C₂₀. For clarity, the diagonal terms are set to 0.

Figure 7:

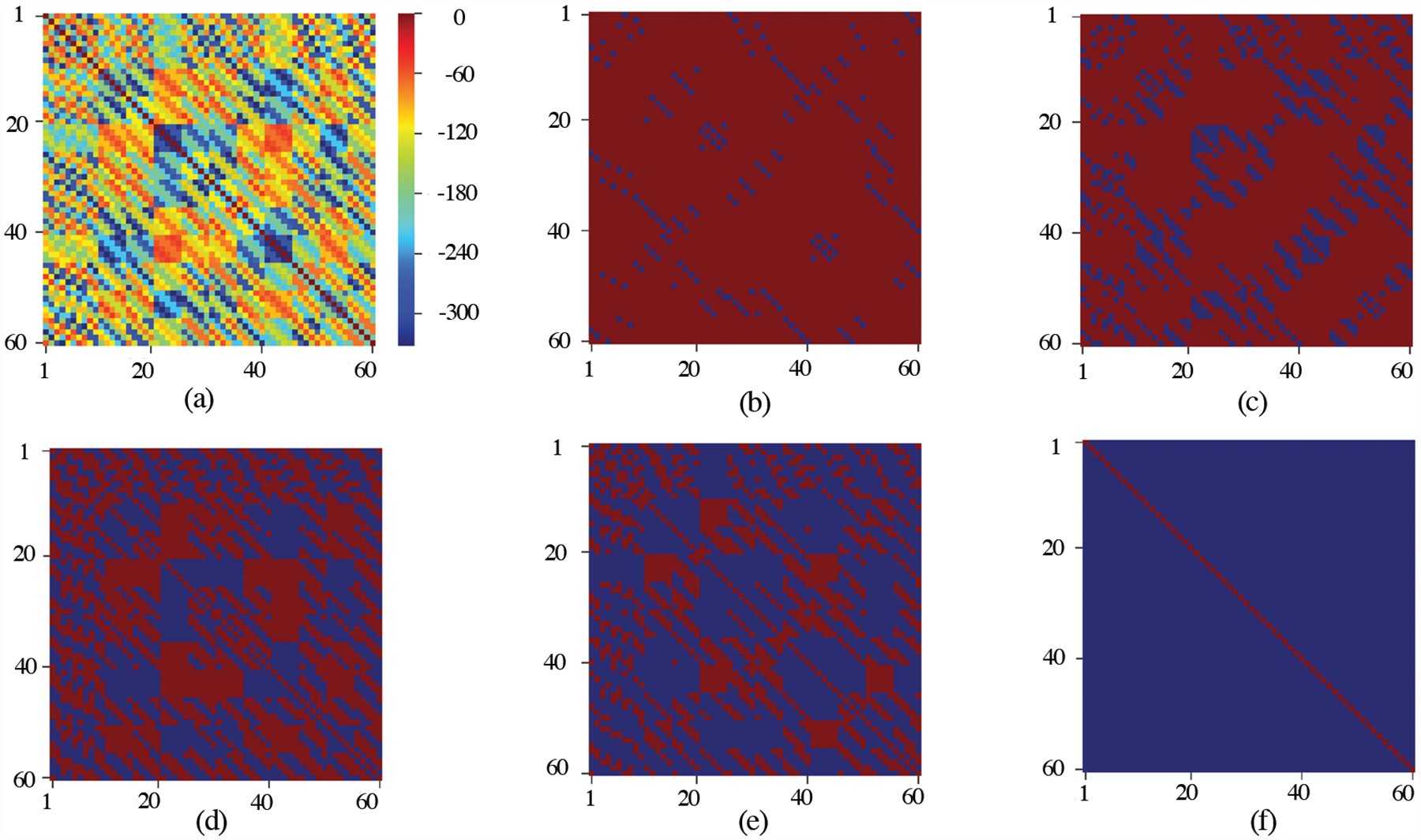
Illustration of persistent multiscale analysis of C₆₀ in terms of 0-combinatorial Laplacian matrices (b)-(f) and their accumulated matrix (a) induced by filtration. As the value of filtration parameter r increases, high-dimensional simplicial complex forms and grows accordingly. (b), (c), (d), (e), and (f) demonstrate the 0-combinatorial Laplacian matrices (i.e., the connectivity among C₆₀ atoms) at filtration r = 1.0 Å, 1.5 Å, 2.5 Å, 3.0 Å, and 3.6 Å, respectively. The blue cell located at the ith row and jth column represents the balls centered at atom i and atom j connected with each other. For clarity, the diagonal terms are set to 0 in all plots.

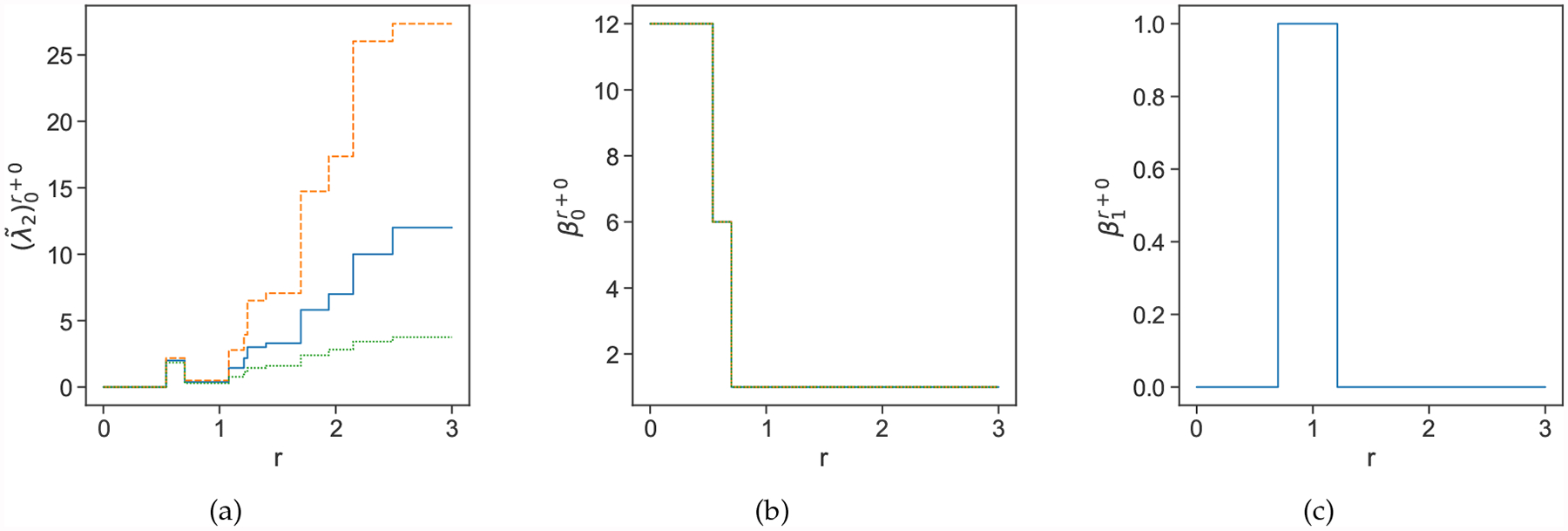
In Figure 8, the blue solid line represents C₂₀ properties and the dash orange line represents C₆₀ properties. For Figure 8(a), the blue line drops at r = 0.72 Å, which means the bond length of C₂₀ is around 1.44 Å. The orange line drops at r = 0.68 Å and 0.72 Å, which means the “double bond” length of C₆₀ is around 1.36 Å and the 6 : 5 bond length is around 1.44 Å. Moreover, the total number of “double bond” is 30, yielding ${\beta }_0^{r+0}=30$ when the radius of solid balls is over 0.68 Å. In conclusion, one can deduce the number of different types of bonds as well as the bond length information from the number of zero eigenvalues (i.e., ${\beta }_0^{r+0}$) under the radius filtration. Furthermore, the geometric information can also be derived from the plot of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$. Each jump in Figure 8(d) at a specific radius represents the change of geometric and topological structure. The smallest non-zero eigenvalue ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ of ${\mathcal{L}}_0^{r+0}$ matrices for C₂₀ changes 5 times in Figure 8(d), which means C₂₀ has 5 different distances between carbon atoms. Furthermore, by Remark 2.1, as ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ of C₂₀ keeps increasing, the smallest vertex connectivity of the connected subgraph continues growing and the topological structure becomes steady. As can be seen in the right-corner chart of Figure 6, the carbon atoms will finally grow to a solid object with a steady topological structure.

Figure 8:

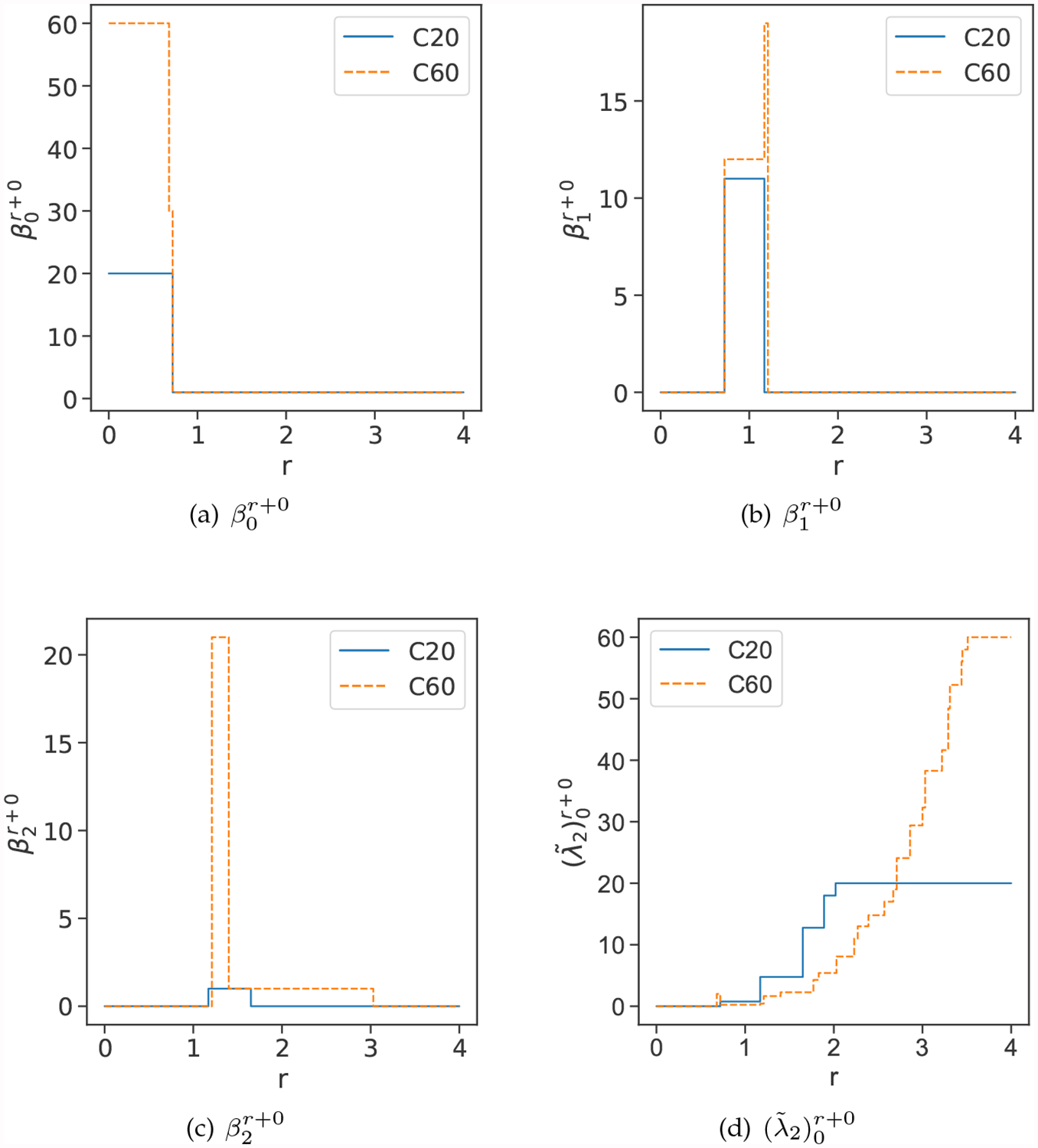
Illustration of persistent spectral analysis of C₂₀ and C₆₀ using the spectra of ${\mathcal{L}}_q^{r+0}$ (q = 1, 2 and 3). (a) The number of zero eigenvalues of ${\mathcal{L}}_0^{r+0}$, i.e., ${\beta }_0^{r+0}$, under radius filtration. (b) The number of zero eigenvalues of ${\mathcal{L}}_1^{r+0}$, i.e., ${\beta }_1^{r+0}$ under radius filtration. (c) The number of zero eigenvalues of ${\mathcal{L}}_2^{r+0}$, i.e., ${\beta }_2^{r+0}$ under radius filtration. (d) The smallest non-zero eigenvalue ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ under radius filtration. The radius grid spacing is 0.01 Å.

Figure 8(b) depicts the changes of Betti 1 value ${\beta }_1^{r+0}$ (i.e., the number of zero eigenvalues for ${\mathcal{L}}_1^{r+0}$) under the filtration r. Since C₂₀ has 12 pentagonal rings, ${\beta }_1^{r+0}$ jumps to 11 when radius r equals to the half of the bond length of l(C₂₀). These eleven 1-cycles disappear at r = 1.17 Å. There are 12 pentagons and 20 hexagons in C₆₀, which results in ${\beta }_1^{r+0}=12$ at r = 0.72 Å, ${\beta }_1^{r+0}=31$ at r = 1.17 Å. All of the pentagons and hexagons disappear at r = 1.22 Å.

As the filtration process, even more structure information can be derived from the number of zero eigenvalues of ${\mathcal{L}}_2^{r+0}$ in Figure 8(c). For C₂₀, ${\beta }_2^{r+0}$ when r = 1.17 Å, which corresponds to the void structure in the center of the dodecahedral cage. The void disappears at r = 1.65 Å since a solid structure is generated at this point. For fullerene C₆₀, 20 hexagonal cavities and a center void exist from 1.12 Å to 1.40 Å yielding ${\beta }_2^{r+0}=21$. As the filtration goes, hexagonal cavities disappear which results ${\beta }_2^{r+0}$ decrease to 1. The central void keeps alive until a solid block is formed at r = 3.03 Å. In a nutshell, we can deduce the number of different types of bonds, the bond length, and the topological invariants from the present persistent spectral analysis.

3.1.2. Persistent spectral predictions of fullerene stability using both harmonic and non-harmonic spectra

Having shown that the detailed fullerene structural information can be extracted into the spectra of ${\mathcal{L}}_q^{r+0}$, we further illustrate that fullerene functions can be predicted from their structures by using our persistent spectral theory in this section. Similar structure-function analysis has been carried out by using other methods [24, 33, 44]. For small fullerene molecule series C₂₀ to C₆₀, with the increase in the number of atoms, the ground-state heat of formation energies decrease [45, 46]. The left chart in Figure 9 describes this phenomenon. Similar patterns can also be found in the total energy (STO-3G/SCF at MM3) per atom and the average binding energy of C_2n. To analyze these patterns, many theories have been proposed. Isolated pentagon rule assumes that the most stable fullerene molecules are those in which all the pentagons are isolated. Zhang et al. [46] stated that fullerene stability is related to the ratio between the number of pentagons and the number of carbon atoms. Xia and Wei [44] proposed that the stability of fullerene depends on the average number of hexagons per atom. However, these theories all focused on the pentagon and hexagon information. More specifically, they use purely topological information to reveal the stability of fullerene. In contrast, we believe that both harmonic persistent spectra and non-harmonic persistent spectra can be used model the structure-function relationship of fullerenes. We hypothesize that the non-harmonic persistent spectra of ${\mathcal{L}}_0^{r+0}$ matrices are powerful enough to model the stability of fullerene molecules. To verify our hypothesis, we compute the summation, mean, maximal, standard deviation, variance of its eigenvalues, and ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ of the persistent spectra of ${\mathcal{L}}_0^{r+0}$ over various filtration radii r. We depict a plot with the horizontal axis represents radius r and the vertical axis represents the particular spectrum value, which is actually the same as Figure 8. Then we define the area under the plot of spectra with a negative sign as

$$A_{\alpha }=-\sum _{i=1}{\Lambda }_i^{\alpha }\delta r,$$ (35)

where δr is the radius grid spacing, in Figure 8, δr = 0.01 Å. Here, α = Sum, Avg, Max, Std, Var, Sec is the type index and thus, ${\Lambda }_i^{\alpha }$ represent the summation, mean, maximal, standard deviation, variance, and the smallest non-zero eigenvalue ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ of ${\mathcal{L}}_0^{r+0}$ at i-th radius step, respectively. The right chart in Figure 9 describes the area under the plot of spectra and closely resembles that of the heat of formation energy. We can see that generally the left chart and the middle chart show the same pattern. The integration of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$ decreases as the number of carbon atoms increases. However, the structural data we used might not be the same ground-state data as in Ref. [46], which results in C₃₆ do not match the corresponding energy perfectly. Limited by the availability of the ground-state structural data, we are not able to analyze the full set of the fullerene family.

Figure 9:

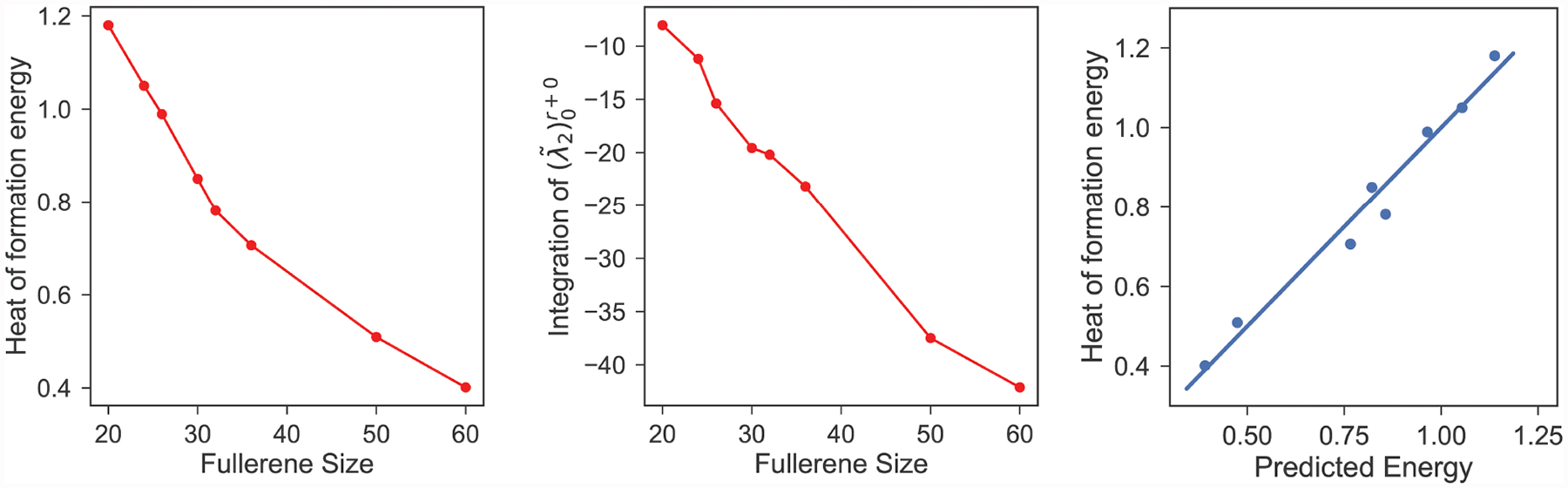
Persistent spectral analysis and prediction of fullerene heat formation energies. Left chart: the heat of formation energies of fullerenes obtained from quantum calculations [46]. Middle chart: PST model using the area under the plot of ${\left({\tilde{\lambda }}_2\right)}_0^{r+0}$. Right chart: Correlation between the quantum calculation and the PST prediction using non-topological spectral analysis (α = Max).

As the present persistent spectral method provides both topological (i.e., harmonic) and non-topological spectral analyses, we are interested in a further comparison of their performances. For the topological spectral analysis, we adopt the model of Xia and Wei [44], which is based in the atom number averaged Betti-2 length for the cavity. The Betti 2 length for the cavity is the longest persistence of ${\beta }_2^{r+0}$ (i.e., the number of zero eigenvalues for ${\mathcal{L}}_2^{r+0}$ under the filtration r. Table 5 presents the predictions obtained from both topological spectral analysis and non-topological spectral analysis. The right chart of Figure 9 plots the correlations between predicted energies and the heat of formation energy of the fullerene molecules computed from quantum mechanics [46]. Clearly, both methods provide very accurate predictions.

Table 5:

The heat of formation energy of fullerenes [46] and its corresponding energies predicted non-harmonic spectral model (α = Max) and harmonic spectral model. The unit is EV/atom.

Fullerene type	C20	C24	C26	C30	C32	C36	C50	C60
Heat of formation energy	1.180	1.050	0.989	0.850	0.781	0.706	0.509	0.401
Non-harmonic spectral energy	1.138	1.050	0.964	0.821	0.857	0.766	0.474	0.391
Harmonic spectral energy	1.224	0.962	0.929	0.861	0.825	0.737	0.564	0.364

To quantitatively validate our model, we apply one of the simplest machine learning algorithms, linear least-squares method, to predict the heat of formation energy. The Pearson correlation coefficient for the α-th method is defined as

$$C_c^{\alpha }=\frac{\sum _{k=1}^N\left(A_{\alpha }^k-{\overline{A}}_{\alpha }\right)\left(E_k-\overline{E}\right)}{{\left[\sum _{k=1}^N{\left(A_{\alpha }^k-{\overline{A}}_{\alpha }\right)}^2\sum _{k=1}^N{\left(E_k-\overline{E}\right)}^2\right]}^{\frac{1}{2}}}$$ (36)

where $A_{\alpha }^k$ represents the theoretically predicted energy of the k-th fullerene molecule, E_k represents the heat of formation energy of the k-th fullerene molecule, and ${\overline{A}}_{\alpha }$ and $\overline{E}$ are the corresponding mean values.

Table 6 lists the correlation coefficient under different type index α and harmonic spectral information of ${\mathcal{L}}_2^{r+0}$. The highest correlation coefficient is close to unity (0.986) obtained with α = Max. The lowest correlation coefficient is 0.942 with α = Sum. We can see that all the correlation coefficients are close to unity, which verifies our hypothesis that the non-harmonic spectra of ${\mathcal{L}}_0^{r+0}$ have the capacity of modeling the stability of fullerene molecules. The performance of the topological spectra is on a bar with that of the best of the non-harmonic spectra. Obvious, our persistent harmonic spectral information and persistent non-harmonic spectral information could be trivially combined in the present machine learning setting to achieve an even higher accuracy. Therefore, our persistent spectral theory works extremely well only with both harmonic and non-harmonic spectra, which means our persistent spectral theory is a powerful tool for quantitative data analysis and prediction.

Table 6:

The correlation coefficients for predictions using different type of statistics of non-harmonic spectra and topological spectra (Top).

Type index	Sum	Avg	Max	Std	Var	Sec	Top
Correlation coefficient	0.942	0.985	0.986	0.969	0.977	0.981	0.979

3.2. Protein flexibility analysis

As clarified earlier, the number of zero eigenvalues of p-persistent q-Laplacian matrix (p-persistent qth Betti number) can also be derived from persistent homology. Persistent homology has been used to model fullerene stability [44]. In this section, we further illustrate the applicability of present persistent spectral theory by a case that non-harmonic persistent spectra offer a unique theoretical model whereas it may be difficult to come up with a suitable persistent homology model for this problem. To this end, we consider a challenging biophysical problem for which current methods do not work well.

The protein flexibility is known to correlate with a wide variety of protein functions. It can be modeled by the beta factors or B-factors, which are also called Debye-Waller factors. B-factors are a measure of the atomic mean-square displacement or uncertainty in the X-ray scattering structure determination. Therefore, understanding the protein structure, flexibility, and function via the accurate protein B-factor prediction is a vital task in computational biophysics [48]. Over the past few years, quite many methods are developed to predict protein B-factors, such as GNM [30], ANM [31], FRI [49, 50] and MWCG [34, 48]. However, all of the aforementioned methods are based on a particular matrix derived from the graph network which is constructed using alpha carbon as nodes and connections between nodes as edges. In this section, we apply our persistent spectral theory to create richer geometric information in B-factor prediction. In particular, we are interested in the prediction of B-factors for which the standard GNM fails to work.

To illustrate our method, we consider a protein whose total number of residues is N. In this work, we employ the coarse-grained C_α representation. Similarly, like in the previous application of fullerene structure analysis, we treat each C_α atom as a 0-simplex at the initial setup and assign it a solid ball with a radius of r. By varying the filtration parameter r, we can obtain a family of ${\mathcal{L}}_0^{r+0}$. For each matrix ${\mathcal{L}}_0^{r+0}$, its corresponding ordered spectrum is given by

$${\left({\lambda }_1\right)}_0^{r+0},{\left({\lambda }_2\right)}_0^{r+0},\cdots ,{\left({\lambda }_N\right)}_0^{r+0}.$$

Suppose the number of zero eigenvalues is m, then, we have ${\beta }_0^{r+0}=m$. Since ${\mathcal{L}}_0^{r+0}$ is symmetric, then eigenvectors of ${\mathcal{L}}_0^{r+0}$ corresponding to different eigenvalues must be orthogonal to each other. The Moore-Penrose inverse of ${\mathcal{L}}_0^{r+0}$ can be calculated by the non-harmonic spectra of ${\mathcal{L}}_0^{r+0}$:

$${\left({\mathcal{L}}_0^{r+0}\right)}^{-1}=\sum _{k=m+1}^N\frac{1}{{\left({\lambda }_k\right)}_0^{r+0}}\left[{\left(u_k\right)}_0^{r+0}{\left({\left(u_k\right)}_0^{r+0}\right)}^T\right],$$

where T is the transpose and ${\left(u_k\right)}_0^{r+0}$ is the kth eigenvector of ${\mathcal{L}}_0^{r+0}$. The modeling of ith B-factor at filtration parameter r can be expressed as

$$B_i^r={\left({\mathcal{L}}_0^{r+0}\right)}_{ii}^{-1},\forall i=1,2,\cdots ,N,$$

and the final model of ith B-factor is given by

$$B_i^{\text{PST}}=\sum _r{w}_r{B}_i^r+w_0,\forall i=1,2,\cdots ,N,$$

where w_r and w₀ are fitting parameters which can be determined from a simple machine learning algorithm, the linear regression, using B-factors from experimental data B^Exp. ³ In this application, we consider the filtration radius from 2 to 6 with the grid spacing of 0.5 and grid spacing of 2 from 6 to 26, then totally 20 different ${\mathcal{L}}_0^{r+0}$ are created at r = 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, and 26. By calculating all the non-harmonic spectra together with their eigenvectors, 20 Moore-Penrose inverse matrices ${\left({\mathcal{L}}_0^{r+0}\right)}^{-1}$ are constructed.

Park et al have carried out the B-factor prediction of small-, medium- and large-sized proteins using GNM and NMA [51]. We collect a total of fifteen medium-sized or large-sized proteins for which the Pearson correlation coefficient of GNM prediction is less than 0.4 reported in an earlier study [51]. Figure 10 plots the flexibility of 1V70 with red color represents for the most flexible regions (the highest B-factor). Obviously, B-factors predicted by PST are very similar to experimental values, whereas GNM predictions differ dramatically from experimental B-factors. This situation can also be seen from Figure 11 where B-factors predicted by PST and GNM are compared with those of experimental results. GNM fail to work for 1V70, 1R7J, and 2FQ3. The Pearson correlation coefficients of GNM, NMA, and PST are compared in Table 7. This study shows that the proposed PST has a great potential in multiscale biophysical modeling and prediction.

Figure 10:

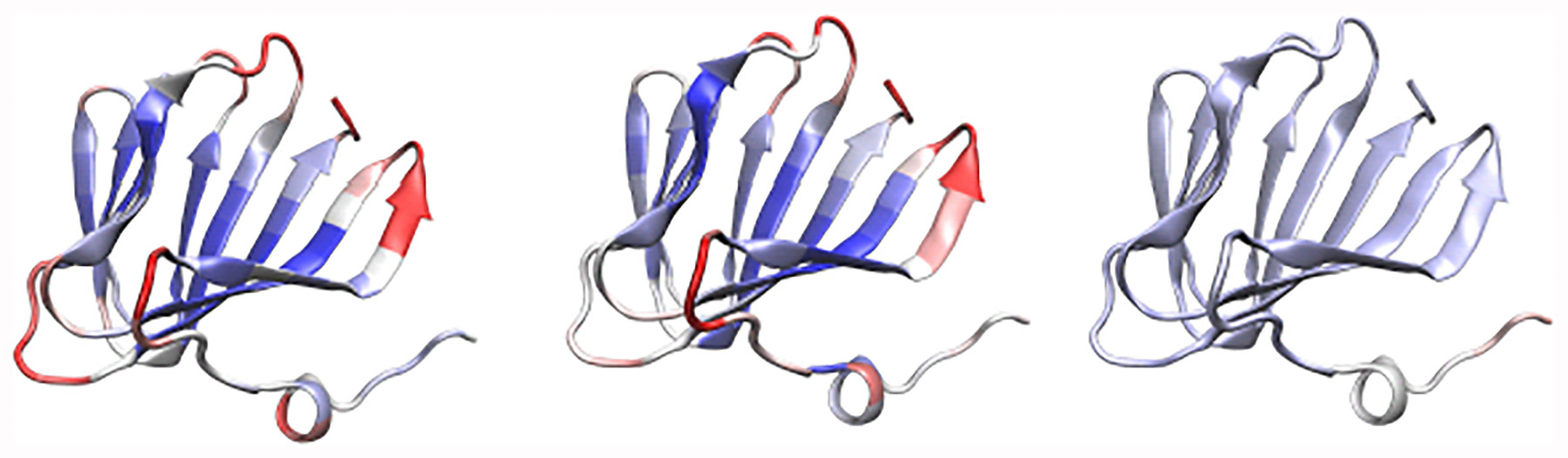
Comparison of protein B-factors obtained by experiment (Left chart), PST (Middle chart), and GNM (Right chart) for protein PDB ID: 1V70, visualized in Visual Molecular Dynamics (VMD) [47]. Red color represents for the most flexible regions.

Figure 11:

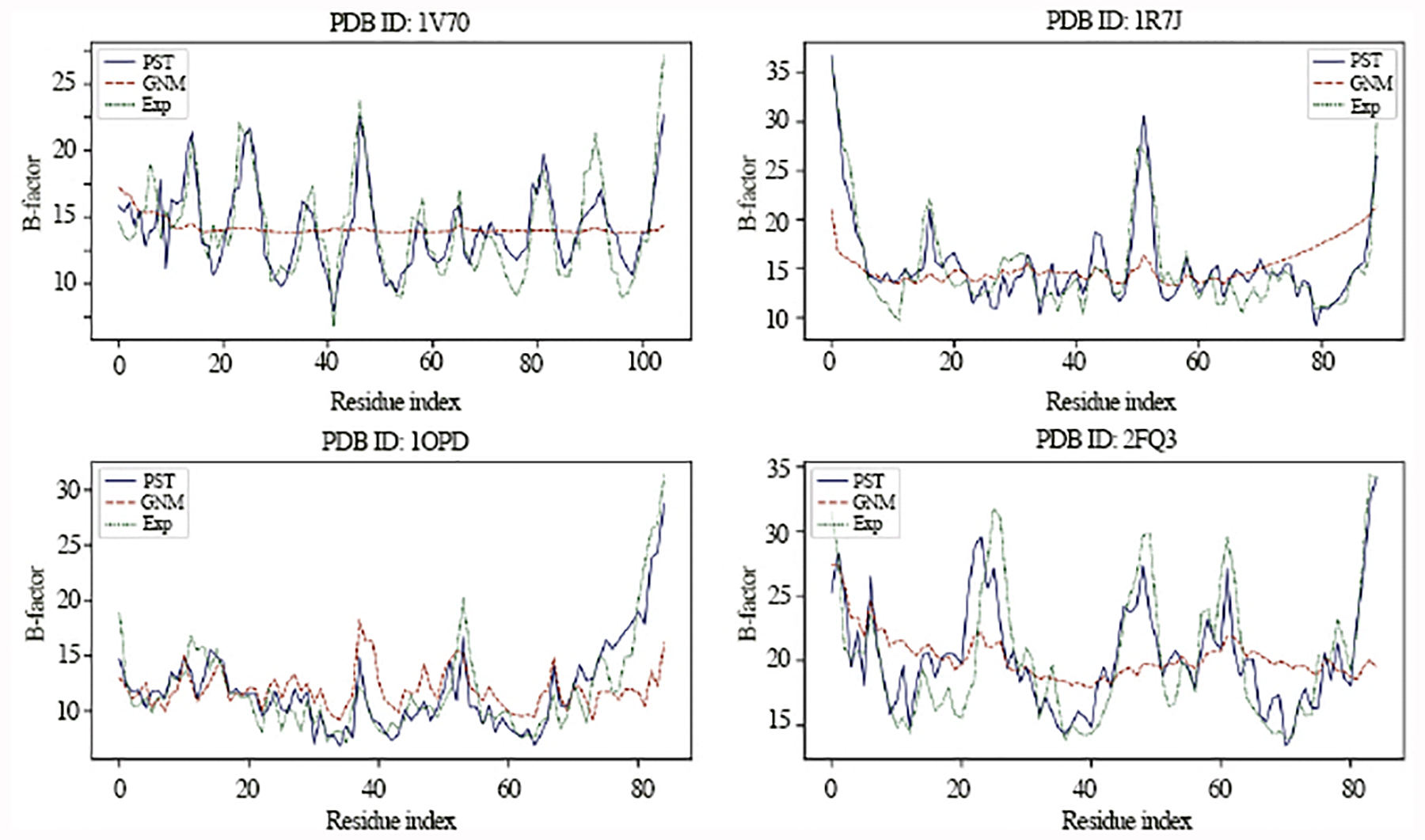
Comparison of experimental B-factors (Exp) and those predicted by PST and GNM for proteins 1V70, 1R7J, 1OPD, and 2FQ3.

Table 7:

Pearson correlation coefficients in B-factor predictions using GNM, NMA, and PST for a group of proteins that are very challenging to GNM. Pearson correlation coefficients for GNM and NMA are extracted from Ref. [51].

PDB ID	GNM	NMA	PST
1OPD	0.398	0.372	0.886
2PKT	−0.286	−0.245	0.745
2FQ3	0.384	0.609	0.808
1R7J	0.368	0.400	0.908
1W2L	0.397	0.130	0.808
5CYT	0.331	0.248	0.624
1V70	0.162	0.265	0.826
1CCR	0.351	0.379	0.708
2VIM	0.212	0.243	0.535
2CG7	0.379	0.355	0.780
1QTO	0.334	0.672	0.853
1WHI	0.270	0.492	0.612
1NKO	0.368	0.583	0.770
1O08	0.309	0.281	0.811
2HQK	0.348	0.715	0.808

4. Conclusion

Spectral graph theory is a powerful tool for data analysis due to its ability to extract geometric and topological information. However, its performance can be quite limited for various reasons. One of them is that the current spectral graph theory does not provide a multiscale analysis. Motivated by persistent homology and multiscale graphs, we introduce persistent spectral theory as a unified paradigm to unveil both topological persistence and geometric shape from high-dimensional datasets.

For a point set $V\subset {ℝ}^n$ without additional structures, we construct a filtration using an (n − 1)-sphere of a varying radius r centered at each point. A series of persistent combinatorial Laplacian matrices are induced by the filtration. It is noted that our harmonic persistent spectra (i.e., zero eigenvalues) fully recover the persistent barcode or persistent diagram of persistent homology. Specifically, the numbers of zero eigenvalues of persistent q-combinatorial Laplacian matrices are the q-dimensional persistent Betti numbers for the same filtration given filtration. However, additional valuable spectral information is generated from the non-harmonic persistent spectra. In this work, in addition to persistent Betti numbers and the smallest nonzero eigenvalues, five statistic values, namely, sum, mean, maximum, standard deviation, and variance, are also constructed for data analysis. We use a few simple two-dimensional (2D) and three-dimensional (3D) structures to carry out the proof of principle analysis of the persistent spectral theory. The detailed structural information can be incorporated into the persistent spectra of. For instant, for the benzene molecule, the approximate C-C bond and C-H bond length can be intuitively read from the plot of the 0-dimensional persistent Betti numbers. Moreover, persistent spectral theory also has the capacity to accurately predict the heat of formation energy of small fullerene molecules. We use the area under the plot of the persistent spectra to model fullerene stability and apply the linear least-squares method to fit our prediction with the heat of formation energy. The resulting correlation coefficient is close to 1, which shows that our persistent spectral theory has an excellent performance on molecular data. Furthermore, we have applied our persistent spectral theory to the protein B-factor prediction. In this case, persistent homology does not offer a straightforward model. We consider a set of 15 challenging proteins for which the most popular biophysical method, Gaussian network model (GNM), fails to work [51]. We show that the additional non-harmonic persistent spectral information provides extremely successful B-factor predictions to this set of challenging proteins.

It is pointed out that the proposed persistent spectral analysis can be paired with advanced machine learning algorithms, including various deep learning methods, for a wide variety of applications in data science. In particular, the further construction of element-specific persistent spectral theory and its application to protein-ligand binding affinity prediction and computer-aided drug design will be reported elsewhere.