Beyond the Michaelis‐Menten: Accurate Prediction of In Vivo Hepatic Clearance for Drugs With Low K _M

Abstract

Clearance (CL) is the major pharmacokinetic parameter for evaluating systemic exposure of drugs in the body and, thus, for developing new drugs. To predict in vivo CL, the ratio between the maximal rate of metabolism and Michaelis‐Menten constant (V _max/K _M estimated from in vitro metabolism study has been widely used. This canonical approach is based on the Michaelis‐Menten equation, which is valid only when the K _M value of a drug is much higher than the hepatic concentration of the enzymes, especially cytochrome P450, involved in its metabolism. Here, we find that such a condition does not hold for many drugs with low K _M, and, thus, the canonical approach leads to considerable error. Importantly, we propose an alternative approach, which incorporates the saturation of drug metabolism when concentration of the enzymes is not sufficiently lower than K _M. This new approach dramatically improves the accuracy of prediction for in vivo CL of high‐affinity drugs with low K _M. This indicates that the proposed approach in this study, rather than the canonical approach, should be used to predict in vivo hepatic CL for high‐affinity drugs, such as midazolam and propafenone.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

☑ For over half a century, in vivo intrinsic drug clearance (CL) has been predicted by simply scaling the in vitro intrinsic drug CL, that is, the ratio between maximal rate of metabolism and Michaelis‐Menten constant (V _max/K _M).

• WHAT QUESTION DID THIS STUDY ADDRESS?

☑ The canonical approach works only when hepatic enzyme concentration is sufficiently lower than the K _M of the drug. We find that such a condition does not hold for drugs with low K _M, and, thus, the canonical approach leads to considerable error in predicting in vivo CL.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

☑ We propose a new approach, which incorporates the saturation of the metabolism rate at high enzyme concentrations. This accurately predicts the intrinsic in vivo CL of high affinity drugs from V _max and K _M estimated with in vitro experiments.

• HOW MIGHT THIS CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE?

☑ The approach proposed in this work improves the accuracy and precision of human hepatic CL prediction using in vitro experiments, which is critical for drug development.

Drug clearance (CL), which has been studied in > 65,000 publications, ¹ is the primary pharmacokinetic (PK) parameter for predicting human systemic drug disposition. ² To predict in vivo hepatic CL (CL_h) from in vitro metabolism studies, well‐stirred, parallel tube, or dispersion liver models have been widely used, which commonly require the estimation of intrinsic CL in the liver. ³ The intrinsic CL_h of a drug has been predicted by scaling the ratio between the maximal rate of metabolism and Michaelis‐Menten constant (i.e., V _max/K _M) estimated from in vitro study using human liver microsomes (HLMs) or hepatocytes. ⁴ This canonical approach assumes that in vivo drug metabolism is accurately captured by the Michaelis‐Menten (MM) equation, similar to in vitro drug metabolism. ⁴ , ⁵

The MM equation becomes inaccurate when a significant fraction of the drug binds to the enzyme. ⁶ , ⁷ , ⁸ To avoid this, the K _M value of the drug needs to be much larger than the hepatic concentration of the enzymes, especially cytochrome P450 (CYP), involved in its metabolism. ⁶ , ⁷ , ⁸ To the best our knowledge, the validity of this condition has not been systematically investigated. In this study, we find that the condition does not hold for many high‐affinity drugs with low K _M, including coumarin (CYP2A6), paclitaxel (CYP2C8), propafenone (CYP2D6), and midazolam (CYP3A4). Thus, under these circumstances, estimating their intrinsic CL_h using the canonical approach based on the MM equation results in considerable error. To resolve this problem, we propose an alternative to the canonical approach based on an enzyme kinetic equation, which is accurate over a much wider range of the ratio of K _M to enzyme concentration than the MM equation. ⁷ , ⁸ This new approach accurately predicts intrinsic CL_h for drugs regardless of the ratio of their K _M values to enzyme concentrations, which dramatically improves the accuracy and precision of in vitro‐in vivo extrapolation (IVIVE) for the CL_h.

Methods

Data collection

Drugs in Table 1 were selected and their K _M, V _max, and in vivo CL_h in Table 2 were obtained using the following criteria:

1. Selection of drug: We selected drugs whose metabolism by a specific major CYP isoform in the liver is the main excretion route for the selected drugs (Table 1 ). Thus, metabolism by other CYP enzymes and CL in other organs have small contributions to the drug CL. Furthermore, we selected drugs whose K _M is less than10·E _T, where E _T is the hepatic concentration of the major CYP isoform involved in drug metabolism. ET is estimated under the assumption that CYPs are evenly distributed in the liver is used (Table 1 ). If the estimated E _T increases considering the subcellular localization of CYPs in the liver (Supplementary Table S1 ), K _M/E _T would be less than 10 for a larger number of drugs than those in Table 1 .

2. K _M and V _max: To estimate the in vitro CL by the major CYP, in vitro K _M and V _max values of the majority of the drugs (Table 2 ) were obtained from previous studies where the values were estimated with product formation by HLM. However, as the values from the product formation study were not available for saquinavir, docetaxel, and valspodar, their K _M and V _max values were obtained from substrate depletion studies. In these in vitro experiment, $E_{\mathrm{T}}\ll K_{\mathrm{M}}$ so that using the MM leads to accurate estimation of K _M and V _max. ⁷

3. Estimation of in vivo CL_h: In vivo CL_h in Table 2 was estimated from total in vivo CL of drugs administered by an i.v. route, except for propafenone and indinavir. As their i.v. route has not been measured, in vivo CL of drugs administrated by an oral route was used. When extrahepatic CL is known, we excluded it from total in vivo CL to estimate in vivo CL_h:

   • For paclitaxel, cyclosporine, midazolam, cabazitaxel, indinavir, and felodipine, we subtracted the estimated renal and/or bile elimination rate of their unchanged forms from their total in vivo CL.

   • For docetaxel, the fraction of its hydroxylated metabolite in the bile, the major elimination pathway, is multiplied to total in vivo CL.

   • For saquinavir, the fraction of its hydroxylated metabolite in systemic circulation is multiplied to total in vivo CL.

Table 1.

Estimated ${\text{CL}}_{\text{int}}^{\text{liver}}$ using the canonical and new approaches

Drugs a	K M (µM) b	Vmax (pmol∙min−1∙pmol CYP−1) c , d	Major CYP	CYP abundance in HLM (pmol/mg)	${\tilde{E}}_{\mathrm{T}}$ (µmol) c,d	E T (µM) e	${\text{CL}}_{\text{int}}^{\text{liver}}$ (mL/min)
							Canonical f	New g
Coumarin	0.75	39.2	2A6	30.7 ~ 56.2 9 , 22	1.77 ~ 5.31	1.03 ~ 3.10	92,457 ~ 277,683	38,924 ~ 54,122
Paclitaxel	5.5	4.64	2C8	26.9 ~ 43.0 9 , 22	1.55 ~ 4.06	0.90 ~ 2.37	1,308 ~ 3,429	1,123 ~ 2,396
Propafenone	0.12	4.83	2D6	9.34 ~ 17.2 11 , 22	0.54 ~ 1.63	0.31 ~ 0.95	21,626 ~ 65,339	5,982 ~ 7,340
Midazolam	1.6	24.4	3A4	32.6 ~ 60.4 11 , 22	1.88 ~ 5.71	1.10 ~ 3.33	28,630 ~ 87,025	16,995 ~ 28,246
Indinavir	2.31	9.28					7,535 ~ 22,905	5,112 ~ 9,382
Cyclosporine	5	4.44					1,666 ~ 5,063	1,366 ~ 3,039
Saquinavir	0.61	40.4					124,247 ~ 377,671	44,443 ~ 58,479
Cabazitaxel	2.1	9.5					8,499 ~ 25,835	5,586 ~ 9,992
Docetaxel	1.1	0.20					348 ~ 1,059	175 ~ 263
Valspodar	1.3	2.49					3,588 ~ 10,906	1,947 ~ 3,062
Felodipine	2.81	36.2					24,156 ~ 73,427	17,381 ~ 33,606

${\text{CL}}_{\text{int}}^{\text{liver}}$, intrinsic clearance of the liver; HLM, human liver microsome; K _M, Michaelis‐Menten constant; V _max, maximal rate of metabolism.

^aSee Methods for the criteria for the drug selections.

^bSee Supplementary Excel File for references of K _M and V _max values.

^cObtained by dividing the measured rate per mg of the microsomes by the rate per pmol CYP with mean population abundance of CYP (pmol/mg): CYP2A6 (45.37), CYP2C8 (32.30), CYP2D6 (13.26), and CYP3A4 (45.07). ⁹ , ¹⁰ , ¹¹ , ²²

^dThe hepatic CYP amount is estimated by multiplying CYP abundance in HLM (pmol/mg) by MPPGL and liver weight (see Methods for details).

^eThe hepatic CYP concentration is estimated based on the assumption that CYPs are evenly distributed (see Methods for details).

^fCanonical ${\text{CL}}_{\text{int}}^{\text{liver}}=\frac{V_{max}}{K_{\mathrm{M}}}·{\tilde{E}}_{\mathrm{T}}$.

^gNew ${\text{CL}}_{\text{int}}^{\text{liver}}=\frac{V_{max}}{K_{\mathrm{M}}+E_{\mathrm{T}}}·{\tilde{E}}_{\mathrm{T}}=\text{Canonical}{\text{CL}}_{\text{int}}^{\text{liver}}·\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}$. See Supplementary Excel File for detailed calculation.

Table 2.

Predicted CL_h using the canonical and new approaches and measured in vivo CL_h

Drugs	Major CYP	f u‐blood a	f u‐mic a	Predicted CLh (mL/min)							In vivo ${\text{CL}}_{\mathrm{h}}$ (mL/min) a , c
				Dispersion model		Well‐stirred model			Parallel tube model
				Canonical	New		Canonical	New	Canonical	New
Coumarin	2A6	0.02	0.99 b	971 ~ 1,357	547 ~ 718		814 ~ 1,151	508 ~ 622	1,048 ~ 1,418	606 ~ 765	625
Paclitaxel	2C8	0.12	0.66	215 ~ 484	187 ~ 364		204 ~ 436	179 ~ 335	219 ~ 507	190 ~ 376	141
Propafenone	2D6	0.06	0.26	1,329 ~ 1,444	822 ~ 919		1,119 ~ 1,320	701 ~ 775	1,400 ~ 1,449	881 ~ 990	400
Midazolam	3A4	0.07	0.54	1,260 ~ 1,436	1,060 ~ 1,256		1,050 ~ 1,288	884 ~ 1,046	1,345 ~ 1,449	1,146 ~ 1,341	429
Indinavir		0.40	0.97	1,190 ~ 1,425	1,028 ~ 1,264		988 ~ 1,256	859 ~ 1,054	1,279 ~ 1,447	1,111 ~ 1,349	624
Cyclosporine		0.07	0.37	281 ~ 669	236 ~ 462		263 ~ 584	223 ~ 418	288 ~ 711	241 ~ 482	209
Saquinavir		0.02	0.58	1,292 ~ 1,440	876 ~ 1,005		1,081 ~ 1,303	742 ~ 841	1,372 ~ 1,449	942 ~ 1,085	452
Cabazitaxel		0.1	0.42 b	1,051 ~ 1,389	855 ~ 1,120		876 ~ 1,193	726 ~ 931	1,135 ~ 1,435	919 ~ 1,209	790
Docetaxel		0.07	0.01 b	1,286 ~ 1,440	1,024 ~ 1,194		1,075 ~ 1,300	855 ~ 991	1,367 ~ 1,449	1,106 ~ 1,283	504
Valspodar		0.02	0.07 b	721 ~ 1,215	467 ~ 650		624 ~ 1,010	422 ~ 568	769 ~ 1,304	488 ~ 689	182
Felodipine		0.01	0.08	1,179 ~ 1,423	1,042 ~ 1,289		979 ~ 1,251	869 ~ 1,077	1,269 ~ 1,446	1,125 ~ 1,369	829

CL_h, hepatic clearance; f _u‐blood, drugs unbound fraction in blood; f _u‐mic, drugs unbound fraction in microsome.

^aSee Supplementary Excel File for references of f _u‐blood, f _u‐mic and in vivo ${\text{CL}}_{\mathrm{h}}$.

^b f _u‐mic of coumarin, cabazitaxel, docetaxel, and valspodar were estimated using this equation, $\frac{1}{C\times {10}^{0.56\log P/D-1.41}+1}$ as they have not been measured. ¹⁷ Microsomal protein concentrations (C) for coumarin, cabazitaxel, docetaxel, and valspodar were 0.03, 0.5, 1, and 1 mg/mL, respectively. Log P = 1.39 for coumarin and Log D _7.4 = 3.3 for cabazitaxel were calculated using ACD/Labs Percepta Platform—PhysChem Module. Log D _7.4 = 6.5 and 4.5 for docetaxel and valspodar were referenced by Bu, 2006.

^cSee Methods and Supplementary Excel File for detailed derivation of in vivo CL_h.

As the extrahepatic CL of valspodar is unknown, total in vivo CL was used as in vivo CL_h. Furthermore, as coumarin and propafenone have multiple metabolism pathways, we used the CL by a specific CYP as in vivo CL_h: for propafenone, CL from the parent to metabolite (5‐OH propafenone) by CYP2D6 and for coumarin, CL from the parent to metabolite (7‐OH coumarin) by CYP2A6.

Estimation of CYP concentration in a whole human liver

The CYP concentration in a whole human liver (${\text{CYP}}_{\text{conc}.}^{\text{liver}}$; Table 1 ) is estimated using the following equations under the assumption that CYP is evenly distributed in the liver:

$$\begin{array}{cc}{\text{CYP}}_{\text{conc}.}^{\text{liver}}(\mathrm{\mu }\mathrm{M})\hfill & =\frac{\text{CYP}\text{amount}}{\text{liver}\text{volume}}\hfill \\ \hfill & =\frac{\text{CYP}\text{abundance}\times \text{MPPGL}\times \text{liver}\text{weight}}{\text{liver}\text{volume}}\hfill \end{array}$$

CYP abundance (pmol/mg) is the amount of CYP enzyme per mg microsomal protein, which is obtained from published data. ⁹ , ¹⁰ , ¹¹ Thirty‐two and 52.5 were used as the lowest and the highest microsomal protein per gram of liver (MPPGL). ¹² , ¹³ Liver weight and density are 1,800 g and 1.05 g/mL, respectively, ¹⁴ which led to the estimation of the liver volume as 1,800/1.05 ~ 1,714 mL.

Simulation and calculation

All the simulation was done using MATHEMATICA 11.0 (Wolfram Research, Champaign, IL). See Supplementary Excel File for the detailed calculation of both canonical and new IVIVE approaches.

Data availability

The datasets generated during and/or analyzed during the current study are available in the Supplementary Excel File .

Results

Detailed derivation of canonical IVIVE for ${\text{CL}}_{\text{int}}$

The MM equation has been used for over a century to describe the enzyme reaction between a single enzyme (e.g., CYP isoform) and a single substrate (e.g., free drug) ¹⁵ :

$$S+E\underset{{\mathrm{k}}_{\mathrm{b}}}{\stackrel{{\mathrm{k}}_{\mathrm{f}}}{⟷}}C\stackrel{k_{\text{cat}}}{\to }P+E$$ (1)

In this system, the free enzyme (E) reversibly binds with the substrate (S) to form the complex (C), and the complex irreversibly dissociates into the product (P) of metabolism and the free enzyme, where the total enzyme concentration, $E_{\mathrm{T}}\equiv C+E$ (µM), is conserved. $k_{\mathrm{f}}$ (µM⁻¹∙min⁻¹) and $k_{\mathrm{b}}$ (min⁻¹) are the forward and reverse rates of substrate binding to the enzyme, and $k_{\text{cat}}$ (min⁻¹) is the catalytic constant, which is the maximal product formation rate per enzyme. The enzyme kinetics (Eq. 1) can be described with a simplified MM model under a suitable condition ⁶ (see Supplementary Note for details):

$$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{k_{\text{cat}}{E}_{\mathrm{T}}S}{S+K_{\mathrm{M}}},$$ (2)

where $K_{\mathrm{M}}=\frac{k_{\mathrm{b}}+k_{\text{cat}}}{k_{\mathrm{f}}}$(µM) is the Michaelis‐Menten constant. When the initial substrate concentration ($S_{\mathrm{T}}$) is substituted into the above equation, the initial velocity of the metabolite formation (v) can be obtained, which is known as the MM equation:

$$v=\frac{k_{\text{cat}}{E}_{\mathrm{T}}{S}_{\mathrm{T}}}{S_{\mathrm{T}}+K_{\mathrm{M}}}.$$ (3)

By fitting the MM equation to the velocity data obtained from in vitro metabolism experiments, the values of $k_{\text{cat}}$ and $K_{\mathrm{M}}$ can be estimated. ¹⁶

In enzyme kinetic field, ${\mathrm{V}}_{\mathrm{m}ax}$ usually indicates the maximal rate of metabolic formation (i.e., $k_{\text{cat}}{E}_{\mathrm{T}}$ µM∙min⁻¹). On the other hand, in the drug metabolism field, ${\mathrm{V}}_{\mathrm{m}ax}$ normalized with pmol CYP or mg protein of the microsomes is commonly used. ¹⁷ That is, the ${\mathrm{V}}_{\mathrm{m}ax}$ value is reported per pmol CYP (i.e., pmol∙min⁻¹∙pmol⁻¹ CYP) when data are obtained using supersomes prepared from recombinant systems expressing human CYP. When HLM are used, it is reported per mg protein of the microsomes (i.e., pmol∙min⁻¹∙mg⁻¹). To convert the rate per mg protein of the microsomes to rate per pmol CYP, the CYP abundance in the HLM sample (pmol/mg) is required. However, as few studies of in vitro enzyme kinetics with HLM measure the CYP abundance in the sample, we use mean population abundance values for the conversion as has frequently been done in other studies. ¹⁷ Through the conversion, we use the unit of pmol∙min⁻¹∙pmol⁻¹ CYP for ${\mathrm{V}}_{\mathrm{m}ax}$ throughout the study. This allows us to replace $k_{\text{cat}}$ with the normalized ${\mathrm{V}}_{\mathrm{m}ax}$ in Eq. 2 and, thus, to follow the conventional notation of IVIVE as described below. Note that the estimation results obtained throughout this work do not change when the pmol∙min⁻¹∙mg⁻¹ is chosen for the unit of ${\mathrm{V}}_{\mathrm{m}ax}$ (see Supplementary Excel File ).

As therapeutic drug concentrations rarely reach their ${\mathrm{K}}_{\mathrm{M}}$ (i.e., $S\ll {\mathrm{K}}_{\mathrm{M}}$ and $S+K_{\mathrm{M}}\approx K_{\mathrm{M}}$, ¹⁸ Eq. 2 can be further simplified:

$$\frac{\mathrm{d}P}{\mathrm{d}t}=\frac{V_{max}{E}_{\mathrm{T}}S}{S+K_{\mathrm{M}}}\approx \frac{V_{max}{E}_{\mathrm{T}}S}{K_{\mathrm{M}}}={\text{CL}}_{\text{int}}^{\text{vitro}}{\mathrm{E}}_{\mathrm{T}}S,$$ (4)

which is referred to as the canonical model in this study. The ${\text{CL}}_{\text{int}}^{\text{vitro}}=\frac{V_{max}}{K_{\mathrm{M}}}$ (mL∙min⁻¹∙pmol⁻¹ CYP) is the intrinsic clearance per enzyme estimated with the in vitro metabolism experiment. This model predicts that the drug is metabolized exponentially with the rate of ${\text{CL}}_{\text{int}}^{\text{vitro}}{E}_{\mathrm{T}}$ (min⁻¹) for varying $E_{\mathrm{T}}$ (µM). This allows for the estimation of the intrinsic hepatic clearance with a simple scaling of $E_{\mathrm{T}}$ . Specifically, by multiplying ${\text{CL}}_{\text{int}}^{\text{vitro}}$ by the amount of hepatic CYP isoform ( ${\tilde{\mathrm{E}}}_{\mathrm{T}}$ (pmol)), the intrinsic hepatic clearance is predicted:

$${\text{CL}}_{\text{int}}^{\text{liver}}={\text{CL}}_{\text{int}}^{\text{vitro}}{\tilde{E}}_{\mathrm{T}}(\text{mL}/min),$$ (5)

where ${\tilde{E}}_{\mathrm{T}}$ can be estimated by multiplying the abundance of CYP (pmol/mg) by mg MPPGL and liver weight. ¹⁹ This is the canonical approach to extrapolate ${\text{CL}}_{\text{int}}^{\text{liver}}$ from ${\text{CL}}_{\text{int}}^{\text{vitro}}$ estimated with in vitro metabolic data. Note that the canonical approach (Eq. 5) assumes that in vivo drug metabolism can be described with the canonical model (Eq. 4) based on the MM model (Eq. 2), similar to in vitro metabolism.

The limitation of the canonical approach

In fact, the MM model (Eq. 2) is accurate under a limited condition when enzyme concentration is sufficiently low (i.e., $E_{\mathrm{T}}\ll K_{\mathrm{M}}+S$ ) that an insignificant fraction of substrate is bound to the enzyme and, thus, the metabolism rate is proportional to the concentration of enzyme. ⁷ , ²⁰ Because therapeutic drug concentrations (S) are typically much lower than $K_{\mathrm{M}}$ (i.e., $S\ll K_{\mathrm{M}})$ , ¹⁸ a much lower enzyme concentration than $K_{\mathrm{M}}$ (i.e., $E_{\mathrm{T}}\ll K_{\mathrm{M}}$ ) is required to use the canonical model (Eq. 4). This is why in vitro experiments have been performed using low concentrations of enzyme (~nM). ²¹

Does $E_{\mathrm{T}}\ll K_{\mathrm{M}}$ hold in the liver? To investigate this question, we first estimated hepatic concentrations of various CYP isoforms ( $E_{\mathrm{T}}$ ) (see Methods for details). To derive the concentration from the amount of hepatic CYP ( ${\tilde{E}}_{\mathrm{T}}$ ) we need to estimate the volume of CYP distribution (V). If CYP is evenly distributed in the whole liver, the volume of CYP distribution would be the liver volume, 1,714 mL. ¹⁴ For instance, the amount of CYP2D6 in the whole liver (i.e., abundance of CYP2D6 in HLM∙MPPGL∙liver weight) is ~0.54–1.63 µmol (Table 1 ). By dividing this with 1,714 mL, we can estimate that the hepatic concentration of CYP2D6 would be ~ 0.31–0.95 µM (Table 1 ).

Surprisingly, $E_{\mathrm{T}}\ll K_{\mathrm{M}}$ does not hold for many drugs with low $K_{\mathrm{M}}$ (Table 1 ). For instance, the $K_{\mathrm{M}}$ of propafenone (~ 0.12 µM) is even lower than the hepatic concentration of its major metabolizing enzyme, CYP2D6 (~ 0.31–0.95 µM). ²² As the validity condition of the MM model ( $E_{\mathrm{T}}\ll K_{\mathrm{M}})$ does not hold, we hypothesized that the canonical approach based on the MM model (Eq. 5) leads to an inaccurate prediction for ${\text{CL}}_{\text{int}}^{\text{liver}}$ of the propafenone. To investigate this, we compared the kinetics of propafenone metabolism simulated using the canonical model (Eq. 4) and the full model (Eq. 8 in Supplementary Note ). As the full model describes the enzyme kinetics (Eq. 1) based on mass action kinetics without the model simplification to derive the MM model (Eq. 2), it accurately captures the drug metabolism regardless of enzyme concentration. First, we considered the concentration of CYP2D6 (0.0017 µM), which is used in in vitro metabolism experiments for propafenone. ²² In this case, as the concentration of CYP2D6 is 100‐fold lower than the $K_{\mathrm{M}}$ of the propafenone, the canonical model accurately captures the drug metabolism simulated by the full model (Figure 1a ). On the other hand, when the concentration of CYP2D6 is increased to its in vivo level (~ 0.95 µM; Table 1 ), the canonical model overestimates the rate of drug metabolism by approximately seven‐fold higher than the full model (Figure 1a inset). This indicates that indeed the canonical approach to extrapolating ${\text{CL}}_{\text{int}}^{\text{liver}}$ from ${\text{CL}}_{\text{int}}^{\text{vitro}}$ (Eq. 5) is inaccurate when the $K_{\mathrm{M}}$ of the drug is not much higher than the hepatic concentration of its metabolizing CYP, and, thus, a significant fraction of the drug is bound to the CYP.

Figure 1.

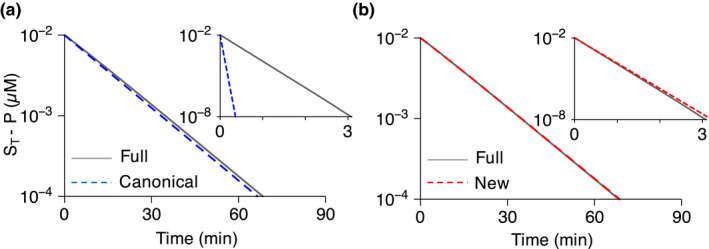
Simulated propafenone metabolism under in vitro (CYP2D6 = 0.0017 µM) and in vivo (CYP2D6 = 0.95 µM) conditions. (a) The canonical model (Eq. 4) accurately simulates propafenone metabolism under the in vitro condition, but not the in vivo condition (inset). Here, $S_{\mathrm{T}}$ represents the initial drug concentration. For the simulations, $V_{max}=4.83$ pmol∙min⁻¹∙pmol⁻¹ CYP and $K_{\mathrm{M}}=0.12\mu M$ are used based on the experimental measurement (Table 1 and S1 ). $E_{\mathrm{T}}=0.0017\mu M$ ²² and $E_{\mathrm{T}}=0.95\mu M$ are used for in vitro and in vivo simulations, respectively (Table 1 ). $k_{\mathrm{f}}=100\mu M/min$ and $k_{\mathrm{b}}=7.17$ min⁻¹ are used for the full model (Eq. 8 in Supplementary Note ) simulation so that $K_{\mathrm{M}}=0.12\mu M$ . $S(0)=0.01$ µM, $C(0)=0$ and $P(0)=0$ . (b) The new model (Eq. 6) accurately simulates the drug metabolism under both in vitro and in vivo conditions (inset). K _M, Michaelis‐Menten constant; V _max, maximal rate of metabolism.

The new approach to extrapolate ${\text{CL}}_{\text{int}}^{\text{liver}}$ from ${\text{CL}}_{\text{int}}^{\text{vitro}}$

With the simple modification of the canonical model (Eq. 4), we can derive an alternative model that accurately describes the hepatic drug metabolism even when the $K_{\mathrm{M}}$ of the drug is not sufficiently higher than the hepatic CYP concentration ⁷ , ⁸ , ²³ , ²⁴ (see Supplementary Note for details):

$$\frac{\mathrm{d}P}{\mathrm{d}t}\approx \frac{V_{max}{\mathrm{E}}_{\mathrm{T}}\overline{S}}{K_{\mathrm{M}}+{\mathrm{E}}_{\mathrm{T}}}={\text{CL}}_{\text{int}}^{\text{vitro}}{\mathrm{E}}_{\mathrm{T}}\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}\overline{S},$$ (6)

where $\overline{S}=S+C$ is the total substrate concentration regardless of its form. This model is referred to as the new model in this study, which leads to a new prediction formula for the intrinsic hepatic clearance:

$${\text{CL}}_{\text{int}}^{\text{liver}}={\text{CL}}_{\text{int}}^{\text{vitro}}{\tilde{E}}_{\mathrm{T}}\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}(\text{mL}/min),$$ (7)

where ${\text{CL}}_{\text{int}}^{\text{vitro}}$ (mL∙min⁻¹∙pmol⁻¹ CYP) is the intrinsic clearance per enzyme and ${\tilde{E}}_{\mathrm{T}}$ (pmol) is the amount of hepatic CYP isoform. Next, we investigated whether the new model (Eq. 6) and, thus, the new formula (Eq. 7) are accurate using the example of propafenone. Indeed, the new model accurately simulates the metabolism of propafenone under both low CYP2D6 (0.0017 µM; Figure 1b ) and high CYP2D6 (0.95 µM) conditions (Figure 1b inset). This indicates that the new formula, which is obtained by simply multiplying $\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}$ with the canonical formula (Eq. 5), can provide accurate prediction of the intrinsic hepatic clearance rate even when ${\mathrm{E}}_{\mathrm{T}}\ll {\mathrm{K}}_{\mathrm{M}}$ does not hold, unlike the canonical formula. Note that as we assume that therapeutic drug concentrations are much lower than $K_{\mathrm{M}}$ , the new approach also predicts that the drug is metabolized exponentially, similar to the canonical approach (Figure 1b ). That is, the qualitative dynamics of hepatic drug metabolism predicted with the canonical and new approach are the same. However, their quantitative prediction of the metabolism rates differ by $\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}$ .

When $E_{\mathrm{T}}\ll K_{\mathrm{M}}$ and, thus, $\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}\approx 1$ , the new formula (Eq. 7) is nearly the same as the canonical one (Eq. 5). On the other hand, as $E_{\mathrm{T}}$ increases, the new formula predicts that ${\text{CL}}_{\text{int}}^{\text{liver}}$ becomes saturated, which differs from the unrealistic prediction of the canonical formula (Eq. 5): the unlimited increase of ${\text{CL}}_{\text{int}}^{\text{liver}}$ with the increase of $E_{\mathrm{T}}$ (Figure 2a ). The difference between the canonical and new formulas becomes notable when $E_{\mathrm{T}}/K_{\mathrm{M}}$ becomes greater than 0.1 (Figure 2a ). Thus, unless the $K_{\mathrm{M}}$ of a drug is 10‐fold higher than its major metabolizing CYP concentration in the liver, the ${\text{CL}}_{\text{int}}^{\text{liver}}$ predicted using the canonical approach should be reduced by multiplying $\frac{K_{\mathrm{M}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}$ . We compared the ${\text{CL}}_{\text{int}}^{\text{liver}}$ predicted using the canonical approach and the new approach for 11 drugs whose $K_{\mathrm{M}}$ is not 10‐fold higher than their major metabolic CYP concentration in the liver (Figure 2b and Table 1 ; see Method for details of drug seletion). For these drugs, the canonical approach considerably overestimates ${\text{CL}}_{\text{int}}^{\text{liver}}$ compared with the new approach.

Figure 2.

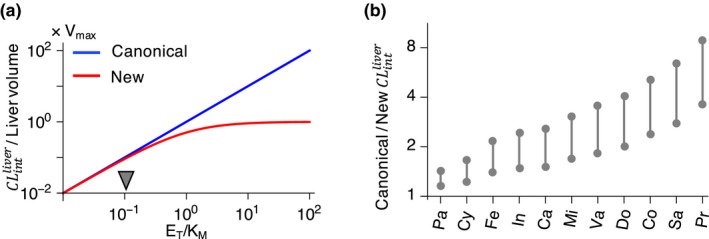
${\text{CL}}_{\text{int}}^{\text{liver}}$ predicted with the canonical approach and the new approach. (a) The canonical approach (Eq. 5) predicts an unlimited increase of ${\text{CL}}_{\text{int}}^{\text{liver}}$ as enzyme concentration increases. On the other hand, the new approach (Eq. 7) predicts the saturation of ${\text{CL}}_{\text{int}}^{\text{liver}}.$ Unless $E_{\mathrm{T}}/K_{\mathrm{M}}<0.1$ , which is highlighted by the arrow, the two approaches lead to different predictions for ${\text{CL}}_{\text{int}}^{\text{liver}}.$ (b) The canonical approach predicts considerably larger ${\text{CL}}_{\text{int}}^{\text{liver}}$ than the new approach for drugs whose $K_{\mathrm{M}}$ is not 10‐fold higher than their major metabolizing CYP concentration in the liver (Table 1 ): Pa, paclitaxel; Cy, cyclosporine; Fe, felodipine; In, indinavir; Ca, cabazitaxel; Mi, midazolam; Va, valspodar; Do, docetaxel; Co, coumarin; Sa, saquinavir; Pr, propafenone. See Table 1 for the detailed calculation of ${\text{CL}}_{\text{int}}^{\text{liver}}$ . See Methods for the detailed description of drug selection. ${\text{CL}}_{\text{int}}^{\text{liver}}$ , intrinsic clearance of the liver; V _max, maximal rate of metabolism; K _M, Michaelis‐Menten constant.; E _T, total enzyme concetnration.

The new approach more accurately predicts CL_h

For drugs whose $K_{\mathrm{M}}$ is not 10‐fold higher than $E_{\mathrm{T}}$ , the canonical approach predicts larger ${\text{CL}}_{\text{int}}^{\text{liver}}$ than the new approach (Figure 2b ). Thus, when the predicted ${\text{CL}}_{\text{int}}^{\text{liver}}$ is substituted into the dispersion model (see Supplementary Note for details), a larger ${\text{CL}}_{\mathrm{h}}$ is predicted with the canonical approach than with the new approach (Table 2 ). Importantly, the predicted ${\text{CL}}_{\mathrm{h}}$ with the canonical approach is much larger compared to experimentally measured ${\text{CL}}_{\mathrm{h}}$ . Such overestimation is considerably reduced with the new approach (Figure 3a,b ). Thus, the new approach improves the accuracy and precision of the prediction for ${\text{CL}}_{\mathrm{h}}$ compared with the canonical approach (Tables 2 and 3 ). Such considerable improvement using the new approach is also observed when other ${\text{CL}}_{\mathrm{h}}$ models, such as the parallel tube model and the well‐stirred model are used (Tables 2 and 3 ).

Figure 3.

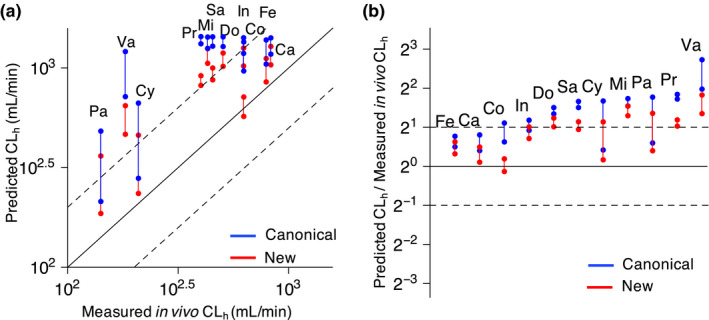
The new approach provides more accurate prediction of hepatic clearance ( ${\text{CL}}_{\mathrm{h}}$ ) than the canonical approach. (a) Relationships between measured in vivo ${\text{CL}}_{\mathrm{h}}$ and predicted ${\text{CL}}_{\mathrm{h}}$ (Table 2 ). Here, the dispersion model is used to predict ${\text{CL}}_{\mathrm{h}}$ based on intrinsic clearance of the liver ( ${\text{CL}}_{\text{int}}^{\text{liver}}$ ) estimated by either the canonical or the new approach (see Methods and Table 2 for details). The solid and dashed lines represent the line of identity and twofold error, respectively. (b) Precision error of ${\text{CL}}_{\mathrm{h}}$ predicted with the canonical and new approaches. Pa, paclitaxel; Cy, cyclosporine; Fe, felodipine; In, indinavir; Ca, cabazitaxel; Mi, midazolam; Va, valspodar; Do, docetaxel; Co, coumarin; Sa, saquinavir; Pr, propafenone.

Table 3.

Accuracy and precision of predicted CL_h using the canonical and new approaches

	Dispersion model		Well‐stirred model		Parallel tube model
	Canonical	New	Canonical	New	Canonical	New
AFE	2.46	1.83	2.14	1.58	2.57	1.94
AAFE	2.46	1.84	2.14	1.62	2.57	1.95
RMSE (mL/min)	709	433	560	305	753	494
R‐RMSE	2.06	1.15	1.67	0.88	2.20	1.28

AAFE, absolute average fold error; AFE, average fold error; CL_h, hepatic clearance; RMSE, root mean squared error; R‐RMSE, relative‐root mean squared error.

Discussion

For drugs with low K _M values (Table 1 ), prediction of in vivo drug clearance from in vitro data using the canonical approach has been unsatisfactory. ¹² , ²¹ , ²⁵ Although various causes of the problem, such as the choice of liver model, ³ , ²⁶ have been proposed, here, we propose that it could be mainly due to the fact that the PK behavior of drugs with low K _M in the liver cannot be captured by the conventional MM equation. The detailed analysis of enzyme kinetics shows that when the K _M of drugs is low and, thus, not 10‐fold higher than the hepatic concentration of their major metabolic CYP ( $E_{\mathrm{T}}$ ), a significant fraction of the drug (~ $\frac{E_{\mathrm{T}}}{K_{\mathrm{M}}+E_{\mathrm{T}}}$ ) is bound to CYP. In this case, the fundamental scaling assumption of the canonical approach (i.e., ${\text{CL}}_{\text{int}}^{\text{liver}}$ doubles as the amount of hepatic enzyme doubles) does not hold, which causes considerable error in predicting ${\text{CL}}_{\text{int}}^{\text{liver}}$ with the canonical approach (Figure 1a ). Thus, we propose an alternative approach (Eq. 7) considering the fact that the saturation of metabolism rate occurs when the enzyme concentration is not sufficiently lower than K _M (Figure 2a ). The new approach accurately predicts the ${\text{CL}}_{\text{int}}^{\text{liver}}$ of 11 drugs with low K _M (Figure 1b and 2b ), which leads to a considerable improvement in predicting their ${\text{CL}}_{\mathrm{h}}$ compared with the canonical approach (Figure 3 and Table 2 ). Such improvement in prediction of ${\text{CL}}_{\mathrm{h}}$ with the new approach proposes the validity check for the canonical approach in the current IVIVE process (Figure 4 ).

Figure 4.

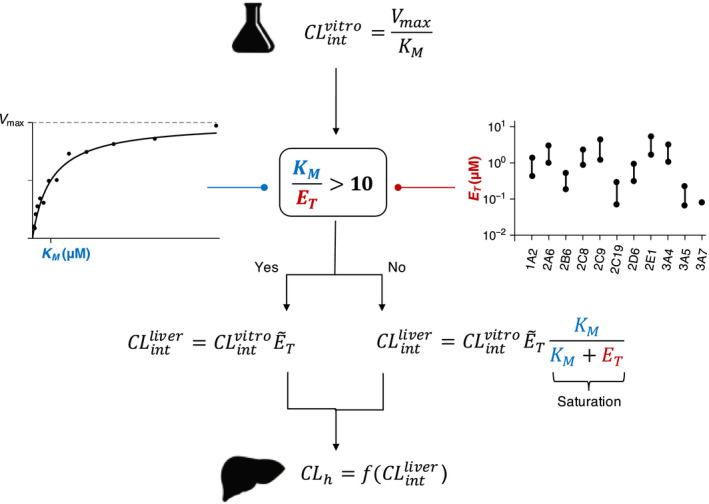
Incorporation of the validity check for the canonical approach into in vitro‐in vivo extrapolation for clearance (CL). If K _M of the drug is not 10‐fold higher than the hepatic concentration of its major CYP (E _T), the canonical approach cannot capture the saturation of metabolism caused by the binding of a significant fraction of the substrate to the enzyme. Thus, to extrapolate ${\text{CL}}_{\text{int}}^{\text{liver}}$ from ${\text{CL}}_{\text{int}}^{\text{vitro}}$ , the new approach should be used, which incorporates the saturation of metabolism. See Supplementary Table S3 and Methods for the detailed estimation procedure for the hepatic E _T. ${\text{CL}}_{\text{int}}^{\text{liver}}$ , intrinsic clearance of the liver; ${\text{CL}}_{\text{int}}^{\text{vitro}}$ in vitro intrinsic clearance of the liver; K _M, Michaelis‐Menten constant; V _max, maximal rate of metabolism.

The V _max and $K_{\mathrm{M}}$ values, needed to compare the canonical and new approaches (Eq. 7), have been reported for a few drugs with low K _M because drug candidates with low $K_{\mathrm{M}}$ might be excluded from drug development due to potential problems of low bioavailability and drug‐drug interactions. Furthermore, we selected drugs that are mainly metabolized by a single CYP enzyme and do not exhibit inhibitory and inducible activities for CYP (see Methods for details). Thus, small number of drugs are used to investigate the accuracy and precision of canonical and new IVIVE (Figure 3 ) compared with recent IVIVE studies. ⁵ , ²⁷ , ²⁸ Thus, further studies are needed with a large number of drugs to fully confirm the advantage of using the new approach over the canonical approach. This might be achieved by considering a large number of drugs metabolized by multiple CYP enzymes. For drugs metabolized by multiple CYPs, the canonical approach estimates the contribution of each CYP to net metabolism with the V _max /K _M and then combines them to estimate global ${\text{CL}}_{\text{int}}^{\text{liver}}$ . ¹⁷ Similarly, our new approach can be extended for drugs with multiple metabolic pathways by simply combining the estimated contribution of each CYP to metabolism with the new approach. It would be interesting in future work to investigate how this extended approach improves the estimation of drug CL.

The values of ${\text{CL}}_{\text{int}}^{\text{liver}}$ and ${\text{CL}}_{\mathrm{h}}$ estimated with the canonical approach in this study (Table 2 ) do not match with those estimated in all previous studies, which have reported values with a large range. For instance, the range of ${\text{CL}}_{\text{int}}^{\text{liver}}$ for midazolam and propafenone reported by previous studies are 8.8 ~ 200 mL/min/kg ²⁵ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³² and 6.5 ~ 644.9 mL/min/kg, ²⁸ , ³⁰ , ³¹ respectively. Thus, our estimations are consistent with those in some previous works (midazolam ²⁵ , ³⁰ , ³¹ , ³² and propafenone ³¹ ), but not the others (midazolam ²⁸ , ²⁹ and propafenone ²⁸ , ³⁰ ). Such differences were mainly attributed to different experimental systems used in previous studies. For instance, they used V _max and $K_{\mathrm{M}}$ obtained with hepatocytes, ²⁸ , ²⁹ whereas we used ones estimated with HLM. Furthermore, they used the estimated values of f _u‐mic and f _u‐blood, ²⁸ , ³⁰ whereas we used experimentally measured ones.

As the CYP amount increases, both the canonical approach and the new approach predict the increase of ${\text{CL}}_{\text{int}}^{\text{liver}}$ and, thus, ${\text{CL}}_{\mathrm{h}}$ , but with different rates: the new approach predicts a lower increase than the canonical approach when $E_{\mathrm{T}}/K_{\mathrm{M}}>0.1$ (Figure 2a ). For instance, if the amount of CYP3A4 in the liver ( ${\tilde{E}}_{\mathrm{T}}$ ) is increased from 1.8 µmol by 10‐fold, the canonical approach predicts that the ${\text{CL}}_{\mathrm{h}}$ of cyclosporine increases by ~ 325%. On the other hand, our new approach predicts the increase by only ~65% because $E_{\mathrm{T}}$ in the denominator of Eq. 7 also increses and, thus, saturation of metabolism occurs. Consistent with the prediction of the new approach, when CYP3A4 is increased by 600 mg rifampin for 11 days, the CL of cyclosporine administered by intravenous route was increased by only ~ 40%, ³³ although rifampin increases CYP3A4 activity in primary human hepatocytes by 10‐fold. ³⁴ Unlike ${\text{CL}}_{\mathrm{h}}$ , as the level of CYP3A4 is much lower in the gut than in the liver, ¹¹ the new approach predicts that the induction of intestinal CYP3A4 greatly increases the CL of cyclosporine in the gut (i.e., the range of $E_{\mathrm{T}}/K_{\mathrm{M}}<0.1$ in Figure 2a ). Indeed, when CYP3A4 is induced by rifampin, the CL of cyclosporine administrated by the oral route, which occurs considerably in the gut, was increased by 270%. ³³ These results indicate that when CYP is induced the saturation of metabolism rate seems to occur for drugs with low $K_{\mathrm{M}}$ in the liver. However, note that p‐glycoprotein‐mediated cellular efflux of cyclosporine can be increased by rifampin, ³⁵ leading to decrease in cyclosporine bioavailability through elevation of efflux in the gut. In addition, hepatic induction of p‐glycoprotein by rifampin may increase hepatic CL of cyclosporine via bile, although hepatic metabolism plays a major role in CL of cyclosporine.

The canonical and new approaches make similar prediction of in vivo ${\text{CL}}_{\mathrm{h}}$ for drugs with high $K_{\mathrm{M}}$ (Figure 3a ). On the other hand, the new approach decreases the prediction of in vivo ${\text{CL}}_{\mathrm{h}}$ compared with the canonical approach when $K_{\mathrm{M}}/E_{\mathrm{T}}<10$ . This seems to be paradoxical as the canonical approach frequently leads to underestimation of in vivo CL for many drugs. ²⁰ , ²⁸ , ³¹ However, interestingly, compared with drugs with high $K_{\mathrm{M}}$ , such an underestimation less frequently occurs for drugs with low $K_{\mathrm{M}}$ , including ones we have discussed (e.g., midazolam and saquinavir), ²⁷ , ³⁰ , ³¹ , ³² , ³⁶ which is consistent with our findings (Figure 3 ). That is, the level of the underestimation of canonical IVIVE seems to vary depending on the $K_{\mathrm{M}}$ of the drug, which could be due to the inaccurate prediction of the canonical approach for drugs with low $K_{\mathrm{M}}$ . Thus, using the new approach, which can provide a consistent prediction regardless of $K_{\mathrm{M}}$ , might be helpful in finding a way to resolve the underestimation problem (e.g., universal scaling regardless of $K_{\mathrm{M}}$ ). ³⁷ Furthermore, as enzyme concentration is typically low (~nM) in the in vitro experiment ⁹ , ¹¹ , ²² and, thus, ${\mathrm{E}}_{\mathrm{T}}\ll {\mathrm{K}}_{\mathrm{M}}+S$ holds, using the MM equation to estimate $K_{\mathrm{M}}$ is valid. However, if such condition does not hold, $K_{\mathrm{M}}$ can be dramatically overestimated, ⁷ which can lead to the underprediction of in vivo ${\text{CL}}_{\mathrm{h}}$ . Such overestimation of $K_{\mathrm{M}}$ can be resolved by using the Eq. 9 in the Supplementary Note (ref. ⁷ ), which might help to resolve underprediction problem of IVIVE.

If the estimated concentration of hepatic CYPs is too high (Table 1 and Figure 4 ), they may not be fully inhibited by CYP inhibitors as CYP inhibitors do not reach sufficient concentrations in vivo to inhibit target CYPs. ³⁸ For instance, the K _i value of voriconazole, a CYP3A4 inhibitors, is 0.66 µM, ³⁹ and hepatic concentration of its free form is 4.96 µM with a typical dose (i.e., 200 mg). ⁴⁰ , ⁴¹ , ⁴² Our estimation of hepatic CYP3A4 concentration is 1.10 ~ 3.33 µM (Table 1 ). When these values are substituted into the formula of K _i (i.e., the ratio between the concentration of complex and reactants), ~ 78–86% of CYP3A4 is expected to form a complex with voriconazole (Table S4 ). However, due to the short half‐life of voriconazole (~ 5 hours), it is questionable to use the static equation of K _i. When the equation is applied to another CYP3A4 inhibitor, fluconazole, which has a long half‐life (~ 22 hours), ⁴³ ~ 93–94% of CYP3A4 is expected to form a complex with fluconazole (Table S4 ). On the other hand, for itraconazole and ketoconazole having high protein‐binding affinity, extremely low fraction of CYP3A4 (i.e., 2% and 1%, respectively) is expected to form a complex (Table S4 ), which raises the question of our estimation for CYP3A4 concentration. In fact, their free form concentration is much less than 10‐fold of K _i. Thus, the static equation of K _i predicts, even when CYP3A4 concentration is extremely low, high fraction of CYP3A4 cannot be in complex with itraconazole and ketoconazole in contrast to their strong CYP3A4 inhibition. This paradox of itraconazole has been resolved by a recent study, which identifies that even metabolites of itraconazole inhibit the CYP3A4 and raises the question of using the concentration of free form of itraconazole to predict its strong inhibitory effect. ⁴⁴ Taken together, the estimation with CYP3A4 inhibitors having weak protein binding affinity (fluconazole and voriconazole), but not with those having strong protein binding affinity (itraconazole and ketoconazole), indirectly support that the estimated CYP concentration (Table 1 ) is in a reasonable range. However, it is difficult to make rigorous conclusion with the static equation of K _i, and more detailed analysis is needed considering the properties of CYP inhibitors, such as selectivity, inhibitory mode, nonspecific binding, and PK behavior.

In this study, to test the validity condition ( $K_{\mathrm{M}}/E_{\mathrm{T}}>10)$ , we used the concentration of CYPs ( $E_{\mathrm{T}}$ ) estimated under the assumption that CYPs are evenly distributed in hepatocytes (Table 1 ). However, the actual concentration of CYP isoforms can be higher because CYPs are primarily localized in the membrane of the endoplasmic reticulum, which is about 20% of the total cell volume. If we adopt the increased concentration of CYP isoforms, the prediction of the CL_h with the new approach changes considerably (Supplementary Figure  S1 and Tables S1 and S2 ). Furthermore, a larger number of drugs than those presented in this study (Table 1 ) fail to satisfy the validity condition of the canonical approach ( $K_{\mathrm{M}}/E_{\mathrm{T}}>10$ ), and, thus, necessitate the new approach presented in this study (Figure 4 ). However, restricting the compartment to the membrane of the endoplasmic reticulum can disrupt the correlation between in vivo and in vitro systems. For instance, it is questionable to use the same value of K _M for both the in vitro system based on a homogenous distribution of the substrate and the in vivo system based on an inhomogeneous cellular localization of the substrate. In particular, if the volumes occupied by substrate and enzyme are different, then even when enzyme concentration is higher than the substrate concentration, the amount of substrate can be in excess of the amount of enzyme. In this case, unlike our analysis based on concentration, the amount of substrate bound to enzyme is negligible and the canonical approach can be still valid. Thus, further study is needed to estimate the drug CL considering the subcellular localization of CYP isoforms in the liver.

When a drug‐enzyme interaction occurs at multiple sites cooperatively, the relationship between substrate concentration and the velocity of metabolism becomes sigmoidal rather than hyperbolic. ¹⁸ , ⁴⁵ In this case, instead of the MM model (Eq. 2), the model based on the Hill equation has been used to investigate CL. ¹⁸ On the other hand, when substrate inhibition is observed, a modified MM model incorporating the inhibition effect of the substrate has been used. ¹⁸ However, similar to the MM model, all of these current models are valid only when the enzyme concentration is sufficiently low, relative to the K _M value, ⁴⁶ which does not always hold in the liver, as shown in this study (Tables 1 and S1 ). Thus, alternative models, which consider the saturation of metabolism at high enzyme concentrations, need to be developed as done in this study.

Funding

This work was supported by a National Research Foundation of Korea Grant funded by the Korean Government (NRF‐2016 RICIB 3008468 to J.K.K., and 2017R1A4A1015860 and 2018M3A9H1021640 to S.K.K.), an EWon fellowship (J.K.K.), a grant from the Korea Health Technology R&D Project through the Korea Health Industry Development Institute funded by the Ministry of Health & Welfare, Republic of Korea (HI17C0927) (H.Y.Y.), and Chungnam National University (H.Y.Y.).

Conflict of Interest

All authors declared no competing interests for this work.

Author Contributions

H.M.B., H.Y.Y., S.K.K., and J.K.K. wrote the manuscript. H.Y.Y., S.K.K., and J.K.K. designed the research. J.K.K. H.M.B., H.Y.Y., S.K.K., and J.K.K. conducted the research. H.M.B., H.Y.Y., S.K.K., and J.K.K. analyzed the data.

Supporting information

Fig S1

Table S1

Table S2

Table S3

Table S4

Supplementary Material

Supplementary Material

Supplementary Material