Individualized SAR Calculations Using Computer Vision-Based MR Segmentation and a Fast Electromagnetic Solver

Abstract

Purpose:

We propose a fast, patient-specific workflow for on-line SAR supervision. An individualized electromagnetic model is created while the subject is on the table, followed by rapid SAR estimates for that individual. Our goal is an improved correspondence between the patient and model, reducing reliance on general anatomical body models.

Methods:

A 3D fat-water 3T acquisition (~2 minutes) is automatically segmented using a computer-vision algorithm (~1 minute) into what we found to be the most important electromagnetic tissue classes: air, bone, fat, and soft tissues. We then compute the individual’s EM field exposure and global and local SAR matrices using a fast electromagnetic integral equation solver. We assess the approach in ten volunteers and compare to the SAR seen in a standard generic body model (Duke).

Results:

The on-the-table workflow averaged 7’44”. Simulation of the simplified Duke models confirmed that only air, bone, fat, and soft tissue classes are needed to estimate global and local SAR with an error of 6.7% and 2.7%, respectively, compared to the full model. In contrast, our volunteers showed a 16.0% and 20.3% population variability in global and local SAR, respectively, which was mostly underestimated by the Duke model.

Conclusion:

Timely construction and deployment of a patient-specific model is computationally feasible. The benefit of resolving the population heterogeneity compared favorably to the modest modeling error incurred. This suggests that individualized SAR estimates can improve electromagnetic safety in MRI and possibly reduce conservative safety margins that account for patient-model mismatch, especially in non-standard patients.

Introduction

The specific absorption rate (SAR) is commonly used for safety evaluation of MRI radiofrequency (RF) systems (1). Global SAR can be relatively well approximated by the total forward power since coil losses and radiated power are relatively low (<10%) and the vast majority of the power goes into the patient (2). Moreover, coil and radiative losses can be simply accounted for using a calibration procedure (3). Local SAR is more difficult to estimate, however, since it is not related in a straightforward manner to the total forward power (4). For example, local SAR hotspots can exist even for reasonable values of the global SAR (4–11). Such hotspots are heavily influenced by the local geometry and typically occur in the arms and the periphery of the body where large surface current loops can form since E-fields are shielded deep in the body and create current flow that largely follow the distribution of conductive tissues (12). The current approach for local SAR supervision is to calculate the 3D distribution of the electric fields (E-fields) in the body using electromagnetic (EM) simulation scaled to the RF excitation pulses. This is done in the factory using generic body models which are representative of the patient population, but of course, are not an anatomical match to the patient being imaged (13–15). A more conservative approach is to use multiple body models and require that the scan satisfies safety in the most conservative one (16–18) or in the model or subset of models most closely matched to the patient (19).

A major limitation of these approaches is that they utilize a relatively small population of body models and the “satisfy all models” approach becomes increasingly conservative as the model population is increased. The potential for patient to model-population mismatches becomes even more problematic when only standard body shapes and model positions are considered for medically diverse patients such as pregnant women, amputees, patients with implants, and subjects requiring unusual body positions/placement in the coil (20–23). Body model position within the coil has been shown to create a large variation in local SAR, with Wolf et al. (24) and Jin et al. (25) reporting a 14–22% change in local SAR due to only a 2.5 cm change in body position. Body model posture can also lead to a large variation in local SAR. Homann et al. (8) reported a ~4-fold difference in local 10g SAR from when the arms were at the side compared to when the arms were crossed on top of the body. The resulting issue with the use of limited standard models analyzed off-line is that the conservative safety margin required to cover the potential patient-model mismatch translates to suboptimal scanning parameters. For SAR-intensive sequences such as turbo spin echo (26) and simultaneous multi-slice excitations (27,28), this may lead to suboptimal scan time duration and image acquisition data rate.

Ideally, local SAR should be assessed on a patient-specific basis and in real time, capturing anatomical variations in the assessment and yielding more appropriate, potentially tighter safety margins even in those patients with non-standard shapes and body positions. To better account for this heterogeneity, a patient specific SAR estimation has been considered potentially valuable (8,29). While showing the potential benefit of the patient-specific approach, these studies could not perform the SAR calculation in a clinically relevant time due to the available EM solvers. For example, Homann et al. (8) reported a computation time of 45 minutes per Tx channel (8 channels) using a Finite Difference Time Domain (FDTD) solver. Other methods have been proposed for real-time assessment of an individual’s local SAR, including approaches based on Electrical Properties Tomography (EPT) (30–40), Global Maxwell Tomography (41–43), and thermoacoustic imaging (44). However, these methods present other challenges in the accurate and timely calculation of local SAR distributions and are not widely used. Recently, Meliado et al. (45) proposed deep learning (DL) as a potential way to rapidly estimate local SAR. Specifically, they trained a conditional generative adversarial network to operate on complex B₁⁺ maps acquired in 23 prostate patients at 7T trained on associated SAR maps computed for those patients offline using FDTD. While very fast (a few ms to generate the local SAR prediction), the method overestimates SAR by ~21% and retains all the standard issues with understanding how a DL approach generalizes to body shapes and patient geometries outside of its training set.

In this work, we propose a fast, patient-specific local SAR estimation approach based on a low-SAR, rapidly acquired MR-generated, body model (46,47) analyzed with an ultra-fast EM solver (48). Since model generation for a patient still on the table necessitates a simplified tissue class set, we first identify the most important tissues for accurate estimation of SAR in the head and neck. We show that modeling only the fat, soft tissues, internal air and bone allows estimation of global and 10g local SAR within 7%, which is in agreement with previous studies (38,39). Guided by these results, we utilize a simple DIXON-based sequence and computer-vision segmenter to create a body model consisting of fat, water, bone, and air. We then compute the E-field distribution in this model using the MAgnetic Resonance Integral Equation (MARIE) software. The total time for creation of the patient specific SAR estimates is less than 8 minutes.

Methods

Overview of patient-specific SAR calculation

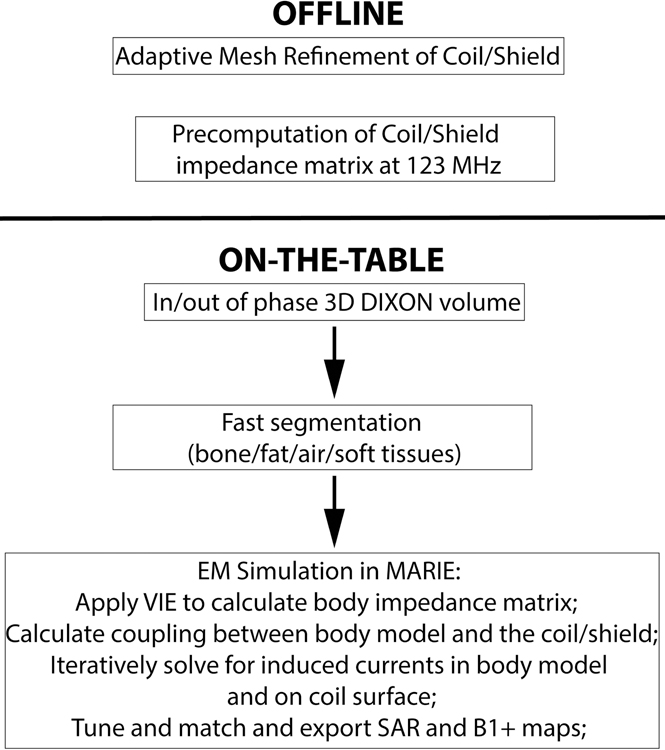
Figure 1 shows the flowchart of our methodology. The method is broken down in two portions. The offline portion is run only once for a specific coil and generates an adaptively meshed coil and an impendence matrix that is valid for all loads at a given frequency. Pre-computation of this impedance matrix speeds up the subsequent on-the-table portion, since it is independent of the specific body model. The on-the-table portion consists of a fast DIXON scan followed by automatic segmentation of the air, bone, fat and soft tissue volumes using a rapid computer-vision segmenter. The final step is computation of the E- and B-fields using the fast EM solver MARIE.

Figure 1:

Flow chart depicting the methodology for fast computation of patient-specific SAR and B₁⁺ maps. The offline phase consists of adaptive mesh refinement and precomputation of the coil/shield impedance matrix at the Larmor frequency. The on-the-table phase consists of the MRI acquisition (3D DIXON), fast segmentation into air, bone, fat, and soft tissue using a computer-vision based segmenter, and EM simulation using MARIE.

Which tissue classes are needed for accurate SAR evaluation?

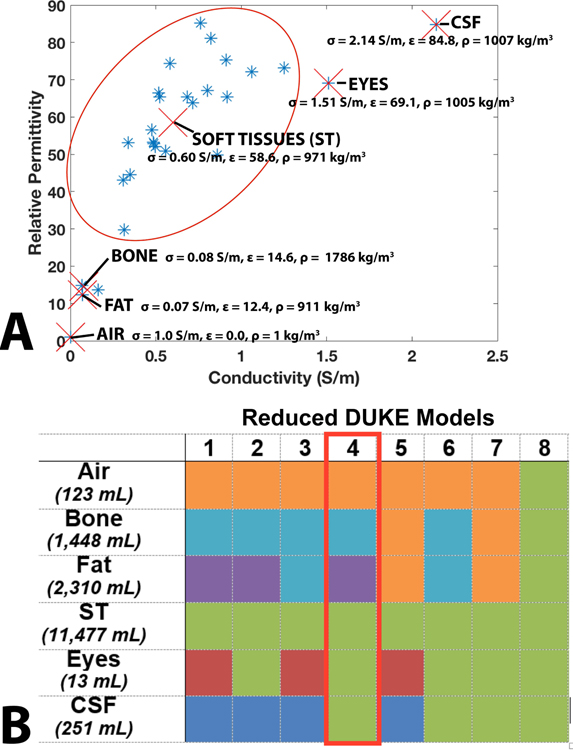
We assessed the impact of the number and choice of tissue classes on global SAR, and local SAR by progressive simplification of the 5 mm isotropic Duke body model (49,50). The original Duke model contains 77 different labeled organs, with relative permittivity (ε), conductivity (σ), and density (ρ) assigned using the Gabriel database (51) (we refer to this full model as “Whole Body Duke”). Note that the Gabriel database only contains 57 tissue classes, so that some labeled organs in Duke are assigned the same tissue class. A truncated version of Duke (“Truncated Duke”) was generated by keeping only the top 425 mm of the original model (this removed some tissue classes that only exist below the thorax, thus the Truncated Duke model has 52 tissue classes). The 52 tissue classes of the Truncated Duke model were then further combined into six major groups: air, bone, fat, soft tissue (ST), eyes, and cerebrospinal fluid (CSF). The tissue groups are shown in Figure 2A and correspond to natural clusters in the relative permittivity vs conductivity graph. The dielectric properties of the groups were chosen as the mean of the dielectric properties of the tissues in each group. Eight simplified body models were then generated from Truncated Duke ( “Reduced Duke Models 1–8”) by further merging those tissue groups. When merging two groups, the dielectric properties of the resulting grouping were assigned the weighted-average (based on volume) of the dielectric properties of the original groups. The different grouping options are shown using a color code in Figure 2B and the resulting weighted-average group merging dielectric properties are shown in Supporting Table S1. Reduced Duke Model 4 (air, bone, fat and soft tissues) is of particular interest because it corresponds to the model that is the easiest to obtain using a single DIXON scan, and is therefore outlined in red.

Figure 2:

A. Conductivity and relative permittivity of the tissue classes present in the Duke body model. Tissues can be naturally classified into air, bone, fat, soft tissues (red oval), eyes, and CSF (marked by red X’s). The average relative permittivity (ε), conductivity (σ), and density (ρ) values for these six classes are also shown in the graph. B. Table summarizing the body model reduction levels studied in this work. The columns indicate different Reduced Duke models numbered from 1 to 8. The rows indicate tissue types. Reduced body models were obtained by grouping some tissue classes together, as indicated by the shared colors. When grouping N tissue classes, the permittivity and conductivity values of the new group were assigned to the weighted average of the N classes (by volume). Reduced Duke Model 4 is highlighted in the red box because it is the most complex model achievable using a single DIXON scan.

Finally, three additional models were created to mimic the fact that, in reality, the portion of the torso located below the coil cannot be reliably imaged and therefore needs to be estimated by extension of the last slice available. We generated Truncated Duke - Chest, Truncated Duke - Muscle, and Truncated Duke - Soft Tissue by assignment of the 100 mm last-slice-extension portion of the model to the average chest properties, muscle and soft tissue, respectively. We used the results of this comparison to inform our segmentation and modeling strategy for the human volunteers.

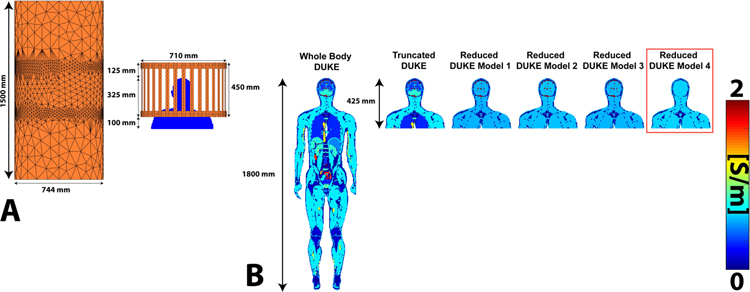
A representative slice of the conductivity for six of the body models (Whole Body Duke, Truncated Duke, and Reduced Duke Models 1–4) is shown in Figure 3. The body models are placed with the eyes at isocenter. Supporting Figure S1 shows all the body models.

Figure 3:

A. Refined coil and shield meshes loaded with the Truncated Duke model. B. Conductivity maps (center coronal slice) of Whole Body Duke, Truncated Duke, and Reduced Duke models 1–4 Reduced Duke Model 4 is outlined in red because it corresponds to the tissue class grouping used in the following volunteer scans.

Fast generation of patient-specific models

We applied this methodology to 10 healthy volunteers imaged in compliance with our Institutional Review Board requirements using a body birdcage coil at 3 Tesla (Siemens Skyra). We scanned 5 males/5 females, age = 23–37 years old, height = 167–193 cm, weight = 134–250 lbs., BMI range = 19.9 to 32.1 kg/m² (variability or standard deviation/mean = 15.5%). The volunteers were scanned head-first and supine in the 3T scanner with the landmark (isocenter) placed just above the eyes. All subjects were scanned with their arms at their sides, but one subject had an additional scan with arms raised above the head.

We chose the DIXON sequence to create the patient-specific body models since it generates distinct fat and water volumes and is fast, low-distortion, and low-SAR (33). The parameters of the sequence were as follows: 1’38” scan time, 500 × 500 × 397 mm³ FOV, 192 × 192 × 128 matrix size, 2.6 × 2.6 × 3.1 mm³ resolution, 4 ms TR, 1.23/2.46 ms TE1/TE2, 10° flip angle, and 6/8 partial Fourier in the partition direction. The output of the DIXON scan is an in-phase and an out-of-phase volume that can be used to obtain the fat and water volumes.

The fat, water and in-phase volumes were segmented into fat, soft tissue, air and bone using a fast automatic computer-vision based segmentation algorithm described previously (46,47). First, all MR images were resliced to 5 mm isotropic resolution. The fat and water volumes yielded the fat and soft tissue classes, respectively, while the in-phase volume was used to estimate the air and bone tissue classes. Specifically, the in-phase volume was used to generate a pseudo-CT by using a groupwise patch-based approach and an MR–CT atlas dictionary built previously for the purpose of attenuation correction in PET/MRI (46,52–54). Segmentation of the bone compartment from the pseudo-CT is easily performed by thresholding the Hounsfield Units. Finally, the body model was extended 100 mm below the last slice in order to more realistically load the body RF coil, as was suggested in Wolf et al. (24). The properties of the extended portion of the body model were set to the average of tissue properties in the chest region of the Duke model (ε = 19.3, σ = 0.499 S/m, ρ = 943 kg/m³). The final patient specific body model was a 5 mm voxel model of 101 × 80 × 108 voxels.

Electromagnetic simulation using MARIE

The MARIE package (48) solves the EM fields in the patient by combination of two distinct solvers: A surface integral equation (SIE) solver, which is used for modeling the impedance matrix of the coil and the shield, and a volume integral equation (VIE) solver used for solving the polarization currents induced in the voxel body model. For this study, we simulated the scanner’s 32-rung high-pass body birdcage coil (diameter = 710 mm, length = 450 mm) and RF shield (diameter = 744 mm, length = 1500 mm), accelerated on an Nvidia Tesla P100 graphical processing unit (GPU). The coil was tuned at 123 MHz (3T) by assigning tuning capacitors to the known values for this clinical coil. The coil was driven in quadrature (1 Amp excitation on the two ports). Figure 3A shows the coil model loaded with the voxel model of Truncated Duke.

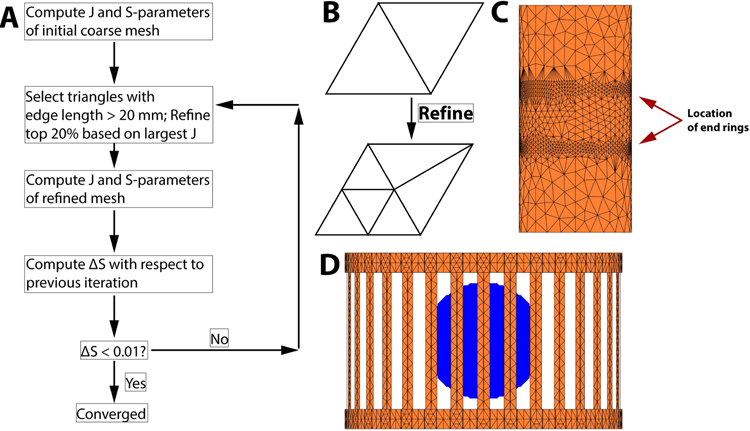
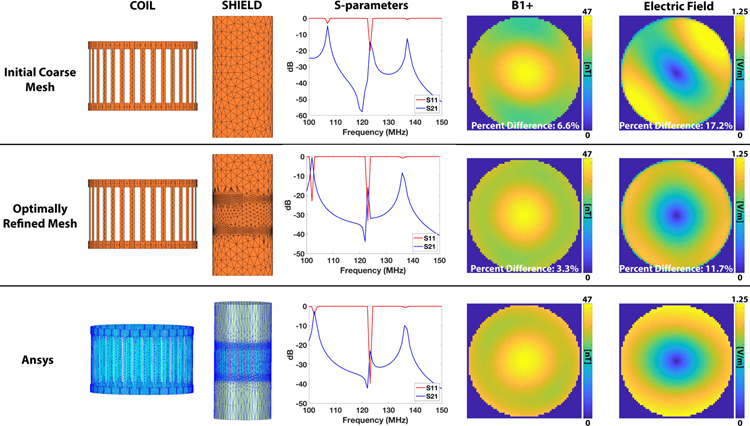
It is known that accurate meshing of the coil and shield is crucial for accurate prediction of the EM fields. Thankfully, the optimal coil and shield mesh producing accurate field estimates do not depend strongly on the patient model and can therefore be determined ahead of time. A good mesh is one that is refined in regions where the current density varies rapidly and is coarse in regions where it does not, thus ensuring accuracy while minimizing computation time. We generated such a mesh by successive refinement of a coarse initial guess following the process summarized in Figure 4 which is similar to that described in Ref. (43). We first start with a coarse mesh and compute the surface current on the coil and shield by full wave simulation (SIE+VIE). We then select the triangle elements with the 20% greatest values of the current density and refine them by bi-section as shown in Figure 4B. Edges smaller than 20 mm are not considered for bisection however, which we found necessary to avoid continuously bi-secting the same triangle elements, thus yielding unreasonably high levels of refinement in some areas of the conducting surfaces. Note that the bi-section may generate points that are not on the coil and shield surfaces anymore. Therefore, a necessary step is to “snap” the newly created point on the coil and shield surface by projection (the exact coil and mesh surface is defined by a high-resolution CAD file). This process is repeated until the maximum S-parameters variation compared to the previous iteration is smaller than 1%. To speed up this process, and since the mesh refinement is expected to be relatively independent from the load, we modeled a uniform sphere of radius 15 cm (ε = 52, σ = 0.55 S/m, ρ = 1000 kg/m³). We validated our mesh refinement process by comparison of the resulting mesh and EM fields to Ansys Electronics (ANSYS, Canonsburg PA), which uses a similar approach (the same loading sphere was simulated).

Figure 4:

A: Adaptive mesh refinement (AMR) process employed in this study The algorithm refines the mesh in areas with the highest values of the surface current (J) and uses the change in S-parameters as the convergence metric. The complete algorithm for the coil/shield studied in this work took 51 minutes 46 seconds (4 iterations). B. Refinement by bisection of triangle edges. C. Final shield mesh showing important refinement close to the end-ring of the coil. D. Final coil mesh loaded with the 15 cm radius uniform sphere used during AMR. There is some refinement in the end rings, which is where the highest surface current is expected.

After refinement, we computed the S-parameters of the coil in the 100–150 MHz range both with MARIE and Ansys Electronics. For both the MARIE and the Ansys Electronics simulations, we optimized of the tuning and matching capacitors and inductors using Ansys Electronics (tuning @ 123 MHz, S11<−20dB) using the co-simulation approach described by Kozlov et al. (55). Fine tuning at the Larmor frequency and matching was performed using matching networks placed on the two quadrature ports (Supporting Figure S2). The equations relating the value of the tuning and matching lumped elements to excitations used in the field solver are shown in Supporting Table S2. These excitations were combined to obtain a single E-field and B-field for the coil. The tuning and matching circuit was optimized for Whole Body Duke and Truncated Duke body models only, with the circuit for Truncated Duke applied to all other models.

The next off-line step was computation of the SIE impedance matrix corresponding to the coil and shield. This impedance matrix depends on the frequency but not on the body model, and therefore can be stored for future simulations.

The “on-the-table” portion of the EM simulation focuses on the coupling between SIE and VIE, which is patient-dependent and therefore cannot be pre-computed. The way to properly couple the SIE and VIE solvers within MARIE is explained in details in Ref. (48) and is outside the scope of the present work. The first step of the “on-the-table” portion of the SIE+VIE solution with MARIE consisted of assembly of the body and coil-body impedance matrices and iterative SIE-VIE solution. The SIE-VIE is in fact a nested iterative process. The inner iteration is the VIE solver. The outer iteration consists in updating the surface current flowing on the coil and shield, which are affected both by the input excitations at the ports and by the polarization current solutions of the VIE calculation. The details have been previously discussed (48,56).

We report fields and SAR values normalized to achieve a given flip-angle (as opposed to a reference input power), which is a more relevant metric for MRI. Specifically, the input power was calibrated for each simulation to generate a 90° average flip-angle in a 30 mm-thick axial slab centered on the eyes after a 1 ms rectangular pulse (this corresponds to an average B₁⁺=5.87 μT) and a duty cycle of 100%. The 10g local SAR was calculated as described in Carluccio et al. (57).

Results

It took four iterations of the refinement process outlined in Fig. 4 to yield S-parameter changes smaller than 1%. Total computation time was ~1 hour (pre-computation). The refined versions of the coil and shield are shown in Figures 4C/D and Figure 5B. Figure 5 shows the coil and shield meshes, S-parameters, and the B₁⁺ and E-field of an axial slice at isocenter for the initial coarse MARIE mesh, the refined MARIE mesh, and the final Ansys Electronics mesh. The mesh refinement process did not significantly alter the coil mesh, but clearly had a large impact on the shield mesh. The position of the end-rings can be clearly seen on the refined shield mesh, which is also a feature of the Ansys Electronics mesh. The detail needed here is due to the fact that the E-field tends to vary rapidly in this region. This refinement impacted the shape of the S-parameter curves and the B₁⁺ and E-field distributions and was needed to achieve good agreement between the refined mesh MARIE predictions of the S-parameters and B₁⁺ and E-field maps and the predictions by Ansys Electronics. Although not a full validation, this simple sanity check insures that the mesh refinement process is working (MARIE was previously fully validated (48)).

Figure 5:

Comparison of the coil & shield meshes, S-parameters, B₁⁺, and electric fields between the initial coarse mesh (top row), optimally refined mesh (center row), and Ansys simulation of the aforementioned 15 cm radius uniform sphere. The geometry of the refinement is similar for MARIE (with refinement) and Ansys with the areas of highest refinement close to the end rings in the coil. Correct refinement of the mesh clearly leads to more accurate S-parameters and E-fields and B₁⁺ maps.

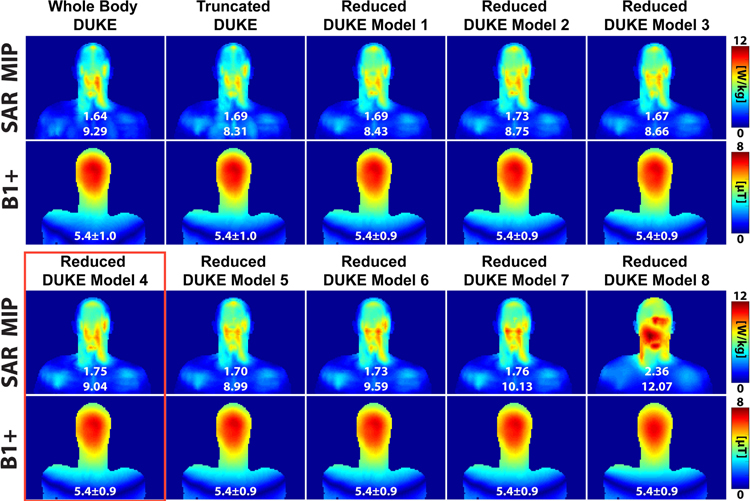
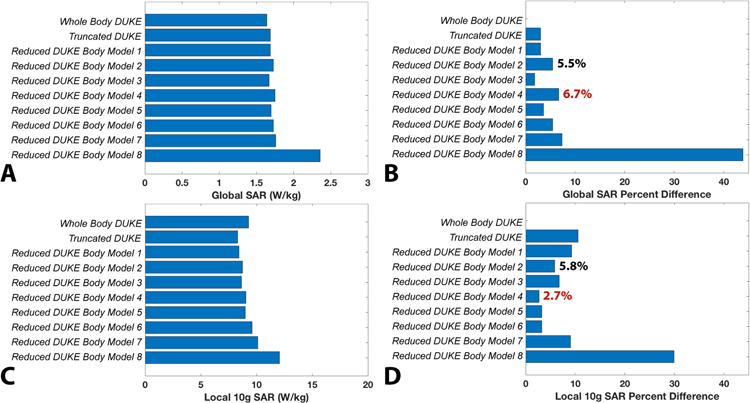
Figure 6 shows the SAR, conductivity, and B₁⁺ maps of the Whole Body Duke, Truncated Duke, and the eight Reduced Duke models. The SAR map shown is the maximum intensity projection of the 10g local SAR. Figure 7A–D shows bar graphs of the global and 10g local SAR for all Duke models (full, simplified and truncated) as well as their percent difference compared to the reference (from the full-detail whole body model). The Reduced Duke model 8, which is truncated and composed of a single tissue class (uniform model), deviated the most from the reference (estimation errors of the global SAR and 10g local SAR are 44% and 30%, respectively). Visually, the SAR distributions for the other 9 models were qualitatively similar, with SAR hotspot locations roughly at similar positions in the head and neck (see Supporting Figure S3). Reduced Duke model 4, which is the most easily obtained using a single DIXON scan and pseudo-CT registration, was associated with a 6.7% global SAR prediction error and a 2.7% 10g local SAR error. Reduced Duke model 2, which has the same tissue classes as model 4 plus CSF, had a 5.5% global SAR error and a 5.8% local SAR prediction error, indicating that addition of this high-conductivity compartment results in a negligible improvement of the modeling accuracy. Additionally, truncation below the shoulders did not have a considerable effect on SAR (estimation error of global SAR and 10g local SAR for Truncated Duke was 3.0% and 10.5%, respectively). The B₁⁺ distributions across all Duke models were very consistent with an inter-body model variability of 0.4%.

Figure 6:

SAR (maximum intensity projection) and B₁⁺ maps (center coronal slice) for the different Duke body models simulated in this work. The numbers in white below the SAR maps are the global and 10g local SAR, respectively. The numbers below the B₁⁺ maps are the mean and standard deviation in μT. Excluding Reduced Duke Model 8, the SAR distributions are similar among the different Duke simplifications and differ mainly in the amplitude of the SAR hotspot. Reduced Duke Model 4 is highlighted in red because it corresponds to the tissue grouping used in the volunteers.

Figure 7:

A. Global SAR in the Duke body models and simplifications. B. Global SAR percent difference for all Duke model simplifications, relative to Whole Body Duke. C. 10g local SAR for all the Duke models. D. 10g local SAR percent difference relative to Whole Body Duke. The percent difference for Reduced Duke Model 4 is in red in B since it represents the tissue grouping used in the volunteers. The percent differences for Reduced Duke Model 2 are in black. This model corresponds to Reduced Duke Model 4 plus CSF.

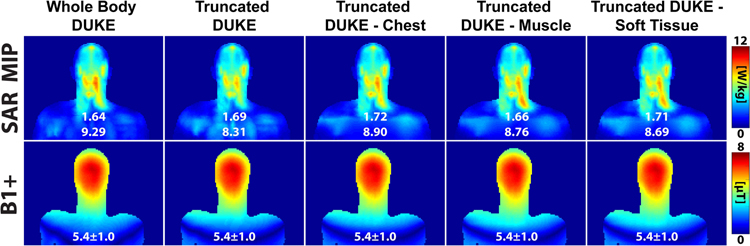
Figure 8 shows the SAR, conductivity, and B₁⁺ maps for different below-the-shoulders model truncation strategies, namely no truncation (Whole Body Duke), truncation without uniform extension (Truncated Duke), and truncation with last-slice-based uniform extension (Truncated Duke - Chest, Truncated Duke - Muscle, and Truncated Duke - Soft Tissue). The 10g local SAR was 5.7% and 6.5% greater in the Truncated Duke - Muscle and Truncated Duke-Soft Tissue models compared to the reference, while Truncated Duke - Chest had a percent difference relative to Whole Body Duke of only 4.2%. The global SAR prediction error was similar among all models (<5%), and B₁⁺ was very consistent. Based on these results, the relative permittivity, conductivity, and density of Truncated Duke - Chest (ε = 19.3, σ = 0.499 S/m, ρ = 943 kg/m³) was applied to the 100 mm body extension of the volunteers body model.

Figure 8:

SAR (maximum intensity projection) and B₁⁺ maps (center coronal slice) of Whole Body Duke, Truncated Duke, Truncated Duke - Chest, Truncated Duke - Muscle, and Truncated Duke - Soft Tissue.

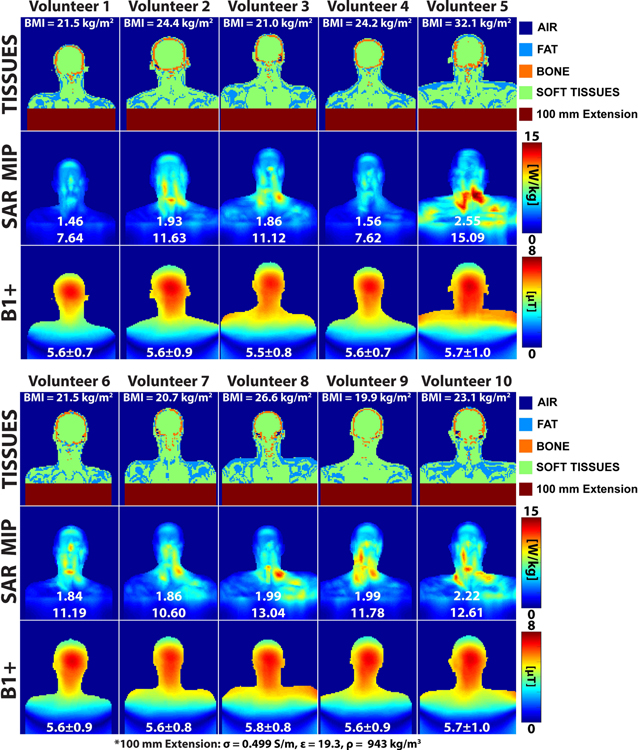
Figure 9 shows the 10g local SAR, conductivity, and B₁⁺ maps for the models of all ten volunteers. The global and 10g local SAR variability of the volunteers were 16.0% and 20.3%, respectively. The range of global SAR values for all volunteers was 1.46–2.55 W/kg while the range of local SAR values was 7.6–15.1W/kg. The local SAR hotspots all tended to occur in the high curvature region of the neck, however there was significant variability of the anatomy in this region which yielded significantly different SAR distributions. Additionally, comparing the volunteer 10g local SAR results to Whole Body Duke (9.29 W/kg) shows that using a generic body model can result in both under- (Volunteers 2–3 and 5–10 by 14–62%) and over-estimations (Volunteers 1 and 4 by 18%) of local SAR in actual volunteers.

Figure 9:

Conductivity (center coronal slice), SAR (maximum intensity projection), and B₁⁺ maps (center coronal slice) for the ten volunteers. The numbers in white below the SAR maps are the global and 10g local SAR. The number below the B₁⁺ maps are the mean and standard deviations in μT.

The importance of accurate modeling of the patient pose is illustrated in Figure 10, which shows a difference in the 10g local SAR between the arms up and arms down positions of nearly 50% (10.6 W/kg vs. 14.9 W/kg, greater in the arms up position within head and neck). Although we do expect greater SAR in the arms up position because of the greater proximity of the arms to the coil in this position, it is interesting to note that the SAR distributions in the upper torso, head and neck were also quite different in these two poses. In contrast, the B₁⁺ maps were much more consistent between volunteers (variability = 1.2%) and poses (arms up = 5.3 μT, arms down = 5.2 μT).

Figure 10:

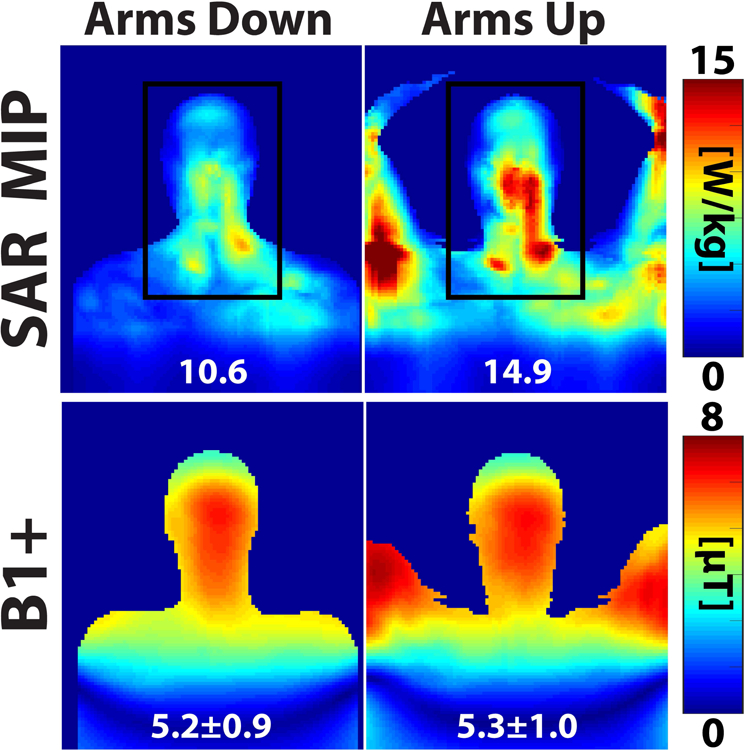
Comparison of SAR and B₁⁺ for a volunteer scanned with her arms along her sides (arms down) and above her head (arms up).

The on-the-table timings for the volunteers were as follows: The DIXON scan for the segmentation required 117 s for each volunteer. The tissue segmentation and creation of the patient specific voxel model required an average ± SD of 56.4 ± 1.8 s for the 10 volunteers. The on-the-table portion of the electromagnetic simulations required an average and SD of 290.3 ± 67.3 s for the 10 volunteers. Thus, the total on-the-table SAR determination time was 463.8 ± 67.9 s.

Discussion and Conclusion

In this study, we developed and demonstrated a new methodology for fast, patient-specific calculation of the SAR and B₁⁺ distribution which brings a personalized medicine strategy to safety prediction in MRI. A key component of the approach is the fast EM solver MARIE, which allows computation of patient-specific SAR in a total of ~8 min. Although this run time is still too long for routine clinical use, we believe it is a good first step in the effort to provide patient-specific safety monitoring. Importantly, we believe that we will be able to reduce this run time to below 2 minutes using a combination of software improvements and basic sequence acceleration methods, described below. Such a short computation time would make the approach more relevant in the clinical setting, especially because the EM computation portion of the method can be run in conjunction with the sequences in the protocols that are not SAR-limited and therefore do not require patient-specific safety monitoring. For example, clinical protocols could easily be rearranged so that the low-SAR sequences are played first, during which SAR is computed, and the high-SAR sequences second once the patient-specific safety parameters are known.

Supporting Table S3 shows the breakdown of the total processing time for each volunteer (acquisition, segmentation, EM simulation). The segmentation time was very similar for each volunteer but the EM computation time was more variable. The longest component of the on-the-table portion was the EM simulation. Of all the EM computation steps (Fig. 1), the longest was the assembly of the coupling matrix (93.4 s in average for all volunteers) followed by the iterative solve (80.4 s average). These on-the-table computation times are longer for bigger volunteers since we use a constant body model resolution of 5 mm, yielding a larger solve domain for large individuals. As shown in Figure 1, some pre-computation is performed offline, i.e. before the patient is being scanned. This takes about 1 hour and is specific to the coil being modeled, but is not specific to the patient.

The DIXON acquisition was performed without any parallel imaging acceleration. It would therefore be rather straightforward to decrease the 117 s acquisition time significantly. Others have achieved CAIPIRINHA-accelerated DIXON acquisitions in the head of ~19 seconds (58). The segmentation step used in this pipeline was implemented in Python, including a few C portions. Thus, faster compute times could be achieved utilizing a higher performance implementation such as those described in Alcain et al. (52) and potentially leveraging deep learning (59). Ultimately, this step can likely be sped-up to less than 10 s. Finally, the development team of MARIE will shortly release an updated version of the software, MARIE 2.0, which contains a number of improvements that dramatically decrease computation time. A first innovation is the possibility to precompute a compact basis for incident fields within the region of interest, which dramatically speeds up the calculation of the RF coil-patient coupling matrix. Although the precomputation is time-consuming, it is performed only once for a given coil and grid size/resolution. A second innovation is the implementation of a new iterative solver, which solves the full-wave EM problem simultaneously for the coil and for the body (60). This considerably speeds up convergence of the field calculation, in contrast with the version used in this work that requires a two-level nested iterative solver to solve the SIE and VIE problems (detailed in ref. (48)). Preliminary results show a simulation time of ~20 s using these improvements, which is a significant reduction from the 4 minutes and 50 seconds reported in the present study.

Our current implementation of the methodology required manually transferring files from the MRI scanner to the segmentation step, and then transferring that output to the EM simulation step. However, the methodology presented here can easily be fully automated and, at term, will require no human intervention beyond starting the MRI pre-scans for generation of the body model. This is important to facilitate translation to the clinic and not slowing down the clinical workflow. To benefit from the additional computation speed up provided by MARIE 2.0, the grid size needs to be fixed, and therefore the acquisition protocols can also be fixed with a FOV large enough to accommodate all subjects. The segmentation and EM simulation steps are already fully automated Matlab implementations and do not require human supervision. While the methodology is not currently automatic, we believe the changes needed to make it fully automatic are straightforward to implement. Eventually, we foresee a completely automatic implementation of the processing and computation pipeline that will run in the background and override the “default”, likely more conservative, file containing the SAR limits with the patient-specific one once the pipeline is fully executed. Additionally, we envision to also include an automatic validation step based on a comparison between the simulated and measured B₁⁺ maps. While we did not perform this comparison in our current implementation, we believe addition of this validation step would also be straightforward to implement for clinical use. Specifically, the B₁⁺ map may be acquired during the SAR computation step to avoid adding time to the overall methodology, and then quickly compared to verify the SAR calculation.

An important finding of our work is the inter-volunteer variation the 10g local SAR of 20.3%. This was greater than the 10g local SAR estimation error due to grouping of the Duke tissues classes into four compartments, e.g. air, bone, fat and soft tissue (2.3%). This indicates that it is more important to generate patient-specific models of the patients being scanned, even imperfect ones with only four tissues classes, than using a highly detailed generic model applied to all patients. This point is clearly seen in Figures 6 and 9, where the variability of SAR and B₁⁺ due to slight changes in the anatomy are evident, and visually much more pronounced than the subtle changes associated with grouping of the Duke tissue classes. It is clear (Fig. 6) that changing the number of tissue classes in Duke does not affect dramatically the spatial pattern of the 10g local SAR distribution. The 10g local SAR distribution, scaled by its maximum, is essentially preserved across the Duke models simulated in this work except for the most extreme simplification (uniform model). In contrast, 10g local SAR patterns are quite different across the volunteers in this study, which shows that the underlying induced current distribution in different patients are shaped by the local anatomy and are therefore best modeled on a patient-specific basis. This situation is even more pronounced for the non-standard patient position shown in Fig. 10, where the volunteer was asked to place her arms above the head. In this case, the Duke-based 10g local SAR prediction failed dramatically (10.6 W/kg compared to 14.9 W/kg for the patient-specific SAR calculation). Our inter-patient variabilities match up with previous studies, which have reported an inter-patient local SAR variability of 17–27% due to variability in body shape and size (8,24,50,61).

We found that a 5 mm isotropic resolution led to a reasonable tradeoff between accuracy of the body model and computation time. The full-wave simulation and coupling matrix assembly times for Duke truncated below the shoulder (with a 100 mm uniform extension) and discretized at 5 mm, 4 mm, and 3 mm isotropic resolutions are shown in Supporting Table S4. EM simulation times were 4.8, 11.3 and 20.2 min for the 5, 4, and 3 mm Duke models, respectively. Both the global and 10g local SAR increased by ~9.1% and ~16.9%, respectively, when the resolution changed from 5 to 3 mm isotropic. Similar results were seen for two of the volunteers in Supporting Table S4. For Volunteer 4, the global and 10g local SAR differed by ~10% and ~5%, respectively, between 5 and 2.6 mm isotropic resolution. For Volunteer 9, the global and 10g local SAR differed by ~7% and ~14%, respectively, between 5 and 2.6 mm isotropic resolution. The increase in SAR with increasing spatial resolution has been reported previously by Wang et al. (62), while earlier work by Collins et al. (63) in the head at 64 MHz and by Homann et al. (8) in the body did not show any significant difference in global or 10g local SAR between different spatial resolutions. Ideally, higher spatial resolutions should be used, however this may not be compatible with the limited time frame available for these computations (should be real-time).

The orbits are vulnerable to thermal damage because of the low perfusion and relatively high conductivity of the vitreous humor and because the lens is known to be particularly temperature sensitive. To further assess SAR values as a function of how the orbits are modeled we created a new model called Reduced Duke - Low Cond. Orbits, with model resolutions of 2.5 and 5 mm. This model is based on the Reduced Duke Model 1, but sets the orbit’s dielectric properties to those of soft tissues (no weighted combination). These results are shown in Supporting Figure S4. Interestingly, the SAR in the eyes of Reduced Duke - Low Cond. Orbits is in fact greater than that of Reduced Duke Model 1. This is due to the fact that the E-fields are greater in the Low Cond. Orbits model (because of the smaller conductivity) than in the Reduced Duke Model 1, and since SAR depends on the square of the electric field the result is also greater even after multiplying by the conductivity. However, comparison of the 2.5 and 5 mm resolution models shows that, although the peak local SAR was not achieved in the eyes, the small SAR hotspots present in the eyes at 2.5 mm (red arrow) is not present in the 5 mm simulation. Therefore, it would be prudent to use a resolution of 2.5 mm or finer in order to capture the eye-SAR which, for some excitations, could very well prove to be the peak local SAR.

In our simulations of the Duke body models, we determined that four tissue classes (soft tissues, air, bone and fat) are sufficient for prediction of both the global and local SAR with reasonable accuracy (<7%). Interestingly, addition of the fifth and sixth most important tissue class for prediction of SAR in the head, eyes and cerebrospinal fluid, respectively, did not have much effect on either global or 10g local SAR. In consequence, we propose a simple body model generation pipeline based on a single DIXON acquisition followed by air, fat and soft-tissue segmentation and addition of the bone compartment using a computer vision-based algorithm. These conclusions echo previous work by Wolf et al (24) and Shao et al. (50). Our choice of truncation of the body model below the chest/shoulders was based on the work by Wolf et al. (24), who found that the computation time decreases substantially in this case without affecting significantly the SAR prediction. It was also shown by Wolf et al. that addition of a small, uniform “body extension” below the truncation line improves simulation of coil loading and thus the SAR prediction accuracy. Thus, we extend our volunteer body models 100 mm below the last z-slice. We found that a good choice of material for this additional dielectric layer was the average of the tissues present in the chest, i.e. soft-tissues, lungs, bone, and fat (ε = 19.3, σ = 0.499 S/m, ρ = 943 kg/m³).

While the workflow presented here was demonstrated for head imaging at 3T using a body coil, it can be adapted to other coils, field strengths, and anatomical locations. Parallel transmission (pTx) in particular can greatly benefit from our approach as safety monitoring is made more complex in this case by interference between the E-fields created by independent transmit channels (64,65). Additionally, our workflow can potentially be incorporated into the pTx workflow for real-time SAR monitoring and optimal pulse design (66,67) although the tissue-class truncation would need to be re-validated for this application. Additionally, an interesting possibility would be to extend the approach presented here to patient-specific temperature prediction. This could be done, for example, by rapid temperature simulation via the Pennes bioheat equation following the SAR calculation, which is relatively straightforward using, for example, GPU-accelerated finite difference temperature modeling (68,69). The Pennes bioheat equation links temperature, SAR, the specific heat capacity of tissue, tissue density, blood perfusion rate and tissue thermal conductivity (1). While there are estimates of all these parameters in the literature, they are not patient-specific and likely have high inter-patient variability. This is similar to assignment of conductivity and permittivity values from databases to the different tissue classes for the EM simulation. The greater relevance of the temperature (and therefore thermal dose) on biosafety therefore needs to be balanced with the likely sensitivity of the temperature estimates to the particular database parameter values assigned, which are not yet completely agreed on and need further study.

Supplementary Material

supp info

Supporting Table S1: Conductivity, relative permittivity, and density of the tissue combinations shown in Figure 2B.

Supporting Figure S1: An extended view of Figure 3B showing all the Duke body models simulated in this study with part A showing the optimally refined coil and shield.

Supporting Figure S2: The tuning and matching circuit we employed is shown here. For each port, one tuning capacitor (C_tune) was used. Additionally, for each port, the matching circuit consisted of two inductors (for example, Lm1 and Lm2 for port 1) in a shunt configuration.

Supporting Table S2: The calculation of the port scaling is shown here for the tuning and matching circuit we employed, shown in Supporting Figure S2. We calculated the optimal values for all the inductors to achieve S11<=−20dB in Ansys (~5–10 s), utilizing the co-simulation approach developed by Kozlov et al. (55). The resulting values were used to calculate the scaling of the B- and E-fields of each port according to the equations seen here (theoretical calculation for port 1 is shown as an example) prior to combination of the fields in quadrature.

Supporting Figure S3: Axial slices of the conductivity and SAR distributions at the 10g local SAR hotspot location. The location of the hotspot differed a little within the head among the Duke models. Reduced Duke Model 4 SAR pattern is very similar to that of Whole Body Duke.

Supporting Table S3: Computation breakdown time for each of the 10 volunteers.

Supporting Table S4: EM computation times for the Truncated Duke models discretized at multiple resolutions, as well as for volunteers 4 and 9. Both the EM solve and coupling matrix assembly times increase with increasing spatial resolution.

Supporting Figure S4: Conductivity, unaveraged SAR, 10g averaged SAR, and electric field distributions for a transverse slice through the eyes (orbits) for Reduced Duke Model 1 and Reduced Duke - Low Cond. Orbits. The model resolutions were 2.5 and 5 mm isotropic. The orbits were a separate tissue class in Reduced Duke Model 1 (1.51 S/m), but set to soft tissue in Reduced Duke - Low Cond. Orbits (0.6 S/m) (all other tissues were the same as in Reduced Duke Model 1). The values of the conductivity, unaveraged SAR, 10g averaged SAR, and electric field distributions of each orbit are also shown. The 10g averaged SAR in the orbits (red arrow) increased from Reduced Duke Model 1 to the Low Cond. Orbits model only slightly. More importantly, the 10g averaged SAR at 2.5 mm resolution revealed a hotspot in the orbits that is not seen at the coarser 5 mm resolution.