Abstract
The greatest restriction to the theoretical study of the dynamics of photoinduced processes is computationally expensive electronic structure calculations. Machine learning algorithms have the potential to reduce the number of these computations significantly. Here, PySurf is introduced as an innovative code framework, which is specifically designed for rapid prototyping and development tasks for data science applications in computational chemistry. It comes with powerful Plugin and Workflow engines, which allows intuitive customization for individual tasks. Data is automatically stored through the database framework, which enables additional interpolation of properties in previously evaluated regions of the conformational space. To illustrate the potential of the framework, a code for nonadiabatic surface hopping simulations based on the Landau–Zener algorithm is presented here. Deriving gradients from the interpolated potential energy surfaces allows for full-dimensional nonadiabatic surface hopping simulations using only adiabatic energies (energy only). Simulations of a pyrazine model and ab initio-based calculations of the SO2 molecule show that energy-only calculations with PySurf are able to correctly predict the nonadiabatic dynamics of these prototype systems. The results reveal the degree of sophistication, which can be achieved by the database accelerated energy-only surface hopping simulations being competitive to commonly used semiclassical approaches.
I. Introduction
Photoinduced ultrafast processes often proceed on multiple electronic states and are controlled by nonadiabatic couplings between electronic and nuclear degrees of freedom. Nonadiabatic couplings are elaborate to calculate, since they require the first-order (nonadiabatic coupling vectors (NACs)) and the second-order (scalar couplings) derivatives of the electronic wavefunction with respect to the nuclear coordinates.1 To study these processes, nonadiabatic dynamics simulations are performed on potential energy (PE) surfaces. The surfaces can be either precomputed and fitted2−4 or computed on the fly, in so-called direct dynamics simulations.5−9 If the PE surfaces are precomputed and fitted, the computational cost of the dynamic simulation can be significantly reduced. Fitted surfaces combined with the multiconfigurational time-dependent Hartree approach (MCTDH)2,3 became the golden standard for nonadiabatic dynamics simulations. But fitting the PE surfaces is a tedious task, in particular for large systems, as PE surfaces have to be accurately fitted globally or along reaction paths, which have to be known before the simulation. On the contrary, in on-the-fly or direct dynamics simulations, the PE surfaces and properties are only computed on demand. This is the standard approach in full-dimensional semiclassical molecular dynamics calculations, like in trajectory surface hopping (TSH) simulations.7,8 In standard implementations of direct dynamics simulations, an electronic structure calculation is launched at each time step independent of whether the properties have been already calculated in this region before. Such an implementation leads to the recomputation of nearby points multiple times, especially if the system is trapped in a bound potential. In this work, the benefits of the two approaches are combined by introducing a database with an effective fitting algorithm. Hereby, in unknown regions of the conformational space, new electronic structure calculations are performed and the results are added to a database. In regions where calculations have already been performed, the fitting algorithm is used to interpolate the stored data and no further electronic structure calculations are needed, as implemented for the direct dynamics variational multiconfiguration Gaussian (dd-vMCG) approach in the Quantics program package.6,10 In recent years, computational statistical learning methods (machine learning, neural networks, deep learning, unsupervised clustering, etc.) have found to provide very promising approaches to construct PE surfaces of high-dimensional systems.11−17 Using these fitted potentials, the computational time for molecular dynamics simulations can be substantially reduced. This was successfully shown for both ground-state molecular dynamics simulations18,19 and (nonadiabatic) excited-state simulations.20−30
In this work, we introduce PySurf, a new software framework for data science applications in computational chemistry. The software package is specifically designed for rapid development and prototyping of new algorithms using the Python programming language at its core.31 The code comes with a powerful Plugin engine, which allows straightforward extensions of the existing functionality with custom modules that naturally fit into the existing environment. Its Workflow engine enables very fast development of customized work and analysis schemes. The implementation of nonadiabatic surface hopping using the Landau–Zener scheme32 is presented. The methodology is applied to a pyrazine model system and to investigate the S2/S1 conical intersection of SO2, based on ab initio calculations. Hereby, standard nonadiabatic surface hopping dynamics simulations are used to sample the important regions of the conformational space. Subsequently, an interpolation scheme is used to predict PE surfaces and gradients based on the stored data. Using fitted properties significantly reduces the computational cost, as no electronic structure calculations are performed, which are typically time determining in direct dynamics simulations. Finally, having global PE surfaces at hand, energy-only calculations are performed, where gradients are calculated directly from the fitted PE surfaces. This opens the possibility to perform nonadiabatic excited-state dynamic simulations, where only energies have to be calculated using electronic structure methods.
The paper is organized as follows: In Section II, the code infrastructure, along with its Plugin and Workflow engines, is presented. Section III introduces the theory applied in our surface hopping simulations, focusing on the energy-only algorithm, and Section IV shows the results of the dynamics simulations for the pyrazine model and the SO2 molecule. Finally, our concluding remarks are given in Section V.
II. Code Infrastructure
PySurf is a new open-source software package written in the Python programming language (Python 3.6+).31 It is designed for data science applications and will be published on Github.33 Its main objective is to provide a simple and powerful environment to both end users and developers. Therefore, the software was specifically designed to be easily extensible. Figure 1 shows a sketch of the main code architecture. The code is divided into three parts. A core framework that defines the basic functionalities (blue). A Plugin engine that allows us to customize each core component (gray) by user-defined functionality. The third part is a specifically tailored database engine (green) based on the Network Common Data Form (NetCDF)34,35 for simple writing and accessing data. The NetCDF3 format, which is the standard file format for many molecular dynamics software packages, like the AMBER36−38 software package, is well suited to store relevant data from electronic structure calculations efficiently in a compact and portable binary format (like coordinates, energies, gradients, and dipole moments).
Figure 1.
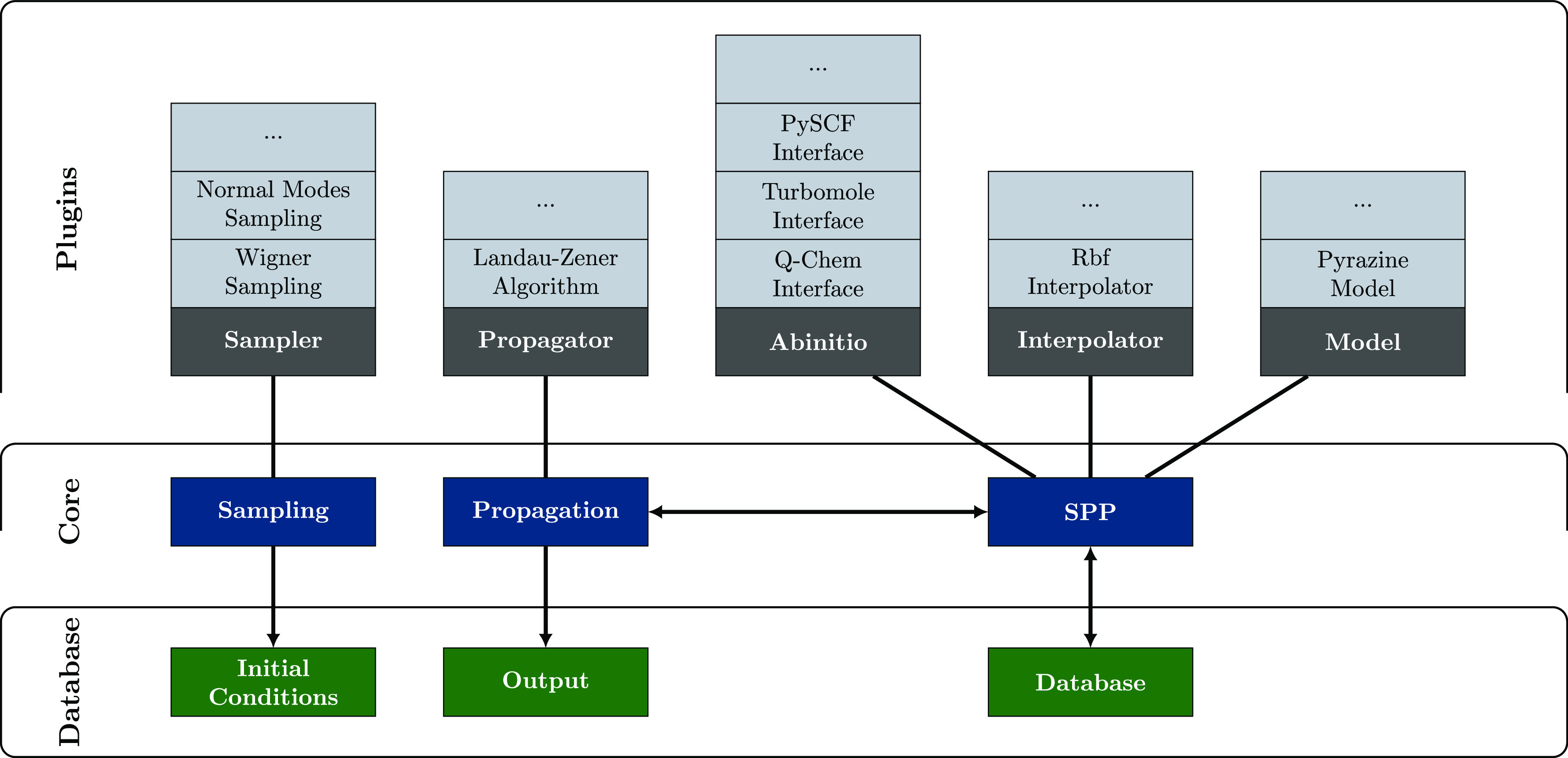
Schematic illustration of the code framework. The core components (blue) provide the general functionality, which can be customized by Plugins (gray), allowing the user to seamlessly add any new feature to the framework. The output (green) is collected in NetCDF databases to ensure fast and efficient data processing. SPP stands for the surface point provider.
Many tasks in computational chemistry can be divided into three main building blocks. The modular design of PySurf tries to match these basic building blocks, i.e., generating geometries, performing electronic structure calculations, and analyzing the results. For instance, geometries are needed for an unrelaxed PE scan along a reaction coordinate, for a semiclassical dynamics simulation or for the calculations of a spectrum. With the generalized sampling and propagation modules, many of these cases can be solved by adding small customized Plugins. At the moment, the package comes with a Wigner39 and a normal mode sampler as well as a velocity Verlet propagator with a Landau–Zener surface hopping algorithm.32 In most tasks, the evaluation of properties at a given geometry is central, e.g., performing an electronic structure calculation for energies and gradients. Therefore, we introduce a corresponding module in the PySurf framework, namely, the surface point provider (SPP). It is responsible for the provision of the properties in a standardized data format at a given geometry. There are already initiatives to provide generalized interfaces to a variety of electronic structure codes like the atomic simulation environment (ASE)40 or QCEngine.41 Existing generalized interfaces (as shown for the ASE in the Supporting Information, SI) can be easily added as Plugins to the SPP as additional ab initio methods. At this moment, interfaces to the Q-Chem,42 Turbomole,43 PySCF,44 and XTB45 program packages are provided. The SPP extends the idea of generalized interfaces further. Depending on the preferences, information is gathered by launching an electronic structure calculation from a model system or from an interpolation scheme. For this work, an interpolator based on SciPy’s46 radial basis function (Rbf) interpolator was implemented as a Plugin. The use of machine learning techniques and methods, borrowed from the realm of artificial intelligence, offers a promising alternative for the interpolation procedure.19 Currently, work in this direction is in progress in our group. All data-intensive output is stored in databases, where it can be easily accessed. The package comes with a variety of predefined analysis tools and a powerful Workflow47 engine, which allows very efficient development of customized Workflows and analysis tools.
II.I. Plugin Engine
A Plugin engine is designed to guarantee PySurf’s modularity and to make it a simple and flexible development platform to prototype and test innovative approaches. It allows extension of the core package by providing Plugins that are seamlessly and natively integrated into the framework.47 Plugins are available for all key components (see Figure 1) and make it trivial to add custom functionality. Due to the modular framework and the design-by-contract principle applied to all components, it is possible to ensure that all functionality is validated at the setup step. Additional user input is added inside the code with the help of a domain-specific language (DSL), which is used to create the input parser automatically.47 The parser validates the given input, making it unnecessary to check user input manually inside the Plugin. This provides several advantages: (i) The specific user input needed for the Plugin is written in the code of the Plugin and there is no need to extend an existing input parser manually. This avoids duplication errors and improves the code readability, leading to very clear codes. (ii) Additionally, the engine can create the documentation automatically from the information provided in the source code using the Sphinx documentation framework.48 Thus, there are no undocumented keywords and the documentation is always up-to-date with the source code.
For most modules, the user input is stored in an input file. If there is no complete input file, e.g., when the code is executed for the first time, the missing user input is asked via a command-line interface. In the SI, we provide examples on how to write a Plugin for a model and an additional sampler. The underlying code package, which implements the Plugin engine, is outside the scope of this manuscript and will be the focus of a complementary publication. Nevertheless, we refer interested readers to ref (47) for more details.
II.II. Workflow Engine
PySurf uses a powerful Workflow engine, which allows the user to intuitively combine and build new custom Workflows, like analysis tools or task sequences with little to no programming skills. A Workflow consists of different functions that are executed sequentially to fulfill a certain task. For the Workflow, a DSL is used, based on a subset of the Python programming language. This has the advantages that more advanced tasks like full-fledged command-line interfaces or error handling can be automatically taken care of for the user. Additionally, before a Workflow is executed, it is checked for type correctness, which can already capture a significant amount of mistakes. Users can add new functions to the Workflow engine either in Python or by combining already existing Workflow functions in a modular approach. The Workflow engine exploits the full modularity of the PySurf package and custom Plugins are automatically usable in the Workflow engine. Examples on how to set up individual Workflows are given in the SI.
III. PySurf: Application Domain
PySurf is a framework with a powerful toolbox to treat and automatize many tasks in computational chemistry. In this work, PySurf is used to implement the Landau–Zener surface hopping scheme for nonadiabatic dynamics simulations. In surface hopping simulations, the computationally most expensive part is the large number of electronic structure calculations that need to be performed for the independent trajectories.9 An obvious way to reduce computational costs is to use the ability of the SPP to fit surfaces based on already precomputed electronic structure data. Similar approaches have been presented by Worth et al.6 for the dd-vMCG method with a modified Shepard interpolation scheme.49,50 For dynamics simulations using Tully’s fewest switches surface hopping (FSSH) algorithm, machine learning models to fit excited-state properties have been implemented.24,29 Combining Tully’s approach with machine learning algorithms demands to fit nonobservables, i.e., NACs. It has been shown that phase correction is necessary for the fitting of NACs in such a dynamics simulation.29 To overcome these circumstances, different surface hopping algorithms that depend only on observables can be used, such as the Landau–Zener32 or the Zhu–Nakamura schemes.51−53 The latter was combined with deep learning algorithms to successfully simulate the S1/S0 transition of CH2NH and 6-aminopyrimidine.22,23 Recently, it has been shown that nonadiabatic dynamics simulations with the Landau–Zener algorithm and the FSSH algorithm produce very similar results.54 The main difference between both approaches is the way how the hopping probability from state i to state j is computed. In Tully’s approach, this is done as a function of the coefficients of the electronic wavefunction and the nonadiabatic coupling vector.55 The Landau–Zener hopping probability, however, is given purely as a function of the energy gap (ΔVij = |Vi – Vj|) between the two states and its second derivative at a certain nuclear position R(t), if there is a minimum in the energy difference at time tc(54)
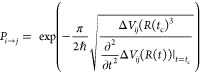 |
1 |
Therefore, nonadiabatic dynamics simulations can be performed using only energies and gradients. This simplicity makes it attractive for excited-state methods, where NACs are not available or too expensive to compute. It is worth mentioning that the Landau–Zener hopping probability reflects the inverse proportionality of the NACs on the energy gap of the PE surfaces. Here we demonstrate that combining the interpolation capability of PySurf with the Landau–Zener algorithm opens up another attractive and cheap doorway for surface hopping simulations. Having global PE surfaces at hand from the interpolation, gradients can be calculated from the fitted energies either by a finite difference scheme or by computing the analytic gradient of the fitting algorithm itself.22,24,29 The latter is common in machine learning libraries that support automated gradient generators.56,57 As the prediction of energies by interpolation is computationally cheap, it is also inexpensive to predict the gradients of the PE surfaces based on the interpolation. This approach, hereafter called energy-only simulations, allows one to perform nonadiabatic molecular dynamics simulation using only energies as input from ab initio calculations. Nuclear gradients needed for the propagation are computed numerically or analytically derived from the fitting algorithm itself. This scheme is of particular interest for electronic structure methods for which the analytic gradients are not available. The general Workflow has the following steps: (i) Filling the database using typical sampling approaches, e.g., Wigner sampling, or performing nonadiabatic dynamics simulations as it is done in this work. (ii) After the conformational space is sampled, nonadiabatic dynamics are performed using only the fitting algorithm until the trajectory leaves the conformational space, where the fit is accurate. If this occurs within the simulation time, it is necessary to extend the database by performing new ab initio calculations. Additionally, a so-called adaptive sampling scheme can be applied. Hereby, the fit is used, whenever it is accurate, else ab initio calculations are performed and are used to extend the database. In the ideal case, the database contains only the data points needed to accurately fit the relevant conformational space and should therefore not show an exponential increase with the number of degrees of freedom. However, this depends on the sampling approach and on the system at hand. The proposed Workflow can be in principle applied in all cases as long as Landau–Zener surface hopping is valid, i.e., it is exact for the two-state case and can be successfully used for transitions that mainly involve two states, which are reasonably well separated from other electronic states, whereas it conceptually fails when more electronic states are within a small energy range. Additionally, the selection of the training data for an accurate fit can be considered as another limiting factor, and so far, no general solution to this problem exists. In the following, we reveal the degree of sophistication that can be achieved by energy-only dynamics being competitive with dynamics using both energies and analytic gradients from ab initio computations.
IV. Results and Discussion
As proof of principle for surface hopping simulations using fitted properties as well as the energy-only algorithm, dynamics simulations of a pyrazine model are performed.58 To analyze the energy-only surface hopping simulations and to validate the accuracy of the fitting algorithm, our results are compared with previous simulations.54,58 Moreover, the population transfer at the S1/S2 conical intersection of SO2 was simulated based on ab initio calculations and compared with the dynamics on interpolated surfaces. The simulations followed a general protocol: First, an independent set of 100 trajectories is propagated to sample the conformational space and the data is stored in a database. Second, the data (i.e., energies and gradients) is used as training data for the fitting algorithm (for SO2, additional data from grid sampling supplements the training data). Subsequently, the quality of the fitted properties has to be checked in the validation step. For this, another set of 100 trajectories, based on independent Wigner sampling, is propagated and the data is stored. The latter data points are compared with the predictions of the interpolator. Finally, the fitted properties are used to perform dynamics simulations with 1000 trajectories (production runs), which are compared with reference calculations. The reference calculations are a set of 1000 trajectories, starting with the same initial conditions as the production calculations, but taking energies and gradients directly from the model or ab initio calculations without interpolation.
IV.I. Pyrazine Models
As the first example of the performance of the energy-only dynamics using PySurf, a pyrazine model is investigated. Pyrazine is a molecule with 24 degrees of freedom and complicated dynamics, which is governed by a conical intersection between the S1 and S2 electronic states. A considerable amount of theoretical investigations, ranging from fully quantum dynamics simulations59 to semiclassical direct dynamics,54 revealed the S1 and S2 vibronic coupling dynamics in pyrazine.
Here we use the two-state model by Sala et al.58 with five dimensions. The model was extended by a harmonic ground-state PE surface using the ground-state frequencies of the equilibrium geometry. Adiabatic energies are obtained by diagonalization of the diabatic matrix. Adiabatic gradients are calculated by a first-order finite difference scheme from the adiabatic energies. The model is implemented in the PySurf framework and is included as an example system in the program package as the PyrazineSala Plugin.
Following the simulation protocol described above, appropriate data has to be fed in the database as training data for the fitting algorithm. To sample relevant data, 100 trajectories, whose initial geometry and velocity are based on a Wigner sampling algorithm, were propagated for 100 fs with a time step of 0.5 fs. The initial state for the trajectories was chosen to be the second excited adiabatic state of the model, which corresponds primarily to the bright B2u(π–π*) state. Energies and gradients of each state at each point along the trajectories were stored in the database. After the simulations, points close to each other were deleted from the database. As the hopping probability is high in regions with small energy gaps (cf. eq 1), two different radii were introduced for points being close to each other. In regions, where the energy difference between two states is smaller than 0.5 eV, points closer than 0.25 in dimensionless normal mode coordinates (using the Euclidean norm) were deleted from the database. In areas, where the surfaces are energetically well separated (energy gap >0.5 eV), points closer than 0.75 (using the Euclidean norm in the dimensionless normal mode coordinates) were deleted from the database. Following that procedure, the number of data sets in the database was reduced from 20 100 to finally 6148 data sets, which corresponds to a reduction of almost 70%. Please note that the fraction of the data that is deleted in the cleaning process may be considered as the first indicator of whether the training data is sufficient. We assume that only a fraction of the complete conformational space is relevant for the simulation and needs to be sampled accurately. Using an equidistant grid, the number of points increases exponentially with the dimensionality. An adaptive sampling scheme may overcome that hurdle, as it samples only the important regions in the conformational space. The latter allows us to treat high-dimensional systems with a limited number of points.
After generating data, it is crucial to test its capabilities and validity. Specifically, it is important to get an estimate of the error that comes with predictions based on the data. For our validation procedure, 100 trajectories, based on independent Wigner sampling, were propagated for 100 fs with a time step of 0.5 fs, using the information from the models, i.e., an independent set of 20 100 data points is created and used as validation data. The energies and gradients of these points are compared to the predictions based on the training data. As a fitting algorithm, a radial basis function (Rbf) interpolator was used with multiquadric basis functions. The width of the multiquadric function was chosen to be ε = 1.0. The root-mean-square deviations (RMSD) is used here to indicate whether the training set and interpolation algorithm are capable to reproduce the desired observables. The RMSD of the energy and gradients for the model are 5.9 and 11 meV, respectively, which confirmed the validity of the employed scheme.
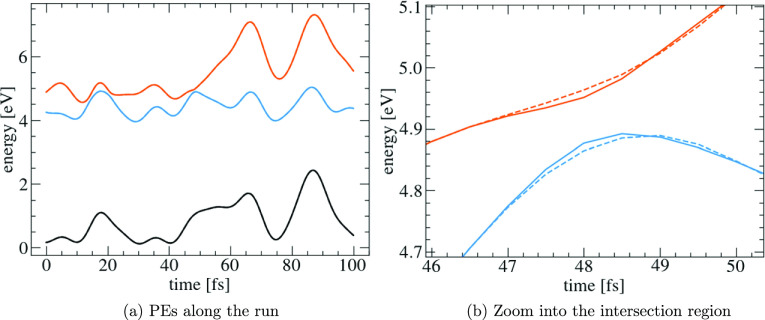
Figure 2a shows the PE surfaces as functions of time of a representative validation trajectory (solid) together with the predictions of the interpolator (dashed). From the figure, it is hard to see any difference as the curves lie on top of each other, reflecting their excellent agreements. The good fitting result relies on appropriate training data. The training trajectories naturally sample the important parts of the conformational space including the areas of high hopping probabilities. Figure 2b shows a close view of the crucial area, i.e., where the S1 and S2 surfaces are close to each other, which is explored by the trajectory after about 48 fs. The fitted PE surfaces (dashed) show a slightly larger energy gap than the model PE surfaces (solid). The difference in the energy gap is about 25 meV. The increase of the energy gap can be explained, as the Rbf interpolator smoothens the PE surfaces. Therefore, it is particularly difficult for the Rbf interpolator to predict the kink at the intersection. More advanced fitting algorithms like neural networks may be better suited to overcome that limitation.
Figure 2.
Comparison of fitted (dashed) and original PE surfaces (solid) along a representative validation trajectory of the five-dimensional (5D) pyrazine model. S0 (black); S1 (blue); and S2 (orange).
After training and validation of the properties, the SPP provides global surfaces for energies, gradients, and optionally other properties, which can be used in further applications. In this study, the PE surfaces and gradients are used to run surface hopping dynamics simulations, which can be directly compared with reference calculations. As reference calculations, 1000 trajectories, based on independent Wigner sampling, are propagated for 100 fs using the fitted PE surfaces and gradients without consultation of the model. For a one-to-one comparison, reference calculations using the same initial conditions and the same random number seeds for the Landau–Zener algorithm were performed. Figure 3 shows the population dynamics for the 5D model of the simulations based on the fitted properties (dashed line) compared to the populations of the reference calculations (solid line). The populations are in very good agreement within the first 20 fs. Subsequently, a more extensive population transfer is observed for the reference simulations, leading to a final population in the S1 state of almost 90%. The simulations using the fitted properties stretch the population transfer slightly, leading to a smaller population of the S1 state and a larger population in the S2 state compared to the reference calculations for the time between 20 and 60 fs. However, they reproduce the modulations of the population curves during the transfer process. From 60 fs to the end, the populations coincide very well again. Considering the accuracy of the surface hopping method in general, which neglects all nuclear quantum effects, using the fitted properties seems an appropriate approximation. A possible explanation for the slightly faster population transfer of the reference data is that it is hard for the Rbf to reproduce the kink of the conical intersection accurately, as shown in Figure 2b. This leads to a larger energy gap and a smaller second derivative close to the conical intersection, leading to an overall smaller hopping probability of the Landau–Zener algorithm.
Figure 3.
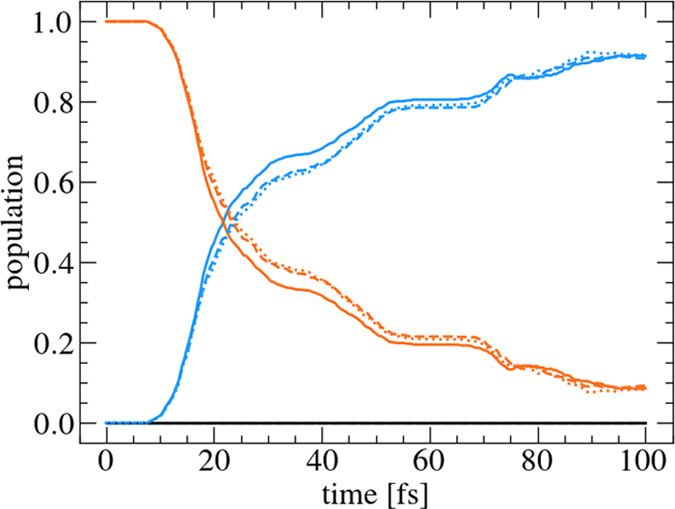
Comparison of the population dynamics of the 5D pyrazine model of the reference (solid), fitted (dashed), and energy-only (dotted) calculations. S0 (black); S1 (blue); and S2 (orange).
As the fitted PE surfaces are available globally, gradients can be numerically calculated from the fitted PE surfaces by a finite difference scheme, as explained above, leading to the so-called energy-only simulations. In Figure 3, the dotted lines show the population dynamics of 1000 trajectories of an energy-only simulation, using the same initial conditions and random seed as for the reference calculations. The populations of the energy-only simulations coincide very well with the populations of the simulation, where also the gradients were fitted. It shows that the additional deviations due to the energy-only algorithm (dotted) are much smaller than the deviations between reference (solid) and fitted calculations (dashed). So, energy-only seems to be a reasonable simplification when accurate PE surfaces are available.
The results are compared with the populations obtained from full quantum calculations and previous trajectory-based semiclassical surface hopping simulations of the same model.54,58 The population transfer from the S2 to the S1 state is slightly slower compared to the previous surface hopping simulations with the Landau–Zener algorithm.54 This can be explained by the fact that in the calculations here, all trajectories start from the adiabatic S2 state. In the previous simulations, trajectories are excited to the bright diabatic B2u state. Subsequently, the system is transformed to the adiabatic representation, leading to slightly different initial conditions, i.e., not all trajectories start from the adiabatic S2 state. Comparing the population transfer obtained from surface hopping simulations, following the scheme proposed here, with full quantum dynamics simulations using the MCTDH method,54 it is apparent that the population transfer is accurately reproduced. To sum up, the different preparation scheme of the initial conditions has more influence on the results than the semiclassical approximations during the simulations.
IV.II. SO2: Ab Initio-Based Example
In the last decade, several studies investigated the excited-state dynamics of SO2, showing that intersystem crossing plays a crucial role.60−62 Moreover, its conical intersection between the two lowest singlet excited states, 11A2 and 11B1, has been studied in detail.63,64 Excitation from the ground state to the 11B1 state is a dipole-allowed transition, which corresponds to the S0–S1 excitation at the Franck–Condon position. It has been shown that excitation to the 11B1 state leads to small intermediate population transfer to S2, but most of the population stays in the S1 state throughout the simulation.63,64 Since we use the system and its S1/S2 conical intersection as a proof-of-principle example for the energy-only approach, trajectories are initially located on the S2 state. This allows us to study a large population transfer from the S2 to the S1 state within 100 fs. Corresponding results for trajectories starting from the S1 state are given in the SI.
The ground-state energy of SO2 has been minimized to obtain the equilibrium geometry. Frequencies and normal mode displacements were calculated at the ground-state minimum energy position and used in the Wigner sampling. To enhance the convergence and stability of the excited-state electronic structure calculations during the dynamics simulations, an additional ghost state (S3) was included, which was not considered in the propagation. As an underlying electronic structure method, time-dependent density functional theory was applied using the B3LYP functional65 and Pople’s 6-31G* basis set,66 as implemented in the Q-Chem program package.42
Following the same protocol as for the model systems, the first 100 trajectories were propagated for 100 fs with a 0.5 fs time step based solely on ab initio calculations and starting from the S2 state. The data was stored in the database, and subsequently, the nearby points were deleted. The threshold for regions with small energy gaps (<0.5 eV) was 0.05 Bohr, whereas for areas where the surfaces are well separated, the radius is 0.1 Bohr (using the Euclidean norm). By this, a database with 1524 data sets was generated. Moreover, a grid in internal coordinates, containing 1759 data points, was added to the training data, to make sure that no extrapolation is needed. The data points are shown in Figure 4 in blue. The fitting was performed in internal coordinates, i.e., atomic distances, reducing the dimensionality of the system from 9 to 3, excluding overall translation and rotation of the molecule during the fitting procedure. The width of the multiquadric basis functions of the Rbf interpolator has been set to ε = 0.35 Bohr. As a validation set, another 100 trajectories were propagated for 100 fs with a time step of 0.5 fs based on independent Wigner sampling. The points of the validation set are illustrated in orange in Figure 4. To validate the fit, the energies of the validation set were compared with the corresponding predictions from the fit, getting an RMSD for the energy surfaces of 35 meV.
Figure 4.
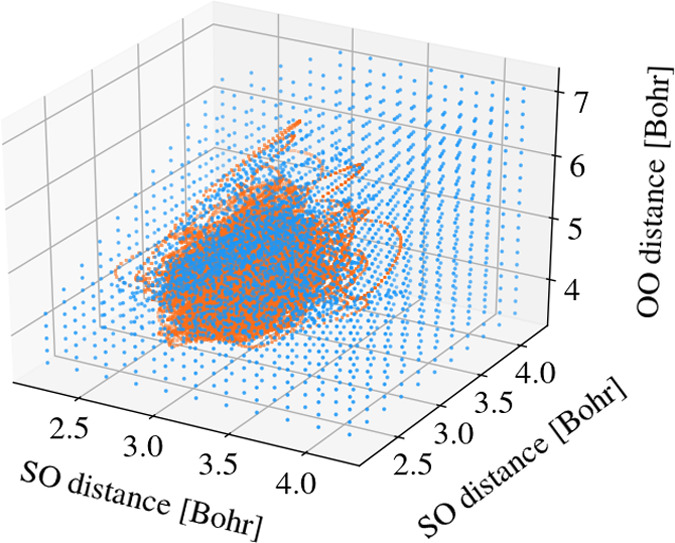
Data points in the space of internal coordinates for the SO2 molecule. The blue points (3283) represent the training set, whereas the orange points correspond to the validation set (20 100).
Figure 5 shows the fitted PE surfaces of the S1 and S2 states along the angular bending mode and the antisymmetric stretching mode, spanning the branching space and thus showing the cone of the conical intersection. The symmetric stretch normal mode is fixed at its equilibrium position.
Figure 5.
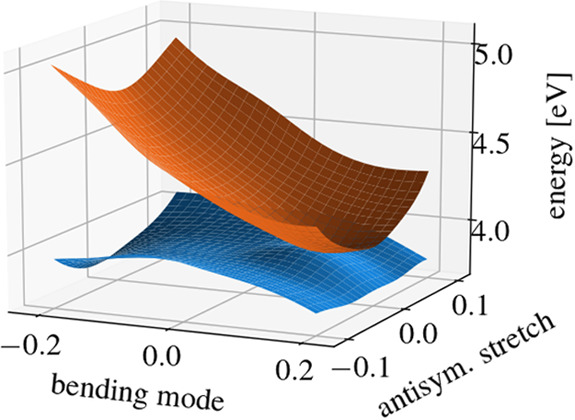
Fitted PE surfaces of SO2, showing the cone of the S1/S2 conical intersection.
Moreover, we have implemented an algorithm for optimization of the conical intersection following the Lagrange multiplier constraint approach proposed by Yarkony et al.,67 utilizing SciPy46 constrained optimization. The obtained structure from the conical intersection optimization on the fitted PE surface is then compared with the structure obtained using the minimum energy crossing point optimization (MECP), as implemented in Q-Chem Software suite.42 The RMSD of the internal coordinates between the latter structures is around 0.01 Å, showing the accuracy of the fitted PE surfaces.
Having the PE surfaces at hand, nonadiabatic surface hopping simulations using the energy-only algorithm were performed. In total, 1000 trajectories based on Wigner sampling were propagated for 100 fs with a time step of 0.5 fs. Another 1000 trajectories with exactly the same initial conditions purely based on ab initio calculations without any support of the database and interpolation were propagated as a reference set. The corresponding population dynamics for the energy-only calculations is shown in Figure 6 (dotted) compared with the populations of the fully ab initio-based reference simulations (solid). The two simulations coincide very well during the first 10 fs, where half of the population is transferred from S2 (blue) to the S1 (orange) state. Between 10 and 40 fs, the energy-only results predict a slightly larger population in the S1 state. Subsequently, the population of the S1 state of the energy-only simulation is a little bit smaller than for the reference calculations. Finally, for both simulations, about 85% of the population is in the S1 state. At about 50 fs, a small population transfer is observed to the ground state (black) for both methods. However, the energy-only simulations predict a larger transfer, which leads to the final occupation of the ground state of more than 5%. The results are also in good agreement with surface hopping simulations using the linear vibronic coupling scheme4 (see SI). Comparing computational times shows the speedup by the interpolation compared to direct ab initio calculations. The interpolator can provide energies and gradients for all states for one geometry roughly 1000 times faster than an electronic structure calculation. Already for this small system, the interpolation gives an enormous speedup, but the benefit gets much larger for larger systems. Developing and applying the derived methodology will open up new doorways for nonadiabatic excited-state dynamic simulations for large molecular systems.
Figure 6.
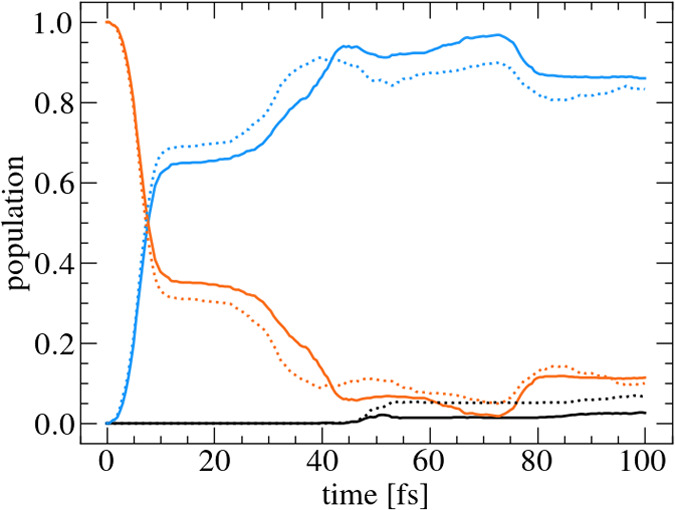
Population dynamics of reference (solid) and energy-only (dotted) calculations for SO2. In the simulations, 1000 trajectories were propagated. S0 (black); S1 (blue); and S2 (orange).
V. Conclusions
PySurf is a modular software package in Python applying state-of-the-art best coding practices. By design, new features, like interpolators, interfaces, and samplers, can be easily and seamlessly added via the Plugin engine. Ab initio calculations are set up and launched from the framework, and their data can be stored in the powerful PySurf database environment. Properties can be interpolated, for example, the interpolation of energies leads to PE surfaces. Once the important areas of the conformational space are sampled, training of the fitting algorithm and the actual evaluation of the surfaces require orders of magnitude less computational time than electronic structure calculations. The Workflow engine provides a toolbox for analysis methods and task sequences. Custom Workflows can be easily developed by combining existing modules or adding functionality in a modular approach. This makes PySurf an excellent development platform for data scientific approaches in computational chemistry.
In this work, the PySurf package was used for nonadiabatic surface hopping simulations. The conformational space was explored, and the data was stored in the database environment and afterward used to produce fitted PE surfaces. With these fitted surfaces, so-called energy-only surface hopping simulations, where gradients are calculated numerically from the PE surfaces, were performed. For the pyrazine model system as well as the S1/S2 conical intersection of the SO2 molecule, the energy-only simulations predicted the dynamics correctly. The proposed protocol allows us to perform surface hopping simulations using only adiabatic energies. Specifically for large molecules and electronic structure methods, where gradients and NACs are costly or not implemented, energy-only dynamic simulations open new possibilities. Furthermore, we are working on more sophisticated fitting procedures for the data, i.e., machine learning techniques like neural networks. Having global PE surfaces at hand and systematically overcoming the technical and conceptual difficulties, PySurf can be further extended to include various algorithms, such as transition-state search, minimum energy crossing points, and conical intersection optimization. This will bring a novel platform for the excited-state nonadiabatic dynamics community.
Acknowledgments
This work is part of the Innovational Research Incentives Scheme Vidi 2017 with project number 016.Vidi.189.044, which is (partly) financed by the Dutch Research Council (NWO).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00825.
SO2 calculations; populations for SO2; Plugin tutorial; and Workflow tutorial (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Conical Intersections: Electronic Structure, Dynamics and Spectroscopy;Domcke W.; Yarkony D.; Köppel H., Eds.; World Scientific: Singapore, 2004. [Google Scholar]
- Beck M.; Jäckle A.; Worth G.; Meyer H.-D. The multiconfiguration time-dependent Hartree (MCTDH) method: a highly efficient algorithm for propagating wavepackets. Phys. Rep. 2000, 324, 1–105. 10.1016/s0370-1573(99)00047-2. [DOI] [Google Scholar]
- Meyer H.-D.; Gatti F.; Worth G. A.. Multidimensional Quantum Dynamics: MCTDH Theory and Applications; Wiley-VCH: Weinheim, 2009. [Google Scholar]
- Plasser F.; Gómez S.; Menger M. F. S. J.; Mai S.; González L. Highly efficient surface hopping dynamics using a linear vibronic coupling model. Phys. Chem. Chem. Phys. 2019, 21, 57–69. 10.1039/C8CP05662E. [DOI] [PubMed] [Google Scholar]
- Ben-Nun M.; Quenneville J.; Martínez T. J. Ab Initio Multiple Spawning: Photochemistry from First Principles Quantum Molecular Dynamics. J. Phys. Chem. A 2000, 104, 5161–5175. 10.1021/jp994174i. [DOI] [Google Scholar]
- Worth G. A.; Robb M. A.; Burghardt I. A novel algorithm for non-adiabatic direct dynamics using variational Gaussian wavepackets. Faraday Discuss. 2004, 127, 307–323. 10.1039/b314253a. [DOI] [PubMed] [Google Scholar]
- Barbatti M. Nonadiabatic dynamics with trajectory surface hopping method. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2011, 1, 620–633. 10.1002/wcms.64. [DOI] [Google Scholar]
- Mai S.; Marquetand P.; González L. Nonadiabatic dynamics: The SHARC approach. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1370 10.1002/wcms.1370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persico M.; Granucci G. An overview of nonadiabatic dynamics simulations methods, with focus on the direct approach versus the fitting of potential energy surfaces. Theor. Chem. Acc. 2014, 133, 1526 10.1007/s00214-014-1526-1. [DOI] [Google Scholar]
- Worth G. Quantics: A general purpose package for Quantum molecular dynamics simulations. Comput. Phys. Commun. 2020, 248, 107040 10.1016/j.cpc.2019.107040. [DOI] [Google Scholar]
- Lorenz S.; Groß A.; Scheffler M. Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett. 2004, 395, 210–215. 10.1016/j.cplett.2004.07.076. [DOI] [Google Scholar]
- Netzloff H. M.; Collins M. A.; Gordon M. S. Growing multiconfigurational potential energy surfaces with applications to X + H2 (X=C,N,O) reactions. J. Chem. Phys. 2006, 124, 154104 10.1063/1.2185641. [DOI] [PubMed] [Google Scholar]
- Behler J.; Parrinello M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401 10.1103/PhysRevLett.98.146401. [DOI] [PubMed] [Google Scholar]
- Behler J.; Reuter K.; Scheffler M. Nonadiabatic effects in the dissociation of oxygen molecules at the Al(111) surface. Phys. Rev. B 2008, 77, 115421 10.1103/PhysRevB.77.115421. [DOI] [Google Scholar]
- Behler J. First Principles Neural Network Potentials for Reactive Simulations of Large Molecular and Condensed Systems. Angew. Chem., Int. Ed. 2017, 56, 12828–12840. 10.1002/anie.201703114. [DOI] [PubMed] [Google Scholar]
- von Lilienfeld O. A. Quantum Machine Learning in Chemical Compound Space. Angew. Chem., Int. Ed. 2018, 57, 4164–4169. 10.1002/anie.201709686. [DOI] [PubMed] [Google Scholar]
- Christensen A. S.; Faber F. A.; von Lilienfeld O. A. Operators in quantum machine learning: Response properties in chemical space. J. Chem. Phys. 2019, 150, 064105 10.1063/1.5053562. [DOI] [PubMed] [Google Scholar]
- Li Z.; Kermode J. R.; De Vita A. Molecular Dynamics with On-the-Fly Machine Learning of Quantum-Mechanical Forces. Phys. Rev. Lett. 2015, 114, 096405 10.1103/PhysRevLett.114.096405. [DOI] [PubMed] [Google Scholar]
- Behler J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901 10.1063/1.4966192. [DOI] [PubMed] [Google Scholar]
- Häse F.; Valleau S.; Pyzer-Knapp E.; Aspuru-Guzik A. Machine learning exciton dynamics. Chem. Sci. 2016, 7, 5139–5147. 10.1039/C5SC04786B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F.; Du L.; Zhang D.; Gao J. Direct learning hidden excited state interaction patterns from ab initio dynamics and its implication as alternative molecular mechanism models. Sci. Rep. 2017, 7, 8737 10.1038/s41598-017-09347-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.-K.; Liu X.-Y.; Fang W.-H.; Dral P. O.; Cui G. Deep Learning for Nonadiabatic Excited-State Dynamics. J. Phys. Chem. Lett. 2018, 9, 6702–6708. 10.1021/acs.jpclett.8b03026. [DOI] [PubMed] [Google Scholar]
- Hu D.; Xie Y.; Li X.; Li L.; Lan Z. Inclusion of Machine Learning Kernel Ridge Regression Potential Energy Surfaces in On-the-Fly Nonadiabatic Molecular Dynamics Simulation. J. Phys. Chem. Lett. 2018, 9, 2725–2732. 10.1021/acs.jpclett.8b00684. [DOI] [PubMed] [Google Scholar]
- Dral P. O.; Barbatti M.; Thiel W. Nonadiabatic Excited-State Dynamics with Machine Learning. J. Phys. Chem. Lett. 2018, 9, 5660–5663. 10.1021/acs.jpclett.8b02469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen W.-K.; Liu X.-Y.; Fang W.-H.; Dral P. O.; Cui G. Deep learning for nonadiabatic excited-state dynamics. J. Phys. Chem. Lett. 2018, 9, 6702–6708. 10.1021/acs.jpclett.8b03026. [DOI] [PubMed] [Google Scholar]
- Williams D. M.; Eisfeld W. Neural network diabatization: A new ansatz for accurate high-dimensional coupled potential energy surfaces. J. Chem. Phys. 2018, 149, 204106 10.1063/1.5053664. [DOI] [PubMed] [Google Scholar]
- Xie C.; Zhu X.; Yarkony D. R.; Guo H. Permutation invariant polynomial neural network approach to fitting potential energy surfaces. IV. Coupled diabatic potential energy matrices. J. Chem. Phys. 2018, 149, 144107 10.1063/1.5054310. [DOI] [PubMed] [Google Scholar]
- Guan Y.; Zhang D. H.; Guo H.; Yarkony D. R. Representation of coupled adiabatic potential energy surfaces using neural network based quasi-diabatic Hamiltonians: 1, 2 2A′ states of LiFH. Phys. Chem. Chem. Phys. 2019, 21, 14205–14213. 10.1039/C8CP06598E. [DOI] [PubMed] [Google Scholar]
- Westermayr J.; Gastegger M.; Menger M. F. S. J.; Mai S.; González L.; Marquetand P. Machine learning enables long time scale molecular photodynamics simulations. Chem. Sci. 2019, 10, 8100–8107. 10.1039/C9SC01742A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westermayr J.; Marquetand P.. Machine learning for electronically excited states of molecules, arXiv:2007.05320. arXiv.org e-Print archive, 2020. https://arxiv.org/abs/2007.05320. [DOI] [PMC free article] [PubMed]
- Van Rossum G.; Drake F. L.. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, 2009. [Google Scholar]
- Belyaev A. K.; Lebedev O. V. Nonadiabatic nuclear dynamics of atomic collisions based on branching classical trajectories. Phys. Rev. A 2011, 84, 014701 10.1103/PhysRevA.84.014701. [DOI] [Google Scholar]
- Menger M. F. S. J.; Ehrmaier J.; Faraji S.. A Framework for DatabaseAccelerated Quantum Chemistry. 2020, http://github.com/mfsjmenger/pysurf.
- Rew R.; Davis G. NetCDF: an interface for scientific data access. IEEE Comput. Graphics Appl. 1990, 10, 76–82. 10.1109/38.56302. [DOI] [Google Scholar]
- Brown S. A.; Folk M.; Goucher G.; Rew R.; Dubois P. F. Software for Portable Scientific Data Management. Comput. Phys. 1993, 7, 304–308. 10.1063/1.4823180. [DOI] [Google Scholar]
- Case D.et al. AMBER 2018; University of California: San Francisco, 2018.
- Salomon-Ferrer R.; Case D. A.; Walker R. C. An overview of the Amber biomolecular simulation package. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2013, 3, 198–210. 10.1002/wcms.1121. [DOI] [Google Scholar]
- Case D. A.; Cheatham T. E.; Darden T.; Gohlke H.; Luo R.; Merz K. M.; Onufriev A.; Simmerling C.; Wang B.; Woods R. J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun L.; Hase W. L. Comparisons of classical and Wigner sampling of transition state energy levels for quasiclassical trajectory chemical dynamics simulations. J. Chem. Phys. 2010, 133, 044313 10.1063/1.3463717. [DOI] [PubMed] [Google Scholar]
- Larsen A. H.; et al. The atomic simulation environment-a Python library for working with atoms. J. Phys.: Condens. Matter 2017, 29, 273002 10.1088/1361-648x/aa680e. [DOI] [PubMed] [Google Scholar]
- Smith D.; Altarawy D.; Burns L.; Welborn M.; Naden L. N.; Ward L.; Ellis S.; Crawford T. The MolSSI QCArchive Project: An open-source platform to compute, organize, and share quantum chemistry data. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2020, e1491 10.1002/wcms.1491. [DOI] [Google Scholar]
- Shao Y.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. 10.1080/00268976.2014.952696. [DOI] [Google Scholar]
- TURBOMOLE GmbH. TURBOMOLE, V7.2; University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 2017.
- Sun Q.; Berkelbach T. C.; Blunt N. S.; Booth G. H.; Guo S.; Li Z.; Liu J.; McClain J. D.; Sayfutyarova E. R.; Sharma S.; Wouters S.; Chan G. K.-L. PySCF: the Python-based simulations of chemistry framework. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1340 10.1002/wcms.1340. [DOI] [Google Scholar]
- Grimme S.; Bannwarth C.; Shushkov P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z=1-86). J. Chem. Theory Comput. 2017, 13, 1989–2009. 10.1021/acs.jctc.7b00118. [DOI] [PubMed] [Google Scholar]
- Virtanen P.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. 10.1038/s41592-019-0686-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Menger M. F. S. J.Colt. 2020, http://github.com/mfsjmenger/colt.
- Brandl G.Sphinx. 2020, https://github.com/sphinx-doc/sphinx.
- Frankcombe T. J.; Collins M. A.; Worth G. A. Converged quantum dynamics with modified Shepard interpolation and Gaussian wave packets. Chem. Phys. Lett. 2010, 489, 242–247. 10.1016/j.cplett.2010.02.068. [DOI] [Google Scholar]
- Frankcombe T. J. Using Hessian update formulae to construct modified Shepard interpolated potential energy surfaces: Application to vibrating surface atoms. J. Chem. Phys. 2014, 140, 114108 10.1063/1.4868637. [DOI] [PubMed] [Google Scholar]
- Zhu C.; Nakamura H.; Re N.; Aquilanti V. The two-state linear curve crossing problems revisited. I. Analysis of Stokes phenomenon and expressions for scattering matrices. J. Chem. Phys. 1992, 97, 1892–1904. 10.1063/1.463178. [DOI] [Google Scholar]
- Zhu C.; Nakamura H. The two-state linear curve crossing problems revisited. II. Analytical approximations for the Stokes constant and scattering matrix: The Landau-Zener case. J. Chem. Phys. 1992, 97, 8497–8514. 10.1063/1.463368. [DOI] [Google Scholar]
- Zhu C.; Nakamura H. The two-state linear curve crossing problems revisited. III. Analytical approximations for Stokes constant and scattering matrix: Nonadiabatic tunneling case. J. Chem. Phys. 1993, 98, 6208–6222. 10.1063/1.464814. [DOI] [Google Scholar]
- Xie W.; Sapunar M.; Došlić N.; Sala M.; Domcke W. Assessing the performance of trajectory surface hopping methods: Ultrafast internal conversion in pyrazine. J. Chem. Phys. 2019, 150, 154119 10.1063/1.5084961. [DOI] [PubMed] [Google Scholar]
- Tully J. C. Mixed quantum-classical dynamics. Faraday Discuss. 1998, 110, 407–419. 10.1039/a801824c. [DOI] [Google Scholar]
- Paszke A.; Gross S.; Chintala S.; Chanan G.; Yang E.; DeVito Z.; Lin Z.; Desmaison A.; Antiga L.; Lerer A. In Automatic Differentiation in PyTorch, 31st Conference on Neural Information Processing Systems (NIPS 2017), 2017.
- Abadi M.et al. Large-Scale Machine Learning on Heterogeneous Systems. 2015, http://tensorflow.org/, software available from tensorflow.org.
- Sala M.; Lasorne B.; Gatti F.; Guérin S. The role of the low-lying dark n* states in the photophysics of pyrazine: a quantum dynamics study. Phys. Chem. Chem. Phys. 2014, 16, 15957–15967. 10.1039/C4CP02165G. [DOI] [PubMed] [Google Scholar]
- Raab A.; Worth G. A.; Meyer H.-D.; Cederbaum L. S. Molecular dynamics of pyrazine after excitation to the S2 electronic state using a realistic 24-mode model Hamiltonian. J. Chem. Phys. 1999, 110, 936–946. 10.1063/1.478061. [DOI] [Google Scholar]
- Mai S.; Marquetand P.; González L. Non-adiabatic and intersystem crossing dynamics in SO2. II. The role of triplet states in the bound state dynamics studied by surface-hopping simulations. J. Chem. Phys. 2014, 140, 204302 10.1063/1.4875036. [DOI] [PubMed] [Google Scholar]
- Xie C.; Hu X.; Zhou L.; Xie D.; Guo H. Ab initio determination of potential energy surfaces for the first two UV absorption bands of SO2. J. Chem. Phys 2013, 139, 014305 10.1063/1.4811840. [DOI] [PubMed] [Google Scholar]
- Lévêque C.; Taïeb R.; Köppel H. Communication: Theoretical prediction of the importance of the 3B2 state in the dynamics of sulfur dioxide. J. Chem. Phys. 2014, 140, 091101 10.1063/1.4867252. [DOI] [PubMed] [Google Scholar]
- Müller H.; Köppel H. Adiabatic wave-packet motion on conically intersecting potential energy surfaces. The case of SO2(1B11A2). Chem. Phys. 1994, 183, 107–116. 10.1016/0301-0104(94)00053-0. [DOI] [Google Scholar]
- Lévêque C.; Komainda A.; Taïeb R.; Köppel H. Ab initio quantum study of the photodynamics and absorption spectrum for the coupled 11A2 and 11B1 states of SO2. J. Chem. Phys. 2013, 138, 044320 10.1063/1.4776758. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Hehre W. J.; Ditchfield R.; Pople J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
- Manaa M. R.; Yarkony D. R. On the intersection of two potential energy surfaces of the same symmetry. Systematic characterization using a Lagrange multiplier constrained procedure. J. Chem. Phys. 1993, 99, 5251–5256. 10.1063/1.465993. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.