D-CCA: A Decomposition-based Canonical Correlation Analysis for High-Dimensional Datasets

Abstract

A typical approach to the joint analysis of two high-dimensional datasets is to decompose each data matrix into three parts: a low-rank common matrix that captures the shared information across datasets, a low-rank distinctive matrix that characterizes the individual information within a single dataset, and an additive noise matrix. Existing decomposition methods often focus on the orthogonality between the common and distinctive matrices, but inadequately consider the more necessary orthogonal relationship between the two distinctive matrices. The latter guarantees that no more shared information is extractable from the distinctive matrices. We propose decomposition-based canonical correlation analysis (D-CCA), a novel decomposition method that defines the common and distinctive matrices from the ${\mathcal{L}}^2$ space of random variables rather than the conventionally used Euclidean space, with a careful construction of the orthogonal relationship between distinctive matrices. D-CCA represents a natural generalization of the traditional canonical correlation analysis. The proposed estimators of common and distinctive matrices are shown to be consistent and have reasonably better performance than some state-of-the-art methods in both simulated data and the real data analysis of breast cancer data obtained from The Cancer Genome Atlas.

1. Introduction

Many large biomedical studies have collected high-dimensional genetic and/or imaging data and associated data (e.g., clinical data) from increasingly large cohorts to delineate the complex genetic and environmental contributors to many diseases, such as cancer and Alzheimer’s disease. For example, The Cancer Genome Atlas (TCGA; Koboldt et al., 2012) project collected human tumor specimens and derived different types of large-scale genomic data such as mRNA expression and DNA methylation to enhance the understanding of cancer biology and therapy. The Human Connectome Project (Van Essen et al., 2013) acquired imaging datasets from multiple modalities (HARDI, R-fMRI, T-fMRI, MEG) across a large cohort to build a “network map” (connectome) of the anatomical and functional connectivity within the healthy human brain. These cross-platform datasets share some common information, but individually contain distinctive patterns. Disentangling the underlying common and distinctive patterns is critically important for facilitating the integrative and discriminative analysis of these cross-platform datasets (van der Kloet et al., 2016; Smilde et al., 2017).

Throughout this paper, we focus on disentangling the common and distinctive patterns of two high-dimensional datasets written as matrices ${\mathrm{Y}}_k\in {\mathbb{R}}^{p_k\times n}$ for k = 1, 2 on a common set of n objects, where each of the p_k rows corresponds to a mean-zero variable. A popular approach to such an analysis is to decompose each data matrix into three parts:

$${\mathrm{Y}}_k={\mathrm{C}}_k+{\mathrm{D}}_k+{\mathrm{E}}_k\text{for}k=1,2,$$ (1)

where C_k’s are low-rank “common” matrices that capture the shared structure between datasets, D_k’s are low-rank “distinctive” matrices that capture the individual structure within each dataset, and E_k’s are additive noise matrices. Model (1) has been widely used in genomics (Lock et al., 2013; O’Connell and Lock, 2016), metabolomics (Kuligowski et al., 2015), and neuroscience (Yu et al., 2017), among other areas of research. Ideally, the common and distinctive matrices should provide different “views” for each individual dataset, while borrowing information from the other. A fundamental question for model (1) is how to decompose Y_k’s into the common and distinctive matrices within each dataset and across datasets.

Most decomposition methods for model (1) are based on the Euclidean space (${\mathbb{R}}^n$, ·) endowed with the dot product. Such methods include JIVE (Lock et al., 2013), angle-based JIVE (AJIVE; Feng et al., 2018), OnPLS (Trygg, 2002; Löfstedt and Trygg, 2011), COBE (Zhou et al., 2016), and DISCO-SCA (Schouteden et al., 2014). A common characteristic among all these methods is to enforce the row-space orthogonality between the common and distinctive matrices within each dataset, that is, ${\mathrm{C}}_k{\mathrm{D}}_k^{⊺}=0$ for k =1, 2. With the exception of OnPLS, these methods impose additional orthogonality across the datasets, that is, ${\mathrm{C}}_k{\mathrm{D}}_{\ell }^{⊺}=0$ for all k and ℓ. A potential issue associated with these methods is that they inadequately consider the more desired orthogonality between the distinctive matrices D₁ and D₂, which guarantees that no common structure is retained therein. Specifically, the first four methods do not impose any orthogonality constraint between D₁ and D₂. Although DISCO-SCA and a modified JIVE (O’Connell and Lock (2016); denoted as R.JIVE) have considered the row-space orthogonality between the distinctive matrices, it may be incompatible with their orthogonal condition that ${\mathrm{C}}_k{\mathrm{D}}_{\ell }^{⊺}=0$ for all k, ℓ = 1, 2 even as p₁ = p₂ = 1.

Rather than the conventionally used Euclidean space (${\mathbb{R}}^n$, ·), the aim of this paper is to develop a new decomposition method for model (1) based on the inner product space (${\mathcal{L}}_0^2$, cov), which is the vector space composed of all zero-mean and finite-variance real-valued random variables and endowed with the covariance operator as the inner product. Specifically, model (1) is a sample-matrix version of the prototype given by

$${\mathit{y}}_k={\mathit{c}}_k+{\mathit{d}}_k+e_k\in {\mathbb{R}}^{p_k}\text{for}k=1,2.$$ (2)

The Euclidean space (${\mathbb{R}}^n$, ·) is hence not an appropriate space for defining the common matrices C_k’s and the distinctive matrices D_k’s, because two uncorrelated non-constant random variables will almost never have zero sample correlation, i.e., the orthogonality in (${\mathbb{R}}^n$, ·). The matrices ${\{{\mathrm{C}}_k,{\mathrm{D}}_k\}}_{k=1}^2$ defined by the aforementioned methods based on (${\mathbb{R}}^n$, ·) are, in fact, estimators of the counterparts defined through model (2) on (${\mathcal{L}}_0^2$, cov). Instead, for model (2), we introduce a common-space constraint for the common vectors ${\{{\mathit{c}}_k\}}_{k=1}^2$, an orthogonal-space constraint for the distinctive vectors ${\{{\mathit{d}}_k\}}_{k=1}^2$, and a parsimonious-representation constraint for the signal vectors x_k := y_k – e_k, k = 1, 2 as follows:

$$\text{span}({\mathit{c}}_1^{⊺})=\text{span}({\mathit{c}}_2^{⊺}),$$ (3)

$$\text{span}({\mathit{d}}_1^{⊺})\perp \text{span}({\mathit{d}}_2^{⊺}),$$ (4)

$$\text{span}(({\mathit{x}}_1^{⊺},{\mathit{x}}_2^{⊺}))=\text{span}(({\mathit{c}}_1^{⊺},{\mathit{c}}_2^{⊺},{\mathit{d}}_1^{⊺},{\mathit{d}}_2^{⊺})),$$ (5)

where $\text{span}({\mathit{v}}^{⊺})=\text{span}({\{v_j\}}_{j=1}^p)=\left\{{\sum }_{j=1}^p{a}_j{v}_j:\forall a_j\in \mathbb{R}\right\}$ is the vector space spanned by entries of any random vector υ = (υ₁, …, υ_p)^⊤, and ⊥ denotes the orthogonality between two subspaces and/or random variables in (${\mathcal{L}}_0^2$, cov). The orthogonal relationship between distinctive matrices D₁ and D₂ is now described by (4).

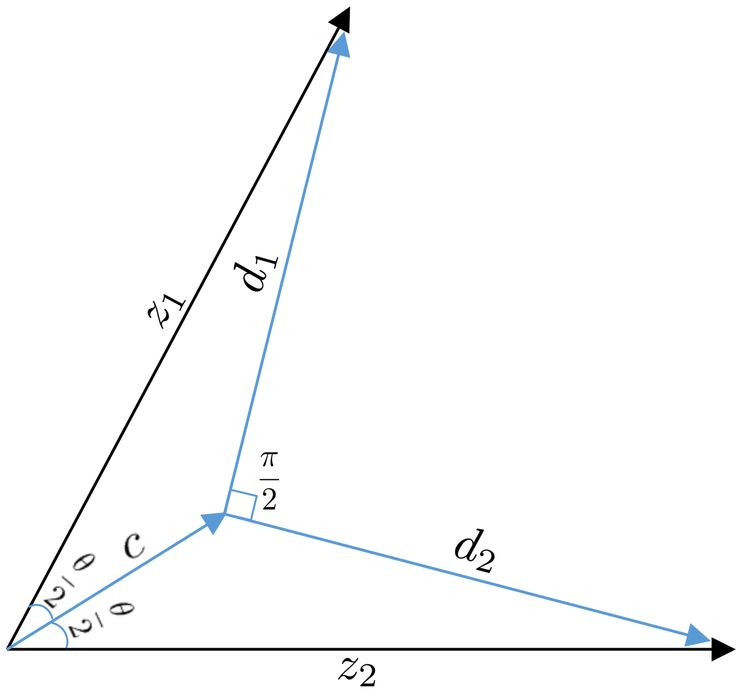
To illustrate the advantage of our proposed constraints over those imposed by the six existing methods mentioned above, we consider a toy example based on model (2) with p₁ = p₂ = 1. Suppose z₁ and z₂ are two standardized signal random variables with the same distribution and corr(z₁, z₂) ϵ (0, 1), i.e., their angle on (${\mathcal{L}}_0^2$, cov), denoted as θ, in (0, π/2) (see Figure 1). We want to decompose them as z_k = c_k + d_k for k = 1, 2. The constraints of JIVE, AJIVE, OnPLS, and COBE translated into space (${\mathcal{L}}_0^2$, cov) do not guarantee d₁ ⊥ d₂, i.e., corr(d₁, d₂) = 0. DISCO-SCA and R.JIVE impose d₁ ⊥ d₂ and c_j ⊥ d_k for all j, k = 1, 2. Restrict $\text{span}(\{z_1,z_2\})=\text{span}({\{c_k,d_k\}}_{k=1}^2)$ as in our (5) to avoid the signal space being represented by a higher dimensional space. Then their orthogonal constraints result in either (i) d₁ = d₂ = 0 or (ii) that only one of d₁ and d₂ is a zero constant, since a two-dimensional space does not tolerate three nonzero orthogonal elements. Scenario (i) indicates z₁ = c₁ ≠ z₂ = c₂ and fails to reveal the distinctive patterns of z₁ and z₂. Scenario (ii) implies unequal distributions of d₁ and d₂, which contradicts the symmetry of z₁ and z₂ about 0.5(z₁ + z₂). However, our proposed constraints and developed method will achieve the desirable decomposition shown in Figure 1, where d₁ ⊥ d₂, c₁ = c₂ = c ∝ 0.5(z₁ + z₂), and moreover, ∥c∥ indicates the extent of 1/θ or corr(z₁, z₂).

Figure 1:

The geometry of D-CCA for two standardized random variables.

Motivated by the toy example above, we introduce a novel method, decomposition-based canonical correlation analysis (D-CCA), which generalizes the classical canonical correlation analysis (CCA; Hotelling, 1936) by further separating common vectors ${\{{\mathit{c}}_k\}}_{k=1}^2$ and distinctive vectors ${\{{\mathit{d}}_k\}}_{k=1}^2$ between signal vectors ${\{{\mathit{x}}_k\}}_{k=1}^2$ subject to constraints (3)-(5). In contrast, classical CCA only seeks the association between two random vectors by sequentially determining the mutually orthogonal pairs of canonical variables that have maximal correlations between the vector spaces respectively spanned by entries of the two random vectors. Another related but different method, the sparse CCA (Chen et al., 2013; Gao et al., 2015, 2017), focuses on the sparse linear combinations of original variables for representing canonical variables with improved interpretability, which is neither required nor pursued by our D-CCA.

The “low-rank plus noise” model y_k = x_k + e_k for each single k can be naturally formulated by a factor model as y_k = B_kf_k + e_k, where the latent factor ${\mathit{f}}_k^{⊺}$ is an orthonormal basis of $\text{span}({\mathit{x}}_k^{⊺})$ with Bk being the coefficient matrix. In factor model analysis (Bai and Ng, 2008), x_k = B_kf_k is called the “common component”, and e_k the “idiosyncratic error”. These two terms should not be confused with our considered common vectors ${\{{\mathit{c}}_k\}}_{k=1}^2$ and distinctive vectors ${\{{\mathit{d}}_k\}}_{k=1}^2$ that are solely based on signals ${\{{\mathit{x}}_k\}}_{k=1}^2$ excluding noises ${\{{\mathit{e}}_k\}}_{k=1}^2$. For general dynamic factor models (Forni et al., 2000), Hallin and Liška (2011) proposed a joint decomposition method, which divides each dataset into strongly common, weakly common, weakly idiosyncratic, and strongly idiosyncratic components (also see Forni et al. (2017) and Barigozzi et al. (2018)). Applying their method to our considered scenarios with no temporal dependence, and additionally assuming no correlations between signals ${\{{\mathit{x}}_k\}}_{k=1}^2$, and noises ${\{{\mathit{e}}_k\}}_{k=1}^2$, then for each y_k, x_k is the sum of strongly common and weakly common components, e_k is the strongly idiosyncratic component, and no weakly idiosyncratic component exists. One may treat their strongly common and weakly common components as the common vector c_k and the distinctive vector d_k, respectively, but the desired orthogonality (4) is still not imposed. Especially when $\text{span}({\mathit{x}}_1^{⊺})\cap \text{span}({\mathit{x}}_2^{⊺})=\{0\}$, x_k is entirely a weakly common component, and thus the orthogonality (4) fails for the toy example shown in Figure 1. See Remark S.l in the supplementary material for more detailed discussions.

Our major contributions of this paper are as follows. The proposed D-CCA method appropriately decomposes each paired canonical variables of signal vectors x₁ and x₂ into a common variable and two orthogonal distinctive variables, and then collects all of them to form the common vector c_k and the distinctive vector d_k for each x_k. The common matrix C_k and the distinctive matrix D_k are defined with columns as n realizations of c_k and d_k, respectively. Three challenging issues that arise in estimating the low-rank matrices defined by D-CCA are high dimensionality, the corruption of signal random vectors by unobserved noises, and the unknown signal covariance and cross-covariance matrices that are needed in CCA. To address these issues, we study the considered “low-rank plus noise” model under the framework of approximate factor models (Wang and Fan, 2017), and develop a novel estimation approach by integrating the S-POET method for spiked covariance matrix estimation (Wang and Fan, 2017) and the construction of principal vectors (Björck and Golub, 1973). Under some mild conditions, we systematically investigate the consistency and convergence rates of the proposed matrix estimators under a high-dimensional setting with min(p₁, p₂) > κ₀n for a positive constant κ₀.

The rest of this paper is organized as follows. Section 2 introduces the D-CCA method that appropriately defines the common and distinctive matrices from the inner product space (${\mathcal{L}}_0^2$, cov). A soft-thresholding approach is then proposed for estimating the matrices defined by D-CCA. Section 3 is devoted to the theoretical results of the proposed matrix estimators under a high-dimensional setting. The performance of D-CCA and the associated estimation approach is compared to that of the aforementioned state-of-the-art methods through simulations in Section 4 and through the analysis of TCGA breast cancer data in Section 5. Possible future extensions of D-CCA are discussed in Section 6. All technical proofs are provided in the supplementary material.

Here, we introduce some notation. For a real matrix M = (M_ij)_{1≤i≤p,1≤j≤n}, the ℓ-th largest singular value and the ℓ-th largest eigenvalue (if p = n) are respectively denoted by σ_ℓ(M) and λ_ℓ(M), the spectral norm ∥M∥₂ = σ₁(M), the Frobenius norm ${\Vert \mathrm{M}\Vert }_F=\sqrt{{\sum }_{i=1}^p{\sum }_{j=1}^n{M}_{ij}^2}$, and the matrix ${\mathcal{L}}^{\infty }$ norm ${\Vert \mathrm{M}\Vert }_{\infty }={\max }_{1\le i\le p}{\sum }_{j=1}^n\mid M_{ij}\mid$. We use M^[s:t,u:v], M^[s:t,:] and M^[:,u:v] to represent the submatrices (M_ij)_{s≤i≤t,u≤j≤v}, (M_ij)_{s≤i≤t,1≤j≤n} and (M_ij)_{1≤i≤p,u≤j≤v} of the p×n matrix M, respectively. Denote the Moore-Penrose pseudoinverse of matrix M by M^†. Define 0_p×n to be the p×n zero matrix and I_p×p to be the p×p identity matrix. Denote diag(M₁, …, M_m) to be a block diagonal matrix with M₁, …, M_m as its main diagonal blocks. For signal vectors x_k’s, denote Σ_k = cov(x_k), Σ₁₂ = cov(x₁, x₂), r_k = rank(Σ_k), r_min = min(r₁, r₂), r_max = max(r₁, r₂) and r₁₂ = rank(Σ₁₂). For a subspace B of a vector space A, denote its orthogonal complement in A by A \ B. We write a ∝ b if a is proportional to b, i.e., a = κb for some constant κ. Throughout the paper, our asymptotic arguments are by default under n → ∞. We reserve {c, c_ℓ}, {c_k} and {C_k} for the common variables, common vectors and common matrices, respectively, and use other notation for constants, e.g., κ₀.

2. The D-CCA Method

Suppose the columns of matrices Y_k, X_k and E_k are, respectively, n independent and identically distributed (i.i.d.) copies of mean-zero random vectors y_k, x_k and e_k for k = 1, 2. We consider the “low-rank plus noise” model for the observable random vector y_k as follows:

$${\mathit{y}}_k={\mathit{x}}_k+{\mathit{e}}_k={\mathbf{B}}_k{\mathit{f}}_k+{\mathit{e}}_k,$$ (6)

where ${\mathrm{B}}_k\in {\mathbb{R}}^{p_k\times r_k}$ is a real deterministic matrix, ${\mathit{f}}_k\in {\mathbb{R}}^{r_k}$ is a mean-zero random vector of r_k latent factors such that cov(f_k) = I_rk×rk and cov(f_k, e_k) = 0_rk×pk, and r_k is a fixed number independent of {n, p₁, p₂}. Write the model in a sample-matrix form by

$${\mathbf{Y}}_k={\mathbf{X}}_k+{\mathbf{E}}_k+{\mathbf{B}}_k{\mathbf{F}}_k+{\mathbf{E}}_k,$$ (7)

where the columns of F_k are assumed to be i.i.d. copies of f_k. We assume that the model given in (6) and (7) is an approximate factor model (Wang and Fan, 2017) that allows for correlations among entries of e_k in contrast with the strict factor model (Ross, 1976) and has $\text{cov}({\mathit{y}}_k)={\mathrm{B}}_k{\mathrm{B}}_k^{⊺}+\text{cov}({\mathit{e}}_k)$ be a spiked covariance matrix for which the top r_k eigenvalues are significantly larger than the rest (i.e., signals are stronger than noises). Detailed conditions for consistent estimation will be given later in Assumption 1. Although approximate factor models are often used in econometric literature (Chamberlain and Rothschild, 1983; Bai and Ng, 2002; Stock and Watson, 2002; Bai, 2003) with temporal dependence on {${\mathrm{F}}_k^{[:,t]}$, ${\mathrm{E}}_k^{[:,t]}$} across t’s, we assume independence across the n samples as in Wang and Fan (2017) since no temporal dependence is quite natural in our motivating TCGA datasets and considered in the six competing methods mentioned in Section 1.

2.1. Definition of common and distinctive matrices

We define the common and distinctive matrices of two datasets based on the inner product space (${\mathcal{L}}_0^2$, cov). The low-rank structure of x_k in (6) indicates that the dimension of $\text{span}({\mathit{x}}_k^{⊺})$ is r_k.

One natural way to construct the decomposition of X_k = C_k + D_k for k = 1, 2 is to decompose the signal vectors as

$${\mathit{x}}_k=\sum _{\ell =1}^{r_k}{\beta }_{k\ell }{z}_{k\ell }={\mathit{c}}_k+{\mathit{d}}_k≔\sum _{\ell =1}^{L_{12}}{\beta }_{k\ell }^{(C)}{c}_{\ell }+\sum _{\ell =1}^{L_k}{\beta }_{k\ell }^{(D)}{d}_{k\ell },$$ (8)

subject to the constraints (3)-(5) with space dimensions L₁₂ ≤ r_min and L_k ≤ r_k, where β_kℓ, ${\beta }_{k\ell }^{(C)}$ and ${\beta }_{k\ell }^{(D)}$ are real deterministic vectors, and random variables ${\{z_{k\ell }\}}_{\ell =1}^{r_k}$, ${\{c_{\ell }\}}_{\ell =1}^{L_{12}}$ and ${\{d_{k\ell }\}}_{\ell =1}^{L_k}$ are, respectively, the orthogonal basis of $\text{span}({\mathit{x}}_k^{⊺})$, $\text{span}({\mathit{c}}_1^{⊺})=\text{span}({\mathit{c}}_2^{⊺})$ and $\text{span}({\mathit{d}}_k^{⊺})$. The desirable contraints (3)-(5) are now equivalent to

$$\{\begin{array}{c}\text{span}({\{z_{1\ell }\}}_{\ell =1}^{r_1}\cup {\{z_{2\ell }\}}_{\ell =1}^{r_2})=\text{span}({\{c_{\ell }\}}_{\ell =1}^{L_{12}}\cup {\{d_{1\ell }\}}_{\ell =1}^{L_1}\cup {\{d_{2\ell }\}}_{\ell =1}^{L_2}),\hfill \\ d_{su}\perp d_{tv}\text{for}s\ne t\text{or}u\ne v.\hfill \end{array}\phantom{\}}$$ (9)

We call ${\{c_{\ell }\}}_{\ell =1}^{L_{12}}$ the common variables of x₁ and x₂, and ${\{d_{k\ell }\}}_{\ell =1}^{L_k}$ the distinctive variables of x_k. The columns of common matrix C_k are defined as the i.i.d. copies of c_k, and those of distinctive matrix D_k are the ones of d_k. The space $\text{span}({\{c_{\ell }\}}_{\ell =1}^{L_{12}})$ represents the common structure of x₁ and x₂, or datasets X₁ and X₂, and the spaces ${\{\text{span}({\{d_{k\ell }\}}_{\ell =1}^{L_k})\}}_{k=1}^2$ correspond to their distinctive structures.

To achieve a decomposition of form (8), our D-CCA method adopts a two-step optimization strategy given in (10) and (11) below. The first step uses the classical CCA to recursively find the most correlated variables between signal spaces ${\{\text{span}({\mathit{x}}_k^{⊺})\}}_{k=1}^2$ as follows: For ℓ = 1, …, r₁₂,

$$\begin{array}{cc}\hfill \{z_{1\ell },z_{2\ell }\}& \in \underset{{\{z_k\}}_{k=1}^2}{\arg \max }\mathrm{corr}(z_1,z_2)\text{subject to}\hfill \\ \hfill \text{var}(z_k)& =1\text{and}{z}_k\in \text{span}({\mathit{x}}_k^{⊺})\setminus \text{span}({\{z_{km}\}}_{m=1}^{\ell -1}),\hfill \end{array}$$ (10)

where $\text{span}({\mathit{x}}_k^{⊺})\setminus \text{span}({\{z_{km}\}}_{m=1}^0)≔\text{span}({\mathit{x}}_k^{⊺})$. Variables ${\{z_{k\ell }\}}_{k=1}^2$ are called the ℓ-th pair of canonical variables, and their correlation is the ℓ-th canonical correlation of x₁ and x₂. Augment ${\{z_{k\ell }\}}_{\ell =1}^{r_{12}}$ with any (r_k – r₁₂) standardized variables to be z_k = (z_k1, …, z_krk)⊤ such that $z_k^{⊺}$ is an orthonormal basis of $\text{span}({\mathit{x}}_k^{⊺})$. A detailed procedure to obtain a solution of ${\{z_k\}}_{k=1}^2$ will be presented later after Theorem 2. An important property of these augmented canonical variables is the bi-orthogonality shown in the following theorem.

Theorem 1 (Bi-orthogonality). The covariance matrix of z₁ and z₂ is

$$\text{cov}(z_1{z}_2)=\left[\begin{array}{cc}\hfill {\mathrm{\Lambda }}_{12}\hfill & \hfill 0_{r_{12}\times (r_2-r_{12})}\hfill \\ \hfill 0_{(r_1-r_{12})\times r_{12}}\hfill & \hfill 0_{(r_1-r_{12})\times (r_2-r_{12})}\hfill \end{array}\right],$$

where Λ₁₂ is a r₁₂×r₁₂ nonsingular diagonal matrix.

Theorem 1 implies that all correlations between $\text{span}({\mathit{x}}_1^{⊺})$ and $\text{span}({\mathit{x}}_2^{⊺})$ are confined between their subspaces $\text{span}({\{z_{1\ell }\}}_{\ell =1}^{r_{12}})$ and $\text{span}({\{z_{2\ell }\}}_{\ell =1}^{r_{12}})$, and moreover, span({z_1ℓ, z_2ℓ}) ⊥ span({z_1m, z_2m}) holds for 1 ≤ ℓ ≠ m ≤ r₁₂. We hence only need to investigate the correlations within each subspace span({z_1ℓ, z_2ℓ}) for 1 ≤ ℓ ≤ r₁₂. The second step of our D-CCA defines the common variables ${\{c_{\ell }\}}_{\ell =1}^{r_{12}}$ by

$$c_{\ell }\propto \underset{w\in ({\mathcal{L}}_0^2,\text{cov})}{\arg \max }\left\{{\text{corr}}^2(z_{1\ell },w)+{\text{corr}}^2(z_{2\ell },w)\right\}$$ (11)

with the constraints

$$\{\begin{array}{c}{z}_{k\ell }=c_{\ell }+d_{k\ell }\text{for}k=1,2,\hfill \\ \text{corr}(d_{1\ell },d_{2\ell })=0,\hfill \\ \text{var}(c_{\ell })\text{increases as}{\rho }_{\ell }≔\text{corr}(z_{1\ell },z_{2\ell })\text{increases on}[0,1].\hfill \end{array}\phantom{\}}$$ (12) (13) (14)

Constraints (12) and (13) are actually the special case of (8) and (9) for two standardized random variables. Constraint (14) indicates that c_ℓ explains more variances of z_1ℓ and z_2ℓ when their correlation p_ℓ increases. Although ρ_ℓ, here referring to the ℓ-th canonical correlation of ${\{{\mathit{x}}_k\}}_{k=1}^2$, is always positive for 1 ≤ ℓ ≤ r₁₂, we include ρ_ℓ = 0 to enable (11) as a general optimization problem for any two standardized variables with nonnegative correlation. The unique solution of (11) is given by

$$c_{\ell }=\left(1-\sqrt{\frac{1-\rho \ell }{1+\rho \ell }}\right)\frac{z_{1\ell }+z_{2\ell }}{2}=\left[1-\tan \left(\frac{{\theta }_{\ell }}{2}\right)\right]\frac{z_{1\ell }+z_{2\ell }}{2},$$ (15)

where θ_ℓ = arccos(ρ_ℓ) is the angle between z_1ℓ and z_2ℓ in (${\mathcal{L}}_0^2$, cov). More desirable than constraint (14), it easily follows from (15) that var(c_ℓ) is a continuous and strictly monotonic increasing function for ρ_ℓ ϵ [0, 1]. We defer the detailed derivation of (15) to the supplementary material (Proposition S.2 and its proof). This solution is geometrically illustrated in Figure 1 with ℓ omitted in the subscriptions. Simply let d_kℓ = z_kℓ for r₁₂ + 1 ≤ ℓ ≤ r_k. The two-step optimization strategy arrives at the following decomposition of form (8): For k = 1, 2,

$${\mathit{x}}_k=\sum _{\ell =1}^{r_k}{\beta }_{k\ell }{z}_{k\ell }={\mathit{c}}_k+{\mathit{d}}_k≔\sum _{\ell =1}^{r_{12}}{\beta }_{k\ell }{c}_{\ell }+\sum _{\ell =1}^{r_k}{\beta }_{k\ell }{d}_{k\ell },$$ (16)

$$\text{with}{\beta }_{k\ell }=\text{cov}({\mathit{x}}_k,z_{k\ell }).$$ (17)

Constraints (3)-(5) or equivalently (9) are satisfied due to the bi-orthogonality in Theorem 1 and the constraints in (12) and (13).

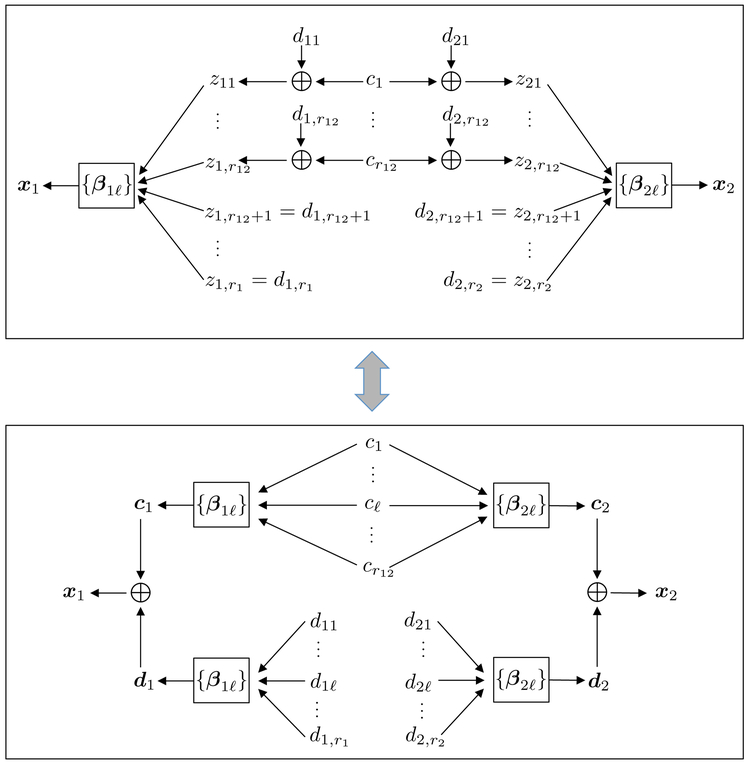
The workflow of D-CCA can be interpreted from the perspective of blind source separation (Comon and Jutten, 2010). Jointly for k = 1, 2, D-CCA first uses CCA to recover the input sources ${\{z_{k\ell }\}}_{\ell =1}^{r_k}$ and the mixing channel ${\{{\beta }_{k\ell }\}}_{\ell =1}^{r_k}$ that generate the output signal vector x_k. Then by the constrained (11), D-CCA discovers the common components ${\{c_{\ell }\}}_{\ell =1}^{r_{12}}$ and the distinctive components ${\{d_{k\ell }\}}_{\ell =1}^{r_k}$, k = 1, 2 of the two sets of input sources ${\{z_{k\ell }\}}_{\ell =1}^{r_k}$, k = 1, 2. Finally, D-CCA separately passes ${\{c_{\ell }\}}_{\ell =1}^{r_{12}}$ and ${\{d_{k\ell }\}}_{\ell =1}^{r_k}$ through the mixing channel ${\{{\beta }_{k\ell }\}}_{\ell =1}^{r_k}$ to form the common vector c_k and the distinctive vector d_k of each k-th output signal vector x_k. Figure 2 illustrates such interpretation of the D-CCA decomposition structure.

Figure 2:

The decomposition structure of D-CCA.

The solution to the CCA problem in (10) may not be unique even when ignoring a simultaneous sign change, but all solutions yield the same c_k and d_k as shown in the following theorem.

Theorem 2 (Uniqueness). All solutions to the problem in (10) for canonical variables ${\{z_{1\ell },z_{2\ell }\}}_{\ell =1}^{r_{12}}$ give the same c_k and d_k defined in (16).

We now present a procedure to obtain the augmented canonical variables {z₁, z₂}. For k = 1, 2, let a singular value decomposition (SVD) of Σ_k be ${\mathrm{\Sigma }}_k={\mathrm{V}}_k{\mathrm{\Lambda }}_k{\mathrm{V}}_k^{⊺}$, where Λ_k = diag(σ₁ (Σ_k), …, σ_rk(Σ_k)) and V_k is a p_k×r_k matrix with orthonormal columns. Let $z_k^{\ast }={\mathrm{\Lambda }}_k^{-1/2}{\mathrm{V}}_k^{⊺}{\mathit{x}}_k$, then we have $\text{cov}(z_k^{\ast })={\mathrm{I}}_{r_k\times r_k}$. Define

$$\mathrm{\Theta }=\text{cov}(z_1^{\ast },z_2^{\ast })={\mathrm{\Lambda }}_1^{-1/2}{\mathrm{V}}_1^{⊺}{\mathrm{\Sigma }}_{12}{\mathrm{V}}_2{\mathrm{\Lambda }}_2^{-1/2}.$$

The rank of Θ is also r₁₂. Denote a full SVD of Θ by $\mathrm{\Theta }={\mathrm{U}}_{\theta 1}{\mathrm{\Lambda }}_{\theta }{\mathrm{U}}_{\theta 2}^{⊺}$, where U_θ1 and U_θ2 are two orthogonal matrices, and Λ_θ is a r₁ × r₂ rectangular diagonal matrix for which the main diagonal is (σ₁(Θ), …, σ_r12 (Θ), 0_{1×(rmin–r12)}). We then define

$$z_k={\mathrm{U}}_{\theta k}^{⊺}{z}_k^{\ast }={\mathrm{\Gamma }}_k^{⊺}{\mathit{x}}_k\text{with}{\mathrm{\Gamma }}_k≔{\mathrm{V}}_k{\mathrm{\Lambda }}_k^{-1/2}{\mathrm{U}}_{\theta k},$$ (18)

which satisfies cov(z_k) = I_rk×rk and corr(z₁, z₂) = Λ_θ. Note that σ_ℓ(Θ) = ρ_ℓ for ℓ ≤ r₁₂ are the canonical correlations between x₁ and x₂.

Now look back to ${\mathit{c}}_k={\sum }_{\ell =1}^{r_{12}}{\beta }_{k\ell }{c}_{\ell }$ that is defined in (16). Plugging (17) and (15) for β_kℓ and c_ℓ in the formula together with ${\{z_j\}}_{j=1}^2$, given in (18), we obtain

$${\mathit{c}}_k=\text{cov}({\mathit{x}}_k,z_k^{[1:r_{12}]}){\mathrm{A}}_C\sum _{j=1}^2{z}_j^{[1:r_{12}]},$$ (19)

where A_C = diag(a₁, …, a_r12) and $a_{\ell }=\frac{1}{2}\left[1-{\left(\frac{1-{\sigma }_{\ell }(\mathrm{\Theta })}{1+{\sigma }_{\ell }(\mathrm{\Theta })}\right)}^{1/2}\right]$ for ℓ ≤ r₁₂. Replacing random vector $z_k={\mathrm{\Gamma }}_k^{⊺}{\mathit{x}}_k$ by its sample matrix ${\mathrm{Z}}_k:={\mathrm{\Gamma }}_k^{⊺}{\mathrm{X}}_k$ in the rightmost of (19) yields

$${\mathrm{C}}_k=\text{cov}({\mathit{x}}_k,z_k^{[1:r_{12}]}){\mathrm{A}}_C\sum _{j=1}^2{z}_j^{[1:r_{12},:]}.$$ (20)

This equation is useful to our design of estimators for C_k and D_k=X_k–C_k in the next subsection.

2.2. Estimation of D-CCA matrices

In this subsection, we discuss the estimation of the matrices defined by D-CCA under model (1) for two high-dimensional datasets. For simplicity, we write the proposed estimators with true ranks r₁, r₂ and r₁₂. In practice, we can replace those unknown true ranks by the estimated ranks given in Subsection 2.3 with a theoretical guarantee provided in Section 3.

Recall that Y_k = X_k + E_k with k = 1, 2. Our first task is to obtain a good initial estimator, denoted by ${\tilde{\mathrm{X}}}_k$, of X_k. Under the approximate factor model given in (6) and (7), our construction of ${\tilde{\mathrm{X}}}_k$ is inspired by the S-POET method (Wang and Fan, 2017) for spiked covariance matrix estimation. Let the full SVD of Y_k be

$${\mathrm{Y}}_k={\mathrm{U}}_{k1}{\mathrm{\Lambda }}_{y_k}{\mathrm{U}}_{k2}^{⊺},$$ (21)

where U_k1 and U_k2 are two orthogonal matrices and Λ_yk is a rectangular diagonal matrix with the singular values in decreasing order on its main diagonal. The matrix ${\tilde{\mathrm{X}}}_k$ is then obtained via soft-thresholding the singular values of Y_k by

$${\tilde{\mathrm{X}}}_k={\mathrm{U}}_{k1}^{[:,1:r_k]}\text{diag}({\widehat{\sigma }}_1^S({\mathrm{Y}}_k),\dots ,{\widehat{\sigma }}_{r_k}^S({\mathrm{Y}}_k)){({\mathrm{U}}_{k2}^{[:,1:r_k]})}^{⊺},$$ (22)

with ${\widehat{\sigma }}_{\ell }^S({\mathrm{Y}}_k)=\sqrt{\max \{{\sigma }_{\ell }^2({\mathrm{Y}}_k)-{\tau }_k{p}_k,0\}}$ and ${\tau }_k={\sum }_{\ell =r_k+1}^{p_k}{\sigma }_{\ell }^2({\mathrm{Y}}_k)/(n{p}_k-n{r}_k-p_k{r}_k)$. Let ${\tilde{r}}_k=\text{rank}({\tilde{\mathrm{X}}}_k)$. Under Assumption 1 that will be given later, it can be shown that ${\tilde{\mathrm{r}}}_k=r_k$ with probability tending to 1 (see the proof of Theorem 3).

We next use ${\tilde{\mathrm{X}}}_k$ to develop estimators for C_k in (20) and D_k=X_k–C_k. Define the estimators of Σ_k and Σ₁₂ as ${\widehat{\mathrm{\Sigma }}}_k=n^{-1}{\tilde{\mathrm{X}}}_k{\tilde{\mathrm{X}}}_k^{⊺}$ and ${\widehat{\mathrm{\Sigma }}}_{12}=n^{-1}{\tilde{\mathrm{X}}}_1{\tilde{\mathrm{X}}}_2^{⊺}$, respectively. Then, based on ${\widehat{\mathrm{\Sigma }}}_k$ and ${\widehat{\mathrm{\Sigma }}}_{12}$, we obtain estimators ${\widehat{\mathrm{V}}}_k$, ${\widehat{\mathrm{\Lambda }}}_k$, ${\widehat{\mathrm{U}}}_{\theta k}=\text{diag}({\widehat{\mathrm{U}}}_{\theta k}^{[1:{\tilde{r}}_k,1:{\tilde{r}}_k]},{\mathrm{I}}_{(r_k-{\tilde{r}}_k)\times (r_k-{\tilde{r}}_k)})$ and ${\widehat{\mathrm{\Lambda }}}_{\theta }$ in the same way as their true counterparts V_k, Λ_k, U_θk and Λ_θ with a r₁×r₂ matrix $\widehat{\mathrm{\Theta }}≔{({\widehat{\mathrm{\Lambda }}}_1^{†})}^{1/2}{\widehat{\mathrm{V}}}_1^{⊺}{\widehat{\mathrm{\Sigma }}}_{12}{\widehat{\mathrm{V}}}_2{({\widehat{\mathrm{\Lambda }}}_2^{†})}^{1/2}$. Define ${\widehat{\mathrm{Z}}}_k^{\ast }={({\widehat{\mathrm{\Lambda }}}_k^{†})}^{1/2}{\widehat{\mathrm{V}}}_k^{⊺}{\tilde{\mathrm{X}}}_k$ and ${\widehat{\mathrm{Z}}}_k={\widehat{\mathrm{U}}}_{\theta k}^{⊺}{\widehat{\mathrm{Z}}}_k^{\ast }$. We have

$$\begin{array}{cc}\hfill & n^{-1}{\widehat{\mathrm{Z}}}_k^{\ast }{({\widehat{\mathrm{Z}}}_k^{\ast })}^{⊺}=n^{-1}{\widehat{\mathrm{Z}}}_k{({\widehat{\mathrm{Z}}}_k)}^{⊺}=\text{diag}({\mathrm{I}}_{{\tilde{r}}_k\times {\tilde{r}}_k},0_{(r_k-{\tilde{r}}_k)\times (r_k-{\tilde{r}}_k)}),\hfill \\ \hfill & \widehat{\mathrm{\Theta }}={\widehat{\mathrm{U}}}_{\theta 1}{\widehat{\mathrm{\Lambda }}}_{\theta }{\widehat{\mathrm{U}}}_{\theta 2}^{⊺}=n^{-1}{\widehat{\mathrm{Z}}}_1^{\ast }{({\widehat{\mathrm{Z}}}_2^{\ast })}^{⊺}\text{and}{n}^{-1}{\widehat{\mathrm{Z}}}_1{({\widehat{\mathrm{Z}}}_2)}^{⊺}={\widehat{\mathrm{\Lambda }}}_{\theta }.\hfill \end{array}$$

From Theorem 1 in Björck and Golub (1973), it follows that $n^{-1/2}{\widehat{\mathrm{Z}}}_1^{[\ell ,:]}$ and $n^{-1/2}{\widehat{\mathrm{Z}}}_2^{[\ell ,:]}$ for ℓ ≤ r_min are the principal vectors of the row spaces of ${\tilde{\mathrm{X}}}_1$ and ${\tilde{\mathrm{X}}}_2$, and moreover, ${\sigma }_{\ell }(\widehat{\mathrm{\Theta }})\le 1$. Let ${\widehat{\mathrm{A}}}_C^{(r)}=\text{diag}({\widehat{a}}_1,\dots ,{\widehat{a}}_r)$ with ${\widehat{a}}_{\ell }=\frac{1}{2}\left[1-{(\frac{1-{\sigma }_{\ell }(\widehat{\mathrm{\Theta }})}{1+{\sigma }_{\ell }(\widehat{\mathrm{\Theta }})})}^{1/2}\right]$ for $\ell \le {\tilde{r}}_{12}≔\text{rank}(\widehat{\mathrm{\Theta }})$ and otherwise ${\widehat{a}}_{\ell }=0$. Define estimators of C_k, D_k and X_k by

$${\widehat{\mathrm{C}}}_k=n^{-1}{\tilde{\mathrm{X}}}_k{({\widehat{\mathrm{Z}}}_k^{[1:r_{12},:]})}^{⊺}{\widehat{\mathrm{A}}}_C^{(r_{12})}\sum _{j=1}^2{\widehat{\mathrm{Z}}}_j^{[1:r_{12},:]},$$ (23)

$${\widehat{\mathrm{D}}}_k={\tilde{\mathrm{X}}}_k-n^{-1}{\tilde{\mathrm{X}}}_k{({\widehat{\mathrm{Z}}}_k^{[1:{\tilde{r}}_{12},:]})}^{⊺}{\widehat{\mathrm{A}}}_C^{({\tilde{r}}_{12})}\sum _{j=1}^2{\widehat{\mathrm{Z}}}_j^{[1:{\tilde{r}}_{12},:]}$$ (24)

and

$${\widehat{\mathrm{X}}}_k={\widehat{\mathrm{C}}}_k+{\widehat{\mathrm{D}}}_k.$$ (25)

Here, we substitute ${\widehat{\mathrm{X}}}_k$ for ${\tilde{\mathrm{X}}}_k$ as the estimator of X_k. The latter can be written as

$$\tilde{\mathrm{X}}={\widehat{\mathrm{C}}}_k^{({\tilde{r}}_{12})}+{\widehat{\mathrm{D}}}_k$$ (26)

with

$${\widehat{\mathrm{C}}}_k^{(r)}≔n^{-1}{\tilde{\mathrm{X}}}_k{({\widehat{\mathrm{Z}}}_k^{[1:r,:]})}^{⊺}{\widehat{\mathrm{A}}}_C^{(r)}\sum _{j=1}^2{\widehat{\mathrm{Z}}}_j^{[1:r,:]}.$$ (27)

Note that ${\widehat{\mathrm{C}}}_k≔{\widehat{\mathrm{C}}}_k^{(r_{12})}$. When $r_{12}\ge {\tilde{r}}_{12}$, we have ${\widehat{\mathrm{C}}}_k={\widehat{\mathrm{C}}}_k^{({\tilde{r}}_{12})}$. But when $r_{12}<{\tilde{r}}_{12}$, ${\widehat{\mathrm{C}}}_k^{({\tilde{r}}_{12})}$ redundantly keeps the nonzero approximated samples of the zero common variable of z_1ℓ and z_2ℓ for $r_{12}<\ell \le {\tilde{r}}_{12}$.

Similar to the decomposition of ${\{{\mathit{x}}_k\}}_{k=1}^2$ given in (16) that is built on the inner product space (${\mathcal{L}}_0^2$, cov), the decomposition of ${\{{\tilde{\mathrm{X}}}_k\}}_{k=1}^2$ in (26) is constructed by an analogy of (12) and (15) on the ${\mathbb{R}}^n$ space with the inner product ⟨u, υ⟩ = u^⊤υ/n for any $\mathit{u},\mathit{v}\in {\mathbb{R}}^n$. We thus have the appealing property ${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0_{p_1\times p_2}$, which corresponds to the orthogonal relationship between the distinctive structures given in (4).

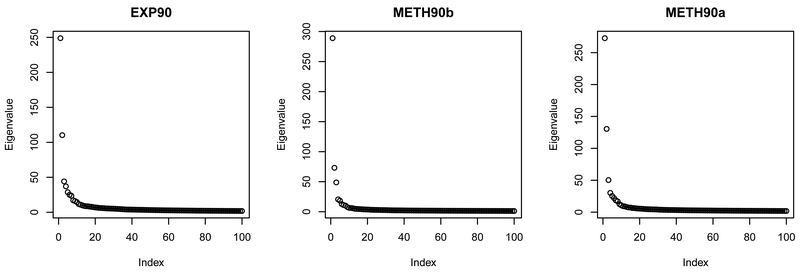
Throughout our estimation construction, the key idea is to develop a good estimator of ${\{{\mathrm{X}}_k,{\mathrm{Z}}_k\}}_{k=1}^2$. Thus, the S-POET method (Wang and Fan, 2017) may be replaced by any other good approach, but with possibly different assumptions. For example, given the cleaned signal data X_k’s, Chen et al. (2013) and Gao et al. (2015, 2017) showed that sparse CCA algorithms can consistently estimate the canonical coefficient matrix Γ_k for ${\mathrm{Z}}_k={\mathrm{\Gamma }}_k^{⊺}{\mathrm{X}}_k$ by imposing certain sparsity on Γ_k’s and that all eigenvalues of cov(x_k) are bounded from above and below by positive constants. These two conditions are not assumed for our proposed method. In particular, their bounded eigenvalue condition contradicts our low-rank structure of signal x_k that introduces the spiked covariance matrix cov(y_k). The sparse CCA algorithms need the cleaned signal data X_k’s available beforehand. Alternatively, they may be directly applicable to the observable data Y_k’s by assuming zero E_k’s, if the bounded eigenvalue condition holds for cov(yk). For the TCGA datasets in our real-data application, the scree plots given later in Figure 6 favorably suggest our spiked eigenvalue assumption. Moreover, the approximate factor model with spiked covariance structure has been widely used in various fields such as signal processing (Nadakuditi and Silverstein, 2010) and machine learning (Huang, 2017), and fits the low-rank plus noise structure considered in the six competing methods mentioned in Section 1. Our paper hence focuses on this spiked covariance model and leaves the extension to sparse CCA models for future research.

Figure 6:

The scree plot of the sample covariance matrix $\frac{1}{n}{\mathrm{Y}}_k{\mathrm{Y}}_k^{⊺}$ for each TCGA dataset.

2.3. Rank selection

In practice, matrix ranks r₁, r₂ and r₁₂ are usually unknown and need to be determined. There is a rich literature on determining r_k, k ϵ {1, 2}, which is the number of latent factors for the high-dimensional approximate factor model. Examples of consistent estimators include but are not limited to Bai and Ng (2002), Onatski (2010), and Ahn and Horenstein (2013). Several heuristic approaches for selecting r₁₂, the number of nonzero canonical correlations for the high-dimensional CCA, have been proposed by Song et al. (2016). In this paper, we apply the edge distribution (ED) method of Onatski (2010) to determine r_k for k = 1, 2 by

$${\widehat{r}}_k=\max \{\ell \le T_k:{\widehat{\lambda }}_{k\ell }-{\widehat{\lambda }}_{k,\ell +1}\ge \delta \},$$ (28)

where ${\widehat{\lambda }}_{k\ell }$ is the ℓ-th eigenvalue of ${\mathrm{Y}}_k{\mathrm{Y}}_k^{⊺}/n$. The upper bound is chosen as $T_k=\min (\#\{i\mid {\widehat{\lambda }}_{ki}\ge \frac{1}{m_k}{\sum }_{\ell =1}^{m_k}{\widehat{\lambda }}_{k\ell }\},m_k/10)$ with m_k = min(n, p_k) which is recommended by Ahn and Horenstein (2013), and parameter δ is calibrated as in Section IV of Onatski (2010). It is believed that r₁₂ > 0 if two variables from different cleaned datasets have a significant nonzero correlation detected by, e.g., the normal approximation test of DiCiccio and Romano (2017). Otherwise, it is unnecessary to conduct the proposed matrix decomposition. We select the nonzero r₁₂ by using the minimum description length information-theoretic criterion (MDL-IC) proposed by Song et al. (2016):

$${\widehat{r}}_{12}=\underset{r\in [1,\min ({\widehat{r}}_1,{\widehat{r}}_2)]}{\arg \min }\left\{n\sum _{l=1}^r\log (1-s_{\ell }^2)+r(r_1+r_2-r)\log (n)\right\},$$ (29)

where s_ℓ is the ℓ-th singular value of ${({\mathrm{U}}_{12}^{[:,1:{\widehat{r}}_1]})}^{⊺}{\mathrm{U}}_{22}^{[:,1:{\widehat{r}}_2]}$ with U₁₂ and U₂₂ defined in (21). The ranks r₁, r₂, and r₁₂ determined by (28) and (29) perform well in our numerical studies.

3. Theoretical Properties of D-CCA Estimators

In this section, we establish asymptotic results for the high-dimensional D-CCA matrix estimators proposed in Subsection 2.2.

Assumption 1. We assume the following conditions for model given in (6) and (7).

• (I)Let λ_k1 > … > λ_k,rk > λ_k,rk+1 ≥ … ≥ λ_k,pk > 0 be the eigenvalues of cov(y_k). There exist positive constants κ₁, κ₂ and δ₀ such that κ₁ ≤ λ_kℓ ≤ κ₂ for ℓ > r_k and min_ℓ≤rk(λ_kℓ – λ_k,ℓ+1)/λ_kℓ ≥ δ₀.
• (II)Assume p_k > κ₀n with a constant κ₀ > 0. When n → ∞, assume λ_k,rk → ∞, p_k/(nλ_kℓ) is upper bounded for ℓ ≤ r_k, λ_k1/λ_k,rk is bounded from above and below, and $\sqrt{p_k}{(\log n)}^{1/{\gamma }_{k2}}=o({\lambda }_{r_k})$ with γ_k2 given in (V) below.
• (III)The columns of ${\mathrm{Z}}_k^{(y)}≔{({\mathrm{\Lambda }}_k^{(y)})}^{-1/2}{({\mathrm{V}}_k^{(y)})}^{⊺}{\mathrm{Y}}_k$ are i.i.d. copies of $z_k^{(y)}≔{({\mathrm{\Lambda }}_k^{(y)})}^{-1/2}{({\mathrm{V}}_k^{(y)})}^{⊺}{\mathit{y}}_k$, where ${\mathrm{V}}_k^{(y)}{\mathrm{\Lambda }}_k^{(y)}{({\mathrm{V}}_k^{(y)})}^{⊺}$ is the full SVD of cov(y_k) with ${\mathrm{\Lambda }}_k^{(y)}=\text{diag}({\lambda }_{k1},\dots ,{\lambda }_{k,p_k})$. The entries of $z_k^{(y)},z_{k1}^{(y)},\dots ,z_{k,p_k}^{(y)}$ are independent with $\mathbb{E}(z_{ki}^{(y)})=0$, $\text{var}(z_{ki}^{(y)})=1$, and the sub-Gaussian norm ${\text{sup}}_{q\ge 1}{q}^{-1/2}{(\mathbb{E}{\mid z_{ki}^{(y)}\mid }^q)}^{1/q}\le K$ with a constant K > 0 for all i ≤ p_k.
• (IV)The matrix ${\mathrm{B}}_k^{⊺}{\mathrm{B}}_k$ is a diagonal matrix, and $\mid {\mathrm{B}}_k^{[i,\ell ]}\mid \le M\sqrt{{\lambda }_{k\ell }/p_k}$ with a constant M > 0 holds for all i ≤ p_k and ℓ ≤ r_k.
• (V)Denote e_k = (e_k1, …, e_k,p_k^)⊤ and f_k = (f_k1, …, f_k,rk)^⊤. Assume ∥ cov(e_k)∥_∞ < s₀ with a constant s₀ > 0. For all i ≤ p_k and ℓ ≤ r_k, there exist positive constants γ_k1, γ_k2, b_k1 and b_k2 such that for t > 0, $\mathbb{P}(\mid e_{ki}\mid >t)\le \text{exp}(-{(t/b_{k1})}^{{\gamma }_{k1}})$ and $\mathbb{P}(\mid f_{k\ell }\mid >t)\le \text{exp}(-{(t/b_{k2})}^{{\gamma }_{k2}})$.

Assumption 1 follows assumptions 2.1-2.3 and 4.1-4.2 of Wang and Fan (2017) which guarantee desirable performance of the initial signal estimators ${\tilde{\mathrm{X}}}_k$’s defined in (22). The diverging leading eigenvalues of cov(y_k) assumed in conditions (I) and (II), together with the approximate sparsity constraint ∥ cov(e_k)∥_∞ < s₀ in condition (V), indicate the necessity of sufficiently strong signals for soft-thresholding. Although Wang and Fan (2017) considered p > n, it is not difficult to relax it to p_k > κ_0n, as given in our condition (II). A random variable is said to be sub-Gaussian if its sub-Gaussian norm is bounded (Vershynin, 2012). Condition (III) imposes the sub-Gaussianity on all entries of $z_k^{(y)}$ with a uniform bound. Simply letting ${\mathit{f}}_k=z_k^{\ast }$ can lead to a diagonal matrix ${\mathrm{B}}_k^{⊺}{\mathrm{B}}_k$ that is required by condition (IV). In condition (V), the approximately sparse constraint is imposed on cov(e_k) rather than E_k. See Wang and Fan (2017) and also Fan et al. (2013) for more detailed discussions of the above assumption.

We consider the relative errors of the proposed matrix estimators in the spectral norm and also in the Frobenius norm. For convenience, we use ∥ · ∥_(·) as general notation for one of these two matrix norms. Define α_Cκ,(·) = ∥C_k∥(·)/∥X_k∥(_·) and α_Dκ,(·) = ∥D_k∥(·)/∥X_k∥(·).

Theorem 3. For k = 1, 2, assume ${\widehat{\mathrm{C}}}_k$, ${\widehat{\mathrm{D}}}_k$, ${\widehat{\mathrm{X}}}_k$ and $\widehat{\mathrm{\Theta }}$ defined in Subsection 2.2 are constructed with true r_k and r₁₂. Suppose that r₁₂ ≥ 1 and Assumption 1 hold. Define $\mathrm{\Delta }={\delta }_{\theta }^{1/2}$ and

$${\delta }_{\theta }=\min \left\{\frac{1}{\sqrt{n}}+\sum _{k=1}^2\sqrt{\frac{p_k\log p_k}{n{\lambda }_1({\mathrm{\Sigma }}_k)}},1\right\}.$$

Then, we have the following relative error bounds of the matrix estimators

$$\frac{{\Vert {\widehat{\mathrm{C}}}_k-{\mathrm{C}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{C}}_k\Vert }_{(\cdot )}}=O_P\left(\frac{\mathrm{\Delta }}{{\alpha }_{{\mathrm{C}}_k},(\cdot )}\right),\frac{{\Vert {\widehat{\mathrm{D}}}_k-{\mathrm{D}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{D}}_k\Vert }_{(\cdot )}}=O_P\left(\frac{\mathrm{\Delta }}{{\alpha }_{{\mathrm{D}}_k},(\cdot )}\right),\frac{{\Vert {\widehat{\mathrm{X}}}_k-{\mathrm{X}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{X}}_k\Vert }_{(\cdot )}}=O_p(\mathrm{\Delta }),$$

and the error bound of canonical correlation estimators

$$\underset{1\le \ell \le r_{\min }}{\max }\mid {\sigma }_{\ell }(\widehat{\mathrm{\Theta }})-{\sigma }_{\ell }(\mathrm{\Theta })\mid =O_P({\delta }_{\theta }).$$

Provided that matrix ranks r₁, r₂ and r₁₂ are correctly selected, Theorem 3 shows the consistency of the proposed matrix estimators in the relative errors that are the norms of estimation errors divided by the norms of true matrices, with associated convergence rates. The ratios α_Cκ,(·) and α_Dκ,(·) in the convergence rates of ${\widehat{\mathrm{C}}}_k$ and ${\widehat{\mathrm{D}}}_k$ can be removed if the relative errors are instead scaled by the norms of the signal matrices.

Although the ED estimators of r₁ and r₂ given in (28) are consistent under some mild conditions (Onatski, 2010), the consistency of the MDL-IC estimator in (29) for r₁₂ is still unclear. However, the following corollary indicates the robustness of our proposed matrix estimators given in (23) and (25) when r₁₂ is misspecified but r₁ and r₂ are appropriately selected.

Corollary 1. For k = 1, 2, assume ${\widehat{C}}_k^{(r)}$, ${\widehat{\mathrm{D}}}_k$ and $\widehat{\mathrm{\Theta }}$ defined in Subsection 2.2 are constructed with the unknown r_k replaced by an estimator ${\check{r}}_k$ satisfying ${\check{r}}_k\stackrel{P}{\to }{r}_k$. Define ${\widehat{\mathrm{X}}}_k^{(r)}={\widehat{\mathrm{X}}}_k^{(r)}+{\widehat{D}}_k$ with $\min (r_{12},{\tilde{r}}_{12})\le r\le r_{\min }$, and ${\sigma }_{\ell }(\widehat{\mathrm{\Theta }})=0$ for $\ell >\min ({\check{r}}_1,{\check{r}}_2)$. Suppose that r₁₂ ≥ 1 and Assumption 1 hold. Then, with Δ and δ_θ defined in Theorem 3, we have

$$\begin{array}{cc}\hfill & \frac{{\Vert {\widehat{\mathrm{C}}}_k^{(r)}-{\mathrm{C}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{C}}_k\Vert }_{(\cdot )}}=O_P\left(\frac{\mathrm{\Delta }}{{\alpha }_{{\mathrm{C}}_k},(\cdot )}\right),\frac{{\Vert {\widehat{\mathrm{D}}}_k-{\mathrm{D}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{D}}_k\Vert }_{(\cdot )}}=O_P\left(\frac{\mathrm{\Delta }}{{\alpha }_{{\mathrm{D}}_k},(\cdot )}\right),\hfill \\ \hfill & \frac{{\Vert {\widehat{\mathrm{X}}}_k^{(r)}-{\mathrm{X}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{X}}_k\Vert }_{(\cdot )}}=O_P(\mathrm{\Delta }),\mathit{and}\underset{1\le \ell \le r_{\min }}{\max }\mid {\sigma }_{\ell }(\widehat{\mathrm{\Theta }})-{\sigma }_{\ell }(\mathrm{\Theta })\mid =O_P({\delta }_{\theta }).\hfill \end{array}$$

Corollary 1 provides an acceptable range, [$\min (r_{12},{\tilde{r}}_{12})$, r_min], for the choice of r₁₂ when r₁ and r₂ are consistently estimated, which can theoretically lead to the same convergence rates (up to a constant factor) as those in Theorem 3. Note that the distinctive matrices ${\widehat{\mathrm{D}}}_k$’s are independent of r₁₂.

4. Simulation Studies

We consider the following three simulation setups to evaluate the finite sample performance of the proposed D-CCA estimators comparing with the six competing methods mentioned in Section 1 and also the decomposition of Hallin and Liška (2011) (denoted as GDFM).

• Setup 1: Let ${\mathit{x}}_1\stackrel{d}{=}{\mathit{x}}_2$, with r₁ = 3, r₁₂ = 1, and λ_ℓ(Σ₁) = 500 – 200(ℓ – 1) for ℓ ≤ 3. Set $z_{k1},z_{k2},z_{k3}\stackrel{i.i.d.}{~}N(0,1)$ for each k = 1, 2. Randomly generate V₁ with orthonormal columns, which is the same for all replications. Let ${\mathit{x}}_k={\mathrm{V}}_1{\mathrm{\Lambda }}_1^{1/2}{z}_k$. Generate $e_{ki},k\le 2,i\le p_k\stackrel{i.i.d.}{~}N(0,{\sigma }_e^2)$ that are independent of ${\{{\mathit{x}}_k\}}_{k=1}^2$. Vary dimension p₁ from 100 to 1,500, the first canonical angle θ₁ = arccos(ρ₁) from 0° to 75° with ρ₁ = corr(z₁₁, z₂₁), and the noise variance ${\sigma }_e^2$ from 0.01 to 16.

• Setup 2: Use the same settings for x₁ and ${\{e_k\}}_{k=1}^2$ as in Setup 1. For x₂, fix p₂ = 300, and set r₂ = 5 and λ_ℓ(Σ₂) = 500 – 100(ℓ – 1) for ℓ ≤ 5. Simulate ${\mathit{x}}_2={\mathrm{V}}_2{\mathrm{\Lambda }}_2^{1/2}{z}_2$ with $z_{21},\dots ,z_{25}\stackrel{i.i.d.}{~}N(0,1)$ and a randomly generated V₂ that is the same for all replications. Let r₁₂ = 1. Vary p₁, θ₁ and ${\sigma }_e^2$ according to Setup 1.

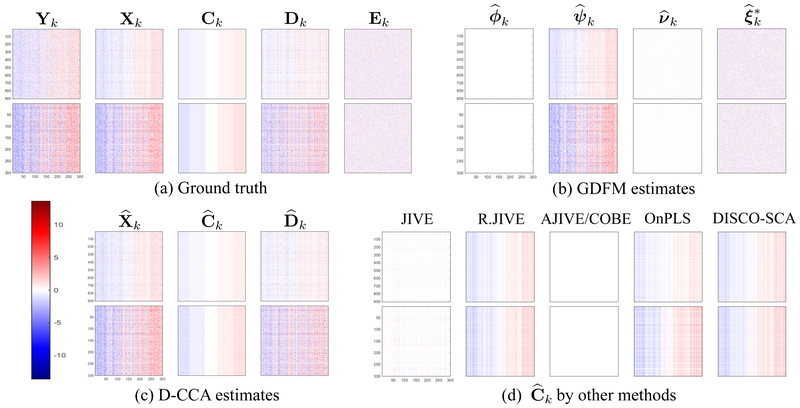
• Setup 3 is for visual purposes: Fix p₁ = 3_p2 = 900, θ₁ = 45°, and ${\sigma }_e^2=1$. Generate two independent variables υ₁ and υ₂ such that $v_1~\text{Unif}(\{0,\pm 1/\sqrt{2},\pm \sqrt{2}\})$ and υ₂ ~ N(0, 1). Let $z_{11}=[v_1+v_2\text{tan}({\theta }_1/2)]/\sqrt{1+{\tan }^2({\theta }_1/2)}$ and $z_{21}=[v_1-v_2\text{tan}({\theta }_1/2)]/\sqrt{1+{\tan }^2({\theta }_1/2)}$. Set ${\mathrm{V}}_k^{[:,1]}=\frac{1}{{\sqrt{p}}_k}{(1,1,\dots ,1)}^{⊺}$ and randomly generate ${\mathrm{V}}_k^{[:,2:r_k]}$ for k = 1, 2. The other settings are the same as those in Setup 2.

We fixed the sample size n = 300 and conducted 1,000 replications for Setups 1 and 2. Setup 3 is only used for the purpose of visually comparing D-CCA with the seven other methods. Setup 3 is similar to Setup 2, but it has the common variable of the first pair of canonical variables following a discrete uniform distribution instead of a Gaussian distribution. We ran a single replication of Setup 3 for the visual comparison in Figure 5. To determine the ranks r₁, r₂, and r₁₂, we respectively used the ED method given in (28) and the MDL-IC method in (29). Additional simulations with AR(1) matrices for ${\{\text{cov}({\mathit{e}}_k)\}}_{k=1}^2$ are given in the supplementary material (Section S.2).

Figure 5:

Color maps for a single replication of Setup 3.

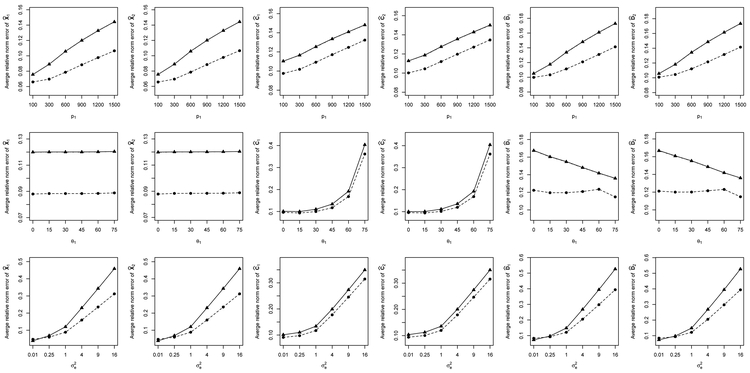
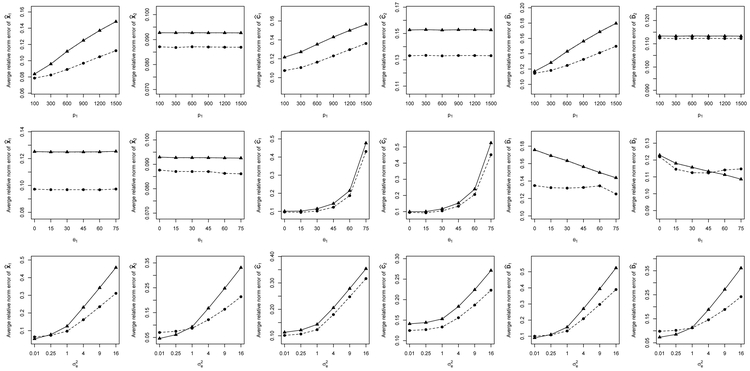
The results obtained by D-CCA for Setups 1 and 2 are summarized in Figures 3 and 4 and Table 1. The first rows of the two figures show the average relative errors (AREs) for θ₁ = 45°, ${\sigma }_e^2=1$ and varying p₁; the second rows are for p₁ = 900, ${\sigma }_e^2=1$ and varying θ₁; and the third rows are for p₁ = 900, θ₁ = 45° and varying ${\sigma }_e^2$. Both figures reveal that the curves based on the estimated ranks almost overlap with those based on the true ranks. The ranks are selected with very high accuracy (>99.7%).

Figure 3:

Average relative errors of D-CCA estimates under Setup 1 in spectral norm (○) and Frobenius norm (△) using true r₁, r₂ and r₁₂, and those in spectral norm (●) and Frobenius norm (▴) using ${\widehat{r}}_1$, ${\widehat{r}}_2$ and ${\widehat{r}}_{12}$.

Figure 4:

Average relative errors of D-CCA estimates under Setup 2 in spectral norm (○) and Frobenius norm (▵) using true r₁, r₂ and r₁₂, and those in spectral norm (●) and Frobenius norm (▴) using ${\widehat{r}}_1$, ${\widehat{r}}_2$ and ${\widehat{r}}_{12}$.

Table 1:

Averages (standard errors) of D-CCA estimates for the first canonical angle/correlation.

(p1, ${\sigma }_e^2$)	θ1 = 0°/ρ1 = 1	θ1 = 45°/ρ1 = 0.707	θ1 = 60°/ρ1 = 0.5	θ1 = 75°/ρ1 = 0.259
Setup 1
(100, 1)	3.59°(0.21°)/0.998(0.000)	44.7°(2.38°)/0.710(0.029)	59.3°(2.88°)/0.509(0.043)	73.5°(3.06°)/0.284(0.051)
(600, 1)	3.61°(0.21°)/0.998(0.000)	44.7°(2.39°)/0.710(0.029)	59.4°(2.89°)/0.509(0.043)	73.5°(3.07°)/0.284(0.051)
(900, 1)	3.61°(0.21°)/0.998(0.000)	44.7°(2.39°)/0.710(0.029)	59.4°(2.90°)/0.509(0.043)	73.5°(3.09°)/0.283(0.052)
(l500, 1)	3.61°(0.21°)/0.998(0.000)	44.7°(2.39°)/0.710(0.029)	59.3°(2.89°)/0.509(0.043)	73.5°(3.08°)/0.284(0.051)
(900, 0.01)	0.36°(0.02°)/1.000(0.000)	44.6°(2.38°)/0.711(0.025)	59.3°(2.89°)/0.508(0.038)	73.5°(3.08°)/0.280(0.046)
(900, 1)	3.61°(0.21°)/0.998(0.000)	44.7°(2.39°)/0.709(0.026)	59.4°(2.90°)/0.507(0.038)	73.5°(3.09°)/0.280(0.046)
(900, 9)	11.0°(0.66°)/0.992(0.001)	45.6°(2.43°)/0.705(0.026)	59.9°(2.92°)/0.504(0.039)	73.7°(3.08°)/0.279(0.046)
(900, 16)	14.9°(0.91°)/0.966(0.004)	46.4°(2.47°)/0.688(0.028)	60.4°(2.93°)/0.492(0.040)	73.9°(3.06°)/0.273(0.047)
Setup 2
(100, 1)	3.58°(0.21°)/0.998(0.000)	44.5°(2.36°)/0.712(0.029)	59.0°(2.83°)/0.514(0.042)	72.7°(2.90°)/0.296(0.048)
(600, 1)	3.59°(0.21°)/0.998(0.000)	44.5°(2.36°)/0.712(0.029)	59.0°(2.83°)/0.514(0.042)	72.7°(2.89°)/0.297(0.048)
(900, 1)	3.60°(0.21°)/0.998(0.000)	44.5°(2.37°)/0.712(0.029)	59.0°(2.84°)/0.514(0.043)	72.7°(2.90°)/0.296(0.048)
(1500, 1)	3.60°(0.21°)/0.998(0.000)	44.5°(2.36°)/0.712(0.029)	59.0°(2.82°)/0.514(0.042)	72.7°(2.89°)/0.296(0.048)
(900, 0.01)	0.36°(0.02°)/1.000(0.000)	44.4°(2.35°)/0.714(0.029)	59.0°(2.82°)/0.515(0.042)	72.7°(2.89°)/0.297(0.048)
(900, 1)	3.60°(0.21°)/0.998(0.000)	44.5°(2.37°)/0.712(0.029)	59.0°(2.84°)/0.514(0.043)	72.7°(2.90°)/0.296(0.048)
(900, 9)	10.9°(0.64°)/0.982(0.002)	45.4°(2.41°)/0.701(0.030)	59.6°(2.87°)/0.506(0.043)	73.0°(2.93°)/0.292(0.049)
(900,16)	14.6°(0.87°)/0.967(0.004)	46.3°(2.45°)/0.691(0.031)	60.0°(2.89°)/0.499(0.044)	73.2°(2.93°)/0.289(0.049)

Consider Figure 3 of Setup 1 as an example. We have nearly identical plots for the two datasets that are generated from the same distribution. From the first row, where all considered cases have almost the same set of average ratios {α_Ck,(·), α_Dk,(·)}, all the AREs become bigger as the dimension p₁ increases. For the second row, the increasing canonical angle θ₁ results in a change in the average ratios α_Ck,2 from 0.997 down to 0.18 and in α_ck,F from 0.74 down to 0.14; α_Dk,2 is stable around 0.78 for the first 5 values of θ₁ and then increases to 0.87 at θ₁ = 75°; and α_Dk,F changes from 0.67 to 0.93. Meanwhile, this leads to increasing AREs of ${\widehat{\mathrm{C}}}_k$ and decreasing AREs of ${\widehat{\mathrm{D}}}_k$, but does not affect the AREs of ${\widehat{\mathrm{X}}}_k$. The third row shows that all the AREs increase as the noise variance ${\sigma }_e^2$ becomes bigger. Note that increasing ${\sigma }_e^2$ is equivalent to decreasing the eigenvalues of Σ_k by scaling ${\sigma }_e^2$ to 1. These results agree with the influence of p₁, α and λ₁(Σ_k) on the convergence rates given in Theorem 3.

For Setup 2, with similar arguments, we find a similar pattern of estimation performance for D-CCA, as shown in the second and third rows and the plots of the first dataset in the first row of Figure 4. For the first row of Figure 4, the considered cases of the second dataset have a fixed dimension p₂ and stable ratios {α_C2,(·), α_D2,(·)}. The corresponding AREs are still acceptable and interestingly are not much impacted by the change in the dimension p₁ of the first dataset. From Table 1, we see that the estimated canonical angles and correlations perform well for Setups 1 and 2 even in the presence of strong noise levels.

The comparison of D-CCA and the seven other methods is shown in Tables 2 and 3, and Figure 5. First consider these methods other than GDFM (Hallin and Liška, 2011). Table 2 reports the results for Setups 1 and 2 when we set p₁ = 900, θ1 = 45° (i.e., ρ₁ = 0.707), and ${\sigma }_e^2=1$. All methods except OnPLS have comparably good performance for the estimation of signal matrices. As expected, D-CCA outperforms all the six competing methods in terms of estimating the common and distinctive matrices. In particular, AJIVE and COBE are unable to discover the common matrices. Figure 5 visually shows a similar comparison based on a single replication of Setup 3. The signal, common, and distinctive matrices are recovered well by the D-CCA method. In contrast, the common matrix estimators estimated from the six state-of-the-art methods significantly differ from the ground truth. AJIVE and COBE still yield zero matrices as the estimators of the common matrices, which appears not reasonable when the first canonical correlation ρ₁ has a high value of 0.707. Table 3 shows the proportion of significant nonzero correlations among the p₁×p₂ pairs of variables between d₁ and d₂ that were detected by the normal approximation test (DiCiccio and Romano, 2017) using each method’s estimates of D₁ and D₂. The procedure of Benjamini and Hochberg (1995) was applied to the multiple tests to control false discovery rate at 0.05. Results are omitted for AJIVE and COBE with ${\widehat{\mathrm{C}}}_k=0$, and also for D-CCA and R.JIVE due to zero correlation estimates by ${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$. All the other methods have a large amount of significant nonzero correlations retained between their distinctive structures.

Table 2:

Averages (standard errors) of norm ratios when p₁ = 900, θ₁ = 45° and ${\sigma }_e^2=1$.

Ratio	Method	Spectral norm	Frobenius norm	Spectral norm	Frobenius norm
		Setup 1		Setup 2
		k = 1 / k = 2	k = 1 / k = 2	k = 1 / k = 2	k = 1 / k = 2
$\frac{{\Vert {\widehat{\mathrm{X}}}_k-{\mathrm{X}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{X}}_k\Vert }_{(\cdot )}}$	D-CCA	0.088(0.010)/0.088(0.010)	0.120(0.006)/0.120(0.006)	0.097(0.012)/0.087(0.017)	0.125(0.007)/0.093(0.006)
	JIVE	0.108(0.005)/0.109(0.005)	0.141(0.004)/0.141(0.004)	0.116(0.005)/0.067(0.004)	0.145(0.004)/0.090(0.002)
	R.JIVE	0.109(0.018)/0.089(0.015)	0.139(0.013)/0.140(0.009)	0.108(0.018)/0.102(0.026)	0.139(0.012)/0.105(0.011)
	AJIVE	0.080(0.004)/0.081(0.004)	0.116(0.003)/0.116(0.004)	0.081(0.004)/0.051(0.002)	0.116(0.003)/0.082(0.002)
	OnPLS	0.390(0.111)/0.399(0.112)	0.315(0.076)/0.321(0.077)	0.397(0.111)/0.550(0.116)	0.320(0.077)/0.331(0.064)
	DISCO-SCA	0.083(0.003)/0.083(0.004)	0.154(0.004)/0.154(0.005)	0.084(0.004)/0.053(0.002)	0.174(0.005)/0.093(0.002)
	COBE	0.080(0.004)/0.081(0.004)	0.116(0.003)/0.116(0.004)	0.081(0.004)/0.051(0.002)	0.116(0.003)/0.082(0.002)
$\frac{{\Vert {\widehat{\mathrm{C}}}_k-{\mathrm{C}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{C}}_k\Vert }_{(\cdot )}}$	D-CCA	0.117(0.028)/0.120(0.027)	0.134(0.028)/0.136(0.027)	0.123(0.028)/0.133(0.036)	0.143(0.029)/0.153(0.038)
	JIVE	0.996(0.009)/0.996(0.008)	1.024(0.014)/1.024(0.013)	0.998(0.009)/0.990(0.015)	1.037(0.025)/1.013(0.019)
	R.JIVE	1.000(0.043)/0.576(0.032)	1.003(0.043)/0.588(0.031)	1.003(0.049)/0.576(0.041)	1.006(0.052)/0.589(0.042)
	AJIVE	1(0)/1(0)	1(0)/1(0)	1(0)/1(0)	1(0)/1(0)
	OnPLS	0.787(0.112)/0.777(0.113)	0.817(0.143)/0.805(0.142)	0.779(0.105)/0.796(0.071)	0.804(0.117)/0.815(0.098)
	DISCO-SCA	1.023(0.065)/1.023(0.066)	1.057(0.087)/1.058(0.089)	0.772(0.183)/1.052(0.112)	0.826(0.227)/1.190(0.237)
	COBE	1(0)/1(0)	1(0)/1(0)	1(0)/1(0)	1(0)/1(0)
$\frac{{\Vert {\widehat{\mathrm{D}}}_k-{\mathrm{D}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{D}}_k\Vert }_{(\cdot )}}$	D-CCA	0.121(0.016)/0.122(0.016)	0.148(0.010)/0.149(0.009)	0.133(0.018)/0.112(0.019)	0.156(0.011)/0.113(0.009)
	JIVE	0.703(0.040)/0.703(0.040)	0.541(0.023)/0.541(0.023)	0.704(0.040)/0.599(0.036)	0.546(0.024)/0.371(0.016)
	R.JIVE	0.689(0.040)/0.405(0.032)	0.535(0.019)/0.337(0.020)	0.690(0.041)/0.350(0.031)	0.536(0.022)/0.238(0.017)
	AJIVE	0.706(0.040)/0.706(0.040)	0.538(0.022)/0.539(0.022)	0.705(0.040)/0.605(0.035)	0.538(0.022)/0.369(0.015)
	OnPLS	0.655(0.093)/0.654(0.095)	0.574(0.064)/0.576(0.066)	0.656(0.094)/0.658(0.113)	0.574(0.063)/0.476(0.057)
	DISCO-SCA	0.704(0.049)/0.704(0.049)	0.558(0.041)/0.559(0.041)	0.532(0.114)/0.628(0.067)	0.462(0.092)/0.432(0.078)
	COBE	0.706(0.040)/0.706(0.040)	0.538(0.022)/0.539(0.022)	0.705(0.040)/0.605(0.035)	0.538(0.022)/0.369(0.015)
$\frac{{\Vert {\widehat{\chi }}_k-{\mathrm{X}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{X}}_k\Vert }_{(\cdot )}}$	GDFM	0.080(0.004)/0.081(0.004)	0.116(0.003)/0.116(0.004)	0.081(0.004)/0.052(0.002)	0.116(0.003)/0.082(0.002)
$\frac{{\Vert {\widehat{\chi }}_k^{\ast }-{\mathrm{X}}_k\Vert }_{(\cdot )}}{{\Vert {\mathrm{X}}_k\Vert }_{(\cdot )}}$	GDFM	0.083(0.003)/0.083(0.004)	0.154(0.004)/0.154(0.005)	0.084(0.004)/0.053(0.002)	0.174(0.005)/0.093(0.002)
$\frac{{\Vert {\widehat{\nu }}_k\Vert }_{(\cdot )}}{{\Vert {\chi }_k^{\ast }\Vert }_{(\cdot )}}$	GDFM	0.080(0.003)/0.080(0.004)	0.099(0.003)/0.099(0.003)	0.082(0.003)/0.047(0.002)	0.128(0.004)/0.044(0.001)

Table 3:

The proportions of significant nonzero correlations between d₁ and d₂ for simulation setups (with p₁ = 900, θ₁=45° and ${\sigma }_e^2=1$) and TCGA datasets. Averages (standard errors) are shown for Setups 1 and 2. Significant correlations are detected by the normal approximation test (DiCiccio and Romano, 2017) using ${\widehat{\mathrm{D}}}_1$ and ${\widehat{\mathrm{D}}}_2$, with false discovery rate controlled at 0.05.

Method	Setup 1	Setup 2	Setup 3	EXP90/METH90b	EXP90/METH90a
D-CCA	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$
JIVE	69.9%(2.5%)	60.8%(3.0%)	98.7%	85.0%	58.2%
R.JIVE	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$	${\widehat{\mathrm{D}}}_1{\widehat{\mathrm{D}}}_2^{⊺}=0$
AJIVE	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$
OnPLS	56.6%(11.1%)	32.7%(8.2%)	52.5%	72.9%	68.6%
DISCO-SCA	50.3%(4.6%)	25.2%(6.7%)	25.1%	67.8%	64.2%
COBE	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$	${\widehat{\mathrm{C}}}_k=0$
GDFM $({\widehat{\mathrm{D}}}_k={\widehat{\psi }}_k)$	70.3%(2.4%)	61.5%(2.7%)	98.6%	100%	100%
GDFM $({\widehat{\mathrm{D}}}_k={\widehat{\psi }}_k+{\widehat{\nu }}_k)$	73.8%(1.8%)	64.8%(2.3%)	97.0%	85.8%	87.0%

Now consider the GDFM method (Hallin and Liška, 2011). We set the sample temporal cross-covariances to be zero in GDFM estimation for our simulated data and TCGA datasets that have no temporal dependence. GDFM decomposes each data matrix by ${\mathrm{Y}}_k={\chi }_k^{\ast }+{\xi }_k^{\ast }=({\varphi }_k+{\psi }_k)+({\nu }_k+{\xi }_k^{\ast })={\chi }_k+{\xi }_k$ with each component’s name shown in Table 6. By Remark S.1 (in the supplementary material), theoretically for our simulated i.i.d. data with no correlations between signals and noises, the weakly idiosyncratic matrix ν_k is zero, and the joint common matrix ${\chi }_k^{\ast }$ and the marginal common matrix χ_k are both equal to the signal matrix X_k. Moreover, the strongly common matrix ϕ_k is zero, when $\text{span}({\mathit{x}}_1^{⊺})\cap \text{span}({\mathit{x}}_2^{⊺})=\{0\}$, i.e., the first canonical correlation ρ₁ between x₁ and x₂ is smaller than 1. The above theoretical results are evidenced by our simulations. In Table 2, the relative errors of estimators ${\widehat{\chi }}_k^{\ast }$ and ${\widehat{\chi }}_k$ to signal X_k are as comparably small as those of ${\widehat{\mathrm{X}}}_k$ by our D-CCA and the other five well performed methods. The similarly small norm ratios of ${\widehat{\nu }}_k$ to ${\widehat{\chi }}_k^{\ast }$ numerically support ν_k = 0. The squares of these quantities are much smaller, and especially in the Frobenius norm are equivalent to matrix-variation ratios. The strongly common matrix estimate ${\widehat{\varphi }}_k$ is zero for the setups, with ρ₁ = 0.707 < 1, considered in the table. These numerical evidences are more clearly seen in Figure 5(b) under a similar setup.

Table 6:

Ranks, variation ratios ($\mathrm{VR}={\Vert \cdot \Vert }_F^2/{\Vert {\widehat{\chi }}_k^{\ast }\Vert }_F^2$), and SWISS scores of GFDM matrix estimates for TCGA datasets.

Matrix Estimate	EXP90 / METH90b		EXP90 / METH90a
	Rank (VR)	SWISS	Rank (VR)	SWISS
${\widehat{\chi }}_k^{\ast }$ (joint common)	4 / 4	0.373 / 0.569	4 / 4	0.378 / 0.850
${\widehat{\chi }}_k$ (marginal common)	3 (0.986) / 3 (0.986)	0.364 / 0.566	3 (0.990) / 3 (0.974)	0.372 / 0.851
${\widehat{\varphi }}_k$ (strongly common)	2 (0.755) / 2 (0.626)	0.288 / 0.348	2 (0.770) / 2 (0.372)	0.302 / 0.613
${\widehat{\psi }}_k$ (weakly common)	1 (0.231) / 1 (0.360)	0.764 / 0.991	1 (0.220) / 1 (0.602)	0.811 / 0.996
${\widehat{\nu }}_k$ (weakly idiosyncratic)	1 (0.014)/ 1 (0.014)	0.987 / 0.760	1 (0.010) / 1 (0.026)	0.997 / 0.812
${\widehat{\psi }}_k+{\widehat{\nu }}_k$	2 (0.245) / 2 (0.374)	0.777 / 0.982	2 (0.230) / 2 (0.628)	0.819 / 0.988
${\widehat{\xi }}_k^{\ast }$ (strongly idiosyncratic)	656 (2.070) / 656 (1.196)	0.985 / 0.987	656 (2.151) / 656 (1.764)	0.977 / 0.989
${\widehat{\xi }}_k$ (marginal idiosyncratic)	657 (2.084) / 657 (1.211)	0.985 / 0.983	657 (2.160) / 657 (1.790)	0.977 / 0.987

5. Analysis of TCGA Breast Cancer Data

In this section, we apply the proposed D-CCA method to analyze genomic datasets produced from TCGA breast cancer tumor samples. We investigate the ability to separate tumor subtypes for matrices obtained from D-CCA in comparison to those obtained from the six competing methods as well as GDFM that are mentioned in Section 1. We consider the mRNA expression data and DNA methylation data for a common set of 660 samples. The two datasets are publicly available at https://tcga-data.nci.nih.gov/docs/publications and have been respectively preprocessed by Ciriello et al. (2015) and Koboldt et al. (2012). The 660 samples were classified by Ciriello et al. (2015) into 4 subtypes using the PAM50 model (Parker et al., 2009) based on mRNA expression data. Specifically, the samples consist of 112 basal-like, 55 HER2-enriched, 331 luminal A, and 162 luminal B tumors.

To quantify the extent of subtype separation, we adopt the standardized within-class sum of squares (SWISS; Cabanski et al., 2010)

$$\text{SWISS}(\mathrm{A})=\frac{\sum _{i=1}^p\sum _{j=1}^n{(A_{ij}-{\stackrel{‒}{A}}_{i,s(j)})}^2}{\sum _{i=1}^p\sum _{j=1}^n{(A_{ij}-{\stackrel{‒}{A}}_i.)}^2}$$

for matrix A = (A_ij)_p×n, where ${\stackrel{‒}{A}}_{i,s(j)}$ is the average of the j-th sample’s subtype on the i-th row and ${\stackrel{‒}{A}}_i$. is the average of the i-th row’s elements. The SWISS score represents the variation within the subtypes as a proportion of the total variation. A lower score indicates better subtype separation. For the mRNA expression data, we filtered out the subset consisting of the 1,195 variably expressed genes with marginal SWISS≤0.9 from the original 20,533 genes, and denote this subset as EXP90. The 2,083 variably methylated probes of the DNA methylation data, originally with 21,986 probes, are included in the analysis. We denote the 881 probes with marginal SWISS≤0.9 as METH90b and the remaining 1,202 probes as METH90a. We conducted the analysis for the pair of EXP90 and METH90b as well as the pair of EXP90 and METH90a.

The ranks and proportions of explained signal variation for the matrix estimators obtained by D-CCA and the six competing methods (except GDFM) are given in Table 4, and their SWISS scores are shown in Table 5. We see in Table 4 that D-CCA, AJIVE and COBE give much lower ranks for the estimated signal matrices ${\{{\widehat{\mathrm{X}}}_k\}}_{k=1}^2$ than the other methods. Particularly for the EXP90 dataset, the rank of ${\widehat{\mathrm{X}}}_1$ obtained by the remaining four methods is inconsistent for the two pairs. As shown in the scree plots of Figure 6, the ranks of signal matrices selected by D-CCA and AJIVE look reasonable because the few most leading principal components of the observed data are captured for denoising, while the signal matrix ranks for the METH90b and METH90a datasets seem to be underestimated by COBE. Using D-CCA, the estimated canonical correlations and angles of signal vectors are (0.934, 0.431) and (20.9°, 64.4°) between the EXP90 and METH90b datasets, and are (0.610, 0.275) and (52.4°, 74.0°) between the EXP90 and METH90a datasets.

Table 4:

Ranks (and proportions of explained signal variation, i.e., ${\Vert \cdot \Vert }_F^2/{\Vert {\widehat{\mathrm{X}}}_k\Vert }_F^2$) of matrix estimates for TCGA datasets.

Matrix	Method	EXP90 / METH90b	EXP90 / METH90a
${\widehat{\mathrm{X}}}_k$	D-CCA	2 / 3	2 / 3
	JIVE	35 / 18	41 / 29
	R.JIVE	40 / 27	44 / 49
	AJIVE	2 / 3	2 / 3
	OnPLS	13 / 10	12 / 10
	DISCO-SCA	13 / 13	17 / 17
	COBE	2 / 1	2 / 2
${\widehat{\mathrm{C}}}_k$	D-CCA	2 (0.472) / 2 (0.301)	2 (0.120) / 2 (0.062)
	JIVE	1 (0.068) / 1 (0.086)	3 (0.236) / 3 (0.167)
	R.JIVE	1 (0.212) / 1 (0.505)	3 (0.274) / 3 (0.602)
	AJIVE	0 / 0	0 / 0
	OnPLS	3 (0.516) / 3 (0.510)	2 (0.455) / 2 (0.166)
	DISCO-SCA	6 (0.732) / 6 (0.571)	8 (0.745) / 8 (0.363)
	COBE	0 / 0	0 / 0
${\widehat{\mathrm{D}}}_k$	D-CCA	2 (0.223) / 3 (0.506)	2 (0.564) / 3 (0.797)
	JIVE	34(0.932) / 17 (0.914)	38 (0.764) / 26 (0.833)
	R.JIVE	39 (0.788) / 26 (0.495)	41 (0.726) / 46 (0.398)
	AJIVE	2 (1) / 3 (1)	2 (1) / 3 (1)
	OnPLS	10 (0.484) / 7 (0.490)	10 (0.545) / 8 (0.834)
	DISCO-SCA	7 (0.268) / 7 (0.429)	9 (0.255) / 9 (0.637)
	COBE	2 (1) / 1 (1)	2 (1) / 2 (1)

Table 5:

SWISS scores for TCGA breast cancer subtypes. Lower scores indicate better subtype separation.

Matrix	Method	EXP90 / METH90b	EXP90 / METH90a
Yk	For all	0.773 / 0.814	0.773 / 0.952
${\widehat{\mathrm{X}}}_k$	D-CCA	0.313 / 0.623	0.313 / 0.925
	JIVE	0.632 / 0.698	0.643 / 0.920
	R.JIVE	0.642 / 0.689	0.647 / 0.931
	AJIVE	0.314 / 0.623	0.314 / 0.925
	OnPLS	0.523 / 0.669	0.515 / 0.905
	DISCO-SCA	0.526 / 0.663	0.553 / 0.904
	COBE	0.314 / 0.545	0.314 / 0.926
${\widehat{\mathrm{C}}}_k$	D-CCA	0.240 / 0.269	0.528 / 0.606
	JIVE	0.831 / 0.831	0.639 / 0.736
	R.JIVE	0.373 / 0.373	0.564 / 0.885
	AJIVE	NA / NA	NA / NA
	OnPLS	0.398 / 0.312	0.419 / 0.494
	DISCO-SCA	0.447 / 0.400	0.470 / 0.717
	COBE	NA / NA	NA / NA
${\widehat{\mathrm{D}}}_k$	D-CCA	0.623 / 0.940	0.320 / 0.979
	JIVE	0.691 /0.741	0.830 / 0.963
	R.JIVE	0.833 / 0.997	0.874 / 0.998
	AJIVE	0.314 / 0.623	0.314 / 0.925
	OnPLS	0.878 / 0.978	0.871 / 0.989
	DISCO-SCA	0.935 / 0.992	0.944 / 0.995
	COBE	0.314 / 0.545	0.314 / 0.926

From Table 5, for the pair of EXP90 and METH90b datasets, the matrix ${\widehat{\mathrm{X}}}_k$ obtained by all the seven methods gains an improved SWISS score compared to the noisy data matrix Y_k. Other than AJIVE and COBE with ${\widehat{\mathrm{C}}}_k=0$, a clear pattern of increasing SWISS scores, from ${\widehat{\mathrm{C}}}_k$ to ${\widehat{\mathrm{X}}}_k$ and then to ${\widehat{\mathrm{D}}}_k$, can be seen for the remaining methods except JIVE. This indicates that an enhanced ability to separate the tumor samples by subtype can be expected when integrating two datasets that can exhibit such a distinction to a moderate extent. Also note that the estimated common matrices of our D-CCA have the lowest SWISS scores. While considering the pair of EXP90 and METH90a datasets, for all the seven methods we find a big gap between the SWISS scores of the two estimated signal matrices, and that the denoised matrix of the METH90a dataset still has nearly no discriminative power with SWISS close to 1. The ability on subtype separation seems more likely to be a distinctive feature of EXP90 dataset comparing to METH90a dataset. The estimated distinctive matrix of EXP90 is thus expected to have a lower SWISS score than its estimated common matrix. However, only D-CCA meets this point, except that AJIVE and COBE yield zero common matrices. The failure of the six competing methods may be caused by their inappropriate decomposition constructions, which are mentioned in Section 1. In particular, from Table 3, we see that a lot of significant nonzero correlations exist among all gene-probe pairs based on the estimated distinctive matrices, respectively, obtained by JIVE, OnPLS and DISCO-SCA.

The GDFM method (Hallin and Liška, 2011) was also applied to the TCGA datasets. Table 6 summarizes the results of GDFM matrix estimates. As estimators of signal matrix X_k, matrix ${\widehat{\chi }}_k$ has comparable rank and SWISS score as those of our D-CCA estimator ${\widehat{\mathrm{X}}}_k$ given in Tables 4 and 5. Besides, ${\chi }_k^{\ast }={\chi }_k$, i.e., ν_k = 0, is numerically suggested by the remarkably small variation ratios of ${\widehat{\nu }}_k$ to ${\widehat{\chi }}_k^{\ast }$ that are likely just induced by estimation errors. With very large ranks and uninformative SWISS scores, both ${\widehat{\xi }}_k^{\ast }$ and ${\widehat{\xi }}_k$ appear to be noises. One may let ${\widehat{C}}_k={\widehat{\varphi }}_k$, ${\widehat{D}}_k={\widehat{\psi }}_k$ (or ${\widehat{D}}_k={\widehat{\psi }}_k+{\widehat{\nu }}_k$), and ${\widehat{\mathrm{X}}}_k={\chi }_k$ (or ${\widehat{\mathrm{X}}}_k={\chi }_k^{\ast }$) for GDFM. Inspecting Table 6 reveals that the discussion given in the preceding paragraph also holds even when we include GDFM.

6. Discussion

In this paper, we study a typical model for the joint analysis of two high-dimensional datasets. We develop a novel and promising decomposition-based CCA method, D-CCA, to appropriately define the common and distinctive matrices. In particular, the conventionally underemphasized orthogonal relationship between the distinctive matrices is now well designed on the ${\mathcal{L}}^2$ space of random variables. A soft-thresholding-based approach is then proposed for estimating these D-CCA-defined matrices with a theoretical guarantee and satisfactory numerical performance. The proposed D-CCA outperforms some state-of-the-art methods in both simulated and real data analyses.

There are many possible further studies beyond the current proposed D-CCA. The first is to generalize the D-CCA for three or more datasets. We may assume that at least two datasets have mutually orthogonal distinctive structures. An immediate idea starts from substituting the multiset CCA (Kettenring, 1971) for the two-set CCA in D-CCA. However, the challenge is that the iteratively obtained sets of canonical variables are not guaranteed to have the bi-orthogonality given in Theorem 1. Hence, we cannot follow the proposed D-CCA to simply break down the decomposition problem to each set of canonical variables, and need a more sophisticated design to meet the desirable constraint. Another direction is to incorporate the nonlinear relationship between the two datasets. The D-CCA only considers the linear relationship by using the traditional CCA based on Pearson’s correlation. It is worth trying the kernel CCA (Fukumizu et al., 2007) or the distance correlation (Székely et al., 2007) to capture the nonlinear dependence. Inspired by the time series analysis of Hallin and Lišska (2011) and Barigozzi et al. (2018), we also expect to generalize D-CCA to general dynamic factor models with comparisons to their methods. These interesting and challenging studies are under investigation and will be reported in future work.