Abstract
We present an analytical hyperelastic constitutive model of the red blood cell (erythrocyte) membrane based on recently improved characterizations of density and microscopic structure of its spectrin network from proteomics and cryo-electron tomography. The model includes distributions of both orientations and natural lengths of spectrin and updated copy numbers of proteins. By applying finite deformation to the spectrin network, we obtain the total free energy and stresses in terms of invariants of shear and area deformation. We generalize an expression of the initial shear modulus, which is independent of the number of molecular orientations within the network and also derive a simplified version of the model. We apply the model and its simplified version to analyze micropipette aspiration computationally and analytically and explore the effect of local cytoskeletal density change. We also explore the discrepancies among shear modulus values measured using different experimental techniques reported in the literature. We find that the model exhibits hardening behavior and can explain many of these discrepancies. Moreover, we find that the distribution of natural lengths plays a crucial role in the hardening behavior when the correct copy numbers of proteins are used. The initial shear modulus values we obtain using our current model (5.9–15.6 pN/μm) are close to the early estimates (6–9 pN/μm). This new, to our knowledge, constitutive model establishes a direct connection between the molecular structure of spectrin networks and constitutive laws and also defines a new picture of a much denser spectrin network than assumed in prior studies.
Significance
This work makes significant contributions to our understanding of the physical basis of red blood cell (RBC) elasticity. We present the first, to our knowledge, microstructure-based elastic model of RBC membranes that accounts for higher densities of spectrin indicated by recent proteomic analysis of RBC proteins, a distribution of spectrin natural lengths obtained from cryo-electron tomography, and the capacity for local cytoskeletal density changes. We show that for the higher spectrin densities indicated by proteomics, accounting for a distribution of molecular lengths in the resting state is essential for reproducing strain-hardening behavior exhibited by the RBC membrane in experiments.
Introduction
The mechanical properties of the membranes of red blood cells (RBCs or erythrocytes) have been extensively studied, but there remains a lack of integrated understanding from the molecular level to the continuum level. On one hand, empirical continuum constitutive laws have been well established, such as the ones described in the monograph by Evans and Skalak (1). In this approach, a two-dimensional hyperelastic constitutive model is derived from thermodynamics using invariants based on assumptions such as isotropy. In early work, Skalak et al. derived a strain energy function of red blood cell membrane based on the invariants of Green’s strain tensor (2). Subsequently, to better separate the shear deformation and the area deformation, Evans and Skalak provided another strain energy function in terms of the area invariant α = λ1λ2 − 1 and shear invariant β = (λ1/λ2 + λ2/λ1 − 2)/2, where λ1 and λ2 are the principal stretch ratios (1). For simplicity, the derivatives of free energy with respect to invariants were assumed to be constants and, as such, define the shear modulus and mean stress resultant (isotropic tension) in the material. In this formulation, the area modulus was defined as the second derivative of the free energy with respect to area, and this was also assumed to be a constant.
Subsequently, the accumulation of experimental evidence indicates that the shear modulus and area modulus are certainly not constants, as would be expected based on the highly nonlinear behaviors of biopolymers with mixed entropic and energetic contributions to free energy (3, 4, 5). Ironically, Dimitrakopoulos found that the original Skalak law (2), which was supplanted by thermodynamically based models, does a reasonable job of explaining the discrepancy in the shear modulus measurements due to its hardening behavior (6), but connections between such models and molecular events are not defined.
From the molecular perspective, several coarse-grained molecular dynamics models have been developed to study the cytoskeletal cortex of RBCs, but no systematic effort has been made to extract the mechanical properties of these coarse-grained molecular dynamics models to reconstruct corresponding continuum strain-dependent constitutive models that could be used for whole-cell simulations of in vivo biological processes or in vitro experiments. One exception is the work of Dao et al., who derived shear and areal moduli for small deformations using a spectrin-level model based on the virial stress (7). Another exception is the work of Svetina et al. (8), who used an energy method based on a random network of ideal springs to make macroscopic predictions of membrane behavior, including micropipette aspirations, and derived expressions for the deformation dependence of the area and shear moduli, although explicit stress-strain relationships were not derived. Thus, although several microscopic models of RBC membranes have been developed, including spectrin-level models (9, 10, 11), with few exceptions, these have not been linked to mechanical behaviors at large deformation via continuum models. In addition, there are recent proteomic data from two independent sources (12,13) showing that whereas the stoichiometry of spectrins and junctional complex proteins are consistent with earlier estimates, copy numbers of RBC proteins such as spectrin are two- to threefold higher than well-accepted values in the literature (14). The predictions of any molecularly based model of red cell membrane behavior need to be re-examined in light of these new data.
In this study, we present a novel, to our knowledge, constitutive description for arbitrarily large deformation that is based on, and connects directly to, spectrin-level behavior as a worm-like chain. In addition, we also derive a simplified version of the constitutive law and give the corresponding analytical solution of the pressure-length relation in micropipette aspiration. Our approach accounts for two important characteristics not found in earlier constitutive models; namely, it exhibits strain-hardening behavior, and it allows for local changes in cytoskeletal density. This latter feature is in keeping with fluorescence imaging experiments showing that the cytoskeleton density does change significantly when cells are aspirated into micropipettes (15), becoming compressed near the pipette entrance and expanded near the tip of the membrane projection. We will explore the effect of the area change on the aspiration curve and measured shear modulus using the microstructure-based model. With microstructure-based strain hardening and cytoskeletal area change, good comparisons with our experiments and those in the literature are demonstrated.
Methods
Constitutive model of the RBC cytoskeleton with orientation distributions of spectrins
We consider the relationship between the molecular free energy of the molecules of the cytoskeletal network and the free energy per unit area of the skeleton. We follow the development of Discher and colleagues (9), which was based on a molecular network model developed by Boey et al. (16). The membrane skeleton was treated as a triangular elastic network in which the springs connecting network nodes have the characteristics of an elastic, worm-like polymer modeled after erythrocyte spectrin. The energy of the triangular network took the form (9)
| (1) |
where is the area per molecule and C is a coefficient preventing network collapse. The attractive potential (Veff (s)) of the “bonds” that represent the spectrin molecules was derived from the force-extension relationship of a worm-like chain (WLC) with both ideal and divergent behavior (17). The approximate interpolation formula of the WLC potential (17) for a bond with node-to-node distance s and maximal separation smax is
| (2) |
where p is the persistence length of the chain segments, kB is Boltzmann’s constant, and T is the absolute temperature. The corresponding force of the effective WLC potential is given as
| (3) |
Discher and colleagues applied these molecular models to obtain predictions both for the distribution of skeletal density in pipette aspirated cells and for the projection length of a biconcave disk being aspirated into a micropipette at different pressures (9). There are three unknown molecular parameters in the model: the maximal molecular length smax, the persistence length p, and the area coefficient C. Writing the molecular lengths relative to their stress-free natural length (s/so) and imposing the condition that the system must be in a minimal energy state at rest, one can solve for one of these parameters (C) in terms of the other two, leaving two coefficients to adjust to vary the mechanical stiffness of the network, p and λmax = smax/so.
Taking so as the resting molecular length, the molecular extension (s/so) is
where t0 is the filament unit orientation in the reference configuration,
is the right Cauchy-Green deformation tensor, and F is the deformation gradient. The molecular extension s/so is related to the material stretch ratios by
| (4) |
where θ0,i = ∈ (1, n) is the angle between the molecular vector for orientation i and the principal axis of extension in the resting state. The energy per unit area must be summed over molecular orientations. Note that in this formulation, n is the number of distinct molecular orientations in the resting state, not the number of elements in a network unit. For example, in a regular hexagonal array, n = 3, but in a random network, n → ∞.
In Appendix B in the Supporting Materials and Methods, we show the detailed derivation of the stress resultants from the energy. The resulting constitutive equations for the skeleton take the form
| (5) |
and
| (6) |
where
| (7) |
| (8) |
and
| (9) |
Note that cα is functionally related to λmax, meaning that there are just two freely adjustable material coefficients (cβ and λmax) in this model. The stress resultants can also be written in terms of shear and isotropic components
| (10) |
and
| (11) |
The expression for can be used to express the dependence of the shear modulus μ on extension as
| (12) |
An important reference point for comparison with other theoretical developments is the value of the modulus at the resting state μ0. Taking the limit at constant area for λ1 1 + ε and λ2 1 − ε, ε → 0, we obtain
| (13) |
This expression is identical to one obtained previously by Dao et al. (7) for the specific case of n = 3. After substituting x0 = 1/λmax = so/smax, recognizing that for a triangular network ρ0 = , and applying algebraic manipulation, we find
| (14) |
Note that
Remarkably, no assumptions about n were made in deriving Eq. 14, demonstrating that it is in fact accurate for all n with the same chain density.
Similarly, from the definition of area modulus Ksk and as detailed in Appendix C in the Supporting Materials and Methods, the area modulus can be expressed as the following forms
| (15) |
There are two forms of special interest. One is the isotropic case λ1 = λ2 = si/s0 = x = ,
| (16) |
and the other is the limit of no deformation at the resting state → 1,
| (17) |
Comparing Eq. 17 with Eq. 13, we find that the initial area modulus is twice the initial shear modulus, = 2μ0.
Simplified shear stress expression
For specific molecular orientations, a simplified expression can be derived to approximate the material behavior to facilitate analytical solutions to certain problems, such as micropipette aspiration. As detailed in Appendix B in the Supporting Materials and Methods, the shear stress resultant in Eq. 10, if the area is incompressible, can be approximated as
| (18) |
The shear modulus is given as
| (19) |
This equation also works for arbitrary n > 2. The detailed derivation and the case of area compressible cytoskeleton can be found in Appendix B in the Supporting Materials and Methods.
Constitutive model of RBC cytoskeleton with natural length distributions of spectrin
When we derived the expressions of the shear stress and energy function, we applied a single value for the natural end-to-end length so in the unstressed state. Recent tomographic studies demonstrate that the resting end-to-end distance of spectrin is not single valued but distributed over some range (18). In this case, we postulate that the energy of the skeleton and corresponding force resultants can be considered to be a superposition of networks with different resting end-to-end distances, weighted according to the frequency at which a given end-to-end distance occurs (at rest). In this case, the shear stress becomes
| (20) |
where φi is the fractional occurrence of a given end-to-end distance so,i. Cryo-electron microscopy (cryo-EM) data (18) show that for mouse erythrocytes, the initial length distribution is given as s0 = [20, 30, 40, 50, 60, 70, 80, 90, 97] nm, with frequencies of f = [1, 17, 30, 38, 19, 17, 6, 1, 1]. Then the fractional weight is φ = [0.00769, 0.13077, 0.23077, 0.29231, 0.14615, 0.13077, 0.046154, 0.00769, 0.00769]. We can also write
| (21) |
, λmax,i = smax/s0,i, and μi is given in Eq. 12 for specific s0,i. Note that the maximal contour length smax is assumed to be the same for all chains regardless of s0,i.
Recent efforts have successfully localized junctional complexes on the red cell membrane using super-resolution microscopy (19), but because this approach requires sparse labeling, not all junctions are labeled, and interjunctional distances cannot be reliably determined. For example, the length distributions in this super-resolution imaging study were calculated as counts/μm2, and the summation of the total counts in their figures gives ∼110 junctions/μm2. This is much lower than the value of ∼730 junctions/μm2 estimated from proteomic data (13) and even significantly lower than the traditional number of ∼270 junctions/μm2 (14).
Analysis of micropipette aspiration
Closed form solution using an analytical model with the simplified constitutive model
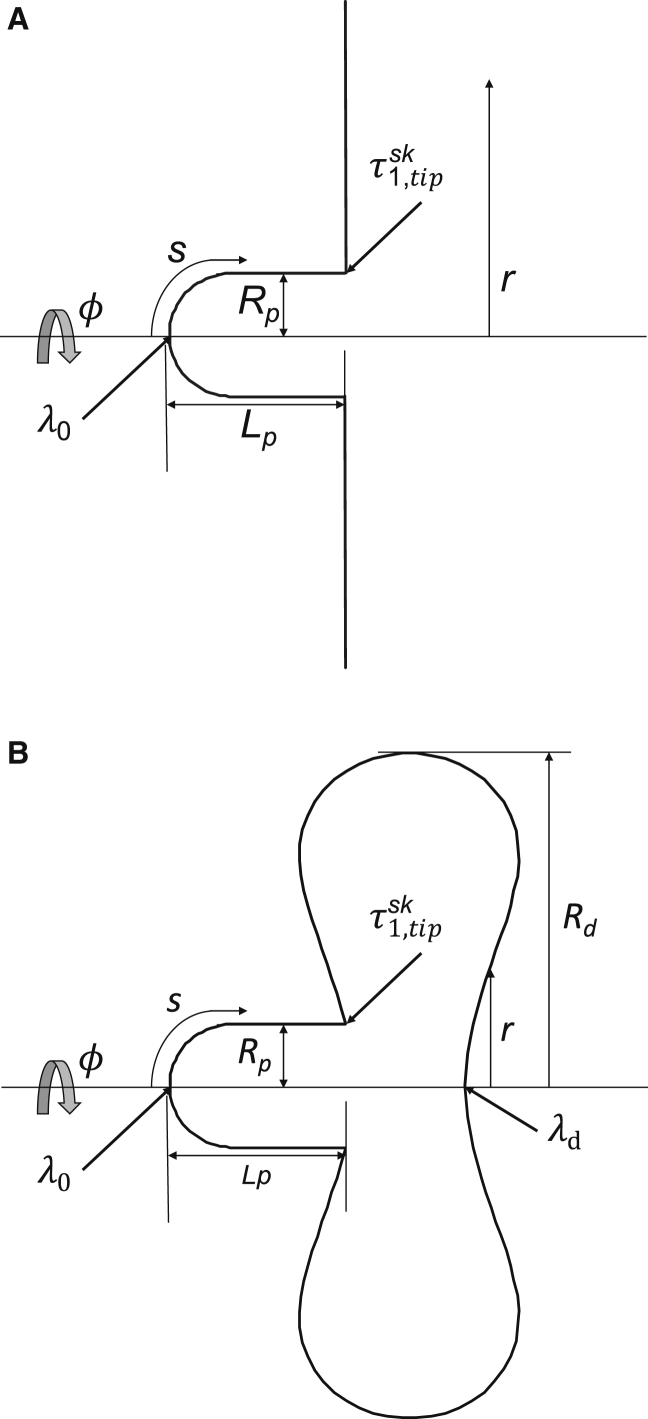
Using the simplifying approximation in Eq. 18, a closed form prediction for the aspirated projection length of the cell as a function of aspiration pressure can be obtained. The cell deformation is approximated as the formation of a cylinder plus hemispherical cap from an infinite membrane plane (Fig. 1 A; (1)). For each projection length, the corresponding meridional tension at the pipette tip is determined, and this in turn is directly related to the predicted aspiration pressure RpΔP = . In this way, a prediction for the projection length as a function of aspiration pressure is generated, in this case from the equilibrium equation in cylindrical coordinates of the flat membrane
| (22) |
Figure 1.
(A) The analytical model for analyzing micropipette aspiration by assuming an infinite flat membrane outside the pipette is shown. (B) The ODE model for analyzing micropipette aspiration by assuming a biconcave shape outside the pipette is shown. A cross section of the axisymmetric cell contour used in the analysis showing coordinate directions is given. Key experimental parameters are the pipette radius Rp and the length of the aspirated membrane projection Lp. The meridional distance along the surface is s, and the radial coordinate is r. The radius of the outer disk Rd is calculated to conserve total surface area. Integration proceeds from the tip of the projection and the center of the disk outside the pipette. The starting stretch ratios λ0 and λd are found such that the membrane stress resultant at the pipette tip is continuous and the total mass of the membrane-associated cytoskeleton is conserved.
In the limit as r → ∞, we take → 0. In this case, the stress at the tip can be obtained by integrating Eq. 22,
| (23) |
where . To evaluate the integral, we make the simplifying assumption that the cytoskeleton is laterally incompressible. From the definition of the principle stretch, we have λ2 = . In the area incompressible case, we can relate the instantaneous position of a material element r to is initial location in the undeformed plane r0 by equating the areas: This implies λ1 = . At the lower limit of the integration, r = Rp, we have λL = λ1|. With these simplifications, recognizing that and using the expression for the stress given in Eq. 18, we evaluate the integral (Eq. 23):
| (24) |
where
and
Because RpΔP = , we have the aspiration pressure ΔP vs. length Lp relation as
| (25) |
Effect of natural length distributions of spectrin
With φi as the fractional weight of contributions for the end-to-end distance s0,i, we have
| (26) |
where cβ,i = and x0,i = s0,i/smax. Note that the maximal contour length smax is assumed to be the same for all chains regardless of s0,i.
Effect of adhesion energy between cell membranes and pipette walls
In a previous study (8), we have provided evidence of an attractive energy between the cell membrane and the micropipette, σap. The effect of such an attractive interaction is to shift the predicted curves for Lp/Rp as a function of ΔPRp along the horizontal axis. Effectively, this transforms Lp/Rp = f (ΔPRp) to Lp/Rp = f (ΔPRp + σap). We introduce σap as a fitted constant for a given pipette on a given day of experiments.
Effect of cytoskeletal area change
We cannot calculate the distribution of cytoskeletal area change analytically because of mathematical difficulties, but if the cytoskeletal area change of the flat membrane is assumed to be uniform, a modified analytical solution can be obtained as
| (27) |
where detailed expressions for the coefficients can be found in Appendix C in the Supporting Materials and Methods.
Numerical solution using an ODE model with the general constitutive model
For the general expressions (Eqs. 5 and 6), we use a numerical approach to solve an ordinary differential equation (ODE) model to obtain predictions for the projection length as a function of aspiration pressure for a micropipette-aspirated biconcave cell (Fig. 1 B). We denote the principal stretches and stress resultant in the meridional direction as λ1 and and in the circumferential as λ2 and . By symmetry, we see that the principal stretch ratios at the tip of the membrane projection in the pipette λ0, and the center of the disk opposite the pipette λd must be isotropic. For a given cell shape (projection length Lp and outer biconcave disk diameter Rd), we find values for λ0 and λd that satisfy the conditions that the meridional tension at the tip of the pipette is continuous and the total mass of the membrane cytoskeleton is conserved (see Appendix A for details of this ODE model in the Supporting Materials and Methods).
Experimental measurements
The projection length of a portion of the red cell membrane aspirated into a micropipette was measured as a function of the aspiration pressure. Measurements were obtained on three different days using large (∼0.85 μm inside diameter) and small (∼0.56 μm inside diameter) micropipettes. Cells were obtained from human donors by simple finger stick under a protocol approved by the Office of Human Subject Protection at the University of Rochester. Cells were suspended in phosphate-buffered saline with 4% v/v of fetal bovine serum to avoid attachments between the cells and glass surfaces. Micropipettes were formed from glass capillaries using a Kopf microelectrode puller and a custom-made microforge. Micropipettes were filled by capillarity with buffer matching the cell suspension buffer, then connected via a continuous, bubble-free water pathway to a water-filled manometer. Zero pressure was set by adjusting the height of the manometer reservoir until suspended particles were motionless in the pipette lumen. Aspiration pressures were applied by adjusting the height of the reservoir using a micrometer with a resolution of 0.01 mm. Cells were observed using an inverted microscope with a 100× oil immersion objective and monochromatic illumination (480 nm). The experiments were recorded using standard video, and the length of the projection as a function of aspiration pressure was measured from the recordings. For each day of experiments, approximately eight cells were measured using the same pressure sequence, and the projection lengths at each pressure were averaged.
Results
We first present results using a single value of resting end-to-end distances s0 for spectrin to illustrate the general behaviors of the model and then introduce a distribution of resting end-to-end distances and demonstrate the importance of having such a distribution to better approximate actual cell behavior.
Parameter selection and stress-strain comparisons
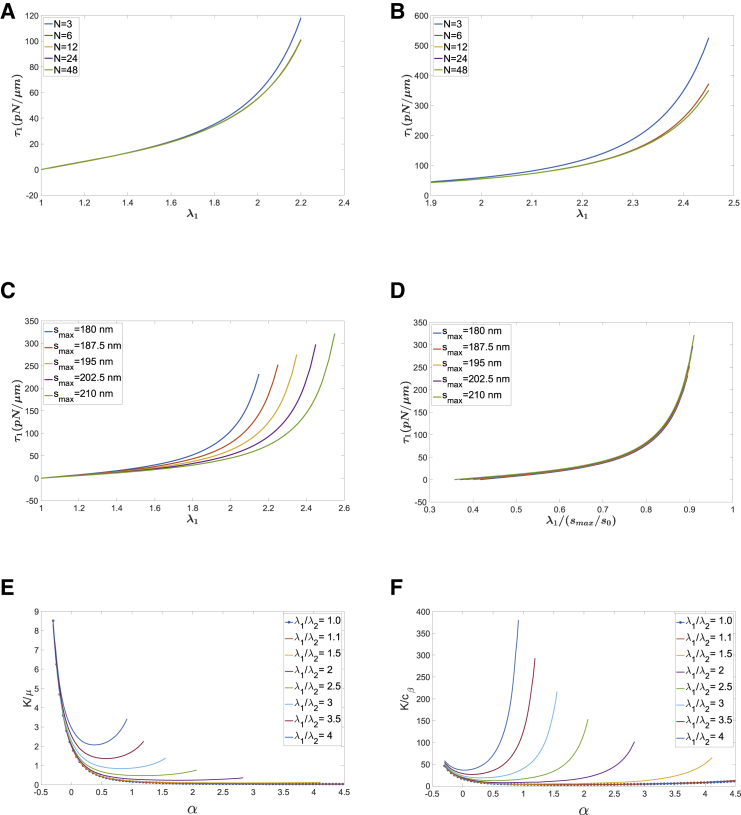
An important advantage of our approach is the ability to see how changing specific characteristics of the molecular network affect the behavior of the membrane in deformation. Some examples of this are shown in Fig. 2. In the native membrane, the orientation of the network elements appears to be random. Thus, an important question to address is how increasing the number of different molecular orientations in the resting state affects the model predictions. This is shown in Fig. 2 A for a simple uniaxial extension (τ2 = 0). For small forces and extension, even a very small number of initial molecular orientations provides a prediction consistent with more complex expressions, but for large extensions, significant differences in the predictions emerge (Fig. 2 B). This implies that the number of distinct molecular orientations in the resting state only affects membrane behavior when molecular extensions approach their maximum. Estimates of accuracy for different numbers of molecular orientations are summarized in Appendix D in the Supporting Materials and Methods. For example, for n = 3, errors in the calculated stress exceed 5% when extensions are greater than 70% of λmax, whereas for n = 6, extensions can be up to 90% of λmax before errors greater than 5% are observed. Similar results were obtained for purely shear deformation (constant skeleton area). As might be expected, results for isotropic expansion of the skeleton showed no dependence on the number of molecular orientations included in the calculations (data not shown). In these examples, the maximal end-to-end distance was set to 200 nm, the persistence length was 25 nm, s0 = 75 nm, and the molecular density was 2200/μm2.
Figure 2.
(A) Stress resultant τ1 as a function of stretch for a uniaxial extension (τ2 = 0), ρ0 = 2200/μm2, p = 25 nm, smax = 200 nm, and s0 = 75 nm. For relatively modest extensions, the stress resultant has little dependence on the number of molecular orientations selected. (B) For large extensions, differences in the predicted stress resultant are found for fewer than 12 molecular orientations, but for n ≥ 12, there is less than a 1% difference in the calculated values when the extension is 95% of its maximum. This is shown for λmax = 2.6 but true for all values tested. (C) Increasing λmax decreases the corresponding stress resultant. (D) As extensions approach the maximum, the curves collapse to a single prediction when expressed as a fraction of λmax, indicating that τ1 could be approximated by a single function of λ1/λmax. (E) The ratio of the area modulus K/shear modulus μ is 2.0 in the resting state but increases with compression and decreases, then increases with expansion. (F) The area modulus increases with compression and decreases with extension until the maximal molecular extension is approached. To see this figure in color, go online.
Dependencies of the predicted stress resultants on molecular density ρ0, persistence length p, and resting molecular length s0 are straightforward because these only appear in the coefficient cβ, which multiplies the entire expression for the stress resultant (Eqs. 5 and 6). Thus, if the ratio of p/s0 is doubled, the stress resultants for the corresponding stretch ratios are halved, and conversely, if the density of molecules is doubled, the stress resultants are doubled. The dependence of the model predictions on the maximal stretch ratio λmax is more complex, but, generally, the stress resultant rises more quickly with extension for smaller values of λmax and increases asymptotically as the extension approaches λmax (Fig. 2, C and D). Interestingly, at higher extensions, normalizing the stretch ratio to λmax collapses the prediction to a single curve (Fig. 2 D). Similar behaviors are exhibited for pure shear deformation.
It is also of interest to understand how the resistance to deformation as reflected in the material constants μ (shear modulus) and K (area modulus) vary with membrane deformation. We have already shown that the ratio of K/μ is 2.0 for small deformations relative to the resting state. This ratio changes substantially, however, as the membrane deforms (Fig. 2 E). Indeed, both moduli vary significantly with membrane expansion. The variation in the area modulus K is shown in Fig. 2 F, and the variation in μ is shown in Appendix D (Fig. S7) in the Supporting Materials and Methods. Note that when the membrane is extended (increasing λ1/λ2), the resistance to dilation increases more rapidly because of the nonlinear increase in resistance to stretch as the maximal stretch ratio is approached.
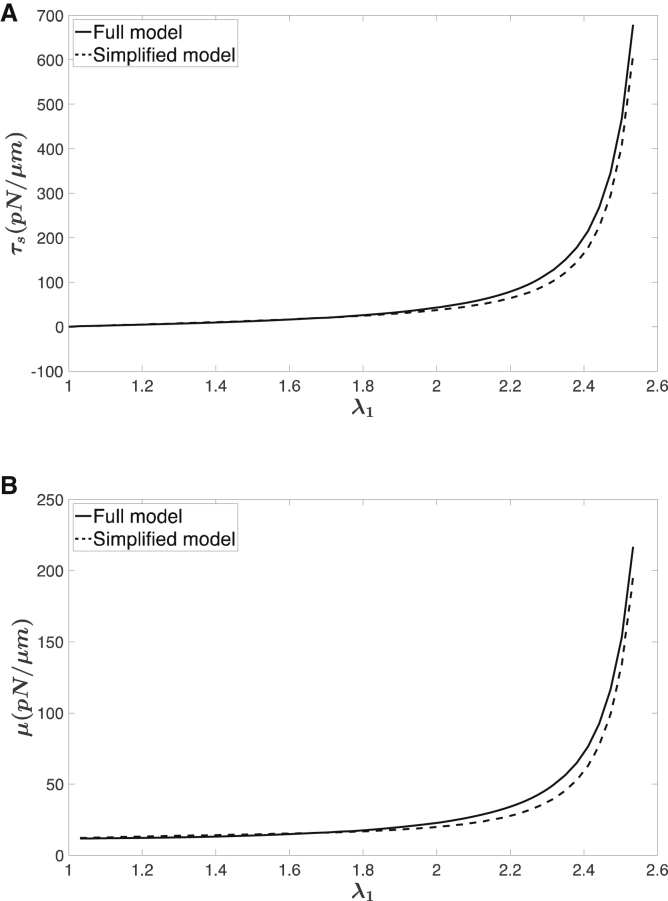
Comparison of the stresses (Fig. 3 A) and shear modulus (Fig. 3 B) obtained using the full model (Eqs. 10 and 12) and the simplified formula (Eqs. 18 and 19) show good agreement over a wide range of extensions.
Figure 3.
Comparison of the stress-strain curves and shear modulus between the full model (Eqs. 10 and 12) and the simplified model (Eqs. 18 and 19). Values for the other parameters used in the calculations: ρ0 = 2200/μm2, p = 25 nm, smax = 200 nm, s0 = 75 nm. (A) Shear stress resultant (area incompressible) is given. (B) Shear modulus (area incompressible) is given.
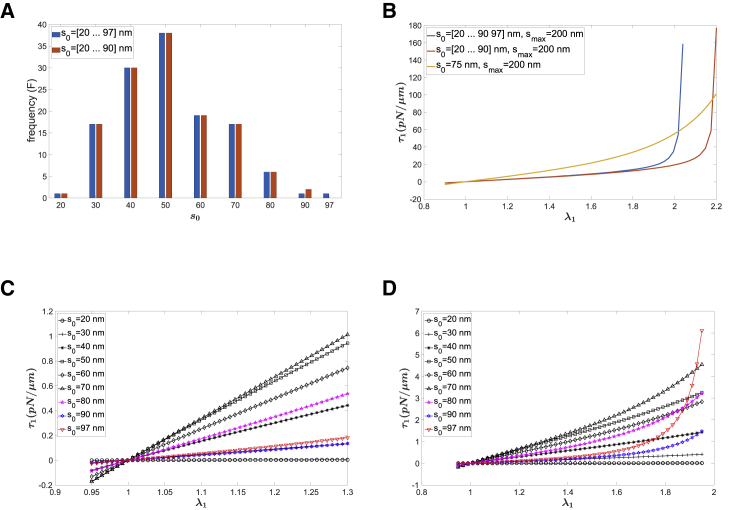
Effects of natural length distributions of spectrins
A recent study using tomographic imaging of intact red cells revealed that there is a distribution of end-to-end distances for spectrin molecules in the undeformed cytoskeleton (18). The reported distribution is reproduced in Fig. 4 A. Even though large values of s0,i occur rarely, they can have a significant impact on stress-strain behavior at larger extensions because of the singularity in molecular force as a function of extension when molecular lengths (s) approach smax. This is illustrated in Fig. 4 B, where the dependence of the force resultant (τ1) on extension is shown for three different but similar distributions, truncated at different values for s0. The distributions with larger values for s0 exhibit the greatest strain-stiffening behavior. Contributions from each individual value of s0 in the distribution are shown for both small (Fig. 4 C) and large (Fig. 4 D) extensions.
Figure 4.
Effect of natural length distributions of spectrin. (A) Distributions of natural length from cryo-EM measurements (18) are shown. (B) Stress resultant τ1 as a function of stretch for two distributions and a single natural length is given. (C) The contributions of each natural length to the total stress resultant τ1 are shown. (D) The same as (C) is shown, but for larger stretch. Values for the other parameters used in the calculations: ρ0 = 2200/μm2, p = 25 nm, smax = 200 nm. To see this figure in color, go online.
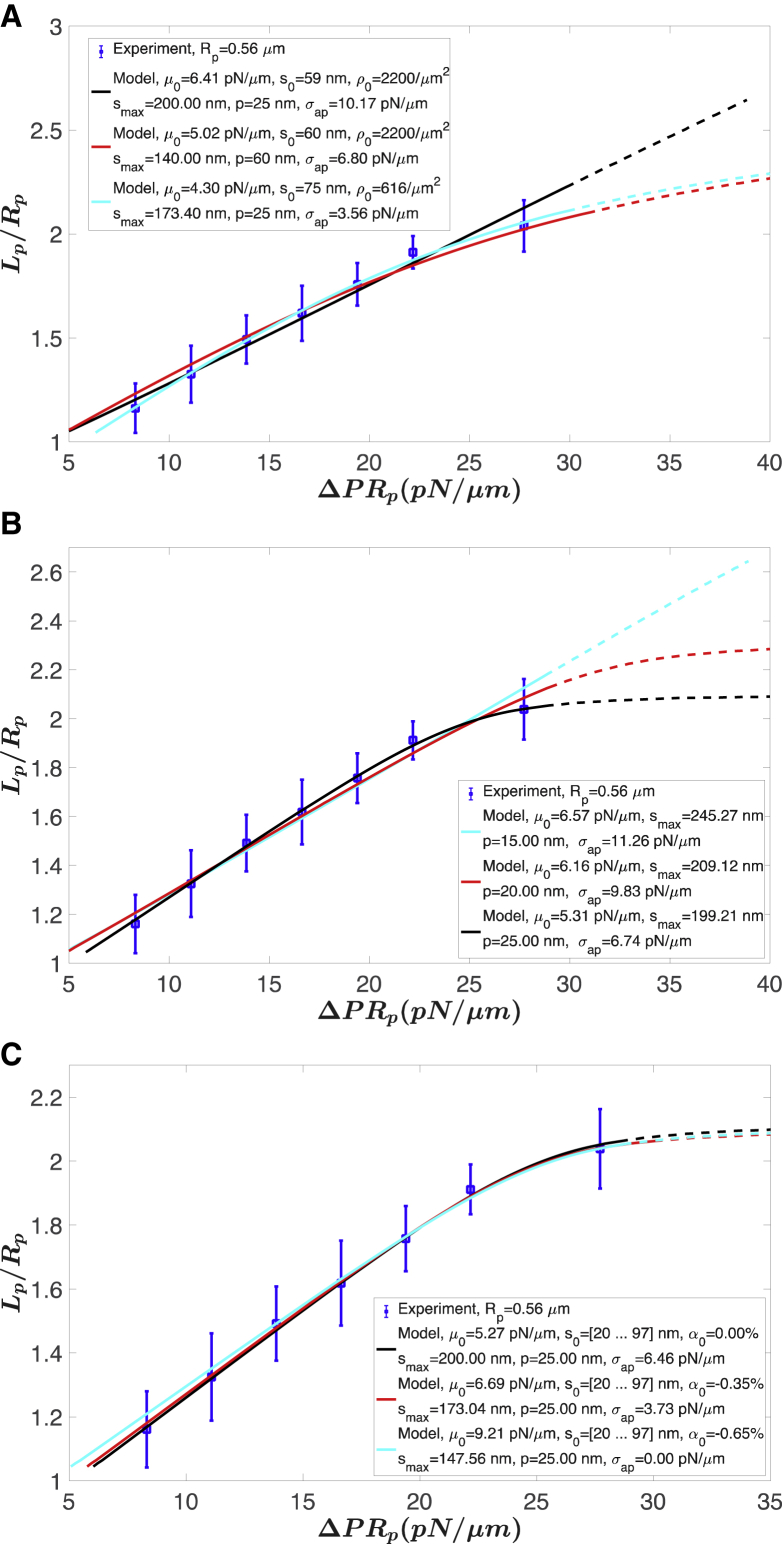
Comparison of the prediction with micropipette aspiration experiments: analytical models
We consider three versions of the analytical models in comparison to experimental measurements. In the first version, we assume a single value for s0 and fit s0 and pipette adhesion energy σap by least-squares regression with a fixed persistence length p and a fixed maximal molecular length smax. We plotted three fits in Fig. 5 A. The best-fit values (black curve in Fig. 5 A) were s0 = 59.25 nm and σap = 10.17 pN/μm for fixed p = 25 nm, smax = 200 nm, and ρ0 = 2200 molecules/μm2. This version of the model does not show obvious hardening unless a small smax = 140 nm and an extremely large p = 60 nm is used (red curve in Fig. 5 A). This is due to the high density of spectrin we used based on proteomic data (2200 molecules/μm2) (12,13). If we use earlier estimates of chain density calculated from a triangular network with an edge length of 75 nm, i.e., ρ0 = = 616 molecules/μm2, it shows hardening at smax = 173 nm and p = 25 nm (cyan curve in Fig. 5 A). Although this result is appealing from the perspective that we observe the expected strain hardening for more reasonable molecular characteristics, the underlying molecular assumptions are inconsistent with recent proteomic results (13). Next, we consider the case in which the values of s0 are fixed but distributed according to electron microscopic tomography (Fig. 4 A; (18)). In this case, we consider three different fixed values for p = 10, 15, and 25 nm, and the values of σap and smax were determined from least-squares regression (Fig. 5 B). Increased persistence length p gives smaller fitted smax and more obvious hardening behavior. Finally, we take into account the possibility that the density of the network may change locally when it is deformed. The ODE model with the general constitutive model (see Comparison of the Prediction with Micropipette Aspiration Experiments: ODE Model) predicts a net compression of the skeleton in the region of the membrane outside the pipette. In keeping with this finding, we postulate an average compression of up to ∼0.65% in the membrane plane outside the pipette. We considered three cases with compressions of 0.0, 0.35, and 0.65%. With fixed p = 25 nm, we obtained smax and σap from the fit (Fig. 5 C). When the compression of the cytoskeleton outside the pipette is larger, we obtain smaller smax (and larger μ0). This implies that allowing redistribution of skeletal density to the membrane portion outside the pipette reduces the appearance of strain hardening (indicated by a downward curvature to the fitted curve) such that smaller values of smax are required to achieve the level of strain hardening (downward curvature) exhibited by the data.
Figure 5.
Comparison of the analytical model predictions with experimental data. (A) Fits with one global natural length without area change are shown. (B) Fits with distributed natural lengths (Fig. 4A) without area change (ρ0 = 2200/μm2) are shown. (C) Fits with distributed natural lengths (Fig. 4A) with an assumed uniform area change α0 on the flat membrane outside the pipette (ρ0 = 2200/μm2) are shown. Dashed curves show the predictions beyond the experimental range. However, it should be noted that such lengths are not accessible experimentally because at longer extensions, folds begin to appear in the membrane, resulting in membrane shapes that are not amenable to analysis. Error bars for experimental data are shown as blue vertical lines. To see this figure in color, go online.
Comparison of the prediction with micropipette aspiration experiments: ODE model
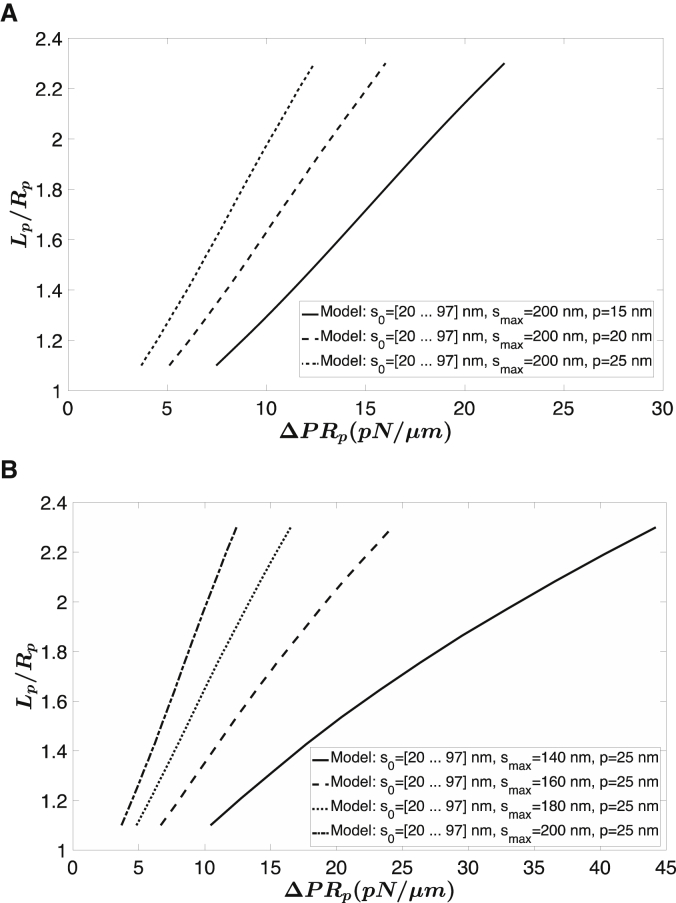
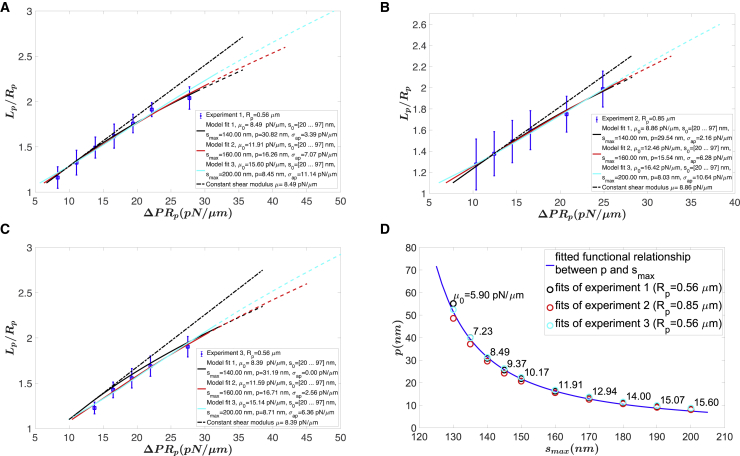
We then apply the ODE model, described in Appendix A in the Supporting Material, to solve the micropipette aspiration numerically by considering the more realistic cell shape shown in Fig. 1 B and employing the full constitutive model (Eqs. 5 and 6) instead of the simplified one. In Fig. 6, A and B, we show the effects of varying the maximal molecular length smax or the persistence length p on the predictions for micropipette aspiration experiments. The initial molecular lengths s0,i were distributed as shown in Fig. 4 A. We observe that both constants affect the slope of the predicted curve, implying that it is possible to compensate for changes in one parameter with changes in the other. On the other hand, although the persistence length p only changes the slope, the maximal molecular length smax changes both the slope and the curvature of the predicted curve. Introduction of the adhesive energy between the cell membrane and the micropipette, σap, enables fitting of the data with a range of value pairs for p and smax. This is illustrated in Fig. 7, in which predicted curves based on three different pairs of values show comparable agreement with the data for each of the 3 days of experiments. In Fig. 7, A and C, the pipette diameter was 1.12 μm, and in Fig. 7 B, the diameter was 1.7 μm. For the fitting procedure, the density of molecules on the surface was set to 2200 molecules/μm2, based on proteomic measurements indicating ∼300,000 tetramers per cell (12,13) and using an average cell area of ∼135 μm2. The distribution of s0 values was fixed according to Fig. 4 A. The value of smax was set at a constant value (140, 160, and 200 nm), and least-squares regression was performed with two free parameters: p and σap. Depending on the value chosen for smax, different values for p and σap were obtained. The value of σap is subject to significant measurement uncertainty because although changes in Lp can be measured very accurately, uncertainty in the location of the pipette tip can lead to errors in its absolute magnitude, and these errors contribute directly to the value of σap. Therefore, changes in the value of σap between different experiments do not necessarily reflect differences that have physical significance. The value of the persistence length p, on the other hand, is of interest because it reflects a molecular property that contributes directly to macroscopic cell behavior. The relationship between the value chosen for smax and the best-fit value for p is given in Fig. 7 D, in which the corresponding initial shear modulus is shown for each pair of p and smax. The initial shear modulus μ0 increased from 5.9 to 15.6 pN/μm with increasing smax. The goodness of fits as reflected by the sum of squared residuals in Fig. 7 for different values of persistence length and maximal length is summarized in Appendix E in the Supporting Materials and Methods.
Figure 6.
Sensitivity of model predictions to parameter values. (A) Effect of persistence length p is shown. (B) Effect of contour length smax is shown. Increasing either p or smax leads to increases in the length of the projection at a given aspiration pressure.
Figure 7.
Comparison of the ODE model predictions with experimental data. Three different experiments are shown. (A) Experiment 1 with Rp = 0.56 μm, (B) experiment 2 with Rp = 0.85 μm, and (C) experiment 3 with Rp = 0.56 μm are shown. (D) Given a value for smax, there is a unique value of p that matches the slope of the data for all three experiments. The relationship between p and smax is shown as the solid line: p = c1, where c1 = 0.0275 and c2 = 101.85. The corresponding initial shear modulus for experiment 1 is shown at each point. Dashed curves show the predictions beyond the experimental range. Error bars for experimental data are shown as blue vertical lines. The database can be found at: https://datadryad.org/stash/share/6ghOC1on3URHVUT55ACqW4W3PgB4TDKefVBDk-7FWKM. To see this figure in color, go online.
Discussion
Derivation of a constitutive model based on molecular parameters facilitates an understanding of how molecular attributes affect membrane deformability. Key molecular characteristics include the density of spectrin on the membrane in the resting state ρ0, the molecular persistence length p, the molecular lengths in the resting network s0, and the maximal molecular extension smax. In the model, the density and the persistence length appear explicitly only in the coefficient cβ, which is directly proportional to the magnitude of the stress for a given deformation. Consequently, the membrane modulus is expected to increase in direct proportion to spectrin density and inversely to the persistence length. In a previous study, a direct proportionality between the membrane shear modulus and the density of spectrin on the membrane has been documented (20), and this is consistent with the formulation we have developed here.
Best-fit values for the persistence length p in our experiments range from 10 to 50 nm. The highest values correspond to the lowest values for smax (Fig. 7 D), the highest degree of strain hardening, and the smallest initial shear modulus (∼5.9 pN/μm). Previously reported values for persistence length fall into the lower end of this range. For single molecules or intact cytoskeletons separated from the bilayer in solution, estimates of persistence length range from 10 to 25 nm (21,22). The persistence length for molecules constrained to remain near the membrane surface might be expected to be slightly smaller or up to 25% larger, based on estimates of the effects of confinement on this characteristic (23). Although the highest values we obtain are above this range, this might be expected given the constraints on spectrin conformation because of multiple membrane attachments. For an intermediate value of p around 25 nm, the fitted smax is around 145 nm and the corresponding initial shear modulus μ0 = 9.37 pN/μm. For the smallest value of p around 8.5 nm, the fitted smax is around 200 nm and the corresponding initial shear modulus μ0 = 15.6 pN/μm, but this case shows very limited hardening for the size of the aspiration lengths studied here.
Strain hardening and the distribution of resting molecular lengths
An important characteristic of the red cell cytoskeleton is strain hardening. In addition to evidence based on determination of the shear modulus using techniques that impose different magnitudes of strain, the pipette aspiration data reported here also show evidence of this in a downward curvature of the data for larger extensions (Fig. 7). Strain hardening is expected for models based on worm-like chain theory because these molecules become asymptotically stiff as they approach their maximal extension. However, the magnitude of the stretch ratios at which this behavior occurs depends critically on the ratio of s0 to smax. Values for the fully extended lengths of spectrin tetramers (smax) are based on rotary-shadowed electron micrographs, which indicated a maximal end-to-end distance of 180–200 nm (24,25). The resting length s0 is typically calculated from estimates of spectrin density and the relationship between density and s0 in triangular networks: ρ0 = . It is important to appreciate the implications of recent proteomic and ultrastructural findings on these values (12,13,18). Until recently, estimates of the number of spectrin molecules on the cell surface were based on density analysis of polyacrylamide gels, which put the number of spectrin tetramers on the surface of a cell at 80,000–120,000 (14). This corresponds to a density of 600–900/μm2 and implies that s0 ranges from 60 to 75 nm. To our knowledge, all existing molecular models of the red cell cytoskeleton assume resting molecular lengths of ∼70 nm. However, recent studies using more modern proteomic techniques put the number of tetramers much higher, ∼300,000 per cell or ∼2200 tetramers/μm2 (12,13). This density corresponds to a value of s0 of ∼40 nm for a triangular network. This much-lower resting s0 will have significant influence on the predictions of existing molecular models.
In relation to strain hardening, the value of s0 = 40 nm implies that maximal molecular extensions in a network could approach a stretch ratio of 4.5–5.0 before significant worm-like stiffening would be observed. In this case, molecular models based on uniform networks would not predict the downward curvature that is evident in the micropipette aspiration data. This dilemma is solved by recent tomographic evidence that end-to-end distances of tetramers in the resting state are not uniform (18). Accounting for this distribution, our molecular-based constitutive model leads to predictions of strain stiffening for extensions of ∼2.0, and results in model predictions for pipette aspiration behavior much closer to what is observed. Additionally, if one reverses the calculation and estimates resting state density from the reported distribution of molecular lengths (using the relationship ρ0 = for triangular networks and performing a weighted sum over the values of s0), one obtains a density of 1740/μm2, a value in excellent agreement with densities based on proteomic results. This last point is strong validation for using both the distributed values for s0 and the higher densities of spectrin indicated by the proteomic measurements.
Literature values for shear modulus
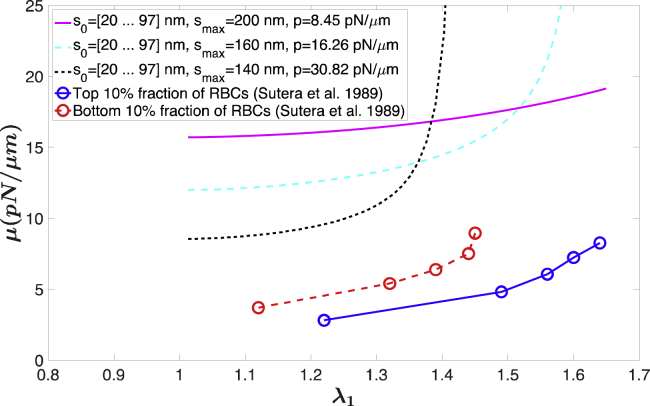
Values reported for the red cell membrane shear modulus in the literature differ significantly. For example, in micropipette aspiration experiments, in which the cell experiences moderate deformation, the shear modulus was measured as values (6–9 pN/μm) (26) or 4.2 pN/μm (27). The shear modulus measured using optical tweezers to stretch red blood cells and produce small deformations was 2.5 pN/μm (28,29), although some other measurements using optical tweezers gave a shear modulus of 5.7 pN/μm (30), 11.1–30 pN/μm (31), or 200 pN/μm (32). In addition to direct measurements of shear modulus, computational modeling studies also required a small shear modulus (∼2.5 pN/μm) to predict the resting biconcave shape and the correct stomatocyte-discocyte-echinocyte shape transition (4,33,34). The ability of different constitutive laws to match experimental measurement are compared in several studies (6,35), but most do not account for strain-hardening behavior. Estimates based on membrane fluctuation measurements (36,37) or tank-treading phenomena (5,38,39), both of which involve relatively small deformations, also tend to produce smaller values. In one interpretation of thermal fluctuation experiments, the shear modulus appears to be very small or almost zero (36,37), whereas experiments on tank treading give a range of shear moduli from 2.81 to 8.95 pN/μm depending on the deformation (5). Although differences in experimental approaches and associated measurement uncertainties as well as different approximations and methods of interpretation likely account for much of the differences in literature values, the strain stiffening captured using the microstructure-based model we present here may also help explain those differences. The value of the modulus in Eq. 21 approximately triples when the stretch ratio increases from 1.0 to 1.4 for smax = 140 nm (Fig. 8). Consistent with this, tank-treading experiments showed that the shear modulus can be tripled when the stretch ratio increases from 1.2 to 1.64 as shown in Fig. 8, although the absolute value of the shear modulus is at least twofold lower than those extracted from micropipette aspiration using this model.
Figure 8.
Shear modulus as a function of the principal stretch from the current model (area incompressible case) and tank-treading experiments. For the curves predicted from the model, parameters from the three cases in Fig. 7A are used, and ρ0 = 2200/μm2. The shear modulus calculated from tank-treading motion of RBCs under shear is from (5). To see this figure in color, go online.
The original analysis of micropipette aspiration, which did not consider strain hardening or cytoskeletal density changes, gave a prediction for the relationship between projection length and aspiration pressure: RpΔP = . Using this approach, the calculated shear modulus was in the range of 6–9 pN/μm (1,26). Our current analysis shows that failing to account for strain hardening results in an overestimate of the initial shear modulus because it reflects an “averaged” value of the increasing shear modulus with deformation. On the other hand, our analysis also shows that failing to account for local changes in skeletal density leads to underestimation of the shear modulus because the constraint of constant density leads to higher shear stresses at the same macroscopic deformation (projection length) (Fig. 5 C). Therefore, these two effects tend to compensate for each other such that the initial shear modulus values we obtain using our current model (5.9–15.6 pN/μm) are not much different than early estimates (6–9 pN/μm).
Values obtained using the simplified models
The simplified models we have derived vastly reduce the computational costs for analyzing experimental data. However, this simplicity comes with some loss of consistency for the molecular coefficients. The approximate model without cytoskeletal area change shows stronger strain stiffening and appears to match two of the three experimental data sets with high accuracy (Fig. 5). It is important to note, however, that maintaining constant cytoskeletal density introduces an important constraint on the deformation, and this accounts for the increased strain stiffening for this model. Indeed, in Fig. 5 C, increasing the assumed cytoskeletal area change for the simplified model results in less hardening. From other experimental evidence, it is clear that local changes in density do occur when the membrane is deformed.
Dynamic remodeling, prestress of the spectrin network, and deformation mechanisms of spectrin
Prior studies considering the molecular basis of red cell membrane elasticity have introduced important potential attributes of the network that we do not consider here, namely dynamic remodeling of the network and the possibility of prestress of the skeleton in the resting state. For example, Fai et al. built a cytoskeletal network model based on cryo-EM tomography (10,18) and demonstrated that faster cytoskeletal reorganization leads to more irreversibly broken spectrin tetramers and a smaller dimensionless tank-treading frequency for a cell undergoing tank treading in shear flow. They also found that when the cell is placed under repeated strains, cytoskeletal dynamics may play a protective role by allowing spectrin tetramers to disconnect before they would break. Zhu and Asaro showed that the unfolding of spectrin can play a significant role in strain-softening of a spectrin network (40). Although these concepts are important considerations, Discher and colleagues report that there was no change in spectrin distribution in their fluorescence-imaged microdeformation experiments over periods of 30 min (15), indicating that if remodeling does occur, it does not have a substantial effect on the distribution of strain in deformed membranes over extended times. Therefore, we believe that our decision not to consider dynamic remodeling in micropipette experiments with much smaller extensions and shorter duration is justified.
It has long been recognized that the red cell membrane is a composite structure and that both the spectrin network and the lipid bilayer contribute to its overall mechanical behavior (1). For the analysis presented here, the bilayer is not expected to make substantial contributions, except to constrain the membrane to a constant surface area, because it offers no resistance to shear deformation, and its resistance to bending is small compared with the force resultants generated as a result of the network deformation during pipette aspiration (1). The composite nature of the red cell membrane, coupled with the very high resistance of the bilayer to surface dilation or compression, raises the theoretical possibility that the skeleton itself may be slightly stretched or slightly compressed at rest, with the bilayer providing a counterbalance to make the net stress in the membrane zero at rest (41,42). The concept of a prestress in the spectrin network was introduced by Discher and colleagues to obtain agreement between their molecular-level red cell network simulations and experiments (9,43). More recently, we have identified a small adhesive energy between the membrane and the pipette surface that likely accounts for the discrepancy they observed for aspirations of biconcave cells (8), making the postulate of a skeletal prestress unnecessary for this case. (Predictions of the network density distribution in aspirated cells with long projections were also improved by inclusion of prestress, but this has not yet been addressed using the microstructure-based model we present here). The possibility of skeletal prestretch was also posited by Turlier et al. in a theory to explain how low-frequency cell fluctuations might be driven by spectrin because of changes in its phosphorylation state (44). Since then, a significant presence of myosin has been documented in red cells (45), which could provide an alternative explanation for the nonequilibrium, low-frequency fluctuations they observed. It could also be argued that long-term stress relaxation should cause network stress resultants to relax to zero over time. In summary, there is no clear evidence to confirm or refute the possibility that prestress may exist.
We consider each spectrin tetramer as a worm-like chain entropic spring in this study. Alternate models of spectrin behaving as a straight helical spring (46) or a Chinese finger trap (47), have been proposed. These models are based on electron micrographs of purified spectrin tetramers or minispectrins. Unfortunately, force-length relationships have not been derived for these cases. If such a force-length relationship existed, it would be straightforward to use the approach described here and incorporate it into our model by changing the potential in Eq. 2. Indeed, a similar approach to the one used here has been used with a model for spectrin as a helical spring to predict membrane behavior (8). That said, there are many experimental images of native spectrin in the actual RBC from quick-freeze, deep-etch, rotary replication procedure (48) or cryo-EM, in which the molecules appear to adopt random worm-like configurations (18), supporting the use of the worm-like chain potential not only here but in many theoretical and computational studies (10).
We note that the stiffening of the membrane at large extensions is reflected in both the thermodynamically defined shear modulus, μ, and the area modulus, K, both of which increase substantially with membrane dilation. It is also of interest that the value of the ratio K/μ also varies substantially from its resting value of 2.0, increasing with compression but decreasing for moderate extensions before increasing at very large extensions. Observations of the distribution of skeletal density in the projections of micropipette-aspirated cells indicated that this ratio should be ∼2.0, but a definitive value was not provided (15). This estimate of the K/μ ratio appears more or less consistent with the predictions of our model, but more detailed calculations would be required to draw a firm conclusion.
Conclusions
The work presented here makes several impactful contributions to our understanding of the physical basis of red blood cell membrane elasticity. First, we have derived a constitutive expression based on molecular properties that allows for local density changes in the deformed red cell cytoskeleton. We have generalized an expression for μ0, the shear modulus for a network near the undeformed shape, previously derived for a network with just three chain orientations (n = 3) (7), and have shown that it is valid for arbitrary n ≥ 3. Furthermore, we have developed the first, to our knowledge, molecularly based elastic model of the red blood cell membrane that accounts for both higher densities of spectrin indicated by proteomic analyses and distributed values of the resting molecular lengths obtained from electron-micrographic tomography. We have shown that for higher spectrin densities indicated by proteomics, accounting for a distribution of resting molecular lengths is essential for reproducing strain-hardening behavior exhibited by the red cell membrane in experiments. We have also obtained a relationship between the values for the maximal extended length of the spectrin tetramer and its persistence length that are consistent with membrane behavior in micropipette aspiration experiments. In addition, an analytical form of the micropipette aspiration with the simplified version of the constitutive law is derived. We find that the model exhibits hardening behavior and can help explain discrepancies found in the literature. In addition, this model can be also used to model other two-dimensional networks of flexible polymers with distributions of orientations and natural lengths, such as nuclear lamins.
Author Contributions
Z.P. and R.E.W. designed the research. Z.F., R.E.W., and Z.P. developed the mathematical models. R.E.W. performed the experiments. Z.F., R.E.W., and Z.P. analyzed the data. All authors contributed equally to writing the article.
Acknowledgments
Z.F. and Z.P. acknowledge support from the National Science Foundation (grant no. 1706436-CBET).
Editor: Ana-Suncana Smith.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.10.025.
Supporting Material
References
- 1.Evans E.A., Skalak R. CRC Press; Boca Raton FL: 1980. Mechanics and thermodynamics of biomembranes. [Google Scholar]
- 2.Skalak R., Tozeren A., Chien S. Strain energy function of red blood cell membranes. Biophys. J. 1973;13:245–264. doi: 10.1016/S0006-3495(73)85983-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Boal D. Second Edition. Cambridge University Press; Cambridge, UK: 2012. Mechanics of the Cell. [Google Scholar]
- 4.Gerald Lim H.W., Wortis M., Mukhopadhyay R. Red blood cell shapes and shape transformations: Newtonian mechanics of a composite membrane: sections 2.5–2.8. In: Gompper G., Schick M., editors. Soft Matter. Wiley-VCH Verlag GmbH & Co. KGaA; 2008. pp. 139–204. [Google Scholar]
- 5.Sutera S.P., Pierre P.R., Zahalak G.I. Deduction of intrinsic mechanical properties of the erythrocyte membrane from observations of tank-treading in the rheoscope. Biorheology. 1989;26:177–197. doi: 10.3233/bir-1989-26207. [DOI] [PubMed] [Google Scholar]
- 6.Dimitrakopoulos P. Analysis of the variation in the determination of the shear modulus of the erythrocyte membrane: effects of the constitutive law and membrane modeling. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:041917. doi: 10.1103/PhysRevE.85.041917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dao M., Li J., Suresh S. Molecularly based analysis of deformation of spectrin network and human erythrocyte. Mat. Sci. Eng. C. 2006;26:1232–1244. [Google Scholar]
- 8.Svetina S., Kokot G., Waugh R.E. A novel strain energy relationship for red blood cell membrane skeleton based on spectrin stiffness and its application to micropipette deformation. Biomech. Model. Mechanobiol. 2016;15:745–758. doi: 10.1007/s10237-015-0721-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Discher D.E., Boal D.H., Boey S.K. Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration. Biophys. J. 1998;75:1584–1597. doi: 10.1016/S0006-3495(98)74076-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fai T.G., Leo-Macias A., Peskin C.S. Image-based model of the spectrin cytoskeleton for red blood cell simulation. PLoS Comput. Biol. 2017;13:e1005790. doi: 10.1371/journal.pcbi.1005790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li J., Dao M., Suresh S. Spectrin-level modeling of the cytoskeleton and optical tweezers stretching of the erythrocyte. Biophys. J. 2005;88:3707–3719. doi: 10.1529/biophysj.104.047332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bryk A.H., Wiśniewski J.R. Quantitative analysis of human red blood cell proteome. J. Proteome Res. 2017;16:2752–2761. doi: 10.1021/acs.jproteome.7b00025. [DOI] [PubMed] [Google Scholar]
- 13.Gautier E.-F., Leduc M., Mayeux P. Absolute proteome quantification of highly purified populations of circulating reticulocytes and mature erythrocytes. Blood Adv. 2018;2:2646–2657. doi: 10.1182/bloodadvances.2018023515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Burton N.M., Bruce L.J. Modelling the structure of the red cell membrane. Biochem. Cell Biol. 2011;89:200–215. doi: 10.1139/o10-154. [DOI] [PubMed] [Google Scholar]
- 15.Discher D.E., Mohandas N., Evans E.A. Molecular maps of red cell deformation: hidden elasticity and in situ connectivity. Science. 1994;266:1032–1035. doi: 10.1126/science.7973655. [DOI] [PubMed] [Google Scholar]
- 16.Boey S.K., Boal D.H., Discher D.E. Simulations of the erythrocyte cytoskeleton at large deformation. I. Microscopic models. Biophys. J. 1998;75:1573–1583. doi: 10.1016/S0006-3495(98)74075-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Marko J.F., Siggia E.D. Stretching DNA. Macromolecules. 1995;28:8759–8770. [Google Scholar]
- 18.Nans A., Mohandas N., Stokes D.L. Native ultrastructure of the red cell cytoskeleton by cryo-electron tomography. Biophys. J. 2011;101:2341–2350. doi: 10.1016/j.bpj.2011.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pan L., Yan R., Xu K. Super-resolution microscopy reveals the native ultrastructure of the erythrocyte cytoskeleton. Cell Rep. 2018;22:1151–1158. doi: 10.1016/j.celrep.2017.12.107. [DOI] [PubMed] [Google Scholar]
- 20.Waugh R.E., Agre P. Reductions of erythrocyte membrane viscoelastic coefficients reflect spectrin deficiencies in hereditary spherocytosis. J. Clin. Invest. 1988;81:133–141. doi: 10.1172/JCI113284. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Svoboda K., Schmidt C.F., Block S.M. Conformation and elasticity of the isolated red blood cell membrane skeleton. Biophys. J. 1992;63:784–793. doi: 10.1016/S0006-3495(92)81644-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Stokke B.T., Mikkelsen A., Elgsaeter A. Human erythrocyte spectrin dimer intrinsic viscosity: temperature dependence and implications for the molecular basis of the erythrocyte membrane free energy. Biochim. Biophys. Acta. 1985;816:102–110. doi: 10.1016/0005-2736(85)90398-0. [DOI] [PubMed] [Google Scholar]
- 23.Cifra P., Benková Z., Bleha T. Persistence lengths and structure factors of wormlike polymers under confinement. J. Phys. Chem. B. 2008;112:1367–1375. doi: 10.1021/jp076355n. [DOI] [PubMed] [Google Scholar]
- 24.Byers T.J., Branton D. Visualization of the protein associations in the erythrocyte membrane skeleton. Proc. Natl. Acad. Sci. USA. 1985;82:6153–6157. doi: 10.1073/pnas.82.18.6153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Liu S.C., Derick L.H., Palek J. Visualization of the hexagonal lattice in the erythrocyte membrane skeleton. J. Cell Biol. 1987;104:527–536. doi: 10.1083/jcb.104.3.527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Waugh R., Evans E.A. Thermoelasticity of red blood cell membrane. Biophys. J. 1979;26:115–131. doi: 10.1016/S0006-3495(79)85239-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chien S., Sung K.L., Tözeren A. Theoretical and experimental studies on viscoelastic properties of erythrocyte membrane. Biophys. J. 1978;24:463–487. doi: 10.1016/S0006-3495(78)85395-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hénon S., Lenormand G., Gallet F. A new determination of the shear modulus of the human erythrocyte membrane using optical tweezers. Biophys. J. 1999;76:1145–1151. doi: 10.1016/S0006-3495(99)77279-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lenormand G., Hénon S., Gallet F. Direct measurement of the area expansion and shear moduli of the human red blood cell membrane skeleton. Biophys. J. 2001;81:43–56. doi: 10.1016/S0006-3495(01)75678-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lenormand G., Hénon S., Gallet F. Elasticity of the human red blood cell skeleton. Biorheology. 2003;40:247–251. [PubMed] [Google Scholar]
- 31.Dao M., Lim C.T., Suresh S. Mechanics of the human red blood cell deformed by optical tweezers. J. Mech. Phys. Solids. 2003;51:2259–2280. [Google Scholar]
- 32.Sleep J., Wilson D., Gratzer W. Elasticity of the red cell membrane and its relation to hemolytic disorders: an optical tweezers study. Biophys. J. 1999;77:3085–3095. doi: 10.1016/S0006-3495(99)77139-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fischer T.M., Haest C.W., Skalak R. The stress-free shape of the red blood cell membrane. Biophys. J. 1981;34:409–422. doi: 10.1016/S0006-3495(81)84859-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Gerald Lim H.W., Wortis M., Mukhopadhyay R. Stomatocyte-discocyte-echinocyte sequence of the human red blood cell: evidence for the bilayer- couple hypothesis from membrane mechanics. Proc. Natl. Acad. Sci. USA. 2002;99:16766–16769. doi: 10.1073/pnas.202617299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Omori T., Ishikawa T., Yamaguchi T. Comparison between spring network models and continuum constitutive laws: application to the large deformation of a capsule in shear flow. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2011;83:041918. doi: 10.1103/PhysRevE.83.041918. [DOI] [PubMed] [Google Scholar]
- 36.Peterson M.A., Strey H., Sackmann E. Theoretical and phase contrast microscopic eigenmode analysis of erythrocyte flicker: amplitudes. J. Phys. II. 1992;2:1273–1285. [Google Scholar]
- 37.Strey H., Peterson M., Sackmann E. Measurement of erythrocyte membrane elasticity by flicker eigenmode decomposition. Biophys. J. 1995;69:478–488. doi: 10.1016/S0006-3495(95)79921-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tran-Son-Tay R., Sutera S.P., Rao P.R. Determination of red blood cell membrane viscosity from rheoscopic observations of tank-treading motion. Biophys. J. 1984;46:65–72. doi: 10.1016/S0006-3495(84)83999-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Drochon A., Barthes-Biesel D., Lelievre J.C. Determination of the red blood cell apparent membrane elastic modulus from viscometric measurements. J. Biomech. Eng. 1990;112:241–249. doi: 10.1115/1.2891179. [DOI] [PubMed] [Google Scholar]
- 40.Zhu Q., Asaro R.J. Spectrin folding versus unfolding reactions and RBC membrane stiffness. Biophys. J. 2008;94:2529–2545. doi: 10.1529/biophysj.107.119438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Boal D.H., Seifert U., Zilker A. Dual network model for red blood cell membranes. Phys. Rev. Lett. 1992;69:3405–3408. doi: 10.1103/PhysRevLett.69.3405. [DOI] [PubMed] [Google Scholar]
- 42.Peng Z., Li X., Suresh S. Lipid bilayer and cytoskeletal interactions in a red blood cell. Proc. Natl. Acad. Sci. USA. 2013;110:13356–13361. doi: 10.1073/pnas.1311827110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Discher D.E. New insights into erythrocyte membrane organization and microelasticity. Curr. Opin. Hematol. 2000;7:117–122. doi: 10.1097/00062752-200003000-00008. [DOI] [PubMed] [Google Scholar]
- 44.Turlier H., Fedosov D.A., Betz T. Equilibrium physics breakdown reveals the active nature of red blood cell flickering. Nat. Phys. 2016;12:513–519. [Google Scholar]
- 45.Smith A.S., Nowak R.B., Fowler V.M. Myosin IIA interacts with the spectrin-actin membrane skeleton to control red blood cell membrane curvature and deformability. Proc. Natl. Acad. Sci. USA. 2018;115:E4377–E4385. doi: 10.1073/pnas.1718285115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.McGough A.M., Josephs R. On the structure of erythrocyte spectrin in partially expanded membrane skeletons. Proc. Natl. Acad. Sci. USA. 1990;87:5208–5212. doi: 10.1073/pnas.87.13.5208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Brown J.W., Bullitt E., McKnight C.J. The physiological molecular shape of spectrin: a compact supercoil resembling a Chinese finger trap. PLoS Comput. Biol. 2015;11:e1004302. doi: 10.1371/journal.pcbi.1004302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Ursitti J.A., Pumplin D.W., Bloch R.J. Ultrastructure of the human erythrocyte cytoskeleton and its attachment to the membrane. Cell Motil. Cytoskeleton. 1991;19:227–243. doi: 10.1002/cm.970190402. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.