Graphical abstract
Keywords: Extracellular matrix, Cell-matrix interactions, Computational modeling, Mechanobiology, Crosslinking
Abstract
Mechanical interactions between cells and the extracellular matrix (ECM) lead to the formation of biophysical cues, notably in the form of cell-generated tension, stiffness, and concentration profiles in the ECM. Fibrillar ECMs have nonlinear stiffnesses, linked to the reorientation of fibers under stress and strain, and nonelastic properties, resulting from the force-induced unbinding of transient bonds (crosslinks) that interconnect fibers. Mechanical forces generated by cells can lead to local ECM stiffening and densification. Cell tension is also propagated through the ECM network. The underlying factors that regulate the relative emergence of these signals are not well understood. Here, through computational simulations of 3D ECM fiber networks, we show that the composition of ECM crosslinks is a key determinant of the degree of densification and stiffening that can be achieved by cell-generated forces. This also regulates the sustainability of tensions propagated through the ECM. In particular, highly transient force-sensitive crosslinks promote nonelastic densification and rapid tension relaxation, whereas permanent crosslinks promote nonlinear stiffening and stable tension profiles. A heterogeneous population of crosslinks with different unbinding kinetics enables ECMs to exhibit accumulation, tension propagation, and stiffening simultaneously in response to mechanical interactions with cells.
1. Introduction
The extracellular matrix (ECM) is a complex network of fibers that provides structural support in tissues. It is also a medium of biophysical and biochemical signals to cells. The ECM can be remodeled by cells, via matrix degradation, matrix production, and mechanical remodeling, thus serving as a channel of cell–cell communication. The mechanical properties of a cell-laden ECM are fundamentally different than a cell-free ECM, highlighting the critical role of active remodeling in conferring physiological tissue properties [1].
It has been shown through various studies that biopolymer networks, including fibrillar ECM, exhibit complex rheological properties, particularly nonlinear stiffening under applied strain and stress. This is apparent in both bulk gel mechanical tests and rheological measurements [2], [3], [4] and local measurements of ECM (via optical tweezers) in the vicinity of contractile cells [5]. Multiple fold increase in the stiffness of the ECM is exhibited when the ECM network is stretched sufficiently.
The ECM also has nonelastic features. Under large strains, fiber network reorganization can occur that does not fully revert when the applied mechanical load is relaxed. Nonelastic phenomenon is observed in many experiments. In bulk rheological measurements, hysteresis and failure can be achieved under large strain amplitudes [3], [4]. At the local scale, imaging experiments have shown that ECM concentration profiles and architectures are permanently rearranged by cells over time, typically resulting in locally densified regions and/or aligned tracks that do not revert completely even after cell relaxation, via decellularization or inhibition of cell contractility [6], [7], [8].
The ECM can therefore exhibit a diverse range of properties that can be tuned by cells as they generate forces. In particular, cell contractility leads to locally stiffened and aligned regions [5]. Stiffening occurs as matrix fibers transition from bending to extension during applied stretch [9]. Thus, stiffening and alignment are typically coupled [10]. The matrix of fibers, along with fibrils within each fiber, are interconnected by molecular bonds, i.e. crosslinks. Crosslinks confer connectivity and elasticity throughout the ECM network. Crosslinks, however, can unbind under tension, which leads to viscoplastic material responses, such as softening and damage, and tension relaxation [6]. Sufficiently large dynamic forces, e.g. via local extension-contraction cycles from numerous highly active cell protrusions, can induce crosslink unbinding and nonelastically accumulate ECM toward the cell periphery [6]. Thus, matrix topography, stiffness, and concentration all can be controlled by cells through force generation in a crosslink-mediated manner.
One perplexing phenomenon is the simultaneous emergence of both stiffening and accumulation of the ECM via cell generated forces. Fibrillar ECMs are nonlinear elastic, as they can stiffen under applied stress and strain [2], [3], [5], [10]. However, they also exhibit nonelastic or viscoplastic properties, as they can be permanently remodeled by applied forces and undergo stress relaxation under applied strain [3], [6], [11]. Our prior study demonstrates that cells can physically and mechanically accumulate ECM to their immediate vicinity (via actin-mediated protrusions) in a nonelastic manner. Nonelastic accumulation is accompanied by stress relaxation as ECM bonds unbind, hence dissipating stored tension, and nonelastic strains [6]. However, despite substantial accumulation of ECM shown in experiments by different cell types, which is indicative of the presence of weak bonds, large stresses and elastic strains are still able to be sustained in the network, indicating that not all stresses are relaxed and not all bonds are broken [5], [6]. This suggests that there are mechanisms that are sustaining large stresses in the network, despite nonelastic ECM accumulation occurring. Here we introduce and quantitatively evaluate a physically and physiologically plausible mechanism – heterogeneity in the crosslink population. Physiologically, there are a variety of bond types and mechanisms that interconnect the ECM, including hydrogen bonds and various crosslinking chemistries, [12], [13], [14], [15], [16], [17], [18], [19] which can span a wide range of force-sensitive unbinding kinetics. Spatial distributions of crosslinks (e.g. regions of high and low crosslinking) can also lead to heterogeneous behaviors.
Here, through computational simulations of discrete ECM fiber networks with dynamic, force-sensitive crosslinks, we demonstrate that ECM networks with fibers interconnected by a heterogeneous population of crosslinks exhibit added versatility and hallmarks of both nonelastic and nonlinear elastic materials. We show that ECMs with a mixture of permanent and transient crosslinks can sustain cell tensions and be stiffened while also enabling matrix fibers to be rapidly and nonelastically accumulated toward the cell surface via dynamic pulling forces.
2. Results
2.1. Simulation setup
We perform discrete fiber network simulations, mimicking cells mechanically interacting with the ECM (see Methods and [6]). We generate a random network of ECM fibers interconnected by crosslinks. One surface of the 3D simulation domain represents the cell surface and local pulling forces are applied in its vicinity, mimicking dynamic forces generated by filopodial-like protrusion-contraction events applied to all fiber segments in close proximity to the cell surface. In our recent study, we applied this model to investigate the impact of dynamic loading force magnitudes and crosslink concentration on ECM remodeling and accumulation by cells [6]. Here, we emphasize the novel aspect of crosslink heterogeneity. We model two different types of crosslinks – transient and permanent. Transient crosslinks can unbind due to force, whereas permanent crosslinks do not unbind due to force. We maintain a constant number of crosslinks in the network and vary the ratio of permanent crosslinks to total crosslinks (RP). An illustration of the dynamic force loading scheme on the ECM network is shown in Fig. 1. Snapshots of different stages during the simulation (before, during, and after the application of dynamic forces) for networks with different crosslink compositions are shown in Fig. 2. Over time, the dynamic loading forces recruit fibers toward the cell surface. With mainly transient crosslinks (Fig. 2, top row), ECM densification is high and the remodeling is nonelastic, as shown by the high accumulation of fibers at the cell surface that do not relax back to initial positions after applied forces are unloaded. With mainly permanent crosslinks (Fig. 2, bottom row), fiber accumulation is substantially reduced and the ECM relaxes back close to its initial state after stopping applied forces. There are also many more fibers simultaneously under high tension during force loading. An intermediate state occurs with a mixture of transient and permanent crosslinks.
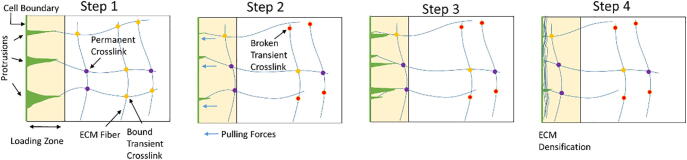
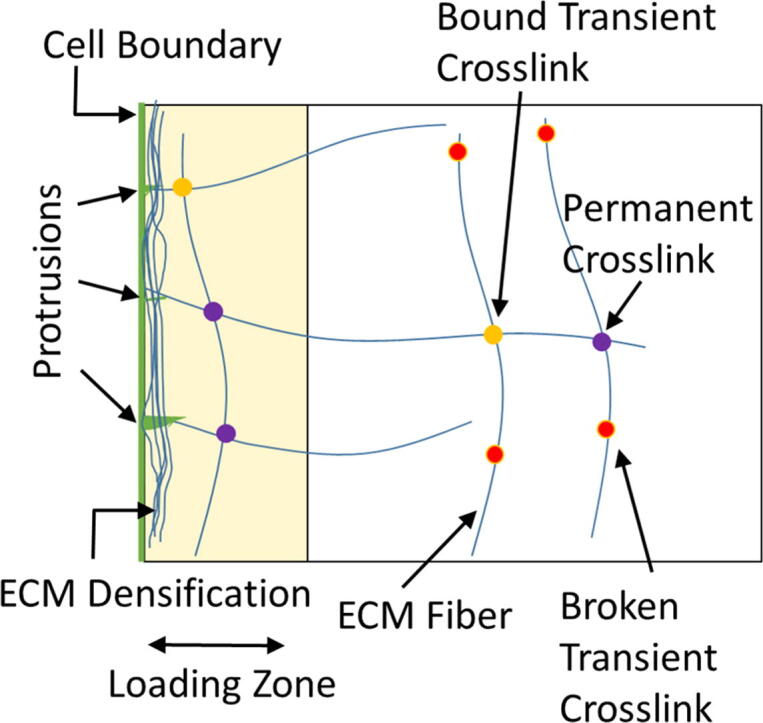
Fig. 1.
Schematic of dynamic force loading in an ECM network with crosslink heterogeneity. Local pulling forces, mimicking dynamic cell protrusion-contraction activity, are generated on fiber segments that enter the cell vicinity, i.e. the loading zone, leading to gradual ECM densification. Crosslinks are either transient (force-sensitive) or permanent (force-insensitive). As transient crosslinks unbind, ECM accumulation and network reorganization become nonelastic. Permanent crosslinks do not exhibit force-induced unbinding.
Fig. 2.
Simulation examples. An initial 3D uniform fiber network is generated without any applied loading forces. Dynamic pulling forces are then applied to fiber segments that are close to the cell surface (within 2 µm of the left surface). After a loading period, applied forces are stopped to allow for network relaxation. ECMs with different RP’s (ratio of permanent crosslinks to total crosslinks) exhibit different amounts of remodeling and nonelastic accumulation. The total number of crosslinks is constant. ECM fibers are color-coded by tension based on the color bar at the right (from −300 to + 300 pN). Yellow points are crosslinks. The left and right surfaces are hard boundaries (fibers cannot go through them). Fibers segments that are at the right surface are bound to it. The other four boundaries are periodic. The simulation domain is 20 × 20 × 20 µm3. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
2.2. Tension profiles of heterogeneous ECM networks
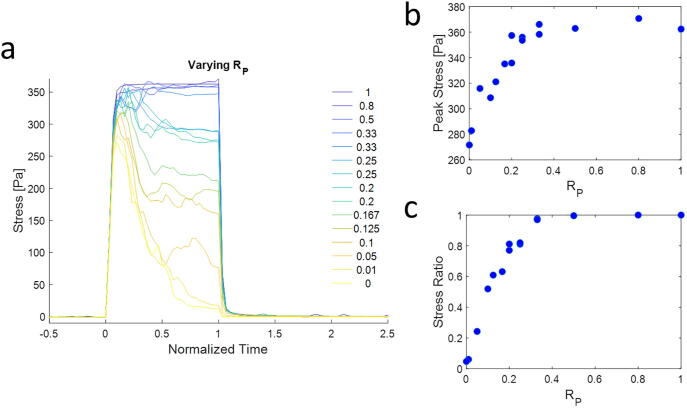
We simulate a range of networks with varying RP, while keeping the total number of crosslinks constant. Transient crosslinks have an unbinding rate that increases exponentially with force based on Bell’s law [20], and permanent crosslinks are insensitive to force. We measure the average tension inside the network under dynamic cell pulling forces. Our results show that the dynamic force loading condition leads to a rapid rise in tension in the network initially (Fig. 3a). Over time, networks with lower RP (more yellow curves) relax tension rapidly, whereas networks with higher RP (more blue curves) undergo less to no relaxation. Lower RP also reduces the peak tension (Fig. 3b) and the amount of sustainable tension (Fig. 3c), as the unbinding of transient crosslinks leads to stress relaxation. We quantify sustainable tension with the stress ratio metric, which is the ratio between the tension right before unloading applied forces (at normalized time = 1) and the peak tension.
Fig. 3.
Stress profiles. a) The stress in the network, calculated by summing the normal tensions of components crossing a plane parallel to the cell surface and then dividing by the area of the surface (20 × 20 µm2), evolves over time for networks with different RP’s. Dynamic forces are applied from normalized time of 0 to 1, followed by cessation of applied forces. High RP leads to stable network stresses, whereas low RP leads to stress profiles that decay over time. b) The peak stress in the network increases with increasing RP up to a plateau. c) The stress ratio is the ratio of the stress at t = 1 (right before applied forces are stopped) and the peak stress. The stress ratio also increases with RP up to a plateau.
2.3. ECM accumulation profiles of heterogeneous networks
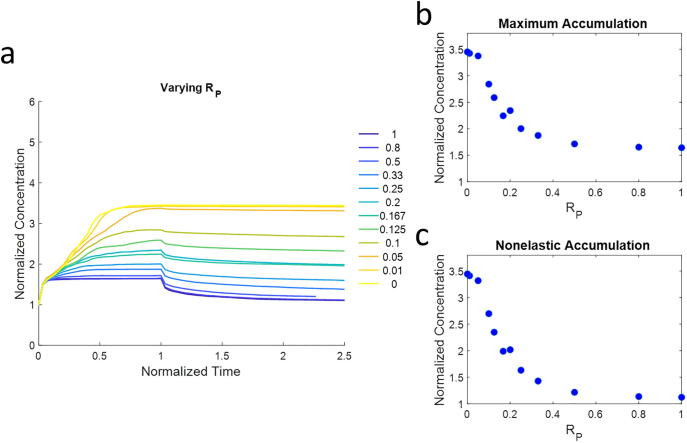
We next quantify the ECM accumulation profile near the cell surface for different crosslink compositions (Fig. 4). We show that network configurations with higher RP’s (more blue curves) have reduced accumulation of ECM toward the cell, and much of the accumulated ECM is reversed after force unloading, indicating elastic recovery. On the contrary, networks with lower RP’s (more yellow curves) exhibit high accumulation of ECM in a nonelastic manner (Fig. 4a). The maximum concentration at the cell surface (which includes both elastic and nonelastic accumulation) decreases with increasing RP (Fig. 4b), and the nonelastic accumulation (remaining concentration after force relaxation) also follows a similar trend (Fig. 4c).
Fig. 4.
ECM accumulation profiles. a) The ECM concentration near the cell surface (within 6 µm) is measured over time. The concentration is normalized to the concentration before force loading. Dynamic forces are loaded at the normalized time from 0 to 1, and applied forces are stopped afterwards to allow for relaxation. High RP leads to low ECM accumulation that reverts, whereas low RP leads to high ECM accumulation that does not revert. b) The peak concentration is measured as a function of RP. This includes both elastic and nonelastic ECM accumulation. c) The nonelastic accumulation (calculated at normalized time = 2, when most simulations have reached a relatively stable state) is measured as a function of RP. At this point, most of the elastic strains have been relaxed.
To compare the accumulation and tension trends relative to crosslink composition, we renormalize the nonelastic accumulation concentration, peak stress, and stress ratio vs. RP plots and overlay them together (Fig. 5). These trends together reveal that a relatively low RP is needed in order to enable networks that can both sustain tension and be susceptible to high ECM accumulation. In particular, the range of RP’s from ~0.05 – 0.3 exhibits both tension sustaining and susceptibility to remodeling properties.
Fig. 5.
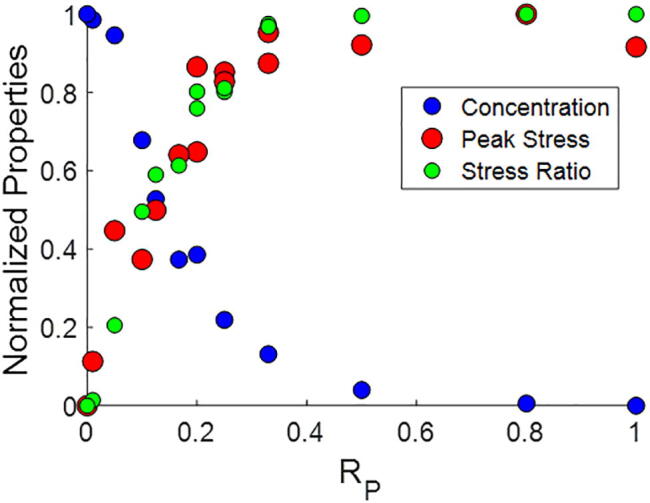
Concentration and stress vs. RP. We overlay the accumulated ECM concentration, peak stress, and stress ratio vs. RP curves, demonstrating nonlinearity in the dependence on RP. There is a range of RP’s that supports both ECM accumulation and sustaining high stresses. Here, for the purpose of comparing, the curves are all renormalized to range between 0 and 1.
2.4. Strain-dependent network stiffness profiles
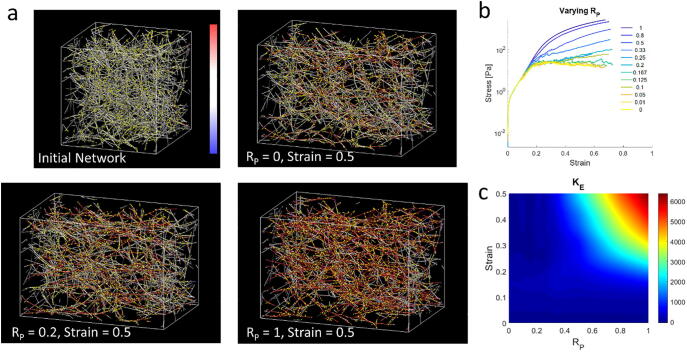
Finally we quantify the differential extensional stiffness (KE) of fiber networks with varying RP. We apply an extensional strain at a constant strain rate on the network and measure extensional stresses and KE (Fig. 6). The initial and strained networks are shown for RP = 0, 0.2, and 1 (Fig. 6a). At relatively high strains (e.g. 0.5), higher RP’s lead to more fibers under high tension. We show that with sufficient permanent crosslinks, the network builds up increasing stress and stiffens (toward a plateau stiffness) under increasing strain, whereas with a low percentage of permanent crosslinks, the network exhibits stress relaxation and failure at relatively low strains and does not undergo high stiffening at high strains (Fig. 6 b,c).
Fig. 6.
Stress and stiffness profiles at varying strain. a) Extensional strain is applied to networks of varying RP, as shown by simulation snapshots. Fibers are color-coded based on tension according to the color bar, which ranges from −300 to 300pN. Yellow spheres are crosslinks. The initial domain size is 20x20x20µm3. b) Extensional stress vs. strain curves are measured for networks with different RP. Networks with low RP exhibit stress decay at high strains. c) Heat map of KE (in Pa) vs. strain and RP shows increased strain-stiffening capacity for networks with high RP. Networks with low RP undergo failure at large strains, and their stiffness is diminished. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3. Discussions
ECM networks exhibit notable properties to which cells are responsive. In particular, mechanical properties, topography, and concentration are key regulators of cell behavior. These properties can also change as a result of mechanical interactions with cells. The ECM stiffens under applied strain and stress [2], [5]. Stiffer environments promote cell behaviors including proliferation, migration, spreading, and contractility [21], [22], [23], [24], [25], [26]. Stiffness further regulates differentiation patterns in stem cells [27], [28] and transformation of tumor cells [29], [30]. As the ECM is stretched, it undergoes alignment as fibers reorient to the direction of strain [10]. Alignment in fibers and microenvironment topography modulate a variety of signaling pathways, including PI3 Kinase and ERK/MAPK, and induce cytoskeletal reorganization and cells to polarize along the long axis of the aligned topography [31], [32], [33]. Rheological measurements of tissues and cell-laden ECMs show that these environments are in a stiffened state that is dependent on active, actomyosin-driven contractility of the embedded cells [1], [5]. Imaging studies have also shown that the vicinity of contractile cells has aligned ECM fibers. These studies demonstrate that cell contractility induces tissue stiffening and matrix fiber alignment and that cell tensions can be sustained in ECM networks to maintain the stiffened state at steady-state.
Furthermore, local ECM concentrations can change as cells mechanically recruit fibers toward their surfaces via dynamic protrusion-contraction cycles and unbinding of ECM crosslinks. Force-mediated ECM remodeling is nonelastic and does not fully recover after cell relaxation, resulting in permanently reorganized architectures and concentration profiles [6]. ECM concentration can modulate receptor-ligand interactions and signaling, and increased ECM concentration is a signature of fibrotic diseases and poor outcome in various solid tumors [34], [35], [36], [37], [38].
In order for the ECM to be able to exhibit all of these empirically demonstrated properties, it has to both sustain tension buildup (without undergoing failure) and allow for nonelastic remodeling. These appear to be paradoxical features, as nonelastic or viscoplastic remodeling typically leads to tension relaxation. Indeed, based on our simulations, if the ECM network has primarily transient or primarily permanent crosslinks, then only parts of these properties are exhibited. However, heterogeneity in crosslink unbinding kinetics enables ECM versatility and confers both tension sustainability and nonelasticity simultaneously in ECM networks (Fig. 3, Fig. 4, Fig. 5, Fig. 6). A permanent crosslink population enables tension to be sustained and ECM stiffening, while a transient crosslink population enables nonelastic densification via dynamic pulling forces. Physiologically, various mechanisms can confer diversity in bond kinetics. There are different types of molecular bonds, including covalent and hydrogen bonds with varying bond strengths, that interconnect the ECM network [15], [16], [17], [18], [19]. Furthermore, the geometry of fibers and spatial distribution of bonds may also influence the effective regional bond strength, e.g. thick fibers with many bonds in close proximity may exhibit lower unbinding rates as forces are more distributed. In tumor microenvironments, the ECM network is often disordered and heterogeneous, with diversity in fiber geometries, local concentration profiles, and dysregulation of crosslinking factors such as tissue transglutaminase and lysyl oxidase [12], [13], [14].
Our computational results demonstrate a nonlinear dependence of network properties on transient and permanent crosslink concentrations (Fig. 5). High levels of permanent crosslinks reduce nonelastic remodeling effects, and predominantly transient crosslinks reduce sustainability of tension buildup and nonlinear stiffening in ECM networks. As permanent and transient crosslinks confer opposing properties, a balanced level of each is required to confer versatile ECM properties and sensitivity to cell-generated forces. A relatively low fraction of permanent crosslinks and correspondingly relatively high fraction of transient crosslinks appear to confer the versatile ECM state, and a shift in this balance will bias the network for increased tension sustainability or increased plastic remodeling during mechanical interactions with cells. Our computational results for networks with RP of ~0.1 – 0.25 demonstrate consistency with previous experimental findings that show ECM accumulation of ~2 – 3.5x relative to background by cells toward their surfaces [6] as well as experimental findings that show that ECMs can sustain stresses of hundreds of Pascals near contractile cells [5]. Without the presence of strong crosslinks, large stresses would rapidly relax over time, and without the presence of weak crosslinks, ECM accumulation at the cell periphery would be low. Moreover, many cell types, including cancer cells and fibroblasts, are known to secrete MMPs, which can degrade the ECM and potentially weaken or degrade crosslinks. This can therefore lead to a reduction in RP as well as in the total concentration of crosslinks in the region where MMPs are active (i.e. near the cell) and thus facilitate ECM accumulation in that region. Notably, however, it has been shown previously that even with MMP inhibition, substantial and similar amounts of ECM densification still occur at the cell periphery, driven by dynamic cytoskeletal forces [6]. Thus, while MMPs may be important and can play supplementary roles in ECM densification, they appear to be dispensable, at least in the early stage ECM accumulation process at the immediate vicinity of cells.
Finally, our computational results can complement future experimental studies that investigate further the impact of crosslink heterogeneity on cell behavior and cell-matrix interactions. Crosslink heterogeneity can be studied experimentally via tunable stress-relaxing hydrogels, e.g. alginate-based gels with different modes of crosslinking (transient ionic bonds vs. strong covalent bonds) [39]. Furthermore, cell-laden ECMs can be fluorescently stained for various cell-secreted crosslinking proteins, and the crosslink concentration profiles can be correlated to ECM accumulation and stress-relaxation properties via imaging and rheometry studies.
4. Conclusion
In this study, we demonstrate that heterogeneity in the unbinding kinetics of ECM crosslinks confers versatility in ECM interactivity, enabling cells to be able to modulate local concentration profiles and generate sustained tension and matrix stiffening via mechanical forces. As ECM concentration and stiffness are both often increased in aggressive solid tumors and cell mechanics is often altered in cancer cells, our study suggests that diversity in ECM bonds is an important mediator of these phenotypes. Thus, ECM crosslink properties and content may be useful diagnostic readouts as well as therapeutic targets toward modulating tumor progression.
5. Methods
5.1. Fiber network model
We perform computational simulations of ECM fiber networks, as described in our previous work [6]. We briefly summarize the model here. Fibers are polymerized initially during a network formation phase and interconnected via crosslinks. Fibers are composed of chains of cylindrical segments (monomeric units). They have elastic extensional and bending potential energies:
| (1) |
| (2) |
where is the potential energy from stretching, is the potential energy from bending, is the extensional stiffness, is the bending stiffness, is the deviation from the equilibrium length, and is the deviation from the equilibrium angle. Crosslinks can unbind following Bell’s equation [20]:
| (3) |
where is the crosslink unbinding rate, is the zero-force unbinding rate, is the mechanosensitivity (i.e. mechanical compliance) of the crosslink, is the magnitude of the extensional force acting on the crosslink (only positive stretching forces contribute), is the Boltzmann constant, and is temperature. Fibers and crosslinks follow the equation of motion (without inertia or thermal forces):
| (4) |
where is the index of the component under consideration, is the cell-generated loading force near the –z boundary, includes all of the mechanical forces from the fiber network components (extension, bending, and volume exclusion [40]), is the drag coefficient, and is the position. Eq. (4) is solved iteratively over time by Euler integration at discrete time steps to determine the position of each component in the network. Crosslink unbinding is modeled stochastically. Each bound crosslink has an unbinding probability at each time step equal to:
| (5) |
Model parameters are listed in SI Table 1. Fiber parameters are based on realistic ECMs, particularly fibrin [17], [41]. The simulation domain is 20 × 20 × 20 μm3 and the left surface represents the cell surface (see Fig. 2). The left and right surfaces are hard boundaries (no fibers can go through), and the other four surfaces have periodic boundary condition. Fiber segments at the right boundary are fixed there. Additional details of the discrete fiber network model in various applications can be found in [6], [40], [42].
We note here that we assume a background of water causing viscous drag. However, in tissue microenvironments, there could be additional damping effects, e.g. due to molecular crowding, that may impact system viscosity and dynamics. System complexity is compounded further by the mechanosensitivity of cell phenotypes to fluid viscosity and molecular crowding [43], [44], [45], [46]. Further studies are warranted for exploring the impact of these factors on cell traction forces, dynamic cell protrusion activity, and ECM densification dynamics.
5.2. Dynamic loading forces
mimics dynamic forces from the numerous dynamic cell protrusions observed in many cells [6], [47], as shown by the schematic in Fig. 1. Fiber segments that are in or newly enter the loading region, i.e. within 2 μm of the cell surface (the left surface of the simulation domain), experience local pulling forces toward the cell surface. These loading forces are continuous and unidirectional (toward the cell surface), and this loading mechanism leads to gradual nonelastic accumulation of ECM at the cell periphery and captures experimental trends from live cells in 3D ECMs [6]. These forces are applied during the force loading phase of the simulations (from normalized time of 0 to 1). After this period, applied forces are stopped and the network relaxes. In these simulations, the pulling force on each segment is 200pN. We previously explored different force magnitudes, which can modulate the network remodeling profiles [6]. Example simulation snapshots are shown in Fig. 2.
5.3. Crosslink heterogeneity
We model crosslink heterogeneity by prescribing two types of crosslinks – transient and permanent. Their difference is exclusively in their mechanosensitivity λ. For transient crosslinks, λ is non-zero, whereas for permanent crosslinks, λ = 0. RP is the ratio of the number of permanent crosslinks to the total number of crosslinks (i.e. permanent crosslinks plus transient crosslinks).
5.4. Computing ECM accumulation
Normalized ECM accumulation at the cell vicinity is calculated by dividing the concentration of ECM within 6 μm from the cell surface by the concentration in the same region right before dynamic force loading. The resulting measurement is therefore the concentration fold change. We compute this over time before, during, and after dynamic force loading. Note that in this study, we consider a normalized time scale (the approximate time when plateau ECM accumulation behavior is observed). Our prior study shows that this leads to reasonable matches between experimental and computational results [6]. Furthermore, the absolute time scale can be influenced and scaled by factors such as the rate of protrusion formation, time scale of protrusion-contraction cycles, and the number and density of simultaneous protrusions generated by cells. These are interesting factors to investigate in subsequent studies. Additionally, cells may adapt to the evolving ECM over time. Mechanosensing and cell-ECM feedback [48], [49], [50], [51], [52] are prominent effects that warrant further exploration in the context of ECM accumulation.
5.5. Computing network stresses
Network stresses are calculated by summing the normal component of forces acting on fibers crossing a plane that is parallel to the cell surface and then dividing by the area of that plane (i.e. 20 × 20 μm2).
5.6. Computing network stiffness
The differential extensional modulus (KE) is computed by taking the derivative of the extensional stress with respect to the applied extensional strain in our simulation networks. In these simulations, we do not apply the same dynamic loading forces as before. Instead, we apply an extensional strain at a constant strain rate on the network. The left and right surfaces are hard boundaries, and fibers are attached to these surfaces. Extensional strain is applied normal to these surfaces (Fig. 6). The remaining four surfaces have periodic boundary condition. We apply a relatively high strain rate (10 s−1) for computational efficiency, and our results are able to demonstrate relative differences between conditions. As the stress vs. strain curves can be noisy due to local unbinding events, we perform data smoothening using linear regression prior to computing KE.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work is supported in part by the U.S. National Institutes of Health National Institute of Biomedical Imaging and Bioengineering (Grant R21EB026630 to M.M.).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.csbj.2020.11.038.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.van Oosten A.S.G., Chen X., Chin L., Cruz K., Patteson A.E., Pogoda K. Emergence of tissue-like mechanics from fibrous networks confined by close-packed cells. Nature. 2019;573:96–101. doi: 10.1038/s41586-019-1516-5. [DOI] [PubMed] [Google Scholar]
- 2.Storm C., Pastore J.J., MacKintosh F.C., Lubensky T.C., Janmey P.A. Nonlinear elasticity in biological gels. Nature. 2005;435:191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 3.Munster S., Jawerth L.M., Leslie B.A., Weitz J.I., Fabry B., Weitz D.A. Strain history dependence of the nonlinear stress response of fibrin and collagen networks. Proc Natl Acad Sci. 2013;110:12197–12202. doi: 10.1073/pnas.1222787110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Roeder B.A., Kokini K., Sturgis J.E., Robinson J.P., Voytik-Harbin S.L. Tensile Mechanical Properties of Three-Dimensional Type I Collagen Extracellular Matrices With Varied Microstructure. J Biomech Eng. 2002;124:214–222. doi: 10.1115/1.1449904. [DOI] [PubMed] [Google Scholar]
- 5.Han Y.L., Ronceray P., Xu G., Malandrino A., Kamm R.D., Lenz M. Cell contraction induces long-ranged stress stiffening in the extracellular matrix. Proc Natl Acad Sci USA. 2018;115:4075. doi: 10.1073/pnas.1722619115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Malandrino A., Trepat X., Kamm R.D., Mak M. Dynamic filopodial forces induce accumulation, damage, and plastic remodeling of 3D extracellular matrices. PLoS Comput Biol. 2019;15 doi: 10.1371/journal.pcbi.1006684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shi Q., Ghosh R.P., Engelke H., Rycroft C.H., Cassereau L., Sethian J.A. Rapid disorganization of mechanically interacting systems of mammary acini. Proc Natl Acad Sci. 2014;111:658–663. doi: 10.1073/pnas.1311312110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ban E., Franklin J.M., Nam S., Smith L.R., Wang H., Wells R.G. Mechanisms of Plastic Deformation in Collagen Networks Induced by Cellular Forces. Biophys J. 2018;114:450–461. doi: 10.1016/j.bpj.2017.11.3739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Onck P.R., Koeman T., Van Dillen T., Van Der Giessen E. Alternative explanation of stiffening in cross-linked semiflexible networks. Phys Rev Lett. 2005;95:19–22. doi: 10.1103/PhysRevLett.95.178102. [DOI] [PubMed] [Google Scholar]
- 10.Vader D., Kabla A., Weitz D., Mahadevan L. Strain-Induced Alignment in Collagen Gels. PLoS ONE. 2009;4 doi: 10.1371/journal.pone.0005902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nam S., Hu K.H., Butte M.J., Chaudhuri O. Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels. Proc Natl Acad Sci USA. 2016;113:5492. doi: 10.1073/pnas.1523906113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cox T.R., Bird D., Baker A.-M., Barker H.E., Ho M.-W.-Y., Lang G. LOX-Mediated Collagen Crosslinking Is Responsible for Fibrosis-Enhanced Metastasis. Cancer Res. 2013;73:1721. doi: 10.1158/0008-5472.CAN-12-2233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Levental K.R., Yu H., Kass L., Lakins J.N., Egeblad M., Erler J.T. Matrix Crosslinking Forces Tumor Progression by Enhancing Integrin Signaling. Cell. 2009;139:891–906. doi: 10.1016/j.cell.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kumar S., Mehta K. Tissue transglutaminase, inflammation, and cancer: How intimate is the relationship? Amino Acids. 2013;44:81–88. doi: 10.1007/s00726-011-1139-0. [DOI] [PubMed] [Google Scholar]
- 15.Theocharis A.D., Skandalis S.S., Gialeli C., Karamanos N.K. Extracellular matrix structure. Adv Drug Deliv Rev. 2016;97:4–27. doi: 10.1016/j.addr.2015.11.001. [DOI] [PubMed] [Google Scholar]
- 16.Kielty C.M., Grant M.E. Connective Tissue and Its Heritable Disorders. John Wiley & Sons, Inc; 2002. The Collagen Family: Structure, Assembly, and Organization in the Extracellular Matrix; pp. 159–221. [DOI] [Google Scholar]
- 17.Litvinov R.I., Gorkun O.V., Owen S.F., Shuman H., Weisel J.W. Polymerization of fibrin: Specificity, strength, and stability of knob-hole interactions studied at the single-molecule level. Blood. 2005;106:2944–2951. doi: 10.1182/blood-2005-05-2039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Weisel J.W. Fibrinogen and fibrin. Adv Protein Chem. 2005;70:247–299. doi: 10.1016/S0065-3233(05)70008-5. [DOI] [PubMed] [Google Scholar]
- 19.Le Guéhennec L., Layrolle P., Daculsi G. A review of bioceramics and fibrin sealant. Eur Cell Mater. 2004;8:1–11. doi: 10.22203/ecm.v008a01. [DOI] [PubMed] [Google Scholar]
- 20.Bell G.I. Models for the specific adhesion of cells to cells. Science (New York, NY) 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 21.Tee S.-Y., Fu J., Chen C.S., Janmey P.A. Cell Shape and Substrate Rigidity Both Regulate Cell Stiffness. Biophys J. 2011;100:L25–L27. doi: 10.1016/j.bpj.2010.12.3744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Discher D.E., Janmey P., Wang Y.-L. Tissue cells feel and respond to the stiffness of their substrate. Science (New York, NY) 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 23.Bangasser B.L., Shamsan G.A., Chan C.E., Opoku K.N., Tüzel E., Schlichtmann B.W. Shifting the optimal stiffness for cell migration. Nat Commun. 2017;8:15313. doi: 10.1038/ncomms15313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pathak A., Kumar S. Independent regulation of tumor cell migration by matrix stiffness and confinement. Proc Natl Acad Sci. 2012;109:10334–10339. doi: 10.1073/pnas.1118073109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Solon J., Levental I., Sengupta K., Georges P.C., Janmey P.A. Fibroblast Adaptation and Stiffness Matching to Soft Elastic Substrates. Biophys J. 2007;93:4453–4461. doi: 10.1529/biophysj.106.101386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Yeung T., Georges P.C., Flanagan L.A., Marg B., Ortiz M., Funaki M. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil Cytoskelet. 2005;60:24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
- 27.Engler A.J., Sen S., Sweeney H.L., Discher D.E. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 28.Chaudhuri O., Koshy S.T., Branco da Cunha C., Shin J.W., Verbeke C.S., Allison K.H. Extracellular matrix stiffness and composition jointly regulate the induction of malignant phenotypes in mammary epithelium. Nat Mater. 2014;13(10):970–978. doi: 10.1038/nmat4009. [DOI] [PubMed] [Google Scholar]
- 29.Wei S.C., Fattet L., Tsai J.H., Guo Y., Pai V.H., Majeski H.E. Matrix stiffness drives epithelial-mesenchymal transition and tumour metastasis through a TWIST1-G3BP2 mechanotransduction pathway. Nat Cell Biol. 2015;17:678–688. doi: 10.1038/ncb3157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Paszek M.J., Zahir N., Johnson K.R., Lakins J.N., Rozenberg G.I., Gefen A. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 31.Doyle A.D., Wang F.W., Matsumoto K., Yamada K.M. One-dimensional topography underlies three-dimensional fi brillar cell migration. J Cell Biol. 2009;184:481–490. doi: 10.1083/jcb.200810041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Kim D.-H., Provenzano P.P., Smith C.L., Levchenko A. Matrix nanotopography as a regulator of cell function. J Cell Biol. 2012;197:351. doi: 10.1083/jcb.201108062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Riching K.M., Cox B.L., Salick M.R., Pehlke C., Riching A.S., Ponik S.M. 3D Collagen Alignment Limits Protrusions to Enhance Breast Cancer Cell Persistence. Biophys J. 2014;107:2546–2558. doi: 10.1016/j.bpj.2014.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hernandez-Gea V., Friedman S.L. Pathogenesis of Liver Fibrosis. Annu Rev Pathol Mech Dis. 2011;6:425–456. doi: 10.1146/annurev-pathol-011110-130246. [DOI] [PubMed] [Google Scholar]
- 35.King T.E., Pardo A., Selman M. Idiopathic pulmonary fibrosis. The Lancet. 2011;378:1949–1961. doi: 10.1016/S0140-6736(11)60052-4. [DOI] [PubMed] [Google Scholar]
- 36.Provenzano P.P., Inman D.R., Eliceiri K.W., Knittel J.G., Yan L., Rueden C.T. Collagen density promotes mammary tumor initiation and progression. BMC Medicine. 2008;6:11. doi: 10.1186/1741-7015-6-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Apte M.V., Park S., Phillips P.A., Santucci N., Goldstein D., Kumar R.K. Desmoplastic Reaction in Pancreatic Cancer: Role of Pancreatic Stellate Cells. Pancreas. 2004;29 doi: 10.1097/00006676-200410000-00002. [DOI] [PubMed] [Google Scholar]
- 38.Whatcott C.J., Diep C.H., Jiang P., Watanabe A., LoBello J., Sima C. Desmoplasia in Primary Tumors and Metastatic Lesions of Pancreatic Cancer. Clin Cancer Res. 2015;21:3561. doi: 10.1158/1078-0432.CCR-14-1051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chaudhuri O., Gu L., Darnell M., Klumpers D., Bencherif S.A., Weaver J.C. Substrate stress relaxation regulates cell spreading. Nat Commun. 2015;6:6365. doi: 10.1038/ncomms7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kim T., Hwang W., Lee H., Kamm R.D. Computational analysis of viscoelastic properties of crosslinked actin networks. PLoS Computational Biology. 2009;5 doi: 10.1371/journal.pcbi.1000439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Collet J.-P., Shuman H., Ledger R.E., Lee S., Weisel J.W. The elasticity of an individual fibrin fiber in a clot. PNAS. 2005;102:9133–9137. doi: 10.1073/pnas.0504120102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Mak M., Zaman M.H., Kamm R.D., Kim T. Interplay of active processes modulates tension and drives phase transition in self-renewing, motor-driven cytoskeletal networks. Nat Commun. 2016;7:10323. doi: 10.1038/ncomms10323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gonzalez-Molina J., Zhang X., Borghesan M., Mendonça da Silva J., Awan M., Fuller B. Extracellular fluid viscosity enhances liver cancer cell mechanosensing and migration. Biomaterials. 2018;177:113–124. doi: 10.1016/j.biomaterials.2018.05.058. [DOI] [PubMed] [Google Scholar]
- 44.Benny P., Raghunath M. Making microenvironments: A look into incorporating macromolecular crowding into in vitro experiments, to generate biomimetic microenvironments which are capable of directing cell function for tissue engineering applications. J Tissue Eng. 2017;8 doi: 10.1177/2041731417730467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zeiger A.S., Loe F.C., Li R., Raghunath M., Van Vliet K.J. Macromolecular Crowding Directs Extracellular Matrix Organization and Mesenchymal Stem Cell Behavior. PLoS ONE. 2012;7 doi: 10.1371/journal.pone.0037904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ang X.M., Lee M.H.C., Blocki A., Chen C., Ong L.L.S., Asada H.H. Macromolecular Crowding Amplifies Adipogenesis of Human Bone Marrow-Derived Mesenchymal Stem Cells by Enhancing the Pro-Adipogenic Microenvironment. Tissue Eng Part A. 2013;20:966–981. doi: 10.1089/ten.tea.2013.0337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Alieva N.O., Efremov A.K., Hu S., Oh D., Chen Z., Natarajan M. Myosin IIA and formin dependent mechanosensitivity of filopodia adhesion. Nat Commun. 2019;10:3593. doi: 10.1038/s41467-019-10964-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Doyle A.D., Yamada K.M. Mechanosensing via cell-matrix adhesions in 3D microenvironments. Exp Cell Res. 2016;343:60–66. doi: 10.1016/j.yexcr.2015.10.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Malandrino A., Mak M., Kamm R.D., Moeendarbary E. Complex mechanics of the heterogeneous extracellular matrix in cancer. Extreme Mech Lett. 2018;21:25–34. doi: 10.1016/j.eml.2018.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Mak M., Spill F., Kamm R.D., Zaman M.H. Single-Cell Migration in Complex Microenvironments: Mechanics and Signaling Dynamics. J Biomech Eng. 2016;138 doi: 10.1115/1.4032188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hytönen V.P., Wehrle-Haller B. Mechanosensing in cell–matrix adhesions – Converting tension into chemical signals. Exp Cell Res. 2016;343:35–41. doi: 10.1016/j.yexcr.2015.10.027. [DOI] [PubMed] [Google Scholar]
- 52.Chen B., Ji B., Gao H. Modeling Active Mechanosensing in Cell-Matrix Interactions. Annu Rev Biophys. 2015;44:1–32. doi: 10.1146/annurev-biophys-051013-023102. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.