Dopamine-Decorated TiO₂ Nanoparticles in Water: A QM/MM vs an MM Description

Abstract

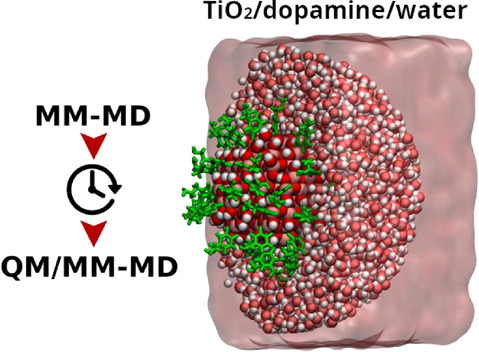
Nanoparticle functionalization is a modern strategy in nanotechnology to build up devices for several applications. Modeling fully decorated metal oxide nanoparticles of realistic size (few nanometers) in an aqueous environment is a challenging task. In this work, we present a case study relevant for solar-light exploitation and for biomedical applications, i.e., a dopamine-functionalized TiO₂ nanoparticle (1700 atoms) in bulk water, for which we have performed an extensive comparative investigation with both MM and QM/MM approaches of the structural properties and of the conformational dynamics. We have used a combined multiscale protocol for a more efficient exploration of the complex conformational space. On the basis of the results of this study and of some QM and experimental data, we have defined strengths and limitations of the existing force field parameters. Our findings will be useful for an improved modeling and simulation of many other similar hybrid bioinorganic nanosystems in an aqueous environment that are pivotal in a broad range of nanotechnological applications.

1. Introduction

Metal oxide nanoparticles (NPs) are receiving increasing attention as carriers for drug delivery.¹⁻³ Titanium dioxide nanoparticles are particularly promising since they may combine transport properties with photoactivity to be applied in photoinduced drug release or in photodynamic therapy.³⁻⁷ Bare nanoparticles are not useful since they tend to agglomerate in an aqueous environment becoming cytotoxic and cannot provide reversible interactions with drugs.⁸ A solution to this is the use of functionalized metal oxide nanoparticles with selected bifunctional ligands that can anchor on the oxide surface on one side but reversibly tether the drug on the other.^9,10 One of the most extensively utilized bifunctional linkers for direct conjugation with metal oxides is the catechol derivative 4-(2-aminoethyl)benzene-1,2-diol or dopamine (DOP),^11,12 which, on one side of the benzene ring, binds the surface through coordination bonds with the enediol portion, whereas, on the other side, the primary amine could potentially remain exposed to the surrounding environment, imparting water dispersibility and acting as a potential handle for biomolecules.^13,14

Current research on nanomedicine aims at optimizing these multifunctional stimuli-responsive nanodevices. The fundamental knowledge of the nature and mechanisms of interaction at an atomistic level would be of great significance to the scientific community involved in this process of development and improvement. For instance, it is crucial to learn how the ligands place and arrange themselves around the nanoparticle and the competition between surface and water interactions.

However, modeling fully decorated metal oxide nanoparticles of realistic size (few nanometers) in an aqueous environment is not a simple task. We need a reasonably accurate and balanced description of NP–ligand, ligand–ligand, NP–water, and ligand–water interactions. A quantum mechanical (QM) description of a system of few nanometers (on the order of a thousand of atoms) immersed in water is beyond the boundaries of state-of-the-art calculations.

The Molecular Mechanics (MM) approach^15,16 could potentially embrace the description of all these interactions within a single level of theory. The price to be paid is the loss of description of the electronic properties of the semiconducting oxide nanoparticle and thus of the chemistry at the interface between the NP and the decorating ligand monolayer.

For this reason, we have decided to apply a hybrid QM/MM scheme¹⁷ where our case study system, namely, the dopamine-decorated TiO₂ nanoparticle, is treated at a QM level of theory, whereas the surrounding water is described at the MM level of theory. We consider this a good compromise in obtaining the required accuracy to describe the chemical and the electronic properties of the NP–ligand system on one side and the mostly physical interaction with the water environment on the other. In this work, we have extended the QM/MM scheme, based on self-consistent charge density functional tight binding (DFTB as shorthand for SCC-DFTB)¹⁸ calculations, that has been developed in a previous study to model bare TiO₂ nanoparticles (2.2 nm with 700 atoms) in water,¹⁹ to the description of the NP/DOP-ligands/water multicomponent system (700 atoms + 46 DOPs + 6386 water molecules). The aims of the present work are, on one side, to assess the accuracy of existing force field parameters derived from the original Matsui–Akaogi parametrization²⁰ for the multiscale modeling of the NP/biomolecule/water interfaces and, on the other, to gain insight into the physics of dopamine-decorated TiO₂ curved NPs of realistic size in an aqueous environment as a relevant hybrid nanosystem for biomedical applications.

The original Matsui–Akaogi force field (hereafter MA-FF) has been successfully applied to the molecular modeling and simulation of complex TiO₂ composites.²¹⁻²⁶ This FF, initially designed for the accurate description of bulk-phase TiO₂ at the classical level, neglects the covalent contribution in the Ti–O bonds compensating with an overestimation of the partial atomic charges and an underestimation of the atomic radii. Recently, Brandt and Lyubartsev²⁷ re-parametrized this original set of MA-FF parameters (hereafter OPT-FF) toward a more accurate description of the TiO₂ surface bond interactions involving undercoordinated Ti and O atoms. The authors included in one of these new potentials a bonding contribution that led to lower partial atomic charges and to more realistic atomic radii for classical TiO₂ atoms.

To shed light on the effects of either neglecting or including the covalent contribution on the prediction of molecular properties at the NP surface, we carried out classical MM-MD simulations of the TiO₂ nanoparticle model covered by DOP ligands either with the original MA-FF or with the OPT-FF, respectively, combined with the GAFF parameters. Furthermore, to better comprehend the role of electrostatics in the structural properties of the monolayer of DOP ligands at the NP interface, we tested three different levels of theory to assign the partial atomic charges to the atoms of the ligands.

Since the short-range LJ (12-6) potential plays a pivotal role in the QM/MM framework adopted in this work,^28,29 we further investigated which FFs provide the most suitable set of LJ (12-6) parameters for the QM/MM modeling and simulations of the NP/DOP-ligands/water system. Moreover, we evaluated the impact that different starting geometries or sampling strategies have on the simulation predictions within different time regimes. For this reason, we have used a multiscale scheme, which we will call Enhanced Temporal Sampling (ETS), combining MM-MD and QM/MM-MD simulations.

The computational methods (MM and QM/MM) and the details of the molecular dynamics (MD) simulations are presented in Section 2. In Section 3, we present and discuss the results of this work through a critical comparison of the different computational approaches: first, we focus on the description of the water ordering and structure around the DOP-decorated TiO₂ NP (Section 3.1); second, we analyze the ligand conformations around the nanoparticle in vacuum and then in the presence of the water environment (Section 3.2). In Section 3.3, we discuss both in qualitative and quantitative terms the description of the H-bond interactions between NP–DOP, DOP–DOP, and DOP–water. Finally, we draw some conclusions on the strengths and limitations of the various approaches used in this work to describe a bioniorganic hybrid multicomponent nanosystem in an aqueous environment and on the physical insight that is possible to achieve.

2. Computational Methods

2.1. Theoretical Background

2.1.1. Molecular Mechanics Molecular Dynamics Method

Within the molecular mechanics molecular dynamics (MM-MD) methodology, one has to define the potential energy functions and their empirical parameters, broadly known as a Force Field (FF), to calculate the forces between pairs of atoms. For convenience, one can divide these functional forms of potential energy into two main groups: bonded and nonbonded potentials.

Herein, we made use of the Generalized AMBER Force Field (hereafter GAFF).^30,31 This FF estimates the total energy of bonded and nonbonded pairwise interactions throughout classical potential forms. The total potential energy of bonded interactions (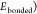 comprehends the sum of bonding stretching (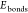), angle bending (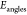), and dihedral torsions (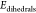) terms. They are given by

1

where k_r, k_θ, and k_n are force constants that keeps the spatial displacement of bonds, angles, and dihedrals around their equilibrium values defined by the r_eq, θ_eq, and γ parameters.

The nonbonded interactions, composed of interactions of electrostatic and nonelectrostatic nature, are modeled by the classical Coulombic potential and the Lennard-Jones 12-6 potential (hereafter LJ (12-6)). The nonbonded potential can be written as

2

Here, A_ij = 4ε_ijσ_ij¹² and B_ij = 4ε_ijσ_ij, in which σ_ij is the interatomic distance between pairs of atoms and ε_ij defines the depth of the attractive potential well. q_i and q_j represent the point charges on atoms i and j, and R_ij stands for the interdistance between a pair of atoms. The cross-terms of the LJ parameters for unlike atoms were obtained using the Lorentz–Berthelot combining rules.³² The Particle Mesh Ewald (PME) method³³ handled the electrostatic interactions for all MM-MD simulations under periodic boundary conditions.¹⁶

It is worth mentioning that such classical approximations are well-suitable for understanding the dynamical process of stable molecular structures by large-scale MD simulations. The major drawback of this approach is that it does not allow the prediction of chemical events such as bond-breaking and bond-making, atomic polarization, and charge transfer.

2.1.2. Quantum Mechanics/Molecular Mechanics Molecular Dynamics Method

The quantum mechanics/molecular mechanics molecular dynamics (hereafter QM/MM-MD) scheme adopted herein relies on the additive-coupling scheme^34,35 in which the total energy can be written as

3

in which the two first terms on the right-hand side of eq 3 stand for the total energy of the QM (E_QM) and the MM (E_MM) subsystems. The E_QM/MM term stands for the total energy of the QM/MM coupling term (eq 4), in which the electrostatic polarization of QM atoms and their respective vdW interactions are accounted for. Thus, the QM atoms (N_QM) are susceptible to polarization by the electric field of external point charges (q_i)around them. These interactions are handled by an electrostatic embedding QM/MM scheme.¹⁷ One can break down the E_QM/MM term in terms of their electrostatic and nonelectrostatic interactions. It can be expressed as

4

where n(r) is the electronic density, Z_α represents the atomic number of atom α, and R_α denotes the nucleic coordinates in the QM subsystem.^35,36 Within this QM/MM formalism, the short-range vdW interactions are modeled by the same potential form as the one adopted in classical GAFF-based MM-MD simulations (eq 2, Section 2.1.1).

2.2. Starting-Point Geometry and ETS Protocol

The starting geometry of the dopamine-decorated anatase TiO₂ nanoparticle (NP-DOPs) is the result of previous works,^14,37,38 as it will be described in the following. TiO₂ spherical nanoparticles were carved from large bulk anatase supercells, setting the radius of the sphere to the desired value of 2.2 nm. Only atoms within that sphere were considered. Some residual very low coordinated Ti atoms or monocoordinated O atoms were either removed or saturated with OH groups or H atoms, respectively. In other words, we used a small number of dissociated water molecules to achieve the chemical stability of the nanoparticle. The stoichiometry of the model is (TiO₂)₂₂₃·10H₂O.³⁷ After a simulated annealing process at 700 K, we have fully relaxed the equilibrated structure with both DFTB and DFT(B3LYP).³⁸ The DFTB-optimized nanoparticle was then progressively functionalized with up to 46 dopamine molecules (33 chelated and 13 bidentate, see Figure 1) and fully optimized again to obtain the high coverage model of NP–DOP used as the starting geometry in this work.¹⁴

Figure 1.

Schematic representation of the binding modes of dopamine on the TiO₂ curved surface.

The water-solvated model was prepared with the use of the PACKMOL program³⁹ by surrounding the “in vacuum”-optimized (with DFTB) structure of NP–DOP within a spherical droplet of classical water molecules.

A fundamental challenge in multiscale modeling and simulation of condensed matter is the efficient sampling of the conformational phase space over time and length scales. Nowadays, ab initio MD simulations have been widely used to understand the hydration effects on metallic surfaces,⁴⁰ although time and length scales in these calculations are still far from those experienced in macroscopic experiments. Even state-of-the-art QM/MM simulations,^41,42 whose classical approximations enhance the phase-space sampling in these calculations, remain in a time and length regime far from the macroscopic scale. One can find relevant studies on simulation artifacts that might arise from the starting-structure dependence,⁴³ short time-scale MD dynamics,⁴⁴ the QM/MM coupling itself,⁴⁵ and sampling-related problems in QM/MM calculations.⁴⁶⁻⁴⁹

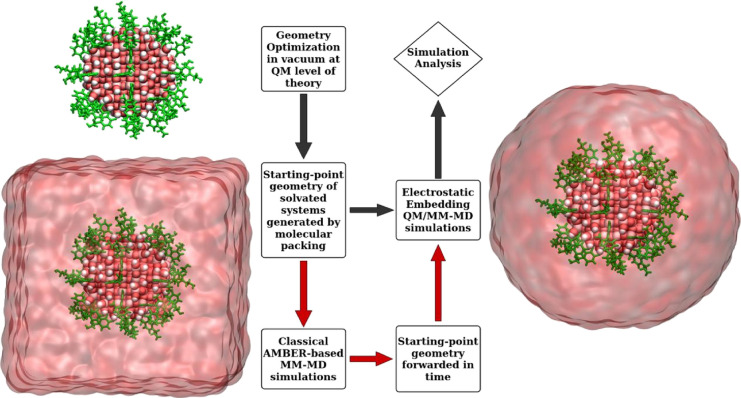
To investigate the implication of starting-point geometry as well as the short time-scale sampling on QM/MM-MD predictions, we have used a multiscale scheme (referred to as ETS) that combines a long-time simulation at the MM level with a QM(DFTB)/MM-MD simulation. This approach is similar to common schemes for simulation of proteins⁵⁰⁻⁵² (where the force field for the preliminary MM-driven propagation is more readily available) but to our knowledge has not yet been utilized for nanoparticle systems of this size. Here, we follow three main steps: (1) a priori relaxation at the classical level forwarding the time-sampling in a regime of nanoseconds; (2) take the last system conformation from the classical simulation in step 1; (3) turn the region of interest to be described at the QM level of theory keeping the set of LJ (12-6) parameters consistent between MM and QM/MM models.

We compare two distinct sets of QM/MM-MD simulations: in the first set, the QM/MM simulation starts from the DFTB-optimized structure of NP–DOP in vacuum, which was solvated with a water droplet by molecular packing, according to the path with gray arrows in Scheme 1; in the second set, we utilize the ETS protocol in which QM(DFTB)/MM-MD simulations were carried out using starting-point geometries taken from the last snapshot of classical MM-MD simulations, as indicated by the red arrows in Scheme 1.

Scheme 1. Simulation Schemes Adopted in the MD Simulations.

The gray arrows indicate the path followed by the conventional sampling (CS) protocol that provides the starting-point geometry by spherical solvation of the optimized SCC-DFTB geometry of NP–DOP via molecular packing. The red arrows indicate the path that uses the starting-point geometry provided by the ETS protocol. The last snapshot from the MM-MD simulation is truncated at 30 Å from the NP centroid stripping off all water molecules outside this distance. No cutoff is applied for the nonbonded interactions in the droplet model calculations.

2.3. Computational Details

2.3.1. Point-Charge Atomic Models

QM calculations at the Hartree–Fock (HF), Density Functional Theory (DFT), and Self Consistent Charge Tight-binding Density Functional Theory (SCC-DFTB) levels of theory generated three different sets of point-charge models for the electrostatic modeling of dopamine atoms. These point-charge models are tagged through this paper as follows: q_HF for the Hartree–Fock point-charge model; q_DFT for the DFT point-charge model; q_DFTB for the SCC-DFTB point-charge model. Moreover, q_HF was obtained following the standard restrained electrostatic potential fitting protocol (RESP)⁵³ on a single dopamine molecule, at the Hartree–Fock level of theory with the 6-31G* basis set (HF/6-31G*). The q_DFT and q_DFTB charge models use Mülliken charges averaged over all dopamine molecules on the nanoparticles during the DFT and DFTB calculations. The partial atomic charges on the dopamine atoms from the HF, SCC-DFTB, and DFT calculations can be found in Table S1 in the Supporting Information.

2.3.2. Classical MM-MD Simulations

All classical MM-MD simulations were carried out with the AMBER16 program.⁵⁴ We used the set of GAFF^30,31 parameters and the quantum Flexible Simple Point Charge water model (hereafter qSPC/Fw)⁵⁵ for modeling organic and water molecules. For the sake of consistency, the LEaP module implemented in the AMBERTools19 suite assigned all bonded and nonbonded parameters for intra- and intermolecular interactions. For performance purposes, all classical MM-MD simulations were carried out in parallel with the SANDER module implemented in the AMBER16 program.⁵⁴

2.3.2.1. Single-Dopamine in Water

The initial structure of dopamine was obtained on the web-server MolView v.2.4 (molview.org). We utilized the LEaP module to add a pre-equilibrated box of qSPC/Fw⁵⁵ water molecules (with dimensions of 30 × 30 × 30 ų) to the single-DOP molecule. Electrostatic and vdW interactions were calculated within a cutoff of 12Å. The Velocity-Verlet algorithm integrated Newton’s equations in time with a time step of 2 fs. A Berendsen thermostat⁵⁶ kept the temperature at 300 K with a damping coefficient of 0.1 (1/ps).

2.3.2.2. Dopamine-Decorated TiO₂ Nanoparticle in Water

The atomic coordinates of the Ti and O atoms in the nanoparticle, as obtained by simulated annealing at 300 K and full atomic relaxation with the DFTB method in ref (14) when 46 dopamine molecules are attached, were kept fixed during all classical MM-MD simulations by Cartesian restraints with force constant equal to 5000 kcal/mol/Ų, the same protocol used in refs (57) and (58). This DFTB-optimized structure was solvated with a pre-equilibrated simulation box containing 6386 qSPC/Fw⁵⁵ water molecules using the LEaP module. To remove possible atomic overlapping after molecular packing of these systems, we carried out a minimization phase with a maximum number of 10000 cycles, with the minimization algorithm switched from the steepest descent to the conjugated gradient after 5000 cycles. A Langevin thermostat heated the system in the NVT ensemble and maintained the target temperature during the MD simulations at 300 K. The equilibration phase was carried out for 10 ns in the isothermal-isobaric (NPT) ensemble to adjust the overall density of the system at P = 1 atm and T = 300 K. The production phase explored 10 ns of the phase space in the NPT ensemble at T = 300 K and P = 1 atm. The LJ parameters for the titanium and oxygen atom-types were taken from either the MA-FF²⁰ or the OPT-FF²⁷ and then assigned according to their coordination numbers. The LJ (12-6) cross-parameters for unlike atom-types were obtained by the Lorentz–Berthelot combining rules. Electrostatic and LJ (12-6) potentials utilized a cutoff of 10 Å (larger cutoff values of 12 and 14 Å were tested, see Figure S1 for comparison). Newton’s equations of motion were solved using the Velocity-Verlet integrator⁵⁹ with a time step of 0.5 fs.

2.3.3. DFT/MM-MD Simulations

The DFT/MM-MD calculation was carried out with the CRYSTAL14^60,61 package at the DFT level of theory, in which Kohn–Sham orbitals were expanded in Gaussian-type orbitals with the all-electron basis set as follows: H|511(p1), C|6-311(d11), N|6-311(d1), and O|8-411(d11). Dispersion forces were included by Grimme’s D* correction. A convergence tolerance of 0.02 eV/Å and 1 × 10^–5 hartree were set to forces and total energy, respectively.

2.3.4. DFTB-MD and DFTB/MM-MD Simulations

The Atomic Simulation Environment (ASE)⁶² interface handled the electrostatic embedding QM/MM scheme¹⁷ between the QM and MM subsystems. We used the DFTB+ program⁶³ for the self-consistent charge density functional tight-binding (hereafter DFTB) calculations. To this end, we adopted the set of parameters MATORG and HBD^64,65 to describe the cross-interactions between TiO₂ and water particles. The hydrogen-bond interaction at the DFTB level was corrected by a hydrogen-bonding damping function with an exponent value set to 4.0.⁶⁶ The convergence tolerance of the self-consistent charge cycle was set to 5.0 × 10^–3. The minimization phase utilized the Berendsen NVT dynamics implemented in ASE, with a target temperature of 300 K and a time constant of 0.01 (1/ps) for the temperature coupling. We carried out the equilibration phase through the Velocity-Verlet integrator with a time step of 1 fs, temperature target of 300 K, and a damping coefficient of 0.1 (1/ps). The production phase was conducted using Berendsen NVT dynamics in ASE, with the temperature kept at 300K, using a damping coefficient of 0.1 (1/ps) and a time step of 1 fs.

2.3.5. Simulation Analysis

For the sake of consistency, we have analyzed all MM-MD simulations in this work using the CPPTRAJ module through the AMBERTools19 suite. VMD⁶⁷ provided the graphical interface to visualize these simulations, and an in-house code generated the VMD-native topology files, thus recovering all atomic parameters (e.g., atomic point-charge, bond-type, etc.) and topological definitions belonging to the QM/MM models.

2.3.5.1. Radial Distribution Function

To obtain the number density profiles, we made use of the gmx-rdf module implemented in GROMACS (version 5.0.5).⁶⁸⁻⁷⁰ The number of particles within a distance r from the NP center was computed and then further normalized by both the bin volume and the number density of bulk water (0.033 Å^–3) at P = 1 atm and T = 300 K. We accounted for all interatomic distances into histograms with a bin width of 0.1 Å.

2.3.5.2. Hydrogen Bonding

To track the hydrogen bond (hereafter H-bond) formation in the MM-MD simulation trajectories, we used the hbond module implemented in the AMBERTools19 suite. We counted as a H-bond formation when the following geometrical criteria were satisfied: (1) the distance between the hydrogen donor (H-donor) and the hydrogen acceptor (H-acceptor) heavy atoms is less than 3.5 Å; (2) the angle formed between the H-donor and H-acceptor, with the hydrogen atom as the vertex, is less than 30°.

2.3.5.3. Molecular Height of Surface-Bonded Dopamine

The molecular height corresponds to the distance from the nitrogen atom of the bonded ligand to the closest titanium atom on the NP surface. These data were analyzed in two different ways: (1) we calculated the molecular height of each ligand and then took a final average over all of them. After that, we plotted it as a function of simulation time; (2) we measured the molecular height of each DOP ligand and then compiled all of them in a single data series. This was turned into normalized histograms and then further fitted using the Gaussian multipeak fitting method. Both analyses included the probability density curve of this quantity to assess an accurate portrayal of the molecular height variable in the course of simulations.

2.3.5.4. Electric Dipole Moment

Dipole Moment Watcher⁶⁷ measured the electric dipole moment resultant of the spatial distribution of a particular charge set in the course of the simulations. Since the partial charges on the QM atoms change every step in the DFTB/MD and DFTB/MM-MD calculations, we adopted the charge set obtained at the last converged SCC cycle to estimate the dipole moment in the DFTB/MM-MD simulation trajectories. We then adopted the same strategy to analyze the simulation data as described in the previous section.

3. Results and Discussion

The results of this work are presented in the next three subsections. In Section 3.1, we focus the attention on water and analyze the performance of different FFs with MM and QM/MM calculations in the description of (i) the water interaction with a curved TiO₂ surface against previous QM data by DFT and DFTB by our group¹⁹ and (ii) the water ordering and structure around the dopamine-functionalized TiO₂ NP. In Section 3.2, we focus the attention on the 46 dopamine molecules anchored to the NP surface, and we first analyze (i) the conformational dynamics in vacuum by comparing the MM and QM/MM results with QM(DFTB) calculations and experimental data⁷¹ and then (ii) the conformational dynamics in water by identifying how the choice of the FFs, the extension of time-sampling, the atomic starting positions, and the electrostatics modeling may affect the results for both MM and QM/MM calculations. In Section 3.3, we discuss the H-bonding description of the multicomponent system with the various approaches used in this work.

For the sake of clarity, simulations are labeled throughout this text according to the FF parameters (capital letters), the simulation method (in capital letters), the surrounding medium (superscript), and the point-charge model (subscript in parentheses). For instance, the acronym MA – MD_(qHF)^WAT stands for classical MD simulations in water using the original Matsui–Akaogi FF with partial atomic charges for dopamine calculated at the HF level of theory. Table 1 presents a summary of the MD simulations carried out in this work.

Table 1. Summary of MD Simulation Details Carried Out in This Study.

simulation details	DFTB/MM-MDCS	DFTB/MM-MDETS	MM-MD(qHF)	MM-MD(qDFT)	MM-MD(qDFTB)
method	QM/MM	QM/MM	MM	MM	MM
initial structure	molecular packing	ETS protocol	molecular packing	molecular packing	molecular packing
point-charge model			HF	DFT	DFTB
time sampling	25 ps	25 ps	20 ns	20 ns	20 ns
medium	vacuum or water	vacuum or water	water	water	water
force field	MA-FF or OPT-FF	MA-FF or OPT-FF	MA-FF or OPT-FF	MA-FF or OPT-FF	MA-FF or OPT-FF

3.1. Description of the Water Interaction with the DOP-Decorated TiO₂ Spherical Nanoparticle

3.1.1. Water Ordering and Structure around the DOP-Decorated TiO₂ Nanoparticle

To analyze the influence of the empirical parameters on the MD simulation predictions of the water ordering around the DOP-functionalized NP surface, we estimate the RDF profiles of water molecules in a periodic cell of 60 × 60 × 60 ų, for simulations combining either the MA-FF or OPT-FF with point charges derived at HF (q_HF), DFTB (q_DFTB), or DFT (q_DFT) QM levels of theory.

Figure 2 shows the normalized RDF as a function of distance from the NP centroid (reference position) to the O_w atoms of water molecules. This analysis revealed a characteristic pattern of water ordering, marked by sharp RDF peaks up to 20 Å from the NP surface in all MD simulations. To facilitate the discussion on the RDF profiles, we split the RDF plot into four main regions, numbered accordingly to the well-defined peaks observed in these profiles. This distance-based model resembles the one proposed by Nosaka and co-workers,⁷² based on experimental measurements. It is useful to identify patterns of water ordering on a metal surface. The authors defined the first solvation shell as the innermost layer containing water molecules strongly adsorbed on the metal surface and having low mobility; the second solvation shell is composed of nonadsorbed water molecules, although with slower mobility than the water molecules in the outer solvation shell. This outer layer is composed of bulk-like water molecules with the highest mobility. These assumptions, based on previously mentioned experimental evidence, are useful to better understand the RDF results below. Figure 2a shows the RDF predictions obtained from the classical MD simulations. Figure 2b shows the RDF curves from the QM/MM-MD simulations. DFTB/MA – MD_ETS^WAT and DFTB/OPT – MD_ETS stand for the QM/MM-MD simulations using either the MA-FF or the OPT-FF, respectively. These FFs are used both in the first MM-MD simulation of the ETS protocol and to provide the empirical parameters for the short-range LJ (12-6) potential. The subscript ETS stands for QM/MM simulations carried out using the ETS protocol (Section 2.2).

Figure 2.

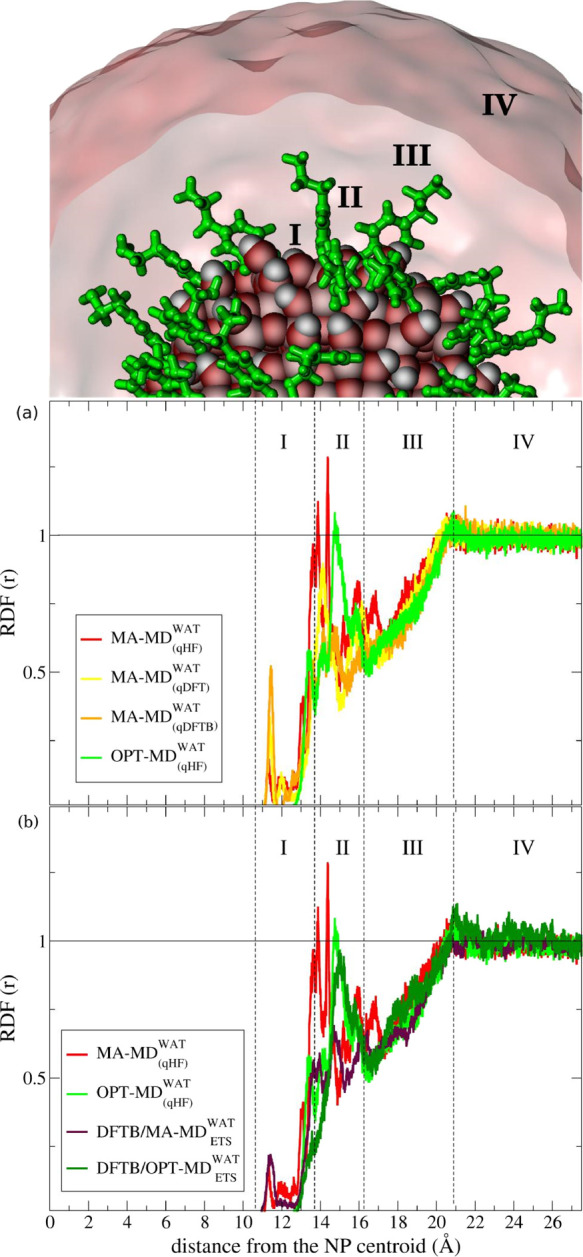
Normalized RDF profiles of water as a function of distance from the NP centroid and their regions of interest numbered with roman numbers from I to IV. The outermost surface Ti atoms are at a distance of 12.2 Å from the NP centroid. The dotted-black vertical lines were traced to define each region of interest in the RDF profile. The horizontal black line is traced at the RDF unit corresponding to the ideal density of bulk water. The subscript ETS stands for starting-point structures provided by the ETS protocol for DFTB/MM-MD simulations. The level of theory used to derive the partial-atomic charges of the DOP ligands for classical simulations are indicated in parentheses. RDF profiles of MM-MD and QM/MM-MD simulations are sketched as follows: MA – MD_(qHF)^WAT (red), MA – MD_(qDFT) (yellow), MA – MD_(qDFTB)^WAT (orange), OPT – MD_(qHF) (light green), DFTB/MA – MD_ETS^WAT (dark violet), and DFTB/OPT – MD_ETS (dark green). Zoomed images illustrating the binding modes of dopamine and its interaction with water are reported in Figure S2.

In Region I (Figure 2a), we observe a considerable difference regarding the RDF prediction by MA-FF and OPT-FF. The innermost RDF peak, which defines the first solvation shell above the NP surface, shows up in Region I in both the MA-FF and OPT-FF predictions, although the latter model has its maximum peak shifted 2.1 Å toward the bulk water compared with the former model. The MA-FF model predicts the first solvation shell at 11.3 Å from the NP center, whereas OPT-FF has its innermost peak at 13.4 Å. The main contribution to this peak comes from water molecules strongly adsorbed at the NP surface. In the MA – MD_(qHF)^WAT simulations, we noticed no exchange of these adsorbed water molecules with others during the MD simulations. Also, the q_HF charges predicted the innermost peak with the lowest intensity, which increases with the q_DFT charges and becomes the highest with the q_DFTB charges.

Regarding the second solvation shell, we notice that the main peak in the RDF profiles for both the MA-FF and OPT-FF models falls into Region II, although in the former model there were also identified smaller contributions in Region I. The OPT – MD_(qHF)^WAT simulation predicts the main peak at 14.8 Å, while the MA – MD_(qHF) simulation shows it at 14.4 Å in this region. Furthermore, we observe a general pattern with a linear increase of water density (Region III) until the RDF profile reaches a plateau at the unit value and is then kept constant at the bulk value in Region IV (Figure 2). All classical simulations showed similar behavior in these regions.

Examining Figure 2b, we can notice a similar discrepancy in the first solvation shell for the innermost peak predictions when using the OPT-FF or MA-FF parameters in the QM/MM calculations. The DFTB/MA – MD_ETS^WAT simulation presents its innermost peak at 11.4 Å, closer of 2.2 Å to the NP centroid if compared with the DFTB/OPT – MD_ETS curve, which has a small shoulder about 13.6 Å in Region I.

In the second solvation shell, the main peak of the DFTB/OPT – MD_ETS^WAT simulation is at 15.0 Å (Region II), i.e., in a similar position to that observed for the OPT-FF simulation. However, the innermost peak observed about 13.6 Å in the latter simulation is almost absent in the DFTB/OPT – MD_ETS simulation. On the other hand, the DFTB/MA – MD_ETS^WAT model is characterized by a substantial decrease in the main-peak intensity compared with the MA – MD_(qHF) curve. Furthermore, the RDF results in Regions III and IV resemble the ones obtained through classical simulation, with a linear ramp of the water density until it reaches a plateau at the bulk value (RDF unit) in Region IV.

Based on the analysis above, one can infer that the main differences in the RDF profile of water by MA-FF and OPT-FF, in both for MM and QM/MM calculations, is in the first solvation shell (Region I) with the simulations using the MA-FF presenting a feature assigned to water molecules directly bound to surface Ti atoms. This discrepancy will be further investigated and discussed in the next paragraph. Another difference is in the position of the second solvation shell peak (Region II), which is shifted at slightly higher distances for simulations by OPT-FF with respect to those by MA-FF.

3.1.2. Water Interaction with Undercoordinated Sites on a Curved Anatase TiO₂ Surface: Comparison with QM Data

MA and OPT force fields were parametrized to reproduce the observed crystal structures of TiO₂ bulk phases and water adsorption enthalpy on rutile TiO₂ flat surfaces under ambient conditions, respectively. It is, therefore, relevant to assess the accuracy of these force fields in the description of water adsorption on a curved TiO₂ surface, and here, we do that by comparison against our previous QM(DFT-B3LYP) and QM(DFTB) calculations on the same spherical NP used in the present study.¹⁹ The binding energies and the Ti–O_water distances of one water molecule adsorbed on three undercoordinated Ti sites on the curved surface are reported in Tables S2 and S3, respectively. The choice of the Ti sites was based on the criterion that the undissociated adsorption mode was preferred to the dissociated one. We can observe a good agreement between the DFT-B3LYP and DFTB binding energies and distances. QM/MM and MM results using MA-FF quite correctly reproduce Ti–O_water distances, although slightly elongated, with reasonably similar binding (±0.5 eV). On the contrary, OPT-FF cannot catch the Ti–O_water coordination but tends to convert the interaction into a double H-bond of the water hydrogens with surface O atoms. This is due to the original parametrization of OPT-FF for water on rutile surfaces, where it either dissociates forming OH on surface Ti atoms or molecularly adsorbed forming H-bonds with surface O atoms. A curved anatase surface presents several undercoordinated Ti sites that can coordinate with molecular water. This situation cannot be described by OPT-FF, whereas MA-FF, although not parametrized specifically for that, can better reproduce DFT and DFTB results, which are confirmed by experimental data from infrared spectroscopy.⁷³

3.2. Conformational Analysis of Dopamine Molecules Anchored to the TiO₂ Spherical Nanoparticles

3.2.1. NP–DOPs in Vacuum: Comparison with QM(DFTB) Results and Experiments

We will first discuss the MD simulations of the dopamine-decorated NP in vacuum to assess the accuracy of MA-FF and OPT-FF in the description of a curved TiO₂/biomolecule interface, based on the comparison with experimental X-ray measurements⁷¹ and QM(DFTB)-MD simulations.

Through an NEXAFS spectroscopic study,⁷¹ it was possible to determine the tilt angle with respect to the surface normal of the phenyl rings in dopamine molecules adsorbed in a monolayer on an anatase (101) TiO₂ single crystal in vacuum: ±5°. This means that the molecules are in a standing up adsorption mode. We can compare this important result with our simulations on the TiO₂ NPs, as detailed in Table S4. In the case of DFTB-MD and OPT-MD, the majority of the molecules are in a standing up configuration with an averaged tilt angle of 12°, which is very close to the experimental value of 5°. On the contrary, in the case of MA-MD, the vast majority of dopamine molecules are in a downward configuration with an averaged tilt angle of 68°. Therefore, OPT-FF is more accurate in reproducing structural properties of biomolecules adsorbed on a TiO₂ surface than MA-FF that seems to overestimate the interaction of the biomolecule with the oxide surface.

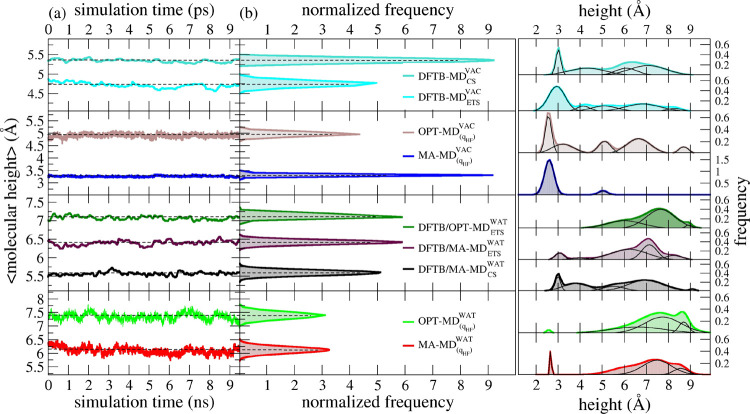
The same conclusions can be derived when we compare the time evolution of the molecular height from the surface for the 46 dopamine molecules anchored to the TiO₂ NP during the MD simulations with DFTB, MA-FF, and OPT-FF in vacuum, shown in the top right part of Figure 3. We can clearly observe that the MA – MD_(qHF)^VAC simulation is characterized by a very intense blue peak centered at about 2.5 Å height (as defined in Section 2.3.5.3). On the contrary, OPT – MD_(qHF) and DFTB – MD_(qHF)^VAC simulations present a wide variety of molecular heights, confirming that many dopamine molecules are in the open-state configuration, similar to what was indicated by the tilt angle.

Figure 3.

(a) Time evolution of the molecular height of surface-bonded DOP and (b) corresponding normalized distribution from time-averaged values of DFTB/MD, DFTB/MM-MD, and classical MM-MD simulations. (c) Nonlinear curve fitting and deconvolution analysis of nonaveraged values of the molecular height of surface-bonded DOP. Black curves represent the deconvolution of their respective nonlinear fitted curves. The level of the theory of the point-charge model used in MM-MD simulations is reported in parentheses. The subscripts VAC and WAT stand for simulations under vacuum and aqueous solvation, respectively. Time units are in picosecond and nanosecond for QM/MM-MD (top) and classical MM-MD simulations (bottom) in their respective x-axis. The simulation methods are distinguished here by the following color scheme: turquoise for DFTB/MD simulations in vacuum; cyan for DFTB/MD simulations using ETS restart in the vacuum medium; black for DFTB/MA-MD simulations with the MA-FF LJ (12-6) parameters in water solvation; dark violet for DFTB/MA-MD simulations with the MA-FF LJ (12-6) parameters using ETS restart in water solvation; dark green for DFTB/OPT-MD simulation with the OPT-FF LJ (12-6) parameters using ETS restart. CS stands for conventional sampling where the starting-point structure for the QM/MM simulations is taken from the optimized structure at the DFTB level and then solvated by molecular packing of water molecules

Therefore, based on the comparison with experiments and DFTB-MD described above, we may conclude that OPT-FF is better suited to describe the TiO₂/biomolecule interface in vacuum than MA-FF.

3.2.2. NP–DOPs in Water: Performance of the Original and the Optimized Matsui–Akaogi Force Field

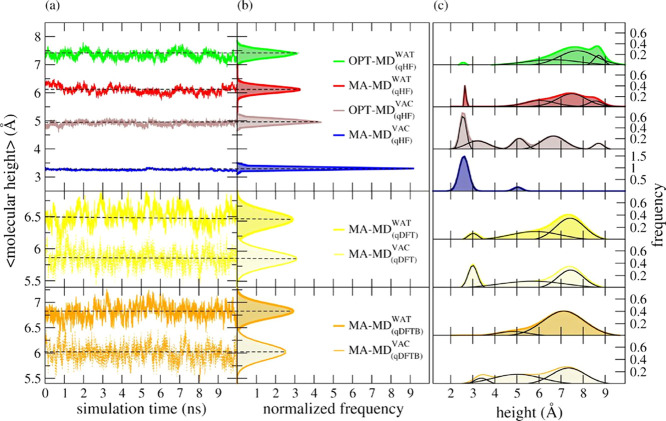
To investigate the effects of different FFs on the conformational-state predictions of surface-bonded DOP ligands, we estimate the molecular heights of these small organic ligands as described in Section 2.3.5.3. This structural property works as an indicator of the preferential conformational state acquired by DOP ligands on the NP surface during the classical simulations. Furthermore, we have tested different partial atomic charge models for the electrostatics modeling of surface-bonded DOP ligands. These partial atomic charges are derived at the HF (q_HF), DFT (q_DFT), and DFTB (q_DFTB) levels of theory. Figure 4a shows the molecular heights of surface-bonded DOP ligands and their probability distribution profiles from the time-averaged values over all DOP ligands (Figure 4b). Figure 4c presents the probability distribution profiles estimated over nonaveraged values of the molecular height for each DOP ligand as well as their respective deconvoluted bands.

Figure 4.

(a) Time evolution of the molecular height of surface-bonded DOP and (b) corresponding normalized probability distribution profiles obtained through classical MD simulations with the original Matsui–Akaogi force field (MA-FF) and its ad hoc optimized set of parameters (OPT-FF). (c) Nonlinear curve fitting and deconvolution analysis of instantaneous values of the molecular height of surface-bound DOP. Black curves represent the deconvolution of their respective nonlinear fitted curves. The level of theory used to fit the point-charge model of DOP is indicated in parentheses. The subscripts VAC and WAT stand for MD simulations under vacuum and aqueous solvation, respectively. The color scheme adopted here is consistent with the one adopted in Figure 2. MD simulations in vacuum were sketched with a lighter color

The deconvolution analysis of the data on the molecular height (Figure 4c) reveals well-defined bands occurring over a wide range of values that can be understood as multiconformational states acquired by the surface-bonded DOP ligands during the MD simulation. Among them, three pre-eminent bands showed up with maximum peaks about 3, 5, and 8 Å. For the sake of comparison, we named those distributions with well-defined maximum peaks higher than 5 Å as “open-state”, while “closed-state” means those distributions with maximum peaks smaller than 5 Å. Peaks with their maximum occurring around 5 Å are defined as “intermediate-state” here. To estimate the occurrence probability of each conformational state, we have integrated the area under the deconvoluted bands in Figure 4c (thin black lines).

Under vacuum conditions, we found that surface-bonded DOP ligands preferred the closed-state rather than the open-state conformation. However, we notice a considerable discrepancy in both the molecular height and the conformational state of surface-bonded DOP between the MA – MD_(qHF)^VAC and the OPT – MD_(qHF) predictions. Figure 4b shows molecular-height averages with maximum peaks at 3.3 and 4.9 Å for the MA – MD_(qHF)^VAC and OPT – MD_(qHF) simulation predictions, respectively. Further examination of the deconvoluted curves in Figure 4c shows a high-intensity peak at 2.6 Å for the MA – MD_(qHF)^VAC simulation, where its main contribution comes from DOP ligands in the closed-state conformation. We also noticed no occurrence of DOP ligands in the open-state region, although a smaller band was observed at 5.1 Å. For the OPT – MD_(qHF) simulation, we also encountered the highest peak occurrence at 2.6 Å, although with a peak intensity about 2 times lower than that predicted by the MA – MD_(qHF)^VAC simulation. This lowering in the peak intensity was compensated by smaller and well-defined bands uniformly distributed along the intermediate- and open-state regions.

In the water environment, regardless of the set of FF parameters applied, we found out that DOP ligands are farther from the NP surface and have higher values than those observed in the vacuum medium. Most of these ligands, mainly driven by electrostatic interactions with water molecules, align themselves toward bulk water. In general, the majority of the DOP ligands has acquired the open-state conformation: simulations by MA-FF and OPT-FF, when combined with q_HF charges, show their main peaks of molecular-height averages at 6.1 and 7.4 Å, respectively; this shift of 1.3 Å between them is 19% smaller than that predicted under vacuum conditions.

Moreover, we observe that the molecular-height predictions by the MA – MD_(qHF)^WAT and OPT – MD_(qHF) simulations present their main difference in the closed-state region. In the former model, we observe a small population at 2.7 Å in both vacuum and water solvation conditions. On the other hand, the OPT – MD_(qHF)^WAT model presents a substantial decrease of DOP ligands in the closed-state conformation, which is compensated by broader distributions populating the intermediate- and open-state conformations.

Based on these results, we learn that the water solvation attenuates the discrepancy between MA-FF and OPT-FF regarding the conformational-state predictions of DOP ligands compared to the vacuum medium. Both FFs predicted a favorable open-state conformation of DOP ligands, which are mainly supported by electrostatic interactions established between the water molecules and the polar moieties of these ligands. However, we note that several DOP ligands remain in the closed-state conformation for the MA – MD_(qHF)^WAT model even when solvated by water. Instead, when the OPT – MD_(qHF) model is applied, we observe the absence of DOP ligands at the closed-state region, compensated by a higher population of DOP ligands acquiring the open-state conformation.

3.2.3. Effects of Time-Sampling and Starting-Point Structures on the QM/MM Simulations

To get insight into the implications of time sampling on the spatial conformation of surface-bonded DOP ligands, we now examine the molecular height of surface-bonded DOP ligands in the presence and absence of aqueous solvation through our multiscale framework. Such analysis also allows a better comprehension of how different strategies to provide the initial structure for QM/MM-MD simulations could affect the predictions of the conformational properties of small organic ligands within different time regimes. At last, we present a direct comparison of the QM/MM-MD against MM-MD simulation predictions for a rational choice of FF parameters to be used in the multiscale simulations of the TiO₂/dopamine interface.

We have estimated the molecular height of surface-bonded DOP ligands along the QM/MM-MD simulations using the same protocol utilized in Section 3.2.1 (see Section 2.3.5.3 for details). Figure 3 shows a quantitative analysis of the time-averaged distance of surface-bonded DOP ligands to the NP surface. We have also performed a histogram analysis of the instantaneous values of the molecular height to get detailed information about the preferred conformation of surface-bonded DOP ligands on the NP surface at the QM/MM level. Figure 3 shows the molecular height of surface-bonded DOP ligands calculated from semiempirical DFTB/MD and DFTB/MM-MD simulations. For the sake of comparison, we have also included the classical MM-MD predictions obtained in Figure 4 (Section 3.2.1).

As presented in detail in Section 2.2, we labeled this approach as ETS (Extended Temporal Sampling) and used it to provide the starting-point structures as input for DFTB/MM-MD simulations with a substantial effect on the conformational state of DOP ligands in aqueous solvation. These QM/MM predictions indicated a majority of surface-bonded DOP ligands in the open-state conformation. We observed that also the choice of LJ parameters has a considerable impact on the conformational state of DOP ligands: the set of MA-FF LJ parameters combined with either the conventional (black curves, Figure 3) or the ETS sampling scheme (dark violet curve, Figure 3c) have their maxima open-state peaks at 6.9 and 7.1 Å, respectively, whereas the DFTB/OPT – MD_ETS^WAT simulation (dark green line, Figure 3c) presents its maximum peak shifted by 0.5 Å toward higher values of molecular height and no peak in the closed-state region (i.e., below 5 Å).

3.2.4. Role of the Electrostatics Modeling

In this section, we investigate the interplay between the electrostatics modeling of DOP ligands and the effects of different point-charge values on the conformational-state predictions. Beyond HF, we tested two additional point-charge sets at the DFT and DFTB levels of theory (q_DFT and q_DFTB). First, we have assigned the partial atomic charges obtained from these QM calculations to the DOP ligand atoms and then carried out MM-MD simulations following the same protocol described in the previous section. Additionally, we have estimated the dipole moment over the MD simulation trajectory for each point-charge model tested herein. In ascending order, we obtain q_DFTB (8.4 D), q_HF (14.2 D), and q_DFT (15.4 D).

Examination of the deconvoluted bands in vacuum (right-hand side panel in Figure 4, Section 3.2.1) reveals that the combination of q_HF with MA-FF parameters induced both the highest peak intensity and probability of finding the DOP ligands in the closed-state conformation (82%). Rather, the use of q_HF combined with the OPT-FF parameters has lowered the main-peak intensity at the closed-state region by 41% besides a substantial increase of smaller and well-defined bands arising toward the open-state region. When q_DFT is used instead, one can observe a decrease in the main-peak intensity by 25% as well as a probability of 38% to find DOP ligands in the open-state conformation. For the MA – MD_(qDFTB)^VAC model, we found no DOP ligands in the closed-state conformation (right-hand side panel in Figure 4, Section 3.2.1). It is also important to point out that, except the MA – MD_(qHF) model, all classical simulations present, at some degree, DOP ligands in the intermediate- and open-state conformations under vacuum conditions.

To investigate if there is a correlation between the dipole and the orientation of bonded DOPs on the NP surface, we evaluated the tilt angle of the phenyl ring of DOP ligands as a function of their dipole moment averaged over all DOPs during the QM(DFTB)-MD and MM-MD simulations in vacuum (Figure S3). We notice that different FFs lead to considerable deviations of the tilt angle, as already discussed in Section 3.2.1, but there, we do not register a clear correlation with the dipole. The experimental tilt angle of dopamine phenyl rings from the surface normal obtained by carbon K-edge NEXAFS under vacuum conditions is about 5°, which is better reproduced by OPT-FF and DFTB MD simulations. In the case of MA-FF simulations, independent of the charge model employed (q_HF or q_DFT), large tilt angles are observed, which indicate overbinding between DOPs and NP surface atoms. We conclude that the tilt angle is more affected by the choice of the FF for the NP than by the choice of the point-charge model for DOPs.

In the presence of water solvation, the major contribution to the molecular height of DOP ligands comes from the intermediate- and open-state conformations. Figure 4 suggests an interplay between the dipole magnitude of surface-bonded DOP described by different point-charge models and the probability to populate different conformational states. For the following combinations, the probabilities of finding DOP ligands in the open-state conformation are 56% for the OPT – MD_(qHF)^WAT model, 53% for the MA – MD_(qDFT) model, 47% for the MA – MD_(qHF)^WAT model, and 94% for the MA – MD_(qDFTB) model. These results show that the combination of MA-FF with the DFTB-derived atomic charges exhibits the highest probability of finding DOP ligands in the open-state conformation, whereas the combination of MA-FF with HF-derived atomic charges exhibits the smallest one. Furthermore, with MA – MD_(qDFTB)^WAT, we did not register any DOP ligands in the closed-state. On the other hand, in the MA – MD_(qHF) and the MA – MD_(qDFT)^WAT simulations, we could observe probabilities of 10 and 1%, respectively, to find DOP ligands in the closed-state conformation. Examination of the deconvoluted curves in Figure 4 shows three distinct populations in the open-state region for both the OPT – MD_(qHF) and the MA – MD_(qHF)^WAT model, whereas both the MA – MD_(qDFTB) and MA – MD_(qDFT)^WAT models show only two well-defined populations in this region.

3.3. H-Bond Description by MM and QM/MM Methods for

3.3.1. An Isolated Dopamine Molecule in a Water Environment

To better comprehend the interplay between the electrostatics modeling and the H-bond nature of DOP in aqueous solvation, we have first performed both classical and QM/MM simulations of a single isolated dopamine molecule solvated in explicit water. Herein, we carried out QM/MM simulations using different QM levels of theory for the atomic-charge derivation. They are (i) DFT, (ii) DFTB/Mülliken, (iii) PM3 charge model. In the DFT QM/MM scheme, the electrostatic interactions are calculated between the electron density of QM atoms with the classical point-charges in the MM region.

Table 2 shows the H-bond formation between the amine group of DOP with the water molecules as either the H-donor or the H-acceptor. For classical MD simulations, the level of theory used to obtain the point-charge models is shown in parentheses. Ensemble averages and standard deviations (in parentheses) were estimated at over 10 ps and 10 ns of the production phase for the QM/MM and MM simulations, respectively.

Table 2. Number of H-Bond Formation between the NH₂ Group of DOP and qSPC/Fw Water Molecules throughout Multilevel Simulations^a,b.

	QM/MM			MM
donor–H···acceptor	DFT	DFTB	PM3	GAFF(qHF)	GAFF(qDFT)	GAFF(qDFTB)
OWAT–H···NDOP	0.7 (0.3)	0.2 (0.2)	0.3 (0.3)	1.3 (0.3)	0.8 (0.3)	0.3 (0.3)
NDOP–H···OWAT	0.4 (0.3)	0.4 (0.3)	0.2 (0.2)	0.9 (0.5)	0.4 (0.4)	0.4 (0.4)

^aDFT, DFTB, and PM3 stand for the levels of QM theory tested in the QM/MM simulations.

^bAverage standard deviation (SD).

Considering the QM(DFT)/MM MD simulation predictions as the reference values, at the classical level, q_DFT yields the best agreement for the H-bond formation between the N_DOP and O_WAT residues. QM(DFT)/MM and QM(PM3)/MM correctly predict the basic/acidic behavior of the NH₂ group and classical water molecules. However, the QM(DFTB)/MM prediction is not correct, with the NH₂ group acting as a better donor than the classical water molecules. Moreover, we notice that QM(DFTB or PM3)/MM predictions (Table 2) underestimated the H-bond formation. The classical calculations for the single DOP, using q_HF or q_DFT point-charge models, correctly describe the classical concept of acid–base in chemistry, with NH₂ groups behaving as better H-acceptors and water molecules as better H-donors. However, one can observe that GAFF(q_HF) overestimates the number of H-bond formation (47% higher than those predicted by the QM(DFT)/MM simulations), whereas the GAFF(q_DFTB) model underestimates it.

To summarize, QM(DFTB)/MM approach tends to underestimate the H-acceptor ability of DOP amino groups, whereas the use of q_HF charges in MM calculations may lead to its overestimation.

3.3.2. Dopamine Molecules Anchored to the NP Surface in a Water Environment

H-bonds are of utmost importance in stabilizing macromolecular structures in aqueous solvation. Since atoms are systematically parametrized in classical FFs to behave accordingly to their chemical nature, one may expect a good (at least qualitative) description of this property from a set of self-consistent empirical FF parameters. However, such an accurate description of H-bonds remains challenging for most QM/MM schemes since these phenomena are mainly driven by electrostatic interactions and occur mostly at the interface between the QM and MM regions.

In this section, we have investigated how different levels of theory used to treat the TiO₂ NP–DOP system in water could affect the number of H-bond formation between solute–solute and solute–solvent residues, based on the assessment made in the previous section for a free dopamine in water.

Table 3 shows the number of H-bonds established between the polar residues in the solvated NP–DOP model during the simulations obtained with the various approaches. For a direct comparison of the O_WAT–H···N_DOP and N_DOP–H···O_WAT H-bond values with the ones for a single DOP in Table 2, we divided the average and standard deviation values by the total number of surface-bonded DOP molecules (46).

Table 3. Number of H-Bond Formation between Solute–Solute and Solute–Solvent Residues of NP in Water Solvation Averaged over 10 ps and 10 ns of Production Trajectories of DFTB/MM-MD and MM-MD Simulations, Respectively^a.

donor–H···acceptor	DFTB/MA-MDETS	DFTB/OPT-MDETS	OPT-MDqHF	MA-MD(qHF)	MA-MD(qDFT)	MA-MD(qDFTB)
OWAT–H···NDOPb	0.3 (0.1)	0.3 (0.1)	1.2 (0.1)	1.4 (0.1)	0.7 (0.1)	0.3 (0.1)
NDOP–H···OWATb	0.3 (0.1)	0.4 (0.1)	0.8 (0.1)	0.5 (0.1)	0.3(0.1)	0.3 (0.1)
ONP–H···NDOP	0.2 (0.5)	0.2 (0.1)	0.6 (0.5)	7.5 (1.2)	1.3 (0.9)	0.2 (0.4)
NDOP–H···NDOP	1.1 (1.0)	1.0 (0.1)	1.5 (1.1)	0.3 (0.6)	0.9 (0.9)	0.9 (0.9)
NDOP–H···ODOP	0.8 (0.8)
NDOP–H···ONP	0.4 (0.7)
ODOP–H···NDOP

^aAverage standard deviation (SD).

^bAverage standard deviation (SD) normalized by 46.

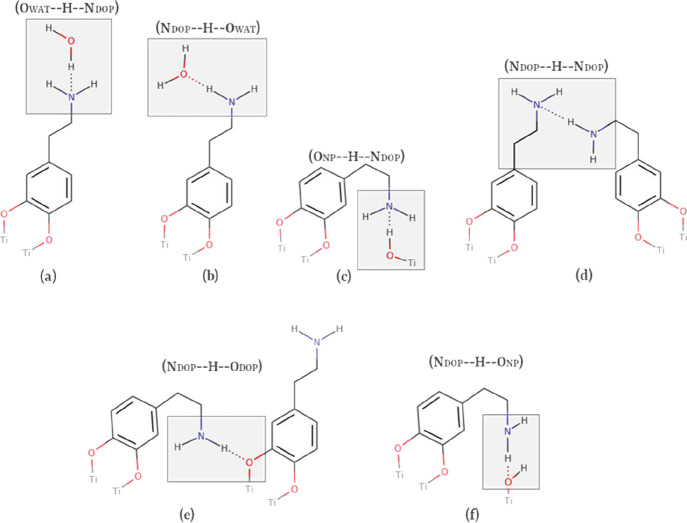
In Table 3, the first capital letter corresponds to the heteroatom in the H-donor group, and the second capital letter stands for the heteroatom belonging to the H-acceptor group. The subscript DOP stands for surface-bonded dopamine, NP for the anatase TiO₂ nanoparticle, and WAT for the water molecules. The H-bonds with nonzero values (Table 3) are sketched in Scheme 2.

Scheme 2. (a–f)2D Representations of the H-Bond Formation Observed during MD Simulations.

The first capital letter stands for the heavy atom in the H-donor group; the second capital letter stands for the heavy atom in the H-acceptor group.

The H-bond formation between the water molecules (O_WAT) and the amine group in the dopamine molecule (N_DOP) is found to be the most recurrent between solute–solvent residues along the MD simulations (see first two entries in Table 3). Apart from DFTB-based simulations, the O_WAT–H···N_DOP H-bond type (Scheme 2a) is the preferred one and MA – MD_(qHF)^WAT shows the highest value for this H-bond type. These results are in line with the fact that DFTB/MM underestimates the N H-accector ability, whereas MM methods with q_HF overestimate it. The second most frequent H-bond type observed is N_DOP–H···O_WAT (Scheme 2b).

Among the H-bonds between the NP and DOPs, the O_NP–H···N_DOP pair (Scheme 2c) is found to be the most common. In the MA – MD_(qHF)^WAT simulation, an exaggerated number of this type of H-bond is registered, in line with the fact that MA-FF tends to bend the DOPs toward the surface in a closed-state conformation (Scheme 2c).

Self-interaction between dopamine residues (N_DOP–H···N_DOP) also occurs with all methods except MA – MD_(qHF)^WAT because, as we just said, with this, FF dopamine molecules are mostly interacting with the NP surface.

Furthermore, we may notice that the N_DOP group has no considerable ability to establish H-bonds with neither the O_DOP nor the O_NP residues (N_DOP–H···O_DOP and N_DOP–H···O_NP in Table 3, respectively). The H-bond formations between these pairs of residues were almost absent in all the simulations.

The data described above, independent of the method used, indicate that surface-bonded DOP ligands favor interactions with water molecules rather than with NP residues. Our results also suggest a dependence between the H-bond description and the electrostatics modeling of the NP models for MM calculations. Both the MM(q_HF) simulations predict for the N_DOP and O_WAT pairs of H-bond interactions, at least in qualitative terms, a correct description of the chemical concept of donor–acceptor interactions based on their electronegativity. On the contrary, DFTB/MM underestimates the H-acceptor ability of amino groups, which was assessed in the previous section against DFT/MM for dopamine in water.

4. Conclusions

This work presents the applicability of state-of-the-art DFTB-based QM/MM and classical MM methodologies to access dynamics and structural properties of a dopamine-functionalized TiO₂ nanoparticle immersed in water, as a model system of the more general class of decorated inorganic nanoparticles.

Critical comparisons of interfacial properties of the dopamine-decorated TiO₂ system, including water ordering and solvation structure, conformational analysis of surface-bonded ligands, and intersystem hydrogen bonding, provide useful guidance for a reasoned choice of the force field parameters.

The original Matsui–Akaogi force field (MA) were parametrized for the description of bulk TiO₂ against experimental lattice parameters, whereas the revised one (OPT) for the description of the rutile flat TiO₂(100) surface/water interface were parametrized against zeta-potential, enthalpy of immersion, and DFT calculations. In this work, we have tested how these FFs perform in the description of a curved anatase TiO₂ surface/biomolecule/water interface, also when used in the multiscale QM/MM scheme.

We observe that MA-FF can better reproduce the QM(DFT and DFTB) results for a single water molecule adsorption on the NP surface Ti sites. This is because OPT-FF was not parametrized to describe Ti–O_W interaction because on rutile water is found to dissociate in Ti–OH and O_surface–H. However, OPT-FF outperforms MA-FF in correctly describing the conformation of dopamine molecules on the TiO₂ surface with respect to the experimental and QM(DFTB) molecular tilt angles in vacuum because MA-FF overestimates the biomolecule interaction with the surface atoms causing an exaggerated bending toward the surface. On this basis, we can infer that even in water MA-FF tends to overestimate the biomolecule–NP interaction with some molecules that prefer to bend toward the surface rather than be solvated by water. A possibility to slightly mitigate this effect is to use MA-FF in combination with (lower) q_DFT charges for N in dopamine instead of q_HF. However, our results on the molecular tilt angle clearly indicate that the choice of the force field is more crucial than the choice of the point charges. Therefore, the take-home message is that OPT-FF provides a more balanced description between NP/DOPs and DOPs/water interactions.

The conformational analysis for the DOP molecules anchored to the NP in water by QM(DFTB)/MM simulations is very similar to that obtained with the corresponding MM (MA vs OPT, respectively).

Regarding the H-bond description, we observed that in QM(DFTB)/MM calculations, the H-acceptor ability of the dopamine amino groups, independent of the FF, is underestimated, whereas in MM calculations (where HF charges are the default), it is overestimated, in both cases with respect to the reference QM(DFT)/MM result.

We have also investigated simulation artifacts due to starting-geometry dependence and short time-scale dynamics through a top-down approach that covers a time regime from picoseconds to nanoseconds. For this, we have combined the QM/MM and MM levels of theory, keeping the same short-range potential, to more effectively explore the conformational space. The results of this investigation indicate that conformational transitions of biomolecules anchored on the NP surface have a direct dependence on the starting-point structure and the time-length sampling in QM/MM calculations. A two-step combined approach (QM/MM following an MM MD simulation) is a common practice in conformational studies of proteins. However, finding an accurate force field in the case of a hybrid system made of metal oxide nanoparticles decorated with several biomolecules is not as straightforward as in the case of proteins, for which force fields are more readily available. This study has shown that the ETS procedure is transferable to these types of systems and the force fields that model them. A future development of this multiscale framework could be the use of coarse-graining (CG) in place of full atomistic simulations, which would allow the conformational space sampling to be further extended.⁷⁴

Before concluding, we wish to remark that this is the first QM/MM study of a TiO₂ NP of realistic size (2.2 nm) fully decorated with biomolecules in a water solvent. Particularly relevant is the fact that the starting geometry of the QM part (NP + biomolecules) of the QM/MM calculations is a fully optimized structure at the QM level from a previous study.¹⁴ Therefore, it is a chemically stable system. Typically, QM/MM calculations start from MM geometries where the chemistry at the interface cannot be correctly described and the models must be based on some chemical assumptions. Also, the QM/MM results have been compared to those from a corresponding MM study based on the same LJ force field parameters, with important implications in the practical aspects of the simulations.

To conclude, through the present work, we have clarified the implications of the empirical parameter choice as well as the sampling-related issues for the dopamine-decorated TiO₂ nanoparticle simulations in water. Besides the scientific impact this has on the specific research field of functionalized metal oxide nanoparticles, the analysis and the protocols derived from our study can be applied to the modeling and simulation of other similar hybrid nanosystems in an aqueous solvent for a broad range of applications.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.0c00483.

• Partial atomic charges on the dopamine atoms from HF, SCC-DFTB, and DFT calculations; binding energies and Ti–O_W distances for a single water molecule on various Ti sites on the NP from DFT, DFTB, QM/MM, and MM calculations; tilt angle of the dopamine phenyl ring with respect to the surface normal from experiments, DFTB, and MM calculations; time evolution of the molecular height of surface-bonded DOP and corresponding normalized probability distribution profiles obtained through OPT-MD simulations at different cutoff values; correlation diagram of dopamine dipole moments and tilt angles from DFTB and MM calculations (PDF)

The authors declare no competing financial interest.