Ground-State Destabilization by Active-Site Hydrophobicity Controls the Selectivity of a Cofactor-Free Decarboxylase

Abstract

Bacterial arylmalonate decarboxylase (AMDase) and evolved variants have become a valuable tool with which to access both enantiomers of a broad range of chiral arylaliphatic acids with high optical purity. Yet, the molecular principles responsible for the substrate scope, activity, and selectivity of this enzyme are only poorly understood to date, greatly hampering the predictability and design of improved enzyme variants for specific applications. In this work, empirical valence bond and metadynamics simulations were performed on wild-type AMDase and variants thereof to obtain a better understanding of the underlying molecular processes determining reaction outcome. Our results clearly reproduce the experimentally observed substrate scope and support a mechanism driven by ground-state destabilization of the carboxylate group being cleaved by the enzyme. In addition, our results indicate that, in the case of the nonconverted or poorly converted substrates studied in this work, increased solvent exposure of the active site upon binding of these substrates can disturb the vulnerable network of interactions responsible for facilitating the AMDase-catalyzed cleavage of CO₂. Finally, our results indicate a switch from preferential cleavage of the pro-(R) to the pro-(S) carboxylate group in the CLG-IPL variant of AMDase for all substrates studied. This appears to be due to the emergence of a new hydrophobic pocket generated by the insertion of the six amino acid substitutions, into which the pro-(S) carboxylate binds. Our results allow insight into the tight interaction network determining AMDase selectivity, which in turn provides guidance for the identification of target residues for future enzyme engineering.

Introduction

Enzymatic catalysis of the formation and breaking of C–C bonds is currently receiving increasing attention.¹ In this context, enzymatic decarboxylation in particular has become highly attractive for the synthesis of optically pure building blocks² and the synthesis of alkenes^1,3−5 and alkanes from biobased precursors.⁶ The release of gaseous CO₂ renders decarboxylases quasi-irreversible, which has been exploited to drive numerous enzymatic cascade reactions.⁷⁻¹¹ In general, enzymatic decarboxylation can proceed in both an oxidative⁴ and a nonoxidative¹ manner. Most nonoxidative decarboxylases employ organic cofactors such as pyridoxyl phosphate, thiamine diphosphate, or an N-terminal pyruvyl group as electron sinks to accommodate the intermediary charge after cleavage of carbon dioxide. Interestingly, three different types of cofactor-independent decarboxylases use substrate-assisted catalysis and thus have the ability to cleave C–C bonds without an internal electron sink. With its highly unusual mechanism, orotidine-5′-phosphate decarboxylase has emerged as a model to study enzymes using ground-state destabilization as a catalytic principle.¹² Among several discussed mechanisms, one uses a so-called “Circe”-effect, in which binding of the phosphate group accommodates the substrate in a binding mode where unfavorable interactions lead to cleavage of a carboxylate group of the substrate. In this vein, the mechanism of phenolic acid decarboxylase (PAD) has been suggested to proceed via a quinone methide intermediate formed by protonation of the substrate double bond.³ This explicitly requires hydrogen bonding of the p-hydroxy group of the substrate with two tyrosine residues. In both cases, the involvement of functional groups of the substrate strictly limits the substrate scope. For instance, PAD decarboxylates differently substituted cinnamic acid derivatives, but all substrates must bear a p-hydroxy group.^1,13

Bacterial arylmalonate decarboxylase from Bordetella bronchiseptica (AMDase, EC 4.1.1.76) was discovered by the Ohta group in the early 1990s, on the basis of a functional screen.^14,15 AMDase catalyzes the stereospecific decarboxylation of α-disubstituted malonic acids, resulting in pure enantiomers of the respective monoacids (Scheme 1). While the acid-catalyzed decarboxylation of prochiral arylmalonates forms racemic product, AMDase catalyzes this reaction stereoselectively. Due to its outstanding stereoselectivity, AMDase has been utilized for the synthesis of a wide range of α-chiral carboxylic acids,¹⁴ including several α-arylpropionates with pharmaceutical activity, such as naproxen^16,17 and flurbiprofen,¹⁸⁻²⁰ α-hydroxy and α-amino acids,²¹ and α-heterocyclic²² and α-alkenyl²³ propionates. Furthermore, combination with metal-catalyzed reduction allows for the synthesis of optically pure α-alkyl propionates.⁹

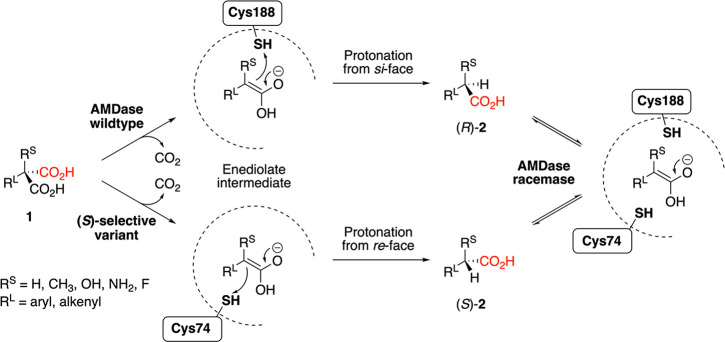
Scheme 1. Reaction Mechanism of Wild-Type AMDase and Its Variants with Inverted Enantioselectivity (When Introducing the G74C Substitution, i.e., Swapping the Catalytic Cysteine from Position 188 to Position 74) and Promiscuous Racemic Activity (When Introducing/Maintaining Cysteines at Both Positions 74 and 188 Simultaneously).

The pro-(R) carboxylate is shown in black, and the pro-(S) carboxylate in red.

Initial studies of AMDase, performed in the absence of a crystal structure, showed that it requires a substituent with a delocalized π-electron system,¹⁵ which can be provided either by an aromatic group or an alkene. The smaller substituent can be a hydrogen or fluorine atom, a methyl group, or an amino or hydroxy group; larger substituents such as an ethyl group are not accepted.^2,15 Several AMDases have been isolated from different bacteria.²⁴⁻²⁷ All show strict preference for the formation of the (R)-enantiomers. Using both enantiomers of pseudochiral ¹³C-labeled malonates, it was shown that AMDase exclusively cleaves the pro-(R)-carboxylate.²⁸

Following from this, the elucidation of several structures of AMDase in both its unliganded and ligand-bound forms^23,29−31 revealed the presence of two binding pockets in the active site. While the first contains several hydrogen-bond donors, the second is mostly composed of hydrophobic residues. Micklefield and co-workers suggested a mechanism that proceeds in two steps: (1) Binding of the pro-(S)-carboxylate in the former pocket, stabilized by several H-bonds, pushes the pro-(R)-carboxylate into a configuration with very unfavorable interactions in the hydrophobic pocket, leading to facile cleavage of the C–C bond and the formation of a planar intermediate.³¹ (2) The donation of a proton by cysteine 188 from one side explains the formation of the pure (R)-products. Ohta and co-workers shifted the position of the catalytic cysteine to the other side, resulting in the formation of pure (S)-enantiomers³² (Scheme 1). While the stereoinversion led the G74C/C188S variant to lose its activity by 20 000-fold, iterative saturation mutagenesis of the hydrophobic pocket partly restored the activity.³³⁻³⁵

Decarboxylation of isotope-labeled malonates confirmed that the (S)-selective variants also cleave the pro-(R)-carboxylate.³³ A variant with both catalytic cysteines present (i.e., C188 intact and the artificial C74 introduced by the G74C substitution) has racemizing activity, which allows for study of the second half-reaction of the mechanism.^36,37 Semiempirical QM/MM calculations³⁷ showed that the racemization proceeds in a stepwise fashion, through stepwise deprotonation and reprotonation of the planar intermediate shown in Scheme 1. Stabilization of this intermediate requires a delocalized π-electron system. The 3.5 kcal mol^–1 energy barrier to the deprotonation step was lower than that of the initial deprotonation of the cysteines (at 25 kcal mol^–1), which might explain the drastic pH-dependence of the G74C/C188G variant.

A quantum mechanical model of AMDase³⁸ confirmed that in the decarboxylation of methylphenyl malonate 1a, C–C bond cleavage is rate-determining. It was argued that enantioselectivity is already determined during substrate binding, as only one binding mode was found to be energetically viable. In the case of a smaller vinyl malonate substrate, it was argued that due to the energetic accessibility of multiple binding modes, both the binding step and the subsequent transition states contribute to the observed selectivity. We note that these calculations were performed with truncated AMDase models, and the results were heavily dependent on model size. A smaller 81 atom model composed of only the substrate and residues forming the dioxyanion hole yielded a small energy difference of only 1.5 kcal mol^–1 between the cleavage of the pro-(R) and the pro-(S) carboxylate groups. However, extension of the model to include several other key residues (to a total of 223 atoms) increased this energy difference to 18.3 kcal mol^–1.

A more recent computational study³⁹ has studied AMDase using the same two cluster models as that found in ref (38), but using soft harmonic confining potentials on the boundaries of the system, rather than the fixed atom model of ref (38). This yielded a smaller energy difference of 6.4 kcal mol^–1 with the larger cluster model, which could also reproduce the enantioselectivity. These differences disclose the complexities found when modeling the system using truncated models. A full enzyme model would provide a better overview of the molecular origins of the observed selectivity. This can be achieved by a complete electrostatic and dynamic treatment within either a QM/MM, an empirical valence bond, or a related framework. In particular, the somewhat nonintuitive results obtained from iterative saturation mutagenesis require a model that takes into account at least the complete first coordination sphere. The hypothetical mechanism for AMDase presented in ref (38) explains the strict preference of AMDase for cleaving the pro-(R)-carboxylate, the inversion of stereopreference in the G74C/C188X variants, and the racemizing activity of the G74C variant. It also provides an energy profile for the reaction and indicates a plausible substrate binding mode. Yet, the predictability of the outcome of amino acid substitutions in the active site is very limited.

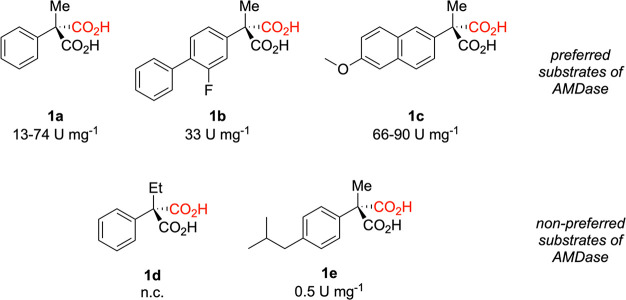
Saturation mutagenesis of (R)-selective^18,23 and (S)-selective^34,35 AMDase variants allowed for significant increases in AMDase activity through very conservative substitutions in the active site. So far, it is very difficult to rationalize why exchanges like L40V, V43I/L, V156L and M159L exert such a remarkable effect on AMDase activity. Moreover, the substrate selectivity of AMDase (Scheme 2) is very difficult to explain: that is, while AMDase catalyzes the decarboxylation of a large series of arylmalonates with a small second substituent (such as H, F, Me), α-ethyl arylmalonates are not converted.^2,15 In addition, while the second substituent might be quite large, AMDase does accept p-isobutylphenyl malonate (which would lead to optically pure ibuprofen) only with very poor catalytic efficiency.³⁵ In both poorly or nonconverted substrates, the inductive effect of the alkyl substituents might impede the stabilization of the planar, charged dienoate intermediate, or their size might lead to steric hindrance.

Scheme 2. Model Compounds Used in This Study and Their Experimentally Observed Acceptance by Wild-Type AMDase.

The pro-(R) carboxylate is shown in black, and the pro-(S) carboxylate is shown in red. Shown here are also the specific activities for each compound (U mg^–1), based on data presented in refs (15, 18, 34, and 35). We note that 1d is fully not converted (n.c.) by AMDase, wherease 1e is converted, but with very low conversion efficiency as shown in Table 1.

Obviously, the activity and selectivity of AMDase can be determined by very subtle interactions in the active site. In order to obtain a dynamic model of the decarboxylation, and to obtain insights into the factors determining substrate acceptance and activity of active-site variants, we investigated the rate-determining first half-reaction (the decarboxylation step) of the decarboxylation of substrates shown in Scheme 2 as catalyzed by wild-type enzyme and substituted variants of AMDase, using the empirical valence bond (EVB) approach.⁴⁰ We have considered the cleavage of both the pro-(R) and pro-(S) carboxylate groups for each substrate and enzyme variant considered in this work, taking into account multiple potential binding modes of each substrate, and coupled this with metadynamics simulations to explore the relative stability of different binding modes at the Michaelis complex. We have also examined how each enzyme variant modulates the hydrophobicity/hydrophilicity throughout the active site to drive catalysis using analysis based on Grid Inhomogeneous Solvation Theory (GIST).⁴¹ Our calculations produce convincing reaction pathways in agreement with experimental observables, pointing to a strongly favored binding mode leading to production of the (R)-enantiomer in wild-type AMDase and to the (S)-enantiomer in variants with the catalytic cysteine transferred to the opposite side of the active site. They rationalize the origins of the tremendous catalytic efficiency of this enzyme, as well as of mutational effects on this activity. Finally (and importantly), our EVB simulations are able to both reproduce and provide a rationale for the unusual substrate acceptance of this enzyme, laying the groundwork for future protein engineering effort on this enzyme.

Methodology

The empirical valence bond (EVB) approach⁴⁰ is our methodology of choice in this study, based on the previous successes of both ourselves and others in using this approach to describe enzyme selectivity.⁴²⁻⁴⁵ Here, we have performed EVB simulations of the decarboxylation of compounds 1a through 1e (Scheme 2) by wild-type and mutant variants of AMDase, specifically by the G74C/V156L/C188G/V43I/A125P/M159L (“CLG-IPL”) variant (compounds 1a, 1b, 1c, and 1e), the G74C/C188G and G74C/C188A variants (compound 1b), and the G74C/C188G variant (compound 1a and 1c). These variants were selected based on the availability of experimental data,^{18,20,23,34,35} with the exception of the G74C/C188A variant for which experimental data is not available. An in-depth description of our simulation protocol and subsequent simulation analysis is provided in the Supporting Information (SI); we provide here a brief summary of our methodology.

Our starting point for simulations of the wild-type enzyme was the structure of wild-type AMDase from Bordetella bronchiseptica, in complex with the potential mechanism-based inhibitor benzylphosphonate (PDB ID: 3IP8(23,46)). Due to the lack of structural data on the enzyme variants of interest to this work, all subsequent mutations were manually generated based on the wild-type crystal structure using the Dunbrack and Cohen backbone-dependent rotamer library,⁴⁷ as implemented into the PyMOL Molecular Graphics System.⁴⁸ The specific side chain rotamers used in the simulations were chosen based on visual inspection for proximity to nearby side chains (to avoid steric clashes), as well as the calculated percentage probability of finding each side chain in a given rotameric state.

Substrates were docked into the active site using AutoDock Vina v. 1.1.2,⁴⁹ which resulted in numerous binding poses. These can be grouped into two representative highly ranked binding poses (Figure S1), the top ranking of which (“Mode I”) has been the focus of this work, for reasons described in the Supplementary Methodology. System setup was performed as described in the SI. Once system setup was complete, all enzyme–substrate complex variants of interest to this work were first equilibrated at the approximate EVB transition state (λ = 0.5) for 30 ns, followed by EVB simulations performed on the end points of the equilibration runs and propagated from the approximate EVB transition states, using the valence bond states shown in Figure S2. Each EVB simulation was performed in 51 individual mapping windows per trajectory of 200 ps length each.

For each system, we performed two independent sets of equilibrations and EVB systems, taking into account the cleavage of each of the pro-(R) and pro-(S) carboxylate groups per compound (the separate equilibrations were necessary as we are propagating from the transition states). Each set of simulations for the cleavage of each carboxylate group was performed in 30 individual replicates (60 per substrate), leading to total cumulative equilibration and EVB simulation time scales of 1.8 and 0.612 μs per enzyme–substrate complex, respectively. Calibration of the EVB parameters was performed as described in Section S1 of the SI. All EVB simulations were performed using the Q6 simulation package⁵⁰ and the OPLS-AA force field,⁵¹ and all EVB parameters necessary to reproduce our work can be found in the SI.

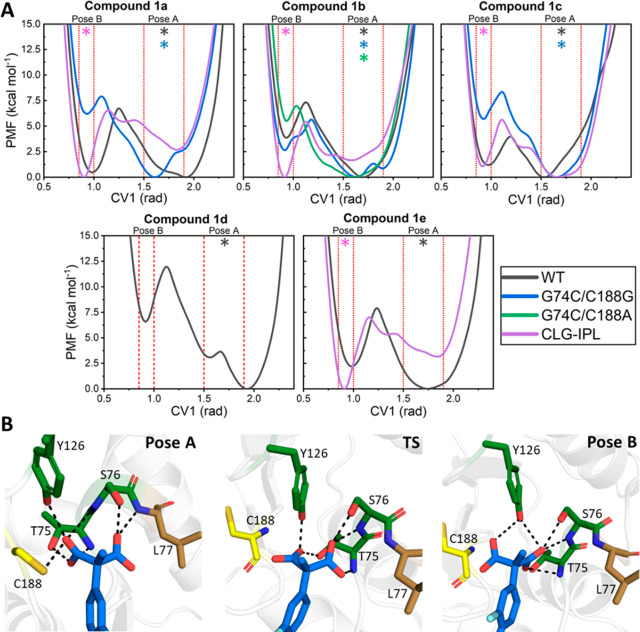
As our EVB simulations appear to sample distinct binding poses for the cleavage of the pro-(R) and pro-(S) carboxylate groups, we also performed well-tempered metadynamics (WT-MetaD)⁵² simulations to calculate the relative populations of the two reactive binding modes at the Michaelis complex. WT-MetaD simulations were performed on the same set of the substrates and enzymes as used in our EVB simulations. Following a standard MD system preparation and equilibration procedure (see the SI Methodology), WT-MetaD simulations were performed in the NPT ensemble (298 K, 1 atm) using the Amber ff14SB⁵³ and GAFF2⁵⁴ force fields (for protein and ligand atoms respectively) and the TIP3P⁵⁵ water model. WT-MetaD simulations were performed using AMBER 18⁵⁶ interfaced with PLUMED v2.7,⁵⁷ with subsequent MD simulation analysis performed using a combination of PLUMED v2.7⁵⁷ and CPPTRAJ.⁵⁸ We used a single collective variable (CV) for all WT-MetaD simulations, which was the mean angle of both carboxylate groups’ orientation in the active site (Figure S3). The combination of both carboxylate groups in a single CV allowed for discrimination of either binding pose independent of which (identical in simulation terms) carboxylate group was orientated where. To prevent the dissociation of any substrate from the active site (or a catalytically competent pose) we applied “Boresch style” restraints⁵⁹ (Figure S4) between atoms on each substrates’ 6-membered ring (which is conserved for all substrates) and Leu77 of the oxyanion hole. Convergence was assessed by monitoring the time evolution of the free energy profile (Figure S5) alongside checking for “diffusive dynamics” (Figure S6) along the CV for each system.

To determine the thermodynamic properties of the water molecules within the AMDase active site, we performed grid inhomogeneous solvation theory (GIST)^41,60 analysis using CPPTRAJ⁵⁸ on the unliganded active sites of the four enzyme variants investigated in this manuscript, as well as three additional variants which are intermediates along the trajectory of improvement in iterative saturation mutagenesis³⁵ from G74C/C188G to CLG-IPL (see the SI Methodology). For this, an additional MD simulation was run for each enzyme for 100 ns, with all protein heavy atoms restrained (as is standard with this approach, see the SI Methodology).⁶⁰ The output of the GIST analysis was used to determine and project the “surface mapped hydrophobicity” onto each substrate atom, using the approach described by Kraml et al.⁶¹ We note that as the GIST analysis was performed on the unliganded states of each enzyme (to identify how each enzyme modulates the active site environment), and the optimal positions of both carboxyl groups are essentially identical across the different substrates for the same binding pose, we focused our GIST analysis on only compound 1b (as this compound was studied by EVB and metadynamics simulations for all four enzymes).

Results and Discussion

Empirical Valence Bond Simulations of AMDase Selectivity Toward Different Compounds

In this work we study decarboxylation of five π-conjugated compounds (Scheme 2) differing in their degree of aromaticity and attached substituents, by both wild-type AMDase and its variants (CLG-IPL, G74C/C188G, and G74C/C188A). The choice of the enzyme to study was led by the fact that wild-type AMDase from B. bronchiseptica converts compounds 1a–c in an (R)-selective fashion,^15,18 whereas compounds 1d–e are curiously either not converted at all (1d) or only very poorly converted (1e).^15,35 The CLG-IPL variant, which carries six amino acid substitutions, was studied here because of its shift to (S)-selectivity^18,35 and the doubly substituted variants were studied for their overall low activity levels after introducing the substitutions.^34,35 Moreover, it has been experimentally demonstrated that even a simple interchange to glycine or alanine at position 188 can have a crucial influence on the enzyme kinetics,^32,34 and therefore we considered variants with both glycine and alanine present at position 188.

The AMDase-catalyzed breakdown of compounds 1a through 1e to produce optically pure (R)- and/or (S)-products is a multistep reaction, initiated through the rate-limiting cleavage of a carboxylic group to yield an sp²-hybridized planar intermediate. This is followed by proton transfer to the intermediate from a nearby amino acid side chain. Critically, it is unclear which carboxylic group of the substrate is preferentially cleaved during this process, as this is not seen in the stereochemistry of the final product. On the basis of isotope-labeling experiments it would appear that, in both the wild-type enzyme^28,31 and the (S)-selective S36N/G74C/C188S variant of AMDase,³³ there is a strong preference for cleavage of the pro-(R) carboxylate group of the substrate. However, as described in the Methodology section, our docking simulations provided multiple possible binding modes in the active site for each substrate considered in this work, although only Mode I-like conformations such as that illustrated in Figure S1 are catalytically productive. Following from this, it can be argued that while variants with the G74C/C188S motif would produce (S)-enantiomers from the same binding mode as would produce (R)-enantiomers in the wild-type enzyme, multiple binding modes would lead to a mixture of the two enantiomers of the α-arylpropionates formed.

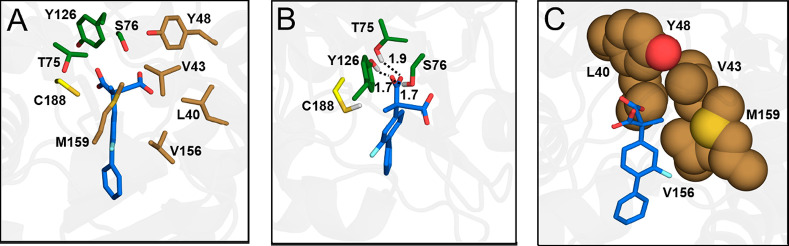
In Mode I, the pro-(S) carboxylate of the substrate is closer to Cys188 and is stabilized by hydrogen bonding interactions from the diaoxyanion hole of AMDase, while the pro-(R) carboxylate of the substrate is partly located in the hydrophobic pocket. Upon equilibration (Figure 1), the substrate rotates slightly such that the pro-(R) carboxylate is fully in the hydrophobic pocket. In contrast, in Mode II, the substrate is rotated by 180° along the z-axis, such that the pro-(R) carboxylate group is instead closer to Cys188, and the pro-(S) carboxylate group is located in the hydrophobic pocket, in contrast to what would be expected from experimental studies.^28,31,33 In addition, EVB simulations of enzyme–substrate complexes with the substrate bound in Mode II provided very high activation free energies in the range of 24–41 kcal mol^–1, further suggesting that this is not a catalytically viable binding mode, and therefore we have not considered Mode II further for detailed analysis. Finally, we independently simulate the cleavage of each of the two carboxylate groups of the substrate, resulting in two different potential decarboxylation routes per compound, allowing us to obtain computational predictions of the pro-(R) vs pro-(S) preference of AMDase toward each compound studied here.

Figure 1.

An illustration of the catalytically preferred binding mode of compound 1b, “Mode I”, after molecular dynamics equilibration in preparation for EVB simulations. (A) An overview of the AMDase binding pocket. (B) A detailed overview of the interactions between the substrate and oxyanion hole. (C) A detailed overview of substrate positioning in the hydrophobic pocket. The corresponding amino acids main chains are for simplicity excluded from the figure. As can be seen, after initial equilibration, the substrate rotates slightly compared to the initial docking pose (Figure S1) such that the pro-(S) carboxylate group of the substrate is stabilized by the dioxyanion hole, and the pro-(R) carboxylate group points toward the hydrophobic pocket. The initial docking poses for both Mode I and Mode II prior to equilibration are shown in Figure S1. We note that compound 1b is selected merely for illustration purposes, and similar binding modes were obtained for all compounds studied in this work.

The results of our EVB simulations of the decarboxylation of compounds 1a through 1e (Scheme 2) by wild-type and variants of AMDase are summarized in Table 1 and Figure 2. This table also shows the corresponding selectivities, kinetics (k_cat), and activation free energies estimated based on experimentally measured activities of each variant toward each compound studied here, where experimental data is available.^{18,20,23,34,35} From this data, it can be seen that our EVB models only show turnover of compounds 1a–c and 1e, in good agreement with experimental observables,^{18,20,23,28,34,35} whereas the activation free energies for compound 1d are very high for the cleavage of both carboxylic groups, suggesting that 1d is not transformed by the enzyme. In cases where experimental data was available to allow for activation free energies to be estimated, we typically obtain activation barriers within ∼3 kcal mol^–1 of the experimental value for cleavage of the energetically preferred carboxylate group. We consider this acceptable due to the lack of experimental data on the reference reaction, necessitating our calculations to be calibrated to density functional theory (DFT) calculations (see SI Section S2), thus introducing uncertainty. In addition, our calculations are able, with reasonable quantitative accuracy, to reproduce the experimentally observed loss of activity upon substitution of C188 to either glycine or alanine,^34,35 as observed in the G74C/C188G and G74C/C188A variants, as well as the fact that the substitution to alanine is more detrimental to the activity of the enzyme than the substitution to glycine.³²

Table 1. Calculated Activation (ΔG^‡) and Reaction Free Energies (ΔG⁰), Obtained Using the Empirical Valence Bond Approach, As Well As Relevant Corresponding Experimental Observables, For the Decarboxylation of Compounds 1a through 1e by Wild-Type AMDase and Variants^a.

system		Pro-(R)		Pro-(S)		experimental data
		ΔG‡	ΔG0	ΔG‡	ΔG0	selectivity	kcat	ΔG‡exp
1a	WT	15.6 ± 0.4	14.0 ± 0.6	26.6 ± 0.6	24.9 ± 0.6	(R)	27923	14.123
	G74C/C188G	23.1 ± 0.6	21.4 ± 0.6	30.3 ± 0.7	28.7 ± 0.6	(S)	0.00435	21.635
	CLG-IPL	26.8 ± 0.7	24.6 ± 0.7	18.1 ± 0.4	17.2 ± 0.4	(S)	3.835	17.435
1b	WT	15.9 ± 0.7	12.9 ± 0.9	20.2 ± 0.7	18.5 ± 0.8	(R)	15.1,18 3120	16.1,18 15.420
	G74C/C188G	17.9 ± 0.9	14.1 ± 0.9	23.4 ± 0.7	21.7 ± 0.7	(S)
	G74C/C188A	20.7 ± 0.9	17.2 ± 1.0	21.2 ± 0.7	18.0 ± 0.9	(S)
	CLG-IPL	16.7 ± 0.5	14.0 ± 0.7	15.8 ± 0.6	12.5 ± 0.7	(S)	23.7,18 7020	15.9,18 15.020
1c	WT	18.0 ± 0.3	17.1 ± 0.3	24.6 ± 0.9	21.5 ± 1.0	(R)	38.718	15.618
	G74C/C188G	22.7 ± 0.4	20.6 ± 0.5	26.9 ± 0.6	25.3 ± 0.7	(S)	0.07734	19.034
	CLG-IPL	22.3 ± 0.7	20.3 ± 0.7	14.4 ± 0.4	13.7 ± 0.5	(S)	4.318	16.918
1d	WT	28.3 ± 0.8	25.8 ± 0.9	32.9 ± 1.8	29.9 ± 1.7
1e	WT	18.0 ± 0.4	16.3 ± 0.5	35.4 ± 0.7	33.7 ± 0.7	(R)	0.2335	19.135
	CLG-IPL	34.4 ± 1.7	31.7 ± 1.5	17.1 ± 0.6	15.9 ± 0.6	(S)	0.5635	18.635

^aAll calculated values are averages and standard error of the mean over 30 individual EVB trajectories per system, as described in the Methodology section, and shown here are data obtained from modeling the decarboxylation of each compound through cleavage of either the pro-(R) or pro-(S) carboxylate groups. WT denotes the wild-type enzyme. Both experimental and calculated activation and reaction free energies are presented in kcal mol^–1. Shown here are also the experimentally observed selectivities for each compound, as well as the corresponding kinetics (k_cat, s^–1) and activation free energies (ΔG^‡_exp) derived from the experimentally observed activities toward each compound by each variant, as presented in refs (18, 20, 23, 34, and 35). The k_cat values were either taken directly from the literature, or were estimated by using the relationship k_cat = (specific activity × molecular weight). The calculated activation free energies were obtained from the k_cat values using transition state theory at temperature 30 °C (for ref (18)), 37 °C (for ref (35)), and 25 °C for the rest. Note that the specific activities were obtained from bar graphs provided in ref (18) and therefore the experimental kinetics and energetics are only approximate. Blank cells denote that experimental data is not available for a given system.

Figure 2.

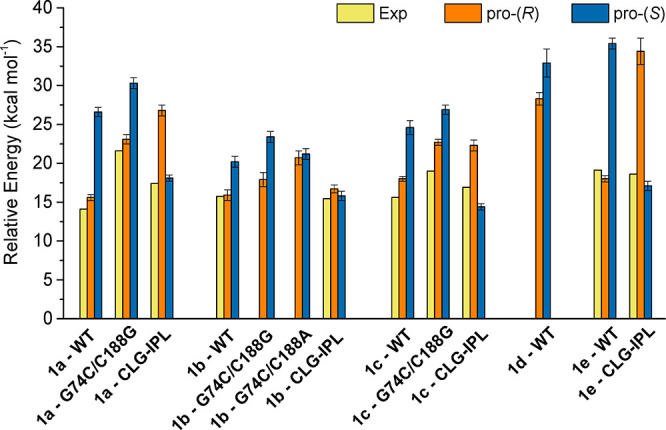
Calculated (pro-(R) and pro-(S)) and, where available, experimental (Exp) activation free energies (ΔG^‡, kcal mol^–1) for the decarboxylation of compounds 1a through 1e (Scheme 2) by wild-type (WT) AMDase and its variants. All calculated values are averages and standard error of the mean over 30 individual EVB trajectories per system, as described in the SI Methodology section. The raw data is provided in Table 1.

In terms of selectivity, it is important to bear in mind that the preference for the cleavage of the bond to a given carboxylate group in the initial decarboxylation step (Scheme 1 and Table 1) does not translate directly to the final product selectivity. That is, all reactions proceed through a common planar intermediate, with the selectivity being determined in the second step of the reaction upon reprotonation of the planar intermediate. This, in turn, is dependent on the binding pose of the substrate in the Michaelis complex, which can, in principle, be any of the three theoretical substrate binding poses to the wild-type AMDase active site as discussed in Section S3 of the SI and illustrated in Figure S7. Nevertheless, we typically observe Michaelis complexes with the substrate in Pose A (Figure 3A) when we model cleavage of the pro-(R) carboxylate group, and Pose B (Figure 3B) when we model cleavage of the pro-(S) carboxylate group. We distinguish here between binding “Modes” (the initial conformations for the equilibration, Figures 1 and S1) and “Poses” (the conformations obtained at the Michaelis complexes following EVB simulations, Figure S7). However, this distinction is purely semantic and made only for clarity of discussion. For representative structures of key stationary points for the cleavage of compounds 1a to 1e by wild-type AMDase, see Figures 3 and S8–S11.

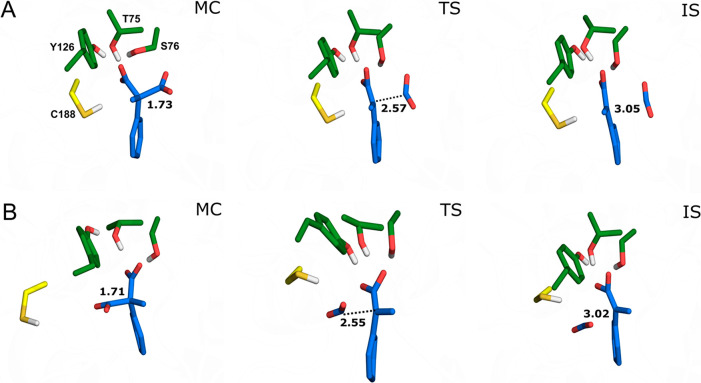
Figure 3.

Representative structures of the Michaelis complexes (MC), transition states (TS), and intermediate states (IS), for cleavage of (A) the pro-(R) and (B) the pro-(S) carboxylate groups of compound 1a by wild-type AMDase, as obtained from EVB simulations of these reactions. For the full reaction mechanism, see Scheme 1. The structures shown here are the centroids of the top ranked cluster obtained from clustering on RMSD, performed as described in the SI. The labeled C–C distances are averages at each stationary point over all trajectories (see Table S1). Corresponding representative structures of key stationary points during simulations of the wild-type AMDase catalyzed decarboxylation of compounds 1b to 1e can be found in Figures S8–S11. The color-coding of key residues follows that of Figure 1A.

For all compounds studied (Scheme 2 and Table 1), we observe preferential cleavage of the pro-(R) carboxylate by wild-type AMDase by 1.5–11 kcal mol^–1 depending on the substrate, as is to be expected due to the destabilization of the pro-(R) carboxylate by unfavorable interactions in the hydrophobic pocket³¹ (Figure 1). We note that this preference is preserved in the case of compounds 1d and 1e, which are observed to be either not (1d) or only very poorly (1e) converted by AMDase.^15,35 On the basis of the schema presented in Figure S7 and the binding poses observed in Figures 3 and S8–S11, this would be expected to lead to the (R)-product in all cases. This is in agreement with isotope-labeling experiments performed by two independent groups^28,31,33 on the (R)-selective wild-type and the (S)-selective variant S36N/G74C/C188S, which have shown that the preferred carboxylate to be cleaved is the pro-(R) carboxylate in both cases.

In the case of the G74C/C188G and G74C/C188A variants, these variants would be expected to result in the formation of pure (S)-enantiomers, due to the proton donating cysteine side chain, which is on the opposite face of the intermediate as compared to the wild type enzyme.^34,35 Once again, this stereoselective protonation is independent of which carboxylate group was cleaved beforehand. Our simulations show preferential cleavage of the pro-(R) carboxylate group (Table 1) with the Michaelis complex bound in Pose A of Figure S7, which is in agreement with the finding, that also (S)-selective AMDase variants might cleave the pro-(R) carboxylate.³³

Finally, in the case of the CLG-IPL variant (which carries six amino acid substitutions: G74C/M159L/C188G/V43I/A125P/V156L), we observe preferential cleavage of the bond to the pro-(S) carboxylate group, although as with the G74C/C188X double mutants, this would still be expected to lead to the (S)-product due to the Michaelis complex being bound in Pose B (Figure S7). We note that while no isotope labeling studies have been performed on the CLG-IPL variant, our modeled (S)-selectivity is in good agreement with the experimentally observed production of pure (S)-enatiomer products.^18,34 In addition, our calculations reproduce both the expected formation of the (S)-enantiomer and the experimental activation free energies for the decarboxylation of compounds 1a through 1c, and 1e by the CLG-IPL variant of AMDase with reasonable quantitative accuracy compared to experiment^18,20,34,35 (Table 1). We note that this is overall a particularly interesting AMDase variant, as each of the hydrophobic residues introduced into this variant (i.e., proline, leucine, isoleucine) have been shown to be very important determinants of AMDase activity.^18,34,35 Following from this, in addition to an activity increase in the decarboxylation of flurbiprofen malonate 1b, this variant showed also remarkable differences in the relative activity toward differently substituted α-aryl propionates.¹⁸

Exploring the Molecular Origin of the Observed Effects on the Activation Free Energies

While our EVB models for the reactions catalyzed by wild-type AMDase and its variants do not provide perfect quantitative agreement with experiment, due to the uncertainties involved in the energetics of the corresponding nonenzymatic reactions (see Section S2 of the SI), they nevertheless appear to provide meaningful qualitative insights into both AMDase substrate preference as well as selectivity toward cleavage of a given carboxylate group. In particular, our model only shows turnover of compounds 1a through 1c and 1e, in good agreement with experiment. We also obtain very high activation barriers for compound 1d, in agreement with the fact that decarboxylation of this substrate is not experimentally observed. In addition, experimentally, the activity of AMDase toward substrate 1e is significantly lower than toward other substrates 1a through 1c.^{18,20,23,34,35} This could be due to the presence of sterically bulky and/or flexible ethyl and isobutyl groups, which would make compounds 1d and 1e challenging to accommodate in the hydrophobic pocket of the AMDase active site, resulting in nonproductive binding modes.

In our simulations, we observe larger motions of these substrates (RMSD of up to 1.9 Å compared to the starting structure) compared to substrates such as 1a, where the substrate RMSD over the course of the simulation is 1 Å or less compared to the starting structure (see Figures S12 and S13). In addition to this, the ethyl and isobutyl groups of compounds 1d and 1e, respectively, are also highly “floppy” and fluctuate extensively across the simulation time (Figure 4), making it more challenging for these compounds to settle into a productive binding mode in the AMDase active site. In conjunction with this, in the case of compounds 1d and 1e we observe greater solvent penetration of the active site compared to the other compounds studied in this work, which will counteract the destabilizing effect of the hydrophobic pocket. Finally, the inductive effect of the alkyl substituents would be expected to destabilize the charged intermediate formed upon cleavage of either carboxylate group, thus making the corresponding decarboxylation also energetically unfavorable through a Hammond effect. Indeed, our EVB simulations (Table 1) support this at least in the case of compound 1d, as the reaction free energy for formation of this charged intermediate is significantly higher (by up to 12.9 kcal mol^–1, in the case of cleavage of the bond to the pro-(R) carboxylate group) for the decarboxylation of this compound compared to the other compounds studied in this work.

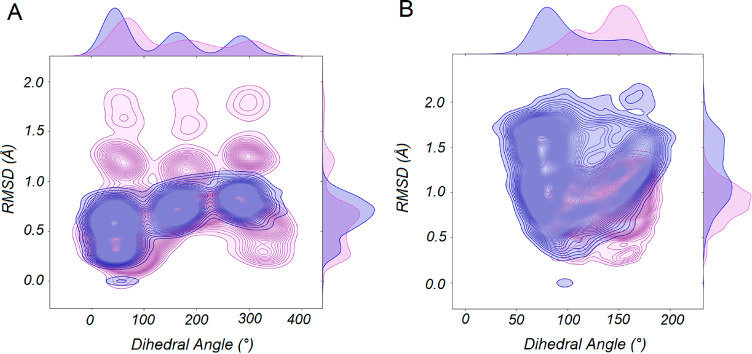
Figure 4.

Joint distribution of the dihedral angles along the ethyl and isobutyl groups of compounds (A) 1d and (B) 1e, as well as the root-mean-square deviations of the substrate (RMSD), during 30 ns molecular dynamics simulations of each compound in complex with wild-type AMDase in preparation for subsequent EVB simulations. In the case of the dihedral angles, the C1–C2–C3–C4 and C1–C2–C3–H1 atoms of the ethyl group and of isobutyl group of 1d and 1e, respectively, were chosen for analysis in each case (see Figure S2). Snapshots were taken every 100 ps of the 30 ns simulations, and thus this analysis was performed on 9000 discrete data points per plot.

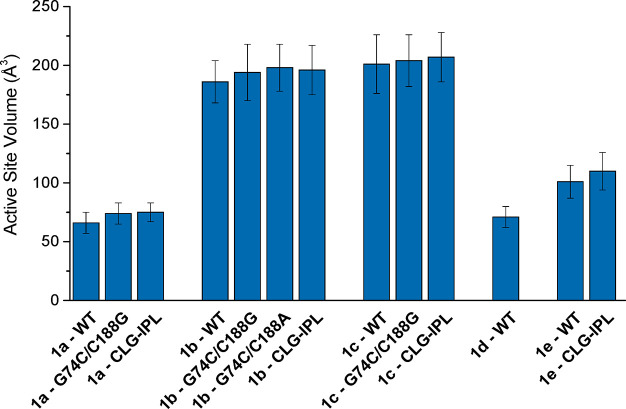
In terms of structural effects, we considered the impact of substrate binding on the active site volume of AMDase, calculated at the Michaelis complexes of wild-type AMDase and its variants in complex with each of compounds 1a through 1e. These were calculated using POcket Volume MEasurer (POVME) 3.0,⁶² as in our previous work.⁶³ As can be seen from Figure 5 and Table S2, the calculated active site volumes largely follow substrate size. That is, the smallest active site volumes are observed in the case of compounds 1a and 1d, which differ only by substitutent (methyl for 1a, ethyl for 1d). This is followed by compound 1e, which has an additional isopropyl group compared to compounds 1a, and finally the multiring substrates 1b and 1c. The standard deviations on the calculated values also increase with increasing substrate size, but only slightly compared to the absolute volumes, suggesting the active site is flexible enough to also accommodate the bulky larger substrates, without being excessively “floppy”.

Figure 5.

Average active site volumes during simulations of wild-type AMDase and its variants in complex with compounds 1b to 1e, calculated using POcket Volume MEasurer (POVME) 3.0.⁶² Data is presented as average values and standard deviations over structures obtained at the Michaelis complexes of 30 independent EVB trajaectories, and analysis was performed on 600 snapshots per system (extracting data every 10 ps of the 200 ps mapping window corresponding to the Michaelis complex of each individual EVB trajectory). The corresponding raw data is presented in Table S2.

We also considered the solvent-accessibility of the active site in our simulations, taking into account that one of the two carboxylate groups is stabilized by a dioxyanion hole while the other (more likely to be cleaved) carboxylate group is located in a hydrophobic pocket. As can be seen from Figure 6 and Table S3, there is significant variety in the number of water molecules in close proximity (within 4 Å) of the carboxylate group being cleaved, with compounds that are turned over by AMDase typically having less than one water molecule close to the reacting group at the transition state, and with this number increasing to as many as two to four (from close to none) in the case of compounds 1d and 1e which either do not or are unlikely to react in the AMDase active site. This is likely due to the high flexibility of these substrates when in complex with AMDase (Figure 4), which provides space for additional water molecules to enter the active site. We note that the number of water molecules for G74C/C188X variants is up to two, which may also contribute unfavorably to their low activity. The importance of sequestering the active site from solvent has been discussed in several prior studies,⁶⁴⁻⁶⁷ and, in particular, a clear correlation between activity loss and increased active site solvation has been shown for several enzymes.^64,66,68,69 Therefore, it is perhaps unsurprising to see yet again for AMDase increased solvent exposure of the active site in conjunction with the binding of compounds 1d and 1e, which are either not turned over at all or only poorly converted by this enzyme, respectively, despite not being significantly structurally different from other compounds that are reactive (Table 1 and Scheme 2).

Figure 6.

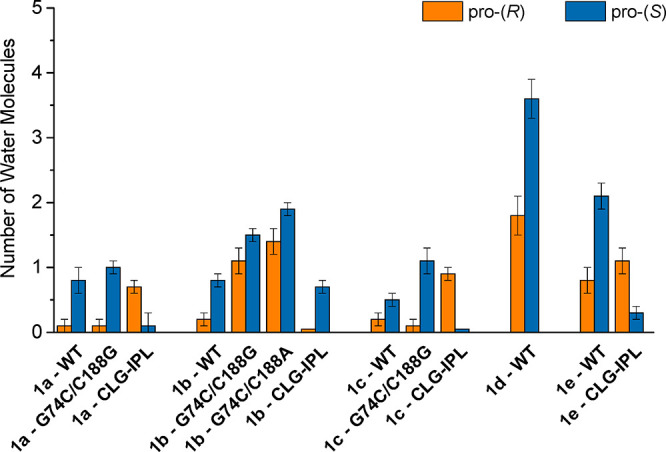
Average number of water molecules within 4 Å of the carboxylate group being cleaved (either pro-(R) or pro-(S), as relevant) during the last 25 ns of our 30 ns equilibration runs at the transition state for each reaction modeled in this work. Data is presented as average values and standard error of the mean over 30 individual trajectories per system, with data collected every 10 ps of simulation time. For the corresponding raw data associated with this figure, see Table S3.

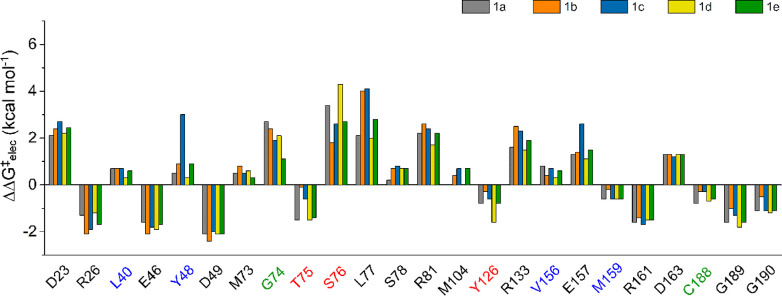
Finally, although hydrophobic effects clearly dominate in determining the selectivity of AMDase (through destabilizing one carboxylate group and sequestering the active site from solvent), we have also considered the electrostatic contributions of individual amino acids to the calculated activation free energies (Figure 7 and Table S4). This is of particular interest to us because, as discussed in Section S4 of the SI, any structural differences between the different transition states involved are minimal. This suggests that energetic differences between different substrates and variants are driven by differences caused by the initial binding pose of the substrate rather than structural effects at the transition state. Electrostatic contributions were estimated by applying the linear response approximation (LRA)^70,71 to our EVB trajectories, as in previous work.^64,66,72 From this data, it can be seen that in the case of wild-type AMDase, where the preferred carboxylate group being cleaved is the pro-(R) carboxylate, the T75 and Y126 side chains from the dioxyanion hole provide modest stabilizing contributions to the developing charge at the transition state, by stabilizing the pro-(S) carboxylate group, although this contribution is offset by a destabilizing contribution from the S76 side chain.

Figure 7.

Electrostatic contributions of individual amino acids (ΔΔG^‡_elec, kcal mol^–1) to the calculated activation free energies for the decarboxylation of compounds 1a to 1e by wild-type AMDase. Data is presented as average values over 30 individual trajectories per system. The corresponding raw data and associated standard error of the mean for each value is shown in Table S4. Amino acids forming the oxyanion hole are highlighted in red, those forming the hydrophobic pocket in blue, and the catalytically important residues at positions 74 and 188 in green. Shown here is data corresponding to the energetically preferred cleavage of the pro-(R) carboxylate group (Table 1). The corresponding figure and raw data for the cleavage of the pro-(S) carboxylate group are shown in Figure S14 and Table S5.

In the case of cleavage of the pro-(S) carboxylate group (Figure S14 and Table S5), this is inversed with stabilizing contributions from T75 and S76, offset by a destabilizing contribution from Y126. Similarly, in the case of the side chains forming the hydrophobic pocket, contributions from all residues but M159 are destabilizing to the cleavage of the pro-(R) carboxylate group (Figure 7), whereas the inverse is observed for cleavage of the pro-(S) carboxylate (Figure S14) where the residues from the hydrophobic pocket make modest stabilizing contributions to the activation free energy for the decarboxylation reaction, and the side chain of M159 is destabilizing. Overall, these contributions are in conceptual agreement with how charge development is localized in the respective transition state. However, the fact that not all residues in the dioxyanion hole or hydrophobic pocket make stabilizing or destabilizing contributions for any given system also indicates that the residue contributions are more complex than that of a simple model where one set of residues stabilizes and the other set of residues destabilizes the decarboxylation reaction.

Finally, we also examined the corresponding contributions to the reactions catalyzed by the G74C/C188G, G74C/C188A, and CLG-IPL variants (Figures S15–S18 and Tables S6–S9). We note that while there are some subtle quantitative differences compared to the wild-type enzyme, these are not significant enough to account for the large energetic differences observed between different systems, as shown in Table 1. Rather, these appear to be determined by changes in solvent penetration of the active site between different variants (due to changes in active site volumes), as well as ground-state effects, as described in the subsequent section.

Exploring Ground-State Effects on the Observed Selectivities

To probe the role of ground-state destabilization in driving AMDase catalysis, we turned to grid inhomogeneous solvation theory (GIST)^41,60 to measure the local hydrophobicity/hydrophilicity throughout the active site. In GIST (see the Methodology for further details), molecular dynamics simulations are analyzed using inhomogeneous solvation theory to produce a detailed grid map of the thermodynamic properties of water for a defined region of interest (i.e., an active site). Here, we used GIST to calculate the solvation free energy of the active site and used this as a measure of the hydrophobicity.⁶¹ This approach explicity considers both nonadditive and cooperative effects on the local hydrophobicity,^41,60,61 both of which are known to play significant roles in modulating the hydrophobicity/solvation free energy.^61,73

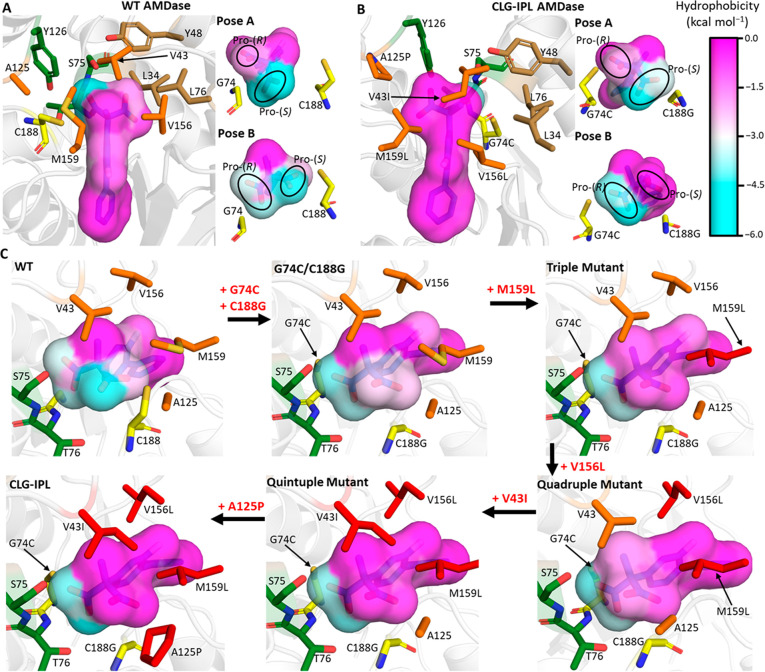
We projected the local hydrophobicity onto both possible reactive binding Poses (A and B) of compound 1b for each enzyme (Figure 8A,B for the wild-type enzyme and the CLG-IPL variant, and Figure S19 for the G74C/C188G and G74C/C188A variants). We first note that the majority of the AMDase active site is hydrophobic, which not only complements its typical range of substrates (Scheme 2) but also likely helps drive substrate binding (through the release of energetically unfavorable water molecules in the active site upon substrate binding). Focusing on the reacting carboxylate groups for wild-type AMDase in Pose A (Figure 8A), we identify clear evidence for ground-state destabilization driving AMDase catalysis, as the cleaving (pro-(R)) carboxylate group is placed into a destabilizing hydrophobic environment, while the pro-(S) carboxylate group is in a stabilizing hydrophilic environment created by the oxyanion hole residues. Consistent with our EVB simulations for wild-type AMDase (Table 1), reactivity through Pose B to cleave the pro-(S) carboxylate group appears to be significantly less favorable.

Figure 8.

Projection of the local active site hydrophobicity onto the two potentially reactive binding poses for (A) wild-type AMDase and (B) the CLG-IPL variant. For both enzyme variants, the local hydrophobicity surrounding each atom of compound 1b is colored according to the scale on the right-hand side, with more negative values indicating a more hydrophilic environment for that atom. For both variants, an overview picture is shown with the catalytic residues colored yellow, the oxyanion hole residues colored green, the (original) hydrophobic pocket residues colored brown, and residues in orange denoting those substituted to obtain the CLG-IPL variant. The smaller pictures associated with both variants describe the local hydrophobicity for either potentially reactive binding mode, with the pro-(R) and pro-(S) carboxylate groups labeled throughout. (C) Progressive construction of the second hydrophobic pocket to allow AMDase activity through binding Pose B. Each enzyme is shown in binding Pose B and colored as described in panels A and B, with the exception that point mutations accumulated along the pathway from G74C/C188G are progressively recolored from orange to red. Calculation and projection of the active site hydrophobicities onto each ligand atom was performed by determining the solvation free energy with GIST^41,60 and then using the mapping procedure described in ref (61). Equivalent projections as in panels (A) and (B) are provided in Figure S19 for the G74C/C188G and G74C/C188A AMDase variants.

In contrast to wild-type AMDase, the CLG-IPL variant was determined by our EVB simulations to preferably react through binding Pose B to cleave the pro-(S) carboxylate group (Table 1). Analysis of Figure 8B shows clear evidence of ground-state destabilization of the pro-(S) carboxylate group in binding Pose B, due to the fact that the six mutations introduced between the wild-type enzyme and the CLG-IPL variant have led to the formation of a new hydrophobic pocket, enabling the CLG-IPL variant to cleave the pro-(S) carboxylate group. Interestingly, the original hydrophobic pocket in the CLG-IPL variant does not appear to have been substantially impacted by these mutations, suggesting that binding Pose A could still be a reasonably reactive binding pose (Figure 8B). This is supported by our EVB simulations, which indicate that while cleavage of the pro-(S) carboxylate of compound 1b is energetically preferred in the CLG-IPL variant, the activation free energy for cleavage of the pro-(R) carboxylate group is only slightly higher than that obtained for cleavage of the pro-(S) carboxylate group.

The CLG-IPL variant was generated from the G74C/C188G variant, using iterative rounds of simultaneous saturation mutagenesis (SSM) experiments,³⁵ in which after each SSM round, a single additional mutation was taken forward for the next round of screening. We aimed to see if we could reproduce the formation of this new hydrophobic pocket over its engineered evolutionary pathway, and therefore performed additional MD simulations and GIST analysis on the three intermediates connecting the G74C/C188G and CLG-IPL variants, projecting the obtained results onto compound 1b in its catalytically preferred binding Pose B (Figure 8C and Table 1). Transitioning from the wild-type enzyme to the G74C/C188G variant removes the steric clash induced by the side chain of C188 with the pro-(S) carboxylate group, allowing the substrate to more optimally orient into the active site and improve the stabilization of the pro-(R) carboxyl in the oxyanion hole. The hydrophobicity of the environment surrounding the pro-(S) carboxylate group notably increases upon the introduction of the M159L subtitution to the G74C/C188G variant, which is consistent with the experimentally observed large increase in activity upon mutation (∼1700-fold increase in k_cat/K_m³⁵). The remaining substitutions from the triple mutant to the sextuple mutant (CLG-IPL) generally have more subtle impact on the substrates’ environment, including alterations in nonreacting regions of the substrate (see e.g., the transition from the triple to quadruple mutant). Nevertheless, there is a clear gradual increase of the hydrophobicity over the evolutionary trajectory, demonstrating that ground-state destabilization through increasing active site hydrophobicity is used to both control selectivity toward cleavage of a given carboxylate group and enhance AMDase catalysis. We note that, in the case of the CLG-IPL variant, the generation of this new hydrophobic pocket was not by design but rather was a serendipitous outcome of the in vitro evolution.³⁵ However, engineering such pockets is clearly an example of a strategy that can also be harnessed in a targeted fashion for the rational engineering of challenging systems such as AMDase and related enzymes, where the selectivity is not being determined at the level of steric hindrance or specific hydrogen bonding interactions (which are much easier to target through rational design).

Differences in the Ground-State Binding Pose Populations

Alongside differences in activation free energies already explored by our EVB simulations, AMDase’s stereoselectivity could (partially) be being regulated at the Michaelis complex, through the differential stabilization of the two plausible reactive binding Poses A and B. To determine the extent to which this controls AMDase selectivty, we performed well-tempered metadynamics (WT-MetaD)⁵² simulations (see the Methodology section) to calculate the relative free energy difference between the two plausible binding poses (Figure 9). Our WT-MetaD simulations used a single collective variable (CV, i.e., a reaction coordinate) to describe the relative orientation of both carboxylate groups independent of which carboxylate group is orientated in whichever direction (see the SI Methodology and Figure S3 for further details). We note that these simulations calculate the relative favorability of either binding pose (which ultimately controls stereoselectivty), and therefore do not inform on differences in binding affinities.

Figure 9.

(A) Free energy profiles describing the relative populations of either binding Pose A or B (Figure S7) for the same combinations of substrates and enzymes as used in our EVB simulations (Table 1). The catalytically preferred binding pose, based on the calculated activation free energies from our EVB simulations, is denoted with a * [colored to match the line color for each enzyme variant, as shown in the color key of panel (A)]. Profiles were obtained using well-tempered metadynamics (WT-MetaD) simulations with a single collective variable (CV1) used to describe the relative orientation of both carboxylate groups of the substrate in the active site. The approximate regions of both binding poses are indicated on each graph. (B) Representative structures (obtained from clustering, see the SI Methodology) of both binding poses and the approximate transition state (TS) between them for wild-type AMDase in complex with compound 1b. Hydrogen-bonding interactions between the substrate and oxyanion hole residues are indicated by dashed lines.

Our WT-MetaD simulations are presented in Figure 9, and show that different substrates and enzyme variants can clearly have a notable impact on the calculated free energy profiles. Regardless, in all cases, we identify two energy minima, which describe Pose A and B (Figure S7) respectively, alongside a TS barrier (located at ∼1.15 rad along the x-axis, Figure 9A) for interconversion between the two binding poses. This barrier describes the approximate point at which interactions between one carboxylate group and the oxyanion hole are breaking, while interactions between the other carboxylate group and the oxyanion hole are forming (Figure 9B). The global free energy minima for the wild-type enzyme and both doubly substituted variants are always located in binding Pose A, which is also their most catalytically favorable reactive pose based on our EVB simulations (Table 1). In contrast, in the CLG-IPL variant, this variant has its free energy minimum located in its EVB determined reactive binding pose (Pose B) for all substrates but compound 1c. However, in the case of this compound, the free energy difference between Poses A and B is only ∼1.5 kcal mol^–1, meaning that these two binding poses can easily interconvert. In fact, if we correct our EVB calculated activation free energy of 14.4 kcal mol^–1 (Table 1) by the approximate free enery required to reach Pose B from Pose A (∼1.5 kcal mol^–1), then we obtain a corrected activation free energy of 15.9 kcal mol^–1, which is in better quantitative agreement with the experimentally observed value of 16.9 kcal mol^–1.¹⁸

Our WT-MetaD results therefore suggest that the optimal reactive binding pose is also the free energy mimina (or very close in energy to it, as in CLG-IPL with compound 1c). Therefore, the preference of this enzyme for cleavage of one carboxylate group over another appears to be determined at multiple stages in the catalytic cycle: first through preferential binding of one substrate binding pose over another, then through selective destabilization of the carboxylate group that is preferentially cleaved by its placement in a solvent-excluded hydrophobic pocket which makes cleavage of this group facile, and finally, through differences in transition state stabilization for cleavage of the pro-(R) and pro-(S) carboxylate groups for each variant.

Conclusions

The unique capacity of cofactor-free decarboxylases to cleave C–C bonds under mild reaction conditions raises several questions regarding the destabilization of carbon–carbon bonds and the stabilization of an intermediary charge without the aid of an electron sink provided by an external cofactor. While its biological role has still not been clarified,² arylmalonate decarboxylase is a unique biocatalyst for the production of optically pure carboxylic acids from prochiral arylaliphatic malonic acids. However, despite increasing insight into the underlying molecular processes involved in the reaction mechanism,^2,23,30 several important questions remain unanswered. While a hydrophobic pocket in the active site was revealed to be a key determinant for AMDase activity,^30,31 the results of amino acid exchanges in this region have often been counterintuitive.^23,34,35 Similarly, restrictions on the substrate scope of this enzyme were difficult to understand.^2,15,35 It remained unclear to which extent steric effects or the reactivity of the substrate control the acceptance of different substrates by AMDase. We were particularly curious to which degree a possible “ground-state destabilization”-driven mechanism or “Circe-effect” guides substrate acceptance, activity, and selectivity.

We note that prior computational work has suggested that the enantioselectivity is determined already at substrate binding, although in some cases the energy differences between the binding modes can be small enough for the decarboxylation transition state to contribute to the enantiodiscrimination.³⁸ Experimentally, the stereoselectivity of the enzyme is believed to depend on the binding mode of the substrate, something that was suggested as early as 1992, where it was also shown that only one carboxylate group is cleaved.²⁸ In contrast, and as we also show here, the substrate spectrum is difficult to rationalize on the basis of binding alone. That is, on the one hand, a delocalized π-electron system (either an aromate or an olefin) is required on the substrate,¹⁵ indicating that transition state stabilization is crucial and that the transition state energy must not be too high for conversion. Here, the ground-state stabilization of flurbiprofen (1b) and naproxen (1c) should be similar, but we observe faster conversion of the former by several variants of AMDase,¹⁸ which reflects the higher reactivity due to the electron-withdrawing fluorine substituent. On the other hand, a slight difference such as one additional carbon atom between 1a and 1d is decisive for conversion,¹⁵ which is difficult to explain by electronic properties alone.

Our EVB simulations help us obtain molecular-level insight into the drivers for the experimentally observed substrate acceptance of AMDase. We are able to reproduce activation free energies for the AMDase-catalyzed decarboxylation of compounds 1a to 1c and 1e by all AMDase variants studied to within 3 kcal mol^–1 of the experimental value (where known). The quantitative accuracy of our calculations is limited by the lack of experimental data against which to calibrate the corresponding nonenzymatic reaction to in all cases, thus limiting us to calibration to quantum chemical calculations as outlined in the SI. However, despite this caveat, in all cases, our simulations are able to correctly predict both the product-selectivity and the substrate discrimination of AMDase. For all compounds, the preference for cleavage of the pro-(R) vs the pro-(S) carboxylate group appears to be driven by substrate positioning in the Michaelis complex, with preferential cleavage of the carboxylate group that interacts most closely with the hydrophobic pocket.

In the case of compound 1d, where no turnover is observed experimentally, our EVB calculations also yield activation free energies of >28 kcal mol^–1, depending on carboxylate group being cleaved. Further analysis of our simulations indicate that this is due to a combination of inadequate substrate binding in the active site due to the presence of the bulky ethyl group, combined with greater solvent penetration into the active site, which is unfavorable for the decarboxylation reaction, and ties in with other computational work⁶⁴⁻⁶⁸ emphasizing the importance of sequestering the active site from solvent. Similar observations are made in the case of compound 1e which is only poorly converted by AMDase.

Following from this, analysis of electrostatic effects have highlighted the complex interplay between individual stabilizing and destabilizing contributions of residues from the dioxyanion hole and hydrophobic pocket for cleavage of the pro-(R) and pro-(S) carboxylate groups. This interplay between stabilizing and destabilizing contributions from the dioxyanion hole and hydrophobic pocket reflect the fact that, in turn, enzyme catalysis can, in theory, be facilitated by either stabilization of the transition state or destabilization of the ground-state, for example by placing the charged carboxylate group to be cleaved in a hydrophobic pocket as in the case of AMDase. While this may seem counterintuitive, there exist many examples of ground-state destabilization playing an important role in catalysis by both natural⁷⁴⁻⁷⁶ and designed enzymes.⁷⁷⁻⁸¹ In particular, the concept of ground-state destabilization in catalysis of decarboxylation reactions has been discussed extensively in the case of orotidine-5′-phosphate decarboxylase (OMPDC),⁸²⁻⁸⁶ a tremendously proficient decarboxylase that provides 31 kcal mol^–1 of transition state stabilization compared to the nonenzymatic reaction.⁸⁷ Like AMDase, OMPDC is one of the few cofactor-free decarboxylases. In the case of OMPDC, evidence has been put forward that catalysis is not due to desolvation effects or ground-state destabilization, but rather due to electrostatic stabilization of the transition state for the decarboxylation reaction,^12,88,89 as well as the involvement of a ligand-gated conformational change that drives catalysis.^90,91

In the present case, our data indicate that electrostatic interactions play a clear role in stabilizing the individual transition states for the AMDase-catalyzed decarboxylation reaction. However, ground-state destabilization clearly appears to be critical for determining the selectivity between different potential transition states, leading to the observed substrate- and product-selectivities. That is, our GIST analysis provides clear evidence of AMDase’s use of ground-state destabilization (through the construction of a hydrophobic environment for the cleaving carboxylate group) to drive enzyme catalysis. We also identified a newly formed hydrophobic pocket present in the CLG-IPL variant which enables catalysis through binding Pose B. Additional simulations of variants along the evolution pathway to CLG-IPL showed a progressive optimization of the hydrophobicity of the active site toward reacting via Pose B. Our WT-MetaD simulations show that for all substrates considered in this work, the optimal reactive binding pose (determined from our EVB simulations) is in almost all cases the most populated binding pose at the Michaelis complex, or very close in energy to it. This indicates that there is already a preference for one binding pose over another at the Michaelis complexes of most variants studies here. Therefore, our simulations clearly demonstrate a role for ground-state destabilization, through creating a hydrophobic cage for the carboxylate group being cleaved, with loss of activity in the case of compounds 1d and 1e being linked to increased stabilization of the carboxylate group being cleaved through greater solvent exposure of the active site, coupled with destabilization of the resulting cationic intermediate through inductive effects.

Our simulations therefore provide clear insights into effects that can be easily manipulated in further engineering of this biocatalytically important enzyme. This is significant both for being able to rationalize the effect of amino acid substitutions on AMDase selectivity, as well as for understanding the mechanistic principles in cofactor-free enzymes that have the capacity to cleave C–C bonds with the limited catalytic set of functional groups provided by the 20 canonical amino acids. This is needed, because enzyme design efforts on this system have been, in large part, hampered by the counterintuitive effects observed after the introduction of mutations, which has negatively impacted predictability. For example, while three substitutions in the active site pocket sufficed to alter the activity of the enzyme by 900-fold,³⁴ the tremendous effect of the substitution of a valine or methionine to a leucine or isoleucine on the enzymatic activity is difficult to understand.^{18,23,34,35,92} In addition, the consequences of mutagenesis on the accommodation of water molecules in the active site or complex stabilizing and destabilizing interactions are extremely difficult to predict, which explains often observed counterintuitive effects, such as a decrease of the racemising activity after creating space in the active site, and an increase after introducing a larger hydrophobic side-chain.⁹²

In the case of AMDase, site-directed random mutagenesis is currently the engineering method of choice. The complexity of the active-site interactions demonstrated by us, particularly in the hydrophobic pocket, indicates why this is the case. Still, our results point out concrete targets for improvement, such as the putative second hydrophobic pocket identified in our GIST analysis. That is, amino acid variation based on the assumption that a sequence space defined by some positions contains improved variants has been successfully demonstrated by us and other, whereas the outcome of defined amino acid substitutions is very hard to predict.^18,23,34 However, as for example in the case of the CLG-IPL variant shown here, it appears that targeting the ground-state destabilization of the substrate by engineering of new hydrophobic cavities into which the substrate can bind could be one straightforward way to rationally manipulate the selectivity of this enzyme.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c10701.

• Additional simulation details, simulation analysis, and all EVB parameters necessary to reproduce this work (PDF)

Author Contributions

^§ These authors contributed equally.

The authors declare no competing financial interest.