Unifying Conceptual Density Functional and Valence Bond Theory: The Hardness–Softness Conundrum Associated with Protonation Reactions and Uncovering Complementary Reactivity Modes

Abstract

In this study, we address the long-standing issue—arising prominently from conceptual density functional theory (CDFT)—of the relative importance of electrostatic, i.e., “hard–hard”, versus spin-pairing, i.e., “soft–soft”, interactions in determining regiochemical preferences. We do so from a valence bond (VB) perspective and demonstrate that VB theory readily enables a clear-cut resolution of both of these contributions to the bond formation/breaking process. Our calculations indicate that appropriate local reactivity descriptors can be used to gauge the magnitude of both interactions individually, e.g., Fukui functions or HOMO/LUMO orbitals for the spin-pairing/(frontier) orbital interactions and molecular electrostatic potentials (and/or partial charges) for the electrostatic interactions. In contrast to previous reports, we find that protonation reactions cannot generally be classified as either charge- or frontier orbital-controlled; instead, our results indicate that these two bonding contributions generally interplay in more subtle patterns, only giving the impression of a clear-cut dichotomy. Finally, we demonstrate that important covalent, i.e., spin pairing, reactivity modes can be missed when only a single spin-pairing/orbital interaction descriptor is considered. This study constitutes an important step in the unification of CDFT and VB theory.

Introduction

The systematic and reliable prediction of regioselective preferences associated with chemical reactions remains an outstanding challenge in computational chemistry.¹⁻⁵ Molecules often contain a multitude of potentially reactive sites, so that manual investigation of the relative energetics of each individual transition and product state, associated with a pair of reaction partners, quickly becomes unfeasible as the size of the investigated system increases. A popular approach aimed at curtailing the explosion of potential reaction pathways involves the definition of so-called “local reactivity descriptors”.⁶⁻⁹

Ideally, a local reactivity descriptor is able to identify the sites in a reactant most prone to undergo the specific reaction type under consideration, so that less favorable alternative reaction pathways can be disregarded. As has been described throughout the literature, the practical performance and reliability of a specific reactivity descriptor is intimately connected to the nature of the interaction between the reaction partners during the bond breaking/formation process.¹⁰⁻¹³

Most general-purpose reactivity descriptors proposed so far can—roughly speaking—be classified into one of two main classes: the descriptor focuses on either so-called “hard–hard” or “soft–soft” interactions. This dichotomous approach (which emerges, among others, from the Klopman–Salem equation¹⁴ and constitutes a cornerstone of the “hard–soft acid base” (HSAB) principle,^15,16 embedded within the conceptual density functional theory (CDFT) framework¹⁷⁻²¹) has been demonstrated to work reasonably well in the limiting situations of either charge-controlled reactivity, i.e., reactions leading to formation of a purely ionic bond, or (frontier) orbital-controlled reactivity, i.e., reactions leading to formation of a purely covalent bond. For example, molecular electrostatic potential (MEP) maps are generally accepted as qualitative guides to predict the preferential binding sites of alkali metal cations, e.g., Na⁺, on organic molecules.^22,23 Fukui functions (or HOMO/LUMO amplitudes), on the other hand, have been used to rationalize regioselectivity in regular electrophilic/nucleophilic substitution reactions.²⁴

In practice, however, many—if not most—reactions are neither entirely charge nor orbital controlled but involve non-negligible contributions of both interaction types.^10,11 The magnitude and importance of the respective electrostatic/(frontier) orbital contribution for specific types of reactions has been the source of heated debates and has given rise to a considerable amount of confusion concerning the appropriateness of one or the other type of local reactivity descriptor in specific situations.^7,8,25

A case in point are protonation reactions. H⁺ is often considered as a prototypical hard electrophile, so one could naively expect that the association of this species with a reaction partner would generally be dominated by electrostatic, i.e., hard–hard, interactions. Indeed, Chattaraj et al.¹² as well as Zielinski and co-workers²⁶ found that partial charges are suitable descriptors for the protonation selectivity in a variety of (bio)organic molecules. Reiher et al., in turn, demonstrated that MEP maps²⁷ as well as electron localization functions (ELF)²⁸ are suitable descriptors to identify potential protonation sites in a number of complex catalytic systems. A similar procedure to identify H⁺ binding sites, based on Foster–Boys orbital localization, has recently been developed by the Grimme group.²⁹

At the same time, very few chemists would mistake the formed R–H bonds in protonated species for an ionic bond; these bonds are generally regarded—and depicted—as covalent ones. Since, as mentioned above, covalent bond formation is usually associated with soft–soft interactions, this realization on its own already appears to contradict the electrostatics-dominated viewpoint on protonation reactions. Furthermore, computational support for an alternative soft–soft point-of-view was very recently provided by Bettens et al., who reported that in the protonation reaction of a variety of alkaline earth and transition metal complexes, e.g., Ca(N₂)₈ and Cr(N₂)₈, the H⁺ species prefer those sites which carry the highest HOMO amplitude, i.e., they prefer to associate to the softest sites of the complex.³⁰

The seemingly conflicting assignments mentioned above raise a number of questions. First and foremost, can these different findings on the nature of the interaction associated with a generic protonation reaction be reconciled? If so, can the relative importance of orbital and charge contributions to the interaction energy between the reactants be distinguished unequivocally and estimated systematically? Finally, can the resulting conclusions for simple protonation reactions be extended to other more complex types of reactions as well?

In the present contribution, we try to answer these questions. To this end, we turn to a valence bond (VB) perspective³¹⁻³⁴ since—as we will demonstrate below—the distinction between charge- and orbital-based interactions emerges organically in this theory, which enables a lucid conceptual treatment of the issues at hand. As will be discussed, our analysis below builds yet another bridge between CDFT and VB theory.³⁵

Computational Details

Geometry optimizations of the various species as well as TD-DFT calculations^36,37 were carried out at the (U)B3LYP/def2-TZVP level of theory³⁸⁻⁴² using the Gaussian09 program.⁴³ The electrostatic potential-fitted (ESP) charge scheme was selected to quantify the atomic charges, since this charge scheme can be expected to optimally describe the electrostatic interaction upon approach of a point charge to the different sites of the considered molecules.^44,45 MEP maps were plotted on an isodensity contour of 0.001 e/au³ with the help of GaussView;⁴⁶ the scale of the maps ranges from −25 (red) to 25 kcal/mol (blue) with a negative electrostatic potential corresponding to a stabilizing interaction with a positive test charge. Inspired by the recent work by Reiher and co-workers on regiochemical descriptors for protonation reactions,²⁷ an in-house PYTHON script was also implemented to read in the “Gaussian.cube” file for pyridine and scan for minima in the electrostatic potential above the potential protonation sites (i.e., in the direction perpendicular to the molecular plane; cf. Supporting Information Section S8 for details). Condensed spin density distributions and Fukui functions were determined from a natural population (NBO) analysis.⁴⁷ Spin density contour maps were plotted at an isodensity value of 0.008 e/au.³

All VB calculations were carried out with the XMVB^48,49 software package at the density functional VB (DFVB) level of theory (which incorporates dynamic correlation)⁵⁰ with a 6-31++G** basis set and a LYP correlation functional on the optimized geometries resulting from the Gaussian09 calculations (the BOVB method⁵¹ was also tested for a selected subset of the considered systems, cf. Section S1 in the Supporting Information). [R···H]⁺ species and the associated basis functions were divided into two fragments, corresponding to molecule R and the H atom. The individual Heitler–London (covalent) and ionic structures corresponding to the bond between these two fragments were considered explicitly in the VB calculations; all other electrons were allowed to delocalize over the full R fragment. The energies associated with specific diabatic states were determined in separate DFVB calculations.

The resulting adiabatic bonding energies calculated at the DFVB/6-31++G**//(U)B3LYP/def2-TZVP level of theory agree within a reasonable margin with the corresponding bonding energies calculated at both the (U)B3LYP/def2-TZVP and the (U)B3LYP/6-31++G***//(U)B3LYP/def2-TZVP levels of theory (cf. Section S2 in the Supporting Information), underscoring the accuracy of the computational methodology used. In the geometry of the dissociated fragments, however, the DFVB/6-31++G**//(U)B3LYP/def2-TZVP calculations systematically overestimate the HL-ionic energetic spacings (as compared to the B3LYP-calculated ones and experimental values). As such, the energy spacings between the HL and the ionic structures in the dissociation limit were corrected by the deviation from the corresponding DFT values (calculated at (U)B3LYP/6-31++G***//(U)B3LYP/def2-TZVP).

Results and Discussion

Qualitative Valence Bond Model for Protonation Reactions

Let us start by introducing some key notions of valence bond theory,³¹⁻³³ needed to model a generic, idealized protonation reaction, i.e., the approach—and subsequent (barrierless) association—of an H⁺ and a (neutral) molecule.

In VB theory, the electronic wave function associated with a chemical system is represented as a superposition of (localized/diabatic) structures. For example, the H–H bond in H₂ can be represented as a mixture between a covalent structure H^•–^•H, also known as the Heitler–London (HL) structure, and two ionic structures, H⁺···H^– and ^–H···H⁺ (cf. Figure 1). In the case of H₂, the ionic structures are degenerate and high lying in energy. At infinite separation of the two H atoms in the gas phase, the energetic gap between these structures and the HL one amounts to the difference between the ionization potential of an individual H atom (I_H = 313.6 kcal/mol) and the electron affinity of an H atom (A_H = 17.4 kcal/mol), i.e., 296.2 kcal/mol³³

1

As the two H atoms approach each other, the ionic structures are stabilized due to electrostatic interaction whereas the HL structure is stabilized by the so-called “spin-pairing”—or (frontier) orbital—interaction, giving rise to the bonding energy. The electrostatic stabilization is usually somewhat stronger than the spin-pairing/covalent interaction, especially when the optimal bond length is short (cf. Coulomb’s law dependence on the point-charge distance). For molecules such as H₂, however, the sheer magnitude of the energetic gap at infinite separation is unsurmountable: the spacing between the diabatic ionic and the HL states remains significant (above 135 kcal/mol) even at the optimal bonding distance. As a consequence of this significant energy gap, the ground-state wave function of H₂ corresponds predominantly to the HL structure; detailed calculations indicate that the mixing of the ionic structures contributes only approximately 4 kcal/mol to the overall bonding energy; the remainder—approximately 100 kcal/mol—can be attributed exclusively to the spin-pairing interaction in the HL structure. As such, the H–H bond in H₂ is truly a covalent bond (Figure 1).

Figure 1.

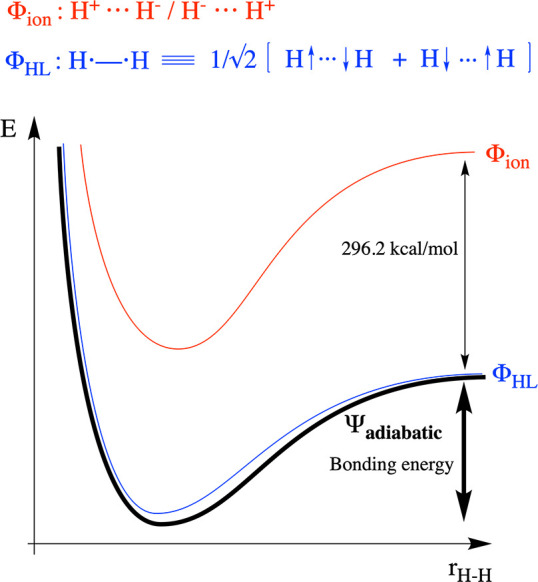
Plots of the energy evolution of the individual diabatic structures (blue and red) and the global adiabatic state (bold black) along the H···H distance (r_H–H). Note that the diabatic curves associated with the ionic structures (in red) barely contribute to the black adiabatic curve: the latter curve only deviates negligibly from the curve associated with the HL structure (blue) in the region around the optimal bonding distance.

The situation is entirely different in the case of NaCl. Analogously to the H₂ case, one can define three (main) diabatic VB structures which contribute to the ground-state wave function of NaCl. For this system, the ionic structures are no longer degenerate: at infinite separation, the Na⁺···Cl^– structure lies a mere 35 kcal/mol above the HL structure (I_Na – A_Cl); the Na^–···Cl⁺ structure lies 286 kcal/mol above the HL structure.⁵² Due to the reduced spacing between the lowest ionic structure and the HL structure (and due to the relative flatness of the curve associated with the latter; recall Na is a poor covalent binder), the ionic structure now easily crosses over the HL one and becomes the most stable diabatic state as the two atoms approach. Indeed, NaCl is unequivocally an ionic compound; its ground state consists almost exclusively of the Na⁺Cl^– structure, and as a consequence, the bond energy for this system is essentially determined by electrostatic interaction with no significant resonance contribution induced by the (spin-paired) HL structure (Figure 2).

Figure 2.

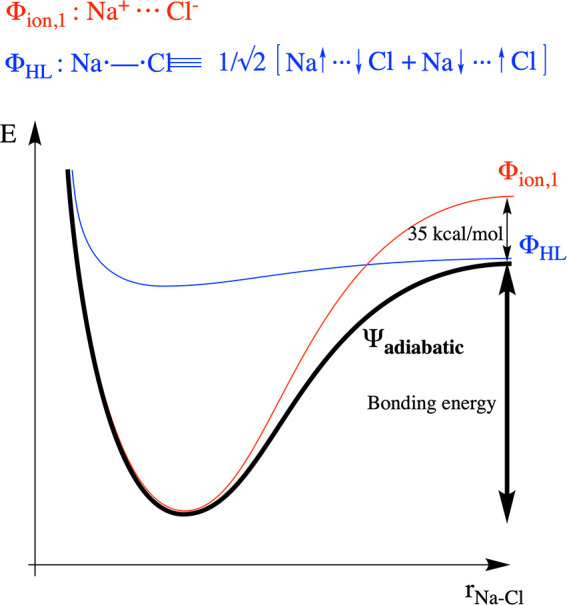
Profile of the bonding interaction and the evolution of energy of the individual diabatic curves and the global adiabatic state associated with this process for NaCl. Note that the diabatic curves associated with the Heitler–London structure (blue) does not contribute significantly to the black adiabatic curve in the region around the optimal bonding distance: the latter curve coincides with the main ionic structure. Note also that the curve associated with Φ_ion,2 is not depicted in this figure due to significant energy gap between this curve and those associated with Φ_ion,1 and Φ_HL, respectively.

Let us now turn to generic protonation reactions, i.e., mutual approach of an H⁺ and a generic (organic/inorganic) molecule R. To facilitate our discussion below we will focus exclusively on the bonding interaction between H and the R fragment; the detailed internal electronic structure of R will not be considered explicitly.

Analogously to the preceding discussions of H₂ and NaCl, one can associate three main VB structures to the [R···H]⁺ system that undergoes protonation; a HL/covalent one (R^+•–^•H) as well as two ionic ones (R: H⁺ and R²⁺ :H^–). In the HL structure, a neutral H^• approaches R^+•, so that the only significant stabilizing interaction that can emerge stems from spin pairing. In the ionic structures, a charged species (H⁺ and H^–, respectively) approaches the R/R²⁺ system, so that—depending on the polarity of the region of R/R²⁺ to which the charged species associates—either an electrostatic stabilization or a destabilization will emerge. It should be evident from the discussions above for H₂ and NaCl that the spacing at infinite separation between the HL and the ionic structures in [R···H]⁺ will determine to a significant extent the nature of the bond being formed.

The energetic separation between the main ionic structure, Φ_ion,1 (R···H⁺), and the HL structure, Φ_HL (R^+•–^•H), can be approximated as

2

with I_R being the vertical ionization potential of R and A_H⁺ the electron affinity of the proton (which is identical to the ionization potential of H, I_H).

The spacing between the HL structure and the second ionic structure, Φ_ion,2 (R²⁺ :H^–), can be approximated as

3

According to eq 2, Φ_ion,1 will be lower than Φ_HL in the dissociation limit in case the (vertical) ionization potential of R is larger than 313.6 kcal/mol, which is the ionization potential of H. For most common molecules this will not be the case. As a reference, the vertical ionization potential of H₂O amounts to 295 kcal/mol; for NH₃, this quantity amounts to 251 kcal/mol, and for ethene and pyridine, it amounts to 243 and 217 kcal/mol, respectively. As such, at infinite separation, the HL structure associated with the protonated system will generally be the lowest diabatic state. However, it should be clear that the energetic spacing between this structure and Φ_ion,1 will be on the lower side: it will range from close to 100 kcal/mol in the case of pyridine + H⁺ to a mere 20 kcal/mol in the case of H₂O + H⁺. This relatively small spacing magnitude is already an indication that the formed bond between R and H⁺ will most likely correspond to neither a purely covalent nor a purely ionic bond (vide infra).

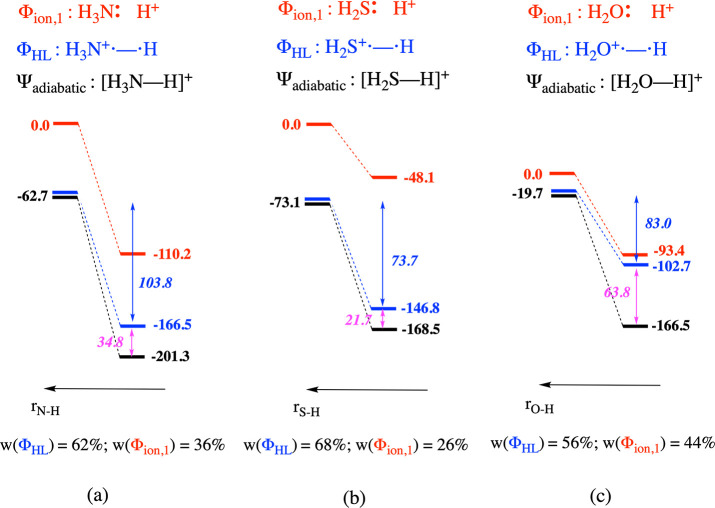
In Figure 3, a concise VB analysis of the R–H bond formation process is shown for some simple single-site model systems, i.e., H₃O⁺, NH₄⁺, and H₃S⁺. A first conclusion that can be drawn from this figure is that for each of the considered bonds the HL structure remains the main contributor to the wave function throughout the entire bond formation process (see Section S3 in the Supporting Information for full bond scanning profiles). Furthermore, the nature of the formed bond is indeed a reflection of the relative spacing of the VB structures at infinite separation, i.e., the relative magnitude of the ionization potential of NH₃, H₂S, and H₂O: the [H₂S–H]⁺ bond is the most covalent, followed by the [H₃N–H]⁺ one, and finally the [H₂O–H]⁺ bond (the weights of the HL structures in the wave functions exceed 68%, 61%, and 55%, respectively).

Figure 3.

Schematic representation of the bonding interaction and the evolution of the energy of the individual diabatic structures and the global adiabatic state associated with this process for (a) [H₃N–H]⁺, (b) [H₂S–H]⁺, and (c) [H₂O–H]⁺. Note that the curve associated with Φ_ion,2 is not depicted in this figure due to the significant energy gap between this curve and those associated with Φ_ion,1 and Φ_HL, respectively. Spin-pairing stabilization energies associated with Φ_HL upon bond formation are depicted in italics in blue; resonance energies are shown in magenta. Weights of the individual structures in the adiabatic wave function at the optimal bonding distance are shown at the bottom of each panel.

Even though our analysis indicates that the R–H bond for each of these model systems is formally covalent in nature at the optimal bonding distance, one can clearly observe that in contrast to the H₂ and NaCl bond, the bulk of the protonation/bonding energy can now no longer be attributed exclusively to either the electrostatic or the spin-pairing interaction: the resonance contribution caused by the mixing between the individual VB structures is no longer negligible. For H₃S⁺, the contribution to the full protonation energy, i.e., E(Φ_ion,1 [dissociated]) – E(Ψ_adiabatic [bonded]), by the resonance energy is still somewhat limited; it is responsible for 22 kcal/mol out of a total of 169 kcal/mol. For NH₄⁺, the contribution by the resonance energy increases slightly to 35 kcal/mol out of 201 kcal/mol; for H₃O⁺, the resonance energy accounts already for almost 40% of the protonation energy: the resonance with the electrostatics-governed ionic structure contributes 64 kcal/mol out of a total of 167 kcal/mol.

Note that the latter resonance energy value approaches 50% of the adiabatic bonding energy (147 kcal/mol), i.e., the energy lowering of the black curve in Figure 3c. As some of us have discussed before, whenever resonance becomes significant and/or starts to take over from either pure electrostatics or spin pairing as the main driver of the bonding interaction, it is arguably more appropriate to categorize the considered bond distinctively as a so-called “charge-shift” bond instead of a covalent or ionic one.⁵³⁻⁵⁶

Thus, from the results for the selected model systems in the previous paragraphs, we can already deduce that the R–H bond in protonated molecules can range from mainly covalent to predominantly charge shift in nature. This variable nature of the formed bond can logically be expected to affect the regioselectivity of proton association as soon as multisite molecules are considered (vide infra). In the case that the formed R–H bond is mainly covalent in nature, i.e., in the case that R^+•–^•H dominates the wave function outright, the spin-pairing interaction can be expected to determine the protonation/bonding energy. The site which facilitates this spin-pairing interaction the most will then be the one at which the proton will preferentially associate.

As discussed at length in a previous contribution, “the site which facilitates the spin-pairing interaction the most” in a multisite/delocalized species is determined by two factors: the intrinsic spin-pairing stabilization and the so-called “resonance penalty”.³⁵

The intrinsic spin-pairing stabilization corresponds to the stabilization associated with the individual (localized) binding sites. This quantity can be probed by considering these binding sites in isolation, e.g., the intrinsic spin-pairing stabilization associated with protonation on the O site of the extended molecule H₂N–OH can be probed by considering the corresponding stabilization induced by protonation of the localized (single-site) analogue H₂O (cf. Figure 3).

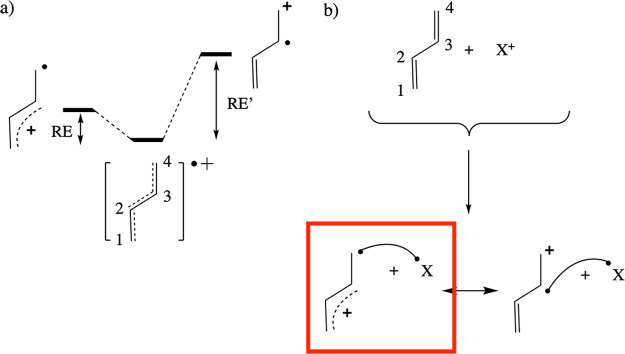
The resonance penalty for protonation reactions corresponds to the delocalization energy lost during the localization of the radical electron in R^+• on the considered association site, since such a localization is a necessary preparation step for the covalent bond formation with the ^•H to occur at this specific location (cf. Figure 4).³⁵

Figure 4.

(a) Radical cation species obtained upon oxidation of the neutral molecule R (here R = butadiene) is a mixture of several (semi)localized/diabatic structures; two such structures are shown for the example system: one in which the radical electron is localized on a terminal carbon (site 4), and one in which the radical electron is localized on a nonterminal carbon (site 3). To each of these localized structures, one can associate a resonance energy (RE), i.e., the amount of energy separating the full, delocalized species from the considered localized structure. (b) When a reaction partner X approaches molecule R and binds to it, the HL structure R^+•–^•X localizes, i.e., the radical electron in R^+• has to end up at a specific site. The energetic cost of this localization process, inherently connected to this reaction, amounts to the corresponding resonance energy (the delocalization energy lost). The lower this RE “penalty” associated with a specific site, the more favorable the spin-pairing interaction will be when the X⁺ binds at this site. For the considered butadiene example (panel a), RE < RE′ (and the intrinsic spin-pairing stabilization is equal), so that the radical electron will preferentially localize on the extremal C sites. Consequently, the HL structure for C₄–X bond formation can be expected to be lower in energy than the HL structure for C₃–X bond formation.

In practice, the site to which the smallest resonance penalty will be associated will be the site at which the spin density of the radical electron in R^+• is the highest. As stated in ref (35), the distribution of the radical electron in R^+• can alternatively be probed through analysis of the HOMO and/or the Fukui function of the uncharged species R. In many cases, the magnitudes of the respective resonance penalties will exceed the relative differences in intrinsic bond strength among different reactive sites, so that the HOMO and/or the Fukui function generally indicates the preferred association site when the spin-pairing/(frontier) orbital interaction dominates the bonding. Thus, under these conditions, the protonation reaction can be expected to adhere to the soft–soft (i.e., orbital control) paradigm we referred to in the Introduction.

In the case that the formed bond has a significant resonance contribution, i.e., the bond is mainly charge shift in nature, the spin-paring interaction will no longer determine exclusively the protonation/bonding energy; the electrostatic interaction in R: H⁺ becomes important as well now since this will provide a major contribution to the bonding (through resonance). In such a case where the electrostatics start to play a similar role as the spin pairing, H⁺ will increasingly tend to associate itself at the site of R which carries the highest negative charge, since association at this site will generally maximize the Coulombic attraction and consequently the bonding energy. Thus, the protonation reaction will increasingly adhere to the hard–hard (or charge-controlled) paradigm we outlined in the Introduction in such a case.

With this analysis we have essentially recovered the principles behind the “hard–hard/soft–soft” regioselectivity dichotomy alluded to in the Introduction, and we are able to understand why some protonation reactions will appear to adhere to the charge-control paradigm, while others may appear to adhere to the orbital-control paradigm; even though strictly speaking, most protonation reactions do not adhere to either of these limiting situations. Note that in this way we have effectively reconciled the seemingly contradicting observations mentioned in the Introduction and we have built yet another bridge between VB theory and CDFT.

As a final side remark, notice that the relative ordering of the overall protonation energies in Figure 3 agrees with the corresponding base strengths: NH₃ is known to act as a basic compound in aqueous solution, whereas H₂S does not exhibit any basic properties in such an environment, i.e., its ability to associate protons is much lower than that of H₂O. In fact, several of the factors which we have identified above as contributing to the protonation energy also emerged—in a modified form—in recent empirical studies aimed at connecting pK_a/pK_b values to CDFT descriptors (cf. Section S4 in the SI for a more in-depth discussion).⁵⁷⁻⁵⁹

Regioselectivity in Protonation Reactions: Sometimes Consideration of a Single Spin-Pairing/Orbital Interaction Descriptor Is Not Enough!

Let us now proceed from the single-site model systems, considered in the previous section, toward a couple of multisite, combined analogues, H₂NOH and H₂NSH, and probe their respective regioselectivity for protonation. Experimental data indicates that for both of these species, proton association will preferentially occur at the N site.⁶⁰ Note that these model systems were also previously considered by Chattaraj et al. to establish the proposed hardness-dominated regioselectivity of protonation reaction.¹²

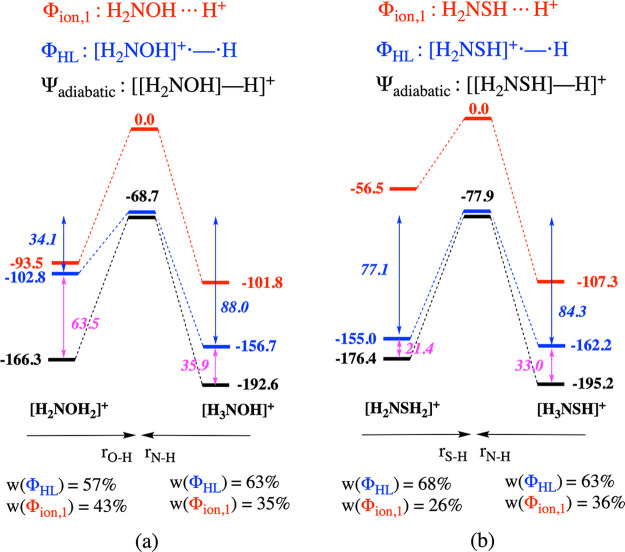
In Figure 5, concise VB analyses for the competing protonated products for both considered species, i.e., H₃N⁺OH versus H₂NOH₂⁺ and H₃N⁺SH versus H₂NSH₂⁺, are presented. Figure 6 contains an overview of some local reactivity descriptors describing, respectively, hard–hard and soft–soft interactions, i.e., the ESP partial charges, together with MEP maps, and the NBO spin densities of the oxidized species (our VB-inspired analogue of the Fukui function, vide supra,³⁵ which effectively corresponds to so-called “Parr functions”,^61,62 cf. Section S5 of the Supporting Information) on the individual sites, for the unprotonated species.

Figure 5.

Schematic representation of the bonding interaction and the energy evolution of the individual diabatic states and the global adiabatic state associated with the protonation of (a) H₂NOH and (b) H₂NSH. The actual site of protonation is indicated by the respective products at the bottom of each energy profile. Note that the profile associated with Φ_ion,2 is not depicted in this figure due to the significant energy distance between this profile and those associated with Φ_ion,1 and Φ_HL, respectively. Spin-pairing stabilization energies upon bond formation are depicted in italics in blue; resonance energies are shown in magenta. Weights of the individual structures in the adiabatic wave function at the optimal bonding distance are shown at the bottom of each panel.

Figure 6.

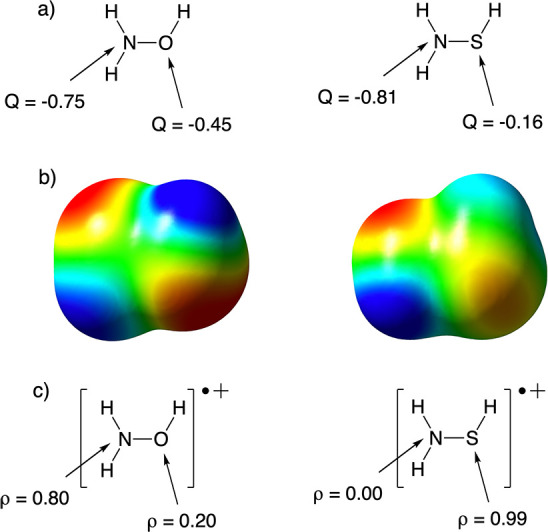
(a) ESP charges (Q) on the N and O/S sites of the neutral, unprotonated species. (b) Corresponding MEP maps (scale ranges from −25 (red) to 25 kcal/mol (blue)). (c) NBO spin densities (ρ) on the N and O/S sites of the oxidized, i.e., radical cation, species.

From a first inspection of Figure 5, it should already be clear that the nature of the considered bonds barely differ from their corresponding single-site analogues in Figure 3: the contributions of the individual VB structures is equivalent and so is the amount of resonance energy between the ionic and the HL structures. Also, the protonation energies are modified only slightly; for the respective N–H bonds formed, the protonation energy decreases 5–10 kcal/mol; for the corresponding O–H and S–H bonds, they increase by a similar magnitude. These observations should not come as a big surprise: H₂NOH and H₂NSH are generally considered as chemically localized species, so the individual sites can be expected to behave in a fairly independent manner.

Nevertheless, how do the local reactivity descriptors presented in Figure 6 fare in “predicting” the regioselectivity, i.e., do they enable the correct identification of the preferential protonation site in the multisite systems?

From Figure 6a one can conclude that for both unprotonated molecules considered, N carries the highest partial charge. Note that this is also reflected in the MEP maps (cf. Figure 6b): the region of the isosurface associated with the lone pair of N is bright red (indicating strong Coulombic attraction of a positive test charge), the hue of the region associated with the O lone pairs is quite similar, but the regions corresponding to the lone pairs of S clearly correspond to a much less negative electrostatic potential. Correspondingly, proton association at the N site leads to the biggest electrostatic stabilization in both systems (cf. the stabilization of the red curves in Figure 5).

The total protonation energy follows the same pattern, i.e., association at N is preferred for both molecules, so that one can phenomenologically conclude that the hard–hard/charge-controlled paradigm is adhered to here, which is in line with the previous findings by Chattaraj et al.¹² What is clearly revealed by our analysis however is that this regioselective preference is not the consequence of the electrostatic interactions dominating in absolute terms over the spin-pairing ones: in fact, the charge interaction is not even the main driver of the bonding in any of the four regioisomers probed!

Turning to the spin densities presented in Figure 6c, one can observe that for H₂NOH this descriptor correctly probes the relative magnitudes of the spin-pairing stabilization during bond formation. The role played by the previously mentioned resonance penalty clearly comes to the forefront in this example. For the N site, carrying the bulk of the spin density in [H₂NOH]^+•, the spin-pairing/(frontier) orbital stabilization is only somewhat lower than the corresponding intrinsic value, which—as mentioned before—can be probed from analysis of NH₄⁺ in Figure 3b (88.0 versus 103.8 kcal/mol). For the O site, carrying a spin density of only 0.2e, the spin-pairing stabilization upon protonation is dramatically reduced compared to the corresponding value obtained from H₃O⁺ (34.1 versus 83.0 kcal/mol).

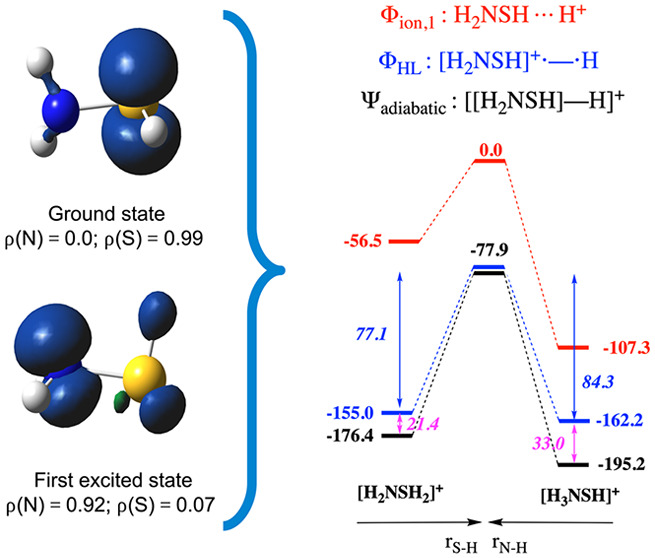
In [H₂NSH]^+•, the spin density is more or less perfectly localized on the S site (ρ = 0.99e). As such, one could expect that almost no resonance penalty would be associated with this site. Indeed, the spin-pairing stabilization associated with this site agrees almost perfectly with the corresponding intrinsic value (77.1 versus 73.7 kcal/mol; cf. Figure 3b). Consequently, one could also expect at the same time a huge resonance penalty to be associated with the N site for this compound. However, this is clearly not the case: the spin-pairing stabilization for the N site in [H₂NSH]^+• deviates only a moderate 20 kcal/mol from the corresponding intrinsic value (84.3 versus 103.8 kcal/mol).

Complementary Reactivity Modes

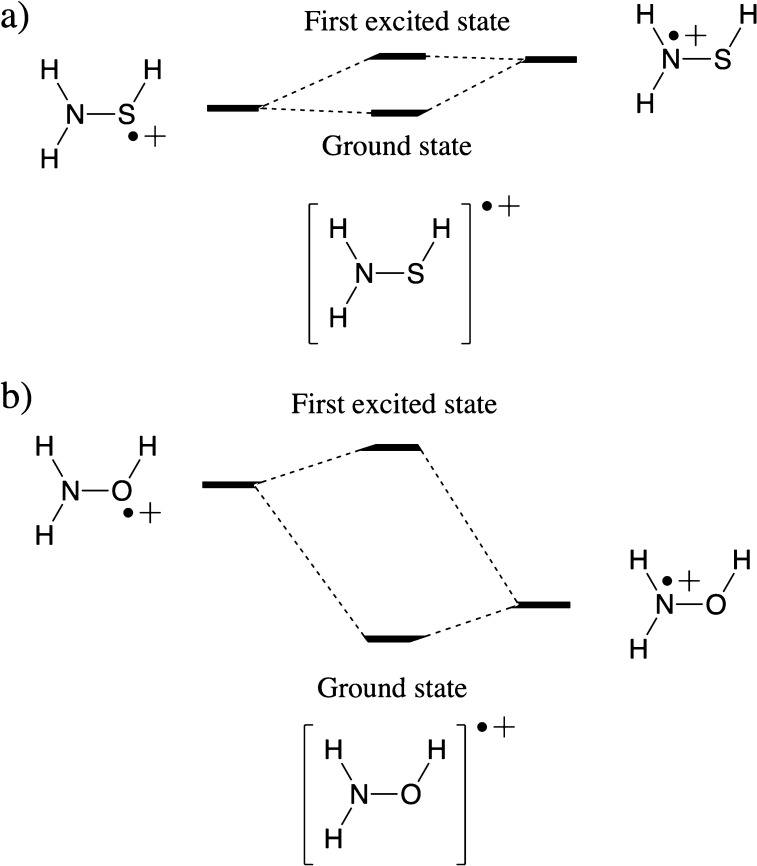
Does this seemingly anomalous resonance penalty associated with the N site constitute a failure of our model outlined above? Not quite; performing a TD-DFT calculation on the oxidized radical species [H₂NSH]^+• straightforwardly reveals the presence of an excited radical cation state a mere 0.18 eV (∼4 kcal/mol) above the ground state. Whereas the spin density in the ground state is localized on the (lone pairs of the) S moiety, the spin density in this—almost degenerate—excited state is primarily localized on the lone pair of the N moiety (ρ_N = 0.92e; cf. the spin density maps associated with both states in Figure 7a).

Figure 7.

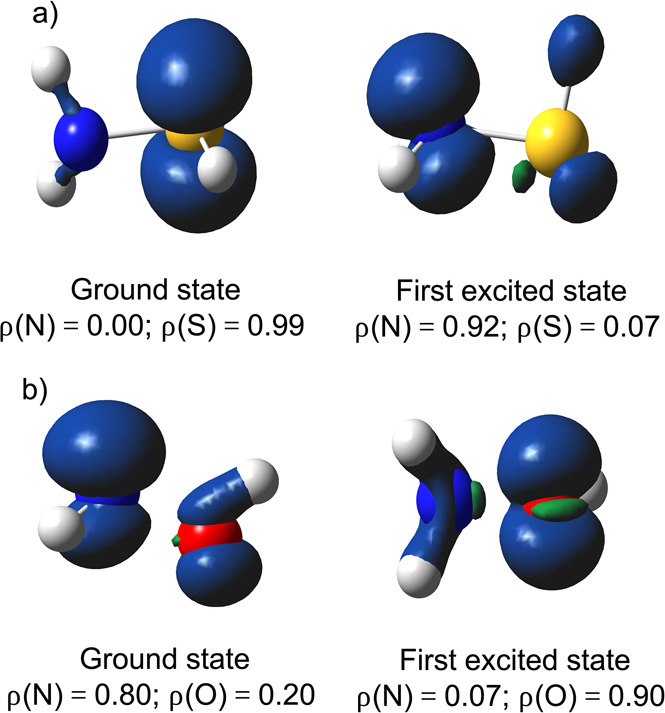
(a) Spin density contour maps for the ground and first excited state of [H₂NSH]^+•. (b) Spin density maps for the ground and first excited state of [H₂NOH]^+•. Contours have been drawn at 0.008 au. Condensed spin densities are shown at the bottom of each respective map.

The appearance of two very close lying states for the radical cation can in fact be readily anticipated from a VB analysis. Recall that in VB theory the wave function is regarded as a superposition of interacting localized structures. In the case of [H₂NSH]^+•, two main VB structures will emerge: one in which the positive charge is located on the N moiety and another in which it is located on the S moiety. From the spacing between E(Φ_ion,1) and E(Φ_HL) in the dissociated geometry for NH₃ and H₂S (i.e., A_H+ – I_R:; cf. Figure 3), one can deduce that the ionization potential for the S moiety is very similar to that for the N moiety (though slightly lower; 240 versus 251 kcal/mol). Consequently, these two localized VB structures are expected to be almost degenerate. Whether these structures interact then depends on the overlap between the local orbitals on the individual moieties. From the geometry of H₂NSH, one can readily deduce that the orbitals containing the lone pairs on S and N lie in almost orthogonal planes (cf. Figure 6), and thus, there will be almost no mixing between these two structures: [H₂NSH]^+• gives rise to two close-lying states indeed, one in which the spin density is localized on the S moiety, and another one in which the spin density is localized on the N moiety (cf. Figure 8a).

Figure 8.

Schematic representation of the mixing between two main VB structures, giving rise to the ground and first excited state, for (a) [H₂NSH]^+• and (b) [H₂NOH]^+•.

According to the discussion in the previous sections, if the two localized structures are close lying in energy, the amount of delocalization energy lost during protonation of the respective sites is more or less equal. Consequently, the resonance penalty associated with protonation of the N is less pronounced than exclusive consideration of the spin density distribution in the ground state of [H₂NSH]^+• would suggest.

In the case of [H₂NOH]^+•, the two most stable VB structures, i.e., the one in which the positive charge is located on the N moiety and the other in which the charge is located on the O moiety, are not close to degeneracy at all; the ionization potential for the N moiety is significantly lower in energy than the ionization potential for the O moiety, cf. the ionization potentials for NH₃ and H₂O (251 versus 293 kcal/mol). Consequently, we now do not end up with two almost degenerate states for [H₂NOH]^+•; there is one state that is clearly lower in energy than the other (according to our calculations, the difference amounts to 0.8 eV, i.e., 19 kcal/mol). The spin density in this ground state is mainly localized on the N moiety. The first excited state is now significantly higher in energy, and in it, the spin density is almost exclusively localized on the O moiety (cf. Figure 7b).

In summary, the analysis above indicates that indiscriminate, exclusive consideration of the ground-state spin density distribution of the oxidized species of a molecule, corresponding to the “ground-state” (nucleophilic) Fukui function in CDFT language, to infer relative propensities to undergo protonation (or more generally speaking, electrophilic attack) is not always sufficient. The appearance of low-lying excited states for this species is generally an indication of hampered mixing between equally favorable localized states. In such a case, the spin distribution in all of the low-lying states needs to be considered; failing to do so will lead to a misinterpretation of the relative soft–soft preference toward protonation/electrophilic attack within the molecule (cf. ref (12)). Note that this issue associated with near-degenerate states has previously been identified and discussed in the CDFT/frontier molecular orbital (FMO) literature, and several mitigation strategies have been explored over the years.^{63−65,65−67}

To underscore this point that low-lying excited states need to be considered as well when gauging reactive sites, an analogous analysis of HSNHSH has been included in Section S6 of the Supporting Information. As demonstrated, TD-DFT calculations reveal again two (relatively) close-lying states for the oxidized species. In this case, the localized orbitals carrying the lone pairs on the two S moieties overlap since they are aligned in space, but the localized orbital carrying the lone pair on the N moiety once more forms an almost perfect angle of 90° with them. Consequently, one of the oxidized species will have its spin delocalized over the two S moieties, while the second state is mainly localized on the N moiety. Furthermore, on twisting the S–N bonds, one can break the delocalization between the S moieties and induce delocalization/interaction between the individual S and N moieties.

Putting together everything we discussed in this section, one can now conclude that the local reactivity descriptors considered describe their respective interaction types reasonably well for the scrutinized systems: partial charges and MEP maps enable identification of the sites that lead to the biggest electrostatic stabilization, and atom-condensed spin densities of the oxidized molecule (in their ground state and potential low-lying excited states) act as a probe to gauge the magnitude of the spin-pairing stabilization.

Consideration of Excited Radical Cation States Reveals Supplementary Reactivity Modes and Some Inherent Limitations of Hard–Hard Descriptors

In this final section, we demonstrate that consideration of excited radical cation states (corresponding to “excited” Fukui functions), analogous to what was done in the previous section, is vital to uncover complementary covalent reactivity modes. In addition, we show that partial charges may sometimes overstate the trends in the electrostatic stabilization patterns upon bond formation.

Let us focus once more on a protonation reaction, this time of pyridine (C₅H₅N). Common chemical knowledge tells us that an approaching H⁺ can associate with pyridine in two distinct ways: either through interaction with the out-of-plane π-system delocalized over the ring or through interaction with the in-plane lone pair on the N moiety. Consideration of the spin density distribution in the ground state of [pyridine]^+• reveals only the in-plane lone-pair attack mode: the spin density on the N atom amounts to 0.83e, and one can unequivocally identify the shape of the lone pair in the spin density contour map (left-hand side of Figure 9). The out-of-plane π-system (covalent) attack mode is only revealed by consideration of the first excited state, which lies a negligible 0.13 eV (∼3 kcal/mol) above the ground state (note that this state ordering can be flipped straightforwardly through (captodative) substitution, cf. Section S7 in the Supporting Information).⁶⁸⁻⁷²

Figure 9.

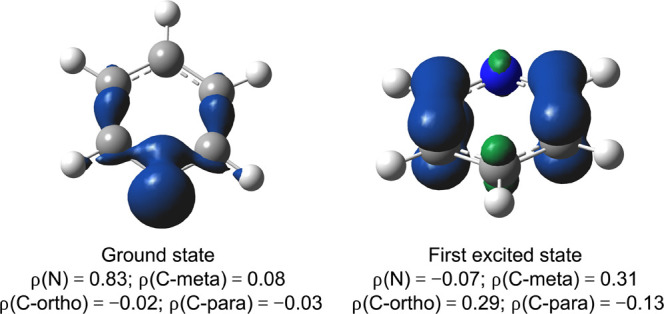
Spin density contour maps for the ground (left) and first excited state (right) of [pyridine]^+•. Contours have been drawn at 0.008 au. Condensed spin densities are shown at the bottom of each respective map.

In this excited state, the bulk of the spin density is delocalized over the C atoms (right-hand side of Figure 9). Out-of-plane attack at the para position is clearly disfavored; the spin density on this site amounts to a mere 0.13e. The density contour map does not enable a clear-cut discrimination between the ortho and the meta attack, though the calculated atom-condensed spin density values seem to suggest an ever-so-slight preference for an attack on the C atom in the meta position.

In analogy with the observations in the previous subsections, one can expect that next to the covalent, i.e., spin-pairing, bonding interaction emerging during the protonation process, there will also be a non-negligible (electrostatics-induced) resonance contribution. To probe preferential sites for the electrostatic interaction, ESP charges and MEP maps were determined once more (cf. Figure 10).

Figure 10.

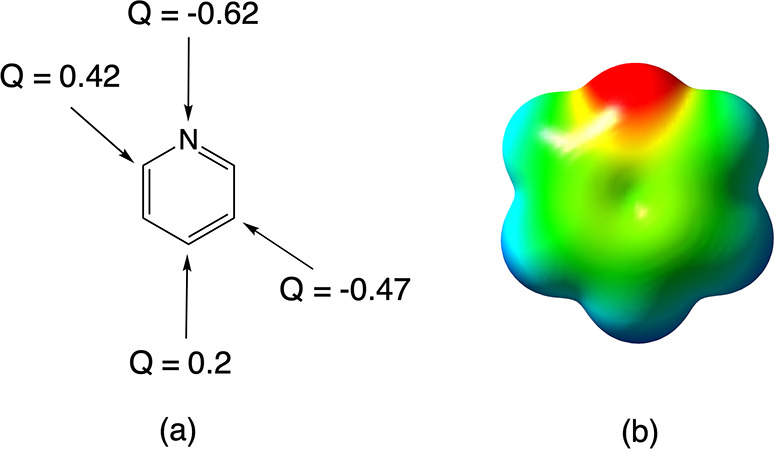
(a) ESP charges (Q) on the different potential protonation sites of pyridine. (b) Corresponding MEP maps (scale ranges from −25 (red) to 25 kcal/mol (blue)).

From this figure, one can readily identify the N site as the association site that should lead to the most electrostatic stabilization: it carries a partial charge of −0.62e, and the region associated with the in-plane lone pair at this site is colored deep red in the MEP map. For the potential C-protonation sites, the MEP maps do not reveal a discernible difference in the propensity to electrostatically stabilize an incoming proton. This uniformity also emerges from a scan for the minimal value of the electrostatic potential above each individual site (cf. Section S8 of the Supporting Information; all minima above the C atoms lie in a range between −3.9 and −6.7 kcal/mol, which are negligible differences compared to the −59.2 kcal/mol value determined for the N site).²⁷

In contrast to the near-uniformity in electrostatic stabilization among the carbon sites emerging from consideration of the electrostatic potential, the partial charges do exhibit a very strong variation: the meta sites in the ring carry a negative charge almost in line with the negative charges on the N atoms (−0.47e), whereas the para site (as well as the ortho sites), on the other hand, carries a positive charge (0.20e and 0.42e, respectively).

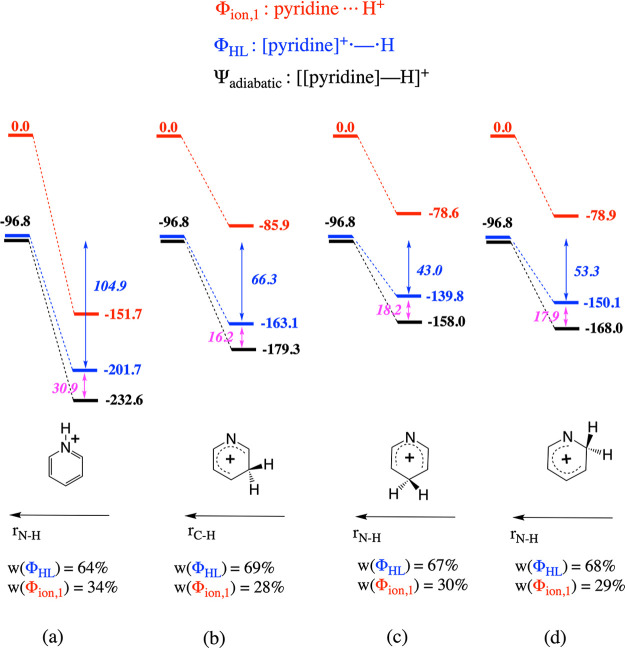
In Figure 11, a full VB analysis is presented for protonation of pyridine. The magnitudes of the spin-pairing interactions associated with the individual protonation sites follow the main trends expected from the spin density values presented in Figure 9. Reaction at the N site is clearly favored, whereas reaction at the C_ortho is the least favorable. In addition, C_meta is indeed more prone to protonation than C_para. Our DFVB results indicate that the spin-pairing interaction for protonation in the meta position is 13 kcal/mol more favorable than in the ortho position, though this is most likely an overestimation considering that our DFT calculations indicate that DFVB overshoots the overall protonation energy difference between the two sites by approximately 4–5 kcal/mol (cf. the comparison in Section S2 in the Supporting Information). In any case, the magnitude of the spin-pairing/orbital interaction difference between these sites is somewhat bigger than what the small spin density differences presented in Figure 9 appeared to suggest, indicating that even though overall, spin density distributions are a good probe to gauge soft–soft interactions, they may sometimes fail to accurately discern the more subtle fluctuations.

Figure 11.

Schematic representation of the bonding interaction and the evolution of energy of the individual diabatic states and the global adiabatic state associated with the protonation of pyridine at (a) the N site, (b) C_meta, (c) C_para, and (d) C_ortho. Note that the profile associated with Φ_ion,2 is not depicted in this figure due to the significant energy gap between this profile and those associated with Φ_ion,1 and Φ_HL, respectively. Spin-pairing stabilization energies upon bond formation are depicted in italics in blue; resonance energies are shown in magenta. Weights of the individual structures in the adiabatic wave function at the optimal bonding distance are shown at the bottom of each panel.

The electrostatic stabilization in its turn also favors unequivocally protonation of the N site (as expected), and we can observe that the variation in the impact of the electrostatics on the total protonation energy associated with the different C sites is indeed negligible: the resonance contribution to the bonds fluctuates in a very narrow range between 16.2 and 18.2 kcal/mol. This is perfectly in line with our preceding discussion of the electrostatic potential characteristics of this molecule. The partial charges thus overestimate the differences in electrostatic potential among the different C sites significantly, even though the qualitative order of the electrostatic stabilization magnitudes (as reflected by the energy lowering of the respective red profiles upon bond formation in Figure 11) is recovered by this descriptor.

Overall, this analysis underscores the limitations of local electrostatic (or hard–hard) descriptors based on point charges: focusing on a single charge in a partial charge model can be misleading—especially as the size of the considered molecule grows—due to the inherent long-range, through-space nature of Coulombic interactions (e.g., the interaction between an approaching proton and the—positively charged—ortho site of pyridine will be counteracted by the simultaneous interactions with the adjacent negatively charged meta and N sites, cf. Figure 10). As such, quantities derived from the electrostatic potentials are arguably more reliable hard–hard descriptors for these types of systems.

Finally, it should be noted that the protonation of pyridine phenomenologically adheres to the (frontier) orbital-control paradigm (i.e., the overall protonation energies follow the order of the magnitudes of the calculated spin-pairing interactions and its corresponding descriptor, cf. the spin densities presented in Figure 9), even though the electrostatic-induced resonance is once more not negligible in this molecule (especially upon attack at the N site). Thus, our results further underscore that the concepts of “hard” and “soft” are subtle and that the common dichotomous treatment found in the literature is not warranted in general.

Conclusions

In this study, we have taken a closer look at the role played by so-called “hard–hard” and “soft–soft” interactions in shaping regiochemical preferences in chemical reactivity. Focusing on a selection of protonation reactions, we demonstrated that these two interaction types contributing to chemical bonding can be readily resolved with the help of VB theory. Our results suggest that the magnitude of either of these interactions—which can best be described as “electrostatic” and “spin-pairing” interactions, respectively, within a VB context—can be probed through careful consideration of appropriate local reactivity descriptors, e.g., electrostatic potential (maps) and/or partial charges to probe the former and the spin density in the oxidized version of the reactant (cf. the Fukui function or HOMO density) to probe the latter.

In contrast to previous reports, we find that most of the investigated protonation reactions cannot be classified as either exclusively charge or (frontier) orbital controlled; instead, our results indicate that these two bonding contributions often interact in more subtle patterns, only giving the impression of a clear-cut dichotomy. As such, a hybrid approach in which descriptors of both interactions types are combined is required in order to accurately and conclusively gauge the reactivity patterns for these reactions.^10,11

Other types of reactions and bond breaking/formation processes, on the other hand, often do exhibit an unequivocally dominant interaction type (e.g., the radical reactions investigated in our previous contributions which are governed by spin-pairing interactions),^35,73 so that corresponding local reactivity descriptors can individually be used to identify and/or assess potential reactive sites and reactive modes in an exhaustive manner. In this regard, we also demonstrated that important complementary covalent, i.e., spin-pairing, reactivity modes can remain concealed when only a single spin-pairing descriptor is considered. Including spin densities of low-lying excited states of the oxidized species in the analysis alleviates this problem. Overall, this study builds additional bridges between conceptual density functional and VB theory and strengthens the conceptual basis of both.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/jacs.0c09041.

• Comparison of the BOVB results with the DFVB results for a selected subset of considered systems, comparison of the DFVB results with the DFT results and experimental data, bond scanning profiles for the protonation reactions, connection between the presented VB framework and the empirical factors identified as driving pK_a values, comparison between the VB analogue of the Fukui function and the conventional Fukui function, spin densities of the ground state and first excited state for [HSNHSH]^+•, tuning of the state ordering through captodative substitution, utility to scan for a minimum electrostatic potential value, and geometries and electronic energies for all the calculated systems (PDF)

The authors declare no competing financial interest.