Giant Transition-State Quasiparticle Spin-Hall Effect in an Exchange-Spin-Split Superconductor Detected by Nonlocal Magnon Spin Transport

Abstract

Although recent experiments and theories have shown a variety of exotic transport properties of nonequilibrium quasiparticles (QPs) in superconductor (SC)-based devices with either Zeeman or exchange spin-splitting, how a QP interplays with magnon spin currents remains elusive. Here, using nonlocal magnon spin-transport devices where a singlet SC (Nb) on top of a ferrimagnetic insulator (Y₃Fe₅O₁₂) serves as a magnon spin detector, we demonstrate that the conversion efficiency of magnon spin to QP charge via inverse spin-Hall effect (iSHE) in such an exchange-spin-split SC can be greatly enhanced by up to 3 orders of magnitude compared with that in the normal state, particularly when its interface superconducting gap matches the magnon spin accumulation. Through systematic measurements by varying the current density and SC thickness, we identify that superconducting coherence peaks and exchange spin-splitting of the QP density-of-states, yielding a larger spin excitation while retaining a modest QP charge-imbalance relaxation, are responsible for the giant QP iSHE. The latter exchange-field-modified QP relaxation is experimentally proved by spatially resolved measurements with varying the separation of electrical contacts on the spin-split Nb.

Over the past decade, it has been shown that the combination of superconductivity with spintronics leads to a variety of phenomena that do not exist separately.¹⁻⁸ In particular, recent discovery and progress in the proximity generation and control of spin-polarized triplet Cooper pairs¹⁻³ at carefully engineered superconductor (SC)/ferromagnet (FM) interfaces in equilibrium allow for the development of nondissipative spin-based logic and memory technologies.

Besides triplet Cooper pairs, nonequilibrium quasiparticles (QPs) in a spin-split SC⁴⁻⁶ have also raised considerable interest. This is because their exotic properties resulting from the mutual coupling between different nonequilibrium imbalances of spin, charge, heat, and spin-heat can greatly enhance spintronics functionality.⁵ For example, the coupling of spin and heat imbalances gives rise to long-range QP spin signals as observed in Al-based nonlocal spin valves⁹⁻¹¹ with a Zeeman spin-splitting field. In addition, a temperature gradient between a normal metal (NM) and a spin-split SC separated by a tunnel barrier induces a pure QP spin current¹² without an accompanying net charge current, analogous to the spin-dependent Seebeck tunneling.^13,14 Substituting the NM by a FM, one can achieve large (spin-dependent) thermoelectric currents^15,16 far beyond those commonly found in all-metallic structures.

Magnon spintronics¹⁷⁻¹⁹ has been an emerging approach toward computing devices in which magnons, the quanta of spin waves, are used to carry, transport, and process spin information instead of conduction electrons. Especially in the low-damping ferrimagnetic insulator yttrium–iron–garnet (Y₃Fe₅O₁₂ = YIG),²⁰ a magnon-carried spin current can propagate over extremely long distances (centimeters at best), and it is free from ohmic dissipation due to the absence of electrons in motion.¹⁷⁻¹⁹ Despite many recent advances¹⁷⁻¹⁹ in this research field, how magnon spin current interacts with and is converted to QP spin and charge currents in a spin-split SC is yet to be investigated.

In this paper, we report three key aspects of the conversion behavior of magnon spin to QP charge via the inverse spin-Hall effect (iSHE) in an exchange-spin-split SC (Nb), directly probed by nonlocal magnon spin-transport¹⁸ (Figure 1a). First, the iSHE in the superconducting state of Nb becomes up to 3 orders of magnitude greater than in the normal state. Second, this enhancement appears only in the vicinity of the superconducting transition temperature T_c when the magnon spin current has an energy comparable to the (singlet) superconducting gap 2Δ^SC of Nb (Figure 1a). Lastly, its characteristic dependence on a dc current density J_dc and the Nb thickness t_Nb indicates that a singularity near the gap edge and a spin-splitting field are both essential for the giant transition-state QP iSHE, the latter of which is experimentally confirmed by performing spatial profiling of the transition-state enhancement by varying the separation distance of electrical contacts on the spin-split Nb layer.

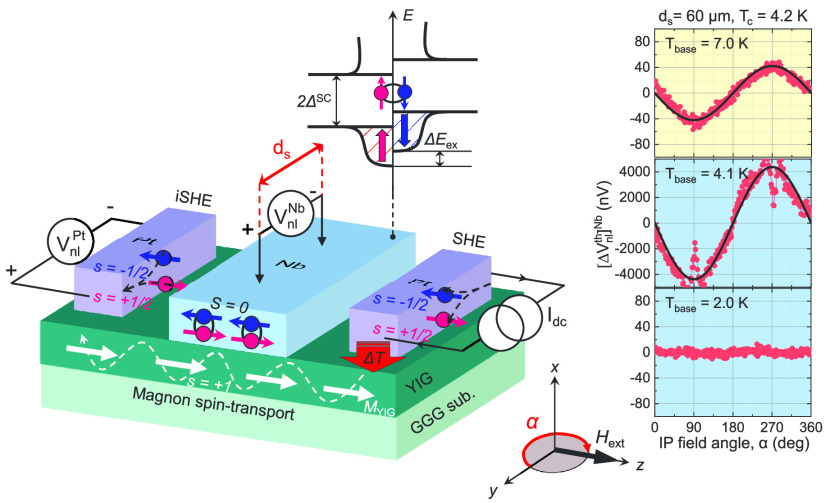
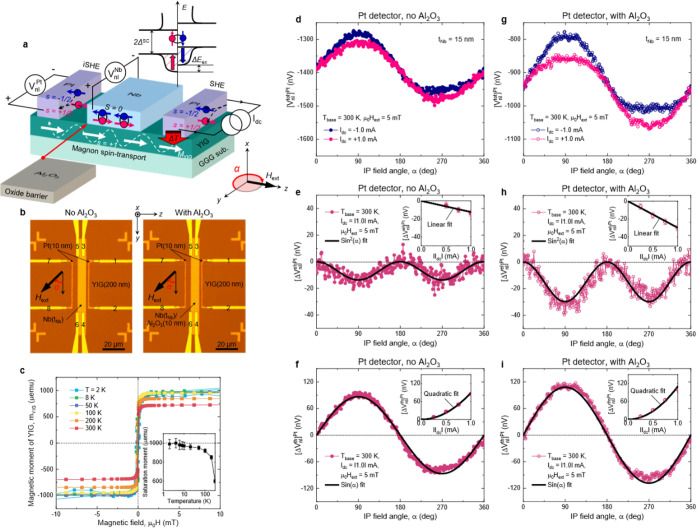
Figure 1.

Nonlocal magnon spin-transport device with a spin-split superconductor. (a) Schematic illustration of the device layout and measurement configuration. When a dc charge current I_dc is applied to the right Pt injector, either electrically or thermally driven magnons accumulate in the ferrimagnetic insulator Y₃Fe₅O₁₂ (YIG) underneath and diffuse toward the left Pt detector. These magnon (s = +1) currents are then absorbed by the left Pt detector, resulting in the electron spin accumulation that is, in turn, converted to a nonlocal charge voltage V_nl^Ptvia the inverse spin-Hall effect (iSHE). Such a conversion process also occurs for the central Nb and thereby V_nl. However, the conversion efficiency changes dramatically when turning superconducting due to the development of quasiparticle (QP) density-of-states with exchange spin-splitting ΔE_ex. Note that in contrast to spin-singlet (S = 0) Cooper pairs in a coherent ground state, the excited QPs can carry spin angular momentum in the superconducting state. (b) Optical micrographs of the fabricated devices with and without a 10-nm-thick Al₂O₃ spin-blocking layer. (c) In-plane (IP) magnetization hysteresis m(H) curves of a bare YIG film, measured at a temperature T of 2–300 K. The inset summarizes the T dependence of the saturation magnetic moment. (d) IP magnetic-field-angle α dependence of nonlocal total voltages [V_nl^tot]^Pt measured with the Pt detector at I_dc = ±1.0 mA at 300 K, for the t_Nb = 15 nm device. From these, electrically ([ΔV_nl]^Pt in e) and thermally ([ΔV_nl^th]^Pt in f) driven magnon components are separated (see main text). Black solid lines in e and f correspond respectively to sin²(α) and sin(α) fits. The estimated magnitude of [ΔV_nl]^Pt ([ΔV_nl^th]^Pt) is plotted as a function of |I_dc| in the inset of e (f), where the black solid line represents a linear fit (quadratic fit). (g–i) Data equivalent to d–f but for the control device with the Al₂O₃ spin-blocking layer.

Results and Discussion

The nonlocal magnon spin-transport devices (Figure 1b) we study consist of two identical Pt electrodes and a central Nb layer on top of 200-nm-thick YIG films, which are liquid-phase epitaxially grown on a (111)-oriented single-crystalline gadolinium gallium garnet (Gd₃Ga₅O₁₂, GGG) wafer (see Methods). Control devices, in which a 10-nm-thick Al₂O₃ spin-blocking layer is inserted between Nb and YIG in an otherwise identical structure, are also prepared for comparison (Figure 1b). Here, we send a dc current I_dc through one Pt (using leads 1 and 2 in Figure 1b) while measuring the in-plane (IP) magnetic-field-angle α dependence of the nonlocal open-circuit voltages [V_nl^Pt(α), V_nl(α)] using both the other Pt (leads 7 and 8) and the central Nb (leads 3 and 4). Note that we apply an external in-plane magnetic field μ₀H_ext of 5 mT, larger than the coercive field of YIG (Figure 1c), to fully align its magnetization M_YIG along the field direction. α is defined as the relative angle of μ₀H_ext (//M_YIG) to the long axis of two Pt electrodes, which are collinear.

As schematically illustrated in Figure 1a, the right Pt acts as a NM injector of magnon spin current across the Pt/YIG interface via either electron-mediated SHE (charge-to-spin conversion)²¹ or spin Seebeck effect (SSE) (heat-to-spin conversion)²² due to the accompanying Joule heating [ΔT ∝ (I_dc)²]. The left Pt serves as an NM detector of the magnon spin current, diffusing through a YIG channel, via electron-mediated iSHE (spin-to-charge conversion), whereas in the same device, the middle Nb functions as an exchange-spin-split SC detector of the diffusive magnon current via QP-mediated iSHE below T_c.⁸

The total voltage measured across the detector is given by V_nl^tot = ΔV_nl + ΔV_nl^th + V₀, where ΔV_nl and ΔV_nl^th are proportional to the magnon spin current and accumulation created electrically (SHE ∝ I_dc)²¹ and thermally [SSE ∝ (I_dc)²],²² respectively. These electrical and thermal magnon currents can be separated straightforwardly by reversing the polarity of I_dc, allowing us to determine the magnitude of each component based on their distinctive angular dependences;¹⁸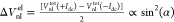 and 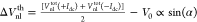. V₀ is an offset voltage that is independent of the magnon spin-transport.

The typical result of such a measurement using the Pt detector at 300 K is displayed in Figure 1d–i, for the t_Nb = 15 nm devices with and without the Al₂O₃ spin-blocking layer. This evidences that both electrically (Figure 1e and h) and thermally (Figure 1f and i) excited magnons transport spin angular momentum over a long distance of 15 μm at room temperature, which is consistent with the original work.¹⁸ We note that from reference devices having the Pt injector/detector only, the room-temperature magnon spin-diffusion length l_sd^m of the YIG is estimated to be around 11(9) μm for the electrically (thermally) driven magnons (Supplementary Section 1). The transporting spin current is absorbed by the middle Nb to a certain extent, given by the difference between the signals with versus without the Al₂O₃ insertion (see Supplementary Section 2 for the quantitative analysis).

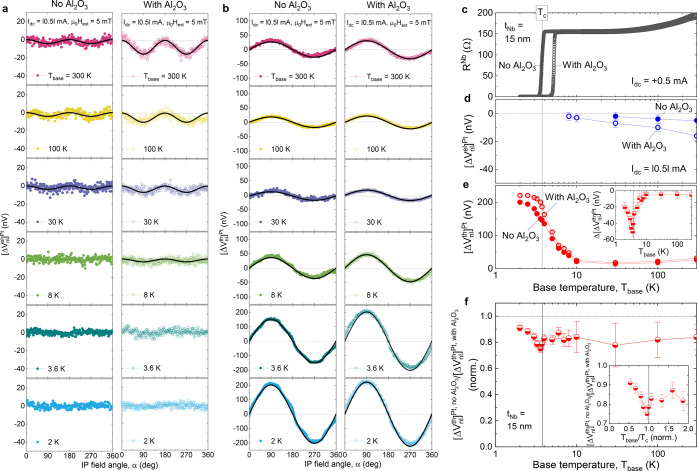
Figure 2a,b,d,e show the temperature T evolution of ΔV_nl^el(α) and ΔV_nl(α) for the t_Nb = 15 nm devices measured by the Pt detector at a fixed I_dc = |0.5| mA (J_dc = |3.3| MA/cm²). As summarized in Figure 2f and g, ⌈ΔV_nl^el⌉^Pt diminishes with decreasing the base temperature T_base, and it almost vanishes for T_base ≤ 10 K, whereas ⌈ΔV_nl⌉^Pt significantly increases at low T_base. Such distinct T_base-dependences are in line with previous experiments^23,24 and theoretical considerations^25,26 that the injection mechanisms for electrical and thermal magnons across the Pt/YIG interface (parametrized by the effective spin conductance and the interface spin Seebeck coefficient, respectively) differ fundamentally. Furthermore, the energy-dependent magnon diffusion and relaxation of the YIG channel may play a role in the transport process.^27,28

Figure 2.

Temperature dependence of nonlocal signals measured by the Pt detector. (a) Electrically driven nonlocal voltages ⌈ΔV_nl^el(α)⌉^Pt as a function of IP field angle α for the t_Nb = 15 nm devices with and without the Al₂O₃ layer, taken at various base temperatures T_base. The black solid lines are sin²(α) fits. (b) Data equivalent to a but for thermally driven nonlocal voltages ⌈ΔV_nl(α)⌉^Pt, along with sin(α) fits (black solid lines). In these measurements, I_dc is fixed at |0.5| mA and the magnetic field μ₀H_ext at 5 mT. (c) Nb resistance R^Nbversus T_base plots for the Al₂O₃-absent and Al₂O₃-present devices, measured using a four-terminal current–voltage method (using leads 3, 4, 5, 6 in Figure 1b) while applying I_dc = 0.5 mA to the Pt injector. A strong suppression of the superconducting transition temperature T_c in the absence of the Al₂O₃ layer (about 1.5 K, at least 1 order of magnitude larger than expected from stray fields of YIG, Supplementary Section 3) indicates the inverse proximity effect;³³ that is, the propagation of YIG-induced exchange spin-splitting into the adjacent Nb. The vertical solid line indicates the superconducting transition temperature T_c of the Nb of the Al₂O₃-absent device. Extracted magnitudes of ⌈ΔV_nl^el⌉^Pt (d) and ⌈ΔV_nl⌉^Pt (e) as a function of T_base for the Al₂O₃-absent and Al₂O₃-present devices. In the inset of e, Δ⌈ΔV_nl^th(T_base)⌉^Pt = ⌈ΔV_nl(T_base)⌉^{Pt,no Al₂O₃} – ⌈ΔV_nl^th(T_base)⌉^{Pt,with Al₂O₃} is also shown. (f) ⌈ΔV_l⌉^{Pt,no Al₂O₃}/⌈ΔV_nl^th⌉^{Pt,with Al₂O₃} as a function of T_base and T_base/T_c (inset).

We below focus on the nonlocal signal from the thermally generated magnons (ΔV_nl^th) since it remains sufficiently large at low T_base for allowing a reliable analysis across T_c. In Figure 2f, we first plot the T_base dependence of ⌈ΔV_nl⌉^Pt without the Al₂O₃ layer normalized by that with the Al₂O₃ layer; ⌈ΔV_nl^th⌉^{Pt,no Al₂O₃}/⌈ΔV_nl⌉^{Pt,with Al₂O₃}. This value reflects how much the magnon spin current is absorbed by the Nb layer. Notably, ⌈ΔV_nl^th⌉^{Pt,no Al₂O₃}/⌈ΔV_nl⌉^{Pt,with Al₂O₃} drops abruptly right below T_c (extracted from the Nb resistance R^Nbversus T_base plot of Figure 2c), and then it rises progressively as the Nb enters deep into the superconducting state, resulting in a downturn at T_base/T_c ≈ 0.95 (inset of Figure 2f). Such a nontrivial behavior is compatible with recent theoretical predictions^29,30 and experimental reports^31,32 on ferromagnetic insulator (FMI)/SC structures, where (spin-singlet) Cooper pairs from the SC cannot leak into the FMI even if the exchange spin-splitting can still penetrate the SC.⁴ So rather well-developed coherence peaks of the QP density-of-states (DOS) at the FMI/SC interface⁵ are accessible to the transporting spin current. This gives rise to an anomalous enhancement of spin absorption by the adjacent SC near T_c. Note that in contrast, for metallic/conducting FM/SC proximity-coupled structures,³³ 2Δ^SC is significantly suppressed at the FM/SC interface, and the superconducting coherence peak effect is therefore fading away.^29,34−38 A slight rise in ⌈ΔV_nl^th⌉^{Pt,no Al₂O₃}/⌈ΔV_nl⌉^{Pt,with Al₂O₃} far below T_c (inset of Figure 2f) is also explained by the development of a (singlet) superconducting gap and the freeze out of the QP population at a lower T_base.^29,34−38

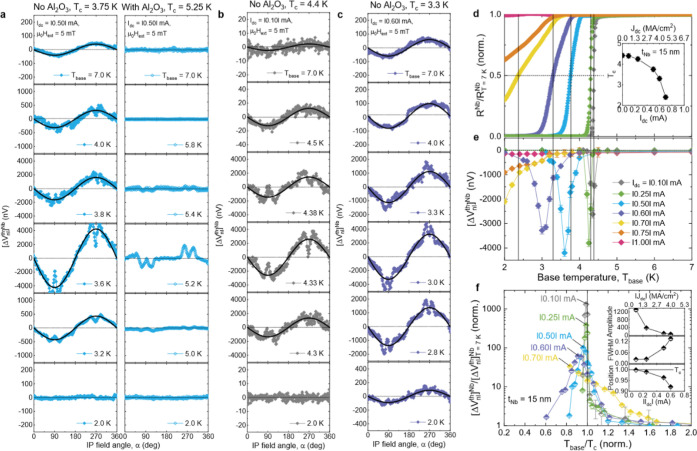
Next, using the Nb detector in the same device, we confirm the above interpretation and demonstrate that the conversion efficiency of magnon spin to QP charge can be dramatically enhanced in the vicinity of T_c. Figure 3a shows the thermally driven nonlocal signal ⌈ΔV_nl^th⌉^Nb for the t_Nb = 15 nm devices with and without the Al₂O₃ (spin-blocking) layer at various T_base around the superconducting transition of the Nb. In the normal state (T_base/T_c > 1), a negative ⌈ΔV_nl⌉^Nb(<0) with several tens of nanovolts is clearly observed. Given ⌈ΔV_nl^th⌉^Pt > 0 (see Figure 2b), this evidences that Nb and Pt have opposite signs in the spin-Hall angle θ_SH, which is in agreement with recent theoretical and experimental studies.³⁸⁻⁴⁰ Intriguingly, upon entering the superconducting state (T_base/T_c < 1), a significant enhancement of ⌈ΔV_nl⌉^Nb up to a few microvolts appears immediately below T_c (T_base/T_c ≈ 0.96), and then it decays toward zero deep in the superconducting state. We note that there exist visible dips in ⌈ΔV_nl^th⌉^Nb at α ≈ 90° and 270° near T_c (Figure 3a), which are also present for the Al₂O₃-inserted control device (Figure 3b) and thus have nothing to do with the magnon spin-transport and QP iSHE. Similar spin-independent signals have been observed in local measurements on NbN/YIG³² and MoGe/YIG⁴¹ bilayers as well and are explained in terms of an Abrikosov-vortex-flow-driven Hall effect under a transverse magnetic field that is close to the upper critical field μ₀H_c2 of (type-II) SC.

Figure 3.

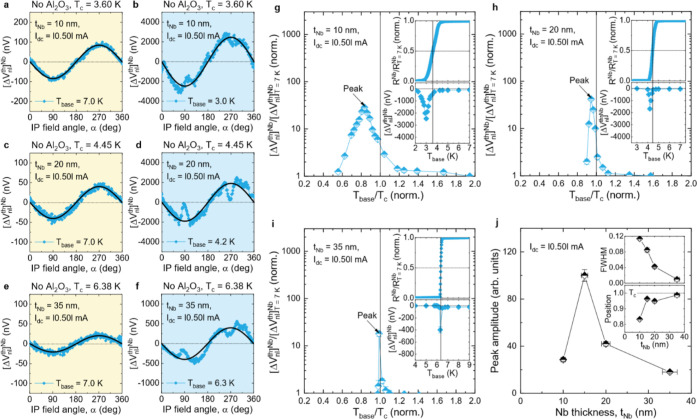
Giant enhancement of nonlocal signals in the transition state of the Nb detector. (a) Thermally driven nonlocal voltages ⌈ΔV_nl^th(α)⌉^Nb as a function of IP field angle α for the t_Nb = 15 nm devices with and without the Al₂O₃ layer, taken at I_dc = |0.5| mA around the T_c of the Nb. The black solid lines are sin(α) fits. (b and c) Data equivalent to a but at I_dc = |0.10| mA (b) and I_dc = |0.60| mA (c), respectively, for the Al₂O₃-absent device. (d) Normalized Nb resistance R^Nb/R_T=7Kversus T_base plots for the Al₂O₃-absent device, measured using a four-terminal current–voltage method (using leads 3, 4, 5, 6 in Figure 1b) with varying I_dc in the Pt injector. The critical temperature T_c is defined as the point where R^Nb = 0.5R_T=7K^Nb. The inset summarizes the measured T_c as a function of I_dc (or J_dc). (e) Estimated magnitude of ⌈ΔV_nl⌉^Nb as a function of T_base for the Al₂O₃-absent device. (f) ⌈ΔV_nl^th⌉^Nb/⌈ΔV_nl⌉_T=7K^Nbversus T_base/T_c plot. The inset displays the |I_dc| (or |J_dc|) dependence of the peak amplitude, width, and position.

To examine the effect of heating power, we measure the T_base dependence of ⌈ΔV_nl^th⌉^Nb (Figure 3b and c) and the normalized R^Nb/R_T=7K (Figure 3d) at various I_dc. As I_dc increases, T_c of the Nb detector is systematically reduced and the transition width becomes broad (Figure 3d). We note that the stronger decay of T_c for I_dc > 0.5 mA is likely caused by the greater injection/excitation of spin-polarized QPs into the Nb detector (see Supplementary Section 3 for a comparison analysis of T_c data between the Al₂O₃-absent and Al₂O₃-present devices). Accordingly, not only a peak of the ⌈ΔV_nl^th⌉^Nb enhancement shifts to a low T_base, but the enhancement regime widens (Figure 3e). For I_dc ≥ |0.7| mA (J_dc ≥ |4.2| MA/cm²), the Nb does not turn fully superconducting down to the lowest T_base = 2 K studied (inset of Figure 3d). The corresponding ⌈ΔV_nl⌉^Nb then remains nonzero at 2 K and is larger than the normal state value (Figure 3e). For a quantitative analysis, we plot the normalized voltage ⌈ΔV_nl^th⌉^Nb/⌈ΔV_nl⌉_T=7K^Nb as a function of the normalized temperature T_base/T_c in Figure 3f. We then find that the transition-state enhancement of ⌈ΔV_nl⌉^Nb/⌈ΔV_nl^th⌉_T=7K can reach up to 3 orders of magnitude at the smallest I_dc = |0.1| mA (J_dc = |0.6| MA/cm²). With increasing I_dc, its peak amplitude decays rapidly, the full-width-at-half-maximum (fwhm) broadens, and the peak is positioned farther away from T_c (inset of Figure 3f). These results ensure that the depressed superconductivity with increasing the heating power has a negative effect on the transition-state enhancement of the QP iSHE.

We perform similar measurements on an additional set of devices with different t_Nb (Figure 4a–f), comparable to or smaller than the superconducting coherence length ξ_SC, and thereby strong t_Nb-dependent superconducting properties (e.g., QP band structure and DOS). Since thin Nb films usually contain a larger amount of grain boundaries, defects, and disorders from the structural inhomogeneity near the growth interface than thick bulk Nb,^42,43 the associated scattering effectively weakens electron–electron and electron–phonon interactions and therefore the smearing-out effect of the QP DOS around the gap edge.⁴⁴ One would predict a greater enhancement of the QP iSHE if the Nb detector is thicker.

Figure 4.

Nb thickness dependence of the giant transition-state enhancement. Representative nonlocal signals ⌈ΔV_nl^th(α)⌉^Nb as a function of IP field angle α for the Al₂O₃-absent devices with different t_Nb of 10 (a and b), 20 (c and d), and 35 nm (e and f), taken above (yellow background) and immediately below (blue background) T_c of the Nb layer. ⌈ΔV_nl⌉^Nb/⌈ΔV_nl^th⌉_T=7Kversus T_base/T_c plots for t_Nb = 10 nm (g), t_Nb = 20 nm (h), and t_Nb = 35 nm (i). In the insets of g−i, the associated R^Nb/R_T=7K^Nb and ⌈ΔV_nl⌉^Nb are plotted as a function of T_base. (j) t_Nb-dependent peak amplitude, width (inset), and position (inset).

However, experiments give a very different result (Figure 4g–i). As t_Nb increases, the peak amplitude of ⌈ΔV_nl^th⌉^Nb/⌈ΔV_nl⌉_T=7K^Nb rises until reaching 15 nm and then drops strongly for thicker Nb detectors, leading to a maximum at t_Nb = 15 nm (Figure 4j). The width and position of the transition-state enhancement, on the other hand, behave as expected for highly and quickly developed coherence peaks in the QP DOS of thick Nb when T_c is crossed: a progressive narrowing of fwhm and a peak shift closer to T_c, respectively, with the increase of t_Nb (inset of Figure 4j). The nontrivial t_Nb-dependent enhancement (Figure 4j) indicates that there is another key ingredient that controls the enhancement amplitude, that is to say, the exchange spin-splitting field,⁴⁻⁶ which has turned out to considerably modify the QP spin relaxation mechanism via a freezing out of elastic/intravalley spin-flip scattering.⁴⁻⁶ Below, we discuss how this exchange-field-frozen spin-flip scattering⁴⁻⁶ is linked to and modifies the QP charge relaxation.

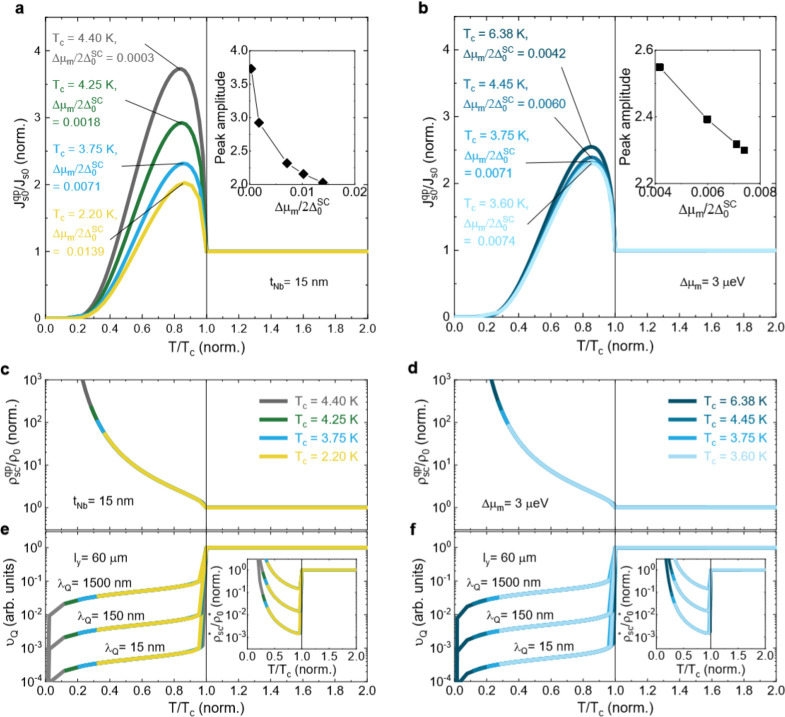
To theoretically describe our results, we first calculate the excited QP spin current density J_s0^qp at the YIG/superconducting Nb interface as a function of the normalized temperature T/T_c for different values of the magnon spin accumulation Δμ_m relative to the zero-T energy gap 2Δ₀ (Figure 5a and b). For this calculation, we employ the recent models^29,30 that explicitly take the superconducting coherence factor into account (see Supplementary Section 4 for full details). Note that the characteristic energy of incoherent magnons which excite spin-polarized QPs in the Nb detector is set by Δμ_m, and the T_c (or 2Δ₀^SC) suppression at a larger Δμ_m is inferred from our data set (Figures 3 and 4). For a quantitative comparison, J_s0 is normalized to its normal state value J_s0.

Figure 5.

Theoretical identification of origins for the giant transition-state enhancement. (a and b) Normalized QP spin current density J_s0^qp/J_s0 at the YIG/superconducting Nb interface as a function of the normalized temperature T/T_c. In this calculation, we use various values of the magnon spin accumulation Δμ_m relative to the zero-T energy gap 2Δ₀. Note that Δμ_m and 2Δ₀^SC are both inferred from our data set (Figures 3 and 4) using relevant theories (see Supplementary Section 4). Each inset summarizes the peak amplitude of J_s0/J_s0versus Δμ_m/2Δ₀^SC. (c and d) Normalized QP resistivity ρ_SC/ρ₀ as a function of T/T_c. (e and f) Volume fraction of QP charge imbalance v_Q as a function of T/T_c. In this calculation, we use three different QP charge-imbalance relaxation lengths, λ_Q = 15, 150, and 1500 nm, in the low-T limit (T/T_c ≪ 1). Insets of e and f display the normalized effective resistivity ρ_SC^*/ρ₀ (=ρ_SC^qpv_Q/ρ₀) of the superconducting Nb.

The calculated J_s0^qp/J_s0 increases largely near T_c (0.8T_c – 0.9T_c), and it decreases exponentially when T < 0.8T_c, reflecting the singularity behavior in a nonequilibrium population of spin-polarized QPs.^29,30,42 In addition, the peak amplitude of J_s0/J_s0 is inversely proportional to Δμ_m/2Δ₀^SC (inset of Figure 5a and b), explaining qualitatively the heating power dependence of the transition-state enhancement (Figure 3f). Nonetheless, this analysis based on the superconducting coherence factor does not capture the mechanism behind the nontrivial t_Nb dependence (Figure 4j).

We next consider the QP resistivity ρ_SC^qp (Figure 5c and d) and the volume fraction of QP charge imbalance v_Q (Figure 5e and f), which together determine the effective resistivity ρ_SC (=ρ_SC^qpv_Q, inset of Figure 5e and f) of the superconducting Nb.^38,45 Here 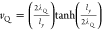,^38,45 where l_y is the spin-active length of the Nb detector, given approximately by the sum of the length of the Pt injector l_y and l_sd^m in our device geometry, and λ_Q is the QP charge-imbalance relaxation length. ρ_SC and ρ_SC^∗ are normalized by their normal-state ones ρ₀ and ρ₀, respectively. We note that if the SC thickness is comparable to or smaller than the QP spin transport length, as relevant to our system,^38,46 the QP-mediated iSHE voltage V_iSHE^qp in the SC can be approximated as 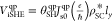, where θ_SH is the QP spin-Hall angle, which is predicted to slightly increase near T_c(45,47) (see Supplementary Section 4 for details), e is the electron charge, and ℏ is the reduced Planck constant. Consequently, J_s0^qp and ρ_SC appear to be governing parameters in V_iSHE^qp.

The most salient aspect of the calculations is that in the vicinity of T_c, v_Q dominates the T-dependent ρ_SC^∗ over ρ_SC, resulting in V_iSHE^qp ∝ λ_Q for given J_s0 and l_y values. This signifies that the QP charge imbalance relaxation is likely responsible for the nontrivial t_Nb-dependent transition-state enhancement (Figure 4j) observed in our system.

We thus propose the following mechanism. If QP charge relaxes through the spin-flip scattering 1/τ_sf^qp and the inelastic scattering 1/τ_in, and 1/τ_sf > 1/τ_in, the effective relaxation time τ_Q^∗ for the QP charge imbalance⁴⁸ is given by 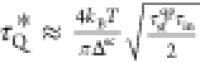where k_B is the Boltzmann constant. Based on the exchange-field-frozen spin-flip scattering⁴⁻⁶ and its proximity nature³³ in an FMI/SC system, one can reasonably assume τ_sf ∝ ΔE_ex ∝ 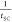. This leads to 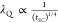and 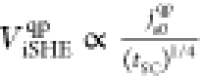. Qualitatively, we can understand the t_Nb-dependent transition-state enhancement (Figure 4j) in the following manner. When t_Nb ≪ ξ_Nb, the superconducting coherence is too weak to inject/excite large QP spin currents across the YIG/Nb interface. In contrast, for t_Nb > ξ_Nb, the exchange spin-splitting-field cannot propagate over the entire depth of such thick Nb and hence the converted QP charge relaxes faster primarily via the spin-flip scattering process. Overall, these two competing effects control the amplitude of the transition-state enhancement by which one would expect a maximum at the intermediate t_Nb ≈ ξ_Nb (around 15 nm for Nb thin films). Note also that the enhancement width and position are determined by J_s0^qp × ρ_SC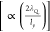, the latter of which decays rapidly to zero below T_c for a strong superconducting Nb.

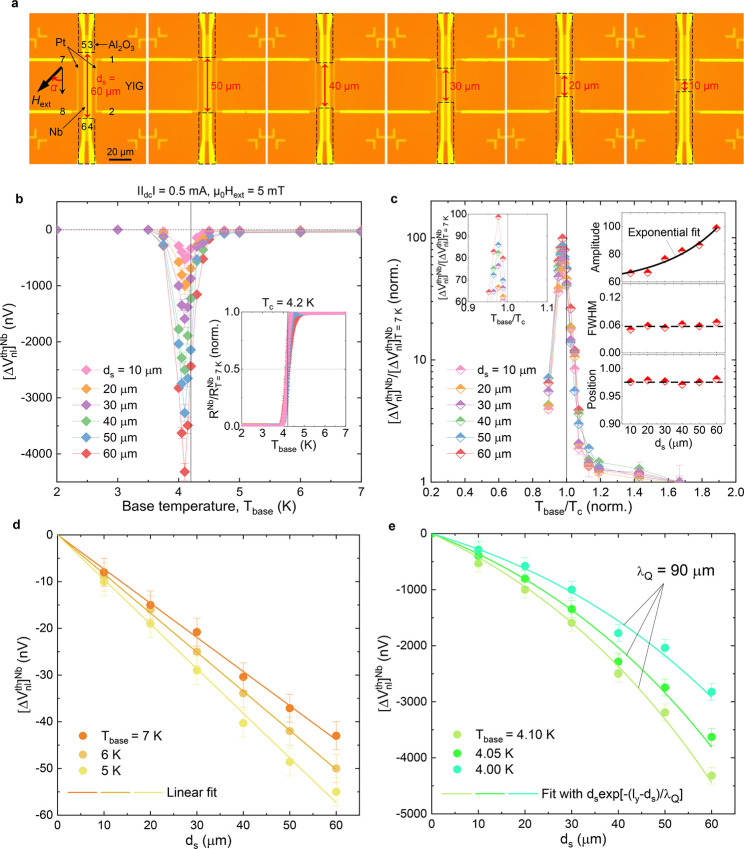
To check the validity of this proposal, we experimentally investigate how the transition-state enhancement scales with the separation distance d_s between Au/Ru electrical contracts on the exchange-spin-split Nb layer (Figure 6a, see Supplementary Section 5). Importantly, while the peak position and width of the transition-state enhancement are almost independent of d_s (Figure 6b and c), the peak amplitude increases quasi-exponentially with the increase of d_s (inset of Figure 6c), reflecting the characteristics of the QP charge-imbalance relaxation effect (see Supplementary Section 5). From the d_s-dependent ⌈ΔV_nl^th⌉^Nb (Figure 6e), we are able to estimate λ_Q in the vicinity of T_c (T_base/T_c = 0.94–0.98) for the spin-split Nb to be around 90 μm. This is surprisingly a few orders of magnitude larger than either commonly assumed⁴⁸ or hitherto reported in Nb films without the presence of spin-splitting fields⁴⁹ and thereby should indicate the significantly exchange-field-modified QP relaxation in our system.

Figure 6.

Spatial profiling of the giant transition-state enhancement. (a) Optical micrographs of the fabricated devices, in which only the separation distance d_s of Au/Ru electrical contacts on the 15-nm-thick Nb layer varies from 10 to 60 μm. (b) Thermally driven nonlocal signals ⌈ΔV_nl^th⌉^Nb as a function of the base temperature T_base for the devices with different d_s. In these measurements, I_dc is fixed at |0.5| mA and the magnetic field μ₀H_ext at 5 mT. The inset shows the normalized Nb resistance R^Nb/R_T=7Kversus T_base plot, which confirms nearly identical superconducting transition T_c of the Nb layer. Note that a relatively higher T_c of the 15-nm-thick Nb layer in these devices than that of the prior device (Figure 3d) is due to the better initial base pressure (<1 × 10^–9 mbar) before film deposition. (c) ⌈ΔV_nl^th⌉^Nb/⌈ΔV_nl⌉_T=7K^Nb as a function of T_base/T_c. The right inset displays the d_s dependence of the peak amplitude, width, and position: the black solid line is an exponential fit, whereas the black dashed lines are given as a guide to the eye. A magnified plot of the peaks is also shown in the left inset. d_s-dependent ⌈ΔV_nl⌉^Nb above (d) and immediately below (e) T_c of the Nb layer. In e, the solid lines are fitting curves to estimate the QP charge-imbalance relaxation length λ_Q (see Supplementary Section 5 for explicit formulas).

Finally, we briefly mention other relevant experiments. It has been previously shown that in all-metallic nonlocal spin-Hall devices,⁸ the giant iSHE (∼2000 times at most) is created by electrical spin injection from Ni₈Fe₂ through Cu into superconducting NbN far below T_c (T_base/T_c = 0.3) and attributed to the exponentially increasing QP resistivity at a lower T. By contrast, a recent experiment has reported that for a YIG/NbN vertical junction³³ the 2–3 times enhanced iSHE voltage by local SSE is measurable only in a limited T range right below T_c (T_base/T_c = 0.96). In this work, the superconducting coherence factor is pointed out as a main source for such an enhancement, and a quantitative description of the data is also provided. In metallic/conducting Nb/Ni₈Fe₂ bilayers,³⁸ a monotonic decay of spin-pumping-induced iSHE appears across T_c, indicating no superconducting coherence effect detectable.

Conclusions

The key findings of our study that help understand these puzzling results are as follows. The spin-to-charge conversion mediated by QPs is substantially enhanced in the normal-to-superconducting transition regime, where the interface superconducting gap matches the magnon spin accumulation. The conversion efficiency and characteristics depend crucially on the driving/heating power and the SC thickness, which is understood based on the two competing effects: the superconducting coherence^29,30,42 and the exchange-field-modified QP relaxation.^4−6,48 The validity of these competing mechanisms is experimentally confirmed by spatially resolved measurements with varying the separation of electrical contacts on the spin-split Nb layer. A quantitative reproduction of the result remains an open question for a theory. The coupling between different nonequilibrium imbalances (magnon, spin, charge, heat, magnon-heat, and spin-heat)^4,12 with exchange spin-splitting and the nonlinear kinetic equations⁴ in the superconducting state should be taken into account rigorously. Moreover, how the magnetic-field-induced screening supercurrents in a spin-split SC contribute to the QP spin-to-charge conversion when coupled with these nonequilibrium modes⁵⁰ remains to be addressed. We speculate that the giant transition-state QP SHE is generic in any FMI/SC system, and its efficiency gets even larger especially with two-dimensional (2D) SCs⁵¹ where the exchange spin-splitting can readily proximity-penetrate the entire depth of the 2D SCs. We also anticipate that such a giant spin-to-charge conversion phenomenon (involving nonequilibrium QPs) can be used as an extremely sensitive probe of spin currents in emergent quantum materials.⁵²

Methods

Device Fabrication

We fabricated the magnon spin-transport devices (Figure 1b) based on 200-nm-thick single-crystalline YIG films (from Matesy GmbH) by repeating a sequence of optical lithography, deposition, and lift-off steps. Note that these YIG films exhibited a very low Gilbert damping of 0.6 × 10^–4 at room temperature, determined via ferromagnetic resonance line width measurements (by Matesy GmbH, https://www.matesy.de/en/products/materials/yig-single-crystal). We first defined the central Nb detector with a lateral dimension of 9 × 90 μm², which was grown by accelerated Ar-ion beam sputtering at a working pressure of 1.5 × 10^–4 mbar. For the control device, a 10-nm-thick Al₂O₃ spin-blocking layer was in situ deposited prior to the Nb deposition. We then defined a pair of Pt electrodes of 1.5 × 50 μm², which were deposited by dc magnetron plasma sputtering at an Ar pressure of 4 × 10^–3 mbar. These Pt electrodes are separated by a center-to-center distance d^Pt–Pt of 15 μm, which is comparable to the typical l_sd^m of single-crystalline YIG films¹⁸ and also to the estimated values from our Pt-only reference devices with different d^Pt–Pt (Supplementary Section 1). The Nb thickness ranges from 10 to 35 nm, whereas the Pt thickness is fixed at 10 nm. Finally, we defined Au(80 nm)/Ru(2 nm) electrical leads and bonding pads, which were deposited by the Ar-ion beam sputtering. Before depositing the Au/Ru layers, the Nb and Pt surfaces were gently Ar-ion beam etched for transparent electrical contacts between them.

Nonlocal Measurement

We measured the nonlocal magnon spin-transport (Figure 1a and b) in a quantum design physical property measurement system at a temperature varying between 2 and 300 K. A dc current I_dc in the range of 0.1 to 1 mA was applied to the first Pt using a Keithley 6221 current source, and the nonlocal voltages [V_nl^Pt(α), V_nl(α)] across the second Pt and the central Nb are simultaneously recorded as a function of in-plane magnetic-field-angle α by a Keithley 2182A nanovoltmeter. α is defined as the relative angle of μ₀H_ext (//M_YIG) to the long axis of two Pt electrodes that are collinear.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsnano.0c07187.

• Estimation of the magnon spin-diffusion length of YIG, quantification of spin currents leaking into the central Nb at room temperature, first-order estimate of the YIG-induced internal field at the Nb/YIG interface, theoretical description of the conversion efficiency of magnon spin to QP charge in the superconducting Nb, spatially resolved measurements by varying the separation of electrical contacts on the spin-split Nb layer (PDF)

Author Contributions

K.-R.J. conceived and designed the experiments. The magnon spin-transport devices were fabricated by K.-R.J. with help from J.-C.J., X.Z., and A.M. The nonlocal transport measurements were carried out by K.-R.J. with the help of J.Y. and J.-C.J. K.-R.J. performed the data analysis and model calculation. S.P.P.P. supervised the project. All authors discussed the results and commented on the manuscript, which was written by K.-R.J.

The authors declare no competing financial interest.