Abstract
Volatility is an inherent fragrance attribute and typically implies a reduced perception over time. One possibility to elongate odor perception is utilizing controlled fragrance-delivery systems. Herein, the Y type of faujasite with different extra-framework cations (abbreviated as ZY, where Z represents Na+, Ca2+, or La3+) was examined as potential carriers for fragrance entrapment and delivery. d-Limonene (Lim) and linalool (Lol) as model fragrances were loaded in the pore space of Y zeolites, yielding composites FG@ZY (FG = Lim, Lol). It was found that the fragrance release profiles correlate highly with the cationic species located in the nonframework. The retention of fragrances in matrices increases in the order NaY < CaY < LaY for either limonene or linalool. Interestingly, the release rate of limonene was significantly slower than that of linalool when encapsulated in the same zeolite, although neat limonene has a much higher saturated vapor pressure than linalool. For instance, the total fraction of aroma released from Lim@LaY over 30 days was about 10%, while the value was ∼20% for Lol@LaY. Based on the density functional theory calculations, the above results could be well rationalized by the electrostatic attraction and shape selectivity of microporous matrices to the dopant molecules.
1. Introduction
Fragrances are indispensable ingredients formulated into everyday consumer products, such as cosmetics, cleaning, personal care items, and so on.1 From the perspective of practical applications, extending the perception of a characteristic scent of perfume compounds is highly desirable but usually hard to achieve due to the inherent volatility of olfactory components.2 Hence, a range of controlled fragrance release systems has been developed, which can be roughly divided into the chemical barrier and physical barrier systems.3 The chemical barrier is based on the concept of profragrance, which is only applicable to fragrant compounds with functional groups. As for the physical barrier, there are concerns that the most commonly applied resinous-type capsules may cause microplastic contamination, resulting from the limited degradability of wall materials.4,5 Recently, inorganic porous materials such as mesoporous silica spheres6−9 and metal–organic frameworks (MOFs)10−13 have been considered to be a promising matrix to encapsulate fragrance, flavor, and essential oils, in which the hosts can stabilize and slow down the evaporation of active ingredients due to the pore/channel confinement effect.
Zeolites are crystalline aluminosilicates formed by corner-sharing [SiO4]4– or [AlO4]5– tetrahedra, which possess periodic one-to-three-dimensional frameworks, unique pore structure, and fine physical and chemical stabilities.14,15 These microporous materials have found widespread applications in industrial fields, including adsorption, ion exchange, separation, and catalysis.16 Since the past decade, zeolites have become prominent nanomaterials for biomedical applications such as drug delivery,17 wound healing,18,19 and targeted in vivo molecular imaging.20 Recently, Strzemiecka and co-workers successfully applied both natural and synthetic zeolites as fragrance carriers and found that the latter is more effective than the former.21 Tekin et al.22 studied the desorption kinetics of a fragrance molecule (triplal) in the X-type zeolites with different average particle diameters 20 and 4 μm, demonstrating that larger crystals have slightly lower desorption rate constants.
Zeolites have many merits as carriers for fragrance encapsulation and controlled release, including high void fraction, good biocompatibility, and low toxicity.14,17,18,21 Nevertheless, there exists a need for a more profound understanding of the sorption and interaction mechanisms of volatile dopants in the microporous matrix.21 Herein, we utilized d-limonene and linalool as model molecules to examine aroma adsorption and retention in a representative Y-type synthetic faujasite (FAU). The choice of both the active component and the carrier was primarily governed by the possibility of probing host–guest interactions in the fragrance-loaded composites. Limonene and linalool represent the main components of the majority of essential oils, which are widely used as a base fragrance ingredient in perfumes, body lotions, household cleaners, and personal care products.1,10 Both are monoterpenoids, but the latter as alcohol has potential interacting sites and a higher polarity relative to the former. Such a structural difference should be reflected in their adsorption and release behavior.
Among the zeolite family, faujasites are of particular interest because they have two independent and interconnecting three-dimensional networks of cavities.23,24 The net negative charge of zeolite is compensated by extra-framework cationic species. One network consists of large cavities, called supercages, which have a diameter of about 12.4 Å. They are linked in a tetrahedral, diamond-type lattice by sharing rings of 12 tetrahedra. These rings have a free diameter of about 7.4 Å.23 The other network is formed by linking smaller cages of a 10.0 Å inner diameter (i.e., sodalite cages) in a tetrahedral, diamondlike lattice, through adjoining rings of six tetrahedra, thus generating hexagonal prisms (D6R), whose opening is of 2.3 Å between sodalite cages. This hierarchical pore structure makes them suitable for selectively adsorbing various organic molecules.25,26 Moreover, the exchangeability of counterions located in both networks of cavities provides flexibility in the regulation of their performance.27 In this work, we focus on the influence of the valence state of cations in the Y-type FAU zeolites (Si/Al ratio of ∼2.5) on the ability to adsorb and preserve the selected model fragrances and try to elucidate the fundamental processes involved through density functional theory (DFT) calculations.
2. Results and Discussion
2.1. Preparation and Characterization of CaY and LaY
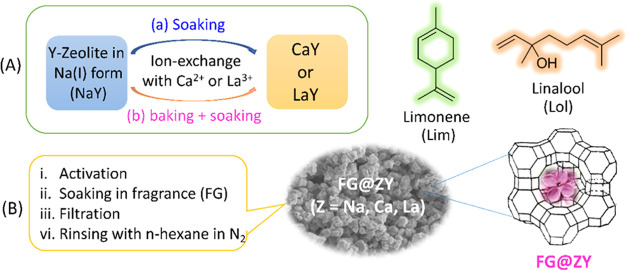
Scheme 1 outlines the ion-exchange process of the Na(I) form of Y zeolite (NaY) with Ca2+/La3+ ions as well as the loading of fragrance in the matrices. As starting materials, NaY has the advantage that it is readily available and can be easily converted into other types with di- and trivalent cations for various applications.17,18,23 The Ca(II)- and La(III)-exchanged zeolites are hereafter named in a simplified way CaY and LaY or CaxY and LaxY when necessary, where x represents the ratio of the equivalent of Ca(II) or La(III) to the total equivalent of cationic species in the zeolite. The value is the equivalent fraction of the ion of interest, indicating the extent of ion exchange. The resulting fragrance-loaded composites are denoted FG@ZY (FG = Lim or Lol; Z = Na, Ca, La).
Scheme 1. Schematic Illustration Showing the Ion Exchange of Y-Type Zeolites (A) and Preparation for Fragrance-Loaded Composites FG@ZY (B) as well as the Structure of Fragrant Molecules Studied in This Work.
Z represents the type of extra-framework cations in the zeolites.
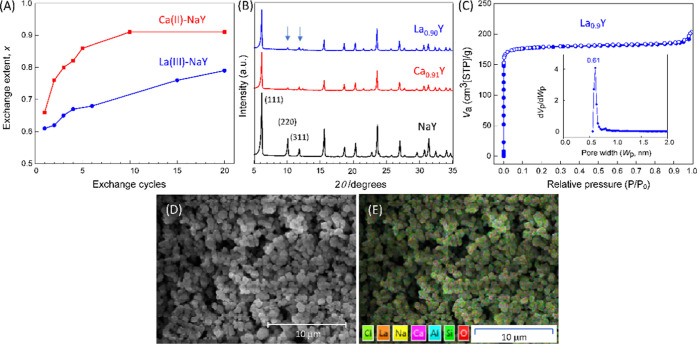
The impregnation method was efficient for the Ca(II)–NaY exchange system. As shown in Figure 1A, the exchange degree (x) increased with the number of soaking and finally reached a platform of 0.91 after ten cycles. However, lanthanum penetrates the zeolite with great difficulty during La(III) exchange and only a moderate extent of exchange (x = ∼0.77) was attained even in the twentieth cycle. Taking into account the fact that the crystalline aluminosilicate is composed wholly of sodalite cages, this result is understandable because the size of the hydrated lanthanum cation of 7.9 Å does not allow passing directly through the six-membered ring openings (d = 2.3 Å) into the small cages.28 Besides, the Coulombic repulsion between the hydrated cations and the anionic sites may be another important factor that impedes the exotic ion from entering the sodalite cage.
Figure 1.
(A) Ion-exchange degree of Ca(II)–NaY and La(III)–NaY systems with increasing soaking cycles. (B) X-ray diffraction (XRD) patterns of the parent zeolite NaY and Ca0.91Y and La0.90Y generated by ion exchange. (C) N2 adsorption–desorption isotherms of La0.90Y as a representative measured at 77 K (inset: the corresponding pore width distribution curve derived from desorption isotherm branches by the HK method). (D) Representative scanning electron microscopy (SEM) image of Ca0.91Y and (E) corresponding overlapped elemental mapping.
To improve the exchange efficiency of the La(III)–NaY system, an alternative strategy was proposed. Specifically, the LaxY samples with a lower exchange extent were subjected to calcination for 6 h at 400 °C and then soaked in a LaCl3 solution. After several calcination–impregnation cycles, a series of La(III)-exchanged zeolites with x values of 0.9–0.97 was obtained (Table S1). It is generally believed that calcination results in the dehydration of hydrated La3+ ions located preferentially in the supercages and, thereby, facilitates migration of the cationic species with a sufficiently small size to the sodalite cage.29−32 Lercher et al.28 demonstrated that lanthanum cations are predominantly stabilized within sodalite cages in the form of multinuclear OH-bridged lanthanum clusters or as monomeric La3+ at the SI sites.
Figure 1B presents the X-ray diffraction patterns of the selected zeolite samples. It shows that the peak positions of Ca0.91Y and La0.90Y are identical to that of their precursor NaY. The retained integrity of the Y-zeolite frameworks was further proved by the SEM/energy-dispersive spectroscopy (EDS) observation (Figures 1D,E, S1, and S2 in the Supporting information, SI). These results suggested the great structural stability of the crystalline aluminosilicate backbone. The obtained XRD patterns for both Ca0.91Y and La0.90Y were characterized by weaker XRD intensities at 2θ of 9–13° compared to NaY, which indicates that the cations have been redistributed in the zeolite.32−34
From N2 adsorption–desorption isotherms (Figures 1C and S3), we can see that these samples show Type I isotherms according to IUPAC classification,35 indicating the microporous nature of Y zeolites. The pore size distribution (Figure 1C inset and Figure S3, descended from the desorption branch) is very narrow, and the most probable pore widths (Wpeak) are 0.59, 0.56, and 0.61 nm for NaY, Ca0.91Y, and La0.90Y, respectively. Comparison of data in Table 1 reveals that the Si/Al ratio and crystallite size of the zeolites as well as the pore structure were not greatly affected by the ion-exchange process, which is consistent with previous reports.36,37 However, the calculated Brunauer–Emmett–Teller (BET) surface area (as,BET) changed significantly, dropping from 829 for NaY to 721 and 714 cm2/g for Ca0.91Y and La0.90Y, respectively.
Table 1. Physicochemical Properties of Zeolite NaY and Its Two Representative Counterparts Containing Ca(II) and La(III) Ionsa.
| Code | x | Si/Al ratio | crystal size (nm) | as,BET (m2/g) | Vp (cm3/g) | Wpeak (nm) |
|---|---|---|---|---|---|---|
| NaY | 2.5 | 600 ± 108 | 829 | 0.34 | 0.59 | |
| Ca0.91Y | 0.91 | 2.4 | 600 ± 90 | 721 | 0.32 | 0.56 |
| La0.90Y | 0.90 | 2.5 | 597 ± 111 | 714 | 0.31 | 0.61 |
2.2. Fragrance Loading in Y Zeolites and Release Behavior
The encapsulation of fragrances was rather straightforward, viz., dipping the activated zeolites in a fragrant oil for 24 h, filtering, and then rinsing the solid with n-hexane in a gentle N2 flow (Scheme 1B). The resulting composites had negligible amounts of solvent residues, which has been evidenced by gas chromatography analysis.
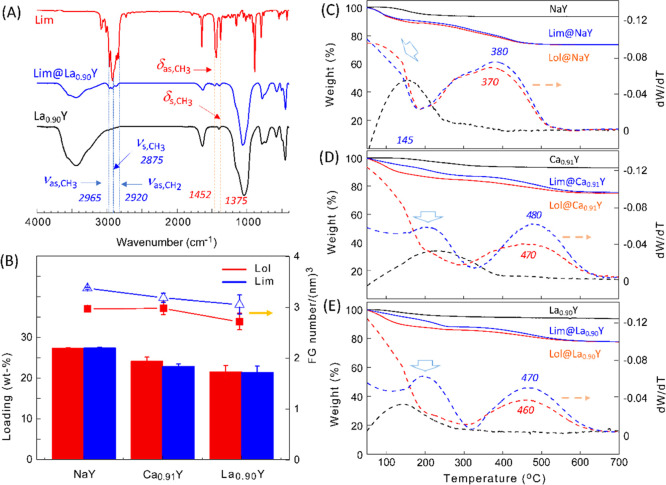
To identify the loading of fragrant molecules in zeolites, Fourier transform infrared (FT-IR) spectroscopy, thermogravimetric analysis (TGA), and XRD methods were used to reveal the interaction between the adsorbate and matrix. As shown in Figures 2A and S4, the characteristic absorption peaks of Lim@ZY and Lol@ZY samples appeared in the range of 2965–2850 cm–1, which are assigned to the C–H stretching vibrations of adsorbed monoterpene compounds. However, there are no signs observed that would describe the interaction of linalool with the matrix because the hydroxyl signals of linalool at 3426 cm–1 merged fully with that of zeolite at around 3440 cm–1 in the spectra of Lol@ZY (Figure S4C,D). From SEM images and XRD patterns of the composites (Figures S5 and S6), the introduction of fragrances does not affect the crystalline structure of the zeolite and its morphology. In the case of FG@NaY, a slight decrease in the intensity of some XRD peaks compared with that of zeolite NaY can be considered a consequence of the variation of spatial positioning of extra-framework cations due to the interaction with adsorbed molecules.33,34
Figure 2.
(A) FT-IR spectra of limonene, La0.90Y, and Lim@La0.90Y as representatives. (B) Fragrance loading capacity of three Y zeolites expressed in weight percent (column) and the molecule number of adsorbate per unit pore volume (line). TG (solid line) and derivative TG (DTG) (dash line) curves of fragrance-loaded composites FG@NaY (C), FG@Ca0.91Y (D), and FG@La0.90Y (E), where black, blue, and red lines represent the zeolite, Lim@ZY, and Lol@ZY samples, respectively.
Figure 2C–E depicts the TGA curves of three zeolites (NaY, Ca0.91Y, and La0.90Y) and their fragrance-loaded composites, respectively. The corresponding loading contents thereby obtained are plotted in Figure 2B. According to various fragrant molecules as well as cationic species, these composites have a loading content (LCw) ranging from 23 to 28% (w/w, relative to the zeolite matrix). When the values were normalized to the number of FG molecules per unit pore volume (LCn) adsorbed in different zeolites, it seems clear that for a specified carrier on which the amount of limonene adsorbed is slightly higher than that of linalool. The difference in adsorption is probably related to the discriminated kinetic diameter of molecules as discussed in the following section. Overall, the loading capacity decreases with decreasing BET surface areas (see Table 1) and the cation content as well in the order NaY > Ca0.91Y > La0.90Y.
Notably, these zeolite composites significantly delayed the thermal evaporation and decomposition of the entrapped fragrances, and the effect was associated with the extra-framework cations. From the derivative TG (DTG) curves in Figure 2C, Lol@NaY lost weight faster than Lim@NaY at the initial release stage before ∼145 °C. The peak top temperature corresponding to the maximum weight loss (Tmax) appeared at 370 and 380 °C for Lol@NaY and Lim@NaY, respectively. These values are much higher than that of free linalool (153 °C) and limonene (138 °C) (see Figure S7). When Ca0.91Y and La0.90Y served as the carrier, the resulting composites displayed different thermal properties from FG@NaY. In detail, both Lol@Ca0.91Y and Lol@La0.90Y showed the DTG patterns similar to that of Lol@NaY, but their Tmax’s shifted to 460–470 °C (Figure 2D,E). In the case of Lim@Ca0.91Y and Lim@La0.90Y, the Tmax reached up to 470–480 °C, and an additional small peak was observed at around 200 °C in their DTG curves. As a general trend, limonene encapsulated in zeolites was less volatile than the corresponding linalool, although in the free state the former has a higher saturated vapor pressure than the latter (Lim: 1.5 ± 0.2 mmHg at 25 °C, bp 176–177 °C; Lol: 0.1 ± 0.8 mmHg at 25 °C, bp 199–200 °C).38 The poorer thermal stability of linalool is probably related to the dehydration of hydroxyl groups, which is prone to occur in the presence of zeolites.16,39
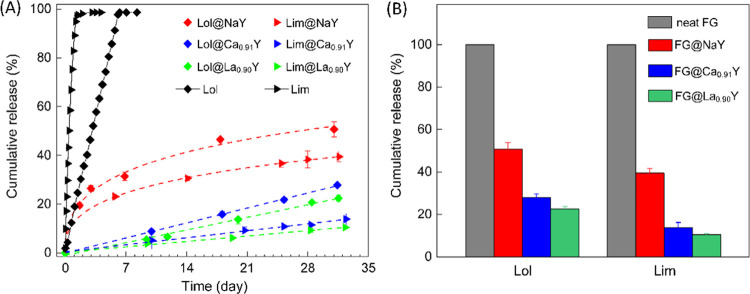
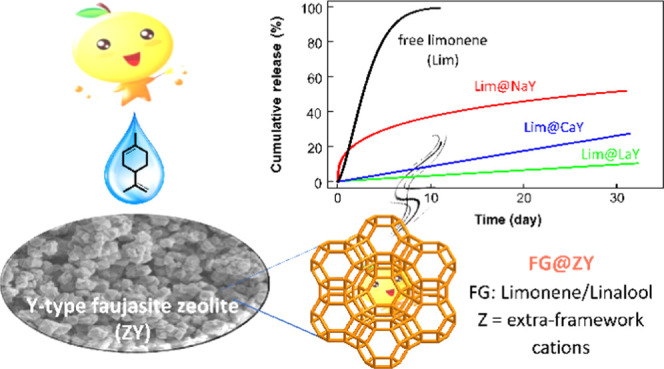
Subsequently, we examined the aroma release behavior of the composite FG@ZYs in comparison to the neat fragrances as the reference at ambient conditions. It can be seen from Figure 3A that both free limonene and linalool evaporated completely in a couple of days, and as expected, the former was lost much faster than the latter. By contrast, the release of fragrance molecules from zeolites was extensively prolonged compared to free fragrances. A comparison of these composites reveals that FG@NaY releases aroma at a faster rate in the first few days and then slows down, whereas its Ca0.91Y and La0.90Y counterparts showed steady and much slower release profiles. Thus, the 30-day total fraction of aroma released from the matrix decreased in the order NaY > Ca0.91Y > La0.90Y, being 51, 28, and 22% for linalool and 39, 19, and 10% for limonene, respectively (Figure 4B). Especially for FG@La0.90Y and FG@Ca0.91Y, the steady aroma release can last for more than one month. Release profiles of both compare very well with those obtained for the encapsulation of fragrances in certain matrices reported earlier, such as MOFs12,13 and polymers,40−42 particularly considering the simplicity of the approach followed.
Figure 3.
(A) Time-elapsed release profiles of FG@NaY, FG@Ca0.91Y, and FG@La0.90Y in comparison to the corresponding free fragrances at ambient conditions (25 °C, ∼70% humidity). Dash lines represent the kinetic curves fitted by the Weibull function for FG@NaY (red) as well as by the zero-order kinetic equation for both FG@Ca0.91Y (blue) and FG@La0.90Y (green). (B) Cumulative release percentages of FG@NaY, FG@Ca0.91Y, and FG@La0.90Y over 30 days. For free limonene and linalool, the release time was two and three days, respectively. Data points represent mean ± standard deviation (SD) from triplicate samples, and error bars represent the standard deviation (n = 3).
Figure 4.
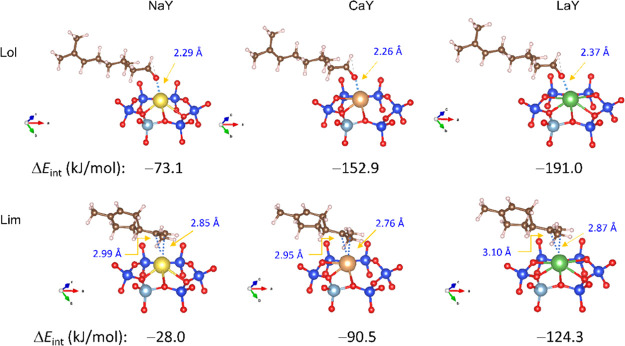
Most stable adsorption configurations of fragrance molecules (Lol and Lim) onto the Y-type zeolites as well as the calculated interaction energies for the adsorption at the PBE + TS/HI level of theory (Si, blue; Al, gray; O, red; Na, yellow; Ca, brown; La, green; C, brown; H, pink). The arrow points to the distance between the metal cation and the coordinating atoms of adsorbed molecules. The integral views showing the optimized configurations at a primitive cell scale are shown in Figure S9.
To gain an insight into the aroma release mechanisms, four mathematic models were applied to fit the obtained release data, including zero-order (r = kt), first-order (r = 1 – e–kt), Higuchi (r = kt0.5), and Weibull (r = 1 – e–(kt)n) models (see Section 4.5). The values of the correlation coefficient (R2) to each model are summarized in Tables S3 and S4. From Figure 3A (red dash lines) and Table S3, the experimental data of both Lim@NaY and Lol@NaY fit well to the Weibull equation with R2 values greater than 0.98. The release rate constant (k) was determined to be 1.7 × 10–7 s–1 for Lol@NaY, which is 1.8-times larger than that of Lim@NaY (6.1 × 10–8 s–1). The two parameters’ exponential function is usually applied to the analysis of drug dissolution and release studies.43 Values of the exponent n lower than 0.75 suggest a Fickian diffusion mechanism, whereas higher values correspond to a non-Fickian delivery of biologically active molecules.44,45 For Lol@NaY and Lim@NaY, the values of n parameter were 0.40 and 0.38, respectively, both below 0.75, suggesting that the release of fragrance from NaY vehicles follows a classical Fickian diffusion, similar to the MOF-based systems reported recently.13
On the other hand, the release process of fragrances from both FG@Ca0.91Y and FG@La0.90Y composites exhibited a zero-order kinetic feature, as shown in Figure 3A (blue and green dash lines) and Table S4 (R2 > 0.99), indicating that the aroma evaporation is linear and independent of the initial load. Such a release behavior is highly desirable because it allows the constant release of entrapped olfactory compounds, thus keeping the smell at a certain level.40 The k values for Lol@Ca0.91Y, Lim@Ca0.91Y, Lol@La0.90Y, and Lim@La0.90Y were 1.0 × 10–7, 4.7 × 10–8, 8.6 × 10–8, and 3.7 × 10–8 s–1, respectively. In other words, the linalool always escapes faster than limonene from the CaY or LaY zeolite matrix, as seen in the Lol@NaY/Lim@NaY pair. These observations revealed that the release kinetics of volatile cargos can be effectively tailored depending on the nonframework cationic species in FAU zeolites.
2.3. Theoretical Computation
To obtain further elucidation of the observed adsorption and retention behavior of limonene and linalool in the zeolites, the interaction of fragrant molecules with the matrices was studied using density functional methods. As depicted in Figure S8, the primitive cell of faujasite contains one supercage and six hexagonal windows connecting the sodalite with the supercage. Taking into account the size of the guest molecules (vide infra), we chose the SII sites in the supercage as the most accessible ones, which are also the most occupied cationic sites.46 To account for the potentiality of the faujasite to capture volatile organics, the previously defined dispersion correction method (TS/HI, Tkatchenko–Scheffler/Hirshfeld)47 is used to compute geometric and energetic parameters involved in the adsorption of limonene and linalool molecules.
Figure 4 presents the most stable adsorption configurations of the two model fragrance molecules onto the zeolites together with the corresponding interaction energies (ΔEint). In the composite Lol@ZYs, the oxygen atom of the alcohol hydroxyl group interacts with the metal cation at distances of 2.29, 2.26, and 2.37 Å for NaY, CaY, and LaY, respectively. The interaction energy in absolute value improves from 73.1 for Lol@NaY to 152.9 for Lol@CaY and to 191.0 kJ/mol for Lol@LaY, which is proportional to the oxidation state of cations. The quite short optimized distances and ΔEint values suggest the formation of a chemical bond between the metal atom and the oxygen atom of the guest molecule, similar to the covalent bonds in bulk materials (e.g., Na–O = 2.32 Å,48 Ca–O = 2.40 Å,49 La–O = 2.37–2.73 Å50). The phenomenon is typical of adsorption between oxygenated species and metals.24
Limonene adsorbs into the zeolites in a π-complexation mode by preferentially interacting its exocyclic vinyl moiety with the metal ions (down panel of Figure 4). The distances between the double bond carbon atoms and the positive ion are slightly longer than those for the conjugated olefin–zeolite adsorption systems reported by Badawi et al.24 For example, they demonstrated that 1,3-butadiene adsorbs on the NaY zeolite via an interaction between the two middle carbon atoms and one Na+ ion with distances of 2.73 and 2.81 Å, respectively. Also, for the Lim@NaY, the double bond carbon atoms are 2.85 and 2.99 Å away from the sodium ion. Similar to the case of Lol@ZYs, the interaction strength of limonene with the matrix increases in the order NaY < CaY < LaY, but the ΔEint value is much small when compared pairwise for a specified zeolite. Among them, the computed interaction energy for the adsorption of limonene onto NaY amounts to −28.0 kJ/mol, being 45.1 kJ/mol lower than that for Lol@NaY.
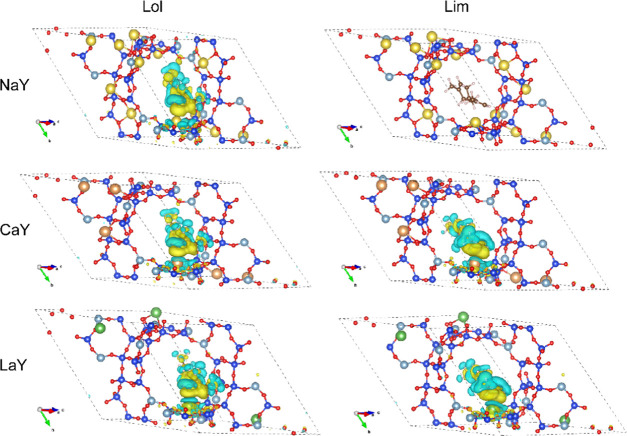
Figure 5 depicts the electron density difference isosurface plots of FG@ZY composites. The plots clearly show an increase in electron density upon adsorption of linalool (blue zone) around Na+, Ca2+, or La3+ ions (the left panel of Figure 5), indicating that there is a metal cation sufficiently close to the guest molecule to interact with the latter through strong electrostatic interactions.51,52 In contrast, the introduction of limonene in the NaY zeolite does not lead to any obvious change in the electron density around Na+ cations. In this case, the van der Waals forces could be considered to be the dominant contribution to the interaction. Nevertheless, for both CaY and LaY zeolites, the electrostatic interaction is likely to occur upon adsorption of limonene, as evidenced by small blue areas around the metal ions in the electron density difference plotted in the right panel of Figure 5.
Figure 5.
Electronic density difference isosurfaces plot upon adsorption of linalool (left panel) and limonene (right panel) onto Y zeolites. The blue (yellow) zones indicate density decrease (increase).
On the other hand, the Bader analysis53 provided further support for the electrostatic interaction mechanism present in the fragrance-loaded systems except for Lim@NaY. As shown in Table 2 by the total Bader charge difference (ΔQ), linalool displays a greater degree of electron transfer relative to limonene during adsorption. It was found that whether limonene or linalool, the ΔQ value increases in the order Na+ < Ca2+ < La3+, which is in line with the Bader charge of the cations located at the SII site in the supercages (Table 3). In other words, the higher the Bader charge of the metal ion, the larger the electronic charge difference for fragrances adsorbed on it and the higher the corresponding interaction energy.
Table 2. Total Electronic Charge Difference (ΔQ) of Fragrances upon Adsorption onto Y-Type Zeolites (ZY) with Various Extra-Framework Cationsa.
| Lol |
Lim |
|||||
|---|---|---|---|---|---|---|
| ZY | NaY | CaY | LaY | NaY | CaY | LaY |
| ΔQ | 0.5670 | 0.6780 | 0.7350 | 0.0268 | 0.0824 | 0.1590 |
Detailed data on the Bader charge of the atoms in linalool and limonene molecules are presented in Tables S5 and S6.
Table 3. Bader Charge (Q) of the Metal Atoms at Site II in the Zeolites with Adsorbed Fragrance Molecules.
| Na | Ca | La | |
|---|---|---|---|
| Lol@ZY | +0.8493 | +1.2018 | +2.6284 |
| Lim@ZY | +0.8557 | +1.1476 | +2.6118 |
Summarizing, the electrostatic interaction is a predominant component to the computed interaction energies, by which we can reasonably explain the fragrance adsorption and release behavior revealed in the previous section. To be specific, the release of both linalool and limonene from the zeolites slows down in the order NaY > Ca0.91Y > La0.90Y (Figure 3), which was attributed to the increased electrostatic attraction of the metal ions to the guest molecules. Also, a decrease in the loading capacity for these zeolites in the same order reported in Figure 2B is consistent with the decrease in the number of cations as binding sites because each of the exchanged Ca(II) and La(III) ions replaced two and three Na+ ions in the parent zeolite NaY, respectively.
Notably, the aroma retention performance of zeolites is difficult to be interpreted solely by the computed interaction energies. As shown in Figure 3, for a given zeolitic matrix, the release rate of limonene is always lower than that of linalool. This result was surprising since based on the intuitionistic knowledge of their chemical structure and the interaction energy calculation (Figure 4), it is anticipated that limonene should escape more quickly than the latter. Furthermore, it has been reported that the confined nanochannels of zeolites would enhance the intermolecular hydrogen-bond interactions of alcohol compounds,54 which also contributes to their retention in the matrix.
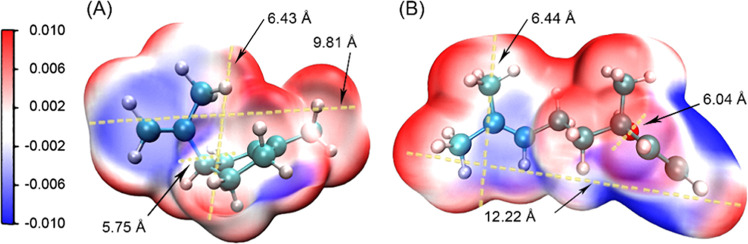
The observation that limonene was better retained within zeolites than linalool may be rationalized from the match between the size and shape of the FAU framework and the sorbate molecules. From the electrostatic potential (ESP) distribution of the two fragrant molecules plotted in Figure 6, limonene shows an overall smaller geometry size relative to linalool, with the kinetic diameters of 9.81, 6.43, and 5.75 and 12.22, 6.40, and 6.04 Å, respectively. This suggests that both can access the faujasite supercage through its 7.4 Å opening. However, the sodalite cage does not allow a sufficiently large space for linalool molecules because its pore diameter (10.0 Å)23 is less than the length of the latter (12.22 Å). On the contrary, it can be expected from limonene to occupy the sodalite cage through a hexagonal window (diameter of 6.6 Å) joining with the supercages (Figure S11). The speculation is supported by the fact that Y-type zeolites were loaded with more limonene and the resulting composite Lim@ZY had higher thermal stability than their corresponding counterparts Lol@ZY (Figure 2B–E). This also means that the limonene molecules confined in sodalite cages would have a longer diffusion path to be passed and therefore release more slowly compared to linalool. Similar size or shape selectivity has also been found in the adsorption and catalytic systems based on MOF and zeolite microporous materials.55−58
Figure 6.
Molecular van der Waals surfaces (au) with electrostatic potential and kinetic diameters. (A) Lim with kinetic diameters (Å) of 9.81, 6.43, and 5.75. (B) Lol with kinetic diameters (Å) of 12.22, 6.40, and 6.04.
3. Conclusions
We utilized the Y-type FAU zeolites to construct fragrance-delivery systems with limonene and linalool as model perfume compounds. The resulting fragrance composites, featuring a moderate loading content (28–32 wt %) and high thermal stability, displayed the characteristics of sustained and steady release. Experimental and computational results have demonstrated a specific contribution of the extra-framework cationic species to aroma retention and release kinetics. The fragrance release rates (FG@NaY > FG@Ca0.91Y > FG@La0.90Y) follow the opposite trend calculated for electrostatic attraction of metal ions with guest molecules by DFT (NaY < CaY < LaY). The fragrance release mechanism from the NaY matrix is a Fickian diffusion, while for CaY- and LaY-based carriers, the aroma transport obeys zero-order kinetics. Also, limonene was found to be entrapped more efficiently in a given zeolite compared with linalool and the aroma evaporation is significantly slower than the latter. The unusual behavior could be attributed to the exact match between the limonene molecule and the pore structure of the zeolite framework, which allows it to penetrate deeply into the sodalite cages and thereby retain longer in the matrix. Overall, this work provides new insights into the host–guest interactions in zeolitic matrices while at the same time introducing a convenient platform for the construction of fragrance-controlled release systems.
4. Experimental Section
4.1. Materials
The zeolite Y in the Na(I) form (denoted NaY) was supplied by Nankai University Catalyst Co., Ltd. (Tianjin, China). d-Linalool (Lol, 98%) and d-limonene (Lim, 95%) were purchased from J&K Scientific (Beijing, China) and used directly. Deionized (DI) water was used in all of the experiments. CaCl2·H2O, LaCl3, and other chemicals of analytical grade were brought from Sinopharm Chemical Reagent Co. Ltd. (Shanghai, China) and used as received.
4.2. Characterizations
Fourier transform infrared (FT-IR) spectra were recorded between 400 and 4000 cm–1 using a Bruker TENSOR II spectrophotometer with 32 successive scans at a resolution of 2 cm–1. Solid samples were mixed with potassium bromide and compressed into a pellet for the measurements, while the neat fragrances were measured by the liquid film method. Powder X-ray diffractometric analysis (PXRD) was performed on a Panalytical X’Pert diffractometer (Netherlands) operated at 40 kV, 40 mA, and 0.02°/min with Cu Kα radiation (λ = 1.5418 Å) in the 2θ range of 5–60°. The morphologies of zeolites and fragrance-loaded composites FG@ZYs were observed by a field-emission scanning electron microscope (SEM) on an SU8010-SEM (Hitachi, Japan). Samples were sputtered with platinum and imaged at an accelerating voltage of 3 kV. The particle size was analyzed by Nano Measurer software (version 1.2.5) and expressed as mean ± standard deviation based on 150 measurements. An energy dispersive spectroscopy (EDS) accessory was also used for imaging and quantifying the element distribution of the samples. The specific surface area and porosity characteristics of zeolites were investigated by N2 adsorption–desorption measurements at 77 K on a BELSORP-max physical adsorption instrument (MicrotracBEL Corp., Japan). Before the tests, the samples were degassed at 120 °C and 1 × 10–5 Pa for 24 h. The specific surface area was calculated by the Brunauer–Emmett–Teller (BET) equation from the adsorption isotherm branch. The total pore volume was obtained at a relative pressure of 0.990. The micropore size distribution was determined by the Horvath–Kawazoe equation from adsorption isotherm data, while the mesopore size distribution was obtained according to desorption isotherm data via the Barrett–Joyner–Halenda (BJH) equation. Thermogravimetric analysis (TGA) of the neat fragrance and zeolite and composites thereof was performed under a N2 atmosphere using a Pyris 1 TGA thermogravimetric analyzer (PerkinElmer). Samples were heated from room temperature to 800 °C at a heating rate of 15 °C/min.
4.3. Preparation of CaY and LaY
Y zeolites with Ca(II) or La(III) counterions were prepared from the precursor NaY according to a previously reported ion-exchange method.25 A typical ion-exchange experiment is as follows: 6 g of NaY was added to an aqueous solution of 1.0 M CaCl2 or LaCl3 (150 mL), and the mixture was stirred at 200 rpm for 24 h at 80–90 °C. After filtration, this procedure was repeated by mixing the isolated solid with a fresh batch of solution. The impregnation of zeolite in the salt solution for 24 h was considered as an ion-exchange cycle. Finally, the separated powder was dialyzed against DI water and lyophilized to yield the desired product as a white solid. The ion-exchange degree (x) was determined by analyzing the Na+ content of the zeolite phase before and after exchange based on the energy-dispersive spectroscopy.
4.4. Encapsulation of Fragrances in Zeolites (FG@ZY)
Encapsulation of fragrances in zeolites was carried out on a Schlenk line. A certain amount of zeolites was placed in a flask, degassed at 120 °C for 6 h, and filled with dry nitrogen. Then, an excess of fragrance was added, and the resulting mixture was stirred at ambient temperature for 24 h and then rinsed with n-hexane several times in a N2 flow to remove residual fragrance on the solid surface. The as-prepared composites (denoted as FG@ZY; Z shows the type of cation in the zeolite) were put into a vial and stored in a desiccator.
The loading content of fragrance in the composites was calculated by the following equation based on thermogravimetric analyses.
| 1 |
where WFG and WZY are the weights of adsorbed fragrance and the carrier, respectively.
4.5. Fragrance Cumulative Release Profiles and Release Kinetics
The fragrance release experiments were carried out at room temperature according to the previously reported procedure.9 At regular intervals, ∼5 mg of sample was taken out from a desiccator with a small air outlet to analyze the fragrance residues by TGA. Each cumulative release percentage of fragrance was derived from three independent measurements and was expressed as the mean ± standard deviation.
Four mathematical models were applied to fit the release profiles of FG@ZY composites, including a first-order equation (eq 2), a Higuchi equation (eq 3), a Weibull equation (eq 4), and a zero-order equation (eq 5).
| 2 |
| 3 |
| 4 |
| 5 |
where r is the fraction of fragrance released at time t to the initial loading content (viz. % cumulative release), k is the release rate constant, and n is a parameter related to the release mechanism.
4.6. Computational Models and Methods
For the consideration of computational cost and convenience, we simplified the standard cubic cell of a faujasite framework (Si192O384)59 into a primitive rhombohedral cell (Si48O96) and replaced 12 Si atoms in the structure with 12 Al atoms to obtain a Si/Al ratio of 3, which was close to the experimental value of about 2.4. Thus, 12 Na+, 6 Ca2+, or 4 La3+ were introduced to balance the negative charges of the framework and were assigned to the following binding sites according to the well-known experimental cationic distribution:46 6 Na+ at SII (supercages), 2 Na+ at SI (D6R cages), 4 Na+ at SI′ (sodalite cages); 1 Ca2+ at SII, 1 Ca2+ at SI, 4 Ca2+ at SI′; and 1 La3+ at SII, 3 La3+ at SI′. The lattice constants are optimized from the Birch–Murnaghan fit to the total energies as a function of the unit cell volume. The lattice parameters of NaY, CaY, and LaY zeolites are as follows: a = b = c = 17.716 Å, α = β = γ = 60°; a = b = c = 17.714 Å, α = β = γ = 60°; and a = b = c = 17.855 Å, α = β = γ = 60°, respectively. The optimized primitive cells of NaY, CaY, and LaY zeolites considered for DFT calculations are shown in Figure S8.
DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP).60 The semilocal Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional was employed in the generalized gradient approximation (GGA) proposed by Perdew et al.61 The electron–ion interactions were described using the projector augmented planewave (PAW) method,62 and the Kohn–Sham equations63 were solved self-consistently until the energy difference between cycles became lower than 10–7 eV. The planewave cutoff energy was set to 450 eV. Gaussian smearing of σ = 0.1 eV was applied to occupations to improve the total energy convergence. The structural relaxations have been performed until all forces were smaller than 0.01 eV/Å. The calculations were done using the Γ-point only due to the large size of the unit cell. The van der Waals interactions were considered using dispersion corrections. To be more specific, we adopted the Tkatchenko–Scheffler scheme with iterative Hirshfeld partitioning, as implemented in VASP by Bučko and co-workers.47,64 This method has been shown to accurately describe the interaction of small molecules with zeolites.24,51,52 The interaction energies (ΔEint) of the fragrance molecules with zeolite Y at 0 K are calculated from eq 6
| 6 |
where EY–F represents the energy of zeolite Y with adsorbed fragrance molecules and EY and EF denote the energy of the empty zeolite and isolated fragrance molecules in the gaseous phase, respectively.
For a given fragrance-loaded composite, the most stable adsorption configuration has been optimized and the difference in electronic density (Δρ) upon adsorption of the fragrant molecule into the zeolite was determined for an improved understanding of the bonding interactions. These adsorption configurations and electronic distribution modes are visualized using VESTA.65 To this end, we have calculated from a relaxed structure of fragrance molecules adsorbed in the zeolite (ZY; Z = Na, Ca or La) the electronic densities of the following fragments: the clean ZY (ρY), the molecule (ρF), and the ZY with the adsorbed molecule (ρY-F). Then, Δρ is calculated from the following expression
| 7 |
Bader’s analysis was also performed to obtain the electronic charge and charge difference of the systems after fragrance adsorption.
The optimized geometries of limonene and linalool molecules were calculated using the DFT PBE0/6-31G(d,p) basis set by Gaussian 09. The molecular van der Waals surfaces, defined as 0.001 au electrostatic potential isosurface by Bader,66 colored by electrostatic potential (ESP), were calculated by Multiwfn67 and shown by Visual Molecular Dynamics (VMD).68
Acknowledgments
This work is supported by the National Key Research and Development Program of China (Grant No. 2016YFA0200301). The authors thank the Computing Platform of the College of Chemical and Biological Engineering at Zhejiang University for the support of simulations. We also thank Na Zheng at the State Key Laboratory of Chemical Engineering at Zhejiang University for her help in SEM/EDS measurements.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c04822.
SEM images, energy dispersion spectra, and N2 adsorption–desorption isotherms of Y-type zeolites; IR spectra, SEM images, and PXRD of fragrance-loaded zeolites; TGA curves of limonene and linalool; periodic model of a primitive cell of zeolites; fragrance adsorption configurations on zeolites; ball-and-stick model of fragrances; graphical representation of the shape selectivity of zeolites Y; preparation and chemical composition of zeolite samples; fragrance release kinetic data; Bader charge differences of fragrance in zeolites (PDF)
Author Contributions
§ Z.L. and J.H. contributed equally to this work.
The authors declare no competing financial interest.
Supplementary Material
References
- Surburg H.; Panten J.. Common Fragrance and Flavor Materials: Preparation, Properties and Uses, 5th ed.; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Herrmann A.The Chemistry and Biology of Volatiles; John Wiley & Sons: Chichester, U.K., 2010. [Google Scholar]
- Herrmann A. Controlled release of volatiles under mild reaction conditions: from nature to everyday products. Angew. Chem., Int. Ed. 2007, 46, 5836–5863. 10.1002/anie.200700264. [DOI] [PubMed] [Google Scholar]
- Bruyninckx K.; Dusselier M. Sustainable chemistry considerations for the encapsulation of volatile compounds in laundry-type applications. ACS Sustainable Chem. Eng. 2019, 7, 8041–8054. 10.1021/acssuschemeng.9b00677. [DOI] [Google Scholar]
- Browne M. A.; Crump P.; Niven S. J.; Teuten E.; Tonkin A.; Galloway T.; Thompson R. Accumulation of microplastic on shorelines woldwide: sources and sinks. Environ. Sci. Technol. 2011, 45, 9175–9179. 10.1021/es201811s. [DOI] [PubMed] [Google Scholar]
- Ciriminna R.; Pagliaro M. Sol-gel microencapsulation of odorants and flavors: opening the route to sustainable fragrances and aromas. Chem. Soc. Rev. 2013, 42, 9243–9250. 10.1039/c3cs60286a. [DOI] [PubMed] [Google Scholar]
- Wang P.; Zhu Y.; Yang X.; Chen A. Prolonged-release performance of perfume encapsulated by tailoring mesoporous silica spheres. Flavour Fragrance J. 2008, 23, 29–34. 10.1002/ffj.1851. [DOI] [Google Scholar]
- Lu Z.; Zhang T.; Shen J.; Xiao Z.; Hu J.; Niu Y.; Yu D.; Chen L.; Zhang X. Effects of fragrance-loaded mesoporous silica nanocolumns on the central nervous system. J. Biomed. Nanotechnol. 2018, 14, 1578–1589. 10.1166/jbn.2018.2607. [DOI] [PubMed] [Google Scholar]
- Wang S.; Jiang D.; Zhou Z.; Shen Y.; Jiang L. A novel photothermo-responsive nanocarrier for the controlled release of low-volatile fragrances. RSC Adv. 2020, 10, 14867–14876. 10.1039/C9RA10662F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaughn J.; Wu H.; Efremovska B.; Olson D. H.; Mattai J.; Ortiz C.; Puchalski A.; Li J.; Pan L. Encapsulated recyclable porous materials: an effective moisture-triggered fragrance release system. Chem. Commun. 2013, 49, 5724–5726. 10.1039/c3cc41236a. [DOI] [PubMed] [Google Scholar]
- Wang H.; Lashkari E.; Lim H.; Zheng C.; Emge T. J.; Gong Q.; Yam K.; Li J. The moisture-triggered controlled release of a natural food preservative from a microporous metal-organic framework. Chem. Commun. 2016, 52, 2129–2132. 10.1039/C5CC09634K. [DOI] [PubMed] [Google Scholar]
- Liu Y.; Wang Y.; Huang J.; Zhou Z.; Zhao D.; Jiang L.; Shen Y. Encapsulation and controlled release of fragrances from functionalized porous Metal–Organic Frameworks. AIChE J. 2019, 65, 491–499. 10.1002/aic.16461. [DOI] [Google Scholar]
- Zhang B.; Huang J.; Liu K.; Zhou Z.; Jiang L.; Shen Y.; Zhao D. Biocompatible cyclodextrin-based metal-organic frameworks for long-term sustained release of fragrances. Ind. Eng. Chem. Res. 2019, 58, 19767–19777. 10.1021/acs.iecr.9b04214. [DOI] [Google Scholar]
- Čejka J.; Corma A.; Zones S.. Zeolites and Catalysis: Synthesis, Reactions and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010. [Google Scholar]
- Kulprathipanja S.Zeolites in Industrial Separation and Catalysis; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2010. [Google Scholar]
- Dusselier M.; Davis M. E. Small-Pore Zeolites: Synthesis and Catalysis. Chem. Rev. 2018, 118, 5265–5329. 10.1021/acs.chemrev.7b00738. [DOI] [PubMed] [Google Scholar]
- Servatan M. Zeolites in drug delivery: progress, challenges and opportunities. Drug Discovery Today 2020, 25, 642–656. 10.1016/j.drudis.2020.02.005. [DOI] [PubMed] [Google Scholar]
- Ninan N.; Muthiah M.; Park I. K.; Elain A.; Wong T. W.; Thomas S.; Grohens Y. Faujasites incorporated tissue engineering scaffolds for wound healing: in vitro and in vivo analysis. ACS Appl. Mater. Interfaces 2013, 5, 11194–11206. 10.1021/am403436y. [DOI] [PubMed] [Google Scholar]
- Yu L.; Shang X.; Chen H.; Xiao L.; Zhu Y.; Fan J. A tightly-bonded and flexible mesoporous zeolite-cotton hybrid hemostat. Nat. Commun. 2019, 10, 1932 10.1038/s41467-019-09849-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ndiege N.; Raidoo R.; Schultz M. K.; Larsen S. Preparation of a Versatile Bifunctional Zeolite for Targeted Imaging Applications. Langmuir 2011, 27, 2904–2909. 10.1021/la2000409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strzemiecka B.; Kasperkowiak M.; Łoźyński M.; Paukszta D.; Voelkel A. Examination of zeolites as fragrance carriers. Microporous Mesoporous Mater. 2012, 161, 106–114. 10.1016/j.micromeso.2012.05.024. [DOI] [Google Scholar]
- Tekin R.; Bac N.; Warzywoda J.; Sacco A. Jr. Encapsulation of a fragrance molecule in zeolite X. Microporous Mesoporous Mater. 2015, 215, 51–57. 10.1016/j.micromeso.2015.05.020. [DOI] [Google Scholar]
- Lutz W. Zeolite Y: synthesis, modification, and properties—a case revisited. Adv. Mater. Sci. Eng. 2014, 2014, 1–20. 10.1155/2014/724248. [DOI] [Google Scholar]
- Hessou E. R.; Jabraoui H.; Hounguè M. T. A. K.; Mensah J.-B.; Pastore M.; Badawi M. A first principle evaluation of the adsorption mechanism and stability of volatile organic compounds into NaY zeolite. Z. Kristallogr. - Cryst. Mater. 2019, 234, 469–482. 10.1515/zkri-2019-0003. [DOI] [Google Scholar]
- Talu O.; Zhang S.-Y.; Hayhurst D. T. Effect of cations on methane adsorption by NaY, MgY, CaY, SrY, and BaY zeolites. J. Phys. Chem. A 1993, 97, 12894–12898. 10.1021/j100151a043. [DOI] [Google Scholar]
- Bezus A. G. Adsorption of ethane and ethylene on X-zeolites containing Li+, Na+, K+, Rb+ and Cs+ cations. J. Chem. Soc., Faraday Trans. 1 1978, 74, 306–315. 10.1039/f19787400306. [DOI] [Google Scholar]
- Kumar P.; Sung C.-Y.; Muraza O.; Cococcioni M.; Al Hashimi S.; McCormick A.; Tsapatsis M. H2S adsorption by Ag and Cu ion exchanged faujasites. Microporous Mesoporous Mater. 2011, 146, 127–133. 10.1016/j.micromeso.2011.05.014. [DOI] [Google Scholar]
- Schüßler F.; Pidko E. A.; Kolvenbach R.; Sievers C.; Hensen E. J. M.; van Santen R. A.; Lercher J. A. Nature and location of cationic lanthanum species in high alumina containing Faujasite type zeolites. J. Phys. Chem. C 2011, 115, 21763–21776. 10.1021/jp205771e. [DOI] [Google Scholar]
- Sherry H. S. The ion-exchange properties of zeolites. I. Univalent ion exchange in synthetic faujasite. J. Phys. Chem. A 1966, 70, 1158–1168. 10.1021/j100876a031. [DOI] [Google Scholar]
- Guzman A.; Zuazo I.; Feller A.; Olindo R.; Sievers C.; Lercher J. A. On the formation of the acid sites in lanthanum exchanged X zeolites used for isobutane/cis-2-butene alkylation. Microporous Mesoporous Mater. 2005, 83, 309–318. 10.1016/j.micromeso.2005.04.024. [DOI] [Google Scholar]
- Klein H.; Fuess H.; Hunger M. Cation location and migration in lanthanum-exchanged zeolite NaY studied by X-Ray Powder Diffraction and MAS NMR spectroscopy. J. Chem. Soc., Faraday Trans. 1995, 91, 1813–1824. 10.1039/ft9959101813. [DOI] [Google Scholar]
- Du X.; Zhang H.; Li X.; Tan Z.; Liu H.; Gao X. Cation location and migration in lanthanum-exchanged NaY zeolite. Chin. J. Catal. 2013, 34, 1599–1607. 10.1016/S1872-2067(11)60622-6. [DOI] [Google Scholar]
- Keawkumay C.; Rongchapo W.; Sosa N.; Suthirakun S.; Koleva I. Z.; Aleksandrov H. A.; Vayssilov G. N.; Wittayakun J. Paraquat adsorption on NaY zeolite at various Si/Al ratios: a combined experimental and computational study. Mater. Chem. Phys. 2019, 238, 121824 10.1016/j.matchemphys.2019.121824. [DOI] [Google Scholar]
- Kozlov K.; Asakura K.; Iwasawa Y. Synthesis and characterization of vanadium (IV) complexes in NaY zeolite supercages. Microporous Mesoporous Mater. 1998, 21, 571–579. 10.1016/S1387-1811(98)00028-6. [DOI] [Google Scholar]
- Thommes M.; Kaneko K.; Neimark A. V.; Olivier J. P.; Rodriguez-Reinoso F.; Rouquerol J.; Sing K. S. W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. 10.1515/pac-2014-1117. [DOI] [Google Scholar]
- Fan M.; Sun J. H.; Bai S.; Panezai H. Size effects of extraframework monovalent cations on the thermal stability and nitrogen adsorption of LSX zeolite. Microporous Mesoporous Mater. 2015, 202, 44–49. 10.1016/j.micromeso.2014.09.011. [DOI] [Google Scholar]
- Noda T.; Suzuki K.; Katada N.; Niwa M. Combined study of IRMS-TPD measurement and DFT calculation on Brønsted acidity and catalytic cracking activity of cation-exchanged Y zeolites. J. Catal. 2008, 259, 203–210. 10.1016/j.jcat.2008.08.004. [DOI] [Google Scholar]
- Royal Society of Chemistry. ChemSpider, a free chemical structure database. http://www.chemspider.com (accessed September 5, 2020).
- Kruger J. S.; Nikolakis V.; Vlachos D. Aqueous fructose dehydration using Brønsted acids zeolites: catalytic activity of dissolved aluminosilicate species. Appl. Catal., A 2014, 469, 116–123. 10.1016/j.apcata.2013.09.030. [DOI] [Google Scholar]
- Ye L.; Li Z.; Niu R.; Zhou Z.; Shen Y.; Jiang L. All-aqueous direct deposition of fragrance-loaded nanoparticles onto fabric surfaces by electrospraying. ACS Appl. Polym. Mater. 2019, 1, 2590–2596. 10.1021/acsapm.9b00457. [DOI] [Google Scholar]
- Kaur R.; Kukkar D.; Bhardwaj S. K.; Kim K.-H.; Deep A. Potential use of polymers and their complexes as media for storage and delivery of fragrances. J. Controlled Release 2018, 285, 81–95. 10.1016/j.jconrel.2018.07.008. [DOI] [PubMed] [Google Scholar]
- Lopes S.; Afonso C.; Fernandes I.; Barreiro M.-F.; Costa P.; Rodrigues A. E. Chitosan-cellulose particles as delivery vehicles for limonene fragrance. Ind. Crops Prod. 2019, 139, 111407 10.1016/j.indcrop.2019.05.057. [DOI] [Google Scholar]
- Papadopoulou V.; Kosmidis K.; Vlachou M.; Macheras P. On the use of the Weibull function for the discernment of drug release mechanisms. Int. J. Pharm. 2006, 309, 44–50. 10.1016/j.ijpharm.2005.10.044. [DOI] [PubMed] [Google Scholar]
- Martínez L.; Villalobos R.; Sánchez M.; Cruz J.; Ganem A.; Melgoza L. M. Monte Carlo simulations for the study of drug release from cylindrical matrix systems with an inert nucleus. Int. J. Pharm. 2009, 369, 38–46. 10.1016/j.ijpharm.2008.10.023. [DOI] [PubMed] [Google Scholar]
- Berger D.; Nastase S.; Mitran R. A.; Petrescu M.; Vasile E.; Matei C.; Negreanu-Pirjol T. Mesostructured silica and aluminosilicate carriers for oxytetracycline delivery systems. Int. J. Pharm. 2016, 510, 524–531. 10.1016/j.ijpharm.2016.02.009. [DOI] [PubMed] [Google Scholar]
- Frising T.; Leflaive P. Extraframework cation distributions in X and Y Faujasite zeolites: a review. Microporous Mesoporous Mater. 2008, 114, 27–63. 10.1016/j.micromeso.2007.12.024. [DOI] [Google Scholar]
- Bučko T.; Lebègue S.; Ángyán J. G.; Hafner J. Extending the applicability of the Tkatchenko-Scheffler dispersion correction via iterative Hirshfeld partitioning. J. Chem. Phys. 2014, 141, 034114 10.1063/1.4890003. [DOI] [PubMed] [Google Scholar]
- Jabraoui H.; Achhal E. M.; Hasnaoui A.; Garden J.-L.; Vaills Y.; Ouaskit S. Molecular dynamics simulation of thermodynamic and structural properties of silicate glass: effect of the alkali oxide modifiers. J. Non-Cryst. Solids 2016, 448, 16–26. 10.1016/j.jnoncrysol.2016.06.030. [DOI] [Google Scholar]
- Hofmeister A. M.; Keppel E.; Speck A. K. Absorption and reflection infrared spectra of MgO and other diatomic compounds. Mon. Not. R. Astron. Soc. 2003, 345, 16–38. 10.1046/j.1365-8711.2003.06899.x. [DOI] [Google Scholar]
- Aldebert P.; Traverse J. P. Study by neutron-diffraction of high-temperature structures of La2O3 and Nd2O3. Mater. Res. Bull. 1979, 14, 303–323. 10.1016/0025-5408(79)90095-3. [DOI] [Google Scholar]
- Chebbi M.; Chibani S.; Paul J. F.; Cantrel L.; Badawi M. Evaluation of volatile iodine trapping in presence of contaminants: A periodic DFT study on cation exchanged-faujasite. Microporous Mesoporous Mater. 2017, 239, 111–122. 10.1016/j.micromeso.2016.09.047. [DOI] [Google Scholar]
- Chibani S.; Medlej I.; Lebegue S.; Angyan J. G.; Cantrel L.; Badawi M. Performance of CuII-, PbII-, and HgII-exchanged mordenite in the adsorption of I2, ICH3, H2O, CO, ClCH3, and Cl2: a density functional study. Chem. Phys. Chem. 2017, 18, 1642–1652. 10.1002/cphc.201700104. [DOI] [PubMed] [Google Scholar]
- Bader R. F.Atoms in Molecules: A Quantum Theory; International Series of Monographs on Chemistry; Oxford University Press: Oxford, 1990; Vol. 22. [Google Scholar]
- Yin Y. C.; Sang X.; Xu X. F.; Ma L. R.; Tian Y.; Wen S. Z.; Luo J. B. Glycerol molecules in nano channels of NaY and USY zeolites. Microporous Mesoporous Mater. 2020, 294, 109919 10.1016/j.micromeso.2019.109919. [DOI] [Google Scholar]
- Melix P.; Heine T. London dispersion governs the interaction mechanism of small polar and nonpolar molecules in metal–organic frameworks. J. Phys. Chem. C 2020, 124, 11985–11989. 10.1021/acs.jpcc.0c02966. [DOI] [Google Scholar]
- Gayubo A. G.; Aguayo A. T.; Atutxa A.; Aguado R.; Olazar M.; Bilbao J. Transformation of oxygenate components of biomass pyrolysis oil on a HZSM-5 zeolite. II. Aldehydes, ketones, and acids. Ind. Eng. Chem. Res. 2004, 43, 2619–2626. 10.1021/ie030792g. [DOI] [Google Scholar]
- Yan P.; Bryant G.; Li M. M.-J.; Mensah J.; Kennedy E.; Stockenhuber M. Shape selectivity of zeolite catalysts for the hydrodeoxygenation of biocrude oil and its model compounds. Microporous Mesoporous Mater. 2020, 309, 110561 10.1016/j.micromeso.2020.110561. [DOI] [Google Scholar]
- Poniedziałek K.; Strzemiecka B.; Kasperkowiak M.; Bielicka-Daszkiewicz K. Assessment of the adsorption strength of fragrances on zeolites via solid-phase extraction. J. Liq. Chromatogr. Relat. Technol. 2017, 40, 353–360. 10.1080/10826076.2017.1306558. [DOI] [Google Scholar]
- Hriljac J. A.; Eddy M. M.; Cheetham A. K.; Donohue J. A.; Ray G. J. Powder neutron diffraction and 29Si MAS NMR studies of siliceous zeolite-Y. J. Solid State Chem. 1993, 106, 66–72. 10.1006/jssc.1993.1265. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Perdew J. P.; Burke K. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Kohn W.; Sham L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
- Bučko T.; Lebègue S.; Hafner J.; Ángyán J. G. Improved density dependent correction for the description of London dispersion forces. J. Chem. Theory Comput. 2013, 9, 4293–4299. 10.1021/ct400694h. [DOI] [PubMed] [Google Scholar]
- Momma K.; Izumi F. VESTA: a three-dimensional visualization system for electronic and structural analysis. J. Appl. Crystallogr. 2008, 41, 653–658. 10.1107/S0021889808012016. [DOI] [Google Scholar]
- Bader R. F. W. Definition of molecular structure: by choice or by appeal to observation?. J. Phys. Chem. A 2010, 114, 7431–7444. 10.1021/jp102748b. [DOI] [PubMed] [Google Scholar]
- Lu T.; Chen F. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- Humphrey W.; Dalke A.; Schulten K. VMD: visual molecular dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.