Identifying Causal Effects With Proxy Variables of an Unmeasured Confounder

Abstract

We consider a causal effect that is confounded by an unobserved variable, but with observed proxy variables of the confounder. We show that, with at least two independent proxy variables satisfying a certain rank condition, the causal effect is nonparametrically identified, even if the measurement error mechanism, i.e., the conditional distribution of the proxies given the confounder, may not be identified. Our result generalizes the identification strategy of Kuroki & Pearl (2014) that rests on identification of the measurement error mechanism. When only one proxy for the confounder is available, or the required rank condition is not met, we develop a strategy to test the null hypothesis of no causal effect.

1. Introduction

Unmeasured confounding is a crucial problem in observational studies. Simpson’s (1951) paradox is an elegant illustration of the type of bias that may arise in causal inference subject to unmeasured confounding. Sometimes an analyst may have access to one or more proxies for the unobserved confounder, for example, a mismeasured version of the confounder. In this case, it may seem natural to directly adjust for the available proxies in order to reduce bias due to unobserved confounding (Greenland, 1980, 1996; Carroll et al., 2006; Ogburn & VanderWeele, 2013; Kuroki & Pearl, 2014). Greenland (1980) suggested that standard adjustment of a binary nondifferential proxy that is independent of the treatment and the outcome after conditioning on the confounder generally reduces bias due to confounding; for a polytomous confounder, however, certain monotonicity assumptions appear indispensable to guarantee such bias attenuation (Ogburn & VanderWeele, 2013). But even when the monotonicity assumptions are met, the approach of Greenland (1980) and Ogburn & VanderWeele (2013) cannot completely eliminate the confounding bias. Greenland & Lash (2008) developed a matrix adjustment method that can completely account for unobserved confounding, but it requires external information on the error mechanism, i.e., the conditional distribution of the proxy given the confounder, and therefore cannot be applied in routine situations where the error mechanism is unknown. Fortunately, when multiple proxies for the confounder are available, as shown by Kuroki & Pearl (2014), one can sometimes identify the error mechanism and thus the causal effect without external information. Kuroki & Pearl (2014) studied identification of the causal effect with two independent proxies in the context of graph-based models, where identification means that the causal effect can be determined uniquely from the joint distribution of observed variables. Figure 1 presents several plausible causal diagrams with proxies for the confounder, where X and Y denote the treatment and the outcome respectively, U denotes the confounder that is not observed, but proxies Z and W of U may be available. Model (a) corresponds to a single nondifferential proxy (Carroll et al., 2006; Greenland & Lash, 2008), and (b)–(c) allow the treatment and the outcome to depend on the proxy, respectively; models (d)–(f) depict situations where two proxies are independent conditional on the true confounder. For graph-theoretic terminology, we refer readers to Pearl (2009). Table 1 presents the corresponding conditional independencies for the diagrams in Figure 1. Practical examples for such diagrams can be found in Carroll et al. (2006), Greenland & Lash (2008) and Kuroki & Pearl (2014). Using the do(x) operator of Pearl (2009), the causal effect of X on Y is

$$\text{pr}\left\{y\right|\text{do}(x)\}=\sum _u\text{pr}(y|x,u)\text{pr}(u),$$

where pr stands for the probability mass function of a discrete variable or the probability density function for a continuous variable. For (d)–(e), Kuroki & Pearl (2014) establish sufficient conditions for nonparametric identification of pr(w | u), which suffices to identify pr{y | do(x)} by applying the matrix adjustment technique of Greenland & Lash (2008).

Fig. 1:

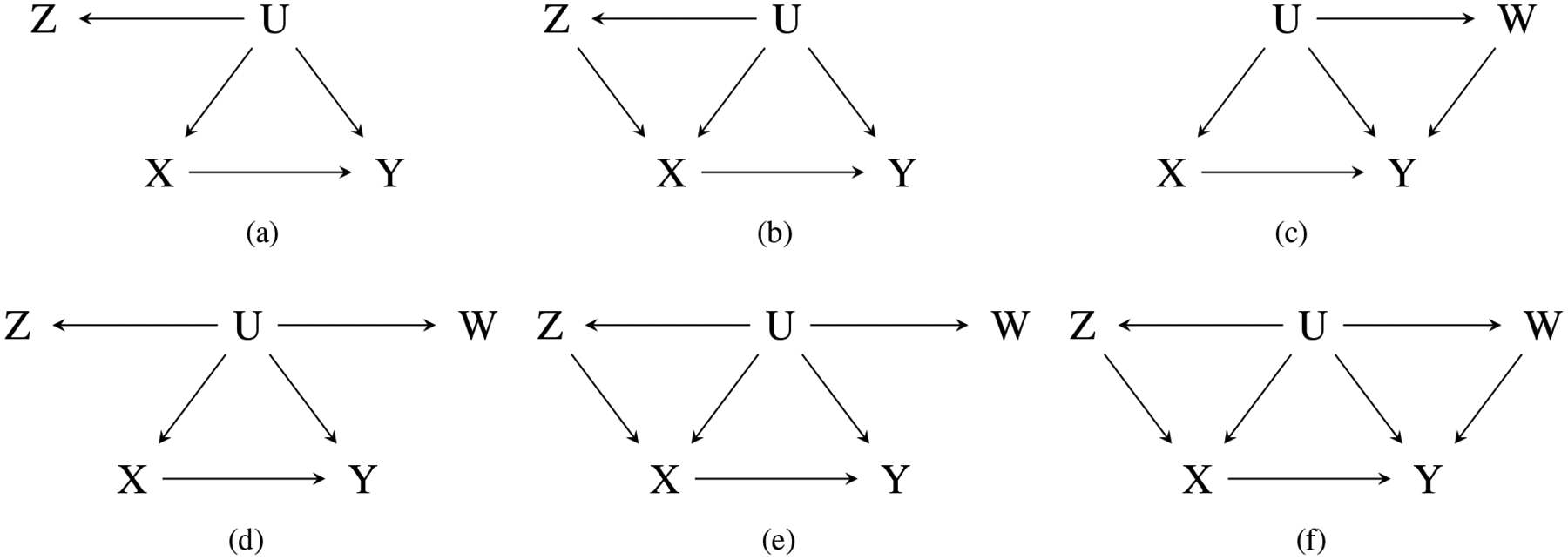
Causal diagrams with confounder proxies.

Table 1:

Conditional independencies of causal diagrams

(a) Z ⫫ (X, Y) | U	(b) Z ⫫ Y | (U, X)
(c) W ⫫ X | U	(d) W ⫫ (Z, X, Y) | U, Z ⫫ (X, Y) | U
(e) W ⫫ (Z, X, Y) | U, Z ⫫ Y | (U, X)	(f) W ⫫ (Z, X) | U, Z ⫫ Y | (U ,X)

Model (f) is more general than (d)–(e). Only under a joint normal model, Kuroki & Pearl (2014) established identification of the causal effect for (f). The nonparametric identification method of Kuroki & Pearl (2014) depends on identification of pr(w | u), and does not apply to model (f), because in general, pr(w | u) is not identifiable in (f). Nonparametric identification of the causal effect for model (f) is not yet available. Below, we propose a novel strategy to nonparametrically identify the causal effect for model (f) without identifying pr(w | u). We consider a categorical confounder in Section 2, and then we generalize the results to the continuous case in Section 3. The required condition is weaker than that of Kuroki & Pearl (2014). Moreover, when only one proxy is available or the proposed identification condition is not met, we establish that it is nonetheless sometimes possible to obtain a valid empirical test of the null hypothesis of no causal effect.

2. Identification with a categorical confounder

As (d) and (e) can be viewed as special cases of model (f) with W ⫫ Y | U, we focus on identification of the causal effect for (f). Suppose W, Z and U are discrete variables, each with k categories. For notational convenience, we use P(W | u) = {pr(w₁ | u), … , pr(w_k | u)}^T, P(w | U) = {pr(w | u₁), … , pr(w | u_k)} and P(W | U) = {P(W | u₁), … , P(W | u_k)} to denote a column vector, a row vector and a matrix that consist of conditional probabilities pr(w | u), respectively. For other variables, vectors and matrices consisting of conditional probabilities are analogously defined: P(U | z, x) = {pr(u₁ | z, x), … , pr(u_k | z, x)}^T, P(U | Z, x) = {P(U | z₁, x), … , P(U | z_k, x)}, and P(y | Z, x) = {pr(y | z₁, x), … , pr(y | z_k, x)}. Model (f) implies that W ⫫ (Z, X) | U and Z ⫫ Y | (U, X), so

$$P(W|Z,x)=P(W|U)P(U|Z,x),$$ (1)

$$P(y|Z,x)=P(y|U,x)P(U|Z,x).$$ (2)

Based on (1) and (2), we identify the causal effect under the condition

P(W | Z, x) is invertible for all x.

This is weaker than the condition of Kuroki & Pearl (2014), which requires invertibility of both P(W | Z, x) and P(y, W | Z, x). Condition (i) is equivalent to requiring that both P(W | U) and P(U | Z, x) are invertible (Banerjee & Roy, 2014, Corollary 5.4), which implies that both W and Z are associated with the confounder U. Condition (i) involves only W, Z and X, and thus can be verified empirically. For the binary case, (i) holds if both Z and W are correlated within each level of X. Under (i), (1)–(2) imply

$$\begin{array}{l}P\left(U|Z,x\right)=P{\left(W|U\right)}^{-1}P\left(W|Z,x\right),\\ P\left(y|Z,x\right)=P\left(y|U,x\right)P{\left(W|U\right)}^{-1}P\left(W|Z,x\right),\end{array}$$ (3)

and thus

$$P(y|U,x)=P(y|Z,x)P{(W|Z,x)}^{-1}P(W|U).$$ (4)

From (4), identification of P(y | U, x) does depend on the error mechanism P(W | U). Letting P(U) = {pr(u₁), … , pr(u_k)}^T with P(W) analogously defined, we have P(W) = P(W | U)P(U). Multiplying P(U) on both sides of (4), we obtain

$$\text{pr}\left\{y\right|\text{do}(x)\}=P(y|Z,x)P{(W|Z,x)}^{-1}P(W).$$ (5)

As a result, identification of pr{y | do(x)} does not depend on P(W | U)! In contrast, the approach of Kuroki & Pearl (2014) requires identification of P(W | U), which rests on the assumption W ⫫ Y | U. When $W\cancel{⫫}Y|U$, i.e., for model (f), however, P(W | U) is in general not identified, and therefore, their approach fails even though the causal effect may still be identified by our formula (5). We illustrate this in the Supplementary Material.

For the binary case, the right hand side of (5) reduces to

$$\frac{\left\{\text{pr}\left(w_1\right)-\text{pr}\left(w_1|z_2,x\right)\right\}\text{pr}\left(y|z_1,x\right)}{\text{pr}\left(w_1|z_1,x\right)-\text{pr}\left(w_1|z_2,x\right)}+\frac{\left\{\text{pr}\left(w_1|z_1,x\right)-\text{pr}\left(w_1\right)\right\}\text{pr}\left(y|z_2,x\right)}{\text{pr}\left(w_1|z_1,x\right)-\text{pr}\left(w_1|z_2,x\right)},$$

which is a weighted average of pr(y | z_i, x), i = 1, 2. It can be viewed as a modified version of the adjustment formula ${\sum }_{i=1}^2\text{pr}\left(y|z_i,x\right)\text{pr}\left(z_i\right)$ suggested by Greenland (1980) and Ogburn & VanderWeele (2013). But their approach can incorporate only one proxy and is biased for pr{y | do(x)} due to confounding. As a second proxy W is available, instead of the weight pr(z), we use a modified weight that can eliminate the bias due to imperfect adjustment of Z.

If W and Z have more categories than U, the causal effect is identifiable as long as P(W | Z, x) has rank k. Identification for this case is achieved by using corresponding coarsening variables W′ and Z′ with k categories such that P(W′ | Z′, x) is invertible.

3. Identification with a continuous confounder

In empirical studies, unobserved confounders may sometimes be continuous. Under model (f), we generalize (5) to the continuous case by assuming the following completeness condition: for all square-integrable function g and for any x,

E{g(u) | z, x} = 0 almost surely if and only if g(u) = 0 almost surely;

E{g(z) | w, x} = 0 almost surely if and only if g(z) = 0 almost surely.

Conditions (ii)–(iii) can accommodate both categorical and continuous confounders. For a categorical confounder with categorical proxy variables, (ii)–(iii) is equivalent to (i). For a continuous confounder, we suppose that both Z and W are continuous. Many commonly-used parametric and semiparametric models such as exponential families (Newey & Powell, 2003) and location-scale families (Hu & Shiu, 2018) satisfy the completeness condition. For nonparametric regression models, results of D’Haultfœuille (2011) and Darolles et al. (2011) can be used to justify the completeness condition, although they focused on instrumental variable estimation. For a review and examples of completeness, see Chen et al. (2014), Andrews (2017) and the references therein.

Letting f denote the probability density function of a continuous variable, instead of the matrix form (3) for the categorical case, identification for the continuous case involves the solution h(w, x, y) to the following integral equation: for any (x, y) and for all z,

$$\text{pr}(y|z,x)={\int }_{-\infty }^{+\infty }h(w,x,y)f(w|z,x)dw.$$ (6)

Equation (6) is a Fredholm integral equation of the first kind. A conventional approach to study its solution is the singular value decomposition (Carrasco et al., 2007, Theorem 2.41). We show existence of its solution under (iii) together with regularity conditions (v)–(vii) in Proposition 1 in the Appendix. The solution to (6) may not be unique, but the causal effect can still be identified.

Theorem 1. Assuming model (f) and condition (ii), for any solution h(w, x, y) to (6),

$$\text{pr}(y|u,x)={\int }_{-\infty }^{+\infty }h(w,x,y)f(w|u)dw,$$ (7)

$$\text{pr}\left\{y\right|\text{do}(x)\}={\int }_{-\infty }^{+\infty }h(w,x,y)f(w)dw.$$ (8)

From the theorem, one can identify the causal effect by first solving (6) and then applying (8) with pr(y | z, x), f(w | z, x) and f(w) obtained from observed variables. While Theorem 1 provides a formal basis for nonparametric inference, specific details on how such inferences can be obtained are beyond the scope of this paper. Nevertheless, we give a semiparametric example.

Example 1. Consider model (f) and assume that f(z, u, w | x) is a normal density for all x; then f(w | z, x) is a normal density function. If one has available pr(y | z, x) and f(w | z, x) = 1/σ(x)ϕ{(w − β₀(x) − β₁(x)z)/σ(x)} from observed variables, with ϕ the standard normal density function and β₁(x) ≠ 0 for all x, then (6) has a unique solution

$$h(w,x,y)=\frac{1}{2\pi }{\int }_{-\infty }^{+\infty }\text{exp}\left\{\frac{\text{i}vw}{\sigma (x)}\right\}\frac{h_2(v,x,y)}{h_1(v)}dv,$$

Where i = (−1)^1/2, h₁(υ) and h₂(υ,x,y) are Fourier transforms of ϕ and pr(y | z, x) respectively $h_1(v)={\int }_{-\infty }^{+\infty }\text{exp}(-\text{i}vz)\varphi (z)dz$ and

$$h_2(v,x,y)=\frac{{\beta }_1(x)}{\sigma (x)}{\int }_{-\infty }^{+\infty }\text{exp}\left\{-\text{i}v\frac{{\beta }_0(x)+{\beta }_1(x)z}{\sigma (x)}\right\}\text{pr}(y|z,x)dz.$$

After obtaining h(w, x, y), we can further identify pr{y | do(x)} from (8).

Example 1 allows X and Y to follow an arbitrary distribution, not necessarily normal, so the model is semiparametric and thus is a generalization of the joint normal model for (X, Y, U, W, Z) considered by Kuroki & Pearl (2014). Under the model of Kuroki & Pearl (2014), Example 1 can be strengthened: one only needs to implement linear regression to obtain $f(y|z,x)~N\left({\alpha }_0+{\alpha }_{1}z+{\alpha }_{2}x,{\sigma }_1^2\right)$ and $f(w|z,x)~N\left({\beta }_0+{\beta }_{1}z+{\beta }_{2}x,{\sigma }_2^2\right)$, then pr{y | do(x)} ~ N(γ₀ + γ₁x, σ²) with γ₁ = α₂ − α₁β₂/β₁ and (γ₀,σ²) presented in the Supplementary Material. One can verify that γ₁ = ∂E(y | u, x)/∂x, which is consistent with the result of Kuroki & Pearl (2014) obtained by an analysis of variance approach that entails normality of (X, Y).

4. Hypothesis testing with proxy variables

Considering a categorical confounder U with k levels, condition (i) implicitly requires that both Z and W have at least as many categories as U, otherwise, the causal effect is in general not identifiable. Nevertheless, as we elaborate below, when one of the proxies has fewer categories than U, we use such proxy variables to test the causal null hypothesis ${ℍ}_0:X⫫Y|U$ in model (f), then we generalize the results to other diagrams. The null hypothesis means that X has no causal effect on Y at any level of U, which is equivalent to pr(y | u) = pr(y | u, x) for all x, y and u. Thus, rejection of the null hypothesis is evidence in favor of causation between X and Y. Because U is not observed, we cannot directly check the divergence between pr(y | u, x) and pr(y | u). Nevertheless, we propose a measure for pr(y | u, x) − pr(y | u) based on proxy variables of U. We assume

X, Z and W have i, j and k categories respectively, with ij ≥ k + 1; and the matrix Q = {P(W | Z, x₁), … , P(W | Z, x_i)} has full row rank.

Under (iv), P(W | U) is invertible (Banerjee & Roy, 2014, Corollary 5.4), and (3) still holds: P(y | Z, x) = P(y | U, x)P(W | U)⁻¹P(W | Z, x) for all x. Denoting q_y = {P(y | Z, x₁), … , P(y | Z, x_i)}^T, we have the decomposition

$$q_y^{\text{T}}=P(y|U)P{(W|U)}^{-1}Q+\{P(y|U,x)-P(y|U)\}P{(W|U)}^{-1}Q.$$ (9)

For fixed y, as x varies, (9) reveals two separate sources of variability of P(y | Z, x): P(W | Z, x) and P(y | U, x). If ${ℍ}_0$ holds, P(W | Z, x) is the only source of variability because P(y | U, x) = P(y | U). Thus, we can test ${ℍ}_0$ by checking whether P(W | Z, x) explains away the variability of P(y | Z, x).

Suppose we have available estimators $\left({\widehat{q}}_y,\widehat{Q}\right)$ that satisfy

$$n^{1/2}\left({\widehat{q}}_y-q_y\right)\to N\left(0,{\Sigma }_y\right)\text{in}\text{distribution,}$$ (10)

$$\widehat{Q}\to Q\text{and}{\widehat{\Sigma }}_y\to {\Sigma }_y\text{in}\text{probability,}\text{with}{\widehat{\Sigma }}_y,{\Sigma }_y\text{positive-definite.}$$ (11)

Letting I denote the identity matrix and

$${\xi }_y=\left\{I-{\widehat{\Sigma }}_y^{-1/2}{\widehat{Q}}^{\text{T}}{\left(\widehat{Q}{\widehat{\Sigma }}_y^{-1}{\widehat{Q}}^{\text{T}}\right)}^{-1}\widehat{Q}{\widehat{\Sigma }}_y^{-1/2}\right\}{\widehat{\Sigma }}_y^{-1/2}{\widehat{q}}_y,$$

then ξ_y is the least-squre residual of regressing ${\widehat{\Sigma }}_y^{-1/2}{\widehat{q}}_y$ on ${\widehat{\Sigma }}_y^{-1/2}\widehat{Q}$, and thus measures the residual variability of P(y | Z, x) not explained by P(W | Z, x). Therefore, we can check how far away ξ is from zero to assess whether ${ℍ}_0$ is correct by using the test statistic $T_y=n{\xi }_y^{\text{T}}{\xi }_y$.

Theorem 2. Assuming model (f), conditions (iv) and (10)–(11), if ${ℍ}_0$ is correct, then n^1/2ξ_y → N(0,Ωy) in distribution, with ${\Omega }_y=I-{\Sigma }_y^{-1/2}{Q}^{\text{T}}{\left(Q{\Sigma }_y^{-1}{Q}^{\text{T}}\right)}^{-1}Q{\Sigma }_y^{-1/2}$ of rank r = ij − k, and $T_y\to {\chi }_r^2$ in distribution.

From Theorem 2, ξ_y asymptotically follows a degenerate multivariate normal distribution, further explaining why ij ≥ k + 1 is required. Given a significance level α, one can reject ${ℍ}_0$ as long as T_y exceeds the (1 − α)th quantile of ${\chi }_r^2$, which guarantees a type I error no larger than α asymptotically. Theorem 2 concerns only one level of the outcome, but in the Supplementary Material we extend to aggregating all levels of a categorical Y. For a categorical outcome, (10)–(11) can be achieved for instance with empirical probability mass functions $\widehat{\text{pr}}(w|z,x)$ and $\widehat{\text{pr}}(y|z,x)$. For a continuous one, (10)–(11) are generally not feasible and discretization is required; however, in many situations where the average causal effect is of interest, one can use q = {E(Y | Z, x₁), … , E(Y | Z, x_i)}^T in construction of the test statistic and perform the test on the mean scale.

The proposed testing strategy is readily generalized to accommodate polytomous W with more than k levels by using an appropriate coarsening of W to construct the test statistic. The proposed test for model (f) applies to (d)–(e). For models (b)–(c), we can test ${ℍ}_0$ by treating one of the proxies as a constant, and to guarantee ij ≥ k + 1, we require Y and X to have more categories than k, respectively. The result equally applies to model (a), which is a special case of (b) and (c). Simulations confirm that our testing strategy performs reasonably well for a moderate sample size, with type I error approximating the nominal level when ${ℍ}_0$ holds and statistical power increasing toward unity when ${ℍ}_0$ does not hold.

5. DISCUSSION

Identifiability of pr(w | u) in models (d)–(e) reflects the well-known fact in latent class analysis that the joint model is identified with at least three independent proxies for the latent factor (Kruskal, 1976; Goodman, 1974; Allman et al., 2009). However, our analysis for model (f) highlights that certain parameters of interest such as the causal effect, is still identifiable with only two independent proxies, even though the latent class model is not completely identified. This work also has promising application in observational studies when negative controls are available (Lipsitch et al., 2010; Gagnon-Bartsch & Speed, 2012; Sofer et al., 2016; Miao & Tchetgen Tchetgen, 2017), in which case, a negative control outcome that is not causally affected by the treatment, and a negative control exposure that does not causally affect the primary outcome, may serve as proxies for the confounder. The proposed methods can accommodate observed covariates by incorporating them into all conditional densities and marginalizing over them to obtain the causal effect. The identification results can be extended by considering multiple confounders U = (U₁, … , U_l) with multiple proxies Z = (Z₁, … , Z_l) and W = (W₁, … , W_l) such that model (f) holds, i.e., W ⫫ (Z, X) | U, Z ⫫ Y | (U, X), in which case, Theorem 1 still applies. For the continuous confounder case, estimation in parametric models, for instance in normal models, is straightforward by linear regression. However, estimation is very challenging in nonparametric models, as it requires solving an integral equation, which we will study elsewhere.

Appendix

We use the singular value decomposition (Carrasco et al., 2007, Theorem 2.41) of compact operators to characterize conditions for existence of a solution to (6). Letting L²{F(t)} denote the space of all square integrable functions of t with respect to a cumulative distribution function F(t), which is a Hilbert space with inner product $\langle g,h\rangle ={\int }_{-\infty }^{+\infty }g(t)h(t)dF(t)$, letting K_x denote the conditional expectation operator: L²{F(w | x)} ↦L²{F(z | x)}, K_xh = E{h(w) | z, x} for h ∈ L²{F (w | x)}, and letting ${\left({\lambda }_{x,n},{\phi }_{x,n},{\psi }_{x,n}\right)}_{n=1}^{+\infty }$ denote a singular value decomposition of K_x, we assume the following regularity conditions:

${\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f(w|z,x)f(z|w,x)\mathit{\text{dwdz}}<+\infty$,

${\int }_{-\infty }^{+\infty }{\text{pr}}^2(y|z,x)f(z|x)dz<+\infty$,

${\sum }_{n=1}^{+\infty }{\lambda }_{x,n}^{-2}{\left|\langle \text{pr}(y|z,x),{\psi }_{x,n}\rangle \right|}^2<+\infty$, then we have the following proposition.

Proposition 1. Given f(w | z, x) and pr(y | z, x), the solution to (6) must exist if conditions (iii) and (v)–(vii) hold together.