Demographic Processes Linked to Genetic Diversity and Positive Selection across a Species' Range

Abstract

Demography determines the strength of genetic drift, which generally reduces genetic variation and the efficacy of selection. Here, we disentangled the importance of demographic processes at a local scale (census size and mating system) and at a species-range scale (old split between population clusters, recolonization after the last glaciation cycle, and admixture) in determining within-population genomic diversity and genomic signatures of positive selection. Analyses were based on re-sequence data from 52 populations of North American Arabidopsis lyrata collected across its entire distribution. The mating system and range dynamics since the last glaciation cycle explained around 60% of the variation in genomic diversity among populations and 52% of the variation in the signature of positive selection. Diversity was lowest in selfing compared with outcrossing populations and in areas further away from glacial refugia. In parallel, reduced positive selection was found in selfing populations and in populations with a longer route of postglacial range expansion. The signature of positive selection was also reduced in populations without admixture. We conclude that recent range expansion can have a profound influence on diversity in coding and non-coding DNA, similar in magnitude to the shift toward selfing. Distribution limits may in fact be caused by reduced effective population size and compromised positive selection in recently colonized parts of the range.

Demography is predicted to affect the magnitude of genetic drift, which in turn lowers the efficacy of directional selection. Across the geographic distribution of a plant, this study shows that the mating system and past species range dynamics, in particular postglacial range expansion, explain population-level genetic variation and the genome-wide signature of positive selection. Selfing populations and those with longer expansion routes have greatly reduced the signatures of selection, pointing to evolutionary constraints in adaptation.

Introduction

Demographic processes are important in population genetics because they determine the strength of genetic drift (Caballero, 1994). In turn, genetic drift shapes genetic variation within and among populations and can reduce the efficacy of selection if selection is weak (Wright, 1931). A rich empirical literature documents that demographic parameters, such as census size and mating system, can explain a considerable amount of variation in within-population genetic diversity (Hamrick and Godt, 1990; Frankham, 1996; Leimu et al., 2006). These demographic parameters may vary on small spatial scales, among local populations, and differences may originate recently in time. Other demographic processes act on larger geographic scales and extend further back in time, such as range expansions (Excoffier et al., 2009) and rear-edge dynamics (Hampe and Petit, 2005). These too can have a large impact on within-population diversity (e.g., Hewitt, 2000). However, the relative importance of demography in determining genetic diversity—via biology, ecology, and population history—and in determining the outcome of directional selection are unresolved (Leffler et al., 2012; Ellegren and Galtier, 2016; Galtier, 2016).

Demography determines the drift-effective population size, N_e (Wright, 1931; Kimura, 1955). The effective population size refers to the size of an ideal stable population with discrete generations, random mating, and random reproductive output that would produce the same quantity of genetic drift as in the real population (Caballero, 1994). The extent to which N_e deviates from the number of reproducing individuals depends on many factors, for example, the mating system (Caballero, 1994). Complete selfing over generations is predicted to cause N_e to be one half that of a randomly mating population (Pollak, 1987; Nordborg, 2000). N_e has two main impacts on subsequent evolution. First, the rate of appearance of new mutations in a population is proportional to N_e, and this affects genetic variation over longer periods of time. Second, the inverse of N_e determines the magnitude of genetic drift, defined as the random change in allele frequency across generations. Genetic drift leads to enhanced fixation or the loss of alleles and, therefore, a loss of genetic diversity in small populations (Wright, 1931). The loss of diversity can be restored quickly only by another local demographic factor, gene flow, which generally increases within-population genetic diversity (reviewed in Felsenstein, 1976). Genetic drift also opposes selection if selection coefficients are smaller than 1/2N_e (Wright, 1931).

In addition to local factors acting recently, more regional demographic processes related to species' range dynamics can also influence genetic diversity because of genetic drift that acted in the more distant past. Such processes include long-term isolation, range retractions due to major disturbances, recolonization, and admixture between formerly separated clusters. These sorts of dynamics are particularly important (and well studied) in species that were strongly affected by the Quaternary Ice Ages in northern-temperate zones (Hewitt, 1999, 2000). Many species survived glacial maxima in small regions with favorable climatic conditions, from which they recolonized the newly ice-free areas at the end of cold periods. This dynamic process is predicted to create a spatial pattern of high genetic diversity in areas of former refuge and a decline in diversity along the expansion routes due to serial founder events and genetic drift (Excoffier et al., 2009). This pattern has been largely confirmed in high-latitude species (Hewitt, 1996, 2000). The opposite end of the distribution, the low-latitude or rear edge, is affected mainly by the dynamics of prolonged isolation and small population size that reduce within-population genetic diversity and increase genetic differentiation among populations (Hampe and Petit, 2005). In contrast to the many studies of neutral genetic diversity after the Quaternary Ice Ages, it is unclear whether genetic drift has opposed directional selection and left a reduced signature of positive selection at leading and rear range edges.

However, genetic drift opposing selection is the focus of theoretical studies on species' range limits. In many evolutionary models of range limits, the environment is assumed to change continuously and with it the value of the trait favored by selection (Sexton et al., 2009). The trait is assumed to have a polygenic basis and selection acts on many loci within the genome (Sexton et al., 2009). Two recent models have predicted stable range limits caused by genetic drift. The first, with a one-dimensional layout of the potential habitat, predicted sharp range limits due to genetic drift opposing selection (Polechová and Barton, 2015). In the second model with a two-dimensional layout of the potential habitat, sharp range limits were established due to genetic drift eroding genetic variation (independent of selection) (Polechová, 2018). While the role of varying genetic drift was not directly explored, the studies suggest that range limits can be caused if genetic drift is enhanced, regardless of the steepness of the environmental gradient, likely leaving a reduced signature of positive selection.

We quantified the relative importance of local demographic parameters (census size and mating system) and species' range dynamics in explaining within-population genomic diversity and signatures of positive selection in the North American Arabidopsis lyrata spp. lyrata (hereafter, A. lyrata). A. lyrata is a short-lived perennial plant, predominantly outcrossing and closely related to the model species A. thaliana. The North American subspecies has a range that extends from North Carolina and Missouri to upstate New York and Ontario (Lee-Yaw et al., 2018). Previous work based on microsatellite data identified an old split between an eastern and a western genetic cluster, with some evidence of range expansion in the north and rear-edge dynamics in the south (Griffin and Willi, 2014). A recent study on pool-sequencing genomic data confirmed the east-west split and suggested that the southern populations in Missouri were even older (Willi et al., 2018). A few selfing and mixed-mating populations were located mostly at the edges of the eastern and western distributions (Griffin and Willi, 2014). Genetic diversity is reduced markedly in these populations, as well as in outcrossing populations at increasing distance from the centers of the two ancestral clusters (Foxe et al., 2010; Griffin and Willi, 2014; Willi et al., 2018). Both selfing and range-edge populations show increased signatures of mutational load, indicating a reduced efficacy of purifying selection (Willi et al., 2018). Here, we first report additional results on the dated phylogeographic history of North American A. lyrata. We then address our main questions: (1) What is the relative importance of local demography (census size and mating system) versus aspects of range dynamics (east-west split, expansion or rear-edge history, and admixture) on within-population genomic diversity in intergenic and coding regions of the genome? (2) Is the imprint of positive selection across the genome related to local and range-level parameters, and is genomic diversity positively related to the imprint of positive selection? Here, the assumption was that demography reflects drift and should therefore influence the efficacy of positive (directional) selection. Finally, we compared genomic diversity estimates based on genome-wide single-nucleotide polymorphism (SNP) frequencies and published microsatellite-based genetic diversity estimates.

Results

Mapping and SNP Calling

The 52 populations included in this study (Figure 1) covered the entire known range of the subspecies lyrata (Schmickl et al., 2010). Pool-sequencing of 25 individuals per population yielded more than 13 billion mapped paired-end reads. After applying the initial read depth cutoff (25–500×) and removing duplicates, an average of 220 million paired-end reads per population (range, 128–323 million) were mapped unambiguously to 67% of the A. lyrata nuclear genome (range, 62%–72%) with a mean depth of 128× (range, 72–188×). The mean number of biallelic SNPs with a minor allele frequency above 0.03 called per population was 1.1 million (range, 0.2–2.1 million). Overall, 1.5% of the sequenced base pairs were SNPs, with the highest percentage for intergenic regions (1.6%), followed by introns (1%) and coding DNA sequences (CDS) (0.8%) (Supplemental Figure 1).

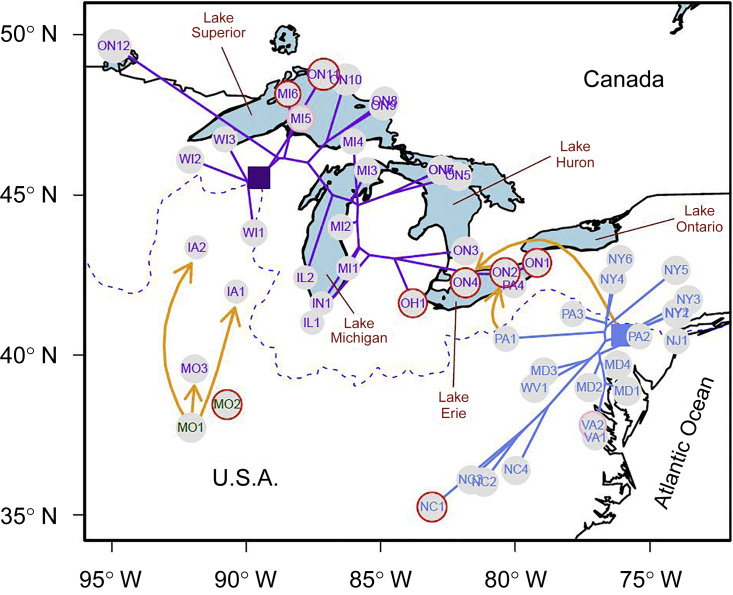
Figure 1.

Map of North American Arabidopsis lyrata Populations Included in this Study.

The populations are indicated by abbreviations (state/province, followed by a number that sorts populations along latitude in the USA and longitude in Ontario, Canada). The two populations of the Ozarks clade are indicated in green, those of the mid-western clade in purple, and those of the eastern clade in blue. For the latter two clades, the relatedness tree starting from the deduced glacial refuge is plotted on the map, in purple for the western clade and in blue for the eastern clade. The position of the most recent common ancestor of populations that appeared after the LGM is represented with squares. Selfing and mixed-mating populations are highlighted by red and pink circles, respectively. The yellow arrows indicate admixture events supported by statistical testing (details in the Results section). The dashed blue line shows the maximum extent of the ice at the last glacial maximum.

Relatedness Tree and Historic Range Dynamics across the Species' Distribution

The geography of postglacial range expansion was inferred by a dated relatedness tree of all populations based on SNP frequencies (Supplemental Figures 2 and 3) and its plotted nodes on the North American map (Figure 1). A second tree produced with another phylogenetic model and on a subset of populations produced the same topology; divergence dates were in good agreement, except for the most recent splits (Supplemental Figure 4). The first split within North American A. lyrata separated Ozark populations in Missouri from all other populations and dated to 253 000 years ago, indicating that these Ozark populations are part of a very old rear edge of the species' distribution (Supplemental Figure 3). The second split was between a mid-western and an eastern clade dating to 169 000 years ago. Within the western clade, the next splits involved populations in northern Missouri and Iowa (MO3, IA1, and IA2, Figure 1, Supplemental Figure 2), with estimated divergence times of 135 000 and 101 000 years ago, respectively (Supplemental Figure 3). These populations are also part of the rear edge, but with younger ages. All other western populations had a common ancestor (Figure 1, purple square, and Supplemental Figure 3, purple circle) from which extant populations in Wisconsin appeared, together with an ancestral population that was the source of all other western postglacial range expansion (Supplemental Figures 2 and 3). Phylogeny and map projection suggested some northward colonization, with extensions to the north shore of Lake Superior and Lake of the Woods, and then eastward colonization to the north shore of Lake Michigan, with two main split-offs, one to the southwestern shore of Lake Michigan and another to the north shore of Lake Huron on Manitoulin Island. Further expansion reached southeastern Lake Michigan, and colonization of the south shore of Lake Huron and Lake Erie followed. The estimated age of the most recent common ancestor for most northern populations in the western clade was 17 000 years (Supplemental Figure 3). In the eastern clade, the most basal population was on the New Jersey coast (NJ1), with a divergence time of about 84 000 years ago (Supplemental Figures 2 and 3). Other eastern populations emerged from an ancestor presumably located in eastern Pennsylvania (Figure 1, blue square, and Supplemental Figure 3, blue circle). Early splits involved populations in southern New York State. Subsequent splits reached further north in New York State or further west in Pennsylvania, south along the Appalachians, and south toward the Atlantic coast. The estimated age of the most recent common ancestor for most northern populations and recently emerged southern populations was about 19 000 years (Supplemental Figure 3).

The relatedness tree included seven admixture events (Supplemental Figure 2), five of which were supported by a four-population test (Figure 1, yellow arrows), one of which was not supported, and one of which could not be tested. Populations around Lake Erie showed a signature of genomic admixture with populations from the east. One migration event originated from the most ancestral population of the eastern cluster to ON1, ON2, ON4, and PA4 with a migration weight (w_m) of 47.8%, and one from eastern PA1 to ON1 and PA4 with a w_m of 38.4%. Four-population testing of the tree [[NJ1, PA1],[ON3, X]], where X is a western population located north of the limit of the Laurentide ice sheet, revealed significant positive Z scores for the four most eastern populations on Lake Erie (Supplemental Table 2). Additional migration events were detected from MO1 to MO3 (w_m = 39.5%), to IA1 (w_m = 25.2%), to the ancestor of IA2 and MO3 (w_m = 20.8%), and to the ancestor of WI1 and WI2 (w_m = 14.7%). Four-population testing was based on the tree [[MO1, MO2],[WI3, X]], where X was a western population. We obtained significant positive Z scores for MO3 and the two Iowa populations, but not for WI1 (Z score = −0.589, P = 0.556) and WI2 (Z score = 0.565 P = 0.572) (Supplemental Table 3). Another admixture event was found from eastern VA2 to the ancestor of MO1 and MO2 (w_m = 30.6%), which could not be tested for significance with the four-population test as there was no other population in the Ozarks clade without a signature of admixture.

Demographic Parameters Linked to Genomic Diversity

The five independent variables had high explanatory power for diversity estimates, with models explaining 68%–77% of the variation for Tajima's π and Watterson's θ (Table 1), and 4%–13% of the variation for Tajima's D (Supplemental Table 4).

Table 1.

Linear Model Testing Relationships between Genomic Diversity and Census Size, the Mating System, Ancestral Cluster, Distance to Cluster Core, and Admixture.

	Intergenic Regions				CDS Regions
	π		θ		π		θ
Source	Estimate	Var. (%)	Estimate	Var. (%)	Estimate	Var. (%)	Estimate	Var. (%)
Intercept	0.0039∗∗∗		0.0038∗∗∗		0.0010∗∗∗		0.0009∗∗∗
log10 (census size)	0.0001	0.76	0.0001	0.79	0.0000	0.72	0.0000	0.70
Mating system (selfing)	−0.0017∗∗∗	31.74	−0.0017∗∗∗	26.35	−0.0006∗∗∗	33.43	−0.0005∗∗∗	28.45
Ancestral cluster (west)	−0.0008∗∗	15.65	−0.0007∗	11.69	−0.0002	9.44	−0.0001	7.76
log10 (distance to core)	−0.0026∗∗∗	26.57	−0.0031∗∗∗	27.47	−0.0010∗∗∗	29.96	−0.0010∗∗∗	30.17
Admixture (yes)	0.0006∗	1.79	0.0005	1.62	0.0002	1.71	0.0002	1.57

Genomic diversity is represented by the weighted medians of Tajima's π and Watterson's θ of intergenic regions and CDS regions (windows of 5000 bp). The sample size for all models was 52 populations. Models explained a large amount of variation: intergenic π, R² = 0.77; θ, R² = 0.68; CDS π, R² = 0.75; θ, R² = 0.69. Estimated intercept and coefficients, and variation explained are reported. Significance is indicated: ∗0.01 < P ≤ 0.05, ∗∗0.001 < P ≤ 0.01, ∗∗∗P ≤ 0.001.

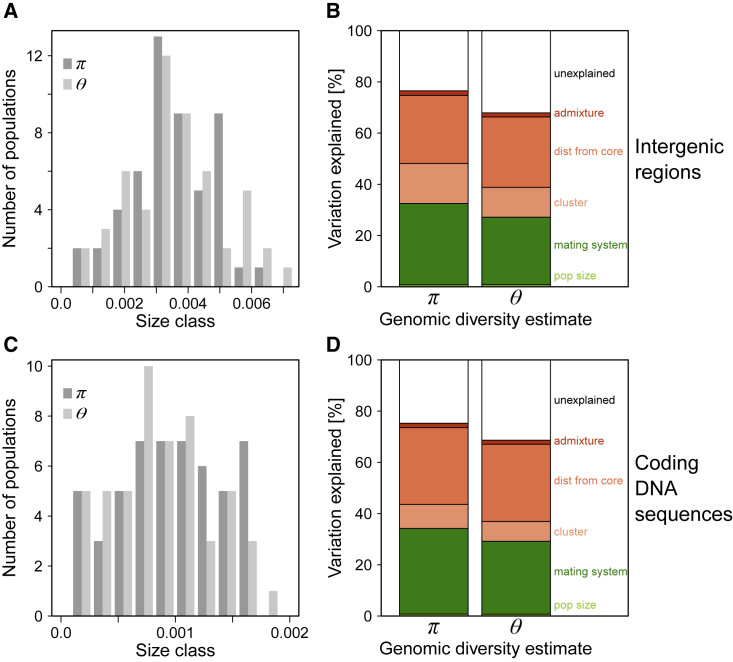
Tajima's π

The weighted median of π across windows of 5000 bp varied among populations, with ranges of 0.0003–0.0059 for intergenic regions and 0.0000–0.0016 for coding regions (Figure 2A). The variables that explained significant amounts of variation in π in intergenic regions—sorted by importance—were the mating system (32%), distance to core, ancestral cluster membership, and admixture, with the species' range variables explaining 44% of the variation (Figure 2B). Two variables explained significant variation in π within coding regions: mating system (33%) and distance to core (30%). Selfing populations had lower π than outcrossing populations, and π decreased with distance from the core (Table 1). Populations of the western genetic cluster had reduced π for intergenic regions, and admixture between clusters increased nucleotide diversity of intergenic regions. The census size did not explain significant variation in π, neither for intergenic nor CDS regions. However, when only outcrossing populations along the expansion route since the last glacial maximum (LGM) were considered (and corrected for distance to core), then small populations of the western cluster had reduced nucleotide diversity compared with large populations (N = 19, P < 0.05 for intergenic and CDS regions). However, small populations in the eastern cluster had enhanced nucleotide diversity (N = 18, P < 0.05 for intergenic and CDS regions).

Figure 2.

Distribution of Population Estimates of Genomic Diversity in North American Arabidopsis lyrata and the Demographic Processes Associated with Them.

Genomic diversity was estimated by Tajima's π and Watterson's θ in intergenic regions (A) and coding DNA (C), and demographic processes at local and species-range scales were considered (B and D). On the local scale, factors included population census size and the mating system, and on the species-range scale, they included an old split between population clusters, distance to core mainly depicting recolonization after the last glaciation cycle, and admixture between ancestral groups. Results of the linear models are presented in Table 1; the sample size was 52 populations.

Watterson's θ

The weighted median of θ across windows of 5000 bp varied among populations, with ranges of 0.0003–0.0069 for intergenic regions and 0.0000–0.0018 for coding regions (Figure 2C, Supplemental Table 1). Variables that explained significant amounts of variation in θ in intergenic regions included distance from the core, the mating system, and ancestral cluster membership (Figure 2D). The local mating system explained 26% of the variation and the large-scale variables together explained 39%. For θ of CDS regions, only distance from the core (30%) and the mating system (28%) were significant. The direction of effects was the same as that for π (Table 1), including the effect of census size of outcrossing populations differing between west and east (two out of four tests with a trend only). In neutral intergenic regions, θ should change linearly with N_e, so we tested whether θ in selfing populations declined more than the predicted (1 + F_IS) compared with outcrossing populations (Pollak, 1987). We tested this by considering only the eight selfing populations (but no mixed-mating ones) and geographically near outcrossing populations (N = 15; one outcrossing population was used in two comparisons). A paired t-test revealed that selfing populations had θ-values for intergenic regions that averaged 26% lower than expected due to inbreeding alone (P < 0.05, two-sided testing; Supplemental Table 5).

Tajima's D

The analysis of Tajima's D of intergenic and CDS regions showed that the overall model was not significant and none of the explanatory variables were significant, except for a positive relationship between distance from core and Tajima's D for intergenic regions (explained 8% of the variation; Supplemental Table 4). This probably reflects a decline in population size toward the edges.

Demographic Parameters Linked to the Signatures of Positive Selection

The two variables depicting genome-wide signatures of positive selection showed an intermediate to strong positive relationship with Tajima's π in intergenic regions (r² = 28% and 63%), which should reflect the drift-effective population size in the absence of between-population gene flow (Table 2A). The first measure was based on the McDonald-Kreitman test applied to individual genes, that is, the fraction of genes with a significant McDonald-Kreitman test, F_genesposSel. Positive selection is deduced if the ratio of non-synonymous to synonymous substitutions, determined relative to an outgroup, is larger than the ratio of non-synonymous to synonymous polymorphisms (D_N/D_S > P_N/P_S, McDonald and Kreitman, 1991), where the latter ratio is assumed to be the reference of neutral evolution (and deleterious mutations are removed by strong negative selection). An important problem is that mutations with a slightly deleterious effect contribute more to P_N than D_N and, therefore, lower the detection of positive selection (Fay et al., 2001). This problem can be alleviated by focusing on polymorphisms with a high minimal frequency (Fay et al., 2001; Messer and Petrov, 2013). The other estimate was based on a derived version of the McDonald-Kreitman test, called asymptotic MK or aMK. Here, the rate of adaptation (α = 1 − P_N/P_S ∗ D_S/D_N) is deduced by estimating its asymptote when P_N/P_S is calculated for each bin of unfolded site-frequency spectra (SFS) for non-synonymous and synonymous sites, α (Messer and Petrov, 2013). This test is reported to be immune to the presence of slightly deleterious mutations interacting with demography and linkage combined with selection (Messer and Petrov, 2013).

Table 2.

Linear Models Testing Relationships between Two Measures of Directional (Positive) Selection and Genomic Diversity in Intergenic Regions (A) or Census Size, the Mating System, Ancestral Cluster, Distance to Cluster Core, and Admixture (B).

	FgenesposSel		α
Source	Estimate	Var. (%)	Estimate	Var. (%)
(A)
Intercept	0.0016∗∗∗		0.0217∗
π, intergenic regions	0.5226∗∗∗	28.04	70.8561∗∗∗	62.72
Depth of sequencing	1.9 ×10−5∗∗∗	17.08
(B)
Intercept	0.0018∗∗∗		0.0335
log10 (census size)	0.0000	0.81	0.0092	0.93
Mating system (selfing)	−0.0009∗	7.63	−0.1086∗∗∗	17.57
Ancestral cluster (west)	−0.0004	5.93	−0.0036	3.67
log10 (distance to core)	−0.0024∗∗	11.50	−0.3292∗∗∗	34.36
Admixture (yes)	0.0013∗∗	9.39	0.0837∗	2.36
Depth of sequencing	2.1 ×10−5∗∗∗	16.63

The response variables are the fraction of genes with a significant McDonald–Kreitman test (F_genesposSel) and the rate of adaptation estimated on non-synonymous versus synonymous sites (α). F_genesposSel was influenced by the depth of sequencing, which was therefore included as a covariate. The sample size was 52 populations. Variance explained by genomic diversity (R²) was 0.28 and 0.63, respectively, for the two variables; variance explained by the model with demographic factors was 0.52 (including depth of sequencing) and 0.59, respectively. Estimated intercept and coefficients, and variation explained are reported. Significance is indicated: ∗0.01 < P ≤ 0.05, ∗∗0.001 < P ≤ 0.01, ∗∗∗P ≤ 0.001.

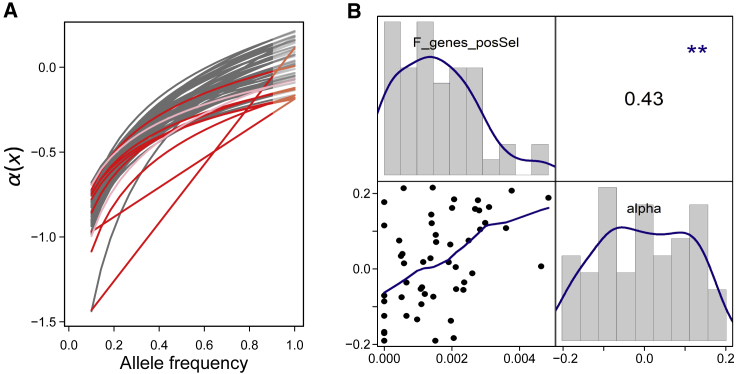
The main model focused on the relationship between signatures of positive selection and demographic factors (Table 2B). Models including all demographic factors explained up to 60% of the variation in the signature of selection among the populations. The mating system was significantly related with F_genesposSel and α, with selfing populations having a lower imprint of positive selection (Figure 3A). In addition, distance from core was consistently linked with F_genesposSel and α; populations farther away from cores had lower signatures of positive selection (Figure 4). For outcrossing populations with a history of recent expansion, there were significant correlations between expansion distance and both F_genesposSel and α (r = −0.49 and −0.74, respectively; N = 37). For outcrossing populations on the rear edge, correlations between rear-edge distance and F_genesposSel and α were −0.35 and −0.25, respectively (N = 5). However, only the southernmost Missouri population had a negative α (−0.07). The mating system and distance from core together explained 52% of the variation in α. Finally, admixture was positively associated with both genomic estimates of selection. F_genesposSel was also positively affected by the depth of sequencing. The values of α ranged from −0.19 to 0.21, and F_genesposSel and α were positively correlated (r = 0.43) (Figure 3B).

Figure 3.

Distribution of and Relationship between Two Population Estimates of Signatures of Positive Selection in North American Arabidopsis lyrata.

The two estimates are the fraction of genes with a significant McDonald-Kreitman test (F_genesposSel) and α. Values of α(x), calculated for each population across bins of site frequency spectra (x, from 0.1 to 0.9) of non-synonymous and synonymous sites, are shown (A). Fitted curves are exponential when possible and linear otherwise. The asymptote (deduced for x = 1) reveals the rate of adaptive evolution in non-synonymous compared with synonymous sites, α. Colors represent populations of the different mating systems: outcrossing in gray, selfing in red, and mixed-mating in pink. In addition, the distribution of the two estimates of positive selection is shown (B). Along the diagonal, histograms of the estimates are plotted, in the lower triangle a scatterplot between the estimates with predictions from a locally fit polynomial model, and in the upper triangle the Pearson correlation coefficient (with significance indicated by stars).

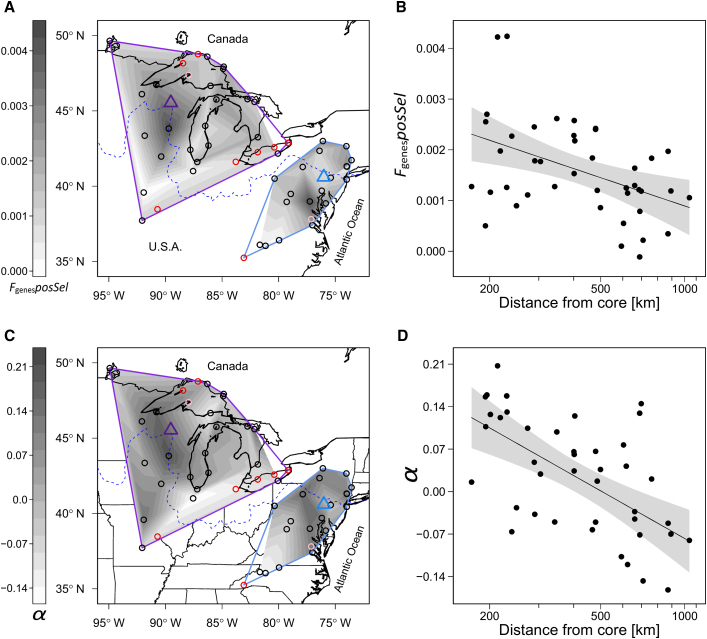
Figure 4.

Geographic Pattern of the Genomic Signatures of Positive Selection in North American Arabidopsis lyrata, and Their Relationship with Distance from Core, Mainly Depicting Recolonization Distance after the Last Glaciation Cycle.

Results are shown on the estimate of the fraction of genes with a significant McDonald-Kreitman test (F_genesposSel) (A and B), and on the rate of adaptation, α, calculated by the aMK method on non-synonymous and synonymous sites (C and D). All panels are based on outcrossing populations only (and after correcting for all factors explaining >1% of variation, except for distance from core). The locations of selfing (red circles) and mixed-mating populations (pink circles) are shown for completeness (A and C). Maps show interpolated estimates within minimum convex polygon hulls surrounding populations of the western and eastern ancestral genetic clusters in purple and blue. Triangles indicate the core areas from which recolonization began after the most recent glacial maximum. Unshaded areas within the polygon hulls are regions with no outcrossing populations. The dashed blue line indicates the maximum extent of the ice sheet during the last glacial maximum. Plots on the right show regression lines (in black) and 95% confidence intervals (gray surface) of the relationship between population estimates of positive selection and distance from core (B and D). Signatures of positive selection declined with increasing distance from the core areas.

Comparison between Microsatellite Diversity and Genome-wide Diversity

Microsatellite and genome-wide diversity estimates were highly correlated (Supplemental Table 6). Heterozygosity estimates, expected heterozygosity at a few microsatellite loci and nucleotide diversity π across genomic regions, had correlation coefficients in the range of r = 0.89–0.93. Frequency-independent estimates of genetic diversity, the allelic richness for microsatellites and Watterson's θ, were correlated to a similar extent. Genomic estimates were even more highly correlated with each other, in particular the same type of diversity estimator but for different genomic regions (range, 0.98–1.00 for both π and θ).

Discussion

Our goal was to compare the relative importance of local and range-wide demographic dynamics in explaining the magnitude of genetic drift and the genome-wide signatures of positive selection in North American A. lyrata. Both types of demographic parameters were clearly important for genetic drift because they explained 70%–80% of the variation in diversity estimates for intergenic and CDS regions (Table 1, Figure 2B and 2D). Two demographic processes were especially relevant in lowering genetic diversity, that is, local shifts in the mating system from outcrossing to selfing and range dynamics, mainly range expansion since the last glaciation cycle. Moreover, genome-wide signatures of positive selection estimated by a McDonald-Kreitman method on the entire SFS were lower in both selfing populations and populations at a greater distance from the region from which expansion started, here called core (Figures 3A and 4). Overall, our results indicate that demographic factors strongly associated with enhanced genetic drift are intermittently linked with reduced signatures of directional selection on a micro-evolutionary scale. Previous inferences of this type have been performed by comparing species, with overall positive (Gossmann et al., 2012) or mixed results (Galtier, 2016).

Demography, Drift, and Genetic Variation

One of the two main factors shaping genetic diversity was the mating system, with selfing populations having much reduced diversity (Table 1, Supplemental Table 5, Figure 2B and 2D). According to theory, generations of self-fertilization should reduce the effective population size (N_e) by one-half relative to a randomly mating population (Pollak, 1987). Here, we confirm that N_e in selfing populations of A. lyrata was reduced by about 26% more than predicted by simple theory (Willi and Määttänen, 2011). Three explanations for a more pronounced decline in N_e in selfing populations have been suggested: selfing populations lose more diversity under background selection compared with outcrossing populations because of higher linkage, selfing populations are less receptive to gene flow, and selfing individuals are better colonizers at the cost of undergoing stronger bottlenecks (Charlesworth et al., 1997; Pannell and Dorken, 2006). The mechanism invoking background selection is plausible because linkage is stronger and extends over longer sequences in selfing compared with outcrossing populations of A. lyrata (Lucek et al., 2019), which should heighten the effect of background selection on reducing genetic diversity (Charlesworth et al., 1997). In our system, the mechanism invoking reduced gene flow into selfing populations is unlikely because gene flow over a few hundred meters to a few kilometers is limited even in outcrossing populations (Willi and Määttänen, 2010, 2011). Finally, we suspect that selfing individuals do not differ in colonizing ability. Selfing in A. lyrata evolved predominantly toward the distribution edges during postglacial expansion, which agrees with a hypothesis of long-distance dispersal and reproductive assurance (Baker, 1955; Stebbins, 1957). However, selfing populations within the range do not occupy large sections of the expansion area, as would be predicted under range expansion and surfing of advantageous alleles (Excoffier et al., 2009). The reason may be that selfing evolved on the expanding wave of recolonization only as the species was about to reach the limits of its ecological niche (southern and northern range edges coincide with niche limits; Lee-Yaw et al., 2018), or it evolved after colonization. A further and very likely explanation for the greater-than-expected decline in N_e is that selfing populations underwent strong bottlenecks when they were founded or since the shift to selfing. A similar scenario has been proposed for the evolution of self-compatible Capsella rubella, which is thought to have speciated via a single selfing individual from self-incompatible C. grandiflora in Mediterranean Europe (Guo et al., 2009). In conclusion, more background selection due to linkage and stronger bottlenecks may explain the greater-than-expected decline in the effective population size in selfing populations.

Postglacial range expansion was about equally important as the mating system for genomic diversity (Figure 2B and 2D). Roughly estimated divergence dates suggest that most populations appeared after the Laurentide ice sheet of the last (Wisconsin) glaciation cycle began to withdraw 19 000 to 20 000 years ago (Clark et al., 2009) (Supplemental Figure 3) from two well-known refuge areas, the Driftless Area and the northeastern USA (Beatty and Provan, 2010). The population phylogeny allowed us to reconstruct the geographic routes of expansion (Supplemental Figures 2–4). In the west, the expansion resembled a single main wave starting at the northern edge of the Driftless Area in Wisconsin and extending eastward to northern Lake Michigan, southward to the Lower Michigan Peninsula, and ending at southern Lake Huron and Lake Erie. In the east, expansion occurred in a star-like manner from a refugial region in the central Appalachians in eastern Pennsylvania, including to the southern Appalachians, and the Atlantic coast in Maryland and Virginia. We conclude that the consistent decline in genomic diversity from core to edge of distribution in the two ancestral clusters was caused by this recent range expansion at the end of the LGM in the north and southeast, combined with rear-edge dynamics in the southwest.

Other demographic processes had lesser effects on genomic diversity (Figure 2B and 2D). An older event in range dynamics, namely the east-west split from about 170 000 years ago (Supplemental Figure 3; 150 000 years ago, Supplemental Figure 4), explained some contemporary genomic diversity in intergenic regions but not in coding regions. An east-west split is common in eastern North American plant and animal species (reviewed in Soltis et al., 2006) and in the case of A. lyrata seems to reflect isolation and differentiation since the Illinoian glaciation. However, the loss of genomic diversity in most western populations may be younger and due to long-term isolation of populations in Missouri and Iowa, and range expansion into northern and eastern regions. Admixture between populations of the three basal clades of North American A. lyrata left only a small and positive imprint on nucleotide diversity in intergenic regions. Two regions with admixture events were detected, one in the southwest and another in the Lake Erie region. For the southwest, the likely scenario is that the Ozarks clade (MO1, MO2) contributed to admixture in populations just to the north (Figure 1, MO3, IA1, and IA2). The Ozarks clade split from the rest of A. lyrata around 253 000 years ago (Supplemental Figure 4; 225 000 years ago, Supplemental Figure 3), presumably soon after the colonization of North America by A. lyrata (the split between the American and European subspecies is about 240 000 years old; Pyhäjärvi et al., 2012). For the Lake Erie region, admixture happened between eastern and western clades, most likely soon after the last glaciation cycle because the populations involved appeared only then. Finally, current census size showed no significant relationship with genomic diversity. Only in the western expansion area was there a positive relationship between census size and nucleotide diversity in intergenic and CDS regions, supporting results of a previous microsatellite study on 18 mostly northern populations (Willi and Määttänen, 2011). This suggests that census size does not capture the effective population size, and that population history and ecology exert overriding effects on genetic variation.

Demography, Drift, and Genome-wide Signatures of Positive Selection

Genome-wide signatures of positive selection varied widely across the 52 populations, with rates of adaptive evolution (α) varying from −0.19 to 0.21 and covering a range of values typically observed in plants (Gossmann et al., 2010). Some populations showed clear genome-wide evidence of adaptive amino acid substitution, while others did clearly not, reflecting considerable variation in the importance of positive selection. This finding warns against pooling a few arbitrary samples to draw species-level conclusions about adaptive evolution, as has been common in the field.

Three demographic parameters were consistently associated with genome-wide signatures of positive selection. First, an outcrossing mating system was positively related to both measures of selection (Table 2, Figure 3A). Glémin et al. (2006) reported a trend toward stronger positive selection in outcrossing taxa in a comparison among species differing in the mating system. Our results for both McDonald-Kreitman tests at the level of genes and aMK testing across the genome agreed that outcrossing populations of A. lyrata had higher rates of adaptive evolution. This result raises two important points. First, even if the result applies generally, it does not mean that selfing populations of A. lyrata are poorly adapted to their environment, but simply suggests that selection must be strong for adaptation to occur. It is known, for example, that selfing populations produce less pollen, and this is presumably an adaptation to selfing (Willi, 2013; Carleial et al., 2017). Second, the weaker signature of directional adaptation in selfing populations comes hand-in-hand with a weaker signature of purifying selection, heightened mutational load, and reduced individual performance (Willi et al., 2018).

The second demographic factor related to genome-wide signatures of positive selection was distance from core. Both estimates of the signature of selection declined with expansion distance (Table 2, Figure 4). For α, the pattern of decreasing signature of selection within increasing distance seemed stronger for longer expansion distance than for rear-edge isolation. Only one population of the rear edge had a negative α, but the sample size for the rear edge was low. This suggests that, in populations that were exposed to enhanced genetic drift due to past range expansion, the efficacy of directional selection was reduced, and adaptive molecular evolution was constrained. Recent theory predicts that genetic drift either opposing directional selection or eroding genetic variation may be important in setting range limits along an environmental gradient (Polechová and Barton, 2015; Polechová, 2018). In our system, a niche-modelling study indicated that the distribution limit of A. lyrata coincides with niche limits in the south and north (Lee-Yaw et al., 2018). In addition, populations at range edges are known to suffer from increased mutational load, presumably due to genetic drift overpowering purifying selection (Willi et al., 2018; Perrier et al., 2020). The current study shows that range-edge populations also suffer from reduced efficacy of directional selection. Both should contribute to lower fitness in populations at range edges and may help establish range limits (Willi and Van Buskirk, 2019).

However, not all directional selection is overpowered by genetic drift toward range edges. In A. lyrata, phenotypic divergence among populations along latitudinal gradients, including populations from southern and northern range edges, indicate that adaptive divergence is underway. Common garden experiments show that A. lyrata from the north grow larger, flower earlier, and are more frost resistant but less heat resistant compared with plants from the south, all pointing to adaptations to living in a cooler environment with a shorter vegetation season (Paccard et al., 2014; Wos and Willi, 2015). This suggests that adaptation to local environmental conditions is possible if directional selection is strong enough, even for populations with a history of genetic drift, while adaptation may be constrained for weaker directional selection (Wright, 1931; Polechová and Barton, 2015). Alternatively, adaptation to local environmental conditions is possible if there is genetic variation for selection to act on, but it fails if genetic drift reduced genetic variation for traits under selection.

We also found a consistent positive relationship between admixture and signatures of positive selection, indicating increased adaptation potential after admixture (e.g., Norris et al., 2020). The impact of admixture on the rate of adaptive evolution was stronger for the fraction of genes under positive selection than it was for α. Contrary results were found for the mating system and distance from core, which explained more variation in α than in the fraction of genes under positive selection. This difference may be due to the sensitivity of the conventional McDonald-Kreitman test to both the number of polymorphic sites and their detection. In agreement with this, we found that populations that were sequenced deeper had higher fractions of genes under positive selection. Therefore, we suspect that the fraction of genes with a significant signature of selection may be a less robust estimate of genome-wide selection than α.

Our results suggest that drawing general conclusions about the prevalence of efficacy of selection and mutational load based on genetic diversity may be valid within species. Here, we found that nucleotide diversity in intergenic regions was highly correlated with other diversity estimates and diversity in other genomic regions, in introns, and in coding DNA. Genetic diversity estimated from >1 million SNPs was closely related to diversity estimated from only 19 microsatellites. Furthermore, the signature of directional selection was linked with nucleotide diversity in intergenic regions, and earlier work has shown that the genomic signature of mutational load is highly associated with genomic diversity in intergenic regions (Willi et al., 2018). We, therefore, propose a “drift syndrome” hypothesis, where neutral marker variation across populations within species captures adaptive evolutionary history and predicts future adaptive potential relatively accurately. Future work should confirm these correlations within and among species, based on genomic data and the magnitude of various demographic parameters. At least for A. lyrata, we conclude that exposure to strong genetic drift has been common over most of the species' range, and that drift in outcrossing and selfing populations has constrained purifying selection and directional adaptation and contributed to setting range limits.

Methods

Population Sampling and Library Preparation

Populations of A. lyrata were collected during the reproductive season in 2007, 2011, and 2014. All, except two populations, had been analyzed previously at 19 microsatellite loci (Griffin and Willi, 2014). Microsatellite genotyping for the two new populations revealed that one of them, ON1, had a population inbreeding coefficient (F_IS) of 0.70 and was therefore predominantly selfing, and the other, ON3, had an F_IS of −0.04 and was outcrossing. For each population, one library was prepared with the Nextera Kit (Illumina, San Diego, CA, USA) from 25 equimolarly pooled DNA samples (following Fracassetti et al., 2015). Each library was paired-end sequenced for 100 bases (PE100) on four Illumina HiSeq2000 lanes, using one-quarter of the lane each time. Barcodes and adapters were removed from sequences. Fracassetti et al. (2015) describe good agreement between SNP frequencies estimated by this approach and individual-level representation sequencing.

Bioinformatics Pipeline

Initial data processing was done for each lane-population combination separately. Raw sequences were trimmed with a base quality threshold of 20 using the Perl script trim-fastq.pl that is part of the software package PoPoolation (Kofler et al., 2011). Trimming was done only from the 3′ end to allow subsequent removal of duplicates. Reads were mapped with BWA-MEM (Li and Durbin, 2009) against the reference using default parameters. The reference was the nuclear genome of A. lyrata v1.0 (Hu et al., 2011) and the chloroplast and mitochondrial genomes of Arabidopsis thaliana from TAIR (Lamesch et al., 2012). Two regions of scaffold II of the A. lyrata reference genome were masked (position ranges, 8746475–8835273 and 9128838–9212301) because they shared very high similarity with the A. thaliana chloroplast genome, suggesting an assembly error in the A. lyrata genome. Data of the different lanes for a population were subsequently merged, and we retained only reads that mapped against scaffolds I–VIII, representing the eight chromosomes of A. lyrata.

Further filtering steps were applied, that is, duplicate reads were removed with the MarkDuplicates tool of Picard v.2.5.0 (http://broadinstitute.github.io/picard/) and only proper paired reads with a mapping quality score above 20 were retained. The reads belonging to three types of regions (intergenic, introns, and CDS) were filtered with BEDTools (Quinlan and Hall, 2010). Distinctions between intergenic, intron, and CDS were based on the newest annotation of A. lyrata (Rawat et al., 2015). Intergenic regions were defined as regions 1000 bp away from the 5′ and 3′ untranslated regions of each gene. For each population, we created pileup files per scaffold-genomic region combination with SAMtools (Li et al., 2009). Pileup files were filtered to retain regions with a depth of coverage per site of 25–500×. Indels (inserts, deletions) were called for each population with the command pileup2indel in VarScan (Koboldt et al., 2012). Regions of 5 bp on each side of an insertion or deletion were identified (identify-genomic-indel-regions.pl) and removed (filter-pileup-by-gtf.pl) with PoPoolation (Kofler et al., 2011). The genomic interspersed repeats were identified in the reference genome with RepeatMasker (Smit et al., 2010) using the default settings for “arabidopsis” and removed from the pileup files. SNPs were called with the command pileup2snp in VarScan (Koboldt et al., 2012) for each population. We retained only bi-allelic SNPs, with a minimum count of the variant allele of 3, a minimum read count frequency of the variant allele of 0.015, a P-value lower than 0.15, and minimum mapping quality of 20. The choice of cutoff parameters was intended to minimize false positives and maximize true rare variants. Finally, SNPs with a strand bias of more than 90% were removed. Further filtering was done for different uses of the SNP datasets.

Population Relatedness Tree

Some results on population relatedness were published in Willi et al. (2018); additional information concerned four-population tests, dates of splits, and using a second method of tree estimation. A first relatedness tree of the A. lyrata populations was estimated with TreeMix (Pickrell and Pritchard, 2012) using 127 725 SNPs present at nucleotide sites across the entire genome and sequenced in all populations. The tree was rooted using SNP frequencies from the Arabidopsis halleri population Ha31 (Fischer et al., 2013). We allowed seven migration events; more did not change the number of significant events. The evaluation was done with the four-population test (Reich et al., 2009) implemented in TreeMix. We accepted the best tree out of 50 that was historically plausible and had the second-highest likelihood. The tree with the highest likelihood placed Lake Erie populations at the base of the eastern cluster, which is historically improbable because the region was under ice during the LGM. Support for that implausible configuration presumably arose from the high degree of admixture in the Lake Erie region. The time calibration of the tree was performed with the chronos function of the R package ape (Paradis et al., 2004) using a “correlated” model with a smoothing parameter (λ) equal to 0 and 10 branch categories. One calibration point was used, the time of the split between Eurasian A. lyrata and A. halleri of 337 400 years ago that had been estimated based on 29 nuclear genes (Roux et al., 2011). Our relatedness tree had branch lengths which were estimated based on frequency data and represented the drift parameter, which is proportional to t/2N_e, where t is the number of generations separating two populations. The chronos function assumes that branch lengths are linearly related to time, as an approximation and neglecting variation due to N_e. A subset of populations was further analyzed with a reversible polymorphism-aware phylogenetic model to cross-validate results (revPoMo; Schrempf et al., 2016). This subset consisted of the A. halleri outgroup population (Ha31), the two populations of the Ozarks clade (MO1 and MO2), three populations of the western clade (IA2, ON10, and IL1), and three populations of the eastern clade (NJ1, NC2, and NY6). The analysis with revPoMo was run with default parameters and 1000 bootstrap replicates. Time calibration was again performed with the chronos function. The timing of splits was set in the context of the Illinoian glaciation, about 190 000–130 000 years ago, and the Wisconsin glaciations, about 75 000–14 500 years ago (McManus et al., 1999).

Estimates of Genomic Diversity and Signatures of Positive Selection

Two estimates of genomic diversity were calculated. We analyzed the pileup files with NPStat (Ferretti et al., 2013) in 5000-bp windows. We provided filtered SNP lists from VarScan with additional restrictions of a minor allele frequency of 0.03 and minimum coverage of 50×, and we set the minimal allele number to 3 (m = 2). For intergenic regions, introns, and CDS regions, we calculated separately Tajima's π or nucleotide diversity (Tajima, 1983), Watterson's θ (Watterson, 1975), and their difference was divided by an approximation of the SD of the difference, Tajima's D (Tajima, 1989). We then took the median across windows weighted by the number of sequenced bps (Supplemental Table 1).

Fraction of Genes with Significant McDonald-Kreitman Test for Positive Selection (F_genesposSel)

Positive selection was depicted by the fraction of genes with a positive McDonald-Kreitman test. For each gene, SNPs of coding regions were classified as synonymous or non-synonymous with the program SnpEff (Cingolani et al., 2012). We input the VarScan SNP lists for CDS regions and a customized SnpEff database produced with the outgroup reference of A. thaliana (TAIR10 reference genome [https://www.arabidopsis.org] after multiple genome alignment with the reference of A. lyrata version 1; Dubchak et al., 2009), with A. lyrata position information, and annotation information from A. lyrata (Rawat et al., 2015). A. lyrata regions without alignment were encoded as missing values. Sites were then filtered for full sequence information for a codon (with a depth of coverage of 25–500×), only one SNP per codon, a minimum depth of coverage of the SNP of 25×, and a position outside of splice regions. Polymorphic sites were restricted to those with a frequency between 0.40 and 0.97; SNPs with a frequency >0.97 were considered to be fixed. The four types of variants, polymorphisms and substitutions of the non-synonymous and synonymous type, were counted for each gene, significance was assessed liberally with Fisher's exact test for 2 × 2 contingency tables, and the sign of the test checked (D_N/D_S > P_N/P_S). We excluded genes for which testing could not be done due to two zeros in a column or row. For synonymous counts, the zeros were replaced with a value of 0.5 to calculate the sign of the test.

Rate of Evolution at Non-synonymous Sites (α)

The rates of evolution at non-synonymous sites were approximated by the asymptote of α when the series of α(x) values was estimated across bins (x) of unfolded SFS for each population. The filtered SnpEff outputs were used to establish SFS for non-synonymous and synonymous sites. Variant frequencies were split into 20 bins between 0.1 and 0.9 (Haller and Messer, 2017), with bin intervals of 0.04. This resolution of SFS was justified given that 25 diploid individuals were sampled per population at an average depth of sequencing of 128×. Occurrences within bins were counted and α(x) calculated by considering the bin class with frequencies >0.98 to represent substitutions. An exponential growth function was fit to α(x) values, and the asymptote of α (at a frequency of 1) extracted from the best-supported model. For 2 out of 52 populations, the exponential model failed and a linear model was used.

Demographic Parameters Linked to Genomic Diversity and Signatures of Positive Selection

The relationship between demographic processes and patterns of genomic diversity and signatures of selection was tested with linear models (type-3 testing, R package car; Fox and Weisberg, 2019) with R 3.6.2 (R Core Team, 2019). Linear models are justified by the theoretical prediction that effective population size is linearly related with π and θ, and that drift affects the outcome of selection by a threshold effect determined by the selection coefficient. Dependent variables were weighted median diversity estimates for intergenic and CDS regions and the estimates for signatures of positive selection. An analysis of the diversity for intron regions was not conducted because estimates were highly correlated with those for exons/coding regions (all r > 0.98, see Results). Five explanatory variables depicted demography: (1) Log₁₀-transformed census size was estimated as the surface area occupied by plants multiplied by a measure of mean local density (Willi and Määttänen, 2011); eight populations were re-assessed for surface area with A. lyrata occurrence in 2018 and mean estimates across the 2 years were taken. (2) Mating system took on the categorical values of predominantly outcrossing or selfing (two mixed-mating populations were considered as selfing). For 18 populations, the mating system was estimated based on progeny arrays (Willi and Määttänen, 2010). For the remaining populations, it was inferred based on F_IS estimated with 19 microsatellite markers (Griffin and Willi, 2014). F_IS is strongly correlated with the multi-locus outcrossing rate assessed by progeny array (N = 18, R² = 0.929, P < 0.001, Figure S1 in Griffin and Willi, 2014). (3) The third explanatory variable was the ancestral cluster membership (east, and west) based on the population relatedness tree (Supplemental Figure 2), reflecting one of the oldest divergences in this species. As the two southernmost Missouri populations, MO1 and MO2, formed an older clade but showed evidence of admixture with the southern populations of the western genetic cluster, they were assigned to the western cluster (considering a third cluster did not improve models). (4) Log₁₀-transformed geographic distance from a core of each of the two ancestral clusters reflected postglacial range dynamics. It was defined as distance from the node from which expansion occurred into areas covered by ice during the LGM (Figure 1, purple and blue squares, and Supplemental Figure 3, purple and blue circles). These ancestral populations were considered to have given rise to the leading edge of the distribution; populations that diverged earlier were considered rear edge relative to the core sites. For populations involved in the postglacial expansion, we calculated the sum of great-circle distances of the map-projected phylogeny (see below) along the entire expansion route back to the core node. For rear-edge populations, we calculated the direct great-circle distance to the core population. Differences between the two types of range dynamics—expansion versus rear edge—were tested further by performing separate correlation analyses on the two types of populations. (5) Admixture events were detected by the four-population test (binary: 0/1; considering migration weight as a continuous variable did not improve models). In summary, the first two variables depicted demographic processes on the local scale, whereas the latter three variables depicted demographic processes on the species-range scale. Continuous explanatory variables were standardized to a mean of 0. The relative importance of the five variables for diversity estimates was assessed with the R package relaimpo (Grömping, 2006) using averaging over orders (Lindeman et al., 1980). Map projection of the phylogeny was done with the phylomorphospace function with the R package phytools (Revell, 2012), which estimated ancestral states for longitude and latitude of internal nodes using maximum likelihood. Interpolation maps were generated with the R package akima (Akima et al., 2016). For the production of maps, further data sources were accessed, for state lines (http://gadm.org/), waterways (http://www.naturalearthdata.com/), and maximum extent of the ice sheet (http://geogratis.gc.ca/api/en/nrcan-rncan/ess-sst/a384bada-a787-5b49-9799-f5d589e97bd3.html; Dyke et al., 2003).

Funding

This work was supported by the Swiss National Science Foundation (PP00P3-123396, PP00P3_146342, 31003A_166322) and the Fondation Pierre Mercier pour la Science, Lausanne.

Author Contributions

Y.W. designed the study, obtained funding, collected plants in the field, analyzed the data, and wrote the manuscript. M.F. designed the study, performed the lab work, analyzed data, and contributed to writing the manuscript. O.B. performed the lab work and commented on the manuscript. J.V.B. collected plants, analyzed data, and commented on the manuscript.

Published: September 11, 2020

Accession Numbers

The pipelines for analyses are accessible at: http://github.com/fraca. Raw sequence data are stored at the European Nucleotide Archive (http://www.ebi.ac.uk/ena) with the accession number PRJEB19338.

The pipelines are accessible at: http://github.com/fraca. Sequence data were stored at the European Nucleotide Archive (http://www.ebi.ac.uk/ena) with the accession number PRJEB19338.