Impact of Vibrational Modes in the Plasmonic Purcell Effect of Organic Molecules

Abstract

By means of quantum tensor network calculations, we investigate the large Purcell effect experienced by an organic molecule placed in the vicinity of a plasmonic nanostructure. In particular, we consider a donor-π bridge-acceptor dye at the gap of two Ag nanospheres. Our theoretical approach allows for a realistic description of the continua of both molecular vibrations and optical nanocavity modes. We analyze both the ultrafast exciton dynamics in the large Purcell enhancement regime and the corresponding emission spectrum, showing that these magnitudes are not accurately represented by the simplified models used up to date. Specifically, both the two-level system model and the single vibrational mode model can only reproduce the dynamics over short time scales, whereas the Fermi’s golden rule approach accounts only for the behavior at very long times. We demonstrate that including the whole set of vibrational modes is necessary to capture most of the dynamics and the corresponding spectrum. Moreover, by disentangling the coupling of the molecule to radiative and nonradiative plasmonic modes, we also shed light into the quenching phenomenology taking place in the system.

The Purcell effect¹ lies at the core of quantum electrodynamics, as it reveals that the radiative properties of any quantum emitter are not inherent to it, but also depend on the electromagnetic (EM) vacuum in its surroundings. A few decades ago, this phenomenon, and in particular, the pursuit for the full inhibition of spontaneous emission at EM band gaps, was one of the driving forces behind the development of photonic crystals.² More recently, much interest has focused on metallic nanocavities.^3,4 The large and spectrally complex photonic density of states associated with plasmonic resonances allows an unprecedented control over spontaneous emission in these nanostructures.^5,6 In recent years, different light sources have been used to probe plasmonic Purcell enhancement phenomena, such as quantum dots,^7,8 solid-state color centers^9,10 or passing electron beams.^11,12

Due to their large transition dipole moments and stability at room temperature, organic molecules have received increasing attention as reliable quantum emitters. In their interaction with plasmonic nanostructures, several topics have been addressed, such as fluorescence enhancement,¹³⁻¹⁷ spectral shaping,¹⁸⁻²⁵ and strong coupling.²⁶⁻³² Unlike other microscopic light sources, for which a two-level system (TLS) description is usually accurate, electronic transitions of organic molecules, from now on excitons, interact strongly with the molecular nuclear vibrations.

Within the TLS approach, only a few time scales play an important role, and in particular, the relative values of the plasmon-exciton exchange rate and their respective losses can be used to distinguish between the weak-coupling and strong-coupling regimes in a fundamental analysis. In contrast, in molecules, the vibronic coupling and the vibrational dynamics introduce several new time scales, such as the coherent nuclear oscillation period or the rate of vibrational energy dissipation and thermalization time, and the simple dichotomy between weak and strong coupling can be expected to give way to a richer phenomenology. For the case of not too large Purcell factors, radiative decay is typically slower than the vibrational relaxation and thermalization times (on the order of 1 ps or less³³), and molecular emission can be assumed to proceed from the lowest excited molecular state, with all vibrational modes in thermal equilibrium. This assumption gives rise to a Fermi’s golden rule (FGR)-based approach in which the emission spectrum of the organic molecule near a plasmonic structure is given by the product of its free-space spectrum and a frequency-dependent Purcell enhancement.^19,20,34 However, as plasmonic structures can achieve Purcell factors on the order of 10⁶,²⁹ radiative decay rates can be decreased from their free-space values in the nanosecond range to femtoseconds, such that radiative decay does not proceed from vibrationally relaxed molecules, the FGR approximation breaks down, and nonequilibrium effects play an important role. More recently, cavity-QED approaches have been able to incorporate the interplay between the exciton and one (or a few) vibrational modes.³⁵⁻³⁹ However, a realistic description of typical organic molecules could require considering hundreds of vibrational modes.

In this Article we present an accurate theoretical framework that is able to treat on an equal footing the electronic, vibrational, and plasmonic degrees of freedom associated with the Purcell effect experienced by organic molecules placed within a metallic nanocavity. Our numerical scheme is based on a quantum tensor network (TN) method,^40,41 which helps provide a complete picture of this phenomenon. In addition, it allows for a validation of the simple models introduced above and also for an in-depth study of the influence of the large number of vibrational modes on the spontaneous emission rate and emission spectrum. We show that while the TLS model is able to reproduce the very short time scales of the spontaneous decay, the FGR approach accounts only for the behavior at very long times. On intermediate time scales, a model that incorporates a single vibrational mode is able to extend the validity of the TLS to slightly longer times. However, we demonstrate that it is mandatory to account for the whole set of vibrational modes to capture most of the time dynamics and the corresponding spectrum.

Model

As a case study, we consider the excited-state dynamics of a single organic molecule placed at the gap center of a silver nanosphere dimer, as sketched in the inset of Figure 1a. This plasmonic structure resembles the two geometries in which the largest Purcell factors have been reported, the so-called nanoparticle on mirror⁴ and bowtie antenna¹⁶ geometries. In this work we have chosen a donor-π bridge-acceptor (D-π-A) organic dye, labeled CPDT,⁴² as a prototypical organic molecule because it displays a significant transition dipole moment and a large Stokes shift (>0.4 eV), yielding excellent absorption and emission capabilities. The Hamiltonian for this hybrid system can be written as [ℏ = 1]

1

where σ_–, b_ω, and a_i,ω denote the lowering operator of the molecular electronic transition, annihilation operator for the molecular vibration, and i-component of the plasmonic mode at frequency ω. Here the index i is either nr or r, representing the nonradiative and radiative plasmonic modes, respectively. Notice that only the latter can be detected in the far-field. The first line in eq 1 describes the free-standing molecule, where we have used a Holstein-type Hamiltonian⁴³ accounting for the continuum of vibrational modes, with coupling strengths λ_ω. The exciton frequency ω_e corresponds to the vertical transition from the vibrational ground state of the electronic ground state. The last part in eq 1 describes the continuum of radiative and nonradiative plasmonic modes, and their coupling, weighted by g_i,ω, to the molecular exciton. This plasmon-exciton coupling can be encoded in the spectral density J_i(ω) = g_i,ω², in a similar way as the vibrational spectral density J_v(ω) = λ_ω does for the vibronic coupling. Note that eq 1 includes optomechanical coupling,⁴⁴ which is usually described in a form where the exciton operators have been adiabatically eliminated. More details of the theoretical model can be found in the Supporting Information, which includes refs (45−57).

Figure 1.

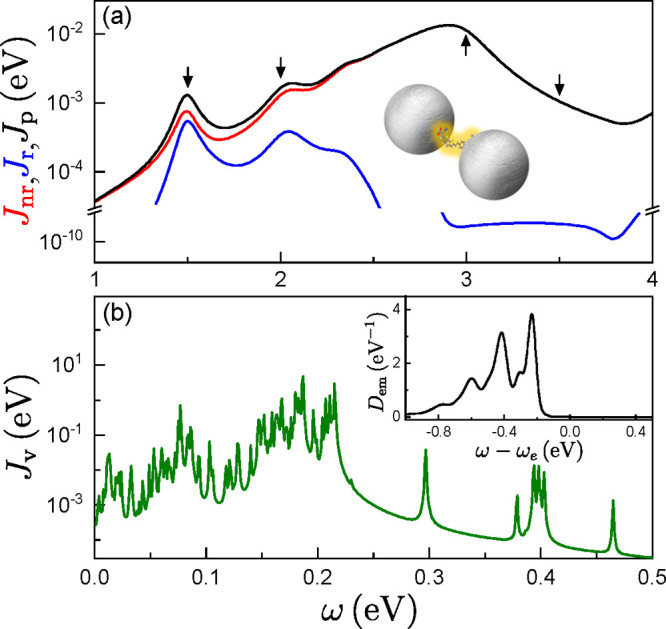
(a) Radiative (i = r, blue) and nonradiative (i = nr, red) plasmonic spectral densities, evaluated at the gap center of a nanosphere dimer, sketched as an inset. The black curve shows the total spectral density, J_p(ω), while the arrows indicate the exciton frequencies in Figures 2 and 3. (b) Vibrational spectral density, J_v(ω), for the CPDT molecule. The inset shows the line shape function, D_em(ω), at T = 300 K.

We numerically solve both the excited-state dynamics and the emission spectrum with our quantum TN method. Importantly, this simulation tool applies a variational algorithm to describe the dynamical evolution of the system wave function. This is expressed as a tensor network, whose truncation must be carefully treated to ensure convergence.^48,51 To make the system described by eq 1 amenable to treatment by this method, the two continua are transformed to a chain form in which each continuum (EM and vibrational) is represented by a chain of nearest-neighbor coupled oscillators, with only the first oscillator coupled to the exciton (see Supporting Information for more details of TN calculations). The first site in the vibrational chain is usually termed the reaction coordinate (RC), whose frequency is given by

2

with 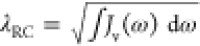being the coupling strength between the RC and the exciton. The remaining sites in the chain essentially act as an effective bosonic environment that leads to the vibrational decay and dephasing of the RC itself.

To shed light into the effect of molecular vibrations and uncover the relevant time scales in the spontaneous emission process, we compare our TN numerical results against three simplified models. As the simplest choice, by discarding all the molecular vibrations, the standard TLS model predicts a decay only dictated by the plasmonic environment, γ_TLS = 2πJ_p(ω_e), where J_p(ω) = ∑_iJ_i(ω) is the total plasmonic spectral density. In a second step, by keeping only the RC within the vibrational chain, we can derive an approach, dubbed here as the single vibration mode (SVM) approximation, in which the RC comprises all the vibrational response. Finally, within the FGR model (see Supporting Information for details), the spontaneous emission rate is simply calculated as the spectral integral of the product of J_p(ω) with the so-called line shape function, D_em(ω), which represents the available optical transitions connecting the ground and the excited electronic states of the molecule under the assumption that the vibrational modes are in thermal equilibrium, leading to

3

As commented above, we consider a silver nanosphere dimer as an example plasmonic cavity, with a 1 nm gap and 20 nm radius. It is embedded in a matrix with refractive index n_D = 2.1, which models a DNA scaffolding.³² The dielectric constant for silver is taken from ref (58). Numerical EM simulations were performed using the finite-element solver of Maxwell’s equations implemented in the commercial package COMSOL Multiphysics. Radiative and nonradiative contributions to the Purcell factor and spectral density were disentangled using the approach in ref (59). As shown in Figure 1a, the plasmonic spectral density is characterized by a radiative dipole mode located at around 1.5 eV, a quadrupole mode at 2.1 eV, and a dominant nonradiative mode, the so-called pseudomode,⁶⁰ emerging at 2.9 eV. A single CPDT molecule is located at the gap center, and we assume that its transition dipole moment (modulus μ = 0.1 e·nm) is pointing along the line that connects the two nanospheres. In the numerical calculations, we assume that the initial state originates from a Franck–Condon excitation, that is, a vertical transition that could result after an ultrashort laser pulse excitation of the electronic ground state. The line shape function within the FGR model in the main text is calculated at T = 300 K, and a comparison with pseudo temperatures simulating the Franck–Condon distribution is provided in the Supporting Information. The temperature in the TN and SVM calculations is effectively zero, as it does not play a relevant role on the ultrashort time scales that we are investigating in this work.

Electronic structure calculations within density functional theory and its time-dependent version are performed to obtain the vibronic coupling constants of the CPDT dye for the displaced harmonic oscillator model. Both the vibrational spectral density and line shape function of the CPDT molecule used in our calculations are shown in Figure 1b. In order to explore different regions of the plasmonic spectral density, we artificially shift the (vertical) exciton energy of the molecule to different values while keeping its vibrational structure fixed. This permits the study of the influence of the different features in the plasmonic spectral density on the molecular dynamics without using molecules with different excitation energies and a different vibrational structure. Therefore, our model should be considered as an archetype for an organic molecule with a complex vibrational spectrum and a large exciton–phonon coupling.

Results and Discussion

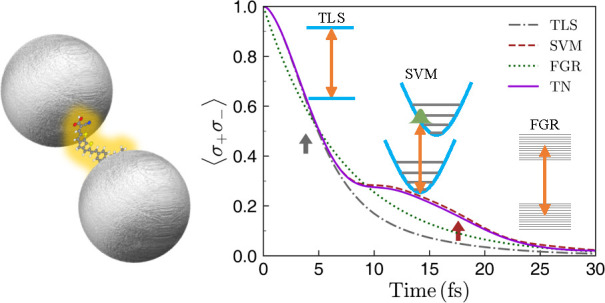
We focus first on the excited-state dynamics. Figure 2 shows the evolution of the exciton population, ⟨σ₊σ_–⟩, evaluated with the TN method at four exciton frequencies. It is compared against the results of the three different models (TLS, SVM, and FGR) for the same cases. First, it is evident that the TLS model largely fails to describe the decay dynamics for all the cases depicted in Figure 2. This failure highlights the importance of going beyond the TLS approach when defining the coupling regimes in the interaction of organic molecules with nanophotonic structures, implying that the simple distinction between weak and strong coupling has to be modified for organic molecules. More specifically, the onset of strong coupling has been identified with the emergence of (Rabi) oscillations in the excited state population dynamics. This picture emerges from a TLS model for the molecule. Our results include molecular features, such as the coherent nuclear oscillation or the rate of vibrational energy dissipation, which also yield an oscillatory behavior of the exciton population even in the Purcell regime, as discussed below. Still, it is interesting to note that TLS seems to be valid up to times of about τ₁ ≈ 4 fs (gray arrows in Figure 2). This is because, soon after its generation, the exciton vibrational wavepacket remains in the vicinity of the Franck–Condon region before exploring the potential energy surface of the excited state.⁶¹ Hence, within a very short time scale, vibrations do not play any role yet and the TLS model describes the molecular decay. This time scale, τ₁, can be estimated as a fraction of the period associated with the RC harmonic motion, T_RC = 2π/ω_RC. Specifically, τ₁ must be shorter than T_RC/4, which is the time that the vibrational wavepacket takes to reach the equilibrium position in the potential energy surface for the excited electronic state. We find that τ₁ ≈ T_RC/6 = 3.8 fs, which is in very good agreement with our numerical results.

Figure 2.

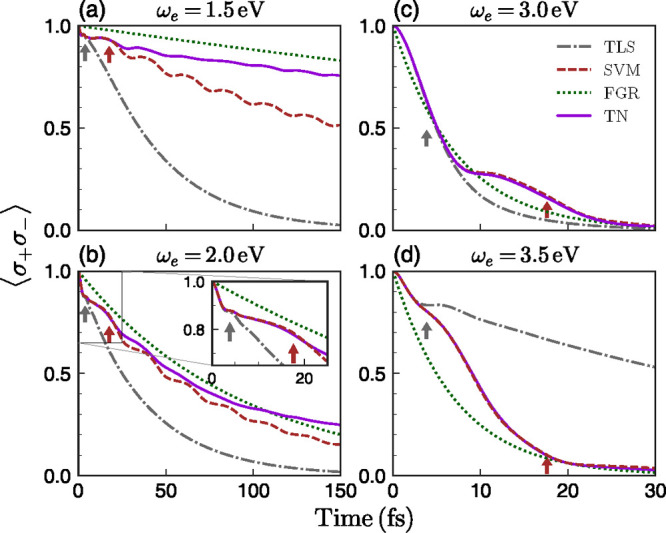
Excited-state dynamics ⟨σ₊σ_–⟩ vs time for different exciton frequencies. In each panel, TLS (gray dash-dotted), SVM (brown dashed), FGR (green dotted), and exact TN (violet solid) predictions are shown. The arrows indicate the positions of τ₁ ≈ π/(3ω_RC) (gray) and τ₂ = 1/γ_d (brown), with ω_RC and γ_d being defined in eqs 2 and 4, respectively. The inset of panel (b) shows a zoom at a shorter temporal range.

When the wavepacket initially moves away from the Franck–Condon region, its dynamics is dominated by the RC, as revealed by the accuracy of the SVM description for all ω_e in Figure 2. This regime holds until both dephasing and decay of the RC into other sites in the TN vibrational chain becomes important. We can estimate this second time scale, τ₂, as the inverse of the coupling between the first (RC) and second sites of the vibrational chain,

4

This estimation gives τ₂ = 1/γ_d = 17.6 fs (brown arrows in Figure 2). This time scale sets the validity of the SVM treatment, and explains that the excellent agreement with TN calculations at high ω_e resides in the large plasmonic coupling experienced by the molecule in this regime.

Following these arguments, it can be understood why the FGR model, in which all vibrational modes are taken into account, works better than the TLS and SVM models at sufficiently long times, as observed in Figure 2. Importantly, it reproduces the general slope of the TN exciton dynamics at long times, which implies a valid estimate of the Purcell factor experienced by the molecule. However, FGR assumes that the vibrational modes at all times are in thermal equilibrium and thus neglects the initial strongly nonequilibrium state and its coherent wave packet motion. The FGR approach thus fails to capture the short-time dynamics and, in particular, cannot represent the weak oscillations observed in the TN calculations.

Let us compare quantitatively the plasmonic Purcell factors that we obtain from the TLS and FGR models at the four exciton frequencies marked by vertical arrows in Figure 1a. The former is given by J_p(ω_e) normalized by its free space counterpart, J₀(ω_e).⁶⁰ The latter results from the ratio between γ_FGR and the free-space decay rate obtained by replacing J_p(ω) by J₀(ω) in eq 3. At ω_e = 1.5 eV, the TLS Purcell factor is 2.0 × 10⁶, while the FGR approximation yields 2.5 × 10⁵, almost 1 order of magnitude apart. Note that, at this exciton frequency, the emission in the TLS is at resonance with the dipolar plasmon mode, while the FGR is Stokes-shifted with respect to it. The discrepancy between TLS (1.1 × 10⁶) and FGR (7.1 × 10⁵) factors is significantly lower at ω_e = 2.0 eV, due to the impact of the dipolar plasmon on the FGR model at this exciton frequency. At ω_e = 3.0 eV, both approximations are in very good agreement (2.1 × 10⁶), a direct consequence of the broad nature of the plasmonic pseudomode sustained by the nanosphere dimer. Finally, the TLS (1.3 × 10⁵) predicts a much slower decay than the FGR (1.3 × 10⁶) above the pseudomode (ω_e = 3.5 eV).

We next examine the frequency-dependent population of the EM modes, 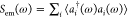. Notice that the sum extends over both radiative and nonradiative plasmonic modes, so we name this physical magnitude the near-field emission spectrum. Within the FGR approach, this quantity is independent of time and can be written as S_em(ω) ∝ D_em(ω)J_p(ω), which gives an intuitive relation between emission peaks and EM spectral density for organic molecules. Figure 3 shows the near-field emission spectra calculated for the four exciton frequencies and the four theoretical approaches in Figure 2, evaluated at t = 150 fs (see Supporting Information for spectra evaluated at the initial and intermediate stage). It is worth pointing out that this corresponds to the total emission accumulated up to this point in time, not an instantaneous emission spectrum. First note that in the left and right panel of Figure 3, emission peaks located at 1.5 and 2.9 eV are clearly seen in TN results, indicating that they are closely related to the dipole mode and pseudomode, respectively. Within the TLS model, only the EM modes close to ω_e contribute to the spontaneous emission process. This leads to single-peaked spectra broadened by the plasmonic environment, very different to the spectra obtained within the TN framework. On the other hand, the SVM approximation largely fails to reproduce the TN spectra for low exciton frequencies (1.5 and 2.0 eV), although it provides a reasonable approximation for higher ω_e. This is in accordance with its better accuracy describing the excited-state decay dynamics for those frequencies (see Figure 2).

Figure 3.

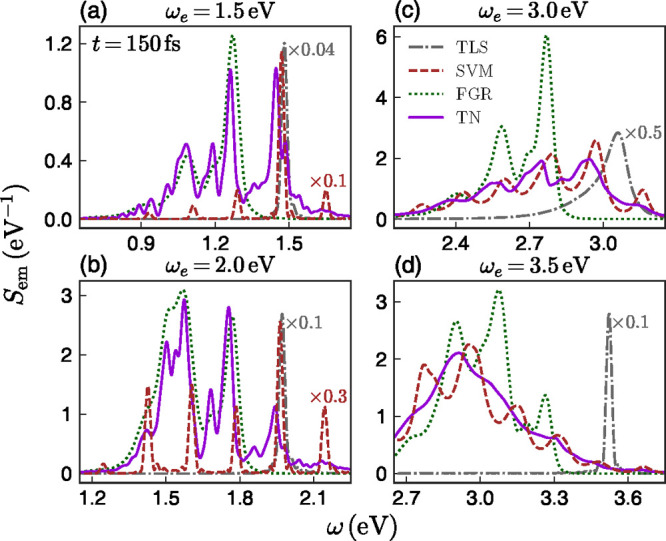
Near-field emission spectra S_em(ω) for four different exciton frequencies. The spectra for the TLS and SVM approximations and full TN method are calculated at t = 150 fs. The line code is the same as in Figure 2. Some spectra have been scaled to facilitate comparison.

In principle, one could have expected that the FGR approach should work better than the other two simplified models, as it incorporates the whole vibration spectrum via the line shape function of the organic molecule. However, as observed in Figure 3, this is not the case for the four chosen ω_e. The FGR approach only works well when the coupling of the molecular exciton with its EM environment is weak enough such that vibrational thermal equilibrium is reached before emission takes place. However, for large plasmon–exciton couplings leading to huge Purcell factors as those associated with plasmonic fields, the molecular exciton decays so fast that vibrational equilibrium is not reached and the spectrum is significantly different from the stationary limit. Our TN calculations show that this fast decay can be utilized to strongly modify the branching ratio of the emission by organic molecules, a phenomenon that has been also reported experimentally.^23,24

Finally, taking advantage of the capability of our TN theoretical framework to separate contributions from plasmonic radiative and nonradiative channels, here we address the interplay between the Purcell effect and the quenching phenomenon. Figure 4 shows the evolution of the population of EM modes, 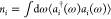(i being either nr or r), as a function of exciton frequency and evaluated at three different times. At very short time scales (t = 5 fs, panel a), the TLS approximation reproduces the TN result, since the molecular wavepacket has not yet explored the molecular vibrations. We can observe that only the coupling to the plasmonic pseudomode (around 2.9 eV) is fast enough to yield a significant EM population in this time scale. The dark nature of this plasmonic resonance translates into a vanishing radiative EM spectrum. The radiative population becomes significant only at longer times, as shown in Figure 4b,c. Specifically, both spectra present a maximum in the vicinity of 1.85 eV, which is a result of maximizing the spectral overlap between D_em(ω) and J_r(ω) and, hence, slightly blue-detuned from the dipolar plasmon mode frequency (1.5 eV) given by the TLS model. Moreover, note that these two panels are very similar, implying that the coupling rate between the molecule exciton and this bright plasmon resonance is faster than 75 fs^–1. Within this exciton frequency range, the effective quantum yield, shown in the inset of Figure 4c, can be as high 30%, despite the fact that the gap in the plasmonic cavity is only 1 nm wide and quenching is expected to be dominant. For higher ω_e, nonradiative components take over, completely quenching the far-field emission of photons by the molecule, as expected. By comparison, the TLS approximation only reproduces qualitatively the TN profiles at longer times, a direct consequence of the discrepancies in the emission spectra in Figure 3.

Figure 4.

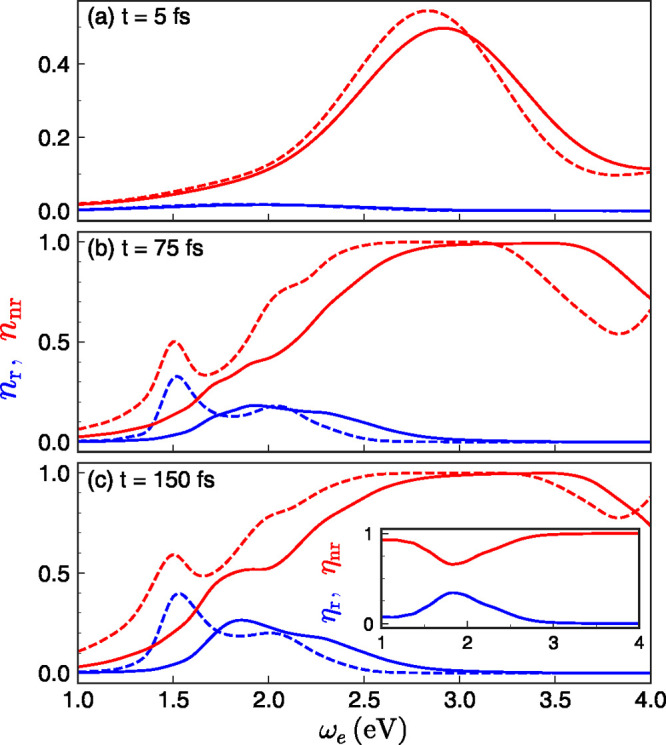
Radiative and nonradiative plasmon population (n_nr and n_r) as a function of exciton frequency ω_e at (a) t = 5, (b) 75, and (c) 150 fs, calculated from the TLS approximation (dashed) and full TN framework (solid). The inset in panel (c) shows the relative contributions of the radiative (effective quantum yield) and nonradiative plasmonic modes.

Conclusion

To conclude, we have applied an accurate quantum tensor network method, able to treat electronic, electromagnetic and vibrational degrees of freedom in light-matter scenarios on an equal footing, to study the Purcell effect occurring when organic molecules interact with plasmonic nanocavities. Using this numerical framework we have tested different simplified models that have been used to analyze this phenomenon lately. We have found that a two-level description of the molecule fairly captures the first steps of the decay process and a simple approach based on the Fermi golden rule can describe its very long time behavior. However, an accurate treatment of the exciton coupling to all the vibrational modes in the organic molecule is mandatory to resolve intermediate time scales. As a consequence, none of the simplified models used up to date are able to provide a precise estimation of near- or far-field emission spectra in hybrid systems involving organic molecules and plasmonic cavities. As an interesting extension of the current work, the influence of nonlinear vibrational mode couplings leading to vibrational energy redistribution could be investigated, as they are not included in the current Holstein-type model and are expected to become important on slightly longer time scales than treated here.^62,63 Our findings also reveal that significant effective quantum yield values can be achieved in situations where strong interaction to nonradiative plasmonic modes takes place and quenching is expected to dominate.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.0c01095.

• More details about the theoretical model, tensor network calculations, Fermi’s golden rule approach, and time-dependent emission spectra (PDF)

The authors declare no competing financial interest.