Individual variations lead to universal and cross-species patterns of social behavior

Significance

To probe the collective nature of social organisms, we measured the duration of food transfer (trophallaxis) and face-to-face events experienced by thousands of barcoded honeybees in a colony, over their entire lifetimes. The interaction time distribution is heavy-tailed, as previously reported for human face-to-face interactions. We develop a detailed theory for the universality of these findings and show that they reflect individual variations in the population. Using a measure of inequality from economics, we quantify these individual differences in both honeybees and humans. We show that bees have individual differences but exhibit less individuality than humans. This work demonstrates how individual variations can lead to universal patterns of behavior across different species and specific mechanisms for social interactions.

Abstract

The duration of interaction events in a society is a fundamental measure of its collective nature and potentially reflects variability in individual behavior. Here we performed a high-throughput measurement of trophallaxis and face-to-face event durations experienced by a colony of honeybees over their entire lifetimes. The interaction time distribution is heavy-tailed, as previously reported for human face-to-face interactions. We developed a theory of pair interactions that takes into account individual variability and predicts the scaling behavior for both bee and extant human datasets. The individual variability of worker honeybees was nonzero but less than that of humans, possibly reflecting their greater genetic relatedness. Our work shows how individual differences can lead to universal patterns of behavior that transcend species and specific mechanisms for social interactions.

How individuals in a community interact with each other gives rise to collective emergent properties of the community (1–5). It reflects the individuals’ personal preference, social roles, the external environment, and other numerous factors applicable to specific context. The distribution of interevent times, or waiting time between two consecutive events, for temporal social networks has been much studied because of its relation to information or disease spreading (3, 4). It has been shown that the heavy tail in the interevent time distribution is due to a decision-based queuing process, in which some tasks are more prioritized than others (6, 7). In contrast, the distribution of contact duration, instead of the interevent time, and its connection to the nature of social interactions have not been studied as much.

We have measured the duration of interactions among thousands of honeybees (Apis mellifera) in a hive, well-known eusocial insects that are easy to experimentally manipulate. Among many possible modes of honeybee social interaction, we focused on trophallaxis, which is mouth-to-mouth liquid food transfer. Trophallaxis occurs not only for feeding but also for communication (8, 9), making it a model system to study social interactions and collective effects (10, 11). To measure the interaction time, all of the honeybees in a colony were fitted with a barcode (12). A high-resolution machine vision camera imaged them at the rate of one frame per second. Then a customized algorithm detected each interaction event by analyzing the images and identified each bee, its position, and its orientation (12) (Materials and Methods).

Note that all of the honeybee data used in this work were originally generated by the authors for separate studies not for the purpose of testing our theory discussed in this paper or even to acquire the data needed for the theory. We used all of the data available to us, which were the trophallaxis social network data acquired in 2013 and analyzed in ref. 12 ($1164\_2013$, $1140\_2013$, $1138\_2013$, $1174\_2013$, and $1170\_2013$, which are trials 1 to 5 in ref. 12) and the trophallaxis social network data acquired in 2016 from colonies with partial treatment with Juvenile Hormone analogue (13, 14) ($789\_$JHA$\_2016$ and $757\_$JHA$\_2016$) (see Materials and Methods for more detail on the colony preparation). Our theory works for all of them, which indicates its robustness.

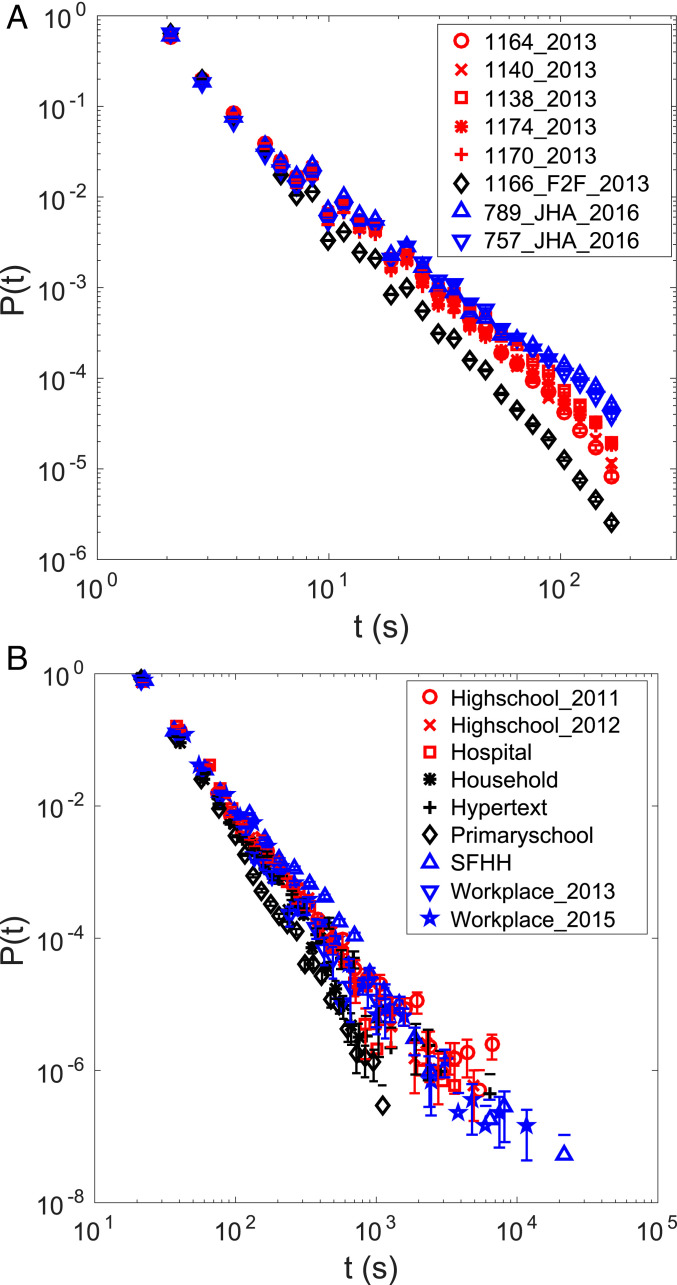
Fig. 1A shows that the distribution of honeybee interaction duration is heavy tailed. The exponents of the power law are –2.4, –2.3, –2.2, –2.2, –2.2, –2.7, –2.0, and –2.0 for each dataset listed in the legend from the top ($1164\_2013$) to the bottom ($757\_$JHA$\_2016$). If every bee were the same and every interaction happened by chance, one might naively expect to see a peaked distribution such as a Gaussian. However, the observed heavy-tailed distribution suggests heterogeneity or variability among the population.

Fig. 1.

(A) Duration of trophallaxis as well as F2F events that are not detected as trophallaxis follows a heavy-tailed distribution. The first number in the dataset name represents the number of observed honeybees in each colony, while the last number represents the year the experiment was performed. Note that the number of individuals in the last two datasets is actually smaller than what was originally observed (676 and 639 instead of 789 and 757, respectively) because we analyzed the data after applying an additional filter to exclude the time series during which the colonies were perturbed by the treatment of JHA, but we decided to keep the name of the datasets. The numbers of interactions used to make the plot are 302,221, 205,787, 191,795, 259,923, 329,170, 1,207,778, 136,529, and 115,965 in the order the datasets are listed in the legend. (B) Human face-to-face (F2F) interaction in various settings exhibits a heavy-tailed distribution. The numbers of interactions used are 10,677, 19,774, 14,037, 32,425, 9,865, 77,520, 26,039, 4,591, and 33,750 in the order the datasets are listed in the legend. In both A and B, error bars indicate the SE. In B, lower error bars for bins with count 1 could not be drawn in logarithmic scale because it extends to 0.

In order to improve the statistical power of our analysis, we also examined F2F events, where honeybees were close and oriented toward each other but not actually engaging in trophallaxis (15). F2F events occur about an order of magnitude more frequently than trophallaxis. F2F events include undetected trophallaxis and possible antennation, but the nature of the honeybee interaction during F2F is not as well defined as trophallaxis. Nevertheless, being F2F is a necessary but not sufficient condition for trophallaxis, so as long as the distance apart is not larger than the length of a honeybee, it would be expected that F2F events scale similarly to trophallaxis events. Indeed, coarse data for temporal networks retain some statistics of the actual interaction including heavy-tailedness of the contact duration distribution (16) (also confirmed by our results in Fig. 1A; see $1166\_$F2F$\_2013$).

In our work, the detection of trophallaxis events is estimated using a two-step filtering process because we are not able to observe directly fluid transfer through the proboscis. Our detection scheme is not subject to tracking error generated by bees that are misoriented or have other individual variations in visibility. Our method, described in detail in our earlier work (12), first selects bee pairs of close enough distance and orientation toward each other. Then we apply a second filter, selecting the bee pairs that are physically connected by proboscis through image processing. Through this second filter, we can filter out the pairs with inaccurate tracking of position or orientation because those pairs would not be connected by the proboscis. Even if there were innately poorly tracked bees, the multiple layers of filtering minimize the detection error on the trophallaxis events. There is quantitative evidence that there is minimal tracking error impact on our results, even without the second filter. The F2F dataset concerns bee pairs that satisfy only the geometric constraint regarding distance and orientation but are not detected as being connected by the proboscis. This dataset has not filtered out the pairs with inaccurate position and orientation through the second filter. However, as shown below, this F2F dataset gives the same power law and scaling laws as the trophallaxis datasets. In other words, the statistics of the data are retained regardless of whether the data have gone through the second filter, which is consistent with the notion that inaccuracy due to positional tracking error was already negligible after the first filter. Our earlier work (12) showed by subsampling of the trophallaxis interaction data at different sampling rates that the statistics of the trophallaxis interaction are robust against subsampling and false negatives, with the statistics of the times between trophallaxis events being robust to detection errors. This strongly suggests that the statistics of the duration of the trophallaxis events will also be robust.

We compared the honeybee data with human data recorded by the SocioPatterns collaboration (16–24) to explore whether there are universal patterns of social interaction. Fig. 1B shows that human F2F interaction time in various settings also exhibits a heavy-tailed distribution. The exponents of the power law are –2.4, –2.7, –2.9, –3.4, –2.7, –3.6, –2.5, –2.9, and –2.6 for each dataset listed in the legend from the top (Highschool$\_2011$) to the bottom (Workplace$\_2015$). Such similarity across different systems indicates an unexpected universality governing the interaction in social systems and suggests that a minimal model (25) should be able to capture the salient features of the interactions.

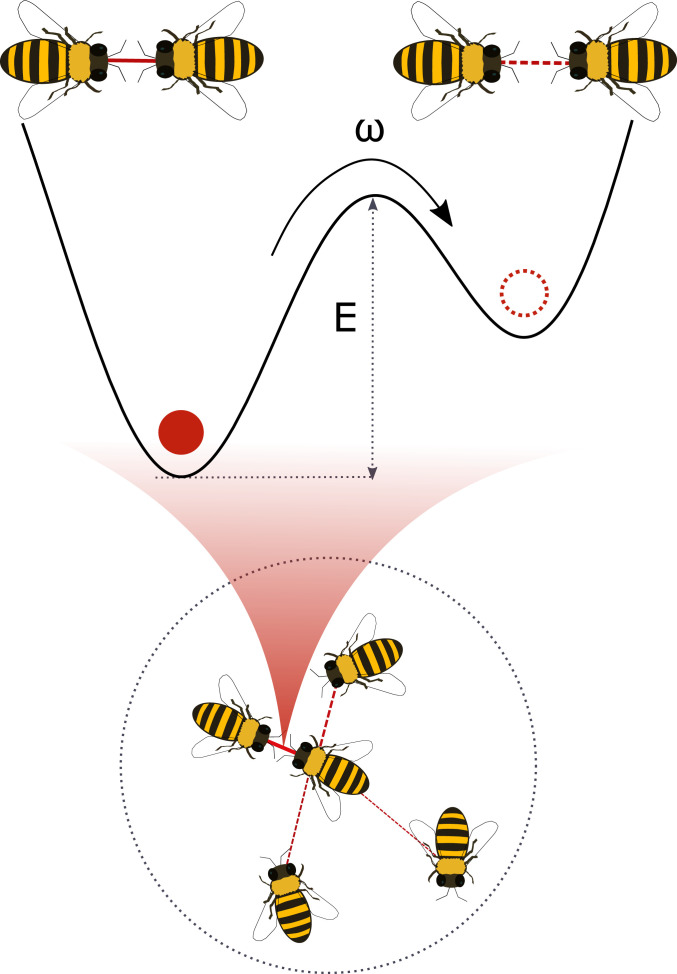
To construct such a minimal model, we treat the social bond between bees as an effective particle. We focus on bees here, but the model is also applicable to humans. The bond is the edge in the usual network representation of social interactions. This effective particle has two states representing an interacting pair and a noninteracting pair. The particle jumps from one state to the other with a fixed rate $\omega$ in the reaction coordinate, as depicted in Fig. 2. Although jumping happens in both directions, we focus on the jumping from the interacting state to the noninteracting state because the interaction time is the waiting time for the first jump in that direction. The distribution of the first jump time $f\left(t,\omega \right)$ is obtained by multiplying the probability not to jump at each time step until time $t$ with the probability density to jump at time $t$. The first part, the probability not to jump until $t$, is ${\left(1-\omega dt\right)}^{t/dt}$, where $dt$ is the interval for a time step. Taking the limit of infinitesimal time steps yields $\underset{dt\to 0}{lim}{\left(1-\omega dt\right)}^{t/dt}=e^{-\omega t}$. The distribution of the first jump time is then given by $f\left(t,\omega \right)=\omega e^{-\omega t}$.

Fig. 2.

Schematic picture for the theory of interaction durations. The dotted circular area indicates the neighborhood of the center bee. The neighbors, or the potential partners, inside the circle are connected with the center bee by a bond. The bond between two bees is represented by a particle in the reaction coordinate. This particle has two states representing an interacting pair and a noninteracting pair, and it changes its state by jumping over the energy barrier $E$ with rate $\omega$. Among the neighbors, the center bee is assumed to primarily interact with a bee with the highest barrier because they form the stablest pair.

Some pairs tend to have longer interactions than others, and this is reflected in their value of $\omega$. To take into account this variability or heterogeneity within the community, we integrate the jump time distribution for a fixed $\omega$ over the distribution of rates $p\left(\omega \right)$. To determine $p\left(\omega \right)$, we use the Kramers theory for escape over a potential barrier (26): the distribution of $\omega$ is related to the distribution of energy barrier heights $E$ through $\omega ={\omega }_0{e}^{-E}$ where ${\omega }_0$ is a constant (26). Here we use a dimensionless energy scale $E$, which is already normalized with possible fluctuations.

We propose that the barrier height distribution $p\left(E\right)$ follows the extreme value distribution for maxima. As illustrated in Fig. 2, a given bee has multiple candidate partners with which to interact. Each possible pair is associated with a certain barrier height. The pair with the highest barrier would spend more time together because it is more difficult for the particle to escape. This partner is thus interpreted as the most likeable and ends up forming a pair. Then the observed energy barrier $E$ is the maximum among the neighbors. The distribution of the maximum is taken to be the Fisher–Tippett–Gumbel distribution for maxima (27, 28), which is appropriate if the parent distribution for barrier heights is localized, as seems reasonable. Then we express $p\left(E\right)=\left(\alpha +1\right)e^{-\left(\alpha +1\right)E}{e}^{-e^{-\left(\alpha +1\right)E}}$ where $\alpha$ is an undetermined parameter. For large $E$, $p\left(E\right)\sim e^{-\left(\alpha +1\right)E}$. We take the large $E$ limit because the heavy-tailed behavior is observed at large $t$. Using $\omega ={\omega }_0{e}^{-E}$, we find that $p\left(\omega \right)\sim {\omega }^{\alpha }$ for small $\omega$, equivalent to large $E$. Combining this $p\left(\omega \right)$ with the exponential pair interaction time distribution, we get

$$f\left(t\right)=\int d\omega p\left(\omega \right)f\left(\omega ,t\right)\sim t^{-\left(2+\alpha \right)}$$ (1)

as the interaction time distribution for the population. The power law form suggests that the assumption about the parent distribution for barrier heights is valid. More details of this calculation are provided in SI Appendix. The quantity $\alpha$ in the exponent connects the community interaction time distribution $f\left(t\right)$ with the distribution of barrier heights $p\left(E\right)$.

We remark that a similar derivation for the heavy-tailed time distribution as shown in Eq. 1 arises in the theory for defect jumping (29) and a model of traps (30, 31) in glass. However, the interpretation of $p\left(E\right)$ in social interactions is different from the analogue in disordered materials. Atoms in a glass successively hop over multiple energy barriers in a rough potential landscape, so the integration over $p\left(E\right)$ is an average over the energy barriers experienced by one atom. On the other hand, our particles for the bond between a pair jump over one energy barrier to change their state. Thus, the integration over $p\left(E\right)$ is an ensemble average over the population.

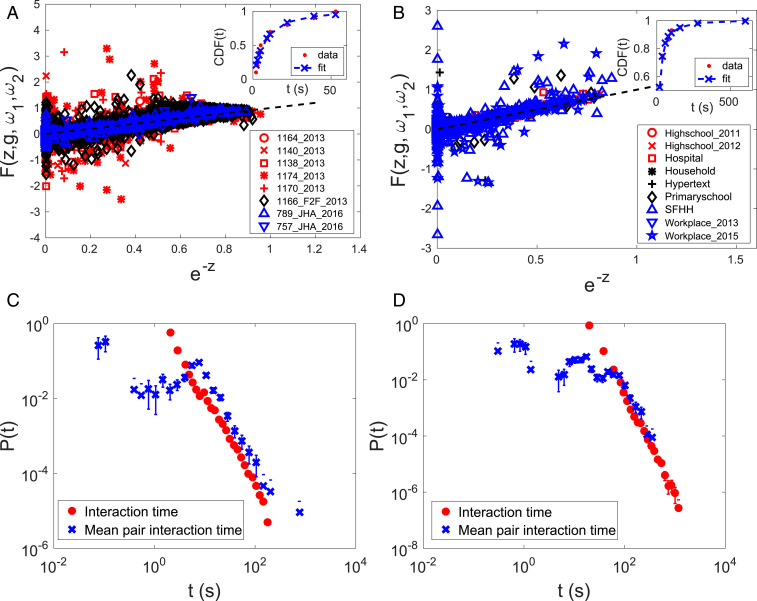
Next we turn to verifications of the predictions of this theory. The simple theory predicts an exponential pair interaction time distribution. The quantile–quantile plots for pair interaction times (Fig. S1) suggest that the pair interaction time distributions for both honeybees and humans are better expressed by hyperexponential distributions, which are weighted sums of two exponential distributions. The theory is not affected by this additive modification, as discussed in SI Appendix. There are so many pairs in each colony that it is not practical to show the goodness of hyperexponential fit for each pair separately. Therefore, we devised a data collapse to show the fit of all pairs in one figure. Only the pairs that yield more than seven points of evaluation for the empirical cumulative distribution function (ECDF) were considered. The cumulative distribution function (CDF) for a hyperexponential function is $Y\left(t\right)=1-g{e}^{-{\omega }_{1}t}-\left(1-g\right)e^{-{\omega }_{2}t}$, where $g$ is the weight and ${\omega }_1$ and ${\omega }_2$ are the rates for each exponential. We define a new variable $z\equiv {\omega }_{1}t$ and rewrite the CDF as $F\left(z,g,{\omega }_1,{\omega }_2\right)\equiv \left(1/g\right)\left(1-Y-\left(1-g\right)e^{-\left({\omega }_2/{\omega }_1\right)z}\right)\hspace{0.17em}=e^{-z}$, where $Y$ is ECDF. Then the $x$ axis only depends on one variable $z$. If the data are well fitted by this functional form, plotting $F\left(z,g,{\omega }_1,{\omega }_2\right)$ against $e^{-z}$ should produce a cloud of data points aligning with the $y=x$ reference line.

Fig. 3 A and B show that most honeybee and human pair interaction times are well fitted to hyperexponential distributions. Fig. 3 A and B, Insets, show the fit of a pair to provide some intuition of the fitting process. The fitted CDF tends to deviate more at small $e^{-z}$, or large $t$, because the CDF value of the fitting function approaches 1 for $t\to \infty$, while the ECDF value is 1 at the longest observed interaction time.

Fig. 3.

(A) Pair interaction time distributions for honeybee pairs are fitted to hyperexponential functions and collapsed together. The numbers of pairs used to generate the plot are 197, 99, 328, 443, 561, 1,806, 46, and 20 in the order the datasets are listed in the legend. The pair interaction time distributions of these pairs were fitted. (Inset) Fitting ECDF of pair interaction times of a pair from $1164\_2013$. (B) The same plot as A but with human pairs. The numbers of pairs used are 37, 82, 59, 58, 39, 143, 98, 15, and 171 in the order the datasets are listed in the legend. (Inset) Fitting ECDF of pair interaction times of a pair from Highschool$\_2011$. (C) Comparison between the scaling of interaction time distribution and mean pair interaction time distribution for $1164\_2013$. (D) The same plot as C but for Primaryschool. The number of mean pair interaction times used is the same as the number of pairs used for fitting, which is listed in A and B. The number of interaction times used is the same as what is listed in Fig. 1. Error bars indicate the SE, and lower error bars for bins with count 1 could not be drawn in logarithmic scale because it extends to 0.

A second prediction from the model is the exponential barrier height distribution. Although $E$ is not a directly measurable variable, the relation $\omega ={\omega }_0{e}^{-E}$ enables us to indirectly measure $p\left(E\right)$ because the mean pair time associated with an energy barrier is $\tau =1/\omega$. The relation $p\left(E\right)\sim e^{-\left(\alpha +1\right)E}$ implies that $p\left(\tau \right)\sim {\tau }^{-\left(2+\alpha \right)}$ for large $\tau$, which has the same exponent as $f\left(t\right)$ in Eq. 1. Therefore, comparing the exponent of the tail of $f\left(t\right)$ and $p\left(\tau \right)$ provides a test of the theory, in particular, the proposed functional form of $p\left(E\right)$.

Fig. 3 C and D demonstrate the same scaling between the tail of $f\left(t\right)$ and $p\left(\tau \right)$ for $1164\_2013$ and Primaryschool, respectively. The comparison of scaling for seven other honeybee datasets and eight other human datasets is shown in SI Appendix, Fig. S4. Here $\tau$ is obtained from fitting parameters $\omega$, not from averaging of pair interaction times, because $\tau$ is the mean pair interaction time associated with a single energy barrier (SI Appendix). If we retain the full form for $p\left(E\right)$, i.e., including the superexponential term in the Fisher–Tippett–Gumbel distribution, $p\left(\tau \right)$ is expected to have a peak at small $\tau$, which may explain the peak in Fig. 3C.

One might think that the identical scaling between $f\left(t\right)$ and $p\left(\tau \right)$ is a consequence of the so-called stable law (32) because $\tau$ is an average of $t$ for pairs. Then, depending on the tail of $f\left(t\right)$, the distribution of $\tau$ would be given either by the central limit theorem, i.e., a Gaussian, or by a power law with the same exponent as $f\left(t\right)$. However, this is not correct, as explained in SI Appendix, because the parent distribution of $p\left(\tau \right)$ is not $f\left(t\right)$ but instead is the pair interaction time distribution $f\left(\omega ,t\right)$.

The two energy barriers suggested by the hyperexponential pair interaction time distribution imply a multidimensional potential landscape of the reaction coordinate. Our model does not limit the number of barriers, allowing the pair interaction time distribution in principle to be an arbitrary sum ${\sum }_i{g}_i{\omega }_i{e}^{-{\omega }_{i}t}$, but the weight of further barriers seems to be too small to contribute to the dynamics. It is evident that different pairs are characterized by different barrier heights, but whether it is a specific pair or a specific individual that determines the barrier height cannot be determined by the analysis so far.

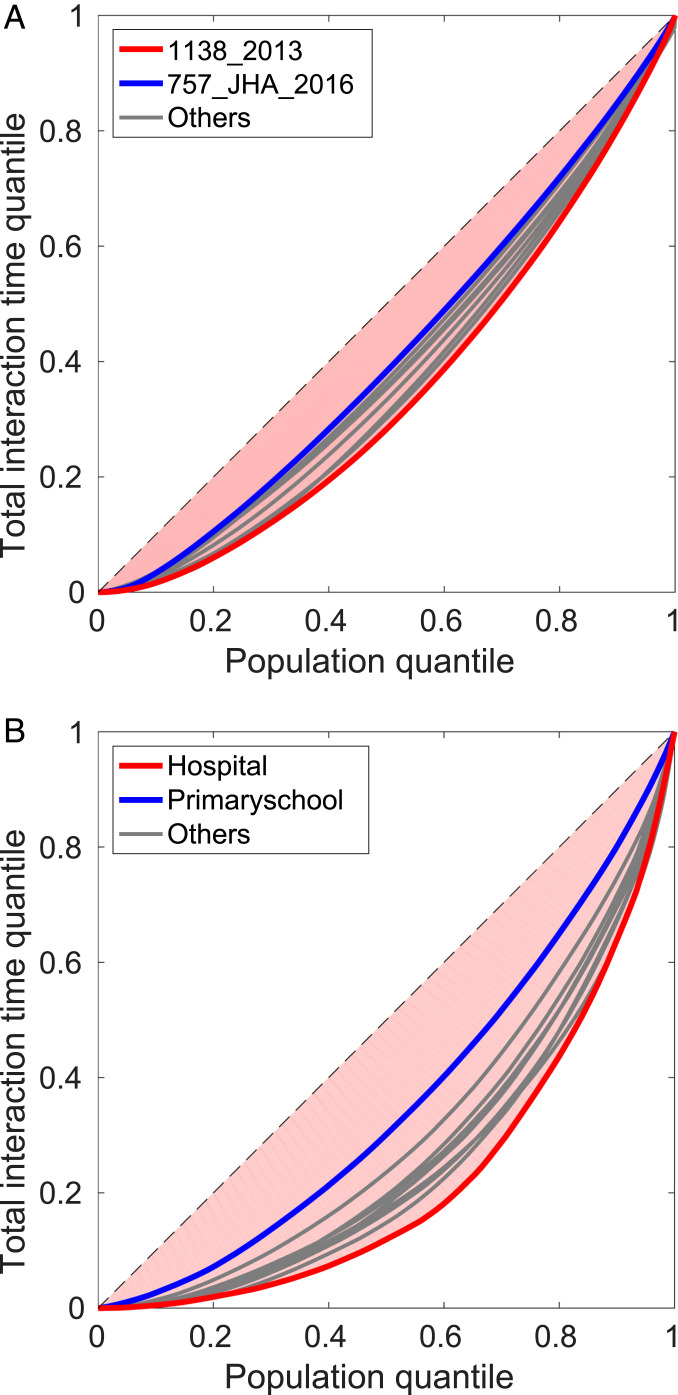
To explore the effect of individuality in social interactions, we calculated the Gini coefficient (33) for 1) the total interaction time spent by each individual, 2) the total number of interactions each individual had, and 3) the total number of partners with which each individual interacted. Widely used to express inequality in economics, the Gini coefficients have recently been used to quantify inequality in the activity level of eusocial insects (34, 35). Fig. 4 shows a graphical representation of the results, known as the Lorenz plot (36), for the total interaction time spent by bees and humans. The Lorenz plots for other variables are shown in SI Appendix, Fig. S5.

Fig. 4.

Lorenz plots of the total time spent for interaction by honeybees and humans. (A) Gini coefficients of bees are as follows: $1164\_2013$, 0.2373; $1140\_2013$, 0.2111; $1138\_2013$, 0.3013; $1174\_2013$, 0.2760; $1170\_2013$, 0.2698; $1166\_$F2F$\_2013$, 0.2089; $789\_$JHA$\_2016$, 0.1941; and $757\_$JHA$\_2016$, 0.1727. The numbers of data points used in the plot are the same as the numbers of individuals in each dataset, which are 1,164, 1,140, 1,138, 1,174, 1,170, 1,166, 676, and 639. (B) Gini coefficients of humans are as follows: Highschool$\_2011$, 0.4333; Highschool$\_2012$, 0.4879; Hospital, 0.5488; Household, 0.5012; Hypertext, 0.4576; Primaryschool, 0.2799; SFHH, 0.4937; Workplace$\_2013$, 0.4493; and Workplace$\_2015$, 0.3753. The numbers of individuals used are 126, 180, 75, 75, 113, 242, 403, 92, and 217.

To read these results, note that in a Lorenz plot the greater the deviation from the $y=x$ reference line, the closer the Gini coefficient to unity, thus indicating a greater level of inequality. More inequality in our data means a greater contribution by individuals to the dynamics, signifying the effect of individuality. Fig. 4A shows that the Gini coefficients for honeybees are in the range 0.2 to 0.3, whereas for humans they are in the range 0.3 to 0.5. Thus, although individual bees are distinct, they are not as different from each other as humans are (Fig. 4B). The Lorenz plots and Gini coefficients for the total number of interactions and total number of partners provided in Fig. S5 show the same trend. The reduced individuality in honeybees compared to humans might be due to the average coefficient of relatedness being $r=0.75$ among workers of the same colony as the queen was inseminated with a single male in these experiments, but further study is needed to verify this conjecture. Since the interaction time is a shared value between a pair, it is nontrivial to completely separate the contribution of individuals. The effect of individuality in social interactions is therefore an open question but one that we have provided the tools to explore. Nevertheless, along with earlier studies of possible chemosensory mechanisms for individual identification (37), our results provide confirmation and quantification of the conjecture from recent work on the personality of honeybee workers as described in ref. 38 that some individuals are more likely to be interactive and engaged in food sharing, while others are less so.

The recently discovered heterogeneous food distribution in the Camponotus sanctus ant colony (39) may suggest individual variations in workers of this other well-known eusocial insect. Although the ratio of transferred food volume to maximal transferable volume during trophallaxis when the donor is a forager is measured to follow the same exponential distribution with the same parameter as the case when the donor is a nonforager (39), it does not necessarily mean the lack of individuality in ants because the individual variations may have been averaged out as the data of many pairs were analyzed collectively. If the data were analyzed for each pair, individual variations may have been observed. It is not the scope of our work, but it would be possible to study the effect of individuality on the food mixing due to trophallaxis of eusocial insects.

We have shown that high-resolution tracking can yield detailed multiscale information about the interactions and behavior of individuals within a community. Our results suggest that individual differences can lead to patterns of behavior that are universal and transcend species, context, and specific mechanisms for social interactions.

Materials and Methods

Animals.

This All experiments took place at the University of Illinois Bee Research Facility, Urbana, Illinois. Experiments for $1164\_2013$, $1140\_2013$, $1138\_2013$, $1174\_2013$, and $1170\_2013$ were performed from July to October 2013. Dataset $1166\_$F2F$\_2013$ was obtained from the same colony as $1164\_2013$. Each experiment started with a colony of 1,200 one-day-old adult worker honeybees (A. mellifera), but the activities of 1,164, 1,140, 1,138, 1,174, 1,170, and 1,166 bees were detected. Datasets $789\_$JHA$\_2016$ and $757\_$JHA$\_2016$ were collected in September and October 2016. Each experiment in 2016 started with a colony of 800 one-day-old adult worker honeybees, but the activities of 789 and 757 bees were detected. After filtering out the period of perturbation caused by the treatment of JHA, we detected the activities of 676 and 639 bees. The details of the experiments in 2013 are described in ref. 12, and here we portray the experiments in 2016 (13). The identification of each honeybee and the detection of trophallaxis were done in the same way as the 2013 experiments (12). The datasets from the 2016 experiments were collected as a part of a different study (13), but no difference with regard to the scaling law exposed in the paper was detected.

To minimize the effects of genetic variation on behavioral analyses, all experiments used adult worker bees from colonies headed by queens that had each been instrumentally inseminated with semen from a single drone. Due to haplodiploidy, this results in an average coefficient of relatedness of 0.75. Honeycomb frames containing pupae were removed from colonies 1 to 2 d prior to the beginning of each experiment and maintained in a dark incubator at $\mathrm{34}°$C and 50% relative humidity (13).

Observation Hive Construction and Monitoring.

Eight hundred 0- to 24-h-old adult workers were cold anaesthetized and tagged (12). The bees were then placed with a barcoded, naturally mated queen into a glass-walled observation hive containing a single one-sided honeycomb frame. Colonies were provided with 300 g of honey and 30 g of artificial bee bread (nine parts honey, nine parts ground pollen, and two parts water). To prevent bees from spreading the honey onto the glass observation window, cells containing honey were covered in wax foundation scented with 5 mL of strawberry or orange food extract (McCormick & Company Inc.) to establish hive identity, thereby facilitating homing during orientation flights and foraging and preventing intracolony conflict during pharmacological treatments (Juvenile Hormone Analogue Treatments). Observation hives were housed in a dark room heated to $\mathrm{32}°$C and maintained at 50% humidity. Images were captured at a rate of one frame per second over the course of the entire experiment; infrared lighting illuminated the colony during periods of image capture from both the front and rear of the hive (via a blacklight) (12). Starting on the second night, the colony entrance was opened to allow the bees access to the exterior environment (12). The glass window of the observation hive was changed twice daily (ca. 9 AM and 8 PM) to prevent debris from obscuring the colony, but the hives were otherwise left undisturbed except during pharmacological treatments (Juvenile Hormone Analogue Treatments).

The barcode and trophallaxis identification was performed as detailed in ref. 12. During the trophallaxis detection, potential interaction partners were first selected according to the geometric constraint. First, the distance between the most anterior point of each bee’s body on the anteroposterior axis was measured, and a bee pair was selected if the distance was between 3.4 and 6.9 mm. Then the selected pair was considered as the potential interaction partners if the angle between each bee’s barcode orientation vector was between $\mathrm{90}°$ and $\mathrm{180}°$. Among the potential partners, the pairs physically connected by the proboscis were detected as doing trophallaxis. On the other hand, the pairs satisfying the geometric constraint but not being connected by the proboscis were classified as F2F. The analyzed F2F dataset used close parameters of the geometric constraint. Identical parameters were used in trophallaxis detection for the 2013 experiment (12), and the more detailed description of the detection procedure is in ref. 12.

Juvenile Hormone Analogue Treatments.

After 5 d of observation, colonies were dismantled, and the bees were placed in Plexiglas cages. The glass observation window was replaced with a transfer glass with removable portholes that could be centered over each sector, and the colony was placed in an area lit by a far-red LED light (Smart Vision Lights). Since far-red wavelengths are barely perceptible to bees, this allowed them to be transferred individually to the Plexiglas cage via forceps without risk of escape. Bees were then cold anaesthetized in groups of three and randomly assigned to one of three treatments: a Juvenile Hormone analogue (JHA) treatment, an acetone vehicle treatment, and a cold-anaesthetized sham treatment (13). Bees in the JHA group were treated topically with the JHA methoprene [200 ng per bee, a dose that is known to induce precocious foraging in bees (40)] dissolved in 1 $\mathrm{\mu }$L of acetone and administered to the abdomen. The vehicle group was treated with 1 $\mathrm{\mu }$L of acetone administered to the abdomen, and the sham treatment group was cold anaesthetized but otherwise untreated. The bees were also painted with a color code (Testor’s Corporation) designating their treatment and photographed, allowing their barcode identification to be linked to their treatment (13). After all of the bees in a colony recovered from anaesthetization, they were returned to their observation hive. Because the colony was physically disturbed, trophallaxis observations from the day of the experiment were not used in any downstream analyses. Monitoring of the colony continued for 7 d after the JHA treatments, after which the colony was disassembled. More details on the JHA treatment and related experiments are in ref. 13.

Code Availability

The custom software to produce printable barcode images, detect barcodes in digital images, and detect trophallaxis is available at https://github.com/gernat/btools. The MATLAB codes used to analyze the data are available at https://github.com/schoi8/heavytail_scaling. The MATLAB code used to calculate the Gini coefficients and to generate the Lorenz plots is available at https://www.mathworks.com/matlabcentral/fileexchange/28080-gini-coefficient-and-the-lorentz-curve.

Data Availability.

The honeybee interaction datasets from the 2013 experiments (12) analyzed in this study are available at http://www.beemonitoring.igb.illinois.edu. The F2F dataset is available at the Illinois Data Bank with the identifier https://doi.org/10.13012/B2IDB-4021786_V1. The honeybee interaction datasets from the 2016 experiments (13) analyzed in this study are available at the Illinois Data Bank with the identifier https://doi.org/10.13012/B2IDB-2712449_V1. The human F2F interaction datasets from the SocioPatterns Collaboration are available at http://www.sociopatterns.org/datasets/.