The Effect of Prenatal treatments on offspring events in the presence of competing events: an application to a randomized trial of fertility therapies

Abstract

When studying the effect of a prenatal treatment on events in the offspring, failure to produce a live birth is a competing event for events in the offspring. A common approach to handle this competing event is reporting both the treatment-specific probabilities of live births and of the event of interest among live births. However, when the treatment affects the competing event, the latter probability cannot be interpreted as the causal effect among live births.

Here we provide guidance for researchers interested in the effects of prenatal treatments on events in the offspring in the presence of the competing event “no live birth”. We review the total effect of treatment on a composite event and the total effect of treatment on the event of interest. These causal effects are helpful for decision making, but are agnostic about the pathways through which treatment affects the event of interest.

Therefore, based on recent work, we also review three causal effects that explicitly consider the pathways through which treatment may affect the event of interest in the presence of competing events: the direct effect of treatment on the event of interest under an intervention to eliminate the competing event, the separable direct and indirect effects of treatment on the event of interest, and the effect of treatment in the principal stratum of those who would have had a live birth irrespective of treatment choice. As an illustrative example, we use a randomized trial of fertility treatments and risk of neonatal complications.

Introduction

Researchers who study the effects of prenatal treatments on events in the offspring face a challenge: the event of interest cannot occur in the absence of a live birth. Failure to produce a live birth—because of conception failure, miscarriage, termination, or stillbirth—is a competing event for events in the offspring.^1,2

A commonly used approach to handle this problem is to restrict the analysis to live births, that is, to individuals who do not experience competing events. When the treatment affects the probability of live birth, however, the estimate from the analysis restricted to live births cannot be interpreted as the causal effect among live births.^3–6 Other proposed approaches do not restrict to live births,^5,7,8 but their practical relevance is unclear.

The statistical literature on competing events is extensive but not always helpful to guide choices among different methods to handle competing events. A key problem is that, with some prominent exceptions,^9–11 the causal interpretation of the statistical estimates has been traditionally left unspecified. Recent work, however, has clarified the definitions of causal effects targeted by conventional statistical approaches and has proposed novel definitions of causal effects in the presence of competing events.^2,12–14

Here, we provide practical guidance for researchers interested in the effects of prenatal treatments on events in the offspring. Using the theoretical framework provided by recent work,^2,12 we review the causal interpretation and practical implications of several approaches to handle the competing event “no live birth”. Specifically, we consider the effects of fertility treatments on the offspring, an increasingly important research area because about 1.7% of births in the U.S.¹⁵ and up to 5% of births in some European countries occur after fertility treatment.¹⁶ In fertility studies, the competing event “no live birth” occurs in over 60% of participants.¹⁷ Throughout, we illustrate the methods using data from a randomized trial of active ovarian stimulation medications and neonatal complications, which we describe first.

The AMIGOS Trial

The Assessment of Multiple Intrauterine Gestations from Ovarian Stimulation (AMIGOS) study was a three-arm randomized trial designed to compare the effects of three active ovarian stimulation medications (letrozole, gonadotropin, and clomiphene) among 900 couples with unexplained infertility undergoing intrauterine insemination.¹⁸ Below we focus on the effect of letrozole versus gonadotropin on the risk of neonatal complications, defined as any of the following: jaundice, respiratory distress, neonatal hospitalization > 3 days, and neonatal intensive care unit admission. We did not include congenital malformations, intrauterine growth restriction, and intracranial hemorrhage as components of the event of interest because these conditions occur before birth. The simplified causal diagram in Figure 1-i introduces our notation and depicts the relationships between key variables. See e-Appendix 1 for a description of the notation.

Figure 1. Causal directed acyclic graphs (DAGs) showing the effect of fertility treatments on neonatal complications.

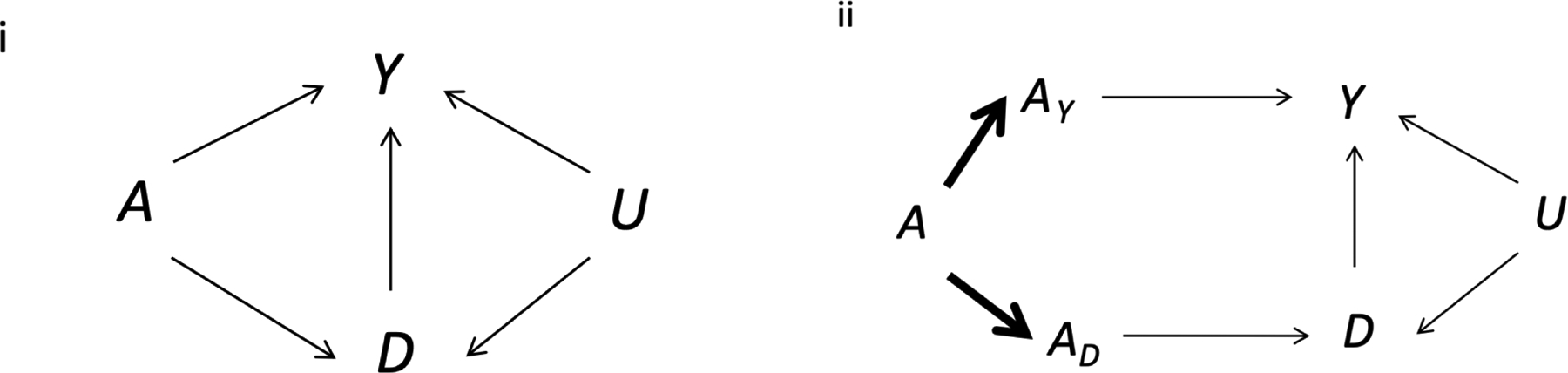
A denotes the treatment (1 for letrozole, 0 for gonadotropin), D the competing event (1 if no livebirth occurs, 0 otherwise), Y the outcome (1 if neonatal complications occur, 0 otherwise), U a set of unmeasured factors that affect both the probability of live birth and of neonatal complications, e.g., partner’s semen quality, maternal health status, or a genetic factor, A_Y is the component of A that directly affects neonatal complications, and A_D is the component of A that directly affects live birth. Graph ii is an extended version of the graph i, in which the treatment components A_Y and A_D are deterministic functions (bold arrows) of A.

As often done,^19–21 we estimated the proportion of live births and the proportion with the event of interest among live births in each treatment group. A live birth occurred in 19% of the 299 women in the letrozole group and in 32% of the 301 women in the gonadotropin group. The difference between these two proportions estimates the effect of the treatment on the probability of live birth, because the trial was marginally randomized.²²

A neonatal complication occurred in 34% of the live births in the letrozole group and in 33.0% of the women in the gonadotropin group (Figure 2). The difference between those proportions estimates the conditional association between the treatment and the event of interest among live births. This conditional association cannot be generally interpreted as the causal effect of treatment among live births because, as shown in Figure 1-i, conditioning on live birth (a collider) is expected to induce selection bias.^3–5 That is, equating the treatment-outcome association in those without the competing event with “the causal effect of treatment (e.g., letrozole vs. gonadotropin) on the event of interest (e.g., neonatal complications) in individuals without the competing event” is generally incorrect under our assumed causal structure (Figure 1-i).

Figure 2. Pregnancy and neonatal outcomes by treatment group, AMIGOS trial (2010–2014).

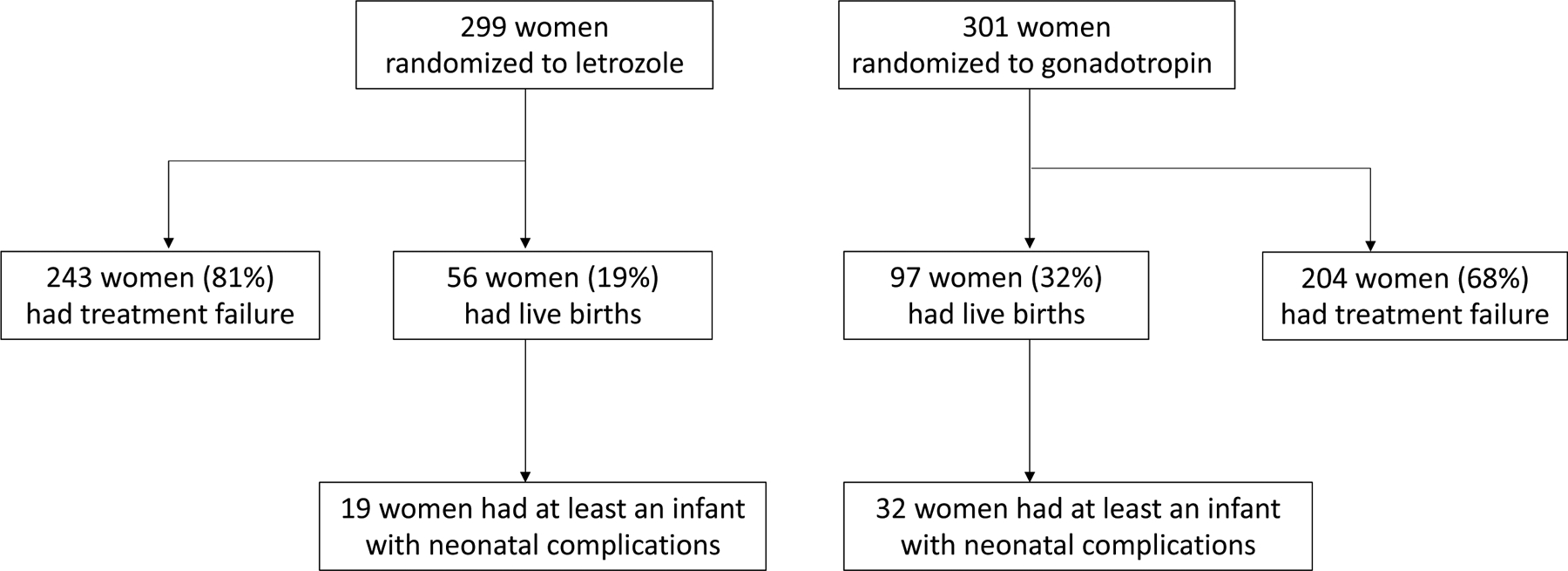
Treatment failure was defined as no live birth due to any of the following: conception failure, miscarriage, termination, and stillbirth.

Neonatal complications were defined as any of the following: jaundice, respiratory distress, neonatal hospitalization > 3 days, and neonatal intensive care unit (NICU) admission. When a multiple birth occurred, a neonatal complication was defined to be present if any of the infants experienced it.

Choosing a fertility treatment in the presence of competing events

From the findings in the previous section, we learn that (i) gonadotropin is, on average, more effective than letrozole in producing a live birth and that, (ii) if a live birth occurs, the risk of neonatal complications is, on average, similar between gonadotropin and letrozole. Consider a couple from the same population as the couples participating in the randomized trial and who needs to decide which of the treatments to use. Given only the average results of this randomized trial without losses to follow-up, which treatment should the couple choose? Under standard decision analysis frameworks²³ applied to our simplified setting, the answer depends on what adverse outcomes (i.e., functions of the joint distribution of live births and complications) the couple wants to minimize.

For example, suppose the couple wants to minimize the probability of a composite event that encompasses neonatal complications (the original event of interest) and no live birth (the original competing event), a commonly used event in perinatal randomized trials.^24–27 Then they would be interested in the risk (cumulative incidence) of the composite event in each treatment group. In our example, there were 19 neonatal complications and 243 failures to produce a live birth in the letrozole group. Therefore, the risk of the composite event was $\frac{243+19}{299}$ =88%. Similarly, the risk of the composite event in the gonadotropin group was $\frac{204+32}{301}$ = 78%.

The risk difference is then 9.2% (95% confidence interval [CI]: 3.4%, 15%), which can be interpreted as “the risk of either no live birth or a live birth with neonatal complications is 9.2 percentage points greater for letrozole compared with gonadotropin”. This risk difference is an estimate of the total effect of treatment on the composite event (Causal effect 1 in this paper). Because one minus the probability of the composite event is just the joint probability of a live birth and no neonatal complications (eAppendix 1), a couple just interested in maximizing the probability of a live birth without neonatal complications would choose gonadotropin.

Now suppose the couple wants to minimize the probability of the event in the offspring, regardless of whether a live birth occurs.^28,29 Then they would be interested in the risk (cumulative incidence) of the offspring event in each treatment group. In our example, the risk of neonatal complication was $\frac{19}{299}$ = 6.4% in the letrozole group and $\frac{32}{301}$ = 11% in the gonadotropin group.

The risk difference is then −4.3% (95% CI: −8.9%, 0.0%), which can be interpreted as “the risk of neonatal complications is 4.3 percentage points lower for letrozole compared with gonadotropin.” This risk difference is an estimate of the total effect of treatment on the event of interest (Causal effect 2) because it combines the direct effect of treatment on the event of interest with its indirect effect mediated by the competing event (paths A → Y and A→D→Y in Figure 1-i).² That is, the total effect is agnostic about whether a treatment reduces the risk of neonatal complications by either reducing the number of neonatal complications among livebirths or simply by reducing the number of livebirths so that no children with neonatal complications may be born.^2,21,30 Distinguishing between these two causal pathways, however, may not matter for any couple who was just interested in minimizing the risk of neonatal complications after one round of fertility treatment: they would choose letrozole. In the next section, we discuss alternative causal effects that have been proposed to distinguish between the causal pathways that yield the total effect; these effects, however, require strong assumptions even when estimated from a randomized trial.

Our above discussion considered only simplified preferences for decision making, assumed that the couple can only have one round of fertility treatment, and assumed that a couple would only weigh three key quantities provided by the trial for each treatment group: (i) the probability of live birth, (ii) the joint probability of live birth and no offspring event, and (iii) the joint probability of live birth and the offspring event. In our example, these probabilities were 19%, 12%, and 6.4% and respectively, for letrozole and 32%, 22%, and 11%, respectively, for gonadotropin (the probability of no live birth and an offspring event is zero). However, before making a decision in practice, many couples will request more information than just these population-averaged risks. For example, they may prefer to base their decision making on risk estimates in subgroups of individuals with characteristics similar to them.

Finally, we ignored the time-varying nature of the competing event “no live birth” during pregnancy (effectively, we assume that gestational age at birth is constant) and consider a randomized trial with no losses to follow-up. As a result, our above calculations are simple and easy to follow. For example, the total effect of treatment on the offspring event is just the contrast of the treatment-specific joint probabilities of live birth and neonatal complications (which can be expressed as the probability of live birth times the conditional probability of neonatal complications among live births) in each group, and the composite effect is the contrast of one minus the treatment-specific joint probability of live birth and no complications (which can be expressed as the probability of no live birth plus the joint probability of live birth and neonatal complications) in each group (eAppendix 1). Extensions of the approaches used here that accommodate more realistic scenarios are reviewed elsewhere.²

Explanation of the pathways in the presence of competing events

We now review three causal effects (or estimands) that explicitly consider the pathways through which treatment may affect the event of interest in the presence of competing events.^2,12–14,31 The numerical estimates for each causal effect in the AMIGOS trial are summarized in Table 1. The formal definitions, identifiability assumptions, and identification formulas can be found elsewhere^2,12–14 and are summarized in eAppendix 1.

Table 1.

Effects of letrozole versus gonadotropin on risks of neonatal complications, AMIGOS trial (2010–2014).

Approach	Causal Estimandsa	Risk difference (95% CI)
1. Total effect of treatment on a composite event	Pr[Qa=1] − Pr[Qa=0]	9.2% (3.4%, 15%)
2. Total effect of treatment on the event of interest	Pr[Ya=1] − Pr[Ya=0]	−4.3% (−8.9%, 0.0%)
3. Direct effect of treatment on the event of interest, not mediated through competing eventsb	Pr[Ya=1,d=0] − Pr[Ya=0,d=0]
a) g-formula estimator		1.1% (−15%, 17%)
b) IP weighted estimator		0.8% (−15%, 16%)
c) doubly robust estimator		0.3% (−16%, 16%)
4. Separable direct and indirect effectsb,c
Separable direct effect when the component of letrozole that affects competing event is kept and the component of gonadotropin that affects competing event is eliminated3	$\text{Pr}\left[Y^{a_Y=1,a_D=1}\right]-\text{Pr}\left[Y^{a_Y=0,a_D=1}\right]$
a) g-formula estimator		0.2% (−2.8%, 3.4%)
b) IP weighted estimator 1		0.2% (−2.9%, 3.2%)
c) IP weighted estimator 2		0.2% (−3.3%, 3.5%)
Separable indirect effect when the component of letrozole that affects neonatal complications is eliminated and the component of gonadotropin that affects neonatal complications is kept	$\text{Pr}\left[Y^{a_Y=0,a_D=1}\right]-\text{Pr}\left[Y^{a_Y=0,a_D=0}\right]$
a) g-formula estimator		−4.5% (−7.4%, −2.1%)
b) IP weighted estimator 1		−4.5% (−7.1%, −1.9%)
c) IP weighted estimator 2		−4.5% (−7.6%, −1.3%)
Separable direct effect when the component of letrozole that affects competing event is eliminated and the component of gonadotropin that affects competing event is kept	$\text{Pr}\left[Y^{a_Y=1,a_D=0}\right]-\text{Pr}\left[Y^{a_Y=0,a_D=0}\right]$
a) g-formula estimator		0.4% (−4.9%, 5.8%)
b) IP weighted estimator 1		0.9% (−4.4%, 6.6%)
c) IP weighted estimator 2		0.4% (−5.0%, 5.9%)
Separable indirect effect when the component of letrozole that affects neonatal complications is kept and the component of gonadotropin that affects neonatal complications is eliminated.	$\text{Pr}\left[Y^{a_Y=1,a_D=1}\right]-\text{Pr}\left[Y^{a_Y=1,a_D=0}\right]$
a) g-formula estimator		−4.7% (−7.9%, −2.1%)
b) IP weighted estimator 1		−5.1% (−8.8%, −2.2%)
c) IP weighted estimator 2		−4.7% (−8.5%, −1.6%)
5. Total (=direct) effect of treatment on event of interest in the unidentifiable subgroup (principal stratum) in which no competing events would occur irrespective of treatment
a) Under monotonicity assumption (33.9 % of population are in the unidentifiable group)	Pr[Ya=1 − Ya=0 | Da=0 = Da=1 = 0]	Upper bound: 0.9% (−14%, 17%) Lower bound: N/A
b) Under cross-world assumptions + parametric assumptionsd	$\frac{\text{Pr}\left[Y^{a=1}|D^{a=0}=D^{a=1}=0\right]/\left\{1-\text{Pr}\left[Y^{a=1}|D^{a=0}=D^{a=1}=0\right]\right\}}{\text{Pr}\left[Y^{a=0}|D^{a=0}=D^{a=1}=0\right]/\left\{1-\text{Pr}\left[Y^{a=0}|D^{a=0}=D^{a=1}=0\right]\right\}}$	risk ratio (95%CI)e: 0.98 (0.48, 1.9)

CI: confidence interval. All 95% CIs were computed from 500 bootstrap samples.

^aLet A denote the treatment (1: letrozole, 0: gonadotropin), D is the competing event (1 if no livebirth, 0 otherwise), Y the event of interest (1 if neonatal complications, 0 otherwise), Q the composite event (1 if no live birth or neonatal complications, 0 otherwise), and U a set of unmeasured factors that affect both the probability of live birth and of neonatal complications. A_Y is the component of A that directly affects neonatal complications, and A_D is the component of A that directly affects live birth. For each individual, Y^a is the counterfactual indicator of event if the individual had been assigned to A=a.

^bAdjusted for treatment (letrozole, gonadotropin), age (<35 or ≥35 years), baseline anti-Mullerian hormone levels (≤1 and >3 ng/ml vs otherwise), history of fertility treatments (yes, no), and history of pregnancy loss (yes, no).

^cStensrud et al¹² for identification formula and IP weighted estimators.

^dWe include the same variables as specified above in the outcome model. The model of live birth includes all the above covariates and the product terms of the covariates.

^eThe method has been described for risk ratio but not risk difference

Causal effect 3: The direct effect of treatment on the offspring event under elimination of all failures to produce a live birth

Suppose we could implement an intervention that (somehow) ensures that all couples have a live birth. Then any effect of treatment on neonatal complications would be necessarily due to a direct effect (A→Y in Figure 1-i) because the indirect effect through the competing event “no live birth” would have been eliminated. This causal effect is the effect of treatment on the event of interest when the value of the mediator “no live birth” is set to zero,² which is an example of a (controlled) direct effect.³² This causal effect, however, raises two problems.

First, the effect estimate is difficult to interpret. Because a procedure to eliminate all competing events (e.g., zero conception failure, miscarriages, and stillbirths) can rarely be imagined in this case, the direct effect remains ill-defined and therefore of unclear utility for decision making.³³

Second, leaving interpretational issues aside, the effect estimate is likely to be biased in many settings. Because the controlled direct effect is defined under a hypothetical intervention to ensure live birth, the analysis needs to be adjusted for the shared causes U of the competing event D and the event of interest Y in Figure 1-i (or by mediators on the pathways U→D or U→Y).^2,4,33 However, these variables are usually not measured, which makes adjustment infeasible.

In our example, we might hypothesize that the following measured variables can act as adequate proxies for the unmeasured common causes of live birth and neonatal complications: age (< 35 years vs. ≥ 35 years), measures of ovarian reserve (anti-Mullerian hormone levels: ≤ 1 and >3 ng/ml vs. otherwise), prior pregnancy loss (yes, no), and prior use of infertility treatments (yes, no). Under the (strong and probably unrealistic) assumption that adjustment for these variables eliminates the selection bias introduced by conditioning on the competing event, we can choose among different adjustment methods, including inverse probability (IP) weighting (that relies on a model for the probability of live birth),³⁴ the plug-in g-formula (that relies on a model for the event of interest among live births),⁹ and doubly robust methods that combine both kinds of models.³⁵ All these methods can also accommodate time-varying prognostic factors in more complex causal structures.

Were we willing to accept that the above direct effect is well-defined and that the above variables are sufficient to adjust for selection bias, the IP weighted risk estimates were 34% in the letrozole group and 33% in the gonadotropin group, and their difference was 0.8% (95% CI: −15%, 16%). The results were similar when we used the g-formula or a doubly robust method (Table 1). In fact, the adjusted estimates were similar to the unadjusted estimates, which suggests that either there was little selection bias or that our adjustment variables were insufficient to reduce it, for example, because we did not adjust for other potential common causes such as paternal semen quality or genetic factors.

Causal effect 4: The separable direct effects of treatment on the event of interest (not through its effect on live birth) and the separable indirect effects of treatment on the event of interest (only through its effect on live birth)

Suppose that each treatment A under study could be decomposed into two components (or, more generally, can be replaced by two treatments) that exert effects through distinct sets of causal pathways (Figure 1-ii). The first component, A_Y, directly affects the risk of neonatal complications without having any effect on live birth. The second component, A_D, only affects the risk of neonatal complications indirectly through its effect on live birth. This decomposition is one way to motivate the separable direct effects¹²— the effect of the first treatment component A_Y on the event of interest when the second component A_D is fixed (that is, there is one separable direct effect for each level of A_D).

Unlike the controlled direct effect, the separable direct effects describe the mechanism by which treatment affects the outcome without relying on hypothetical interventions to ensure live birth. If each treatment could be actually decomposed in practice, then, rather than having only a binary choice of treatment A, future couples would be able to choose among 4 possible treatment combinations of A_Y and A_D, which would alter our discussion about decision making in the previous section.

When, as in our trial, the treatments A_Y and A_D cannot be independently administered (even if they exist), we need strong assumptions to obtain valid estimates of the separable direct effects. First, the treatment decomposition assumption must be justified by subject matter knowledge. We discuss possible decompositions of gonadotropin and letrozole in more detail in eAppendix 2. Second, even if the treatment decomposition assumption holds, the identification of the separable direct effects (like that of the controlled direct effect) also requires adjustment for the shared causes U of the competing event and the event of interest (or by mediators on the pathways U→D or U→Y) (Figure 1-ii).¹² When, as is often the case, these variables are not measured, the separable direct effects cannot be validly estimated.

Were we willing to make the assumption of treatment decomposition and of sufficient adjustment given the covariates available, then our estimate of the first separable direct effect above by the g-formula would be 0.2% (95%CI: −2.8%, 3.4%) when A_D is fixed to the letrozole component, and 0.4% (95% CI: −4.9%, 5.8%) when A_D is fixed to the gonadotropin component. The separable direct effect estimates were small compared with the total effect estimates, which suggests that letrozole lowered the risk of neonatal complications mainly through its effect on reducing the number of livebirths. The results were similar when we used IP weighting (Table 1).

Causal effect 5: The total effect of treatment on the event of interest in the subgroup in which no competing event would occur irrespective of treatment

Imagine we could identify the subset of women who would have a live birth regardless of whether they are assigned to letrozole or gonadotropin. In this so-called “principal stratum”^9,10 there are no competing events and therefore the total effect of treatment equals the direct effect of treatment not mediated by the competing event. The average causal effect of treatment for women in the principal stratum, which is also known as the survivor average causal effect (SACE),³⁶ however, can differ from the effect in other women. Furthermore, in practice, it is impossible to identify the women who would have a live birth under either treatment level.

The principal stratum effect can only be quantified under strong and untestable assumptions. For example, suppose we assumed that (1) no women in the study population would experience a live birth under letrozole but not gonadotropin (a monotonicity assumption) and (2) compared with women who received gonadotropin and had a live birth (i.e., the 97 mothers in the gonadotropin arm), those who received letrozole and had a live birth (i.e., the 56 mothers in the letrozole arm), on average, would have had a higher risk of neonatal complications if they had been treated with gonadotropin.¹³ Then, it can be shown that 34% of the trial participants would be in this principal stratum, and the upper bound of the effect¹³ would equal the unadjusted estimate in the analysis restricted to live births, that is, 0.9% (95% CI: −14%, 17%). The monotonicity assumption (1), however, is likely to be violated in our example because some women may respond to letrozole but not gonadotropin.³⁷

Approaches that avoid monotonicity require other strong and untestable assumptions. For example, an alternative method requires five other conditions.¹⁴ One of those conditions forces investigators to make assumptions about the relation between events under two treatment values in the same individual, something that is referred to as a cross-world assumption.³⁸ Specifically, to use this method, we would need to believe that, in women who had a live birth under a particular treatment (say, letrozole), knowing whether these women would also have a live birth under the other treatment (say, gonadotropin) would not improve our ability to predict the neonatal complications under letrozole after adjusting for the measured variables. Additional parametric assumptions required by this method would not hold if, for example, the effect of letrozole on neonatal complications varied across unmeasured confounders.¹⁴ Were we willing to make all these assumptions in our example, then our estimate of the risk ratio of neonatal complications in the principal stratum would be 0.98 (95% CI: 0.48, 1.9).

Discussion

The effect of a prenatal treatment on events in the offspring is a particular instance of the effect of a treatment on an event of interest in the presence of competing events.^2,12–14 Using concepts from the recent literature on competing events, we reviewed several possibilities for data analysis in a randomized trial of fertility therapies and neonatal complications with no losses to follow-up.

A randomized trial without losses to follow-up provides valid estimates of three quantities that can be used by couples to support their treatment decisions: the probability of live birth, the joint probability of live birth and offspring event, and the joint probability of no live birth and no offspring event in each treatment group. The total effect of treatment on a composite event that includes both no live birth and the event of interest (Causal effect 1)^5,7 and the total effect of treatment on the offspring event (Causal effect 2)² are constructed using these probabilities. While these effects provide relevant information for couples seeking fertility treatment, decision making in real life usually relies on additional information, e.g., subgroup-specific information, information on other undesirable outcomes, ethical considerations, cost, and etc.

Researchers can also consider three additional causal effects that describe the pathways by which the treatment exert its effects: the controlled direct effect, the separable direct effect, and the principal stratum effect. However, the relevance of these causal effects to decision making is not always straightforward. Also, valid estimation of these effects requires very strong assumptions even in a randomized trial without loss to follow-up.^{2,12–14,31,39}

The controlled direct effect (Causal effect 3) relies on the existence of a hypothetical intervention that prevents the competing event from occurring.² In our example, it is very hard to imagine how competing events such as conception failure or miscarriage could be eliminated. In general, the controlled direct effect is only recommended when a hypothetical intervention to eliminate the competing events can be plausibly articulated.

The separable direct effect (Causal effect 4) eliminates the interpretational complications of the controlled direct effect but require strong assumptions about the decomposition of treatment into two components that exert effects through different causal pathways.¹² While it may be hard to justify in our trial, the treatment decomposition assumption may be more plausible in other settings. Consider for example, intracytoplasmic sperm injection (ICSI), an in vitro fertilization procedure that involves the sperm selection and injection of the sperm cell into the cytoplasm of the egg. The selection of a sperm cell increases the chance of live birth (but selection might not affect the risk of autism), while injection of the sperm may affect epigenetic methylation and then the risk of autism (but might not cause competing events).⁴⁰ More generally, considering a hypothetical decomposition of the treatment may help researchers clarify their notion of direct treatment effects and motivate the development of new therapies.¹²

Finally, the principal stratum direct effect (Causal effect 5) eliminates the interpretational complication of the controlled direct effect (Causal effect 3) by targeting an unknown subset of the population and requires additional strong assumptions.^13,14 For example, the monotonicity assumption generally will not hold unless we are comparing one treatment that is always superior than the other in producing live birth. A possible example in the fertility therapies setting in which monotonicity may hold is in vitro fertilization versus ovarian stimulation only; however, such comparison is rarely of clinical interest.

To focus on the problem of competing events, our example was oversimplified. First, we only considered a baseline treatment (i.e., assignment to either gonadotropin or letrozole), which did not vary during the follow-up. Second, even though Causal effects 1–4 were developed for survival or time-to-event settings,^2,12 we only considered whether a live birth or whether neonatal complications occurred, but not the time of their occurrence. (Note that point identification of Causal effect 5 has not been developed for time-to-event settings.¹⁴) If gestational age at birth differs between treatment groups, this simplification is questionable for events that, like neonatal complications, depend on gestational age. In our example, the mean gestational age was similar in both treatment groups (38.1 weeks for letrozole, 37.6 weeks for gonadotropin). For a fixed gestational age, this simplification does not matter for estimating the total effect on cumulative risk, but it does generally matter for estimating the direct effects, which rely on adjustment for time-fixed (baseline) and time-varying variables.

In conclusion, this paper reviews the causal interpretation and practical implications of different methods to handle the competing event “no live birth” in studies of the effects of prenatal treatments on events in the offspring. When choosing a particular method, researchers need to consider the interpretation of the causal effect, its relevance for decision makers —patients, doctors, other stakeholders —and scientists, and whether the assumptions required to identify the causal effect are tenable.²