Reference charts for body composition parameters by dual‐energy X‐ray absorptiometry in European children and adolescents aged 6 to 18 years—Results from the Austrian LEAD (Lung, hEart, sociAl, boDy) cohort

Summary

Background

DXA is a widely used technique to assess body composition. Reference values based on a large general population cohort of European children and adolescents were missing. The aim of this study was to provide age‐ and sex‐specific reference percentiles of body composition parameters for European children and adolescents and to compare them to the American NHANES cohort. Additionally, exponents accounting best for height biases were analysed.

Methods

DXA scans of 1573 participants, aged 6 to 18 years, recruited from 2011 to 2019 by the Austrian LEAD study, a representative population‐based cohort, have been used to create reference charts using the LMS model.

Results

Reference charts displaying percentile curves and the corresponding reference values are provided. Fat mass parameters were higher in females, while lean mass parameters were higher in males. Compared to the NHANES cohort medians of FMI and LMI were always lower. For FMI, BMI, LMI and ALMI the best fitting exponent were 2.5, 3, 3 and 3.5 respectively

Conclusions

The present study provides reference charts for children and adolescents aged 6 to 18 years, for body composition parameters assessed by DXA. The charts enable comparison to a European general‐population cohort and indicate that reference populations should be chosen with caution.

1. INTRODUCTION

Obesity and overweight have increased in children worldwide throughout the last decades. ¹ The continuing increase is alarming since studies report a strong association between childhood obesity and premature death in adulthood. ² , ³ Emerging evidence suggests that muscle mass abnormalities already present in early childhood are a relevant risk factor for metabolic diseases and adverse health outcomes in later life. ⁴ Hence, the assessment and monitoring of body composition should start at a young age. Various techniques for the assessment of body composition exist. The high precision and accuracy, as well as the meanwhile clinical availability, make dual‐energy X‐ray absorptiometry (DXA) a widely used imaging technique for the assessment of body composition. ⁵ , ⁶ DXA can assess fat mass (FM), bone mass, and lean mass (LM). ⁶ While primarily used to measure bone mineral density, to predict the risk for bone fractures, the assessment of FM and LM has become more common in the last years as well. ⁶ Compared to body mass index (BMI), FM indexed by height² (FMI) reflects the amount of body fat more precisely, since BMI cannot differentiate between the different components of body weight. BMI therefore is only a surrogate marker of the amount of body fat. ⁷ LM indexed by height² is often used as a marker of skeletal muscle mass, primarily when measured at the limbs as appendicular LMI (ALMI). ⁴ , ⁸ However, the interpretation of individuals' DXA measurement results requires appropriate reference values. Reference percentiles, based on sufficiently large samples, representative for the general population, are needed to detect deviations from a standardised range. Reference percentiles for body composition parameters need to consider age, sex and ethnicity. ⁹ Since differences between DXA devices have been reported, they are further only applicable to the same DXA systems they have been measured with. ¹⁰ , ¹¹ Moreover, patients need to be compared to subjects of the same population, since variations in body composition and proportions between populations have been reported. ¹² Until now, the only recommended reference percentiles ¹³ have been derived from the dataset of the American National Health and Nutrition Examination Survey (NHANES) cohort. ¹⁴ , ¹⁵ Reference curves based on DXA measurements of children and adolescents, representative for a European population, are currently not available.

Indexing anthropometric and body composition parameters by height² is widely performed to account for biases due to height. Whether indexing with the exponent 2 for height is appropriate for children and adolescents have been challenged lately. ⁴ , ¹⁶ , ¹⁷

The first aim of the study was to provide age‐ and sex‐specific reference percentiles of the main body composition parameters for European children and adolescents aged 6 to 18 years, measured with a Lunar Prodigy DXA. The second aim was to compare them to the reference percentiles based on the American NHANES cohort. The third aim was to evaluate whether indexing by squared height is appropriate for body weight, FM, LM and ALM or whether superior exponents exist.

2. MATERIALS AND METHODS

2.1. Study design and cohort

The LEAD study (clinical trial number: NCT01727518) is a longitudinal observational study, investigating a random sample of participants, recruited from the general population of Austria, a central European country. A precise description of the recruitment strategy, the objectives, and the methodology, as well as the external validity of the LEAD Study, has been published previously. ¹⁸ In short, the study cohort was recruited, stratified by age, sex and residential area, based on the Austrian inhabitants' register and is representative of the Austrian population in terms of age and gender distribution. ¹⁸ It should be considered that the study population is only representative for Caucasians. For this analysis, only cross‐sectional data of participants from the age of 6 to 18 years with valid whole‐body DXA scans, which were examined between 2011 and 2019, were included. In total, 1637 participants aged 6 to 18 years satisfied the inclusion criteria for the LEAD study (signed informed consent and had valid lung function data available) during this time period, 64 of them had to be excluded: 28 as legal representative did not give permission for DXA examination, and 36 due to entry errors. Therefore, 1573 had valid DXA measurements and were included for the analysis of the present manuscript. Three participants had a diagnosis of diabetes mellitus, and two of them were treated with insulin, while one was taking oral glucose‐lowering drugs, two had a diagnosis of a renal disease, and one was taking systemic glucocorticoids. None of the included participants had a diagnosis of cancer or osteoporosis or was taking diuretic medications. Participants exceeding the weight limit of the DXA scanner table (159 kg) could not be considered for this analysis. Further general exclusion criteria were pregnancy and current breastfeeding, which did not apply to any of the participants of this analysis. We did not apply exclusion criteria to other specific groups (e.g. participants with a diagnosis of diabetes mellitus) to make sure that our sample represents the true general population well.

2.2. Ethics

The study was conducted according to the Declaration of Helsinki (2008) and approved by the local ethics committee of Vienna (protocol number: EK‐11‐117‐0711). Informed consent was signed by all participants and for minors by either their parents or legal representatives.

2.3. Measurements

2.3.1. Anthropometrics/body composition

As the Austrian LEAD Study is a single‐centre study, all whole‐body measurements were taken with the same Lunar Prodigy (GE Lunar Corp.; Madison, Wisconsin) DXA scanner. The quality control and calibration procedure were performed according to the manufacturers' recommendations. Before the first measurement of the day, a phantom was used to ensure quality control. Positioning was standardized and revised before each participants' measurement by a trained technician, who also post‐verified that the scan was appropriate. To assess precision and repeatability, a random sample of 30 participants was measured twice, and the coefficient of variation (CV) was calculated as the root mean square standard deviation divided by the mean. The CV was found to be 1.15% for total FM, 1.33% for %FM, 0.71% for total LM, 2.12% for appendicular LM, 2.82% for FM trunk and 2.53% for FM limbs.

All participants of the LEAD study were examined after completing a fasting period of 8 hours. Jewellery (e.g. earrings, watches, necklaces, bracelets, rings, removable piercings), shoes, jeans, all clothes with zippers or press buttons and bras containing a wire were taken off prior to the measurement.

Whole‐body measurements of FM, LM, as well as LM and FM of the limbs and FM of the trunk were derived from the DXA scanner dataset. All parameters were analysed using the paediatric version of the software enCORE (version 17, 2016). Height was measured using a stadiometer, and weight was measured with a high‐precision scale (Exacta Classica by Soehnle).

The following indices were calculated as described below:

• FMI (kg/m²): calculated as FM divided by height²,

• %FM: calculated as FM (kg) divided by total body weight (kg),

• FM trunk/limbs (kg): calculated as FM trunk divided by the sum of FM of arms and legs

• LMI (kg/m²): calculated as LM divided by height²,

• appendicular LMI (ALMI, kg/m²): the sum of LM of arms and of legs divided by height²,

• BMI (kg/m²): calculated as body weight divided by height²,

• fitted FMI (kg/m^x): calculated as FM divided by height^x,

• fitted LMI (kg/m^x): calculated as LM divided by height^x,

• fitted ALMI (kg/m^x): calculated as ALM divided by height^x,

• fitted BMI (kg/m^x): calculated as weight divided by height^x.

2.4. Statistics

The dataset was stratified by sex and grouped by age with steps of 2 years (eg, 6.0 to <8.0 years), for which descriptive analyses were conducted. Extreme outliers (standardized residuals >10) were identified by using a linear model, but no outliers were found for any parameter presented in this manuscript. Reference curves were created using the LMS method described by Cole and Green, ¹⁹ which is explained in the method section of the corresponding adults' manuscript in greater detail. ²⁰ In contrast to the descriptive analysis, the LMS model uses the exact age in a continuous manner as input, such that splitting the data into arbitrary age groups is not needed. The degrees of freedom of the L, M and S curves were chosen by first fitting multiple models, and then selecting the final model based on the Bayesian Information Criterion (BIC). To prevent overfitting due to a relatively smaller amount of data points, we limited the reachable degree of freedom for the M‐curve to a maximum of four. For the L‐ and S‐curves, the highest degrees of freedom attained were one and five, respectively. The L, M and S parameter curves of the selected model were used to construct percentile curves (3rd, 10th, 25th, 50th, 75th, 90th, 97th) for the original data, which were then plotted as reference charts. To check whether the selected model yields reasonable percentiles, the percentage of data points lying below each percentile curve was calculated. In addition, we calculated with the corresponding age‐ and sex‐specific L, M and S values the Z‐scores for each individual using the following formula: $\mathit{\text{Zscore}}=\frac{{\left[\frac{y}{M\left(t\right)}\right]}^{L\left(t\right)}-1}{L\left(t\right)S\left(t\right)}$ (t = age, y = value of DXA measurement). We tested whether the distribution of the Z‐scores corresponds to a standard Gaussian distribution by the Kolmogorov‐Smirnov test (P < .05, using multiple testing correction), which could not be rejected for any parameter evaluated.

To compare our results to the NHANES cohort, we plotted the curves corresponding to the 3rd, median and the 97th percentile based on the NHANES reference values ¹⁵ next to our median curves. Moreover, we calculated LMI Z‐scores for participants of the LEAD Study, using the published L, M and S values of NHANES ¹⁵ and tested whether the resulting distribution still corresponded to a standard Gaussian distribution by Kolmogorov‐Smirnov test (P < .05, using multiple testing correction). For FMI, Duran et al used a more flexible target distribution, which is not symmetric around zero (=skewed). Therefore, they most likely were not able to transform the data into a standard Gaussian distribution. This was not the case for us, that is, the LMS model could be fit for all parameters. Our LMS models were constructed using the R (2004‐2016 The R Foundation for Statistical Computing http://www.R-project.org) package VGAM (https://cran.r-project.org/web/packages/VGAM/index.html). The developed R script was published on Github (https://github.com/FlorianKrach/LMS-model).

To find the optimal exponent x, such that indexing by height power x gives a constant relation between height and the indexed quantity, linear regression analysis was used. For an exponent x, the indexed values were calculated as “original value” divided by height power x. Then, these indexed values were regressed on height, and the optimal exponent was chosen as the one for which the regression coefficient was closest to 0. The exponent was rounded (next 0.5 [this rounded exponent also coincided with the optimal exponent when regarding only exponents n/2, for integer numbers n]), and we developed reference charts for the parameters indexed with the new exponent using the same method as described above. All descriptive analyses were conducted with either R (http://www.R-project.org) or python (https://www.python.org).

3. RESULTS

3.1. Population characteristics

Table 1 shows the descriptive characteristics of the studied population. In total, 1573 children and adolescents aged 6 to 18 years were included (males 51.7%).

TABLE 1.

Descriptive characteristics of the study population

Age	6‐18 years	6‐8 years	8‐10 years	10‐12 years	12‐14 years	14–16 years	16‐18 years
Total
Sample size (n)	1573	346	363	242	194	200	228
Height (cm)	147.3 ± 19.3	124.8 ± 6.4	135.3 ± 7.4	146.3 ± 7.8	160.2 ± 8.4	167.7 ± 8.4	172.5 ± 8.9
Weight (kg)	42.6 ± 17.7	25.3 ± 5.2	32.0 ± 7.7	39.7 ± 10.1	51.1 ± 11.6	60.6 ± 13.5	65.5 ± 11.1
BMI (kg/m2)	18.7 ± 3.9	16.1 ± 2.3	17.3 ± 3.0	18.4 ± 3.6	19.8 ± 3.5	21.5 ± 4.3	22.0 ± 3.1
%FM	30.0 ± 7.9	29.8 ± 6.2	31.4 ± 7.8	31.6 ± 7.5	29.8 ± 8.2	30.1 ± 8.4	26.6 ± 8.5
FM (kg)	12.6 ± 7.1	7.5 ± 3.2	10.2 ± 4.9	12.7 ± 6.2	15.3 ± 7.2	18.1 ± 8.4	16.8 ± 6.7
LM (kg)	28.7 ± 12.0	17.1 ± 2.7	21.0 ± 3.6	25.9 ± 4.6	34.2 ± 6.4	40.5 ± 7.9	46.2 ± 8.9
ALM (kg)	12.9 ± 6.3	6.9 ± 1.5	8.9 ± 2.0	11.5 ± 2.4	15.8 ± 3.4	18.8 ± 4.4	21.9 ± 5.2
Males
Sample size (n)	814	159	195	129	102	97	132
Height (cm)	149.6 ± 20.6	124.9 ± 6.5	135.9 ± 7.6	146.4 ± 7.5	161.0 ± 9.0	171.8 ± 8.7	177.5 ± 6.8
Weight (kg)	44.6 ± 19.1	25.6 ± 5.1	32.2 ± 8.1	40.3 ± 9.8	51.9 ± 12.0	64.4 ± 15.5	69.5 ± 10.4
BMI (kg/m2)	18.9 ± 4.0	16.3 ± 2.2	17.2 ± 3.0	18.7 ± 3.7	19.8 ± 3.4	21.8 ± 5.0	22.0 ± 2.9
%FM	27.2 ± 7.9	27.4 ± 5.7	28.9 ± 7.5	30.7 ± 7.8	27.8 ± 8.8	26.1 ± 8.9	21.3 ± 6.0
FM (kg)	11.8 ± 7.1	7.0 ± 2.8	9.5 ± 5.1	12.6 ± 6.4	14.5 ± 7.3	17.0 ± 9.8	14.5 ± 6.2
LM (kg)	31.2 ± 13.6	17.9 ± 2.7	21.8 ± 3.7	26.6 ± 4.2	35.7 ± 7.0	45.2 ± 8.3	52.1 ± 6.3
ALM (kg)	14.3 ± 7.2	7.2 ± 1.5	9.3 ± 2.1	11.9 ± 2.3	16.7 ± 3.8	21.5 ± 4.5	25.3 ± 3.8
Normal weight a	58%	61%	56%	51%	55%	56%	70%
Overweight a	18%	13%	20%	22%	24%	14%	15%
Obesity a	10%	12%	10%	13%	8%	13%	3%
Females
Sample size (n)	759	187	168	113	92	103	96
Height (cm)	144.7 ± 17.4	124.7 ± 6.4	134.5 ± 7.0	146.1 ± 8.3	159.3 ± 7.6	163.8 ± 6.0	165.7 ± 6.7
Weight (kg)	40.4 ± 15.8	25.0 ± 5.4	31.8 ± 7.3	38.9 ± 10.4	50.2 ± 11.2	57.0 ± 10.2	60.1 ± 9.9
BMI (kg/m2)	18.5 ± 3.8	16.0 ± 2.3	17.4 ± 3.0	18.0 ± 3.6	19.7 ± 3.7	21.2 ± 3.6	21.9 ± 3.4
%FM	33.0 ± 6.6	31.8 ± 6.0	34.2 ± 7.2	32.7 ± 7.1	32.0 ± 7.0	33.8 ± 6.0	33.9 ± 5.7
FM (kg)	13.4 ± 7.0	8.0 ± 3.3	11.0 ± 4.6	12.9 ± 6.1	16.1 ± 7.0	19.2 ± 6.7	20.0 ± 6.2
LM (kg)	25.9 ± 9.2	16.5 ± 2.5	20.0 ± 3.4	25.0 ± 5.0	32.6 ± 5.3	36.1 ± 4.4	38.1 ± 4.9
ALM (kg)	11.4 ± 4.6	6.7 ± 1.4	8.5 ± 1.9	11.1 ± 2.6	14.8 ± 2.7	16.4 ± 2.5	17.2 ± 2.7
Normal weight a	60%	63%	52%	54%	61%	63%	71%
Overweight a	17%	16%	24%	14%	15%	19%	11%
Obesity a	7%	5%	11%	9%	4%	5%	5%

Note: Table shows mean ± SD or prevalence (%).

Abbreviations: BMI, body mass index; yrs, years.

^aNormal weight: Z‐scores −1 to 1, overweight: Z‐scores >1 to ≤2, obesity: Z‐scores >2 (Reference: WHO 2007).

3.2. Reference charts

Reference curves of the 3rd, 10th, 25th, 50th, 75th, 90th, 97th percentiles were constructed with the LMS method and are shown for anthropometric parameters (BMI, height, weight; Figure 1), FM parameters (FMI, %FM and FM trunk/limbs; Figure 2 ), as well as LM parameters (LMI , ALMI; (Figure 3), for males and females separately. The corresponding reference values for each percentile and the L, M and S values for each age (in 1‐year steps) are provided in Table S2. Fat mass parameters (FMI, %FM, FM trunk/limbs) reached higher values in females compared to males, while lean mass parameters (LMI, ALMI) were higher in males

FIGURE 1.

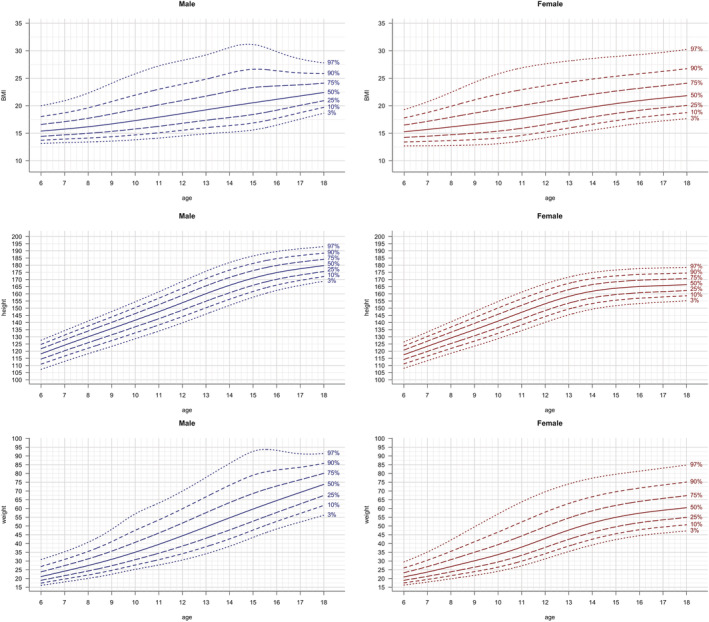
Anthropometric parameters: height, weight and BMI vs age. Lines indicate 3rd, 10th, 25th, 50th, 75th, 90th and 97th percentile. Age in years, height in cm, weight in kg, BMI in kg/m²

FIGURE 2.

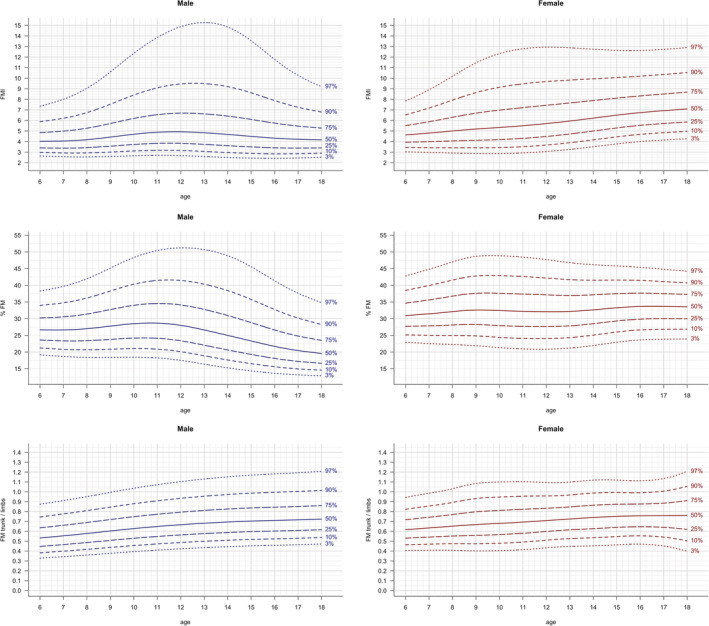
FM parameters: FMI, %FM and FM trunk/limbs vs age. Lines indicate 3rd, 10th, 25th, 50th, 75th, 90th and 97th percentile. Age in years, FMI in kg/m², FM trunk/limbs in kg

FIGURE 3.

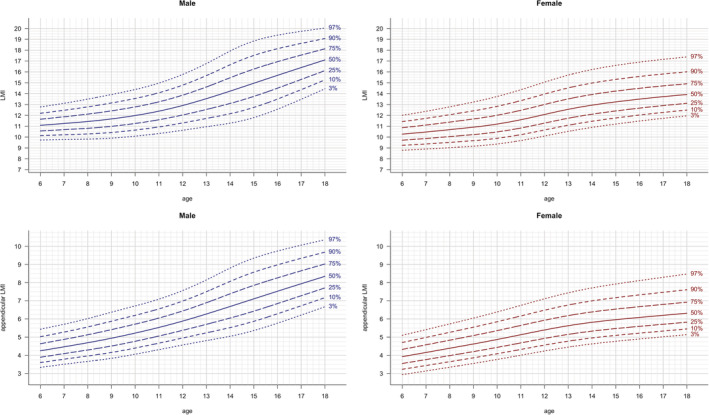
LM parameters: LMI and ALMI vs age. Lines indicate 3rd, 10th, 25th, 50th, 75th, 90th and 97th percentile. Age in years, LMI in kg/m², ALMI in kg/m²

3.3. Evaluation of our LMS models

The age‐ and sex‐adjusted Z‐scores of FMI, LMI and ALMI were calculated using the L, M and S values for all participants of the LEAD cohort. The distributions of the Z‐scores of each parameter were all found to correspond to a standard Gaussian distribution.

3.4. Comparison with results from the NHANES cohort

The age‐ and sex‐adjusted modelled 3rd, 50th, and 97th percentile for non‐Hispanic white children based on the NHANES cohort data, as published by Duran et al, ¹⁵ and the respective percentiles based on the LEAD cohort data, are shown in Figure 4. Comparison between the NHANES' and the LEAD's median curves of FMI showed that values were higher in the American cohort and that the distance between medians varied from 0.68 to 1.26 kg/m² in females (for ages 8.0 and 18.0 years, respectively) and from 0.14 to 1.03 kg/m² in males (for children aged 11.6 and adolescents aged 18.0 years, respectively). Between the male LMI median curves, the largest difference was 0.79 kg/m² for 15.7 years old males, while the smallest difference was 0.25 kg/m² at the age of 11.4 years. Comparing the LMI median curves for females, the largest distance was 0.78 kg/m² at the age of 10.8 years, and the smallest difference was 0.2 kg/m² for adolescents aged 18 years. Between the 3rd percentile, differences were smaller with a maximum of 1 kg/m² for LMI in males, 0.4 kg/m² in females, 0.3 kg/m² for FMI in males and 0.5 kg/m² for FMI in females. Differences between the 97th percentile were larger with maximums of 2.4 kg/m² in male LMI, 1.3 kg/m² in female LMI, 5.5 kg/m² in male FMI and 6.4 kg/m² in female FMI. The smallest differences were 0.6 kg/m² in male and female LMI, 0.4 kg/m² in female FMI and 2.0 kg/m² in FMI of males.

FIGURE 4.

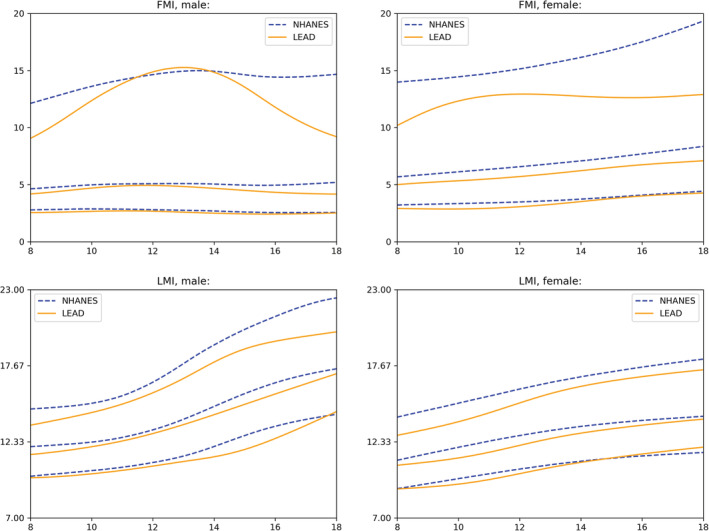
Comparison between the 3rd, 50th, and 97th reference percentiles of the NHANES and the LEAD cohort

The Kolmogorov‐Smirnov test was used to investigate if the LMI Z‐scores for the LEAD participants calculated with the NHANES reference values also satisfy the null hypothesis of following a standard normal distribution. This was rejected, and graphical investigation of the histogram of Z‐scores showed that the mean of the distribution was shifted to the left (Figure S1).

3.5. Fitted body composition parameters

For the original FMI, LMI, ALMI and BMI we found a regression coefficient of 0.022, 0.084, 0.056 and 0.114, respectively. The exponent 2.5 was optimal for FM (regression slope 0.004), while for LM and body weight the exponent 3 was optimal (regression slopes −0.002 and −0.008 respectively). For ALM, 3.5 was the best fitting exponent (regression slope of −0.001). We call the indexed values with the optimal exponent the respective fitted values, that is, fitted FMI (fFMI), LMI (fLMI), ALMI (fALMI) and BMI (fBMI). The corresponding charts are shown in Figure 5.

FIGURE 5.

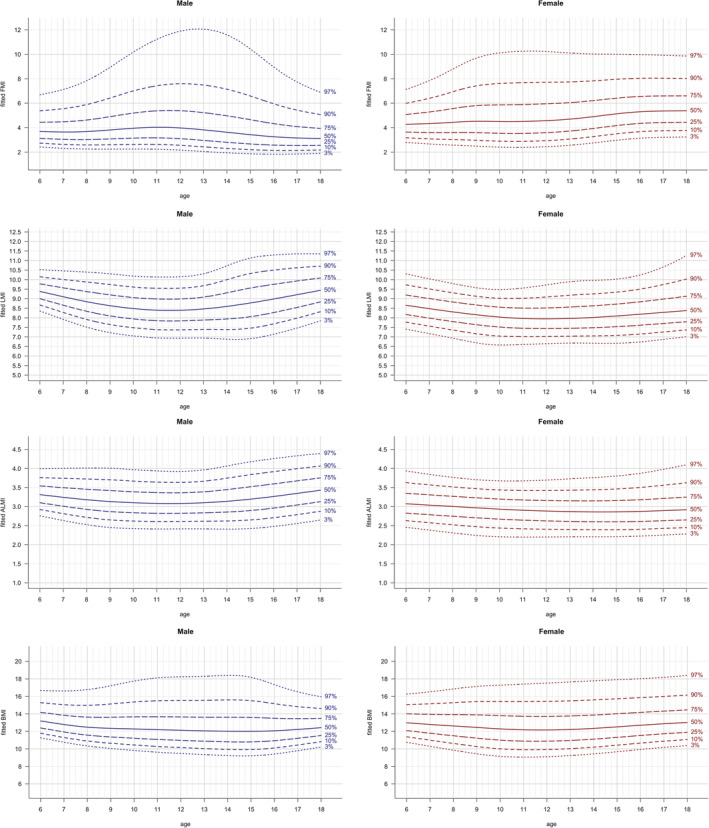
Fitted body composition parameters: fFMI, fLMI, fALMI, fBMI vs age. Lines indicate 3rd, 10th, 25th, 50th, 75th, 90th and 97th percentile. Age in years, fFMI in kg/m^2.5, fLMI in kg/m³, fALMI in kg/m^3.5 and fBMI in kg/m³

4. DISCUSSION

The present manuscript provides age‐ and sex‐related reference charts for different body composition parameters, based on 1573 European children and adolescents aged 6 to 18 years. It is the first study showing reference curves of FMI, LMI and ALMI, derived from DXA scans of a large European general population cohort of Caucasian children and adolescents.

Due to the rising epidemic of non‐communicable disease, and body composition being known as an important risk factor, ²¹ the assessment of nutritional status has become an integrative part of several prevention strategies. Lately, it has been strongly emphasised that body composition charts should be added to growth charts, which are already commonly applied in paediatrics. The clinical importance is based on the fact that not only growth but also nutritional status can be monitored more precisely in order to identify individuals at risk early. ²² DXA is a commonly used technique for the assessment of body composition due to its wide clinical availability and high precision. Several studies have reported that body composition parameters analysed by DXA show an excellent agreement with the gold standard techniques computed tomography (CT) and magnetic resonance imaging (MRI) measurements. ⁶ , ²³ Compared to CT and MRI, advantages of DXA are the low exposure to radiation dosage, similar to the average background radiation, and its fast scanning time, ⁵ , ⁶ , ²⁴ both especially relevant for the examination of young children. To allow the comparison of patients' results to the general population, age‐ and sex‐specific reference charts are needed. In addition to their clinical importance, reference values are further required in research addressing the effects of nutritional abnormalities. This is of great importance, as only little is known about the relationship between body fat and health‐related risks in the young population. ¹⁹ Besides the detection of an excessive amount of body fat, there is a growing interest in investigating the consequences of lean mass abnormalities. ⁴ Reference values illustrating the natural range of values observed in the general population can be used to subsequently define cut‐offs associated with health‐related risks.

In general, the International Society of Densitometry (ISCD) considers reference curves based on the NHANES dataset as most appropriate for comparison to the US population, but encourages to determine its applicability to other populations. ¹¹ , ¹³ Since differences between population have been emphasised, ¹² relevant discrepancies might also exist in children as already seen in adults. ²⁰ Reference charts based on a sufficiently large dataset of measurements from European children and adolescents have not been available so far. We provide for the first time, reference charts based on a large European general population cohort, created by using the same approach as applied for the US population's recommended percentiles. Moreover, we provide reference charts for children and adolescents for the parameter ALMI based on a large dataset, which is described as a more precise marker of skeletal muscle mass than LMI. ⁹ Since studies indicate that low muscle mass is associated with an increased risk for metabolic and cardiovascular diseases and adverse health outcomes, its monitoring has been urged specifically. ²⁵

4.1. Reference charts

In line with the previously published results for adults, ²⁰ we found that patterns of the widely used body composition parameters differ between sexes. FMI values were found to be lower in male compared to female children and adolescents, while LMI and ALMI values were higher in males. LMI and ALMI increased both with age during childhood and adolescence, while FM trunk/limbs increased only slightly in children and adolescents. The distinct shape of the upper percentile curves of FMI (Figure 2), which also remained after adjusting with the fitted exponent (fFMI, Figure 5), in male adolescents in the LEAD cohort might be due to relatively smaller sample size for ages between 12 and <16 years (see Table 1) leading to higher uncertainty and the larger variance of the samples within this group. Another potential reason might be that growth patterns in children vary, especially during puberty (eg, gaining weight before a growth spurt or vice versa).

4.2. Evaluation NHANES

To investigate potential population discrepancies, we evaluated if the U.S. NHANES reference percentiles ¹⁵ (for non‐Hispanic, white children applicable to GE Lunar DXA scanners) are suitable for the LEAD cohort, as a representative sample of a central European country. The distribution of the age‐ and sex‐adjusted Z‐scores of LMI (Figure S1), calculated with the L, M and S values provided by NHANES for all LEAD participants included in this analysis, was found to be non‐compliant to a standard Gaussian distribution. This indicates that the NHANES reference percentiles do not fit well for a European sample. The shift of the mean to the left indicates that the present sample (in this case the LEAD cohort) shows on average lower values than the reference sample (NHANES), as Z‐scores get smaller when the median increases. This means that after applying the NHANES reference values to our cohort, more participants are labelled with a low Z‐score and fewer participants with a high Z‐score. The distribution of the Z‐scores of other body composition parameters could not be compared as no LMS model was fit for FMI. Furthermore, ALMI, to the authors' best knowledge, has not been analysed in children and adolescents of the NHANES cohort yet. The aforementioned results are supported by all plots in Figure 4, as they show that the values of LMI and FMI in males and females were higher in the NHANES cohort compared to the LEAD cohort. The higher FMI values in the American NHANES cohort are not surprising since the prevalence of obesity is estimated to be much higher in the United States than in European regions such as Austria (33.7% vs 18.4%). ²¹ In accordance, the prevalence of obesity in children is also estimated to be highest in the United States. ²⁶ The close relationship between fat and lean mass ⁹ might explain that LMI was subsequently higher. However, the differences between the median values of LMI were smaller compared to those of FMI.

Taken together, those results indicate that the NHANES reference values should be used with caution for cohorts outside the United States, at least for non‐Hispanic white children. Worth noting, since overweight in Austria is estimated to be comparable to other countries of central and north‐western Europe, ²⁷ we consider the LEAD reference values to be suitable for populations with similar anthropometric characteristics. However, this needs to be validated in other European cohorts.

4.3. Fitted body composition parameters

Even though the exponent 2 is widely used to account for height when computing indexed values, its appropriateness has been questioned for children and adolescents. ¹⁶ , ¹⁷ We evaluated how well this exponent accounts for height, and whether there exists a better one. Our data suggest that for the commonly used BMI a better fitting exponent would be 3, which has already been found by other studies as well. ¹⁶ For FMI and LMI the best fitting exponents were 2.5 and 3 respectively, which is again in line with previously published results by other cohorts. ⁴ For ALMI we found that indexing height with the exponent 3.5 fits best. Using the exponent 2 overestimates the age‐related increase. Our results suggest that the increase observed in Figures 2 and 3 is more related to growth in height than to gain in FM or LM solely. It seems that the amount of FM and LM relative to the height power the fitted exponent does not change much with age. Therefore, we hypothesize that if adjusted for height correctly, age‐independent cut‐off values might exist for fitted body composition parameters as well as for fBMI in children and adolescents. However, it should be considered that this finding is based on cross‐sectional data only.

Since most studies and clinicians use FMI, LMI and ALMI indexed by squared height, we also provide reference charts for them, but nevertheless, we suggest to use the new, fitted body composition parameters to prevent effects due to height. Moreover, we emphasize that this finding should be evaluated in other general population cohorts.

4.4. Limitations

Due to scanner differences, reference values are only applicable to the Lunar Prodigy model, ¹¹ and as the LEAD cohort is a representative sample for Caucasians only, the reference values are not applicable to other ethnicities. Worth noting, since our data was gathered in a single centre, measurements taken at another location might have a bias. It should be considered that the data set consisted of only 1573 DXA measurements, but to the authors' best knowledge, this is a large sample size compared to other European cohorts.

4.5. Strengths

The strengths of this study are the random population‐based recruitment of the study sample, which is representative for a central European country, ²⁷ as well as the standardised, single‐centre measurements. The third strength is the mathematical approach with the LMS model, with which a possibly non‐linear dependence on age is accounted for continuously. Moreover, this model handles heteroscedasticity that occurs across age and fits the percentiles accordingly.

The provided reference charts enable clinicians an easy and fast evaluation of their patients' results in the every‐day clinical setting (the charts can be provided on request in a larger format), and the reference values provided in Tables S2 can be used by researchers to compare their study sample to the LEAD cohort. Additionally, Z‐scores can be calculated by using the L, M and S values for each age.

Importantly, reference values illustrate the range of values observed in the general population but do not provide information on the relationship between certain values and their association with adverse outcomes. For the definition of clinically validated cut‐offs, the association with health‐related risks has to be investigated. To the authors' best knowledge, no cut‐offs for body composition measurements, neither in adults nor in children and adolescents have been validated yet. We would like to emphasize the need for these cut‐offs and are aiming to address this in a future project.

To provide the reference values for each exact age and to enable comparison and calculation of the Z‐scores easily, we developed a tool that can be accessed on https://leadstudy.at/publikationen/.

5. CONCLUSION

This study provides age‐ and sex‐related reference charts for widely used anthropometric and body composition parameters for children and adolescents aged 6 to 18 years. It reveals differences between two large cohorts of different populations (American vs Central European). Moreover, it shows that the widely used indices may not be appropriate and that the fitted values for FMI, LMI, ALMI and BMI might be superior.

CONFLICT OF INTEREST

All authors declare no conflict of interest related to the manuscript.

AUTHOR CONTRIBUTIONS

Alina Ofenheimer analysed data and wrote the manuscript; Robab Breyer‐Kohansal conducted the study and reviewed the manuscript; Sylvia Hartl conducted the study and reviewed the manuscript; Otto C. Burghuber conducted the study and reviewed the manuscript; Florian Krach analysed data and reviewed the manuscript; Frits M. E. Franssen reviewed the manuscript; Emiel F. M. Wouters reviewed the manuscript; Andrea Schrott researched data; Marie‐Kathrin Breyer conducted the study and reviewed the manuscript.

Supporting information

Figure S1. Comparison between NHANES and LEAD cohort according to Z‐scores distribution of LMI. Distribution of LMI Z‐scores calculated with the NHANES reference values (pink) and the LEAD reference values (green) for participants of the LEAD cohort.

Tables S2. Reference values for percentiles (3rd, 25th, 10th, 50th, 75th, 90th, 97th) of different body composition parameters (BMI, height, weight, FMI, %FM, FM trunk/limbs, LMI, ALMI, fFMI, fLMI, fALMI, fBMI).

Ofenheimer A, Breyer‐Kohansal R, Hartl S, et al. Reference charts for body composition parameters by dual‐energy X‐ray absorptiometry in European children and adolescents aged 6 to 18 years—Results from the Austrian LEAD (Lung, hEart, sociAl, boDy) cohort. Pediatric Obesity. 2021;16:e12695 10.1111/ijpo.12695