Significance
To survive and to thrive, plants rely on their ability to sense multiple environmental signals, such as gravity or light, and respond to them by growing and changing their shape. To do so, the signals must be transduced down to the cellular level to create the physical deformations leading to shape changes. We propose a multiscale theory of tropism that takes multiple stimuli and transforms them into auxin transport that drives tissue-level growth and remodeling, thus modifying the plant shape and position with respect to the stimuli. This feedback loop can be dynamically updated to understand the response to individual stimuli or the complex behavior generated by multiple stimuli such as canopy escape or pole wrapping for climbing plants.
Keywords: plant tropism, biomechanics, morphoelasticity, rod theory, mathematical model
Abstract
Plant tropism refers to the directed movement of an organ or organism in response to external stimuli. Typically, these stimuli induce hormone transport that triggers cell growth or deformation. In turn, these local cellular changes create mechanical forces on the plant tissue that are balanced by an overall deformation of the organ, hence changing its orientation with respect to the stimuli. This complex feedback mechanism takes place in a three-dimensional growing plant with varying stimuli depending on the environment. We model this multiscale process in filamentary organs for an arbitrary stimulus by explicitly linking hormone transport to local tissue deformation leading to the generation of mechanical forces and the deformation of the organ in three dimensions. We show, as examples, that the gravitropic, phototropic, nutational, and thigmotropic dynamic responses can be easily captured by this framework. Further, the integration of evolving stimuli and/or multiple contradictory stimuli can lead to complex behavior such as sun following, canopy escape, and plant twining.
Plant tropism is the general phenomenon of directed growth and deformation in response to stimuli. It includes phototropism, a reaction to light (1); gravitropism, the reaction to gravity (2, 3); and thigmotropism, a response to contact (4), among many others (Fig. 1). The study of tropisms in plants dates back to the pioneering work of giants such as Darwin (5) and Sachs (6) and has been a central topic for our understanding of plant physiology ever since. Tropisms form a cornerstone subject of modern plant biomechanics (7) and crop management strategies (8), as well as systems biology and plant genomics (9). Being sessile by nature, plants lack the option to migrate and must adapt to their ever-changing environment. The growth response of individual plants to environmental cues will determine the yield of a crop in unusually windy conditions, will decide the future of rainforests in a world driven by climate change, and may be key for colonizing foreign environments such as Mars.
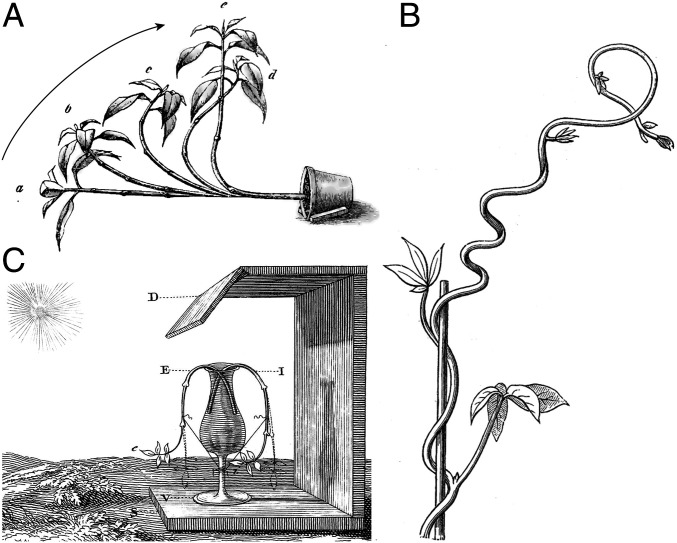
Fig. 1.
Classic experiments on tropic responses. (A) Gravitropism: A potted plant realigns itself with gravity (13). (B) Thigmotropism: A twining vine develops curvature when in contact with a pole (6). (C) Phototropism: A plant reorients itself toward the light source [18th century experiments by Bonnet (14), correctly interpreted by Duhamel du Monceau (15, 16)].
Mathematical modeling plays an invaluable role in gaining a better understanding of tropisms and how plants may respond to a change in their environment (10). Yet, a general mathematical description of tropisms is a grand challenge. First, the growth response tends to be dynamically varying: A sunflower grows to face the sun, but as it grows the sun moves, so the environmental influence—the intensity of light impacting on each side of the sunflower—is changing during the process. Similarly, a tree branch may align with the vertical in a gravitropic response, decreasing the likelihood of breaking under self-weight; however, the growth response itself may increase the branch weight and thus change the stimulus (11). Second, while there exist numerous experimental setups that enable one to carefully isolate a particular stimulus, a plant typically receives multiple stimuli at the same time and in different locations (12). The resulting movement is an integration of multiple signals.
Third, any tropism is fundamentally a multiscale phenomenon. Transduction of an environmental cue takes place from the organ to the cell and involves, ultimately, molecular processes. A hormonal response is induced, which leads to different cells expanding at different rates in response to the chemical and molecular signals. However, one cannot understand the change in shape of the plant and its position in relation to the direction of the environmental stimulus at this level. To assess the effectiveness of the growth response, one needs to zoom out. The net effect of a nonuniform cell expansion due to hormone signaling is a tissue-level differential growth (1) as depicted in Fig. 2. At the tissue level, each cross-section of the plant can be viewed as a continuum of material that undergoes nonuniform growth and/or remodeling (17). Differential growth locally creates curvature and torsion, but it also generates residual stress (18). As a result, the global shape of the plant and its material properties evolve in time. To characterize this global change, and to update the position of the plant in the external field, a further zooming out to the plant or organ level is appropriate. At the plant level, the global shape, material properties, and positioning in the external stimulus are well described by a physical filament: Here, the plant is viewed as a space curve endowed with physical properties dictated by the lower-level tissue scale, and its shape and motion can be described by the theory of elastic rods, which has been applied to multiple biological contexts, from DNA and proteins to physiology and morphogenesis (19–22).
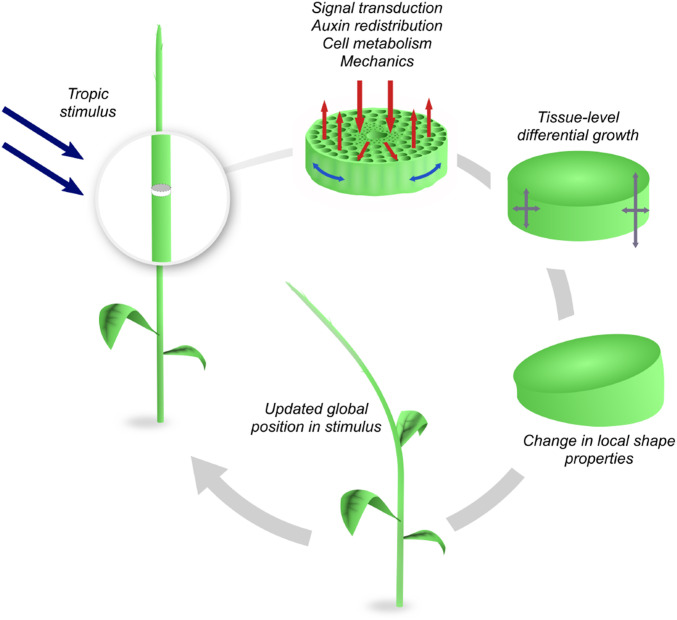
Fig. 2.
Tropism is a multiscale dynamic process: The stimulus takes place at the plant or organ level and its information is transduced down to the cellular level, creating a tissue response through shape-inducing mechanical forces that change the shape of the organ. In the process, the plant reorients itself and, accordingly, the stimulus changes dynamically.
The challenge of formulating a mathematical model of tropism is further complicated by the remarkable variation in plants and the multiple types of tropism. Within a single plant, a tropic response may refer to the growth and movement of the entire plant or a subset: a single branch, vine, stem, or root. Here, we use the word “plant” to refer to the entire class of plant structures that may undergo such growth responses. Moreover, even within a single plant, multiple environmental cues will combine and overlap in effecting mechanotransductive signals, hormonal response, differential growth, and ultimate change in shape (23); e.g., a sunflower exhibiting phototropism still perceives a gravitational signal.
At the theoretical level, a variety of approaches have recently been proposed. Growth kinematics models successfully describe the tropic response at the plant level (7, 24, 25), but do not include mechanics and cellular activities. A number of large-deformation elastic rod descriptions of tropic plant growth have also been proposed (26–31); these involve a full mechanical description at the plant level, with phenomenological laws for the dynamic updating of intrinsic properties such as bending stiffness and curvature and even branching and self-weight (32), but specific cell- and tissue-level mechanisms are not included. Multiscale formulations have also appeared, including functional–structural plant models (8, 33, 34) and hybrid models with vertex-based cell descriptions (35, 36). These computational approaches have the potential to incorporate effects across scales but are limited to small deformations compared to the ones observed in nature.
The goal of this paper is to provide a robust mathematical theory that links scales and can easily be adapted to simulate and analyze a large number of overlapping tropisms for a spectrum of plant types. Our mathematical and computational framework includes 1) large deformations with changes of curvature and torsion in three-dimensional space; 2) internal and external mechanical effects such as internal stresses, self-weight, and contact; and 3) tissue-level transport of growth hormone driven by environmental signals. By considering the integration of multiple conflicting signals, we also provide a view of a plant as a problem-solving control system that is actively responding to its environment.
1. Multiscale Modeling Framework
The key to our multiscale approach is to join three different scales: stimulus-driven auxin transport at the cellular level, tissue-level growth mechanics, and organ-level rod mechanics.
A. Geometric Description of the Plant
We start at the organ scale and model the plant as a growing, inextensible, unshearable elastic rod following the formalism of ref. 17, chap. 5 that extends the classical Cosserat rod theory (37–40) to growing filaments. A morphoelastic rod is a one-dimensional filamentary object that can bend and twist with some penalty energy. The rod cannot be elastically stretched, but it can increase in length by addition of mass, leading to a growth stretch. Let describe its centerline, where is the initial arc length measured from the base of the plant toward its tip (Fig. 3A). Together with the fixed Cartesian basis, , we define, at each point on the curve a local orthonormal basis , oriented such that aligns with the tangent in the direction of increasing , and denote directions in each cross-section from the centerline to two distinguished material points. From the director basis, the Darboux vector is defined as and encodes the rod’s curvature, torsion, and twist (17). For a given curvature vector, the shape of the rod, and the evolution of the basis, is determined, for boundary conditions , by integrating the system of equations
| [1] |
Here denotes the total axial growth stretch of each section mapping the initial arc length to the current arc length (41). The general basis specializes to the Frenet–Serret frame by taking and to be the curve’s normal or to the so-called Bishop frame (or parallel transport frame) by taking and (42, 43). At each value of , the cross-section is defined by a region , where , are local variables describing the location of material points in the respective directions , .
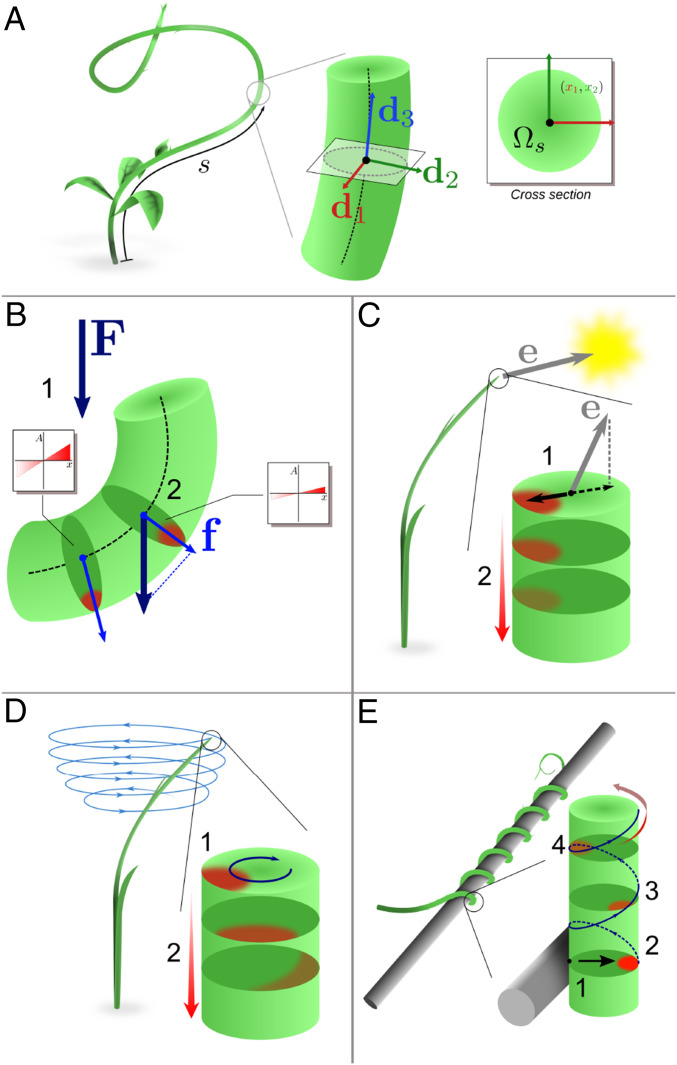
Fig. 3.
(A) Each cross-section of the rod is parameterized by its arc length (oriented acropetally) and equipped with a local material basis . (B) Gravitropism: The gravity vector (1) is sensed in each cross-section and causes lateral auxin flow (2). (C) Phototropism: The light vector is sensed at the plant apex and results in the establishment of an apical auxin profile (1) that is transported basipetally with attenuation (2). (D) The circumnutation is generated by an internal oscillator with pulsation associated with rotating auxin profile at the apex (1). The apical profile is transported basipetally (2), generating curvature and torsion. (E) Thigmotropic pole wrapping is triggered by a contact (1) eliciting an asymmetrical auxin profile (2), which is in turn transported helically (3) to the rest of the plant with signal attenuation (4).
In terms of the local geometry, any material point in the plant can be represented by its arc length and its position on the cross-section at as follows:
| [2] |
We can now use this representation to formulate the stimuli.
B. The Stimuli
Tropic stimuli are characterized by their origin, sign, and direction (44). Signal origin includes chemicals, water, humidity, gravity, temperature, magnetic fields, light, and touch. Tropisms can have a sign: positive if the plant grows toward or in the direction of the stimulus or negative if it moves away from the stimulus. The direction of tropism describes the orientation of the response with respect to a directed stimulus: Exotropism is the continuation of motion in the previously established direction, orthotropism is the motion in the same line of action as the stimulus, and plagiotropism is the motion at an angle to a line of stimulus.
Physically, stimuli are fields acting in space at a point and changing over time . They can be either scalar fields, , e.g., chemical, temperature, or light intensity; vector fields, , e.g., geomagnetic field, gravity, or light direction; and, possibly, tensor fields (e.g., mechanical stress—not considered here). These stimuli are in general functions of both space and time which makes plant tropism a physical theory of fields (which is appropriate since plants grow in physical fields). Since a stimulus is defined at points in space, we must also take into account the orientation and the position of the plant in space. For example, the cellular response to light in phototropism is linked to the relative orientation of the plant in relation to the light source. In the case of a vector stimulus , we must therefore decompose the stimulus in the local basis:
| [3] |
The quantities are the components of the stimulus as felt by the plant. Next, we link an external stimulus to the cellular response.
C. Cellular Response and Auxin Transport
At the cellular level, deformations take place through anelastic expansions of the cell walls in response to turgor-induced tension (45, 46). We refer to any geometric change of cellular shape as growth. While detailed models of these cellular processes are available (47–49), they do not easily extend to the continuum level; hence, for simplicity we adopt here a coarse-grained view in which the anelastic expansions are connected locally via a single hormone concentration field that plays the role of a morphogen. This is in line with other models of morphogen-mediated growth (e.g., ref. 50). Here, we consider the phytohormone auxin which is known to play a central role in plant growth and remodeling. Indeed, laterally asymmetrical auxin redistribution is broadly accepted as a universal mechanism underlying tropisms (51, 52). A lateral gradient is controlled via the relocalization of auxin transporters in response to tropic signals (53). In shoots, higher levels of auxin are generally associated with faster growth. The resulting asymmetrical growth of cells elicits global curvature at the organism level through pathways that are not completely understood (54). Therefore, in our model auxin flux is a function of tropic signal and growth is taken to depend only on auxin concentration.
We assume that auxin is transported by diffusion and advection and locally removed by various mechanisms such as conjugation or direct oxidation (55–57). These effects are modeled through a standard reaction–advection–diffusion equation (58) for the auxin concentration :
| [4] |
where is the auxin flux, is a parameter that characterizes the rate of auxin turnover, and captures any sources or sinks. The flux is a sum of a diffusive component and a stimulus component , although a simple scaling analysis with estimated auxin diffusion and velocity (SI Appendix, section 4A) suggests that the process is advection dominated, and so we restrict our attention to the zero diffusion limit . Depending on the particular tropism, the information about the stimuli is contained either in or in a boundary or source term. The auxin transport, Eq. 4, is combined with a no-flux condition at the outer boundary of each cross-section, where is an outward normal vector to the boundary .
D. Tissue-Level Growth and Remodeling
Once the auxin distribution is known from the solution of Eq. 4, we can relate the growth field at the tissue level to the concentration . Here, we use the general theory of morphoelasticity (17) that assigns at each point of the plant a growth tensor dictating the deformation due to growth. Physically, this tensor field integrates the multiple contributions of local pressure, cell material properties, and tissue geometry, all regulated via the cell metabolic and genetic activity (47) into a single object describing the local change of shape of an elementary volume element (59). This growth tensor may be different in different directions (anisotropic growth) and/or spatially varying (heterogeneous growth) (60) to encode changes in both length and girth. However, here we assume that growth takes place, locally, only along the axial direction and not in the cross-sectional direction. This assumption implies that there is no change in thickness, an effect that could be of importance in some systems. Then, the only nontrivial component of the growth tensor is a single function that describes the change of axial length of an infinitesimal volume element (SI Appendix, section 2). An initially straight filament of length with constant at all points would grow to a new straight filament of length (18). If, however, varies from point to point, the same filament would tend to bend and twist as shown in Fig. 2.
Next, we connect the axial growth function to the concentration of auxin via a growth law of the form
| [5] |
where is a baseline level of auxin, characterizes the rate at which an increase in auxin generates growth, and
is the average of the growth field, with the area of the cross-section. The term provides a pointwise measure of the strain induced by differential growth and models autotropism, the observed tendency to grow straight when subject to other tropisms. The underlying mechanisms of autotropism are poorly understood, but studies using radiolabeled auxin suggest that this straightening response does not depend on auxin but rather is sensed via an actomyosin-dependent mechanism (61, 62).
E. Change in Local Shape and Properties
The axial growth function is defined at the tissue scale and, as such, does not directly give the change in curvature and torsion of the plant. Indeed, the change of shape depends not only on but also on the internal mechanical balance of the forces generated by each growing volume element. Following the general theory given in ref. 18 and its adaptation to the particular case of plants given by the growth law Eq. 5, we compute the intrinsic curvatures and elongation of the growing plant (SI Appendix, section 3). In the absence of autotropism (), these curvatures (given by the vector ), which define the shape of the plant in the absence of body force and external loads, evolve via
| [6] |
| [7] |
| [8] |
| [9] |
Here and for the rest of this paper, we have assumed that the cross-section is circular with radius , area , and second moment of area .
F. Rod Mechanics Set the Plant Position in the Stimulus Field
Once the intrinsic curvatures and elongation of the plant following growth have been updated, the plant position and orientation are updated by solving the Kirchhoff equations (41, 63) for the balance of linear and angular momentum for given external forces such as self-weight, wind, or contact forces (see SI Appendix, section 1 for details on the Kirchhoff equations).
Since at this scale the plant is treated as a one-dimensional structure, its equilibrium shape is easily computed even in complex nonplanar geometries. Once the deformation is determined, the multiscale cycle is completed by updating the map between external stimulus and cell-scale response with respect to the updated orientation, and the process is repeated.
G. Summary
The flow of information between different spatial scales for a given stimulus field proceeds as follows: 1) Given an initial plant shape, a stimulus impacts auxin transport and thus local concentrations of auxin via the transport equation (Eq. 4); 2) the local auxin concentration changes the local growth field that impacts the intrinsic curvatures and axial extension of the plant via Eqs. 6–9; and 3) the new intrinsic curvatures and external conditions determine the new mechanical equilibrium of the plant, thus changing the plant position and shape in the stimulus field.
The theoretical objective in this work is to bridge the divide between cell-based descriptions of auxin transport and plant-level descriptions of tropism kinematics. In the examples below, we demonstrate how the tissue-level transport and growth equations may be mathematically combined to yield explicit evolution rules for the curvature and axial growth at the rod level. In this way, the multiscale flow can be efficiently simulated and analyzed for a variety of tropic responses. It is also worth noting that a significant amount of biology exists between the cell-scale and the tissue-level models we propose, therefore we largely opt for qualitative investigation of complex behavior, with further experimental and theoretical work needed to refine parameter selection.
2. Examples
A. Gravitropism
Gravitropism has been extensively studied both experimentally and theoretically. The classic description is based on the so-called “sine rule” in which the change in curvature follows the sine of the angle with the direction of gravity (64). While it is successful in capturing observed behavior in gravitropic experiments, it is mostly phenomenological and is applicable only to planar geometry. Here, we show that the sine rule emerges naturally from our formulation but that it can be generalized to include three-dimensional deformations that are generated when the entire plant is forced to change its orientation in time.
The stimulus for gravitropism is the vector field which can be written in the plant frame of reference as , where is the gravity force acting in the plane of the cross-section. Since it is believed that plants are insensitive to the strength of gravitational field (65), it is sufficient to use a unit vector representing only the direction of gravity; i.e., we scale the gravitational acceleration to 1. If , no tropic response will occur. Gravity perception relies on specific cells called statocytes distributed along the shoot (66). Statocytes contain dense organelles, statoliths, that sediment under the effect of gravity. Tilting of the plant causes statoliths to avalanche and to form a free surface perpendicular to the gravity vector, providing orientational information to the cell (67). It has been observed that the gravitropic response depends upon the angle between the statoliths free surface and the vertical, but not upon the intensity of the gravitational field or the pressure of statoliths against the cell membrane (65). A possible mechanism is that the contact between the statoliths and the cell membrane may trigger relocalization of PIN membrane transporters and a redirection of auxin flux (67). Here, we follow this hypothesis and, accordingly, assume that gravity drives an advective flow of auxin . If the statocytes are uniformly distributed within the stem volume, then is constant. We assume also a source and sink of auxin on each cross-section, representing a continual axial auxin flow, and that auxin transport occurs on timescales much shorter than the one associated with growth. Combining the transport equation (Eq. 4), the growth law (Eq. 5) (in the absence of autotropism for simplicity), and the evolution laws given by Eqs. 6–9, we obtain (SI Appendix, section 4B) the gravitropic curvature and axial extension models:
| [10] |
| [11] |
Here, is a single constant characterizing the rate of change of curvature due to gravity and associated with a timescale of gravitropic reaction , where is a characteristic axial length, say the length of the plant; characterizes the constant rate of auxin turnover (Eq. 4); and the parameter is the net auxin available in the cross-section (SI Appendix, section 4B). Note that the right-hand side of Eq. 11 is proportional to the net “excess auxin,” given by the integral of over the section, while the quantity does not appear in Eq. 10. The existence of such an auxin threshold is observed both in local biosynthesis and developmental processes (68, 69) and has been adopted in models (e.g., ref. 70). In our model, curvature may develop without axial extension: For axial extension the net auxin must exceed a threshold, while curvature development conceptually derives from a redistribution and thus asymmetry of auxin.
In the particular two-dimensional case where the plant can only bend around the single axis and all external forces can be neglected, we have , , and the curvature . Defining to be the inclination angle, Eq. 10 reads
| [12] |
which is the classic and widely used sine law of gravitropism (24).
The general evolution equations (Eqs. 10 and 11) can be used for more complex gravitropic scenarios. Consider, for instance, an experiment in which the base of the plant stem is at a fixed angle from the horizontal and the base is rotated, as shown in Fig. 4A and used in experiments to study gravitational setpoint angles (71). Then, in the frame of reference of the plant, the direction of gravity is constantly changing. Here, we consider the case of zero-axial growth and neglect self-weight (see C. Photogravitropic Response for these additional effects). The tropic response will generate curvature and torsion, depending on the angle and the rotational velocity of the base as shown in Fig. 4.
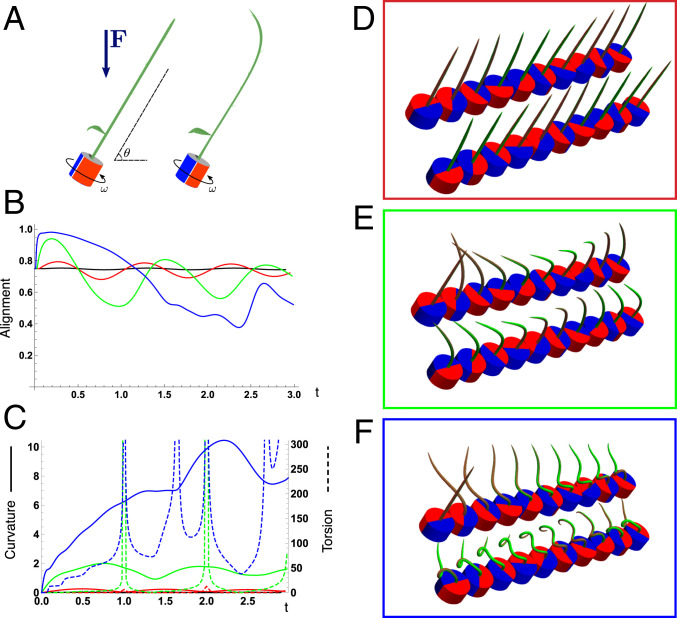
Fig. 4.
Gravitropism with a rotating base. (A) A base is tilted with respect to the vertical and then rotated about the axis with speed so that one revolution is completed every time unit. Gravitropic response is simulated for varying values of gravitropic sensitivity (black), 1 (red), 10 (green), and 50 (blue). (B and C) Alignment with the vertical (B) and curvature and torsion (C) are plotted against time for three base rotations. (D–F) Snapshots for cases of (D) slow reaction, ; (E) intermediate reaction, ; and (F) fast reaction, . The sequence is read left to right, top to bottom, and the base rotation is counterclockwise. Further simulation details and parameters are provided in SI Appendix, section 8.
For visualization purposes, we fix the base rotation rate to one turn per unit time and vary the tropic reaction rate of the plant, which is equivalent to a fixed reaction rate and varying base rotation rate via a rescaling of time. In Fig. 4, we simulate three full rotations of the base with varying reaction rates (SI Appendix, Movies S1–S4). The evolving morphology is characterized by three metrics: an alignment metric in Fig. 4B that measures how closely aligned with the vertical the plant is (a value of one is attained if the entire plant is vertical) and curvature and torsion in Fig. 4C that broadly measure deviation from a straight configuration (details in SI Appendix, section 5).
Consider first the slowest reaction morphology (equivalent to the case of fastest base rotation), given by the black curves in Fig. 4 B and C. Since the plant’s response time is much slower than the base rotation, the gravitropic response is averaged out and the plant hardly deviates from the straight configuration, never improving its alignment and generating effectively no curvature or torsion. The plant is almost perfectly straight at all times (snapshots not included). The red curves denote a case with increased but still small reaction rate (fast base), which generates only small oscillations in alignment and curvature. In this regime, the plant is effectively “confused”; the local gravitational field is changing too quickly for the plant to make any progress toward alignment with the gravitational field (Fig. 4D).
As the reaction rate is increased (or the base rotation decreased), interesting morphologies emerge. In the case of the intermediate reaction rate (green curves in Fig. 4 B and C), the plant begins to curve toward the vertical during the first quarter rotation of the base, bending about the axis and increasing its alignment. However, as the base continues to rotate, the curvature initially developed has the tip pointing away from the vertical, so the alignment decreases, and the plant now must bend about the orthogonal axis. As the base completes its first rotation and the “desired” axis for bending returns to the original , an inversion occurs (Fig. 4E, and more visible in Movie S3), creating a large spike in torsion that remains bounded and continuous. This basic process repeats with each rotation.
Finally, increasing the reaction rate (or slowing the base) further creates highly complex morphologies as evidenced by the blue curves in Fig. 4 B and C. Here the plant quickly aligns with gravity and attains near perfect alignment in the first 10th of the first rotation. As the base rotates away from this aligned state, we see an interesting phenomenon: The tip of the plant is able to react and maintain alignment with the vertical, but since the base of the plant is clamped at an ever-changing angle, a loop forms, starting at the base and working its way to the tip (Fig. 4F). This is accompanied by strong variations in the total alignment and increasingly high curvature, with repeated spikes in torsion as extra twist is removed. Our simulations of this case beyond three rotations suggest that while the basic process of loops generated at the base and working to the tip continues, the morphology does not settle down into a fixed oscillatory pattern, highlighting the potential for complex dynamics generated by this highly nonlinear system.
Phototropism.
It was Darwin, at the end of the 19th century, who demonstrated that exposure of the plant apex to a light source was necessary to induce tropic bending (5, 72). Later on, Boysen-Jensen proposed that bending is induced by a diffusive substance, later identified as auxin, that carries the tropic information from the apex to the rest of the shoot (73, 74). These early observations are the basis of the popular Cholodny–Went model (75, 76) stating that phototropism relies upon three broad mechanisms: 1) sensing of light direction at the tip of the shoot; 2) establishment of a lateral asymmetry of auxin concentration at the tip; and 3) basipetal transport of this asymmetrical distribution, resulting in differential growth along the shoot (77–79).
We model these three steps by considering axial transport of auxin, with an asymmetrical distribution that is established at the shoot apex by the stimulus, treated as a point source of light. We suppose that auxin flows basipetally with advective velocity and turnover , for which the transport equation is
| [13] |
Here the derivative in space is taken with respect to the current arc length . Additional source/sink terms can be used to model axial extension without changing the evolution of the curvature (SI Appendix, section 4C). We account for the amount and distribution of auxin at each section via a boundary condition at the tip () and define that depends on the light source located at in space and a scalar representing its intensity. We then define the unit vector from the plant tip to the light source and write it in the plant reference frame , as shown in Fig. 3C. The vector in the cross-section distinguishes the light side of the tip from the dark side and defines the asymmetrical distribution of auxin:
| [14] |
where characterizes the sensitivity of the phototropic response.
For constant velocity , and in the absence of autotropic effects, Eqs. 13 and 14 can be solved exactly (SI Appendix, section 4C), leading to the phototropic curvature model:
| [15] |
| [16] |
where is a single parameter from which the phototropic response time is defined as . The exponential decay in Eq. 15 is due to the turnover of auxin so that less is available at the base, while the time shift of accounts for the transport time to the section at arc length , leading to time-delay differential equations. The change of curvature thus depends on three quantities: 1) the orientation of the tip with respect to the light source ago; 2) the amount of auxin available for the phototropic signal, which depends on the turnover ; and 3) the plant’s response sensitivity, characterized by . Bending occurs over a characteristic dimensionless bending length within the tip of the plant.
B.1. Fixed light source—no growth.
We consider first a fixed light source and restrict our attention to the case of zero axial growth so that for all time and the transport equation is solved in the reference variables. For a given transport time , the response of the plant is determined by the characteristic dimensionless bending length and the response time as shown in Fig. 5.
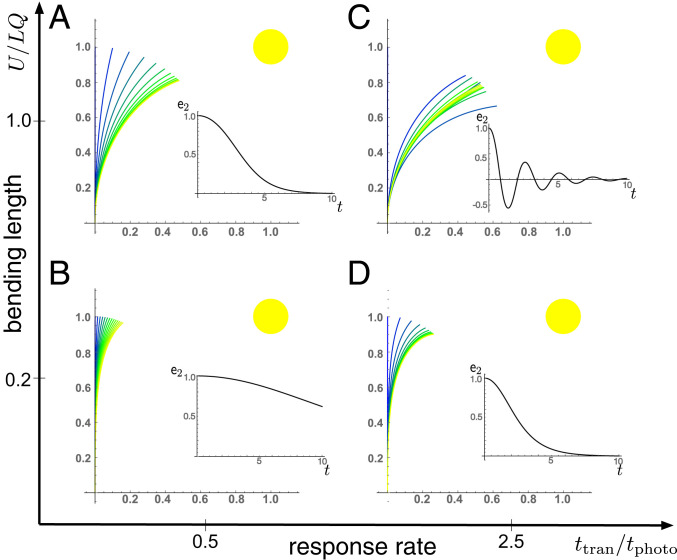
Fig. 5.
(A–D) Planar phototropic shape evolution for a fixed light source and with no axial growth, for small and large values of the ratio of response rate to transport rate and dimensionless bending length . (A–D, Insets) Alignment is characterized by , such that when the tip is pointed at the source for this planar case. Further simulation details and parameters are provided in SI Appendix, section 8.
With small bending length, the response is localized close to the tip, and the plant is much slower to orient (comparing Fig. 5 A and B). Increasing the response rate naturally produces a faster orientation and potentially an overshoot. If axial auxin transport is much faster than the growth response (), then the auxin is effectively in steady state at each growth step (as we have assumed for the cross-sectional transport). This implies that the delay can be neglected and the curvature response at each point depends on the current orientation of the tip. In this case, since the response is characterized entirely by the orientation of a single point, the motion is very simple: The plant bends to orient with the light, with no oscillations about the state in which the tip is perfectly oriented with the light ().
Contrast this behavior with gravitropism, in which an oscillation about the vertical state is typical unless a strong autotropism response is added. The difference between the gravitropic model and the phototropic model for fast transport is that during gravitropism, each cross-section tries to align itself with gravity, thus creating a conflict at the global level that results in an oscillatory motion; while during phototropism each cross-section tries to align the tip with the light, so there is no conflict. However, with delay, such a conflict does exist, due to the fact that each cross-section is accessing a previous state of the tip. Thus, in the regime , and if the bending length is not too short, a damped oscillation about the preferred orientation is observed, as shown in Fig. 5C.
B.2. Moving light source
Next, we consider a moving source, and in particular we simulate a day–night cycle of a plant following a light source (the Sun) as shown in Fig. 6A. The intensity is also taken to be sinusoidal, so that the phototropic signal is strongest at noon and the signal vanishes at sunset. For fast response and long bending length, the plant bends significantly and successfully tracks the moving light source (Fig. 6B). However, at night and without a signal, the motion halts (Movie S5). The plant remains bent toward sunset the entire night and does not display the nocturnal reorientation observed in many plants (80, 81). With a nonvanishing autotropic term in Eq. 5, we obtain an autophototropism curvature model of the form
| [17] |
| [18] |
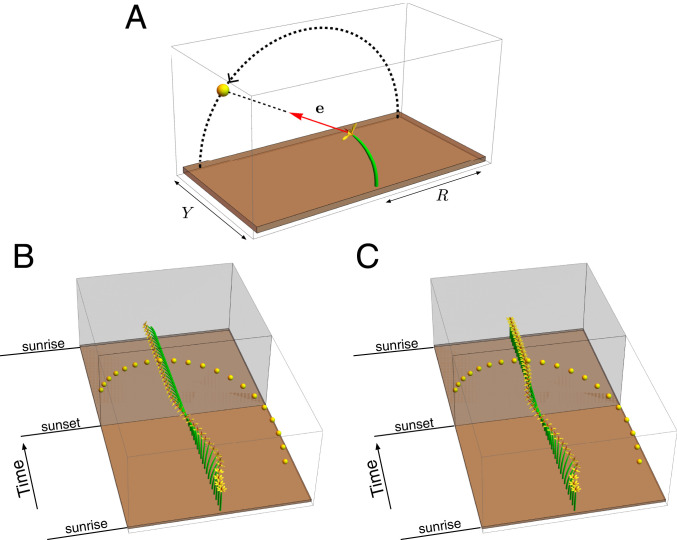
The additional terms serve to straighten the plant in the absence of any other signal. This is evident in Fig. 6C, in which we see that the motion during the day is very similar, while at night the stem straightens back to the vertical (Movie S6). We note that in heliotropic plants such as the common sunflower, Helianthus annuus, there are additional mechanisms, not considered here, based on circadian rhythms to reorient the plant at night to face eastward in anticipation of the next sunrise (82).
Fig. 6.
(A) Geometry of the phototropic response stimulated by a light source that follows a circular path of radius , shifted a distance in the transverse “horizon.” (B) A full day–night cycle with fast response and long bending length. (C) The addition of autotropic terms enables the plant to return to the vertical during night, when the phototropic signal is absent. Further simulation details and parameters provided in SI Appendix, section 8.
C. Photogravitropic Response
Next, we demonstrate the delicate balance that must exist in the presence of tropic responses to multiple stimuli. We simulate two different scenarios of a plant responding to simultaneous but conflicting gravitropic and phototropic signals. Following ref. 12, we assume that the effects of multiple stimuli are additive (SI Appendix, section 4F). This assumption is based on the existence of separate pathways for signal transduction leading to the redistribution of auxin. However, it is known that these pathways share common molecular processes and there are nontrivial interactions between different tropisms (83) that are not included here.
C.1. Fixed horizontal light source.
We consider a growing plant subject to self-weight and initially oriented vertically, but with a fixed light source located in the transverse horizontal direction. The evolution of the plant can then be characterized by the ratio of response rates to gravitropic versus phototropic signals and the ratio of density to bending stiffness, which controls the degree of deformation under self-weight.
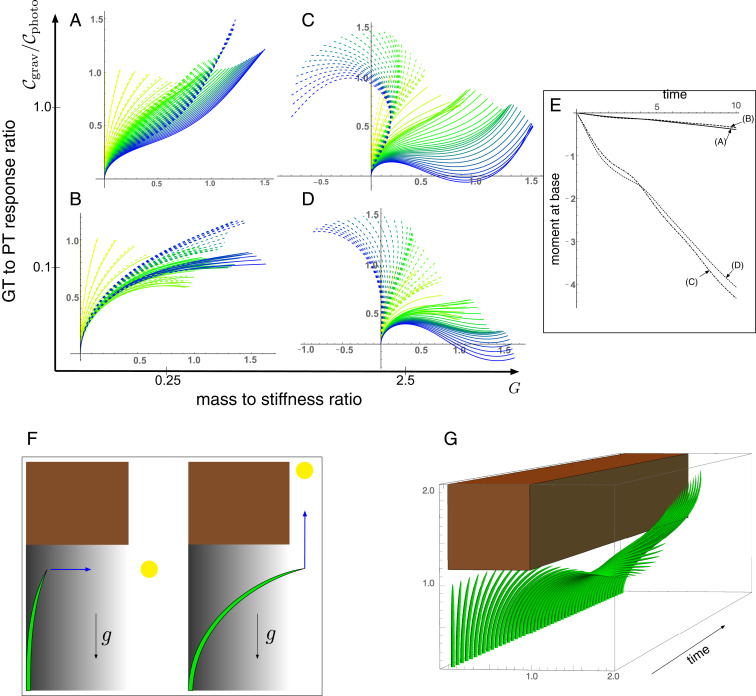
In Fig. 7 A–D we show the evolving morphology of the plant in this two-dimensional parameter space, plotting both the deformed shape (solid lines) and the reference unstressed shape (dashed lines). In Fig. 7 A and B, the effect of self-weight is relatively minimal, and the evolution is primarily driven by the conflicting phototropic signal acting horizontally to the right and the vertical gravitropic signal. With increased mass, there is an increased mechanical deformation due to self-weight, so that significant disparity develops between the deformed and reference shapes. In this regime the balance of signals has greater importance for the fate of the plant. Comparing Fig. 7 B and D, the initial phases are similar, but as the plant lengthens and extends to the right in Fig. 7D, self-weight deforms the plant significantly, with half of the plant below the base level by the end of the simulation. Such a deformation could signal failure by creating large torque at the base. In Fig. 7E we plot the moment at the base, where the stress is highest, against time for each case, and as expected the moment is significantly higher for larger mass.
Fig. 7.
Gravitropism versus phototropism. In A–E, a fixed light source is located to the right, at the point (4,1), while gravity points vertically downward. For each parameter set, the tropic response is simulated for the same total time and with equivalent axial growth. The evolving plant shape, deformed under self-weight, is shown in increasing time from yellow to blue, with the unstressed shape appearing as a dashed line. The moment at the base for the four cases is plotted against time in E. F depicts the setup for a plant escaping from the shade under a rigid obstacle. The phototropic signal points either horizontally, if the tip is under the shade, or vertically, if the tip is out of the shaded region. (G) A sample simulation showing a successful escape. Further simulation details and parameters are provided in SI Appendix, section 8.
Intuitively, we expect that this problem could be alleviated by increasing the gravitropic response rate. Comparing Fig. 7 C and D, the evolution with higher gravitropic response in Fig. 7C does show decreased sagging. However, the moment at the base is in fact higher in Fig. 7C. Increasing the gravitropic response rate even further does ultimately alleviate the problem—consider that the plant remains mostly vertical if gravitropism dominates phototropism—nevertheless, this example highlights the delicate and potentially counterintuitive nature of this balance.
C.2. Escaping from the shade.
The results above suggest a view of a plant as a problem-solving agent that actively responds to the signals in its environment. A typical problem that many plants have to solve is access to light (84). For instance, consider a plant growing underneath a canopy (85) as shown in Fig. 7 F and G. While the tip is in the shaded region, diffuse lighting creates a phototropic stimulus to grow horizontally, orthogonal to the gravitational signal. If the tip emerges from under the shade, phototropism and gravitropism align, and the plant will attempt to grow vertically. In this mixed-signal scenario, the success or failure of the plant in emerging from under the canopy is down to how the competing signals are integrated and the relative importance of self-weight. An example of a successful escape is shown in Fig. 7G. Note that determining the mechanical forces acting in the plant is crucial in this example: Once the tip is outside of the shade, both signals try to align the entire length of the plant with the vertical, and this leads to physical contact between the plant and the corner of the canopy. Determining the morphology beyond this point thus requires determining the mechanical contact force (SI Appendix, section 6), which would not be possible in a purely kinematic description.
D. Pole Dancing
A fascinating plant motion is the mesmerizing dance that climbing plants, such as twiners, perform to first find a pole and then wrap around it. Like any dance, this event requires a complex integration of stimuli to achieve a well-orchestrated sequence of steps: 1) finding a pole, 2) contacting the pole, and 3) proceeding to wrap around the pole. A common mechanism for searching for a climbing frame is circumnutation, a combination of circular movement and axial growth causing the tip to move up in a sweeping spiral path, as first described by Darwin (5, 26, 86). When the plant makes contact with a pole, it must then interpret its orientation with respect to the pole in order to wrap around it. Here the stimulus is mechanical: The physical contact of the plant with the pole results in a change of curvature, a response referred to as thigmotropism. Since initially the plant samples only a very small region of the pole, the stimulus field is highly localized. As the plant wraps around the pole, new contact points are established to propagate the helical shape upward.
D.1. Circumnutation.
Experiments suggest that, depending on the plant, circumnutation is driven by an internal oscillator, a time-delay response to gravity, or a combination of the two (87, 88). Here, following the hypothesis of an internal oscillator, we show that the basic nutating motion emerges naturally from an internal oscillator at a single point combined with axial auxin transport (89). We consider an auxin source at the point from which an auxin differential is transported axially. The auxin transport equation may be solved in a similar manner to that in the phototropism case with an added rotational component in the local frame of the cross-section due to an internal oscillator (Fig 3D). Taking for simplicity a constant rotation rate , we obtain (details in SI Appendix, section 4D) the circumnutation curvature model:
| [19] |
| [20] |
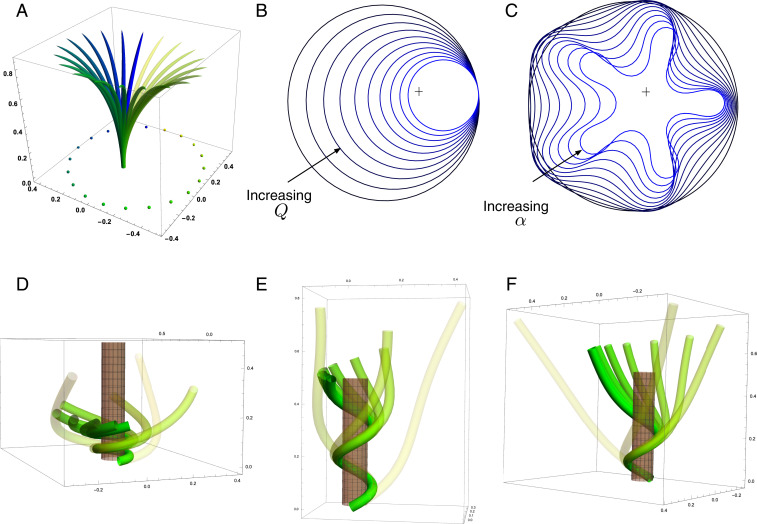
Since the signal here is internal, there is no feedback from the environment and the morphology of the plant is predetermined by the turnover , the transport velocity , the response rate , and the rotation rate . In Fig. 8A we illustrate a sample motion with auxin source at the tip. Fig. 8B demonstrates the impact of auxin turnover: High turnover means the motion is constrained to a region very close to the tip and thus the elliptical shape of the tip pattern is small. More complex tip patterns may also be generated if there is nonuniformity in the internal oscillator (Fig. 8C).
Fig. 8.
(A–F) Circumnutation (A–C) and thigmotropism (D–F). (A) Snapshots of a sample circumnutation motion, with tip pattern projected onto the plane. In B and C, tip patterns are plotted for varying parameters (the location of the plant base is indicated by the cross). In B, an increase in turnover decreases the size of the tip pattern. In C, a nonconstant angular velocity of the oscillator is given by , generating a tip pattern with fivefold symmetry, and increasingly noncircular with increasing . In D–F, the wrapping around a pole due to thigmotropism at a single contact point is simulated for the same total time, for different parameter regimes: With a low rotational component (D) the torsion is low, a high rotational component with low turnover (E) generates rapid wrapping and high torsion, while wrapping is much slower with high turnover (F). Further simulation details and parameters are provided in SI Appendix, section 8.
D.2. Thigmotropism.
Two interesting observations can be made when a twining plant makes first contact with a pole: 1) Torsion is generated via a localized contact around a single point, and 2) a rotation is induced; i.e., the orientation of the tangent of the plant with respect to the axis of the pole changes. These observations suggest that this contact is sufficient to generate locally a helical shape and that the pitch of the helix is fixed by internal parameters as opposed to the angle at which contact is made (90, 91).
To show how pole wrapping can be obtained within our framework consistently with these observations, we consider a plant with a single contact point located at and at position on the boundary with angle in the plane -. The contact induces an auxin gradient at this point, with maximal auxin on the opposite side of the contact point, i.e., , and the auxin is transported by an advective flux with both an axial component and a constant rotational component with angular velocity (Fig. 3E). The transport equation can be solved exactly (SI Appendix, section 4E), and we obtain the following thigmotropism curvature model:
| [21] |
| [22] |
Solving these equations leads to exact expressions for the intrinsic curvatures from which we extract the geometric curvature and torsion (SI Appendix, section 8F). The curvature increases linearly in time until it reaches a maximal value determined by the pole radius (the intrinsic curvature may keep increasing, but the actual curvature may not due to the mechanical contact). For a pole of radius and plant radius the helix radius is fixed, while the helical angle depends on the rotation rate and is found to satisfy .
For given axial velocity , the resulting helical shape is determined solely by the geometry of the pole and the rotational component , while the wrapping rate depends on the turnover and the response rate . In Fig. 8 D–F we illustrate three different regimes: low rotational component with low turnover (D), high rotational component with low turnover (E), and high rotational component with high turnover (F) (Movies S7–S9). Note that at time where is the final curvature, the contact point spreads to a contact region, creating a wave of contact and auxin signal that propagates along the length of the plant. Here, we restrict our attention to the signal from the first contact point. The separate curvature models for circumnutation and pole wrapping can now be combined to simulate the process of searching for a pole, making contact, and wrapping (Movie S10).
3. Model Validation
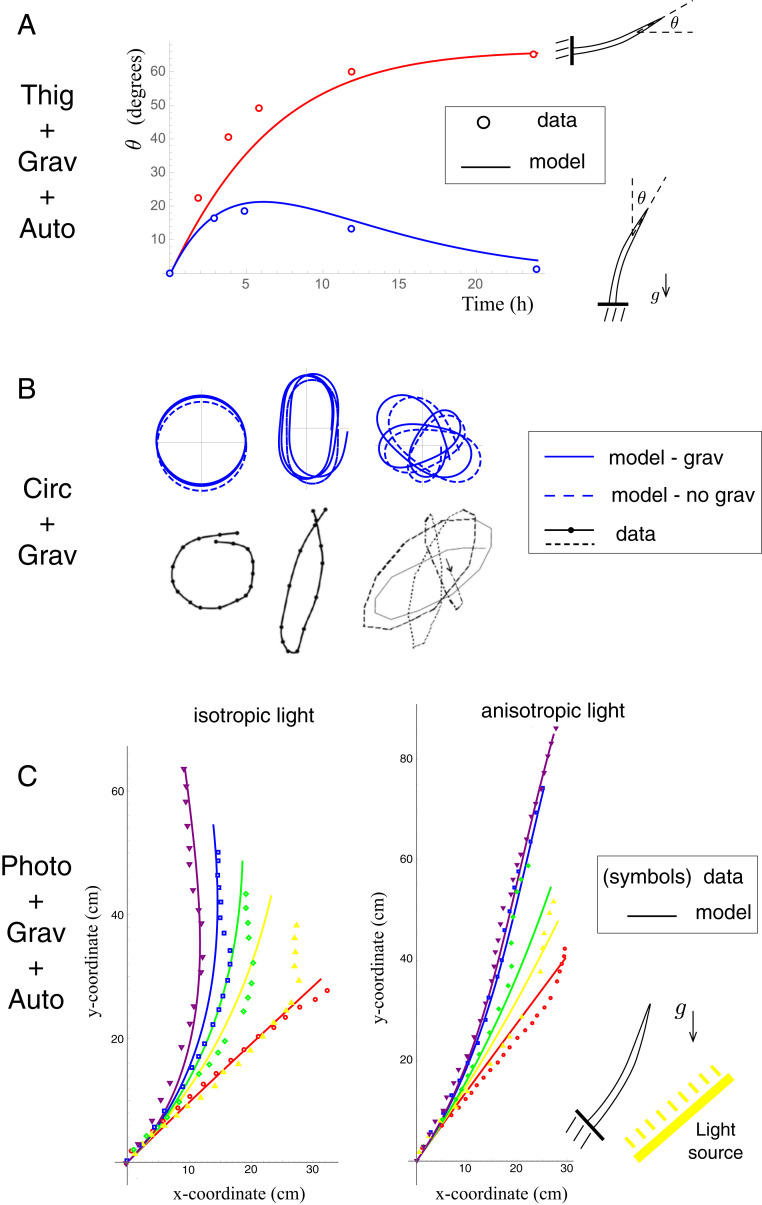
The tropic scenarios we have considered thus far were not focused on specific plants or experiments, but rather with the aim of demonstrating a diverse range of complex behavior. To validate the framework as a general construct, in Fig. 9 we compare model output with data in three distinct experimental scenarios that together include all of the tropisms we have modeled: Fig. 9A includes data on thigmotropic curvature generation (92) and gravitropic bending, Fig. 9B shows a diversity of tip patterns measured during circumnutation (93), and Fig. 9C plots the evolving shape of saplings bending to align with gravity and exposed to isotropic (Fig. 9 C, Left) or anisotropic (Fig. 9 C, Right) light (94) (see SI Appendix, section 9 for details of these experiments and model comparison). In each case, the model is able to reproduce, qualitatively and quantitatively, the experimental observations, demonstrating a robustness of the framework across a range of plant types and combined tropic responses.
Fig. 9.
A comparison of model output with experimental observations for a variety of tropic responses. (A) Mechanical perturbation is applied to cucumber hypocotyls situated vertically, causing them to bend (blue data and curves), after which they recover the vertical; a horizontally situated plant bends toward the vertical under gravitropism (red data and curves). (B) Multiple tip patterns are observed in sunflowers; these circumnutation patterns are reproduced by the model with (solid curves) and without (dashed curves) gravitropic effects. (C) Tree saplings are inclined at an angle and subjected to either isotropic (Left) or anisotropic (Right) light. The shape of the plants is extracted at five times and discretized along the length (symbols). Continuous two-dimensional shapes (solid curves) obtained by our model combining gravitropic, phototropic, and autotropic effects are included at the same time points.
A second type of validation is obtained by considering the simplification of our models to existing purely kinematic models. A number of geometric models exist in the literature, positing the evolution of the plant’s curvature as a function of time, and have been systematically validated against data and observations. The sine law (Eq. 12) is an example of such a kinematic model. Similarly, planar kinematic phototropic (12) and circumnutation models (95) have been proposed and we show explicitly in SI Appendix, section 7 that they can be reproduced from the models we have derived under particular geometric restrictions and/or parameter limits. Our framework both generalizes these descriptions and enables potential insight into how changes at the level of auxin transport and tissue growth might be seen in organ-level kinematics.
4. Conclusion
Plant motion in response to environmental stimuli is a process of extreme biological and ecological relevance. While the pioneering biologists of the 19th century investigated the global motion of plants via clever experiments devised to create conflicting signals and generate complex plant morphologies, most of the work of the 20th century was focused on the molecular and cellular processes, seeking signaling pathways and relevant proteins involved in tropic response. We have combined this accumulated knowledge with recent progress in the physical and computational modeling of living structures to develop a general framework for tropism that relates stimuli to shape. To do so, we modeled auxin transport and the mechanisms by which environmental stimuli are integrated into cellular activities, tissue-level growth, leading ultimately to a change in shape at the plant scale viewed as a morphoelastic structure.
We have demonstrated the power of this framework through a series of examples including key effects such as axial growth, autotropism, gravitropism, phototropism, thigmotropism, self-weight, circumnutation, contact mechanics, and three-dimensional deformations. The specific tropic scenarios we have considered were chosen to illustrate the range of complex behaviors capable of being simulated. The study of individual stimuli provided new models for the evolution of curvatures for different forms of tropisms. These models can be confronted and refined, iteratively, against data and experiments as needed. Further, we demonstrated the potential for multiple and potentially conflicting stimuli to create problems for the plant to solve. The resulting plant behaviors indicate a need for a delicate balance between competing tropisms to achieve a particular task. In each particular scenario, we have opted for parsimony over complexity in terms of modeling choices, to highlight qualitative features and how auxin-level differences may become apparent in plant-level morphology.
The work presented here integrated information at the tissue and organ levels. This approach needs to be expanded to include cell-based and molecular-level descriptions to fully link the scales for tropisms and plant growth. At the cell to tissue scale, the link between auxin and growth in Eq. 5 is a lumped description of a complex process that involves cell wall tension and turgor pressure (96). In principle, additional modeling layers could also be added between the stimulus and auxin response, including for example transcription factors and protein production and interactions. Both of these extensions likely require explicit cell-based modeling. However, our framework is such that if the output from a cell model is the value of the piecewise continuous axial growth function , then the evolution of the curvatures given by Eqs. 6–8 still applies and can be used to infer the global changes of geometry. Another important extension is to include branching processes since most of these filamentary structures include multiple branches. Branches can easily be included within a rod theory, at the additional cost of including extra parameters, such as length and orientation of each segment, and new growth laws for the placement of each segment (28, 32).
This work provides a theoretical platform for understanding plant tropisms and generating complex morphologies. As well as linking to cellular and subcellular scales, a key future direction is connecting with experiments dedicated to controlling multiple stimuli and generating complex morphologies. For instance, we showed that a relatively simple experimental setup like a rotating base under gravity can generate a wide range of plant shapes. Such steps espouse an approach that is both multiscale and multidisciplinary. Indeed, plants refuse to obey the rules of a single scientific discipline. They are not simply genetic or cellular entities, nor are they purely physical objects or ecological atoms. They reach for the sun; they bend under gravity; they feel their neighbors; they grow, twist, curve, and dance in the fresh air and in the dark caves. If we have any hope to understand them, we will need to respect their plurality, break down our own disciplinary barriers, and fully integrate our scientific knowledge from subcellular to ecological levels.
Supplementary Material
Acknowledgments
The support for A.G. by the Engineering and Physical Sciences Research Council of Great Britain under research Grant EP/R020205/1 is gratefully acknowledged. We thank János Karsai for permission to use his flower parameterization in Fig. 6 and the reviewers for their constructive criticism.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
See online for related content such as Commentaries.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2016025117/-/DCSupplemental.
Data Availability.
Mathematica notebook files data have been deposited in the Oxford University Research Archive (https://doi.org/10.5287/bodleian:EoydP5kOP).
References
- 1.Firn R. D., Digby J., The establishment of tropic curvatures in plants. Annu. Rev. Plant Physiol. 31, 131–148 (1980). [Google Scholar]
- 2.Band L. R., et al. , Root gravitropism is regulated by a transient lateral auxin gradient controlled by a tipping-point mechanism. Proc. Natl. Acad. Sci. U.S.A. 109, 4668–4673 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Bastien R., Bohr T., Moulia B., Douady S., Unifying model of shoot gravitropism reveals proprioception as a central feature of posture control in plants. Proc. Natl. Acad. Sci. U.S.A. 110, 755–760 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Simmons C., Söll D., Migliaccio F., Circumnutation and gravitropism cause root waving in Arabidopsis thaliana. J. Exp. Bot. 46, 143–150 (1995). [Google Scholar]
- 5.Darwin C., The Power of Movement in Plants (Appleton, 1897). [Google Scholar]
- 6.Sachs J., Lectures on the Physiology of Plants (Oxford University Press, English ed., 1888). [Google Scholar]
- 7.Moulia B., Fournier M., The power and control of gravitropic movements in plants: A biomechanical and systems biology view. J. Exp. Bot. 60, 461–486 (2009). [DOI] [PubMed] [Google Scholar]
- 8.Vos J., et al. , Functional–structural plant modelling: A new versatile tool in crop science. J. Exp. Bot. 61, 2101–2115 (2009). [DOI] [PubMed] [Google Scholar]
- 9.Esmon C., Pedmale U., Liscum E., Plant tropisms: Providing the power of movement to a sessile organism. Int. J. Dev. Biol. 49, 665–674 (2005). [DOI] [PubMed] [Google Scholar]
- 10.Sato E., Hijazi H., Bennett M., Vissenberg K., Swarup R., New insights into root gravitropic signalling. J. Exp. Bot. 66, 2155–2165 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mattheck C. M., Mattheck C., Design in Nature: Learning from Trees (Springer Science & Business Media, 1998). [Google Scholar]
- 12.Bastien R., Douady S., Moulia B., A unified model of shoot tropism in plants: Photo-, gravi- and propio-ception. PLoS Comput. Biol. 11, e1004037 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pfeffer W. F. P., Pflanzenphysiologie: Ein Handbuch der Lehre vom Stoffwechsels und Kraftwechsels in der Pflanze (W. Engelmann, 1904). [Google Scholar]
- 14.Bonnet C., Mémoires d’Histoire Naturelle. Recherches sur l’Usage des Feuilles (l’Imprimerie de Samuel Fauche, Libraire du Roi, 1779). [Google Scholar]
- 15.du Monceau D., Louis H., La Physique des Arbres, Où IL Est Traité de l’Anatomie des Plantes Et de l’Économie Végétale, Vol. 2: Pour Servir d’Introduction au Traité Complet des Bois Et Forests; Avec une Dissertation sur l’Utilité des Méthodes de Botanique, Et une Explication des Termes Propres à cette Science, Et Qui Sont en Usage pour l’Exploitation des Bois Et des Forêts (Guerin H. L. and Delatour L. F., 1758). [Google Scholar]
- 16.Whippo C. W., Hangarter R. P., Phototropism: Bending towards enlightenment. Plant Cell 18, 1110–1119 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Goriely A., The Mathematics and Mechanics of Biological Growth (Springer, 2017). [Google Scholar]
- 18.Moulton D. E., Lessinnes T., Goriely A., Morphoelastic rods III: Differential growth and curvature generation in elastic filaments. J. Mech. Phys. Solid. 142, 104022 (2020). [Google Scholar]
- 19.Tabor M., Klapper I., “Dynamics of twist and writhe and the modeling of bacterial fibers” in Mathematical Approaches to Biomolecular Structure and Dynamics, Mesirov J. P., Schulten K., Sumners D. W., Eds. (Springer, 1996), pp. 139–159. [Google Scholar]
- 20.Klapper I., Biological applications of the dynamics of twisted elastic rods. J. Comput. Phys. 125, 325–337 (1996). [Google Scholar]
- 21.Schlick T., Modeling superhelical DNA: Recent analytical and dynamic approaches. Curr. Opin. Struct. Biol. 5, 245–262 (1995). [DOI] [PubMed] [Google Scholar]
- 22.Thompson J. M. T., van der Heijden G. H. M., Neukirch S., Supercoiling of DNA plasmids: Mechanics of the generalized ply. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 458, 959–985 (2002). [Google Scholar]
- 23.Muthert L. W. F., Izzo L. G., Van Zanten M., Aronne G., Root tropisms: Investigations on earth and in space to unravel plant growth direction. Front. Plant Sci. 10, 1807 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bastien R., Douady S., Moulia B., A unifying modeling of plant shoot gravitropism with an explicit account of the effects of growth. Front. Plant Sci. 5, 136 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Meroz Y., Porat A., Tedone F., Palladino M., Marcati P., A general 3d model for growth dynamics of sensory-growth systems: From plants to robotics. Front. Robotics AI 7, 89 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Goriely A., Neukirch S., Mechanics of climbing and attachment in twining plants. Phys. Rev. Lett. 97, 184302 (2006). [DOI] [PubMed] [Google Scholar]
- 27.Chelakkot R., Mahadevan L., On the growth and form of shoots. J. R. Soc. Interface 14, 20170001 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Faruk Senan N., O’Reilly O., Tresierras T., Modeling the growth and branching of plants: A simple rod-based model. J. Mech. Phys. Solid. 56, 3021–3036 (2008). [Google Scholar]
- 29.Guillon T., Dumont Y., Fourcaud T., A new mathematical framework for modelling the biomechanics of growing trees with rod theory. Math. Comput. Model. 55, 2061–2077 (2012). [Google Scholar]
- 30.O’Reilly O. M., Tresierras T. N., On the evolution of intrinsic curvature in rod-based models of growth in long slender plant stems. Int. J. Solid Struct. 48, 1239–1247 (2011). [Google Scholar]
- 31.O’Reilly O. M., Modeling Nonlinear Problems in the Mechanics of Strings and Rods (Springer, 2017). [Google Scholar]
- 32.Jirasek C., Prusinkiewicz P., Moulia B., “Integrating biomechanics into developmental plant models expressed using L-systems” in Plant Biomechanics 2000: Proceedings of the 3rd Plant Biomechanics Conference Freiburg-Badenweiler, August 27 to September 2, 2000, Spatz H.-Ch., Speck T., Eds. (Georg Thieme Verlag, Stuttgart, Germany: ), pp. 615–624. [Google Scholar]
- 33.Evers J., van der Krol A., Vos J., Struik P., Understanding shoot branching by modelling form and function. Trends Plant Sci. 16, 464–467 (2011). [DOI] [PubMed] [Google Scholar]
- 34.Surovy P., Yoshimoto A., Application of a functional-structural plant model (FSPM) to optimize a management regime. FORMATH 12, 173–189 (2013). [Google Scholar]
- 35.Fozard J., Bennett M., King J., Jensen O., Hybrid vertex-midline modelling of elongated plant organs. Interface Focus 6, 20160043 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jensen O. E., Fozard J. A., Multiscale models in the biomechanics of plant growth. Physiology 30, 159–166 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Antman S. S., Nonlinear Problems of Elasticity (Springer, New York, NY, 2005). [Google Scholar]
- 38.Pai D. K., “Strands: Interactive simulation of thin solids using Cosserat models” in Computer Graphics Forum, Drettakis G., Seidel H.-P., Eds. (Blackwell Publishers, Oxford, UK, 2002), vol. 21, pp. 347–352. [Google Scholar]
- 39.Manning R. S., Maddocks J. H., Kahn J. D., A continuum rod model of sequence-dependent DNA structure. J. Chem. Phys. 105, 5626–5646 (1996). [Google Scholar]
- 40.Chouaieb N., Goriely A., Maddocks J. H., Helices. Proc. Natl. Acad. Sci. U.S.A. 103, 9398–9403 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Moulton D. E., Lessinnes T., Goriely A., Morphoelastic rods Part 1: A single growing elastic rod. J. Mech. Phys. Solid. 61, 398–427 (2012). [Google Scholar]
- 42.Carmo M. P. D., Differential Geometry of Curves and Surfaces (Prentice-Hall, Englewood Cliffs, NJ, 1976). [Google Scholar]
- 43.Bishop R. L., There is more than one way to frame a curve. Am. Math. Month. 82, 246–251 (1975). [Google Scholar]
- 44.Braybrook S. A., Peaucelle A., Mechano-chemical aspects of organ formation in Arabidopsis thaliana: The relationship between auxin and pectin. PloS One 8, e57813 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Lockhart J. A., An analysis of irreversible plant cell elongation. J. Theor. Biol. 8, 264–275 (1965). [DOI] [PubMed] [Google Scholar]
- 46.Cosgrove D. J., Growth of the plant cell wall. Nat. Rev. Mol. Cell Biol. 6, 850–861 (2005). [DOI] [PubMed] [Google Scholar]
- 47.Boudon F., et al. , A computational framework for 3D mechanical modeling of plant morphogenesis with cellular resolution. PLoS Comput. Biol. 11, e1003950 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bassel G. W., et al. , Mechanical constraints imposed by 3D cellular geometry and arrangement modulate growth patterns in the Arabidopsis embryo. Proc. Natl. Acad. Sci. U.S.A. 111, 8685–8690 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Daher F. B., et al. , Anisotropic growth is achieved through the additive mechanical effect of material anisotropy and elastic asymmetry. eLife 7, e38161 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kennaway R., Coen E., Green A., Bangham A., Generation of diverse biological forms through combinatorial interactions between tissue polarity and growth. PLoS Comput. Biol. 7, e1002071 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Muday G. K., Auxins and tropisms. J. Plant Growth Regul. 20, 226–243 (2001). [DOI] [PubMed] [Google Scholar]
- 52.Gilroy S., Plant tropisms. Curr. Biol. 18, R275–R277 (2008). [DOI] [PubMed] [Google Scholar]
- 53.Esmon C. A., et al. , A gradient of auxin and auxin-dependent transcription precedes tropic growth responses. Proc. Natl. Acad. Sci. U.S.A. 103, 236–241 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Vanneste S., Friml J., Auxin: A trigger for change in plant development. Cell 136, 1005–1016 (2009). [DOI] [PubMed] [Google Scholar]
- 55.Rose S., Rubery P. H., Bopp M., The mechanism of auxin uptake and accumulation in moss protonemata. Physiol. Plantarum 58, 52–56 (1983). [Google Scholar]
- 56.Woodward A. W., Bartel B., Auxin: Regulation, action, and interaction. Ann. Bot. 95, 707–735 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Benková E., et al. , Local, efflux-dependent auxin gradients as a common module for plant organ formation. Cell 115, 591–602 (2003). [DOI] [PubMed] [Google Scholar]
- 58.Runions A., Smith R. S., Prusinkiewicz P., “Computational models of auxin-driven development” in Auxin and Its Role in Plant Development, Zažímalová E., Petrášek J., Benková E., Eds. (Springer-Verlag Wien, 2014), pp. 315–357. [Google Scholar]
- 59.Rodriguez E. K., Hoger A., McCulloch A. D., Stress-dependent finite growth in soft elastic tissues. J. Biomech. 27, 455–467 (1994). [DOI] [PubMed] [Google Scholar]
- 60.Coen E., Rolland-Lagan A. G., Matthews M., Bangham J. A., Prusinkiewicz P., The genetics of geometry. Proc. Natl. Acad. Sci. U.S.A. 101, 4728–4735 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Okamoto K., et al. , Regulation of organ straightening and plant posture by an actin–myosin xi cytoskeleton. Nature Plants 1, 1–7 (2015). [DOI] [PubMed] [Google Scholar]
- 62.Harmer S. L., Brooks C. J., Growth-mediated plant movements: Hidden in plain sight. Curr. Opin. Plant Biol. 41, 89–94 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Nizette M., Goriely A., Towards a classification of Euler–Kirchhoff filaments. J. Math. Phys. 40, 2830–2866 (1999). [Google Scholar]
- 64.Galland P., Tropisms of Avena coleoptiles: Sine law for gravitropism, exponential law for photogravitropic equilibrium. Planta 215, 779–784 (2002). [DOI] [PubMed] [Google Scholar]
- 65.Chauvet H., Pouliquen O., Forterre Y., Legué V., Moulia B., Inclination not force is sensed by plants during shoot gravitropism. Sci. Rep. 6, 35431 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Morita M. T., Directional gravity sensing in gravitropism. Annu. Rev. Plant Biol. 61, 705–720 (2010). [DOI] [PubMed] [Google Scholar]
- 67.Pouliquen O., et al. , A new scenario for gravity detection in plants: The position sensor hypothesis. Phys. Biol. 14, 035005 (2017). [DOI] [PubMed] [Google Scholar]
- 68.Mousdale D., Fidgeon C., Wilson G., Auxin content and growth patterns in auxin-dependent and auxin-autotrophic plant cell and tissue cultures. Biol. Plantarum 27, 257 (1985). [Google Scholar]
- 69.Chandler J. W., Local auxin production: A small contribution to a big field. Bioessays 31, 60–70 (2009). [DOI] [PubMed] [Google Scholar]
- 70.Bozorg B., Krupinski P., Jönsson H., A continuous growth model for plant tissue. Phys. Biol. 13, 65002 (2016). [DOI] [PubMed] [Google Scholar]
- 71.Roychoudhry S., Del Bianco M., Kieffer M., Kepinski S., Auxin controls gravitropic setpoint angle in higher plant lateral branches. Curr. Biol. 23, 1497–1504 (2013). [DOI] [PubMed] [Google Scholar]
- 72.Whippo C. W., Hangarter R. P., Phototropism: Bending towards enlightenment. Plant Cell 18, 1110–1119 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Boysen-Jensen P., La transmission de l’irritation phototropique dans l’avena. Bull. Acad. Sci. Lett. Montpellier 3, 1–24 (1911). [Google Scholar]
- 74.Christie J. M., Murphy A. S., Shoot phototropism in higher plants: New light through old concepts. Am. J. Bot. 100, 35–46 (2013). [DOI] [PubMed] [Google Scholar]
- 75.Cholodny N., Wuchshormone and tropismen bei den pflanzen. Biol. Zentralblatt 47, 604–629 (1927). [Google Scholar]
- 76.Went F. W., Wuchsstoff und wachstum. Rec. Trav. Bot. Neerl. 25, 1–116 (1928). [Google Scholar]
- 77.Went F. W., Thimann K. V., “Phytohormones” in Experimental Biology Monographs, Bard P., et al., Eds. (The Macmillan Company, New York, 1937). [Google Scholar]
- 78.Hart J. W., Plant Tropisms and Other Growth Movements (Chapman & Hall, 1992). [Google Scholar]
- 79.Christie J. M., Phototropin blue-light receptors. Annu. Rev. Plant Biol. 58, 21–45 (2007). [DOI] [PubMed] [Google Scholar]
- 80.Stanton M. L., Galen C., Blue light controls solar tracking by flowers of an alpine plant. Plant Cell Environ. 16, 983–989(1993). [Google Scholar]
- 81.Vandenbrink J. P., Brown E. A., Harmer S. L., Blackman B. K., Turning heads: The biology of solar tracking in sunflower. Plant Sci. 224, 20–26 (2014). [DOI] [PubMed] [Google Scholar]
- 82.Atamian H. S., et al. , Circadian regulation of sunflower heliotropism, floral orientation, and pollinator visits. Science 353, 587–590 (2016). [DOI] [PubMed] [Google Scholar]
- 83.Correll M. J., Kiss J. Z., Interactions between gravitropism and phototropism in plants. J. Plant Growth Regul. 21, 89–101 (2002). [DOI] [PubMed] [Google Scholar]
- 84.Ballaré C. L., Pierik R., The shade-avoidance syndrome: Multiple signals and ecological consequences. Plant Cell Environ. 40, 2530–2543 (2017). [DOI] [PubMed] [Google Scholar]
- 85.Ballaré C., Scopel A., Roush M., Radosevich S., How plants find light in patchy canopies. A comparison between wild-type and phytochrome-b-deficient mutant plants of cucumber. Funct. Ecol., 9 859–868 (1995). [Google Scholar]
- 86.Isnard S., Silk W. K., Moving with climbing plants from Charles Darwin’s time into the 21st century. Am. J. Bot. 96, 1205–1221 (2009). [DOI] [PubMed] [Google Scholar]
- 87.Brown A. H., Circumnutations: From Darwin to space flights. Plant Physiol. 101, 345–348 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Agostinelli D., DeSimone A., Noselli G., Nutations in plant shoots: Endogenous and exogenous factors in the presence of mechanical deformations. bioRxiv:2020.07.06.188987 (6 July 2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Stolarz M., Circumnutation as a visible plant action and reaction: Physiological, cellular and molecular basis for circumnutations. Plant Signal. Behav. 4, 380–387 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Silk W. K., On the curving and twining of stems. Environ. Exp. Bot. 29, 95–109 (1989). [Google Scholar]
- 91.Silk W. K., Growth rate patterns which maintain a helical tissue tube. J. Theor. Biol. 138, 311–328 (1989). [Google Scholar]
- 92.Jaffe M. J., Takahashi H., Thigmotropism and the inodulation of tropistic curvature by mechanical perturbation in cucumber hypocotyls. Physiol. Plantarum 80, 561–567 (1990). [Google Scholar]
- 93.Stolarz M., Circumnutation as a visible plant action and reaction. Plant Signal. Behav. 4, 380–387 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Coutand C., Adam B., Ploquin S., Moulia B., A method for the quantification of phototropic and gravitropic sensitivities of plants combining an original experimental device with model-assisted phenotyping: Exploratory test of the method on three hardwood tree species. PloS One 14, e0209973 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Bastien R., Meroz Y., The kinematics of plant nutation reveals a simple relation between curvature and the orientation of differential growth. PLoS Comput. Biol. 12, e1005238 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Mirabet V., Das P., Boudaoud A., Hamant O., The role of mechanical forces in plant morphogenesis. Annu. Rev. Plant Biol. 62, 365–385 (2011). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Mathematica notebook files data have been deposited in the Oxford University Research Archive (https://doi.org/10.5287/bodleian:EoydP5kOP).