Opposing Influence of Top-down and Bottom-up Input on Excitatory Layer 2/3 Neurons in Mouse Primary Visual Cortex

Summary

Processing in cortical circuits is driven by combinations of cortical and subcortical inputs. These inputs are often conceptually categorized as bottom-up, conveying sensory information, and top-down, conveying contextual information. Using intracellular recordings in mouse primary visual cortex, we measured neuronal responses to visual input, locomotion, and visuomotor mismatches. We show that layer 2/3 (L2/3) neurons compute a difference between top-down motor-related input and bottom-up visual flow input. Most L2/3 neurons responded to visuomotor mismatch with either hyperpolarization or depolarization, and the size of this response was correlated with distinct physiological properties. Consistent with a subtraction of bottom-up and top-down input, visual and motor-related inputs had opposing influence on L2/3 neurons. In infragranular neurons, we found no evidence of a difference computation and responses were consistent with positive integration of visuomotor inputs. Our results provide evidence that L2/3 functions as a bidirectional comparator of top-down and bottom-up input.

Highlights

• •Layer 2/3 neurons show widespread subthreshold mismatch responses
• •Mismatch response sign is predicted by visual flow and locomotion-related responses
• •Layer 5/6 has a scarcity of depolarizing mismatch responses
• •Visual flow and locomotion speed have opposing signs of influence only in layer 2/3

Jordan and Keller use whole cell recordings in mice navigating in virtual reality to show that neurons only in superficial cortical layers have a special property: they integrate visual flow and locomotion speed with opposing signs, allowing them to compute bidirectional mismatches between actual and expected visual flow speeds.

Introduction

Predicting the sensory consequences of self-motion is a central component of feedback guided motor control and allows the brain to infer whether sensory stimuli are self-generated or externally generated (Crapse and Sommer, 2008). It is still unclear how the nervous system learns and represents the relationships between movement and sensory feedback. One brain structure involved in complex sensorimotor learning processes is the neocortex (Lalazar and Vaadia, 2008; Makino et al., 2016). Cortical areas receive both bottom-up sensory-driven input and top-down input that is thought to signal contextual and motor-related information (Engel et al., 2001). The primary visual cortex (V1) of mice receives bottom-up visual input from the lateral geniculate nucleus, as well as top-down input from various other cortical areas, including higher-order visual cortices, retrosplenial cortex, and anterior cingulate cortex (Leinweber et al., 2017; Oh et al., 2014; Zhang et al., 2016). These top-down inputs convey various contextual signals, including attention (Zhang et al., 2014), spatial information (Fiser et al., 2016; Saleem et al., 2018), head direction (Vélez-Fort et al., 2018), and locomotion-related signals (Leinweber et al., 2017).

There are different, though not mutually exclusive, ideas about the computational purpose of integrating bottom-up and top-down inputs. Locomotion-related input may function to increase the signal-to-noise ratio of visual responses by enhancing visual responses in V1 (Niell and Stryker, 2010). During locomotion, neuromodulatory inputs are more active (Larsen et al., 2018; Reimer et al., 2016), and there is widespread depolarization of cortical neurons (Bennett et al., 2013; Polack et al., 2013), indicating a locomotion-related state change that likely underlies the increased gain of visual responses (Fu et al., 2014; Polack et al., 2013). Another idea is that V1 integrates positively weighted sums of locomotion speed and visual flow speed to estimate an animal’s speed through the world (Saleem et al., 2013). This was based on the finding that neurons in V1 can be driven by locomotion in absence of visual input (Keller et al., 2012) and often have activity that correlates positively with both visual flow speed and locomotion speed (Saleem et al., 2013). It has also been proposed that layer 2/3 (L2/3) neurons compute a difference between visual and locomotion-related input to convey visuomotor prediction errors (Keller and Mrsic-Flogel, 2018). This interpretation is based on the computational framework of predictive processing (Rao and Ballard, 1999) and the discovery of a subset of L2/3 neurons that strongly respond to a sudden mismatch between visual flow feedback and locomotion speed (Keller et al., 2012; Zmarz and Keller, 2016). In predictive processing, one of the key circuit elements is prediction error neurons. These neurons compare top-down inputs that convey a prediction of sensory input with bottom-up sensory-driven inputs, rendering them responsive to differences between the two. Top-down and bottom-up inputs could be compared using a divisive mechanism (Spratling, 2008; Spratling et al., 2009) or a subtractive mechanism (Keller and Mrsic-Flogel, 2018; Rao and Ballard, 1999). In the latter case, the weights of these two types of input would be balanced and opposing in a given prediction error neuron. If bottom-up sensory input is excitatory, then the effect of top-down input should be inhibitory, and vice versa.

The predictive processing framework postulates the existence of two types of prediction error neurons: positive prediction error neurons that subtract a top-down prediction from the sensory input and negative prediction error neurons that subtract sensory input from the top-down prediction (Keller and Mrsic-Flogel, 2018; Rao and Ballard, 1999). The mismatch-responsive neurons found in L2/3 using calcium imaging are consistent with the latter type of neurons. V1 receives both bottom-up excitation and visually driven inhibition (Attinger et al., 2017), as well as a combination of excitatory and inhibitory top-down inputs (Gilbert and Li, 2013; Leinweber et al., 2017; Zhang et al., 2014). If the strengths of the two sources of input were balanced and opposing in individual neurons, prediction error responses would arise from a temporary imbalance between the two inputs.

To test for the existence of a balance between top-down and bottom-up inputs, we performed intracellular recordings in V1 of mice exploring a virtual reality environment. We found widespread responses to visuomotor mismatch in L2/3 excitatory neurons ranging from strongly hyperpolarizing to strongly depolarizing. The magnitude and sign of these responses is associated with differences in electrophysiological properties, visual responses, and membrane potential (V_m) dynamics during locomotion. Moreover, the influence of visual input and that of locomotion-related input on V_m were opposing, consistent with the hypothesis that L2/3 computes a difference between the two inputs. By contrast, deep-layer neurons did not show this characteristic, instead exhibiting depolarizing responses to both types of input.

Results

We made blind whole-cell recordings in V1 of mice head-fixed on a spherical treadmill with locomotion coupled to visual flow feedback in a virtual reality environment (Figures 1A and 1B; Leinweber et al., 2014). At the beginning of each recording, full-field visual flow was coupled to mouse locomotion. This coupling was interrupted by suddenly halting visual flow for 1 s at random times to generate visuomotor mismatch events (Keller et al., 2012). To minimize the influence of changes in eye position, we used full-field visual flow halts that induce a uniform mismatch stimulus independent of eye position and that do not trigger eye movements (Figure S1; Keller et al., 2012; Zmarz and Keller, 2016). Following the closed-loop session, we decoupled locomotion and visual flow to measure the effects of each on neuronal activity separately. Visual stimuli consisted of 1 s full-field, fixed-speed flow of the virtual tunnel walls, presented at random times. We made whole-cell recordings from 54 neurons. Putative interneurons, with an input resistance exceeding 100 MΩ, or a spike half-width below 0.6 ms (Gentet et al., 2012; Pala and Petersen, 2015), were excluded from all analyses. These criteria do not exclude lower-input-resistance, non-fast-spiking interneurons (Gentet et al., 2012). In total 15% of neurons were excluded, leaving 46 putative excitatory neurons in the sample (Figure S2).

Figure 1.

Whole-Cell Recordings during Visuomotor Coupling and Mismatch

(A) Schematic of whole-cell recordings at the L2/3 depth and of the visuomotor virtual reality setup.

(B) Mice were habituated on the setup for 5 to 7 days before whole-cell recording experiments. Experiments consisted of an initial closed-loop phase, during which visual flow feedback was coupled to locomotion interspersed with visual flow halts (mismatches). In a second open-loop phase, visual flow was presented in 1 s pulses of visual flow independent of locomotion.

(C) Example V_m trace (black) from a depolarizing mismatch (dMM) neuron. Dotted lines indicate 0 cm/s. Visuomotor mismatch events are marked by an orange bar and shading.

(D) Average V_m response (top) and firing rate histogram (bottom) for mismatch trials for the example neuron shown in (C) (averaged over 45 mismatch events). Shading indicates SEM. The value in gray bold italics indicates the mean pre-stimulus voltage.

(E) As in (C), but for a neuron with a hyperpolarizing mismatch (hMM) response.

(F) Average V_m response to mismatch for the example neuron in (E). Shading indicates SEM over 15 trials. The value in gray bold italics indicates the mean pre-stimulus voltage. This neuron did not show spontaneous spikes, so the spike histogram is omitted.

Subthreshold Mismatch Responses Are Widespread in Putative L2/3 Excitatory Neurons

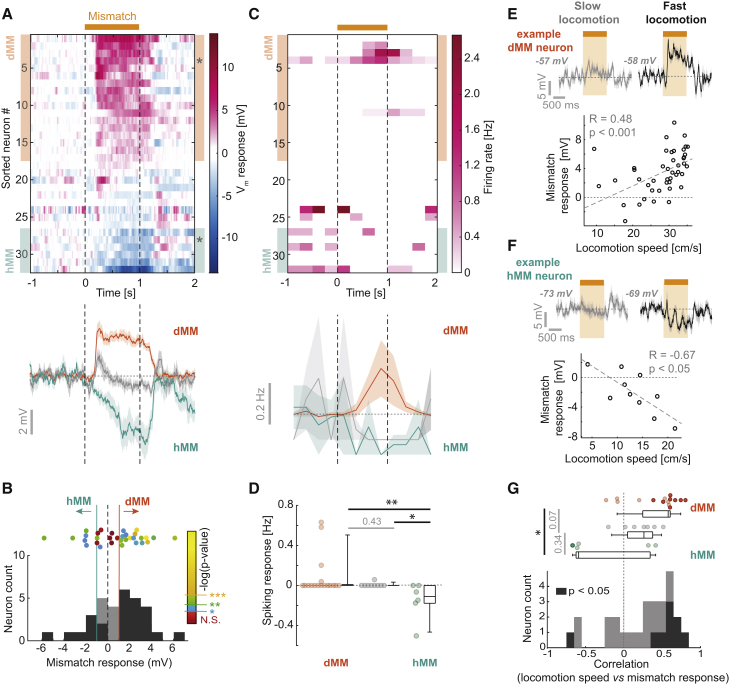
We first assessed the visuomotor mismatch responses of 32 putative L2/3 excitatory neurons recorded within 400 μm of the cortical surface. Consistent with mismatch responses described previously using calcium imaging (Keller et al., 2012; Zmarz and Keller, 2016), we found neurons with depolarizing responses to mismatch (Figures 1C and 1D). We also found neurons with hyperpolarizing responses (Figures 1E and 1F). Across neurons, the distribution of mismatch responses was unimodal, with 78% (25/32) responding significantly (see STAR Methods; Figures 2A, 2B, and S3A). We operationally defined neurons as either depolarizing mismatch (dMM, n = 17) neurons or hyperpolarizing mismatch (hMM, n = 6) neurons if their average mismatch response was above 1 mV or below −1 mV, respectively. This threshold value is arbitrary, and our results are robust using a range of thresholds. The remaining neurons (9 of 32, denoted as unclassified) did not exceed the average 1 mV threshold but often showed brief depolarizing responses at the onset and/or the offset of mismatch. The different signs of mismatch response could not be explained by regression to a common reversal potential, because mismatch responses were not related to pre-stimulus voltage (Figure S3B). Mean mismatch responses were comparable in magnitude to the standard deviation (SD) of V_m for most neurons (Figure S3C), and the mean fraction of trials with responses larger than 2 SDs across all neurons was 28% ± 19% (Figure S3D). Potentially because of this trial-to-trial variability, spiking responses were less common in the dataset but overall reflected the subthreshold responses (Figures 2C and 2D). Different response types were intermixed, because they could be recorded from the same craniotomy (Figures S3E–S3G).

Figure 2.

Subthreshold Mismatch Responses Are Widespread in L2/3, and Responses Correlate with Locomotion Speed

(A) Top: heatmap of average V_m responses to mismatch for 32 neurons, sorted by average response. Neurons classified as dMM and hMM are marked by orange and turquoise shading, respectively. Asterisks indicate examples shown in Figure 1. Bottom: average V_m response to mismatch across 17 dMM neurons (orange), 6 hMM neurons (turquoise), and 9 unclassified neurons (gray). Shading indicates SEM over neurons.

(B) Histogram of average mismatch responses. In dark gray are counts of neurons with a significant response (p < 0.05, paired t test between pre- and post-mismatch average V_m). Turquoise and orange lines indicate hMM and dMM thresholds, respectively. Shown above the histogram are mismatch responses colored according to their p value. ^∗p < 0.05, ^∗∗p < 0.01, ^∗∗∗p < 0.001.

(C) Top: heatmap of the average spiking rate during mismatch. Color coding and sorting are as in (A). Bottom: average mismatch-induced change in the spiking rate for the same groups of neurons as in (A). Shading indicates SEM over neurons.

(D) Boxplots comparing spiking rate responses to mismatch for dMM neurons (orange, n = 17), unclassified neurons (gray, n = 9), and hMM neurons (turquoise, n = 6). One-way ANOVA: p < 0.01, F-statistic = 12.5; dMM versus hMM: p < 0.01, dMM versus unclassified: p = 0.43, hMM versus unclassified: p < 0.02, rank-sum test. Boxplots show median, quartiles, and range-excluding outliers (see the Statistics section in STAR Methods for details).

(E) Top: average V_m response for the 10 mismatch events with the highest (black) and lowest (gray) locomotion speeds for an example dMM neuron. Shading indicates SEM over trials. Values in gray bold italics indicate the mean pre-stimulus voltage. Bottom: scatterplot between average locomotion speed and mismatch response for 45 trials. The dashed gray line shows linear regression.

(F) As in (E), but for an example hMM neuron. Average V_m responses were calculated from five trials with the lowest (gray) and highest (black) locomotion speeds.

(G) Histogram of correlation coefficients between locomotion speed and mismatch response. In dark gray are counts of neurons with a significant correlation (p < 0.05). Boxplot compares values for dMM neurons (orange, n = 15), hMM neurons (turquoise, n = 5), and unclassified neurons (gray, n = 7), with significant correlations shown as dark data points. One-way ANOVA on ranks: p < 0.02, chi-square = 8; dMM versus hMM: p < 0.02, dMM versus unclassified: p = 0.07, hMM versus unclassified: p = 0.34, rank-sum test. Boxplots show median, quartiles, and range-excluding outliers.

See Table S1 for inclusion criteria.

We previously found that mismatch responses scale with locomotion speed (Keller et al., 2012; Zmarz and Keller, 2016). Congruently, 30% of neurons exhibited significant correlations between mismatch response and locomotion speed across trials (Figures 2E–2G). The sign of this correlation was significantly different between dMM neurons and hMM neurons (Figures 2G and S3H). Given that during mismatch the difference between predicted and actual visual flow speed is simply a function of the locomotion speed, an increase in mismatch response with increasing locomotion speed is consistent with an increased prediction error.

Mismatch Response Sign Is Associated with Different Electrophysiological Properties

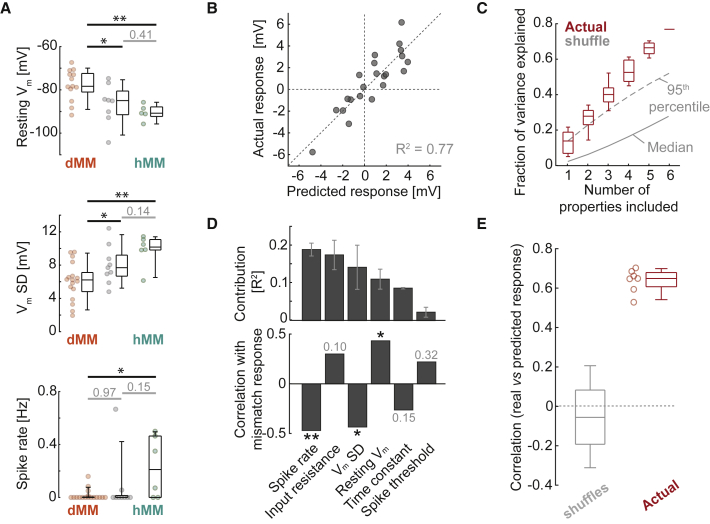
Biophysical properties can be tuned by the profile of synaptic input received by the neuron (Angelo et al., 2012; Desai et al., 1999). We found that certain electrophysiological properties correlated with mismatch responses, including initial resting V_m, variance in V_m (when stationary), and baseline spike rates (Figure 3A). To test whether a neuron’s mismatch response was predictable from its electrophysiological properties, we used multiple linear regression to predict mismatch responses using the following six properties: initial resting V_m, input resistance, V_m variance (during stationary periods), baseline spike rate, membrane time constant, and spike threshold (see STAR Methods). The variance in mismatch response explained by the linear model was 77% when using all six properties and was significantly higher than for shuffle controls (p < 0.0001) (see STAR Methods; Figures 3B and 3C). The contribution of each electrophysiological property to the variance explained ranged between 5% and 25%, with no single property dominating the effect (Figure 3D). Using leave-one-out analysis, we found there were significantly higher positive correlations between predicted and actual mismatch responses when the model was generated using actual data compared with randomly permuted controls (actual: 0.65 ± 0.06; shuffle controls: −0.06 ± 0.21; p < 0.001) (see STAR Methods; Figure 3E). Thus, responses to mismatch were correlated with electrophysiological properties, potentially indicating differences in synaptic inputs and/or cell-type-specific and intrinsic properties.

Figure 3.

Mismatch Responses Are Predictable from Electrophysiological Properties

(A) Boxplots to compare properties between dMM, hMM, and unclassified categories. From top to bottom: resting V_m (one-way ANOVA: p < 0.01, F-statistic = 6.5; dMM versus hMM: p < 0.01, dMM versus unclassified: p < 0.05, hMM versus unclassified: p = 0.41, t test), standard deviation (SD) of V_m during stationary periods (one-way ANOVA: p < 0.01, F-statistic = 6.5; dMM versus hMM: p < 0.01, dMM versus unclassified: p < 0.05, hMM versus unclassified: p = 0.14, t test), and baseline spike rate (one-way ANOVA: p = 0.06, F-statistic = 6.5; dMM versus hMM: p < 0.05, dMM versus unclassified: p = 0.97, hMM versus unclassified: p = 0.15, t test).

(B) Scatterplot between predicted mismatch response (from a multiple linear regression model including six electrophysiological properties) and actual mismatch response for each neuron.

(C) Fraction of variance in mismatch response explained as a function of the number of electrophysiological properties included in the model. Red boxplots show data for all model subsets. In gray are the median (solid line) and 95^th percentile (dashed line) for shuffle controls, in which mismatch responses were randomly permuted with respect to electrophysiological properties.

(D) Top: bar plot of the average additional R² when including each electrophysiological property in the linear model. Bottom: bar plot of correlation coefficients between each electrophysiological property and mismatch response. ^∗p < 0.05; ^∗∗p < 0.01.

(E) Results of leave-one-out analysis. Plotted in red are correlation coefficients between predicted and actual mismatch responses (for the neurons left out during model generation) for all seven model subsets including five or six properties. The gray boxplot shows the values for models generated with data in which mismatch responses were randomly permuted relative to electrophysiological properties.

Mismatch Responses Are Anticorrelated with Visual Flow Responses in Putative L2/3 Excitatory Neurons

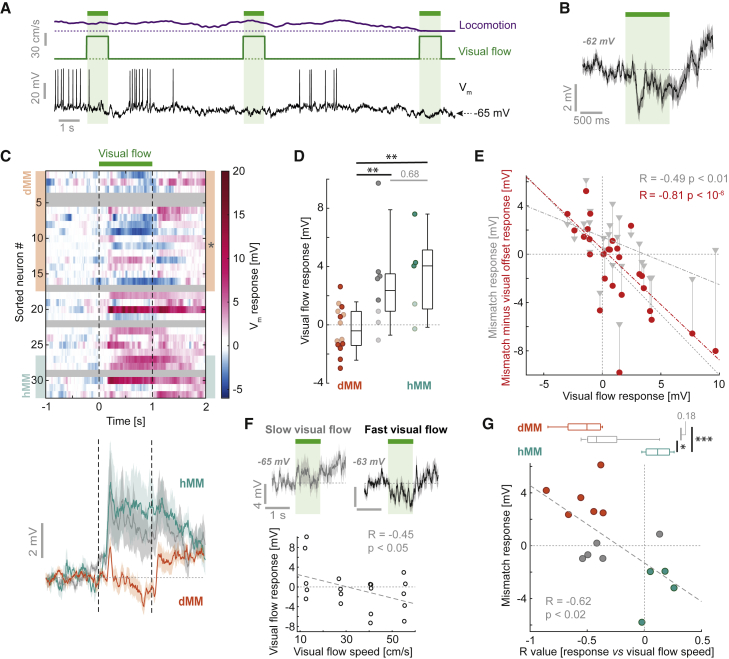
The observed mismatch responses either could be computed by L2/3 neurons as a difference between predicted and actual visual flow input or could simply be inherited from inputs to these neurons. If the responses are inherited, hyperpolarization would simply reflect a mismatch-triggered inhibitory input, and depolarization would reflect a mismatch-triggered excitatory input. However, if mismatch responses are driven by a reduction in visually driven input, we should find an opposing relationship between mismatch responses and visual responses. If visual input is excitatory, then its removal during mismatch would evoke hyperpolarization. Similarly, assuming visual input is inhibitory, removal of this input would evoke depolarization. To test this, we analyzed responses to 1 s visual flow stimuli, presented at random times independent of locomotion. Given that these stimuli are not predictable from locomotion or stimulus history, they constitute a positive prediction error (i.e., more visual flow than predicted). Because visual flow responses during locomotion and during stationary periods were correlated (Figures S4A–S4C), we included all presentations in our analysis. We lost 5 putative L2/3 pyramidal neurons before being able to record visual responses. 60% of the remaining neurons responded significantly to visual flow presentations (Figures 4A–4C; see STAR Methods). Subthreshold responses to visual flow were significantly different in dMM and hMM neurons (mean ± SD, dMM: −0.3 ± 1.6 mV, n = 14; hMM: 3.5 ± 3.0 mV, n = 5; p < 0.003, t test) (Figure 4D), and there was a significant negative correlation between visual flow response and mismatch response (R = −0.49, p < 0.01, n = 27) (Figure 4E). The different signs of visual response could not be explained by regression to a common reversal potential, because spiking responses largely reflected subthreshold responses (Figure S4E), and pre-stimulus V_m was a poor predictor of visual flow response (Figures S4F and S4G). Visual responses were comparable in magnitude to mismatch responses (Figure S4H).

Figure 4.

Visual Flow Responses Inversely Relate to Mismatch Responses in L2/3 Neurons

(A) Example V_m trace (black) recorded from a dMM neuron during the open-loop phase. Brief 1 s visual flow stimuli (shaded green) evoked hyperpolarization. Dotted lines indicate 0 cm/s.

(B) Average V_m response to visual flow stimuli for the example neuron in (A). Gray shading indicates SEM over 42 trials. The value in gray bold italics indicates the mean pre-stimulus voltage.

(C) Top: heatmap of the average V_m response to visual flow stimuli across all L2/3 neurons, sorted as in Figure 2A. Gray shading marks neurons for which we did not have sufficient data. Bottom: average response across 14 dMM neurons (orange), 5 hMM neurons (turquoise), and the remaining 8 neurons (gray). Shading indicates SEM over neurons. The asterisk indicates the example shown in (A).

(D) Average V_m responses to 1 s visual flow stimuli, compared for 5 hMM, 14 dMM, and 8 unclassified neurons. Dark data points indicate significant responses, p < 0.05, paired t tests. One-way ANOVA: p < 0.01, F-statistic = 6.5; dMM versus hMM: p < 0.003, dMM versus unclassified: p < 0.01, hMM versus unclassified: p = 0.68, t test.

(E) Scatterplot between average visual response and average mismatch response (gray triangles) for 27 L2/3 neurons. For red data points, the average response to visual flow offset was subtracted from the mismatch response. Dashed gray and red lines show linear fits to the respective data.

(F) Top: average response to visual flow stimuli of the lowest two (gray, 7 trials) and the highest two (black, 11 trials) visual flow speeds for an example neuron. Shading indicates SEM over trials. Values in gray bold italics indicate the mean pre-stimulus voltage. Bottom: scatterplot between visual flow speed and visual flow response across trials for the example neuron.

(G) Scatterplot between correlation coefficients (between visual flow speed and visual flow response) and mismatch response. Boxplots above compare values for 6 dMM (orange), 4 hMM (turquoise), and 5 unclassified neurons (gray). One-way ANOVA: p < 0.002, F-statistic = 12.5; dMM versus hMM: p < 0.001, dMM versus unclassified: p = 0.18, hMM versus unclassified: p < 0.02, t test.

In addition to responses to visual flow onset, we found that many neurons exhibited depolarizing responses or persistent depolarization after visual flow offset (Figure 4C). One interpretation of this is that the offset of visual flow results in separate excitatory input to L2/3 neurons. Consequently, mismatch responses would arise from a reduction in visual flow-driven input and a parallel increase in input driven by the visual flow offset. Correcting the mismatch responses for this visual flow offset response revealed a strong anticorrelation between visual flow and mismatch responses (R = −0.81, p < 10⁻⁶, n = 27) (Figure 4E; see STAR Methods). In a subset of neurons, we presented four distinct visual flow speeds (Figure 4F). In dMM neurons, visually driven hyperpolarization increased with visual flow speed, resulting in negative correlations between visual flow speed and V_m response (mean R value ± SD, = −0.54 ± 0.21, n = 6) (Figure 4G). By contrast, in hMM neurons, visually driven depolarization increased with visual flow speed, resulting in positive correlations (mean R value ± SD = 0.1 ± 0.1, n = 4; dMM versus hMM: p < 0.001, t test). Overall, the opposing relationship between visual responses and mismatch responses is consistent with the latter arising from transient removal of visual flow input.

The Influence of Locomotion on V_m Differs Depending on Mismatch Response

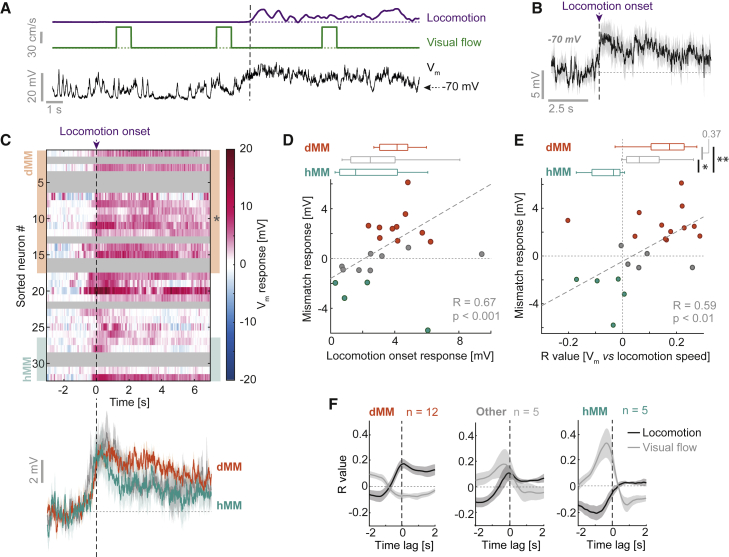
Computing visuomotor prediction errors requires a top-down input to convey a prediction of visual flow given movement. If a motor-related input is used to compute prediction error responses, we would expect to find that the motor-related input to a given neuron is correlated with the strength of the mismatch responses and anticorrelated with the strength of visual response. Thus, dMM neurons should receive motor-related excitation, whereas hMM neurons should receive motor-related inhibition (Keller and Mrsic-Flogel, 2018). Complicating this analysis somewhat, locomotion is associated with a brain state change, likely driven by neuromodulatory inputs (Fu et al., 2014; Polack et al., 2013). We quantified the influence of locomotion on L2/3 neurons in the open-loop condition in absence of coupled visual flow. Consistent with previous work (Bennett et al., 2013; Polack et al., 2013), we observed during locomotion a systematic depolarization in V_m that began before locomotion onset, a reduction in V_m variance, and only a small change in spike rates across the dataset (Figures 5A–5C and S5A–S5C). Although all neurons depolarized, locomotion onset responses correlated positively with mismatch responses (Figure 5D). Locomotion also caused visual responses to become more depolarizing (Figures S4A–S4D), consistent with previous findings (Bennett et al., 2013). These results are consistent with a neuromodulatory state change causing widespread depolarization of neurons (Polack et al., 2013), alongside a separate locomotion-related drive that correlates with mismatch response. To minimize the influence of state transitions associated with locomotion onsets and offsets, we analyzed the correlation between V_m and locomotion speed only during times of locomotion (see STAR Methods; Figure S7). We found that dMM neurons depolarized with increasing locomotion speed, whereas hMM neurons hyperpolarized with increasing locomotion speed (dMM: mean R value ± SD = 0.14 ± 0.13, n = 12; hMM: −0.06 ± 0.07, n = 5; p < 0.005, t test) (Figure 5E). This is consistent with a locomotion-related excitation onto dMM neurons and inhibition onto hMM neurons that both scale with locomotion speed, in addition to state-dependent depolarization.

Figure 5.

The Influence of Locomotion on V_m Differs Depending on Mismatch Response

(A) Example V_m trace (black) from a neuron during locomotion onset (vertical dashed line) in the open-loop condition. Dotted lines indicate 0 cm/s.

(B) Average V_m response to locomotion onset (purple dashed line) for the example neuron in (A). Shading indicates SEM over 4 trials. The value in gray bold italics indicates the mean pre-locomotion voltage.

(C) Top: heatmap of average V_m responses to locomotion onset for all L2/3 neurons. Responses are sorted as in Figure 2A. Gray shading marks neurons for which we did not have sufficient data. Bottom: average locomotion onset response across 10 dMM neurons (orange), 4 hMM neurons (turquoise), and 8 unclassified neurons (gray). Shading indicates SEM over neurons.

(D) Scatterplot between locomotion onset response and mismatch response for 22 neurons. Boxplots compare responses for 4 hMM neurons (turquoise), 10 dMM neurons (orange), and 8 unclassified neurons (gray). One-way ANOVA, p = 0.43, F-statistic = 0.9.

(E) As in (D), but for correlation coefficients between locomotion speed and V_m (when excluding stationary periods). Boxplots above compare values for 12 dMM (orange), 5 hMM (turquoise), and 5 unclassified neurons (gray). One-way ANOVA, p < 0.02, F-statistic = 5.8; dMM versus hMM: p < 0.005, dMM versus unclassified: p = 0.37, hMM versus unclassified: p < 0.05, t test.

(F) Average cross-correlations between V_m and locomotion speed (black) or visual flow speed (gray). Negative time values indicate locomotion/visual speed preceding V_m. Shading indicates SEM over neurons.

If mismatch responses are the result of opposing visual flow and locomotion speed inputs, the effects of locomotion speed and visual flow speed on V_m should have opposing signs. This was indeed the case: the correlation coefficients between V_m and locomotion speed were positively correlated with mismatch responses (R = 0.59, p < 0.01) (Figures 5E, 5F, and S7), whereas the correlation coefficients between V_m and visual flow speed showed a similarly strong negative correlation with mismatch responses (R = −0.54, p < 0.01). Consistent with this, in the closed-loop condition, the change in V_m during locomotion (and concurrent visual flow) did not depend on mismatch response (Figure S5D), whereas the difference in locomotion-related V_m changes between closed-loop and open-loop epochs was anticorrelated with mismatch response (Figure S5E). Although we cannot determine from our data whether locomotion and visual flow inputs are perfectly coincident, we found that the timing of the peak cross-correlation of V_m with locomotion was well matched with that of the cross-correlation of V_m with visual flow (Figure 5F). These data are consistent with L2/3 mismatch-responsive neurons computing the difference between a visual flow input and a locomotion-related input using balanced and opposing excitatory and inhibitory input.

Infragranular Layers Integrate Visual and Motor-Related Input Differently from L2/3

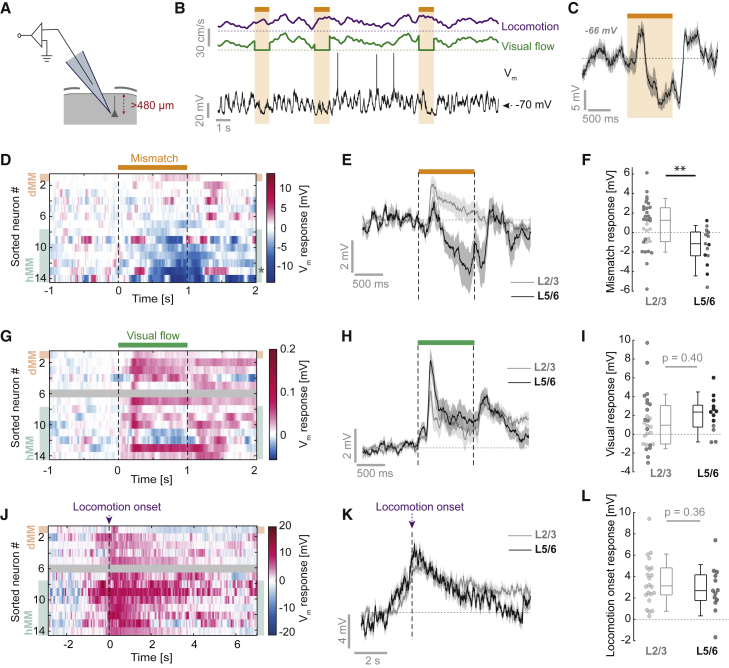
It has been suggested that infragranular layers 5 and 6 (L5/6) are computationally distinct from L2/3 (Harris and Mrsic-Flogel, 2013; Rao and Ballard, 1999). To probe for layer specificity in mismatch computation, we examined responses of neurons recorded between 480 and 750 μm from the cortical surface (Figure 6A), which we consider putative L5/6 excitatory neurons (n = 14). These L5/6 neurons had higher input resistances and higher firing rates than L2/3 neurons (Figures S6A and S6B), consistent with differences previously found between L5 and L2/3 neurons (de Kock and Sakmann, 2009; Lefort et al., 2009; Sakata and Harris, 2009). In contrast to L2/3 neurons, only 36% (5/14) of neurons responded significantly to mismatch (Figures 6B and 6C). Depolarizing responses (exceeding 1 mV, dMM) were rare (1 of 14 neurons), whereas half of the neurons (7 of 14) exhibited hyperpolarizing responses (exceeding −1 mV, hMM) (Figures 6D and S6C). Congruently, there was no evidence of positive correlations between mismatch response and locomotion speed in L5/6 neurons (Figure S6D). Overall, there was a significant difference between average mismatch responses in L2/3 and L5/6 neurons (mean ± SD, L2/3: 0.8 ± 2.4 mV, 32 neurons; L5/6: −1.5 ± 2.0 mV, 14 neurons; p < 0.01, t test) (Figures 6E and 6F). The paucity of dMM responses in L5/6 could be the result of (1) reduced bottom-up visual inhibition, (2) reduced excitatory locomotion-related input, (3) a lack of balanced and opposing tuning between these inputs, or (4) any combination of these. To examine these possibilities, we first analyzed visual flow responses. 70% of L5/6 neurons had significant responses to visual flow, all of which were depolarizing (Figure 6G). However, we found no evidence of a significant difference in average visual responses between L5/6 and L2/3 neurons (mean ± SD, L2/3: 1.3 ± 2.8 mV, 27 neurons; L5/6: 2.0 ± 1.9 mV, 13 neurons; p = 0.40, t test) (Figures 6H and 6I). In L5/6 neurons, we also found no evidence of a correlation between visual responses and mismatch responses (Figure S6E). Next, we looked at locomotion onset responses in L5/6 neurons. Nearly all L5/6 neurons underwent depolarization beginning before locomotion onset that was similar to that of L2/3 neurons (mean ± SD, L2/3: 3.5 ± 2.2 mV; L5/6: 2.8 ± 2.2 mV; p = 0.36, t test) (Figures 6J–6L). However, unlike in L2/3 neurons, locomotion did not affect visual responses in L5/6 neurons (Figures S4C–S4D), similar to findings in the somatosensory cortex (Ayaz et al., 2019).

Figure 6.

Deep-Layer Neurons Show a Lack of dMM Responses

(A) Neurons recorded at a vertical depth greater than 480 μm were classified as putative L5/6 neurons.

(B) Example V_m trace (black) from a putative L5/6 neuron recorded during the closed-loop condition with mismatch stimuli (orange bar and shading). Dotted lines indicate 0 cm/s.

(C) Average V_m response to mismatch stimulus for the example neuron in (B). Shading indicates SEM over 13 trials. The value in gray bold italics indicates the mean pre-locomotion voltage.

(D) Heatmap of average V_m responses to mismatch across all L5/6 neurons. Neurons are sorted by average mismatch response. Neurons were assigned dMM (orange shading) or hMM (turquoise shading) according to the same criteria used for L2/3 neurons: mismatch responses of at least 1 or −1 mV, respectively.

(E) Average response to mismatch across all L5/6 neurons (black, 14 neurons) compared with the average response to mismatch across all L2/3 neurons (gray, 32 neurons). Shading indicates SEM over neurons. Average pre-mismatch voltages were −68 ± 8 mV for L2/3 neurons and −64 ± 9 mV for L5/6 neurons.

(F) Average mismatch responses of L2/3 and L5/6 neurons. Dark data points indicate neurons with a significant response to mismatch. ^∗∗p < 0.01, t test.

(G) As in (D), but for visual flow responses. Gray shading indicates a neuron with insufficient data.

(H) As in (E), but for visual flow responses. Average pre-visual stimulus voltages were −64 ± 8 mV for L2/3 neurons and −63 ± 9 mV for L5/6 neurons.

(I) As in (F), but for visual flow responses. Dark data points indicate neurons with a significant response to visual flow.

(J) As in (D), but for locomotion onset responses. Average pre-running onset voltages were −64 ± 8 mV for L2/3 neurons and −62 ± 7 mV for L5/6 neurons.

(K) As in (E), but for locomotion onset responses.

(L) As in (F), but for locomotion onset responses.

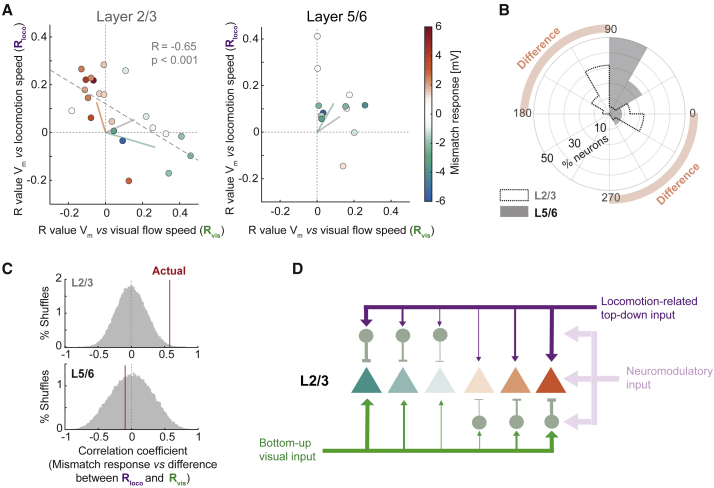
Finally, we compared how V_m in L2/3 and L5/6 neurons scaled with locomotion speed and visual flow speed. V_m in L2/3 neurons tended to exhibit a positive correlation with visual flow and a negative correlation with locomotion, or vice versa, resulting in a significant anticorrelation between the two correlation values (R = −0.65, p < 0.001, n = 22 neurons) (Figures 7A and S7). In contrast, V_m in L5/6 neurons tended to exhibit positive correlations with both visual flow and locomotion (Figures 7A and S7). To quantify this difference between L2/3 and L5/6 neurons, we computed the angle from 0° in the two-dimensional scatterplot of correlation values for each neuron. This angle is between 0° and 90° for neurons with positive correlations for both visual flow and locomotion and either between 90° and 180° (negative prediction error) or between 270° and 360° (positive prediction error) for neurons with opposing signs of the correlations. We found that this distribution is bimodal for L2/3 neurons, with a significantly higher proportion of neurons with angles corresponding to opposing signs of correlation than that observed in L5/6 neurons (L2/3: 17 of 22 neurons; L5/6: 2 of 12 neurons; p < 0.002, tea tasting exact test) (Figure 7B). The distribution of angles for L2/3 and L5/6 neurons were significantly more anticorrelated than expected by chance (p < 0.01) (see STAR Methods). The difference between the correlation of V_m with locomotion and the correlation of V_m with visual flow was a good predictor of mismatch responses in L2/3 neurons (R = 0.58, p < 0.01), but not in L5/6 neurons (R = −0.10, p = 0.75) (Figure 7C). Thus, the relative lack of dMM responses in L5/6 neurons is likely a result of a lack of balanced and opposing tuning between visual and locomotion-related inputs. Altogether, opposing visual and locomotion-related inputs necessary to compute visuomotor mismatch responses is a specific feature of L2/3 neurons and appears to be absent from L5/6 neurons, indicative of separate computational roles of L2/3 and L5/6 in visuomotor integration.

Figure 7.

L2/3 Neurons, but Not L5/6 Neurons, Integrate Locomotion and Visual Inputs with Opposing Signs

(A) Scatterplots of the correlation coefficient between V_m and visual flow speed and the correlation coefficient between V_m and locomotion speed for 22 L2/3 neurons (left) and 12 L5/6 neurons (right). The gray dashed line is a linear regression to the data. Pale solid lines indicate the average population vector for hMM neurons (turquoise), dMM neurons (orange), and unclassified neurons (gray).

(B) Histogram of the angles in (A) for each neuron. The two histograms are significantly anticorrelated (p < 0.02, see STAR Methods).

(C) Difference between the correlation of V_m with visual flow and the correlation of V_m with locomotion speed is a good predictor of mismatch responses in L2/3 neurons (R = 0.58, vertical red line denoted as actual), but not in L5/6 neurons (R = −0.1, vertical red line). Gray histograms are shuffle controls in which correlation coefficients were scrambled across neurons.

(D) Schematic of a hypothesized L2/3 circuit. Excitatory neurons (triangles) have visuomotor mismatch responses ranging from strong depolarization (orange) to strong hyperpolarization (turquoise), reflecting the balance between bottom-up and top-down excitation and inhibition. Inhibitory interneurons are shown in gray. Locomotion also evokes a state change affecting all neurons via neuromodulatory input. The width of the arrows indicates the relative strength of the input.

Discussion

Our results are consistent with the key postulate of the predictive processing framework: visuomotor mismatch responses observed in L2/3 of V1 are the result of a difference computation between predicted visual flow and actual visual flow (Keller and Mrsic-Flogel, 2018; Rao and Ballard, 1999). Although the visuomotor integration characteristics of L5/6 could support several models, they are consistent with a role in maintaining an internal representation by integrating over L2/3 and top-down input (Keller and Mrsic-Flogel, 2018). This interpretation assumes that visual flow responses are mainly bottom-up driven and locomotion responses are mainly top-down driven.

Several limitations of current-clamp recordings should be kept in mind when interpreting our results. First, we cannot directly determine from changes in V_m the underlying changes in excitatory and inhibitory inputs. A depolarizing response, for example, can be caused by an increase in excitatory input or a decrease in inhibitory input. Second, somatic recordings do not have direct access to inputs arising on distal dendrites, particularly in awake in vivo recordings, in which input resistances are typically low (Figure S2A). Consequently, inhibition is underestimated if it arises primarily on distal dendritic compartments or when it shunts depolarizing currents rather than evoking overt hyperpolarization. The sources of the visually driven inhibition onto negative prediction error neurons are somatostatin-positive interneurons (Attinger et al., 2017), which preferentially target the apical dendrites of L2/3 excitatory neurons (Markram et al., 2004). This could explain why we only see overt hyperpolarization to visual flow in a subset of dMM neurons. To overcome these limitations, ideally one would want to use genetically encoded voltage indicators to measure voltage changes in the dendrites optically.

It is possible that hMM and dMM neurons are differentially tuned for visual features such as grating orientation and that dMM responses arise from relief from a form of cross-orientation suppression. In the limited recording time of intracellular recordings, it would be difficult to quantify mismatch responses and visual tuning curves in the same neurons. However, a purely visual explanation of the difference between dMM and hMM neurons would not account for the effect of locomotion-related input anticorrelating with that of the visual flow input (Figures 5F and 7A). This is consistent with suprathreshold mismatch responses not being accounted for by visual responses alone (Zmarz and Keller, 2016). In addition, cross-orientation suppression likely is not driven by intra-cortical inhibition but instead is the consequence of reduced thalamic drive (Freeman et al., 2002). Thus, a model based purely on bottom-up visually driven responses cannot account for our results.

Assuming hMM and dMM neurons correspond to positive and negative prediction error neurons, why signal the two types of errors in separate populations of neurons? In the midbrain dopaminergic system, positive and negative reward prediction errors are thought to be encoded bidirectionally in individual neurons via increases and decreases in firing rate (Schultz et al., 1997). In the case of cortical L2/3 neurons, baseline firing rates are probably too low to reliably signal with a decrease in firing rate. Splitting negative and positive prediction error responses into two separate populations of neurons alleviates this problem. In addition, this could simplify learning, because the activity of prediction error neurons could be used directly as an error signal to drive plasticity (Hertäg and Sprekeler, 2020).

How many spiking responses to mismatch would we expect, assuming the predictive processing framework were a useful model? A simple upper bound on this would be half of the prediction error neuron population: half responds to positive prediction errors, and the other half responds to negative prediction errors. However, here we probed prediction errors by breaking the coupling between forward locomotion and backward visual flow, which represents only a small fraction of the total space of visuomotor coupling a mouse will experience. V1 receives top-down input that conveys predictions of visual input given locomotion (Leinweber et al., 2017), spatial location (Fiser et al., 2016), and visual surround (Keller et al., 2020). In addition, V1 receives inputs that convey vestibular signals (Vélez-Fort et al., 2018) and auditory signals (Ibrahim et al., 2016; Iurilli et al., 2012). In principle, all these top-down inputs could be associated with a population of prediction error neurons selective for a particular type of error. We previously found that L2/3 neurons responsive to the omission of a visual input expected based on spatial location are different from those that respond to the visuomotor mismatches we used here (Fiser et al., 2016). Thus, there likely is some specificity in the coding of prediction errors. Although L5/6 neurons in our study did not have the opposing influence of locomotion and visual flow input necessary to compute prediction errors, it is possible that they compute prediction errors in different dimensions, for example, when integrating vestibular and visual signals. Furthermore, only 2 of 14 of our infragranular recordings were recorded at the layer 6 depth (>600 μm), and it is possible that in larger datasets, distinct visuomotor integration characteristics may be observed for layer 6 neurons.

Calcium imaging experiments show that 20%–30% of L2/3 neurons respond to mismatch (Attinger et al., 2017; Keller et al., 2012)—a proportion larger than that estimated to respond to one particular natural scene (3%) or one particular drifting grating (12%) (Yoshida and Ohki, 2020). Not surprisingly, the subthreshold tuning for mismatch is broader than the suprathreshold tuning. However, only 10% of our L2/3 neurons show spiking responses to mismatch. Potential causes of this smaller fraction of suprathreshold responses could be internal solution dialysis, the higher rate of mismatch presentation used during the whole-cell recordings, or intracellular calcium rises independent of spiking activity during calcium imaging. Although the cause of this discrepancy is unclear, it does not alter our conclusions.

Altogether, we find L2/3 neurons with responses consistent with signaling either positive or negative prediction errors, which can be explained by opposing visual and locomotion-related inputs. This computation appears confined to L2/3 neurons. It is conceivable that the two functional neuron types in L2/3 are associated with different synaptic input distributions and possibly gene expression profiles. Identifying molecular markers for these different neuron types would allow us to test the hypotheses put forward in the predictive processing framework.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
All data and code used to generate figures.	This manuscript	https://data.fmi.ch/
Experimental Models: Organisms/Strains
Mus musculus: C57BL/6J	Charles River Laboratories	IMSR_JAX:000664
Software and Algorithms
MATLAB, 2019	https://www.mathworks.com/products/matlab.html	RRID: SCR_001622
LabView	https://www.ni.com/en-us/shop/labview.html	RRID: SCR_014325
Python3	https://www.python.org/	RRID: SCR_008394
Panda3D	https://www.panda3d.org/	N/A
MultiClamp Commander	https://www.moleculardevices.com/	N/A

Resource Availability

Lead Contact

Requests for further information and resources should be directed to the lead contact, Georg Keller (georg.keller@fmi.ch).

Materials Availability

No new unique reagents or mouse lines were generated in this study.

Data and Code Availability

All data and analysis code are available online at https://data.fmi.ch/.

Experimental Model and Subject Details

All animal procedures were approved by and carried out in accordance with guidelines of the Veterinary Department of the Canton Basel-Stadt, Switzerland.

Subjects

32 experimentally naive C57BL/6J mice (RRID:IMSR_JAX:000664) were used in this study, procured from Charles River Laboratories. Mice were a mixture of males and females and aged between 6 and 10 weeks of age at the time of electrophysiological recording.

Method Details

Head implant surgery

Mice were anesthetized using a mix of fentanyl (0.05 mg/kg), medetomidine (0.5 mg/kg) and midazolam (5 mg/kg). Analgesics were applied perioperatively. Lidocaine was injected locally on the scalp (10 mg/kg s.c.) prior to surgery, while metacam (5 mg/kg, s.c.), and buprenorphine (0.1 mg/kg s.c.) were injected just after completion of the surgery. An incision was made in the skin above the cranium and the periosteum was completely removed from the skull. The surface of the skull was roughened with a dental drill. To optimize stability of the brain for later recordings, a blunt tool was used to apply gentle force to one of the parietal skull plates just anterior to bregma until small forces applied to either intra-parietal or parietal skull plates did not result in relative movement of the bones. In this position, layers of tissue glue (Histoacryl, B.Braun, Germany) were used to fuse the skull plates along the sutures. Tissue glue was then applied to the whole skull surface, and a custom-made titanium head-bar was glued to the skull. At this point, right V1 was marked 2.5 mm lateral to the midline, just anterior to the lambdoid suture. Dental cement was used to fix the head-bar in place and build a recording chamber around V1. Anesthesia was then antagonized (Flumazenil, 0.5 mg/kg and Atipamezole, 2.5 mg/kg i.p.), and the mouse was allowed to recover for 3 days. Buprenorphine or Metacam were provided as a general analgesia on the subsequent 2 days.

Whole cell recordings

Micropipettes (5 MΩ to 8 MΩ resistance) were fabricated using a PC-100 puller (Narishige, Tokyo, Japan) from 1.5 mm diameter filamented borosilicate glass (BF150-86-10, Sutter, California, USA). A small 1 mm craniotomy and durectomy were made over the right primary visual cortex (spanning 2 mm to 3 mm lateral from the midline) under isoflurane anesthesia. To stabilize the brain, the craniotomy was covered in a layer (0.5 mm to 1 mm) of 4% low-melting point agar (A9793, Sigma-Aldrich), dissolved in bath recording solution. The recording chamber was submerged in bath recording solution (126 mM NaCl, 5 mM KCl, 10 mM HEPES, 2 mM MgSO₄, 2 mM CaCl₂, 12 mM glucose, brought to pH 7.4 using NaOH, with a final osmolarity 280 mOsm to 290 mOsm). The mouse was allowed to recover from isoflurane anesthesia for at least 20 minutes head-fixed prior to recordings, which were only attempted after the mouse had displayed regular locomotion behavior. Whole cell recordings were performed blindly by lowering the micropipette, back-filled with intracellular recording solution (135 mM KMeSO₃, 5 mM KCl, 0.1 mM EGTA, 10 mM HEPES, 4 mM Mg-ATP, 0.5 mM Na₂-GTP, 4 mM Na₂-phosphocreatine, brought to pH 7.3-7.4 with KOH, with an osmolarity 284 mOsm to 288 mOsm), through the agar and 50 μm into the tissue with high pressure (> 500 mbar) applied to the micropipette. The micropipette was visually targeted at the center of the craniotomy. Micropipette resistance was monitored in voltage clamp via observing the electrode current while applying 15 mV square pulses at 20 Hz. Brain entry was detected by a step change in the current (Margrie et al., 2002), and at this point the descent axis was zeroed. Once a depth of 50 μm from the surface was reached, pipette pressure was lowered to 20 mbar and neuron hunting began. This consisted of advancing the electrode in 2 μm steps until a substantial and progressive increase in pipette resistance was observed for at least 3 consecutive steps. Pressure in the pipette was then rapidly lowered to 0 mbar, and often a small negative pressure was applied to aid in forming a gigaohm seal. Once this was achieved, the pipette was then carefully retracted by up to 4 μm, and break-in achieved using suction pulses. Electrophysiological properties were determined in the first 60 s of the recording using a series of current steps from −0.4 nA to 0.3 nA, and the evoking of action potentials was used to confirm the neuronal nature of the cell. All recordings took place in current clamp mode. Pipette capacitance and series resistance were not compensated. Data were acquired and Bessel low-pass filtered below 4 kHz using a MultiClamp amplifier (Molecular Devices, California USA) and digitized at 20 kHz via custom-written LabView software. Voltage values have not been corrected for the junction potential between the internal solution and bath solution (−8.5 mV), owing to the difficulty of measuring junction potentials accurately in vivo. Recordings were terminated if series resistance displayed a substantial increase, as monitored by 25 ms or 50 ms current pulses between −0.1 nA and −0.25 nA applied at 1 Hz throughout the recording. Access resistance was estimated offline from the voltage drop in the 1 ms after current step onset and ranged between 25 MΩ and 140 MΩ for included data (65 MΩ ± 27 MΩ, mean ± SD). For all data included the average membrane potential during stationary periods was more hyperpolarized than −45 mV (on average −61 mV ± 7 mV, mean ± SD; 95% were more hyperpolarized than −55 mV), and spike amplitudes on average were 47 mV ± 16 mV (mean ± SD).

Virtual reality

During all recordings, mice were head-fixed in a virtual reality system as described previously (Leinweber et al., 2014). Briefly, mice were free to run on an air-supported polystyrene ball, the rotation of which was coupled to linear displacement in the virtual environment projected onto a toroidal screen surrounding the mouse. From the point of view of the mouse, the screen covered a visual field of approximately 240 degrees horizontally and 100 degrees vertically. The virtual environment presented on the screen was a virtual tunnel with walls consisting of continuous vertical sinusoidal gratings. Prior to the recording experiments, mice were trained in 1 h to 2 h sessions for 5 d to 7 d, until they displayed regular locomotion.

Visual stimuli

During the first segment of each recording, visual flow feedback was coupled to the mouse’s locomotion speed. At random intervals averaging at 7 s, 1 s long halts in visual feedback were presented (referred to as ‘mismatch’ stimuli). After at least 3 minutes of this protocol, the visual feedback was stopped (i.e., no visual flow coupled to locomotion speed), and instead 1 s full-field fixed-speed visual flow stimuli were presented at random intervals (mean ± SD, 8.1 s ± 1.3 s), regardless of locomotion behavior. In a subset of recordings (12 of 27), these stimuli all had one fixed visual flow speed, and in the remaining subset (15 of 27), four different visual flow speeds were presented in a pseudorandom sequence.

Quantification and Statistical Analysis

All data analysis was performed using custom-written MATLAB (2019) (Mathworks) code.

Statistics

For each comparison, first a Lilliefors test was used to test for normality of the distribution. In the case of comparisons involving normal distributions across more than one group (e.g., hMM, dMM and unclassified L2/3 neurons), first a one-way ANOVA was performed. If the distribution was not normal, a one-way ANOVA on ranks was used instead. In the case of a significant result (p < 0.05), either t tests or rank sum tests were used to determine which comparisons were significant (the latter test being used in cases of non-normally distributed data or data comparisons where variance was unequal as determined by a Bartlett test). To test for significant differences in variance in non-normally distributed samples, a Brown-Forsythe test was performed. Box and whisker plots are all drawn such that the box represents the inter-quartile range and median, and the whiskers represent the 10^th and 90^th percentiles. For all correlations, a method of fitting robust to outliers was used (MATLAB function Fitlm) based on bisquare weighting of residuals.

Cell numbers:

In total, we recorded from 54 neurons from 32 mice. Only one craniotomy was performed per mouse. Typically, only one (13 mice), or two neurons (13 mice) would be recorded per mouse, but in rarer cases three neurons (5 mice) would be recorded. Between recordings, mice would be re-exposed to fully coupled visuomotor experience for at least 10 minutes. Of the 54 neurons recorded, 6 neurons were excluded as putative interneurons as they had an input resistance higher than 100 MΩ. A subset of interneuron types (e.g., somatostatin-expressing neurons) have been described to have high input resistances (Gentet et al., 2012; Pala and Petersen, 2015). Two neurons were excluded due to spike half-widths below 0.6 ms (putative parvalbumin-expressing neurons). Consistent with the excluded neurons being interneurons, other electrophysiological features differed between these excluded neurons and the remaining putative excitatory neurons, including higher baseline spike rates and more depolarized resting membrane potentials (Figure S2). 32 of the remaining 46 putative excitatory neurons were recorded at a vertical depth of less than 400 μm below the cortical surface. We refer to these as putative L2/3 neurons. Of these, 27 underwent both the visuomotor coupled and open-loop parts of the protocol, and the remaining 5 underwent only the former part. Of the 27 neurons with both parts of the protocol, 15 were presented with visual stimuli of four different speeds, while the remaining 12 were presented with only one visual flow speed. The neurons for which we do not have data in the open-loop condition are represented as uniform gray on response heatmaps of visual flow and locomotion onset response. 14 neurons were recorded at vertical depths greater than 480 μm, with a maximum depth of 723 μm (2/14 were recorded at L6 depths of > 600 μm, so the dataset is likely dominated by L5 neurons). We refer to these as putative L5/6 neurons. Of these, 13 underwent both the visuomotor coupled and open-loop parts of the protocol, and the remaining 1 underwent only the former part. Of the 13 neurons with both parts of the protocol, 12 were presented with four different visual flow stimuli of different speeds, and the remaining 1 neuron was presented visual flow stimuli of one speed only. Note that neurons are included in each analysis depending on availability of the relevant data.

Spike half-widths and subtraction

Spikes were detected from peaks exceeding −30 mV membrane potential. Spike half-width was measured as the duration of the average spike waveform that exceeded half of the spike amplitude. For all average membrane potential response plots, spikes were removed from membrane potential traces by replacing them with a linear interpolation from the membrane potential recorded 2 ms prior to spike peak, and that recorded 3 ms after spike peak. Voltage responses to the 25 ms or 50 ms duration current pulses used to track access resistance were removed similarly, by replacing them with a linear interpolation from the time just before the current pulse turned on to that 70 ms later.

Mismatch responses

Presentation of visual flow halts (mismatches) occurred independent of locomotion speed. As only halts during non-zero visual flow speed would result in a change of the visual stimulus, mismatch events were defined as visual flow halts that occurred during an average locomotion speed exceeding 4 cm/s in the 2 s prior to and after onset of mismatch stimulus. The average number of mismatch presentations per neuron was 15 ± 9 (mean ± standard deviation). To calculate average V_m responses, spikes and current pulses were removed as described above and the V_m was baseline-subtracted by the average membrane potential in a window 1 s prior to mismatch for each trial. The mean of all resulting V_m traces was then taken to generate the average response. The average response for each neuron was taken as the mean V_m response during the entire 1 s of mismatch presentation. The significance of this response was determined by performing a paired t test between the average V_m 1 s before mismatch and that in the 1 s during mismatch. Mismatch responses were cross-validated in neurons with at least 10 mismatch trials by calculating mismatch responses in odd and even trials separately (Figure S3A). Spiking responses were generated by taking the mean spike count in 250 ms time bins aligned to mismatch onset. To assess the signal to noise ratio of subthreshold mismatch responses, standard deviation of the baseline membrane potential was calculated for each neuron from a distribution of sham-triggered changes in V_m (average V_m in 0-1 s baseline subtracted for the average V_m in the 1 s prior to the sham-trigger) during locomotion(Figures S3C and S3D).

Correlation between mismatch responses and locomotion speed

To test the relationship between mismatch responses and locomotion speed, we averaged the locomotion speed 1 s prior to mismatch onset and computed the correlation coefficient of this value with average mismatch response (averaged across the 1 s of mismatch) across trials for each neuron. Only neurons with at least 7 valid mismatch trials, and a range of at least 10 cm/s in locomotion speed were included. To generate correlation coefficients less sensitive to outliers, a method of fitting robust to outliers was used (MATLAB function Fitlm) based on bisquare weighting of residuals.

Electrophysiological properties and multiple linear regression analysis:

A series of current steps from −0.4 nA to 0.3 nA were applied to the neuron at least 3 times at the beginning of the recording to determine input resistance. In all cases, mice were stationary at the time of these current steps. The total resistance was calculated by averaging the voltage response for each current step value and measuring the slope between the average response 25 ms to 125 ms after current step onset against the injected current. This was done separately for negative and positive current injection, as the former consistently showed a lower resistance than the latter (in part due to voltage sag during negative current injection). The access resistance was estimated by taking the slope between the current injected and the voltage response in the first 1 ms. Input resistance was calculated as the difference between total resistance and access resistance. Resting membrane potential was defined as the intersection between zero current and the voltage axis. Note that resting membrane potential would often depolarize by a few mV before stabilizing during the first 3 to 5 minutes of the recording, presumably as the intracellular solution diffuses throughout the neuron. As such, membrane voltages read out at later time points (e.g., in Figure S5) are different to the initial resting membrane potentials assessed just after break-in. The membrane time constant was estimated by finding the time at which the voltage change fell below 1/e of the difference between 1 ms after current step (−0.1 nA) onset and steady state (estimated as the voltage in the window 45 ms - 50 ms after the onset). Since many cells were silent during zero current injection, spike thresholds were calculated for spikes evoked during the I-V curve (after offline removal of the voltage drop across the series resistance), all of which were overshooting. For each spike, the spike threshold was determined as the voltage at the peak rate of change of the slope of the spike waveform. The median of these spike thresholds was then taken as the measure of spike threshold for the neuron. Spike thresholds measured in this way were similar to those measured in previous in vivo studies of L2/3 in primary visual cortex (−40 mV ± 5 mV, mean ± SD) (Bennett et al., 2013; Polack et al., 2013).

In order to determine whether mismatch responses could be predicted from electrophysiological properties, we used a multiple linear regression analysis including six physiological properties: spike threshold, initial resting membrane potential, input resistance, spike rate prior to mismatch stimuli, variance in membrane potential during stationary epochs, and membrane time constant. For each regression, we included 1 to 6 of these properties, in all possible combinations, and determined the variance in mismatch response explained by each model. Since not all properties were measured for each neuron, including more properties in the regression leads to a reduction in sample size which could account for some of the increase in variance explained as more properties are included. To assess this, we performed controls in which mismatch responses were randomly permuted with respect to the sets of electrophysiological properties (10000 permutations per regression). The contribution of each variable to model performance was assessed for all neurons where all data were available. The R² of model subsets including a given electrophysiological property were compared to the R² of the same subsets missing the property. The average change in R² was then averaged for all model subsets, for each individual property. To assess the performance of the models on data not included in model generation, we used all model subsets including 5 or 6 properties, and systematically generated the model excluding one of the 32 L2/3 neurons. We then used the resulting model to predict the response of the left-out neuron and determined the correlation between predicted and actual mismatch responses for the full dataset. This was then compared to 10000 models in which mismatch response was randomly permuted with respect to electrophysiological properties.

Changes in membrane potential dynamics during locomotion

To measure membrane potential average and variance, as well as spiking activity during locomotion and stationary periods (Figure S5), only the data from the open-loop condition were used. The data were binned into 500 ms time bins, and spike count, median membrane potential and locomotion speed were calculated for each time bin. The locomotion speed trace was smoothed in a 1 s time window prior to this calculation. For quantification of V_m during stationary periods, all V_m values corresponding to times when the locomotion speed was below a threshold of 4 cm/s were pooled, and the mean and standard deviation of these values were calculated for each neuron. The same was then done for locomotion periods where the locomotion speed exceeded the 4 cm/s threshold.

To determine the time of locomotion onsets, we detected points where the smoothed locomotion velocity crossed a threshold of 0.8 cm/s and exceeded 4 cm/s in the following 1 s. Average locomotion onset responses were then calculated for each neuron where there were at least 2 locomotion onsets. These were baseline-subtracted by the average membrane potential in the 2.5 s prior to locomotion onset for each trial before averaging all traces. Locomotion onset responses were taken for each neuron as the average response 0 s to 6 s after locomotion onset.

Calculation of cross-correlations (Figures 5E, 5F, and S7):

Cross-correlations were calculated between membrane potential and locomotion for the open-loop condition only. For this, the locomotion trace and visual flow trace recorded at 1 kHz were smoothed using a 500 ms time window. Membrane potential was binned in 1 ms time windows. Times during which the mouse was stationary (locomotion < 4 cm/s), and times during which visual flow stimuli were presented, as well as 1 s after the presentation, were excluded. We then computed the cross-correlation between locomotion trace and membrane potential in a window of −2000 ms to +2000 ms. A similar procedure was used for the cross-correlation between membrane potential and visual flow, again excluding periods when the mouse was stationary. For each neuron, the overall correlation coefficient for the locomotion-V_m correlation was taken as the average cross-correlation for time delays between −500 and +500 ms, as this is where the cross-correlation averaged across the L2/3 and L5/6 samples combined peaked (Figure S7B). For each neuron, the overall correlation coefficient for the visual flow-V_m correlation was taken as the average cross-correlation for time delays between −1000 and 0 ms, as this is where the cross-correlation averaged across the L2/3 and L5/6 samples combined peaked (Figure S7B). Only neurons with at least 25 s of locomotion in absence of visual flow were included in these analyses (n = 22 L2/3, n = 12 L5/6).

To compare correlations for L5/6 and L2/3 datasets (Figure 7), we calculated an interaction angle for each neuron as the arcus tangent of the ratio of the locomotion-V_m correlation and visual flow-V_m correlation. Polar histograms were then made for the L2/3 and L5/6 datasets separately (Figure 7B). The neuron counts for each angular bin were then correlated between L5/6 and L2/3 datasets, generating an R value of −0.1. To test if the resulting anticorrelation was significant, L5/6 and L2/3 interaction angles were pooled, random subsets corresponding to the sample sizes of the L5/6 and L2/3 datasets were drawn, and the correlation coefficients between the shuffled sample distributions were obtained. An R value was then calculated for the correlation between the resulting two polar histograms. This was repeated 10000 times to generate a distribution of correlation coefficients.

To determine how well the correlations for visual flow speed and locomotion speed predicted a neuron’s mismatch response (Figure 7C), we computed the correlation coefficient between the difference of the two correlation coefficients (R value_locomotion - R value_visual) and the mismatch responses, for L2/3 and L5/6 neurons separately. As a shuffle control, we then randomly permuted the visual flow correlation and locomotion correlation values across neurons 100000 times to create a shuffle distribution.

Visual flow responses

Visual onsets were defined as the time the visual flow speed crossed a threshold of 0.8 cm/s. The membrane potential for each presentation was baseline subtracted by the average V_m in the 1 s prior to visual flow onset. The response was then averaged in the 1 s window of visual flow across all trials, regardless of locomotion behavior. The significance of this response was determined for each neuron by performing a paired t test between the average V_m 1 s before visual flow onset, and that in the 1 s during visual flow for all included trials. For the subset of neurons which were shown four different visual flow speeds, responses were averaged regardless of visual flow speed. To determine the effect of locomotion on visual flow responses (Figures S4A–S4D), visual flow presentations were separated according to locomotion speed: locomotion trials were defined as trials in which the average locomotion speed in the 1 s prior to and 1 s during visual flow both exceeded 4 cm/s. Stationary trials were defined as trials in which the locomotion speed in these two epochs both were less than 4 cm/s. For correlations between visual flow speed and visual response (Figures 4F and 4G), only trials in which the mouse was locomoting above 4 cm/s were included, and the correlation coefficient between the visual flow speed and membrane potential response across trials was generated for each neuron.

Correlation between visual flow response and mismatch response

For the correlation between mismatch response and visual response across neurons (Figure 4E), we first calculated the correlation between the mismatch response (as averaged across the 1 s of mismatch) versus the visual response (as averaged across the 1 s of visual response). To account for any response to visual flow offset, we computed the visual offset response as the average membrane potential response in the 1 s after visual flow offset, baseline subtracted using the average membrane potential in the 1 s prior to visual flow onset. This visual flow offset response was then subtracted from the mismatch response, and the correlation was calculated between the resulting values and the visual flow response.

Pupil movements

Mismatch induced eye movements were quantified in 20 mice not used in the whole cell recordings experiments (Figure S1). Eye position and pupil dimeter were recorded in response to visuomotor mismatches. We measured pupil diameter for all mismatch trials and z scored the data for each trial. For each mouse, these z scored data were then averaged to quantify the average mismatch induced pupil diameter response. This was repeated for sham trials using random triggers. We quantified mismatch induced eye movements by comparing the x and y pupil positions in the 1 s before to that in the 1 s during mismatch.

Published: October 21, 2020