Hybrid methods for combined experimental and computational determination of protein structure

Abstract

Knowledge of protein structure is paramount to the understanding of biological function, developing new therapeutics, and making detailed mechanistic hypotheses. Therefore, methods to accurately elucidate three-dimensional structures of proteins are in high demand. While there are a few experimental techniques that can routinely provide high-resolution structures, such as x-ray crystallography, nuclear magnetic resonance (NMR), and cryo-EM, which have been developed to determine the structures of proteins, these techniques each have shortcomings and thus cannot be used in all cases. However, additionally, a large number of experimental techniques that provide some structural information, but not enough to assign atomic positions with high certainty have been developed. These methods offer sparse experimental data, which can also be noisy and inaccurate in some instances. In cases where it is not possible to determine the structure of a protein experimentally, computational structure prediction methods can be used as an alternative. Although computational methods can be performed without any experimental data in a large number of studies, inclusion of sparse experimental data into these prediction methods has yielded significant improvement. In this Perspective, we cover many of the successes of integrative modeling, computational modeling with experimental data, specifically for protein folding, protein–protein docking, and molecular dynamics simulations. We describe methods that incorporate sparse data from cryo-EM, NMR, mass spectrometry, electron paramagnetic resonance, small-angle x-ray scattering, Förster resonance energy transfer, and genetic sequence covariation. Finally, we highlight some of the major challenges in the field as well as possible future directions.

I. INTRODUCTION

In order to solve many of the large, pressing problems in science and medicine, methods to determine accurate structures of proteins and protein complexes are necessary. Understanding protein structure gives us an enhanced ability to understand and manipulate protein function. Obtaining accurate protein structures can significantly facilitate the discovery of mechanisms of the machinery of life. Once structures are determined and mechanisms of action are better understood, new therapeutics can be developed much more rapidly, often enhanced by the use of computer-aided structure-based drug discovery (SBDD) methods.¹ For example, with the determination of a protein structure, SBDD can drastically reduce the number of small molecules to be screened experimentally, excluding the most unlikely binders based on computational predictions.

There are some experimental methods that can be used to determine the structures of proteins at resolutions where the positions of heavy atoms can be elucidated (<3 Å), namely, x-ray crystallography, nuclear magnetic resonance (NMR) spectroscopy, and cryo-electron microscopy (cryo-EM). These methods have been and will continue to be central to the field of structural biology.^2–4 Determined structures are typically deposited in the Protein Data Bank (PDB), making them available to the scientific community. However, while the data collected from these methods can be used to unambiguously determine the 3D coordinates of most or all of the atoms, they each offer some unfortunate shortcomings. While x-ray crystallography is still the most common structure determination method used for stable, ordered proteins (accounting for ∼89% of protein structures in the PDB⁵), determining the proper crystallization conditions for a specific protein system can take months to years. Another downside of x-ray crystallography is that it can be difficult to obtain the structures of large complexes. On the other hand, NMR (∼7% of protein structures in the PDB⁵) is beneficial in that it is the most commonly used method to determine an ensemble of structures, providing information on conformational flexibility, which has made it more amenable to intrinsically disordered proteins.⁶ The downside to NMR as a full structure determination method is that it is typically limited to smaller structures (with some exceptions) due to issues with peak overlapping and line broadening. Finally, cryo-EM (∼3% of protein structures in the PDB⁵) continues to increase in popularity due to its benefits such as not requiring crystallization and utilizing conditions that are relatively native-like. Despite these benefits, density maps at high resolution currently cannot be routinely achieved, and the method is typically limited to large structures (although a benefit over x-ray crystallography and NMR is that it can be used on very large complexes). Additionally, all three of these methods require large amounts of sample as compared to some other experimental methods discussed later (although cryo-EM can be performed using much less sample than the other two methods). Despite the strong interest in protein structure determination, there is currently a huge gap between the number of known sequences and experimentally determined structures deposited in the PDB, highlighting the difficulties of structure elucidation. At the time of writing, there were about 185 × 10⁶ known sequences in the UniProt database,⁷ while there were only about 163 000 structures containing proteins in the PDB,⁵ with many exhibiting high sequence similarity to each other. While there are many reasons for this discrepancy (many of which are due to the described limitations), one reason is conformational heterogeneity. Dynamic systems that cannot be fully described by a single structure are typically harder to fully characterize experimentally (e.g., they are difficult to crystallize). Nonetheless, these methods undoubtedly will remain central to protein structure determination in the future, and advances are still being made, but it would be beneficial to the field to have the ability to consistently construct accurate structures of protein systems using data from easier-to-perform experimental methods.

There are many examples of experimental methods that are more accessible, easier to perform, and that provide some structural information, but from which the data alone are not enough to fully establish the structure of a protein. These data are sparse, in that they do not contain enough information to fully constrain the structure, but are also often simultaneously ambiguous (not specific, allowing for multiple interpretations) and uncertain (high false-positive signals).⁸ Nevertheless, some types of experimental data may provide enough information for full structure determination but are not practically usable in that way due to a lack of full understanding of the structural connection. For example, NMR chemical shifts (CSs) provide a large amount of information (as they are very sensitive to changes in structure), but currently, the translation between CS and structure is not perfectly understood. In summary, the experimental data that cannot practically be used for full protein structure determination may inherently not provide enough information (e.g., not enough measurements, ambiguity, and uncertainty) or may not be understood well enough for translation to the protein structure (or in many cases, a combination of the two).

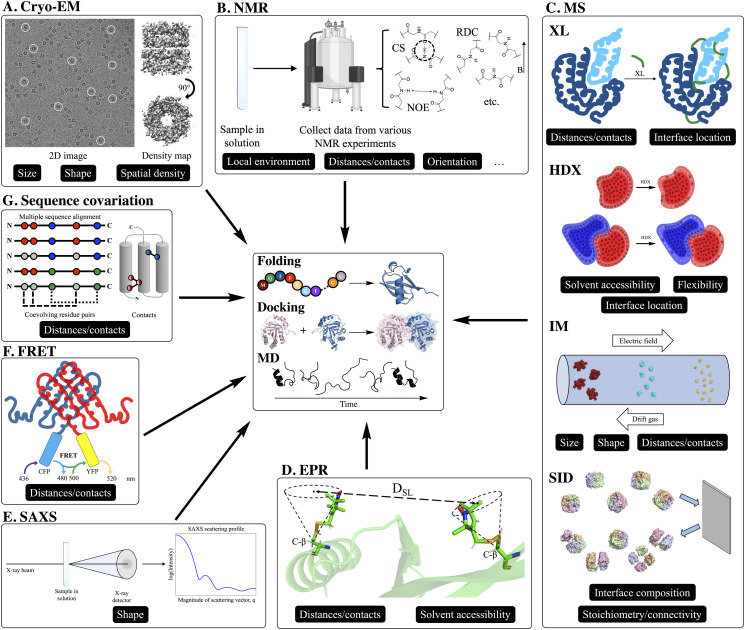
Some examples of techniques that can be used to collect these types of data are cryo-EM (when high-resolution density maps cannot be obtained), NMR (when a full collection of structure determination experiments are not performed), mass spectrometry (MS), electron paramagnetic resonance (EPR) spectroscopy, small-angle x-ray scattering (SAXS), Förster resonance energy transfer (FRET) spectroscopy, and genome sequencing (for the analysis of co-evolving residues). These methods will each be highlighted in more detail later in this Perspective, but, in general, they provide structural information such as size, shape, solvent accessibility, interface location/composition, distances/contacts, spatial density, orientation, local environment, flexibility, and stoichiometry/connectivity. Figure 1 shows representations for each experimental method as well as tags indicating what type of structural information that they can provide for modeling efforts. While knowing these types of information can be very beneficial, unfortunately they do not unambiguously specify the three-dimensional atomic coordinates.

FIG. 1.

Representations of each featured experimental method used for computational modeling. In this Perspective, we discuss how each method has been used for computational modeling in the form of de novo folding from the sequence (tertiary structure prediction), protein–protein docking (quaternary structure prediction), and molecular dynamics (physics-based protein dynamics simulation), as shown in the center panel. In the outer panels, each experimental method is tagged based on the type of structural information provided by its data. The categories are size, shape, solvent accessibility, interface location/composition, distances/contacts, spatial density, orientation, local environment, flexibility, and stoichiometry/connectivity. (a) Cryo-EM 2D projection image of the GroEL complex,⁴⁵ a homo 14-mer with D7 symmetry, in vitreous ice is shown on the left. Some examples of individual projections of the complex in different orientations are circled. On the right, the reconstructed 3D density map of the complex at 3.5 Å resolution (EMDB: 8750) is shown in two orientations. Cryo-EM density maps provide information on size, shape, and spatial density. (b) Representations of the most common forms of NMR data used for integrative structural modeling. Chemical shifts (CSs) provide information on local environments, nuclear Overhauser effect (NOE) provides distance between atom pairs, and residual dipolar coupling (RDC) provides information on inter-nuclei vector orientations. (c) Representations of various mass spectrometry (MS) methods that encode structural information into protein/peptide mass. Chemical cross-linking (XL) provides distances between residues that are cross-linked by fixed-length reagents and can provide the interface location when performed on a complex. In hydrogen–deuterium exchange (HDX), the exchange rates (from H to D of backbone amide hydrogens) provide information on solvent exposure and flexibility. By performing HDX on monomers and the complex (ΔHDX) and analyzing the difference, the interface location can also be determined. Ion mobility (IM) provides information on size and shape by separation, where larger proteins travel (left to right in this figure) through the bath gas with a lower velocity. This velocity can be used to calculate an averaged 2D collision cross section. If enough measurements are made on a protein complex and monomers, distances between subunits can also be approximated. Surface-induced dissociation (SID), which is exclusively used on complexes, can provide information on overall complex stoichiometry and subunit connectivity by breaking apart non-covalent interface interactions. Additionally, depending on the amount of energy required to break certain interfaces, a metric that depends on interface composition can also be measured. (d) Electron paramagnetic resonance (EPR) provides distances between paramagnetic spin labels, commonly nitroxide (spin-labeled residues shown as sticks). Because of the movement of spin labels, the location can be modeled using a cone as shown in this figure. The solvent accessibility of the paramagnetic labels can also be measured. (e) Small-angle x-ray scattering (SAXS) provides information on shape in the form of a scattering profile (scattering intensity as a function of spatial frequency), which can be approximated from the 3D structure. (f) Förster resonance energy transfer (FRET) can be measured by attaching a donor and acceptor fluorophore to the protein (either in vivo or in vitro) such as cyan fluorescent protein (CFP, shown in cyan) and yellow fluorescent protein (YFP, shown in yellow). The measured FRET efficiency (E_FRET) is dependent on the distance between the probes. (g) By performing a multiple sequence alignment with a large number of evolutionarily related sequences and identifying coevolving residue pairs, distance restraints or contacts can be determined.

An alternative approach for protein structure determination is to use computational prediction methods. Over the past 20–30 years, a large number of software packages and online tools have been developed toward structural modeling of proteins, many freely available for use. These algorithms can be broadly broken down into three categories: protein folding (prediction of the tertiary structure from the sequence), protein–protein docking (prediction of the quaternary structure from the structures of the monomers), and molecular dynamics [MD, short timescale (usually ns to μs) sampling of conformational dynamics of a protein]. As outlined in Levinthal’s paradox, computational protein structure prediction methods realistically cannot sample all possible backbone conformations of a protein but rather generally rely on stochastic approaches. For protein folding, most algorithms use Monte Carlo methods, sampling different backbone conformations by iteratively inserting small fragments of backbone coordinates (with similar sequences) obtained from the PDB⁹ and scoring the conformations with scoring functions that generally contain knowledge- and/or physics-based terms.¹⁰ Some examples of programs that can be used for ab initio protein structure prediction are Rosetta,^9,11–13 BCL,^14,15 QUARK,¹⁶ TOUCHSTONE II,¹⁷ and I-TASSER.¹⁸ Structure prediction can be further facilitated if the structures of similar sequences are available in the PDB (homology modeling). Some examples of homology modeling methods are RosettaCM,¹⁹ Modeller,²⁰ SWISS-Model,²¹ and MOE.²² Quaternary structure prediction methods can either dock chains together (locally or globally) or build entire complexes using symmetry. Specifically for local docking, Monte Carlo methods are common. These methods sample many orientations between different protein chains and score models based on shape agreement and energetic enhancement of the interface(s). For global docking, fast Fourier transform methods (FFT) are generally used. FFT methods sample the large conformational space with high efficiency and evaluate the fit between subunits based on shape complementarity. Some methods for protein–protein docking are RosettaDock,^23,24 Rosetta SymDock,²⁵ DOT,²⁶ HADDOCK,²⁷ ZDOCK,²⁸ ClusPro,²⁹ PatchDock/SymmDock,³⁰ and FTDOCK.³¹ Finally, while it is certainly powerful to obtain or predict a static structure, many proteins can adopt multiple different physiologically relevant conformations in vivo. MD offers the ability to sample some of these different structures, which can then be used to gain crucial insight into the function. MD algorithms typically use classical, physics-based force fields^32–35 (molecular mechanics, either all atom or coarse-grained) to simulate the dynamics and model the structure in relevant solution conditions (proteins are typically embedded in explicit water boxes with periodic boundary conditions during the simulations). Some programs that can be used to perform MD simulations are NAMD,³⁶ Amber,³⁷ GROMACS,³⁸ Desmond,³⁹ CHARMM,⁴⁰ and OpenMM.⁴¹ While these methods for protein structure prediction and modeling have been very successful, de novo modeling remains a challenge.

Due to the challenges of both computational modeling and interpreting the data of experimental methods, it has become increasingly popular to incorporate restraints [reward or penalty functions that quantify the agreement with the experiment in some way, i.e., (1) based on deviation from the experiment using a forward model or (2) using geometric functions derived from the experiment] from sparse experimental data into modeling algorithms. While we generally refer to the experimental methods as either techniques that routinely elucidate high-resolution structures or those that provide some structural information, but not enough to fully determine atomic coordinates; in reality, the computational methods using these data exist on a spectrum. Depending on the amount of information provided as well as the understanding of those data with relation to the structure, the methods exist somewhere in the spectrum of de novo structure prediction (from the sequence only), structure prediction using sparse experimental data, and full structure determination (x-ray crystallography, NMR, and cryo-EM). While not a focus of this Perspective, we note that dynamic systems with large conformational heterogeneity may especially require integrative modeling. For these systems, however, it is important to be aware that multiple conformations may be present in the data and are relevant to the function. Because of the popularity of integrative modeling, the biennial Critical Assessment of Structure Prediction (CASP) competition added structure prediction categories for modeling with multiple varieties of data from experiments such as NMR, SAXS, cross-linking MS, small-angle neutron scattering (SANS), and FRET in CASP13.⁴² In addition to the incorporation of restraints from the experimental data into the existing structure modeling algorithms, software exclusively focusing on structure modeling based on the experimental data, such as the Integrative Modeling Platform (IMP),^43,44 has also been developed. In this Perspective, we highlight many different ways that the experimental data have been incorporated into protein tertiary structure prediction, protein–protein docking, and MD. This Perspective will focus on methods that generate experimental restraints from cryo-EM, NMR, MS, EPR, SAXS, FRET, and genetic sequence data.

II. INTEGRATIVE MODELING: COMBINING EXPERIMENTAL DATA AND COMPUTATIONAL MODELING

A. Cryo-electron microscopy

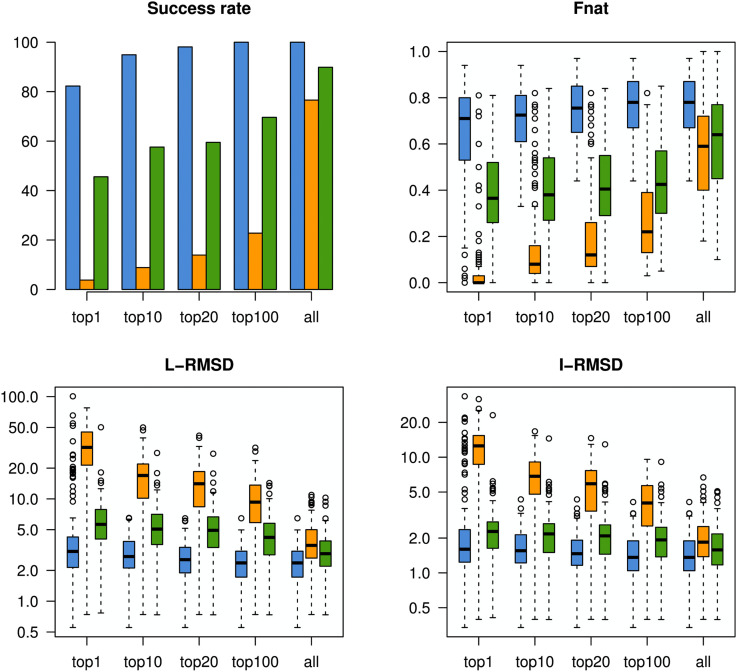
Cryo-EM is performed by rapidly freezing an aqueous protein sample in a thin layer of vitreous ice and then analyzing the frozen sample with electron microscopy. From this analysis, 2D images of individual molecules in many different orientations can be obtained. After taking numerous measurements and obtaining thousands of 2D projections, a 3D density map of the protein can be reconstructed by combining projections of single particles in different rotational orientations. An example for GroEL, a homo 14-mer with D7 symmetry, is shown in Fig. 1(a): the 2D image on the left and density map on the right. However, the resolution of cryo-EM density maps can vary significantly (∼1.25 Å to >20 Å).^46,47 At low resolutions, the overall shape and topography can be observed. As the resolution increases to ∼5 Å to 7 Å, secondary structure elements such as alpha helices and beta sheets become visible, but side chains are not resolved until ∼3 Å or higher resolution is obtained. Recent years have seen a resolution revolution, where the number of high-resolution structures (and structures in general) deposited in the Electron Microscopy Data Bank (EMDB) has increased significantly.⁴⁸ For example, in as late as 2014, no maps with a resolution higher than 3 Å had yet been deposited in the EMDB, while in 2019 alone, 265 maps of such resolution were released. Over the same time frame, the total number of deposited maps has increased from 2725 to 11 363. Despite this success, high-resolution maps are not yet routinely obtained from cryo-EM experiments, and thus, many medium- to low-resolution density maps are available for modeling. Over the years, numerous computational methods have been developed to model the structure of proteins based on these density maps.⁴⁹ In a recent protein–protein docking study, it was shown that the information contained in even very low-resolution density maps (∼20 Å) was more useful for integrative modeling than contact or interface information.⁵⁰ Results from this study showing the effectiveness of the different types of information for modeling are shown in Fig. 2. In this Perspective, we will focus on computational methods that use density maps for rigid fitting, flexible fitting (refinement), and de novo modeling. However, it is important to point out that the sophisticated computational algorithms have been developed to construct 3D structures from the obtained 2D projections.^51–53 Additionally, methods have also been developed to identify secondary structural elements (SSEs) from a density map (of which many modeling methods take advantage).^54–58

FIG. 2.

Comparison of the utility of different types of information (green: contacts; orange: interface; and blue: EM density) for protein–protein docking. Docking results for a benchmark set of 162 complexes were evaluated based on the success rate (percentages of cases with a good model in the top N = 1, 10, 20, 100, or all), Fnat (fraction of native contacts), L-RMSD (ligand RMSD), and I-RMSD (interface RMSD). For all metrics, information on EM density was the most beneficial for integrative modeling. Reprinted with permission from de Vries et al., Biophys. J. 110(4), 785–797 (2016). Copyright 2016 Cell Press.

The original computational methods developed to model the structure based on cryo-EM density maps were rigid fitting methods. Rigid fitting methods attempt to place previously obtained high-resolution structures into density maps without altering the tertiary structures. One of the first algorithms to perform rigid fitting was Situs.⁵⁹ This method uses an exhaustive docking approach to sample all possible conformations. Other examples of rigid fitting methods have been developed based on rotational/translational search (EMfit),⁶⁰ fast Fourier transform,^61–63 grid-threading Monte Carlo,⁶⁴ spherical harmonics for rotational sampling (ADP_EM),⁶⁵ and geometric hashing (BCL::EM-Fit).⁶⁶ While rigid fitting methods are often used with tertiary structures obtained experimentally, generated homology models of monomers have been built into complexes using rigid modeling.⁶⁷

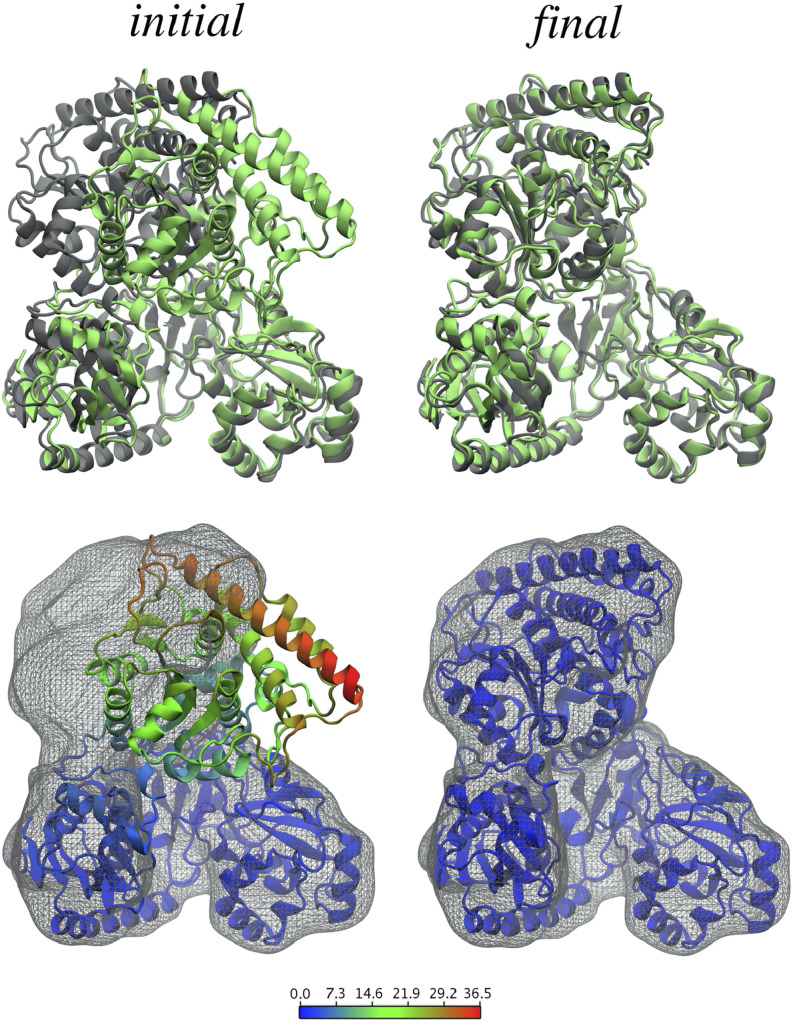
Flexible fitting methods, which perform fitting into density maps, while allowing changes in tertiary structure, have since become more common as structure refinement tools. One branch of these methods uses molecular dynamics simulations to sample structures while using the well-established MD force fields combined with cryo-EM density maps to energetically guide the sampling. The molecular dynamics flexible fitting (MDFF,^68,69 using NAMD) method was developed to guide the structures of biomolecules toward density maps by including a density map-based potential function. MDFF has been shown to be very robust as it can also be performed on membrane proteins,⁷⁰ it can include additional symmetry restraints,⁷¹ and further advances have been made such that it can be used with a wide range of resolutions (even down to sub-5 Å).^72,73 An example of the drastic improvement in terms of agreement with a density map that can be obtained using MDFF is shown in Fig. 3. A similar approach to flexible fitting has been performed using Amber, where the potential was based on cross correlation between the density map and the structure.⁷⁴ In addition to all-atom modeling, a coarse-grained, Gō-model (which translated the initial structure to C-α positions and native potentials between the C-α’s) has been used to simulate proteins based on density maps.⁷⁵ Finally, REMDFit that increases conformational fitting trials with a variety of different force constants has been developed.⁷⁶

FIG. 3.

Improvement in fit to the density map using MDFF for acethyl-CaA synthase. Target structures and simulated density maps are shown in gray, and the initial and fitted structures are shown in green (top) and colored by backbone RMSD (Å) per residue (bottom). After MDFF, there was a significant improvement both in density map fit and RMSD. Reprinted with permission from Trabuco et al., Structure 16(5), 673–683 (2008). Copyright 2008 Cell Press.

As an alternative to using MD to sample conformations for EM-based structure refinement, and to possibly obtain more diverse backbone sampling, normal mode analysis (NMA) can also be used. In NMA, backbones are sampled by perturbing the structure along normal modes, collective motions where bonds vibrate with the same phase and frequency.⁷⁷ Methods have been developed to use NMA to distort the structure away from its starting state and toward agreement with the density map. In order to probe more physically realistic deformations, NMFF-EM only considers low-energy motions of the protein to guide the structure toward the low-resolution density maps.^78,79 Rather than excluding high-energy normal modes, iMODFIT uses all normal modes for its coarse-grained density map fitting.⁸⁰ Because of this, a larger range of conformations can be sampled including large scale conformational changes. Similarly to NMFF-EM, iMODFIT samples only the low frequency vibrations and can efficiently sample using internal coordinates.⁸¹

In addition to cryo-EM-based flexible fitting with MD and NMA, structure refinement can also be performed using Rosetta.⁸² The density-based refinement performs particularly well on high-resolution density maps (<4.5 Å). In short, segments (fragments) of the protein are optimized within the density map by first rigid body minimizing, then optimizing the side chain rotamers, and finally minimizing torsions with the inclusion of density agreement into the force field. A similar, automated approach can be used to refine models of complexes into large density maps.⁸³ Additionally, exploiting the orthogonality of the force fields, MDFF has been successfully combined iteratively with Rosetta to refine the structures of both soluble and membrane proteins based on cryo-EM density maps.^84–87 By iterating between the two cryo-EM structure refinement protocols, these methods have been successful in reducing the RMSD (root-mean-square deviation) to the native model beginning with models at about 5 Å RMSD.

While flexible fitting into EM density maps can be very advantageous, obtaining the starting structure for the modeling can, of course, be a challenge. For this reason, de novo methods have been developed to essentially predict the structures based on the sequence and the cryo-EM density maps. The first such method, EM-Fold, was originally designed to predict folds of proteins using medium-resolution density maps (∼5 Å to 10 Å, where density rods corresponding to secondary structure elements are visually identifiable).^88,89 The method fits secondary structure elements (identified from the sequence by secondary structure prediction methods) into manually identified density rods in the density map. After using a Monte Carlo search algorithm for rod placement, Rosetta is used to build in the missing side chains and loops. EM-Fold has been applied to predict the structures of multiple large proteins (up to ∼400 residues) within cryo-EM density maps.^90,91 Another tool, Gorgon, can be used to build de novo models using density maps in the range of 3.5–10 Å resolution.⁹² Gorgon uses a feature detection tool, SSEHunter,⁵⁴ to identify the secondary structure in the density maps and builds coarse-grained models using geometric modeling techniques. In addition to structure refinement based on density maps, Rosetta can also model structures de novo using maps at high resolutions (3 Å–5 Å).^93,94 Rosetta uses its fragment assembly Monte Carlo simulated annealing method to sample backbone conformations but chooses fragments that agree best with the density map based on a scoring function. After iterating between model generation and fragment scoring, density-guided refinement is performed on the best models. Along with proteins, RNA can be modeled into density maps in Rosetta as well.⁹⁵ Pathwalking (part of the EMAN package) uses a very different approach to de novo modeling with cryo-EM density maps using the traveling salesman problem as an inspiration.^96–98 Pathwalking essentially determines a valid path of C-α atoms through the density map for a given number of residues, which then need to be refined, and a specific sequence needs to be mapped onto the structure. Along with its other modeling tools for cryo-EM and x-ray crystallography, Phenix can be used to model structures de novo into high-resolution density maps through its phenix.map_to_model tool with the goal of automatically mapping the structure using a strategy similar to an experienced biochemist’s intuition.^99,100 In short, the method looks for regions of strong density to place secondary structures and subsequently branches out from the strongest density backbone region to place the side chains. Finally, all-atom refinement is performed. Another de novo modeling method, MAINMAST, outputs multiple models with confidence scores.^101,102 The method first identifies points of high density and connects them into a minimum spanning tree, which is subsequently refined into essentially a C-α model. Finally, the top models are converted to all-atom and further refined using MDFF. In addition to full-sequence structural modeling, individual fragments of a protein can be modeled into a cryo-EM density map using FragFit, which searches the PDB for similar sequences of the fragment and models the structure of that fragment into the overall structure of the protein based on the density map.¹⁰³ While machine learning techniques have previously been used in the cryo-EM modeling pipeline (picking of 2D single particle images^104–110 and SSE identification from density maps^55–58), it has recently been used for de novo modeling.¹¹¹ Using a deep learning approach that included three cascaded convolutional neural networks, a method has been developed to produce confidence maps for major components of the structure (such as SSEs, backbone, and C-α locations). This has been further converted into backbone traces, and then, the sequence is mapped onto the trace to obtain full atomic structures. In the spirit of blind competitions, EMDataResource has organized modeling competitions using cryo-EM density maps.¹¹² In the most recent competition in 2019, 13 groups predicted structures for 4 high-resolution density maps (1.8 Å–3.1 Å), many of which were very accurate. Future model challenges are expected to expand to medium-resolution (3 Å–4 Å) maps of more complicated systems.

In addition to cryo-EM-guided de novo modeling (effectively from the sequence), protein–protein docking has also been performed using ATTRACT-EM, docking with very low-resolution (∼20 Å) density maps.¹¹³ Starting from the structures of the monomers, ATTRACT-EM assembles many starting structures and restrains the further refinement based on symmetry and the agreement with the density map, with final models being refined further. In the Integrative Modeling Platform (IMP), a Bayesian scoring function to quantify the agreement between structures and density maps has been developed.¹¹⁴ The input to this integrative modeling is the structures of the monomers. From these structures, monomers are fitted into their portions of the density maps, and they are assembled into complexes using Monte Carlo replica exchange. Importantly, the scoring function includes prior information, such as how well the monomer agreed with their portions of the density map.

Cryo-EM is certainly one of the fastest growing techniques in protein structure determination. Modeling approaches are used for both high- and low-resolution density maps obtained from cryo-EM to study many different systems involving proteins and protein complexes. For cryo-EM, the biggest challenge is dealing with heterogeneous and dynamic systems where multiple conformations may blur the overall density map. Moving forward, cryo-EM will likely become the prime structure determination method, elucidating protein structures for many systems that have long evaded traditional techniques such as x-ray crystallography and NMR.

B. Nuclear magnetic resonance spectroscopy

As previously mentioned, solution NMR can be used to uniquely determine the 3D structure for some small protein systems. However, doing so requires the collection of a full set of structure determination data from a variety of different NMR experiments. Depending on the experiment, prior to collecting data, the proteins need to be expressed in isotopically labeled media using NMR active ¹³C and/or ¹⁵N isotopes. Optimizing the expression medium and conditions to produce large amounts of sample is incredibly expensive and challenging due to the inherent cost of isotopically labeled materials. While the specific experiments performed to determine the protein structure with NMR can vary, typically, this requires assigning the peaks of the 2D HSQC (heteronuclear single quantum coherence) spectra in order to determine the sequence positions of observed amide chemical shifts and then performing 2D NOESY (nuclear Overhauser effect spectroscopy) experiments to determine which atoms are close in space, as well as some other experiments to determine additional restraints. Assigning the backbone peaks of the HQSC spectra can be very time consuming and expensive, requiring multiple separate experiments [such as 3D HNCACB and 3D CBCA(CO)NH] which require days to weeks of data collection for each. In addition, because of the continuous data collection time necessary for these experiments, the proteins must be very stable in solution. Once enough distance restraints from NOESY as well as additional restraints such as dihedral angles and inter-nuclei vector orientation are defined (such that the restraints are abundant and not sparse), an ensemble of structures can nearly unambiguously be determined using simulated annealing. Despite the successes of the technique, typically, a full set of restraints can only be determined for small proteins (although there are some exceptions with more advanced techniques). Even then, the data collection and analysis can be very expensive and time consuming (typically months to years and thousands of dollars). However, some useful structural restraints can be determined from NMR experiments on a larger variety of systems without performing a full set of structure determination experiments, saving time and money. In this Perspective, we will highlight computational methods that can incorporate sparse data from NMR into protein structure prediction and modeling.

The restraints derived from sparse NMR data that are used for structural modeling most commonly come in three forms: chemical shifts (CSs), distance restraints from NOE, and orientational restraints from residual dipolar coupling (RDC), as displayed in Fig. 1(b). Chemical shifts provide information on the local environment for specific atoms, which has been incorporated into modeling in multiple different ways, but, in general, tools are used to predict CSs from the structure,^115–118 which can then be compared to CS values derived from the experiment. NOE is a relaxation technique, where the basic idea is to alter the spin on one nucleus and measure the effect that has on a different nucleus. Because the intensity of the measurement is dependent on the distance between two atoms, NOE can provide through-space distance restraints for atoms that are within approximately 5 Å. While NOE is an important part of full structure determination from NMR as described above, often, sparse amounts of these restraints can be measured and input into computational modeling methods. Finally, RDC arises when proteins in solution align to the magnetic field, facilitated by the alignment medium. When this happens, the amount of dipolar coupling observed is dependent on the angle between the inter-nuclei vector and the magnitude of the magnetic field. These measurements can provide orientational restraints for computational modeling as RDCs can be predicted from the structure and compared to the experiment.¹¹⁹ In addition to using these sparse data for structural modeling (i.e., using them as restraints in structure prediction and simulations, which will be the focus of the rest of this section), NMR data have also been used to parameterize^120,121 and evaluate^122–126 molecular mechanics force fields.

Chemical shifts, which are obtained in the early stages of any NMR structure determination protocol as previously described, can be used to guide protein structure prediction as they encode information about local environments. Many of the CS-based structure prediction methods use tools such as TALOS, which can be used to predict secondary structure or torsion angles from CS.^127–129 One of the first methods to incorporate chemical shifts into structure prediction was CHESHIRE.¹³⁰ In CHESHIRE, the secondary structures are predicted based on both sequence and chemical shifts, which are then used to predict backbone torsion angles. These torsion angles are subsequently used to select fragments from the PDB, which are then used for Monte Carlo fragment insertion. While these fragments are typically selected based on the local sequence similarity for ab initio modeling, choosing them based on CS data ensures that the fragments have backbones that are more native-like. In a benchmark, CHESHIRE predicted native-like structures for 11 proteins with up to 123 residues. A similar approach is taken in CS-Rosetta.^131–133 When Rosetta performs Monte Carlo simulations to sample the protein structure, it does so by inserting backbone angles of fragments obtained from the PDB. Similar to CHESHIRE, CS-Rosetta includes a CS-based bias into the fragment selection in order to select fragments with a similar local environment as well as a sequence. The difference is that CS-Rosetta’s fragment selection is performed by directly comparing experimental CS to predicted CS for fragments in the PDB (rather than first predicting bb torsions and then using that to select fragments). This method has been shown to be successful even when only sparse chemical shift assignments are available. While CS-based de novo methods such as CS-Rosetta and CHESHIRE have been successful, they are typically only viable for smaller proteins (up to ∼125 residues). To overcome this size limitation, CS data can also be incorporated into homology modeling for proteins with the available homologs. In Rosetta, this has been done by using the CS data to identify homologs of the target sequence and to align it to templates (alignment method called POMONA), with RosettaCM used for the homology modeling (CS-RosettaCM).¹³⁴ In a benchmark (proteins between 100 and 400 residues), the method predicted accurate structures (<2.5 Å) in 15/16 cases. In addition to tertiary structure prediction, CS values can be used to predict elements of the secondary structure, which could be additionally helpful for modeling. MICS was developed to do this and used a neural network to develop a model that can accurately predict the locations of helix capping and β-turn motifs as they are inherently dependent on the local environment and thus chemical shifts.¹³⁵

Distance restraints from NOE can be incredibly useful because one of the most difficult aspects of computational structure prediction methods is to correctly identify contacts that are close in space but far in sequence. For example, this is one of the reasons why the structures of proteins with high beta sheet content are often more difficult to predict. One of the first computational methods to illustrate the usefulness of NOE restraints into structure prediction was RosettaNMR.¹³⁶ The developed approach was to alter the scoring function to take into account the sparse NOE restraints (∼1 per residue). Another method that was developed to use NOE restraints for structure prediction is TOUCHSTONEX.^137,138 This method uses a coarse-grained approach where proteins are represented by C-α, C-β, and side chain center of mass and an energy function that includes a pairwise energy term that is dependent on the NOE-derived atom–atom distances. Additionally, NOE restraints have been incorporated into I-TASSER (I-TASSER-NMR).¹³⁹ In this approach, a scoring function is used to not only evaluate distance restraints for a single pair of atoms at a time but also to include the probability that the NOE restraint could be assigned to a different pair.

Furthermore, RDCs can be used in protein structure modeling, providing information on the inter-nuclei vector orientations. RDC’s were incorporated into RosettaNMR by including an additional score term with the Rosetta scoring function that quantified the agreement between predicted¹¹⁹ and experimental RDC’s.¹⁴⁰ Another method, REDCRAFT, has also been developed to model structures using RDC data.¹⁴¹ In this method, RDC fitness for each pairwise residue–residue interaction is ranked and the structure is built up one residue at a time based on this RDC agreement. While RDC data provide useful information to include into structure prediction, RDC’s are not typically used as the exclusive NMR restraint for structure prediction.

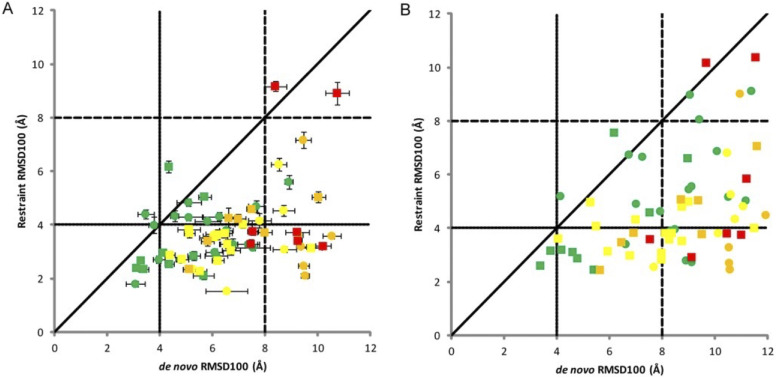
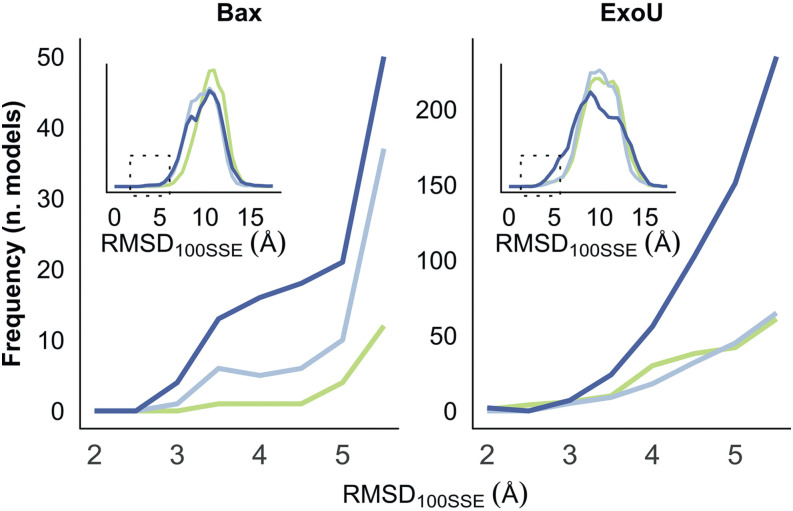
Because they can provide different types of orthogonal information and are sometimes collected at the same time, incomplete sets of CS, NOE, and RDC can be even more beneficial to structure prediction when used together. Even unassigned NMR data of the three types have been shown to effectively predict accurate structures using Rosetta.¹⁴² After initial structure generation, a Monte Carlo method was used to search for assignments that best match the data and structures. This method was able to identify correct folds in all cases, and refinement was able to identify high-resolution models in some cases. As integrative modeling has become more popular and strategies have been developed to model structures with NMR data, many methods now commonly incorporate multiple types of sparse NMR data into their structure prediction methods. CS, NOE, and RDC data have been used to build complexes in Rosetta from the sequence.¹⁴³ This strategy is to use CS data to build monomers (CS-Rosetta) as previously described and dock them together with the NOE interface and RDC restraints to predict the accurate structures of homodimers. In this method, the RDC restraints were incorporated by quantifying the deviation of predicted and experimental RDC as a scoring function into docking. Another method, MFR (molecular fragment replacement) also uses NMR restraints from CS, NOE, and RDC to produce backbone models of a protein.¹⁴⁴ In this method, backbone data (CS and RDC) are used to select fragments, and RDC and optionally NOE are used during the fragment assembly process. The biggest benefit of this method is the speed. Additionally, CS, NOE, and RDC data can be used for coarse-grained modeling in BCL::Fold and BCL::MP-Fold.^145,146 In a benchmark which included dozens of small proteins and some very large (6 with more than 220 residues), the correct protein fold was sampled in 65/67 cases. Figure 4 shows the improvement of sampling when NMR restraints were included. Again in Rosetta, a combination of NOE and RDC restraints was used to predict structures in CASP13.¹⁴⁷ In this method, low-resolution models were produced using NOE distance restraints and RosettaCM was used to refine based on NOE and RDC restraints. In the blind test set, more than half of the proteins were predicted with a RMSD of less than 3.5 Å.

FIG. 4.

NMR restraints improved native-like sampling in BCL. Each point signifies one protein. Points are colored based on size (green: <150 residues; yellow: ≥150 and <250 residues; orange: ≥250 and <400 residues; and red: ≥400 residues) and shaped based on type (circle: soluble and square: membrane). (a) The mean RMSD100 with error bars of ±1 SD of the top 10 models with (y-axis) and without (x-axis) NMR restraints. (b) The RMSD100 of the top model with and without NMR restraints. Reprinted with permission from Weiner et al., Proteins 82(4), 587–595 (2014). Copyright 2014 John Wiley and Sons.

While the most common types of NMR data used for modeling are CS, NOE, and RDC, other types of sparse data have been used for structure prediction as well. For example, paramagnetic restraints from NMR have also been used for structure prediction with RosettaNMR.¹⁴⁸ As a supplement to the CS and NOE data, paramagnetic relaxation enhancements (interactions between nuclear spins and paramagnetic metals or nitroxide spin-labels) can provide long distance restraints (up to 40 Å, compared to ∼5 Å for NOE). Similar to RDC, orientational restraints from pseudocontact shifts (PCS) can be obtained and used for modeling in RosettaNMR. In a large benchmark (of both structure prediction and docking), both overall sampling and the RMSD of the predicted structure improved when the paramagnetic NMR data were included. While NMR is typically performed in the solution state for protein structural characterization, restraints can also be derived from solid-state NMR. Some examples include magic-angle-spinning assignments,¹⁴⁹ distance restraints,¹⁴⁹ and angular restraints.¹⁵⁰

In addition to structure prediction, NMR-based restraints can be incorporated into molecular dynamics simulations (outside of the use of MD to refine high-resolution structures). These simulations are typically used for structure refinement, with the goal of sampling a structure or an ensemble of structures that is in good agreement with both the experimental data and the molecular mechanics force field. The restraints can sometimes be used for long MD simulations as well. As early as the mid-1990s, distance restraints from NOE were incorporated into MD simulations using GROMOS, showing the proof of principle of such methods.¹⁵¹ Furthermore, restraints from CS, RDC, and/or NOE were incorporated into MD simulations using GROMACS,^152,153 Amber,¹⁵⁴ and ALMOST.¹⁵⁵ Regardless of the MD platform, PLUMED is another useful tool for incorporating restraints into MD simulations.^156,157 The strength of PLUMED is its versatility as it can not only be used with several different MD packages (such as NAMD, Amber, and GROMACS) but can moreover be utilized to incorporate many different types of restraints. While it can be used to incorporate experimental data-based restraints, in general, it is commonly used for NMR-restrained simulations. An example application of PLUMED is to incorporate chemical shifts into MD simulations as collective variables (based on the difference between predicted and experimental CS) to guide the simulations toward agreement with the experimental data without explicitly altering the force field.¹⁵⁸ In another example, PLUMED was incorporated into cryo-EM- and CS-based structure refinement with Rosetta and MD.⁸⁷ For heterogeneous systems (such as disordered proteins), PLUMED-ISDB¹⁵⁹ (integrative structural and dynamic biology) can be used to determine an ensemble of structures based on ensemble-averaged and noisy experimental data using a Bayesian, metainference approach. While it can be used with multiple types of experimental data, NMR data such as CS, J-couplings, and RDC are commonly used.^160,161

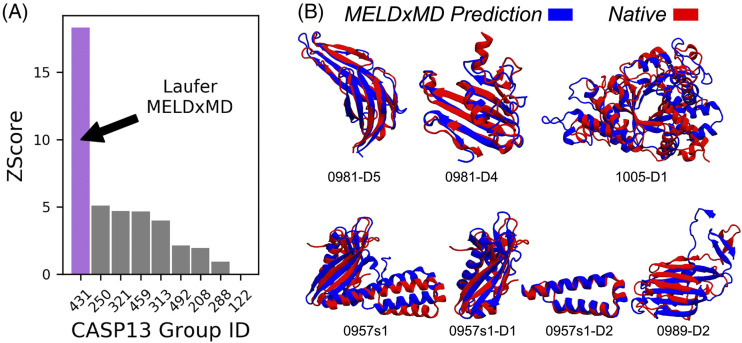
MELD (Modeling Employing Limited Data) takes a slightly different approach for structural modeling with the experimental data.^8,162 Like PLUMED, it can, in principle, take multiple different types of experimental data but was specifically designed to be used with general experimental data that are very sparse and sometimes incorrect. In order to account for the fact that some of the data may be missing or incorrect, MELD uses a Bayesian scoring function, where the Amber force field is used to evaluate the prior probability and the experimental data are used to evaluate the likelihood probability. The likelihood and prior probabilities are combined to define the scoring function using OpenMM for sampling. The innovation in MELD is to exclude the weakest restraints from the energy evaluation, which are determined to be unreliable. For example, in the incorporation of both NMR and EPR restraints, it was determined that 65% of the data were reliable and thus included into the scoring function. In a benchmark, MELD generated structures with low RMSD (less than 2.5 Å) for the majority of tested cases. In the NMR data category in CASP13, MELDxMD was the best structure prediction method (results shown in Fig. 5), illustrating the success of the approach.

FIG. 5.

MELDxMD was the highest ranked group in NMR data-assisted CASP13 (2018). (a) MELDxMD (431) had the highest Z-score in the category. (b) Predicted structures for CASP targets are shown with reference to the native structures. Five of these predicted structures were best in CASP. Reprinted with permission from Robertson et al., Proteins 87(12), 1333–1340 (2019). Copyright 2019 John Wiley and Sons.

We have highlighted many different techniques that can be used with NMR to obtain structural and dynamic information on both ordered and disordered protein systems. While size limitation remains a significant challenge, the large amount of information (such as distances/contacts and local environment) that can be provided by NMR data has made it one of the most popular tools for structure elucidation and integrative modeling.

C. Mass spectrometry

In recent years, mass spectrometry (MS) has become an increasingly popular tool to study proteins and protein complexes due to some important advances starting in the late 1980s. The initial problem with using MS on proteins and peptides was the need to softly ionize the molecules into the gas phase for analysis in order to preserve their covalent bonds or even structures. Until the invention of soft ionization techniques such as electrospray ionization (ESI)¹⁶³ and matrix-assisted laser desorption/ionization (MALDI),¹⁶⁴ this was not possible. These inventions sparked the development of new mass analyzers and ultimately techniques to determine structural information on proteins. These techniques can be broken down into two categories: bottom-up and top-down. In bottom-up MS, proteins are enzymatically digested into small peptides and these peptides are separated and analyzed using tandem MS (MS/MS). Alternatively, in top-down MS, intact proteins are separated and ion-trapped using tandem MS. Many pre-MS ion activation or chemical modification methods have been developed to infer structural information from MS experiments.

Ultimately, MS can be used to measure the mass-to-charge ratio of a molecule. While this information is useful for an entire protein (especially when analyzing complex mixtures), structural information is gained by analysis of results after different pre-MS steps are performed. These pre-MS steps have been developed in order to encode structural information into the mass of the protein or protein fragments. Many of these methods have then been incorporated into computational pipelines to model protein structures. The MS-based methods highlighted in this Perspective are chemical cross-linking, covalent labeling (such as hydrogen–deuterium exchange and hydroxyl radical footprinting), ion mobility, and surface-induced dissociation. While the structural data obtained from these MS-based methods are not enough to fully elucidate the structure, MS does not suffer from many of the drawbacks of the typical structure determination methods. MS can handle complex mixtures, does not require crystallization, can be performed on both large and small systems (up to megadalton-sized complexes), and requires small amounts of sample (μl of sample at low μM concentrations). Finally, as will be described in Secs. II C 1–II C 4, the types of structural information that can be obtained from MS experiments are very diverse.

1. Chemical cross-linking

Chemical cross-linking (XL, CX, or CL) has been combined with MS (XL-MS) using a bottom-up approach. The general idea of the method is to chemically connect two atoms that are close in space, while the protein is in a native-like environment. In XL-MS, the native protein in solution is incubated with a bifunctional cross-linking reagent, as depicted in Fig. 1(c). After cross-linking, the proteins are enzymatically digested into smaller peptide fragments, cleaving some peptide bonds, but keeping the newly created cross-links intact. The peptides are then separated and analyzed by liquid chromatography and tandem MS. If the sequence location of the cross-links can be determined from the peptides, this analysis provides information about which residues are interacting (i.e., close in space), often across protein–protein interfaces. Based on the length of the cross-linking reagent (which can be up to about 35 Å depending on the reagent), distance restraints can be inferred and included in computational structure prediction algorithms.¹⁶⁵ Cross-linking information can be extremely beneficial for computational modeling because contacts that are close in space, but far in sequence, are generally hardest to predict.

Workflows have been developed in Rosetta to individually use the data from cross-linking experiments for de novo modeling, homology modeling, or protein–protein docking. These methods were first developed to use detected cross-linked residue distances as restraints in model generation as well as to filter models after structure generation.^166,167 Distance restraints from XL-MS have also been used with homology modeling using I-TASSER,¹⁶⁸ XLinkDB¹⁶⁹ [a combination of Modeller and PatchDock from the Integrative Modeling Platform (IMP)], and MD refinement.¹⁷⁰ Cross-linking data have been used to model the interaction between Psb27 and Photosystem II, combined with protein–protein docking.¹⁷¹ The top-ranked (without incorporating the XL) docked models did not match the XL data, so the data were necessary to properly model the structure. Additionally, software is available to detect cross-links such as Mass Spec Studio, which was validated based on its ability to improve protein–protein docking when used with available software.¹⁷² More recently, chemical cross-link data have been used to build full quaternary structures from the sequence using Rosetta.¹⁷³ This has been done by generating tertiary models using de novo or homology modeling and then docking those models to form the complex (all done without guiding the predictions with XL data). Next, the models were filtered based on the agreement between the number of cross-links observed and the lysine–lysine distances in the predicted models. Models that passed the filter were refined by docking at higher resolution and rescored based on lysine–lysine distances of experimentally observed cross-links and the Rosetta scoring function to select the predicted structures. In addition in Rosetta, flexible peptide docking has been performed using experimentally determined cross-links as filters to select good models.¹⁷⁴

Rather than simply using XL data as restraints, the importance of cross-link distance restraints being surface accessible (rather than through the protein) has furthermore been examined by calculating the surface accessible surface distance using Jwalk and using that in a scoring function to score homology models based on XL data.¹⁷⁵ In another study, a statistical XL-based potential based on distance calculations from the protein data bank was developed and incorporated into the Rosetta ab initio folding as a proof of principle.¹⁷⁶ This force field improved tertiary structure prediction by including the probability that cross-linked residues are surface accessible.

In addition to detecting if and where cross-links bind to generate distance restraints or use in a scoring function, it is possible to quantify the number of cross-links between two residues (quantitative chemical cross-linking). Based on the intensity of different cross-links, this type of analysis can give information on dynamics and can sometimes detect multiple conformations. It has been shown that multiple relevant protein conformations can be modeled based on cross-link intensity by combining xTract with docking.¹⁷⁷

2. Covalent labeling

While XL-MS methods gain insight into residue–residue distances, covalent labeling methods gain insight into solvent accessibility and flexibility. Covalent labeling (CL) reagents can bind to proteins in solution and thus chemically alter their masses (either irreversibly or reversibly). The structural hypothesis is that the reagents bind more favorably or more rapidly to residues that are more solvent-exposed and more flexible. The general workflow for covalent labeling MS (CL-MS) methods is to incubate the protein in solution with the labeling reagent for a certain period of time to allow the labeling reagents to bind to the protein. Then, the protein is enzymatically fragmented into peptides (bottom-up), which are separated and analyzed by tandem MS to determine the binding location of the labels within the sequence by detecting the change in mass (although it can sometimes be a challenge to determine the exact, residue-resolved locations since measurements are generally performed on peptides). Covalent labeling strategies can be employed in many different flavors (depending on the labeling reagent used) but can generally be broken down into specific and non-specific labeling methods. Specific covalent labeling reagents bind to particular amino acids or amino acid functional groups. Common methods are available to target arginine, carboxylic acids, cysteine, histidine, lysine, tryptophan, or tyrosine.¹⁷⁸ On the other hand, non-specific labeling reagents can label most or all of the amino acid types. The most commonly used non-specific labeling methods are hydroxyl radical footprinting (HRF) and hydrogen–deuterium exchange (HDX). While both types of covalent labeling can provide useful structural information, the use of non-specific methods to this point has been more successful in structural modeling since they provide more information by labeling more residue types; therefore, this Perspective will highlight methods that incorporate HDX and HRF into modeling. To make structural hypotheses, it is also important that covalent labels do not cause changes to the overall structure of the protein. However, this effect is minimal when small labels are used (such as with HDX and to a lesser extent HRF)¹⁷⁸ and also when the experiment is performed sufficiently fast [such as fast photochemical oxidation of proteins (FPOP)].¹⁷⁹ It has been shown using simulated CL data with noise that labeling the following residues provides the most useful information toward tertiary structure prediction because of their abundance in sequence: L, G, R, V, and S.¹⁸⁰

a. Hydrogen–deuterium exchange.

Hydrogen–deuterium exchange, a non-specific covalent labeling method, has been used for a long time to study biomolecules (since the 1930s for small systems) but has become very popular when combined with MS (HDX-MS). As the pre-MS, covalent labeling step, the protein is incubated in a D₂O buffer solution. In this solution, some hydrogens in the protein are able to exchange with deuterium, as shown in Fig. 1(c). After some time, the exchange is quenched and continued in the CL-MS pipeline, as previously described. This experiment is repeated for many different incubation times so that kinetics can be determined. Rate constants or protection factors derived from rate constants at each measured position are commonly reported in the literature. However, it is not uncommon to report percent deuteration incorporation of certain positions at certain time points. Because of fast back-exchange for side-chain hydrogens (after quench) and slow exchange for carbon-bound hydrogens (prior to quench), only the amount of exchange from backbone amide hydrogens is measured (starting at the third residue in each fragment). One major difficulty of HDX is to convert the data collected on peptides to the residue level, although many methods have been developed to facilitate this conversion.^181,182 For HDX to occur at a given position, it is particularly important that the amide hydrogens be both exposed and flexible (i.e., not participating in a hydrogen bond) in order to rapidly exchange because hydrogen-bonded hydrogens are much less likely to exchange with deuterium.

HDX data have been successfully incorporated with homology modeling to predict structures. In one study, using a two-step homology modeling strategy, where the sequence alignment was adjusted after the first step to better match the HDX data, the models were further evaluated based on solvent exposure.¹⁸³ Of the predicted models, the best model showed a strong correlation (R² = 0.94) between the backbone solvent-accessible surface area (SASA) and percent deuterium incorporation measured with HDX at the peptide level. This analysis leads to new mechanistic hypotheses for the system. In a different study, correlations between the number of deuterons and the backbone SASA for each peptide were used to analyze homology models of IκBε generated with two different templates (both with strong correlations).¹⁸⁴ The templates differed in length and the HDX analysis, showing a good correlation in the extended region, was used to justify an additional structured ankyrin repeat in the target.

In addition to homology modeling, HDX data have been successfully incorporated into protein–protein docking. Differential HDX (ΔHDX), performing HDX-MS experiments on the monomers separately and comparing to HDX of the complex, can provide useful information specifically on the location of the protein–protein interface. Interface residues are likely to exchange rapidly in the monomer but may exchange slower in the complex as they generally become more buried and less flexible upon binding. However, it is important to note that changes in non-interface residues upon binding (protection or deprotection) can also occur due to the general stabilization of the complex as well as allosteric effects. Figure 1(c) shows an example of the difference in deuteration that could occur in the unbound and bound forms. To demonstrate this, the hUNG-UGI complex was docked using DOT and outputs were filtered based on HDX data.¹⁸⁵ For peptides observed in both the monomer and the complex, the difference between the number of deuterons in the monomer and the complex was measured (this number indicates the number of backbone amide hydrogens at the interface). The filtering step required that the same number of residues in the fragment was within a 7 Å interaction distance of the other subunit and this part of the interface. This filtering was shown to enrich the number of native-like structures in the prediction. In another study, ΔHDX was used to help identify the binding interface between two partners and was combined with RosettaDock, which was also restrained using inter-subunit cross-links.¹⁸⁶ In addition to using HDX to identify the interface, models were evaluated based on SASA and HDX agreement, which resulted in a model with a RMSD of less than 2 Å. Similar analyses have been done with protein–ligand complexes.^{181,187–189}

Since HDX is a solution-based approach, it can provide information on the ensemble of structures present in the solution. Because of this, it is beneficial to use HDX data in conjunction with MD simulations. It has been shown that HDX data can discriminate between native and non-native folds from conformations generated in an MD simulation.¹⁹⁰ This was done by predicting the deuterium uptake based on near contacts and hydrogen bonds from the structures and comparing it to the experimental results. In addition to actually modeling HDX during MD simulations, the simulations themselves have been extensively used to better understand and predict the HDX results. For example, MD simulations have been used to predict the peptide-resolved HDX data based on solvent accessibility. These data were calculated over the simulation based on both residue SASA and whether the amide NH interacts with a water molecule. The predictions correlated well with the experimental results.^191,192 Numerous other methods have been developed that quantify some combination of hydrogen bonding, solvent accessibility, and RMSF (root-mean-square fluctuation).¹⁹³

b. Hydroxyl radical footprinting.

In contrast to HDX, HRF methods irreversibly alter the mass of the protein at certain positions. The strategy is to introduce hydroxyl radicals into solution to interact with the side chains of exposed residues. The resulting mass change is very dependent on the amino acid type, for example, the radical can abstract hydrogens from aliphatic residues or directly attack sulfur atoms or aromatic rings. Although there are many different ways to introduce the hydroxyl radicals (such as radiolysis of water with electrons, x rays, or gamma radiation, transition metal-dependent chemical reactions with peroxide, or high-voltage electrical discharge in water), one of the most common methods that has been used in structure prediction is through peroxide photolysis, called fast photochemical oxidation of proteins (FPOP). In FPOP, hydroxyl radicals are produced in situ by UV laser-based photolysis of hydrogen peroxide. The radicals then alter the mass of a broad range of amino acid types with different intrinsic reactivities that have been tabulated. Similarly to HDX, FPOP rate constants can be determined for each residue and from the rate constants, protection factors (intrinsic reactivity divided by rate constant) are generally derived. The structure-based hypothesis for this metric is that a higher protection factor should correlate with less solvent exposure due to the lack of accessibility of the radicals.

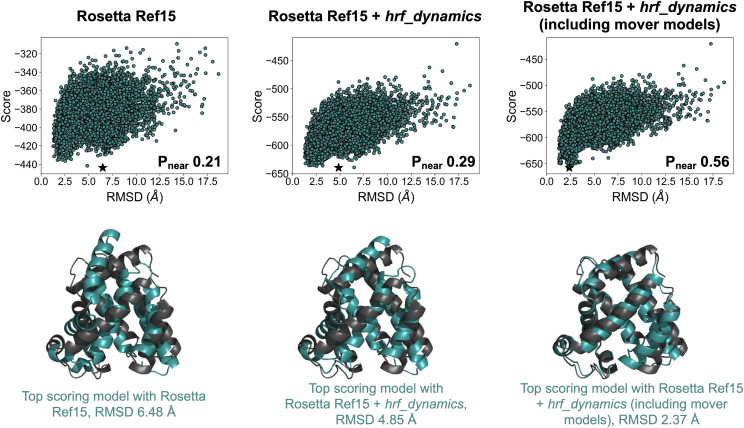
Based on this hypothesis, correlations between structure and FPOP data have been examined.¹⁹⁴ The average SASA derived from MD simulations normalized by the sequence context, calculated for residues with high and moderate hydroxyl radical reactivity, was shown to be strongly correlated with a normalized protection factor (PF). Analyzing the frames from unfolding simulations, this metric was able to discriminate well between native-like and non-native-like models based on RMSD. Furthermore, FPOP has been incorporated into a de novo tertiary structure prediction framework.¹⁹⁵ Based on an observed correlation between neighbor count, a surface-accessibility measure of the number of neighboring residues within a specific distance, and natural logarithm of PF, a model to predict FPOP data from structure was developed. This model was incorporated into an FPOP-quantifying scoring term, which was used to rescore models generated in Rosetta. Structure prediction was improved with the inclusion of FPOP data. Furthermore, accounting for side chain flexibility through MD and Rosetta movers has been shown to improve the observed correlation between residue exposure and experimental PF.¹⁹⁶ Incorporation of this improved correlation into a scoring function produced improvement in model selection for tertiary structure prediction as well. Extracting the top 20 scoring models and generating 30 additional structures for each using a combination of Rosetta movers chosen to boost side-chain sampling further improved the predicted structure in all cases. An example is shown in Fig. 6 for myoglobin. The selected model (based on score) improved from 6.48 Å (left) when no HRF data were included to 4.85 Å (middle) and when HRF data were included and further improved to 2.37 Å (right) when additional side-chain sampling was allowed using the mover models.

FIG. 6.

The inclusion of HRF data improved structure prediction for myoglobin. Top shows score vs RMSD plots and quality of funneling metric, P_near, for 20 000 ab initio models (top scoring model for each shown with a star). Bottom shows a comparison of top scoring model (cyan) to the crystal structure (gray). Results are shown for when no HRF data were included (left), when hrf_dynamics score was included (middle), and when hrf_dynamics score was included with further sampling using Rosetta movers for the top 20 models (right). Figure credit: Sarah Biehn.

3. Ion mobility

Ion mobility (IM), a top-down, native MS approach, provides structural information not on specific residues, but rather on the shape of the entire protein or protein complex. In IM, the entire native protein, rather than broken into peptides, is softly ionized in the gas phase and accelerated through a bath gas (commonly nitrogen or helium) and subsequently analyzed with MS. The velocity of each ion as it passes through the bath gas depends on its size and shape (as well as charge and other experimental factors), which can then be translated into a rotationally averaged collision cross-sectional area (CCS). Figure 1(c) illustrates this separation, showing smaller ions moving faster through the bath gas (left to right). This experimentally derived CCS can then be used for structural modeling. While there is a plethora of different computational methods to predict the experimentally measured CCS from the 3D coordinates of a protein, selecting the best method can be challenging because there is usually a tradeoff between accuracy and computation time. Briefly, some methods simply calculate the average projection area over multiple rotations of the protein [projection approximation (PA)^197,198 and exact hard-spheres scattering (EHSS)¹⁹⁹], while some also take gas–protein interaction energy and multiple gas–protein collisions into account [trajectory method (TJM),^200,201 diffuse trajectory method (DTM),²⁰² and projection superposition approximation (PSA)²⁰³]. Rather than predicting the CCS from a single structure, the structure relaxation approximation (SRA), a method to predict IM spectra from an ensemble of structures for a specific charge state, has been developed.²⁰⁴ The SRA uses short timescale molecular dynamics simulations to sample structures in the correct charge states and uses the predicted CCS values from the PSA of snapshots to predict the overall IM spectra.

IM CCS data have been incorporated into structure prediction of protein complexes using the IMP. In these studies, coarse-grained models of large complexes were generated in the IMP.^205,206 By applying a scoring function based on the agreement between predicted (PA) and experimental CCS, the candidate models were ranked and clustered to predict a native-like model. In a benchmark, the predicted coarse-grained structures were in good agreement with structures in the PDB. It is also possible to generate distance restraints between subunits in a complex using IM.²⁰⁷ For example, IMMS_modeler was developed (within the IMP) to further predict coarse-grained models of protein complexes using IM data and clustering. In this method, IM is used to determine the CCS, as described previously. Then, based on this CCS value, a radius for each individual subunit is determined (assuming a rough sphere shape). After performing the experiment on individual subunits as well as different subcomplexes, rough intersubunit distance restraints were determined and input into the modeling method. This method was successful in identifying coarse-grained topologies of complexes.^208–210

In addition to predicting the structures of complexes, some work has been done toward incorporating CCS biasing into MD simulations. By using a simplified, but very fast model for CCS prediction that is based on the radius of gyration (developed based on the correlation between the radius of gyration and the predicted CCS using EHSS) combined with MD, it has been shown that unfolding of a protein can be modeled based on the CCS.²¹¹ Such a method has many potential future uses such as structurally modeling or calculating the free energy change between collision-induced unfolding and transitions between conformations.

4. Surface-induced dissociation

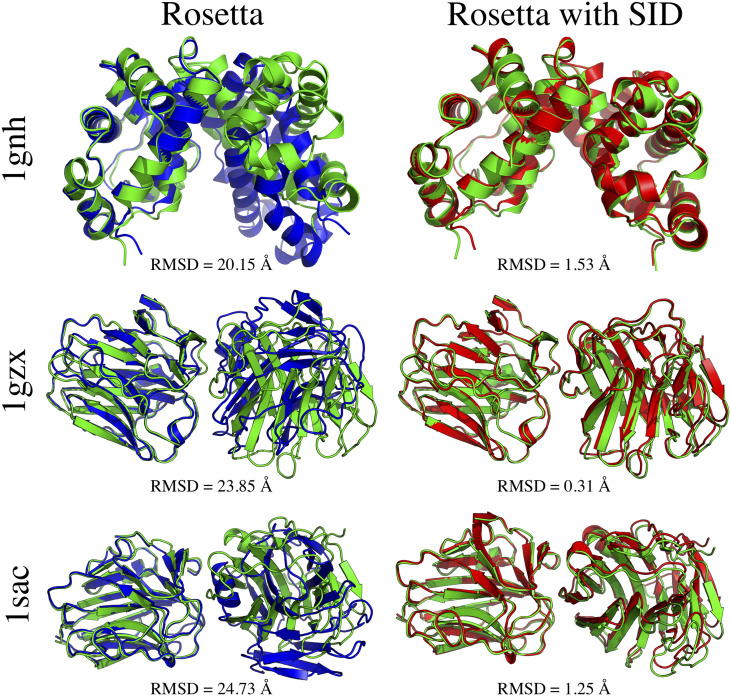
While surface-induced dissociation (SID) has been around for a while (originally used on small molecules and peptides), because of the advances of MS technology, it has recently become a viable method to study the structures of protein complexes.^212–215 Similar to IM, in the top-down (native MS) SID approach, whole protein complexes are softly ionized into the gas phase. Using some amount of applied voltage, they are then collided with a rigid surface, where they can break apart into intact monomers or smaller subcomplexes; an example of possible breakages is shown in Fig. 1(c) for a homotetramer. The resulting proteins are then analyzed using MS to determine the relative intensity of each product. The dissociation pattern depends on the lab-frame energy (acceleration energy) of the complex, provided thorough the applied voltage. The experiment is repeated multiple times with different acceleration energies. While SID is frequently used to determine connectivity and stoichiometry of protein complexes,^216–218 it has recently been shown that it can also measure a form of interface strength.²¹⁹ It was hypothesized that weaker interfaces would break at lower acceleration energies, while stronger interfaces would stay intact until a high enough acceleration energy was provided. Based on this, a quantitative measure called appearance energy (AE, lab-frame acceleration energy at which the subcomplexes resulting from the breakage of a specific interface reach 10% of the relative intensity of the original complex) was developed. A model to predict AE from the structure was developed, which was based on interface properties such as size and hydrogen bonding.²¹⁹ Based on this model, a scoring function was developed to quantify the agreement between the experimental and predicted AE for each docked pose. The inclusion of SID data into the Rosetta scoring function improved the ranking of docked poses and ultimately improved the predicted structures obtained from docking.²²⁰ The structures of three cases where RMSD improved by more than 18 Å when SID data were included are shown in Fig. 7.

FIG. 7.

Comparison of predicted subcomplexes with (left, blue) and without (right, red) the inclusion of SID data into protein–protein docking. The native structures are shown for reference (green). RMSD (Å) to the mobile chain is shown. RMSD improved by >18 Å when SID data were included for these cases. Reprinted with permission from Seffernick et al., ACS Cent. Sci. 5(8), 1330–1341 (2019). Copyright 2019 American Chemical Society (ACS). Further permissions related to the material excerpted should be directed to the ACS.

While in its infancy compared to other methods, mass spectrometry has grown in popularity in terms of providing useful information about the protein structure. While further developments need to be made for MS to establish itself as a pillar of structure determination, it has become a prime method for the collection of sparse data (with small amounts of sample), which contain information of many types (such as distances and solvent accessibility). As MS methods become more widely commercialized and used, and the data become better understood, MS may develop into one of the most important tools for structure elucidation.

D. Electron paramagnetic resonance spectroscopy

Similar to NOE with NMR, electron paramagnetic resonance (EPR) spectroscopy can be used to determine distances between atoms, often measured through site-directed spin labeling (SDSL-EPR). To do this, specific residues are mutated to cysteine and labeled with a paramagnetic spin label (typically nitroxide), as shown in Fig. 1(d). Similar to NMR NOE, the measurement of the magnetic dipolar interaction depends on the strength of the magnetic field and the distance between the two probes, with the difference being that NMR depends on the spin of nuclei and EPR depends on the spin of electrons. Originally, this technique could be used to measure medium- to long-range distances between probes (∼8 Å to 20 Å), but the development of pulse EPR methods such as double quantum coherence (DQC) and double electron–electron resonance (DEER) has increased the measurable distance range to ∼20 Å to 80 Å. This increased range has made it possible to probe a larger number of interactions and thus obtain more data. This is particularly significant because to use EPR data in structure prediction, the locations of the labels are often scanned over to determine many distance restraints. While in this Perspective, we will mainly focus on structure modeling methods, these distance measurements have also been used to identify the secondary structure of alpha helices^221,222 and beta sheets.^223,224 By systematically scanning the placement of paramagnetic probes, the distances between residues that are close in sequence can be compared to canonical distances between residues in helices and sheets, which are well established. Additionally, conformational changes can be detected using EPR based on measured distances.^225–227 Along with measuring distances, it is possible to measure the accessibility of the spin label probe which can give some information about solvent accessibility at that position.²²⁸

In Rosetta, restraints from EPR have been used for de novo structure prediction using both distance and solvent accessibility information from EPR experiments.²²⁹ Importantly, because the paramagnetic portion of the spin labels does not occur at the location of any atom in the protein, a technique to properly model the location was necessary. For this, in Rosetta, a cone centered at the C-β position was used to map the possible locations of the electron with respect to an actual atom in the protein, as shown in Fig. 1(d). In the original implementation, these locations and the measured distances of the interaction of spin labels were used to generate restraints for the scoring function using the same scoring function as RosettaNMR uses for NMR NOE distance restraints. To account for the solvent accessibility portion, a correlation was observed between spin-label accessibility and the number of C-β neighbors within 8 Å (negative correlation: higher accessibility corresponds to higher solvent exposure, which means fewer C-β neighbors). It was shown that fewer than one restraint per four residues was needed to accurately predict structures. An updated version (RosettaEPR) used a statistical, knowledge-based potential along with the positions on the cone to influence the scoring method for the distance portion.²³⁰ Currently, rotamers of spin labels (such as methanethiosulfonate spin label) can be used to explicitly model the distances between the backbone and the relevant electron.²³¹ Using the approach with the knowledge-based cone potential, large membrane proteins can be modeled using BCL::MP-Fold, including the EPR terms into the Monte Carlo SSE assembly.²³² The use of EPR data enriched the sampling with native-like structures. A similar approach has also been used in BCL::Fold to assemble the structures of large soluble proteins (up to 200 residues). The use of EPR data improved the RMSD of the predicted structure.²³³ As mentioned in Sec. II B, EPR distance restraints have been incorporated into MELD (along with NMR NOE).⁸ More recently, RosettaDEER has been developed as a scoring method for structure prediction.²³⁴ In this method, the scoring function explicitly predicts the DEER decay traces and spin-label distance distributions fast enough for on-the-fly calculation. RosettaDEER improves on the cone-based scoring function as it includes more information from the experiment. RosettaDEER showed a significant improvement in sampling as compared both to the cone-based method and to when no experimental data were used, as shown in Fig. 8.

FIG. 8.

Comparison of sampling for Bax and ExoU de novo folding using DEER data to predict structures. RosettaDEER showed improvement in sampling over the previous cone method and when no EPR restraints were included. Reprinted with permission from Del Alamo et al., Biophys. J. 118(2), 366–375 (2020). Copyright 2020 Cell Press.

Along with structure prediction, EPR data can be included in molecular dynamics simulations. Tools have been developed in CHARMM-GUI (DEER Facilitator) not only to measure the distribution of spin-pair distances from a simulation (Spin-Pair Distributor) but also to include distance restraints from EPR into a simulation (reMD Prepper).²³⁵ This is done by explicitly modeling the rotamers of the spin labels. Comparison of distance distributions from experiment and simulation has been shown to be in excellent agreement.

EPR has been around for a while and has contributed meaningful structural information (such as distances and solvent accessibility) for many systems. However, the uncertainty in EPR data can still be relatively high possibly due to the length of the spin labels. If the size of spin labels can be reduced, the accuracy of integrative modeling efforts may improve significantly.

E. Small-angle x-ray scattering

While x-ray diffraction methods have, for years, been used to analyze the structures of crystallized molecules, including proteins as described previously, it is also possible to measure the x-ray scattering of molecules in solution using small-angle x-ray scattering (SAXS). SAXS provides information on both the overall shape and the oligomeric state of a protein while the protein is under native-like conditions in solution. In SAXS, x rays are passed through a target sample and the scattered photons are detected at small angles (typically ∼0.1° to 10°), as shown in Fig. 1(e). Scattering occurs because of constructive or destructive interference with electrons that resonate at the same frequency as the incident x rays. The SAXS profile (scattering intensity as a function of spatial frequency) of the protein of interest is obtained by subtracting the scattering profile of the buffer from the scattering profile of the sample (protein and buffer). The profile can then be converted into the pairwise distribution function, an approximate distribution of pairwise atomic distances of the macromolecule, using an inverse Fourier transform method.²³⁶

One of the most important advantages of SAXS compared to some other methods is that the protein stays in solution during the experiment (and thus does not need to be crystallized) and is not artificially disrupted (for example, with labeling reagents), which allows SAXS to provide information on the ensemble of conformations of the protein in near-native conditions. Because of this, SAXS is very amenable to multi-domain proteins and intrinsically disordered proteins. While SAXS has many advantages, there are also some important disadvantages. Whereas x-ray diffraction of crystals can provide high-resolution structural information, measuring the scattering of x rays in solution significantly decreases the resolution (typically ∼10 Å–20 Å or lower). Because of this low resolution, it is typical to combine the data obtained from SAXS with data determined from other structure determination methods. It has become very common to use computational structure prediction methods with SAXS data to model the structures of proteins. In addition to SAXS, a similar experimental method, small-angle neutron scattering (SANS), has been used to some extent for structural modeling (generally low-resolution modeling of membrane proteins, sometimes combined with SAXS).^237–241 Because structure prediction methods using SANS data are not as well developed at this stage, we will focus on SAXS in this Perspective.

Many methods are available to predict the SAXS profile from a structure so that the agreement with SAXS data can be measured in a variety of ways.^242–244 A common strategy to use SAXS profiles for structural modeling is to filter/rank the predicted structures based on their agreement with SAXS data. Another common strategy to model the data is to use the predicted structures to choose an ensemble that, when the structures are combined, matches the data. While the first approach is more common for structure prediction and docking, both strategies can be performed using the FoXS family of analysis tools.^245,246 Using FoXS, a model can be evaluated based on the agreement with a SAXS profile, which could be used in structure prediction (as can be done for protein–protein docking using FoXSDock, described in the next paragraph). The second approach can be performed using MultiFoXS, where an ensemble of structures is generated based on an input structure. The structures in the ensemble are then evaluated based on the SAXS agreement, and probabilities are output for the top models. Another method, BILBOMD, takes a similar approach, generating different conformations using molecular dynamics and then using those frames to determine a representative ensemble that matches the SAXS data.²⁴⁷

Because of the topological information gained from SAXS profiles, the data have been very useful for the modeling of protein complexes through protein–protein docking. The first such method to combine SAXS data with docking, pyDockSAXS (which has since been incorporated as a webserver), uses an approach that ranks potential docked structures based on a scoring function and SAXS agreement after unrestrained docking.^248,249 FoXSDock, another online SAXS-based docking server takes a similar approach, rescoring docked poses (generated using PatchDock) based on the agreement with the SAXS profile of the complex.^245,246 Another notable method for protein–protein docking with SAXS data is ClusPro.^250–252 The method for docking with SAXS data in ClusPro is performed with a few simple steps. First, 70 000 structures are obtained using unrestrained docking using the PIPER method in ClusPro. These structures are filtered down to the top 2000 based on the agreement with the obtained SAXS profile by predicting the SAXS profile for each structure and calculating the χ-score agreement. Finally, the resulting 2000 structures are ranked based on their PIPER energies, and the resulting top 1000 structures are clustered to produce 10 clusters. In a benchmark, the inclusion of SAXS data improved the model selection. It has also been shown by simulating the experimental data based on crystal structures that iSPOT could combine both SAXS and footprinting data to filter docked structures and identify a native-like model.²⁵³

While most protein–protein docking methods use SAXS data to rank the predicted structures as a post-processing step, some methods use the data during the structure generation phase. In theory, this should enrich the sampling of native-like structures as compared to docking without the SAXS data. ATTRACT-SAXS can generate and rank structures based on SAXS data alone.²⁵⁴ This approach is particularly significant because the method relies only on assessing the interface energy but does not require forcefield to assess energies for all atoms. ATTRACT-SAXS uses a scoring function based on SAXS agreement as the energy function for the Monte Carlo sampling and clusters top models to select a predicted structure. In a benchmark, ATTRACT-SAXS was able to improve the sampling of native-like structures when including SAXS and outperformed some other available methods. A few predicted structures are shown in Fig. 9. While ATTRACT-SAXS generates structures based on data alone, another study that included SAXS data during docking was performed using RosettaDock.²⁵⁵ This method incorporated SAXS restraints into the low-resolution docking phase along with using the Rosetta energy function and significantly improved both sampling and structure prediction.

FIG. 9.

Docked structures generated using ATTRACT-SAXS for an easy [(a) 2GTP], medium [(b) 1B6C], and hard [(c) 3F1P] case. Docked models are shown in green and red, and the crystal structure is shown in gray along with the cluster rank, IRMSD, LRMSD, and fnat. For comparison, the simulated SAXS profiles are also shown along with the experimental curves. Reprinted with permission from Schindler et al., Structure 24(8), 1387–1397 (2016). Copyright 2016 Cell Press.

Some alternative approaches are also available for protein modeling with SAXS data. It has shown that principal component analysis and SAXS data with clustering can be used to classify ab initio predicted models.²⁵⁶ Additionally, DecodeSAXS, a machine learning algorithm, has been developed to generate 3D models of proteins from SAXS profiles.²⁵⁷

SAXS profiles can furthermore be useful for modeling of multi-domain proteins. Due to flexible linker regions, the whole structures of multidomain proteins can be particularly difficult to obtain with x-ray crystallography, but it is not uncommon to obtain the structures of the stable regions. SAXS data, when used with those structures of stable domains, can be used to model the flexible linker regions. This type of prediction can be done using SAXSDom.²⁵⁸ Based on the input structures of the domains, the sequence (i.e., the sequence and location of the linker region), and the SAXS profile, the method performs Monte Carlo sampling on the linker region and evaluates each move based on the agreement with the SAXS profile of the entire protein. A similar approach can be used with algorithms in ATSAS.²⁵⁹ Using BUNCH,²⁶⁰ multidomain proteins can be modeled from the structures of the individual domains, but also CORAL can be used to build up those multidomain monomers into complexes.

Due to the encoding of flexibility into the data (since data are collected in native-like solution conditions), molecular dynamics simulations have been used in combination with SAXS in multiple different ways. For example, coarse-grained MD simulations have been used to predict the SAXS profile for a protein.²⁶¹ By simulating the structure and analyzing the trajectory, a better estimate can be made toward the experimental profile than with just the crystal structure because of the use of dynamic information. Additionally, restraints based on SAXS data have been incorporated into MD simulations using a quick on-the-fly SAXS energy to bias the simulation.²⁶² The method was used on intrinsically disordered proteins, a good test case due to their high intrinsic flexibility, to create an ensemble of structures that agreed very well with the experimental SAXS data. Finally, a hybrid resolution MD method (hySAXS) has been developed to incorporate SAXS data into a simulation. In a comparison to an MD simulation without the incorporation of the data, the SAXS-based simulation was better able to reproduce a separate set of data from NMR.

While SAXS provides information on shape and oligomeric state, the data are sparse and require integrative modeling. Using data from SAXS has been successful for protein–protein docking because it breaks degeneracy in the overall symmetry of the protein. However, when used in CASP (for tertiary structure prediction), SAXS has not thus far provided a huge advantage. While SAXS data are useful, the sparsity of the data might make the method best used in conjunction with orthogonal data from other methods.

F. Förster resonance energy transfer

Förster resonance energy transfer (FRET) occurs when a fluorescent donor and acceptor are in close proximity in space. In FRET, the donor is excited, and then, energy is transferred to the acceptor non-radiatively by dipole–dipole coupling. In order for FRET to occur, there must be overlap between the emission spectra of the donor and the excitation spectra of the acceptor, and the distance between the donor and the acceptor must be somewhere between 10 and ∼90 Å (depending on the pair). For example, one of the most common FRET tag pairs is cyan fluorescent protein (CFP) and yellow fluorescent protein (YFP). In this pair, CFP excites at 436 nm and emits at 480 nm, while CYP excites at 500 nm and emits at 520 nm.²⁶³ For proteins, FRET is usually performed by attaching the donor and acceptor to termini of different subunits within a complex in order to probe their interactions. Figure 1(f) shows a representation of CFP and YFP attached to proteins. FRET is often measured and reported as FRET efficiency (E_FRET), which is dependent on the distance between donor and acceptor (R) as well as the Förster distance (R₀) and number of acceptors (a). In many cases, the Förster distance can be estimated so that the distance between donor and acceptor can be derived, which can be used for modeling. One benefit of using FRET for structural modeling is that it can be either performed in vitro [also known as single molecule FRET (smFRET), provides information about individual molecules] or in vivo (which can give information about protein–protein interactions inside a cell). In general, the fluorescent proteins are not as well behaved for smFRET, but, in principle, smFRET provides access to subpopulations for heterogeneous systems. Some drawbacks are that the fluorescent labels need to be attached and can only provide distance information on the positions at which they are attached and that uncertainty in the derived distances can be high.

In general, smFRET can be used to determine distances between the centers of the covalently attached fluorophores if careful considerations are made. One way to use these data for modeling is to provide restraints for protein–protein docking.²⁶⁴ While considering the centers of the covalently attached fluorophores as dummy atoms, docked structures can be ranked based on their distance agreement between the dummy atoms and the FRET-derived distance restraints. Using a similar approach, the FPS (FRET positioning and screening) toolkit has been developed for docking of protein and DNA using FRET restraints.²⁶⁵ This method ranks structures based on FRET distance agreement while taking into account spatial distributions of the fluorophores. In another study, a Bayesian scoring function has been developed to fully model the statistics and Markov chain Monte Carlo was used to sample the posterior distribution to obtain structures.²⁶⁶

FRET measured in vivo can be modeled in the Integrative Modeling Platform (IMP) using a Bayesian approach to predict the structures of complexes.²⁶⁷ In the IMP method, the FRET efficiency (E_FRET) is replaced by the FRET_R index, which is a ratio between the fluorescence intensity of the donor excitation wavelength and the fluorescence intensity of the acceptor emission wavelength. The Bayesian scoring function uses a forward model for FRET_R (including noise) with the goal of maximizing the probability of the structure based on the data and prior information. In a benchmark of large ternary and quaternary complexes, the scoring function selected models in good agreement with the native at the positions of the FRET tags (N or C terminal), but the overall agreement with the entire model was worse (data shown in Fig. 10), which indicated to the authors that FRET data should be most helpful when supplemented with additional experimental data as is particularly convenient in the IMP.

FIG. 10.

Benchmark of FRET-based modeling in the integrative modeling platform. The accuracy (average C-α RMSD between crystal structure and 20 most probable models) of the modeled structures as a function of noise and data sparseness is shown for (a) all residues and (b) N- and C-terminal residues. Because the FRET tags were placed on the termini, the accuracy of the models was significantly better [(b) vs (a)]. (c) The ensemble of the most probably models compared to the native for 1FRT and 1M56. Reprinted with permission from Bonomi et al., Mol. Cell Proteomics 13(11), 2812–2823 (2014). Copyright 2014 American Society for Biochemistry and Molecular Biology (United States).

FRET data have also been used to model intrinsically disordered proteins (IDP). In one study, many different FRET-based distance restraints were generated by combining different FRET pairs at different locations in α-synuclein.²⁶⁸ Then, different conformations of α-synuclein were generated in PyRosetta by performing Monte Carlo simulations. These conformations were analyzed using harmonic potential restraints based on the collected library of FRET distance data. The structures that best matched the FRET data similarly matched other experimental data for α-synuclein. In another study, FRET data were used to model the structures of IDPs bound to polyethylene glycol (PEG), an organic polymer.²⁶⁹ In this method, the structures of the IDPs were sampled using flexible-meccano and TRaDES and were evaluated by predicting the FRET efficiency from the predicted IDP structures and comparing that to the experimentally measured FRET efficiency. Then, these structures of IDPs were inserted into coarse-grained MD simulations of PEG and scored based on their interaction to predict the structure of the complex.

FRET data have been used for structural modeling for a handful of cases; however, the data may be too sparse for modeling without including other information as well. Even the most successful methods note noise as an issue because of the need for the attachment of the fluorescent proteins. However, one advantage is the ability to run the experiment in vivo and obtain information about interactions inside living cells.

G. Contact inference from sequence co-evolution

In addition to explicitly collecting experimental data to be input into a computational structure prediction method, information derived from sequence data stored in a database such as UniProt can also be incorporated into structure prediction algorithms. As previously described, obtaining information on which residues in a protein interact (specifically interactions that are not close in sequence) can be very beneficial for structure prediction mainly due to the difficulty in sampling a large number of long-range contacts. This type of information, contact information, can be obtained by analyzing large numbers of evolutionarily related protein sequences and searching for covariation between two residues in the sequence. Occasionally, mutations in one residue are accompanied by covariant mutations in an interacting residue. For example, consider two interacting residues packed tightly in the core of a protein. If one of the residues were to mutate to a larger amino acid in order to retain the same shape and function of the entire protein, the other interacting residue would have incentive to mutate to a smaller residue. This process is called genetic covariation. If co-evolving residues in a target sequence can be located when analyzing evolutionarily related sequences, contacts can be predicted and then used as restraints for structure prediction, although sophisticated statistical and machine learning techniques are needed to analyze the data. A cartoon example of identification of coevolving residue pairs (left) and their underlying contacts (right) is shown in Fig. 1(g). Because of the large number of protein sequences that have been experimentally determined and the useful information that can be obtained, this approach has become increasingly popular in recent years.

Although contact prediction contests have been included in CASP since 1999 (CASP2), the rapid increase in available sequences and other advances, such as filtering out indirect effects,²⁷⁰ has made contact predictors based on co-evolution data more popular and successful. Because of these reasons, many different contact predictors have been developed which approach the residue–residue contact prediction (either inter- or intra-protein) using statistical models^271–280 and also machine learning.^281–285 Knowledge of the predicted contacts could then be input into a structure prediction protocol. Once a sufficient number of sequences became available for the input into such modeling, EVfold was able to predict structures to within 2.7 Å–4.8 Å RMSD based on the co-evolutionary data.²⁸⁶ Using Rosetta, it was shown that structure prediction using the predicted contact maps would be useful if the target sequence is more similar to the queried sequences than to a structure in the protein data bank for which homology modeling could be used.²⁸⁷ Since these developments, many different structure prediction methods have been developed to incorporate the predicted contacts from covariation (many of which have subsequently been improved to predict histograms of contact data rather than binary contact prediction),^288–297 culminating in AlphaFold.^298,299 AlphaFold’s structure prediction method made a notable impact at CASP13 (2018), with significantly better structure prediction results than have ever been seen before. While some contact predictors only predict binary contacts, AlphaFold’s deep learning algorithm instead creates an energy landscape based on the predicted distances between pairs. One of the most significant differences between AlphaFold’s potential and other structure prediction force fields is that the energy landscape is so smooth that it does not require the generation of a large number of structures through stochastic Monte Carlo methods. Instead, a simple gradient descent method is sufficient to find the structure with the lowest energy. Figure 11 shows the comparison to other methods in CASP13. AlphaFold correctly predicted structures for 24/43 domains, 10 more than the next closest method.

FIG. 11.

Performance of AlphaFold (A7D) in CASP13 (2018). Number of free modeling domains predicted for a given TM-score threshold for AlphaFold (blue) and other groups (red). Reprinted with permission from Senior et al., Proteins 87(12), 1141–1148 (2019). Copyright 2019 John Wiley and Sons.

The viability of utilizing sequence co-evolution in modeling has recently been accelerated by large amounts of available data and developments in deep learning. Because the use in structure prediction is relatively new, intrinsic limitations of the information it can provide are unknown. Nonetheless, the method has the potential to play an important role in structure determination and could also become part of all integrative modeling approaches in the future.

III. FUTURE DIRECTIONS AND CHALLENGES

In this Perspective, we have summarized computational techniques that perform protein structure prediction, protein–protein docking, and/or molecular dynamics simulations by including experimental data from cryo-EM, NMR, MS, EPR, SAXS, FRET, and/or sequence covariation to improve modeling accuracy. While improvements in algorithms and data availability have resulted in dramatic improvements in modeling accuracy over the last decade, there are still challenges ahead.

One challenge for integrative modeling approaches is to properly account for the experimental error and noise. While doing so can improve modeling results even with partially incorrect or incomplete data, perfectly accurate modeling with sparse data cannot be reasonably expected. In addition to modeling experimental error and noise for dynamic systems, it can also be very important to model ensembles of multiple conformations. Another challenge and reason for inaccurate modeling is error in forward models, which predict the data from the structure. This might be a reason why many methods are only successfully able to rank models after generation, rather than being used during the sampling phase. Improvements in understanding and theory of experimental techniques should improve these forward models over time.

The understanding of the relationships between experimental data and structure is one reason why integrated approaches can fail. One way to gain a more accurate understanding of experimental data and successfully use the information in modeling is to make datasets more easily available. For example, databases such as the Electron Microscopy Data Bank (EMDB) and UniProt have made a large amount of data available for cryo-EM- and sequence covariation-based modeling. Databases to unify and store data from other experimental methods would be tremendously beneficial to protein structure modeling efforts. While unifying large amounts of experimental data is certainly a huge challenge, we hope that the successes of computational modeling highlighted in this Perspective demonstrate the demand for these types of resources.

Despite the recent success of AlphaFold²⁹⁸ in covariation-based modeling, accurate tertiary structure prediction remains a huge challenge. AlphaFold’s structure prediction results in CASP13 (2018) were the best ever seen, but the method still failed to accurately predict structures (TM score > 0.7) of 19/43 domains. One of the reasons for AlphaFold’s success, besides the use of state-of-the-art neural networks to derive sequence-dependent potentials, is the quantity of data available for multiple sequence alignment used to predict distances and contacts (∼185 × 10⁶ available sequences⁷). While in the long-term, it is potentially shortsighted to place limits on deep learning methods such as AlphaFold, current implementations may be dependent on the amount of distance information stored in the aligned, evolutionarily relevant sequences. One possible solution could be to include more data, specifically data from experimental methods that contain structural information as outlined in this Perspective, into the structure prediction potentials.

Numerous computational methods outside of AlphaFold incorporate multiple types of experimental data into their structure prediction methods. When doing so, we hypothesize that it is most beneficial to combine methods that provide orthogonal information. In Fig. 1, we have roughly categorized the data obtained from the featured experimental methods based on the type of structural information they provide. The categories are size, shape, solvent accessibility, interface location/composition, distances/contacts, spatial density, orientation, local environment, flexibility, and stoichiometry/connectivity. For example, when deciding which methods to combine, it might be most advantageous to obtain some information on overall shape (e.g., SAXS or cryo-EM), some information on solvent exposed residues (e.g., covalent labeling or EPR), and some information on contacts (e.g., sequence co-evolution, FRET, XL, EPR, and NOE). This type of combined information could have the potential to synergistically improve structure prediction. However, one of the main challenges in the combination of multiple types of experimental restraints is to properly weight the information, ideally in a probabilistic approach based on their accuracy and uncertainty. For example, Bayesian approaches in the Integrative Modeling Platform (IMP)^43,44 and Modeling Employing Limited Data (MELD)^8,162 are specifically designed to statistically model the probabilities and noise.

While monomer fold prediction methods such as AlphaFold are very important, much of the biological function is mediated by protein–protein interactions, where the majority of proteins exist at least transiently as part of a complex. In this Perspective, we have discussed several experimental methods that can specifically provide information about these protein–protein interfaces, such as hydrogen–deuterium exchange (covalent labeling), chemical cross-linking, surface-induced dissociation, Förster resonance energy transfer, and electron paramagnetic resonance. Using these methods to collect data on interfaces as well as other methods that provide information on the entire complex should facilitate the prediction of these complex structures. For example, it is feasible to use some information to predict monomer structures and some other information to predict the relative orientations of those monomers as they form a complex, assuming that they do not undergo significant backbone conformational changes upon binding.

During protein structural modeling efforts, computer algorithms for conformational sampling are almost always used. Conversely, one such unconventional approach to sampling is used in Foldit. Foldit, a video game with a Rosetta backend, takes advantage of the intuition of “citizen scientists” to explore the conformational space of proteins that are visually presented in interactive puzzles.³⁰⁰ In Foldit, players can sample different structures by manually changing positions of backbones and side chains as well as using built-in tools which perform some small algorithmic refinement, such as gradient-based minimization and combinatorial side-chain rotamer packing. This strategy of crowdsourcing the sampling using Foldit has been successful in terms of predicting the structures of real proteins in multiple studies.^301–304 Foldit has also been incorporated into the classroom to teach students about the protein structure in a more interactive manner.^305–307 Recently, cryo-EM density maps have been integrated into Foldit puzzles, allowing the players to fit proteins into visualized density maps.³⁰⁸ In a comparison to other automated cryo-EM density flexible fitting tools, Foldit players were able to identify a structure of S. entomophila afp7. Of course, using Foldit to determine a structure based on a density map is considerably more time consuming than automated algorithms, but the method was able to produce a structure with better side-chain placement in the density map and which was more geometrically plausible, as shown in Fig. 12. Moving forward, it would be interesting to see Foldit players building structures using information from other experimental data, such as labeled residues from covalent labeling and contacts from a variety of experimental methods.

FIG. 12.

(a) Comparison of models for Afp7. The Foldit structure is rendered in green, the microscopist structure in gray, the Phenix model in magenta, and the Rosetta model in yellow. The electron potential map is contoured at 2σ. (b) Comparison of the Ramachandran outlier and allowed backbone conformations. (c) Comparison of Molprobity Clashscore—in both cases, lower is better. (d) Comparison of three different map-to-model correlation coefficients in which higher values are better. (e) Map-to-model FSC curves for Microscopist (gray), Foldit (green), Phenix (pink), ARP w/ARP (orange), and Buccaneer (blue) models. Reprinted with permission from Khatib et al., PLoS Biol. 17(11), e3000472 (2019). Copyright 2019.

In conclusion, the field of structural biology has the potential to solve many important problems; however, protein structure determination remains a challenge. While methods have been developed to experimentally determine the structures of proteins (x-ray crystallography, NMR, and cryo-EM), they each have limitations and are not appropriate in all cases. On the other hand, many experimental methods that provide some sparse structural data are available. These data can be incorporated into computational protein modeling algorithms such as de novo folding, protein–protein docking, and molecular dynamics. Over the past few decades, many combined experimental/computational methods have been successfully developed and benchmarked as described in this Perspective. In the future, significant advancements to data collection and modeling of the methods highlighted in this Perspective will be made. There is little doubt that new experimental methods will be developed and used for protein structure modeling as well. For example, cryo-EM, which has become one of the most popular methods for integrative modeling, was not thought of in this light even 20 years prior. Current and future methods have tremendous potential to facilitate structure determination of proteins and protein complexes.

DATA AVAILABILITY

Data sharing is not applicable to this article as no new data were created or analyzed in this study.