De Novo Protein Design for Novel Folds Using Guided Conditional Wasserstein Generative Adversarial Networks

Abstract

Although massive data is quickly accumulating on protein sequence and structure, there is a small and limited number of protein architectural types (or structural folds). This study is addressing the following question: how well could one reveal underlying sequence–structure relationships and design protein sequences for an arbitrary, potentially novel, structural fold? In response to the question, we have developed novel deep generative models, namely, semisupervised gcWGAN (guided, conditional, Wasserstein Generative Adversarial Networks). To overcome training difficulties and improve design qualities, we build our models on conditional Wasserstein GAN (WGAN) that uses Wasserstein distance in the loss function. Our major contributions include (1) constructing a low-dimensional and generalizable representation of the fold space for the conditional input, (2) developing an ultrafast sequence-to-fold predictor (or oracle) and incorporating its feedback into WGAN as a loss to guide model training, and (3) exploiting sequence data with and without paired structures to enable a semisupervised training strategy. Assessed by the oracle over 100 novel folds not in the training set, gcWGAN generates more successful designs and covers 3.5 times more target folds compared to a competing data-driven method (cVAE). Assessed by sequence- and structure-based predictors, gcWGAN designs are physically and biologically sound. Assessed by a structure predictor over representative novel folds, including one not even part of basis folds, gcWGAN designs have comparable or better fold accuracy yet much more sequence diversity and novelty than cVAE. The ultrafast data-driven model is further shown to boost the success of a principle-driven de novo method (RosettaDesign), through generating design seeds and tailoring design space. In conclusion, gcWGAN explores uncharted sequence space to design proteins by learning generalizable principles from current sequence–structure data.

INTRODUCTION

A fundamental science question about proteins, the workhorse molecule of life, is their sequence–structure–function relationships.¹ Anfinsen and co-workers studied the renaturation of fully denatured ribonuclease² and eventually established a thermodynamic hypothesis: native conformations of proteins in physiological milieu correspond to the solute–solvent systems’ lowest Gibbs free energy.³ Since then, the direct exploration of the sequence–structure relationship has led to both the forward problem of structure prediction from sequence⁴ as well as the inverse problem of sequence design for desired structures.^5,6 With the data quickly accumulating on protein sequence and structure, a central question in this study is as follows: how well can one reveal deep insights into sequence–structure relationships to empower inverse protein design?

The forward problem of protein structure prediction, especially ab initio prediction without templates, is often solved by energy minimization. Even this classical principle-driven approach has benefited from data. Examples include the use of structural fragments for efficient sampling and the use of structure and sequence data for training scoring functions. A recent wave of data comes from protein sequences without paired structures. Specifically, sequence coevolution can be exploited to infer residue–residue structure contacts^7–9 and enhance protein structure prediction significantly.^10–12 As witnessed in recent CASP (Critical Assessment of Structure Prediction), the latest revolution is in the prediction of residue–residue distances even for proteins with few homologue sequences, which is enabled by advanced deep neural network architectures (especially deep residual networks) that learn from the sequence, structure, and coevolution data.^13,14

The inverse problem of protein design is often similarly pursued following the energy minimum principle.^15–17 Current protein (re)design algorithms fall in three classes: (1) exact algorithms such as dead-end elimination, A*, and cost function networks,^18–21 (2) approximation algorithms such as relaxed integer programming and loopy belief propagation,^22,23 and (3) heuristic algorithms such as genetic algorithms and Markov chain Monte Carlo (MCMC).^24,25 The more challenging de novo protein design assumes that, along with the sequence, even the exact backbone structure is unknown.²⁶ Rather, the desired structure is described by the composition and the relative arrangement of secondary structure elements. The (energy minimum) principle-driven RosettaDesign tools²⁵ have made great success for de novo protein design.^27–30

In contrast to the forward problem, the inverse problem of de novo protein design has witnessed limited impacts from deeply exploiting data with advanced artificial intelligence technologies (especially deep learning),^31,32 despite impressive progress in fixed-backbone protein design.^33–37 Meanwhile, the impacts of deep generative models, represented by Generative Adversarial Networks (GAN)³⁸ and Variational Auto-Encoder (VAE),³⁹ have reached the sibling fields of inverse design for DNA,^40,41 RNA,⁴² small molecules,^43,44 and peptides.⁴⁵

Our study focuses on developing deep generative models for the inverse problem of de novo protein design. The specific design goal here is an arbitrary structural fold, a global pattern of protein structures characterized by the content and organization of secondary structures.⁴⁶ Despite the growth of protein structure data, the number of structural folds remains around 10³ lately. To design sequences for a novel fold, our models overcome the unique challenges from the design space, the design objective (desired properties), and the mapping in between.

The first challenge, a numerical one, comes from the much more daunting protein sequence space. Compared to aforementioned molecular designs, protein sequences have more choices at each position (20 standard amino acids versus four nucleotides) and are much longer, leading to the dimensionality of 20^L ≫ 4^K where L > K.

The second challenge, a conceptual and mathematical one, is that, the fold space is a discrete domain that has not been completely observed.⁴⁷ Therefore, a generalizable representation is needed to design a novel fold (a value in the discrete space) never seen in training data. In contrast, aforementioned deep generative small-molecule designs often target either a continuous property (such as logP) or a discrete one with desired values observed in training data.

The last challenge is the knowledge gap about the complex sequence–fold relationship. Protein folds are products of both convergent and divergent evolution,⁴⁸ and sequences in the same structural fold do not necessarily share a common evolutionary origin.⁴⁶ In other words, although very similar sequences are often in the same fold (with not-so-rare exceptions), very dissimilar sequences (even when their sequence identities are below 20%) can belong to the same fold as well. By definition, no sequence similarity is implied within a fold. This complex sequence–fold mapping makes it extremely difficult to learn from the data. In contrast, designing RNAs benefits from the fact that desired structures can often be readily translated to regular base-pairing patterns in the sequence space.

To overcome the aforementioned challenges in de novo protein fold design, we present a study exploiting current data and developing advanced technologies for faster, broader, and deeper exploration of the protein sequence space while seeking principles underlying protein structure folds. Specifically, we have developed a semisupervised, guided conditional Wasserstein GAN (Figure 1) by making the following innovative contributions:

Figure 1.

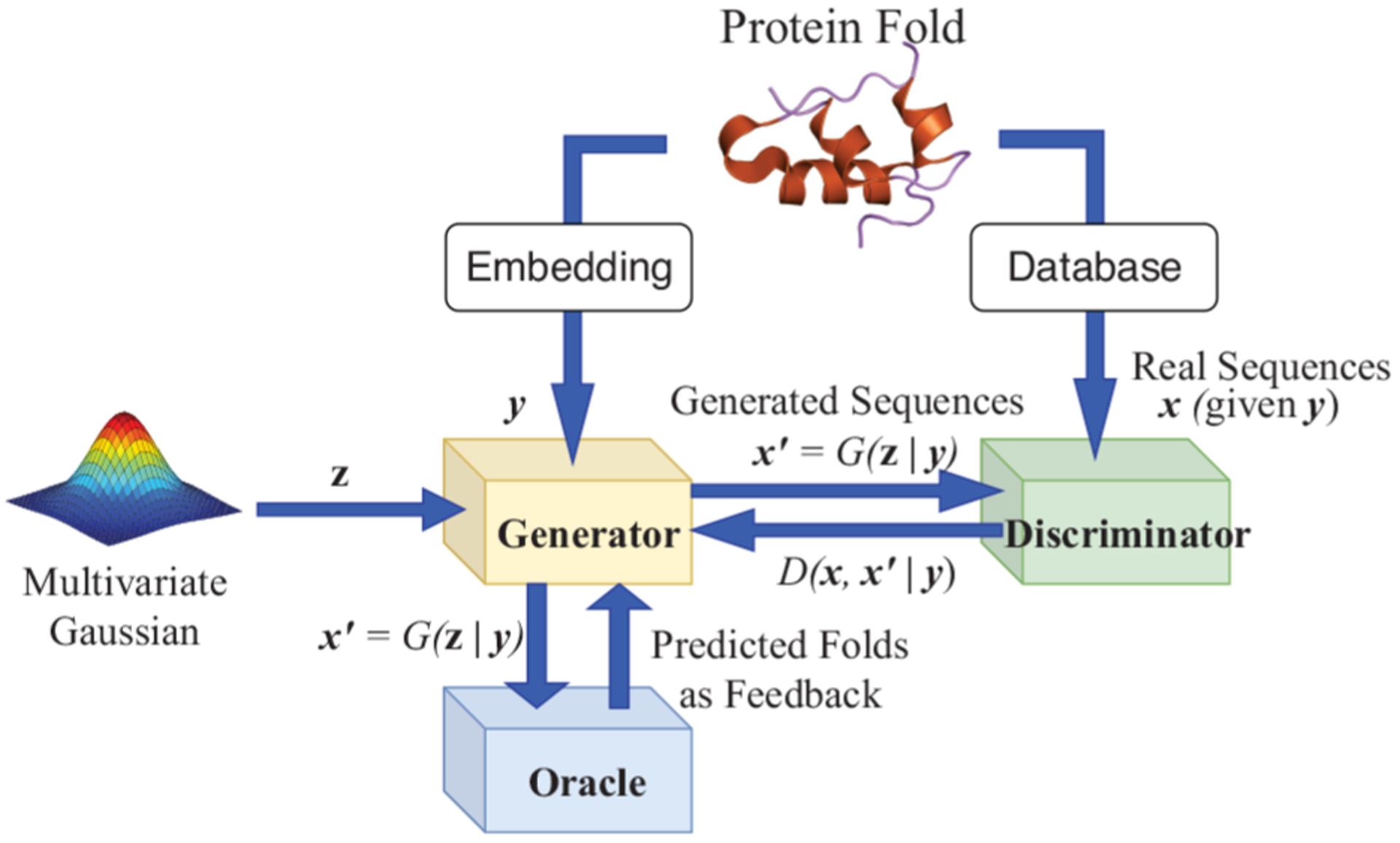
Architecture of guided conditional Wasserstein GAN.

1. We have extended WGAN with two component networks (generator and discriminator/critic) to three-component gcWGAN by introducing an “oracle” that provides real-time feedback on generator’s output quality and an additional loss term fully differentiable for model training.

2. For the new component, the oracle, we have developed an ultrafast sequence-to-fold classifier that is capable of online feedback during model training, whereas the state-of-the-art fold classifiers cannot address the need. We have accomplished this by using less processed inputs (sequence only) and more advanced model architecture (residual neural networks).

3. For the conditional input of gcWGAN, we have embedded structural folds into low-dimensional vectors in a nonparametric way (kernelized PCA) that preserves distance metrics in the fold space. The fold representation also allows for generalizability to describe novel folds.

4. For training gcWGAN, we have exploited abundant protein sequences without paired structures, in addition to those with paired structures, and trained our models in a semisupervised manner.

We systematically assess our models’ capability on designing novel protein folds, including a newly published one. gcWGAN-generated protein sequences are predicted to resemble natural proteins in biophysical properties and stability/fold origins, and their functions are predicted to be specific to target folds. Compared to a recent study based on conditional VAE,³¹ our models generate proteins that are comparably or more accurate in desired folds, yet much more diverse and often more novel in sequence. Our data-driven gcWGAN, when integrated with the principle-driven RosettaDesign, boost the amount of successful designs and design efficiency.

MATERIALS AND METHODS

In this section, we first introduce models and training strategies that are our major contributions. For models, we describe the overall architecture and mathematical foundation of our gcWGAN and then include more details about the newly introduced oracle network (ultrafast sequence-to-fold predictor) as well as the newly developed conditional input (representation of an arbitrary fold). For training, we introduce our three-step semisupervised strategy that exploits sequences without paired structures to overcome training instability and increase “protein-like” designs.

After describing the data used for gcWGAN training, validation, and testing, we focus on assessment. We have comprehensive assessments of model-generated sequences, including oracle-assessed success rates (yield ratios), predicted biophysical and biological properties, and structure-based quality prediction (TM-scores), as well as diversity and novelty.

We end the section with how to integrate our data-driven gcWGAN into principle-driven RosettaDesign to boost success: initializing sequence search or/and reducing design space.

GAN Models for De Novo Protein Design.

The architecture of gcWGAN is illustrated in Figure 1. There are three components of the model, all of which are neural networks: the generator, the discriminator, and the oracle. The generator is fed with a random input z and a conditional input y (a representation of any given fold) and produces artificial amino-acid sequences $\tilde{x}$. The discriminator tries to tell apart the artificial sequences $\tilde{x}$ and the real (natural) ones x for the given fold. With training sequences and their folds, the generator and the discriminator compete against each other and improve each other iteratively in the training process. Meanwhile, a third network, the oracle, takes artificial sequences from the generator, predicts their chances of belonging to the target fold, and guides the training of the generator and the discriminator. Once the model is trained, the generator becomes a protein sequence designer for any arbitrary desired fold that is represented as the conditional input y.

Details of gcWGAN are elaborated next. We begin with background information for GAN, WGAN, and conditional WGAN, where the generator, the discriminator (also called the critic in WGAN), and the Wasserstein loss are explained. We proceed to describe our guided cWGAN (gcWGAN) with the additional oracle network (a sequence-to-fold predictor here) and accordingly an additional loss term that is fully differentiable to regularize the generator and the critic. With the overall architecture of gcWGAN explained, we detail its oracle that provides ultrafast fold classification to guide gcWGAN training and its conditional input that represents a desired fold.

Conditional Wasserstein GAN (cWGAN).

Generative Adversarial Network (GAN),³⁸ a class of generative models, represents a game between a generator G and a discriminator D. The generator’s objective is to generate artificial data from a noise input that is close to real data, and the discriminator’s goal is to discriminate the generated data from the real ones.

Compared to the original GAN,³⁸ Wasserstein GAN (WGAN)^49,50 uses Wasserstein distance rather than Jensen–Shannon divergence in the loss function. This change overcomes training difficulties in GAN, such as difficulty to reach Nash equilibrium,⁵¹ low dimensional support, vanishing gradients and mode collapsing.⁴⁹ WGAN has been extended to conditional WGAN (cWGAN) where both the generator and the discriminator (more often referred to as the critic in WGAN) are conditioned on an additional supervised event y, where y can be any kind of auxiliary information or data such as a discrete label,⁵² sequence,⁵³ image,⁵⁴ or speech.⁵⁵

We consider conditional WGAN (cWGAN) (formulated using the Kantorovich–Rubinstein duality) with a penalty on the gradient norm imposing a soft version of the Lipschitz constraint.⁵⁰ The formulation is as follows:

$$\begin{gathered} \underset{G}{\text{min}}\underset{D}{\text{max}}{L}_1=\underset{G}{\text{min}}\underset{D}{\text{max}}\{{\mathbb{E}}_{x~{\mathbb{P}}_r}[D(x\mid y)]-{\mathbb{E}}_{\tilde{x}~{\mathbb{P}}_g}[D(\tilde{x}\mid y)] \\ -{\lambda }_1{\mathbb{E}}_{\widehat{x}~{\mathbb{P}}_{\widehat{x}}}\left[{\left({\Vert {\nabla }_{\widehat{x}}D(\widehat{x}\mid y)\Vert }_2-1\right)}^2\right]\} \end{gathered}$$ (1)

where y is the embedding of the protein fold (explained in the Conditional Input to gcWGAN: Fold Representation section); x denotes real sequences generated from ${\mathbb{P}}_r$, the real data distribution; and $\tilde{x}$ denotes artificial sequences generated from ${\mathbb{P}}_g$, the model distribution. ${\mathbb{P}}_g$ is implicitly defined by distribution p(z) of noise z because $\tilde{x}=G(z\mid y)$. Moreover $\widehat{x}~{\mathbb{P}}_{\widehat{\mathit{x}}}$ is implicitly defined as uniformly sampling along straight lines between pairs of points sampled from ${\mathbb{P}}_g$ and ${\mathbb{P}}_r$ for a given label y. This is inspired by the fact that the optimal critic contains straight lines, with the l2 norm of the gradient equal to 1, connecting coupled points from ${\mathbb{P}}_g$ and ${\mathbb{P}}_r$. Hyper-parameter λ₁ enforces the importance of gradient penalty in the loss function and is set at 10 without tuning.⁵⁰ The pseudocode of cWGAN with gradient penalty is given in the Supporting Information (SI) Section 4.1 or Section S4.1 in short.

Guided cWGAN (gcWGAN).

In principle, cWGAN could guide the sequence generation specifically for a desired fold. However, limited resolution of fold embedding could present a barrier. We have thus developed a novel GAN model, guided cWGAN (or gcWGAN), with an additional “oracle” network inside (detailed in the Oracle in gcWGAN: Fold Prediction section). The oracle provides feedback to the generator on how well generated sequences might possess the desired property (an arbitrary fold here). Specifically, this feedback is sequence-predicted fold probabilities in our case and introduced as an additional “regularization” term R to L₁ in the loss function

$$\underset{G}{\text{min}}\underset{D}{\text{max}}{L}_2=\underset{G}{\text{min}}\underset{D}{\text{max}}\left\{L_1+{\lambda }_{2}R\right\}$$ (2)

where the hyper-parameter λ₂ is used to balance the two terms.

$$\begin{gathered} R=-{\mathbb{E}}_{\tilde{x}~{\mathbb{P}}_g}[I_{\text{target}}(\tilde{x})\text{log}O(\tilde{\mathit{x}}) \\ +\left(1-I_{\text{target}}(\tilde{x})\right)\text{log}(1-O(\tilde{x}))] \end{gathered}$$ (3)

where $O(\tilde{x})={\sum }_{k=1}^{K_{\prime }}{p}_k(\tilde{x})$, the sum of probabilities for the top K′ (10 in this study) fold predictions from the oracle. Ideally, $I_{\text{target}}(\tilde{x})$ is an indicator function that equals 1 when the target fold is among the top K′ predictions from the oracle. But this definition would lead to a nondifferentiable expression without gradients needed for back-propagation. We thus introduce $I_{\text{target}}(\tilde{x})\approx \text{ReLU}\left(p_{\text{target}}(\tilde{x})-p_{K^{\prime }}(\tilde{x})\right)$ and $1-I_{\text{target}}(\tilde{x})\approx \text{ReLU}\left(p_{K^{\prime }}(\tilde{x})-p_{\text{target}}(\tilde{x})\right)$. So if the target fold is within top K′ predictions, $p_{K^{\prime }}(\tilde{x})-p_{\text{target}}(\tilde{x})<0$ and its ReLU assigns zero to $1-I_{\text{target}}(\tilde{x})$; otherwise, zero is assigned to $I_{\text{target}}(\tilde{x})$.

The pseudocode of gcWGAN is given in SI Section S4.2. Model architectures of the critic and the generator are in SI Section S4.3.

Now that the overall architecture of gcWGAN is explained, we use the next two subsubsections to introduce the oracle network (i.e., an sequence-to-fold online predictor) and the conditional input to gcWGAN (i.e., a representation of an arbitrary fold).

Oracle in gcWGAN: Fold Prediction.

The newly introduced “oracle” in gcWGAN comments on the quality of generated sequences toward desired property y. In our case, it is a sequence-to-fold predictor used both for guiding sequence generation during model training and for filtering generated sequences afterward. So that the oracle in gcWGAN can be in sync with the generator and the critic updates, it has to generate extremely high throughput yet somewhat accurate fold predictions, which state-of-the-art fold predictors including DeepSF⁵⁶ cannot address. In response to this need, our oracle is a revised model based on DeepSF. It uses less features for speed and more advanced network architecture for accuracy compared to DeepSF, which is detailed as follows.

First, DeepSF uses input features including amino-acid sequence, position-specific scoring matrix, predicted secondary structure, and predicted solvent accessibility, whereas our oracle only uses sequence (one-hot encoding). The features other than sequence are very informative for fold prediction but unfortunately require computationally expensive multiple sequence alignment. Considering that our model for protein fold design involves millions of generated sequences during training, online calculation of nonsequence features for oracle feedback is infeasible (each sequence demands around 10 min or more for nonsequence features).

Second, DeepSF involves a 1D deep convolutional neural network, whereas our oracle is deeper with 10 more layers of residual convolutional layers and a larger filter size (40 versus 10). The architecture change is to compensate for the loss of informative nonsequence features. In the end, a softmax layer predicts the probability for each 1215 folds (slightly increased from 1195 in DeepSF due to SCOPe update).

More details about the oracle, including its architecture, can be found in SI Section S3.

Conditional Input to gcWGAN: Fold Representation.

The inputs to the generator include a multivariate Gaussian variable (z) and a conditional input (y) describing the desired property (an arbitrary fold here). For the conditional input, we aim at low-dimensional fold representations that are (1) representative enough for preserving the information about the known folds and (2) generalizable enough for describing a novel fold. Considering that the growth of the fold space in recent years has been slow and likely near saturation,⁵⁷ we focus on the space containing the 1232 basis folds (SCOPe v. 2.07) and perform dimension reduction using kernel principal component analysis (kPCA).^58,59

Specifically, we do not start with describing individual folds but instead find “distances” between fold pairs, using symmetrized TM-scores as pairwise similarity (kernels) and the nearest positive definite matrix as the Gram matrix. We then used kPCA to construct a space spanned by orthonormal PCs where inner products reproduce the aforementioned pairwise distances. In this way, any fold with a structure blueprint can be represented with coordinates in the subspace spanned by the top K PCs. More details can be found in SI Section S2.

Training Strategies for gcWGAN.

Semisupervised Training.

In gcWGAN, the oracle is pretrained and fixed, and the generator and the critic are trained with a series of “warm starts”. The idea is to facilitate generated sequences to be “protein-like” (for instance, able to fold into stable and functional structures).

To this end, we have developed a three-step semisupervised strategy to train gcWGAN by exploiting abundant protein sequences without paired structures. Specifically, we first train cWGAN using unsupervised protein sequences from UniRef50 (see the Data section) while fixing their y (fold embedding) at the center of all fold representations. We then retrain cWGAN using the supervised sequences (see the Data section) with corresponding fold representations but initialize model parameters at the optimal values from the unsupervised step (warm start). In the third and final step, we train our gcWGAN using the supervised sequences and initialize the generator/critic parameters at the optimal values from the previous semisupervised cWGAN model (again, warm start).

Besides improving the chance of generating relevant protein sequences, the three-step semisupervised setting could also overcome the instability of gcWGAN training.

Hyperparameter Tuning.

While training cWGAN or gcWGAN, we consider three common hyper-parameters: (1) the initial learning rate for the Adam optimizer, (2) the number of critic iterations, and (3) the noise length. Assuming that optimal hyper-parameters are similar between cWGAN and gcWGAN, we sequentially tune them for cWGAN by training cWGAN for 100 epochs. For gcWGAN, the three common hyper-parameters are adopted at the optimal values for cWGAN, and its λ₂ is tuned further.

To tune the hyper-parameters, we select four criteria for the intermediate assessment of sequences at each epoch. The criteria are of increasing biological relevance: (1) mathematical convergence through the critic’s loss, (2) low ratio of the “nonsense” sequences (how often padding characters appears between or in front of amino-acid characters to produce invalid sequences), (3) low ratio of padding characters at the end of valid sequences, and (4) sequence novelty through low sequence identity between generated sequences and real representative sequences for a given fold. Sequence novelty was adopted so that models do not just mimic sequence-fold patterns observed. In our study, it was found insensitive to hyper-parameters considered and was not a determinant of their optimal values or trained models. As our designs are targeting a fold rather than a specific (fixed-backbone) structure, sequence recovery was not adopted as a criterion here or for assessment. More details are in SI Section S5.

Data.

Sequences labeled with structural folds are retrieved from SCOPe v. 2.07⁴⁶ and filtered at 100% identity level. Lengths are between 60 and 160. The resulting labeled data consist of 20,125 sequences (over 35% of the original) labeled with 781 of the original 1232 folds, across all seven fold classes (a–g) and three “difficulty” levels based on sequence abundance (at least 51 sequences for easy, at most five for hard, and in between for medium). More details are provided in SI Section S1.

The labeled data set is split into training (70%), validation (15%), and test (15%) sets with stratified sampling to preserve the fold–class distribution. Folds do not overlap among sets, and their statistics are in Table S2. The training sequence statistics are in Table S3. Sequence and structure representatives of each fold are chosen for postanalysis (SI Section S2).

In addition, 31,961 unlabeled sequences without paired structures, in the same length interval, are obtained from UniRef50.⁶⁰

Assessment.

Once the generator is trained, we feed it with the desired structural fold (in its embedding y) and generate sequences to pass the nonsense check and then the oracle’s check.

The intermediate, valid sequences (before the final, oracle’s check) are generated up to 10⁵ per fold and assessed across all folds using the oracle, a fold classifier (see details in SI Section S7). The final sequences (after passing the oracle) are generated 10 per fold and assessed over selected folds using Rosetta, an ab initio structure predictor. cVAE and Rosetta pipelines are in SI Sections S8 and S9.

Assessing Intermediate Designs.

We first estimate “yield ratios” (success rates) for generated valid sequences (passing the nonsense check). Specifically, a sequence is declared a “yield” if its top-10 oracle-predicted folds include the target and the yield ratio is the portion of those yields. When the target fold is novel and undefined in the oracle, we use its neighbor (a.188 in our case).

Physical and Biological Assessment of Final Designs.

We next assess the (bio)physical and biological significance of the oracle-filtered designs generated for all 31 test folds whose yield ratios are at least 1 × 10⁻⁵ (yielding folds). We generate up to 1000 such sequences, and a time limit of 2 days was adopted for low-yielding folds. We apply to these designs sequence-based predictors of biophysical properties and protein functions. Details are provided in SI Sections S11 and S12.

Stability.

We use an instability index (Guruprasad et al. PEDS 1990) that has been widely used and is available in BioPython v.1.76.⁶¹ An instability index above 40 is recommended to suggest an unstable protein.

Other Physical Properties.

We also calculate for generated sequences aromaticity value,⁶² grand average hydropathicity (GRAVY),⁶³ isoelectric point (pI),⁶⁴ and normalized molecular weight⁶⁵ using BioPython.

Functional Annotations.

For 25 of the 31 yielding test folds that have experimentally validated functional annotations (Gene Ontology or GO terms), we predict GO terms of generated sequences (40 for each fold) using NetGO.⁶⁶ We then calculate the GO similarity between each generated sequence and the structural representative of its target fold using GOGO.⁶⁷ We remove from the similarity the background—the average GO similarity to the representative sequences of other (off-target) folds. The resulting Δ GO-similarity being above 0 indicates fold specificity of designed sequences, in the sense of protein function.

Origins of Stability.

Protein stability is often attributed to hydrophobic collapse and hydrogen bonds. We thus use Rosetta to predict structures of sequences designed for selected folds. We then calculate buried nonpolar surface area (NPSA), hydrogen bond energy, and Rosetta total energy, which were shown to correlate well with protein stability experimentally.⁶⁸ More details are in SI Section S11.2

Origins of Folds.

We investigate deeply into an α fold (a.35) to examine one physical origin of the fold: hydrogen bond patterns. We use Rosetta to predict structures and compare such patterns between generated and natural sequences. More details are in SI Section S11.3

Structural Assessment of Final Designs.

We last analyze the fold accuracy of the final designs (those yields) by predicting their structures using Rosetta v3.10.²⁵ As ab initio structure prediction is computationally expensive (10⁴ core-hours per sequence), we choose six representative test folds across fold classes (a–d and g), sequence abundance (easy to hard, reflecting “designability”), and yield ratios (above 0.01 for high and otherwise for low), as seen in Table 1. In addition, to check the model performance for prospective, novel folds, we also select a recently published fold (PDB ID: 6H5H).⁶⁹ Note that the fold is not completely observed in 6H5H. So we used a design structure (polb1) in the study whose first 71 residues are experimentally verified in 6H5H and the last 20 residues form two helices bending back to the N-term helix.⁶⁹ Compared to the representative structures of 1232 basis folds, the structure has TM-scores below 0.5.

Table 1.

Representative Test Folds for Structural Assessment

	High Yield	Low Yield
Easy	b.2	a.35
Medium	c.94	g.44
Hard	c.56	d.146

For each of the seven selected folds, we predict 10 structures for each of the first 10 final sequences. We generate 10,000 trajectories for each sequence. Among the 10,000 predictions, we retain around 10% energetically lowest ones with an energy-cutoff of 200, cluster those with a cluster radius of 2.5 Å in RMS and a maximum cluster count of 10, and report the 10 cluster centers as final structure predictions.

Structure Accuracy.

We align each structure prediction of a designed sequence to the known, representative structure of its target fold, using TM-align⁷⁰ and calculate its TM-score (the reference being the target structure). We use TM-scores as a continuous measure on how likely the designs belong to the target folds. A TM-score between 0 and 1 indicates very likely the same fold when it is above 0.5 and nonrandom similarity when it is above 0.3.⁷¹

Sequence Diversity and Novelty.

We perform pairwise alignment of the 100 final sequences for each fold and calculate the distribution of sequence identity to measure diversity. We also do so between each designed sequence and the known natural ones for each target fold to calculate maximum sequence identity and measure sequence novelty. As a sequence identity value above 0.3 would indicate close homologues whose structures are very likely similar, we regard 0.3 as a threshold below which generated sequences are diverse or novel.

Incorporating gcWGAN into Principle-Driven De Novo Design.

We tested two ways to incorporate our data-driven gcWGAN into a principle-driven protein design method, RosettaDesign: initialize sequence search with specific seed designs and reduce search space with predicted sequence profiles (only top amino acids giving the probability above varying thresholds are allowed for each residue). In each setting, we run 20 parallel jobs of RosettaDesign for 4 days. Due to the computational expenses, we restrict the study to the novel fold. More details including the RosettaDesign scripts can be found in SI Section S10.

RESULTS

Fold Representation as Input.

To construct a low-dimensional fold representation as the conditional input to gcWGAN, we performed kernel PCA for the fold space spanned by the 1232 basis folds. The first 20, 200, and 400 principal components (PCs) explained around 15%, 50%, and 75% of the variance, respectively (Figure S2). As the dimension of fold representation determines that of the conditioning variable y in cWGAN and a higher dimension causes more demanding model training, we chose the space spanned by the first 20 PCs as a lower-dimensional representation of fold space. An analysis on the resolution of the fold representation shows that the explained variance of the 20 PCs reach 60% for 40 cluster centers of the 1232 original folds (Figure S3). Visualization of the fold representations shows that folds are well clustered, consistent with their class membership (Figure S4), where α/β and α + β folds’ representations distributed between the clusters of α and β folds.

Fold Prediction as Oracle.

We next assess the oracle in gcWGAN that, during training, gives feedback on the generated sequences’ chances of belonging to the target fold. We compared, in Table S4, the original DeepSF using all features or sequence only and our oracle (modified DeepSF) using sequence only. For the test set, top-10 predictions from DeepSF impressively achieved an accuracy of 0.94 using all features, whereas they only did that for 0.69 using just sequence. By modifying the model architecture, our oracle using just sequence increased the accuracy to 0.74. Meanwhile, our oracle only uses milliseconds to predict for each sequence, whereas DeepSF spends minutes on nonsequence feature calculations alone. Therefore, our oracle is a somewhat ambiguous yet ultrafast fold predictor that is suitable for the framework of gcWGAN.

Semisupervision Improves Training for gcWGAN.

We report hyper-parameter tuning results in Figures S6–S9 and Table S5. We also showcase the benefit of semisupervision in Figure S10. The training of gcWGAN was warmed up with parameters initialized at trained values of the semisupervised cWGAN. Compared to using supervised cWGAN (skipping unsupervised pretraining), semisupervised gcWGAN training reached lower overall losses in the last 20 of the 100 epochs (p-value being 0.05 and 0.04 according to one-sided paired t-test and Wilcoxon signed-rank test, respectively; see Table S6). The trend was maintained with the last 20 of 100 more epochs during training (both p-values being around 0.02). Moreover, semisupervision increased yield ratios for five of the six test folds by 24%–687% (Figure S11).

Oracle Feedback Increases Yields.

For intermediate sequence designs, we first examine their yield ratios for all test folds in Table 2. Training and validation results for cWGAN and gcWGAN can be found in Table S7. gcWGAN with oracle feedback improved the yield ratio for an average test fold by around 79% compared to cWGAN and did so by more than 39% for five out of seven fold classes (especially class g or small proteins for which an improvement of 933% was reached) and did so by over 93% for difficult cases that are the least designable. Two factors affect the yield ratios: (1) Easy folds with abundant sequence availability are with higher yield ratios for the training or test set because of more data or more designability. (2) Folds for which the oracle is more accurate see higher yield ratios.

Table 2.

Yield Comparison among cVAE, cWGAN, and Guided-cWGAN for the Test set

	cVAE		cWGAN		gcWGAN
	yield ratio	fold coverage	yield ratio	fold coverage	yield ratio	fold coverage
all	7.5 × 10−3	0.084	1.4 × 10−3	0.327	2.5 × 10−3	0.290
Fold Class Breakdowns
a	<1 × 10−5	0.000	7.9 × 10−5	0.286	2.8 × 10−4	0.250
b	5.3 × 10−2	0.200	3.5 × 10−3	0.467	7.0 × 10−3	0.267
c	2.2 × 10−5	0.125	8.6 × 10−3	0.750	1.2 × 10−2	0.750
d	1.4 × 10−5	0.049	7.5 × 10−4	0.268	1.1 × 10−3	0.195
e	<1 × 10−5	0.000	<1 × 10−5	0.000	<1 × 10−5	1.000
f	<1 × 10−5	0.333	2.2 × 10−5	0.333	<1 × 10−5	0.000
g	1.1 × 10−3	0.182	9.1 × 10−5	0.182	9.4 × 10−4	0.455
Sequence-Availability Class Breakdowns
easy	2.2 × 10−3	0.625	1.3 × 10−2	1.000	2.1 × 10−2	0.875
medium	3.6 × 10−2	0.136	8.1 × 10−4	0.500	1.4 × 10−3	0.364
hard	<1 × 10−5	0.013	4.6 × 10−4	0.208	8.9 × 10−4	0.208

We also incrementally generate up to 10⁵ sequences for each of the six selected folds. We observe that gcWGAN with feedback increased the yield efficiency by 39%–917% for five of them (Figure S12).

gcWGAN Improves Yield Ratios for Most Folds Compared to cVAE.

We compared yield ratios between gcWGAN and a recent cVAE-based software for protein design³¹ in Table 2 (all folds and breakdowns) and Table S12 (six selected folds). Overall, gcWGAN had higher yield ratios for four of seven fold-classes and comparable ones for another two. The average yield ratio is higher with cVAE, which is very misleading because the average for cVAE was dominated by an extremely high yield ratio (0.79) for only one fold (Table S11). This test fold (b.9) is actually in cVAE’s training set (the closest example used in cVAE had a TM score at 0.56, indicating the same fold; see Table S13). Once the cVAE training folds are removed from our test sets, gcWGAN has a higher yield ratio on average and in almost every subset (Table S10).

Importantly, gcWGAN achieved yield ratios over 1 × 10⁻⁵ for 29% of test (or shared test) folds, whereas cVAE only did 8.4% (4.8%). For all six selected test folds, gcWGAN increased the yield ratios by 1 to 2 orders of magnitude. Note that three of our six test folds turned out to be in cVAE’s training set (Table S13), as the information had not been available until recent.

All the yield ratios are relatively low—gcWGAN achieved around 2% on average even for folds with abundant sequences or 0.4% for folds with high oracle accuracy. We however note that many sequences declared nonyields by the imprecise oracle could be false negatives. We also note that low yield ratios can be overcome with high throughput and do not affect accuracy as we show in structural evaluation.

Although sequence identity to natural sequences is not necessarily a fit to assess fold design (to be detailed next), we compared cVAE, cWGAN, and our gcWGAN in this regard for completeness (Table S14). We used intermediate designs from cWGAN and gcWGAN before the final oracle filter. We found that all methods had sequence identity around 0.2 for test folds, although cVAE shows a slight overfit. To contexualize the seemingly low sequence identity level, we examined the identity distributions for natural sequence pairs of the same fold (as well as superfamily and family). We note that around 66% and 89% of them (at 90% sequence redundancy level) are with an identity below 0.2 and 0.3, respectively, highlighting the challenge of fold design. Interestingly, the mean identity for natural sequences within a fold is 0.21, similar to the value for model-generated sequences within an average test fold. Nevertheless, the lack of sequence similarity within a fold echoes the definition of fold (purely by what and how secondary structure elements are arranged and not by common evolutionary origins). It also highlights the challenge to design and assess protein sequences for a target fold. More details are in SI Section S7.3.

gcWGAN Designs Physically and Biologically Meaningful Sequences.

We next examine whether the designed sequences are physically and biologically sound. Figure 2a shows that, unlike random ones, gcWGAN-designed sequences are similar to natural sequences in instability index (both mean and distribution; more details in Sec. S11.1). An instability index below 40 is considered a sign of protein stability. Compared to random sequences whose average instability index was 45.49, gcWGAN-designed sequences had an average instability index of 39.63, close to and slightly edging natural sequences (39.88). The instability indices of gcWGAN designs were also lower in distribution compared to random sequences (p-value = 2.1 × 10⁻¹⁸ according to one-sided K–S test). In particular, 61.2% of gcWGAN-designed sequences were of instability index below 40, compared to 56.1% for natural sequences and 0% for random sequences.

Figure 2.

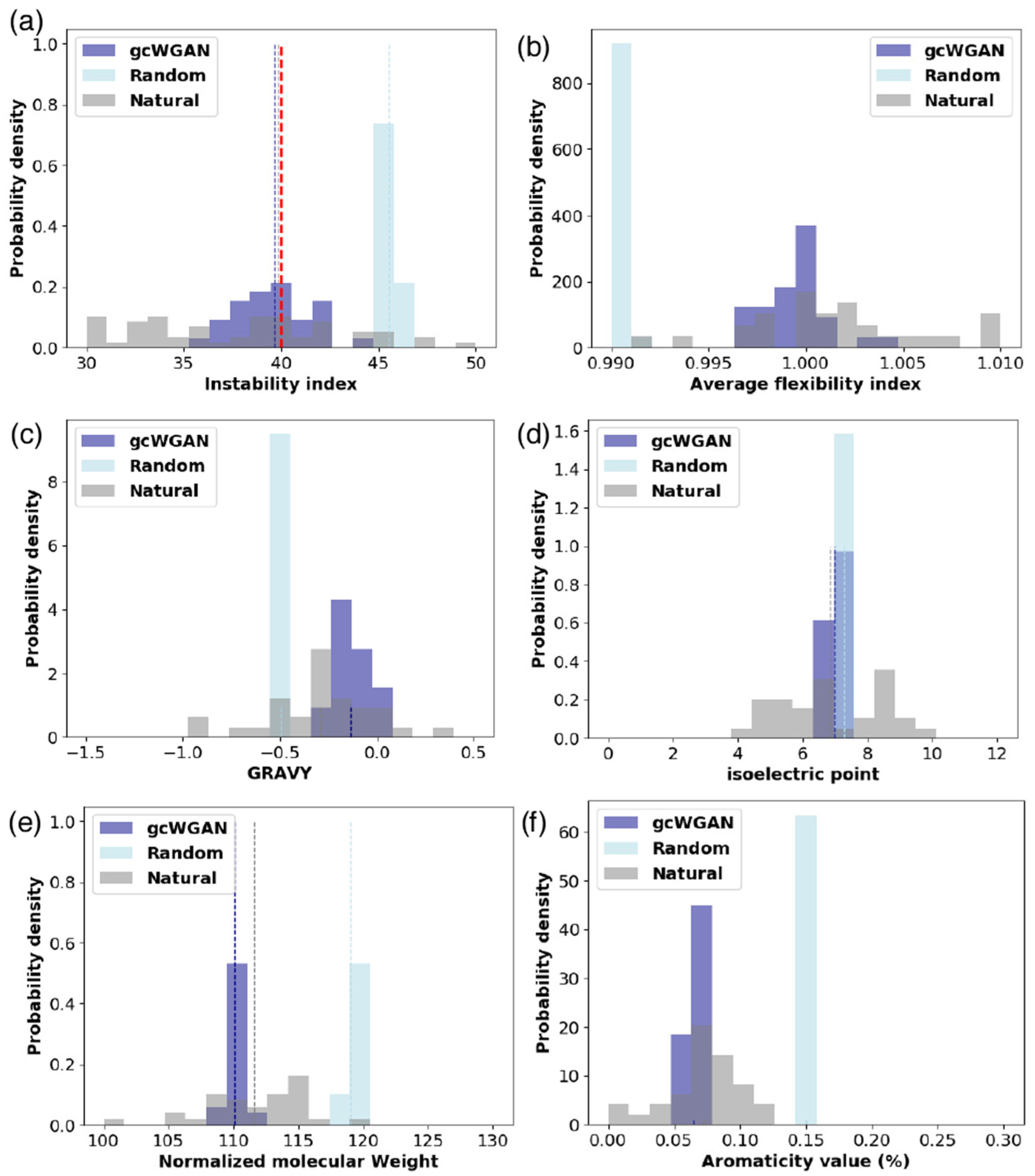
Distributions of the biophysical properties for random, generated, or natural sequences: (a) instability index, (b) average flexibility index, (c) GRAVY, (d) isoelectric point, (e) normalized molecular weight, and (f) aromaticity value. Vertical dashed lines indicate means of the same colored bars, except that red ones indicate thresholds.

We note that, unlike principle-driven protein design (such as Rosetta) whose design objective can explicitly include stability optimization, our data-driven approach learns from rather than optimizes against natural sequences. So gcWGAN designs are not supposed to be more stable than natural sequences, although some Rosetta designs were shown to before.

We also examined other biophysical properties. Figure 2b–f shows that, compared to random sequences, generated sequences are much closer in distribution to natural sequences in flexibility, grand average hydropathy (GRAVY), Isoelectric point (pI), normalized molecular weight, and aromaticity. We provide distances between means or distributions of generated and natural sequences in Table S17.

To explain the physical origins of predicted stability of generated sequences, we further compared the distributions of generated and natural sequences in buried nonpolar surface area, hydrogen bond energy, and Rosetta overall energy in Figure S16 (marginalized 2D distributions). We again found similar distributions between the two sets of sequences.

To examine physical origins of folds, we have investigated one α fold (a.35) to compare residue-level hydrogen-bonding patterns between a designed sequence (with Rosetta-predicted structures) and three natural sequences (with crystal structures). Figure S17–18 indicate that, even though the three natural sequences and the generated ones have different lengths, common characteristic hydrogen-bond patterns potentially contributed to their sharing the fold, such as the extensive close-to-diagonal lines indicating α helices and a common off-diagonal block indicating helix packing.

For the last part of this subsection, we have examined protein functions (GO terms) predicted for generated sequences and those known to natural sequences. Out of 25 yielding test folds with experimentally annotated protein functions, we show in Figure 3 the ΔGO similarity between generated and natural sequences of target folds (with background similarity to natural sequences of off-targets removed). We find that the designed sequences have above-zero ΔGO similarity with statistical significance (p-value from t-test being 2 × 10⁻¹⁰⁹ for molecular function and 4 × 10⁻⁶¹ for biological process). These results suggest that gcWGAN-generated sequences are much more functionally similar to their target folds than they are to off-targets, supporting the fold specificity of these designs in the sense of protein function.

Figure 3.

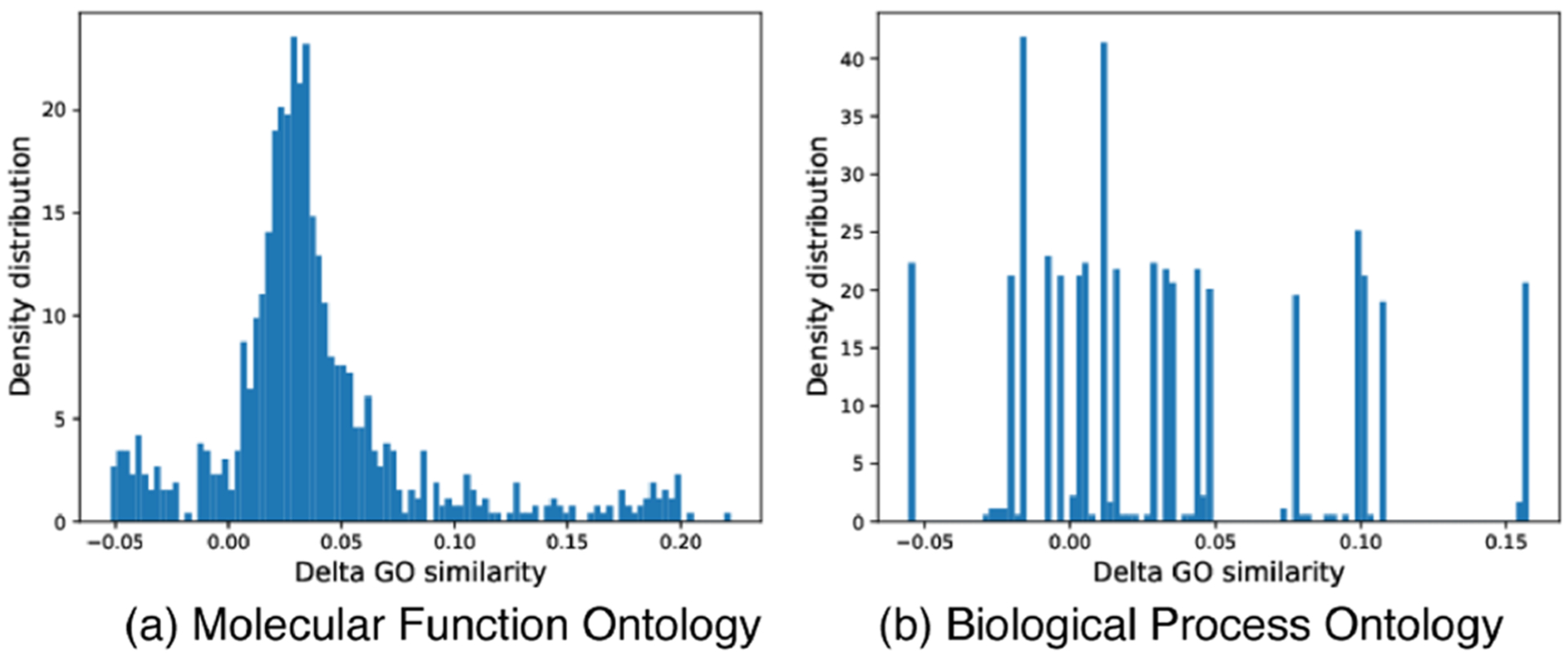
ΔGO-similarity between designed and natural sequences of target folds, with the background similarity to off-target folds removed.

gcWGAN Designs Sequences of Comparable or Better Accuracy Compared to cVAE.

We proceed to examine final sequence designs (the yields) using Rosetta-based structure prediction, for six selected test folds (not seen in the training set thus regarded novel). For each fold, we designed 10 sequences using either gcWGAN or cVAE and predicted 100 structure models using Rosetta. The distributions of the structures’ TM-scores (Figure 4), when compared to corresponding ground truth, showed that gcWGAN outperforms cVAE. Specifically, gcWGAN (oracle-filtered) had higher TM-score distributions than cVAE for four of six folds with p-values way below 1 × 10⁻⁶. Taken together, gcWGAN could design protein sequences more specific to target folds than off-targets. It can sometimes do so with good accuracy: the best TM-score is not always above 0.5 but often well above 0.4.

Figure 4.

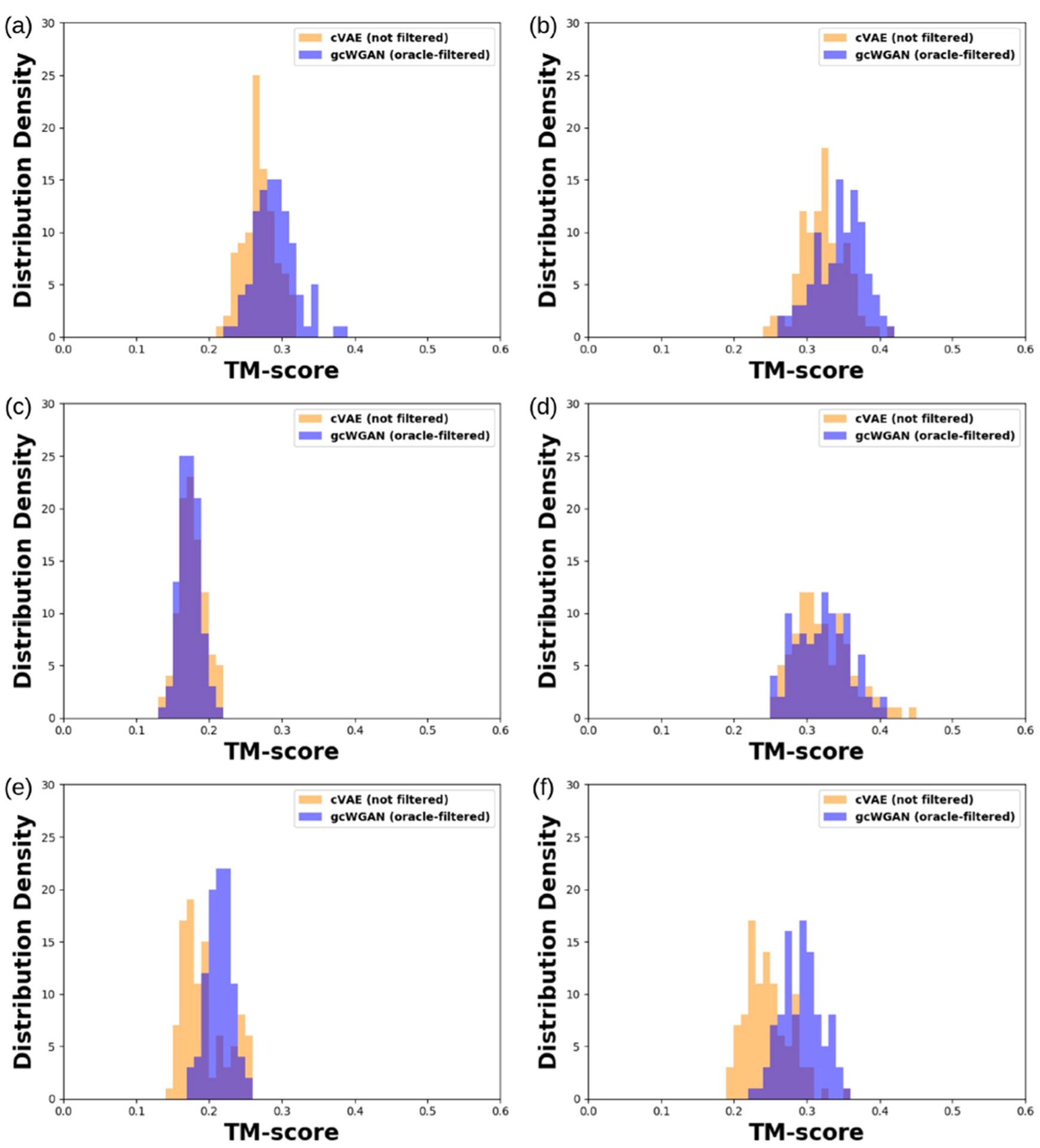
Distribution of the TM-scores between cVAE/gcWGAN designs and the ground truth for six selected, representative test folds: (a) b.2, (b) a.35, (c) c.94, (d) g.44, (e) c.56, and (f) d.146.

We also compared gcWGAN and cVAE on a novel fold not even in the 1232 basis folds for fold embedding. When applying the filter on gcWGAN designs for the novel fold, we selected neighbor folds according to TM alignment and chose a.188. gcWGAN improved the best TM score compared to cVAE albeit without an advantage in distribution (Figure 5a). Impressively, the best sequence/structure combination from gcWGAN had a TM-score of 0.46, very close to the threshold to indicate the same fold. The predicted structure is superimposed to the ground truth in Figure 5c.

Figure 5.

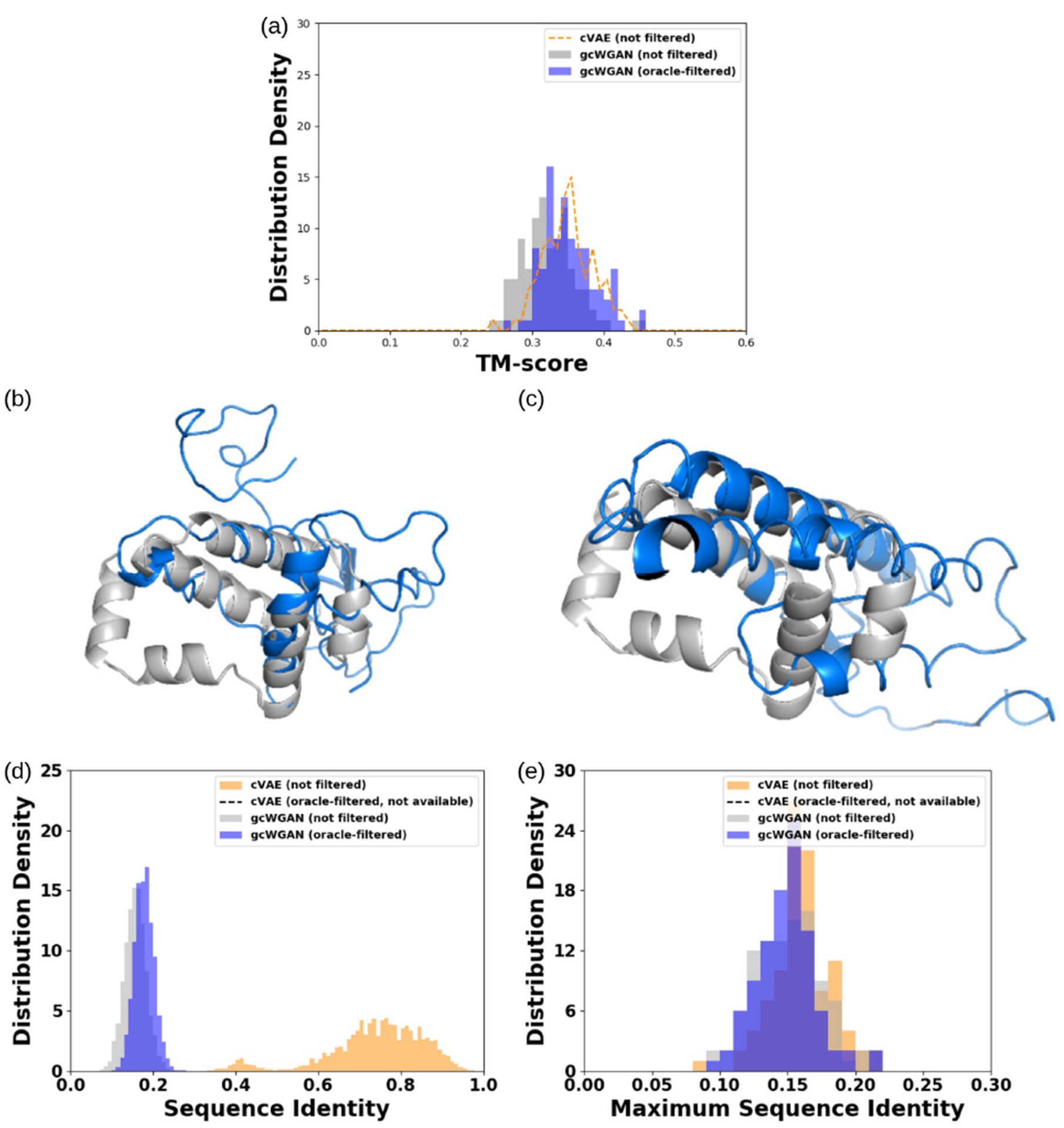
Assessing gcWGAN designs targeting a completely novel fold when the oracle gives feedback on the closest basis fold a.188. (a) TM-score distribution. (b) Best gcWGAN design (not filtered) (blue) and the ground truth (gray) (TM-score = 0.45). (c) Best gcWGAN design (oracle-filtered) (TM-score = 0.46). (d) Sequence diversity (more with lower identity). (e) Sequence novelty (more with lower identity).

gcWGAN Designs More Diverse and More Novel Sequences Compared to cVAE.

Besides the fold accuracy, we also examine the diversity among the designed protein sequences as well as their novelty compared to known representative sequences. For both the six test folds and the completely novel fold, gcWGAN designs for the same fold are of low sequence identity below 0.3, whereas most cVAE designs are close homologues with sequence identity above 0.3 (Figure 5d and Figure 6). Apparently, gcWGAN could explore much more diverse regions of the sequence space, while maintaining decent fold specificity and accuracy as examined earlier.

Figure 6.

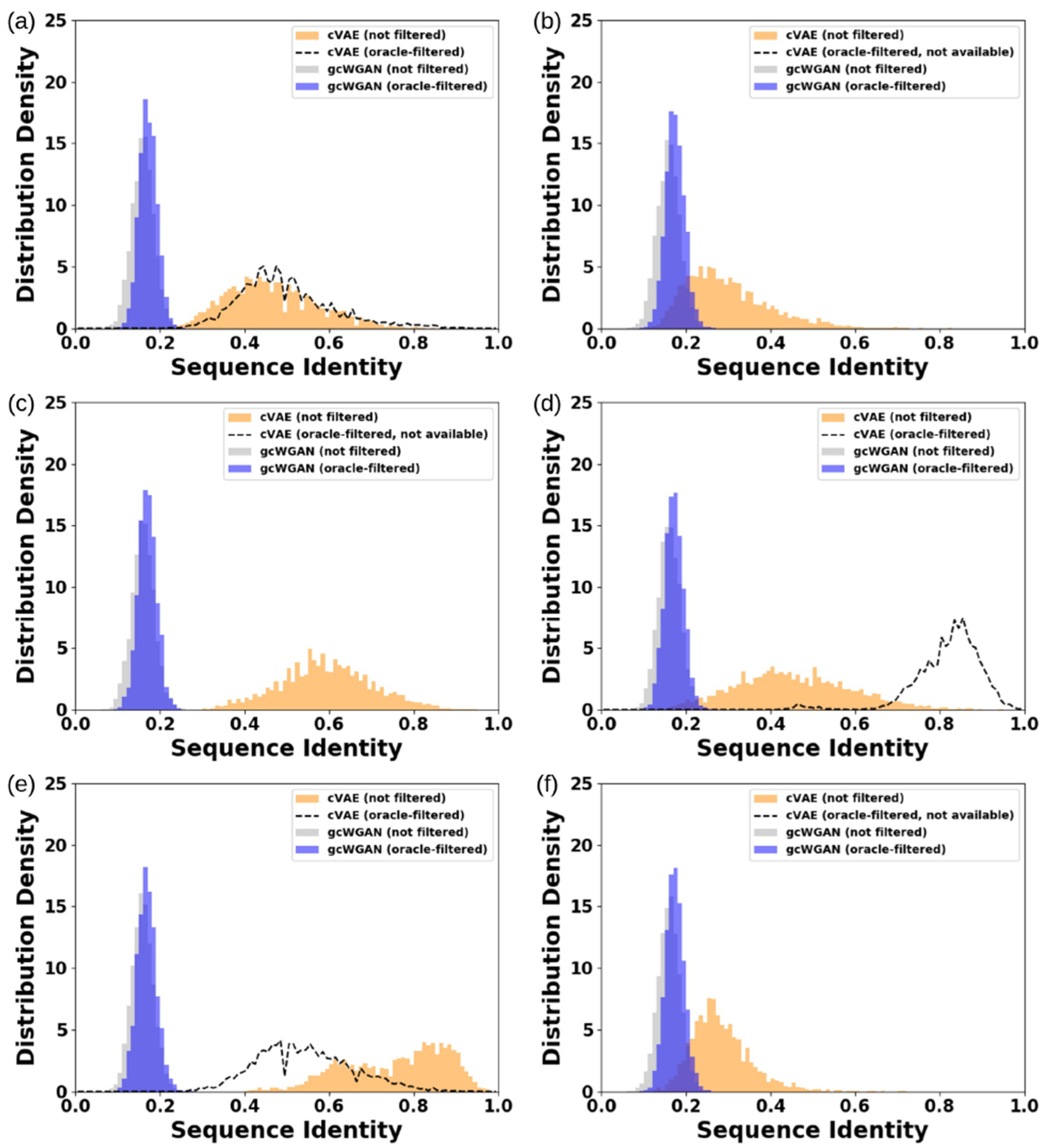
Comparing sequence diversity between cVAE and gcWGAN designs for the six selected cases: (a) b.2, (b) a.35, (c) c.94, (d) g.44, (e) c.56, and (f) d.146. Lower sequence identity indicates more diversity and that below 0.3 indicates no close homologues.

Moreover, gcWGAN designs are almost entirely of sequence identity lower than 0.3 compared to the closest, known representative sequence for the desired fold (Figure 5e and Figure 7). In contrast, cVAE designs are often close homologues of a known representative sequence with sequence identity above 0.3. In particular, the best cVAE design for b.2 and g.44 are of sequence identity at 0.62 and 0.43, respectively, whereas such gcWGAN designs are of sequence identity at 0.20 and 0.17, respectively, while giving better or comparable TM-scores for target folds. Therefore, gcWGAN is exploring uncharted regions in the sequence space.

Figure 7.

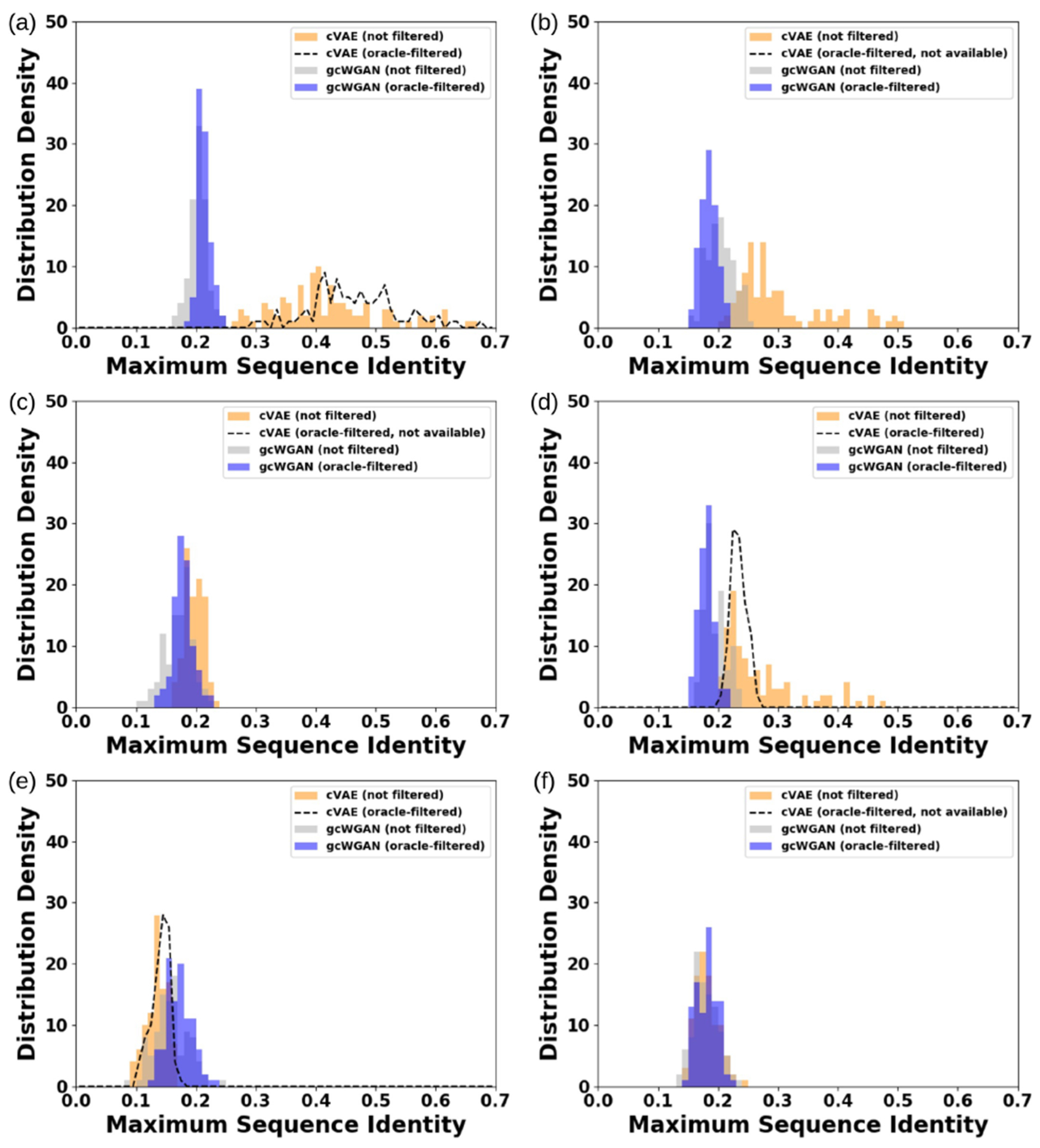
Comparing sequence novelty between cVAE and gcWGAN designs for the six selected cases: (a) b.2, (b) a.35, (c) c.94, (d) g.44, (e) c.56, and (f) d.146. Lower sequence identity indicates more novelty and that below 0.3 indicates no close homologues to known sequences of the same fold.

cWGAN and gcWGAN have similar and improved sequence diversity/novelty compared to cVAE, which was regardless of the application of the final, oracle filter (Figures 6 and 7 and Figures S19–22). (Applying the final filter to cVAE was only feasible for three of the six test folds as no sequence was accepted in 2 days in those cases.) Therefore, the improved diversity and novelty of gcWGAN designs were not attributed to filters but to our design of the Wasserstein distance replacing Jensen–Shannon divergence in GAN. In addition, gcWGAN improves yield ratios compared to cWGAN, as previously shown in Table 2, suggesting that the increased yield (success) is due to the oracle feedback.

Integrating Data- and Principle-Driven Approaches for De Novo Protein Design.

Targeting the novel fold not even in the basis set for fold representation learning, we use RosettaDesign for de novo protein design without and with gcWGAN incorporated. gcWGAN provides specific designs to initialize sequence search or/and sequence profiles to reduce design space for Rosetta.

Table 3 shows that the best RosettaDesign result for the novel fold had a TM score of 0.53, similar to the best gcWGAN design (0.46). Table 3 also shows that, even without design-space reduction (prob. cutoff being 1), simply using gcWGAN designs as Rosetta “seeds” would double the count of successful designs (from 7 to 14), judging by whether they are predicted to follow the secondary structures and topological constraints of the target fold (RosettaDesign criteria). These designs are predicted to adopt the target fold, judging from TM-scores being close to or above 0.5. In addition, gcWGAN design profiles can drastically reduce the design space by up to 10¹² without reducing the successful designs. Interestingly, even when the design space is reduced by 10⁷⁶, a level where the original Rosetta fails to find a successful design, RosettaDesign with gcWGAN initialization can still produce six successful designs with good quality. Sequence identities of all successful designs are below 0.2, which is not necessarily wrong considering the low sequence similarity that we observed earlier in natural sequences of the same fold. Our results attest to the power of integrating principle- and data-driven approaches to de novo protein design.

Table 3.

Comparison of RosettaDesign and RosettaDesign + gcWGAN Using gcWGAN Sequences (to Initialize Search) and Profiles (to Reduce Design Space)

		RosettaDesign			RosettaDesign + gcWGAN
Prob. cutoff	Design space reduction	# Success	Best TM	Identity	# Success	Best TM	Identity
1 (All)	–	7	0.53	0.16	14	0.49	0.15
0.99	1.81 × 104	7	0.42	0.17	11	0.46	0.09
0.95	1.12 × 1012	4	0.37	0.19	13	0.47	0.16
0.9	9.77 × 1018	5	0.49	0.14	9	0.50	0.12
0.5	1.04 × 1076	0	-	-	6	0.45	0.16

CONCLUSIONS AND DISCUSSION

We have designed novel deep generative models for de novo protein design targeting novel structure folds. Here, we utilize both sequence data with and without structures in a semisupervised setting and an ultrafast oracle for fold recognition as feedback. As summarized below, our results reveal the value of current protein data toward unraveling sequence–structure relationships and utilizing resulting knowledge for inverse protein design.

Over model-designed sequences for nearly 800 folds of diverse class and difficulty (including over 100 test folds not seen in the training set), we first globally assess their performances using the oracle, an ultrafast yet imprecise fold predictor. Compared to a data-driven alternative (cVAE), our gcWGAN model generates more yields (according to the oracle) for nearly all target folds and achieves much more coverage of target folds. These designs are also predicted to be stable and specific for target folds in the sense of physics and functions.

For selected representative test folds and a novel fold not seen in the 1232 basis folds, we assess gcWGAN designs using a structure predictor. We find that gcWGAN designs are comparable or better in fold accuracy compared to cVAE. Notably, gcWGAN designs are much more diverse, which can be attributed to that WGAN with its implicit model and Wasserstein distance overcomes known limitations of VAE.^49,72,73 Moreover, gcWGAN designs are often novel in sequence rather than close homologues of known proteins. This indicates that gcWGAN is exploring uncharted regions in the sequence space, using what it learns from the data about sequence–fold relationships rather than simply mimicking the data.

Among major factors affecting gcWGAN performances, fold representation and oracle’s accuracy need the most improvement. Currently, our fold representation is learned in a nonparametric way (kPCA) preserving distance metrics. But its resolution is limited as we choose a low-dimensional subspace for computational concerns. Our oracle is ultrafast yet highly ambiguous and imprecise, so the feedback has limited performance boost. Very accurate yet expensive fold predictors (such as the original DeepSF) acting as the final filter could still improve the performance not during but after the training stage. Interestingly, folds with few sequences known in nature, thus potentially less designable, also appear to be more difficult for the data-driven gcWGAN approach even though those sequences and folds are never known to gcWGAN during training.

gcWGAN designs proteins much faster than principle-driven structure-based methods (10⁻³ s versus at least 10⁵ core hours) and thus can provide seed designs and tailor a much reduced design space for the latter. Indeed, our experiments show that, through the aforementioned two ways of incorporation into Rosettadesign, gcWGAN significantly improves the success for the novel fold, suggesting the potential of integrating principle-and data-driven approaches to de novo protein design.