Abstract
The great saphenous vein (GSV) has served as a coronary artery bypass graft (CABG) conduit for over 50 years. Despite prevalent use, first-year failure rates remain high compared to arterial autograft options. Amongst other factors, vein graft failure can be attributed to material and mechanical mismatching that lead to apoptosis, inflammation, and intimal-medial hyperplasia. Through the implementation of the continuum mechanical-based theory of “stress-mediated growth and remodeling,” we hypothesize that the mechanical properties of porcine GSV grafts can be favorably tuned for CABG applications prior to implantation using a prolonged but gradual transition from venous to arterial loading conditions in an inflammatory and thrombogenic deficient environment. To test this hypothesis, we used a hemodynamic-mimetic perfusion bioreactor to guide remodeling through stepwise incremental changes in pressure and flow over the course of 21-day cultures. Biaxial mechanical testing of vessels pre-and post- remodeling was performed, with results fit to structurally-motivated constitutive models using non-parametric bootstrapping. The theory of “small-on-large” was used to describe appropriate stiffness moduli, while histology and viability assays confirmed microstructural adaptations and vessel viability. Results suggest that stepwise transition from venous-to-arterial conditions results in a partial restoration of circumferential stretch and circumferential, but not axial, stress through vessel dilation and wall thickening in a primarily outward remodeling process. These remodeled tissues also exhibited decreased mechanical isotropy and circumferential, but not axial, stiffening. In contrast, only increases in axial stiffness were observed using culture under venous perfusion conditions and those tissues experienced moderate intimal resorption.
Keywords: perfusion culture, vein arterialization, vascular remodeling, bypass grafting
INTRODUCTION
Stenosis and failure of coronary artery bypass grafts (CABGs) generally follow a well-characterized pattern of cell infiltration, proliferation, and extracellular matrix (ECM) deposition forming a new layer between the intima and media, narrowing the lumen and obstructing perfusion of the myocardium.42 This process, known as intimal hyperplasia, is a primary cause of the 6% failure rate of CABGs within the first year.5 Moreover, multivessel disease and a lack of suitable autologous candidates lead to frequent use of great saphenous veins (GSVs) for CABGs that fail at significantly higher rates in the near, mid, and long term.3,15 While this phenomenon is hardly controversial, researchers continue to work towards methods of avoiding these maladaptive processes with little clinical success.
Mechanical discrepancies between the graft and host tissue play a significant role in vein graft failure.17 A classical and generally accepted theory contends that blood vessels are structured to optimally distribute mechanical loads in their native hemodynamic environment, wherein they operate under what is referred to as the homeostatic stress state.13,14 Sustained deviations from native hemodynamic loading perturb the local mechanical environment of the vessel wall, stimulating an adaptive remodeling process which seeks to restore the homeostatic stress state via phenotypic modulation of resident vascular cells.22 Indeed, previous investigations have demonstrated the capacity of vessels to restore homeostatic values of stress following perturbations to both wall shear and circumferential stress due to changes in blood flow and pressure, respectively.25,31 Although this phenomenon has been observed in vivo, few studies have achieved comparable results in vitro.7,18,19 In this investigation, we seek to manipulate mechanical loads in vitro to confirm prior in vivo observations and theories of stress homeostasis and to explore whether we can manipulate veins towards mechanical properties more suited to the arterial circulation than fresh venous tissue.
The use of GSVs for CABG results in transplantation from a relatively steady, low pressure, low flow environment to the higher pulsatility, higher flow, and higher pressure of the coronary circulation. The acute mechanical deviations experienced by autologous grafts upon introduction to the coronary circulation thus include increased circumferential and axial tensile wall stresses and flow-induced shear stress at the intima,37 which can be significant and potentially beyond the restoration capacity of adaptive remodeling.19 Others have proposed an ex vivo tissue culture strategy to guide vein-to-artery adaptation, whereby transitioning between native in situ loads and expected grafted loads would be divided into smaller steps or a continuous gradual increase.26 Thus, each step would perturb the local mechanical environment enough to initiate remodeling but not so much to prevent full restoration of mechanical homeostasis via adaptive processes. This stepwise process is repeated until the graft vessel is at mechanical homeostasis under the target loads.26 Similarly, using a constrained mixture model of vascular growth and remodeling, simulations predict gradual loading would increase a vein’s likelihood of successful adaptation.38
In this investigation, we build upon our previous ex vivo culture experiments (i.e., gene expression, microscopy, viability) to assess the effects of stepwise transition from venous to arterial hemodynamics on GSV adaptive remodeling using a pulsatile perfusion bioreactor.34,36 We hypothesize that GSVs experiencing gradual transition to coronary loading conditions, and in the absence of a systemic inflammatory system and circulating platelets, will undergo adaptive growth and remodeling and be better mechanically suited to the coronary circulation, while avoiding intimal hyperplasia and maladaptive remodeling. This adaptive remodeling, in theory, should include increased deformed inner radius and wall thickness at arterial pressures without the thickened intima and denuded endothelium characteristic of early intimal hyperplasia. To help elucidate and translate these findings into “growth-and-remodeling” theory, state-of-the-art constitutive models using nonparametric bootstrapping are employed to illustrate best-fit parameters from nonlinear regression while employing the theory of “small-on-large” for appropriate linearization around physiological operating points.
MATERIALS AND METHODS
Tissue Harvesting and Preparation
A total of 23 GSVs were initially isolated from freshly slaughtered American Yorkshire sows (200 ± 20 kg; 36 ± 6 months old) at a local abattoir. All vessels used in this investigation originated from animals raised for human consumption and do not fall under IACUC protocol. Vessels were stored and transported on ice in Moscona’s saline solution supplemented with 20 U/mL heparin, 1% penicillin/streptomycin, 1% amphotericin-B, and 1% gentamycin. Under sterile conditions in a biological hood, excess perivascular tissue was removed using forceps and spring scissors, and branches were ligated with sterile 3-0 silk suture. For each vessel, one section approximately 40 mm in length, was mounted to custom barbed glass cannulae within a glass bioreactor (Adams & Chittenden Scientific Glass, Berkeley, CA) and the sample was extended to 1.4x its unstretched length (suture-to-suture) to approximate in situ axial stretch, with this stretch ratio determined from preliminary mechanical testing of GSVs prior to culture using established techniques.11,44 A second section 10-mm in length was mounted to barbed female luer lock fittings for day 0 biaxial mechanical testing. Vessel segments were isolated from similar anatomical locations for each test.
Ex Vivo Vessel Culture
A detailed description of the bioreactor can be found in Prim et al. 2018.34,36 Briefly, the glass vessel chamber was incorporated into a flow loop containing a roller pump, pressure transducer, downstream resistor, compliance chamber, and media reservoir, all contained within a sterile incubator at 37 °C and 5% CO2. The culture medium in the vessel chamber (150 mL) and reservoir/flow loop (300mL) was DMEM containing phenyl-red and supplemented with 10% fetal bovine serum, 1% penicillin/streptomycin, 1% amphotericin-B, and 1% gentamycin, which was replaced every 7 days. Carbamylcholine chloride (10−5 M) was used initially to induce endothelial cell-dependent relaxation to prevent vasospasm at the initiation of culture. Controlled mechanical loading parameters were the volumetric flow rate (Q) and pressure (P), whereby GSVs were cultured for 21 days under either in situ loading conditions (Venous: Q = 0.17 ±0.03 mL/s; P = 15 ±1.9 mmHg) or stepwise loading from in situ to coronary pulsatile loading conditions (Arterial: Q = 0.52 ±0.13 mL/s; P = 102 ± 8.4 mmHg). For each 3 day interval (21 days, 7 total intervals), flow and pressure were calculated to achieve an equal percent increase at each step (ΔQ = 17.3% and ΔP = 31.5%) (Figure 1). Vessels were monitored daily for shifts in pH and/or contamination. Phenylephrine HCl (10−5 M) was used as an intermediate marker of smooth muscle viability by observing contraction prior to media exchange. Any contaminated cultures or vessels that failed the vasoreactivity assay were immediately terminated. At the end of each culture, one section (15 mm) was cut from the middle of the sample and mounted to female barbed luer lock fittings for biaxial mechanical testing; one section (1 mm) was cut for tissue viability assessment; and one section (3 mm) was cut and prepared for histological analysis.
Figure 1.
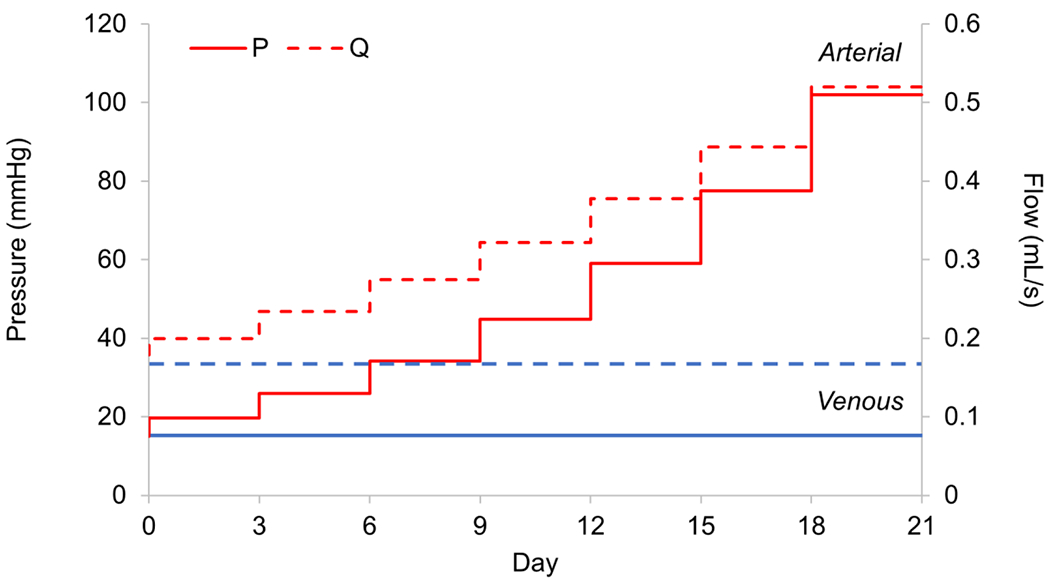
Mean venous (blue) and stepwise venous-to-arterial (Arterial; red) perfusion culture conditions for 21 days. For the transition culture scenario, increases in pressure (solid lines) and volumetric flow (dashed line) were made at 3-day intervals with concatenate increases in pulsatility (not shown). Flow increased by 17.3% each step and pressure by 31.5%. Axial extension remained constant throughout.
Biaxial Mechanical Testing
Mechanical testing protocols followed in a similar fashion to our previous work using a customized Bose BioDynamic 5270 device with 22 N force transducer having a 10−5 N resolution and 50 Hz maximum sampling frequency.37,45 Briefly, samples were secured to female barbed luer lock fittings using 3-0 braided silk suture, and unstretched suture-to-suture length was recorded. Samples were then mounted in the testing chamber of the device, taking care to avoid twisting or overstretching of the vessel, and length of the axial control arms were adjusted to the previously recorded unstretched values. Axial force and luminal pressure gauges were tared after mounting but before data acquisition. The testing chamber and flow loop were filled with PBS supplemented with 10−5 M sodium nitroprusside warmed to 37 °C to ensure complete SMC relaxation.
After clearing air bubbles from the flow loop, the pressure was increased from 0-200 mmHg at increasing axial stretch while taking note of the corresponding axial force values, and the axial stretch at which axial force remained constant throughout pressurization was noted as the approximate in vivo stretch. Axial extension and pressurization preconditioning protocols were performed prior to collecting data. For these, pressure was set to 100 mmHg, and samples were stretched at 0.05 mm/s to the aforementioned in vivo stretch plus 10 percent for 8 cycles. Next, with axial stretch set at the approximate in vivo value, pressure was increased from 0-200 mmHg at 1 mmHg/s for 8 cycles. To refine the in vivo stretch estimation, in consecutive trials vessels were pressurized to 60, 100, and 140 mmHg, axial stretch was increased from 1 to the approximate in vivo value plus 10%, and axial force was recorded throughout. When plotted together as axial stretch versus axial force, the point at which the three curves intersected was assumed to be the in vivo axial stretch.10,30
For data collection, samples were subjected to quasistatic inflation at three axial stretches: the in vivo value, ~10% above in vivo, and ~10% below in vivo. At each axial stretch, pressure was increased from 0-200 mmHg at 1 mmHg/s, with outer diameter, and axial force recorded at 20 mmHg increments. This procedure was repeated for 3 trials at each of the 3 axial stretch values. Thus, each vessel was tested in triplicate and the mean values of response variables were analyzed. In contrast, grouped data represent averaged values for each of the groups: Day 0, (n=10) and hemodynamic-mimetic perfusion tissue culture at venous (Venous; n=4) or stepwise venous-to-arterial transitional perfusion conditions (Arterial; n=6), groups. All Day 0 mechanical and histological data were paired to their Venous or Arterial group counterparts.
Viability and Histological Analysis
At the termination of 21-day cultures, 1 mm ring sections were cut from perfused samples and incubated in 0.5 mg/ml methylthiazol tetrazolium (MTT; Sigma-Aldrich, Munich, Germany) in sterile Moscona’s saline at 37 C for 1 hour. Images were collected using the microscope-mounted DSLR described above. Yellow MTT solution is reduced to an insoluble purple formazan product in the presence of metabolically active and viable cells, so relative tissue viability was quantified via threshold analysis of purple pixels to total cross-section area in ImageJ (National Institutes of Health). Any vessels that failed the MTT colorimetric assay, and their Day 0 counterparts, were excluded from the analysis. For histology, sections were fixed in 4% paraformaldehyde, embedded in paraffin, sectioned at 5 pm with a microtome and stained with hematoxylin/eosin or Masson’s trichrome.
Data Analysis
Following mechanical testing, ring sections 1 mm thick were cut from the center of tested samples, placed in a shallow dish of PBS, and images collected using a DSLR camera (Canon USA, Long Island, NY) mounted to a dissecting microscope (Carl Zeiss Microscopy GmbH, Jena, Germany) using an adapter lens (Micro Tech Lab, Graz, Austria). A radial stress-relieving cut was made in each ring, and the cut sectors equilibrated for 20 minutes before images were collected of the stress-free configuration. ImageJ (NIH) was used to measure inner arc length Li, outer arc length Lo, and cross sectional area A. From these data, stress-free thickness H and opening angle Φ could be calculated using
| (1) |
Here we assume that our vessels experience axisymmetric finite elastic deformation due to applied pressure and longitudinal extension and are cylindrically shaped homogeneous and incompressible tubes. By deactivating smooth muscle contractility with sodium nitroprusside, we consider only the passive mechanical properties resulting from extracellular matrix components – primarily collagen, elastin, and ground substance.44 Given tissue incompressibility, we calculate the deformed inner radius ri as
| (2) |
where the deformed outer radius ro and axial stretch xz are measured at each loading state. The mid-wall circumferential λθ and axial λz stretches are
| (3) |
where l and L are the deformed and undeformed lengths of the vessel segment.
Mean circumferential σθ and axial σz, experimental wall stresses are
| (4) |
where h is the deformed wall thickens, P the luminal pressure, and F the axial force.
Poiseuille flow was assumed so that steady wall shear stresses were estimated by
| (5) |
where μ =8.9×10−4 Pa-s approximates the dynamic viscosity of the culture media. Our experimental configuration prevented real-time measurements of inner radii so these were assessed post-facto under fully passive conditions and would tend to underestimate the shear stresses experienced in culture.
The lumen area compliance is given as
| (6) |
where ΔP is the change in pressure and Δri the corresponding change in radius.35
Theoretical Framework
We utilized a structurally-motivated constitutive model initially proposed by Holzapfel, Gasser, and Ogden (HGO), and later modified to include four collagen fiber families distinguished by orientation.1,21 This model separates the isotropic (iso) from the anisotropic (aniso) contributions to the total strain energy so that
| (7) |
and
| (8) |
Here c is a material parameter used to represent the isotropic contribution to the total strain energy while and represent the anisotropic material parameters of the individual fiber families. C = FTF is the right Cauchy-Green deformation tensor, a one-point symmetric tensor independent of rigid both motion and F = diag(λθ,λz,λr) is the deformation gradient tensor. Enforcing incompressibility det(F) = 1 enables radial stretch to easily be calculated as λr = 1/(λθλz). Ic and are the first and fourth principal invariants of C, respectively, defined as
| (9) |
Mk = (0, sin αk, cos αk) is a unit vector oriented in the direction of the kth fiber at an angle αk relative to the axial direction.21,37,45 Although convention varies in the literature, we assume here that α1 = 0 represents axially oriented fibers, α2 = π/2 the circumferentially oriented fibers, and the diagonal fibers were symmetric and helically arranged so that , and .
The Cauchy stress for an incompressible hyper-elastic material under finite deformations is given as
| (10) |
where is the Lagrange multiplier used to enforce incompressibility and I the identity matrix. The term containing is deemed the reaction stress while the other term, is the deformation-dependent (extra) stress. Now, if we assume trr is much less than tθθ or tzz, we can let trr ≈ 0 and the problem is reduced to one of plane stress. Then from (10), , and using the chain rule we have,
| (11) |
Next, we utilize the theory of “small-on-large” to determine appropriate stiffness linearizations that are based on the complex but fully nonlinear anisotropic strain energy function. This function also allows the inclusion of residual stresses.1 For small displacements the linearized moduli can be found by using the following (for details see Baek et al. 20071),
| (12) |
where δ is the Kronecker delta, Fo the deformation gradient relating the undeformed reference to the finitely deformed configuration about which linearization is performed, and Co the associated components of the right Cauchy-Green tensor at that configuration. Biaxial stiffnesses are then calculated using the chain rule for second-order partial differential equations so that from (12) we get,
| (13) |
The most relevant conditions for calculating stiffness are those that are physiological. In this study, however, these include both venous (~20 mmHg) and arterial (~100mmHg) culture pressures at in vivo axial stretches. These reference pressures were chosen to be slightly greater than those measured in live but anesthetized pigs in the supine position.20,27 The corresponding stretches were also used to calculate the total stored energy and biaxial state of stress.
From the nonzero equilibrium equations, the modeled pressure and force can be found from
| (14) |
and
| (15) |
The constitutive model parameters are found by minimizing the objective function between the experimentally measured (exp) and modeled (mod) pressure and force
| (16) |
with n the total of j observations and the over-bar denoting the mean value of pressure or force. This particular objective function has been found to be the best fit for biaxial data at both high and low stretches.4,11 Then a multivariate regression analysis was performed on this objective function using the Isqnonlin from MATLAB’s optimization toolbox (MathWorks; Natick, MA). Random unknown parameters are generated for each initial parameter with bounds assigned so that , and 0 < α < π/2.
Non-parametric Bootstrap
Multi-parametric models may exhibit local minima that fail to represent the material’s biaxial behavior uniquely and have non-Gaussian distributions.43 These can generate undesirable model behavior under certain conditions. To address this problem, a non-parametric bootstrap method has been developed that relies on resampling with replacement of experimental data.12,24 To produce bootstrapping distributions we define a matrix X consisting of n total experimental observations taken from each of the unique biaxial testing protocols so that xj = {Pexp (j), Fexp (j), λθ(j), λz(j)}, j = 1,2,…,n. Then for each bootstrapping iteration a unique dataset X* is created from a randomized resampled version of X at j. All values of X have the same probability of being resampled and X* contains the same total number of observations as X. Values from X already included in X* are not excluded from the dataset. In doing so, a redistribution of weight is assigned to each piece of data at random. Nonlinear regression analysis is then performed for each bootstrapping iteration using a minimization of the objective function shown in (16). The pointwise estimate is considered representative of the underlying material behavior if it is near the peak value in a bootstrapping distribution. For simplicity, visual inspection of bootstrapping results was sufficient while the identification of modes and local minima are described elsewhere.12
Statistical Comparisons
A two-way analysis of variance (ANOVA) was used to test the effects of culture conditions on geometric and mechanical variables. A Tukey-Kramer post hoc test was performed to identify groups with statistical significance considered at p<0.05.
RESULTS
The overall success rates for Venous and stepwise Arterial cultures and subsequent mechanical testing were 40% and 75% respectively with only paired pre- and post-cultured tissues considered in the analysis. Moderate variability was found using the MTT and vasoreactivity assays (Figure 2) for pre- and post-culture conditions. No observed changes in the vessel zero-stress configuration reached statistical significance due to a large sample variance (Table 1). However, trends towards increased stress-free wall thickness (Day 0 - H = 0.48 ± 0.23; Venous - H = 0.59 ± 0.15; Arterial - H = 0.62 ± 0.07 mm) and decreased opening angles (Day 0 - Φ = 90.6 ± 31.7; Venous - Φ = 56.5 ± 33.3; Arterial - Φ = 71.5 ± 21.4 deg) were observed in culture groups.
Figure 2.

Representative MTT colorimetric metabolic activity assay of stained rings from porcine great saphenous veins (GSV) (a) fresh and (B) viable 21-day stepwise Arterial transitional culture.
Table 1.
Stress-free configuration geometries for GSVs at Day 0, after 21 days of venous culture (Venous), or after 21 days of stepwise venous-to-arterial transitional culture (Arterial). No statistical significance were found between groups for these variables.
| Day 0 | Venous | Arterial | |
|---|---|---|---|
| Inner Arc Length (mm) | 8.36 ± 1.72 | 6.92 ± 2.19 | 8.15 ± 2.29 |
| Outer Arc Length (mm) | 11.4 ± 1.61 | 10.6 ± 1.40 | 12.0 ± 2.25 |
| Unloaded Wall Thickness (mm) | 0.48 ± 0.23 | 0.59 ± 0.15 | 0.62 ± 0.07 |
| Opening Angle (Deg) | 90.6 ± 31.7 | 56.5 ± 33.3 | 71.5 ± 21.4 |
Averaged biaxial inflation-extension data is presented for all pre- (Day 0) and post-culture (Venous and Arterial) groups with constitutive modeling results superimposed onto experimental datasets (Figure 3). Large sample-to-sample variations were apparent in all groups. Still, the model was an excellent fit for the individual and averaged data with root-squared-mean errors (RMSE) of 0.090, 0.071, and 0.101 for the Day 0, 21-day Venous, and 21-day Arterial culture groups, respectively. Non-parametric bootstrapping revealed point-wise estimates to be near the peak of bootstrapped distributions without demonstrating local minima (Figure 4). Of note, the isotropic coefficient represents a nearly minimum value within the search space of the minimization function, while the parameters were significantly higher for the Arterial culture group; anisotropy is typically associated with the contribution of collagen, so these findings, together with the phenomenological increase in fiber angle observed in both 21-day culture groups may suggested collagen remodeling but would need to be confirmed with direct experimentation.
Figure 3.
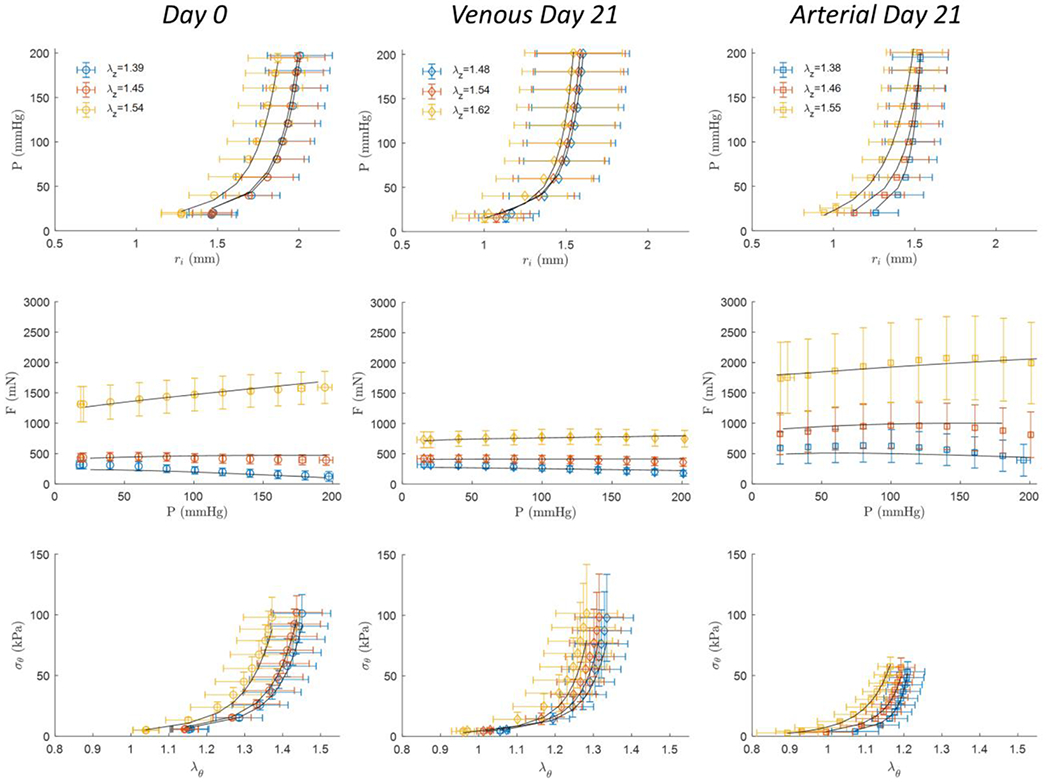
Biaxial mechanical testing results of GSVs (left) at Day 0 (n=10), or after 21-days of (middle) Venous (n=4), or (right) stepwise Arterial (n=6) perfusion culture conditions. All measured data represent mean values ± the standard deviation and are shown at (red), above (yellow), and below (blue) the in vivo axial stretch ratio. Black curves illustrate data fitted to the constitutive model.
Figure 4.

Results from the non-parametric bootstrap of the 4-fiber-family HGO model for GSVs at Day 0, and after 21 days of Venous or stepwise Arterial.
Structural and mechanical values were compared between pre- and post-culture vessels at venous (20 mmHg) or arterial (100 mmHg) conditions (Figure 5). This approach facilitated comparisons of discrete metrics of interest under common loading conditions. As an illustrative point, the Day 0 Venous group deformed inner radius was considerably lower (ri = 1.30 ± 0.36 mm) than the Day 0 Arterial group (ri = 2.17 ± 0.28 mm) due to the different assessment pressures and passive distension. Thus when comparing the passive wall shear stress at Day 0 - Venous (τw = 1.17 ± 1.35 Pa) to Day 0 - Arterial (τw = 0.50 ± 0.22 Pa), the latter appear lower due to the passive radii increase (note the term in denominator of equation (5)) despite the increase in volumetric flow. Overall, the deformed inner radius decreased in the 21 day stepwise Arterial culture group (ri = 1.48 ± 0.35 mm; p=0.022) while the deformed wall thickness increased significantly from Day 0 (h = 0.48 ± 0.05 mm) to day-21 Arterial (h = 0.76 ± 0.15 mm; p=0.027).
Figure 5.
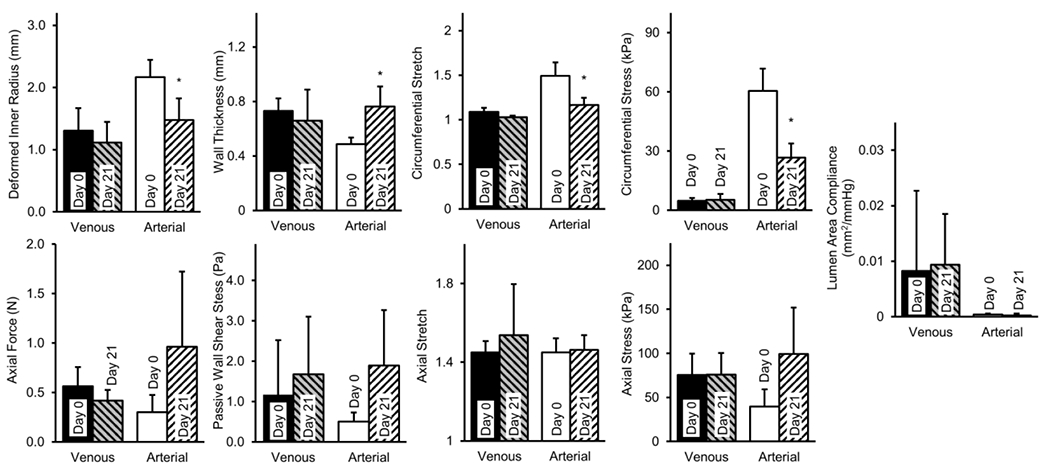
Passive structural and mechanical properties of GSVs before (Day 0; N=10) and after (Day 21) hemodynamic-mimetic perfusion tissue culture at venous (Venous; N=4) or stepwise venous-to-arterial transitional perfusion conditions (Arterial; N=6). As a discrete metric of comparison, Venous and Arterial vessels are illustrated mechanically at 20 and 100 mmHg respectively; furthermore, Day 0 represents a single pooled cohort illustrated mechanically under both venous (20 mmHg) and arterial (100 mmHg) loads. Wall shear stresses are shown at fully dilated conditions. All values are mean ± std. (*) Denotes statistical significance at p<0.05 between Day 0 and Day 21 for venous or arterial conditions.
These morphometric decreases manifested as changes in mean circumferential stress at arterial conditions (σθ = 60.4 ± 11.4 to σθ = 26.6 ± 7.25 kPa; p=0.004) but did not restore the value experienced at pre-culture venous conditions (σθ = 4.81 ± 1.38 kPa) for the duration of the experiment. Circumferential stretch also decreased from Day 0 (λθ = 1.49 ± 0.15) to day-21 in the Arterial group (λθ = 1.17 ± 0.08; p=0.015), again still exceeding that of Day 0 Venous group (λθ = 1.09 ± 0.05). No statistically significant changes were observed in any metrics for Venous culture compared to Day 0. The axial stretch at which pressurization was force-invariant remained similar for all experimental groups. Axial force and stress however, trended upwards when comparing Day 0 (F = 0.300 ± 0.174 N, σz = 39.7 ± 19.4 kPa) to 21 Days Arterial (F = 0.964 ± 0.758 N, σz = 99.2 ± 52.48 kPa) culture.
Consistent with canonical nonlinear mechanical behavior, lumen area compliance was higher at Day 0 Venous (CA = 8.2x10−3 ± 0.0145 mm2/mmHg) than Day 0 Arterial pressures (CA = 4.2x10−4 ± 1.6x10−4 mm2/mmHg) without differences found after Arterial culture. Progressive increases in stiffness moduli were apparent with increases in pressure about which the linearization was performed (Figure 6). Specifically, circumferential stiffness moduli decreased in the Arterial group ( MPa) compared to Day 0 ( MPa) at 100 mmHg and above. In contrast, the axial stiffness moduli was similar for the Day 0 ( MPa) and Arterial groups ( MPa) while the venous ( MPa) culture experienced decreases in axial stiffness. All vessels were stiffer axially than circumferentially. Day 0 and Venous culture groups had similar biaxial strain energy profiles, while Arterial cultures resulted in a circumferential stiffening which shifted the strain energy function towards an anisotropic behavior characterized by a decreased isotropic and an increased anisotropic contribution (Figure 7).
Figure 6.
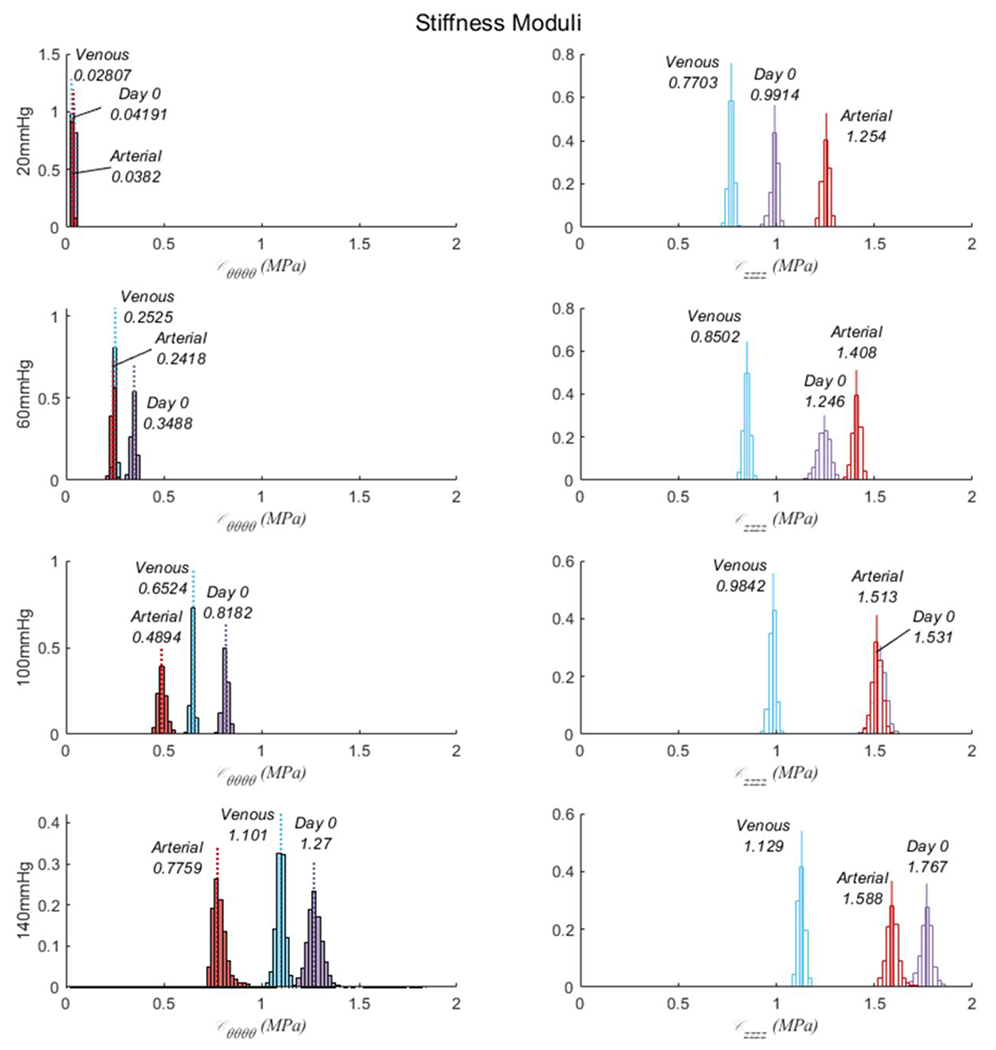
Bootstrapped stiffness moduli for the circumferential (left) and axial (right) directions linearized around 20, 60, 100, and 140 mmHg for GSVs at Day 0, and after 21 days of Venous or stepwise Arterial.
Figure 7.
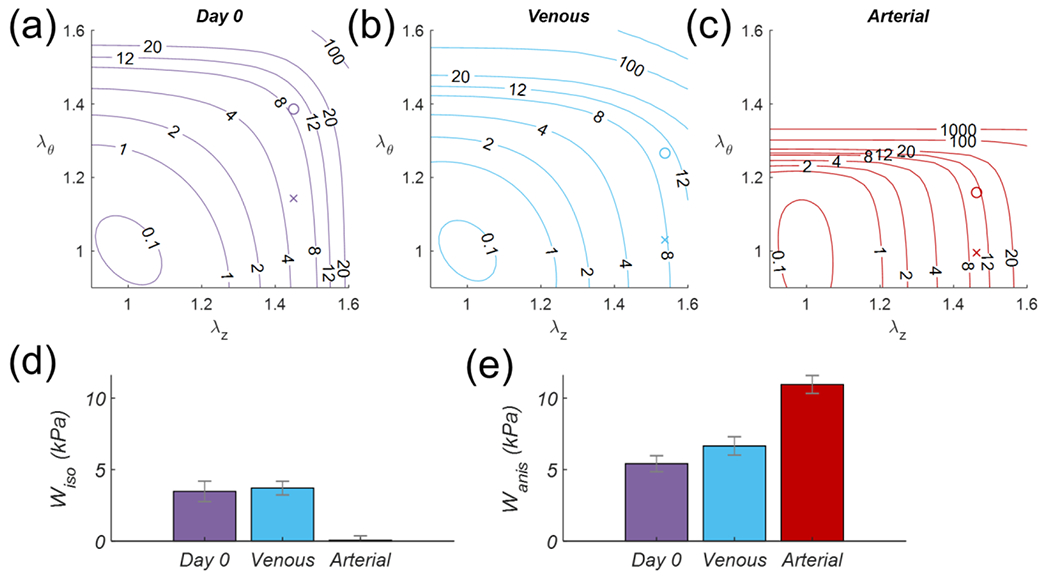
GSV total stored energy (top) contour plots as a function of biaxial stretch for (a) Day 0, or after 21 days of (b) Venous or (c) stepwise transition Arterial culture. Symbols “o” and “x” illustrate the stretch state at 20 mmHg and 100 mmHg respectively, (d) Isotropic and (e) anisotropic contribution to the total strain energy at 100 mmHg.
Qualitatively stained cross-sections at Day 0 and post-culture illustrate the muscular media as the thickest layer in these veins with interspersed collagen fibers and a prominent external elastic membrane with elastic fibers found in the adventitia (Figure 8). This organization is unique compared to other medium-sized veins where the adventitia is the dominant muscular layer.40 Histologically, we did not see evidence of increased elastogenesis in Arterial or Venous cultures compared to Day 0. Endothelial cell nuclei could be found in successful tissue cultures. Medial and adventitial cell nuclei appeared evenly distributed across the medial layer of Day 0 and Arterial cultures (Supplement 1) but were more heterogeneous in the Venous cultures. Likewise, healthy and apoptotic cell nuclei were sometimes evenly distributed throughout the wall following tissue culture, but others demonstrate heterogeneity of apoptotic nuclei gathering in clusters.
Figure 8.
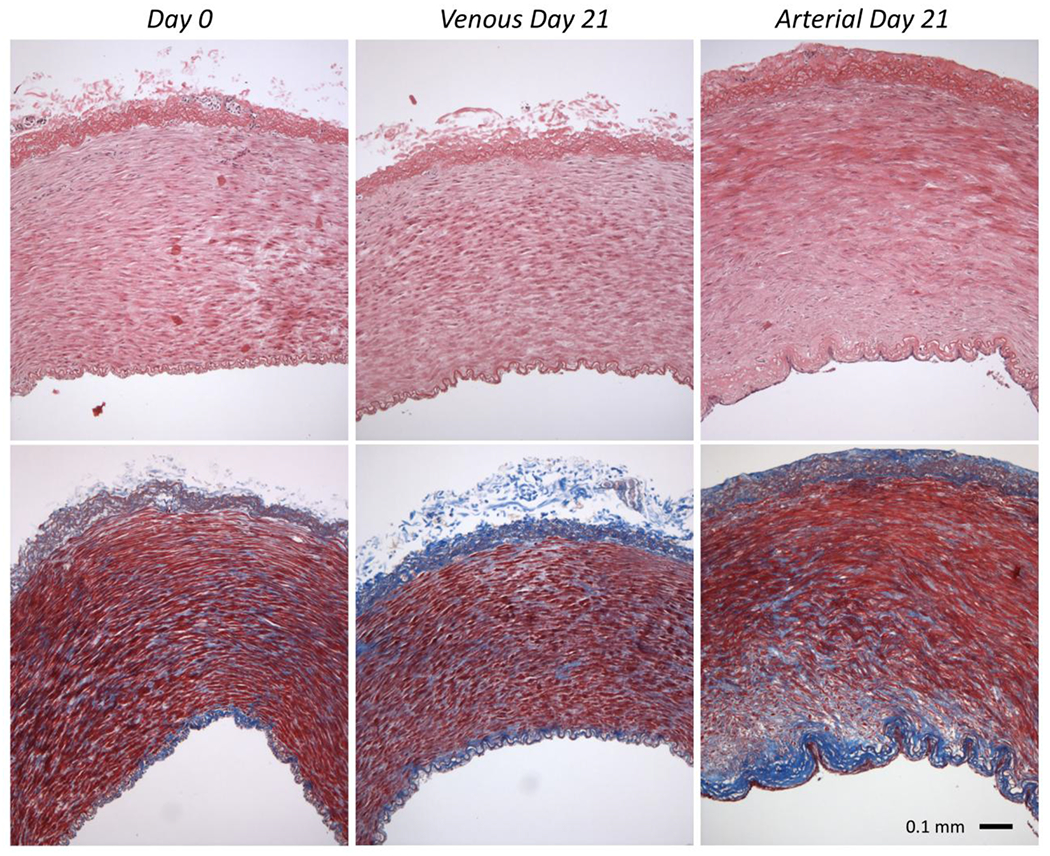
Representative histological samples of GSV cross-sections using (top) hematoxylin and eosin and (bottom) Masson’s Trichrome staining of (left) Day 0 or after 21 days of (middle) Venous or (right) stepwise transition Arterial culture.
DISCUSSION
In this investigation, we build upon previous observational studies of acute graft biomechanics and CABG perfusion culture in order to guide adaptive remodeling through stepwise increases in media pressure and volumetric flowrate from native (Venous) to grafted (Arterial) hemodynamic-replicated environments over 21-days.34,37 The primary indicator of success herein is the restoration of tissues towards native homeostatic stress states (and surprisingly, strain) while maintaining tissue viability. Initially designed as a stress feedback experiment, the kinetics of extracorporeal growth failed to match their in vivo counterparts within a duration acceptable for experimental viability thus, as a proxy for circumferential stress and wall shear stress feedback, pressure and flow were gradually increased at 3-day intervals over the course of 21-day cultures and tissues were analyzed mechanically after culture. Although numerous factors affect tissue growth such as nutrition, cytokines, and the chemical environment, the current work focused on mechanobiological cues that guide adaptation of GSVs. Constitutive models contained herein represent the acute pre- and post-remodeled configurations and can be used to motivate vascular growth-theory. As such, the current work contributes to the complex field of vascular mechanobiology.
In the present investigation, GSVs subjected to 21-day stepwise remodeling cultures (i.e., Arterial samples) demonstrated significant mechanobiological changes compared matched pre-culture samples (i.e., Day 0) and GSVs subjected to 21-day ex vivo culture simulating native venous conditions (i.e., Venous). These observations corroborate the numerous prior in vivo and ex vivo investigations demonstrating vascular remodeling in response to altered mechanical loads. We, and others, posit that such remodeling occurs to achieve some level of stress homeostasis, with circumferential stresses believed to be a primary driver of remodeling.23 Specific to this experiment is the question of whether GSVs subjected to persistent loads characteristic of the arterial circulation would seek to regain their native stress states (i.e., Day 0) or would undergo some level of “reprogramming” and seek to achieve stress homeostasis characteristic of native arteries. Prior to culture we observe that circumferential stresses are significantly higher for GSVs under arterial loads than venous loads (Day 0 – Venous σθ = 4.81 ± 1.38 kPa; Day 0 – Arterial σθ = 60.4 ± 11.4 kPa). Following 21-day stepwise remodeling culture, we see that circumferential stresses under arterial loads are significantly lower than Day 0 – Arterial (Day 21 – Arterial σθ = 26.6 ± 7.25 kPa; p=0.004). In prior work, we quantified and compared the mechanical response of common CABG graft tissues and native coronary arteries under mechanical loads characteristic of their native in situ loading environment and the grafted coronary environment.37 In that investigation, we observed mean circumferential stresses of 66.7 kPa for porcine left anterior descending (LAD) coronary arteries under loads characteristic of the native coronary environment. Taken together, these observations suggest that the vascular remodeling observed herein may occur as GSVs seek to regain circumferential stress homeostasis characteristic of their native in situ loading conditions, though this hypothesis should be confirmed through further investigations and would likely differ in an implant model.
Thrombosis, intimal-medial hyperplasia, and atherosclerosis are the leading causes of vein graft disease and reoperation following bypass surgery.33 Through perfusion tissue culture, we induce tissue growth and adaptation in an anti-thrombogenic and inflammatory environment, conceptually demonstrating a method by which such maladaptive processes may be avoided in autologous or tissue-engineered vascular grafts. For our stepwise Arterial samples, growth occurred in the form of vessel dilation and wall thickening and coincided with a trend towards reduced opening angles. A decreased opening angle suggests non-uniform but biased outward growth which would be a positive indicator of success, while increases in opening angle suggest inward or maladaptive remodeling (i.e., intimal hyperplasia).14 Histology supports growth of these tissues occurring in both inward and outward directions.
Naturally, changes to vessel morphometry and mechanical properties are driven by remodeling and reorganization of intramural cells and ECM. Prior investigations by others have characterized the phenotypic plasticity of vascular SMCs, including phenotypic switching that occurs between the “contractile” and “synthetic” phenotypes in response to altered mechanical stimuli,16,39 and our prior work has demonstrated altered expression of genes associated with vascular remodeling, such as MMP2 and TIMP1, after 6-hour and 7-day ex vivo culture, suggestive of synthetic SMC activity.34 Furthermore, deposition of additional ECM proteins (e.g., collagen type IV) or ground substance may contribute to the medial thickening observed herein. While not a primary focus of this investigation, future efforts should seek to characterize the extent to which phenotypic switching occurs due to the stepwise remodeling approach described herein, whether those phenotypic changes differ from those seen in clinical CABG procedures, and the extent to which observed medial thickening is due to hypertrophy, hyperplasia, and/or protein deposition. Furthermore, future investigations should seek to understand whether elastogenesis is observed as result of stepwise remodeling cultures. Likewise, intimal resorption (localized atrophy), decreased the opening angle in venous cultures that failed to increase in size.13
The stepwise remodeling approach and findings described herein appear to corroborate and build upon prior investigations of vascular remodeling. While collagen generally has a half-life of weeks to months in quiescent tissues, some have found evidence of much higher rates in perturbed vasculature and other tissues.9,32,41 In vivo experiments have also shown wall thickening over 80% within 21 days,28 so it is reasonable to suspect significant structural remodeling even if homeostasis is not fully regained under coronary conditions. Moreover, we know that ex vivo tissue culture nominally affects gene expression within several hours, with prolonged changes over 21 days.34 Finally, inflammation is known to have a role in this in vivo process but is unlikely to have significantly influenced findings in the ex vivo experiments described herein.9,29
Constitutive modeling techniques provide an additional analytical framework to describe and contextualize these experimental phenomena. The biasing of anisotropic strain energy to the overall strain energy function in GSVs cultured under stepwise arterial conditions supports the idea that these vessels accumulated collagen and this concept is supported qualitatively by histological sections. Surprisingly, this growth manifested as axial, not circumferential stiffening per stiffness moduli (Figure 6) using the theory of “small-on-large”.1 At a continuum scale, axial stress may be secondary and compensatory in order to achieve the dominant circumferential and shear stress demands.23
The most widely accepted view of mechanical homeostasis and remodeling is that stresses correlate closest with tissue homeostasis and deviations in stresses from homeostasis drive remodeling.7,14,23 While flow rate and pressure directly correlate to wall shear and circumferential stress, these are not calculated in real-time in our experiment, requiring a direct measure of inner diameter and is thus a limitation in our study. Structural remodeling can occur over weeks as opposed to days and morphological changes may be limited enough through 21 days to make reasonable stress approximations. Prior experience suggests that tissue viability decreases dramatically after 28 days and further culture may have diminishing results.8 Though further experimentation is necessary, these findings provide evidence to support previous hypotheses of mechanical homeostasis and remodeling in the vasculature.
The use of abattoir sourced tissues, rather than inbred animals, resulted in considerable variation amongst groups (see error bars Figure 3). Although the animal-to-animal variation is a better representation of genetic variations in human populations, we did not adjust volumetric flowrate or pressure to the individual specimen since these were not known a priori. However, only matched pre- and post-remodeled data was used in our analysis to better represent individual specimen’s growth characteristics. We also note that stresses borne by smooth muscle cells, deemed active stresses, are not calculated as our fully passivated tissues.44 In addition, although material heterogeneity and large opening angles were observed in our samples, for simplicity purposes and to facilitate linking these models with established tissue-culture techniques, veins were modeled using a thin-walled theory. A thick-walled approach however, could have a small effect on the best-fit modeling parameters with advantages realized through the inclusion of layer-specific information, constituent area fractions, and inclusion of material deposition stretches.2 The role of spatial gradients of stress on growth and remodeling is a subject of ongoing theoretical and experimental investigations.6 Overall, we acknowledge these to be limitations in our study.
The native porcine GSV has a narrower lumen when compared to the left anterior descending artery of the coronary circulation, a potential anastomosing tissue.37 The adaptive diameter response of our GSVs to stepwise arterial cultures through vessel homeostasis was fortuitous with the remodeled geometry a better match for the anastomosing coronary vessels. Such a response is not coincidental as the microstructural configuration of healthy arteries of the coronary circulation, and indeed all vasculature, are configured to be nearly optimal in order to distribute loads in their local hemodynamic environment.13,14 Overall, the presented technique can be adapted for other graft tissues and procedures such as a modulated arteriovenous fistulae and peripheral artery bypass. Success would expand the number of vessels that could be used as grafts; however, care must be taken to ensure sufficient remodeling can take place for the duration of viable culture.
The use of autologous CABG procedures remains a primary intervention to treat severe coronary artery disease, and the GSV remains one of the primary conduits used for these procedures, despite lower rates of long-term patency and increased risk of graft failure.3,15 This investigation builds upon prior work by our collaborators and others to demonstrate that GSVs subjected to stepwise changes in mechanical loads, as opposed to the large acute changes experienced in a CABG procedure, can maintain viability and remodel structurally, potentially driven by resident vascular cells seeking to regain stress homeostasis. While it is possible that human vessels manipulated in a similar manner in clinical practice may increase graft viability, support long-term patency, and decrease failure rates, this protocol would pose significant feasibility issues and is unlikely to be tenable for the vast majority of cases. There may be potential to apply these techniques to tissue engineered grafts, though de novo tissue engineered vascular grafts have also experienced significant technical hurdles that have limited clinical applicability.
Knowing the significant drawbacks to GSVs as CABG conduits, the techniques described herein may be applied to evaluate alternative autologous vascular tissues for use in CABG procedures. Ex vivo vascular tissue culture may be used in conjunction with biaxial mechanical testing look beyond vessel morphometry to identify graft alternatives most capable of adapting to the coronary circulation, and this technique could be completed in the low-risk laboratory environment in order to de-risk the use of novel tissues prior to any attempted use in the clinic. At minimum, these experimental techniques demonstrate that vessels can be successfully maintained in ex vivo tissue culture for 3-weeks with precise control of mechanical stimuli, which can be applied in combination with other analytical techniques as we continue to understand the complex phenomena of vascular remodeling.
Supplementary Material
Acknowledgments
The authors would like to acknowledge the contributions of Boran Zhou (PhD), Shahd Hasanain (BS), Colton Kostelnik (BS), Laurel Carter (MD) and Nicole Carey (MD) for their technological contributions to the project.
Funding
This work is supported by the National Institutes of Health under grant numbers (R21 EB022131, R01HL133662, and P20GM103444)
Footnotes
Publisher's Disclaimer: This Author Accepted Manuscript is a PDF file of an unedited peer-reviewed manuscript that has been accepted for publication but has not been copyedited or corrected. The official version of record that is published in the journal is kept up to date and so may therefore differ from this version.
Conflicts of Interest
No benefits in any form have been or will be received from a commercial party related directly or indirectly to the subject of this manuscript.
References
- 1.Baek S, Gleason RL, Rajagopal KR, and Humphrey JD. Theory of small on large: potential utility in computations of fluid–solid interactions in arteries . Comput. Methods Appl. Mech. Eng 196:3070–3078, 2007. [Google Scholar]
- 2.Bellini C, Ferruzzi J, Roccabianca S, Di Martino ES, and Humphrey JD. A microstructurally motivated model of arterial wall mechanics with mechanobiological implications. Ann. Biomed. Eng 42:488–502, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Benedetto U, Raja SG, Albanese A, Amrani M, Biondi-Zoccai G, and Frati G. Searching for the second best graft for coronary artery bypass surgery: a network meta-analysis of randomized controlled trials. Eur J Cardiothorac Surg 47:59–65, 2015. [DOI] [PubMed] [Google Scholar]
- 4.Bersi MR, Ferruzzi J, Eberth JF, Gleason RL Jr., and Humphrey JD. Consistent Biomechanical Phenotyping of Common Carotid Arteries from Seven Genetic, Pharmacological, and Surgical Mouse Models. Ann. Biomed. Eng 42:1207–1223, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carey JS, Danielsen B, Milliken J, Li Z, and Stabile BE. Narrowing the gap: Early and intermediate outcomes after percutaneous coronary intervention and coronary artery bypass graft procedures in California, 1997 to 2006. J Thorac Cardiovasc Surg 138:1100–1107, 2009. [DOI] [PubMed] [Google Scholar]
- 6.Chen YC, and Eberth JF. Constitutive function, residual stress, and state of uniform stress in arteries. J. Mech. Phys. Solids 60:1145–1157, 2012. [Google Scholar]
- 7.Cyron CJ, and Humphrey JD. Growth and remodeling of load-bearing biological soft tissues. Meccanica 52:645–664, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dummler S, Eichhorn S, Tesche C, Schreiber U, Voss B, Deutsch MA, Hauner H, Lahm H, Lange R, and Krane M. Pulsatile ex vivo perfusion of human saphenous vein grafts under controlled pressure conditions increases MMP-2 expression. Biomed Eng Online 10:62, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Eberth JF, Popovic N, Gresham VC, Wilson E, and Humphrey JD. Time course of carotid artery growth and remodeling in response to altered pulsatility. Am J Physiol Hear. Circ Physiol 299:H1875–83, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Eberth JF, Taucer AI, Wilson E, and Humphrey JD. Mechanics of carotid arteries in a mouse model of marfan syndrome. Ann. Biomed. Eng 37:1093–1104, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ferruzzi J, Bersi MR, and Humphrey JD. Biomechanical Phenotyping of Central Arteries in Health and Disease: Advantages of and Methods for Murine Models. Ann. Biomed. Eng 41:1311–1330, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ferruzzi J, a Vorp D, and Humphrey JD. On constitutive descriptors of the biaxial mechanical behaviour of human abdominal aorta and aneurysms. J. R. Soc. Interface 8:435–450, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fung YC What are the residual stresses doing in our blood vessels? Ann. Biomed. Eng 19:237–249, 1991. [DOI] [PubMed] [Google Scholar]
- 14.Fung YC, and Liu SQ. Strain distribution in small blood vessels with zero-stress state taken into consideration. Am. J. Physiol 262:H544–552, 1992. [DOI] [PubMed] [Google Scholar]
- 15.Goldman S, Zadina K, Moritz T, Ovitt T, Sethi G, Copeland JG, Thottapurathu L, Krasnicka B, Ellis N, Anderson RJ, and Henderson W. Long-term patency of saphenous vein and left internal mammary artery grafts after coronary artery bypass surgery: Results from a Department of Veterans Affairs Cooperative Study. J. Am. Coll. Cardiol 44:2149–2156, 2004. [DOI] [PubMed] [Google Scholar]
- 16.Gomez D, and Owens GK. Smooth muscle cell phenotypic switching in atherosclerosis. Cardiovasc Res 95:156–164, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gooch KJ, Firstenberg MS, Shrefler BS, and Scandling BW. Biomechanics and Mechanobiology of Saphenous Vein Grafts. J. Biomech. Eng 140:020804, 2018. [DOI] [PubMed] [Google Scholar]
- 18.Gusic RJ, Myung R, Petko M, Gaynor JW, and Gooch KJ. Shear stress and pressure modulate saphenous vein remodeling ex vivo. J Biomech 38:1760–1769, 2005. [DOI] [PubMed] [Google Scholar]
- 19.Gusic RJ, Petko M, Myung R, William Gaynor J, and Gooch KJ. Mechanical properties of native and ex vivo remodeled porcine saphenous veins. J Biomech 38:1770–1779, 2005. [DOI] [PubMed] [Google Scholar]
- 20.Hocking KΜ, Sileshi B, Baudenbacher FJ, Boyer RB, Kohorst KL, Brophy CM, and Eagle SS. Peripheral venous waveform analysis for detecting hemorrhage and iatrogenic volume overload in a porcine model. Shock 46:447–452, 2016. [DOI] [PubMed] [Google Scholar]
- 21.Holzapfel GA, Gasser TC, and Ogden RW. A New Constitutive Framework for Arterial Wall Mechanics and a Comparative Study of Material Models. J. Elast. Phys. Sci. solids 61:1–48, 2000. [Google Scholar]
- 22.Humphrey JD Cardiovascular Solid Mechanics: Cells, Tissues, and Organs. New York, USA: Springer, 2002.doi: 10.1007/978-0-387-21576-1 [DOI] [Google Scholar]
- 23.Humphrey JD, Eberth JF, Dye WW, and Gleason RL. Fundamental role of axial stress in compensatory adaptations by arteries. J Biomech 42:1–8, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kamenskiy A, Seas A, Deegan P, Poulson W, Anttila E, Sim S, Desyatova A, and MacTaggart J. Constitutive description of human femoropopliteal artery aging. Biomech. Model. Mechanobiol 16:681–692, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kamiya A, and Togawa T. Adaptive regulation of wall shear stress to flow change in the canine carotid artery. Am J Physiol 239:H14–21, 1980. [DOI] [PubMed] [Google Scholar]
- 26.Kassab GS, and Navia JA. Biomechanical considerations in the design of graft: the homeostasis hypothesis. Annu Rev Biomed Eng 8:499–535, 2006. [DOI] [PubMed] [Google Scholar]
- 27.Kinsky Μ, Ribeiro N, Cannesson M, Deyo D, Kramer G, Salter M, Khan M, Ju H, and Johnston WE. Peripheral venous pressure as an indicator of preload responsiveness during volume resuscitation from hemorrhage. Anesth. Analg 123:114–122, 2016. [DOI] [PubMed] [Google Scholar]
- 28.Langleben D, Szarek JL, Coflesky JT, Jones RC, Reid LM, and Evans JN. Altered artery mechanics and structure in monocrotaline pulmonary hypertension. J. Appl. Physiol 65:2326–2331, 1988. [DOI] [PubMed] [Google Scholar]
- 29.Latorre M, and Humphrey JD. Modeling mechano-driven and immuno-mediated aortic maladaptation in hypertension. Biomech. Model. Mechanobiol 17:1497–1511, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Van Loon P Length-force and volume-pressure relationships of arteries. Biorheology 14:181–201, 1976. [PubMed] [Google Scholar]
- 31.Matsumoto T, and Hayashi K. Mechanical and dimensional adaptation of rat aorta to hypertension. J Biomech Eng 116:278–283, 1994. [DOI] [PubMed] [Google Scholar]
- 32.McAnulty RJ, and Laurent GJ. Collagen synthesis and degradation in vivo. Evidence for rapid rates of collagen turnover with extensive degradation of newly synthesized collagen in tissues of the adult rat. Coll. Relat. Res 7:93–104, 1987. [DOI] [PubMed] [Google Scholar]
- 33.Parang P, and Arora R. Coronary vein graft disease: pathogenesis and prevention. Can. J. Cardiol 25:e57–e62, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Prim DA, Menon V, Hasanian S, Carter L, Shazly T, Potts JD, and Eberth JF. Perfusion Tissue Culture Initiates Differential Remodeling of Internal Thoracic Arteries, Radial Arteries, and Saphenous Veins. J. Vase. Res 55:255–267, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Prim DA, Mohamed MA, Lane BA, Poblete K, Wierzbicki MA, Lessner SM, Shazly T, and Eberth JF. Comparative mechanics of diverse mammalian carotid arteries. PLoS One 13:e0202123, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Prim DA, Potts J, and Eberth JF. Pulsatile Perfusion Bioreactor for Biomimetic Vascular Impedances. J. Med. Device. 12:041002, 2018. [Google Scholar]
- 37.Prim DA, Zhou B, Hartstone-Rose A, Uline MJ, Shazly T, and Eberth JF. A Mechanical Argument for the Differential Performance of Coronary Artery Grafts. J. Mech. Behav. Biomed. Mater 54:93–105, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ramachandra AB, Humphrey JD, and Marsden AL. Gradual loading ameliorates maladaptation in computational simulations of vein graft growth and remodelling. J. R. Soc. Interface 14:20160995, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rensen SSΜ, a F P. Doevendans M, and van Eys GJJM. Regulation and characteristics of vascular smooth muscle cell phenotypic diversity. Neth. Heart J 15:100–108, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ross M, and Pawlina W. Histology: A Text and Atlas. In: Histology: A Text and Atlas. 2004, pp. 184–191. [Google Scholar]
- 41.Sodek J, and Ferrier JM. Collagen remodelling in rat periodontal tissues: compensation for precursor reutilization confirms rapid turnover of collagen. Coll. Relat. Res 8:11–21, 1988. [DOI] [PubMed] [Google Scholar]
- 42.de Vries MR, Simons KH, Jukema JW, Braun J, and Quax PHA. Vein graft failure: from pathophysiology to clinical outcomes. Nat. Rev. Cardiol 13:451–470, 2016. [DOI] [PubMed] [Google Scholar]
- 43.Yin FCP, Chew PH, and Zeger SL. An approach to quantification of biaxial tissue stress-strain data. J. Biomech 19:27–37, 1986. [DOI] [PubMed] [Google Scholar]
- 44.Zhou B, Prim DA, Romito EJ, McNamara LP, Spinale FG, Shazly T, and Eberth JF. Contractile Smooth Muscle and Active Stress Generation in Porcine Common Carotids. J. Biomech. Eng 140:014501, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhou B, Wolf L, Rachev A, and Shazly T. A structure-motivated model of the passive mechanical response of the primary porcine renal artery. J. Mech. Med. Biol 14:1450033, 2014. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


