Visual number sense in untrained deep neural networks

Visual number sense can arise spontaneously in untrained deep neural networks in the complete absence of learning.

Abstract

Number sense, the ability to estimate numerosity, is observed in naïve animals, but how this cognitive function emerges in the brain remains unclear. Here, using an artificial deep neural network that models the ventral visual stream of the brain, we show that number-selective neurons can arise spontaneously, even in the complete absence of learning. We also show that the responses of these neurons can induce the abstract number sense, the ability to discriminate numerosity independent of low-level visual cues. We found number tuning in a randomly initialized network originating from a combination of monotonically decreasing and increasing neuronal activities, which emerges spontaneously from the statistical properties of bottom-up projections. We confirmed that the responses of these number-selective neurons show the single- and multineuron characteristics observed in the brain and enable the network to perform number comparison tasks. These findings provide insight into the origin of innate cognitive functions.

INTRODUCTION

Number sense, an ability to estimate numbers without counting (1, 2), is an essential function of the brain that may provide a foundation for complicated information processing (3). It has been reported that this capacity is observed in humans and various animals in the absence of learning. Newborn human infants can respond to abstract numerical quantities across different modalities and formats (4), and newborn chicks can discriminate quantities of visual stimuli without training (5). In single-neuron recordings in numerically naïve monkeys (6) and crows (7), it was observed that individual neurons in the prefrontal cortex (PFC) and other brain areas can respond selectively to the number of visual items (numerosity). These results suggest that number-selective neurons (number neurons) arise before visual training and that they may provide a foundation for an innate number sense in the brain. However, details of how this cognitive function emerges in the brain are not yet understood.

Recently, model studies with biologically inspired artificial neural networks have provided insight into the development of various functional circuits for visual information processing (8–11). For example, the brain activity initiated by various visual stimuli has been successfully reconstructed in deep neural networks (DNNs) (12–14), and the visual pattern designed to maximize the response of DNNs also maximized the spiking activity of cortical neurons beyond their naturally occurring levels (15). These results suggest that studies using DNN models can provide a possible scenario for the mechanism of the brain activities encoding visual information.

Previous studies using DNNs have suggested that number-selective response can emerge from unsupervised learning of visual images (16–18) without training for numbers (19). However, the number-selective responses observed in these models were mostly dependent on low-level visual features, such as the total area of the stimulus; thus, an additional learning process was required to achieve the abstract number sense (19, 20). A recent study showed that neurons with abstract number sense can emerge in DNNs after being trained for the classification of natural images (21), implying that the abstract number sense could be initiated by the learning of statistical properties of natural scenes. However, it still remains unclear whether such nonnumerical training processes are factors crucial to the emergence of a number-selective response.

Important clues were found from a randomly initialized, untrained feedforward network able to initiate various cognitive functions (22). It was reported that selective tunings, such as number-selective responses, can emerge from the multiplication of random matrices (23) and that the structure of a randomly initialized convolutional neural network can provide a priori information about the low-level statistics in natural images, enabling the reconstruction of the corrupted images without any training for feature extraction (24). Furthermore, a recent study showed that subnetworks from randomly initialized neural networks can perform image classification (25), implying the ability of a randomly initialized network to engage in visual feature extraction.

Here, we show that abstract number tuning of neurons can spontaneously arise even in completely untrained DNNs and that these neurons enable the network to perform number discrimination tasks. Using an AlexNet model designed on the basis of the structure of a biological visual pathway, we found that number-selective neurons are observed in randomly initialized DNNs in the complete absence of learning and that they show the single- and multineuron characteristics of the types observed in biological brains following the Weber-Fechner law. The responses of these neurons enable the network to perform a number comparison task, even under the condition that the numerosity in the stimulus is incongruent with low-level visual cues such as the total area, the size, and the density of visual patterns in the stimulus. From further investigations, we found that the neuronal tuning for various levels of numerosity originated from the summation of monotonically decreasing and increasing activity units in the earlier layers (16–18, 26), implying that the observed number tuning emerges from the statistical variation of bottom-up projections. Our findings suggest that number sense can emerge spontaneously from the statistical properties of bottom-up projections in hierarchical neural networks.

RESULTS

Emergence of number selectivity in untrained networks

We simulated the response of AlexNet, a conventional DNN that models the ventral visual stream of the brain (table S1) (8). The network consists of five convolutional layers for feature extraction and three fully connected layers for object classification. In the current study, to investigate the selective responses of neurons rather than the performance of the system, the classification layers were discarded and the responses of units in the last convolutional layer (Conv5) were examined. We tested the number-selective responses of neurons for images of dot patterns depicting numbers spanning from 1 to 30 (Fig. 1A) (27). With a test design introduced in earlier work (21), we used three different sets of stimuli to ensure the invariance of the observed number tuning for certain geometric factors, in this case the stimulus size, density, and area (set 1, circular dots of the same size; set 2, dots equal the total dot area; and set 3, items of different geometric shapes with an equal overall convex hull).

Fig. 1. Spontaneous emergence of number selectivity in untrained neural networks.

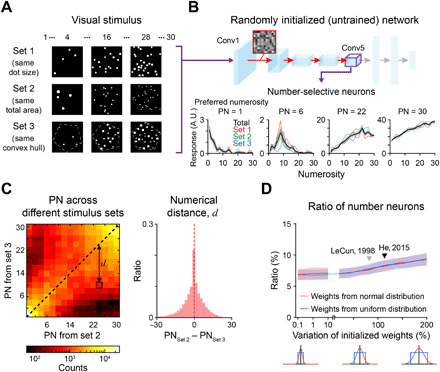
(A) Examples of the stimuli used to measure number tuning (21). Set 1 contains dots of the same size. Set 2 contains dots with a constant total area. Set 3 contains items of different geometric shapes with an equal overall convex hull (white dashed pentagon). (B) Top: Architecture of the untrained AlexNet, where the weights in each convolutional layer were randomly initialized by a controlled normal distribution (28). Bottom: Examples of tuning curves for individual number-selective network units observed in the untrained AlexNet. A.U., arbitrary unit. (C) Left: The preferred numerosity (PN) outcomes measured with different stimulus conditions are significantly correlated with each other, implying consistency of the preferred numerosity. Right: The average numerical distance between PNs of each number-selective neuron measured with different stimulus conditions is close to zero. Dashed lines indicate the average. (D) Ratio of number-selective neurons is consistently observed, even when the weight variation was substantially reduced from the original random initialization condition (28), suggesting that the emergence of number-selective neurons does not strongly depend on the initialization condition. Black and gray triangles indicate the degree of weight variation for the standard random initialization suggested previously (28, 29).

To examine whether number tuning of neurons can arise even in completely untrained DNNs, we devised an untrained network by randomly initializing the weights of filters in each convolutional layer (Fig. 1B, top) (28). Unexpectedly, we found that number-selective neurons were observed in this untrained network (Fig. 1B, bottom; 8.52% of Conv5 units). We also found that the preferred numerosity (PN) of number-selective neurons was consistent across different stimulus types (Fig. 1C and fig. S1) and across new stimulus sets of the same type (fig. S1). The response of number-selective neurons to the PN remained consistently stronger than that to other numerosities, even when change in the other low-level visual cues (including size, rotation angle, and color) was applied to the images (fig. S2). To confirm that number-tuned units appear consistently across different conditions of random initialization, we varied the width of random weight distribution (normal and uniform) in each layer, under different initialization methods (28, 29). We confirmed that number-selective neurons are consistently observed (Fig. 1D), even when the weight variation was substantially reduced (10⁻³ times smaller) from the original condition (Fig. 1D, black and gray triangles) of random initialization.

Previously observed characteristics of tuned neurons in monkeys (27), including the Weber-Fechner law, were also reproduced by number neurons in the untrained AlexNet (Fig. 2). First, the distribution of the PN covered the entire range (1 to 30) of the presented numerosity, but number neurons preferring 1 or 30 were most frequently observed. Thus, the ratio of neurons increases as the PN decreases to 1 or increases to 30, with a profile similar to the experimental observation in monkeys (Fig. 2A) (27). In addition, we observed that the average tuning curves indicating the preference of each numerosity were a good fit to the Gaussian function, particularly on a logarithmic scale, as observed in biological brains (Fig. 2B, *P < 10⁻⁴⁰, Wilcoxon rank sum test) (27). We found that the sigma of the Gaussian fit (σ) of the averaged tuning curve increases proportionally with increase in the PN on a linear scale. Moreover, it remains constant on a logarithmic scale (Fig. 2C; linear, slope = 0.29; log, slope = 0.044) following the Weber-Fechner law (27).

Fig. 2. Tuning properties of number-selective neurons in the untrained network.

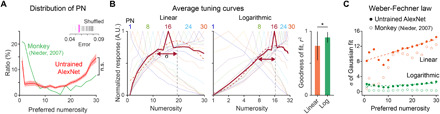
(A) Distribution of preferred numerosity in the network and the observation in monkeys (27). Inset: The root mean square error between the red and green curves (untrained versus data) is significantly lower than that in the control with the distribution of shuffled preferred numerosity (tall pink line; P < 0.05, n = 100). (B) Left and middle: Average tuning curves of different numerosities on a linear scale and on a logarithmic scale. Right: The goodness of the Gaussian fit (r²) is greater on a logarithmic scale, as reported (27). *P < 10⁻⁴⁰, Wilcoxon rank sum test. (C) The tuning width (sigma of the Gaussian fitting) increases proportionally on a linear scale and remains constant on a logarithmic scale, as predicted by the Weber-Fechner law (n = 100) (27).

It is notable that the tuning properties of the untrained AlexNet examined in Fig. 2 are similar to those of the AlexNet trained for the classification of natural images (pretrained AlexNet; ILSVRC2010 ImageNet database was used for training) (fig. S3) (8). One noticeable difference between the number tuning of the two networks was that the ratio of number-selective neurons to the total neurons was significantly smaller in the pretrained AlexNet (untrained, 8.52% versus pretrained, 3.65% of Conv5 units; fig. S3E, left). Our analysis suggests that this difference could be dependent on the bias of the average convolutional weights in the pretrained network. We found that the average weights in the pretrained network were negatively shifted (−0.13, in unit of the SD of convolutional weights), while those of untrained networks were set to 0 (28). Additional simulation shows that when the weights of untrained networks are shifted with a similar negative bias, the ratio of number-selective neurons decreases in a manner similar to that of a pretrained network (fig. S3E, right). This observation implies that strong negative bias reduces the probability that a stimulus image will generate a nonzero response of the rectified linear unit (ReLU) activation function in Conv5, and thus also reduces the probability of generating number-selective responses.

Numerosity comparison by number-selective neurons

Next, we determined whether these number-selective neurons could perform a number comparison task (Fig. 3A; see Materials and Methods for details), as performed in previous model studies (19, 20). In the task, two images of dot patterns were presented to the network, and a support vector machine (SVM) was trained with the response of 256 number-selective neurons to determine which stimulus had greater numerosity. The measured correct performance rate of the network was found to be 85.1 ± 1.7% (Fig. 3B, red solid bar). This is significantly higher than that of the SVM trained with the response of nonselective neurons (Fig. 3B, red open bar; number neurons versus nonselective neurons, *P = 1.28 × 10⁻³⁴, Wilcoxon rank sum test). The performance of the number-selective neurons was also higher than that when the SVM was directly trained with stimulus images [Fig. 3B, gray solid bar; number neurons versus images (red solid versus gray solid bar), *P = 1.28 × 10⁻³⁴, Wilcoxon rank sum test]. This implies that number-selective neurons encode numerosity information exclusively, rather than those other visual features extracted from the stimulus images.

Fig. 3. Number neurons can perform numerosity comparison, reproducing statistics observed in animal behaviors.

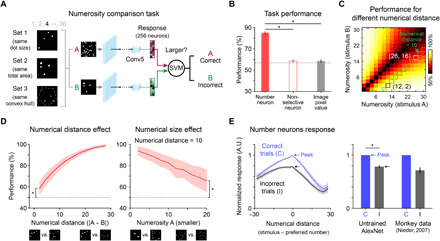
(A) Number comparison task using the SVM. (B) Task performance in the case that the response of number neurons, nonselective neurons, and the pixel values of raw stimulus images were provided to train the SVM. The dashed line indicates the chance level. (C) Performance of numerosity comparison across different combinations of numerosities. (D) Left: Performance as a function of the difference between two numbers. The performance increases as the number difference increases (numerical distance effect) and is significantly higher than the chance level for all cases (*P = 8.70 × 10⁻¹⁷, Wilcoxon rank sum test). Right: Even when the difference between two numbers is identical [e.g., 12 versus 2 and 26 versus 16; black versus white squares in (C)], the performance is greater for the pairs of small numbers (numerical size effect; *P = 3.25 × 10⁻¹⁷, Wilcoxon rank sum test). (E) Left: Average activity of number-selective units as a function of the numerical distance. Right: Response to the preferred numerosity; note that the response during correct trials is significantly higher than that during incorrect trials, as observed in actual neurons recorded from a monkey prefrontal cortex during a numerosity matching task (*P = 2.82 × 10⁻³⁹, Wilcoxon rank sum test) (27).

Subsequently, we found that the performance of the network shows profiles of numerosity comparison similar to those observed in humans and animals. In the performance of numerosity comparison across different combinations of numerosities (Fig. 3C), the performance increases as the numerical distance between two numerosities increases (numerical distance effect; Fig. 3D, left; for a difference = 2, *P = 8.70 × 10⁻¹⁷, Wilcoxon rank sum test), as observed in humans and monkeys (30, 31). Across the pairs of identical numerical distance (e.g., 10; green solid boxes in Fig. 3C), the performance was higher for the pair of smaller numerosities (numerical size effect; Fig. 3D, right; for 20 versus 30, *P = 3.25 × 10⁻¹⁷, Wilcoxon rank sum test). To investigate the contributions of the number-selective neurons for correct choices in greater depth, we compared the average tuning curves obtained in correct and incorrect trials, as in previous experimental studies (27). As expected, the average response to the PN in incorrect trials significantly decreased to 78.3% of that in correct trials (Fig. 3E; *P = 2.82 × 10⁻³⁹, Wilcoxon rank sum test), as observed in the numerosity matching task with monkeys (27). This result suggests that the selective responses of the observed number neurons can provide a network capable of comparing numbers.

Abstract number sense independent of low-level visual cues

In the conventional numerosity comparison task (19, 21, 32) with two numerosities presented in different images, it is possible that the numerosity in the image is estimated by low-level visual cues correlated with the numerosity. For example, the total area of the stimulus is proportional to the numerosity in stimulus sets 1 and 3 (Fig. 4A), which means that the images with greater numerosity have larger total area in 79.8% of the image pairs used in the test. This implies that the SVM may have achieved high performance by comparing the total area of the stimulus, instead of encoding the abstract numerosity.

Fig. 4. Abstract number sense independent of low-level visual features.

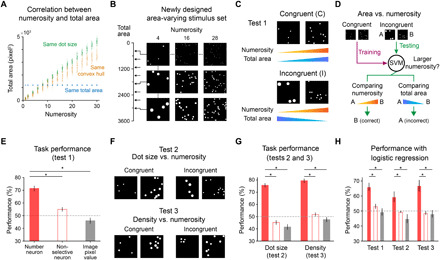
(A) Correlation between the numerosity and total area of the stimuli used for the task in Fig. 3. (B) Newly designed stimulus set with greater variation of the total area (eightfold variation; 120π to 960π pixel²) (16). (C) Image pairs were grouped as congruent and incongruent pairs, depending on the correlation between the values of numerosity and the total area. (D) In the revised task, the SVM was trained with the response to congruent pairs but was tested using incongruent pairs. (E) Task performances when the SVM was trained with the response of number neurons, of nonselective neurons, and with pixel values of raw stimulus image, respectively (*P = 1.28 × 10⁻³⁴, Wilcoxon rank sum test). (F) Similar classification of image pairs by dot size and density. (G) Task performances with image pairs in (E) suggest that number-selective neurons encode the abstract number sense independent of low-level visual features of the stimulus (*P = 1.28 × 10⁻³⁴, Wilcoxon rank sum test). (H) Task performances with the logistic regression as a classifier, instead of SVM (*P = 1.28 × 10⁻³⁴, Wilcoxon rank sum test).

To address this critical issue, we designed a revised comparison task appropriate for testing the abstract numerosity independent of other low-level visual features, which is reported previously in both experimental (33, 34) and model (16) studies. First, we designed a new stimulus set using various levels of the total area (16) (Fig. 4B; eightfold variation on the area; 8^1/2 = 2.83-fold on the one-dimensional scale). The performance of the network with this new stimulus set was 83.0 ± 1.5%, practically equivalent to that in the previous result. This suggests that the performance of the network for number comparison task does not substantially depend on the stimulus area. Next, we classified test image pairs into congruent (C) and incongruent (I) cases, depending on whether the values of numerosity and the low-level visual features in each pair, such as the total area, were correlated or not (Fig. 4C). In the revised task, the SVM was trained with congruent pairs but was tested with incongruent pairs, so that the network could generate a correct answer only when it encoded the abstract numerosity of a stimulus image, independently of other visual cues such as total area (Fig. 4D).

As a result, the SVM trained with the response of number neurons achieved the correct ratio of 71.4 ± 2.1% (Fig. 4E). Although the performance in this strict task appears to be slightly lower than that in the original task (85.1 ± 1.7%; Fig. 3B), it is still significantly higher than that with nonselective neurons and that with pixel information about stimulus images [Fig. 4E; number neurons versus nonselective (red solid versus red open bar), *P = 1.28 × 10⁻³⁴; number neurons versus images (red solid versus gray solid bar), *P = 1.28 × 10⁻³⁴, Wilcoxon rank sum test], implying that number neurons encode the abstract numerosity of a stimulus image, independently of other visual cues.

A similar task was repeated for other visual cues by classifying image pairs by congruency to the dot size or to the local density of dots (Fig. 4F). Similarly, the correct performance ratio of the network was 75.7 ± 1.7% and 79.5 ± 1.6%, respectively [Fig. 4G; number neurons versus nonselective (red solid versus red open bar), *P = 1.28 × 10⁻³⁴ for dot size, *P = 1.28 × 10⁻³⁴ for density; number neurons versus images (red solid versus gray solid bar), *P = 1.28 × 10⁻³⁴ for dot size, *P = 1.28 × 10⁻³⁴ for density, Wilcoxon rank sum test]. We also observed similar results with the performance using the logistic regression instead of the SVM, suggesting that these results do not rely on a particular type of classifier for numerosity estimation [Fig. 4H; 66.1 ± 2.7%, 59.5 ± 3.5%, and 66.9 ± 3.7% for tests 1, 2, and 3 using number neurons; number neurons versus nonselective (red solid versus red open bar), *P = 1.28 × 10⁻³⁴, 1.28 × 10⁻³⁴, 1.28 × 10⁻³⁴; number neurons versus images (red solid versus gray solid bar), *P = 1.28 × 10⁻³⁴, 1.53 × 10⁻³⁴, 1.28 × 10⁻³⁴, Wilcoxon rank sum test]. These results indicate that number-selective neurons can perform number comparison tasks by encoding the abstract numerosity, instead of low-level visual features.

Number tuning by monotonically decreasing and increasing units

Subsequently, we examined how number-selective neurons emerge in untrained random feedforward networks on the basis of the summation coding model in previous studies (Fig. 5A) (16–18, 26). In our model neural network, important clues were found in the neurons observed in the earlier layer (Conv4), the responses of which monotonically decrease or increase as the stimulus numerosity increases (Fig. 5B). We found that these neural responses do not substantially vary due to changes of the total stimulus area (16), virtually realizing area-invariant, monotonically increasing and decreasing responses to stimulus numerosity (fig. S4, A and B; see Materials and Methods for details; 1129 ± 253 decreasing units and 5620 ± 898 increasing units in Conv4; 1.74 ± 0.39% and 8.66 ± 1.39% of all Conv4 units). Notably, the ratio of monotonic units is less than 0.3% in Conv1 and Conv2, whereas it sharply increases to approximately 10% in Conv3 (fig. S4C). These results suggest that the hierarchy across the three convolutional layers is required to generate monotonic activities in the current randomly initialized networks, while such activities could arise in a single layer if the network has been trained for numerosity estimation (17). The average width (sigma of the Gaussian fit) of the decreasing response curves was smaller than that of the increasing units (Fig. 5B, insets; mean ± SD of the sigma = 8.28 ± 2.55 for decreasing units, 13.2 ± 0.94 for increasing units; P < 10⁻⁴⁰, Wilcoxon rank sum test), as observed in the number neurons in Conv5 (PN = 1 versus 30; Fig. 2C).

Fig. 5. Emergence of number tuning from the weighted sum of increasing and decreasing unit activities.

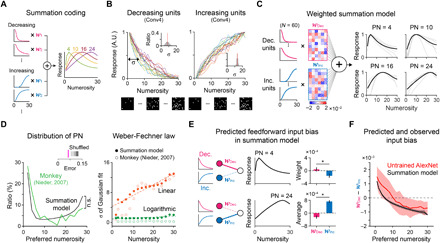
(A) Summation coding model (16–18, 26). (B) Monotonically decreasing/increasing neuronal activities as the numerosity increases were observed in earlier layers. Inset: The sigma of the Gaussian fit. Red solid lines indicate the average. (C) Number tuning as the weighted summation of decreasing/increasing units. Black solid lines, the average of individual tuning curves. (D) Left: Distributions of the preferred numerosity from the model simulation and observations in monkeys (27). Inset: The similarity test as performed in Fig. 2A (P < 0.01, n = 100). Right: The tuning width increases proportionally on a linear scale and remains constant on a logarithmic scale, as predicted by the Weber-Fechner law (27). (E) In the model simulation, neurons tuned to smaller numbers receive strong inputs from the decreasing units and receive weak inputs from the increasing units and vice versa. Right: The average weights of units preferring 4 and 24. (F) Weight bias of all number neurons observed in Conv5 of the untrained AlexNet. As predicted by the model simulation, the neurons tuned to smaller numbers receive stronger inputs from decreasing units and vice versa.

We hypothesized that these increasing and decreasing units can be the building blocks of number-selective neurons tuned to various numerosity values, as in the summation coding model suggested previously (16–18, 26). To test this idea, we performed a model simulation that holds that tuning curves tuned to various preferred numbers develop from a combination of increasing and decreasing unit activities. For this, 60 increasing and decreasing units were modeled as log-normal distributions peaking at 1 and 30, respectively (Fig. 5C, left), from the Gaussian parameters observed in the untrained AlexNet (see Materials and Methods for details). From 1000 repeated trials of simulations in which the weights of feedforward projections were randomly sampled from the Gaussian distribution of the untrained AlexNet (28), we found that number-selective neurons of all PNs can arise from the weighted sum of increasing and decreasing units (Fig. 5D). The number of tuned neurons increased as the PN decreases toward 1 or increases toward 30 (Fig. 5D, left), as observed in monkey experiments (27). In this simulation, we also confirmed that the sigma of the Gaussian fit of the average tuning curve follows the Weber-Fechner law, similar with that in the untrained AlexNet (Fig. 5D, right; linear, slope = 0.27; log, slope = 0.016).

We found that the number-selective neurons generated by this simulation show a predicted bias of feedforward weights between decreasing and increasing units such that neurons tuned to smaller numbers receive strong inputs from the decreasing units and receive weak inputs from the increasing units, while neurons tuned to larger numbers receive stronger inputs from increasing units (Fig. 5E; P < 10⁻⁴⁰; Wilcoxon rank sum test; Fig. 5F, black solid curve). We confirmed that this feedforward bias was also observed in Conv5 of the untrained AlexNet (Fig. 5F, red solid curve), implying that the observed neuronal tuning for various levels of numerosity originated from the summation of the monotonically decreasing and increasing activity units in the earlier layers. We also observed that monotonic units in Conv4 provide stronger inputs to number neurons than to the other neurons in Conv5 (fig. S4D), implying that number tuning in Conv5 arises from the monotonic units in Conv4.

DISCUSSION

Using biologically inspired DNN models, we showed that number neurons can spontaneously emerge in a randomly initialized DNN without learning. We found that a statistical variation of the weights in feedforward projections is a key factor to generate neurons tuned to numbers. These results suggest that neuronal tunings that initialize the abstract number sense could arise from the statistical complexity embedded in the deep feedforward projection circuitry.

Notably, we devised a new numerosity comparison task (Fig. 4) able to validate the abstract number sense independent of other low-level visual cues. Previously, it was suggested that the reported number sense might be observed because of the correlation between the numerosity and other continuous magnitudes such as total area, because it is hardly possible to design visual stimuli in which numerosity is completely independent of other nonnumerical visual magnitudes (e.g., if the total area is fixed, then the single dot size must decrease as numerosity increases) (35). However, this scenario was refuted in a number of commentaries (36–40) and after further studies (41, 42), from the fact that the observed number sense does not depend on various visual features in each controlled test. To address this issue carefully, we devised a new numerosity comparison task that could be successfully performed, only when the network makes decisions based on estimation of abstract numerosity. This new test can be used for future studies of abstract numerosity in behavioral tests of both animals and artificial neural networks.

Although AlexNet is not an impeccable model of the ventral visual pathway, the current results provide a possible scenario for understanding the developmental mechanism of number-selective neurons with unrefined feedforward projections (6, 7). Notably, this mechanism could also be applied to the other cognitive functions in the brain, such as the orientation selectivity in the primary visual cortex (V1). Regarding this issue, our previous studies showed that neuronal orientation tuning, and its spatial organization across the cortical surface, can emerge from the early circuits of the retina without any refinement of feedforward and recurrent circuits by visual experience (43–47). Extending this notion, our current results obtained from artificial DNNs may provide insight into the emergence of cognitive functions observed in early brains before learning begins with sensory inputs, which can be fine-tuned by various types of synaptic plasticity during the developmental process (48, 49).

It must be also noted that our current model is about how number sense arises initially and does not consider the complete process of development of number sense in adult animals. The training of DNN on natural images does not reconstruct all the changes in the properties of biological number tuning through lifelong experience. For example, we observed that the tuning curves of both untrained and pretrained networks are well fitted to a logarithmic scale (Fig. 2C and fig. S3B). However, the number tuning in infants on a logarithmic scale becomes a linear scale as they grow to adults (50), probably by experience with number system and by learning mathematics. We expect that a DNN model trained on numerical tasks would be able to implement the entire development process of number tuning, including the transition from a logarithmic to a linear scale by experience.

The biological implications of our results also provide a testable prediction for experimental studies about the anatomical substrates of the summation model in the brain. Number-selective neurons in the brain are observed mostly in the PFC (27, 34, 51), and neurons of monotonically increasing and decreasing activities are observed in the lateral intraparietal area (LIP) (33). Although the functional circuits from the LIP to the PFC for numerosity estimation has not been thoroughly examined anatomically, these two regions are observed to coactivate during the visual tasks of subjects (52). Such a correlation might be due to feedforward projection from the LIP to the PFC, considering that the LIP showed shorter latency than the PFC during a task involving visual categories (53). These results imply the possibility that the PFC and LIP are regions of interest that house the actual number neurons and their key component units. Further tests, to determine such as whether the number tuning in PFC weakens when the neural activity of the LIP is silenced, may validate the summation model as an underlying mechanism of number tuning in the brain.

In summary, we conclude that the number tuning of neurons can spontaneously arise in a completely untrained hierarchical neural network, solely from the statistical variance of feedforward projections. These results highlight the computational power of randomly initialized networks, as studied in relation to reservoir computing (54, 55) or zero-shot training for visual tasks (56, 57). Our findings suggest that various neural tunings may originate from the random initial wirings of neural circuits, providing insight into the mechanisms underlying the development of cognitive functions in hierarchical neural networks.

MATERIALS AND METHODS

Neural network model

AlexNet (8) was used as a representative model of a convolutional neural network. It consists of five convolutional layers with ReLU activation, followed by three fully connected layers. The detailed designs and hyperparameters of the model were determined on the basis of earlier work (8). On the basis of the architecture described above, the untrained version of AlexNet was investigated. For each layer, the values of the weights were randomly sampled from a normal distribution, where the mean of weights was set to 0, and the SD of the weights was determined to balance the strength of input signals across convolutional layers (bias = 0) (28). All simulations underwent 100 trials.

Stimulus dataset

The stimulus sets (Fig. 1A) were designed on the basis of earlier work (21). Briefly, images (size, 227 × 227 pixels) that contain N = 1, 2, 4, 6 … 28, 30 circles were provided as inputs to the network. To ensure the invariance of the observed number tuning for geometric factors such as the stimulus size, density, and area, three stimulus sets in which spatial overlap between the dots is avoided were designed. In set 1, dots were located at random locations but with a nearly consistent radius (generated by the normal distribution; mean = 7, SD = 0.7). In set 2, the total area of the dots remains constant (1200 pixel²) across different numerosities, and the average distance between neighboring dots is constrained in a narrow range (90 to 100 pixels). In set 3, a convex hull of the dots was fixed as a regular pentagon; the circumference of which is 647 pixels. The shape of each dot was determined to be that of a circle, a rectangle, an ellipse, and a triangle with an equal probability for each. Fifty images were generated for each combination of the numerosity and the stimulus set, meaning that 50 × 16 × 3 = 2400 images were used in total to evaluate the responses of the network units. Area-varying stimulus sets with eight levels of the total area (120π, 240π, 360π … 960π pixel²) (Fig. 4B) were designed on the basis of previous work (16). For each level, the total area of the dots remains constant across different numerosities, as in set 2 in Fig. 1A.

Analysis of the responses of the network units

The responses of network units in the final convolutional layer (after ReLU activation of the fifth convolutional layer) were analyzed. Similar to the method used to find number-selective neurons in monkeys (27) and to detect number-selective network units (21), a two-way analysis of variance (ANOVA) with two factors (numerosity and stimulus set) was used. To detect number-selective units generating a significant change of the response across numerosities but with an invariant response across stimulus sets, a network unit was considered to be number selective if it exhibited a significant change for numerosity (P < 0.01) but no significant change for the stimulus set or interaction between two factors. In contrast, a network unit was considered to be nonselective if it exhibited a significant change for the stimulus set (P < 0.01) but no significant change for the numerosity or for the interaction between two factors. The PN of a unit was defined as the numerosity that induced the largest response on average among the responses for all presentations. The tuning width of each unit was defined as the sigma of the Gaussian fit of the average tuning curve on a logarithmic number scale.

To determine the average tuning curves of all number-selective units, the tuning curve of each unit was normalized by mapping the maximized response to 1 and was then averaged across units using the PN value as a reference point. To compare the average tuning curves across different numerosities, the tuning curve of each unit was averaged across units preferring the same numerosity and was then normalized by mapping the minimized and maximized responses to 0 and 1, respectively.

Numerosity comparison task for the network

A numerosity comparison task was designed to examine whether number-selective neurons can sufficiently perform a numerical task that requires an estimation of numerosity from images. For each trial, a sample and a test stimulus (randomly selected from 1, 2, 4 … 28, 30) were presented to the network, and the resulting responses of the number-selective neurons were recorded. Then, an SVM was trained with the responses of 256 randomly chosen neurons (10 trials of sampling for each untrained network) to predict whether the numerosity of the sample stimulus is greater than that of the test stimulus. In this case, 100 sample stimuli were generated for each form of numerosity (1600 stimuli in total), and the test stimuli for each sample were generated while avoiding the numerosity of the corresponding sample stimulus. To calculate the average tuning curves for the correct and incorrect trials, the tuning curve of each neuron was normalized so that response for the PN in the correct trial was mapped to 1.

Model simulation for weighted summation of increasing and decreasing units

A model simulation was designed to show that the summation of decreasing and increasing unit activities (Fig. 5B) can reproduce the number-selective activities of all numerosities. The tuning curve of a model output neuron (R) was defined by

$$\mathit{R}=\text{ReLU}(\mathrm{\Sigma }{\mathit{w}}_{\text{Dec},\mathit{i}}{\mathit{r}}_{\text{Dec},\mathit{i}}+\mathrm{\Sigma }{\mathit{w}}_{\text{Inc},\mathit{i}}{\mathit{r}}_{\text{Inc},\mathit{i}})$$() 1

where w_Dec,i and w_Inc,i are the weight of the ith decreasing or increasing units, respectively, and r_Dec,i and r_Inc,i indicate their tuning curve. The decreasing and increasing unit activities (r) were modeled as log-normal distributions peaking at 1 and 30, respectively, mimicking the tuning curves observed in Conv4 of the untrained AlexNet. The tuning width of 60 decreasing or increasing sample units was randomly sampled from the Gaussian distribution, modeled following the statistics measured in the untrained AlexNet [means ± SD = 1.94 ± 1.5 (decreasing), 2.19 ± 1.5 (increasing)]. The feedforward weight (w) was also randomly sampled from the Gaussian distribution estimated from the untrained AlexNet. In a trial, 10,000 output neurons were generated, and 1000 trials were performed for the simulation.

The definition of increasing (or decreasing) units in Conv4 of the untrained AlexNet was adapted from previous work (16). In detail, those units were defined by regressing the response of unit i (R_i) with the logarithm of numerosity (N) and total area (A) across the entire image set (fig. S4; all variables used in the regression were scaled from 0 to 1)

$${\mathit{R}}_{\mathit{i}}={\mathrm{\beta }}_{\mathit{N}}\text{log}(\mathit{N})+{\mathrm{\beta }}_{\mathit{A}}\text{log}(\mathit{A})+\mathrm{\epsilon }$$ () 2

Increasing (or decreasing) units were defined if the regression explained at least 10% of the variance (R² > 0.1) in its response and the regression coefficient of the total area, β_A, was smaller than 0.1, so that the response of increasing (or decreasing) units increases (or decreases) as the stimulus numerosity increases but does not vary across the change of total area of the stimuli.

Statistical analysis

All statistical variables, including the sample sizes, exact P values, and statistical methods, are indicated in the corresponding texts or figure legends. The one-sided Wilcoxon rank sum test was used for most comparison analyses, except for the comparison between two different distributions of the PN (bootstrap analysis; the root mean square error between two curves was compared with that in the control with a shuffled distribution; Figs. 2A and 5D). Shaded areas or error bars indicate the SD in Figs. 1D, 2 (A and B), 3 (B, D, and E), 4 (E, G, and H), and 5 (E and F), and figs. S3 (B to E) and S4 (C and D), and indicate the SE in Fig. 1B and figs. S2D and S3A.

Code availability

MATLAB (MathWorks Inc.) with deep learning toolbox was used to perform the analysis. The MATLAB codes used in this work are available at https://github.com/vsnnlab/Number (DOI: 10.5281/zenodo.4118252).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/7/1/eabd6127/DC1

View/request a protocol for this paper from Bio-protocol.