Airflows inside passenger cars and implications for airborne disease transmission

We assess the impact of airflow on airborne coronavirus transmission risk to occupants in passenger cars.

Abstract

Transmission of highly infectious respiratory diseases, including SARS-CoV-2, is facilitated by the transport of exhaled droplets and aerosols that can remain suspended in air for extended periods of time. A passenger car cabin represents one such situation with an elevated risk of pathogen transmission. Here, we present results from numerical simulations to assess how the in-cabin microclimate of a car can potentially spread pathogenic species between occupants for a variety of open and closed window configurations. We estimate relative concentrations and residence times of a noninteracting, passive scalar—a proxy for infectious particles—being advected and diffused by turbulent airflows inside the cabin. An airflow pattern that travels across the cabin, farthest from the occupants, can potentially reduce the transmission risk. Our findings reveal the complex fluid dynamics during everyday commutes and nonintuitive ways in which open windows can either increase or suppress airborne transmission.

INTRODUCTION

Outbreaks of respiratory diseases, such as influenza, severe acute respiratory syndrome (SARS), Middle East respiratory syndrome, and now the novel coronavirus [severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)], have taken a heavy toll on human populations worldwide. They are redefining a myriad of social and physical interactions as we seek to control the predominantly airborne transmission of the causative, SARS-CoV-2 (1–3). One common and critical social interaction that must be reconsidered is how people travel in passenger automobiles, as driving in an enclosed car cabin with a copassenger can present a risk of airborne disease transmission. Most megacities (e.g., New York City) support more than a million of these rides every day with median figures of 10 daily interactions per rider (4). For maximum social isolation, driving alone is clearly ideal, but this is not widely practical or environmentally sustainable, and there are many situations in which two or more people need to drive together. Wearing face masks and using barrier shields to separate occupants do offer an effective first step toward reducing infection rates (5–10). However, aerosols can pass through all but the most high-performance filters (8, 11), and virus emissions via micrometer-sized aerosols associated with breathing and talking, let alone coughing and sneezing, are practically unavoidable (12–21). Even with basic protective measures such as mask wearing, the in-cabin microclimate during these rides falls short on a variety of epidemiological guidelines (22) with regard to occupant-occupant separation and interaction duration for a confined space. Preliminary models indicate a buildup of the viral load inside a car cabin for drives as short as 15 min (23, 24), with evidence of virus viability within aerosols of up to 3 hours (25, 26).

To assess these risks, it is critical to understand the complex airflow patterns that exist inside the passenger cabin of an automobile and, furthermore, to quantify the air that might be exchanged between a driver and a passenger. Although the danger of transmission while traveling in a car has been recognized (27), published investigations of the detailed airflow inside the passenger cabin of an automobile are unexpectedly sparse. Several works have addressed the flow patterns inside automobile cabins, but only in the all-windows-closed configuration (28–30)—most commonly used so as to reduce noise in the cabin. However, intuitively, a means to minimize infectious particles is to drive with some or all of the windows open, presumably enhancing the fresh air circulating through the cabin.

Motivated by the influence of pollutants on passengers, a few studies have evaluated the concentration of contaminants entering from outside the cabin (31) and the persistence of cigarette smoke inside the cabin subject to different ventilation scenarios (32, 33). However, none of these studies have addressed the microclimate of the cabin and the transport of a contaminant from one specific person (e.g., the driver) to another specific person (e.g., a passenger). In addition to this being an important problem applicable to airborne pathogens, in general, the need for a rigorous assessment of these airflow patterns inside the passenger cabin of an automobile seems urgent in the current coronavirus disease 2019 worldwide public health crisis.

The current work presents a quantitative approach to this problem. Although the range of car geometries and driving conditions is vast, we restrict our attention to that of two people driving in a car (five-seater), which is close to the average occupancy and seating configuration in passenger cars in the United States (34). We then ask the question: What is the transport of air and potentially infectious aerosol droplets between the driver and the passenger, and how does that air exchange change for various combinations of fully open and closed windows?

To address this question, we conducted a series of representative computational fluid dynamics (CFD) simulations for a range of ventilation options in a model four-door passenger car. The exterior geometry was based on a Toyota Prius, and we simulated the flow patterns associated with the moving car while having a hollow passenger cabin and six combinations of fully open and closed windows, named as front left (FL), rear left (RL), front right (FR), and rear right (RR) (Fig. 1). We consider the case of two persons traveling in the car—the driver in the front left-hand seat (assuming a left-hand drive vehicle) and the passenger sitting in the rear right-hand seat, thereby maximizing the physical distance (≈1.5 m) between the occupants. For the purposes of simulation, the occupants were modeled simply as cylinders positioned in the car interior.

Fig. 1. Schematic of the model car geometry, with identifiers the FL, RL, FR, and RR windows.

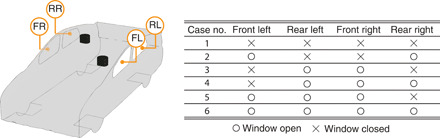
The two regions colored in black represent the faces of the driver and the passenger. Table on the right summarizes the six configurations simulated, with various combinations of fully open and closed windows.

As a reference configuration (Fig. 1, Config. 1), we consider driving with all four windows closed and a typical air-conditioning flow—with air intake at the dashboard and outlets located at the rear of the car—that is common to many modern automobiles (35). The intake air was modeled to be fresh (i.e., no recirculation) with a relatively high inflow rate of 0.08 m³/s (36).

The numerical simulations were performed using Ansys Fluent package, solving the three-dimensional, steady Reynolds-averaged Navier-Stokes (RANS) equations using a standard k-ε turbulence model (for details, see Methods). The RANS approach for turbulence, despite its known limitations (37), represents a widely used model for scientific, industrial, and automotive applications (38). A more accurate assessment of the flow patterns and the droplet dispersion is possible using large-eddy simulations or using fully resolved direct numerical simulations, which have a significantly higher computational cost. This is beyond the scope of the present work.

We simulated a single driving speed of v = 22 m/s [50 miles per hour (mph)] and an air density of ρ_a = 1.2 kg/m³. This translates to a Reynolds number of 2 million (based on the car height), which is high enough that the results presented here should be insensitive to the vehicle speed. The flow patterns calculated for each configuration were used to estimate the air (and potential pathogen) transmission from the driver to the passenger and, conversely, from the passenger to the driver. These estimates were achieved by computing the concentration field of a passive tracer “released” from each of the occupants and by evaluating the amount of that tracer reaching the other occupant (see Methods).

Here, we first describe the pressure distributions established by the car motion and the flow induced inside the passenger compartment. Following that, we describe the passenger-to-driver and driver-to-passenger transmission results for each of the ventilation options and, last, conclude with insights based on the observed concentration fields, general conclusions, and implications of the results.

RESULTS AND DISCUSSION

Overall airflow patterns

The external airflow generates a pressure distribution over the car (Fig. 2), forming a high-pressure stagnation region over the radiator grille and on the front of the windshield. The peak pressure here (301 Pa) is of the order of the dynamic pressure (0.5 ρ_av² = 290 Pa at 22 m/s). Conversely, as the airflow wraps over the top of the car and around the sides, the high airspeed is associated with a low-pressure zone, with the local pressure well below atmospheric (zero gauge pressure in Fig. 2). This overall pressure map is consistent with other computations of flows over automobile bodies (39) and gives a physical preview to a key feature—that the areas near the front windows and roof of the car are associated with lower-than-atmospheric pressures, while the areas toward the rear of the passenger cabin are associated with neutral or higher-than-atmospheric pressures.

Fig. 2. Pressure distributions around the exterior of the car associated with a vehicle speed of 22 m/s (50 mph).

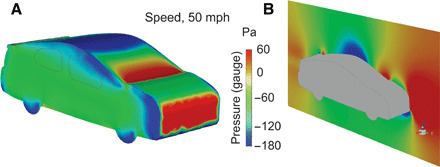
(A) Surface pressure distribution. (B) Pressure distribution in the air at the midplane. The color bar shows the gauge pressure in pascals and emphasizes the midrange of pressures: [−180, 60] Pa. At this speed, the full range of gauge pressure on the surface is [−361, 301] Pa.

A typical streamline (or pathline) pattern in the car interior is shown in Fig. 3, where the RL and FR windows are opened (Config. 3 in Fig. 1). The streamlines were initiated at the RL window, which is the location of a strong inflow (Fig. 3, bottom right), due to the high-pressure zone established by the car’s motion (Fig. 2). A strong air current (~10 m/s) enters the cabin from this region and travels along the back seat of the car before flowing past the passenger sitting on the RR side of the cabin. The air current turns at the closed RR window, moves forward, and most of the air exits the cabin at the open window on the FR side of the vehicle, where the exterior pressure is lower than atmospheric (Fig. 2). There is a much weaker air current (~2 m/s) that, after turning around the passenger, continues to circulate within the cabin. A small fraction of this flow is seen to exit through the RL window.

Fig. 3. Streamlines computed for the case in which the RL and FR windows are open.

The streamlines were initiated at the RL window opening. The streamline color indicates the flow velocity. Insets show the FR and RL windows colored by the normal velocity. The RL window has a strong inflow (positive) of ambient air, concentrated at its rear, whereas the FR window predominantly shows an outward flow (negative) to the ambient.

The streamline arrows indicate that the predominant direction of the recirculation zone inside the cabin is counterclockwise (viewed from above). These streamlines, of course, represent possible paths of transmission, potentially transporting virus-laden droplets or aerosols throughout the cabin and, in particular, from the passenger to the driver.

As already indicated, for the particular ventilation option shown here, the overall air pattern—entering on the RL and leaving on the FR—is consistent with the external pressure distributions (Fig. 2). The elevated pressure toward the rear of the cabin and the suction pressure near the front of the cabin drive the cabin flow. This particular airflow pattern was confirmed in a “field test” in which the windows of a test vehicle (2011 Kia Forte hatchback) were arranged with the RL and FR windows open, with two occupants (driver in the FL seat and a passenger in the RR seat) as in Config. 3. The car was driven at 30 mph on a length of straight road, and a flow wand (a short stick with a cotton thread attached to the tip) and a smoke generator were used to visualize the direction and approximate strength of the airflow throughout the cabin. By moving the wand and the smoke generator to different locations within the cabin, the overall flow patterns obtained from the CFD simulations—a strong air stream along the back of the cabin that exits the FR window, and a very weak flow near the driver—were qualitatively confirmed (see the Supplementary Materials). Different ventilation configurations generate different streamline patterns (e.g., figs. S4 and S5) but most of these can be linked to the pressure distributions established over the car body (Fig. 2).

An important consideration when evaluating different ventilation options in the confined cabin of a car is the rate at which the cabin air gets replenished with outside fresh air. This was measured by Ott et al. (32) for a variety of cars, traveling at a range of speeds, and for a limited set of ventilation options. In these measurements, a passive tracer (representing cigarette smoke) was released inside the cabin, and the exponential decay of the tracer concentration was measured. Assuming the cabin air to be well mixed (32), they estimated the air changes per hour (ACH)—a widely used metric in indoor ventilation designs.

From the simulations, we can precisely compute the total flow of air entering (and leaving) the cabin, and, knowing the cabin volume, we can directly compute the ACH. Such a calculation yields a very high estimate of ACH (of the order of thousands; see fig. S6), but this is misleading, since the assumption of well-mixed cabin air is an oversimplification. Instead, a more relevant quantification of the ACH was obtained using a residence time analysis for a passive scalar released at multiple locations within the passenger cabin. The time taken for the concentration at the outlets to decay below a threshold value (1% of the initial value) was computed, and the inverse of this time yields effective values for ACH (Fig. 4), which compare favorably with those reported by Ott et al. (32), after correcting for the vehicle speed (40).

Fig. 4. Air change rate (or ACH) calculated on the basis of a residence time analysis for different configurations.

Here, the air change rate is given by 1/τ_r, where τ_r is the residence time in hours. Uncertainty estimate is based on the turbulence level.

As one might expect, the-all-windows-open-configuration (Config. 6) has the highest ACH—approximately 250, while among the remaining configurations, the-all-windows-closed-configuration (Config. 1) has the lowest ACH of 62. However, what is somewhat unexpected is that the ACH for the configuration with windows adjacent to the driver and the passenger (FL and RR, respectively; Config. 2) are opened is only 89—barely higher than the all-windows-closed configuration. The remaining three configurations (Configs. 3 to 5) with two or three open windows all show a relatively high efficacy of about 150 ACH. The reason for these differences can be traced back to the overall streamline patterns and the pressure distributions that drive the cabin flow (Fig. 2). A well-ventilated space requires the availability of an entrance and an exit and a favorable pressure gradient between the two (41, 42). Once a cross-ventilation path is established (as in Config. 3 or Fig. 3), opening a third window has little effect on the ACH.

It is important to point out that the ACH for Config. 3 is higher than that for Config. 2, despite the apparent mirror symmetry of the open windows. This occurs because of two effects. First, the locations of the occupants relative to the open windows influences the residence time of the released scalar, which is used in estimating the ACH (32). Second, the cylinders representing the driver and passenger also cause a reduction in the airflow in Config. 2 where the occupants are seated next to the open windows. We will later show that the ACH gives only a partial picture and that the spreading of a passive scalar can show marked variations between Configs. 3 and 5, despite their nearly constant ACH.

Driver-to-passenger transmission

The flows established through the cabin provide a path for air transmission between the two occupants and hence a possible infection route. Our focus here is on transmission via aerosols, which are small enough (and noninertial) that they can be regarded as faithful tracers of the fluid flow (43, 44).

We begin by addressing the problem from the viewpoint of an infected driver releasing pathogen-laden aerosols and potentially infecting the passenger. Figure 5 shows a comparison of the spreading patterns of a passive scalar released near the driver and reaching the passenger (for details, see Methods). To obtain a volumetric quantification, the average scalar concentration in a 0.1-m-diameter spherical domain surrounding the passenger’s face is also computed, as shown in Fig. 5B.

Fig. 5. Driver-to-passenger transmission.

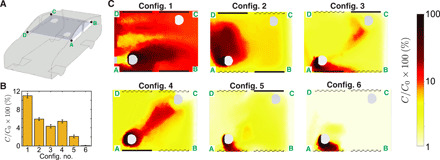
(A) Schematic of the vehicle with a cut plane passing through the center of the inner compartment on which the subsequent concentration fields are shown. (B) The bar graph shows the mass fraction of air reaching the passenger that originates from the driver. (C) Heatmaps showing the concentration field of the species originating from the driver for different window cases. Note that the line segment A–D is at the front of the car cabin, and the flow direction in C is from left to right. Dashed lines represent open windows, and solid lines indicate closed windows. Here, C₀ is the initial mass fraction of passive scalar at the location of the injection, where C/C₀ = 1. Error bars in (B) are 1 SD of the concentration field around the passenger.

The all-windows-closed configuration (Config. 1), relying only on air-conditioning, fares the worst and results in over 10% of the scalar that leaves the driver reaching the passenger. In contrast, the all-windows-open setting (Config. 6) appears to be the best case, with almost no injected scalar reaching the passenger. An overall trend of decreasing transmission is observed when the number of open windows are increased. However, there is some variability between the different configurations, the reasons for which may not be clear until one looks at the overall flow patterns (e.g., Fig. 3).

Concentration fields of the scalar (Fig. 5C) are examined in a horizontal plane A-B-C-D within the car cabin roughly at head height of the occupants (Fig. 5A). The scalar field concentration is the highest where all four windows are closed (Config. 1). We note that this driving configuration might also represent the most widely preferred one in the United States (with some seasonal variations). A two-windows-open situation, wherein the driver and the passenger open their respective windows (Config. 2), might be assumed as the logical thing to do for avoiding infection from the other occupant. Although this configuration does improve over the all-windows-closed situation, shown in Fig. 5B, one can see from the concentration field that Config. 2 does not effectively dilute the tracer particles and that the passenger receives a fairly large contaminant load from the driver. To explain this result, we looked more closely at the airflow patterns. In analogy with the streamlines associated with Config. 3 (Fig. 3), Config. 2 establishes a strong air current from the open RR window (RR) to the open FL window, along with a clockwise recirculating flow within the cabin as viewed from above. Although this flow pattern is weak, it increases the transport of tracer from the driver to the passenger. Moreover, the incoming air stream in Config. 2 enters behind the passenger and is ineffective in flushing out potential contaminants emanating from the driver.

An improvement to this configuration can be achieved if two modifications are possible: (i) a change in the direction of the internal circulation and (ii) a modified incoming airflow that impinges the passenger before leaving through the open window on the front. This has been realized when the RL and FR are open (Config. 3) (Fig. 5C), same as the configuration shown in Fig. 3). Now, the incoming clean air stream from the RL window partially impinges on the passenger (seated in the RR seat) as it turns around the corner. This stream of air might also act as an “air curtain” (45), and hence, the concentration of potentially contaminated air reaching the passenger is reduced.

The remaining configurations (Configs. 4 to 6) will be treated as modifications made to Config. 3 by opening more windows. Configuration 4 has three windows open (Fig. 5C). Since this represents opening an additional (RR) window, it may be unexpected to find a detrimental effect on the concentration field and the ACH (comparing Configs. 3 and 4 in Fig. 5, B and C). The increase in the concentration can be linked to the modified airflow patterns that result from opening the third (RR) window. First, opening the RR window leads to a reduction in the flow turning at the RR end of the cabin, since a fraction of the incoming air gets bled out of this window (fig. S4). Because of this diversion of the airflow, the region surrounding the passenger is less effective as a barrier to the scalar released by the driver. Second, the modified flow also creates an entrainment current from the driver to the passenger, which further elevates the scalar transport.

When the third open window is the FL (Config. 5), this leads to an improvement, nearly halving the average concentration when compared to when the additional window is the RR (Config. 3). The reason for this is apparent from the concentration field (Fig. 5C), since with the FL window near the driver open, the relatively low pressure near the front of the car creates an outward flow that flushes out much of released species. With the substantially reduced initial concentration field near the driver, the fraction reaching the passenger is proportionately reduced. Thus, among the configurations with three windows open, Config. 5 might provide the best benefit from the viewpoint of driver-to-passenger transmission.

Last, when all four windows are opened (Config. 6), we can again use the exterior pressure distribution to predict the flow directions. The streamlines enter through the rear windows and leave via the front windows. However, unlike the configuration with only two windows open (Fig. 3), the overall flow pattern is substantially modified (fig. S5), and the streamlines obey left-right symmetry and, for the most part, do not cross the vertical midplane of the car. In this configuration, the flow is largely partitioned into two zones creating two cross-ventilation paths in which the total airflow rate is nearly doubled when compared to the two- and three-windows-open configurations (fig. S6).

Passenger-to-driver transmission

In this section, we look into the particle (and potential pathogen) transmission from the passenger to the driver. Comparing the spreading patterns of a passive scalar within the car cabin (Fig. 6), the general trend suggests a decreasing level of transmission as the number of open windows is increased, similar to the results found for the driver-to-passenger transmission. The all-windows-closed configuration (Config. 1) shows the highest concentration level at the driver (~8%). This value, however, is lower than the 11% reported for the inverse transport, i.e., from the driver to the passenger (Fig. 5B), a difference that can be attributed to the fact that the air-conditioning creates a front-to-back mean flow.

Fig. 6. Passenger-to-driver transmission.

(A) Schematic of the vehicle with a cut plane passing through the center of the inner compartment on which the subsequent concentration fields are shown. (B) The bar graph shows the mass fraction of air reaching the driver that originates from the passenger. (C) Heatmaps showing the concentration field of the species originating from the passenger for different window configurations. Dashed lines represent open windows, and solid lines indicate closed windows. Here, C₀ is the initial mass fraction of passive scalar at the location of the injection, where C/C₀ = 1. Error bars in (B) are 1 SD of the concentration field around the driver.

As before, the lowest level of scalar transport corresponds to all-windows-open scenario (Config. 6), although we note that the concentration load here (about 2%) is noticeably higher than that for the driver-to-passenger transmission (about 0.2%). The streamline patterns for this configuration (fig. S5) show that the air enters through both the rear windows and exits through the respective front windows. There is, therefore, an average rear-to-front flow in both the left and right halves of the cabin, which enhances transmission from the passenger to the driver.

Among the remaining configurations (Configs. 2 to 5), Config. 3 shows a slightly elevated level of average concentration. The counterclockwise interior circulation pattern is at the heart of this transmission pattern. A substantial reduction in the average concentration can be achieved by additionally opening the rear window adjacent to the passenger (Config. 4). This allows for much of the scalar released by the passenger to be immediately flushed out through the rear window, analogous to the way in which opening the driver-adjacent (FL) window helps to flush out the high-concentration contaminants from the driver before they can circulate to the passenger (Fig. 5C, Config. 5).

Concluding remarks

In summary, the flow patterns and the scalar concentration fields obtained from the CFD simulations demonstrate that establishing a dominant cross-ventilation flow within the car cabin is crucial to minimize potentially infectious particle transport between car occupants. With this flow pattern established, the relative positions of the driver and passenger determine the quantity of air transmitted between the occupants.

It is, perhaps, not unexpected that the most effective way to minimize cross-contamination between the occupants is to have all the windows open (Config. 6). This establishes two distinct airflow paths within the car cabin, which help to isolate the left and right sides, and maximizes the ACH in the passenger cabin. Nevertheless, driving with all windows open might not always be a viable or desirable option, and, in these situations, there are some nonintuitive results that are revealed by the calculations.

The all-windows-closed scenario (Config. 1) with only air conditioning providing exchange appears to be the least effective option. Perhaps most unexpected is that an intuitive option—of opening the windows adjacent to each occupant (Config. 2)—is effective but not always the best among the partial ventilation options. Configuration 3, in which the two windows farthest from the occupants (FR and RL, respectively) are open, appears to give better protection to the passenger. The particular airflow patterns that the pressure distributions establish—channeling fresh air across the rear seat and out the FR window—help to minimize the interaction with the driver in the FL position.

The role of car speed cannot be ignored when addressing the transport between the vehicle’s occupants. Since the Reynolds number of the flow is high, the airflow patterns will be largely insensitive to how fast the car is driven. However, the ACH is expected to depend linearly on the car speed (40) and, consequently, the slower the car speed, the lower the ACH, the longer the residence time in the cabin, and hence the higher the opportunity for pathogenic infection (see fig. S7). We expect fully open windows to be the most efficient at reducing the contamination of the cabin environment. The flow patterns resulting from partially open windows, which can be a common driving setting, will be the focus of a future investigation.

The findings reported here can be translated to right-hand-drive vehicles, of relevance to countries like the United Kingdom and India. In those situations, similar but mirrored flow patterns can be expected. Furthermore, although the computations were performed for a particular vehicle design (loosely modeled on a Toyota Prius), we expect the overall conclusions to be valid for most four-windowed passenger vehicles. However, trucks, minivans, and cars with an open moonroof could exhibit different airflow patterns and hence different scalar transport trends.

There are, to be sure, uncertainties and limitations in our analysis approach. The steady RANS simulations solve for time-averaged turbulent flow, while the transmission of scalar particles that might represent pathogenic aerosols will be affected by large-scale, unsteady, and turbulent fluctuations, which are not fully captured in the present work. These effects could change the amount of tracer emitted by one occupant and reaching the other (46). Furthermore, buoyancy of the ejected multiphase cloud and temperature variations with the ambient can cause increased lifetimes for respiratory microdroplets (21), which are not accounted for in the present work. Nevertheless, despite these caveats, these results will have a strong bearing on infection mitigation measures for the hundreds of millions of people driving in passenger cars and taxis worldwide and potentially yield safer and lower-risk approaches to personal transportation.

METHODS

The car geometry was chosen on the basis of the basic exterior of a Toyota Prius. The interior was kept minimal and composed of two cylindrical bodies representing the driver and the passenger. The computer-aided design model for the car geometry was prepared using SOLIDWORKS, and subsequent operations including domain discretization (meshing) and case setup were carried out using the Ansys Fluent module.

The steady RANS equations with a standard k-ε turbulence model was solved on an unstructured grid, made up of about 1 million tetrahedral grid cells. The domain size was 6h × 5h × 3h in the streamwise, normal, and spanwise directions, respectively, where h is the car height. A vehicle speed of v = 22 m/s (50 mph) was set as the inflow condition upstream of the front of the car body. A pressure outlet condition was applied at the exit. The simulations were iterated until convergence was achieved for the continuity and momentum equations and the turbulence dissipation rate E. Each simulation run took roughly 1.5 hours of computational time on a standard workstation. A grid independence study was performed, which established that the resolution adopted was sufficient for the quantities reported in the present work.

The mixing and transport of a passive scalar were modeled by solving species transport equations describing an advection-diffusion equation. Separate simulations were performed for the scalar released near the driver and then for its release near the passenger’s face. The scalar was set to be a noninteracting material, i.e., with an exceedingly low mass diffusivity, which meant that only advection and turbulent diffusion contributed to its transport dynamics. This approach mimics the mixing of a high Schmidt number material, such as dye or smoke, which are commonly used as a tracers in turbulent fluid flows (47). The injection rate of the species was very low so that it did not influence the airflow. This was verified by comparing the concentration fields for various injection rates, which showed negligible variation. This strategy was followed so that the turbulent diffusion effects were also captured in the analyses.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/sciadv.abe0166/DC1