A thermodynamic atlas of carbon redox chemical space

Significance

Carbon redox chemistry plays a fundamental role in biology. However, the thermodynamic and physicochemical principles underlying the rise of metabolites involved in redox biochemistry remain poorly understood. Our work introduces the theory and techniques that allow us to quantify and understand the global energy landscape of carbon redox biochemistry. We analyze the space of all possible oxidation states of linear-chain molecules with two to five carbon atoms and generate a detailed atlas of the thermodynamic stability of metabolites in comparison to nonbiological molecules. Although the emergence of life required the underlying chemistry to bootstrap itself out of equilibrium, a quantitative understanding of the environment-dependent thermodynamic landscape of prebiotic molecules will be extremely valuable for future origins of life models.

Abstract

Redox biochemistry plays a key role in the transduction of chemical energy in living systems. However, the compounds observed in metabolic redox reactions are a minuscule fraction of chemical space. It is not clear whether compounds that ended up being selected as metabolites display specific properties that distinguish them from nonbiological compounds. Here, we introduce a systematic approach for comparing the chemical space of all possible redox states of linear-chain carbon molecules to the corresponding metabolites that appear in biology. Using cheminformatics and quantum chemistry, we analyze the physicochemical and thermodynamic properties of the biological and nonbiological compounds. We find that, among all compounds, aldose sugars have the highest possible number of redox connections to other molecules. Metabolites are enriched in carboxylic acid functional groups and depleted of ketones and aldehydes and have higher solubility than nonbiological compounds. Upon constructing the energy landscape for the full chemical space as a function of pH and electron-donor potential, we find that metabolites tend to have lower Gibbs energies than nonbiological molecules. Finally, we generate Pourbaix phase diagrams that serve as a thermodynamic atlas to indicate which compounds are energy minima in redox chemical space across a set of pH values and electron-donor potentials. While escape from thermodynamic equilibrium toward kinetically driven states is a hallmark of life and its origin, we envision that a deeper quantitative understanding of the environment-dependent thermodynamic landscape of putative prebiotic molecules will provide a crucial reference for future origins-of-life models.

Redox reactions are fundamental to biochemistry. Recent work has uncovered quantitative thermodynamic principles that influence the evolution of carbon redox biochemistry (1–3). This line of work has focused on the three main types of redox reactions that change the oxidation level of carbon atoms in molecules: reductions of carboxylic acids (–COO) to aldehydes (–C=O); reductions of aldehydes and ketones to alcohols (hydroxycarbons) (C–O); and reductions of alcohols to hydrocarbons (C–C). The “rich-get-richer” principle states that more reduced carbon functional groups have higher standard redox potentials (1–3). Thus, alcohol reduction to a hydrocarbon is more favorable than aldehyde/ketone reduction to an alcohol, which in turn is more favorable than carboxylic acid reduction to an aldehyde. This explains why, across all six known carbon fixation pathways, adenosine triphosphate is invested solely (with ribulose-5P kinase as the single exception) to drive carboxylation and the reduction of carboxylic acid functional groups (2, 4). Quantitative analysis of biochemical redox thermodynamics has also explained the emergence of NAD(P) as the universal redox cofactor. With a standard redox potential of −320 mV, NAD(P) is optimized to reversibly reduce/oxidize the vast majority of central metabolic redox substrates (3). In addition, since its standard potential is ∼100 mV lower than that of the typical aldehyde/ketone functional group, it effectively decreases the steady-state concentration of potentially damaging aldehydes/ketones in the cell (3). Finally, other physicochemical properties like hydrophobicity and charge act as constraints that shape the evolution of metabolite concentrations (5).

Although the emergence of early self-reproducing systems requires the underlying chemistry to be out of thermodynamic equilibrium, a quantitative and comprehensive understanding of the underlying energy landscape would be very valuable. For example, high abundance of a given compound in a mixture of thermodynamically equivalent molecules could be ascribed to a kinetics-enabled, energy-driven process. However, the most likely scenario is that even at equilibrium, some compounds may be significantly more favorable than others, establishing the initial conditions for subsequent out-of-equilibrium processes. In addition, kinetics of catalysis and thermodynamics are highly intertwined, jointly contributing to effective reaction rates (6–8). Therefore, a comprehensive and quantitative understanding of the underlying thermodynamic landscape could help inform kinetic models of prebiotic redox chemistry.

Despite these motivations, the thermodynamic and physicochemical principles underlying the rise of carbon redox biochemistry remain very poorly understood. Here, we combinatorially generate the chemical space of all possible redox states of linear-chain n-carbon compounds (for n = 2 to 5). We partition each n-carbon linear-chain redox chemical space into biological metabolites and nonbiological compounds and systematically explore whether metabolites involved in biochemical redox reactions display features that would be unexpected elsewhere in redox chemical space. To compare physicochemical and thermodynamic properties of the biological and nonbiological molecules, we use cheminformatic tools and a recently developed quantum-chemical approach to estimate standard reduction potentials (E^o′) (3) of biochemical reactions.

In addition to generating a molecular energy landscape of broad applicability to the study of biochemical evolution, our analysis provides specific insight on redox biochemistry, which we summarize in the following five major conclusions: 1) the oxidation level and asymmetry of aldose sugars makes them unique in that they have the highest possible number of connections (reductions and oxidations) to other molecules; 2) biological compounds (metabolites) tend to be enriched for carboxylic acid functional groups and depleted for aldehydes/ketones; 3) metabolites tend to have, on average, higher solubilities and lower lipophilicities than the nonbiological molecules; 4) across a range of pH and electron-donor/-acceptor potentials, metabolites tend to have, on average, lower Gibbs energies relative to the nonbiological compounds; and 5) by adapting Pourbaix phase diagrams—an important conceptual tool in electrochemistry—to the study of redox biochemistry, we find that the n-carbon linear-chain dicarboxylic acids and fatty acids (e.g., succinate and butyrate in four-carbon redox chemical space) are the local minima in the energy landscape across a range of conditions and thus may have a spontaneous tendency to accumulate. Our results suggest that thermodynamics may have played an important role in driving the rise of dominant metabolites at the early stages of life and yield insight into the principles governing the emergence of metabolic redox biochemistry.

Results

Aldose Sugars Have the Maximal Number of Redox Connections.

We combinatorially generated all possible redox states of n-carbon linear-chain compounds (for n = 2 to 5 carbon atoms per molecule) and studied the properties of the resulting chemical spaces (Fig. 1). For every molecule in n-carbon redox chemical space, each carbon atom can be in one of four different oxidation levels: carboxylic acid, ketone or aldehyde, hydroxycarbon (alcohol), or hydrocarbon (Fig. 1A). Molecules in redox chemical space are connected to each other by three different types of two-electron reductions (or the reverse oxidations) that change the oxidation level of a single carbon atom: reduction of a carboxylic acid to an aldehyde; reduction of an aldehyde/ketone to a hydroxycarbon; and reduction of a hydroxycarbon to a hydrocarbon. In order to make the redox chemical space model system tractable to analysis, we decreased its complexity by excluding carbon–carbon bond cleavage/formation reactions (e.g., reductive carboxylations or oxidative decarboxylations), keto–enol tautomerizations, intermediate carbon–carbon double-bond formation, intramolecular redox reactions, or different stereoisomers for a given molecular oxidation level (see SI Appendix, Table S1 for how the number of compounds increases when these reactions are included). In what follows, we focus the majority of our analysis on the properties of the four-carbon linear-chain redox chemical space (see SI Appendix, Figs. S7–S14 for corresponding results in two-, three-, and five-carbon linear-chain redox chemical space).

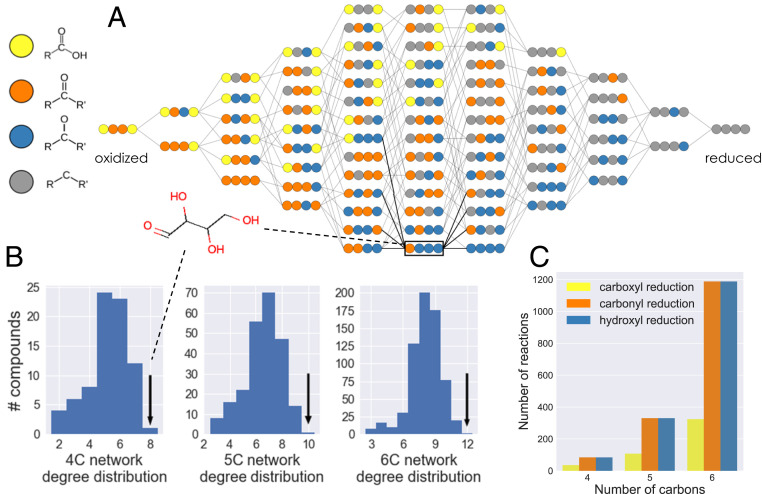
Fig. 1.

The structure of n-carbon linear-chain redox chemical space. (A) The redox chemical space defined by the set of all possible four-carbon linear chain molecules that can be generated from three different types of redox reactions: reduction of a carboxylic acid to an aldehyde group; reduction of an aldehyde/ketone group to a hydroxycarbon (alcohol); and reduction of a hydroxycarbon to a hydrocarbon (and corresponding oxidations). Carbon atoms are represented as colored circles, with each color corresponding to an oxidation state: yellow, carboxylic acid; orange, aldehyde/ketone; blue, hydroxycarbon; and gray, hydrocarbon. Compounds within each column have the same molecular oxidation state and are organized from most oxidized (left) to most reduced (right). (B) The degree distributions for the four-, five-, and six-carbon linear-chain redox chemical spaces. In all cases, the aldose sugar is the only compound with the maximal number of possible reductions and oxidations (black arrows). (C) Number of reactions in the four-, five-, and six-carbon linear-chain redox chemical spaces that belong to each of the three types of redox reactions considered.

The four-carbon linear-chain redox chemical space contains 78 molecules connected by 204 reactions. The molecules span 11 different molecular oxidation levels, from the fully oxidized 2,3-dioxosuccinic acid (2 carboxylic acids and 2 ketones) to the fully reduced alkane butane (Fig. 1A); 84 reactions reduce aldehydes/ketones to hydroxycarbons (or oxidize hydroxycarbons to aldehydes/ketones), and the same number reduce hydroxycarbons to hydrocarbons (or oxidize hydrocarbons to hydroxycarbons). Since carboxylic acids are restricted to carbon atoms at the edges of a molecule (i.e., carbon nos. 1 and 4 in 4-carbon linear-chain molecules), only 36 reactions reduce carboxylic acids to aldehydes (or oxidize aldehydes to carboxylic acids) (Fig. 1C).

The number of reactions that connect a molecule to its oxidized or reduced products—the redox degree of a molecule—ranges from 2 to 2n (Fig. 1B). In n = 4-carbon redox chemical space, we find that only a single molecule in the network, the aldose sugar erythrose (and its stereoisomers), has the maximal degree value of 2n = 8. This holds true for all redox chemical spaces regardless of the number of carbon atoms: only the corresponding aldose sugars in the two-, three-, five-, and six-carbon redox chemical spaces have the maximal-degree value, 2n (Fig. 1B). This is explained by the fact that the n-carbon aldose sugar satisfies the two constraints required to have the maximal number of redox connections: 1) each atom must be in an “intermediate” oxidation level that can be both oxidized and reduced. Therefore, all inner carbon atoms (i.e., atom nos. 2 and 3 in four-carbon linear-chain molecules) must be in the hydroxycarbon oxidation level, while carbon atoms at the edges (i.e., atom nos. 1 and 4) can be either in the aldehyde or hydroxycarbon oxidation level. 2) The molecule must not be symmetric under a 180° rotation along its center. Thus, the two edge atoms must be in different oxidation levels. This leads uniquely to the aldose sugar molecular redox-state configuration.

Biological Compounds Are Enriched in Carboxylic Acids and Depleted of Aldehyde/Ketone Groups.

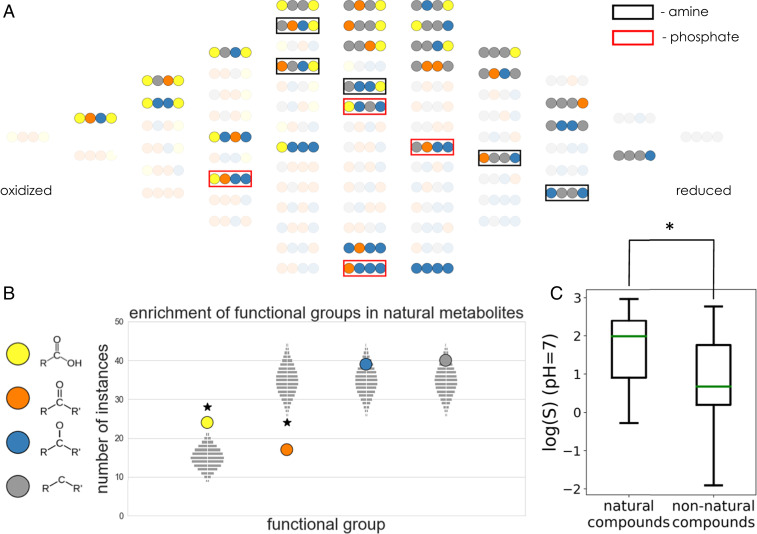
What distinguishes the subset of compounds in redox chemical space that appear in cellular metabolism from those that do not? To address this question, we subdivided the 78 molecules from the full 4-carbon redox chemical space into 30 biological compounds (also referred to from here onward simply as metabolites or “natural” compounds), which were identified based on matches with Kyoto Encyclopedia of Genes and Genomes (KEGG) database entries (9, 10), and the remaining 48 “nonbiological” compounds (Fig. 2A). Compounds in KEGG that correspond to molecules in redox chemical space but have alcohol groups substituted by amines or phosphates were considered a match, as these functional groups have the same oxidation level (see Materials and Methods for further details). For example, the metabolites oxaloacetate and aspartate have the same oxidation level at every carbon atom but differ by the substitution of an alcohol into an amine; both are considered a match to the corresponding molecule in our network. Similarly, we consider metabolites with carboxylic acid groups that are activated with either thioesters or phosphates groups as matches to molecules in redox chemical space.

Fig. 2.

Functional-group statistics and aqueous solubilities of biological compounds in the four-carbon linear-chain redox chemical space. (A) The subset of molecules in four-carbon linear-chain redox chemical space that matches biological metabolites in the KEGG database. Compounds that match KEGG metabolites but with alcohol groups substituted by either amines or phosphates are marked with black and red squares, respectively. (B) Enrichment and depletion of functional groups in the set of biological compounds. The vertical position of each colored circle corresponds to the number of times each functional group appears in the set of biological compounds. The light gray rectangles show the corresponding expected null distributions for random sets of molecules sampled from redox chemical space. See SI Appendix, Fig. S1 for statistical analysis of functional-group pairs and triplets. (C) Comparison of predicted aqueous solubility log(S) at pH 7 for biological and nonbiological compounds in the four-carbon linear-chain redox chemical space. Biological compounds have significantly higher solubilities than the nonbiological set (P < 0.005).

As a first comparison between metabolites and nonbiological compounds, we analyzed the enrichment or depletion of functional groups (i.e., carbon atom oxidation levels) in the two categories (Fig. 2B). Specifically, we counted the number of times that each functional group appears in the set of metabolites and compared it to analytically derived expected null distributions for random sets of compounds (Materials and Methods). We found that in four-carbon linear-chain redox chemical space, metabolites are significantly enriched in carboxylic acids (P < 0.001) while being significantly depleted for ketones (P < 0.001) (Fig. 2B). We find similar trends in three- and five-carbon redox chemical spaces (SI Appendix, Figs. S8–S11). Since all but one molecule in two-carbon redox chemical space are biological metabolites, this space is not amenable to such statistical analysis. Furthermore, after normalizing for observed single functional-group statistics (see Materials and Methods for further details), we computed the null distributions for higher-order functional-group patterns, i.e., pair (2mer) and triplet (3mer) patterns (SI Appendix, Fig. S1). According to our analysis, only the 2mer pattern with a hydroxycarbon next to a hydrocarbon is depleted in the metabolites, albeit not significantly (P = 0.05). The number of times that all other 2mer and 3mer functional-group patterns appear in metabolites—including the highly uncommon dicarbonyl pattern—can be explained by the underlying single functional-group statistics.

We then asked whether the observed functional-group enrichments and depletions translate to differences in physicochemical properties of the metabolites and the nonbiological compounds. In particular, the significant enrichment of carboxylic acids is likely expected to result in higher average solubility and lower lipophilicity for the natural relative to the nonnatural compounds. However, given the fact that solubility and lipophilicity depend on the combination of all functional groups in a given molecule—with polar groups like carboxylic acids increasing solubility and nonpolar groups like hydrocarbons decreasing it—and that there is a enrichment (albeit not statistically significant) of hydrocarbons in the natural compounds, the combined effect of these two trends may be nontrivial. We therefore explicitly computed the solubility (logS) and lipophilicity (as captured by the octanol–water distribution coefficient [logD]) at pH 7. Indeed, we find that, in correlation with their enrichment for carboxylic acid functional groups, metabolites have significantly higher solubilities (P < 0.005) (Fig. 2C) and significantly lower logD values (P < 0.01) (SI Appendix, Fig. S2) than the set of nonbiological compounds. We observe similar trends in three- and five-carbon redox chemical spaces (SI Appendix, Figs. S9 and S13).

Metabolites Have on Average Lower Gibbs Energies than Nonbiological Compounds.

We next focused on estimating the energy landscape of our redox compounds, with special attention to the question of whether metabolites and nonbiological compounds display different patterns in this landscape. We used a recently developed calibrated quantum-chemistry approach (3) to accurately predict the apparent standard redox potentials $E^{o\prime }\left(\text{pH}\right)$ of all reactions in n-carbon linear-chain redox chemical space (n = 2 to 5). Previous work has shown that the calibrated quantum-chemistry method achieves significantly better accuracy than the group-contribution method (GCM) (3), the most commonly used approach to estimate thermodynamic parameters of biochemical compounds and reactions (11–14). Briefly, the quantum-chemistry method relies on density functional theory with a double-hybrid functional (15, 16) to compute the differences in molecular electronic energies and utilizes a two-parameter calibration against available experimental data. We computed the energies of several geometry-optimized conformations of the fully protonated species of each compound. We then estimated the standard redox potential $E^o$ of the fully protonated species as the difference in electronic energies of the products and substrates, ΔE_electronic. Using cheminformatic pK_a estimates (Marvin 17.7.0, 2017; ChemAxon) and the Alberty Legendre transform (17, 18), we converted the standard redox potentials to transformed standard redox potentials $E^{o\prime }\left(\text{pH}\right),$ which depend on pH. Finally, in order to correct for systematic errors in the quantum-chemistry calculations and the cheminformatic pK_a estimates, we calibrated—via linear regression—the transformed standard redox potentials $E^{o\prime }\left(\text{pH}\right)$ against a dataset of available experimental values (see Materials and Methods for further details).

We note that the improvement in accuracy of the quantum-chemical approach over GCM is particularly striking for the linear-chain compounds in our redox chemical spaces. This is most apparent for the set of aldehyde/ketone to hydroxycarbon reductions (SI Appendix, Fig. S3): while GCM prediction is no better than an average value predictor (R² = −0.04), the redox potentials predicted with the calibrated quantum-chemistry method correlate linearly with experimental values (Pearson r = 0.50). GCM accounts only for the difference in group energies of products and substrates to estimate redox potentials. Thus, for redox reactions, it effectively ignores the molecular environment surrounding the reduced/oxidized carbon atom, collapsing all of the potentials associated to aldehyde/ketone functional-group reductions to two values (the average aldehyde and ketone reduction energies), thus lowering its prediction accuracy (SI Appendix, Fig. S3). Therefore, the use of our calibrated quantum-chemical method is essential in order to accurately predict and analyze the energetics of n-carbon linear-chain redox chemical spaces.

We used the predicted $E^{o\prime }\left(\text{pH}\right)$ values to generate the energy landscape of redox chemical space. To do this, we assumed that each compound is coupled to an electron donor/acceptor with a given steady-state redox potential, E(electron donor). This potential could represent that set by a steady-state ratio of NAD⁺/NADH or other abundant redox cofactor inside the cell (19). Alternatively, in the context of prebiotic chemistry, it could represent the potential associated with a given concentration of molecular hydrogen in an alkaline hydrothermal vent or different iron oxidation states in prebiotic oceans (20, 21). Given a value of E(electron donor), we convert the $E^{o\prime }\left(\text{pH}\right)$ of each reaction into a Gibbs reaction energy, using $\mathrm{\Delta }{G}_r\left(\text{pH}\right)=-nF\left(E^{o\prime }\left(pH\right)-E\left(\text{electron}\hspace{0.17em}\text{donor}\right)\right)$ (where n is the number of electrons and F is Faraday’s constant). The set of Gibbs reaction energies for all redox transformations—as a function of pH and electron-donor potential—defines the energy landscape of our redox chemical space (Fig. 3A and SI Appendix, Figs. S5 and S6).

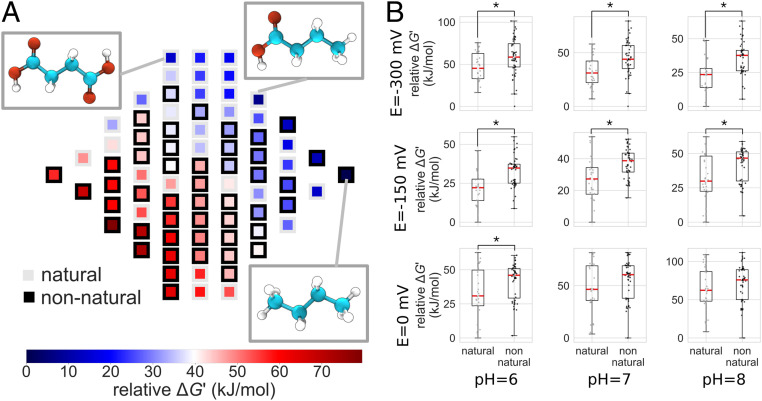
Fig. 3.

Thermodynamic landscape of the four-carbon linear-chain redox chemical space. (A) Relative Gibbs energies of metabolites at pH 7 and E(electron donor/acceptor) = −300 mV. Gibbs energies are normalized relative to the metabolite with the lowest energy. Compounds within a column (same molecular oxidation state) are sorted from highest (bottom) to lowest (top) relative energies. The structures of the three compounds that are local minima in the thermodynamic landscape are shown: succinate (Top Left Inset), butyrate (Top Right Inset), and butane (Bottom Right Inset). These compounds have lower Gibbs energies than all of their neighboring molecules accessible by a reduction or oxidation. (B) Relative Gibbs energies of biological and nonbiological compounds for a range of pH and E(electron donor/acceptor) values. At each value of pH and E(electron donor/acceptor), Gibbs energies are normalized relative to the compound with the lowest energy. Asterisks indicate statistically significant differences of average values (Welch’s t test; P < 0.05).

A notable finding of this analysis is that, across a range of cofactor potentials, metabolites in four-carbon linear-chain redox chemical space have, on average, significantly lower relative Gibbs energies than the nonbiological compounds (Fig. 3B). We find a similar trend for metabolites in three- and five-carbon linear-chain redox chemical space (SI Appendix, Figs. S10–S14); however, because of the few number of nonnatural compounds in three-carbon redox chemical space, the trend there is not statistically significant (SI Appendix, Fig. S10). An important exception to this general trend (and one that is conserved across spaces with different numbers of carbon atoms) is that the aldose sugars (e.g., erythrose), the ketose sugars (e.g., erythrulose), and the sugar alcohols (e.g., threitol) have a higher relative Gibbs energy than all compounds in redox chemical space across a large range of pH and electron-donor potential.

A Pourbaix Phase Diagram of Redox Chemical Space Maps Local Minimal-Energy Compounds.

In addition to the trends observed for average energy differences between biological and nonbiological compounds, the relative energies of individual compounds change as a function of pH and E(electron donor) (SI Appendix, Figs. S5 and S6). To further investigate the detailed structure of the thermodynamic landscape, we set out to map which molecules are local minima at each value of pH and E(electron donor). A molecule is a local minimum in redox chemical space if its Gibbs energy is lower than that of all of its neighbors with whom it is connected through a reduction or an oxidation. We adapt Pourbaix phase diagrams, a powerful standard visualization tool in the field of electrochemistry (22), to the problem of mapping out regions of pH, E(electron donor) phase space in n-carbon linear-chain redox chemical space. In a Pourbaix diagram, the predominant equilibrium states of an electrochemical system and the boundaries between these states are mapped out as a function of two-phase space parameters. Fig. 4 shows a Pourbaix phase diagram representation of four-carbon linear-chain redox chemical space (see SI Appendix, Figs. S7, S8, and S12 show the corresponding Pourbaix diagrams for two-, three-, and five-carbon linear-chain redox chemical spaces).

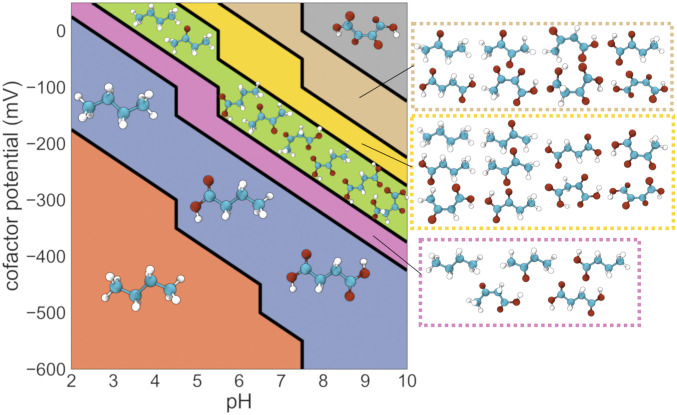
Fig. 4.

Pourbaix phase diagram for the four-carbon linear-chain redox chemical space. Molecules that are local minima in the energy landscape at each region of pH, E(electron donor/acceptor) phase space are shown. At low pH and E(electron donor/acceptor) values, butane is both the global and the only local minimum-energy compound. At intermediate values of pH and E(electron donor/acceptor), several metabolites emerge as local minima and would thus tend to accumulate. For example, the metabolites oxaloacetate, acetoacetate, and α-ketobutyrate emerge as local energetic minima in the region of phase space shown in green. Finally, in the upper right corner of the phase diagram, characterized by higher values of both pH and E(electron donor/acceptor), the fully oxidized four-carbon compound 2,3-dioxosuccinic acid emerges as the only local (global) minimum.

At the lower left corner of the diagram in Fig. 4, in the region corresponding to more acidic pH values and more negative electron-donor potentials, the fully reduced four-carbon alkane butane is the only local (and the global) energy minimum (Fig. 4). Thus, assuming all compounds are kinetically accessible, butane would be expected to accumulate in these conditions. The structure of redox chemical space becomes richer as pH and E(electron donor) increase. Succinate and the four-carbon short-chain fatty acid (SCFA) butyrate—two biologically important metabolites—emerge as two additional local minima at more oxidative regions of the phase diagram (Fig. 4). Both succinate and butyrate consist of inner carbon atoms in the hydrocarbon (fully reduced) oxidation level and edge carbon atoms in either the hydrocarbon or the carboxylic acid (fully oxidized) state. Notably this pattern—where the n-carbon linear-chain dicarboxylic acid (oxalate, malonate, succinate, and glutarate for two-, three-, four-, and five-carbon atoms, respectively), the fatty acid (acetate, propionate, butyrate, and valerate), and the alkane (ethane, propane, butane, and pentane) emerge as the only local minima in a large region of phase space—is conserved in redox chemical spaces with different number of carbon atoms (SI Appendix, Figs. S7, S8, and S12). Further increases in either pH or electron-donor potential result in the emergence of additional compounds, both metabolites and nonbiological molecules, as local energy minima in the landscape (Fig. 4 and SI Appendix, Figs. S7, S8, and S12).

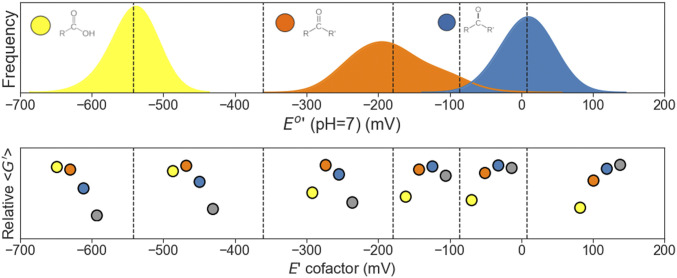
Can we predict from simple physicochemical principles the identity of the local minimal-energy compounds? A simple mean-field toy model (Fig. 4C) that focuses on the average standard redox potentials $<E^{o\prime }\left(\text{pH}\right)>$ of the different carbon functional groups can help intuitively predict which metabolites accumulate at given values of pH and E(electron donor). Fig. 5, Upper shows the distributions of standard potentials at a fixed pH (pH 7) for all compounds in four-carbon redox chemical space categorized by the type of functional group undergoing reduction. Given a fixed value of E(electron donor), the average redox potentials for each functional-group category can be used to compute average Gibbs reaction energies for each type of carbon redox transformation via the following equation: $\mathrm{\Delta }{G}_{\text{r}}\left(\text{pH}\right)=-nF\left(<\hspace{1em}{E}^{o\text{'}}\left(\text{pH}\right)>-E\left(\text{electron}\hspace{0.17em}\text{donor}\right)\right)$ (where n is the number of electrons and F is Faraday’s constant). We use this to generate Fig. 5, Lower, which schematically shows the relative average Gibbs energies of the four different carbon oxidation levels at different values of E(electron donor) at pH 7. The boundaries delimiting different regions of the E(electron donor) axis mark the values where the rank-ordering of relative average Gibbs energies for the four carbon oxidation-level changes.

Fig. 5.

A mean-field toy model explains the identity of molecular oxidation states of local minima. The schematic diagram illustrates how the average standard redox potentials of different carbon functional groups dictate the identity of the minimal-energy compounds. Top shows the distributions of standard redox potentials (pH 7) of all reactions in the four-carbon linear-chain redox chemical space, grouped according to the functional group that is reduced during the transformation: carboxylic acid (yellow), aldehyde/ketone (orange), and hydroxycarbon (blue). Bottom shows—for different values of E(electron donor/acceptor)—the resulting relative average Gibbs energies of the functional groups. For example, in the region where E(electron donor/acceptor) is between about −360 and −190 mV, aldehydes/ketones (orange) have, on average, the highest relative Gibbs energy, followed by hydroxycarbons (blue), carboxylic acids (yellow), and hydrocarbons (gray). Therefore, minimal-energy compounds will have inner carbon atoms (atom nos. 2 and 3 in four-carbon molecules) that equilibrate to the hydrocarbon oxidation state and edge carbon atoms (atom nos. 1 and 4) that equilibrate to either the carboxylic acid or the hydrocarbon oxidation state.

As an illustrative example, we focus on region III in Fig. 5, which is approximately delimited by the values $-360\hspace{0.17em}\text{mV}\le E\left(\text{electron}\hspace{0.17em}\text{donor}\right)\le -180\hspace{0.17em}\text{mV}.$ In this region, the reduction of carboxylic acids to aldehydes (yellow to orange) is highly unfavorable (alternatively, the oxidation of aldehydes to carboxylic acids is highly favorable). On the other hand, the reduction of ketones to hydroxycarbons (orange to blue), as well as the reduction of hydroxycarbons to hydrocarbons (blue to gray), are thermodynamically favorable. Thus, at pH 7 and for this range of E(electron donor) values, the edge carbon atoms (atom nos. 1 and 4 in the four-carbon linear-chain compounds) are driven to either the most-oxidized (carboxylic acid) or the most-reduced (hydrocarbon) oxidation level, while the inner carbon atoms (atom nos. 2 and 3)—which cannot exist in the carboxylic acid oxidation level—are driven to the hydrocarbon oxidation level. This corresponds precisely to the molecular oxidation levels of dicarboxylic acids, fatty acids, and alkanes (e.g., succinate, butyrate, and butane), the local and global minimal-energy compounds in this region of pH, E(electron donor) phase space.

Discussion

In this work, we introduced the chemical spaces of all molecular oxidation levels of n-carbon linear-chain compounds and analyzed their structural, physicochemical, and thermodynamic properties. In some respects, our work is related to that of Morowitz et al. (23) in that it similarly explores the chemical properties of a portion of chemical space in search for possible traces of their relevance to the rise of biological systems. However, our work does not rely on chemical databases—which may be biased toward certain categories of compounds (24)—but rather analyzes a portion of chemical space in a way that is general, unbiased, and potentially arbitrarily extendible. In addition, while Morowitz et al. imposed a priori solubility, oil–water partition coefficients and combustion energies as criteria for the selection of metabolism-like organic compounds, our work systematically compares metabolites to the rest of the molecules in redox chemical space and demonstrates significant differences in these physicochemical parameters.

Our results are applicable and agnostic to “genetics-first” (25–28), or “metabolism-first” (29–32), scenarios for the early stages of life. Thermodynamics is a fundamental constraint in chemistry, and comprehensively and accurately mapping out the energy landscape of well-defined portions of redox chemical space should be of value to a wide variety of prebiotic chemistry models involving carbon redox chemistry. Thus, our capacity to estimate the thermodynamic landscape of molecules in a key region of the chemical space relevant to living systems could be equally valuable for metabolism-first studies aimed at characterizing possible avenues toward primitive organized autocatalytic networks, as well as for genetics-first studies exploring conditions conducive to the formation of nucleotides.

Examining the connectivity of redox chemical space, we found that aldose sugars—e.g., glyceraldehyde (n = 3), erythrose (n = 4), ribose (n = 5), and glucose (n = 6) and their corresponding stereoisomers—are unique in that they are the only compounds with the highest possible number of oxidative and reductive connections (2n) to neighboring molecules. Whether this maximal number of connections, coupled to their relatively high Gibbs energies, played a role in the emergence of aldose sugars as key players in cellular metabolism remains to be explored. One hypothesis is that a high degree value in redox chemical space could influence their role as central metabolic hubs in metabolic networks, optimally positioning them as high-energy substrates with many biochemical roads leading to a wide variety of compounds (33). However, a preliminary statistical analysis revealed that the connectivity of aldose sugars in the KEGG compound of metabolic reactions is not significantly high in comparison to other compounds (Dataset S1). It is also possible that, among the compounds with high energy, those accessible through multiple routes (i.e., with high connectivity) would have a higher chance of becoming incorporated into a rising metabolism. Although these interpretations are purely speculative, the quantitative knowledge provided by our work provides the basis for further exploration.

We found that the set of biological compounds is significantly enriched for carboxylic acid functional groups and have, on average, significantly higher solubilities (logS at pH 7) than the set of nonbiological compounds. In addition to an increase in aqueous solubility, other reasons for why carboxylic acids may have been selected during the evolution of metabolism potentially include a decrease in permeability across lipid membranes (34). This is reflected in the predicted values of octanol–water distribution coefficients, logD(pH 7) for the biological and nonbiological compounds (SI Appendix, Fig. S2). In addition, the enrichment for carboxylates may have enhanced the ability of enzymes to recognize small molecule substrates. Our analysis also showed that biological compounds are significantly depleted in aldehyde/ketone functional groups. Notably, in the four-carbon network, only one biological compound, diacetyl—which appears in the metabolic networks of yeast and several bacterial species (35, 36)—contains two ketone functional groups. This is consistent with the fact that aldehyde/ketone groups are significantly more reactive than carboxylic acids or hydroxycarbons and can cause oxidative damage, spontaneously cross-link proteins, inactivate enzymes, and mutagenize DNA (37).

Our analysis brings to the field of origin of life a recently developed quantum-chemical method for calculating biochemical redox potentials (3) that can have multiple applications for studying early biomolecules irrespective of any specific hypothesis on putative early pathways or on whether genes or metabolism emerged first. Our thermodynamic calculations, which rely on a recently developed calibrated quantum-chemistry approach that was shown to have better accuracy than cheminformatic methods (3), revealed that metabolites have, on average, lower Gibbs energies than the nonbiological set of compounds across a range of pH and electron-donor potentials. One could speculate on the relevance of these results in the context of the very early stages of the emergence of metabolism. In particular, there may have been a stage, prior to the rise of efficient catalysis, in which prebiotic carbon redox chemistry had not bootstrapped itself completely yet out of the equilibrating forces of thermodynamics. Under these circumstances, the equilibration process would have led to accumulation of a pool of compounds, which could serve as initial substrates or replenishing intermediates for downstream, kinetically controlled processes such as autocatalytic cycles or pathways that synthesized monomers for replicative polymers. Importantly, the identity of these thermodynamically favored and metabolite-enriched molecules depends on the values of the two environmental parameters (pH and environmental redox-couple potential), as shown in our Pourbaix phase diagrams. For example, low potential and acidic regions of phase space—e.g., E(electron donor) = −350 mV, pH 7—lead to accumulation of few metabolites (e.g., succinate and butyrate in four-carbon chemical space), whereas other regions of phase space—e.g., E(electron donor) = −200 mV, pH 7—would accumulate a more complex ensemble of compounds. Future work could explore whether particular ensembles of metabolite-enriched compounds (i.e., regions of phase space) are better primed to evolve into prebiotic pathways.

The resulting thermodynamic landscape also revealed in detail which compounds—both biological and nonbiological—are energetic local minima as a function of pH and E(electron donor) and would thus tend to accumulate. We find that some regions of phase space—such as those leading to the production of large quantities of volatile short hydrocarbons like butane and other alkanes—would be problematic for prebiotic chemistry. Indeed, although bacterial alkane production has been described (38, 39), the high volatility of these compounds likely limits their role in metabolism. However, as mentioned above, other regions of phase space would be expected to lead to complex metabolite-enriched mixtures of molecules that could provide a rich source of starting substrates for downstream kinetically controlled processes. Furthermore, spatial or temporal gradients of the environmental parameters—which have been proposed in the context of origins of life models (40, 41)—would open up the possibility of complex dynamic behavior, shifting the balance between different local minima. Finally, although our work dissects the energy minima of each isolated n-carbon redox chemical space, these are, in reality, embedded in a larger chemical space. Recent developments will help dissect and understand the properties of such expanded chemical networks (42, 43).

In the context of known living organisms, in the Pourbaix phase diagram representation of four-carbon linear-chain redox chemical space, the biological metabolites succinate and butyrate are local minima across a range of physiologically relevant pH and E(electron donor) values. Succinate is a key intermediate in the tricarboxylic acid cycle (TCA) cycle, with numerous recently elucidated signaling functions (44, 45). Interestingly, succinate accumulation occurs in a number of different organisms, including bacteria such as Escherichia coli (46), Mycobacterium tuberculosis (47), as well as several bacterial members of the human gut microbiome (48–51) and the bovine rumen (52–55); fungi such as the yeast Saccharomyces cerevisiae (56) and members of the genus Penicillium (57); green algae (58); parasitic helminths (59); the sleeping sickness-causing parasite Trypanosoma brucei (60); marine invertebrates (61); and humans (52–55). More specifically, our observations are consistent with the behavior of the TCA cycle under anaerobiosis and hypoxia (62–65). In these conditions, the reactions of the TCA cycle operate like an “incomplete fork,” with a portion of the pathway running in a reductive (“counterclockwise”) modality, i.e., oxaloacetate sequentially reduced to malate, fumarate, and succinate. Thus, despite the fact that in these examples, succinate is part of biochemical networks of higher complexity than our redox chemical space, its empirically observed accumulation is consistent with its identity as a local energy minimum. We also note that the SCFA butyrate accumulates to high (millimolar) levels in the gut lumen as a product of bacterial fermentation (66, 67). We found that this pattern—where the n-carbon linear-chain dicarboxylic acid and the fatty acid emerge as the only local minima in a large region of phase space—is conserved in the Pourbaix diagrams for redox chemical spaces with different numbers of carbon atoms (SI Appendix, Figs. S7, S8, and S12). Therefore, in analogy to succinate accumulation, it would be reasonable to search for evidence of n-carbon linear-chain dicarboxylic acid accumulation in different biological systems under physiological conditions matching the relevant region of phase space. Studying glutarate accumulation in hypoxic and/or acidic conditions would be particularly enticing, since pathways for its biosynthesis (e.g., as part of lysine metabolism) are conserved across many species.

There are several caveats and limitations associated with our analysis. The first one is that our redox chemical-space analysis is based solely on thermodynamics and does not account for kinetics. Thus, we assume that all molecular oxidation levels are accessible, effectively ignoring kinetic constraints. While it is clear that the emergence of early self-reproducing systems requires the underlying chemistry to bootstrap itself out of equilibrium, our quantitative and comprehensive analysis of the underlying energy landscape of redox reactions should be of value to prebiotic chemistry models. Furthermore, it may be interesting for future work to explore the relative role of thermodynamic and kinetic control in establishing early metabolism and ask whether kinetically controlled pathways that kick-started life were preceded by a prebiotic chemical era predominated by a strongly biased thermodynamically dominated mixture of compounds.

In our study, we explicitly did not want to bias our results toward biologically relevant molecules and redox reactions, and therefore the set of redox transformations considered here is not restricted to only those catalyzed by present-day enzymatic reaction mechanisms. For instance, the reduction of a hydroxycarbon (alcohol) functional group to a hydrocarbon occurs enzymatically through a C=C double-bond intermediate (for example, the reduction of malate to succinate occurs via fumarate). Therefore, a hydroxycarbon functional group that is incapable of undergoing elimination cannot undergo such a reduction using known enzymatic mechanisms. Since it is plausible that these transitions could have occurred through nonenzymatic mechanisms in prebiotic chemistry, we purposefully did not exclude these instances from our analysis.

In addition, our redox chemical space ignores further biochemical details: we do not include intramolecular redox transformations (where an electron transfer within a molecule changes the oxidation level of two different carbon atoms) or keto–enol tautomerizations; we do not account for non–linear-chain carbon compounds nor the different possible stereoisomers of a given molecular oxidation level (e.g., l-malate vs. d-malate), which may differ in energy; and we do not consider functional-group activation chemistry (e.g., the conversion of carboxylic acids to thiols), which has an important effect on thermodynamics. Finally, our partitioning of molecules into metabolites and nonbiological compounds relies on what is found in the KEGG database, which is only a proxy for the absolute set of compounds that partake in nature’s redox biochemistry.

However, despite these caveats, we propose that our simplified redox chemical space is rich enough to serve as a baseline for a better understanding of the underlying thermodynamic and physicochemical principles of carbon redox biochemistry. In future work and following recent exciting developments in the field of heuristically aided quantum chemistry (42, 43, 68, 69), our chemical space model could be expanded to include the additional types of biochemical transformations mentioned above and begin to account for kinetic accessibility. It would be particularly interesting to include carboxylation and decarboxylation reactions (both reductive/oxidative and nonreductive/nonoxidative), which would effectively connect the different n-carbon redox chemical spaces to each other but would significantly increase the complexity of the analysis. Including additional types of reactions such as aldol/retro–aldol reactions and hydrations/dehydrations would fully map the chemical space model to experimentally tractable reaction networks (21, 70–72).

Finally, given the importance of redox chemistry at the early stages of life’s history, it is possible to think of our landscape as a generalization of the space of metabolites found in current living systems (9, 10, 73). By taking into account this extended space, future models for the rise and evolution of biochemistry (42, 69, 74) could more specifically compare the evolutionary trajectory of life as we know it to alternative paths potentially involving transiently relevant molecules and reactions (31, 75).

Materials and Methods

To generate the reactions, we used the RDKit cheminformatics software to design simplified molecular-input line-entry system (SMILES) reaction templates (reaction strings), which, when applied to a compound, will reduce it according to the functional groups detected. In order to classify compounds in the full redox networks as biological or nonbiological, we looked for matches in the KEGG database of metabolic compounds using the RDKit toolbox. To compute the null distribution for the expected number functional-group patterns in n-carbon molecules, we derived the analytical solution for the probability of observing m instances of a given functional group in a sample size N (SI Appendix). For functional-group patterns of larger size, we computed the null distributions empirically by sampling compounds from redox chemical space. For all tests of statistical significance (i.e., differences in solubilities, n-gram counts, octanol–water partition coefficients, Gibbs energies of biological vs. nonbiological compounds), we performed Welch’s unequal variance t test.

We used the cheminformatics software ChemAxon (Marvin 17.7.0, 2017; ChemAxon) to predict the pH-dependent solubility, logS(pH), and octanol–water distribution coefficients, logD(pH). To predict standard redox potentials with quantum chemistry, we computed the electronic structure and energy of the fully protonated species of each metabolite using the Orca quantum-chemistry software (SI Appendix). We then calibrated predictions against available experimental data using linear regression. Our group-contribution calculations to estimate redox potentials rely on the method as implemented by Noor et al. (14).

Data Availability.

All study data are included in the article, SI Appendix, and Datasets 1–4.