Artificial intelligence analysis of magnetic particle imaging for islet transplantation in a mouse model

Abstract

Purpose

Current approaches to quantification of magnetic particle imaging (MPI) for cell-based therapy are thwarted by the lack of reliable, standardized methods of segmenting the signal from background in images. This calls for the development of artificial intelligence (AI) systems for MPI analysis.

Procedures

We utilize a canonical algorithm in the domain of unsupervised machine learning, known as K-means++, to segment the regions of interest (ROI) of images and perform iron quantification analysis using a standard curve model. We generated in vitro, in vivo, and ex vivo data using islets and mouse models and applied the AI algorithm to gain insight into segmentation and iron prediction on these MPI data. In vitro models included imaging the VivoTrax labeled islets in varying numbers. In vivo mouse models were generated through transplantation of increasing numbers of the labeled islets under the kidney capsule of mice. Ex vivo data were obtained from the MPI images of excised kidney grafts.

Results

The K-means++ algorithms segmented the ROI of in vitro phantoms with minimal noise. A linear correlation between the islet numbers and the increasing prediction of total iron value (TIV) in the islets was observed. Segmentation results of the ROI of the in vivo MPI scans showed that with increasing number of transplanted islets, the signal intensity increased with linear trend. Upon segmenting the ROI of ex vivo data, a linear trend was observed in which increasing intensity of the ROI yielded increasing TIV of the islets. Through statistical evaluation of the algorithm performance via intraclass correlation coefficient validation, we observed excellent performance of K-means++ based model on segmentation and quantification analysis of MPI data.

Conclusions

We have demonstrated the ability of the K-means++ based model to provide a standardized method of segmentation and quantification of MPI scans in an islet transplantation mouse model.

Introduction

Magnetic particle imaging (MPI) is an emerging modality that directly detects the magnetization of iron oxide nanoparticles, with advantages including: high specificity and sensitivity, linear quantitative ability, and high potential for clinic translation (1, 2). Implemented in various realms of biomedical research, this relatively novel imaging modality has invoked scientific inquiry in a new and advanced area of molecular imaging and analysis and showed significant advancements for development of theranostics and precision medicine (3). Its reliance on superparamagnetic iron oxide (SPIO) nanoparticle signals to generate positive contrast images sets a new standard for quantitative imaging and biology. However, due to the newfound presence of MPI in the field, selection bias for segmentation of imaging data exist, there is a gap between tedious meticulous imaging analysis work and robust quantification of imaging signals (4). Henceforth, it is crucial to direct efforts towards combining the realm of MPI with Artificial Intelligence (AI), which enables rapid, high-throughput analysis of data systems and structures. Through its use in analysis of regions of interest (ROI) in preclinical and clinical scans, with a focus on rapid quantification, monitoring, and prognosis/predictive capability in multiple imaging modalities such as MRI, PET, and CT, it has become clear that AI may allow one to bypass hurdles faced in biomedical image quantification (5–8). These problems include issues with accurate and reliable signal quantification, mainly due to the high degree of intra and inter-rater variability and selection bias resulting from the imaging specialist or radiologist under which the image is scrutinized (9) (10) (11). These problems are exaggerated in the realm of MPI due to its novelty in the field, and intrinsic problems including the inability to define a determinate boundary for a ROI in an MPI scan (12). Therefore, the image and its ROI becomes subject to selective bias from the rater at hand and a proper signal may become outweighed by that which is false positive or false negative; Henceforth, quantification becomes highly unreliable and difficult for subsequent analysis. In accordance with these issues exists the time-consuming cost of freehand selection and manual analysis of MPI image scans (12). Commonly used deep learning algorithms within the field of AI, such as the Convolutional Neural Network (CNN), are able to provide high-throughput and robust analysis within molecular imaging domains of interest, although these often come with limitations – such algorithms require a large volume of labeled data for training the neural network and can only function within a narrow range of new data (13, 14). However, other types of AI algorithms within the domain of unsupervised machine learning (ML), namely clustering based approaches, can be optimized for functioning on a wide variety of data and do not require a large volume of training data to perform with a high degree of accuracy (5). Here, we propose to develop and use the K-means++ clustering-based, unsupervised machine learning algorithm to provide a novel method/tool for image segmentation and quantification in the MPI domain, using SPIO labeled human islets in a mouse model of islet transplantation as an example. While islet transplantation has emerged as a clinical modality to treat type 1 diabetes patients, it is hampered by islet loss during early post-transplant period (15). Previously, we demonstrated that islets labeled with magnetic nanoparticles can be imaged after transplantation using MRI (16, 17), which is limited by low sensitivity and reliance on a negative contrast (18, 19). This calls for a positive contrast, high sensitivity quantitative imaging modality and sophisticated image analysis tools to track the dynamic nature of transplanted islets in vivo (18, 19). Therefore, monitoring changes in MPI signal through machine learning- enhanced segmentation and quantification can provide insight into such issues. The purpose of the algorithm used here is to provide a mechanism for rapid and highly specific segmentation of an ROI from an MPI scan, and subsequent analysis of the ROI in order to predict the total accumulation of SPIO nanoparticles within the islet cells. A similar algorithm based on K-means has been applied previously in various realms of biomedical imaging (20–22).Currently, there is a lack of both minimal standardized methods for segmentation and quantification of MPI and advanced analysis tools to calculate the total iron content within a signal cluster. In this study, we develop and evaluate the performance of a novel K-means++ based linear regression model to predict total iron value of an auto-segmented ROI from an MPI scan of an in vivo mouse model of transplanted human islets labeled with SPIO nanoparticles. While in previous studies we showed an MPI signal originated from the labeled transplanted islets, a novel, automated mechanism for TIV prediction for transplanted cells imaged with MPI is needed (23). Granting the ability to do so will allow for rapid segmentation and quantification analysis of an ROI and estimation of the total iron content, unlocking the capability to monitor immediate and longitudinal studies of transplanted human islets with greater accuracy and throughput in the molecular imaging modality of MPI. Importantly, the proposed approach can be applied to a variety of transplanted labeled cells (i.e. stem cells) imaged using MPI.

Methods and Materials

Development of K-means++ segmentation algorithm for MPI analysis

In order to properly implement the K-means++ algorithm, we accurately segmented the ROIs from an MPI scan. First, we extracted the pixel array from the raw DICOM file and found the threshold value using the Otsu method (24). The algorithm first calculated histograms, probabilities and mean for each level of pixel values in order to find the best suitable threshold value. It iterated through each intensity level. Through this process, the pixel intensity value with maximum variance was calculated which separates foreground from background. After this, the algorithm then located small, insignificant bright spots called salt noise from the image (25) (Fig. 1). This rendered an image with particular regions which we assume to be the various ROI locations, including the main ROI and any reference fiducial markers in the scan. This was achieved by erosion followed by a dilation of image values. After thresholding and locating our pixels of interest, we labeled isolated blocks of pixel values with a common label. For example, the main ROI is a concentrated block of information at the center of the image and was labelled as 0. At the corner of the MPI or the edge of the image scan the pixels are designated a separate label such as 1 (Supplemental Fig. 1). Therefore, using the size of the zone of this information, we considered the bigger zone of information as the main ROI and smaller zone of information was taken as the reference fiducial marker. This preprocessing method is reliable in that each image generated followed a pre – determined pattern, which allowed the algorithm to function on a wide domain of MPI generated images since fiducial markers are often included, in relatively standard positions, alongside the main object/region of interest being scanned.

Figure 1.

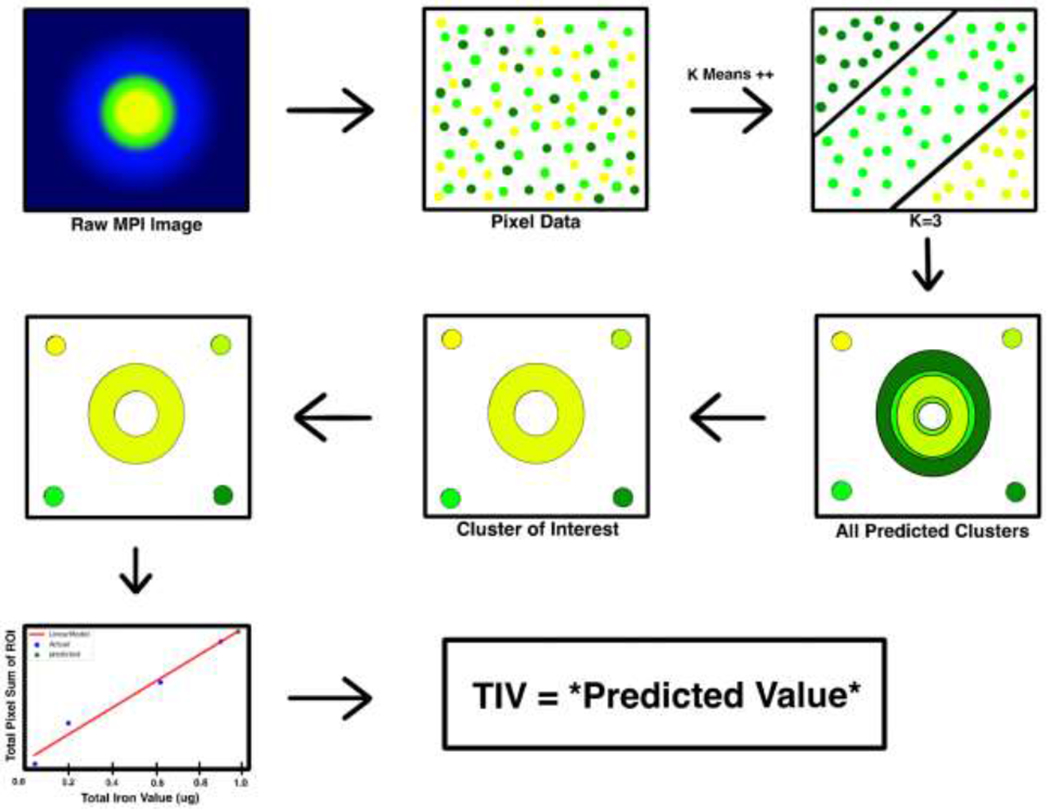
Overview of the K-means++ algorithm and standard curve for total iron value (TIV) prediction. Raw MPI Image is loaded into the algorithm, and a k – value is chosen in orderto cluster the data points for segmentation. The cluster of interest is then selected from the predicted clusters. A standard curve is then generated based on the total pixel sum value and corresponding total iron value of the 4 reference markers. This standard curve is used to estimate the unknown TIV of the segmented ROI of interest.

Furthermore, MPI generated DICOM images may use different objects and not just “blobs” of pixel clusters, hence, it is important to segment such complex shapes and objects within the identified regions. In addition, it is also important to separate the pixel values of dispersion generated by the object, termed “noise”, from the actual pixel values that represent the object – in this case being the SPIO nanoparticle clusters within any given construct being scanned. Therefore, after the aforementioned preprocessing steps, we used K-means++ based segmentation for each image region separately. The K-means++ algorithm iteratively partitioned the data into k distinct groups, termed “clusters”. These groups were distinct and non-overlapping, where each data point (pixel value in our case) belonged to only one distinct cluster. In this, the algorithm tried to maximize the inter cluster distance and minimize the intra cluster distance. The algorithm used the proposed clustering equation shown below:

$$J=\sum _{i=1}^m\sum _{k=1}^K{w}_{ik}\Vert x^i-{\mu }_k{\Vert }^2$$

Where w_ik= 1 for data point xⁱ if it belongs to cluster k; otherwise, w_ik = 0. μ_k represents the centroid of the cluster of xⁱ. To calculate the distance between pixel values, the canonical distance metric employed in our algorithm was the Euclidian distance. A centroid in the conventional K-means algorithm was defined the center point of all the data points that belong to that cluster. In this study we used K-means++, a variant of original K-means with smarter initialization only at the onset of clustering (26) (27). Initial centroids were selected from the available data points, and a new point was chosen as a centroid based on its distance from the nearest, previously chosen centroid, which represents an initialization mechanism termed sequential initialization. This type of sequential initialization is what differentiates K-means++ clustering from normal K-means, which uses completely randomized initialization at the onset of clustering. However, it is important to note that this was only done for the initial assignment of centroids at the initialization phase of the algorithm, for the next few rounds centroids are recalculated from the aggregate of all pixels in the current class and this process iterates until there are no further assignments or readjustments to be made of pixels to the newly calculated centroids (Fig. 1). We choose k values for centroids that cover the entire range of data points; This value for k can be considered the number of different pixel clusters represented in our dataset. This was done by parameter optimization in which we compared the results for k = 2,3,5, and 7 clusters, and applied the elbow method to determine variance such that the minimum sum squared of errors (MSSE) was the lowest and stable for the chosen k cluster (28). Following K-means++ segmentation, the pixel values of all members of our cluster of interest were summed to give us the total pixel sum of our segmented ROI(s).

3D printed phantom preparation and MPI protocol:

For phantom imaging and optimization of the algorithm, two 3D printed constructs were generated – an ‘S’ and a “Circle” phantom shape using the J750 3D printer (Stratasys, Ltd., Eden Prairie, MN). SPIO nanoparticle solutions (VivoTrax, Magnetic Insight, Inc., Alameda, CA) of various concentration were prepared in PBS (Supplemental Fig. 3, 4). A known amount (μl) of the resulting diluted VivoTrax solution (5.5mg/ml of iron) was injected into the prospective 3D printed phantoms, and the TIV (Concentration x μl injected) was recorded for use in validating and comparing the prediction of the proposed k-means++ based algorithms to the actual TIV injected into the constructs. For the ratio model, one fiducial marker of 10% VivoTrax solution was placed in the standard marker holder at the top of the MPI bed. Four fiducial markers (10%, 20%, 30%, and 40% of diluted VivoTrax solutions, 1μl each) were taped to four corners of the MPI bed for the Standard Curve (SC) model. Finally, the phantoms were then placed on the MPI bed and 2D scans were initiated & executed using the MOMENTUM MPI imager (Magnetic Insight, Inc., Alameda, CA). 2D MPI images were acquired with the following parameters: 4cm×6 cm field-of-view (FOV), a 6 T/m selection field gradient, a drive field strength of 20 mT peak amplitude and a 45.0 kHz drive frequency. The MPI images were reconstructed using x-space reconstruction.

Nanoparticle labeling of human islets and in vitro MPI of human islet phantoms

Human pancreatic islets were received from Integrated Islet Distribution Program (IIDP, City of Hope, Duarte, CA) and incubated in CMRL media with 5% FBS. Human islets were labeled with 280 μg/mL VivoTrax in the same media and incubated for 48 hours at 37°C with 5% CO₂ (23), and were washed three times using PBS. Human islet phantoms were comprised of different numbers of VivoTrax labeled islets (25, 50, 100, 200, 400 and 800 islet equivalents, IEQ) in 50 μl of PBS. 2D MPI (MOMENTUMTM imager) images of human islet phantoms (6 groups, n = 2) were acquired with the same aforementioned parameters for phantom imaging.

In vivo and ex vivo MPI of transplanted human islets in a mouse model

All animal experiments were performed in compliance with the National Institutes of Health guide for the care and use of laboratory animals (NIH publications No. 8023, revised 1978) and approved by the Institutional Animal care and Use Committee at Michigan State University. Different numbers of VivoTrax labeled human islets (25, 50, 100, 200, 400 and 800 IEQ) in PBS were transplanted under the left kidney capsule of NOD.scid mice (6 groups. n=2, The Jackson Laboratory, Bar Harbor, ME) (23). Mice were imaged using an MPI scanner (MOMETUM MPI imager, Magnetic Insight Inc., Alameda, CA) 1 day and 3 days post islet transplantation. One 3D MPI and subsequent 2D MPI images were acquired. 2D MPI images were acquired with the following parameters: 6 cm×12 cm FOV, a 3 T/m selection field gradient, a drive field strength of 20 mT peak amplitude and a 45.0 kHz drive frequency. 3D images were acquired with a FOV of 6 cm × 6 cm × 12 cm, 55 projections with a total imaging time including reconstruction of ~35 minutes. Anatomic CT reference images were also acquired using the whole-body microCT scanner (QuantumGX, Perkin Elmer, Hopkinton MA). MPI images were co-registered to CT for 3D scans using VivoQuant Imaging Software (Invicro, Boston, MA,). At the completion of the imaging session, mice were sacrificed, the left kidney was excised and imaged ex vivo with the MPI scanner using 2D scan parameters as described above.

Immunofluorescence staining of labeled human islets and grafts under the kidney capsule

Paraffin-embedded sections of labeled human islets and sections of the grafts under the kidney capsule were incubated with anti-dextran primary antibody (StemCells, Inc., Newark, CA) or anti-insulin primary antibody (Santa Cruz Biotechnology, Dallas, TX), followed by a Texas red-labeled secondary antibody (Abcam, Cambridge, MA) and a FITC-labeled secondary antibody (Abcam, Cambridge, MA), respectively. All sections were mounted with a mounting medium containing DAPI (Vector Laboratories, Burlingame, CA) and analyzed using an Eclipse 50i fluorescence microscope (Nikon, Tokyo, Japan).

Intraclass correlation coefficient and inter-rater reliability validation

To measure the accuracy and determine reliability of the K-means++ algorithm, the model’s output and analysis of the ROIs were compared to the manual segmentation and TIV prediction results from board-certified radiologists. They segmented the ROI manually using the VivoQuant Imaging Software (Invicro, Boston, MA), and total pixel sum values were extracted for TIV analysis from the ROIs using the ratio method. For statistical analysis, SPSS statistical software (IBM, Armonk, NY) was used to calculate Intraclass Correlation Coefficient (ICC), which provides a measure of the Inter-rater reliability amongst various raters (neural network and radiologists) and indicates the accuracy of the model in segmenting proper ROI from pixel field. A two-way mixed model with a confidence interval of 95% was selected, and a measure of absolute agreement was calculated with the ICC. The greater the ICC value, the more reliable the model is due to the greater degree of correlation amongst the rater’s values. In order to account for reliability of the Ratio model and SC model, and precedence of one of these models over the other, ICC was calculated in accordance to both of these models. ICC was also calculated to measure agreement of TIV prediction between board-certified radiologist (rater), who uses the ratio method by convention, and the algorithm which estimates TIV from the proposed SC model. In cases where TIV is truly known and calculated at time of scanning, such as that when the phantoms are imaged, the calculated (actual) TIV is used to calculate ICC. An F test with a true value of 0 was used to calculate statistical significance (p < 0.05) of the ICC results.

Statistical analysis

All experiments performed in duplicate were repeated using independent samples. Differences between the time points and between experimental and control groups were assessed by a Student t test and corrected by the ANOVA using SPSS statistics (IBM, Armonk, NY); the repeated two-way ANOVA was used for the time course analysis; a p value ≤ 0.05 was considered statistically significant.

Results

Parameter optimization and k value selection

In an effort to apply the proposed unsupervised machine learning algorithm effectively, the proper number of centroid (clusters), k, have to be determined to ensure accurate segmentation of the ROI from the MPI in a diverse dataset. For parameter optimization, different values for k (2, 3, 5, and 7) were chosen and input into the algorithm and the output segmentation was observed (Fig. 2). Here, the algorithm was applied to an ‘S’ shaped phantom of 1.2 μg of iron. When k =2, the algorithm was unable to decipher the boundaries of true nanoparticle signal and produced a significant amount of noise in its final segmentation output (Fig. 2A). As the value of k was increased to 3 and 5, the algorithm predicted with a greater degree of specificity and accuracy, where minimal noise was included in the segmented result (Fig. 2A). However, as the number of clusters increases from 5 to 7 k, the algorithm tends to overshoot in its predictions and segments regions of the image to exclude true nanoparticle signals thus compromising the integrity of segmentation by including false negative predictions (Fig. 2A). Furthermore, as the number of clusters decreases from 5 to 3, the algorithm includes a slight degree of noise in the final output and therefore undershoots in the prediction, ineffectively rendering a false positive in its segmentation output. Through application of the elbow method and validation by board-certified radiologists, the optimum value for k was chosen to be 5 clusters, under which the MSSE tends to stabilize without further decrease (Fig. 2B). Therefore, due to the minimal amount of error associated with the value of 5 potential pixel clusters (centroids) within an image, this value for k was used throughout the rest of the study to accurately segment the MPI Image scans under investigation and perform subsequent analysis on the segmented ROI for prediction of TIV.

Figure 2.

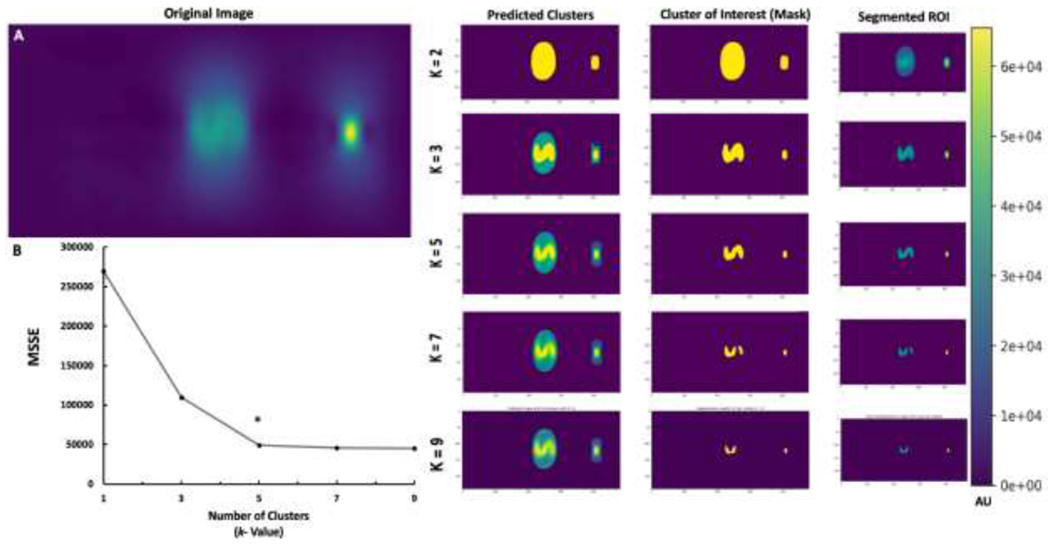
K-means++ segmentation and parameter optimization for selected k value. A. Segmentation ROI of k value = 2 clusters, k value = 3 clusters, k value = 5 clusters, and k value = 7 clusters; B. Elbow method graph indicating minimum sum squares of error (MSSE) per selected k value. The size of the ‘S’ phantom was 15mm.

In Vitro K-means++ Segmentation and TIV Prediction of VivoTrax labeled human islets

After validating the algorithm’s performance in segmenting ROI for phantom constructs and predicting the corresponding TIV, the Kmeans++ based SC algorithm was applied to islet phantoms containing increasing numbers of VivoTrax-labeled human islets (Fig. 3A). Here the K-means++ algorithms segmented only the ROI with minimal noise, indicating that the algorithm regarded only the true signals from the nanoparticle clusters and reduced the background significantly. After segmentation of the ROI from the MPI scan, the algorithm predicted TIV of the cellular ROI using the Standard Curve (SC) model. Through its predictions, we observed a linear correlation between the increasing number of IEQ, which was concomitant with increasing signal intensity, and the increasing prediction of TIV in the islets (Fig. 3B). As the number of IEQ increased from 100 to 800, the predicted TIV also increased from about 0.05 to .40. ICC validation of TIV prediction by the SC algorithm indicated good inter-rater reliability since the correlation coefficient (0.812 for single measures) was below the threshold of 0.9 for excellent ICC. Any variations in TIV prediction amongst raters were likely due to differences in ROI size and threshold. This includes potential false positives by the rater, due to the presence of salt noise, or false negative segmentation by the highly specific K-means++ segmentation algorithm (Supplemental Table 4). Nonetheless, a relatively high degree of inter-rater reliability permits the application of the SC algorithm to the in vitro model. Islet labeling with VivoTrax was also confirmed by fluorescence microscopy where the signal from insulin (green) co-localized with the signal from dextran staining (red) (Fig. 4).

Figure 3.

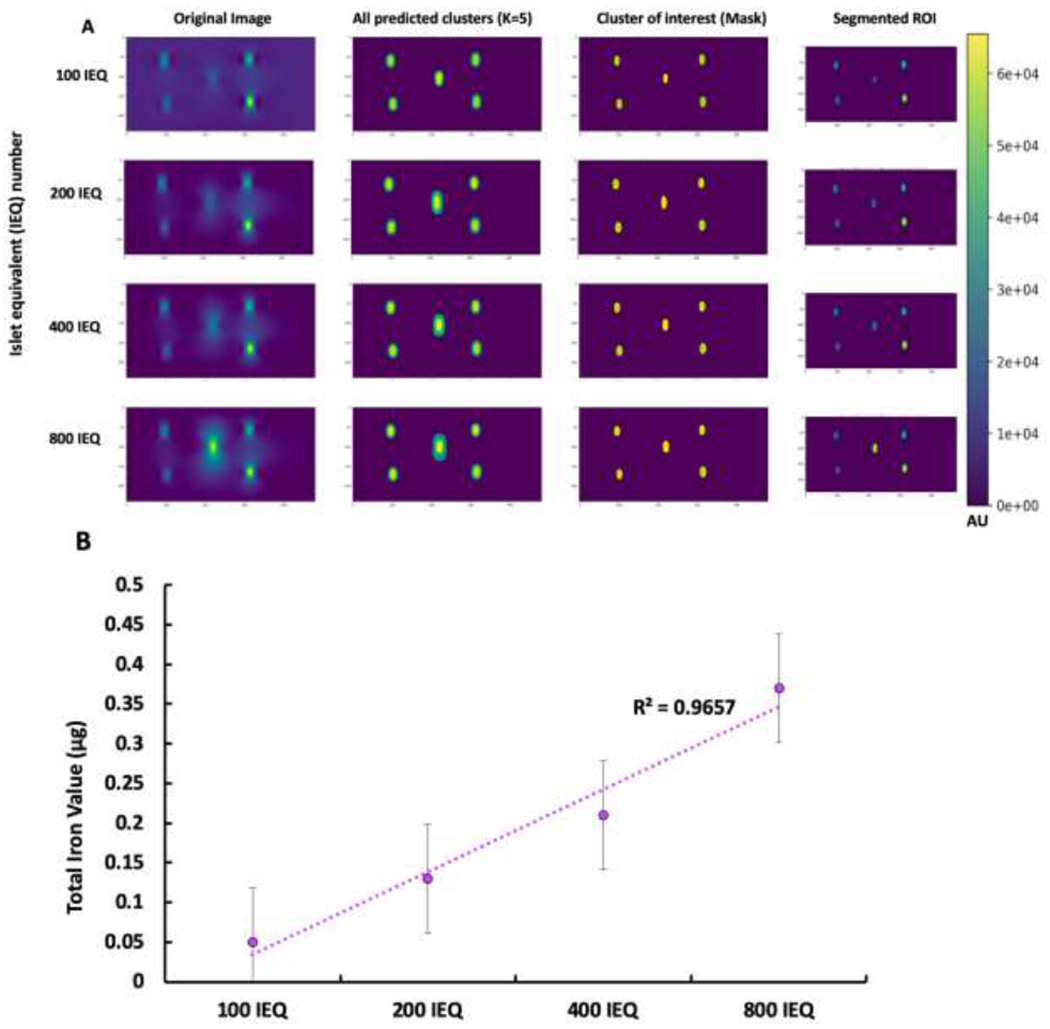
K-means++ segmentation and TIV prediction of human islet in vitro. A. Segmentation of increasing number of IEQ: 100 IEQ, 200 IEQ, 400 IEQ, and 800 IEQ. B. TIV prediction of islet numbers. Note a linear increase in signal intensity of the segmented ROI with the higher number of islets in phantoms. Phantoms with larger islet numbers accumulated significantly higher number of nanoparticles resulting in higher iron content. The size of the ‘Circle’ phantom was 30mm.

Figure 4.

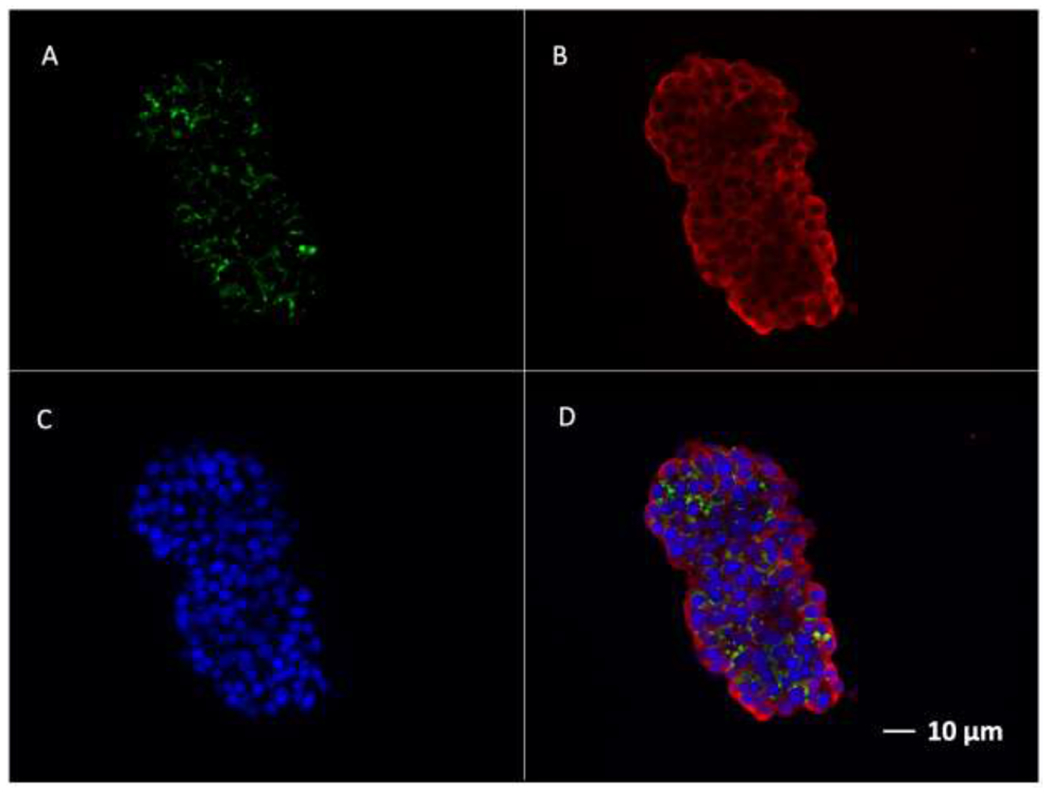
Fluorescence immunostaining of human islets labeled with VivoTrax. A. Staining for dextran using anti-dextran antibody (Green); B. Staining for insulin using anti-insulin antibody (Red); C. DAPI staining of cell nucleus (Blue)s; D. Merged images. Bar=10μm.

In vivo MPI and K-means++ ROI segmentation/ TIV prediction of transplanted human islets

After successful transplantation of human islets under the left kidney capsule, which was monitored using a 3D MPI co-registered with CT, the proposed machine learning algorithm was applied to the in vivo model (Fig. 5). Subsequent 2D scans of all mice that received labeled islet transplant were fed into the K-means++ segmentation algorithm and the extracted ROI was analyzed using the SC model for TIV prediction (Fig. 6). Here, segmentation results of the ROI of the MPI scans showed that with increasing number of transplanted islets per graft, the signal intensity increased with linear trend and the ROI appeared larger (Fig. 6A). Noticeably, in certain MPI scans, islands of pixels, which likely result from dispersed clusters of nanoparticles, were segmented by the algorithm. This is crucial for accurate quantification of an ROI from an MPI scan as it does not include bleeding of nanoparticle signal or relative noise in the final segmented ROI, a feat that has been difficult to achieve manually by image specialists as they often incorporate the entire region in one freehand selection, without accounting for individual islands or clusters. This introduces noise and error into the final calculation when analyzing the ROI or attempting to quantify TIV within the region. However, due to the highly specific segmentation of our clustering-based algorithm, the SC model was able to predict TIV from the extracted ROIs, indicating a linear trend as the number of islets in vivo was increased from 100 to 800 (Fig. 6B). ICC validation of these results indicated a high degree of inter-rater reliability and a near-excellent ICC score (p < 0.005, Supplemental Table 4). Furthermore, the in vivo prediction of total iron amount, although difficult to validate due to the constantly shifting, dynamic biology of the nanoparticle cluster environment of the islet graft under the kidney capsule, can provide insight into future longitudinal studies using TIV for obtaining information regarding cellular nanoparticle content over time. In this case, a slight decrease in ROI, and therefore a decrease in TIV prediction was observed at one to three days after transplantation. This is likely due to islet cell death followed by iron release and subsequent uptake by macrophages normally observed during early post-transplant period (29).

Figure 5.

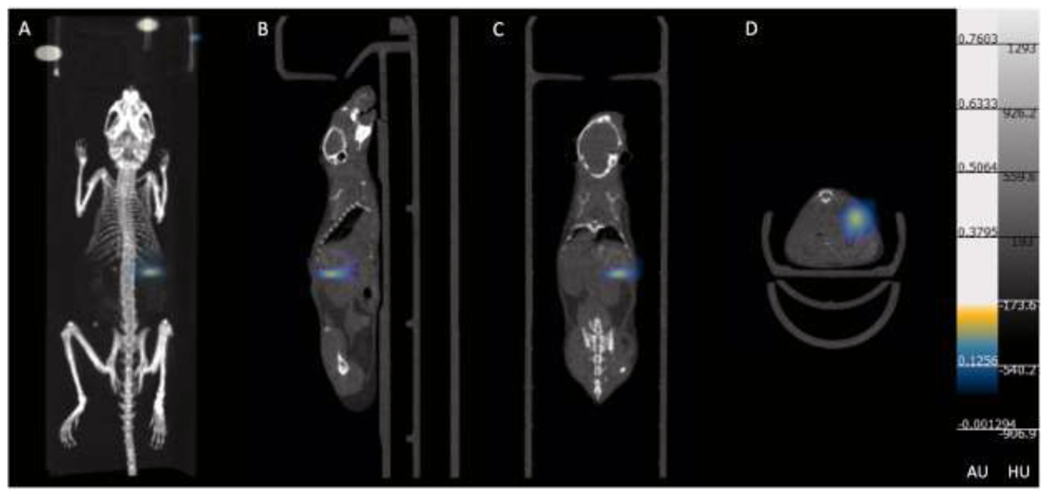
3D MPI scan and CT overlay of islets transplanted under the left kidney capsule. A. 3D MPI/CT merged image; B. Sagittal view of MPI/ CT image; C. Coronal view of MPI/CT image; D. Axial view of MPI/CT image.

Figure 6.

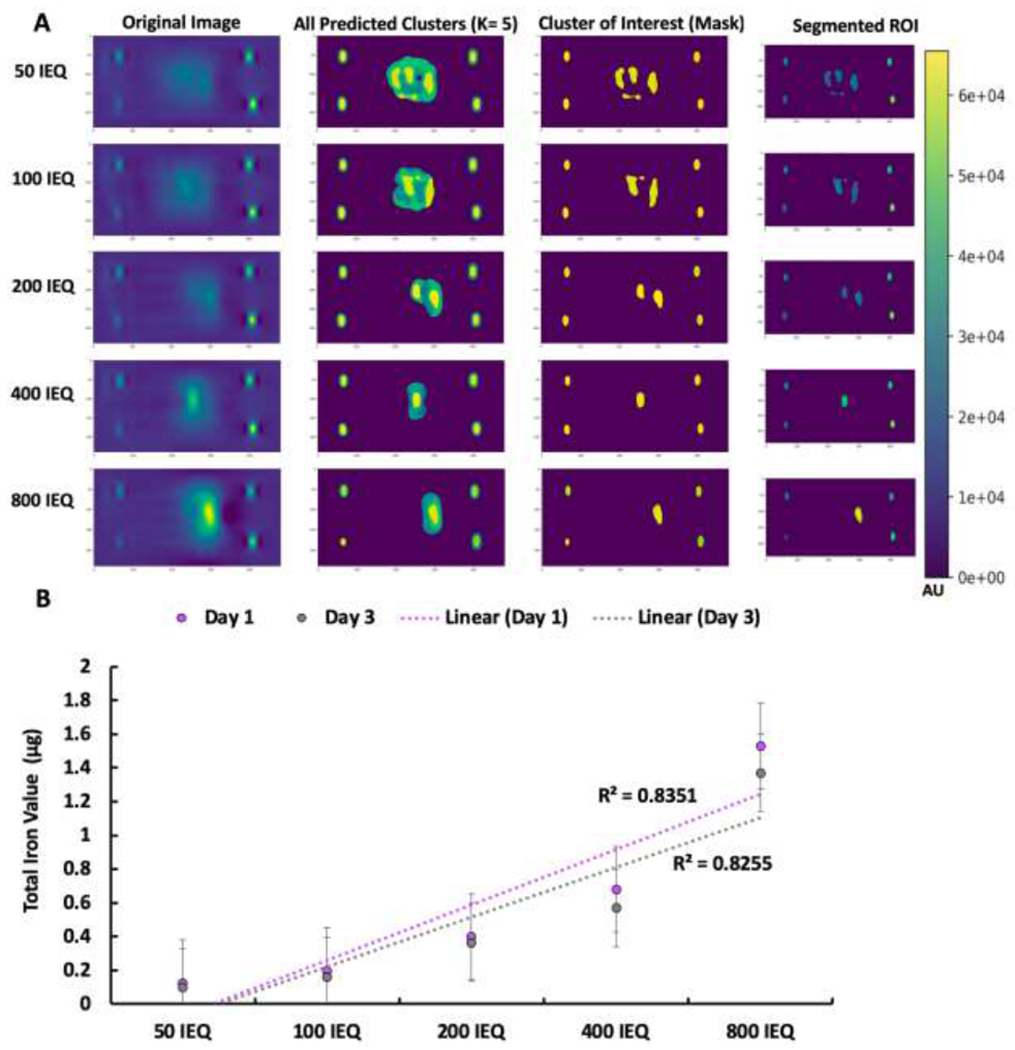
K-means++ segmentation and SC model TIV prediction of in vivo MPI of transplanted islets. A. K-means++ segmentation of transplanted islets: 50 IEQ, 100 IEQ, 200 IEQ, 400 IEQ, and 800 IEQ; B. TIV prediction from extracted ROIs using SC model.

Ex vivo kidney MPI, K-means++ segmentation and TIV prediction

We next performed 2D MPI ex vivo scans of the excised kidneys in order to apply the K-means++ SC model algorithm for segmentation and TIV prediction of the ROI (Supplemental Fig. 5). As evident in application of the algorithm to the phantoms, upon segmenting the ROI of the MPI scans of the kidney with transplanted islet grafts ex vivo, a linear trend was observed in which increasing pixel intensity of the ROI yielded increasing TIV of the islets under the kidney capsule (Supplemental Fig. 5). ICC validation of the algorithm ex vivo indicates a great degree of inter-rater reliability in TIV prediction of the ex vivo image scans, underscoring the algorithm’s ability to perform with qualified accuracy in ROI segmentation and analysis (Supplemental Table 5). The presence of iron in transplanted islets was also confirmed histologically by staining for insulin and dextran. As shown in Supplemental Fig. 6, there was an excellent co-localization of the signals in the excised tissue samples from the kidney grafts.

Discussion

Application of artificial intelligence in the form of an unsupervised machine learning algorithm, namely K-means++ for segmentation in conjunction with linear regression (SC model) for TIV prediction, enabled automated, rapid and high-throughput quantification of MPI Images. K-means is a clustering-based, unsupervised machine learning technique entirely based on pixel values (30). Since this study aimed to develop an advanced MPI data analysis method associated with an unsupervised machine learning problem where we don’t have a high volume of labeled dataset, K-means++ clustering seemed like a reasonable choice. The algorithm groups similar pixel values into clusters. The number of groups is pre-defined and is a limitation of K-means++ algorithm in that it has to undergo initial parameter optimization in order to function within a domain, in this case being MPI signals. However, since we are using a predetermined scale range of total iron values from 0.5 to 7.5 μg (low to high signal intensity generated) we can circumvent this limitation to a high degree. Therefore, using K-means++ we generated clusters and isolated the maximum value cluster as our cluster of interest. Then using the segmentation map from K-means++ which acts as a mask from the original image, pixel values were identified by using pixel indices to segment the original MPI image and only showed the segmented clusters of interest. Using the original pixel intensity values from the MPI file, we calculated the sum of pixel intensities in our segmented ROI(s). Initial parameter optimization through application of the elbow method allowed for use of the algorithm in a diverse domain of studies ranging from in vitro phantom to in vivo and ex vivo animal models. Through validating the performance of the SC model in comparison to the ratio model for TIV prediction, it is evident that quantification of the iron content of an ROI within an MPI scan can be propagated through the use of AI. From segmentation results of phantoms of different structures, both ‘S’ and ‘Circle’ shapes, it is evident that the algorithm can function with a high degree of specificity for true SPIO nanoparticle signals with little regard for bleeding of signal or noise, even in the presence of spatial complexity of signal patterns. This ability of the algorithm to segment portions of an ROI that does not include noise, and segment islands of pixels is unprecedented in the field of MPI and molecular imaging in that conventional methods in ROI analysis by freehand selection of imaging specialists often include a great deal of noise in ROI extraction and analysis. Furthermore, the ability of the algorithm to generate a standard curve from which TIV is predicted permits a highly robust computational mechanism for iron quantification in an ROI. This has previously been difficult to achieve manually without application of certain software and calculation of a linear correlational equation or a linear regression model for prediction, or reliance on a ratio method which incorporates only the total pixel sum and TIV of one single fiducial marker. Use of the proposed algorithm in vitro, in vivo, and ex vivo demonstrated the ability to segment, quantify, and perform analysis of labeled human pancreatic islet signals from an MPI scan in a rapid and high throughput manner. The accuracy of the algorithm in comparison with an imaging specialist, as fortified by the high degree of inter-rater reliability via ICC validation across all in vitro, in vivo, and ex vivo of our mouse model qualifies the ability of this algorithm to segment and calculate total iron content of an MPI ROI with trustable validity. In some cases, the algorithm included less salt noise and false positives in its ROI prediction, and this might allow for greater TIV prediction than that of an imaging specialist.

In vivo studies showed that the complex biology of an animal model yields potential dispersal and scattering of iron signals, and this introduces a great deal of variability and error in manual analysis of the ROI. Previously, the task of quantification of cellular iron uptake was rendered obsolete and the metric of TIV of cells in vitro or in vivo was rarely considered in the field without use of additional devices and modalities (31). Through the described algorithm, however, the total iron content could be rapidly monitored and analyzed. Due to the ability of artificial intelligence to segment an ROI and quantify total pixel sum and predict TIV with high throughput and reliability, this process becomes more approachable and applicable in a variety of settings where MPI cell imaging is applied in vivo (2, 32, 33). The histology and imaging correlation allow for the anatomical verification of the colocalization of the dextran coated nanoparticles accumulated in the transplanted cells. This is done through monitoring graft cells location within the subject through use of MPI coregistered with CT for anatomical reference as to where the cells are distributed. The histology portion confirms that the cells that endocytosed the dextran coated nanoparticles and are generating the signals in the MPI are indeed transplanted insulin releasing cells. This is signified by the co-staining for insulin and dextran under the kidney capsule.

There are several limitations of our study. Although the algorithm was built to segment and analyze 2D MPI data for this study, it can be expanded and applied to 3D datasets by working on multiple slices instead of one. This is important for in vivo imaging of mice with MPI as often these are 3D scans. This current algorithm only accounting for a single 2D slice of MPI data instead of the typical 3D data that is retrieved for mice scanning, the lack of a proper ground truth and reliance on reference markers to estimate total iron amount calls for further exploration in this area. Employing deep learning or other forms of machine learning where the algorithm can be better trained on total iron value predictions but can still use K-means++ for segmentation would serve as ideal algorithm for accurate segmentation and TIV prediction of an MPI 3D ROI in our future studies. Another limitation of our study is that the current Kmean++ algorithm was only tested for one MPI tracer. Beside VivoTrax (Resovist), there are several commercially available SPIOs including another clinical approved tracer Feraheme (Ferumoxytol), which has a different magnetic field distortion property from VivoTrax. Nonetheless, a clear relationship between the increasing total pixel sum and TIV prediction of an ROI is indicative of the fact that the K-means++ segmentation algorithm and SC model are capable of segmenting the ROI and predicting TIV with similar trends across in vitro, in vivo, and ex vivo studies. This underscores the opportunity to exploit the proposed unsupervised machine learning technique for segmentation and ROI analysis of iron accumulation in various applications related to cell-based therapies including endogenous cell labeling for cancer (34) and diabetes treatment (35).

Conclusion

Here, we demonstrated the application of the K-means++ based approach to pancreatic islet transplantation model for a novel, standardized method of segmentation and quantification analysis of MPI scans. However, this method has the potential to be extended to other cell types such as induced pluripotent stem cells or CAR T cells where MPI signal quantification and analysis of TIV, indicative of nanoparticle uptake, can be quickly and accurately quantified. This tool may be useful in monitoring signal fluctuation in transplanted cells, such as graft loss from signal decay post-transplant in longitudinal studies. Furthermore, this machine learning approach extends the analytical potential of AI to the novel realm of MPI and its use in clinically translatable therapies such as islet transplantation for type 1 diabetes.