Summary
Chaos behavior has been observed in various cellular and molecular processes. Here, we modeled reversible phosphorylation dynamics to elucidate a design principle for autonomous chaos generation that may arise from generic enzymatic reactions. A comprehensive parameter search demonstrated that the reaction system composed of a set of kinases and phosphatases and two substrates with two modification sites exhibits chaos behavior. All reactions are described according to the Michaelis-Menten reaction scheme without exotic functions being applied to enzymes and substrates. Clustering analysis of parameter sets that can generate chaos behavior revealed the existence of motif structures. These chaos motifs allow the two-substrate species to interact via enzyme availability and constrain the two substrates' dynamic changes in phosphorylation status so that they occur at different timescales. This chaos motif structure is found in several enzymatic reactions, suggesting that chaos behavior may underlie cellular autonomy in a variety of biochemical systems.
Subject Areas: Biochemical Mechanism, Molecular Biology, Enzyme Engineering, Biophysics
Graphical Abstract
Highlights
-
•
Two substrates with reversible two-site phosphorylation can exhibit chaos behavior
-
•
The chaos does not require autocatalysis or allosteric regulation of enzymes
-
•
The chaos is a result of the coupling of two substrates via enzyme availability
Biochemical Mechanism; Molecular Biology; Enzyme Engineering; Biophysics
Introduction
The spontaneous activation of chemical reactions is the basis of cellular autonomy. Biological oscillators play an important role in the control of the autonomous and temporal activities that occur in cells. Examples include autonomous rhythmicity observed in the circadian cellular clock process (Nagoshi et al., 2004), cell cycle progression (Murray and Kirschner, 1989), and rhythmic neuronal firing (Izhikevich, 2007). Such activities can span timescales from milliseconds to hours. Biological oscillators are also thought to play an important role in autonomous pattern formation from body segmentation in mammals (cm scale) (Palmeirim et al., 1997) and the positioning of cell division machinery inside unicellular prokaryotes (μm scale) (Raskin and de Boer, 1999). These oscillators are often modeled as feedback loops composed of genetic, biochemical, and cellular events that exhibit limit cycle oscillation over a wide period range (Goldbeter, 2002). Biological systems are composed of multiple oscillators, which in many cases interact with each other. For example, it was recently demonstrated that the segmentation clock period is modulated by intercellular coupling of genetic oscillators (Yoshioka-Kobayashi et al., 2020). Such coupling also occurs within cells among oscillators that drive various physiological functions, e.g., circadian clocks influence cell cycle progression (Matsuo et al., 2003; Yang et al., 2010) and, in turn, cell cycle phase influences the circadian clock (Bieler et al., 2014). Such coupling of multiple oscillators may help produce robust oscillation (Droin et al., 2019; Yan and Goldbeter, 2019b).
In certain conditions, coupled oscillators may exhibit more complex dynamics including multirhythmicity and chaos behavior (Gerard and Goldbeter, 2012; Yan and Goldbeter, 2019a). Indeed, chaos behavior may play a fundamental role in the functioning of biological systems; it has been suggested that autonomous and complex systems (such as living systems) converge on the edge of chaos (Kauffman, 1992; Langton, 1990). Autonomous chaos behavior has been observed and modeled extensively in various biological layers; early examples include the peroxidase enzymatic reaction (Olsen and Degn, 1977), neuronal firing (Aihara et al., 1985; Skarda and Freeman, 1987), and cAMP signaling in Dictyostelium (Durston, 1974; Martiel and Goldbeter, 1985). Chaos behavior continues to be recognized for its importance in modern biology. For example, a recent modeling study of the sleep-wake cycle suggested that the transition between chaos behavior and regular oscillation may underlie the state alteration from sleep-associated to wake-associated neuronal firing patterns (Rasmussen et al., 2017). In such studies, mathematical models are used to understand and predict how complex and autonomous behavior occurs when cellular and molecular activities are modulated. However, it is often difficult to understand how chaos behavior arises from a biochemical reaction system because the biological networks that give rise to chaos behavior can involve multiple gene expression networks, cell-cell interactions, and the complex regulation of molecules.
In modern research, a synthetic biology approach is increasingly being employed to gain mechanistic insights into the autonomous generation of complex behaviors from biological components. In this approach, the aim is to design complex responses from relatively simple model systems. Protein networks shaped by enzymatic reactions and protein-protein interactions have recently been studied using a synthetic biology approach, leading to the de novo design of protein logical circuits (Chen et al., 2020; Fink et al., 2019; Gao et al., 2018). Complex responses have also been observed in nuclear-free cytosolic extract systems, where protein networks, rather than genetic circuits, play a role to elicit autonomous responses (Pomerening et al., 2003, 2005). Therefore, the design of protein networks in cells may improve understanding of how the complex responses exhibited by individual cells originated. Mathematical models can facilitate the design of synthetic protein-based circuits for autonomous activity including chaos. These models must be detailed enough to map to measurable biochemical parameters but also contain a small enough number of components to facilitate experimental design.
In the present study, we use modeling of biological autonomous chaos to interrogate the general design principles of biological chaos that can be realized in a set of ubiquitous molecular systems. Reversible phosphorylation is a well-understood mechanism by which protein activity is regulated. A typical model of reversible phosphorylation assumes a set of antagonizing enzymes (a kinase and a phosphatase) and a substrate (Conradi and Shiu, 2018; Kholodenko, 2006). The enzymes catalyze the phosphorylation and dephosphorylation of the substrate following the Michaelis-Menten reaction scheme. Despite its simplicity and generality, this reaction scheme can generate various complex behaviors; in particular, reversible phosphorylation with two or more modification sites in one-substrate molecule can exhibit biostability (Markevich et al., 2004), multistability (Thomson and Gunawardena, 2009), and autonomous oscillation (Conradi et al., 2019; Jolley et al., 2012; Suwanmajo and Krishnan, 2015). In addition, the spatiotemporal dynamics of this system include traveling waves (Markevich et al., 2006) and the Turing pattern (Sugai et al., 2017). The generic applicability of the reversible phosphorylation model to the modeling of various types of posttranslational modification enables researchers to investigate a typical molecular mechanism that produces complex behaviors from a combination of simple enzymatic reactions.
Specifically, we demonstrate here that chaos behavior can arise from a reversible phosphorylation model entirely described by the Michaelis-Menten reaction scheme. The system does not assume typical allosteric regulation of enzymes in which the enzymes' reaction rates are actively modulated by the substrate, explicit autocatalytic activities, or any other exotic control of the enzymes. The complexity of our model system arises from its composition, which includes two-substrate species each of which has two modification sites. We found that typical combinations of reaction parameters create chaos motifs that allow each of the two substrates to behave as an oscillator and to couple with each other through the availability of shared enzymes. This motif structure can be found in several well-known kinases. Therefore, our model will help researchers to identify and perhaps design possible enzymatic reaction components that can induce autonomous complex outputs in cells.
Results
A coupled dual-phosphorylation system shows chaos behavior
The simplest type of reversible phosphorylation scheme is a system with a single substrate that has one phosphorylation site (Figure S1A). However, this scheme can be modeled as a one-dimensional system by applying the Michaelis-Menten approximation, and thus, oscillation and chaos are impossible (Jolley et al., 2012; Strogatz, 1994). Therefore, we next consider a similar reversible phosphorylation system but single substrate contains two phosphorylation sites. In this system, we previously found that reversible two-site phosphorylation in a single substrate system can have a limit cycle oscillation (Jolley et al., 2012). We assessed whether the same system could exhibit chaos behavior. The system consists of a single substrate with two phosphorylation sites, which are phosphorylated and dephosphorylated by a kinase and a phosphatase, respectively (Figure S1A). All the reactions follow the Michaelis-Menten reaction scheme. Parameters were randomly sampled from an exponential distribution bounded between 1 and 1000 min−1 for reaction rate constants (k) and between 0.01 and 1000 μM for binding constants (Km). Note that a low Km value indicates strong binding between an enzyme and the substrate. The parameter range corresponds to reasonable values typically used in other simulation studies (Chickarmane et al., 2007; Jolley et al., 2012; Liu et al., 2011; Markevich et al., 2004; Qiao et al., 2007; Shankaran et al., 2009; Sugai et al., 2017) and within the distribution of kcat and Km values observed in various enzymes (Bar-Even et al., 2011). Through the numerical integration of the system with 10,000,000,000 randomly sampled parameter sets, we identified 12,636,210 parameter sets that exhibit limit cycle oscillation but did not find any parameters that exhibit chaos behavior, suggesting that the single-substrate system is not complex enough to include chaos behavior.
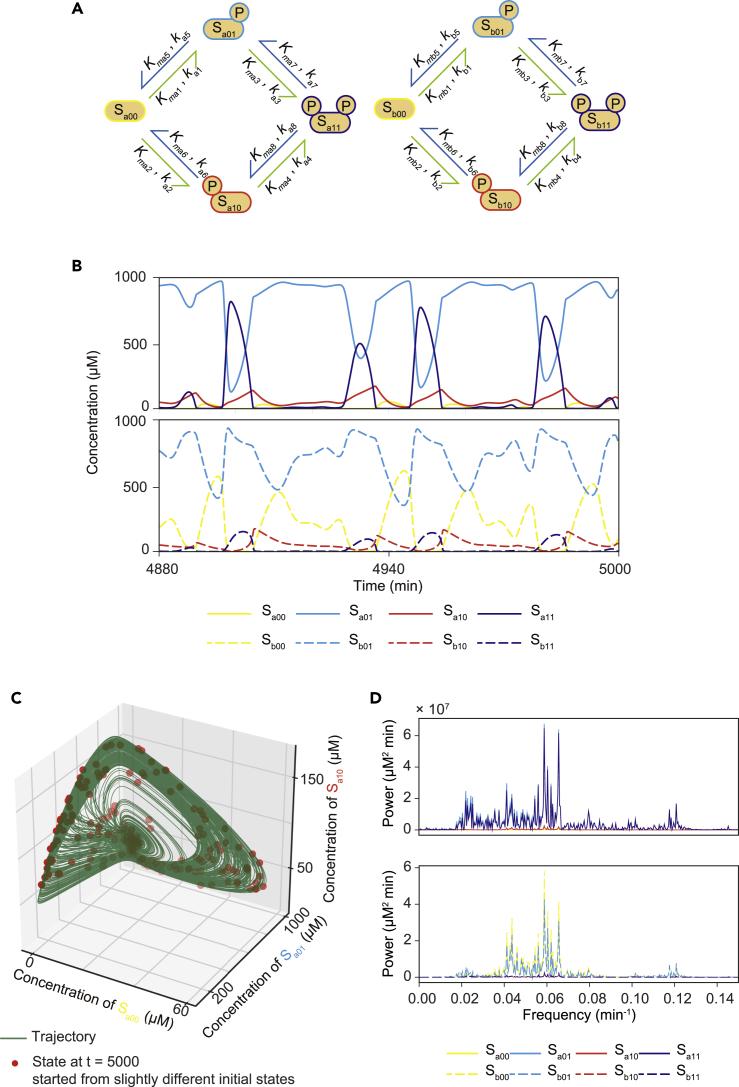
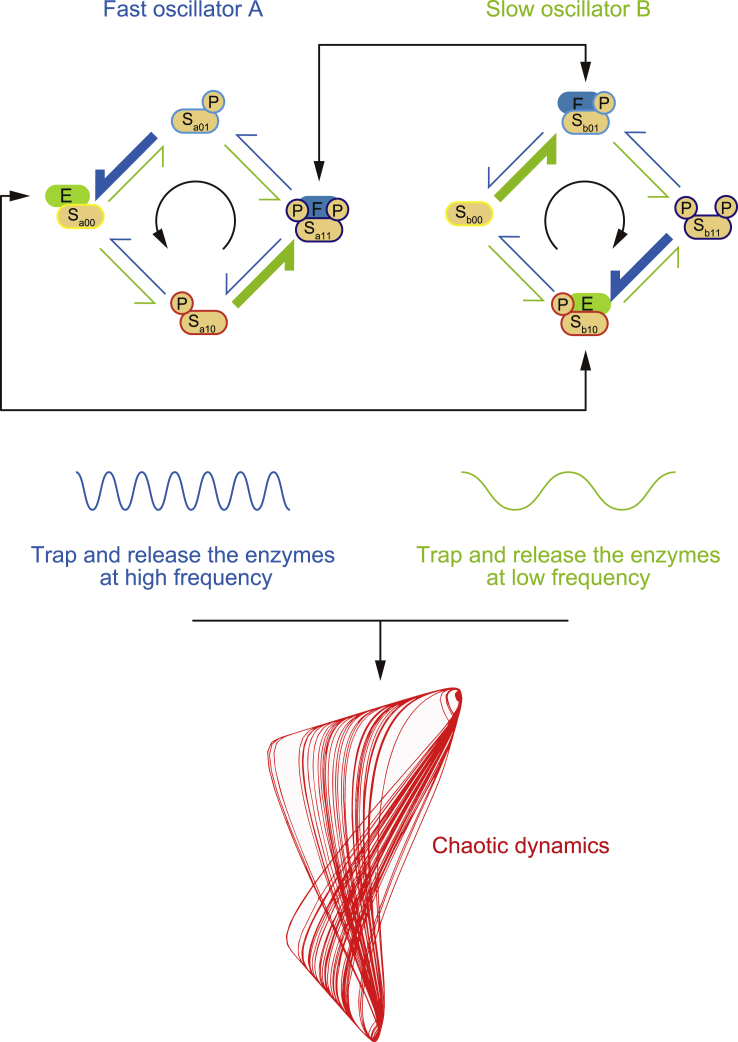
We therefore considered a dual-substrate system consisting of two types of substrate, named Sa and Sb (Figure 1A). Each substrate has two phosphorylation sites that are modified reversibly by a shared kinase (E) and a shared phosphatase (F). Sa has four phosphorylation states, named Sa00, Sa01, Sa10, and Sa11; Sb also has four phosphorylation states, named Sb00, Sb01, Sb10, and Sb11. The states Sa00 and Sb00 are unphosphorylated substrate states, whereas Sa01, Sa10, Sb01, and Sb10 are substrate states with single phosphorylation at either one of the modification sites. The remaining states, Sa11 and Sb11, are substrate states with phosphorylation at both of the two modification sites.
Figure 1.
A coupled dual-phosphorylation system shows chaos behavior
(A) A reaction network comprising a two-substrate (i.e., Sa and Sb) system. Each substrate undergoes a reversible phosphorylation cycle at two residues. The phosphorylation (green arrows) and dephosphorylation (blue arrows) reactions are catalyzed by a shared kinase and phosphatase, respectively. All the reactions follow a Michaelis-Menten reaction scheme characterized by parameters for reaction speed k and enzyme-substrate affinity Km.
(B) An example time course of chaotic phosphorylation dynamics.
(C) The example chaotic trajectory from t = 0 min to t = 5,000 min is projected to Sa00-Sa01-Sa10 space (green line). Red dots indicate the phosphorylation states at t = 5,000 min obtained from 200 runs of the simulation with slightly different initial conditions.
(D) Power spectrum of the example chaotic trajectory analyzed by fast Fourier transform (FFT).
See also Figure S1.
This dual-substrate system showed chaos behavior with some parameter sets (hereafter called “chaos parameter sets”). With chaos parameter sets, the system never converged to a stable state or limit cycle oscillation (Figure 1B). The chaos behavior was further validated by showing that small changes in the initial state could lead to a variety of different states after the system had evolved to a certain time (Figure 1C). The power spectrum of chaos orbitals showed a broad spectrum rather than a few peaks with strong power intensity (Figure 1D). These features distinguish the chaos parameter sets from parameters resulting in limit cycle oscillations (hereafter called “oscillation parameter sets”) (Figures S1B–S1D).
Conserved parameter motifs in the chaos parameter sets
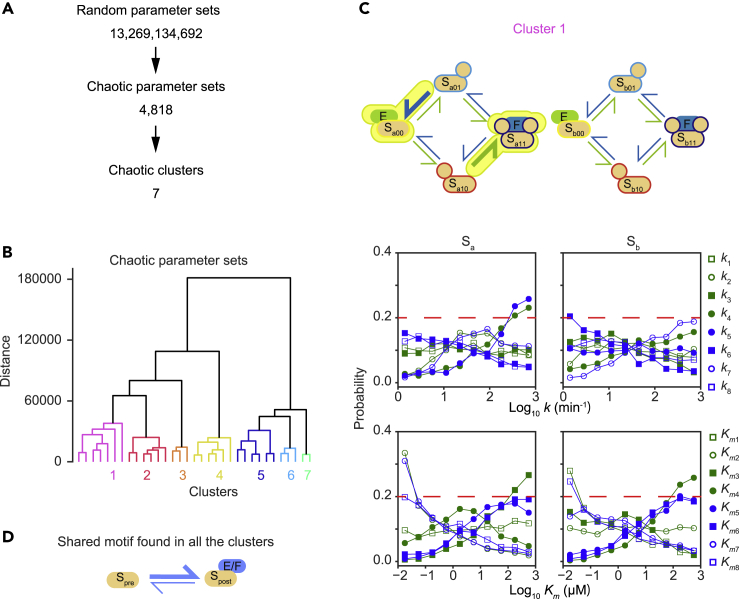
To ascertain whether a specific parameter region was related to chaos behavior in the parameter space, chaos parameter sets were collected by a random parameter search within the same distribution of kcat and Km values described above. This random search revealed 4,818 chaos and 286,255 oscillation parameter sets from 13,269,134,692 randomly generated parameter sets (∼0.0000363% for chaos and ∼0.00216% for oscillation parameter sets) (Figure 2A).
Figure 2.
Shared motifs in chaotic parameter sets
(A) Workflow for chaotic motif identification.
(B) Clustering of chaotic parameter sets with Ward's algorithm. The chaotic parameter sets were standardized by considering phosphor-site symmetries.
(C) Schematic representation and parameter histograms for the largest cluster. Reaction constants (k) for which the distribution exceeds the probability 0.2 (red dotted lines) at the highest value are denoted as fast reactions. Michaelis constants (Km) for which the distribution exceeds the probability 0.2 at the lowest value are denoted as high-affinity enzyme-substrate bindings. The fast reactions are shown as thick arrows, while the high-affinity bindings are indicated by attaching the kinase (E) or phosphatase (F) to the edge of the corresponding substrate species.
(D) A shared design motif found in all clusters. A fast reaction produces a substrate species that has high affinity with either E or F.
See also Figure S2.
To identify a typical motif structure of the chaos parameter sets, hierarchical clustering analysis was performed on the collected chaos parameter sets. Seven clusters were defined by setting a threshold to the clustering dendrogram (Figure 2B). To elucidate the characteristic combination in each cluster, we identified the fast reaction rate based on the criterion that the probability of the corresponding k parameter exceeds a certain threshold (0.2; for details, see Transparent methods) at the highest parameter bin (1000 min−1). Similarly, we identified the stable substrate-enzyme complex based on the criterion that the probability of corresponding Km exceeds the threshold at the lowest parameter bin (0.01 μM). Figure 2C (upper section) shows a schematic view of the chaos parameter sets classified as cluster 1. This scheme highlights the positions of large k values (fast reaction speeds) and small Km values (stable enzyme-substrate complex formation). The parameter distributions of clusters 2–7 are shown in Figure S2. The histograms in each panel indicate the parameter distributions (Figures 2C and S2).
We found that all the clusters included a shared motif structure in at least one part of the phosphorylation/dephosphorylation pathway (as highlighted by yellow coloring trimmed with green or orange in Figures 2C and S2 [discussed later]). The shared motif structure shown in Figure 2D is characterized by a fast reaction that produces stable binding of the substrate (Spost) with either the kinase or phosphatase that is not the same enzyme catalyzed in the fast reaction (i.e., if the fast reaction is a phosphorylation reaction, the product is stably bound with a phosphatase not a kinase.) For example, in cluster 1 (Figure 2C), a kinase reaction with a high ka4 value produces Sa11, which involves stable binding with the phosphatase as indicated by the low Kma7 value. In the same way, the other motif is composed of a phosphatase reaction with a high ka5 value that produces Sa00, which involves stable binding with the kinase as indicated by a low Kma2 value.
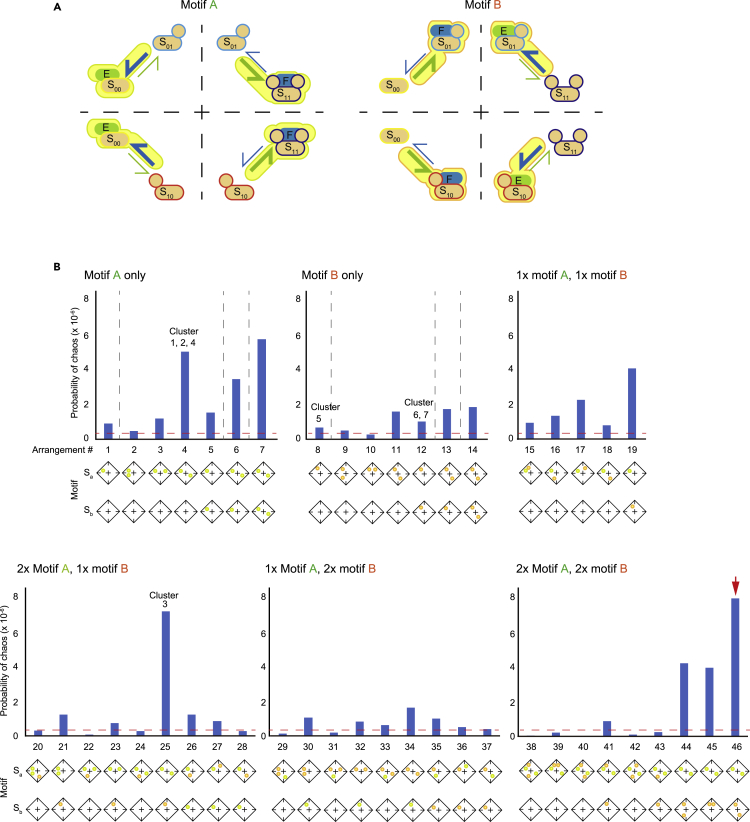
Motif arrangements necessary for chaos behavior
The motifs can be categorized into two types (named motif A and B, respectively) by considering the symmetry of a state transition diagram (Figure 3A). In motif A, a fast reaction is assigned such that a fully phosphorylated (S00) or fully dephosphorylated product (S11) is produced. On the other hand, motif B is composed of a fast reaction that produces a single phosphorylated substrate (S01 or S10). S00 and S11 can be converted by converting the kinase and phosphatase; thus, they have a symmetrical relationship. S01 and S10 are also symmetrical because they can be converted by converting the position of two phosphorylation residues. However, S00 cannot be converted into S01 or S10 by a symmetrical conversion because S00 binds to and is a substrate for a kinase only. In contrast, S01 and S10 can bind to and be a substrate for either a kinase or a phosphatase. Similarly, S11 cannot be symmetrically converted to S01 or S10. These asymmetries make motif A and motif B independent. Either type of motif can be found in each of the chaos clusters. In Figures 1C and S2, motif A is highlighted in yellow trimmed with green and motif B is highlighted in yellow trimmed with orange.
Figure 3.
Functional significance of the number and arrangement of chaos motifs
(A) The chaos motif can be subdivided into two types. Motif A comprises either an unphosphorylated substrate (S00) or fully phosphorylated substrate (S11) as a high-affinity substrate that tightly binds to kinase E or phosphatase F, respectively. Motif B comprises a single phosphorylated substrate (S01 or S10) as a high-affinity substrate species. In both motifs, the fast reactions that produce high-affinity species are catalyzed by enzymes that are not tightly bound to the produced high-affinity species. In Figures 2 and S2, motif A is shown in yellow with a green border, while motif B is shown in yellow with an orange border.
(B) The motif structures were imposed in the parameter search by applying biased k and Km values. The positions of imposed motifs are indicated in the diagrams below each bar chart. A rhombus divided into four subspaces represents the reaction structure shown in (A). For example, the upper left space indicates the conversion between S00 and S01. When a green circle is shown in any of the four subspaces, motif A is imposed at the reversible phosphorylation scheme corresponding to the subspace. Similarly, an orange circle denotes motif B imposed at the indicated subspace. Bar charts indicate the probability of chaotic parameter sets found in the presence of each imposed motif. In the bar charts, motif arrangements correspond to the clusters found in the random parameter search (Figures 2 and S2), which are indicated as cluster numbers. The red arrow indicates the motif arrangement with the highest probability of chaos behavior.
See also Figure S3.
To investigate whether the presence of a motif structure is important to chaos behavior in the two-substrate system, we performed a biased parameter search. Each motif could be placed into four symmetrical positions on a reaction diagram of each Sa and Sb substrate (Figure 3A). We tested a scenario in which each substrate could have up to two motif As and two motif Bs, respectively. According to the symmetry within the reaction diagram, 46 patterns of different motif biases cover all possible arrangements of motifs (Figure 3B). Among the 46 motif arrangements, 35 were more likely to show chaos behavior than a system without any motif bias. These 35 motif arrangements included those that correspond to the clustering analysis results (e.g., cluster 1–7). For example, a structure that has motif A in the positions Sa01→Sa00 and Sa10→Sa11 corresponds to cluster 1, 2, and 4 and shows a higher probability of having chaos behavior than in the parameter search without any motif bias (Figure 3B: arrangement #4).
The biased parameter search suggested that motifs with specific arrangements contribute to chaos behavior (Figure 3B). First, the probability of chaos behavior increases when motif A or motif B are placed in rotationally symmetrical positions (e.g., conversion between S00↔S01 or between S11↔S10); arrangements #4, #6, and #7 show higher chaos probabilities as they contain two motif As in rotationally symmetrical positions, while arrangements #11, #13, and #14 also exhibit higher chaos probabilities by containing two motif Bs in rotationally symmetrical positions. Second, comparisons between arrangements with only motif A or motif B show that arrangements with motif A tend to have chaos behavior more than those with motif B. Third, a certain arrangement of both motif A and motif B substantially increases the probability of chaos behavior. This is evident by comparison of the probabilities of arrangements #6, #13, and #25; all of these arrangements have motif A or B in the positions Sa00↔Sa01, Sa11↔Sa10, and Sb00↔Sb01; however, arrangement #25, which contains two motif As in substrate Sa and one motif B in substrate Sb, has a higher probability of chaos behavior than arrangements #6 and #13. It should also be noted that even if the number of included motifs increases, the inappropriate motif arrangement decreases chaos probability to a probability lower than that observed with an unbiased parameter search (e.g., arrangement #38). Among the 46 arrangements, the highest chaos probability was observed for an arrangement of Sa with two motif As in rotationally symmetrical positions and Sb with two motif Bs in rotationally symmetrical positions (arrangement #46: red arrow in Figure 3B).
With two motif As or two motif Bs in rotationally symmetrical positions, the substrate phosphorylation-dephosphorylation reaction tends to flow in a cyclic order. For example, if motif A is placed in the symmetrical positions Sa01→Sa00 and Sa10→Sa11 (e.g., arrangement #4), the fast dephosphorylation reaction leads to a counter-clockwise phosphorylation-dephosphorylation cycle (Sa01→Sa00→Sa10→Sa11→Sa01 …) (see Figure 4A). This cyclical bias with stable enzyme-substrate binding is a typical motif arrangement where limit cycle oscillation occurs in a single-substrate system (Jolley et al., 2012). Accordingly, two-substrate systems with two motif As or motif Bs in rotationally symmetrical positions have a higher probability of limit cycle oscillation, as well as chaos behavior (Figure S3A). Such correlation can also be observed for other motif arrangements; for example, a motif arrangement with a high probability of chaos behavior tends to have a high probability of oscillation (Figures S3A and S3B). This relationship is to be expected, given that chaos behavior is often caused by the coupling of oscillators. However, a high probability of oscillation does not fully account for a high probability of chaos behavior because arrangement #46, which has the highest probability of chaos behavior, does not have the highest probability of oscillation (Figure S3B, red arrow). Thus, arrangement #46 retains reaction features that are important for chaos behavior.
Figure 4.
Critical parameters for the oscillation-chaos transition
(A) Schematic diagram of the stereotypical chaos/oscillation parameter sets.
(B) Bifurcation analysis of stereotypical chaos parameter sets (n = 97), all of which preserve a motif arrangement shown in the schematic representation. A heatmap shows the results of bifurcation analysis. White circles indicate the centroid of the 97 stereotypical parameter sets. The color of the heatmap represents, for a set of stereotyped parameters, the probability of chaos behavior (red), oscillation (green), or convergence to some steady state (blue) when each indicated parameter is fixed to an indicated value. For example, if all 97 parameter sets had chaos behavior, the color would be red, but if half the parameter sets had chaos behavior and the other half had oscillation, the color code would be brown (50% red +50% green).
(C) The analysis method is the same as that in (B), except that the indicated parameter and its symmetrical pair (e.g., ka1 and ka8, Kmb4 and Kmb5) are simultaneously fixed to an indicated value.
See also Figure S4.
The chaos motif arrangements create two oscillator structures
To investigate the mechanism underlying the generation of chaos behavior, we considered stereotypical chaos parameter sets (n = 97) based on motif arrangement #46 (Figures 3B and 4A). For comparison, we also considered stereotypical oscillation parameter sets (n = 97) based on motif arrangement #46. Both stereotypical parameter sets had symmetrical structures because the setting parameters in the symmetrical positions (e.g., ka1 and ka8) had identical values.
Bifurcation analyses were performed with the stereotypical parameter sets. Bifurcation maps for stereotypical chaos sets support the importance of motif structure (Figures 4B and 4C). The motif A structure in substrate Sa is implemented by high ka4/5 and low Kma2/7 values. Indeed, in the bifurcation maps, chaos behavior is restricted in the range of the highest ka4/5 and lowest Kma2/7 values. These constrains appear to be important for avoiding the system's convergence to a fixed steady state because high ka4/5 and low Kma2/7 values are also critical for oscillation in the stereotypical oscillation parameter sets (Figure S4). For substrate Sb, motif B is implemented by high kb1/8 and low Kmb4/6 values. Similar to substrate Sa, chaos behavior is restricted within the range of high kb1/8 and low Kmb4/6 values, although this constrain appears to be less important than for motif A in substrate Sa. The importance of a motif B in substrate Sb is characteristic of chaos behavior because these parameters have a negligible impact in the bifurcation map of the stereotypical oscillation parameter sets (Figure S4). In other words, the appropriate arrangement and parameter space of both motif A in substrate Sa and motif B in substrate Sb are important for chaos behavior.
Another constrain can be found in ka2. Chaos behavior and oscillation are restricted in the narrow range of ka2/7 values (Figures 4 and S4). Indeed, ka2/7 is critical for period determination in an oscillator composed of a similar motif A arrangement because this rate constant determines the time required to convert all the enzyme-trapping statuses (Sa00 and Sa11) to nontrapping statuses (Jolley et al., 2012). In contrast, the period-determining parameter for a motif B oscillator is kb3/6. By comparing the parameter ranges of chaos behavior for ka2/7 and kb3/6 with those of an oscillation, it was found that the faster cycle (higher ka2/7) for the Sa oscillator relative to that of the Sb oscillator appears to be important for chaos behavior. This expected period difference appears not to be important for oscillation because changes to kb3/6 do not affect the steady-state behavior of the stereotypical oscillation parameter sets (Figure S4).
Coupling of fast and slow oscillators is raised by a combined motif A and motif B arrangement
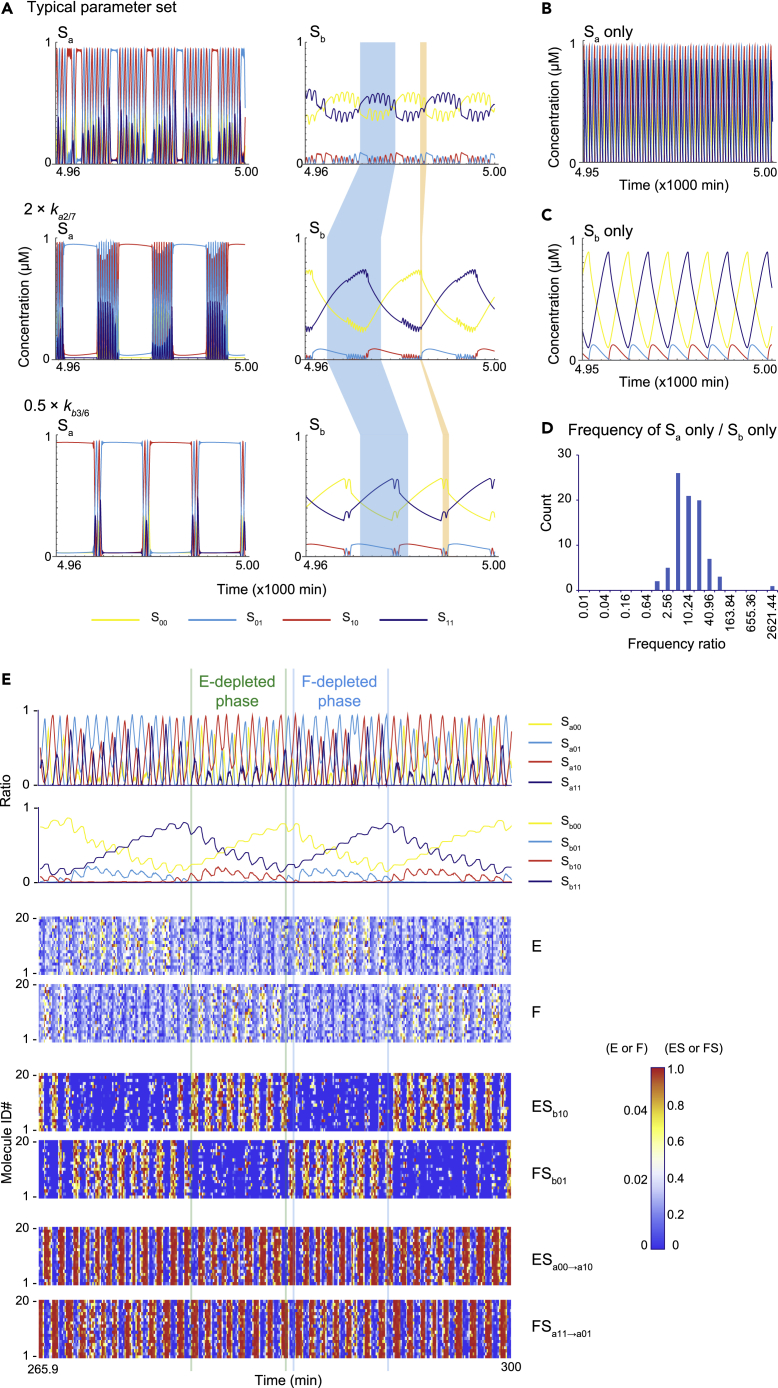
To further investigate the underlying mechanism of chaos behavior, we chose one example among the stereotypical chaos parameter sets (Table S1). The system with this example parameter set showed chaos behavior characterized by a mixture of fast and slow dynamics in the trajectory of phosphorylation statuses (Figure 5A). In Figure 5A, the approximate period of slower dynamics is shown by a blue band, whereas that of faster dynamics is shown by an orange band (see the Sb plot in Figure 5A). These short and long periods are sensitive to changes in ka2/7 and kb3/6 values, which are reaction parameters suggested to be critical for periods of Sa- and Sb-based oscillation (Jolley et al., 2012). A two-fold increase in ka2/7 further shortens the short period (2× ka2/7: orange band in Figure 5A) while the long period is further lengthened (2× ka2/7: blue band in Figure 5A). On the other hand, a two-fold decrease in kb3/6 lengthens the long period (0.5× kb3/6: blue band in Figure 5A) without markedly affecting the short period (0.5× kb3/6: orange band in Figure 5A). Because the short period is sensitive to ka2/7, we suggest that the dynamics of substrate Sa are primarily responsible for the fast oscillatory component of chaos behavior. The slow oscillatory component may be largely determined by the coupling of Sa and Sb because both ka2/7 and kb3/6 affect the longer period.
Figure 5.
Dissection of timescales encoded by the chaos motifs
(A) Time course of chaotic dynamics for a representative chaos parameter set, the representative parameter set with a two-fold increase in the parameter values for symmetrical ka2 and ka7, or the representative parameter set with a 0.5-fold decrease in the parameter values for symmetrical kb3 and kb6. The dynamics are mainly composed of oscillatory dynamics of high and low frequency. A typical period of high-frequency oscillation is shown as an orange stripe, whereas that of a low-frequency oscillation is shown as a blue stripe.
(B) Time course of oscillatory dynamics for the representative parameter set when the amount of Sb is fixed to zero. In the absence of Sb, the parameter set gives oscillation in Sa with high frequency.
(C) Time course of oscillatory dynamics for the representative parameter set when the amount of Sa is fixed to zero. In the absence of Sa, the parameter set gives oscillation in Sb with low frequency.
(D) Comparison of frequency differences encoded by oscillatory dynamics intrinsically driven by Sa and Sb. For the 97 stereotypical chaotic parameter sets, the amount of Sa or Sb was fixed to zero. In total, 85 of the stereotypical parameter sets showed oscillation for the remaining Sb or Sa dynamics. The ratio of Sa-frequency and Sb-frequency indicates that the Sa substrate is responsible for the high-frequency oscillation in the stereotypical parameter sets.
(E) The upper two plots indicate time evolution of Sa and Sb at each phosphorylation state based on the stochastic simulation. The lower heatmaps illustrate the fraction of time that each sampled enzyme or substrate molecule (numbered as #1 to #20) spend in an indicated form (e.g., substrate-unbound free E, ES complex from Sb10→Sb11) during a 0.1 s epoch. Sa molecules trap E and F reciprocally at high frequency, while Sb molecules slowly trap and release the E and F, thereby driving low-frequency rhythmicity.
The different roles of Sa and Sb were further validated by removing one of the Sa or Sb substrates from the chaos system. If the amount of Sb is set to zero with all other parameters maintained, the remaining Sa substrate shows a limit cycle oscillation with a period comparable to the fast oscillatory component of the chaos system (Figure 5B). On the other hand, if the amount of Sa is set to zero, the remaining Sb substrate shows an oscillation with a longer period than that of a Sa-only oscillation (Figure 5C). The different intrinsic periods of Sa-only and Sb-only oscillations are conserved among the stereotypical parameter sets; among the 97 stereotypical parameter sets, 85 showed oscillations in the absence of Sa or Sb. In most cases, a Sa-only oscillation had a higher frequency (i.e., shorter period) than a Sb-only oscillation (Figure 5D). The unimodal distribution of frequency difference suggests that the coupled Sa and Sb oscillators tend to behave chaotically when the frequency ratio is not too low or high. These results support the hypothesis that a Sa oscillator with an intrinsically shorter period contributes to the faster dynamics of chaos behavior and a Sb oscillator with an intrinsically longer period contributes to the slower dynamics, while the coupling between Sa and Sb dynamics is required for the slower dynamics of chaos behavior.
In agreement, a mixture of fast and slow dynamics was observed under increased Sa-enzyme affinity (i.e., decreased Kma2/7) conditions (Figure S5A). Fast dynamics are absent if the affinity of the Sa-enzyme is significantly decreased (Figure S5B), suggesting that Sa-enzyme affinity is important for producing fast dynamics. In addition, increasing Sb-enzyme affinity disrupts fast dynamics (Figure S5C), while decreasing Sb-enzyme affinity disrupts slower dynamics (Figure S5D); this suggests that setting Sb-enzyme affinity at an appropriate strength is important for the coexistence of fast and slow dynamics.
The phosphorylation dynamics of Sa and Sb affect each other through the availability of a shared kinase and phosphatase. The availability of free enzymes is restricted by the presence of substrate species with high affinities to these enzymes (i.e., enzyme sequestration). Therefore, the results presented above suggest that enzyme sequestration by substrate Sa may be important for fast dynamics, whereas slower dynamics are likely related to enzyme sequestration by substrate Sb. Given this possibility, we aimed to directly visualize the behavior of a free kinase, free phosphatase, and the sequestered enzymes using a stochastic simulation (Figure 5E). This stochastic simulation did not presuppose the quasi-steady-state assumption of the Michaels-Menten reaction scheme. Instead, the dynamics of the enzyme-substrate complex were simulated explicitly. In the stochastic simulation, fast and slow dynamics were still observable in Sa and Sb phosphorylation states. Consistent with this, the availability of the free kinase (E) and free phosphatase (F) fluctuated in fast and slow dynamics. This fluctuation in the slow dynamics of E and F was represented as E-depleted and F-depleted phases, which were well matched with the presence of ESb10→b11 and FSb01→b00 complexes, respectively, both of which are Sb complexes with high affinities to E and F, respectively. On the other hand, ESa00→a10 and FSa11→a01 complexes, which are Sa complexes with high affinities to E and F, respectively, showed clear oscillations that were well matched with fast dynamics. In summary, the stochastic simulation demonstrated that enzyme sequestration by Sb species represents the slow dynamics of free enzyme availability, whereas enzyme sequestration by Sa species dominates the fast dynamics of phosphorylation statuses. The dynamics of chaos behavior may result from the coupling of Sa and Sb substrates via the availability of enzymes, which varies across timescales (Figure 6).
Figure 6.
Coupling of posttranslational oscillators encoding different timescales
In a stereotypical arrangement of motif structure, the chaotic dynamics arise from a coupling of two-substrate modification cycles communicated by the competitive availability of shared enzymes, E and F. One substrate (Sa) intrinsically drives the reciprocal sequestration of the enzymes at high frequency, and the other substrate (Sb) intrinsically drives the enzyme sequestration at low frequency. The coupling of two such posttranslational oscillators encoding at different timescales can result in chaotic dynamics without the need for external signals or any typical allosteric regulation of enzymes.
Discussion
Reversible phosphorylation networks in living cells
To the best of our knowledge, this study is the first computational demonstration of a biochemical system described only by the Michaelis-Menten reaction scheme exhibiting chaos behavior. Our model can be discriminated from a set of molecular models employing the synthesis and degradation of components (Decroly and Goldbeter, 1982). Although the coupling of oscillators is understood to be one of the typical mechanisms underlying chaos generation, the model of reversible phosphorylation described by the Michaelis-Menten scheme helps connect the design principle to the possible molecular properties. We previously showed that a similar two-site phosphorylation system could be an autonomous oscillator (Jolley et al., 2012). Mathematically, the model of Jolley et al. (2012) is closely related to the oscillator model of KaiC protein (Rust et al., 2007), a unique cyanobacteria protein with autokinase and autophosphatase activities. Nonetheless, the model described by the generic Michaelis-Menten scheme allows us to directly compare parameter (k and Km) combinations, leading to the theory that several kinases, including mammalian proteins, may meet the requirements for composing autonomous oscillators. The work in the present study may be similarly useful, and below we discuss how a cellular reversible phosphorylation network can be a chaos generator without the need for eccentric assumptions related to the properties of enzymes and substrates.
We employed a model with two substrates, each of which had two modification sites modified by a shared kinase and phosphatase pair. This setting includes some degree of complexity but should also be commonly observed in the phosphorylation networks of cells. A previous mass spectrometry analysis revealed that at least 75% of the complete proteome is phosphorylated (Sharma et al., 2014) and that many substrates are phosphorylated at multiple residues. On the other hand, the number of kinases and phosphatases is much smaller than the substrate variety (Manning et al., 2002). Thus, different substrates share a kinase/phosphatase pair for modification of phosphorylation residues. Kinases are also known to modify a variety of non-motif substrate sequences at a different reaction rates (Miller and Turk, 2018; Ubersax and Ferrell, 2007), although kinases do have preferred substrate sequences, or consensus sequences, at which the kinase preferentially phosphorylates target residues. Therefore, a set of shared kinases and phosphatases is naturally observed in the phosphorylation network of cells.
Given this situation, it is reasonable to assume that the number of phosphorylation residues and the number of substrates sharing enzymes is greater than (and therefore more complex than) that in our model. Nevertheless, our model could be applied to more complex phosphorylation networks in which more than two phosphorylation sites and substrate species exist. By extending the complexity of multisite phosphorylation in a substrate, it may even be possible to implement the two (distinct) substrates modeled in this study at distinct protein regions within the same substrate molecule. A similar condition can be found in phosphorylation control of the mammalian circadian protein PERIOD (PER) 2, a relatively large (∼100 kDa) protein that is mostly annotated with an intrinsically disordered region (Gustafson and Partch, 2015). A previous study demonstrated that the same kinase, casein kinase I (CKI) δ/ε, phosphorylates at multisite phosphorylation clusters located at two distinct protein regions within PER2 (Zhou et al., 2015). Therefore, the phosphorylation of the two regions may compete with each other through different affinities to the CKIδ/ε kinase. Though it is currently unknown whether this circadian kinase-substrate pair exhibits autonomous chaotic phosphorylation, we expect that the phosphorylation network modeled in the present study could be implemented in a variety of molecules.
Typical chaos motifs found in actual kinases
We found that a typical chaos motif and combination of motifs had chaotic phosphorylation dynamics. Because the k and Km values of known kinases vary by a few orders of magnitude (Bar-Even et al., 2011) and even the same kinase can show different k and Km values depending on substrate sequences (Ubersax and Ferrell, 2007), it should be possible to identify enzyme and substrate pairs that satisfy typical chaos motifs.
The chaotic motif shown in Figure 3A requires the formation of a tight complex between the enzyme and the substrate/product. The arrangement of the motif structure with frequent occurrence of chaos behavior, as shown in Figure 2, suggests that it is important for an enzyme to modify the substrate in a specific order. These structures are common to the formation of oscillators from reversible phosphorylation (Jolley et al., 2012), and the properties required of the enzyme are also common to the formation of oscillators in several aspects. For example, CKIδ/ε is a candidate kinase that could achieve a chaotic motif structure. CKIδ/ε tightly binds to PERs and other substrate proteins (Aryal et al., 2017). Moreover, the substrate/product binding property is conserved even with short peptide substrates (Shinohara et al., 2017), which plays a role in the temperature-insensitive phosphorylation rate of this kinase. In addition, CKIδ/ε has a unique consensus sequence of pS-X-X-S∗ (pS: pre-phosphorylated serine; X: any amino acid; and S∗: target serine), which allows the CKIδ/ε to sequentially phosphorylate the repeated S-X-X-S sequence from N- to C-terminus. Interestingly, the PER protein substrates have the repeated S-X-X-S sequence, which is known to be involved in the frequency control of circadian clock oscillation. Recent studies found that a CKIδ/ε isoform could phosphorylate serine at the N-terminal proximity of the S-X-X-S repeat and thereby prime for sequential phosphorylation (Fustin et al., 2018; Narasimamurthy et al., 2018). Therefore, CKIδ/ε and substrates with repeated S-X-X-S consensus sequences could be the building blocks for producing posttranslational chaos generators. We note that sequential phosphorylation and substrate/product complex formation is also found in other kinase/substrate pairs involved in cellular signaling pathways such as cell cycle control (Miller and Turk, 2018; Valk et al., 2014).
Comparison of the posttranslational oscillator and chaos generator
Our comparisons of chaos behavior and oscillation probabilities among the various combinations of motif A and B imply that the chaos generator prefers motif A over motif B (see Figure S3B). Compared with motif A, motif B has a higher tendency to exhibit oscillation rather than chaos behavior. This is consistent with a previous study (Jolley et al., 2012), which indicated that for single-substrate systems with two reversible phosphorylation sites, a single-substrate system composed from motif B [“cluster 1” oscillator described by Jolley et al. (2012)] has a higher probability of exhibiting oscillation than that composed from motif A [“cluster 2” oscillator described by Jolley et al. (2012)].
Given that typical chaos behavior is generated by the coupled posttranslational oscillators in our system, a question arises: why is a higher chaos behavior probability derived from the presence of motif A rather than from a two-substrate system composed with motif B that shows the highest probability of oscillation? The importance of motif A for the generation of chaos behavior can be understood based on the coupling mechanism of the two substrates, which occurs through enzymatic shearing. Our stochastic simulation indicated that enzymes are trapped and released by Sb species over a slower time course (Figure 5G). To achieve enzyme trapping by Sb, it is necessary that the enzymes are released from Sa species. The Sa system shown in Figure 5 is composed of motif A (see Figure 4A for the schematic view). From this viewpoint, enzymes are released according to the oscillation process driven by motif A; focusing on kinase (E) in the Sa species, Sa is mostly trapped by the Sa00 substrate through high kinase-Sa00 affinity (low Kma2 values). The bound kinase (E) is then released from the Sa00 when the cyclic phosphorylation/dephosphorylation event proceeds from Sa00 to Sa10. The same scenario can also be applied to the release of trapped phosphatase (F) by Sa11. Therefore, the trapped enzymes need to be released through the course of the (de)phosphorylation cycle. This is not the case for an oscillator composed of motif B (i.e., the Sb system in Figure 4A); the kinase (E) trapped by Sb10 is not involved in the cyclic reaction in which Sb10 is dephosphorylated by the phosphatase, nor is the kinase released in the course of the phosphorylation/dephosphorylation cycle. This scenario is validated by the bifurcation analysis shown in Figure 4. The kinase trapping of Sa can be very tight, as indicated by the bifurcation map in which the chaos area of Kma2 reaches the edge of the smallest parameter boundary (∼0.01 μM). Figure S5A also shows that fast and slow dynamics can persist even with a very high affinity between Sa00-kinase and Sa11-phosphatase (low Kma2/7 values). In contrast, the kinase trapping of Sb should be tight but to a lesser extent than that of Sa; the chaos area of Kmb4 is within the smaller parameter range but cannot reach the smallest boundary (Figure 4). Where Kmb4 values are too low, the enzyme may not be released from Sb10 efficiently, and the coupling between Sa and Sb might consequently be disrupted.
In summary, although motif B is potent in exhibiting autonomous oscillation, motif A is beneficial to the coupling status of substrates with other substrate molecules through enzymatic sharing. This suggests that by combining different motif structures in different arrangements, it is possible to design biochemical networks that are suitable for generating not only oscillators that induce constant rhythms but also chaos generators that elicit spontaneous and complex dynamics in posttranslational modification.
Conclusion
Recent study demonstrated that chaos can arise from relatively simple transcriptional control models (Heltberg et al., 2019), and our study further suggests that autonomous chaos behavior can also arise from a generic mechanism of reversible multisite phosphorylation. Therefore, multisite phosphorylation networks could be sources of the spontaneous properties of cellular function, such as the stochastic nature of cellular differentiation (Furusawa and Kaneko, 2001) and the spontaneous and excitable activation of intracellular signaling observed in unicellular organisms (Devreotes et al., 2017). Thermal fluctuations in molecular activity, as well as transduction and amplification, have previously been modeled as a source of spontaneous activation in intracellular biochemical reactions (Oosawa, 2001, 2007; Ooyama and Shibata, 2011; Shibata and Ueda, 2008; Ueda and Shibata, 2007). The present study suggests that spontaneous and chaotic dynamics may also be generated from the ubiquitous setting of reversible posttranslational networks. As a similar line of research, it will also be interesting to investigate how the enzyme-substrate network avoids chaos behavior if spontaneous action leads to uncontrollable outcomes (Gelens et al., 2015).
Limitations of the study
In this study, we did not conduct an analysis of chaos system based on the analytical solution of mathematical models. Instead, we used a set of analysis based on random parameter searching, numerical integration of ordinary differential equations, and clustering analysis of chaos parameter sets. These analyses have limitations in the interpretation of the obtained results. First, although we could not find chaos in the system with single substrate having two phosphorylation sites, we cannot exclude the possibility that chaos can be observed with certain parameter combinations in the system of single substrate. Second, the mechanism of chaos generation explained in this study (e.g. Figure 6) is based on the stereotypical parameter combination illustrated as in Figure 4, and it is highly likely that there are certain parameter sets yielding chaos dynamics by the mechanism that are difficult to be categorized as “two-coupled fast and slow oscillators”. Finally, since the random parameter search was performed against reversible phosphorylation models with the Michaelis-Menten approximation, the results of the random parameter search may show different trends in the distribution of the chaotic parameters if similar reversible phosphorylation systems are modeled without using the Michaelis-Menten approximation.
Resource availability
Lead contact
Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Hiroki R. Ueda (uedah-tky@umin.ac.jp)
Materials availability
This study did not generate new unique reagents.
Data and code availability
The code generated during this study are available at GitHub https://github.com/DSP-sleep/PT_Chaotic_Oscillators.
Methods
All methods can be found in the accompanying Transparent Methods supplemental file.
Acknowledgments
This work was supported by grants from the Brain/MINDS JP21dm0207049, Science and Technology Directorate Platform Program for Advanced Biological Medicine JP21am0401011, AMED-CREST JP21gm0610006 (AMED/MEXT) (H.R.U.), Grant-in-Aid for Scientific Research (S) JP25221004 (JSPS KAKENHI) (H.R.U.) and Scientific Research (C) JP20K06576 (JSPS KAKENHI) (K.L.O.), HFSP Research Grant Program RGP0019/2018 (HFSP) (H.R.U.), ERATO JPMJER2001 (JST) (H.R.U.) and an intramural Grant-in-Aid from the RIKEN BDR (H.R.U.). The authors would like to thank Enago (www.enago.jp) for the English language review.
Author contributions
H.Q.Y., K.L.O., and H.R.U. designed the study. H.Q.Y. performed most of the simulation study. H.Q.Y., K.L.O., and H.R.U. analyzed the mechanism of chaos generation and wrote the manuscript.
Declaration of interests
H.R.U. is a member of the iScience's editorial advisory board.
Published: January 22, 2021
Footnotes
Supplemental Information can be found online at https://doi.org/10.1016/j.isci.2020.101946.
Supplemental information
References
- Aihara K., Matsumoto G., Ichikawa M. An alternating periodic-chaotic sequence observed in neural oscillators. Phys. Lett. A. 1985;111:251–255. [Google Scholar]
- Aryal R.P., Kwak P.B., Tamayo A.G., Gebert M., Chiu P.L., Walz T., Weitz C.J. Macromolecular assemblies of the mammalian circadian clock. Mol. Cell. 2017;67:770–782 e776. doi: 10.1016/j.molcel.2017.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bar-Even A., Noor E., Savir Y., Liebermeister W., Davidi D., Tawfik D.S., Milo R. The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry. 2011;50:4402–4410. doi: 10.1021/bi2002289. [DOI] [PubMed] [Google Scholar]
- Bieler J., Cannavo R., Gustafson K., Gobet C., Gatfield D., Naef F. Robust synchronization of coupled circadian and cell cycle oscillators in single mammalian cells. Mol. Syst. Biol. 2014;10:739. doi: 10.15252/msb.20145218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Z., Kibler R.D., Hunt A., Busch F., Pearl J., Jia M., VanAernum Z.L., Wicky B.I.M., Dods G., Liao H. De novo design of protein logic gates. Science. 2020;368:78–84. doi: 10.1126/science.aay2790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chickarmane V., Kholodenko B.N., Sauro H.M. Oscillatory dynamics arising from competitive inhibition and multisite phosphorylation. J. Theor. Biol. 2007;244:68–76. doi: 10.1016/j.jtbi.2006.05.013. [DOI] [PubMed] [Google Scholar]
- Conradi C., Mincheva M., Shiu A. Emergence of oscillations in a mixed-mechanism phosphorylation system. Bull. Math. Biol. 2019;81:1829–1852. doi: 10.1007/s11538-019-00580-6. [DOI] [PubMed] [Google Scholar]
- Conradi C., Shiu A. Dynamics of posttranslational modification systems: recent progress and future directions. Biophysical J. 2018;114:507–515. doi: 10.1016/j.bpj.2017.11.3787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Decroly O., Goldbeter A. Birhythmicity, chaos, and other patterns of temporal self-organization in a multiply regulated biochemical system. Proc. Natl. Acad. Sci. U S A. 1982;79:6917–6921. doi: 10.1073/pnas.79.22.6917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devreotes P.N., Bhattacharya S., Edwards M., Iglesias P.A., Lampert T., Miao Y. Excitable signal transduction networks in directed cell migration. Annu. Rev. Cell Dev. Biol. 2017;33:103–125. doi: 10.1146/annurev-cellbio-100616-060739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Droin C., Paquet E.R., Naef F. Low-dimensional dynamics of two coupled biological oscillators. Nat. Phys. 2019;15:1086–1094. doi: 10.1038/s41567-019-0598-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Durston A.J. Pacemaker mutants of Dictyostelium discoideum. Dev. Biol. 1974;38:308–319. doi: 10.1016/0012-1606(74)90009-8. [DOI] [PubMed] [Google Scholar]
- Fink T., Lonzaric J., Praznik A., Plaper T., Merljak E., Leben K., Jerala N., Lebar T., Strmsek Z., Lapenta F. Design of fast proteolysis-based signaling and logic circuits in mammalian cells. Nat. Chem. Biol. 2019;15:115–122. doi: 10.1038/s41589-018-0181-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furusawa C., Kaneko K. Theory of robustness of irreversible differentiation in a stem cell system: chaos hypothesis. J. Theor. Biol. 2001;209:395–416. doi: 10.1006/jtbi.2001.2264. [DOI] [PubMed] [Google Scholar]
- Fustin J.M., Kojima R., Itoh K., Chang H.Y., Ye S., Zhuang B., Oji A., Gibo S., Narasimamurthy R., Virshup D. Two Ck1delta transcripts regulated by m6A methylation code for two antagonistic kinases in the control of the circadian clock. Proc. Natl. Acad. Sci. U S A. 2018;115:5980–5985. doi: 10.1073/pnas.1721371115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao X.J., Chong L.S., Kim M.S., Elowitz M.B. Programmable protein circuits in living cells. Science. 2018;361:1252–1258. doi: 10.1126/science.aat5062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelens L., Huang K.C., Ferrell J.E., Jr. How does the Xenopus laevis embryonic cell cycle avoid spatial chaos? Cell Rep. 2015;12:892–900. doi: 10.1016/j.celrep.2015.06.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerard C., Goldbeter A. Entrainment of the mammalian cell cycle by the circadian clock: modeling two coupled cellular rhythms. PLoS Comput. Biol. 2012;8:e1002516. doi: 10.1371/journal.pcbi.1002516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbeter A. Computational approaches to cellular rhythms. Nature. 2002;420:238–245. doi: 10.1038/nature01259. [DOI] [PubMed] [Google Scholar]
- Gustafson C.L., Partch C.L. Emerging models for the molecular basis of mammalian circadian timing. Biochemistry. 2015;54:134–149. doi: 10.1021/bi500731f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heltberg M.L., Krishna S., Jensen M.H. On chaotic dynamics in transcription factors and the associated effects in differential gene regulation. Nat. Commun. 2019;10:71. doi: 10.1038/s41467-018-07932-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izhikevich E.M. MIT Press; 2007. Dynamical Systems in Neuroscience. [Google Scholar]
- Jolley C.C., Ode K.L., Ueda H.R. A design principle for a posttranslational biochemical oscillator. Cell Rep. 2012;2:938–950. doi: 10.1016/j.celrep.2012.09.006. [DOI] [PubMed] [Google Scholar]
- Kauffman S.A. Origins of order in evolution: self-organization and Selection. In: Varela F.J., Dupuy J.-P., editors. Understanding Origins: Contemporary Views on the Origin of Life, Mind and Society. Springer Netherlands; 1992. pp. 153–181. [Google Scholar]
- Kholodenko B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langton C.G. Computation at the edge of chaos: phase transitions and emergent computation. Physica D Nonlinear Phenomena. 1990;42:12–37. [Google Scholar]
- Liu P., Kevrekidis I.G., Shvartsman S.Y. Substrate-dependent control of ERK phosphorylation can lead to oscillations. Biophysical J. 2011;101:2572–2581. doi: 10.1016/j.bpj.2011.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning G., Whyte D.B., Martinez R., Hunter T., Sudarsanam S. The protein kinase complement of the human genome. Science. 2002;298:1912–1934. doi: 10.1126/science.1075762. [DOI] [PubMed] [Google Scholar]
- Markevich N.I., Hoek J.B., Kholodenko B.N. Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 2004;164:353–359. doi: 10.1083/jcb.200308060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markevich N.I., Tsyganov M.A., Hoek J.B., Kholodenko B.N. Long-range signaling by phosphoprotein waves arising from bistability in protein kinase cascades. Mol. Syst. Biol. 2006;2:61. doi: 10.1038/msb4100108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martiel J.L., Goldbeter A. Autonomous chaotic behaviour of the slime mould Dictyostelium discoideum predicted by a model for cyclic AMP signalling. Nature. 1985;313:590–592. doi: 10.1038/313590a0. [DOI] [PubMed] [Google Scholar]
- Matsuo T., Yamaguchi S., Mitsui S., Emi A., Shimoda F., Okamura H. Control mechanism of the circadian clock for timing of cell division in vivo. Science. 2003;302:255–259. doi: 10.1126/science.1086271. [DOI] [PubMed] [Google Scholar]
- Miller C.J., Turk B.E. Homing in: mechanisms of substrate targeting by protein kinases. Trends Biochem. Sci. 2018;43:380–394. doi: 10.1016/j.tibs.2018.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray A.W., Kirschner M.W. Cyclin synthesis drives the early embryonic cell cycle. Nature. 1989;339:275–280. doi: 10.1038/339275a0. [DOI] [PubMed] [Google Scholar]
- Nagoshi E., Saini C., Bauer C., Laroche T., Naef F., Schibler U. Circadian gene expression in individual fibroblasts: cell-autonomous and self-sustained oscillators pass time to daughter cells. Cell. 2004;119:693–705. doi: 10.1016/j.cell.2004.11.015. [DOI] [PubMed] [Google Scholar]
- Narasimamurthy R., Hunt S.R., Lu Y., Fustin J.M., Okamura H., Partch C.L., Forger D.B., Kim J.K., Virshup D.M. CK1delta/epsilon protein kinase primes the PER2 circadian phosphoswitch. Proc. Natl. Acad. Sci. U S A. 2018;115:5986–5991. doi: 10.1073/pnas.1721076115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olsen L.F., Degn H. Chaos in an enzyme reaction. Nature. 1977;267:177–178. doi: 10.1038/267177a0. [DOI] [PubMed] [Google Scholar]
- Oosawa F. Spontaneous signal generation in living cells. Bull Math. Biol. 2001;63:643–654. doi: 10.1006/bulm.2001.0236. [DOI] [PubMed] [Google Scholar]
- Oosawa F. Spontaneous activity of living cells. Bio Syst. 2007;88:191–201. doi: 10.1016/j.biosystems.2006.05.006. [DOI] [PubMed] [Google Scholar]
- Ooyama S., Shibata T. Hierarchical organization of noise generates spontaneous signal in Paramecium cell. J. Theor. Biol. 2011;283:1–9. doi: 10.1016/j.jtbi.2011.05.016. [DOI] [PubMed] [Google Scholar]
- Palmeirim I., Henrique D., Ish-Horowicz D., Pourquie O. Avian hairy gene expression identifies a molecular clock linked to vertebrate segmentation and somitogenesis. Cell. 1997;91:639–648. doi: 10.1016/s0092-8674(00)80451-1. [DOI] [PubMed] [Google Scholar]
- Pomerening J.R., Kim S.Y., Ferrell J.E., Jr. Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell. 2005;122:565–578. doi: 10.1016/j.cell.2005.06.016. [DOI] [PubMed] [Google Scholar]
- Pomerening J.R., Sontag E.D., Ferrell J.E., Jr. Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat. Cell Biol. 2003;5:346–351. doi: 10.1038/ncb954. [DOI] [PubMed] [Google Scholar]
- Qiao L., Nachbar R.B., Kevrekidis I.G., Shvartsman S.Y. Bistability and oscillations in the Huang-Ferrell model of MAPK signaling. PLoS Comput. Biol. 2007;3:1819–1826. doi: 10.1371/journal.pcbi.0030184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raskin D.M., de Boer P.A. Rapid pole-to-pole oscillation of a protein required for directing division to the middle of Escherichia coli. Proc. Natl. Acad. Sci. U S A. 1999;96:4971–4976. doi: 10.1073/pnas.96.9.4971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rasmussen R., Jensen M.H., Heltberg M.L. Chaotic dynamics mediate Brain state transitions, driven by changes in extracellular ion concentrations. Cell Syst. 2017;5:591–603 e594. doi: 10.1016/j.cels.2017.11.011. [DOI] [PubMed] [Google Scholar]
- Rust M.J., Markson J.S., Lane W.S., Fisher D.S., O'Shea E.K. Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science. 2007;318:809–812. doi: 10.1126/science.1148596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shankaran H., Ippolito D.L., Chrisler W.B., Resat H., Bollinger N., Opresko L.K., Wiley H.S. Rapid and sustained nuclear-cytoplasmic ERK oscillations induced by epidermal growth factor. Mol. Syst. Biol. 2009;5:332. doi: 10.1038/msb.2009.90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharma K., D'Souza R.C., Tyanova S., Schaab C., Wisniewski J.R., Cox J., Mann M. Ultradeep human phosphoproteome reveals a distinct regulatory nature of Tyr and Ser/Thr-based signaling. Cell Rep. 2014;8:1583–1594. doi: 10.1016/j.celrep.2014.07.036. [DOI] [PubMed] [Google Scholar]
- Shibata T., Ueda M. Noise generation, amplification and propagation in chemotactic signaling systems of living cells. Bio Syst. 2008;93:126–132. doi: 10.1016/j.biosystems.2008.04.003. [DOI] [PubMed] [Google Scholar]
- Shinohara Y., Koyama Y.M., Ukai-Tadenuma M., Hirokawa T., Kikuchi M., Yamada R.G., Ukai H., Fujishima H., Umehara T., Tainaka K. Temperature-sensitive substrate and product binding underlie temperature-compensated phosphorylation in the clock. Mol. Cell. 2017;67:783–798 e720. doi: 10.1016/j.molcel.2017.08.009. [DOI] [PubMed] [Google Scholar]
- Skarda C.A., Freeman W.J. How brains make chaos in order to make sense of the world. Behav. Brain Sci. 1987;10:161–173. [Google Scholar]
- Strogatz S.H. Addison-Wesley Pub.; 1994. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering (Reading, Mass. [Google Scholar]
- Sugai S.S., Ode K.L., Ueda H.R. A design principle for an autonomous post-translational pattern formation. Cell Rep. 2017;19:863–874. doi: 10.1016/j.celrep.2017.03.081. [DOI] [PubMed] [Google Scholar]
- Suwanmajo T., Krishnan J. Mixed mechanisms of multi-site phosphorylation. J. R. Soc. Interface. 2015;12:20141405. doi: 10.1098/rsif.2014.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomson M., Gunawardena J. Unlimited multistability in multisite phosphorylation systems. Nature. 2009;460:274–277. doi: 10.1038/nature08102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ubersax J.A., Ferrell J.E., Jr. Mechanisms of specificity in protein phosphorylation. Nat. Rev. Mol. Cell Biol. 2007;8:530–541. doi: 10.1038/nrm2203. [DOI] [PubMed] [Google Scholar]
- Ueda M., Shibata T. Stochastic signal processing and transduction in chemotactic response of eukaryotic cells. Biophysical J. 2007;93:11–20. doi: 10.1529/biophysj.106.100263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valk E., Venta R., Ord M., Faustova I., Koivomagi M., Loog M. Multistep phosphorylation systems: tunable components of biological signaling circuits. Mol. Biol. Cell. 2014;25:3456–3460. doi: 10.1091/mbc.E14-02-0774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J., Goldbeter A. Multi-rhythmicity generated by coupling two cellular rhythms. J. R. Soc. Interface. 2019;16:20180835. doi: 10.1098/rsif.2018.0835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan J., Goldbeter A. Robust synchronization of the cell cycle and the circadian clock through bidirectional coupling. J. R. Soc. Interface. 2019;16:20190376. doi: 10.1098/rsif.2019.0376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q., Pando B.F., Dong G., Golden S.S., van Oudenaarden A. Circadian gating of the cell cycle revealed in single cyanobacterial cells. Science. 2010;327:1522–1526. doi: 10.1126/science.1181759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshioka-Kobayashi K., Matsumiya M., Niino Y., Isomura A., Kori H., Miyawaki A., Kageyama R. Coupling delay controls synchronized oscillation in the segmentation clock. Nature. 2020;580:119–123. doi: 10.1038/s41586-019-1882-z. [DOI] [PubMed] [Google Scholar]
- Zhou M., Kim J.K., Eng G.W., Forger D.B., Virshup D.M. A Period2 phosphoswitch regulates and temperature compensates circadian period. Mol. Cell. 2015;60:77–88. doi: 10.1016/j.molcel.2015.08.022. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The code generated during this study are available at GitHub https://github.com/DSP-sleep/PT_Chaotic_Oscillators.