Development of New Tuberculosis Drugs: Translation to Regimen Composition for Drug-Sensitive and Multidrug-Resistant Tuberculosis

Abstract

Tuberculosis (TB) kills more people than any other infectious disease. Challenges for developing better treatments include the complex pathology due to within-host immune dynamics, interpatient variability in disease severity and drug pharmacokinetics-pharmacodynamics (PK-PD), and the growing emergence of resistance. Model-informed drug development using quantitative and translational pharmacology has become increasingly recognized as a method capable of drug prioritization and regimen optimization to efficiently progress compounds through TB drug development phases. In this review, we examine translational models and tools, including plasma PK scaling, site-of-disease lesion PK, host-immune and bacteria interplay, combination PK-PD models of multidrug regimens, resistance formation, and integration of data across nonclinical and clinical phases. We propose a workflow that integrates these tools with computational platforms to identify drug combinations that have the potential to accelerate sterilization, reduce relapse rates, and limit the emergence of resistance.

1. INTRODUCTION

With over 1.4 million deaths in 2018, tuberculosis (TB) claimed more lives than any other infectious disease. In addition, 10 million new cases of TB were estimated globally. Though the incidence rate has declined, the cumulative reduction in incidence rate from 2015 to 2018 was only 6.3%, noticeably short of the 20% milestone set by the End TB Strategy for 2020 (1).

First-line treatment can be highly effective against drug-susceptible tuberculosis (DS-TB). In clinical trials, the standard 4-drug, 6-month regimen produces cure rates of over 95% (2–4). However, in practice, this complex regimen often fails to meet these cure rates due to the lengthy duration of therapy, excessive toxicity, and general lack of adherence (5). Furthermore, drug-resistant TB remains a major threat (roughly 500,000 new cases in 2018) (1), highlighting the need for more treatment options.

Fortunately, recent successes in TB drug discovery and development have produced a number of new drug approvals, late-stage drug candidates, and new compounds entering the clinical phases of development (6, 7). This progress has resulted in a new challenge in TB drug development: With many possible combinations, how do development teams prioritize regimens to test in resource- and cost-intensive clinical trials?

Rational selection of new drugs is challenging for several reasons, including the need for multidrug regimens, the challenges inherent in translating nonclinical results into predictions of clinical outcomes, and the lack of consistent biomarkers across development phases (8–15). Large, late-phase clinical trial failures emphasize the need for better tools in the nonclinical and early clinical spaces to address these challenges. Although there is no consensus on a definitive TB drug development pathway, it is clear that efforts spanning all levels of research provide new and distinct insights (8). It is not the lack of data but a lack of data integration across these platforms that remains the greatest challenge in constructing a rationally designed treatment regimen (9).

Quantitative pharmacology and model-informed drug development are recognized as methods to overcome the limitations of individual models and single experiments and combine data derived from multiple platforms (15–19). This review focuses on current approaches to translate nonclinical experiments into safer, shorter treatment for DS-TB and multidrug-resistant tuberculosis (MDR-TB). Specifically, we focus on computational methods spanning empirical, pharmacokinetic-pharmacodynamic (PK-PD), and systems approaches that complement experimental models to strengthen clinical predictions. We discuss tools that are being implemented to address unique challenges in translating between species, and we summarize previous work that uses computational approaches to predict clinical outcome.

2. DATA AVAILABLE FOR MODELING

Nonclinical data form the cornerstone of rational drug selection. Here, we highlight experimental models that are used to inform translational modeling. These experimental models have been extensively reviewed elsewhere (10, 19–21).

2.1. In Vitro

Most TB drug discovery and development programs rely on potency metrics obtained through in vitro assays. In vitro assays are the most rapid approach to determine drug efficacy, and assay parameters can be easily adjusted to test efficacy in different conditions. Traditionally fixed drug concentrations are tested, but assays that use changing, or dynamic, drug concentrations such as the hollow fiber system (HFS) have also been developed.

2.1.1. Fixed concentration assays.

Static concentration growth inhibitory and time-kill assays obtained from high-throughput screening in early discovery are used to calculate PK-PD target calculations in late preclinical development and clinical trial simulations (19). Today, the field is evolving rapidly to design more sophisticated assays that, while still resorting to static concentrations, integrate a variety of growth media and assay conditions to partially recapitulate the microenvironment found at sites of active TB disease (13, 14) and to specifically target persisters (22). The major limitations of static concentration assays are the relatively short testing period, compound instability, and the absence of the dynamic drug exposures seen in vivo. Despite these limitations, one could argue that the two latest additions to the TB drug arsenal, bedaquiline (BDQ) and delamanid, were developed using these potency metrics to support in vivo dose finding and efficacy studies. While these assays have thus proven useful and effective, optimizing new regimens will require more refined approaches and PK-PD translational tools.

2.1.2. Dynamic concentration using the hollow fiber system.

The HFS has been used extensively to test the activity of antibiotics under conditions that simulate a desired PK profile (23). The HFS adds a critical dynamic layer to the in vitro assessment of drug activity, since the shape of the concentration-time profile influences microbial kill rates and resistance emergence (19, 20, 24). Outputs include colony-forming unit (CFU) counts as well as time to positivity (TTP) in the Mycobacteria Growth Indicator Tube culture system, but the model is also amenable to sampling bacterial and host cell products useful for profiling metabolites or gene or protein expression (20). The HFS has recently been qualified by the European Medicines Agency as a predictive nonclinical model for TB drug development (24, 25) and endorsed by the US Food and Drug Administration.

The major limitation of the HFS is the absence of components of the immune response, although it has been adapted to assess the response of Mycobacterium tuberculosis (Mtb) to fluctuating drug concentrations inside of macrophages (26). Additional challenges relate to reproducing drug exposures at the various sites of infection, accounting for highly protein-bound and/or tissue-avid drugs and the tendency of some drugs to bind to system components (19). These issues are particularly relevant to modeling TB treatment, given the heterogeneous pathology and bacterial phenotypes observed and the recent trend toward advancing TB drug candidates with high lipophilicity and other challenging physicochemical and pharmacological traits. For these reasons, the outputs from the HFS and other in vitro systems are best utilized in tandem with outputs from in vivo infection models.

2.2. In Vivo

In vivo models allow assessment of drug efficacy within a complex system that includes the presence of an immune system and physiological processes that contribute to drug exposure. In vivo models can be adapted for longer testing periods than in vitro models, can study multiple bacterial subpopulations at one time, and have more relevant outputs like relapse rates. Here, we discuss three commonly used in vivo models in TB research: mouse, rabbit, and nonhuman primate models.

2.2.1. Mouse models.

Typically, mouse models are used for the first test of efficacy in vivo due to the relatively low logistical requirements, including low costs and ease of handling (10). Although several different inbred and outbred strains are available, experiments using BALB/c mice have provided the largest database for in vivo efficacy studies of TB drugs (27). Data outputs such as bacterial burden (most commonly reported as CFU counts) over time in whole-lung homogenates and the proportion of relapse over time have shown predictive value for determining the efficacy of drug regimens and quantifying exposure-response relationships (14, 15). Comprehensive data sets exist for drugs used as monotherapy and in combination with others (27–33).

In mouse infection models, parameters such as the size of the infectious dose and the length of the incubation period prior to treatment can be modulated to establish distinct infection models with varying bacterial burdens, replication rates, and host immune effects (27, 34). Genetically immune-deficient athymic nude mice, which do not develop an effective adaptive immune response to Mtb infection, have been used to estimate the effect of the adaptive immune response on bacterial number and drug activity. Athymic nude mice require longer treatment durations and are more prone to resistance emergence, suggesting that there is utility in modeling treatment outcomes in the context of advanced immune-compromising conditions (35, 36). As such, the type of infection model (e.g., the inoculum size and incubation period) and the underlying development of the adaptive immune response (e.g., host genetic background) are essential factors determining bacterial burden, survival, and drug response, which in turn can affect the interpretation of the drug’s effect (10, 14, 34).

Despite the spectrum of experimental controls of infection, most mouse strains fail to show caseation necrosis, a hallmark of human TB pathology (20). Therefore, mouse infection models using BALB/c, C57BL/6, Swiss, athymic nude, and other commonly used strains are principally models of intracellular infection. Certain mouse strains have shown a propensity to develop caseating lung lesions upon Mtb infection (e.g., C3HeB/FeJ, Nos2^−/−) and now enable studies of large populations of bacteria residing extracellularly in the necrotic centers of these lesions (37–39) and lesion drug distribution (33, 40). Thus, C3HeB/FeJ and other similar mouse strains provide an economic way to generate lesion-level PK-PD data.

2.2.2. Rabbit model.

The rabbit model of active TB presents multiple pulmonary lesion types, each taking different trajectories over time in response to immune pressure and drug treatment, thus reproducing the dynamic pathology observed in humans (41–43). These aspects allow the rabbit model to be useful in PK-PD and target attainment investigations in plasma and at the site of the disease. Recent technological advances have improved the quantification of lesion-level TB drugs (44’46). Specifically, laser-capture microdissection followed by drug quantitation combines the fully quantitative feature of LCMS (liquid chromatography coupled to mass spectrometry) analysis of tissue homogenate with the high spatial resolution (up to 30–50 mm) of MALDI (matrix-assisted laser desorption/ionization) mass spectrometry imaging. For example, drug levels can be measured in uninvolved lung, the outer cellular rim rich in lymphocytes, the inner cellular rim rich in foamy macrophages, the outer edge of the necrotic core or caseum, and the center of the caseum. Measured drug concentrations can be related to the concentrations required to inhibit growth or kill resident bacterial populations. Extensive plasma and lesion PK data sets are available for rifampin (RIF), isoniazid (INH), pyrazinamide (PZA) (47, 48), and several fluoroquinolones (47, 49–51). Comprehensive data sets, including plasma PK, lesion PK, potency against persisters in caseum, and lesion-centric efficacy measured by CFU counts and chromosome equivalents, are available for PZA (43, 47, 48, 52) and three fluoroquinolones (46).

2.2.3. Nonhuman primate model.

Compared with other animal models, nonhuman primates (NHPs) often closely recapitulate the plasma PK and metabolism of small-molecule drugs in humans. In addition, NHP models best capture most of the disease pathologies seen in human TB. FDG-PET/CT (fluorodeoxyglucose positron emission tomography/computed tomography) has been used to track longitudinal lesion-level responses to immune pressure and drug treatment within the same animal (53–55). When combined with measurements of bacterial burden and drug concentrations in plasma and lesions, PET-CT imaging is a powerful tool for generating plasma-based and lesion-centric PK-PD models. PK and efficacy studies in rhesus and cynomolgus macaques, as well as in marmosets, have delivered comprehensive data sets for metronidazole, RIF and INH (56), several oxazolidinones (57), and the standard four-drug regimen compared to a combination of INH and streptomycin (58). Most live births in marmosets are twins, thus comparison of results from siblings treated with different drugs or regimens allows for direct comparisons that exclude host factors as a source of variability in drug response (59).

3. TRANSLATIONAL APPROACHES: IMPORTANCE, ADVANTAGES, AND DISADVANTAGES

Translational approaches can be divided into two broad categories: empirical and mechanistic (Figure 1). Empirical methods build relationships between variables and outcomes without the need for or an explanation of the mechanism. Conversely, mechanistic models approximate biological phenomena. In drug discovery and development, mechanistic and semi-mechanistic models include integration of relevant physiological and pharmacological relationships between the host, the drug(s), and the bacteria (17, 27). Here, we summarize the approaches and reflect on the potential advantages and disadvantages of each approach.

Figure 1.

Examples of empirical and mechanistic models. (a) Empirical models use a top-down approach to link predictive variables to outcomes. Clemens et al. (64) use in vivo dose-response data and a parabolic response surface to empirically predict effective drug-dose combinations. (b) Mechanistic models use a bottom-up or middle-out approach to recapitulate biological processes. Pienaar et al. (80) simulate host-drug-bacteria dynamics at a molecular level to compare efficacies of fluoroquinolones. Figure adapted with permission from References 64 and 80.

3.1. Empirical (Nonpharmacological) Approach

Empirical models are considered to be simpler models, as they are easier to implement than mechanistic models (60). The era of big data has led to increasing artificial intelligence techniques that provide predictive algorithms and has made empirical approaches highly efficient (61).

A challenge in selecting the best TB drug regimen is the number of experiments required as the number of drugs increases. Using machine learning, Horwitz and colleagues (62) were able to show that multidrug-dose relationships from in vitro assays can be described by a parabolic surface using stepwise regression, which was further optimized by machine-learning algorithms and tested in BALB/c mice (63, 64) (Figure 1). This approach reduced a theoretical 30.5 billion experiments needed to test 14 drugs to only three phases of 85–155 drug-dose combinations at each phase. Although only a narrow range of combinations was tested in mice, one of the selected regimens (clofazimine, BDQ, and PZA) prevented relapse in mice after only 3 weeks of treatment (64), confirming prior evidence of its rapid sterilizing activity in mice (65). Regression analysis methods could also be applied to increasing amounts of in vivo data in efforts to evaluate the predictive accuracy of nonclinical models and to validate an optimized approach to better translate clinical outcomes from nonclinical data.

A limitation to this approach is that extrapolation of nonclinical efficacy data to the human system of disease and clinical outcomes is not straightforward, and drug targets or pathways that are important to translation could be missed. Additionally, a layer of data is lost, as continuous data are not utilized. Integrating changes over time that are essential to describing disease progression and drug cure would require a mechanistic approach.

3.2. Mechanistic (Pharmacological) Approach

Mechanistic approaches that examine drugs at a pharmacological level and may improve the translation of TB drugs are summarized in Figure 2.

Figure 2.

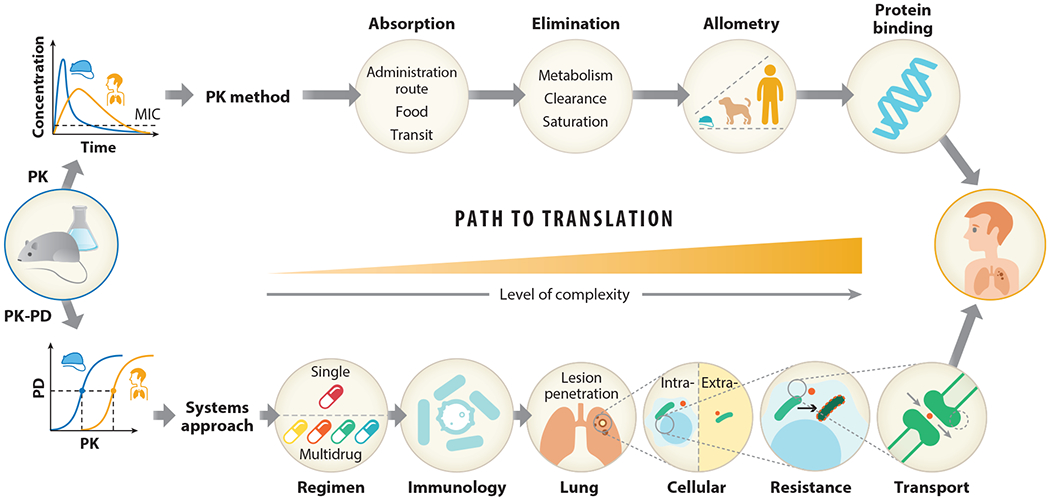
Pathway to translating nonclinical to clinical outcomes for TB. Different pathways exist to translate preclinical to clinical outcomes. Two methods reviewed here include a PK approach and a systems approach. The PK approach can be used to predict equivalent drug exposure between nonclinical models and humans. Here, the assumption is that the outcomes will be comparable between species if drug exposure is matched. However, with the complexity of TB disease, a more systems-like approach may be necessary, as species differences in disease pathology do not capture the full spectrum of outcomes in patients. This approach therefore incorporates host-specific differences and models host-bacteria-drug dynamics at the site of action to make more accurate predictions in patients. Abbreviations: MIC, minimum inhibitory concentration; PK, pharmacokinetics; PD, pharmacodynamics; TB, tuberculosis.

3.2.1. Pharmacokinetics-pharmacodynamics.

Traditionally, PK-PD translation involves identifying the human dose that produces the exposure with demonstrated efficacy in an animal model (13). While this approach gives a broad idea of a safe and effective dose, it relies on strong assumptions, including (a) that scaling between species is predictable and reliable, (b) that the antibacterial effects of the host immune system are equivalent between species, and (c) that drug exposures and effects are not impacted by other drugs through drug-drug interactions. Thus, PK-PD approaches are an attractive option to refine predictions and incorporate additional knowledge.

In general, the purpose of PK-PD studies is to define a relationship between dose and response. With this, PK-PD models can identify the optimal dose and dosing schedule and can simulate alternate regimens. PK-PD modeling has evolved from empirical, descriptive approaches to mechanistic approaches that include properties such as host antimicrobial effects, disease progression, and target site drug distribution (66). The movement toward models with more biological plausibility has improved the predictive accuracy and our ability to extrapolate from them. Mechanism-based PK-PD methods consider time, unlike time-collapsed methods/measures such as AUC, C_max, or time relative to minimum inhibitory concentration (MIC), and reflect gradual killing effects, with changes in concentration as opposed to a binary kill-no kill measure assumed by MIC.

In addition to the time course of drug concentration and response, PK-PD models can include submodels that describe the underlying biological system (66–68). The biological system is the setting in which the drug-bacteria interplay takes place. The primary effect of the biological system is often attributed to the adaptive immune system of the host organism, which can combat the infection and limit growth or reduce bacterial burden without drugs (27, 34). Thus, capturing its effect in a model is critical to establish an uninflated and translatable drug effect (28). Additionally, the heterogeneous lesions of active TB are primarily driven by the immune response (69). These structures add an additional obstacle for drug movement to the site of the disease. Therefore, the time delay for distribution into the site of action is an important component in a PK-PD model.

PK-PD modeling and simulation can substantially reduce uncertainty, time, and cost in high-level decision-making in all phases of development (11, 12, 70). Section 4 of this review highlights both addressable and ongoing challenges in TB drug development that PK-PD modeling can improve, including site-of-disease or lesion PK, immunology, and combination regimens. The translational toolbox is composed of key components that we believe must be implemented in order to accurately translate from nonclinical experiments to clinical outcomes (Figure 3).

Figure 3.

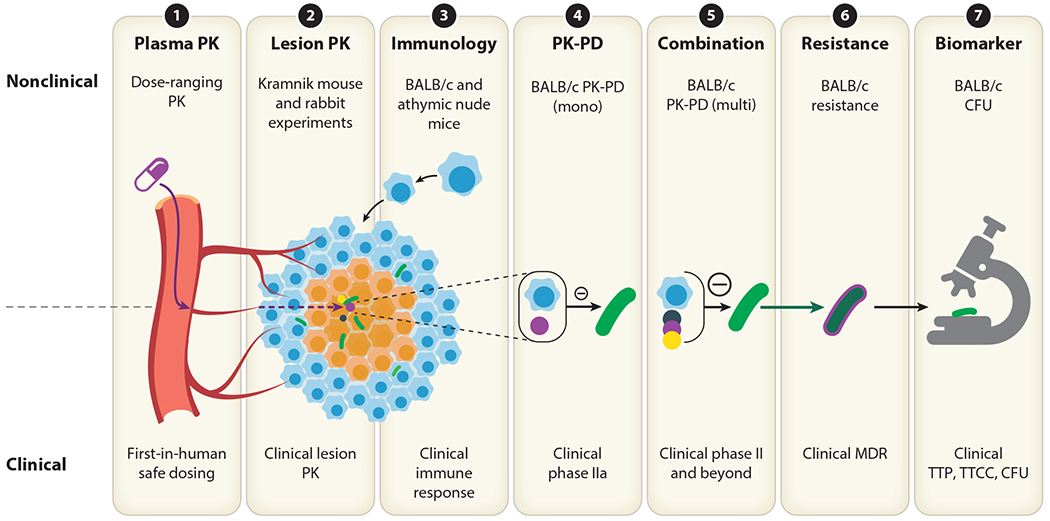
Modeling tools important for a translational platform. Each modeling tool listed is an essential component for predicting clinical outcomes. (①) Plasma pharmacokinetics (PK) studies are a cornerstone to translation. Efficacy, safety, and tissue distribution parameters can be linked to plasma concentration, and plasma PK can inform first-in-human dosing. (②) Lesion PK studies can determine whether a new drug is likely to reach the site of action, including heterogeneous lesions. Mechanistic PK models can simulate predicted levels in patient lesions. (③) Comparing and modeling responses in immune-competent and immune-compromised animal models can predict anticipated differences in host immune response and natural disease progression. (④, ⑤) Monotherapy and combination pharmacokinetics-pharmacodynamics (PK-PD) models link drug concentration to drug effect and are a cornerstone of defining optimal drug combinations. (⑥) Resistance models incorporate mechanisms related to the emergence of resistance to therapy over time. (⑦) Biomarkers of disease progression and treatment response in different species should be aligned using statistical models to link nonclinical and clinical readouts that determine outcome.

3.2.2. Systems pharmacology.

Systems pharmacology models use a bottom-up approach to characterize networks of pharmacology, pathology, and biological systems. The increase in nonclinical data available to TB researchers ranges from in vitro assays to unique animal models, making a quantitative systems pharmacology (QSP) approach useful for integrating data and uncovering optimal therapeutics. Differing time scales; specific sites of disease compartments; immune considerations (71); population PK (72); drug resistance (73); and bacterial dynamics, including intracellular survival and metabolomic changes in bacteria (74), can be integrated using QSP methodology.

Existing systems pharmacology models of TB have focused on the host-bacteria relationship. Kirschner et al. (71) have become the leading group in describing within-host infection, which is summarized in their review. Their systems pharmacology models are capable of describing the spectrum of latent to active TB and account for how patients move between these states (75, 76). These models aim to reconstruct the immune response involved in forming granulomas and has culminated in GranSim, an agent-based model that provides two- and three-dimensional spatial models of the lung parenchyma, immune cells, and their interaction over time (73, 77–81) (Figure 1). This work has further been expanded by other groups to include oxygen dynamics and antibiotic treatment within granulomas and the modeling of the access of drugs and oxygen to bacteria in relation to their distance from blood vessels (82). A multiscale, whole-lung and lymphatic model has been built based on these principles that can integrate heterogeneity similar to that found in patients, potentially leading to the opportunity to consider a cure across multiple sites of infection within the same patient (83).

This work has provided a scaffold to examine factors that limit the efficacy of antimycobacterial drugs and how systems pharmacology models can guide optimization for current and future drugs. Importantly, when building a systems model, care is needed to reduce the model to its essential parts. Large systems models can cause a loss of confidence when they become unwieldy and contain pathways and networks that may not offer real insights.

4. TRANSLATIONAL TOOLBOX

The translational toolbox refers to the essential components for translating nonclinical data to clinical outcomes (Figure 3). In this section, we summarize seven essential components and highlight published work.

4.1. Plasma Pharmacokinetics

Before testing in vivo efficacy of a new compound, developers test oral bioavailability through PK studies (14). Animal plasma PK is essential to determine the potential of a compound to attain reasonable exposures in vivo and, later, to establish PK-PD indices in efficacy studies and determine first-in-human dosing projections. Dose-ranging and dose fractionation studies establish human-equivalent doses, drivers of efficacy, and important nonlinearities in absorption and clearance. Allometric scaling is a weight-based empirical approach to extrapolate animal PK to humans (84). However, protein binding, metabolic pathways, and transport may be species-specific and thus limit the utility of allometric scaling (though renally excreted drugs are generally well predicted). Physiologically based PK modeling (models using parameters based on physiology) improves scaling between species but is much more complex (85). Additional absorption, distribution, metabolism, and excretion studies like human hepatocyte studies to identify drug-drug interactions and investigation of maximal tolerated dose and food effects add insight to drug behavior in patients.

4.2. Lesion Pharmacokinetics

Drug distribution to the site of action has become increasingly appreciated as a core PK-PD determinant (9, 66). Pulmonary lesions begin as cellular granulomas, organized structures made of various immune cell types, and evolve to necrotizing granulomas as a result of host cell and bacterial lysis. Thus, TB lesions are primarily made of two major compartments: cellular and necrotic, the latter being devoid of vascular supply (86). Drugs vary greatly in the manner in which they partition into cellular and necrotic portions of lesions, which can create stark differences in drug exposures between intracellular and extracellular sites of infection (and even into foamy and non-foamy macrophages) in the same lesion and alter PK-PD relationships based on plasma exposure. Differential vascularization and vascular efficiency (87), immune cell types (51), protein binding (88), drug physicochemical properties (89), and interindividual PK variability (90) all affect tissue distribution. In addition, the microenvironments and bacterial phenotypes differ at these sites of infection, which can further alter PK-PD relationships (33, 91, 92). Bacterial populations exhibit differential persistence in the face of immune pressure (93) and drug exposure (52), due to various metabolic and physiologic adaptations to the local environment (22). Mtb isolated from caseum in rabbit lung lesions is profoundly drug tolerant compared to bacteria grown in laboratory media (52).

PK modeling of lesion compartments implements an effect compartment to describe drug distribution from plasma (66),

$$\frac{d{C}_{\mathrm{lesion}}}{dt}={\text{K}}_{\mathrm{pl–lesion}}\left({\text{R}}_{\mathrm{pl–lesion}}\times C_{\mathrm{plasma}}-C_{\mathrm{lesion}}\right),$$ 1.

and has been used to model PK in rabbits (47) as well as in patients undergoing lung resection (90). Moxifloxacin (MFX) was predicted to be the most efficacious fluoroquinolone (80) using these methods, and PZA was demonstrated to be active against Mtb residing in difficult-to-sterilize necrotic lesions (33, 43, 94). Incorporation of differential drug exposure and drug susceptibility in the calculation of lesion-centric PK-PD parameters can improve translation to PK-PD models. Taking lesion-centric PK-PD parameters into consideration could lead to the rational design of combination regimens made of agents that together reach and kill all bacterial populations.

4.3. Immune System Quantification/Bacterial Growth Dynamics

Due to the important role of the host adaptive immune response on impacting treatment effect, various mathematical models have been developed to describe bacterial infection and the resulting immunological responses in animal models of TB (71, 73, 81, 83, 95–98). The enormous amount of data from mouse models of TB has provided great advantages in modeling the bacterial infection and the underlying development of immune responses. In a bacterial growth submodel, the net change in bacterial number (B) over time on growth is described by a one-compartment model with one first-order rate for bacterial replication (K_g) and one first-order rate for natural death (K_d):

$$\frac{dB}{dt}={\text{K}}_{\text{g}}\times B-{\text{K}}_{\text{d}}\times B.$$ 2.

In addition, a logistic function can describe a growth plateau as it approaches a maximum population (B_max) (99–101):

$$\frac{dB}{dt}={\text{K}}_{\text{g}}\times B\times \left(1-\frac{B}{{\text{B}}_{\max }}\right).$$ 3.

The decrease of bacterial replication rate and plateau of bacterial burden are believed to be mainly caused by the onset and development of the adaptive immune response. The impact of the adaptive immune response on bacterial replication was previously described as a nonlinear (sigmoidal) function of bacterial load, with maximal immune effect (Kg) and a bacterial load that stimulates half of the maximal effect (B₅₀) (102–105):

$$\frac{dB}{dt}={\text{K}}_{\text{g}}\times B\times \left(1-\frac{B}{{\text{B}}_{\max }}\right)-\frac{{\text{K}}_{\text{B}}\times B}{{\text{B}}_{50}+B}\times B.$$ 4.

This effect has also been described using a sigmoidal function of time of incubation with maximal immune effect (K_T) and incubation time that stimulates half of the maximal effect (T₅₀) (28):

$$\frac{dB}{dt}={\text{K}}_{\text{g}}\times B\times \left(1-\frac{B}{{\text{B}}_{\max }}\right)-\frac{{\text{K}}_{\text{T}}\times t}{{\text{T}}_{50}+t}\times B.$$ 5.

The effect has been further described by two sigmoidal functions depending on both bacterial number and time of incubation in order to differentiate the immune effect at the same incubation time but with different bacterial load or the effect with the same bacterial load but at different incubation time (27). Considering the evolution of bacterial populations in vivo from actively replicating bacilli to nonreplicating bacilli, this adaptive immune effect is added onto the bacterial growth as an inhibitory effect to slow bacterial replication (27):

$$\frac{dB}{dt}={\text{K}}_{\text{g}}\times B\times \left(1-\frac{{\text{K}}_{\text{B}}\times B^{\gamma B}}{{\text{B}}_{50}^{\gamma B}+B^{\gamma B}}\right)\times \left(1-\frac{{\text{K}}_{\text{T}}\times t^{\gamma \text{T}}}{{\text{T}}_{50}{}^{\gamma \text{T}}+t^{\gamma \text{T}}}\right)-{\text{K}}_{\text{d}}\times B.$$ 6.

Incorporation of the immune system is a critical step in PK-PD modeling. Without it, the drug effect becomes inflated, and the efficacy predictions can be overshot or overly optimistic.

4.4. Pharmacokinetics-Pharmacodynamics

As previously discussed, static MIC does not consider the change in drug exposures over time or in different lesions, while a PK-PD approach does so and can therefore provide better predictions. Clewe et al. (106) developed a multistate tuberculosis pharmacometric (MTP) model based on in vitro time-kill studies. The MTP model consists of three bacterial growth states (fast, slow, and nonmultiplying) and could serve as a framework for accurate characterization of drug effects on different bacterial states. The model was extended by Wicha et al. (107) to successfully predict treatment outcomes in an HFS model, a mouse TB model, and a human phase IIa study.

Establishing PK-PD relationships from in vivo experiments requires integrating the contribution of the immune system. Using BALB/c mouse data, we modeled the interplay between bacterial growth, the adaptive immune response, lung pathology, and TB drugs (28). Our translational model platform includes a quantitative model of the interplay of bacterial growth and immune response, allowing the characterization of the net exposure-response relationships of rifapentine (RPT), RIF, and MFX. This translational PK-PD model adequately predicted long-term outcomes observed in recent clinical trials, including REMox-TB (4) and RIFAQUIN (2). In addition, this model showed that it had the ability to be applied to ongoing trials, in which it predicted minimal risk of relapse at 1 year following 4 months of treatment with high-dose, RPT-containing regimens in TBTC study 31 (NCT02410772; https://clinicaltrials.gov/ct2/show/NCT02410772) and with high-dose, RIF-containing regimens in the RIFASHORT trial (NCT02581527; https://clinicaltrials.gov/ct2/show/NCT02581527). These works illustrate that experimental data, when combined with appropriate considerations of differential bacterial states and the immune system, can improve predictions of clinical outcomes.

4.5. Combination Regimens

Combination therapies are the cornerstone for TB treatment, based on superior efficacy and reduced risk of drug resistance (108). With multiple diverse sites of infection and bacterial subpopulations, it is unlikely that a single drug will ever replace combination therapy.

Much effort has been devoted to exploring the interaction between drug pairs. The most commonly used methods can be summarized as effect based and dose-effect based. Effect-based methods compare the effect resulting from the combination of two drugs (E_AB) directly to the effects of its individual components (E_A, E_B). The Bliss independence model is one of the most popular effect-based methods. It quantifies interaction with a combination index (CI), where the combination effect can be less than (CI >1), similar to (CI = 1) or greater than (CI < 1) the expected additive effect from individual agents (109–111):

$$\mathrm{CI}=\frac{E_{\text{A}}+E_{\text{B}}-E_{\text{A}}{E}_{\text{B}}}{E_{\mathrm{AB}}}.$$ 7.

Alternatively, dose-effect-based methods compare the amount or concentration of each drug that produces the same effect (112) and are based on the mathematical framework known as Loewe additivity (113). Under the assumption that the mathematical relation of single dose A and B to reach the combination effect by pair of doses (a, b) is

$$\frac{a}{\text{A}}+\frac{b}{\text{B}}=1,$$ 8.

CI could be defined as

$$\frac{a}{\text{A}}+\frac{b}{\text{B}}=\mathrm{CI},$$ 9.

where CI > 1 indicates an effect produced by the dose pair (a, b) that is less than the expected effect from additivity. Graphical approaches such as isobologram and response surface analysis are also widely utilized, as they are conceptually straightforward, but crucial drawbacks include difficulties in quantitative interpretation and the inability to use graphical analysis for longitudinal data.

As combinations of three or more drugs are typically administered for TB, an urgent task is to develop an analytical framework for when drug pair analysis cannot be applied. Wood et al. (114) developed a simple equation for drug combinations in Escherichia coli and Staphylococcus aureus, and Zimmer et al. (115) have extended the Bliss independence model in which the effects of all drugs in the mixture are the product of their effective doses (calculated by the model) rather than true doses (dose administered). CI could be evaluated using the ratio of effective and true doses for individual drugs. The general pharmacodynamic interaction (GPDI) model was built on this work and developed for the analysis of TB drug combinations (116). The GPDI model was adapted from a competitive inhibition model (117); however, it uses an estimable interaction term (INT) that allows both positive and negative shift of the PD parameter (EC₅₀):

$$E_{\text{A}}=\frac{{\text{E}}_{\text{maxA}}\times C_{\text{A}}}{\left(\text{E}{\text{C}}_{50\text{A}}\times \left(1+\frac{\text{IN}{\text{T}}_{\text{AB}}\times C_{\text{B}}^{H_{\text{INT},\text{AB}}}}{{{\text{EC}}_{50}}_{\text{INT},\text{AB}}^{{}^{H_{\text{INT},\text{AB}}}}+C_{\text{B}}^{H_{\text{INT},\text{AB}}}}\right)\right)+C_{\text{A}}}.$$ 10.

The GPDI model considers that two drugs could simultaneously be both a perpetrator and victim drug, and thus both positive and negative shifts of EC₅₀ are allowed by the value INT, which could be between −1 and ∞. One of the highlights of the GPDI model is that, for the first time, PD interactions are considered a function of concentration, which could be bidirectional with a change in time. Such a model has been implemented in three- and four-drug combinations (118, 119).

A major limitation to studying drug combinations is the number of experiments required to capture all possible combinations at multiple dose levels. Diagonal measurement of N-way drug interactions (DiaMOND) was recently proposed to address this problem (120). DiaMOND assumes that in a checkerboard assay only regions with the most information about the shape of the contour are needed. Therefore, for a triplet drug interaction, only dose responses of single drugs and the combination 1:1:1 mixtures are required to be sampled for analysis of interactions within the combination, making the DiaMOND method a more efficient method to inform experimental design of drug combinations.

Using these approaches, synergy and antagonism can be established early in development to evaluate the efficacy of novel regimens.

4.6. Drug Resistance Models

Resistance to TB drugs has been an inevitable consequence of clinical usage. Resistance to the new TB drugs BDQ and delamanid has already occurred (121–123). New regimens that are designed to prevent resistance before reaching patients are required.

Two resistance mechanisms can be considered in modeling approaches, namely genetic resistance and phenotypic resistance (drug tolerance). The Mtb genome mutates spontaneously at random, with frequencies ranging between 10⁻⁶ and 10⁻¹⁰ per generation for standard drugs (124). Genetic resistance due to chromosomal mutations leads to acquired MDR-TB and extensively drug-resistant TB. Phenotypic resistance can occur due to epigenetics, protein modification, and metabolic and physiologic reversible adaptations in the presence of drugs and can lead to prolonged treatment and relapse (125, 126). Phenotypic resistance can ultimately promote genetic resistance (121).

To model resistance, in vitro methods can predict the minimum selection concentration of drugs, explained as the minimum concentration at which resistant bacteria are selected for but not killed (127). This work follows the mutant selection window paradigm that hypothesizes that drug-resistant mutants are selected within a window that spans from the MIC of wild-type growth and the upper boundary of concentration-inhibiting growth for the most resistant strains (128, 129). These windows of resistance selection may be pronounced in heterogeneous lesions like granulomas (90, 130, 131), in which differential drug distribution into lesion compartments may result in low drug exposures.

Mechanistic PK-PD models can quantify longitudinal wild-type and resistant bacteria data using genetic and phenotypic principles (102). To model genetic resistance, a preexisting subpopulation model can be used, whereby the resistant compartment is initiated with an estimated fraction of already-resistant bacteria that may have a fitness cost modeled through slower growth (132, 133). Drugs preferentially kill the more drug-sensitive, wild-type bacteria, leading to an increase of the less susceptible bacteria. Different EC₅₀ or E_max values can be estimated for the two subpopulations (134). Alternatively, the appearance of new mutants can be modeled with a first-order rate constant (99, 135). Expansion of this model has included sequential mutations in which bacteria mutate with a relative loss in fitness and then mutate again to regain fitness (136). A similar approach in the GranSim platform is used to model mono-resistance in heterogeneous granulomas (137).

Phenotypic resistant models include adaptive and persister models. For adaptive modeling, changes in E_max, EC₅₀, or growth rate are modeled over time in discrete populations, allowing for a gradually increasing resistant subpopulation that changes the initial mixed population to a homogeneous population that is more difficult to kill (101). Variants of this model include on-off binding to increase or decrease this process in the presence of drugs (138). The persister model uses phenotype switching between a normal-growing population and a slow-growing persister population that is assumed to be responsible for poor outcomes (139).

Multidrug-resistant models likely require additional mechanisms of resistance. The mutation rate of INH+RIF-resistant bacteria has been estimated to be 1,000-fold higher than the respective mono-resistant rates, which suggests that with each resistant generation, bacteria are primed for further resistance (140).

4.7. Biomarkers

While there are many new biomarkers under investigation, animal models of TB and in vitro assays measure bacterial burden by counting CFUs. CFU counts are the gold standard of bacterial burden and are used across historical data to measure and compare new drug performance in clinical development programs (141). Translation of preclinical solid-culture CFU counts to clinically used liquid culture TTP, time to culture conversion (TTCC), and sputum smear tests is necessary to accurately predict patient outcomes in clinical trials.

Animal models study the total population of Mtb in the lung, including bacteria in closed lesions (142), whereas clinical measures use sputum samples from patients that reveal only those bacteria at the surface of lung and cavities and are often discrete or binary measures. A translational model to consolidate these different data types, from different infection sites and possibly measuring different bacterial subpopulations, is required.

Diacon et al. (143) showed that CFU counts can be replaced by faster and less laborious TTP measures to assess early bactericidal activity (144). Models to describe liquid-culture CFU and TTP measurements have revealed negative correlations with a gradient shift to higher bacterial burden in TTP compared to CFU counts at later time points, showing that, over time, the increase in TTP is inflated compared to the decrease of CFU counts (145). Therefore, TTP seems to be able to account for a subpopulation of bacteria not reflected in CFU counts (145, 146). This relationship between CFU counts and TTP in patients was modeled using machine learning with a Gompertz model, which was reported to be the best fit:

$$\log \left(CFU\right)=\frac{TTP-\left(562.318e^{-0.789e^{-{0.195}_t}}\right)}{-64.111e^{-1.002e^{-{0.248}_t}}}.$$ 11.

This model was included in the MTP model discussed under PK-PD tools (106). CFU and TTP values are made available at early clinical trial stages (phase IIa), and TTCC has become an important end point for later-stage trials. Several studies showed that TTCC could be an early predictor of treatment success in drug-resistant TB patients after the first 2 months (147–150). To our knowledge, no study has reported a mathematical relationship between CFU/TTP and TTCC. As one of the most important end points and a potential predictor for resistance, filling the gap between CFU/TTP and TTCC could serve as a powerful translational tool.

5. CONCLUSION

The arsenal of new drugs in the pipeline imposes new challenges for the TB community, and quantitative tools are needed to refine results and predict clinical outcomes with higher confidence. In the wake of clinical trial failures, TB drug developers must utilize lessons learned and find new ways to provide safe, novel regimens for testing in TB patients. Importantly, the growing body of technological and methodological advances should be implemented and integrated. As an essential component to modern drug development, translational modeling serves as a platform to connect experimental data and create networks of knowledge. We believe that the use of the translational tools presented here can build confidence into deciding which regimens should be tested; fill in the gaps of experimental uncertainty; and ultimately produce safe, effective, and novel regimens for testing in TB clinical trials.