Nuclear mechanics within intact cells is regulated by cytoskeletal network and internal nanostructures

Abstract

The mechanical properties of the cellular nucleus are extensively studied as they play a critical role in important processes, such as cell migration, gene transcription, and stem cell differentiation. While the mechanical properties of the isolated nucleus have been tested, we lack measurements about the mechanical behavior of the nucleus within intact cells and specifically about the interplay of internal nuclear components with the intracellular microenvironment, because current testing methods are based on contact and only allow studying the nucleus after isolation from a cell or disruption of cytoskeleton. Here we used all-optical Brillouin microscopy and three-dimensional chemomechanical modeling to investigate the regulation of nuclear mechanics in physiological conditions. We observed that the nuclear modulus can be modulated by epigenetic regulation targeting internal nuclear nanostructures such as lamin A/C and chromatin. We also found nuclear modulus is strongly regulated by cytoskeletal behavior through a robust mechanism conserved in different culturing conditions. Given the active role of cytoskeletal modulation in nearly all cell functions, our work will enable to reveal highly relevant mechanisms of nuclear mechanical regulations in physiological and pathological conditions.

1. Introduction

As the largest organelle of most eukaryotic cells, nucleus is not only a container of genetic material but also a mechanosensor that can respond to external mechanical cues.^[1] Recent progress in mechanobiology has unveiled the critical role of the mechanical properties of the cellular nucleus, suggesting the nuclear mechanics regulates many important functions through mechanotransduction.^{[2, 3]} For example, in cell migration through confined microenvironments, a process central to tissue development, immune cell trafficking and cancer metastasis, the cellular nucleus is thought to act as a mechanical barrier due to its size and stiffness.^[4] Mechanically, it is expected that lower nuclear modulus should favor migration; indeed, it has been found that highly motile tumor cells have softer nuclei than normal cells;^[5] however, the behavior of internal regulators of nuclear stiffness, i.e. lamin A/C and chromatin, suggests a more complex scenario in which both dynamic regulation of nuclear mechanics and external cytoskeletal activity are potentially involved.^{[6, 7]} Although extensive studies have been conducted to understand the physical organization of the nucleus and to reveal mechanically regulated pathways, a direct understanding of the mechanical behavior of the nucleus within intact cells is incomplete, mainly due to the limitation of existing technologies.

The nucleus is mechanically interconnected with the surrounding cytoskeleton;^{[8, 9]} as a result, it is necessary to study nuclear mechanics in its physiological environment. This is however challenging because most of the current techniques need physical contact as they extract the modulus by applying a force on the sample and measuring its deformation, while the nucleus is not physically accessible within a cell.^{[4, 10, 11]} With current technology, either the nucleus is isolated for direct contact or the external force needs to be transmitted through the cell cytoskeleton which can, in turn, induce alterations in the physical properties of both cytoskeleton and nucleus. As a result, while the role of nuclear internal nanostructures (e.g. lamin, chromatin) has been studied thoroughly in isolated nuclei, the effect of the intracellular environment on nuclear mechanics has not been fully captured. Recently, an emerging technique – deformation microscopy – has revealed high-resolution strain maps of cells under deformation in vitro and in vivo, thus providing mechanistic insight into nuclear mechanics with compromised intracellular components, such as lamin A/C and the linker of nucleoskeleton and cytoskeleton complexes.^{[12, 13]} However, because the distribution of deforming loads within a cell is unknown, discriminating the intrinsic role of the nuclear modulus remains difficult.

In this work, we investigated the internal and external regulators of nuclear mechanics within intact live fibroblast cells using both experimental and computational approaches. Experimentally, we used Brillouin microscopy, which can provide direct information on the longitudinal modulus of the nucleus by probing localized light-matter interactions on the scale of ~200 nm. Brillouin microscopy has previously demonstrated non-disturbing characterization of cellular mechanics.^[14-18] Although the rigorous relationship between high-frequency longitudinal modulus, characterized by Brillouin technique, and traditional quasi-static Young’s or shear modulus, obtained with contact-based techniques is not established in soft biological matter, empirically strong correlations have been observed in many physiological and pathologic processes, suggesting the biomechanical changes occurring within cells alter both moduli in the same direction.^{[17, 19, 20]} Here, we validated Brillouin measurements for the characterization of nuclear mechanics and used it to directly quantify the changes of longitudinal modulus of the cellular nucleus in response to both epigenetic regulation and cytoskeletal manipulation. Computationally, to elucidate the underlying factors that regulate nuclear mechanics, we developed a three-dimensional (3D) chemomechanical model^[21] that can describe how cytoskeletal components modulate actomyosin contractility that mediates alterations in nuclear morphologies and modulus.

Using Brillouin microscopy and the chemomechanical modeling, we revealed a comprehensive picture of nuclear mechanics within intact cells regulated by its physical nanostructure and its micromechanical intracellular environment. We found an important role of the intracellular cytoskeletal network on nuclear mechanics, which was predicted by the 3D chemomechanical model and reproduced by experiments with Brillouin microscopy. We further confirmed this cytoskeletal manipulation consistently regulated nuclear mechanics for cells in different microenvironments. Taken together, we revealed that both the nuclear internal nanostructure and the cytoskeletal-nuclear connections can modulate the nuclear modulus in intact cells, which is crucial to understand the role of nuclear mechanics in various cellular functions and activities.

2. Results

2.1. Brillouin characterization of nuclear longitudinal modulus

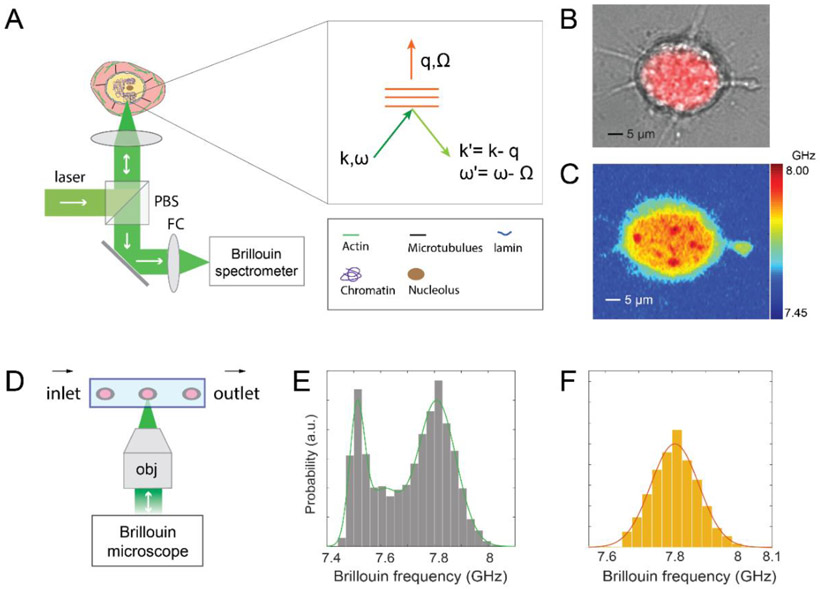
The sub-micron imaging capabilities of Brillouin microscopy are demonstrated in Figure 1. Using only optical means, Brillouin microscope can probe the subcellular components without contact or mechanical perturbation (Figure 1A), which is an ideal tool for quantifying nuclear mechanics of cells in different microenvironments. In this work, the mechanical properties of the cellular nucleus were investigated in both attached and suspended conditions. For attached cells, scanning a sample across the beam focus, a Brillouin map of the mechanical properties of the cell can be obtained (Figure 1B&1C). Brillouin images clearly identify subcellular structures such as cytoplasm and nucleus based on their mechanical properties. For suspended cells, to achieve high throughput measurement, we combined high-resolution Brillouin microscopy with microfluidic device. As a result, we can quantify the intact nuclear mechanics of cell populations as they flow through the microfluidic channel according to our previously established protocol (Figure 1D-1F, Methods).^[16] We approximated the nucleus as an elastic material due to the nearly instantaneous character of our measurements; however, previous experiments have indicated that the nucleus behaves as a viscoelastic material, with both elastic response and time-dependent viscous response.^[1] Given that the viscous relaxation time is on the order of 1-300 s,^{[7, 22]} our elastic treatment is suitable for several cell activities that require long times to occur (e.g. transendothelial migration).^[23] We reported our results in terms of both Brillouin shift and Brillouin-derived longitudinal modulus (Methods).

Figure 1. Characterization of nuclear mechanics with Brillouin technique.

(A) Principle of using a confocal Brillouin microscope to measure nuclear mechanics of a cell. The light red and yellow regions indicate cytoplasm and nucleus, respectively. (inset) the phase-matching condition indicates that the induced Brillouin frequency shift is equal to the frequency (a few GHz) of hypersonic acoustic waves Ω. ω and k represent the frequency and wave vector of incident light, and ω' and k' are the frequency and wave vector of scattered light, respectively. (B) co-registered bright-field and florescent image of a cell with its stained nucleus. (C) corresponding Brillouin image of the same cell. The color bar has a unit of GHz. (D) schematic of Brillouin flow cytometry. (E) original flow data of cell population with the fitting of the histogram’s profile. (F) extracted signature of the nucleus. The details of the data extraction procedure are provided in Methods.

2.2. Brillouin microscopy measurement of epigenetic regulation of nuclear mechanics

The relationship between longitudinal modulus at high frequency, sampled by Brillouin technology, and traditional mechanical moduli in quasi-static conditions is not known for soft matters such as cells and tissue. However, over the past years in several materials (biopolymers, tissue, cell), a high empirical correlation has been found.^[14] Before interpreting Brillouin microscopy as indicators of nuclear modulus, we therefore benchmarked Brillouin signatures to traditional mechanical measurements for known effects. Specifically, we epigenetically modulated internal nano-structural components of the nucleus (e.g. lamin A/C, and chromatin) as their mechanical effects on the nucleus have been previously characterized with gold-standard contact-based mechanical techniques on isolated nuclei.

2.2.1. Decrease of intact nuclear modulus with lamin A/C knockdown

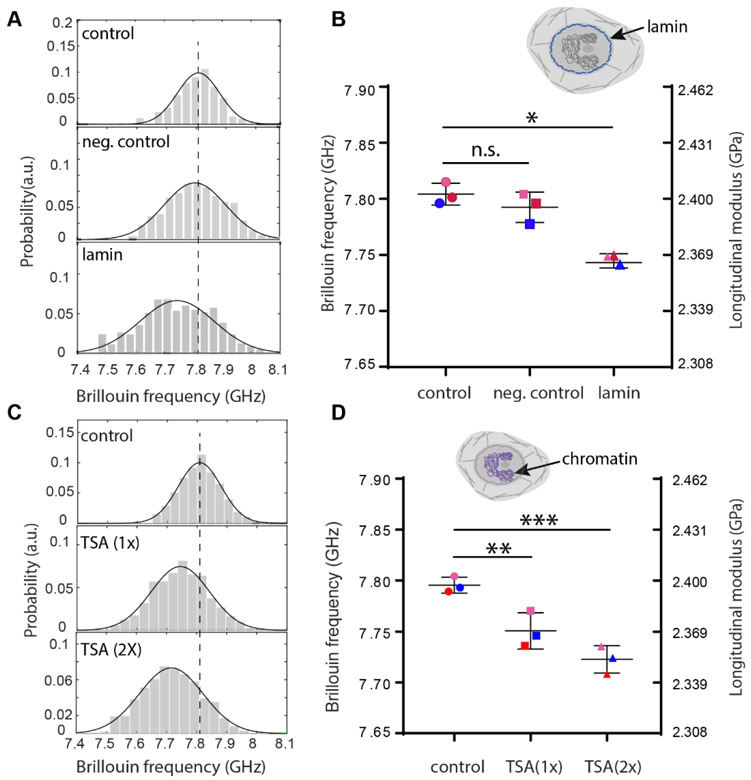
Previous studies have found lamin A/C had a critical influence on the mechanical properties of the nucleus.^{[7, 22, 24]} Here, to study the effect of lamin A/C expression on the nuclear mechanics of intact cells, we used live NIH 3T3 cells and knocked down lamin A/C expression with siGENOME-lamin A/C-control siRNA and DharmaFECT 1 transfection reagent, which silenced lamin A/C genes through RNA interference. As a negative control experiment, a different siRNA with a scrambled sequence (hence no known cellular target) was used to treat the second group of cells. Figure 2A show representative results of nuclear modulus in cell population untreated, treated with scrambled sequence siRNA, and with lamin A/C knocked down, respectively. Successful knockdown was confirmed by immunofluorescent labeling of lamin A/C (Figure S8). The averaged Brillouin shift as well as longitudinal modulus of the intact nucleus showed a statistically significant decrease after lamin A/C knockdown but no statistically significant change with scrambled control (Figure 2B). The measured longitudinal modulus decreased about 1.61%, which would correspond to a ~24% decrease of the Young’s modulus by using a previously established correlation relationship between Brillouin-derived longitudinal modulus and standard elastic moduli^[14] (see Methods); as comparison, previous results on both isolated and intact nuclei with conventional contact-based methods have shown decreases ranging from 33% to 65%, depending on the cell line and knockdown level (Table S1).^{[4, 7, 22, 24-26]} The nuclear modulus decrease upon lamin knockdown was also predicted by our model (see section 3.2.1 and Fig. S8).

Figure 2. Regulation of intact nuclear modulus of suspended cells by epigenetic factors.

(A) Representative flow results of cellular nucleus from control (n=122), negative control (n=195) and knockdown (n=114) groups, respectively after lamin A/C knockdown. Histograms represent measured data and solid curves are fitted results. The dotted line indicates the peak location of the control group. (B) Averaged Brillouin shifts of three repeated groups. Data points show the mean of all independent repeats (n=69, 114, 162 for the second repeat and n=149, 198, 305 for the third repeat, respectively); the bars show the standard deviation. The color of the dots represents different repeated groups. n.s.: not statistically significant. Inset cartoon highlights the structure of lamin in the cell model. (C) Representative flow results of cellular nucleus from control (n=171), 1-unit-dose treatment (n=439) and 2-unit-dose treatment (n=84) groups after chromatin decondensation with trichostatin A (TSA). (D) Averaged Brillouin shifts of three repeated groups (n=117, 319, 220 for the second repeat and n=161, 245, 301 for the third repeat, respectively). Inset cartoon highlights the structure of chromatin in the cell model. *p<0.01. **p<0.02, ***p<0.003. Statistical significance is determined by performing paired t-test with all repeats.

2.2.2. Decrease of intact nuclear modulus with chromatin decondensation

Next, we focused on the main component of the nucleus interior, i.e. chromatin, which packs a histone-DNA complex to prevent DNA damage and control gene expression as well as DNA replication. In numerous cellular activities, chromatin behaviors such as condensation and decondensation crucially affect the mechanical phenotype of the nucleus.^{[6, 22]} To evaluate the effect of chromatin behavior on nuclear mechanics, we used trichostatin A (TSA), an epigenetic modifier that inhibits histone deacetylase (HDAC) and causes chromatin decondensation.^[27] Cells were treated with two different doses of TSA and the corresponding modulus of the nucleus was compared with the control group. Figure 2C shows representative results of nuclear modulus in cell populations untreated, treated with 1 unit and 2 units of TSA, respectively. Figure 2D shows averaged Brillouin shifts from all repeated groups. The longitudinal modulus of the nucleus display dose-dependent decreases upon treatment with TSA, as large as 1.81%. This would correspond to about 27% decreases of the Young’s modulus by using the empirical correlation relationship obtained from cells. Nuclear softening after chromatin decondensation has also been observed in many other cell lines with existing methods, and the relative decreases vary from 26% to 56%, depending on nuclear status, treatment protocol and sensing methods (Table S2).^{[26, 28-31]} The nuclear modulus decrease upon chromatin decondensation was also predicted by our model (see section 3.2.1 and Fig. S9).

Upon epigenetic regulation (i.e. lamin knockdown and chromatin decondensation), the variation of high-frequency longitudinal modulus of the nuclear mechanics measured by Brillouin technique consistently shows the same trend as the Young’s modulus measured by conventional methods at low frequency, indicating the underlying biochemical, physical and/or structural changes in the nucleus affect both moduli in the same direction, as previously demonstrated in cell and tissue measurements.^{[14, 20]}

2.3. Role of cytoskeletal components in nuclear mechanics

2.3.1. Mechanisms of nuclear mechanotransduction

Growing evidence suggests that cytoskeleton-mediated transmission of physical forces from the extracellular matrix (ECM) to the nucleus alters nuclear mechanics and architecture which, in turn, can impact the cell’s ability to sense and respond to its mechanical environment by regulating important nuclear functions like gene expressions in both normal and diseased cells.^[9] To study the mechanisms of force transduction in fibroblasts, we developed a 3D chemomechanical model that accounts for all the key cellular components involved in the transmission of physical signals from the ECM to the nucleus. We first used the model to elucidate the underlying mechanisms through which mechanical forces are transduced from the extracellular environment to the nucleus leading to alterations in the properties of the nucleus. We then used the model and our Brillouin experiments in the next section to show how disruption of cytoskeletal components (e.g., actin filaments and microtubules) can impact the mechanical properties of the nucleus by affecting these signal transmission mechanisms.

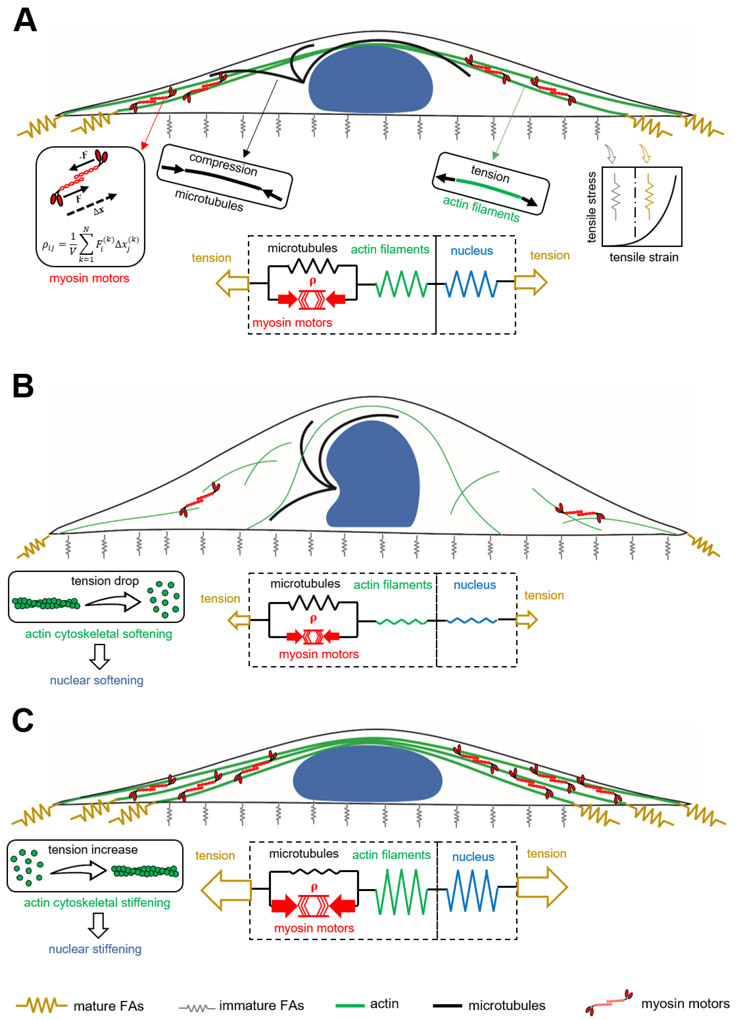
The cytoskeleton in our model is composed of three elements including (i) the myosin motors (active force-generating element), (ii) the microtubule network, and (iii) the actin filament network. As shown in Figure 3A, the contractile force generated by an individual phosphorylated myosin molecular motor can be modeled as a force dipole which is a pair of equal but oppositely directed forces. The spatial density of these force dipoles in our coarse-grained model is treated as a symmetric tensor ρ_ij whose components represent cell contractility in different directions. Starting with isotropic (independent of direction, ρ₁₁ = ρ₂₂ = ρ₃₃) and uniform (independent of spatial location) contractility, our first goal is to determine how the cell contractility ρ_ij changes with physical properties of the microenvironment including substrate stiffness, area, and shape. Note that cells have been shown both experimentally^[32] and theoretically^[33-35] to respond to increases in substrate stiffness and area by promoting actomyosin contractility and generating more contractile forces.

Figure 3. A 3D chemomechanical feedback model for nuclear and cytoskeletal mechanics.

(A) A fibroblast cultured on a large rectangular fibronectin-coated micropatterned substrate. (B) Disruption of actomyosin contractility leads to softening of both cytoskeleton and nucleus. (C) Disruption of the microtubule network promotes actomyosin contractility which, in turn, leads to stiffening of both cytoskeleton and nucleus.

We hypothesize that the average of contractility in all three directions, $\frac{1}{3}{\rho }_{kk}=({\rho }_{11}+{\rho }_{22}+{\rho }_{33})∕3$, is related to the average of stress in the actin filament network, $\frac{1}{3}{\sigma }_{kk}$, and the tension anisotropy, σ_a, as follows

$$\frac{{\rho }_{kk}}{3}=f_m\frac{{\sigma }_{kk}}{3}+f_m{\sigma }_a+f_0{\rho }_0$$ (1)

where this stress-dependent feedback mechanism is regulated by the feedback parameters f_m and f_a (see Supporting Information 1 Section 1). Note that in the absence of tension (σ_kk = 0), f₀ regulates the mean contractility $\frac{1}{3}{\rho }_{kk}$ and relates it to the cell contractility in the quiescent state (initial contractility) ρ₀. As a result of this feedback mechanism, we are able to capture the experimental observations ^{[36, 37]} in which the cell contractility, ρ_ij, the stiffness of the actin network, ${\mathrm{C}}_{ijkl}^{(\mathrm{A})}$, and the stress it carries, σ_ij, increase with substrate stiffness, area, and aspect ratio (Figures S1-S3).

We first use the model to demonstrate the generation of actomyosin contractility in fibroblasts. As the cell is seeded on its adhesive substrate, both contractility ρ_ij and actin network stiffness ${\mathrm{C}}_{ijkl}^{(\mathrm{A})}$ are uniform (independent of spatial location) and isotropic (independent of direction). The adhesion layer in our continuum model (Figures 3A & S4) is treated as a set of initially soft and uniform nonlinear mechanical elements representing the initially weak connections between the cell and its rigid substrate. For an elongated substrate geometry, the initially uniform and isotropic contractility ρ_ij generates a non-uniform and anisotropic stress field on the adhesion layer which experiences higher tensile stresses at the two ends along the long axis of the cell (Figures 3A, S4, S5). In response to these tensile stresses, the adhesion layer stiffens at the two ends representing the stress-dependent formation of mature focal adhesions which connect the cell to its substrate (Figures 3A, S4, S5). The resistance against cell contraction at the mature focal adhesions and the subsequent generation of the local tensile stresses along the long axis of the cell at these mature focal adhesions activate the Rho-Rock and the Ca²⁺ signaling pathways ^[38] which promote myosin phosphorylation and subsequently increase the contractility ρ_ij, anisotropically (Figure S6). The polarization of ρ_ij along the long axis of the cell is accompanied by the polarization of stress in the actin filament network σ_ij (Figure S6) and subsequently stiffening of the actin network ${\mathrm{C}}_{ijkl}^{(\mathrm{A})}$ along the long axis of the cell (Figure S5) capturing the fact that cells respond to tension by increasing their cytoskeleton stiffness through recruitment and alignment of actin filaments in the direction of the tensile stress.^[39]

The model next shows that the increase in actomyosin contractility and the subsequent remodeling of the cytoskeleton can change nuclear morphology and stiffness through cytoskeletal physical links (e.g. stress fibers) that directly transmit the local tensile stresses generated at the mature focal adhesions to the nuclear envelope lamina network . The nucleus is composed of a fibrous thin elastic layer, representing the nuclear lamina network, filled with a linear material which represents chromatin (see Figure S7 and Supporting Information 1 Sections 2 and 3). The model shows that a 60% decrease (corresponding to 66% knockdown of lamin A/C in experiment) in the initial elastic modulus of the nuclear envelope lamina network yields a drop of 26% in the effective elastic modulus (Figure S8E), which is similar as the one extracted from our experiment (24% decrease). In addition, a 60% decrease in the elastic modulus of the chromatin results in a drop of 15.5% in the effective elastic modulus (Figure S9), capturing the nuclear softening extracted from our experiment upon TSA treatment.

The nucleus is assumed to be initially a sphere as the cell is seeded on the substrates. The generation of the polarized contractility and the subsequent formation of stress fibers impose vertical and lateral inward compressive forces on the nuclear envelope which, in turn, cause the nucleus to be flattened and elongated (Figure 4A-4D)^[40]. In addition to these inward traction forces generated by stress fibers, the nuclear envelope is also subjected to outward traction forces from the nuclear interior including (i) the mechanical forces due to the resistance of chromatin against deformation, and (ii) the internal pressure due to fluid content and chromatin decondensation. The inward and outward traction forces are balanced by the mechanical forces generated in the nuclear envelope due to the resistance of the nuclear lamina network against deformation (Figure S7). Our simulations show how the resistance of the lamina network against stretching generates tension in the nuclear envelope as the nucleus deforms from an initially round to an elongated and flattened morphology with the generation of actomyosin contractility in the cytoskeleton (Figure 4A-4D). Since the nuclear envelope is modeled as a fibrous material,^[41] it stiffens in tension to capture the experimentally observed (i) tension stiffening of the lamina network,^[26] and (ii) increase of lamin A/C level with actomyosin contractility which perhaps is required to prevent the nuclear envelope from rupture.^[7] Our simulations show that with developing polarized actomyosin contractility in the cytoskeleton, the nucleus is compressed and it becomes elongated and flattened, while tension is generated in the nuclear envelope lamina. Next, we apply both experimental and computational approaches to test the role of cytoskeletal components on the mechanical phenotypes of the nucleus by disrupting the actin and microtubule networks individually.

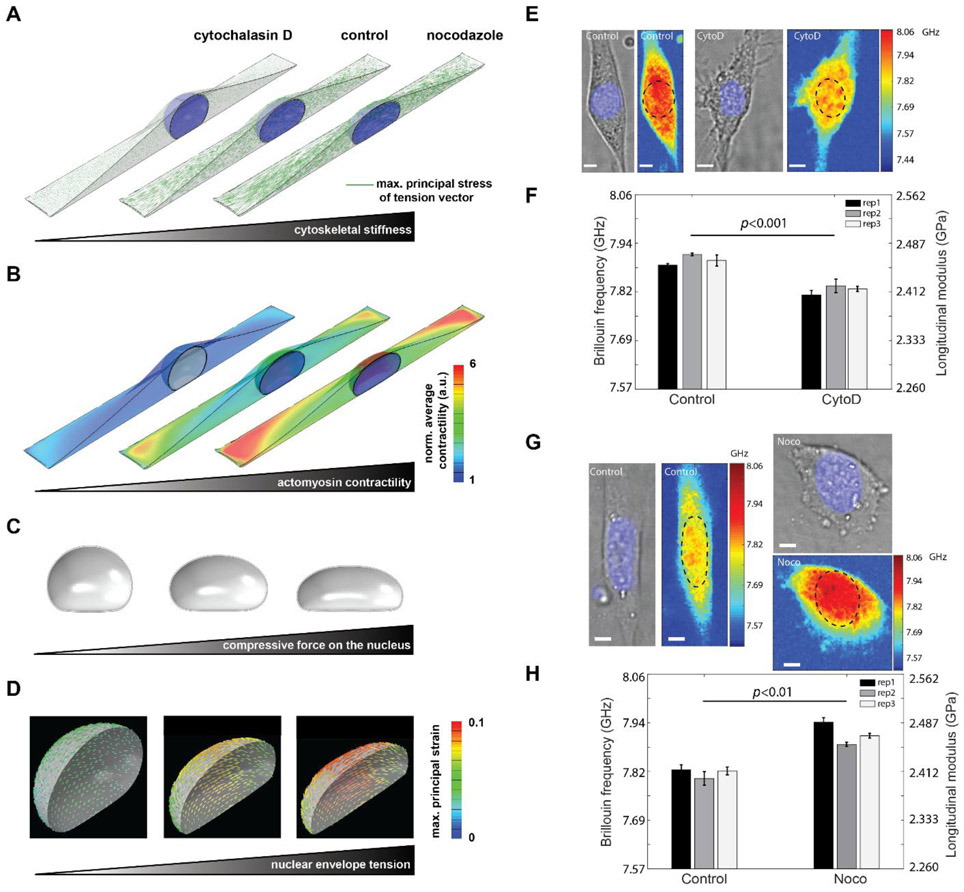
Figure 4. Regulation of intact nuclear moduli of attached cells by cytoskeletal modification.

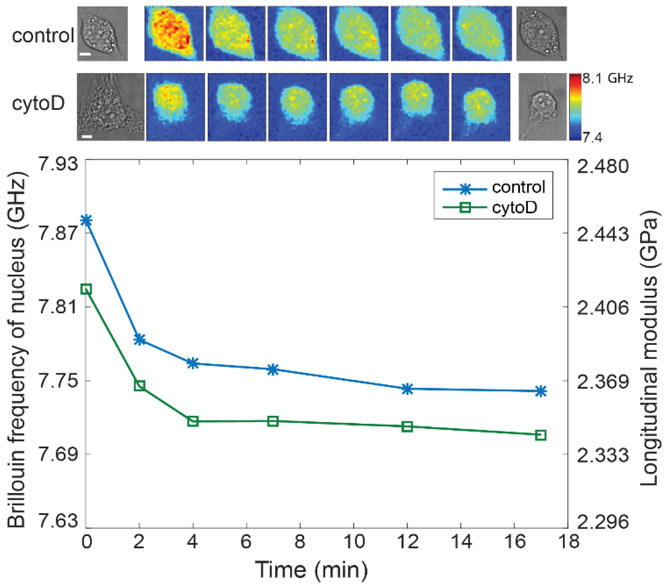
Fibroblasts were simulated on a large rectangular fibronectin-coated micropatterned substrate with a surface area of 1600 μm² and an aspect ratio of 1:5. Simulation results of (A) cytoskeletal stiffness. The green line indicates the maximum principal stress of the tenson vector at each location, and the length represents the amplitude of the stress. (B) actomyosin contractility. The value is normalized to the minimum value. a.u. arbitray unit. (C) compression force. (D) nuclear envelope tension. Our simulations show how disruption of cytoskeletal components (actin filaments and microtubules) upon treatment with CytoD and Nocodazole changes actomyosin contractility and cytoskeletal organizations and subsequently impacts nuclear morphology and the mechanical forces that the nucleus experience. (E) Representative cell images after CytoD treatment in experiment. Colormaps are corresponding Brillouin images. The dashed circle indicates the location of the nucleus. (F) Repeated results of nuclear Brillouin shifts after CytoD treatment in experiment. Colors indicate different experiments. The bar plots indicate the averaged Brillouin shift of the nucleus. The error bar is s.e.m. (G) Representative results of nuclear Brillouin shifts after Nocodazole treatment in experiment. (H) Repeated results of nuclear Brillouin shifts after Nocodazole treatment in experiment. The scale bar is 5μm, and the color bar has a unit of GHz. In each repeat, ≥ 6 cells were measured from both control and treated groups. Statistical significance is determined by the paired t-test of three repeats.

2.3.2. Decrease of intact nuclear moduli of attached cells due to actin depolymerization

Noncontact nature of the Brillouin technology enabled us to directly interrogate the effect of mechanical connection between cellular cytoskeleton and nucleus within intact cells. First, we modulated the actin network by treating NIH 3T3 cells with Cytochalasin D (CytoD), which is frequently used to depolymerize actin filaments. Cells were cultured on a glass bottom dish and stained with DAPI, a blue-fluorescent dye for labeling the nucleus. Confocal fluorescent images clearly show the actin filament was disrupted after CytoD treatment (Figure S10A). Brillouin images and co-registered bright-field/fluorescent images were recorded with Brillouin microscopy and bright-field/fluorescent microscopy, respectively. The averaged modulus of the nucleus can be extracted by co-localizing Brillouin image with fluorescent image, as shown in Figure 4E. After CytoD treatment, the averaged longitudinal modulus of the nucleus decreased about 2.01%, which would correspond to a 30% decrease in the Young’s modulus by using the empirical correlation relationship obtained from cells (Figure 4F). Direct measurements of cytoskeletal-induced regulation of nuclear mechanics are not available for comparison, but previously, a 65% decrease in Young’s modulus of isolated nuclei compared with intact nuclei was observed^[42] by penetrating the cytoskeleton with a needle-equipped AFM instrument. This corroborates the mechanical effect of the actin cytoskeleton on the nucleus shown by our measurements.

To investigate the mechanism behind nuclear softening observed in our experiments upon CytoD treatment, we simulated depolymerization of actin filaments using our 3D chemomechanical model. To this end, we decrease the stiffness of the actin network, ${\mathrm{C}}_{ijkl}^{(\mathrm{A})}$, in our simulations which leads to a significant decrease in cytoskeletal tension (Figure 4A) and subsequently cytoskeletal softening. From our experiment, we calculated the elastic modulus of the cytoskeleton dropped 32% after CytoD treatment (Figure S10). This agrees with the 41% drop predicted by the model (Figure S10C) and other experiments.^[43] Furthermore, our simulations show that the cell contractility ρ_ij significantly decreases with depolymerization of actin filaments (Figure 4B) in agreement with experimental results.^[44] As a result, the actomyosin contractility dependent compressive forces on the nucleus significantly decrease and nuclear height increases (Figure 4C). Finally, as the nucleus becomes round, the nuclear envelope tension is released and subsequently the nuclear envelope lamina network becomes softer (Figure 4D). These simulations show that the nuclear softening observed in our experiments upon CytoD treatment is correlated with the reorganization of cytoskeletal structures and its subsequent release of mechanical forces from the nucleus. This is further shown in Figure S12A where nuclear projected area decreases 5.4% with decreasing actomyosin-dependent compressive forces on the nucleus upon CytoD treatment, which was also captured in the experiment (6.7% decrease).

2.3.3. Increase of intact nuclear moduli of attached cells due to microtubule disruption

Next, we used Brillouin microscopy to measure nuclear modulus of NIH 3T3 cells treated with Noco, which is known to disrupt microtubules. Cells from both control and treated groups were cultured on a polyacrylamide gel substrate with a shear modulus of 16.3 kPa, and the results are shown in Figure 4G & 4H. We observed a significant increase in the modulus of the nucleus after disruption of microtubules. The averaged longitudinal modulus of the nucleus increased about 2.21% after Noco treatment, which would correspond to a 33% increase of the Young’s modulus by using the empirical correlation relationship obtained from cells.

We then simulated depolymerization of microtubules by decreasing the stiffness of the microtubule network $C_{ijkl}^{(MT)}$ as described in Supporting Information 1 Section 1.2. Microtubules are known to experience compressive forces and buckle due to cell contractility.^[45] Buckling of microtubules has been observed to increase (decrease) with increasing (decreasing) cell contractility upon treatment with thrombin (CytoD)^[46]. Consistent with these experimental observations, microtubules in our model bear compression due to the cell contractility ρ_ij, while part of this internally generated stress is transmitted to the nucleus and the ECM through the tensile stress in the actin network, σ_ij, yielding the following force balance equation

$${\rho }_{ij}=-C_{ijkl}^{(MT)}{\epsilon }_{kl}^{(MT)}+{\sigma }_{ij}$$ (2)

where ${\mathrm{C}}_{ijkl}^{(\text{MT})}{\epsilon }_{kl}^{(\text{MT})}$ is the compressive stress in the microtubule network while ${\epsilon }_{kl}^{(\text{MT})}$ is the strain tensor of the microtubule network (Supporting Information 1 Section 1 and Figure S13). Figure 4B shows that depolymerization of microtubules leads to an increase in the cell contractility ρ_ij in our model. The increase in cell contractility is consistent with experimental studies ^[47] where higher levels of phosphorylated myosin light chain (p-MLC) were observed upon depolymerization of microtubules. The experimentally observed increase of cell contractility with depolymerization of microtubules was attributed to the activation of GEF-H1 ^[48] (a RhoA-specific guanine nucleotide exchange factor) where the activated GEF-H1 was observed to promote cell contractility through activation of the Rho-Rock signaling pathway. Our simulations show that the increase in the cell contractility ρ_ij generates higher tension in the actin filament network σ_ij (Figure 4A) and stiffens the actin filament network in the direction of σ_ij representing the formation of stress fibers as experimentally observed.^[49] As a result, actomyosin-driven compressive forces on the nucleus increases, nuclear height decreases, tensile stresses in the nuclear lamina network increase and the nuclear envelope stiffens (Figures 4C&4D). These simulations show that the nuclear stiffening observed in our experiments upon Nocodazole treatment is correlated with the increase in actomyosin contractility and the subsequent remodeling and stiffening of the cytoskeleton which can in turn apply higher mechanical forces to the nucleus through cytoskeletal physical links. In addition, from our experiment, we calculated a 33% increase of cytoskeletal elastic modulus after Nocodazole treatment, which is in agreement with our simulations where we observed 26% stiffening of the cytoskeleton upon microtubule depolymerization (Figure S11). Furthermore, we observed the projection area of the nucleus increased 13% after Nocodazole treatment in experiment, while the simulation predicted an increase of 7% (Figure S12B).

Cellular stiffening after microtubules disruption has been observed by measuring whole cell body with AFM nano-indentation ^[50] and micromanipulated microbeads,^[8] but no study has previously been able to directly quantify the behavior of nuclear mechanics upon cytoskeletal modifications to our knowledge. Together with the data of actin depolymerization, our results depict a mechanical connection between cytoskeleton and nucleus, in which the nucleus is subjected to a complex force field and its elastic modulus will be modulated when the force balance is altered.

2.3.4. Conserved modulation of nuclear mechanics by cytoskeletal factors during cell detachment

Cells can adapt to different microenvironments through cytoskeletal remodeling and thus change the stiffness of cytoskeleton, ^[51] but how the nuclear mechanics will be affected during this process has not been explored yet. The detachment of adherent cells is an important activity in biological processes. For example, epithelial-mesenchymal transition (EMT) has been known to play a crucial role during the embryonic development and tumorigenic progression.^[52] During the process of EMT, epithelial cells lose their polarity and detach from the basement membrane, and eventually become mesenchymal cell phenotype with enhanced migratory capacity and invasiveness. In addition, for stem cell therapy used in regenerative medicine, the adherent stem cells have to be detached from culture substrate and proliferated in suspension, later on transplanted into host tissue . Previous studies have shown that the detachment of adherent cells in vitro by trypsinization will remodel the actin cytoskeleton and thus alter the morphology as well as the mechanical phenotype of cells.^{[53, 54]} Here, we investigated how the cytoskeletal alternation will affect the nucleus mechanics during the course of and after the cell detachment.

Cell detachment with trypsin is known to alter the actin filament thus releases the pre-stress within the cytoskeleton, which is suspected to soften the cells.^[46] For detached cells in suspension, the actin filament will be reorganized into the cortical layer that maintains the elastic strength of the cells.^[55] To test the effect of trypsin during detachment, we used Brillouin microscope to continuously monitor the moduli of individual cells as they were exposed to trypsin (0.25% trypsin+EDTA) (Figure 5 and Figure S14). The time-lapse Brillouin image of a representative cell from the control group (first-row images) indicates both the cytoskeletal and nuclear modulus decreased rapidly within the first 2 minutes right after the trypsin was added. This softening effect continued afterward but slowed down over time. The corresponding longitudinal modulus of the nucleus decreased about 3.03% after 17 minutes (Figure 5, blue curve with asterisk mark), indicating the nucleus was also softened due to the disruption of actin filaments by trypsin. As a comparison, we performed a similar experiment on cells treated with CytoD. The measured results of a representative CytoD-treated cell (Figure 5, second-row images and green curve with square marker) show a similar trend as the untreated cell but with smaller longitudinal modulus. These results suggest that under normal cell culture condition, trypsinization only disrupts a portion of actin filament and the mechanical connection between cytoskeleton and nucleus is still functioning during cell detachment.

Figure 5. Changes of the nuclear modulus of the representative attached 3T3 cells during detachment with trypsin.

The images in the first and second rows on top show the representative cells from control and CytoD-treated groups, respectively. The scale bar is 5 μm, and the color bar has a unit of GHz. The markers indicated the averaged Brillouin shift of the nucleus corresponding to each Brillouin image, and the lines are guides of eye.

2.3.5. Conserved modulation of nuclear mechanics by cytoskeletal factors in suspended microenvironments

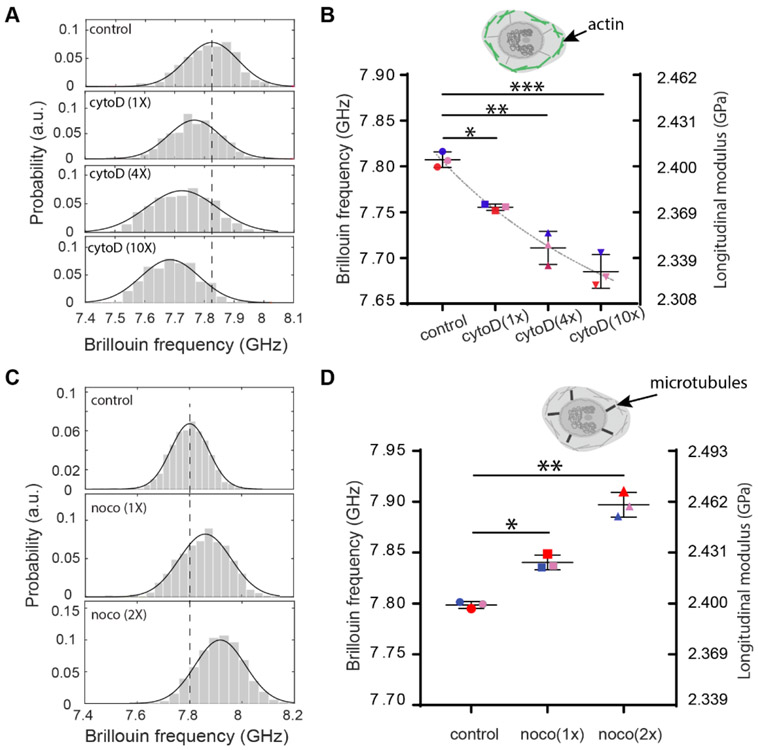
To test the existence of this mechanical connection for cells in suspended microenvironments, we repeated the cytoskeletal manipulation experiments on cells in suspension with Brillouin flow cytometry.^[16] First, we modulated the actin network by treating NIH 3T3 cells with different doses (1X, 4X, and 10X) of CytoD. Similar to the case of attached cells, we observed increasing nuclear softening with increasing doses of CytoD. At the highest dose of 10X (0.5μg mL⁻¹), the average longitudinal modulus of the nucleus dropped 3.22%, which would correspond to ~48% decrease of Young’s modulus (Figures 6A&6B) by using the empirical correlation relationship obtained from cells. We then measured nuclear modulus of NIH 3T3 cells treated with two different doses of Noco. As shown in Figures 6C&6D, we observed an increase in average longitudinal modulus of the nucleus of two groups about 2.55% at highest dose, which corresponds to 38% increases in the Young’s modulus by using the empirical correlation relationship obtained from cells. This indicates dose-dependent stiffening of the nucleus upon disruption of microtubules, which is consistent with the results of attached cells as well as the model prediction.

Figure 6. Regulation of intact nuclear moduli of suspended cells by cytoskeletal modification.

(A) Representative results of cellular nucleus from control (577), 1-unit-dose treatment (n=98), 4-unit-dose treatment (n=279) and 10-unit-dose treatment (n=368) groups after CytoD treatment. Histograms represent measured data and solid curves are fitted results. The dotted line indicates the peak location of the control group. (B) The averaged Brillouin shifts of three repeated groups (n=132, 365, 115, 220 for the second repeat and n=119, 204, 127, 61 for the third repeat, respectively). Data points show the mean of all independent repeats, and the bars show the standard deviation. The colors represent different repeated groups. The dotted line indicates the trend of the decrease. Inset cartoon highlights the structure of cytoskeleton in the cell model. (C) Representative results of cellular nucleus from control (n=349), 1-unit-dose treatment (n=255) and 2-unit-dose treatment (n=371) groups after Nocodazole treatment. (D) The averaged Brillouin shifts of three repeated groups(n=81, 258, 247 for the second repeat and n=390, 106, 172 for the third repeat, respectively). Inset cartoon highlights the structure of microtubules in the cell model. *p<0.02, **p<0.01, and ***p<0.003. Statistical significance is determined by performing paired t-test with all repeats.

In short, we reveal here that the nuclear mechanics can be modulated by the cytoskeletal network for fibroblast cells. Trypsinization during the course of cell detachment would disrupt a portion of the actin filament and thus decreased the overall stiffness of the cell. However, the mechanical connection between cytoskeleton and nucleus maintained and was still functioning for cells in suspended microenvironments.

3. Discussion

3.1. Feasibility of Brillouin technique

We have demonstrated Brillouin microscopy is sensitive to drug-induced perturbation of both nuclear internal structures and cytoskeleton. In many physiological conditions, the changes of nuclear mechanics are comparable to the perturbation induced by dosages used in our experiment. For example, stem cell differentiation involves changes in multiple structural components of the nucleus, including altered expression of lamin A/C. While differentiated cells express lamin A/C, the naïve stem cells do not. Pajerowski et al has shown the nuclear stiffness of naïve stem cells is about 45% of differentiated cells, and this stiffness change can be fully replicated by knocking down lamin A/C with a human-derived epithelial cell line.^[22] In addition, prior to differentiation, pluripotent stem cells comprise a naïve state and a primed state, and the nucleus in the primed state is 25% softer than that in the naïve state due to the histone modification as well as the global decondensation of chromatin. This situation can be mimicked by TSA treatment on stem cells with similar amount of dosage used in our experiment.^[30] Furthermore, nuclear mechanics are highly relevant with many human diseases such as the premature aging disease Hutchinson-Gilford progeria syndrome,^[56] in which the patient nuclei can be more than 50% stiffer than healthy cells possibly due to the accumulation of progerin at the nuclear lamina.^{[57, 58]}

3.2. Current limitations of Brillouin technique

Brillouin microscopy provides a non-contact sensing of high-frequency longitudinal modulus, which is not directly related to the quasi-static Young’s modulus measured by most of the contact-based methods, such as AFM, micropipette aspiration and optical/magnetic tweezers.^[1] However, numerous experiments have confirmed that, for biological samples including cells, strong correlations are found in many physiological and pathologic processes, thus an empirical relation can be established after careful calibration to interpret Brillouin-derived longitudinal modulus in terms of Young’s modulus. The underlying reason can be understood by approximating the biological materials as a mixture of fluid and solid constituents.^[17] As both constituents will be involved in biomechanical changes (e.g. water content changes, polymerization) and affect both longitudinal and Young’s moduli in the same direction, phenomenological correlations can be observed. However, because the contribution of the fluid and solid constituents to the biomechanical changes are sample dependent, a prior calibration is required before correlating two moduli for specific sample.

The spatial resolution of the confocal Brillouin microscope is mainly determined by the voxel size of the focused laser beam, which depends on the numerical aperture of the objective lens used in the experiment. In addition, if the voxel of interest contains more than one material, the overall shape of the Brillouin spectrum will be a combination of Brillouin signatures of all materials inside.^{[59, 60]} In such context, fitting the spectrum with single-peak Lorentzian shape may introduce artefact at the interface of two materials with distinct Brillouin signatures, therefore double-peak fitting could be necessary to remove the artefact. Similar to single-photon confocal microscope, the penetration depth of the Brillouin microscope is limited by the transparency of the sample. For embryonic tissue, Brillouin microscope has been shown to reach the depth of about 200 μm.^[61]

4. Conclusion

We studied the underlying mechanisms that regulate the nuclear mechanics of intact cells upon intracellular modifications using all-optical Brillouin microscopy and 3D chemomechanical modeling. We observed mechanical changes of the nucleus in intact cells due to the epigenetic modulation of nanoscale nuclear components, such as lamin A/C and chromatin. We found an important role of the cytoskeleton on the modulus of the nucleus, which was predicted by our 3D chemomechanical model and reproduced by our experiments with Brillouin microscope, indicating that nuclear mechanics is strongly affected by cytoskeletal behavior. Specifically, our results show that depolymerization of the actin filament network leads to lower nuclear modulus, while disruption of the microtubules leads to higher nuclear modulus. We also demonstrated that cytoskeletal regulation on nuclear mechanics was conserved for cells in different microenvironments. Therefore, the mechanical phenotypes of the nucleus in intact cells are regulated by both the nuclear nanostructure and cytoskeletal network. Since the mechanical phenotypes of the nucleus are relevant to important cell processes through mechanotransduction, our study can help understand intracellular mechanisms that alter nuclear mechanics and thus affect cell functions in various physiological and pathological conditions.

4. Experimental Section

Brillouin instrumentation

Brillouin scattering is an inelastic scattering process analogous to Raman scattering where the incident light undergoes a frequency shift after the interaction with matter. While Raman scattering provides chemical information of material by probing molecular bond vibrations, Brillouin scattering provides high-resolution mechanical information of the material as it is caused by collective motion of molecules on ~200 nm scale in biological materials . This collective motion of molecules can be thought of as microscopic acoustic waves, i.e. periodic and traveling modulation of the density and refractive index of material. When light hits the material, part of it is scattered and experiences a Doppler frequency shift due to the interaction with this propagating hypersonic acoustic wave (Figure 1A). Because the propagation of the acoustic wave is governed by the mechanical properties of the material, measuring the induced frequency shift with a Brillouin spectrometer can provide direct measurement of the material’s longitudinal modulus. Integrated Brillouin spectrometer with a high-resolution optical microscopy modality, Brillouin microscope can sense the localized mechanical properties with sub-micron resolution in 3D.^[14]

We combined a Brillouin microscope with a microfluidic devices to perform population-based measurement with a throughput of ~200 cells per hour. The Brillouin microscope consisted of a high-resolution Brillouin spectrometer and an inverted microscope (IX81, Olympus). A ~10 mW continuous-wave laser (Torus, Laser Quantum, 532 nm) was used to illuminate the sample. The objective lens with effective numerical aperture (NA) of 0.4 (Olympus LUCPLFLN40X) was used to focus the laser beam into a beam spot of 0.8 μm by 0.8 μm by 4.4 μm. The scattered light was collected by the same objective lens and sent into the spectrometer via a single mode fiber (Thorlabs). The Brillouin spectrometer consisted of a two-stage virtually imaged phased arrays (VIPAs) in cross-axis configuration.^{[14, 62]} A PMMA-made microfluidic chip (microfluidic ChipShop, GmbH) was used for the flow experiment. The channel had a size of 150 μm (width) by 50 μm (depth) by 50 mm (length). The inlet of the channel had three sub-channels to achieve sheath flow condition. The chip was installed on the holder stage of the microscope so that the illumination beam can be focused into the channel from its bottom side. A home-built bright-field microscope was installed on top of the chip to monitor the flow status and guide the data acquisition. The prepared cell suspension was first loaded into a syringe and then delivered into the channel by a syringe pump. The flow speed of cells was about 30 μm s⁻¹. During the running of flow experiments, the Brillouin spectrometer was continuously recording spectra at a rate of 20 Hz.

Brillouin images of attached cells were acquired with a confocal Brillouin microscopy that has a similar configuration to the one mentioned above. Attached cells were imaged by point scanning them through the laser spot with a motorized stage. In these 2D imaging experiments, instead of using 532-nm laser source, we used a 660-nm laser with ~20 mW to remove phototoxic^[63] and used an objective lens with NA of 0.7 (Olympus LUCPLFLN60X) to achieve appropriate spatial resolution of 0.58 μm by 0.58 μm by 2.8 μm. The measured Brillouin shift at 660 nm was scaled to 532 nm based on the wavelength relationship. The scanning step size was set as 1μm in trypsin detachment experiments, and 0.5 μm in the rest of the experiments, both with exposure time of 40 ms. Cell viability was checked by monitoring the absence of blebs during and after each experiment.^[63]

Data post-processing

Data post-processing was done with a home written Matlab (MathWorks) program. Each Brillouin scattering peak in the spectrum was fitted to a single-peak Lorentzian shape with a least-squares fitting protocol. The distance of the adjacent Brillouin scattering peaks was used to calculate Brillouin shift. As a cell flows across the focused laser beam, multiple subcellular positions will be sampled by the continuously running Brillouin spectrometer. We first created a histogram (Figure 1E) showing the distribution of Brillouin shifts from the time-trace of the acquired raw data after removing the signature of the medium. This histogram contains mechanical signatures of points sampled in the cellular cytoplasm and the nucleus. The signature of the medium can be identified by flowing and measuring the medium only. The histogram of mechanical signatures of cytoplasm and nucleus were fitted with a linear combination of two Gaussian distributions. Since the cellular nucleus is generally stiffer than cytoplasm, the signature of the nucleus (Figure 1F) can be readily extracted based on the peak location of the fitted curve. The validity of this post-processing method has been previously proven by comparing the extracted result with both 2D images of the cell population and co-localized fluorescent cellular image.^[16]

Calculation of longitudinal modulus from Brillouin shift

The longitudinal modulus M' = Ω_B²·λ²·ρ/4n², where Ω_B is the measured Brillouin frequency shift at backward scattering geometry, λ is the wavelength of the incoming light, n is the refractive index of the sample, and ρ is the mass density. To derive longitudinal modulus M', the ratio of density to index of refraction ρ/n² needs to be known. The refractive index of the nucleus (n=1.354) was taken from the measurement with 3D optical diffraction tomography.[64] Considering the cell as a mixture of liquid medium and solid matters (i.e. proteins), the absolute density of the nucleus can be calculated from the refractive index measurement.[65, 66] Here, with the protein density of 1.37 g/mL,[67] we obtained the density of nucleus as ρ = 1.022 g/mL. The longitudinal modulus of the nucleus was then calculated from the measured Brillouin shift by using constant value of refractive index and density mentioned above. To estimate the longitudinal modulus of the cytoplasm, the constant value for density (1.055 g/mL) and refractive index (1.37) was used. Although both parameters may vary due to condition change, their ratio has been found to be approximately constant in cells.[14]

Estimation of relative change of Young’s modulus with Brillouin-derived longitudinal modulus

Brillouin shift is a direct measure of the high-frequency longitudinal modulus of a sample. For many biological samples, empirically it has been shown that the longitudinal modulus determined by Brillouin shift has a log-log linear relationship to quasi-static Young’s modulus E' through log(M') = a log(E')+b, where the coefficients a and b depend on the material. Thus, the relative changes of Young’s modulus and longitudinal modulus are related by δE'/E' = (1/a)δM'/M'.^[14] For cells, the value of coefficient (a = 0.0671) was obtained by calibration with AFM measurement, which was then used as constant here to estimate the relative change of Young’s modulus based on Brillouin derived longitudinal modulus.

The Brillouin frequency shift can be measured by the Brillouin spectrometer with a precision of 10 MHz at 532 nm. Considering the Brillouin shift of cellular sample is around 7.5 GHz, the relative precision of Brillouin frequency is 0.13%. According to the relationship between longitudinal modulus and Brillouin shift, the relative precision of longitudinal modulus is 0.26%. Further considering the conversion between longitudinal modulus and Young’s modulus, the relative precision of Young’s modulus is about 3.87%.

Cell culture

NIH/3T3 cells with early passage number were used for all the experiments. Cells were purchased from American Type Culture Collection (ATCC^® CRL-1658™); after purchase, cells were frozen at early passage. Fresh cells from stock were cultured in DMEM with 10% fetal calf serum and 1% penicillin-streptomycin at 37°C with 5% CO₂. To prepare cell suspension for flow experiments, cells were detached with 0.25% Trypsin-EDTA (Thermo Fisher Scientific), centrifuged, and re-suspended in a solution of phosphate-buffered saline (PBS) without Mg²⁺ and Ca²⁺ to a final concentration of ~10⁵ to 10⁶ cells per ml. Previous studies show that concomitant with the actin cytoskeleton remodeling, the nuclear volume shrinks quickly and becomes round within ~10 min after detachment.^[54] To eliminate the artifact of trypsin-induced nucleus rounding, ^[22] we started the flow experiments at least ~15 min later after detachment.

Lamin A/C knockdown

Transfection was performed using DharmaFECT 1 (T-2001-01, Dharmacon) following the manufacturer’s recommendations. Briefly, NIH/3T3 cells were seeded in poly-D-lysine (100 μg mL⁻¹) coated 6-well plates at 15,000 cells cm⁻². After 18 hours, cells were rinsed, incubated with transfection medium, and prepared as follows. A 500 nM solution of siGENOME lamin A/C siRNA (D-001050-01-05, Dharmacon) and a solution of 50x diluted DharmaFECT 1 were made with serum-free DMEM, and then combined in a 1:1 ratio. After incubating for 20 minutes, this solution was added to antibiotic-free complete medium (DMEM + 10% fetal calf serum) in a 1:4 ratio to yield transfection medium. After 72 hours incubation with transfection medium, cells from nine wells were harvested and pooled, then immediately assessed with flow cytometry. A non-transfected control and a non-targeting transfection control using siGENOME non-targeting siRNA #1 (GE: D-001210-01-5) were simultaneously prepared.

Immunocytochemistry experiments

Transfection was performed in the same manner as Lamin A/C knockdown, but cells were instead seeded on poly-D-lysine coated glass-bottom dishes at 15,000 cells cm⁻². After the 72 hour incubation, samples were rinsed and directly fixed with 10% neutral buffered formalin for 15 minutes, preserving the attached morphology. Cells were then permeabilized with 0.1% Triton-X 100 for 15 minutes; blocked with 2% BSA for 20 minutes; incubated overnight with mouse anti-lamin A/C (ab8984, Abcam), diluted 1:250; and incubated with goat anti-mouse IgG Alexa fluor 594 conjugate (A-11032, ThermoFisher), diluted 1:500, for one hour. All steps were performed at room temperature, except for incubation with primary antibody at 4°C, and samples were rinsed three times with PBS between each step. Antibody solutions were prepared in 1% BSA.

Chromatin decondensation

1.25 million cells were seeded per T75 flask overnight in complete growth medium. Cells were then incubated at 37°C and 5% CO₂ in complete medium containing 50 (1-unit dose), or 100 (2-unit dose) ng mL⁻¹ trichostatin A (T8552, Sigma Aldrich) for two hours. Following the incubation, the cells were harvested, prepared for the flow experiment as described above, and immediately measured.

Microtubule disruption

For flow experiments, 1.5-1.8 million cells were seeded per T75 flask overnight in a complete growth medium. Cells were then incubated at 37°C and 5% CO₂ in complete medium containing 10 (1-unit dose), or 20 (2-unit dose) μg mL⁻¹ Nocodazole (M1404, Sigma Aldrich) for two hours. Following the incubation, the cells were harvested, prepared for the flow experiment as described above, and immediately measured. For experiments with attached cells, cells were placed on polyacrylamide gel substrate with a shear modulus of 16.3 kPa, and then incubated in complete medium containing 20 μg mL⁻¹ Nocodazole for two hours before imaging. Polyacrylamide gel substrate for cell seeding was prepared as described before.^[14]

Actin filament disruption

For flow experiments, Cytochalasin D (CytoD) powder (C8273, Sigma Aldrich) was resuspended in DMSO to make a stock solution 5 mg mL⁻¹. The stock solution was further diluted in the complete cell medium to 0.05 μg mL⁻¹ (1-unit dose), 0.2 μg mL⁻¹ (4-unit dose), and 0.5 μg mL⁻¹ (10-unit dose) concentrations. For each concentration, a fully confluent T75 flask of 3T3 cells was incubated in the CytoD solution for 30 min. Cells were then harvested and re-suspended in PBS solution before the flow experiment. For experiments with attached cells, we cultured cells on coverslip glass (μ-Dish, Ibidi). Cells were incubated in the CytoD solution with concentration of 0.5 ug mL⁻¹ for 30 min before imaging.