Abstract
The targeted inactivation of individual oncogenes can elicit regression of cancers through a phenomenon called oncogene addiction. Oncogene addiction is mediated by cell-autonomous and immune-dependent mechanisms. Therapeutic resistance to oncogene inactivation leads to recurrence but can be counteracted by immune surveillance. Predicting the timing of resistance will provide valuable insights in developing effective cancer treatments. To provide a quantitative understanding of cancer response to oncogene inactivation, we developed a new 3-compartment mathematical model of oncogene-driven tumor growth, regression and recurrence, and validated the model using a MYC-driven transgenic mouse model of T-cell acute lymphoblastic leukemia. Our mathematical model uses imaging-based measurements of tumor burden to predict the relative number of drug-sensitive and drug-resistant cancer cells in MYC-dependent states. We show natural killer (NK) cell adoptive therapy can delay cancer recurrence by reducing the net-growth rate of drug-resistant cells. Our studies provide a novel way to evaluate combination therapy for personalized cancer treatment.
Subject terms: Oncogenes, Computational models
Introduction
Cancers are initiated by genetic changes that occur in oncogenes and tumor suppressor genes. While many genetic changes are required to establish a tumor, the therapeutic inactivation of a single driver oncogene has been shown to induce significant tumor regression in animal models and human cancers. This dependence of cancers on a single oncogene for their survival is termed oncogene addiction1–4. Oncogene addiction has led to identification of many therapies that target oncogenes including gefitinib for lung adenocarcinomas, trastuzumab for breast cancers, and imatinib for chronic myelogenous leukemia (CML) and gastrointestinal stromal tumors (GIST)1. Despite targeted oncogene inactivation, cancers eventually evolve to develop therapeutic resistance, ultimately resulting in treatment failure and cancer recurrence5,6. It remains unclear how cancers evolve to acquire these mutations to become resistant to therapies and whether these mutant cells are pre-existing or only acquired after therapeutic inactivation.
MYC is a driver oncogene that is overexpressed in a wide range of human cancers, including hematopoietic, breast, liver, colon, ovarian, lung carcinomas, osteosarcomas, glioblastomas, melanoma and myeloid leukemias7,8. MYC is a transcription factor that globally regulates gene expression response to cellular growth, proliferation, metabolism, adhesion, survival and DNA repair, as well as more complex programs such as stemness, angiogenesis and the immune response9–15. As shown in clinically relevant transgenic mouse models, MYC driven cancers are oncogene addicted3,16,17.
Upon MYC inactivation, the majority of tumor cells are eliminated (Fig. 1a). However, MYC oncogene addiction involves both tumor-intrinsic pathways including proliferation arrest, apoptosis, and differentiation, as well as tumor-extrinsic pathways including the shut-down of angiogenesis and cellular senescence, which are processes mediated by the host immune system3,11,16–21. Thus, in the absence of an intact immune system, MYC inactivation fails to elicit complete and sustained tumor regression18,21 and eventually a tumor recurs due to the resistance to MYC inactivation and the restoration of MYC expression22. However, the timing of occurrence of resistance and the frequency of mutation acquisition are difficult to predict during tumor development and treatment.
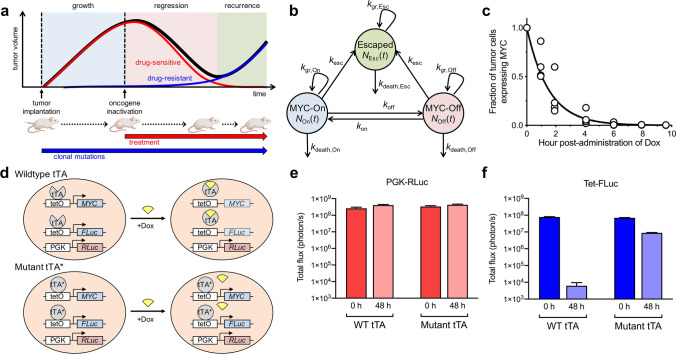
Figure 1.
Combined mathematical model and transgenic mouse model to quantify tumor growth, regression and relapse upon oncogene inactivation. (a) Kinetics of tumor growth, regression and recurrence following treatment-induced oncogene inactivation. (b) Generalizable 3-compartment mathematical model to study drug-sensitive and drug-resistant tumor cell sub-populations following oncogene inactivation. (c) Measurement of the kinetics of MYC inactivation via in vivo tumor biopsy following doxycycline (Dox) treatment. MYC expression was measured by RT-PCR and normalized to the level before treatment. (d) Experimental model used to study oncogene addiction and to measure tumor burden and oncogene expression, based on a conditional MYC-driven mouse model using the Tet-system. Cancer cells were virally transduced with a PGK-RLuc reporter and a Tet-inducible FLuc reporter. In wildtype cancer cells treated with Dox, both MYC and FLuc are inactivated, while RLuc remains active. If the cancer cells acquire a mutation in the tTA region where Dox is binding, the cancer cells become resistant to Dox, enabling MYC and FLuc expression to persist in the tumor. Therefore, RLuc signal was used to measure the total tumor burden and FLuc signal provided an indirect measurement of in vivo MYC expression. (e–f) Examination of RLuc and FLuc reporters in vitro. Luciferase signal was measured in the wildtype cells or in tTA mutant cells in the presence or absence of Dox.
Mutation acquisition and drug resistance cannot be detected easily using non-invasive methods. Molecular imaging has been widely used in animal models and patients to measure tumor burden and to monitor different biological processes including metabolism, apoptosis, and immune cell trafficking non-invasively23,24. However, little information about resistance, including the timing of mutation acquisition and the proportion of drug-sensitive and resistant cells, has been obtained with current imaging approaches. Other methods to detect drug resistance using tissue biopsy are tedious, subject to confounding measures of tumor heterogeneity, and limited by the number of samples. A non-invasive imaging method that provides gross tumor measurements and enables understanding of the mechanisms of drug resistance and tumor recurrence would be valuable.
Mathematical models have been previously used to describe tumor growth, tumor evolution and therapeutic response25–32. In the study of cancer drug resistance, for example, stochastic models have been used to determine the likelihood of whether a cancer will have resistant clones at the time of cancer detection33 or during the patient’s lifetime34,35, but these results are difficult to extrapolate to a specific patient. In contrast, deterministic models have been used to indicate the average number of resistant cells before and after treatment36. We have previously shown that quantitative imaging combined with classifier algorithms may be useful for clinically stratifying cancer patients who may benefit from oncogene-targeted therapeutics25. We now aim to understand how imaging measurements alone may be used to understand the mechanism of oncogene addiction and the kinetics of tumor regression and recurrence.
Here, we develop a new quantitative, biologically validated mathematical model of tumor regression and recurrence upon oncogene inactivation that utilizes imaging-based tumor burden measurements to characterize the emergence of therapeutic resistance. We validated the predicted number of drug-sensitive and drug-resistant tumor cells in a conditional transgenic mouse model of MYC-driven T-cell acute lymphoblastic leukemia (T-ALL) in which MYC expression can be controlled temporally through the tetracycline-regulated system (Tet system)3. By administration of doxycycline, MYC is inactivated quickly and the cancers regress. We used our mathematical model to characterize treatment conditions that lead to regression or recurrence in individual immune-compromised mice. We showed that the adoptive transfer of natural killer (NK) cells, and simulated combination treatments varying the death and growth rates of drug-sensitive and drug-resistant populations, may lead to sustained regression of T-ALL. Our study provides an understanding of the mathematical framework underlying therapeutic resistance and the role of the immune system in this process, which can be employed to evaluate new personalized therapeutic approaches for better cancer treatment in the future.
Results
Development of a compartmental model of oncogene-dependent cancer dynamics
We developed a 3-compartment model that describes the dynamic processes of cancer growth, regression and recurrence following administration of a targeted therapeutic or treatment (drug) that inactivates a key driver oncogene (Fig. 1b, Table 1). The total cancer burden is composed of cancer cells in three mutually exclusive states: (1) drug-sensitive cancer cells in an oncogene-activated state (On); (2) drug-sensitive cancer cells in an oncogene-inactivated state (Off); and (3) drug-resistant cells in a persistent oncogene-activated state (Esc), regardless of the presence of drug. The total number of cancer cells at a given time t is equal to the sum of the number of cells in each state, i.e., NTotal(t) = NOn(t) + NOff(t) + NEsc(t). For the experimental mouse model studied here, we assumed that the number of cells N(t) in each state is correlated with optical imaging signal S(t), i.e., STotal(t) = SOn(t) + SOff(t) + SEsc(t).
Table 1.
Model state variables and parameters.
| Description (units) | |
|---|---|
| State variable | |
| NOn(t) | Number of drug-sensitive cancer cells in On state |
| NOff(t) | Number of drug-sensitive cancer cells in Off state |
| NEsc(t) | Number of drug-resistant cancer cells in Escaped state |
| NTotal(t) | Number of cancer cells in all states |
| SOn(t) | Optical signal (total flux) of drug-sensitive cancer cells in On state (photon/s) |
| SOff(t) | Optical signal (total flux) of drug-sensitive cancer cells in Off state (photon/s) |
| SEsc(t) | Optical signal (total flux) of drug-resistant cancer cells in Escaped state (photon/s) |
| STotal(t) | Optical signal (total flux) of cancer cells in all states (photon/s) |
| Parameter | |
| kgr,On | Growth rate of drug-sensitive cancer cells in On state (day-1) |
| kdeath,On | Death rate of drug-sensitive cancer cells in On state (day-1) |
| knetgr,On | Net-growth rate of drug-sensitive cancer cells in On state (day-1) |
| kgr,Off | Growth rate of drug-sensitive cancer cells in Off state (day-1) |
| kdeath,Off | Death rate of drug-sensitive cancer cells in Off state (day-1) |
| knetdeath,Off | Net-death rate of drug-sensitive cancer cells in Off state (day-1) |
| kgr,Esc | Growth rate of drug-resistant cancer cells in Escaped state (day-1) |
| kdeath,Esc | Death rate of drug-resistant cancer cells in Escaped state (day-1) |
| knetgr,Esc | Net-growth rate of drug-resistant cancer cells in Escaped state (day-1) |
| kEsc,On | Rate of escape of On cells to Escaped state (day-1) |
| kEsc,Off | Rate of escape of Off cells to Escaped state (day-1) |
| kesc | Generalized rate of escape of drug-sensitive cells to Escaped state (day-1) |
| koff | Rate of oncogene inactivation (day-1) |
| NOn(0) | Initial number of drug-sensitive cancer cells in On state |
| NOff(0) | Initial number of drug-sensitive cancer cells in Off state |
| NEsc(0) | Initial number of drug-resistant cancer cells in Escaped state |
| NTotal(0) | Initial number of cancer cells in all states |
| SOn(0) | Initial optical signal (total flux) of drug-sensitive cancer cells in On state (photon/s) |
| SOff(0) | Initial optical signal (total flux) of drug-sensitive cancer cells in Off state (photon/s) |
| SEsc(0) | Initial optical signal (total flux) of drug-resistant cancer cells in Escaped state (photon/s) |
| STotal(0) | Initial optical signal (total flux) of cancer cells in all states (photon/s) |
Cancer cells proliferate or die according to state-dependent growth or death rates, kgr,On, kdeath,On, kgr,Off, kdeath,Off, kgr,Esc and kdeath,Esc. These growth and death rates may be: (a) dependent on oncogene-activation status (e.g., On cells may grow and/or die at the same rate as Esc cells); (b) dependent on drug-sensitivity status (e.g., On cells may grow and/or die at the same rate as Off cells; or (c) independent of cancer state (e.g., each cell state has independent rates of growth and death). Furthermore, these rates may be affected by treatment (drug, radiation, etc.) and/or cancer-immune system interactions.
Only drug-sensitive (On and Off) cells are assumed to be affected by oncogene-targeted therapy. Upon oncogene inactivation, On cells undergo rapid oncogene inactivation to the Off state at rate koff. Upon removal of treatment, Off cells may revert to the On state at rate kon3,19,37,38. Drug-sensitive cells may acquire genetic mutations at rate kesc and become resistant to targeted therapy against the specific oncogene, thereby becoming drug-resistant cells.
The general 3-compartment model consists of a set of ordinary differential equations and is based on the principle of mass balance, in which the change in the number of cells in each state is the summation of the influx of cells into the state minus the efflux of cells from the state. These equations are as follows:
| 1a |
| 1b |
| 1c |
Similar equations may be used if cell state is monitored using optical imaging signal S(t), which has been shown to correlate with tumor cell number39:
| 1d |
| 1e |
| 1f |
All model variables and parameters are summarized in Table 1. We note that this model is generalizable to virtually any driver oncogene and corresponding targeted therapy. The model can be further adapted for other study designs. For example, if a tumor cell population N(t) with growth rate kgr reaches a carrying capacity K due to limited resources, a logistic function can be incorporated, i.e., .
Application of the 3-compartment model to MYC-driven T-cell acute lymphoblastic leukemia
To determine whether a deterministic approach can account for gross changes in tumor burden before and after oncogene inactivation, we adapted the general 3-compartment model to study the doxycycline-mediated inactivation of MYC using Tet-regulated transgenic T-ALL3. To initially reduce the complexity of the model parameter space, we developed a subset (submodel) of the general 3-compartment model (Supplementary Fig. 1a) to describe the following in vivo conditions: (1) the host is an immune-deficient NSG mouse lacking T cells, B cells, and NK cells which would otherwise alter growth and death rates of cancer cells; (2) a known number of T-ALL cells is implanted subcutaneously in the flank of the NSG mouse at a given time; (3) the T-ALL cells can be MYC-inactivated by continued doxycycline administration via drinking water. Validation of this model in a simplified experimental animal setting is ideal because the number of cancer cells in specific states can be monitored using highly sensitive, in vivo bioluminescence imaging (BLI), in which the luminescence produced is proportional to the number of viable cells39. The incorporation of other model features, including immune components and heterogeneous cancer cell types with varying drug sensitivity, can be incorporated later as the appropriate biological data becomes available.
The 3-compartment model for doxycycline-mediated MYC regulation in -ALL is based on the following set of assumptions that correspond to our experimental study:
In the absence of doxycycline, the oncogene inactivation rate koff is assumed negligible (koff = 0), and the cells in the MYC-On state remain activated.
In the presence of doxycycline, the oncogene activation rate kon is assumed negligible (kon = 0), and the cells in the MYC-Off state remain inactivated.
The rate of escape, kesc, is assumed same for both MYC-On and MYC-Off cells, and therefore represents a deterministic (average) rate of escape summarizing the experimental time course being studied.
Cells that have acquired mutations enabling resistance are in an irreversible drug-resistant (Esc) state, and all Esc cells have at least one mutation enabling resistance.
Initial conditions NOff(0) = NEsc(0) = 0 are based on the assumption that all cancer cells are initially in the On state, i.e., NOn(0) > 0. Similarly, SOff(0) = SEsc(0) = S0, where S0 is the non-zero background optical imaging signal.
To reduce the number of parameters, we further simplified the model to include only the net rates of growth or death in each tumor cell state as follows (Supplementary Fig. 1a):
| 2a |
| 2b |
| 2c |
such that MYC-activated states have a positive net-growth rate (i.e., proliferation exceeds death), and that MYC-inactivated states have a positive net-death rate (i.e., death exceeds proliferation). The simplified 3-compartment model (Supplementary Fig. 1a) is the minimal model to account for tumor growth, regression, relapse, as well as the kinetics of MYC inactivation and escape, during the time course of doxycycline treatment. This model can further be reduced to other submodels that account for complete regression (Supplementary Fig. 1b,c).
The initial tumor burden represents the total number of tumor cells in all states at any time t, i.e., NTotal(t) = NOn(t) + NOff(t) + NEsc(t), which has been shown to be proportional to BLI signal39. We assume that there is an imaging resolution threshold (background signal, b) for measuring tumor burden. For clinical imaging, b may be the minimum spatial resolution required to distinguish the smallest lesion (e.g., a pixel or voxel). For in vivo animal optical imaging, b may be a non-zero photon flux acquired in a healthy mouse. We assumed that cancer BLI signal for each state will only be detectable if it surpasses an optical background threshold b = S0.
Measuring rate of MYC inactivation by doxycycline
For the MYC-driven T-ALL, we first measured the rate of oncogene inactivation (koff), which may vary depending on the treatment and dosage. If the rate of oncogene inactivation is much slower relative to cancer cell proliferation, then it may be possible for the MYC-On cells to continue growing before treatment takes effect. Following intraperitoneal administration of doxycycline, we measured the MYC inactivation rate in vivo by acquiring a tissue biopsy of the same tumor at various times and measuring the amount of MYC mRNA via qPCR (Fig. 1c). MYC mRNA was no longer detectable in 99% of T-ALL cells within 6.7 h of doxycycline administration. We calculated the half-time of MYC inactivation (t1/2 = 1.04 h) and the corresponding inactivation rate (koff = (ln 2)/t1/2 = 16.01 day-1), which was significantly faster than the observed cancer cell doubling time (1–2 days). This inactivation rate was assumed to be similar for all mice in our study.
Bioluminescence imaging to monitor cancer growth and oncogene expression
Cancer cells in all states may be monitored quantitatively using real-time non-invasive reporter gene imaging. We chose to use a conditional MYC-driven T-ALL cell line in which MYC is inactivated via the Tet system by administration of doxycycline3,18. We tracked T-ALL cells noninvasively by imaging stable expression of the BLI reporter gene Renilla luciferase (RLuc) under the control of a constitutive PGK promoter40. In the presence of substrate coelenterazine, PGK-RLuc enables tracking of all T-ALL cells noninvasively in vivo, immediately after subcutaneous cell implantation, and before and after doxycycline-mediated MYC inactivation.
To monitor the number of MYC-expressing T-ALL cells, we incorporated a Tet-inducible firefly luciferase reporter (Tet-FLuc, Fig. 1d). Both MYC and FLuc are controlled by the Tet system. Thus, Tet-FLuc reporter enables non-invasive in vivo imaging of MYC expression over time. We generated single-cell clonal populations (clone B11 and E12) of the T-ALL cells dually stably transfected with PGK-RLuc and Tet-FLuc (4188-PGK-RLuc/Tet-FLuc) to enable simultaneous, sensitive monitoring of all T-ALL cells (RLuc) and the MYC-expressing subset (FLuc). We validated the dual-reporter system in vitro and found that while RLuc expression remained high after 48 h of MYC inactivation via doxycycline, FLuc expression decreased 8000-fold (Fig. 1e,f). We have previously shown that tumor recurrence results from the emergence of mutations in the tetracycline transactivator (tTA) region of the Tet system22. Here, we also showed that the mutant tTA cells become doxycycline-resistant and maintain high expression of both MYC and FLuc (Fig. 1e,f). Therefore, using the Tet-regulated system and dual-luciferase labeled cells, we were able to monitor total tumor burden (RLuc) and MYC expression (FLuc) at any given time by in vivo imaging.
We next examined how the timing of MYC inactivation contributed to recurrence or complete regression by administering doxycycline either: (a) when the tumor was already large (0.8 cm3); or (b) when the tumor was small (immediately after T-ALL cell injection). For each treatment scenario, we fitted the 3-compartment model to measurements of total tumor volume (RLuc signal) to estimate rates of tumor growth (knetgr,On, knetgr,Esc,), death (knetdeath,Off,), and oncogene escape (kesc). Each treatment scenario is described below and parameter estimates are provided in the Supplementary Tables 1–10.
Modeling cancer recurrence after MYC inactivation
When large tumors were treated with doxycycline to inactivate MYC (Fig. 2a–h), RLuc measurements showed that tumor initially regressed but ultimately recurred (Fig. 2a,b). The 3-compartment model fitted well to total tumor burden data (Fig. 2c,d) and indicated that tumor net-growth and net-death rates were similar between mice (Fig. 3a and Supplementary Tables). The rate of MYC escape (kesc), however, differed by several log orders between mice in the same treatment group (e.g., ranging from 3.41 × 10–11 to 2.18 × 10–7 day−1 in Supplementary Table 10), suggesting a mutation event occurring in as few as 20 million cells per day and a diverse mutation frequency even in cancers initiated by a single clonal population of cells in genetically identical subjects (Fig. 3a). We note that kesc was estimable with a high degree of uncertainty (112–721% CV, Supplementary Tables 4–7,10), which is difficult to validate non-invasively in the same mouse. The net-growth rates of the doxycycline-resistant population were estimable with reasonable precision (13–53% CV, Supplementary Tables 4–7,10). Therefore, the 3-compartment model was able to characterize which doxycycline-resistant cell populations were fast-growing (e.g., 1.4-day doubling time for NSG18) or slow-growing (e.g., 2.1-day doubling time for NSG37). This suggested that although measurements of gross tumor burden cannot be used to distinguish a specific rate of mutation acquisition for a given mouse, the model is capable of determining which clones are aggressive.
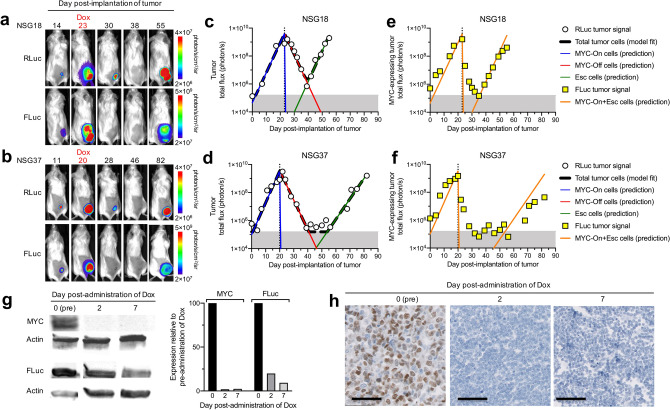
Figure 2.
Modeling in vivo bioluminescence imaging (BLI) measurements of tumor burden in mice with recurring tumors. (a, b) BLI of PGK-RLuc and Tet-FLuc signals in two representative NSG mice treated with doxycycline (Dox) on (a) day 23 or (b) day 20 after tumor transplantation. (c–f) Quantitative analysis of the RLuc and FLuc signals from (a, b). (c, d) The simplified 3-compartment model was fitted (dashed black line) to RLuc signal (white circles), shown superimposed with the predicted population of MYC-On cells (blue line), MYC-Off cells (red line), and Escaped cells (green line). Shaded grey region (below 1.60 × 105 photon/s) indicates imaging signal is below the limit of detection. (e, f) The model-predicted MYC-expressing tumor cell population (orange line) superimposed with Tet-FLuc signal (yellow squares). (g) Western blot of MYC and FLuc protein expression in the tumors collected before, or 2 or 7 days after MYC inactivation. (h) Immunohistochemistry staining of MYC in the tumors collected before, or 2 or 7 days after MYC inactivation. Scale bar is 50 µm.
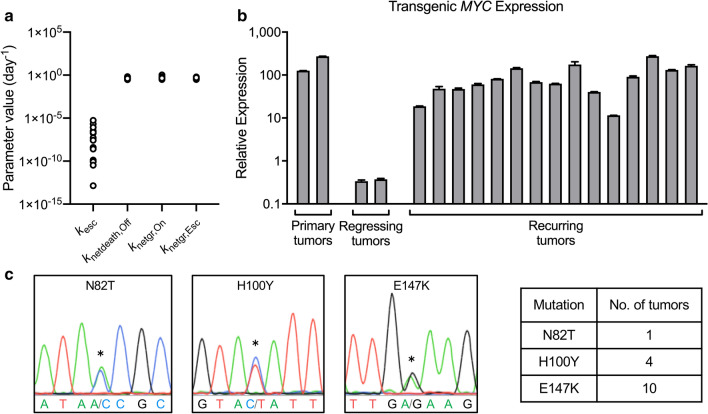
Figure 3.
Quantitative analysis of tumor growth, death, and escape rates and associated tTA mutations. (a) Summary of parameter estimates from n = 15 mice with tumor recurrence: kesc (day−1), knetdeath,Off (day−1), knetgr,On (day−1), knetgr,Esc (day−1). (b) Transgenic MYC expression measured by qPCR showed that every recurring tumor exhibited high transgenic MYC expression. (c) Example chromatograms and table summarizing the N82T, H100Y and E147K mutations detected in the recurring tumors.
We used the model’s estimated parameter values for each mouse to predict the amount of tumor burden in the doxycycline-sensitive (MYC-On and MYC-Off) and doxycycline-resistant (Escaped) states. As a single clonal cancer population, we assumed all cells were initially in a doxycycline-sensitive MYC-On state (blue curve, Fig. 2c,d, Supplementary Fig. 2). Doxycycline administration quickly converted MYC-On cells to a doxycycline-sensitive MYC-Off state (red curve, Fig. 2c,d, Supplementary Fig. 2). The model predicted that 4188-PGK-RLuc/Tet-FLuc cells acquired resistance to MYC inactivation (green curves in Fig. 2c,d and Supplementary Fig. 2) and became imaging-detectable (green curve exceeded the grey shaded region) as early as day 22 in some mice (e.g., NSG17, Supplementary Fig. 2) and as late as day 53 in others (e.g., NSG37, Fig. 2). Furthermore, the model suggested that these Escaped cells could have been detected in these mice as early as day 17 and 45, respectively, if the imaging limit of detection were improved 15-fold (lowered to 1 × 104 photon/s). Therefore, with only a gross BLI measurement of tumor burden, the model can be used to predict the number of drug-sensitive cancer cells at any time. This information is not easily obtained via an invasive biopsy and may be useful for evaluating the efficacy of a MYC-targeted drug.
To validate the 3-compartment model structure, we compared the predicted proportion of cells expressing MYC (orange curve, Fig. 2e,f, Supplementary Fig. 2) to in vivo measurements of MYC expression. For all mice, the model predicted that the MYC-expressing population regressed immediately. However, the FLuc signal lingered for 2–7 days post-administration of doxycycline. We hypothesized that the remaining Tet-FLuc signal was the result of accumulated trace leftover FLuc signal in millions of cancer cells. To confirm this, we measured MYC and FLuc protein levels in excised treated tumors collected before, and at 2 and 7 days after doxycycline administration (Fig. 2g, Supplementary Fig. 3). MYC was quickly inactivated, as the model predicted, which is consistent with our earlier in vivo measurements (Fig. 1c), while FLuc expression decreased at a slower rate consistent with our BLI measurements (Fig. 2e,f). The inactivation of MYC was further confirmed by immunohistochemical staining of MYC in these excised tumors (Fig. 2h). Therefore, based on our Tet-FLuc measurements and protein expression data, we validated that the model-predicted kinetics of the MYC-expressing cell population were highly reflective of the in vivo cell state.
We next examined the mechanism of cancer recurrence in the transgenic T-ALL mouse model. Our previous work demonstrated that recurrence occurs through the restoration of MYC expression and mutation of the doxycycline-responsive tet-repressor (tetR) domain of tTA22. We measured the transgenic MYC expression in all the recurring tumors and sequenced the tTA region. All tumor samples (n = 15) showed high expression of transgenic MYC compared to regressing tumors (Fig. 3b) and exhibited at least one of three different mutations (N82T, H100Y, E147K) corresponding to the tetR domain of tTA, consistent with our previous reports22 (Fig. 3c).
Modeling cancer regression after MYC inactivation
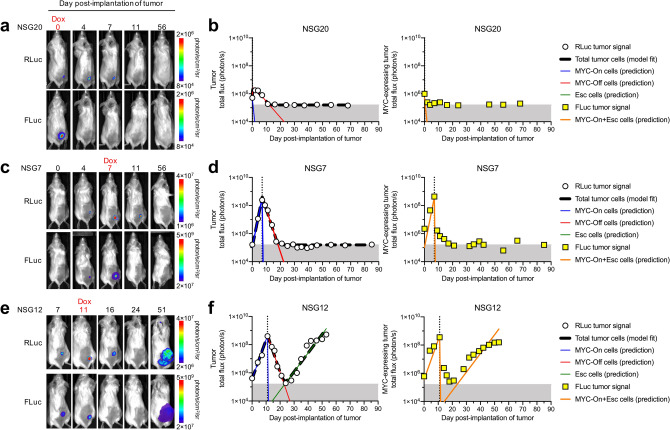
We hypothesized that earlier treatment of the cancers prior to mutation acquisition would increase the likelihood of complete regression. To test this, we inactivated MYC in separate sets of mice at various times post-implantation of cancer cells and used subsets of the 3-compartment model (Supplementary Fig. 1b,c) to describe each mouse’s RLuc measurements of total tumor burden (Fig. 4 and Supplementary Figs. 4, 5). We found that when cancers were treated on the day of implantation or up to 7 days post-implantation, all cancers regressed completely (Fig. 4a–d and Supplementary Figs. 4, 5). We observed when treatment was administered as late as 11 days post-implantation of cells, 2 of 3 cancers relapsed (Fig. 4e,f and Supplementary Figs. 4, 5). This suggests that for the T-ALL 4188-PGK-RLuc/Tet-FLuc cells, complete regression may be best achieved when treatment is initiated during the first week of cancer growth.
Figure 4.
Bioluminescence imaging (BLI) of PGK-RLuc and Tet-FLuc signals in three representative NSG mice treated with doxycycline (Dox) on (a, b) day 0, (c, d) day 7, or (e, f) day 11 after tumor transplantation. (b, d, f) The simplified 3-compartment model was fitted (dashed black line) to RLuc signal (white circles), shown superimposed with the predicted population of MYC-On cells (blue line), MYC-Off cells (red line), and Escaped cells (green line). Shaded grey region (below 1.60 × 105 photon/s) indicates imaging signal is below the limit of detection. The model-predicted MYC-expressing tumor cell population (orange line) is shown superimposed with Tet-FLuc signal (yellow squares).
Model-predicted therapeutic effect of natural killer (NK) cells
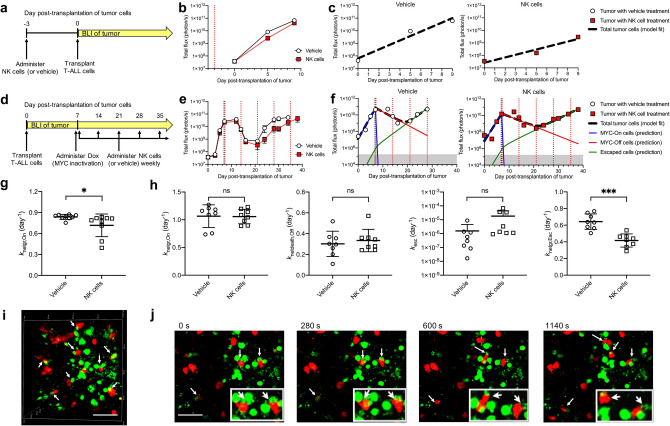
The 3-compartment model serves as a quantitative framework to study how immune cells may alter the kinetics of tumor growth and death. We applied our mathematical model to study how NK cells affect cancer progression and treatment (Fig. 5). We have recently shown that NK cells can alter the fate of MYC-driven cancers41. Here, we first examined the net growth and death rates of cancer cells in the presence and absence of NK cells in immune-deficient NSG mice (Fig. 5a, Supplementary Fig. 6). Compared to the mice without NK cell transfer, the mice receiving syngeneic NK cell (CD3− NKp46+) adoptive transfer 3 days before T-ALL transplantation showed significantly slower cancer growth (0.72 vs. 0.84 day−1, p < 0.04 using an unpaired t-test, Fig. 5b,c,g). We further validated this using intravital microscopic (IVM) imaging. We visualized NK cells (red, derived from mCherry transgenic mice) infiltrating in the tumor microenvironment and actively attacking cancer cells (green, labeled with PGK-GFP) in real time in live mice (Fig. 5i–j, Supplementary Videos 1–2).
Figure 5.
Bioluminescence imaging (BLI) and mathematical modeling analysis showed NK cells delayed (a–c) tumor growth and (d–f) recurrence. (a) NK cells were adoptively transferred 3 days before intravenous T-ALL-FLuc cell transplantation. (b) FLuc measurement of tumor burden in mice with or without NK cell transfer (mean ± SEM of n = 9 mice per group). (c) Representative growth curve for a mouse without or with NK cell transfer. (d) T-ALL-FLuc cells were intravenously transplanted into NSG mice on day 0. On day 7, doxycycline (Dox) was administered. Either NK cells or a saline control were transferred on day 7 and weekly thereafter. (e) BLI measurement of tumor burden in mice with or without NK cell transfer (mean ± SEM of n = 8 mice per group). (f) Examples of model fits to BLI measurements in representative mice without or with NK cell transfer. The simplified 3-compartment model was fitted (dashed black line) to FLuc data (white circles), shown superimposed with the predicted population of MYC-On cells (blue line), MYC-Off cells (red line), and Escaped cells (green line). Shaded grey region (below 1.60 × 105 photon/s) indicates imaging signal is below the limit of detection. (g) Comparison of knet,growth,On in mice shown in (a–c). *p < 0.05. (h) Comparison of the parameter estimates for mice shown in (d–f). ***p < 0.0001. (i–j) Intravital microscopic imaging showed NK cells (mCherry-labeled, red) attacking T-ALL cells (GFP-labeled, green). (i) 3D imaging of interactions of NK cells and tumor cells. (j) Time-lapse imaging showed NK cells (red) actively attacking T-ALL cells (green). Zoomed-in images are shown n inset. Interactions of NK cells and tumor cells are indicated by white arrows. Scale bar = 20 µm.
We then used the 3-compartment model to examine the potential changes in net-growth and net-death rates of the cancer cells following repeated weekly NK-cell adoptive transfer during cancer regression and recurrence (Fig. 5d–f, Supplementary Fig. 7). In this experiment, NK cells were adoptively transferred on the day of MYC inactivation and then weekly thereafter. As measured via BLI, cancer recurrence was delayed in the mice that received NK cell transfer compared to mice receiving a saline control. We found that mice receiving NK-cell adoptive transfer showed slower post-treatment net growth rates (0.42 vs. 0.64 day−1, p < 0.0001 using an unpaired t-test, Fig. 5h). These results demonstrated that NK cell-based therapy may be particularly effective against MYC-driven lymphoma. NK cell adoptive therapy after MYC inactivation did not significantly impact the pre-treatment net growth (knetgr,On), post-treatment net death (knetdeath,Off), or escape (kesc) rates, suggesting that knetdeath,Off is primarily controlled by autonomous processes such as apoptosis and proliferative arrest, and kesc is independent of NK cell interactions (Fig. 5h).
Model-based simulations to sustain cancer regression using oncogene-targeted therapeutics
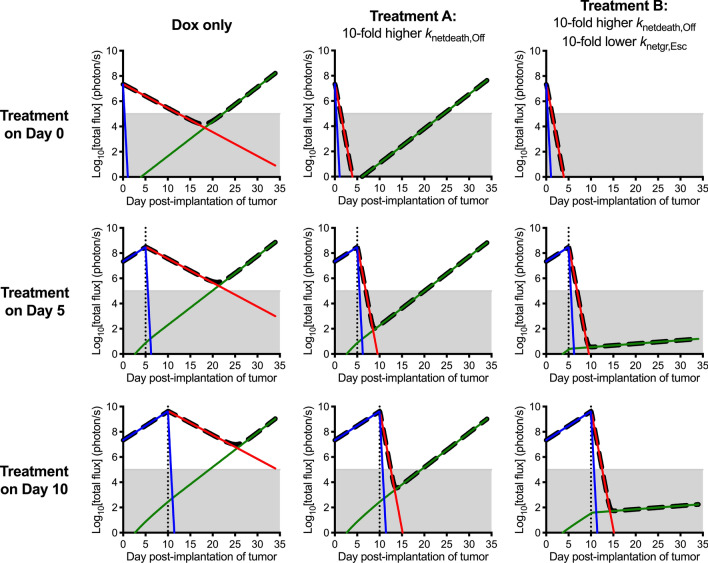
We next used the 3-compartment model and mean values of the optimized parameter estimates (Fig. 3a) to simulate later-stage (50-fold larger) cancers and the potential effectiveness of other therapeutic strategies (Fig. 6). These strategies include starting treatment at an earlier time and leveraging treatments that decrease the growth rate and increase the death rate of drug-sensitive cancer cells. The model indicated that sustained cancer regression is difficult to achieve in the absence of the immune system ven if MYC is inactivated arly(e.g., at diagnosis). In contrast, a hypothetical treatment (Treatment A) that increases the death rate of drug-sensitive cells by tenfold may prolong the emergence of a resistant cell population, but the model suggests that even then the cancer eventually recurs. Ultimately a single drug or panel of drugs (Treatment B) that utilizes a combined approach of increasing drug-sensitive cell death and decreasing drug-resistant growth would effectively prolong recurrence. These examples illustrate the potential ability of a biologically validated mathematical model to simulate the effects of timing and combinations of treatments (chemotherapy, adoptive cell therapy) to optimize sustained regression. Therefore, the model may help quantitatively evaluate the potential role of candidate therapies and immune effectors to target MYC and other oncogenes during the process of cancer growth and regression.
Figure 6.
Comparison of doxycycline (Dox) treatment to two hypothetical treatments for a simulated lesion of 1 × 107 T-ALL cells. Shown are the MYC-On (blue), MYC-Off (red), and Escaped (green) cell populations following a one-time treatment dosing on the indicated day. Shaded grey region indicates tumor burden not detectable with imaging. Treatment A has a tenfold higher knetdeath,Off relative to Dox, and Treatment B has a tenfold higher knetdeath,Off and tenfold lower knetgr,Esc relative to Dox.
Discussion
We established and validated a new 3-compartment model that quantifies the expression levels of a driver oncogene such as MYC in individuals with an oncogene-addicted cancer. The model used imaging-based measurements of tumor burden, which can be commonly obtained in the clinic, to quantify the kinetics of cancer growth, regression, and recurrence in various treatment stages of an individual’s cancer, and to characterize the emergence and progression of resistant clones. The mathematical model can quantify the effectiveness of novel drugs or treatments such as NK cell adoptive transfer, which we showed delayed cancer recurrence by slowing down the net-growth rate of resistant tumor cells. Our approach can aid in the design and evaluation of optimal treatment regimens involving single or combined oncogene-targeted strategies with the incorporation of immune-based therapies.
Our mathematical model quantitatively links the mechanism of oncogene inactivation to cancer response in a transgenic MYC-driven cancer. We have reported that oncogene addiction involves both autonomous and immune-dependent mechanisms3,11,16–21. Cancers recurred due to mutation and restoration of MYC in the immune-deficient host22. Our mathematical model showed that even cancers derived from a single clonal cell in genetically identical hosts can acquire therapeutic resistance at drastically different rates, suggesting that mutation acquisition occurs stochastically among individuals. The kinetics of cancer regression were highly dependent on cancer intrinsic changes, but the clearance of the resistant cell population likely requires the immune system18,21. We quantified the rate at which NK cells eliminate treatment-resistant cancer cells, which may help optimize NK-cell therapy to further reduce cancer recurrence (Fig. 5). Other immune components such as CD4+ T cells are also required to eradicate cancer recurrence by different mechanisms18,21. This suggests that combination targeted and immune therapies may best reduce cancer recurrence, and our mathematical model provides a new way to analyze these outcomes quantitatively for each therapy.
The 3-compartment model is the minimal model needed to describe the mechanisms of oncogene inactivation and mutation acquisition and provides a fundamental quantitative starting point to study how the immune system may affect the success of a cancer treatment. We will focus next on incorporating additional compartments into the minimal model to account for regulatory effects of the immune system, including NK cells, CD4+ and CD8+ T-cells, and macrophages18,20,21,41. We are developing new imaging techniques to track different immune populations such as activated T cells and NK cells in vivo42–46. Novel and specific imaging probes can now visualize and quantify cellular changes including proliferation47, apoptosis48 and senescence49. The development of more sophisticated mathematical models is becoming possible with advancements in functional and anatomical imaging modalities that boast improved temporal and spatial resolution23,24. These mathematical models may eventually describe the spatial heterogeneity of the tumor microenvironment and include stochastic cellular processes that are critical for small tumors (birth, death, and clonal evolution of cells).
The predictive capability of any computational model is limited to the data at hand but can be refined using more sensitive imaging and detection methods that boast higher temporal and spatial resolution. For example, in this study, we used BLI to measure disease burden of a mouse model of T-ALL. The development of advanced biomedical imaging techniques to monitor immune cell trafficking will enable further biological and kinetic studies of tumor regression and recurrence in animals and patients. Machine learning-based approaches are now becoming capable of predicting patient relapse at the time of diagnosis50, by leveraging extensive data sets involving thousands of measurements to train and validate the model. As state-of-the-art genomic and proteomic methods evolve in the decades to come, thereby enabling the detection and monitoring of early mutations in cancer, we envision that mechanistic modeling and artificial intelligence-based approaches may be integrated to understand, improve and predict the outcome of personalized medicine approaches.
We utilized experimentally validated biological hypotheses underlying oncogene addiction to develop a general mechanistic model that may now aid in the design, evaluation, and analysis of personalized therapeutics in many ways. First, our model can be adapted for other driver oncogenes, oncogene-addicted cancers, and targeted therapeutics. Second, our model can simulate potential treatment options or combinations of treatments including immune therapy, to identify the optimal timing and dosage for a given individual, based on experimentally validated and mechanistically modeled concepts of oncogene addiction. These treatments may include new targeted therapies, alone or in combination with adoptive immunotherapy, and will be critical for establishing the success of personalized medicine.
Methods
Cloning and cell culture
The conditional murine T-ALL cell line 4188 was derived from SRα-tTA/Tet-O-MYC mice. The cells were cultured in RPMI 1640 medium (Invitrogen) supplemented with 10% fetal bovine serum, 1% Anti-Anti and 50 µM 2-mercaptoethanol (Sigma-Aldrich). MYC was inactivated with doxycycline (20 ng/ml, Sigma-Aldrich, T7660).
The RLuc sequence was cloned into a pMSCV retroviral vector (Clontech, CA). The Tet-inducible luciferase reporter (Tet-3G-Fluc) was purchased from Clontech. Virus production and infection were performed as previously described17. Retrovirus was produced using the Phoenix retroviral packaging system (ATCC, VA). Lentivirus was produced using HEK293T cells (ATCC, VA). Leukemia cells were spin infected and selected with geneticin (400 µg/ml) and puromycin (2 µg/ml). Two single cell clones (B11 and E12) were finally selected for further in vivo experiments.
Tumor transplantation and in vivo bioluminescence imaging
The generation and characterization of the Tet-system transgenic lines of conditional expression of MYC have been described3. We subcutaneously transplanted 2 × 105 PGK-RLuc- and Tet-FLuc-labeled MYC T-ALL cells (clone B11 or E12) in the flanks of 4- to 8-week-old NSG mice (n = 38). At specified times, or when the tumors reached a volume of 0.8 cm3, MYC was inactivated to induce tumor regression by treating mice with doxycycline (100 μg/ml i.p. injection on the first day and in drinking water (100 μg/ml) in the following days). The processes of tumor growth, regression and recurrence were monitored via bioluminescence imaging (BLI) of RLuc expression. MYC expression was monitored indirectly via BLI of Tet-FLuc expression. All BLI measurements were acquired using the Ami system (Spectral Instruments Imaging). For each mouse, RLuc substrate coelenterazine (50 µg in 150 µl saline) was injected intravenously and images were acquired immediately. Six hours later, FLuc substrate D-luciferin (33 mg/ml, 100 μl) was injected intraperitoneally and images were acquired after 10 min. BLI signals were quantified using Aura software (Spectral Instruments Imaging).
Compared to RLuc, FLuc has a longer emission wavelength and is therefore brighter and more efficient in penetrating light through tissue. To address this quantitatively, the minimum and range of signal for both FLuc and RLuc were calculated for each mouse and then averaged for each group of mice studied. The FLuc signal was normalized to the RLuc range using the following equation:
| 3 |
where FLuc1(t) is the raw FLuc signal at time t; FLuc2(t) is the normalized FLuc signal at time t; FLucmin and RLucmin are the minimum detected FLuc and RLuc signals, respectively; and FLucrange and RLucrange are the differences between the maximum and minimum FLuc and RLuc signals, respectively.
We performed in vivo RLuc and FLuc imaging on healthy mice (n = 10 age-matched mice without tumor xenografts) to determine the limit of detection of bioluminescence signal (1.58 × 105 photon/s for RLuc; 1.64 × 105 photon/s for FLuc). We defined any signal above 1.60 × 105 photon/s to be imaging-detectable.
For the experiments with NK cell adoptive transfer, syngeneic NK cells were isolated from FVB/N mice (4–8 weeks old) by magnetic activated cell sorting with a NK cell selection kit (Miltenyi Biotec). Flow cytometry was performed to confirm the purity of the isolated NK cells. We intravenously injected 3 × 106 PGK-FLuc labeled T-ALL cells (line 4188) into 4- to 8-week-old NSG mice (n = 16). Tumor engraftment was monitored by BLI. All mice were treated with doxycycline to inactivate MYC 7 days post-transplantation of tumor cells. Eight of 16 mice were subjected to adoptive transfer of NK cells (1 × 106 week). In another experiment, one dose of NK cells (1 × 106 cells) was adoptively transferred 3 days before tumor transplantation to evaluate the role of NK cells in tumor growth.
All animal experiments were approved by Stanford University's Administrative Panel on Laboratory Animal Care (APLAC) and were performed in accordance with institutional and national guidelines.
Quantification of MYC mRNA using qPCR and Sanger sequencing of relapsed tumors
To measure the kinetics of MYC inactivation in vivo, mice were treated with doxycycline by intraperitoneal injection (100 μg/ml) when tumor volume reached 0.8 cm3. Samples were collected from the same tumor at 0, 1, 2, 4, 6, 8, and 10 h post-injection of doxycycline. To examine the levels of transgenic MYC in relapsed tumors, all tumor tissue was excised and collected at each experimental endpoint. Total mRNA was extracted from the tumor samples and relapsed tumors using an RNA extraction kit (RNeasy Mini Kit, Qiagen). Transgenic MYC mRNA expression was measured in triplicate using SYBR-based quantitative PCR and measurements were normalized to Ubiquitin C (UBC) mRNA levels. The primers used for transgenic MYC were: MYC-F, GGTCACACCCTTCTCCCTTC; MYC-R, AGCAGCTCGGTCACCATC.
To check whether the recurring tumors acquired mutations in the tTA gene, we excised all recurring tumors and extracted genomic DNA with a DNA extraction kit (NucleoSpin Tissue, Macherey–Nagel). The tTA region was amplified by PCR from genomic DNA using the Herculase II Fusion kit and directly sequenced in Stanford PAN facility (F-primer, CCTCAGTGGATGTTGCCTTT; R-primer, CCTGCACCTGAGGAGTGAAT).
Western blotting and immunohistochemistry staining
Proteins were extracted using Bicine/CHAPS lysis buffer. Lysates were then separated via gel electrophoresis (Bio-Rad) and transferred to PVDF membranes using standard protocols. MYC and FLuc protein levels were detected using an anti-MYC (ab32072, Abcam)51 or anti-FLuc (ab21176, Abcam)52 antibody, respectively. The blot was imaged using a LI-COR scanner and analyzed by ImageJ.
Paraffin-embedded tumor sections were deparaffinized by successive incubation in xylene, 95% ethanol, 90% ethanol, and 70% ethanol, followed by PBS. Epitopes were unmasked by steaming in DAKO antigen retrieval solution for 45 min and then rinsed twice in PBS. The sections were blocked using DAKO blocking solution, and then immunostained overnight at 4 °C using primary antibodies (MYC, 1:150, Epitomics). Sections were then washed with PBS and incubated with biotinylated anti-rabbit IgG (1:300, Vector Labs) for 30 min at room temperature, then with the ABC kit (Vector Labs) for 30 min at room temperature. Sections were developed using 3,3′-diaminobenzidine (DAB, Vector Labs), counterstained with hematoxylin, and mounted with Permount. Images were obtained on a Philips Ultrafast Scanner.
Intravital microscopic imaging (IVM)
Syngeneic NK cells were isolated from 4- to 6-week-old CAG-mCherry mice by magnetic activated cell sorting with a NK cell selection kit (Miltenyi Biotec). Adoptive transfer of 1 × 106 NK cells to NSG mice was performed 3 days before tumor transplantation. For IVM imaging, dorsal skinfold chamber surgery was performed according to an established protocol53. Then 2 × 106 GFP-labeled MYC T-ALL cells (line 4188) were transplanted subcutaneously in the chamber. After 4 days, tumor cells and NK cells were imaged simultaneously in vivo under a multiphoton microscope (Nikon A1 MP +) using a 10 × water immersion objective.
Model fitting and parameter estimation
All model fits and simulations were performed using the simulation, analysis and modeling software SAAM II (The Epsilon Group). For the T-ALL experimental data studied here, the 3-compartment model used for curve fitting consisted of Eqs. 1d, 1e, 1f, 2a, 2b, and 2c, with kon = 0, and is depicted schematically in Supplementary Fig. 1a. Briefly, the rate of MYC inactivation (koff) was estimated by fitting a monoexponential decay function to MYC expression data measured by RT-PCR (Fig. 1c). Then, for each mouse, Eqs. 1d, 1e, 1f, 2a, 2b, and 2c were fitted to the total tumor BLI signal (e.g., RLuc total flux, shown in Supplementary Figs. 2, 4, 5, and 6) to estimate rate constants knetgr,On, knetgr,Esc, knetdeath,Off and kesc. Best fitted curves were shown as black dashed lines (e.g., Fig. 2c for NSG mouse #18). Optimal parameter estimates for all mice in this study are provided explicitly in Supplementary Tables 1–10. Parameter estimates for each mouse were then used to predict (i.e., simulate) the number of cells in the MYC-On (blue curve), MYC-Off (red curve), and Esc (green curve) states.
The Akaike Information Criterion (AIC) was used to compare model fits, with the best fit indicated by the lowest AIC value54. All data generated and analyzed in this study are included in this published article (and its Supplementary Information files).
Supplementary Information
Acknowledgements
We would like to thank Dr. Yulin Li, Dr. Anja Deutzmann, Dr. Renumathy Dhanasekaran, Dr. Wadie Daniel Mahauad Fernandez, and members of the D.W.F. and S.S.G. laboratories for their helpful discussion and suggestions; Dr. Jiamin Chen and Dr. John Bell for their discussion of deep sequencing of mutations; and the Stanford Center for Innovation in In-Vivo Imaging (SCI3). The mouse in Figure 1a was drawn using BioRender. This work is funded in part by National Institutes of Health (NIH) U01 Grant CA188383 (D.W.F. and S.S.G.), Emerson Foundation (D.W.F.), R01 CA170378 PQ22 (D.W.F.), PQ7 5R01CA20873503 (D.W.F.), R351R35CA253180 (D.W.F.), Stanford BioX (D.W.F. and S.S.G.), the Department of Defense through the Breast Cancer Research Program under award number W81XWH-18-1-0342 (S.S.H.), the Weston Havens Foundation (L.T.), Special Fellow Award (LLS 3366-17) from The Leukemia and Lymphoma Society (S.S.), ASH Scholar Award (S.S.), and the Stanford University Asia-Medical Fund J. Huang Medical Fellowship (J.W.).
Author contributions
S.S.H., L.T., S.S.G. and D.W.F. conceived the study and experimental design. S.S.H. designed the mathematical model and computational analysis strategy. L.T., S.S., M.L. and J.W. performed the biological experiments. S.S.H., L.T., D.W.F. and S.S.G. analyzed the data. S.S.H., L.T., S.S., S.S.G. and D.W.F. wrote the paper.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: Sharon S. Hori and Ling Tong.
Sanjiv S. Gambhir is deceased.
Contributor Information
Sharon S. Hori, Email: shori@stanford.edu
Dean W. Felsher, Email: dfelsher@stanford.edu
Supplementary Information
The online version contains supplementary material available at 10.1038/s41598-020-78947-2.
References
- 1.Weinstein IB, Joe A. Oncogene addiction. Cancer Res. 2008;68:3077–3080. doi: 10.1158/0008-5472.CAN-07-3293. [DOI] [PubMed] [Google Scholar]
- 2.Felsher DW. Oncogene addiction versus oncogene amnesia: perhaps more than just a bad habit? Cancer Res. 2008;68:3081–3086. doi: 10.1158/0008-5472.CAN-07-5832. [DOI] [PubMed] [Google Scholar]
- 3.Felsher DW, Bishop JM. Reversible tumorigenesis by MYC in hematopoietic lineages. Mol. Cell. 1999;4:199–207. doi: 10.1016/s1097-2765(00)80367-6. [DOI] [PubMed] [Google Scholar]
- 4.Felsher DW. Cancer revoked: oncogenes as therapeutic targets. Nat. Rev. Cancer. 2003;3:375–380. doi: 10.1038/nrc1070. [DOI] [PubMed] [Google Scholar]
- 5.Kwak EL, et al. Irreversible inhibitors of the EGF receptor may circumvent acquired resistance to gefitinib. Proc. Natl. Acad. Sci. USA. 2005;102:7665–7670. doi: 10.1073/pnas.0502860102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kobayashi S, et al. EGFR mutation and resistance of non-small-cell lung cancer to gefitinib. N. Engl. J. Med. 2005;352:786–792. doi: 10.1056/NEJMoa044238. [DOI] [PubMed] [Google Scholar]
- 7.Pelengaris S, Khan M, Evan G. c-MYC: more than just a matter of life and death. Nat. Rev. Cancer. 2002;2:764–776. doi: 10.1038/nrc904. [DOI] [PubMed] [Google Scholar]
- 8.Chen H, Liu H, Qing G. Targeting oncogenic Myc as a strategy for cancer treatment. Signal. Transduct. Target. Ther. 2018;3:5. doi: 10.1038/s41392-018-0008-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Eilers M, Eisenman RN. Myc's broad reach. Genes Dev. 2008;22:2755–2766. doi: 10.1101/gad.1712408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Dang CV. c-Myc target genes involved in cell growth, apoptosis, and metabolism. Mol. Cell. Biol. 1999;19:1–11. doi: 10.1128/mcb.19.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gouw AM, et al. The MYC oncogene cooperates with sterol-regulated element-binding protein to regulate lipogenesis essential for neoplastic growth. Cell Metab. 2019;30:556–572.e555. doi: 10.1016/j.cmet.2019.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Das B, et al. MYC regulates the HIF2α stemness pathway via nanog and Sox2 to maintain self-renewal in cancer stem cells versus non-stem cancer cells. Cancer Res. 2019;79:4015–4025. doi: 10.1158/0008-5472.CAN-18-2847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Casey SC, Baylot V, Felsher DW. The MYC oncogene is a global regulator of the immune response. Blood. 2018;131:2007–2015. doi: 10.1182/blood-2017-11-742577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gouw AM, Toal GG, Felsher DW. Metabolic vulnerabilities of MYC-induced cancer. Oncotarget. 2016;7:29879–29880. doi: 10.18632/oncotarget.7223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gabay M, Li Y, Felsher DW. MYC activation is a hallmark of cancer initiation and maintenance. Cold Spring Harb. Perspect. Med. 2014;4:a014241. doi: 10.1101/cshperspect.a014241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jain M, et al. Sustained loss of a neoplastic phenotype by brief inactivation of MYC. Science. 2002;297:102–104. doi: 10.1126/science.1071489. [DOI] [PubMed] [Google Scholar]
- 17.Wu CH, et al. Cellular senescence is an important mechanism of tumor regression upon c-Myc inactivation. Proc. Natl. Acad. Sci. USA. 2007;104:13028–13033. doi: 10.1073/pnas.0701953104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Rakhra K, et al. CD4(+) T cells contribute to the remodeling of the microenvironment required for sustained tumor regression upon oncogene inactivation. Cancer Cell. 2010;18:485–498. doi: 10.1016/j.ccr.2010.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shachaf CM, et al. MYC inactivation uncovers pluripotent differentiation and tumour dormancy in hepatocellular cancer. Nature. 2004;431:1112–1117. doi: 10.1038/nature03043. [DOI] [PubMed] [Google Scholar]
- 20.Dhanasekaran R, et al. MYC and Twist1 cooperate to drive metastasis by eliciting crosstalk between cancer and innate immunity. Elife. 2020;9:e50731. doi: 10.7554/eLife.50731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Casey SC, et al. MYC regulates the antitumor immune response through CD47 and PD-L1. Science. 2016;352:227–231. doi: 10.1126/science.aac9935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Choi PS, et al. Lymphomas that recur after MYC suppression continue to exhibit oncogene addiction. Proc. Natl. Acad. Sci. USA. 2011;108:17432–17437. doi: 10.1073/pnas.1107303108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.James ML, Gambhir SS. A molecular imaging primer: modalities, imaging agents, and applications. Physiol. Rev. 2012;92:897–965. doi: 10.1152/physrev.00049.2010. [DOI] [PubMed] [Google Scholar]
- 24.Massoud TF, Gambhir SS. Integrating noninvasive molecular imaging into molecular medicine: an evolving paradigm. Trends Mol. Med. 2007;13:183–191. doi: 10.1016/j.molmed.2007.03.003. [DOI] [PubMed] [Google Scholar]
- 25.Tran PT, et al. Survival and death signals can predict tumor response to therapy after oncogene inactivation. Sci. Transl. Med. 2011;3:103–199. doi: 10.1126/scitranslmed.3002018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Norton L. A Gompertzian model of human breast cancer growth. Cancer Res. 1988;48:7067–7071. [PubMed] [Google Scholar]
- 27.Goldie JH, Coldman AJ. A mathematic model for relating the drug sensitivity of tumors to their spontaneous mutation rate. Cancer Treat. Rep. 1979;63:1727–1733. [PubMed] [Google Scholar]
- 28.Laird AK. Dynamics of tumor growth. Br. J. Cancer. 1964;13:490–502. doi: 10.1038/bjc.1964.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bozic I, et al. Evolutionary dynamics of cancer in response to targeted combination therapy. Elife. 2013;2:e00747. doi: 10.7554/eLife.00747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lahouel K, et al. Revisiting the tumorigenesis timeline with a data-driven generative model. Proc. Natl. Acad. Sci. USA. 2020;117:857–864. doi: 10.1073/pnas.1914589117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Altrock PM, Liu LL, Michor F. The mathematics of cancer: integrating quantitative models. Nat. Rev. Cancer. 2015;15:730–745. doi: 10.1038/nrc4029. [DOI] [PubMed] [Google Scholar]
- 32.Hori SS, Gambhir SS. Mathematical model identifies blood biomarker-based early cancer detection strategies and limitations. Sci. Transl. Med. 2011;3:109–116. doi: 10.1126/scitranslmed.3003110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Iwasa Y, Nowak MA, Michor F. Evolution of resistance during clonal expansion. Genetics. 2006;172:2557–2566. doi: 10.1534/genetics.105.049791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Komarova NL, Wodarz D. Drug resistance in cancer: principles of emergence and prevention. Proc. Natl. Acad. Sci. USA. 2005;102:9714–9719. doi: 10.1073/pnas.0501870102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Komarova N. Stochastic modeling of drug resistance in cancer. J. Theor. Biol. 2006;239:351–366. doi: 10.1016/j.jtbi.2005.08.003. [DOI] [PubMed] [Google Scholar]
- 36.Tomasetti C, Levy D. An elementary approach to modeling drug resistance in cancer. Math. Biosci. Eng. 2010;7:905–918. doi: 10.3934/mbe.2010.7.905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Schönig, K. & Bujard, H. in Generating Conditional Mouse Mutants via Tetracycline-Controlled Gene Expression Vol. 209 Transgenic Mouse Methods and Protocols (eds Hofker, M. H. & Deursen, J. V.) Ch. 5, 69–104 (Humana Press, London, 2011). [DOI] [PubMed]
- 38.Shachaf CM, et al. Genomic and proteomic analysis reveals a threshold level of MYC required for tumor maintenance. Cancer Res. 2008;68:5132–5142. doi: 10.1158/0008-5472.CAN-07-6192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hori SS, Lutz AM, Paulmurugan R, Gambhir SS. A model-based personalized cancer screening strategy for detecting early-stage tumors using blood-borne biomarkers. Cancer Res. 2017;77:2570–2584. doi: 10.1158/0008-5472.CAN-16-2904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bhaumik S, Gambhir SS. Optical imaging of Renilla luciferase reporter gene expression in living mice. Proc. Natl. Acad. Sci. USA. 2002;99:377–382. doi: 10.1073/pnas.012611099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Swaminathan S, et al. MYC functions as a switch for natural killer cell-mediated immune surveillance of lymphoid malignancies. Nat. Commun. 2020;11:2860. doi: 10.1038/s41467-020-16447-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Keu KV, et al. Reporter gene imaging of targeted T cell immunotherapy in recurrent glioma. Sci. Transl. Med. 2017;9:2196. doi: 10.1126/scitranslmed.aag2196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Natarajan A, Mayer AT, Reeves RE, Nagamine CM, Gambhir SS. Development of novel immunoPET tracers to image human PD-1 checkpoint expression on tumor-infiltrating lymphocytes in a humanized mouse model. Mol. Imaging. Biol. 2017;19:903–914. doi: 10.1007/s11307-017-1060-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Mayer AT, Gambhir SS. The immunoimaging toolbox. J. Nucl. Med. 2018;59:1174–1182. doi: 10.2967/jnumed.116.185967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Alam IS, et al. Imaging activated T cells predicts response to cancer vaccines. J. Clin. Invest. 2018;128:2569–2580. doi: 10.1172/JCI98509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Mayer AT, et al. Practical immuno-PET radiotracer design considerations for human immune checkpoint imaging. J. Nucl. Med. 2017;58:538–546. doi: 10.2967/jnumed.116.177659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Peck M, et al. Applications of PET imaging with the proliferation marker [18F]-FLT. Q. J. Nucl. Med. Mol. Imaging. 2015;59:95–104. [PMC free article] [PubMed] [Google Scholar]
- 48.Ye D, et al. Bioorthogonal cyclization-mediated in situ self-assembly of small-molecule probes for imaging caspase activity in vivo. Nat. Chem. 2014;6:519–526. doi: 10.1038/nchem.1920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang Y, et al. Real-time imaging of senescence in tumors with DNA damage. Sci. Rep. 2019;9:2102. doi: 10.1038/s41598-019-38511-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Good Z, et al. Single-cell developmental classification of B cell precursor acute lymphoblastic leukemia at diagnosis reveals predictors of relapse. Nat. Med. 2018;24:474–483. doi: 10.1038/nm.4505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Wang L, et al. A genetically defined disease model reveals that urothelial cells can initiate divergent bladder cancer phenotypes. Proc. Natl. Acad. Sci. USA. 2020;117:563–572. doi: 10.1073/pnas.1915770117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Amoasii L, et al. In vivo non-invasive monitoring of dystrophin correction in a new Duchenne muscular dystrophy reporter mouse. Nat. Commun. 2019;10:4537. doi: 10.1038/s41467-019-12335-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ritsma L, et al. Surgical implantation of an abdominal imaging window for intravital microscopy. Nat. Protoc. 2013;8:583–594. doi: 10.1038/nprot.2013.026. [DOI] [PubMed] [Google Scholar]
- 54.Akaike H. New look at statistical-model identification. IEEE Trans. Automat. Contr. 1974;19:716–723. doi: 10.1109/Tac.1974.1100705. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.