Biomimetic six-axis robots replicate human cardiac papillary muscle motion: pioneering the next generation of biomechanical heart simulator technology

Abstract

Papillary muscles serve as attachment points for chordae tendineae which anchor and position mitral valve leaflets for proper coaptation. As the ventricle contracts, the papillary muscles translate and rotate, impacting chordae and leaflet kinematics; this motion can be significantly affected in a diseased heart. In ex vivo heart simulation, an explanted valve is subjected to physiologic conditions and can be adapted to mimic a disease state, thus providing a valuable tool to quantitatively analyse biomechanics and optimize surgical valve repair. However, without the inclusion of papillary muscle motion, current simulators are limited in their ability to accurately replicate cardiac biomechanics. We developed and implemented image-guided papillary muscle (IPM) robots to mimic the precise motion of papillary muscles. The IPM robotic system was designed with six degrees of freedom to fully capture the native motion. Mathematical analysis was used to avoid singularity conditions, and a supercomputing cluster enabled the calculation of the system's reachable workspace. The IPM robots were implemented in our heart simulator with motion prescribed by high-resolution human computed tomography images, revealing that papillary muscle motion significantly impacts the chordae force profile. Our IPM robotic system represents a significant advancement for ex vivo simulation, enabling more reliable cardiac simulations and repair optimizations.

1. Introduction

Ex vivo heart simulators provide an important platform to drive innovation in cardiac surgery. These simulators are used to design and analyse surgical techniques and devices for optimized implementation in human patients. The simulators feature programmable pumps that expose heart valves to their physiologic environment—including relevant pressure and flow waveforms—while haemodynamic, strain and motion metrics are recorded. Numerous previous studies feature analyses of disease states and optimization of surgical valve repair techniques and devices [1–8]. These studies are unique in their ability to immediately inform the current practice of cardiac surgery and have already had a meaningful impact on patient care through the analysis of surgical repairs [9,10]. However, the fidelity of these biomechanics analyses and surgical optimizations is dependent on the ability of the simulator to accurately mimic the in vivo environment, particularly for patient-specific surgical optimization.

A significant limitation of current mitral valve ex vivo simulation is the inability to include the complex motion of the papillary muscles. In vivo, the papillary muscles move with each heartbeat, translating and rotating relative to the valve annulus [11], which in turn crucially affects the motion and forces on the chordae tendineae and the leaflets, and thus the function of the valve. This complex papillary muscle motion will not only have an impact on the analysis of healthy valve mechanics ex vivo, but it will also play an important role in generating mitral valve disease models due to altered papillary muscle motion. In particular, secondary mitral regurgitation is typically a result of ventricular processes affecting the cardiac trajectories of the papillary muscles and annulus [12,13]. Including this motion in ex vivo simulation will significantly improve our ability to capture the full dynamics of the mitral valve and increase the reliability of our surgical repair analyses and optimizations. Though previous studies report the capability of adjusting papillary muscle placement within the simulator, the papillary muscles remain fixed in place during cardiac cycles [14,15]. The use of robotics to simulate or augment natural cardiac movement has been implemented for a range of applications including motion compensation during surgery [16,17] and implantable soft robotic devices to assist ventricular contraction [18,19]. Recently, there have been developments in the use of soft robotics to simulate gross cardiac wall motion ex vivo [20,21], though the complex and unique motion of papillary muscles for valvular simulation and analysis has not yet been tackled. Here, we present the design and implementation of a dual image-guided papillary muscle (IPM) robotic system, consisting of coupled waterproofed six-axis robotic platforms that mimic the native motion of the papillary muscles during ex vivo simulation. The effect of simulating papillary muscle motion can not only provide insight into the biomechanics of the mitral valve but also has important implications for all ex vivo mitral valve studies and surgical valve repair.

2. Materials and methods

2.1. Image-guided papillary muscle robot design

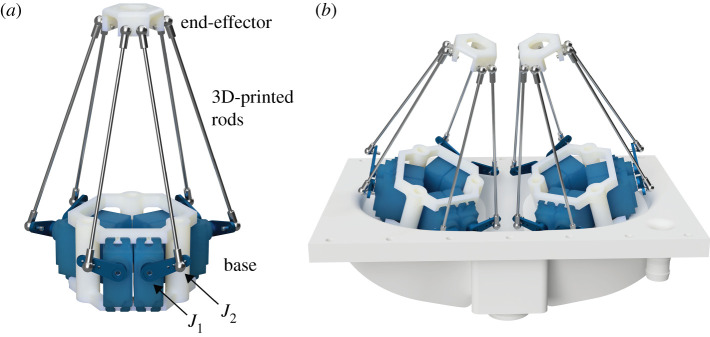
Each IPM robot uses a modified Stewart platform design consisting of six servo motors with actuating rods that extend to an end-effector platform with preformed suture perforations for papillary muscle attachment (figure 1a). Using servo motors, as opposed to the more typical linear actuators, allows us to reduce the response time of our system, enabling a higher system bandwidth. Because this mechanism provides three translational and three rotational degrees of freedom, any position and orientation within the reachable system workspace can be uniquely specified by a combination of servo joint angles. Thus, with two IPM robots, we can fully mimic the complex native motion of each papillary muscle for both position and orientation axes to drive both papillary muscles within a heart simulator. The IPM robot was specifically designed to match the anatomical geometry of the animal model and the geometric constraints of our left heart simulator. Each IPM robot was constructed using a custom 3D-printed housing for the six waterproofed servo motors. Carbon's MPU100 (Carbon, Redwood City, CA) was used as the material for all 3D-printed components [22], though each component could also be machined from a corrosion resistant metal to prevent deformation over a longer period of time. A modified heart simulator left ventricular chamber was built to mount the IPM robots, allowing for additional operating space without collisions between the legs or servo arms (figure 1b).

Figure 1.

Diagram of the IPM robot. (a) A single IPM robot. J₁ denotes the first joint at the base of the servo arm and J₂ denotes the second joint connecting the servo arm to the 3D-printed rod. (b) Render of the dual IPM robotic system mounted on the base plate of the left ventricular chamber in the heart simulator. The platforms are both angled 15° towards the centre for additional operating space.

To drive the coupled IPM robots, we designed a custom software package that both calculates the kinematics of our system to drive the servo motors and graphically simulates the state of the system in real time. Due to the high number of degrees of freedom of each IPM robot and the use of revolute joints as opposed to linear actuators, controlling the highly nonlinear kinematics of the platform presents several mathematical challenges. The forward kinematics of this system, which would allow for the calculation of end-effector positions from joint angles, presents a highly complex, nonlinear system of equations typically requiring iterative approaches to solve. However, the inverse kinematics, which allows us to calculate joint angles from given end-effector positions, is a less computationally expensive problem and can be applied to calculate joint angles in real time [23]. Additionally, to inform the design of such a system, we performed both singularity and computational operating space analyses during our iterative design approach, described below. A simple position validation test—detailed in electronic supplementary material S1—was also performed to examine the approximate accuracy of the IPM motion.

2.2. Singularity analysis

The IPM robot, which is a modified and miniaturized form of a Stewart platform, could become theoretically uncontrollable due to a singularity; we determined the conditions for this singularity and formulated our design geometry to avoid it. Electronic supplementary material S2 contains the proof showing that, with linear actuators, when the base and end-effector are similar and highly symmetric, such a singularity occurs. Thus, we chose not to use an end-effector and base that are semiregular hexagons with the same relative proportions. Instead, we used semiregular hexagons that were dissimilar. The selected end-effector side lengths were 0.95 cm and 1.9 cm, while the base lengths were 1.6 cm, 7.4 cm. Hence the two hexagons have unequal side length ratios 1.9/0.95 = 2 and 7.4/1.6 = 4.6. We also computationally verified that these parameters allow significant variation away from the hypersurface defining the singularity (S2). Additionally, we did not use linear actuators; in figure 1a, controlling joint J₂ would be equivalent to a linear actuator, but we instead controlled joint J₁.

2.3. Computational operating workspace validation

To calculate the workspace of our IPM robot and ensure the papillary muscle motion falls within these limits, we used the Stanford Sherlock supercomputing cluster to perform a computational analysis of our defined system and unique geometric constraints. Using the inverse kinematics of our system to verify whether a position and orientation was physically reachable by the platform, we iterated over a six-dimensional boundary set to determine the geometry of the system workspace [24]. The Sherlock cluster represents a 192-fold computational enhancement over a standard computer (2 GHz, quad-core Intel i5) allowing us to iterate over 1.4 × 10¹⁰ unique positions and orientations using 384 computing cores.

2.4. Papillary muscle trajectory translation

To determine the physiologic motion of the papillary muscles, the mitral valve annulus and papillary muscles were tracked using CEMRG software (London, UK) for a de-identified dataset of high-resolution computed tomography (CT) scans of an adult human heart with 10 images over the course of one cardiac cycle. In the left heart simulator, the annulus is sewn to a flexible mount that allows it to passively undergo a conformational change between a saddle shape and a flat ring during the cardiac cycle to approximate the natural annulus motion while its centre remains fixed. However, in vivo, the annulus centroid also translates as the heart beats. Thus, the papillary muscle trajectories were adjusted to compensate for this native annulus translation. Additionally, using a series of rotation matrices calculated in MATLAB (Mathworks, Natick, MA) that match the geometry of our physical system, these trajectories were transformed to superimpose motion of the cardiac cycle from CT images onto our physical IPM robot end-effectors.

Using a series of rotation matrices along with our robot-controlled system, these tracked CT data allowed us to mimic the exact positions and orientations of the native papillary muscle cardiac trajectory with our IPM robot. The centroid of the three points prescribing the motion of each papillary muscle defined the position of the end-effector, while the plane that contained all three points defined the orientation of the end-effector. However, in order to interpret this orientation plane of the points as a control parameter, we additionally calculated the Euler body angles of the three points. This was done by calculating the plane's orthogonal vector and then performing arctangent operations to find the body angles. After transforming these points to match our system geometry and calculating their positions and orientations, we inputted these trajectories into our software platform which calculated the appropriate joint angles for each servo motor of the IPM robot.

2.5. Left heart simulator

To test the impact of this motion on the mitral valve apparatus, we recorded the forces on the chordae tendineae of a mitral valve in real time, comparing the forces when the IPM robots were synchronized to mimic native motion versus a stationary state to match the current state of the art in ex vivo simulation. Ex vivo simulation typically uses porcine mitral valves as a human analogue [6,14,25–28]. In this study, mitral valves were carefully excised from locally obtained fresh porcine hearts, preserving the annulus, leaflets, papillary muscles and chordae tendineae; in select circumstances, a valve could not be tested on the day of explanation and was placed in vacuum-sealed bag with normal saline and frozen for preservation. To mount the valve within our custom left heart simulator [6,7,10], a small cuff of left atrium was also preserved as the attachment for a 3D-printed, elastomeric, silicone sewing ring fixed between the left atrial and left ventricular simulator chambers. The sewing ring material provided elasticity to reduce annulus fixation and the left atrial cuff aided in retaining the natural elasticity of the valve. The valve was mounted to the sewing ring with six interrupted 2–0 braided polyester sutures for alignment as well as a continuous running 2-0 polypropylene suture as a haemostatic suture line. The haemostatic line was locked to prevent inadvertent restrictive annuloplasty. Due to the importance of consistency in fixing the IPM robots to the valve, hearts with aberrant papillary muscle anatomy were excluded. Each papillary muscle was sewn to a 3D-printed end-effector platform using four interrupted, pledgeted, 2-0 braided polyester horizontal mattress sutures. The papillary muscles were cut prior to mounting such that each would be properly positioned on the end-effectors in a native configuration when the IPM robot was at its origin, thus providing the maximum range of reachable space. Each end-effector's position was then further refined to mimic in vivo placement inside the left heart simulator using the IPM robot's six degrees of freedom. The in vivo papillary muscle trajectory was then superimposed onto this native home position.

The design of our custom left heart simulator has been previously described [6,7,10]. The simulator features a pulsatile linear piston pump (ViVitro Superpump, ViVitro Labs, Victoria, BC, Canada) programmed to produce a physiologic waveform in compliance with ISO 5840 standards for in vitro valve testing. Pressure was recorded using ventricular, aortic, and left atrial pressure transducers (Utah Medical Products Inc., Midvale, Utah), while flow was recorded using electromagnetic flow probes (Carolina Medical Electronics, East Bend, North Carolina). To ensure proper transduction of the flow meters, 0.9% normal saline was used as the test fluid. Peripheral resistance and compliance in the system were initially titrated with a 70 28-mm leakless disc valve (ViVitro). During testing, the mechanical mitral valve was replaced by a porcine valve with both papillary muscles fixed to the IPM robots, and 10 cycles of haemodynamic data were collected in both stationary and robotic motion states. A synchronizing signal pulse from the linear piston pump controller was used to drive the timing of the IPM robot motion.

Forces on the chordae tendineae were measured with calibrated fibre Bragg grating (FBG) strain gauge sensors (DTG-LBL-1550 125 µm FBGS International, Belgium) as previously described [7,10,29]. FBGs are optical strain gauges with a thin profile and low mass, enabling the use of the sensors on multiple chordae without disrupting the haemodynamics and mechanics of the valve apparatus. The sensors were fixed to native chordae using CV-6 PTFE flanking the 4 mm strain gauge with care taken to ensure the length of chord between the two sutures matched the 4 mm length of the strain gauge. The section of chordae between the sutures was then cut with no change in overall chordal length to direct the entire force to the FBG sensor. Multiple native chordae (n = 3–5) were instrumented for each valve, including primary and secondary chordae in both posterior and anterior positions. Each chord is unique in its geometry, anatomical placement and cross-sectional area, and thus there will be native force differences between each chord. To ensure a paired comparison for each chord, no adjustments to FBG instrumentation were made between exposing the valve to the stationary and papillary muscle motion conditions. Maximum chordal forces were calculated as well as the rate of change of force with respect to time (dF/dt) at the onset of systole.

2.6. Statistical analysis

Statistical significance was defined at p < 0.05 for all tests. Chordal force and rate of change of force variables are reported as mean ± standard deviation. Non-parametric Friedman tests were used to compare continuous chordal force and rates of change of force variables between stationary and motion groups. This test accounts for non-normally distributed forces and for the fact that the experimental method included separate data collection stages for each valve. Maximum chordal forces were calculated as the average force during systole, and dF/dt was calculated as the average rate of change of force on a given chordae tendineae with respect to time at the onset of systole.

3. Results

3.1. Computational operating workspace simulation

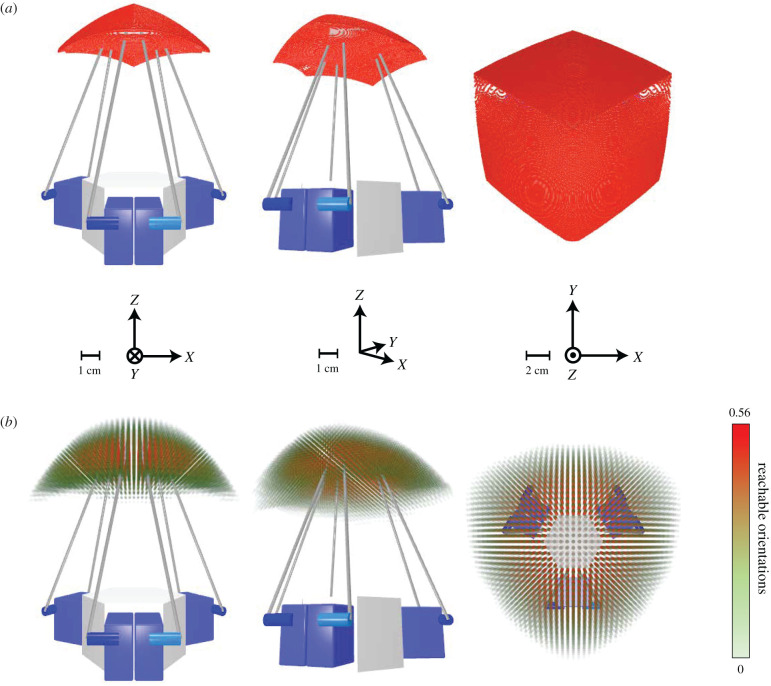
Because this system has six degrees of freedom, in order to conduct a full workspace analysis, we iterated over six dimensions. We additionally performed a three-dimensional iteration for intuitive visualization. For the three-dimensional iteration, we kept a constant, neutral orientation, absent of any rotation and mapped the end-effector centroid (figure 2a). This precise but less accurate set gave a general approximation of the true workspace with a superior resolution (0.11 mm), allowing us to more intuitively visualize the space. The six-dimensional iteration (i.e. accounting for both position and orientation of the end-effector) was more computationally expensive, leading to a lower resolution set (3.33 mm and 3.75°), but provided a more accurate approximation of the real workspace. To visualize this space, we mapped the positions in our virtual simulator and encoded orientation information via colour and opacity. The more orientations that the robot can reach at a given position, the redder in colour and the higher opacity the overlaid point is, with the bounds being set to [ − π/2, π/2]. This six-dimensional iteration visualization is shown in figure 2b. Calculated workspace limits are shown in table 1. These results confirmed that the IPM robot workspace for our system encompassed the limits of the human papillary muscle trajectory used in this study.

Figure 2.

Range-of-motion simulation results. Simulation results calculating the total range of motion of the IPM robot end-effector via inverse kinematics iteration on the Stanford Sherlock supercomputing cluster. Axes and scale for each view are indicated. (a) Three-dimensional iteration, with a fixed, neutral orientation, absent of rotation, and a resolution of 0.11 mm. (b) Six-dimensional iteration with a resolution of 3.33 mm and 3.75°. Greater opacity and red colour indicate a higher relative frequency of reachable orientations for a given position with a maximum reachable orientation frequency of 0.56. For reference, a relative frequency rate of reachable orientations of 1 indicates a position where every permutation of orientations with the bounds of [−π/2, π/2] for each axis is reachable. The dynamic range of the reachable orientation percentages was exponentially tuned for better visibility.

Table 1.

Sherlock computing cluster simulated workspace ranges for the IPM robot end-effector.

	X-axis range (cm)	Y-axis range (cm)	Z-axis range (cm)
three dimensions	[−5.0136, 5.0136]	[−5,2539, 5.7891]	[−1,7476, 1.8023]
six dimensions	[−6.6667, 6.6667]	[−6.3333, 7.6667]	[−4, 1.6667]

3.2. Implementation in the heart simulator

Three porcine valves were tested in our custom left heart simulator and successfully affixed to the final dual IPM robotic system (figure 3a,b). Multiple chordae tendineae were instrumented with high-resolution FBG strain gauge sensors for a total of 10 chordae instrumented across the valves (figure 3c). The left heart simulator subjected each valve to physiologic pressures and flows, while the IPM robots were synchronized to simulate in vivo papillary muscle motion (see electronic supplementary material movie).

Figure 3.

Heart simulator experimental setup. (a) Diagram of the custom left heart simulator with stationary papillary muscles. From Imbrie-Moore [8], used with permission from Elsevier. (b) Picture of the dual Stewart platform system sewn to papillary muscles of a porcine mitral valve to mimic the motion of the heart during ex vivo cardiac simulation experiments. (c) High-resolution FBG strain gauge sensor instrumenting a chordae tendineae; the sensor is calibrated to correlate strain to force. The chord is severed between the two suture attachment points, denoted by red arrows, to transmit all force through the sensor.

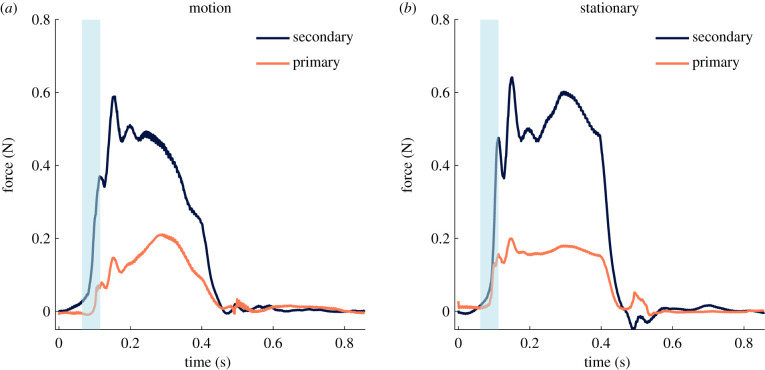
No significant difference was found for any haemodynamic parameters between the stationary and robotic actuated motion states tested, including mean arterial pressure, diastolic pressure, systolic pressure, mean atrial pressure, mean ventricular pressure and regurgitant fraction. However, a clear difference was observed when analysing the force profiles. Figure 4a shows the forces in the robotic state with primary and secondary chordae separated and figure 4b shows the forces in the stationary state. In both cases, the force tracings are averaged across at least four cardiac cycles to produce an average cardiac cycle tracing; variability cycle to cycle was extremely low with a standard deviation of less than 0.01 N in peak forces across cycles. Qualitatively, the smoother force profile of the chordae with the coupled IPM robots driving the papillary muscles to mimic their natural motion is far more similar to previously reported in vivo force results [30–33]. We can examine this force tracing difference quantitatively through an analysis of the yank on the chordae, a term denoting the rate of change of force over time (dF/dt). The onset of systole was selected as the region for the rate of change of force analysis because this region of the chordal force profile experiences a dramatic spike in force with maximum dF/dt as the valve is first subjected to the rising left ventricular pressure. dF/dt at the onset of systole was significantly lower for the robotic motion state compared with the stationary state in both primary chordae (3.14 N s⁻¹ versus 5.33 N s⁻¹, p = 0.046) and secondary chordae (5.13 N s⁻¹ versus 13.16 N s⁻¹, p = 0.025). A lower dF/dt is an indicator that the force on the chordae rises more smoothly; note that no significant difference was found between the maximum force measured on the chordae for either primary or secondary chordae tendineae between the stationary and robotic actuated states.

Figure 4.

Primary and secondary chordae tendineae forces. (a) Composite force tracings over the course of a cardiac cycle for primary and secondary chordae for the coupled IPM robotic system simulating the papillary muscle motion. (b) Composite force tracings for the system in a stationary position to mimic the current state of ex vivo experimentation. The approximate region analysed for the rate of change of force (dF/dt) is highlighted in blue for both motion and stationary IPM configurations. Note that this figure shows the composite tracing across multiple chordae and valves; due to the fact that each valve has a unique anatomical geometry which causes slight offsets in the force profiles, the onset of systole region was defined for each case. dF/dt at the onset of systole is significantly lower for the robotic motion state compared with the stationary state in both primary chordae (3.14 N s⁻¹ versus 5.33 N s⁻¹, p = 0.046) and secondary chordae (5.13 N s⁻¹ versus 13.16 N s⁻¹, p = 0.025).

4. Discussion

Ex vivo cardiac simulation provides a robust means to quantitatively analyse cardiac biomechanics and offers a platform to optimize surgical techniques. Thus, each step advancing this simulation to more closely match the in vivo environment significantly improves our ability to design optimal devices and surgical techniques. This work presents a coupled six-axis robotic Stewart platform system that mimics the native motion of papillary muscles for an important advancement in ex vivo simulation. The system was designed with six degrees of freedom to capture the complex translation and rotation in native papillary muscle motion, prescribed by high-resolution CT images. We also conducted thorough mathematical and supercomputer-enabled numerical analyses to ensure our system geometry avoided singularity conditions and operated within our physical boundary requirements. From our computational simulation results, we found that our physical system has a larger relative reachable area across the XY-plane, while being most limited in the Z-direction. Intuitively, this matches the description of this kind of parallel manipulator, as the Z-direction workspace is approximately limited to twice the length of the servo horn. This analysis proved invaluable for informing our design as it allowed us to fine-tune the physical geometry of our system to better match the workspace of the papillary muscle trajectory to our IPM robot workspace.

Ultimately, the IPM robots mounted in our ex vivo left heart simulator enabled high-resolution analysis of haemodynamics and chordal force profiles with the simulation of in vivo papillary muscle motion. In particular, the introduction of papillary muscle motion, when compared with the traditional stationary ex vivo testing configuration, resulted in a dF/dt at the onset of systole that was significantly lower for both primary and secondary chordae. A lower dF/dt in the robotic actuated state indicated that the papillary muscle motion likely acts to cushion the sharp increase in force on the chordae at the onset of systole. The lack of significant difference in peak force was expected given that we ensured that the position of the papillary muscles in the stationary mode was in accordance with the papillary muscle in vivo systolic position; thus, in both stationary and papillary muscle motion modes, the valve would be in similar configurations during systole when the left ventricular pressure is highest, and therefore seeing similar maximum force levels. However, it is possible that the sharp spike in force at the onset of systole would be slightly attenuated with the cushioning effect of papillary muscle motion. With increased testing and additional valves, we may be able to elucidate if this attenuation exists and, if so, to what extent. The recorded forces were slightly lower than expected given previous ex vivo data [29,34,35]. This is likely due to instrumenting chordae tendineae prior to the tests when they are not under physiologic tension, thus resulting in a slight mismatch in effective chordae and strain gauge length. In future experiments, the end-effectors can be lowered to induce proper tensioning while the strain gauge instrumentation is performed.

Though this IPM robotic system brings us closer to a more representative ex vivo cardiac simulation, there are limitations. There is a potential mismatch between the valve being tested and the papillary muscle trajectory selected for the IPM robots to simulate. Only in the very specific case where the valve motion was measured in vivo prior to ex vivo experimentation would this mismatch be eliminated. With a future large animal experiment, the importance of this valve-specific trajectory could be determined. In vivo forces could be measured in a porcine or ovine model while CT or magnetic resonance images are recorded, then the valve could be explanted and tested in the heart simulator with the IPM robots mimicking the exact in vivo motion. Additionally, although no significant haemodynamic differences were observed, we propose a more in-depth analysis of coaptation area and tenting height in future studies to further elucidate any changes in valvular biomechanics with the introduction of papillary muscle motion.

There are also future areas of refinement for ex vivo cardiac simulation; one such area that could represent the next significant step towards a fully accurate simulator is the motion of the mitral valve annulus. Though our elastic valve sewing ring provided the flexibility to passively undergo conformational changes over the course of a cycle, the exact annular motion has yet to be prescribed in a simulator. Another area of improvement lies in the FBG sensors. Though the sensors represent an advancement over alternative strain gauges used to measure forces on chordae which have a larger footprint and mass [34,36,37], there will nonetheless be a mismatch in the stiffness of the FBG sensor in comparison with the native chordae. In manufacturing increasingly shorter FBGs, we have sought to mitigate this source of error by replacing only a fraction of the chord and thus retaining the overall viscoelastic properties. Future work to continue to shorten the sensor and to manufacture sensors using polymer-based fibres rather than silica-based fibres could refine the force-sensing measurement system further.

We showed that including the papillary muscle motion in these simulations significantly impacts the chordal force profile, and thus our novel IPM robotic system can be used in future ex vivo experimentation to more accurately replicate the in vivo environment. With our IPM robots, new minimally invasive devices that place artificial chordae in regurgitant mitral valves can be analysed in future studies incorporating the full motion of the papillary muscles, thus more accurately simulate the in vivo forces on both the native and artificial chordae. Moreover, with this advancement, we can study the biomechanics of chordal tethering from ventricular dilatation induced papillary muscle displacement on functional mitral regurgitation as well as papillary muscle head optimization through the use of high-resolution CT data from patients with cardiac disease.

Data accessibility

The software to drive the IPM robots is available at: https://osf.io/3a8y6/.

Authors' contributions

A.M.I., M.H.P. and Y.J.W. designed and implemented the final IPM system as well as wrote the manuscript. M.S. performed mathematical singularity analysis. M.H.P. performed computational workspace analysis. A.M.I., M.H.P., M.J.P., R.K., H.W., Y.Z., J.M.F., A.B., C.C., C.H., D.D. and Y.J.W. were involved in project development. A.M.I., M.H.P., M.J.P. and H.L. performed experimentation. All authors contributed to the editing and revising of the manuscript.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the National Institutes of Health (NIH R01 HL152155 and NIH R01 HL089315-01, Y.J.W.), the American Heart Association (17POST33410497, M.J.P.), the National Science Foundation Graduate Research Fellowship Program (DGE-1656518, A.M.I.-M.) and a Stanford Graduate Fellowship (A.M.I.-M.). The content is solely the responsibility of the authors and does not necessarily represent the official views of the funders.