Intrinsic electronic conductivity of individual atomically resolved amyloid crystals reveals micrometer-long hole hopping via tyrosines

Significance

The ability to understand and modulate protein conductance is central to many biological processes and for the technological applications of electronic biomaterials. However, measurements of intrinsic protein conductivity are lacking. Here, we employ a four-electrode method to measure contact-free electronic conductivity of an individual protein microcrystal that exhibits efficient hole transport over micrometers via stacked tyrosines. Combined experimental and computational studies show that both the energetics and proximity of the proton acceptor to tyrosine determine the rate of hole transport. Our mechanistic studies on model systems with atomic-resolution structures may help identify design principles to engineer electronic conductivity in proteins of interest for a wide range of applications, including artificial photosynthesis, biocatalysis, prevention of oxidative damage, and nucleic acid biosynthesis.

Abstract

Proteins are commonly known to transfer electrons over distances limited to a few nanometers. However, many biological processes require electron transport over far longer distances. For example, soil and sediment bacteria transport electrons, over hundreds of micrometers to even centimeters, via putative filamentous proteins rich in aromatic residues. However, measurements of true protein conductivity have been hampered by artifacts due to large contact resistances between proteins and electrodes. Using individual amyloid protein crystals with atomic-resolution structures as a model system, we perform contact-free measurements of intrinsic electronic conductivity using a four-electrode approach. We find hole transport through micrometer-long stacked tyrosines at physiologically relevant potentials. Notably, the transport rate through tyrosines (10⁵ s⁻¹) is comparable to cytochromes. Our studies therefore show that amyloid proteins can efficiently transport charges, under ordinary thermal conditions, without any need for redox-active metal cofactors, large driving force, or photosensitizers to generate a high oxidation state for charge injection. By measuring conductivity as a function of molecular length, voltage, and temperature, while eliminating the dominant contribution of contact resistances, we show that a multistep hopping mechanism (composed of multiple tunneling steps), not single-step tunneling, explains the measured conductivity. Combined experimental and computational studies reveal that proton-coupled electron transfer confers conductivity; both the energetics of the proton acceptor, a neighboring glutamine, and its proximity to tyrosine influence the hole transport rate through a proton rocking mechanism. Surprisingly, conductivity increases 200-fold upon cooling due to higher availability of the proton acceptor by increased hydrogen bonding.

Many biological processes require electron transport over far longer distances than the 25 Å allowed by single-step tunneling (1). The aromatic amino acids tyrosine and tryptophan, strategically placed between cofactors in proteins, can provide the critical stepping-stones for multistep hopping by acting as intermediaries along the electron transfer route as in Photosystem II and ribonucleotide reductase (1, 2). In addition, chains of aromatic residues have been proposed to move hole carriers from enzyme active sites to the exterior of proteins to avoid oxidative damage caused by redox cofactors, but direct experimental evidence of charge transport beyond the nanometer scale is lacking (3, 4). The ubiquity of such chains observed in proteins, and the established role of aromatic amino acids in the above biological processes, motivates mechanistic studies of how electron transport via aromatic residues can scale over mesoscopic (hundreds of nanometers) to microscopic distances (1, 2).

A remarkable example of biological long-distance electron transport is by soil (5, 6) and sediment bacteria (7, 8) that carry electrons to remote acceptors hundreds of micrometers (5, 9) to centimeters away (7–10), 10,000 times the size of the cell. This long-distance transport enables bacteria to get rid of electrons derived from metabolism and survive in harsh environments that lack soluble, membrane-ingestible electron acceptors such as oxygen. Polymerized cytochromes produced by soil bacteria function as “microbial nanowires” by transporting electrons through seamlessly stacked hemes (5, 6). In addition, filamentous proteins produced by both soil (11) and sediment bacteria (8) have been shown to be conductive, even in the absence of cytochromes (8). However, the underlying conductivity mechanism is unclear. Aromatic residues present in these filamentous proteins of soil (11) and sediment bacteria (10) have been proposed to carry electrons over long distances. However, this hypothesis is open to question because previous studies of DNA conductivity have shown that charge transport through aromatic bases is not possible beyond nanometer distances (12, 13), even using a very large driving force (>5 V) and synthetic bases (13).

As the structures and composition of the abovementioned filamentous proteins produced by soil and sediment bacteria are unknown, here we use amyloid proteins with stacked tyrosine residues as a model system to evaluate the possibility and mechanism of long-distance electron transport via aromatic residues (Figs. 1 and 2A). Many soluble proteins aggregate into an insoluble amyloid state to form elongated, unbranched fibrils that are associated with several fatal diseases, such as Alzheimer’s, type II diabetes, and some types of cancers (14). Amyloids are attractive model systems to evaluate protein conductivity mechanisms due to their unique ability to form several distinct, highly ordered, self-replicating, and stable biomimetic structures (Fig. 1). Short peptide-based amyloids are particularly attractive because of their computationally guided, autonomous, and high-precision synthesis as well as their diverse chemical properties and biocompatibility.

Fig. 1.

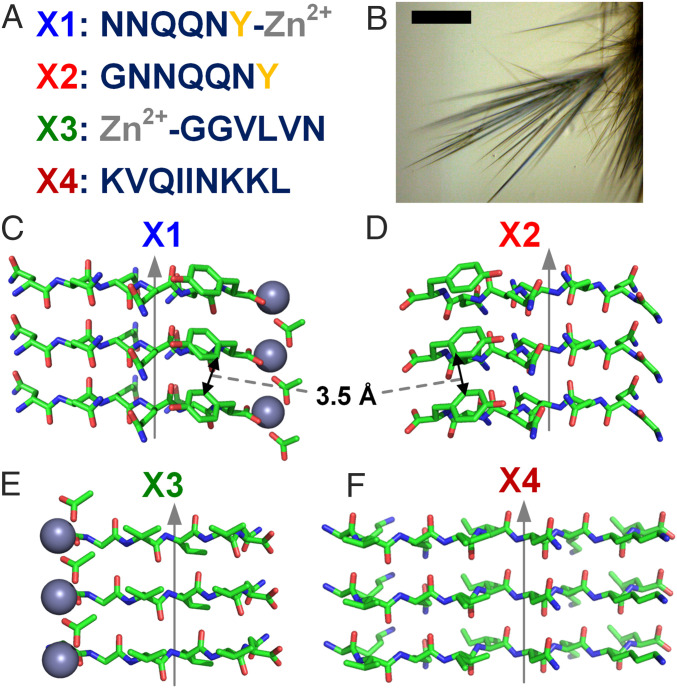
Strategy to evaluate protein conductivity mechanism using short peptides as building blocks for model systems. (A) Amino acid sequences of the short peptides used with tyrosine (yellow) and zinc (gray) highlighted. (B) Light microscopy image of microcrystals. (Scale bar, 50 µm.) (C–F) Atomic structures of microcrystals with gray arrows indicating the direction of the fibril axis. (C) X1, Zn²⁺NNQQNY (PDB ID 5K2E); (D) X2, GNNQQNY (PDB ID 5K2G); (E) X3, Zn²⁺GGVLVN (PDB ID 3PPD). (F) X4, KVQIINKKL (PDB ID 6NK4). Tyrosine edge-to-edge distances are 3.5 Å. Chemical elements are shown as follows: green, carbon; blue, nitrogen; red, oxygen; and gray, zinc.

Fig. 2.

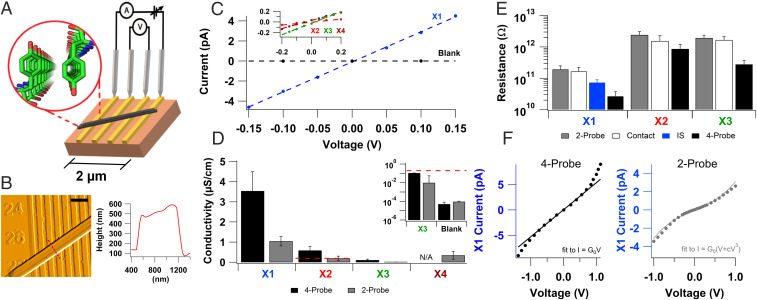
Intrinsic conductivity measurements of amyloids reveal micrometer-long charge transport through stacked tyrosines. (A) A schematic for measuring the intrinsic conductivity of a protein crystal (black) using four probes. (Inset) Atomic structure of X1 showing stacked tyrosines. (B, Left) AFM image of X1 crystal spanning multiple electrodes and (Right) corresponding height profile at the red dotted line. (Scale bar: B, 1 µm.) (C) Representative current–voltage (I–V) curves taken by two-probe electrical measurements. The dashed lines are linear fits to the data shown. (Inset) Zoomed I–V curve for low-conductive microcrystals. (D) Comparisons of the four-probe (black) and two-probe (gray) conductivity of the microcrystals. (Inset) Zoomed values (below X2 two-probe dashed red line) on a log scale. (E) Average resistance values of microcrystals measured using two-probe, contact, AC impedance spectroscopy (IS), and four-probe methods. Bars represent mean + SEM of multiple replicates [n (two-probe) = 19, 8, 9, 4, and n (four-probe) = 8, 9, 6 for X1, X2, X3, and X4, respectively. n (IS) = 11]. (F) Comparison of current–voltage profile for X1 measured using (Left) four- and (Right) two-probe method.

In addition to their biomedical importance, amyloids are attractive biomaterials due to their high stability and capacity to reproduce themselves by seeding, enabling the development of self-repairing and replicating biomimetic materials (14). However, two major bottlenecks remain in the use of amyloids as a model system to evaluate conduction mechanisms and for the development of protein-based multifunctional biomaterials. First, like most proteins, amyloids lack electronic or optical functionality (15, 16), and in prior studies of protein conductivity, high contact resistance—either between proteins or at the protein–electrode interface—has been shown to mask the intrinsic electronic properties (17). Second, in contrast to over 100,000 structures of globular proteins, only a few dozen amyloid fibril structures are available (14), and conformational changes induced by experimental conditions hinder the elucidation of structure–function correlations.

To address both these bottlenecks, here we employ a strategy to measure intrinsic conductivity of pristine amyloid microcrystals, with atomic resolution structures (18, 19), aiming to correlate structure with function by avoiding modification or tagged molecules that can induce large conformational changes (20–22). We use individual microcrystals with defined geometry to perform measurements of charge transport through stacked tyrosines, or along the fibril axis (Fig. 1). Notably, we employ a four-electrode system with ionically blocking electrodes and measure steady-state electronic current (9, 17) to avoid artifacts due to contact resistance (23, 24), polarization resistance (25), and ionic currents (23), which are known to mask the intrinsic conductivity of the protein (23, 26). Our studies show that amyloid proteins can efficiently transport charges over micrometer distances under ordinary thermal conditions without any need for redox-active metal cofactors. In contrast to single-step tunneling commonly observed in proteins, we find evidence for a hopping mechanism, previously observed experimentally only in synthetic conjugated molecular wires (27, 28), to account for long-distance conductivity.

Results

Strategy to Measure Contact-Free Electron Transport in Proteins to Determine Intrinsic Conductivity.

Although charge transfer over nanometers is well documented in several protein systems (29), contact-free DC conductivity measurements of intrinsic charge transport have not been performed for any well-defined proteins, to our knowledge. During charge transfer, electrons are exchanged between donor and acceptor molecules within nanometer distances and remain localized on the protein. In contrast, conductivity measurements involve the passage of charge through a protein without charge residing on the protein (30). Such conductivity measurements are extremely challenging due to contact resistances obscuring the intrinsic conductivity, as most of the applied voltage drop occurs across the contacts (23, 26). Even single-molecule measurements have shown that protein conductance is strongly affected by the nature of contacts (23, 26, 27). Therefore, previous measurements of single-molecule protein conductance have emphasized the pressing need to inject charges into the protein interior via ligands or good contacts for reliable determination of protein conductance (26).

To avoid artifacts due to electrode polarization and contact resistance developed at the interface between the protein and electrode (17), here we employ a four-electrode setup in which we applied the current (I) to the outer two electrodes and measured the direct current (DC) voltage (V) across the inner two electrodes (Fig. 2A). As no current can flow through the inner circuit due to the high impedance of the voltmeter, this method eliminates artifacts due to contacts and electrode polarization and enables the determination of intrinsic conductivity (17). Furthermore, the carrier injection can be controlled precisely by ensuring current conservation between the outer two electrodes and maintaining the voltage between the inner electrodes corresponding to thermal energy (k_BT). This setup thus avoids any electrochemical processes or the need for photosensitizer to generate high oxidation states of aromatic residues (29). By eliminating hot carrier injection, this method enables measurements of conductivity in its truest sense to evaluate whether there are free charge carriers that can move under ordinary thermal conditions (31). We had previously applied the four-probe method to measure networks of microbial nanowires, which eliminates the contact resistance between the protein and electrode (9). However, the interfilament contact resistance dominated the overall response, leading to 1000-fold lower conductivity (9) than individual nanowires (5, 6). Therefore, here we measure individual protein crystals with atomic-resolution structures using four-probe to determine the intrinsic conductivity mechanism.

Micrometer-Long Chains of Stacked Tyrosines Confer Conductivity to Amyloids.

We selected for comparison four amyloid fibril-forming peptides with atomic-resolution structures to probe how charge transport is affected by periodic stacking of tyrosine and metals (non–redox-active Zn²⁺): 1) X1, Zn²⁺NNQQNY; 2) X2, GNNQQNY; 3) X3, Zn²⁺GGVLVN; and 4) X4, KVQIINKKL (Fig. 1). These fibril-forming peptides form elongated microcrystals (Fig. 1B) where, like natural amyloid fibrils, the peptides form extended parallel β-sheets whose constituent β-strands run perpendicular to the fibril axis, with both fibrils and microcrystals having similar diffraction patterns (32). In contrast to large macromolecular systems, the minimalistic nature of this system (six- to nine-residue peptides and metal ion) is helpful in identifying components essential for engineering desired functionalities.

We individually placed each microcrystal on gold electrodes separated by 300-nm nonconductive gaps and located their electrode contacts using atomic force microscopy (AFM) (Fig. 2B). We performed measurements at atmospheric pressure.

All four peptide microcrystals showed conductivity with linear (ohmic) current–voltage behavior in two-probe measurements (Fig. 2C). We calculated the microcrystal conductivity from the measured conductance using a conformal mapping technique accounting for the microcrystal and electrode device dimensions (9). We found that X1 had the highest conductivity among all four microcrystals (Fig. 2D) and even the lower conducting microcrystals had higher conductivity than a blank device (93.4 ± 31.6 pS/cm) (Fig. 2D, Inset). As expected, four-probe measurements showed higher conductivity than two-probe, and the conductivity of X1 was significantly higher (P ≤ 0.05) than the conductivity of the other peptides (Fig. 2D).

The mean four-probe conductance of a single X1 microcrystal was 74.8 ± 19.9 pS, which is the highest conductance reported for a single amyloid protein macrostructure (33). Although conductance values have been reported in networks of amyloid and peptide fibrils (34–37), the lack of a consistent, uniform macromolecular conformation of amyloids as well as the dependence of conductance values on electrode and sample geometries prevented direct comparisons between these measurements (38). The electrical resistance of the sample measured using two-probe is dependent on the crystal size and the nature of contacts, whereas the four-probe conductivity is an intrinsic property of the material. The mean four-probe conductivity of the X1 microcrystal was 3.5 ± 0.96 µS/cm (Fig. 2D), which is the highest conductivity for amyloids reported to date, to our knowledge. As expected, the conductivity through proteins without metal cofactors is lower than the conductivity of other conducting proteins such as the polymerized cytochrome filaments of Geobacter sulfurreducens that transport electrons via stacked hemes rather than tyrosines (5, 6). The X2 microcrystal that lacked metal ions, but contained stacked aromatics, showed a sixfold lower conductivity (0.59 ± 0.20 µS/cm) than X1. The X3 microcrystal that lacked tyrosines showed the lowest four-probe conductivity (0.11 ± 0.045 µS/cm), which is 32 times lower than X1. Our studies thus show that although other amino acids can also contribute to protein conductivity, stacked tyrosines provide a more efficient transport path for conductivity. The microcrystals of X4 that lacked both tyrosines and metal ions were too short for four-probe measurements; they exhibited low two-probe conductivity (0.35 ± 0.20 µS/cm). Both X3 and X4 lack stacked tyrosines; however, the two-probe conductivity of X4 was higher than both two- and four-probe conductivity of X3. This could be due to the differences in contact resistances as our results show that two-probe resistance values are comparable to the contact resistance (Fig. 2E). It could also be due to the basic residues (lysines) included in the X4 sequence, but intrinsic conductivity is required for direct comparison (39). Both X1 and X2 have tyrosines with a suitable arrangement for π-stacking interactions at 3.56 Å (40). Therefore, our measurements indicate that stacked tyrosines can transport charges over micrometer distances even in the absence of strong oxidants that are typically required to oxidize individual tyrosines for conductivity (41).

The contact resistance (the difference between measured two- and four-probe resistances) for all microcrystals was substantially higher or comparable to the intrinsic (four-probe) resistance (Fig. 2E), demonstrating the large influence of contacts on conductivity measurements of proteins. For X3 and X1, the contact resistance was about sixfold higher than the intrinsic resistance, whereas for X2 it was twofold higher. All measurements confirm that significant contact resistance masks the true conductivity of these proteins in the two-probe setup because most of the voltage drop occurs across the contacts. Differences in measured contact resistances are likely due to differences in microcrystal shape, composition, and size. Our results demonstrate that contact resistance plays a significant role in measurements of protein conductivity, even for samples with lower conductivity. Our micrometer-scale studies thus complement and extend previous single-molecule studies that have shown that contact resistance masks the intrinsic conductance of biomolecules (23, 24, 42).

To complement DC conductivity measurements, we performed alternating current (AC) impedance spectroscopy (IS) to separate electronic and ionic conductivity (9). IS of a single X1 microcrystal showed that there was no major ionic contribution to the sample conductivity (SI Appendix, Fig. S1). Acidic and basic side chains have been known to increase the ionic conductivity in some cases (39, 43). Therefore, the lack of charged residues in the X1 peptide is consistent with the lack of ionic current in these microcrystals. Resistance values extracted from an equivalent circuit analysis of these AC measurements were comparable to DC resistance values, thus validating our measurement approach that measured conductivity by four-probe is primarily electronic in nature (Fig. 2E).

Increased Structural Rigidity of Amyloids due to Metal Ions Enhances Conductivity.

The conductivity of X1 was higher than X2 despite having nearly identical structures with close tyrosine stacking. The main difference between these two structures is the introduction of Zn²⁺ in X1 instead of glycine (Fig. 1 C and D). As the tyrosines and surrounding residues are conserved, it would be expected that both microcrystals have similar conductivity. However, redox activity or charge transfer involving tyrosine is typically proton-coupled owing to the high acidity of oxidized tyrosine (pK_a −2) (44), which gives rise to proton-coupled electron transfer (PCET). Because tyrosine participates in PCET, any changes in the hydrogen bonding network surrounding tyrosine can modulate the rate of charge transfer (44, 45). Notably, in both X1 and X2, tyrosine is within close hydrogen bonding distance to the nearest glutamine side chain, positioning the glutamine as a probable proton acceptor for proton transfer (PT) (45). The tyrosine OH could be stabilized in a stretched configuration by hydrogen bonding interactions with the amide oxygen or nitrogen of the glutamine, analogously to the PT mechanism from Tyr to Gln proposed for the blue light using FAD (BLUF) domain protein (46–48).

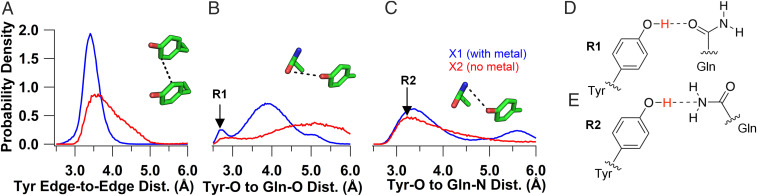
We performed molecular dynamics (MD) simulations at 300 K to investigate ensembles of conformations of X1 and X2 and examine their hydrogen-bonding networks. To analyze structural changes involving charge transfer residues, we monitored three key distances over the MD trajectories: tyrosine edge-to-edge, tyrosine hydroxyl–oxygen (Tyr–O) to glutamine amide–oxygen (Gln–O), and Tyr–O to glutamine amide–nitrogen (Gln–N) (Fig. 3 A–C). The comparison of X1 and X2 revealed that Zn²⁺ stabilizes the microcrystal structure of X1, as evidenced by the wider tyrosine edge-to-edge distance distribution in X2, with a larger tail compared to X1, which could reduce electron hopping in X2 (Fig. 3A). There was no significant difference in crystal packing of X1 and X2 to explain the difference in distributions (32).

Fig. 3.

Tyrosine stacking and proton acceptor availability govern conductivity. MD simulations at 300 K to compare the order of X1 (blue) and X2 (red) crystals. (A–C) Probability density distributions of the separation between key residues. (A) Tyrosine edge-to-edge distance. (B) Tyrosine hydroxyl–oxygen to glutamine amide–oxygen distance with the R1 conformation labeled at the 2.7-Å peak of X1. (C) Tyrosine hydroxyl–oxygen to glutamine amide–nitrogen distance with the R2 conformation labeled at the 3.24-Å peak in X2. Insets show the distances measured with a black dotted line. (D) Chemical representation of the R1 and (E) R2 rotamers.

Analysis of the other key distances showed that the glutamine can form two distinct rotamer forms designated R1 and R2, with the Gln–O or Gln–N closest to the tyrosine, respectively (Fig. 3 D and E). X1 can stably form the R1 conformation (2.7 Å from Tyr-O to Gln-O), which becomes more prominent as temperature is lowered (Fig. 3B and see Fig. 6C). In addition, it has a high likelihood of remaining at distances around 3.8 Å for Tyr–O to Gln–O and 3.4 Å for Tyr–O to Gln–N at 300 K (Fig. 3B). PT rates are known to depend strongly on the proton donor–acceptor distances (44, 48). Therefore, our analysis suggests that when the R1 conformation is stabilized by Zn²⁺, the Gln–O is the preferred proton acceptor in X1, whereas when the R1 conformation is not stabilized both the Gln–O and N are equally accessible. In contrast, the X2 microcrystal was more likely to form the R2 conformation at 300 K as evidenced by the larger probability of short Gln–N distances (3.2 Å), indicating the most probable proton acceptor in X2 is the Gln–N (Fig. 3C). Considering that X1 and X2 would primarily utilize the closest available proton acceptor for PCET, charge transfer would likely be overall slower in X2 because it has larger mean tyrosine edge-to-edge separations and proton donor–acceptor distances when compared to X1.

In addition to hydrogen bond network changes from thermal fluctuations, electronic effects that modulate the pK_a of any residues surrounding the charge transfer region could also regulate PCET (45). Although Zn²⁺ is not redox active and cannot directly take part in electron transport, it could potentially lower the pK_a of residues by up to 4 pH units which would facilitate PCET (49). However, our density functional theory (DFT) calculations showed that Zn²⁺ does not significantly change the pK_a of tyrosine in X1 microcrystals (SI Appendix, Table S3), confirming that it must play a primarily structural role. In summary, X1, which contains a readily available proton acceptor and rigid tyrosine stacking, displays higher conductivity than X2. This suggests that ordered metal incorporation likely enhances conductivity by making the structure more rigid, preventing thermal fluctuations from disrupting the charge transport pathway and stabilizing the R1 conformation

DFT Suggests Hole Conductivity due to Proton Rocking and the Energetics of Proton Acceptor Determines the Transport Rate.

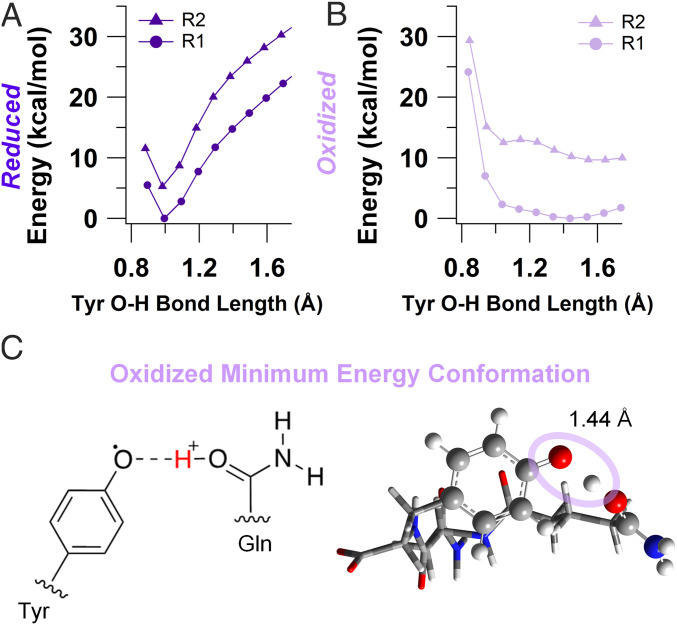
Our MD simulations combined with conductivity measurements indicated that the surrounding hydrogen-bonding network was fundamental to charge transport in the highest conducting amyloids, X1, by maintaining close tyrosine stacking and short proton donor–acceptor distance for PCET. To explore the possibility that proton transfer can occur in X1, we performed DFT calculations on model amyloid chains (SI Appendix, Fig. S2 and Table S4). Due to the presence of both R1 and R2 rotamers in our MD simulations (Fig. 3 D and E), we included both forms in our calculations. Relaxed potential energy scan calculations, in which geometry optimizations were performed at fixed tyrosine O–H distances with a polarizable continuum model for water, revealed that both reduced conformations (R1 and R2) had a single minimum at a tyrosine O–H bond distance of 1 Å, suggesting that proton transfer does not occur (Fig. 4A). In contrast, potential energy profiles for the oxidized R1 conformation indicated that there was no barrier to PT as the potential energy curve has a single-well shape characteristic of strong hydrogen bonds (Fig. 4B) (50). The oxidized R2 conformation was characterized by a low-barrier hydrogen bond with a barrier of 0.5 kcal/mol that can be overcome by thermal energy (Fig. 4B). Thus, our DFT calculations showed that PT can readily proceed when the tyrosine is oxidized in the R1 conformation (Fig. 4C), while it is unlikely to occur in the reduced state. Furthermore, the R1 conformation is thermodynamically favored in the reduced form (5.3 kcal/mol) and even more so after oxidation (11.4 kcal/mol), consistent with the MD simulations for X1 (see Fig. 6C and SI Appendix, Tables S5 and S6). In the oxidized R1 conformation, the small energetic difference between protonated and deprotonated Tyr suggests that the proton can move back and forth readily. Therefore, we conclude that the single-well potential or proton transfer in this conformation may indicate a proton rocking mechanism, where the proton can be delocalized in the barrierless energy well, in a manner similar to TyrZ in Photosystem II and Tyr122 in ribonucleotide reductase (45). This proton rocking mechanism does not require long-range proton transport and is therefore consistent with our impedance experiments that did not show any ionic conductivity (SI Appendix, Fig. S1). Calculations performed in polarizable continuum models resembling the dielectric environments inside and on the surface of proteins showed nearly identical results (SI Appendix, Fig. S5 and Tables S4–S6).

Fig. 4.

DFT calculations confirm proton transfer in oxidized X1. Relaxed potential energy scan for reduced (A) and oxidized (B) X1 in R1 and R2 conformations. Energy is normalized to the minimum value of R1 scans. (C) Chemical structure of oxidized minimum energy conformation (Left) and the DFT optimized geometry (Right). The oval highlights the tyrosine O–H bond and the optimized bond length. Chemical elements are colored as follows: gray, carbon; blue, nitrogen; red, oxygen; white, hydrogen.

Stacking Substantially Lowers the Redox Potential of Tyrosine.

Specific hydrogen-bonding networks and hydrophobic protein environments can change the effective oxidizing potential of tyrosine (45). Our contact-free conductivity measurements through stacked tyrosines were performed under ordinary thermal conditions at low bias potentials (Fig. 2C). To understand the origin of conductivity at low bias, we investigated the oxidation potential of tyrosine in the case of X1. We performed DFT calculations of tyrosine in the R1 conformation of X1 using implicit solvents with several dielectric constants and found that the maximum oxidation potential was +0.8 V vs. SHE or +5.2 V vs. vacuum (SI Appendix, Table S7). Comparison of one- and two-layer models of X1 showed that tyrosine stacking lowers the oxidation potential by ∼150 mV (SI Appendix, Table S8). The calculated oxidation potential of tyrosine in X1 is in proximity with reported values for the Fermi level of gold electrodes (approximately +5.1 V vs. vacuum) (51). This proximity between the redox potential of the tyrosine and the Fermi level of the electrode allows for charges to be injected even at low applied bias.

On the other hand, the oxidation potential of tyrosine in the R2 conformation was roughly 340 mV higher than R1 in all dielectric environments due to the facile proton transfer that stabilizes the oxidized R1 species. As the R1 conformation is also the thermodynamically favored conformation in the reduced state, we propose that the charge transport mechanism involves proton rocking in the R1 conformation.

Resistance Increases Linearly with Protein Length, Suggesting a Hopping Mechanism.

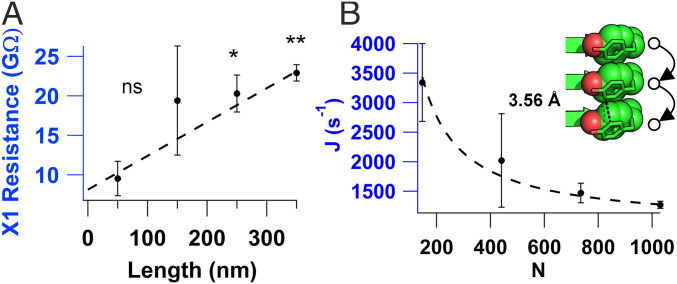
The electrical resistance was measured as a function of microcrystal length (Fig. 5A) to probe the mechanism of charge transport through the highest conducting amyloids (X1). The four-probe technique was adapted such that the first two probes remained stationary and the last two moved by one electrode after each measurement until the desired length was reached. The resistance vs. length relationship for X1 agreed well with the expected linear relationship of a hopping conductor. The calculated conductance from the linear fit yielded a conductivity of 4.8 ± 0.76 µS/cm in agreement with our measurements (Fig. 2D). Although many proteins are shown to transport electrons by tunneling with the resistance increasing exponentially with distance (23, 26), computational studies on longer peptides have predicted a transition from tunneling to hopping as a dominant transport mechanism (52). In addition, computational studies on proteins have predicted hopping transport (53, 54). Our finding of linearly increasing resistance suggests hole hopping between closely stacked tyrosines as a dominant mechanism of conductivity (Fig. 5). Using a steady-state hopping theory, we estimated the hopping rate between tyrosines by using $J=\left(k_{up}+k_{hop}/N\right)$, where $k_{hop}$ is the hopping rate and $k_{up}$ is related to injection rate from the electrode into the crystal (55). By converting resistance into electron flux, and distance into the number of hopping steps, we found that hopping rate was ∼10⁵ s⁻¹ and $k_{up}$ was ∼10² s⁻¹ at 100 mV for X1 (Fig. 5B). These rate measurements suggest that transport through tyrosines is 1,000-fold faster than the charge injection into the protein. This rate was estimated with the assumption that all tyrosines in the crystal contribute to measured current under uniform electric field. However, due to coplanar geometry of electrodes, the electric field is not uniform and possible defects in the crystal may lower the number of tyrosines participating in the transport. Therefore, the estimated rate represents a lower limit (29). Nevertheless, the hopping rate measured at ordinary thermal conditions is comparable to rates for charge transfer in protein crystals with heme or metal cofactors (55–57) measured by photochemical injection methods.

Fig. 5.

Resistance increases linearly with crystal length, consistent with a hopping mechanism. (A) Four-probe resistance vs. length measurements of X1. P values: *P < 0.05; **P < 0.01. (B) Electron flux (J) vs. number of carriers calculated from A. Values represent mean ± SEM (n = 3). (Inset) Schematic of hole hopping through tyrosines with their edge-to-edge distance labeled.

Higher Availability of the Proton Acceptor Leads to a 200-Fold Increase in Amyloid Conductivity.

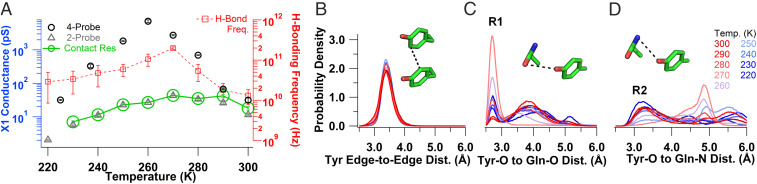
Our DFT calculations and resistance vs. length measurements suggest that proton rocking coupled with electron hopping is a likely mechanism for charge transport in X1. To further investigate the mechanism of conductivity, we analyzed the temperature dependence of the conductivity as measured in a four-probe configuration (Fig. 6A, black). The conductivity increased exponentially to 260 K and then decreased exponentially to 225 K. The response was reversible without any hysteresis. An Arrhenius fit to the data for the 225 to 260 K range, using $\sigma \left(T\right)={\sigma }_0\exp \left(T_0/T\right)$, yielded an activation energy (k_BT₀) of 0.77 eV. As nanoscale measurements have also reported similar activation energy, our measurements thus establish that proteins can extend transport from nanometers to micrometers with no change in the activation energy (29).

Fig. 6.

Exponentially increasing crystal conductivity upon cooling near physiological temperatures due to increased availability of proton acceptor. (A) Temperature dependence of the X1 conductance measured with a four-probe (black circles) and two-probe (gray triangles) arrangement. The green circles and solid line indicate the inverse of the contact resistance. Errors shown are fit errors to the linear region of an I–V curve measured as in Fig. 2 at each temperature. The calculated hydrogen bonding frequency between Tyr–O and Gln–O is also shown (red squares) with the SEM reported for each temperature (n = 6). (B–D) MD simulations from 300 to 200 K to determine changes in X1 structure upon cooling. (B) Tyrosine edge-to-edge distance. (C) Tyrosine hydroxyl–oxygen to glutamine amide–oxygen distance with the labeled R1 conformation. (D) Tyrosine hydroxyl–oxygen to glutamine amide–nitrogen distances with the labeled R2 conformation. (Insets) The corresponding distances are indicated with a black dotted line with the residues colored as in Fig. 1.

In contrast to the four-probe arrangement, two-probe measurements (Fig. 6A, gray) showed a much weaker temperature dependence. The slopes in the major regions, 220 to 260 K and 260 to 300 K, decreased by twofold and sevenfold, respectively, compared to four-probe (Fig. 6A and SI Appendix, Table S9). Notably, the changes in slope led to an activation energy of 0.30 eV in the two-probe measurements, which is substantially lower than 0.77 eV measured using four-probe. Therefore, our studies indicate that the true activation energy can be severely underestimated when using the two-probe method due to large contact resistance.

Notably, the potentials corresponding to the measured activation energy are comparable to the potentials that enhance conductivity for both the two- and four-probe measurements of current–voltage curves (Fig. 2F). The four-probe measurement showed an increase in conductance around 0.7 V indicated by linear behavior with a different slope. The two-probe showed an increase around 0.3 V with behavior that fit well to a linear plus cubic relationship, consistent with a Simmons model of a tunneling barrier forming at the contacts (58). This response was reversible because reversing the polarity yielded similar nonlinear region with similar slope (Fig. 2F). These comparative measurements demonstrate that contact resistance strongly affects the two-probe measurements and the increase in current at low potentials is likely due to a barrier bending effect that decreases the contact resistance at higher bias (58). Therefore, it is important to evaluate the role of contacts in prior studies that used two-probe and bulk methods to evaluate charge transport through aromatic amino acids, including tyrosines (59–62).

The large differences in slopes between two- and four-probe further underscore how contacts mask the true nature of protein conductance and why is it critical to measure intrinsic conductivity to determine underlying transport mechanisms. We found that contact resistance dominates the two-probe measurements (Fig. 6A, green circles). Thus, our measurements show that the contact resistance masks the true temperature dependence of protein conductivity in the two-probe approach, making it difficult to resolve the underlying conduction mechanism. This is important because previous studies have found different transport mechanisms based on temperature dependencies that were impacted by the contact resistance.

To understand the mechanism underlying a 200-fold increase in conductivity upon cooling, we performed MD simulations in the temperature range of 300 to 220 K (Fig. 6 B–D). Our MD simulations at 300 K had indicated that the side chains involved in charge transfer experienced substantial thermal fluctuations. Therefore, we examined these same key distances as the temperature was lowered. We found that the tyrosine edge-to-edge distance was well preserved for all temperatures with a peak around 3.4 Å (Fig. 6B). The Tyr–O to Gln–O distance distribution sharpened to a prominent peak at 270 K and then returned to a broader distribution at 220 K (Fig. 6C). We also computed temperature-dependent hydrogen-bonding frequencies to account for both donor–acceptor distance and orientation. The probability of forming a hydrogen bond between Tyr–O and Gln–O (R1 conformation) increased by 15-fold when cooling from 300 to 270 K (Fig. 6A). In contrast, hydrogen bonding between the Tyr–O and Gln–N (R2 conformation) was at least an order of magnitude less frequent than in the R1 conformation for all temperatures (SI Appendix, Fig. S6). The observed increase in probability to form a hydrogen bond with the proton acceptor upon cooling in R1 is consistent with the increased conductivity (Fig. 6A), indicating that the PT mechanism through the R1 conformation results in the most efficient charge transport. Thus, the observed temperature dependence of the X1 microcrystal can be explained by a competition between the increasing availability of a proton acceptor and the decreasing thermal energy available for hopping as the temperature is lowered, resulting in a crossover at 260 K.

Discussion

Recent studies have identified the critical need to develop model systems to understand the mechanism of charge transport in proteins (4). Here, we utilize four fibril forming short peptides with atomically resolved structures to determine how charge transport is influenced by the protein environment, aromatic residues, and metal ions. Our combined experimental and computational analysis suggest that PCET confers conductivity in amyloid microcrystals. The high conductivity of the X1 microcrystals compared to the other examined microcrystals suggests that the presence of periodically stacked aromatic residues can mediate efficient charge transport with the availability of a nearby proton acceptor. Using a four-electrode setup, we measure intrinsic charge transport unaffected by contacts or other typical artifacts to determine the length and temperature dependencies of conductivity. With recent advances in fabrication of nanoscale electrodes down to subnanometer (63), this method could be widely applicable to a large number of biomolecular systems irrespective of their size (6, 9, 17).

It has been suggested that chains of redox active amino acids could serve a biological role by mediating hole hopping to prevent oxidative damage of enzyme active sites (3). Here, we provide direct evidence that proteins can transport charges over micrometer distances under low applied bias potentials via stacked tyrosine residues. Our study shows that carefully structured protein environments can lead to tyrosine oxidation well below the standard oxidizing potential and without any need for a photosensitizer to generate a high oxidation state. We also found that rigidity of the structure, enhanced by the incorporation of a metal ion, is important in maintaining the efficiency of the charge transport pathway as suggested by the higher conductivity of X1 than X2 microcrystals. Both structures showed higher conductivity than metal-incorporated peptide microcrystals that lacked tyrosine residues (X3), demonstrating the crucial role of aromatic residues as a hopping step for transport. We have thus employed both theory and experiments to develop a model for charge transport in these peptide crystals.

Computational studies on modeling of current in filaments of Shewanella oneidensis have also invoked multistep hopping models (54). These studies concluded that to account for observed currents, charge localizing sites need to be within 1 nm even if reorganization energies are assumed to be zero (54). However, structural studies found that cytochromes on these filaments are up to 40 nm apart (64). Therefore, it has been proposed that diffusion of cytochromes along the filaments confer the conductivity to filaments (64). A hopping model (53) has also been invoked for the electron transfer through monomeric cytochromes (65). While we have demonstrated long-range hole hopping through closely stacked tyrosines, there are many ways for proteins to carry out charge transport, and more studies are needed to understand the varying mechanisms.

We expect that these results will motivate the synthesis of new peptides to test predictions of computational models. These findings can help to facilitate a bottom-up atomic-level approach to conductive protein design with structure–function correlation studies leveraging atomic-resolution structures of amyloid crystals. Our methodology will help to set standards for reporting protein conductivity for accurate comparison of different protein systems. In addition, the suggested critical role of the glutamine rotamer conformation is similar to the proton transfer mechanism proposed for the BLUF domain protein (46). Therefore, the suggested transport mechanism may help address long-standing questions about how protein architecture influences electron transport (1) for a wide range of applications that all employ aromatic residues and PCET, including artificial photosynthesis, biocatalysis, prevention of oxidative damage, and nucleic acid biosynthesis.

Materials and Methods

Preparation of Peptide Microcrystals.

Crystals X1 (18), X2 (18), and X3 (19) were prepared as described previously. Microcrystal X4 was prepared by purchasing KVQIINKKL synthetic peptide from GenScript. KVQIINKKL was crystallized using the hanging-drop method with a 2:1 mixture of 20 mg/mL KVQIINKKL and 0.2 M lithium citrate, 20% PEG 3350. All microcrystal hanging-drop samples were diluted in their respective crystallization reservoir buffer for storage and subsequent single-crystal conductivity measurements.

Sample Preparation for Conductivity Measurements.

Nanoelectrode devices were washed with acetone, isopropanol, ethanol, and water twice, and then plasma cleaned for 2 min on a low setting (Harrick Plasma Cleaner; PDC-001-HP). All microcrystals were suspended in their respective reservoir buffer at varying dilutions. Appropriate dilutions of the original microcrystal stock solution (1:100) were made with either reservoir buffer or water, and 3 to 4 µL was dropped onto a clean device. Devices were first dried in a desiccator for ∼25 min. Excess dried buffer was removed with filter paper. Samples were checked under the MPI probe station optics, and if necessary, a microcrystal was moved onto the center of electrodes using a titanium probe needle. For all samples, the area of the device around the electrodes was cleaned with water and dried with filter paper to remove residual buffer. All samples were air dried overnight and mounted onto a metal puck for imaging by AFM in air (Oxford Instruments, Cypher ES, or Bruker Dimension Fastscan). All experiments were performed at atmospheric pressure in ambient air.

DC Conductivity Measurements.

Connections to device electrodes were made with a probe station (MPI TS50) inside a Dark Box. Current and voltage were applied using a semiconductor parameter analyzer with preamplifiers (Keithly 4200 A-SCS) allowing for 1-fA current and 0.5-μV resolution. Two-probe DC conductance measurements utilized two-probe needles to contact the device on two adjacent electrodes. A fixed voltage was applied to the two electrodes for a minimum of 200 s in sampling mode until a steady current was reached. Voltage–current points were fit with a line, and the slope was used to determine conductance (G). In four-probe DC measurements, contacts were made with four gold electrodes connected by a microcrystal. Current was applied to the outer two electrodes in the range of ±1 to 100 pA. The current was held for a minimum of 200 s, and the voltage difference at steady state was recorded from the two inner electrodes. The slope of the subsequent V–I curve was used to determine intrinsic sample resistance. For resistance vs. length measurements, the setup started in the four-probe setup; the last two probes were moved over by one electrode such that the four probes spanned five electrodes. The resistance was measured, and the last two probes were again moved by one electrode. This process was repeated three times to reach 350 nm. For measuring conductivity using both two- and four-probe measurements, linearity of current and voltage was maintained by applying appropriate voltage and current, respectively.

Temperature-Dependent DC Conductivity Measurements.

The sample was placed in a cryostat (Quantum Design DynaCool PPMS), and conductivity was measured using the Keithly 4200 A-SCS. Both two- and four-probe DC measurements were performed at each temperature once the temperature reached an equilibrium. Activation energy was calculated by an Arrhenius fit to the natural logarithm of conductivity vs. the inverse temperature.

Conductivity Calculations.

Conductivity of the microcrystals was calculated by using the conformal mapping technique: $\sigma =\left(-\pi G/L\right)\ast \ln {\left(\left(1/4\right)\left(\tanh \left(\pi a/2g\right)/\tanh \left(\pi b/2g\right)\right)\right)}^{-1}$, where G is the conductance (in siemens), a is half the separation of electrodes (150 nm), b is the width of the electrode plus a (450 nm), L is the length of the microcrystal in contact with the electrode, and g is the height of the microcrystal (9). In our case, g = L because the microcrystals are very regular in shape. A table of all crystal conductivities, average resistance, and average heights can be found in SI Appendix, Table S10. Conductivity of a blank device was calculated using the formula σ = KG, where K is the cell constant (66). The conductivity value for resistance vs. length was calculated by using the linear fit at 300 nm to get a resistance value and then using the equation above. Flux at 0.1 V was calculated by assuming all tyrosines within the crystal are active carriers and that transport occurs only along the crystal’s long axis. Additionally, we assumed every charge transport path is independent of one another and thus adds linearly to the flux. The height of the crystal was 200 nm. Assuming a square cross-sectional area and 0.5 active Tyr per nm² (from the structure), we calculated the flux per path of stacked tyrosines (Fig. 5B). Length was converted to number of hopping steps by dividing the distance by edge-to-edge separation of Tyr (3.5 Å). Contact resistance in Fig. 6 was calculated as the difference between the two- and four-probe resistances at each temperature of two separate crystals.

Data Availability.

Protein structure data have been deposited in the Protein Data Bank (PDB ID code 6NK4). All study data are included in the article and SI Appendix.