Abstract
Detection of incident hepatitis C virus (HCV) infections is crucial for identification of outbreaks and development of public health interventions. However, there is no single diagnostic assay for distinguishing recent and persistent HCV infections. HCV exists in each infected host as a heterogeneous population of genomic variants, whose evolutionary dynamics remain incompletely understood. Genetic analysis of such viral populations can be applied to the detection of incident HCV infections and used to understand intra-host viral evolution. We studied intra-host HCV populations sampled using next-generation sequencing from 98 recently and 256 persistently infected individuals. Genetic structure of the populations was evaluated using 245,878 viral sequences from these individuals and a set of selected features measuring their diversity, topological structure, complexity, strength of selection, epistasis, evolutionary dynamics, and physico-chemical properties. Distributions of the viral population features differ significantly between recent and persistent infections. A general increase in viral genetic diversity from recent to persistent infections is frequently accompanied by decline in genomic complexity and increase in structuredness of the HCV population, likely reflecting a high level of intra-host adaptation at later stages of infection. Using these findings, we developed a machine learning classifier for the infection staging, which yielded a detection accuracy of 95.22 per cent, thus providing a higher accuracy than other genomic-based models. The detection of a strong association between several HCV genetic factors and stages of infection suggests that intra-host HCV population develops in a complex but regular and predictable manner in the course of infection. The proposed models may serve as a foundation of cyber-molecular assays for staging infection, which could potentially complement and/or substitute standard laboratory assays.
Keywords: viral infection, infection stage, quasispecies, cyber-molecular assay, machine learning
1. Introduction
Hepatitis C virus (HCV) infection remains a major cause of morbidity and mortality, with an estimated 70 million people being HCV infected worldwide in 2015 (Blach et al. 2017). HCV infection is the leading cause of chronic liver diseases and hepatocellular carcinoma worldwide, contributing to the death of more than 350,000 people in 2015 (Blach et al. 2017). Hepatitis C outbreaks continue to occur, posing a serious challenge to public health (Zibbell et al. 2015). HCV is highly mutable. As a result, each infected individual hosts a heterogeneous population of genetically related HCV variants or ‘quasispecies’ (Domingo, Sheldon, and Perales 2012). Substantial diversity of intra-host viral populations plays a crucial role in disease progression and epidemic spread (Ramachandran et al. 2011; Skums, Bunimovich, and Khudyakov 2015; Campo et al. 2016). However, intra-host dynamics of HCV and other RNA viruses remain poorly understood. One of the most important questions is the relative contribution of random and deterministic evolutionary factors in disease progression or, using the metaphor of Gould (1990), whether it is possible to ‘replay the tape of life’ for the virus evolution inside a host. This question is of high importance for biomedical research, as predictability of viral evolution potentially implies the power to understand and control the disease (Lassig, Mustonen, and Walczak 2017; Seo et al. 2020), which may result in advanced diagnostic and treatment strategies.
In this article, we study evolutionary factors associated with the transition between HCV infection stages. In more than 50 per cent of cases untreated HCV infection proceeds to the chronic phase, which can lead to the development of liver cirrhosis and/or hepatocellular carcinoma (Seo et al. 2020). Accurate recent or persistent staging of HCV infection is important for biomedical applications. In clinical settings, it may inform the patient management and treatment strategy. In epidemiology, identification of acute cases allows for detection and investigation of recent transmissions and outbreaks and provides information on disease incidence. Understanding of changes in intra-host HCV populations at different stages of infection would constitute a large step towards reliable forecasting of viral evolutionary dynamics.
Recent HCV infection is usually assessed using clinical symptoms and time since seroconversion. HCV infection may, however, remain asymptomatic for years while seroconversion is not frequently detected, preventing accurate identification of infection stages. Several laboratory methods have been reported for distinguishing acute and chronic stages of infection (Bowen and Walker 2005; Araujo et al. 2011). Detection of HCV RNA in the absence of anti-HCV activity in serum specimens was used as an indication of recent HCV infection (Tsertsvadze et al. 2016). Although a strong marker, it has a very short duration and cannot be used for reliable detection of acute infections.
Advent of next-generation sequencing (NGS) presented an opportunity to sample and analyse unprecedented large numbers of intra-host viral variants from numerous infected individuals. HCV variants sampled by NGS have been used to detect stages of HCV infection (Astrakhantseva et al. 2011; Montoya et al. 2015). The stage detection methods are generally based on the assumption that intra-host viral evolution is driven by the continuous immune escape resulting in genetic diversification. Consequently, quantitative measures of genetic diversity of intra-host viral variants are assumed to be most useful for staging. However, several recent reports contested the veracity of this assumption. In particular, after initial diversification, intra-host HCV populations may actually lose heterogeneity and stop diverting at later stages of infection (Ramachandran et al. 2011; Gismondi et al. 2013), with certain viral variants persisting in infected hosts for years (Ramachandran et al. 2011; Palmer et al. 2014). Furthermore, this process is accompanied by an increase of negative selection over the course of HCV infection (Lu et al. 2008; Ramachandran et al. 2011; Gismondi et al. 2013; Campo et al. 2014). These findings suggest a high level of intra-host adaptation at late stages of infection (Skums, Bunimovich, and Khudyakov 2015) and indicate that genetic heterogeneity is not a reliable marker for infection staging, and more elaborate metrics are needed to understand HCV evolution and to accurately classify recent and persistent HCV infection.
Here, we present a new approach for staging HCV infection using quantitative genomic measures to evaluate diversity, information content, effective dimensionality, topological structure, evolutionary dynamics, and physico-chemical properties of intra-host HCV variants and populations. Analysis of features’ distributions at early and late stages of infection suggests that intra-host HCV populations evolve in a complex but regular and predictable manner. Based on these findings, we propose a multi-feature machine learning classifier for staging HCV infection. The model allows for more accurate detection of recent HCV infection than models based only on population diversity and provides new insights into mechanisms of infection progression.
2. Materials and methods
2.1 Data collection and preprocessing
We analysed intra-host HCV populations sampled from recently (N = 98) and persistently (N = 256) infected persons collected as described in (Lara, Teka, and Khudyakov 2017). The E1/E2 junction of the HCV genome (L = 246 nt), which contains the hypervariable region 1 (HVR1), was sequenced using the GS FLX System and the GS FLX Titanium Sequencing Kit (454 Life Sciences, Roche, Branford, CT). Obtained sequences were processed using the error correction and haplotyping algorithm K-mer Error Correction (KEC) (Skums et al. 2012), which produced 245,878 unique viral haplotypes with frequencies. Sequences of each population were aligned using MUSCLE (Edgar 2004). Since obtained average numbers of sequences for recent and persistent populations were different (∼n = 295 and ∼n = 846, respectively), the features studied in this paper were normalized, when appropriate.
2.2 Features calculation
The analysed features could be loosely split into four groups: genomic features, complexity features, network features, and biochemical features. The features are summarized in Table S1 (see Supplementary Table S1). We assumed that a given intra-host population contains n unique haplotypes with frequencies Sixteen features corresponding to this population constitute its ‘feature vector’.
2.2.1 Genomic features
These features are obtained by direct comparison of sequences from each population.
‘Distance-based’ features include ‘mean and SD’ of pairwise hamming distance distribution (‘Features 1 and 2’), and the ‘conservation score (Feature 3)’ of the population consensus sequence calculated with the NUC44 scoring matrix (Nguyen, Guo, and Pan 2016). We also used the so-called ‘mutation frequency’ feature (Feature 4) (Montoya et al. 2015), which is defined as the mean distance between all haplotypes and the most frequent haplotype. All four features measure the population diversity.
Diversity was also quantified using three ‘entropy-based’ features. Suppose that the intra-host population is fixed. For the genomic position , let be a collection of -mers (subsequences of length ) of all haplotypes starting at that position. The positional -entropy is defined as the entropy of the frequency distribution of -mers starting at :
| (1) |
Here is the set of unique elements of is a -mer, and refers to the relative frequency of inside . An ‘average positional k-mer entropy’ (Feature 5) is the mean of positional -entropies over all positions. For , the feature (Feature 6) is an entropy of observed haplotype frequencies, while for , it is an average position-wise single nucleotide variant (SNV) entropy (Feature 7). In our model, we used entropies (Feature 7), (Feature 6), and (Feature 5).
Next, we estimated the frequency of ‘transversions (Feature 8)’ (mutations between purines and pyrimidines) among all observed mutations within the population. This feature is suggested by previous studies (Powdrill et al. 2011) that reported higher frequencies of transitions over transversions in HCV populations.
‘Selective pressure’ was measured using the DN/DS ratio (Feature 9), which has been calculated as the ratio of rates of non-synonymous (DN) and synonymous (DS) substitutions with respect to the most frequent genomic variant.
2.2.2 Complexity features
‘PCA complexity (Feature 10)’ is derived from principal component analysis (PCA). PCA has been widely used to quantify patterns of genomic population structure, and the idea to use the number of principal components that explain a given portion of variation to estimate the effective number of subpopulations inside a population has been described and justified in Patterson, Price, and Reich (2006) and Cavalli-Sforza, Menozzi, and Piazza (2018). In our case, for each population, we transform its alignment into numerical matrix M by transforming nucleotides as A = 0001, C = 0010, T = 0100, G = 1000. The complexity is then defined as the percentage of principal components required to explain at least per cent of the observed genetic variance, that is , where are the eigenvalues of a covariance matrix of M. In this study, we used the complexity with . This can be justified by several arguments. First, the value is large enough to reflect the significant portion of the population’s genomic composition. Second, each population in general can be characterized by the area under the curve , which takes into account all possible values of . However, if M is non-singular, then, given that is monotonically increasing, as and as , this area is accurately enough reflected by the value at the middle point of the curve’s domain.
‘Kolmogorov complexity (KC) (Feature 11)’ is the classical concept of information theory, which quantifies the descriptive/information complexity of a string over a finite alphabet (Li and Vitanyi 2019). Informally it is defined as the highest possible degree of compression of a given string without loss of information. Although the exact value of KC (Feature 11) is algorithmically incomputable, it can be efficiently approximated using data compression techniques. In our case, each viral sequence has been transformed into a binary string (as described above), and these strings have been concatenated into a string of length |s|. Following Kaspar and Schuster (1987), the normalized KC (Feature 11) was estimated as . Here is a ‘Lempel-Ziv complexity’ of s defined as the number of unique substrings encountered by a computational process that constructs s by adding its symbols one by one; and is the asymptotical expected Lempel-Ziv complexity of a random string of length (for more detailed description, see Lempel and Ziv 1976; Kaspar and Schuster 1987). Under this definition, ‘simpler strings’ (i.e. strings with more regular structure) have lower complexity.
2.2.3 Network features
This group of features is derived from the analysis of ‘genetic networks’ of HCV populations, which represent a ‘sequence space’ (Kaspar and Schuster 1987) of a virus. Formally, for each patient, its genetic network is a graph, whose vertices represent sampled viral haplotypes, and edges connect variants that differ by at most mutations (by default ) (Fig. 1). With each vertex we associate the frequency of the corresponding haplotype. In the case of a large population size accompanied by a high mutation rate and a fast reproduction time, genetic networks constructed using NGS data represent population structures significantly more accurately than phylogenetic trees (Campo et al. 2014). Their structure is shaped by various factors, such as epistasis, founder effects, and selection pressures that affect the virus over the course of infection (Ramachandran et al. 2011; Schaper, Johnston and Louis 2012). For each network, the following four features have been calculated.
Figure 1.
(A) Examples of genetic viral networks for a persistently infected individual and (B) for a recently infected. The viral network of the recently infected host has the structural properties typical for scale-free networks.
‘Robustness/selection balance (Feature 12)’ has been measured by the correlation between vectors of vertex frequencies and eigenvector centralities. The latter is the principal eigenvector of the adjacency matrix A of . In the classical quasispecies model, vertex centralities are indicative of the mutational robustness of corresponding viral variants, while a high frequency may be indicative of a higher fitness or a higher mutational robustness (van Nimwegen, Crutchfield, and Huynen 1999).
Topological structures of genetic networks have been assessed using two features. The first of them is a normalized ‘s-metric (Feature 13)’ (Li et al. 2005) which measures how close a network is to being scale free. Here, is a degree (number of neighbors) of a vertex , and the normalization factor represents the order of magnitude of the maximum non-normalized -metric for -vertex network. Scale-free networks are ubiquitous in biological and social systems and share specific properties such as a power-law degree distribution, small diameter, and presence of hubs.
The second network structural feature is the average clustering coefficient C (Feature 14), which measures the degree to which network vertices tend to cluster together. It reflects the probability that a random connected vertex triplet is complete (i.e. every pair of vertices is connected by an edge) and is calculated as follows: .
‘Evolutionary dynamics (Feature 15)’ feature estimates an age of the genetic network using a dynamic evolutionary model. The general idea is to simulate variant frequencies using a system of ordinary differential equations (ODE) (Feature 15) and estimate an age of the network as the time when simulated frequencies achieve the best agreement with observed frequencies. Due to the inherent uncertainty of quantitative features of the model, we do not use the actual estimated age as a feature for infection staging, rather we classify patients based on the qualitative behaviour of the function describing the deviation of simulated and observed frequencies over time.
Formally, we separate each intra-host viral population into subpopulations corresponding to connected components of the genetic network. For each subpopulation, viral evolution is described by the dynamical system (equations (2–5)), partially inspired by the ideas from Wodarz (2003) and Rong et al. (2010).
| (2) |
| (3) |
| (4) |
| (5) |
Variable represents numbers of uninfected target cells, variables represent cells infected by virions with th genome, variables represent virions with th genome in the host’s serum, and variables represent -cell antibodies targeting the ith genome. The constants are model parameters representing various rates. In this study, we used the values of these parameters estimated in Dahari et al. (2009) and Rong et al. (2010). According to the model, uninfected hepatocytes are produced by differentiation of precursor cells at a constant rate , proliferate by a logistic growth law with a rate due to the limited liver cell carrying capacity and die at rate . Cells are infected by a variant at a rate and, after being infected, are eliminated by the cross-immunoreactive Cytotoxic T Lymphocytes (CTLs) at rate . The virions with the th genome are introduced to the blood by the cells infected by the variant at the rate , where is a probability of mutation between variants and , is the Hamming distance between genomes and , is the length of the genomes, and is the mutation rate. Specific B-cell antibodies eliminate the corresponding virions at a rate . They are stimulated by the corresponding viral variants at the rate and decays at a rate in the absence of stimulation.
An estimated age of the network could be defined as the time when simulated frequencies achieve the best agreement with observed frequencies, that is , where is a Jensen–Shannon divergence between distributions and . However, numerical features in equations (2–5) could be uncertain or patient specific. As a result, the estimated numerical values of for different patients cannot be directly compared and used for the classification. More reliable classification can be achieved using qualitative characteristics of the deviation function , which are not significantly affected by the parameters’ variation. Intuitively, if the model (2–5) adequately describes the evolution of viral populations, then the model for recent populations achieves the best agreement between model-based and observed frequencies for earlier populations, and the agreement deteriorates with time. Similarly, for older populations, the agreement is low at earlier times and increases till it reaches a maximum at some late time point. Thus, in general, recent and old populations are expected to be characterized by deviation functions with descending and ascending trends, respectively. Based on this idea, we classify viral subpopulation as recent or old based on the coefficients of the approximation of by the exponential function .
It is known that some patients have mixtures of components under different types of selection (Campo et al. 2014). In particular, chronically infected hosts may have components of different ages, and the overall age of infection should be defined by the oldest component. Given this, the classification of a patient was performed separately for each connected component of the genetic network. The patient is classified as persistently infected, if at least one of the connected components is old, and as recently infected, if all of them are recent. The prediction age variable (Feature 15) is set to be equal to in the first case and in the second case.
2.2.4 Biochemical feature
This feature (Feature 16) assesses the physico-chemical properties of sequences from viral populations. In brief, a large set of physico-chemical parameters is considered for each sequence from a given population. The goal is to synthesize the information from all sequences into a single population feature that is added to the other features for the final analysis. This is done first by applying a prediction model to assess whether a given sequence has a physico-chemical profile associated with recent or persistent infection, using the method described below. The biochemical index of an entire population is then defined as the probability that a random sequence from this population has a profile pointing to persistent infection.
Feature selection, feature extraction, and training of the classification model were done using a balanced training set of 3,933 sequences (1,965 sequences for the persistent class and 1,968 sequences for the recent class). First, following the general pipeline described in Lara et al. (2018), we generated the initial set of 600 physico-chemical features to evaluate the biochemical feature space of nucleotide sequence variants of HCV HVR1. Briefly, feature vector representations of HVR1 were constructed using dinucleotide-based auto-covariance formula (Liu et al. 2015), where is a physico-chemical index and is the distance separating two nucleotide dimers along the nucleotide sequence. We initially used 148 physico-chemical indexes to construct biochemical features of DNA dimers (Lara, Teka, and Khudyakov 2017). The auto-covariance formula (Liu et al. 2015), where = 148 and = 1, was used to compute a preliminary 148-long variable feature vector representation for each HCV HVR1 sequence. Next, we measured the Pearson correlation coefficient of each index to the persistent and recent classes to select the best class-correlated indexes. A total of ten physico-chemical indexes, comprising the 148-long variable feature vectors, were found to have statistically significant feature-class correlation (R threshold value and after multiple testing correction), which incorporated the following indexes of DNA dimers (Lara, Teka, and Khudyakov 2017): the thermodynamic indexes (Breslauer-dH and Breslauer-dG), structural indexes (twist-tilt, slide-rise, protein-DNA twist, slide-2, and twist-1), the nucleotide composition index (G-content), and the energy indexes of DNA (stabilizing energy of Z DNA and enthalpy; Friedel et al. 2009; Chen et al. 2014). These ten class-correlated indexes were selected to recompute the auto-covariance per physico-chemical index (with = 10 and = 60), thus generating 600-long variable feature vector representations of HVR1 sequences.
Next, to decrease the dimensionality of feature vectors and to optimize the feature space representation of HVR1 in relation to the persistent/recent classes, we further processed the feature vectors using machine learning-based feature selection techniques (Tsuruoka, Tsujii, and Ananiadou 2009). We used the class-attribute interdependence maximization (CAIM) algorithm (Kurgan and Cios 2004) to automatically generate class-related binary values for each of the continuous physico-chemical values. The obtained 600-long binary feature vectors were then processed by the correlation-based feature selection (CFS) algorithm, which automatically finds the most class-informative feature subset based on a Merit scoring (Wang et al. 2005). The CFS algorithm found a feature subset of 54 variables with a Merit score = 0.6. These 54-dimensional CFS-selected features were used as the final biochemical feature representation of HVR1 sequences.
After that, CFS-selected feature vectors of the sequences were used as input data to train a stochastic gradient descent (SGD) classifier (Zhang 2004; Seo et al. 2020). Briefly, the SGD classifier implements regularized linear models with stochastic gradient descent learning and is a very efficient approach, with linear training cost, which can easily be scaled to big data problems. Selection and tuning of the hyperparameters of the SGD classifier was done using the GridSearchCV module in Scikit-learn Python library. The hyperparameters of the selected probabilistic logistic regression classifier were as follows: loss function = ‘log’, alpha = ‘0.1’, n_iter = 100, class_weight = ‘balanced’, and random_state = 42. Five-fold cross-validation training of the SGD classifier was done using Scikit’s StratifiedKFold function (parameters: n_splits = 5, shuffle = True, and Random_state = 42).
Finally, the trained SGD classifier was used to predict the class probability of all observed HCV HVR1 sequences inside each host. Then the composite biochemical feature of each intra-host population was computed as where n is the number of populations’ haplotypes, and and are the frequency and the predicted class probability of the ith haplotype.
2.3 Machine learning classifier
Feature vectors of recently and chronically infected hosts were used to train machine learning classifiers for infection stage prediction. Given a labelled training set comprising feature vectors together with their class labels (recent or persistent), each classifier is fitted to the training data by adjusting its model features and assigns labels for unlabelled feature vectors using the trained model. In this study, we used Support Vector Machines (SVM) with linear and polynomial kernel and Logistic Regression. Both approaches are classical supervised learning methods that construct a hyperplane in the multidimensional Euclidean space, which serves as a separator for feature vectors from classes of recently and persistently infected hosts.
3. Results
3.1 Stage-specific distributions of features
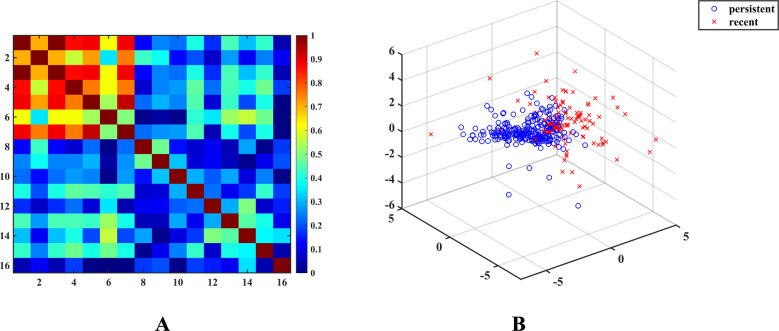
Our model consists of sixteen diverse features categorized in four groups: genomic features, complexity features, network features, and biochemical features. The three features (-entropy, SNV entropy, and conservation score; Features 3, 5, and 7, respectively) were found to be in high correlation with Feature 1 and with each other (Fig. 2A). For the remaining thirteen features, there is a small to medium correlation between them (Fig. 2A), demonstrating that they reflect different properties of intra-host viral populations.
Figure 2.
(A) Heatmap of absolute values of pairwise correlations between features. (B) 3-Dimensional projection of recently and persistently infected hosts (with highly correlated features removed).
Feature vectors of recent and persistent populations are separable from each other (Fig. 2B). For the features, Mann–Whitney U test suggests statistically significant difference between recent and persistent intra-host populations (Table S1).
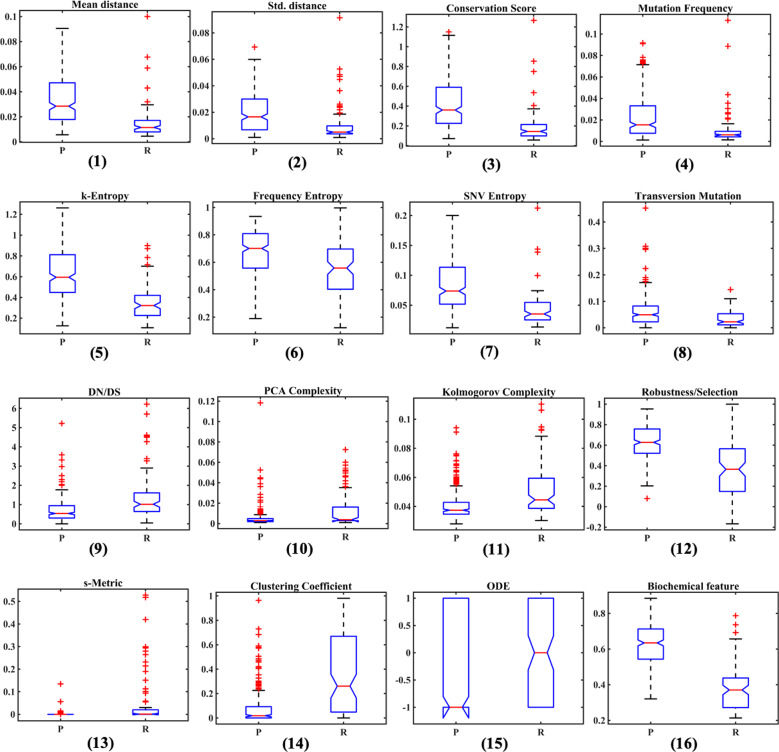
As expected, diversities are on average higher for persistent than recent populations (Fig. 3 (1–7)). Higher genetic diversity of persistent populations is accompanied by significantly lower PCA (p < 0.01) and KCs (Features 10 and 11) (Fig. 3 (10, 11)). The decrease of complexity points to a higher level of adaptation and organization of intra-host populations (see Discussion). The emergence of intra-host adaptation is further supported by the increase in negative selection (Feature 9) (Fig. 3(9)) at later stages of HCV infection. It can be claimed that this trend is not due to spurious correlations associated with the difference in numbers of sequences for recent and persistent populations. When the patients with less than q sampled sequences are discarded, then the numbers of sequences for recent and chronic patients are more balanced (∼1,139 and ∼1,340 in average, respectively, for q = 200 and ∼1,350 and ∼1,594, respectively, for q = 300), and the trend to have lower PCA and KCs (Features 10 and 11) for persistent populations remain to be statistically significant (). Furthermore, the significant difference between PCA complexities (Feature 10) of recent and persistent populations is observed for different values of the variance threshold. Indeed, the areas under the curves , (), for persistent populations P remain significantly lower than for recent populations ().
Figure 3.
Box plots of feature distributions for persistent (left box plot on each graph) and recent (right box plot on each graph) intra-host HCV populations. The plots are in the same order as in Supplementary Table S1.
Recent and persistent HCV populations are also separable by an ODE feature (Feature 15) (Fig. 3 (15)). However, it should be noted that the minimal JS divergence between model-based and observed frequencies is significantly lower for recent than for chronic patients (∼0.07 vs 0.12, respectively, ). Thus, the immune escape-based model (2–5) describes recent populations more accurately than persistent populations. This observation could point to a declining role of immune escape.
Transition mutations were overwhelmingly more frequent than transversion mutations (Feature 8) for both classes of samples. This fact agrees with the previously published results (Powdrill et al. 2011), although the magnitude of difference vary along the genome: HVR1 transitions are times more frequent than transversions, while a seventy-five-fold difference was reported for NS5B (Powdrill et al. 2011). However, prevalence of transversions was times higher in persistent populations (Fig. 3 (8)). This property of intra-host viral evolution also agrees with previous studies (Duchene, Ho, and Holmes 2015) on the between-host level that suggests that the propensity of transition/transversion ratio to decline could be associated with the growth of genetic saturation.
Genetic networks of recent and persistent intra-host populations possess different structural properties. Networks of recent populations have significantly higher s-metrics and clustering coefficients (Features 13 and 14) (Fig. 3 (13, 14)). It indicates that, in contrast to the persistent populations, they tend to have structural properties more typical for scale-free networks, including the power-law degree distribution with clearly manifested hubs (high-degree vertices), with their vertices having propensity to cluster (Fig. 1). This observation reflects the role of founder viral variants at the earlier stage of infection (see Discussion). A significantly higher correlation between frequencies and network centralities of variants in persistent populations (Feature 12) (Fig. 3 (12)) indicates that the population structure at later stages is significantly influenced by mutational robustness, while at earlier stages, it is basically defined by founders.
Finally, individual sequences of recent and persistent populations have distinct physico-chemical properties (Feature 16) (Fig. 3 (16)).
3.2 Machine learning classification
Mutation frequency, -entropy, and frequency entropy (Features 4, 5, and 6) have been excluded from the prediction model as they are highly correlated with Feature 1 and with each other. The remaining thirteen features were used to train SVMs and Logistic Regression classifiers for binary classification of intra-host viral populations labelled as ‘persistent’ and ‘recent’. Although these classifiers do not necessarily require removal of highly correlated features, they were dropped to reduce a likelihood of overfitting. Accuracy of classifiers has been assessed using a two-step cross-validation. First, to account for the bias associated with unequal numbers of cases with persistent () and recent () infection, repeated random subsampling of ninety-eight populations from the persistent sample data set was performed. For each of the balanced training sets ten-fold cross-validation was carried out.
The average prediction accuracies are reported in Table 1. Classification performance evaluation of all methods indicates a high accuracy of infection stage inference, with SVM with quadratic kernel demonstrating the highest accuracy of .
Table 1.
Prediction accuracies of machine learning methods.
| Method | Mean prediction accuracy | 95% CI |
|---|---|---|
| SVM—linear kernel | 95.07% | (94.909, 95.233) |
| SVM—quadratic kernel | 95.18% | (95.004, 95.356) |
| Logistic regression | 92.98% | (92.908, 93.051) |
SVM classifier with quadratic kernel has been compared to the previously published HCV infection staging models (Montoya et al. 2015) which classify intra-host viral populations as recent or persistent using frequency entropy (Feature 6), SNV entropy (Feature 7), or mutation frequency (Feature 4). The Receiver Operating Characteristic (ROC) curves of the classifiers are shown in Fig. 4. Previously proposed methods (, , and , respectively) were less accurate in comparison with the SVM classifier (, thus suggesting that diversity features alone are not sufficient for accurate distinction between recent and persistent cases. SVM classifier performed at the expected lower accuracy on randomly labelled data sets (average ), thus indicating that the associations between feature distributions and infection stages are likely due to the structural and evolutionary factors rather than to random statistical correlations in the data.
Figure 4.
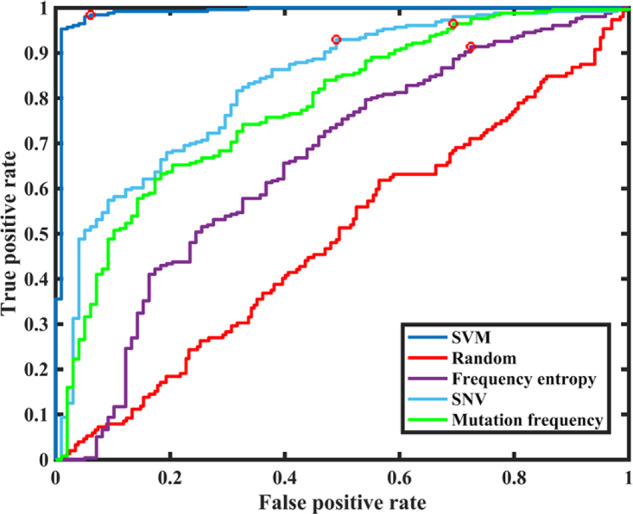
ROC curves of classification models.
4. Discussion
We present the results of comprehensive analyses of the structure of intra-host viral populations using a large set of samples from individuals with recent and persistent infection, which significantly exceeds data sets used in earlier studies (Montoya et al. 2015). Amplicons covering HCV HVR1 have been sequenced by NGS. Intrinsically disordered regions (IDRs) of proteins like HVR1 seem to be most useful for application in models to identify viral clinical properties from sequences. It has an extensive epistatic connectivity across the entire HCV polyprotein (Lara et al. 2011) and is associated with immune escape (Law et al. 2018), drug resistance (Aurora et al. 2009; Lara et al. 2011), and virulence (Lara and Khudyakov 2012). Consequently, IDRs play an important role in viral adaptation to the host environment, making regions like HVR1 sensitive ‘sensors’ that accurately reflect intra-host biological changes during the infection process.
Our results indicate significant differences in the structure of HCV populations sampled from recently and persistently infected hosts and suggest that intra-host HCV populations develop in a complex but ordered and predictable manner during the course of infection. This form of evolutionary regularity manifests itself in the presence of viral genetic features strongly associated with stages of infection. Utilization of these features for machine learning allowed us to train classifiers capable of inferring infection stage from HCV sequence data with accuracies as high as 95 per cent. Our study confirms a previously established positive correlation between infection stage and intra-host viral diversity (Araujo et al. 2011; Shen et al. 2014; Montoya et al. 2015). However, because of complexities in the structural development of intra-host populations affected by bouts of selective sweeps and negative selection during chronic infection (Skums, Bunimovich, and Khudyakov 2015; Raghwani et al. 2016), simple metrics of genetic heterogeneity are insufficient for the accurate staging of HCV infections. High accuracy could be achieved by using a combination of features measuring different structural and evolutionary properties of viral populations. Furthermore, most of the analysed features are easily computable and do not require computationally intensive phylogenetic and phylodynamic inference. Thus, the proposed prediction models may serve as accurate and scalable ‘cyber-molecular assays’ for staging infection, which could potentially complement and substitute standard laboratory assays. In particular, the proposed models are currently being incorporated into Global Hepatitis Outbreak and Surveillance Technology (GHOST) (Longmire et al. 2017)—a web-based molecular surveillance system developed and maintained by Centers for Disease Control and Prevention (CDC). Moreover, the overall strategy described in this study may serve as a foundation for cyber-molecular diagnostics (Campo and Khudyakov 2020).
All feature changes described in this study reflect major trends of intra-host viral evolution that have been previously explored and described (Ramachandran et al. 2011; Duchene, Ho, and Holmes 2015; Skums, Bunimovich, and Khudyakov 2015). Some changes such as the increase of transversions and genetic heterogeneity of viral populations seem to be more directly than others associated with duration of infection and linked to high mutability and genetic saturation (Duchene, Ho, and Holmes 2015; Montoya et al. 2015). Changes of other features are likely associated with variation in selection pressures operating at different stages of infection.
The dynamics of analysed features suggests that intra-host HCV evolution at the initial stage of infection is largely different from evolution at later stages of infection. In particular, the physico-chemical properties of HVR1 variants appear to be influenced by and responsive to intra-host environmental factors specific to the recent and persistent stages of HCV infection. The change of properties is likely to be associated with different evolutionary mechanisms operating at different infection stages. Early evolution is likely defined by a founder-flush process (Templeton 2008; Ramachandran et al. 2011) which rapidly generates massive selectable genetic heterogeneity. This is reflected, in particular, by pronounced scale-free properties of recent genetic networks. Indeed, star-like networks (the simplest scale-free networks), just like star-like phylogenies, typically represent populations that recently underwent a population expansion from a single founder. For HCV, transmissions of higher multiplicity have been observed (Li et al. 2012); furthermore, the population could expand by the time of sampling. In that case, the observed genetic network may not be exactly star-like, but multiple founder variants (median = 4; Friedel et al. 2009) should still serve as most central vertices, resulting in more general scale-free structure. Evolution of recent populations seems to be driven by positive selection (DN/DS > 1). In such settings, the contribution of mutational robustness is less pronounced, resulting in the lower values of the robustness/selection balance feature (Feature 12) for recent populations. In particular, the network centres are likely founders transmitted from their previous hosts, some of which may be less fit than newly generated variants in the new host, resulting in the eventual decrease of their observed frequencies over time.
In contrast, later stages are likely to be defined by the virus adaptation to the host environment and varying immune selection pressures. The process of adaptation results in an orderly development of intra-host viral populations which is reflected by the increase of negative selection and decrease of PCA and KCs (Features 10 and 11). The major role here is played by epistasis. For HCV, it is frequently detected in the form of coordinated substitutions, which are organized into a complex network of epistatic connectivity (Campo et al. 2008). Coordinated substitutions reflect selection pressures acting on intra-host viral populations and represent dependence of phenotypic effects of mutations on other mutations or on genetic background to which these mutations occur (Campo et al. 2008). HCV epistatic interactions have been shown to be associated with host factors (Lara et al. 2011; Lara, Purdy, and Khudyakov 2014), drug resistance (Aurora et al. 2009; Lara and Khudyakov 2012; Thai et al. 2012), disease severity (Lara et al. 2014), and coinfections (Dahari et al. 2009). Many features analysed here could be essentially linked with the underlying epistatic networks. For example, high complexity indicates a high level of randomness of a sequence, whereas low complexity implies the presence of specific structural patterns inside a sequence (Li and Vitanyi 2019). The reduction in complexity of the late-stage intra-host HCV populations indicates increase in epistatic connectivity among polymorphic sites resulting from strong functional constraints experienced by these populations. Such constraints shape adaptation of viral populations to specific intra-host environments. At the earlier stages of infection, nucleotide changes are seemingly more random, resulting in populations with higher dimensionality. Changes in physico-chemical properties based on auto-correlation also likely reflect variations in the structure of epistatic networks established during early and late stages of infection in addition to variation in the strength of connectivity in these networks (Lara, Teka, and Khudyakov 2017).
Given the above observations, it is unlikely that the entire intra-host HCV evolution is driven by a single evolutionary mechanism. The changes of evolutionary parameters are consistent with the hypothesis that intra-host HCV evolution is not a simple accrual of genetic heterogeneity resulting from the ‘arms race’ between the virus and the host’s immune system or a random genetic drift within the space of effectively neutral genomic variants. It is rather a complex process defined by the recurring presentation of a succession of selection challenges specific to each stage of infection (Ramachandran et al. 2011; Skums, Bunimovich, and Khudyakov 2015). In this process, different modes of evolution can be dominant at different stages. The arms race seems to drive intra-host HCV evolution at its early stages, as indicated by the positive selection, smaller impact of mutational robustness and the fact that ODE model (Feature 15) (2–5) describes recent populations quite accurately. However, the ‘perpetual arms race’ model is inconsistent with the observed increase of negative selection, long-term persistence of particular genomic variants (Ramachandran et al. 2011; Palmer et al. 2014), and antigenic convergence (Campo et al. 2012). Similarly, strong coordination of variability and functionality among genomic sites is unlikely to be established as a result of a neutral evolution and should be the result of selection. However, it is quite possible that the stable ‘end game’ or equilibrium population observed at its later stages will be ‘internally’ neutral (under the network neutrality definition from van Nimwegen, Crutchfield, and Huynen 1999). Such a population can be located at a local fitness landscape plateau and form a neutral genetic network, where fitnesses of its nodes are equal and greater than for variants outside the network. This can lead to the higher impact of mutational robustness on the relative variant frequencies ‘inside’ this network (van Nimwegen, Crutchfield, and Huynen 1999). However, it should be remembered that the viral fitness landscape is essentially dynamic and is defined by emerging immune responses and cross-immunoreactivity between current and past viral genotypes (Skums, Bunimovich, and Khudyakov 2015). Thus, the currently observed internally neutral network should have been selected over the course of evolution.
The most intriguing stage of intra-host HCV evolution is the transition between two aforementioned stages, that is, between the immune escape under positive selection and a conditionally stable state under the negative selection. The reported results are consistent with the hypothesis that this transition can be caused by the development of specific cooperative interactions among intra-host viral variants (Skums, Bunimovich, and Khudyakov 2015; Domingo-Calap et al. 2019). Under this model, HCV immune adaptation is associated with antigenic cooperation among intra-host HCV variants (Ramachandran et al. 2011; Skums, Bunimovich, and Khudyakov 2015), due to complementary roles played by viral variants in mitigation of neutralizing immune responses defined by their topological location in cross-immunoreactivity networks (Campo et al. 2012). This model posits that intra-host viral populations evolve as quasi-social systems of functionally complementary variants (Skums, Bunimovich, and Khudyakov 2015; Domingo-Calap et al. 2019). Such functional differentiation enables HCV adaptation to the changing intra-host environment as a group of cooperators rather than independent variants.
Supplementary data
Supplementary data are available at Virus Evolution online.
Funding
PS and AZ were supported by National Institutes of Health, (grant number: 1R01EB025022). PIB was supported by Georgia State University Molecular Basis of Disease fellowship. The funders had no role in study design, data collection and analysis, or preparation of the manuscript.
Data availability
The proposed method’s scripts are available in the following GitHub repository https://github.com/compbel/recentvschronic. The data can be obtained from the CDC according to the US government guidelines.
Supplementary Material
Acknowledgements
Research was conducted as approved by the Institutional Review Board of the Centers for Disease Control and Prevention, Atlanta, GA (protocol 7270.0). The findings and conclusions in this report are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention and Georgia State University.
Conflict of interest: None declared.
References
- Araujo A. C. et al. (2011) ‘ Distinguishing Acute from Chronic Hepatitis C Virus (HCV) Infection Based on Antibody Reactivities to Specific HCV Structural and Nonstructural Proteins’, Journal of Clinical Microbiology, 49: 54–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astrakhantseva I. V. et al. (2011) ‘ Differences in Variability of Hypervariable Region 1 of Hepatitis C Virus (HCV) between Acute and Chronic Stages of HCV Infection’, In Silico Biology, 11: 163–73. [DOI] [PubMed] [Google Scholar]
- Aurora R. et al. (2009) ‘ Genome-Wide Hepatitis C Virus Amino Acid Covariance Networks Can Predict Response to Antiviral Therapy in Humans’, The Journal of Clinical Investigation, 119: 225–36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blach S. et al. (2017) ‘ Global Prevalence and Genotype Distribution of Hepatitis C Virus Infection in 2015: A Modelling Study’, The Lancet Gastroenterology & Hepatology, 2: 161–76. [DOI] [PubMed] [Google Scholar]
- Bowen D. G., Walker C. M. (2005) ‘ Adaptive Immune Responses in Acute and Chronic Hepatitis C Virus Infection’, Nature, 436: 946–52. [DOI] [PubMed] [Google Scholar]
- Campo D. S. et al. (2008) ‘ Coordinated Evolution of the Hepatitis C Virus’, Proceedings of the National Academy of Sciences of the United States of America, 105: 9685–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campo D. S. et al. (2012) ‘ Hepatitis C Virus Antigenic Convergence’, Scientific Reports, 2: 267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campo D. S. et al. (2014) ‘ Next-Generation Sequencing Reveals Large Connected Networks of Intra-Host HCV Variants’, BMC Genomics, 15: S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campo D. S., Khudyakov Y. (2020) ‘ Machine Learning Can Accelerate Discovery and Application of Cyber-Molecular Cancer Diagnostics’, Journal of Medical Artificial Intelligence, 3: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campo D. S. et al. (2016) ‘ Accurate Genetic Detection of Hepatitis C Virus Transmissions in Outbreak Settings’, Journal of Infectious Diseases, 213: 957–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cavalli-Sforza L. L., Menozzi P., Piazza A. (2018) The History and Geography of Human Genes. Princeton, NJ: Princeton University Press. [Google Scholar]
- Chen W. et al. (2014) ‘ PseKNC: A Flexible Web Server for Generating Pseudo K-Tuple Nucleotide Composition’, Analytical Biochemistry, 456: 53–60. [DOI] [PubMed] [Google Scholar]
- Dahari H. et al. (2009) ‘ A Mathematical Model of Hepatitis C Virus Dynamics in Patients with High Baseline Viral Loads or Advanced Liver Disease’, Gastroenterology, 136: 1402–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domingo-Calap P. et al. (2019) ‘ Social Evolution of Innate Immunity Evasion in a Virus’, Nature Microbiology, 4: 1006–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domingo E., Sheldon J., Perales C. (2012) ‘ Viral Quasispecies Evolution’, Microbiology and Molecular Biology Reviews, 76: 159–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchene S., Ho S. Y. W., Holmes E. C. (2015) ‘ Declining Transition/Transversion Ratios through Time Reveal Limitations to the Accuracy of Nucleotide Substitution Models’, BMC Evolutionary Biology, 15: 36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edgar R. C. (2004) ‘ MUSCLE: Multiple Sequence Alignment with High Accuracy and High Throughput’, Nucleic Acids Research, 32: 1792–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedel M. et al. (2009) ‘ DiProDB: A Database for Dinucleotide Properties’, Nucleic Acids Research, 37: D37–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gismondi M. I. et al. (2013) ‘ Dynamic Changes in Viral Population Structure and Compartmentalization During Chronic Hepatitis C Virus Infection in Children’, Virology, 447: 187–96. [DOI] [PubMed] [Google Scholar]
- Gould S. J. (1990) Wonderful Life: The Burgess Shale and the Nature of History. New York: W. W. Norton & Company. [Google Scholar]
- Kaspar F., Schuster H. G. (1987) ‘ Easily Calculable Measure for the Complexity of Spatiotemporal Patterns’, Physical Review A, 36: 842–8. [DOI] [PubMed] [Google Scholar]
- Kurgan L. A., Cios K. J. (2004) ‘ CAIM Discretization Algorithm’, IEEE Transactions on Knowledge and Data Engineering, 16: 145–53. [Google Scholar]
- Lara J., Khudyakov Y. (2012) ‘ Epistatic Connectivity among HCV Genomic Sites as a Genetic Marker of Interferon Resistance’, Antiviral Therapy, 17: 1471–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lara J., Purdy M. A., Khudyakov Y. E. (2014) ‘ Genetic Host Specificity of Hepatitis E Virus’, Infection, Genetics and Evolution, 24: 127–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lara J. et al. (2011) ‘ Coordinated Evolution among Hepatitis C Virus Genomic Sites Is Coupled to Host Factors and Resistance to Interferon’, In Silico Biology, 11: 213–24. [DOI] [PubMed] [Google Scholar]
- Lara J., Teka M., Khudyakov Y. (2017) ‘ Identification of Recent Cases of Hepatitis C Virus Infection Using Physical-Chemical Properties of Hypervariable Region 1 and a Radial Basis Function Neural Network Classifier’, BMC Genomics, 18: 880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lara J. et al. (2018) ‘ HCV Adaptation to HIV Coinfection’, Infection, Genetics and Evolution, 65: 216–25. [DOI] [PubMed] [Google Scholar]
- Lara J. et al. (2014) ‘ Computational Models of Liver Fibrosis Progression for Hepatitis C Virus Chronic Infection’, BMC Bioinformatics, 15: S5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lassig M., Mustonen V., Walczak A. M. (2017) ‘ Predicting Evolution’, Nature Ecology and Evolution, 1: 77. [DOI] [PubMed] [Google Scholar]
- Law J. L. M. et al. (2018) ‘ Role of the E2 Hypervariable Region (HVR1) in the Immunogenicity of a Recombinant Hepatitis C Virus Vaccine’, Journal of Virology, 92: e02141-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lempel A., Ziv J. (1976) ‘ On the Complexity of Finite Sequences’, IEEE Transactions on Information Theory, 22: 75–81. [Google Scholar]
- Li H. et al. (2012) ‘ Elucidation of Hepatitis C Virus Transmission and Early Diversification by Single Genome Sequencing’, PLoS Pathogens, 8: e1002880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li L. et al. (2005) ‘ Towards a Theory of Scale-Free Graphs: Definition’, Internet Mathematics, 2: 431–523. [Google Scholar]
- Li M., Vitanyi P. (2019) An Introduction to Kolmogorov Complexity and Its Applications. Cham, Switzerland: Springer. [Google Scholar]
- Liu B. et al. (2015) ‘ Pse-in-One: A Web Server for Generating Various Modes of Pseudo Components of DNA, RNA, and Protein Sequences’, Nucleic Acids Research, 43: W65–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Longmire A. G. et al. (2017) ‘ GHOST: Global Hepatitis Outbreak and Surveillance Technology’, BMC Genomics, 18: 916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu L. et al. (2008) ‘ HCV Selection and HVR1 Evolution in a Chimpanzee Chronically Infected with HCV-1 over 12 Years’, Hepatology Research, 38: 704–16. [DOI] [PubMed] [Google Scholar]
- Montoya V. et al. (2015) ‘ Differentiation of Acute from Chronic Hepatitis C Virus Infection by Nonstructural 5B Deep Sequencing: A Population-Level Tool for Incidence Estimation’, Hepatology, 61: 1842–50. [DOI] [PubMed] [Google Scholar]
- Nguyen K., Guo X., Pan Y. (2016) Multiple Biological Sequence Alignment: Scoring Functions, Algorithms and Evaluation. Hoboken, NJ: John Wiley & Sons. [Google Scholar]
- van Nimwegen E., Crutchfield J. P., Huynen M. (1999) ‘ Neutral Evolution of Mutational Robustness’, Proceedings of the National Academy of Sciences of the United States of America, 96: 9716–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmer B. A. et al. (2014) ‘ Analysis of the Evolution and Structure of a Complex Intrahost Viral Population in Chronic Hepatitis C Virus Mapped by Ultradeep Pyrosequencing’, Journal of Virology, 88: 13709–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson N., Price A. L., Reich D. (2006) ‘ Population Structure and Eigenanalysis’, PLoS Genetics, 2: e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powdrill M. H. et al. (2011) ‘ Contribution of a Mutational Bias in Hepatitis C Virus Replication to the Genetic Barrier in the Development of Drug Resistance’, Proceedings of the National Academy of Sciences of the United States of America, 108: 20509–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raghwani J. et al. (2016) ‘ Exceptional Heterogeneity in Viral Evolutionary Dynamics Characterises Chronic Hepatitis C Virus Infection’, PLoS Pathogens, 12: e1005894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramachandran S. et al. (2011) ‘ Temporal Variations in the Hepatitis C Virus Intrahost Population During Chronic Infection’, Journal of Virology, 85: 6369–80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rong L. et al. (2010) ‘ Rapid Emergence of Protease Inhibitor Resistance in Hepatitis C Virus’, Science Translational Medicine, 2: 30ra32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaper S., Johnston I. G., Louis A. A. (2012) ‘ Epistasis Can Lead to Fragmented Neutral Spaces and Contingency in Evolution’, Proceedings of the Royal Society B: Biological Sciences, 279: 1777–83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seo S. et al. (2020) ‘ Prevalence of Spontaneous Clearance of Hepatitis C Virus Infection Doubled from 1998 to 2017’, Clinical Gastroenterology and Hepatology, 18: 511–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shen C. et al. (2014) ‘ Transmission and Evolution of Hepatitis C Virus in HCV Seroconverters in HIV Infected Subjects’, Virology, 449: 339–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skums P., Bunimovich L., Khudyakov Y. (2015) ‘ Antigenic Cooperation among Intrahost HCV Variants Organized into a Complex Network of Cross-Immunoreactivity’, Proceedings of the National Academy of Sciences of the United States of America, 112: 6653–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skums P. et al. (2012) ‘ Efficient Error Correction for Next-Generation Sequencing of Viral Amplicons’, BMC Bioinformatics, 13: S6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Templeton A. R. (2008) ‘ The Reality and Importance of Founder Speciation in Evolution’, Bioessays, 30: 470–9. [DOI] [PubMed] [Google Scholar]
- Thai H. et al. (2012) ‘ Convergence and Coevolution of Hepatitis B Virus Drug Resistance’, Nature Communications, 3: 789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsertsvadze T. et al. (2016) ‘ The Natural History of Recent Hepatitis C Virus Infection among Blood Donors and Injection Drug Users in the Country of Georgia’, Virology Journal, 13: 22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsuruoka Y., Tsujii J., Ananiadou S. (2009) ‘Stochastic gradient descent training for L1-regularized log-linear models with cumulative penalty’ in Proceedings of the Joint Conference of the 47th Annual Meeting of the ACL and the 4th International Joint Conference on Natural Language Processing of the AFNLP: Volume 1—ACL-IJCNLP’09. Suntec, Singapore: Association for Computational Linguistics (ACL).
- Wang Y. et al. (2005) ‘ Gene Selection from Microarray Data for Cancer Classification: A Machine Learning Approach’, Computational Biology and Chemistry, 29: 37–46. [DOI] [PubMed] [Google Scholar]
- Wodarz D. (2003) ‘ Hepatitis C Virus Dynamics and Pathology: The Role of CTL and Antibody Responses’, Journal of General Virology, 84: 1743–50. [DOI] [PubMed] [Google Scholar]
- Zhang T. (2004) ‘Solving large scale linear prediction problems using stochastic gradient descent algorithms’ in Twenty-First International Conference on Machine Learning—ICML’04. Banff, Alberta, Canada: The International Machine Learning Society (IMLS).
- Zibbell J. E. et al. (2015) ‘ Increases in Hepatitis C Virus Infection Related to Injection Drug Use among Persons Aged ≤30 years—Kentucky, Tennessee, Virginia, and West Virginia, 2006–2012’, Morbidity and Mortality Weekly Report, 64: 453–8. [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The proposed method’s scripts are available in the following GitHub repository https://github.com/compbel/recentvschronic. The data can be obtained from the CDC according to the US government guidelines.