Probabilistic colocalization of genetic variants from complex and molecular traits: promise and limitations

Summary

Colocalization analysis has emerged as a powerful tool to uncover the overlapping of causal variants responsible for both molecular and complex disease phenotypes. The findings from colocalization analysis yield insights into the molecular pathways of complex diseases. In this paper, we conduct an in-depth investigation of the promise and limitations of the available colocalization analysis approaches. Focusing on variant-level colocalization approaches, we first establish the connections between various existing methods. We proceed to discuss the impacts of various controllable analytical factors and uncontrollable practical factors on outcomes of colocalization analysis through realistic simulations and real data examples. We identify a single analytical factor, the specification of prior enrichment levels, which can lead to severe inflation of false-positive colocalization findings. Meanwhile, the combination of many other analytical and practical factors all lead to diminished power. Consequently, we recommend the following strategies for the best practice of colocalization analysis: (1) estimating prior enrichment level from the observed data and (2) separating fine-mapping and colocalization analysis. Our analysis of 4,091 complex traits and the multi-tissue expression quantitative trait loci (eQTL) data from the GTEx (v.8) suggests that colocalizations of molecular QTLs and causal complex trait associations are widespread. However, only a small proportion can be confidently identified from currently available data due to a lack of power. Our findings set a benchmark for current and future integrative genetic association analysis applications.

Introduction

The advancements in genetic association analysis of complex and molecular traits have uncovered a large volume of putative causal genetic variants. Subsequently, utilizing genetic association discoveries to explore the molecular mechanisms of complex disease etiology has become a standard practice in human genetics research. Various types of analytical approaches designed for the integrative analysis of data from expression quantitative trait loci (eQTL) mapping and genome-wide association studies (GWASs) of complex traits have shown promise in implicating molecular pathways connecting genetic variations, molecular phenotype changes, and complex diseases.1, 2, 3, 4, 5, 6

Colocalization analysis is an integrative analysis technique that aims to identify genetic variants introducing simultaneous phenotypic changes in multiple molecular and/or complex traits. Although colocalization analysis is not constrained by the types of phenotypes investigated, we focus our discussions in this paper on a single complex trait and one type of molecular trait, e.g., gene expressions. The discoveries from this class of analyses have resulted in molecular insights of complex diseases, e.g., atherosclerosis,⁷ the age of onset of menarche and menopause,⁸ and cardiovascular disease.⁹

There are two broad types of colocalization analysis approaches in the current literature. The first kind, represented by regulatory trait concordance (RTC)² and joint likelihood mapping (JLIM),¹⁰ makes claims that causal GWAS hits and eQTL signals co-exist within a genomic region consisting of tightly linked genetic variants. We refer to this type as locus-level colocalization analysis. The second kind, illustrated by coloc,¹¹ eCAVIAR,¹² and ENLOC/fastENLOC,^6,13 attempts to uncover colocalization signals at the single SNP/variant resolution using probabilistic quantifications. We refer to this type as SNP-level colocalization analysis. The common obstacle for both types of colocalization analysis is linkage disequilibrium (LD) among candidate SNPs. Hypothetically, with complete linkage equilibrium, colocalization analysis becomes relatively trivial, and various approaches from both types converge. With the presence of LD, a SNP-level colocalization may not be identifiable. That is, multiple competing scenarios may be indistinguishable based solely on the observed association data. (See the example of two perfectly linked SNPs illustrated in Wen et al.¹³) Thus, the quantification of SNP-level colocalization evidence should acknowledge such uncertainty explicitly. Furthermore, relevant additional information, e.g., enrichment level of eQTLs in GWAS hits, should be incorporated to aid in the identification of more likely scenarios. Based on the above considerations, probabilistic analysis in the Bayesian framework becomes a natural choice for SNP-level colocalization analysis; all aforementioned SNP-level colocalization methods utilize Bayesian probabilistic modeling approaches. (In this paper, we use the terms “SNP-level colocalization analysis” and “probabilistic colocalization analysis” interchangeably.)

Probabilistic colocalization analysis at the variant level faces many challenges, both analytically and practically. Analytical factors—for example, prior specifications and model assumptions required for likelihood computation (e.g., consideration of allelic heterogeneity)—are known to have drastic impacts on analysis outcomes. Practically, even when the ideal analytical strategies are applied, the power of colocalization analysis can still be limited by the underlying association data, e.g., the power of marginal association analysis. In this paper, we take a divide-and-conquer strategy to systematically investigate various analytical and practical factors in probabilistic colocalization analyses. We attempt to isolate each factor through analytical derivation and numerical experiments and to quantify its effects on potential false positive and false negative findings. We seek to identify a set of best analytical strategies that enable robust and powerful probabilistic colocalization analysis. Also, we hope to practically illustrate the natural limitations of colocalization analysis based on the currently available data and establish a baseline for future development in integrative genetic research.

Material and methods

For probabilistic colocalization analysis, we focus our discussion on three representative methods: coloc,¹¹ eCAVIAR,¹² and ENLOC/fastENLOC.^6,13 A comprehensive overview of the three methods and additional approaches is provided in Section 1 of the supplemental material and methods.

Statistical framework of probabilistic colocalization analysis

Let the binary indicators γ and d denote the latent causal association status of a given variant with respect to the complex and gene expression traits of interest, respectively. The probabilistic quantification of colocalization for the variant is essentially to evaluate the conditional probability,

$$\text{Pr}\left(\gamma =1,d=1|\text{eQTL}\text{data},\text{GWAS}\text{data}\right).$$ (Equation 1)

All known probabilistic colocalization approaches aim to compute Equation 1, which is carried out by applying the Bayes rule, i.e.,

$$\text{Pr}\left(\gamma =1,d=1|\text{eQTL }\text{data},\text{GWAS}\text{data}\right)$$ (Equation 2)

$$\propto \text{Pr}\left(\gamma =1,d=1\right)P\left(\text{eQTL data},\text{GWAS }\text{data }|d=1,\gamma =1\right),$$

where eQTL data and GWAS data represent the genotype and phenotype data collected for eQTL mapping and GWAS analysis, respectively. Noticeably, the computation requires an explicit specification of the prior probability $\text{Pr}\left(\gamma =1,d=1\right)$ and the likelihood function $P\left(\text{eQTL}\text{data},\text{GWAS }\text{data }|d=1,\gamma =1\right)$.

The prior quantity, $\text{Pr}\left(\gamma =1,d=1\right)$, reflects the frequency of colocalization sites in all interrogated variants and can be equivalently specified by the product of $p_d:=\text{Pr}\left(d=1\right)$ and $\text{Pr}\left(\gamma =1|d=1\right)$, i.e.,

$$\text{Pr}\left(\gamma =1,d=1\right)=\text{Pr}\left(\gamma =1|d=1\right)\text{Pr}\left(d=1\right).$$ (Equation 3)

In ENLOC/fastENLOC, a set of parameters (α₀, α₁), referred to as “enrichment parameters,” are introduced to parameterize $\text{Pr}\left(\gamma =1|d\right)$, i.e.,

$$\text{logit}\left[\text{Pr}\left(\gamma =1|d\right)\right]={\alpha }_0+{\alpha }_{1}d,$$ (Equation 4)

where α₁ is the log odds ratio quantifying the enrichment level of molecular QTLs in GWAS hits. Note that, with the specification of α₀, α₁ and the frequency of causal eQTLs, p_d, the frequency of the causal GWAS hits, $p_{\gamma }:=\text{Pr}\left(\gamma =1\right)$, is induced.

In the implementation of coloc, the priors are defined by $p_1:=\text{Pr}\left(\gamma =0,d=1\right)$, $p_2:=\text{Pr}\left(\gamma =1,d=0\right)$, and $p_{12}:=\text{Pr}\left(\gamma =1,d=1\right)$. The equivalent parametrization by (p_d, α₀, α₁) is given by

$$p_d=p_1+p_{12}$$

$${\alpha }_0=\text{log}\left[\frac{p_1}{1-p_1-p_2-p_{12}}\right]$$

$${\alpha }_1=\text{log}\left[\frac{p_{12}\left(1-p_1-p_2-p_{12}\right)}{p_1{p}_2}\right]$$

The third approach, eCAVIAR, makes a simplifying assumption that the causal status of γ and d are a priori independent. In the ENLOC parameterization, this independence assumption implies that there is no enrichment of eQTLs in GWAS hits, i.e.,

$$\left(p_d,{\alpha }_0=\text{log}\left[\frac{p_{\gamma }}{1-p_{\gamma }}\right],{\alpha }_1\equiv 0\right).$$

Or equivalently,

$$\text{Pr}\left(\gamma =1,d=1\right)=\text{Pr}\left(\gamma =1\right)\text{Pr}\left(d=1\right)=p_{\gamma }\cdot p_d.$$

Given the equivalence of different formulations in all methods, our subsequent discussion in the results section will focus on the ENLOC/fastENLOC parameterization because of its convenient interpretation.

Results

Analytical strategies in colocalization analysis

We consider two aspects of the analytical strategy in probabilistic colocalization approaches:the prior specification and the likelihood computation.

Specification of enrichment prior

We perform a series of numerical experiments to evaluate the sensitivity of colocalization analysis outcomes with respect to the enrichment parameter specification. In these experiments, we fix the frequencies of causal eQTLs and GWAS hits, p_d and $p_{\gamma }$, and consider α₁ the only free parameter. To isolate the effect of prior specification, we only consider computing the colocalization probability for a single SNP assumed to be in complete linkage equilibrium with other candidate variants. Particularly, we consider weak, modest, and strong association evidence from respective eQTL or GWAS analysis for the variant and examine the effect of varying enrichment levels on the magnitude of resulting SNP-level colocalization probabilities. The details on the design of the numerical experiment are provided in Section 3 of the supplemental material and methods.

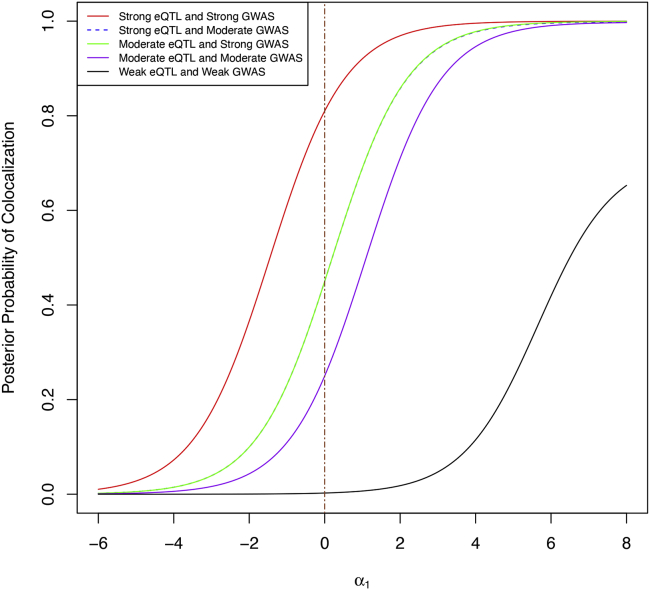
The results are summarized in Figure 1. Based on our real data analysis of 4,091 GWAS traits and the eQTL data from the GTEx project (Figure 5), we consider ${\alpha }_1\in \left[\mathrm{0,5}\right]$ a meaningful range in practical colocalization analysis. Within this range, SNP-level colocalization probabilities are generally sensitive to the enrichment prior specification. However, depending on the combination of strength of evidence from individual association studies, different combination categories are differentially impacted. Specifically, when the eQTL and GWAS association evidence are both strong or weak, the resulting colocalization probabilities are relatively stable with respect to the changes of the enrichment prior. This phenomenon can be intuitively explained: when the marginal association evidence is highly informative (including the case that association evidence is weak, i.e., the evidence for no association is strong), the likelihood for colocalization is overwhelming, and the prior impact is diminished. On the other hand, SNPs with modest association evidence from either GWAS or eQTL analysis are most sensitive to the prior specification, as a strong enrichment assumption can significantly increase the corresponding probability of colocalization.

Figure 1.

The impact of pre-defined enrichment level (α₁) on the SNP-level colocalization probability

The different curves represent different combined levels of marginal association evidence for a particular SNP from the eQTL and GWASs. Informed by our real data analysis of 4,091 GWAS traits and the eQTL data from the GTEx project, we consider ${\alpha }_1\in \left[\mathrm{0,5}\right]$ a meaningful range for practical colocalization analysis. Within this range, all categories show different levels of sensitivity to the specification of the enrichment parameter.

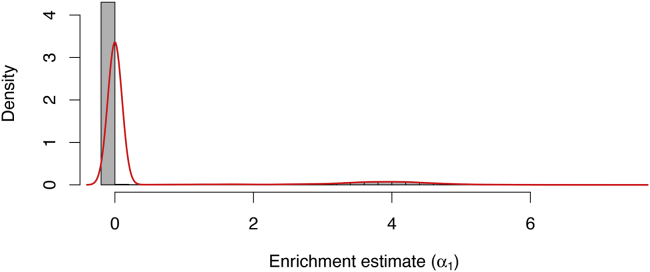
Figure 5.

Enrichment estimates from all tissue-trait pairs in the phenomexcan analysis

The histogram displays a bimodal distribution, with a sharp peak at α₁ = 0 and a wide peak centered around α₁ = 4.

The sensitive nature of probabilistic colocalization analysis should caution practitioners. Because colocalization analysis is often treated as a discovery process similar to a hypothesis testing procedure, false positives, i.e., type I errors, should be carefully guarded against. From the numerical experiment, we observe that aggressively setting a high enrichment value tends to flag many more colocalization sites than setting a conservative value. However, this is also dangerous for inflating false-positive colocalization findings. Thus, we conclude that a conservative enrichment prior is, in principle, acceptable and may be preferable. Nevertheless, simply setting α₁ = 0 in all circumstances can be too conservative and lead to a severe loss of power.

Given the observations from the above experiments, great care is warranted in prior specifications. For an ideal Bayesian analysis, the required prior information should be derived from historical analyses of similar types. In the case that such historical information is unavailable, we recommend to estimate required hyper-parameters from the observed data. One of the established estimation procedures is implemented in ENLOC/fastENLOC, where p_d, α₀, and α₁ are estimated by jointly analyzing the eQTL and GWAS data via a multiple imputation procedure¹³ (a summary of the procedure is provided in Section 2 of the supplemental material and methods). This estimation procedure, designed specifically for dealing with the latent association status in both eQTLs and GWAS hits, has shown the ability to provide robust and reliable enrichment estimates in our simulation studies (see results). Recently, Wallace et al.¹⁴ proposes to perform a sensitivity analysis of the priors for identified colocalization signals. While we completely agree that understanding prior sensitivity is critical for practitioners, it should be noted that sensitivity analysis alone does not justify selecting a specific set of priors.

Likelihood computation and accounting for allelic heterogeneity

The likelihood computation in probabilistic colocalization analysis refers to the evaluation of $P\left(\text{eQTL}\text{data},\text{GWAS}\text{data }|d,\gamma \right)$ in Equation 2. In the current practice, eQTL and GWAS data are typically obtained from non-overlapping cohorts, and all methods compute the likelihood by

$$P\left(\text{eQTL}\text{data},\text{GWAS}\text{data }|d,\gamma \right)=P\left(\text{eQTL}\text{data }|d\right)P\left(\text{GWAS}\text{data }|\gamma \right).$$ (Equation 5)

There are two different strategies for evaluating likelihood. The first strategy, adopted by eCAVIAR and fastENLOC, recovers the required likelihood information from multi-SNP fine-mapping analyses of eQTL and GWAS data. The second strategy, used by coloc, directly computes each trait’s marginal likelihood from summary statistics under a simplifying assumption of no allelic heterogeneity. Allelic heterogeneity (AH) refers to the phenomenon of distinct genetic variants at a locus simultaneously affecting the same phenotype. Under the assumption of no AH, there is, at most, one causal SNP within a locus for a given trait. Henceforth, we refer to such an assumption as the “one causal variant” (OCV) assumption. The primary rationale for the OCV assumption is computational (rather than biological): if the assumption holds, the LD information within the locus of interest becomes obsolete for likelihood evaluation, and the computation can be carried out analytically based on single-variant association test statistics.15, 16, 17

In colocalization analysis of eQTLs and GWAS hits, a locus is typically defined as the cis region of a target gene, e.g., a 2 Mb window centered around the transcription start site.¹⁸ At such a scale, AH is a widespread phenomenon in gene regulations based on overwhelming evidence from recent large-scale eQTL studies.^18,19 While it may work reasonably well for some complex traits, the OCV assumption is likely often violated in the analysis of molecular traits. Here, we are interested in exploring its implications on both false-positive and false-negative findings in colocalization analysis.

We first conduct simulation studies using real genetic data from the GTEx project and simulate gene expression and complex trait data based on linear regression models. To isolate the effect of AH, we focus on simulating strong genetic effects for all eQTLs and GWAS hits. (As shown in the previous section, these signals are robust to the misspecification of enrichment parameters.) Furthermore, both expression and complex trait data are independently generated from the same genotype data, which ensures LD mismatch is not a factor in the analysis. Our simulation considers the following scenarios for each gene-trait pair within a genomic locus:

• 1single causal variants in both eQTL and GWAS data, no colocalization
• 2AH in eQTL data (two causal eQTLs per gene), a single causal variant in GWAS data, no colocalization
• 3single causal variants in both eQTL and GWAS data, single colocalization event
• 4AH in eQTL data (two causal eQTLs per gene), a single causal variant in GWAS data, single colocalization event

The first two scenarios are designed to investigate potential false-positive findings, and the last two are for false-negative findings. The assembled data for analysis consist of different mixtures of the four scenarios, such that we could evaluate both the type I and the type II errors. The simulation details are provided in the Section 4 of the supplemental material and methods.

We use two different methods to analyze the simulated data. Particularly, we apply the default coloc method to represent methods making the OCV assumption and without explicit modeling of AH. We apply fastENLOC to represent methods that explicitly model potential AH. We provide the true priors for coloc analysis, and the fastENLOC analysis estimates the enrichment prior directly from the data. The results of our simulations are in Table 1. In all of our simulated scenarios, we find that both types of approaches control the false discovery rate (FDR). However, when AH is presented, the power of coloc is approximately half of the power of fastENLOC. The relative ratio of power between the two types of approaches is expected. When two independent eQTL signals co-exist, coloc identifies one signal with a stronger signal-to-noise ratio as the sole casual eQTL, which leads to a false-negative finding when the unselected eQTL overlaps the causal GWAS hit.

Table 1.

The impact of modeling consideration of AH on FDR and power in colocalization analysis

AH modeling	Dataset
	scenarios (1,2,3)		scenarios (1,2,4)
	FDR	power	FDR	power
Yes	0.047	0.997	0.041	0.971
No	0.039	0.937	0.044	0.411

fastENLOC and coloc are selected to represent the approaches with and without explicit AH modeling, respectively. Both approaches maintain the proper false discovery rate levels in all settings. However, the power difference is quite large when AH is indeed present in the molecular QTL data (i.e., scenarios (1,2,4)).

Even though the simulation study does not indicate apparent inflation of FDR, there are some theoretical concerns on potential false positives related to the OCV assumption. First, some implementations of the assumption, e.g., coloc, enumerate all possible causal association configurations from both traits to compute the normalizing constants and desired colocalization probabilities. Under the simplifying assumption of OCV, there are (p + 1)² possibilities precisely (where p represents the number of SNPs in the locus). If the assumption is violated, many more necessary scenarios are uncounted (the total possibilities without constraints are 2^p). This factor can lead to under-estimating the normalizing constants and over-estimating the colocalization probabilities. Second, false positives can be carried over from single-SNP analysis in the marginal studies. It is known that some non-causal SNPs that are in partial LD with multiple causal SNPs can generate the most significant single-SNP association evidence.¹⁹ Such false-positive findings based on single-SNP association evidence are maintained and carried over into the colocalization analysis under the OCV assumption. Consequently, it becomes a source of false-positive colocalization findings. In contrast, methods that explicitly perform multi-SNP fine-mapping analysis can effectively dissect different scenarios by accounting for LD. Hence, they are unlikely to suffer from such false-positive findings. In summary, we conclude that the OCV assumption can, in theory, lead to anti-conservative quantifications of colocalization probabilities. Although the extent of the anti-conservativeness may not lead to observable inflations of FDR within our simulations, its effect can be observed in the numerical experiments examining the calibration of the reported colocalization probabilities (Section 5.1 of the supplemental material and methods and Figure S1).

It is worth emphasizing that the OCV assumption may not be invalid in all scenarios, but it is inappropriate at the scale of genomic regions commonly used in molecular QTL studies for molecular QTL mapping analysis. More generally, our recommendation for dealing with likelihood computation in colocalization analysis is to apply specialized multi-SNP association techniques. We note that state-of-the-art of fine-mapping approaches^8,17,20 all have the ability to account for AH without making the OCV assumption. It is also intuitive that colocalization analysis should be based on the best possible fine-mapping results. This is because the inaccuracy from poor likelihood computation will inevitably translate into inaccuracy in subsequent probabilistic quantification of colocalization. The emergence of fast and accurate Bayesian multi-SNP association analysis methods, e.g., FINEMAP,²¹ DAP-G,¹⁷ and SuSIE,⁸ make it feasible to practically separate fine-mapping and colocalization analyses with affordable computational costs. The current implementation of fastENLOC can take the fine-mapping results from any of those Bayesian methods and perform colocalization analysis.

Practical factors in colocalization analysis

There are many practical factors in colocalization analysis that analysts have little control over. Nevertheless, their impacts on the outcomes are profound. Having established the fundamental inference principles, we proceed to assess the empirical performance of probabilistic colocalization analysis and investigate the other performance-impacting factors using realistically simulated eQTL and GWAS data.

Empirical assessment of probabilistic colocalization analysis

To construct a simulated dataset that resembles real applications of colocalization analysis, we simulate 20,000 non-overlapping genes with 1,500 SNPs within each cis-region. The scale of the simulated datasets resembles real applications of genome-wide colocalization analysis. We use the real genetic data from 400 participants of the GTEx project. In order to circumvent the issue of LD mismatch in this particular experiment, we use the same set of genotype data to simulate both the expression and complex trait phenotypes. Within each cis region, the causal eQTLs are randomly selected from a series of independent Bernoulli trials, such that on average there are three causal eQTLs per gene (i.e., p_d = 2 × 10⁻³). Similarly, we sample causal GWAS SNPs conditional on the simulated eQTL status using the probability model (Equation 1) with a true α₁ value of 4. As a result, the simulated dataset consists of 2,103 colocalized association signals distributed in 2,001 unique genes. Given the truly causal SNPs for each gene, we independently generate the molecular and complex trait data for the 400 individuals based on standard multiple linear regression models. Specifically, each causal variant-trait pair’s genetic effects are independently drawn from the distribution N(0,1). The residual errors for each trait and each individual are also independently generated from the standard normal distribution. Additional simulation details are provided in Section 5 of the supplemental material and methods.

To analyze the simulated dataset, we first perform separate Bayesian fine-mapping analyses for the simulated eQTL and GWAS datasets using the software package DAP-G.¹⁷ Utilizing the resulting probabilistic annotations, we apply fastENLOC to estimate the enrichment parameters with the default shrinkage setting. As expected, the estimated enrichment parameter α₁ is slightly under-estimated, but reasonably close to the true value (${\hat{\alpha }}_1=3.644$ with the standard error 0.039). We then perform colocalization analysis using fastENLOC using the estimated and true enrichment parameters, respectively. For comparison, we also run coloc with its default prior model parameters and the true parameters, respectively. Note that the differences between coloc and fastENLOC results based on the true enrichment parameters should reflect the difference in fine-mapping analysis, including the consideration of AH.

We first examine the false positive rate and the power at 5% FDR level for different analysis settings (Table 2). We find that severe inflation of type I errors only occurs at the coloc run with its default model priors (which significantly exceeds the true enrichment parameter). All other analysis settings, including the coloc run with the true enrichment parameters, show proper control of the desired false discovery rate. For the methods that control the type I errors, the power seems low across the board (Table 2). The under-estimation of the enrichment parameter (α₁) due to shrinkage only explains a small fraction of the power loss. Although the power and type I error analysis only focus on high colocalization probability values, our conclusion extends to the full probability spectrum. Additional inspection of the calibration of the regional colocalization probabilities (RCPs) also confirms that various methods yield conservative colocalization results when supplied with the true enrichment prior (Figure S1 and Section 5.1 of the supplemental material and methods).

Table 2.

Realized false discovery rates and power of colocalization analysis in simulated data

Method	Number of discoveries	Realized FDR	Power
fastENLOC (estimated prior)	406	0.034	0.186
fastENLOC (true prior)	458	0.046	0.208
coloc (default prior)	472	0.258	0.175
coloc (true prior)	200	0.045	0.095

The table shows an overall assessment of power and realized FDR (controlled at 5% level) for various colocalization approaches. Only coloc with its default subjective prior shows severely inflated type I errors. The enrichment priors are justified for the remaining approaches, and they properly control the FDR. The power (for methods properly controlling FDR) is overall quite low in this setting that resembles realistic applications.

We identify two primary sources of false-negative errors by an in-depth examination of the simulated data and the corresponding analysis results. We refer to these two sources as class I and class II false-negative errors in colocalization analysis. Specifically, we define

• 1Class I false negatives: lack of power in association analysis of individual traits
• 2Class II false negatives: inaccurate quantification of association evidence at SNP level for individual traits

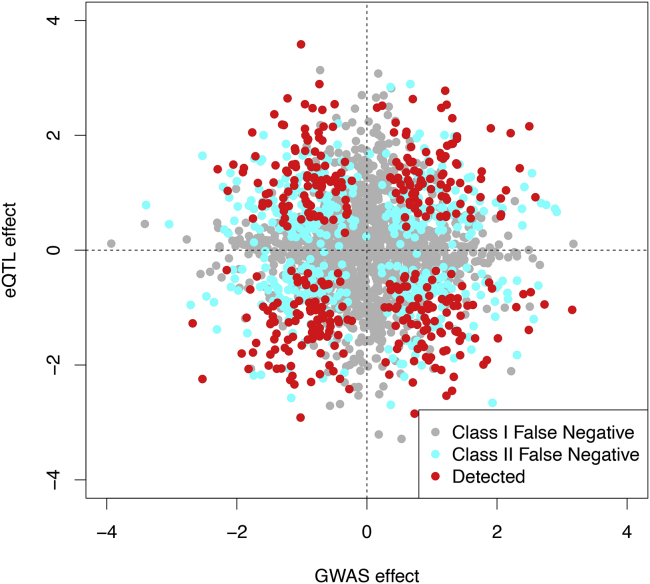
The class I false negatives (FNs) represent the cases of failure in detecting at least one type of association signals (eQTL or GWAS) in genetic association analysis. The class II FNs represent the scenarios where both types of association signals are correctly uncovered at locus level, but the inaccurate SNP-level quantifications imply that the causal variants for the two types of traits are unlikely overlapping. In our simulation studies, 59.0% (1,240) and 22.0% (463) of the true colocalization signals fall into the class I and II false negatives categories, respectively. To better visualize the two FN classes, we plot the true eQTL and GWAS effects of the colocalized signals with their corresponding labeled categories based on the fastENLOC results in Figure 2. Most points representing class I FNs (gray) are closely located around the axes, indicating at least one of the genetic effects (eQTL or GWAS) is too small to be detected by the corresponding association analysis. Marginally, at the 5% FDR level, the power for GWAS and eQTL is 44% and 62%, respectively. In comparison, most points representing class II FNs (cyan) and detected signals (red) are scattered around the two diagonals.

Figure 2.

Classification of all colocalized SNPs

All truly colocalized variants from our realistic simulations, classified as either a class I false negative, class II false negative, or successfully detected by fastENLOC. We see the expected pattern that most points near one of the axes are class I false negatives, while points far away from both tend to be detected by fastENLOC.

The impacts of class I FNs are easy to understand and well expected. As neither eQTL mapping nor genetic association analysis of complex traits achieves high power in practice, this class of FNs remains a primary source for failures in identifying colocalization sites.

A proportion of class II false negatives can be explained by a “threshold” effect. For example, some modest eQTL signals barely clear the bar to qualify for significant eQTL findings, but the underlying evidence is not strong enough to ensure a significant colocalization discovery. Additionally, the class II FNs can occur even when the association signals for both GWAS and eQTL can be narrowed down into the same genomic locus with high confidence. This is because, at the SNP level, it remains difficult to pinpoint the causal variants for both traits due to the combination of LD and insufficient sample size. The phenomenon of class II FNs is also closely related to a well-known fact in fine-mapping analysis: the lead (i.e., the most significant) SNPs that emerge from association analysis may not be the true causal SNPs.^22,23 Incidental correlation between the genotypes of non-causal SNPs (in LD with the true causal variant) and residual errors from the outcome variable could lead to stronger empirical correlation, especially with limited samples. There is generally a higher level of mismatching between lead and causal SNPs when the underlying studies are underpowered. In any association analysis, Bayesian or frequentist, the lead SNPs are always regarded as the most plausible causal SNPs from the data. When the mismatch of lead and causal SNPs occurs in at least one trait, all algorithms are led to believe there is a lack of evidence for SNP-level colocalization, even though the signal clusters for both traits are correctly identified.

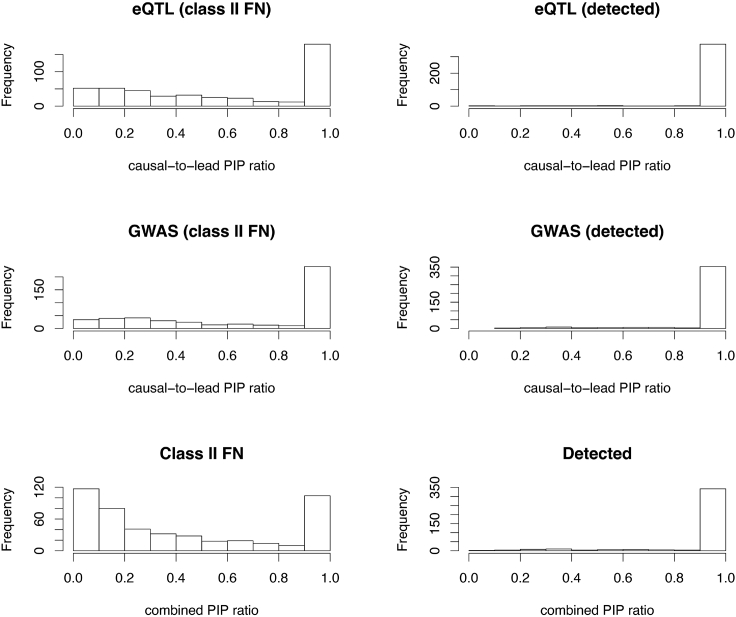
To provide a visualization, we compute a ratio of posterior inclusion probabilities (PIPs) for the causal SNP versus the lead SNP (causal-versus-lead PIP ratio) in each signal cluster harboring a true colocalized signal for both simulated eQTL and GWAS data. The PIPs for a SNP, $\text{Pr}\left(\gamma =1|\text{GWAS data}\right)$ and $\text{Pr}\left(d=1|\text{eQTL data}\right)$, quantify the strength of association evidence in the GWAS and eQTL data, respectively. The PIP ratio = 1 indicates that the lead SNP is indeed the causal SNP (or they are in perfect LD). We further compute a combined ratio by multiplying the two trait-specific causal-versus-lead PIP ratios for each signal cluster. Note that the combined ratio = 1 suggests the causal SNPs are identified as lead SNPs in both traits, whereas the combined ratio < 1 indicates that in at least one trait, the lead SNP and the causal SNP do not match. The comparison of various PIP ratios between detected and class II false-negative signals is shown in the histograms of Figure 3. The overall patterns in Figure 3 indicates that in detected colocalization signals, the vast majority of causal SNPs are indeed lead SNPs in both traits; many mismatches between causal and lead SNPs lead to false negatives in identifying the colocalized signals.

Figure 3.

PIP ratios for all signal clusters

The first column of histograms represents the ratio of causal SNP PIP to lead SNP PIP for all class II false negatives from the eQTL simulated dataset, the GWAS dataset, then both combined. The second column represents the same ratio, but among all successfully detected colocalizations from the respective datasets.

Both classes of false-negative errors are intrinsic to genetic association analysis and are well known. However, it is somewhat surprising to observe that the combined effects from these factors have such a drastic effect on the power of colocalization analysis—even when the association analysis for individual traits is considered relatively well powered.

In practice, when the truth is unknown, we can still assess the relative power of the colocalization analysis based on the estimates of $p_d,p_{\gamma }$, and α₁. The expected number of colocalization sites based on the enrichment analysis can be computed by $M{p}_{\gamma }/\left(1+\frac{p_d}{1-p_d}\text{exp}\left(-{\alpha }_1\right)\right)$, where M represents the total number of genetic variants. In this simulation, the fastENLOC estimates

$${\hat{p}}_{\gamma }=1.3\times {10}^{-3},{\hat{p}}_d=5.4\times {10}^{-4},{\hat{\alpha }}_1=3.644,$$

and the expected number of the colocalization sites is ∼800, which represents a lower bound estimate of true colocalization sites (due to the conservative estimate of α₁ and the class I FNs). The number of detected sites at the 5% FDR level is roughly half of the expected sites. Henceforth, we refer to this proportion as the rejection-to-expectation (rej-to-exp) ratio, representing an upper-bound estimate of the empirical power of the colocalization analysis.

Mismatching LD structures

Most existing colocalization analysis approaches are built on the experimental scheme known as the two-sample design, where the eQTL and GWAS data do not share common samples. While this design allows for using valuable eQTL resources, e.g., GTEx data, for analyzing a wide range of GWAS data collected from many different cohorts, it raises some practical concerns. To our knowledge, all existing methods implicitly assume that the LD structures between the two association samples are identical, which is at best questionable when the two sets of association data are collected from different cohorts. In general, there is a lack of empirical evaluation of how different levels of mismatching between LD structures affect colocalization analysis outcomes. To address this issue, we design a simulation experiment utilizing multi-population genetic data to quantify the effects of mismatching LD patterns on colocalization analysis with two-sample designs.

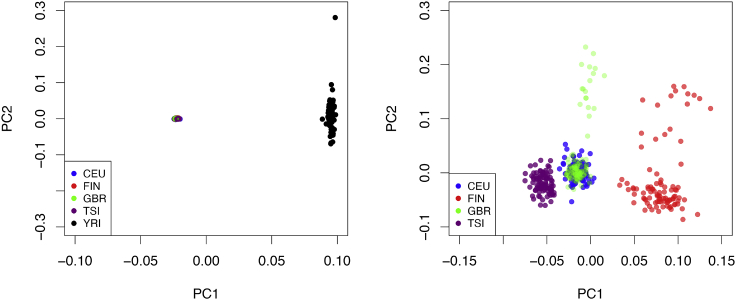
We take the genetic data from the GEUVADIS project, which consists of samples from four European populations—CEPH (CEU), Toscani (TSI), British (GBR), and Finnish (FIN)—and one African population, Yoruban (YRI) (Figure 4).²⁴ We select the SNPs located within a 200 kb cis-region from 6,977 protein-coding and lincRNA genes, each of which contains at least 500 candidate SNPs. For each gene, we first sample the causal eQTL and GWAS SNPs from its candidate cis-SNPs. We then simulate a single eQTL dataset using the FIN data. We subsequently generate 5 GWAS datasets using the genotype data and pre-determined GWAS association status for all 5 population groups. Note that the LD patterns are perfectly matched for the Finnish population for GWAS and eQTL analysis, which forms a baseline for evaluating the effects of LD mismatching. Additional simulation details are provided in Section 6 of the supplemental material and methods.

Figure 4.

Population structures represented by PCA plots in GEUVADIS data

The left panel show the PCA plots (PC1 versus PC2) with the samples from all populations. The right panel shows the PCA plots using European samples only. Based on these plots, we expect maximum LD mismatch between YRI and any European population.

We analyze the five pairs of eQTL-GWAS data using fastENLOC. Our comparisons focus on the enrichment estimates, false-positive colocalization findings, and power. The results are summarized in Table 3. In all cases, we do not observe any inflation of false-positive colocalization findings—the false discovery rates are properly controlled in all datasets. The impact of LD mismatch is reflected by the under-estimation of the enrichment parameters and the diminished power, especially in noting that the power of GWAS discovery (which is perfectly correlated with estimated $p_{\gamma }$) is not substantially different in all populations. In the extreme case of mismatch, i.e., the analysis of YRI GWAS data and FIN eQTL data, we find that the enrichment parameter α₁ is most severely underestimated, and the resulting power is reduced to 50% of the perfectly matching association data (i.e., FIN GWAS and FIN eQTL). We also note that the underestimation of the enrichment parameter only explains a small proportion of the loss: even when the true enrichment parameter is used, the power of colocalization analysis from analyzing the YRI GWAS data remains significantly lower than the other European datasets. Within the European populations, the effects of LD mismatch on colocalization analysis are also noticeable. The comparison within the European populations may also be complicated by differences in sample sizes, where TSI and CEU have the largest (n = 92) and smallest (n = 78) sample sizes, respectively. The sample size difference is directly linked to the power of GWAS discovery.

Table 3.

LD mismatch impact on enrichment estimation, FDR, and power

Datasets	${\hat{\alpha }}_1$	${\hat{p}}_{\gamma }$	Realized FDR	Power
FIN versus FIN	4.076	1.25 × 10−3	0.029 (0.036)	0.129 (0.129)
FIN versus GBR	3.964	1.23 × 10−3	0.023 (0.027)	0.102 (0.103)
FIN versus TSI	3.935	1.27 × 10−3	0.023 (0.028)	0.101 (0.099)
FIN versus CEU	3.842	1.10 × 10−3	0.030 (0.047)	0.075 (0.077)
FIN versus YRI	3.438	1.19 × 10−3	0.001 (0.006)	0.065 (0.067)

The enrichment estimates $\left({\hat{\alpha }}_1\right)$ and from all combinations of eQTL and GWAS datasets we used for this analysis. The estimated frequency of GWAS hits $\left({\hat{p}}_{\gamma }\right)$ reflects the GWAS power of each GWAS dataset. (Note that true $p_{\gamma }=1.92\times {10}^{-3}$.) The quantities in parentheses show the realized FDR and power when using the true enrichment parameter in the colocalization analysis.

Overall, in relative terms, our observation suggests that the power loss suffered from the LD mismatching is qualitatively less severe than from the imperfect power of individual association analysis—as long as the eQTL and the GWAS samples are from reasonably close populations. In addition, the power loss caused by LD mismatching may be compensated by increased power in single-trait association analysis.

Colocalization analysis of 4,091 GWAS datasets and GTEx eQTL data

To provide a comprehensive summary of colocalization analysis using the current available GWAS and eQTL data, we analyze 4,091 complex trait datasets and the final release of the GTEx data (v.8) from 49 tissues.^6,18 In total, we perform colocalization analysis on 200,459 trait-tissue pairs using fastENLOC. The biological implications from the colocalization analysis, coupled with PrediXcan analysis,⁴ have been reported and discussed in Pividori et al.⁶ In this section, we focus on the technical aspect of the colocalization analysis and provide a high-level summary of the colocalization results for a wide range of complex traits with currently available GWAS and eQTL datasets. The fastENLOC output for all trait-tissue combinations can be downloaded using the URLs in Table S1. Additional details of data processing and analysis are given in Section 7 of the supplemental material and methods.

We first examine the empirical distribution of the enrichment estimates, ${\hat{\alpha }}_1$, over the 200,459 trait-tissue pairs. The histogram in Figure 5 shows the empirical distribution of the enrichment estimates. We observe a clear bi-modal distribution: the estimates from the vast majority of the trait-tissue pairs are close to 0, and there is also a noticeable peak centered around α₁ = 4. Upon close inspections, we find the vast majority of complex traits with near 0 eQTL enrichment have few significant GWAS hits, which may be attributed to the lack of power in the corresponding studies.

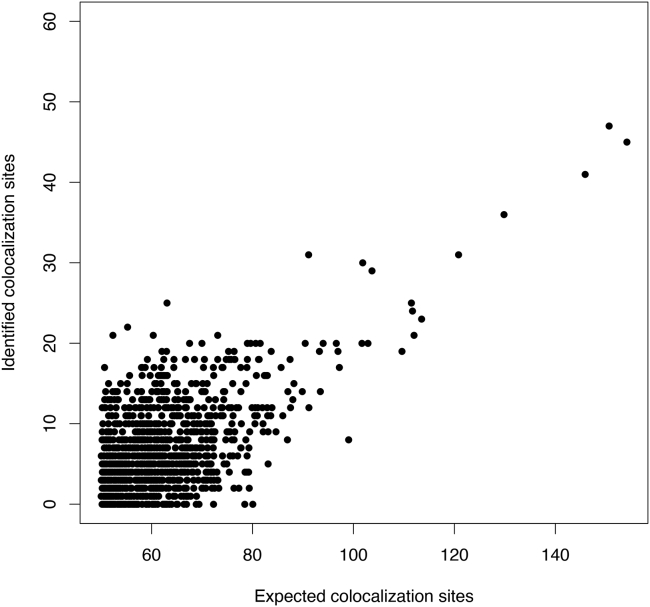
Next, we inspect the significant findings from the analysis of each individual trait-tissue pair. Based on the enrichment analysis results, we compute the expected number of colocalization sites for each trait-tissue pair. Additionally, we identify high-confidence colocalization sites at the 5% FDR level based on the output of RCP values using the Bayesian FDR control procedure. In total, 15,975 sites pass this type I error control threshold in all trait-tissue pairs. We consider the trait-tissue pairs with more than 50 expected colocalization sites as “well powered.” For this set of trait-tissue pairs, we compare the expected colocalization sites and the identified high-confidence sites at the 5% FDR level (Figure 6). The average rej-to-exp ratio in this set is 10.7% (median = 9.43%). This result indicates that the current colocalization analysis is (severely) under-powered for most trait-tissue pairs.

Figure 6.

The comparison of the calculated expected colocalization sites and the detected high-confidence sites among well-powered trait-tissue pairs

This apparent lack of power falls in line with our findings from our simulations.

Discussion

In this paper, we have systematically explored both the analytical and the practical factors that impact the performance of probabilistic colocalization analysis for a molecular and a complex trait. We identify a single analytical factor, i.e., the specification of prior enrichment levels, that can lead to a significant inflation of false-positive findings, and we recommend estimating the critical enrichment parameters directly from the data. On the other hand, we find that a combination of analytical and practical factors, including modeling considerations for AH, LD mismatch, and imperfect power in association analyses, could severely diminish the power of SNP-level colocalization discoveries. As a result, current approaches often fail to identify the majority of colocalization signals in practical applications, even when they are appropriately applied. We argue that understanding the promise and limitations of the current state-of-the-art is critical for the practitioners to properly anticipate and correctly report their findings. For colocalization analysis of currently available molecular QTL and GWAS data, we may need to embrace the noticeable discrepancy between “expected colocalized signals” and the actual identified “significant colocalization findings.”

There are many ways in which we can improve the power of existing colocalization methods based on our findings in this paper. For example, analytical strategies in improving the enrichment estimation, applying better fine-mapping methods, and explicitly modeling varying LD patterns across datasets will most likely result in enhanced power. Nevertheless, we suspect that improving the quality of the GWAS and molecular QTL datasets should have a more direct and visible impact. We note that most existing molecular QTL studies are limited by the high-throughput phenotyping cost and have modest sample sizes and relatively high experimental noise. The state-of-the-art eQTL annotations generated by the GTEx project are derived from bulk tissues of <1,000 samples. The current technology advancement, e.g., applying single-cell technology for molecular QTL mapping, combined with proven statistical strategies for data aggregation, e.g., a meta-analysis of molecular QTLs, could significantly enhance colocalization discoveries.

Another promising direction for improving colocalization analysis is to incorporate additional genomic information. This can be achieved by expanding the current prior model $\text{Pr}\left(\gamma =1,d=1\right)$ to $\text{Pr}\left(\gamma =1,d=1|\text{additional }\text{genomic}\text{annotations}\right)$. The additional genomic features can be obtained from other relevant molecular phenotype studies, e.g., studies of methylation, chromatin accessibility, and histone modification. This added information provides a more relevant “local” genomic context for each candidate locus, hence improving both the sensitivity and specificity of the colocalization analysis.

Although our discussions in this paper are exclusively illustrated using two complex traits, the general principles extend to the analysis of multiple traits.^25,26 All of the analytical and practical factors that we have discussed impact SNP-level colocalization analysis for more than two traits. If not adequately dealt with, the resulting adverse effects can be even more severe. For example, both classes of false-negative errors discussed in the section of realistic power assessment increase with more traits considered. Additionally, the existing enrichment estimation procedure via multiple imputation does not scale well regarding a large number of traits (i.e., ≥5). Therefore, extending the best practice of colocalization analysis from two traits to multiple traits remains a critical challenge.

Colocalization analysis is also connected to other types of integrative analysis approaches, e.g., transcriptome-wide association studies (TWASs). In analyzing eQTL and GWAS data, a TWAS utilizes the same input data sources as the colocalization analysis. However, its results have some unique causal implications provided that a set of assumptions is met.²⁷ Despite the difference in their theoretical origins, positive findings from the two analyses can be driven by similar signals. Recent studies⁶ find that integrating colocalization analysis into a TWAS can improve its sensitivity and specificity. More generally, the two prevailing types of integrative analysis approaches can complement each other. Thus, further exploration of their connections and distinctions becomes an important future direction.

Data and Code Availability

The harmonized summary statistics from 4,091 complex trait GWASs and the multi-tissue eQTL annotations derived from the GTEx (v.8) data are made publicly available (see web resources). The source code and scripts for data generation and data analysis in the numerical experiments (fastENLOC) are available in the Github repository.

Declaration of interests

The authors declare no competing interests.

Published: December 11, 2020

Web resources

• coloc, https://cran.r-project.org/web/packages/coloc/index.html

• eCAVIAR, http://genetics.cs.ucla.edu/caviar/

• fastENLOC, https://github.com/xqwen/fastenloc

• fastENLOC analysis of 4,091 complex traits and GTEx v8 data (detailed results), https://tinyurl.com/y6cx9ovm

• fastENLOC data generating and analysis scripts/code for the numerical experiments, https://github.com/xqwen/fastenloc/tree/master/promise_and_limitation_paper/

• GEUVADIS data, https://www.internationalgenome.org/data-portal/data-collection/geuvadis

• GTEx, https://www.gtexportal.org/home/

• Harmonized summary statistics for 4,091 complex-trait GWAS, https://zenodo.org/record/3629742/files/harmonized_imputed_gwas.tar

• Multi-tissue eQTL annotations derived from the GTEx (v8) data, https://tinyurl.com/yyfser9a

• phenomeXcan, http://apps.hakyimlab.org/phenomexcan/

• Summary results from fastENLOC analysis of 4,091 complex traits and GTEx v8 data, https://doi.org/10.5281/zenodo.3530669