Leveraging phenotypic variability to identify genetic interactions in human phenotypes

Summary

Although thousands of loci have been associated with human phenotypes, the role of gene-environment (GxE) interactions in determining individual risk of human diseases remains unclear. This is partly because of the severe erosion of statistical power resulting from the massive number of statistical tests required to detect such interactions. Here, we focus on improving the power of GxE tests by developing a statistical framework for assessing quantitative trait loci (QTLs) associated with the trait means and/or trait variances. When applying this framework to body mass index (BMI), we find that GxE discovery and replication rates are significantly higher when prioritizing genetic variants associated with the variance of the phenotype (vQTLs) compared to when assessing all genetic variants. Moreover, we find that vQTLs are enriched for associations with other non-BMI phenotypes having strong environmental influences, such as diabetes or ulcerative colitis. We show that GxE effects first identified in quantitative traits such as BMI can be used for GxE discovery in disease phenotypes such as diabetes. A clear conclusion is that strong GxE interactions mediate the genetic contribution to body weight and diabetes risk.

Introduction

In Cappadocia, Turkey, traces of an asbestos-like, cancer-causing fiber was found in the materials of villagers’ homes and was prevalent in the air. However, this alone could not explain an epidemic where 50% of all Cappadocia villagers died from mesothelioma, compared to only 4.6% of asbestos miners with at least 10 consecutive years of work.¹ After nearly 3 years of living among the villagers, Roushdy-Hammady et al. documented a Cappadocia villager pedigree and described a highly penetrant Mendelian transmission of disease.² Once the pathogenic BAP1 mutations were found,³ follow-up experimental studies^{4, 5, 6} illuminated how BAP1 and asbestos exposure synergistically cause dangerous oncogenic effects in a gene-environment (GxE) interaction.⁷

This example is one of only a few well-characterized GxE interactions in humans, which have mostly appeared as modulators of Mendelian disorders’ penetrance.⁷ In human genetics, the primary focus has been characterizing the average relationship between individual genetic variants and a phenotype. Although researchers have identified thousands of associations across a spectrum of human phenotypes at the single variant level,⁸ research in model organisms and cell cultures has constantly shown that genetic effects are context dependent.^{9, 10, 11, 12, 13} As one example, the genetic effects governing lifespan in Drosophila melanogaster within one environment do not alter lifespan within another environment.¹⁰ The incomplete penetrance for many common human diseases, such as the APOE E4 allele on Alzheimer disease risk or smoking on lung cancer risk, implies important genetic and environmental modifiers of disease onset.^{14, 15, 16, 17}

Although GxE interactions are expected to be numerous, it is debated how important these interactions are to human genetics.^{18, 19, 20, 21, 22, 23} If they play a significant role, identifying these interactions can enable more accurate genetic prediction,¹² especially at the individual level. Current state-of-the-art prediction models use polygenic scores (PGSs),²⁴ which combine additive effects of genetic variants into a single risk measure. Clinical and environmental factors are used to improve model prediction, but potential interactions with genetic information are not commonly considered. Additionally, PGSs have poor transferability across populations,²⁵ possibly driven by environmental factors. If genetic effects on human phenotypes vary from person-to-person as a result of interactions, then more individualized prediction could be realized by first identifying genetic interactions and estimating their effects.

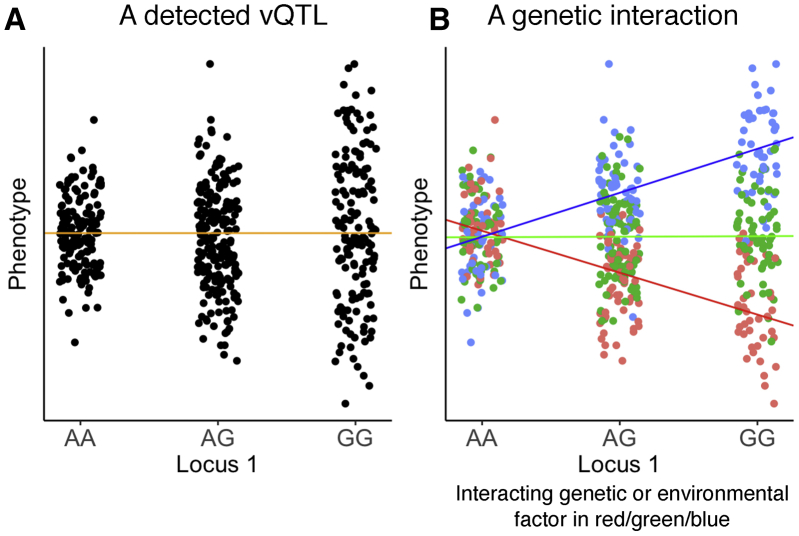
Because there is modest power to detect interactions in large human population cohorts, efficiently identifying the interactions remains an important statistical and computational challenge. To address these difficulties, we make use of a previously characterized observation that most GxE interactions with large effect size can be revealed as a change in the variance of a quantitative phenotype during a one-SNP-at-a-time genome-wide association study (GWAS) (Figure 1).^{26, 27, 28, 29, 30} This insight lets us identify strong GxE interactions associated with a given quantitative trait via a two-step approach. First, we look for genome-wide SNPs that are associated with the variance of the trait, thus identifying what are known as variance quantitative trait loci (vQTLs).^30,31 Second, we use these vQTLs to screen for potentially strong GxE interactions associated with the same phenotype. Scanning for vQTLs involves just a single test per SNP, so it provides a powerful inroad for discovering genetic interactions by nominating loci as promising candidates for an interaction.

Figure 1.

vQTLs could arise from a genetic interaction

(A) We refer to a genetic variant associated with the variance of the phenotype as a variance QTL (vQTL). The orange line, representing the line of best fit, has slope close to 0 and indicates that the mean of the phenotype does not change with a difference in genotype.

(B) A vQTL could also arise from a genetic interaction. The displayed data in (B) is the same data as in (A), except the points are colored to reflect the genotype at a second locus or the level of an environmental variable. This second factor interacts with locus 1 to create a mean-based interaction effect, and this mean-based interaction effect gives the appearance of a vQTL at locus 1. Data in both figures are simulated.

In the present study, we introduce a statistical framework to nominate SNPs for GxE interaction testing by leveraging differences in the means (muQTLs) and the variances (vQTLs) of a phenotype. We apply these methods to study the genetic basis of variation in body mass index (BMI) levels.^32,33 We further explore the role for interactions across human disease and perform in silico functional analyses for implicating relevant cell types and pathways, providing new insights into the architecture of human phenotypes.

Material and methods

Description and implementation of variance tests

We implemented several statistical methods to test a SNP for an association with the variance of a quantitative phenotype within a population dataset. First, we introduce the deviation regression model (DRM), where a linear regression is performed between individuals’ minor allele counts and the absolute difference between an individual’s phenotype value and the population phenotype medians within each genotype (after covariate adjustment). In the DRM, each individual j with genotype i has phenotypic value Y_ij. The genotype is coded as i = 0, 1, or 2, determined by the minor allele count. The median phenotype value is calculated for all individuals with categorical genotype i, ${\tilde{Y}}_i$. The absolute value of the difference between Y_ij and ${\tilde{Y}}_i$ is calculated as follows:

$$Z_{ij}=\left|Y_{ij}-{\tilde{Y}}_i\right|$$ (Equation 1)

The Z_ij values for each individual j represent the deviation from the within-genotype phenotype medians. Next, SNPs are tested for association with Z_ij values via linear regression and the minor allele counts are used as a numeric covariate. The effect size and p values for the SNP covariate in the regression are used as proxies for the variance effect size and significance of association with phenotypic variance. In practice, covariates are regressed out from Y_ij prior to calculating Z_ij.

The DRM is a similar approach to the Brown-Forsythe (BF) test, which allows for non-linear associations through an ANOVA model instead of a linear model.³⁴ We note that an ANOVA model requires categorical predictors, while a regression such as the DRM can be applied to continuous predictors representing imputation-derived minor allele dosages. Furthermore, we note that the BF test adjusts an individual’s phenotype values via the within-genotype median values, while the Levene’s test (LT) uses the within-genotype mean values.³⁵ The use of the median instead of the mean allows the BF test to be more robust than the LT to non-normality. The use of both approaches within genetic association studies has been discussed previously.³⁶

In our study, we compared the DRM to a number of other variance tests in R: the BF test,³⁴ the LT,³⁵ the extended Levene’s test for generalized scale (gS),³⁷ a two-step squared residual approach (TSSR),³⁸ squared residual value linear modeling (SVLM),³⁹ the double generalized linear model (DGLM),³¹ Bartlett’s test for equality of variances⁴⁰ (BT), and the Fligner-Killeen test for homogeneity of variances (FK).⁴¹ We omit the famLRTV method due to the authors’ finding that there is similar performance with LT.⁴² We omit the Bayesian heteroscedastic linear regression model due to the authors’ previous finding that there is decreased power to find interaction candidates compared to LT.⁴³

BF was implemented with the “leveneTest()” function with default arguments (median-centered) from the “car”⁴⁴ package, while LT was implemented with the “center = ‘mean’” argument. We implemented gS, an approach that extends BF, by using the “gJLS” package.³⁷ TSSR, an easy-to-apply approach employed in Yang et al.,³⁸ was implemented as linear regression on the squared mean-centered phenotype. SVLM³⁹ is similar to TSSR, except it also adjusts for the SNP mean effect prior to calculating the residuals; this was manually implemented. The DGLM, which jointly uses a linear model on the phenotypic means and a log-linear model on the variances,⁴⁵ was implemented with the “dglm()” function from the “dglm” package;³¹ the results from the variance test are reported. BT⁴⁰ and FK⁴¹ were implemented with the “bartlett.test()” and “fligner.test()” functions from the “stats” package.

Simulations of genotypes and phenotypes for method comparison

We compared methods for identifying variance differences by using statistical power and false positive rates (FPR) as the performance benchmarks. In the FPR scenario, we simulated a single SNP with minor allele frequency (MAF) = 0.4 by using a W ∼Binom(2, 0.4) independent random variable. In the power testing scenario, we simulated a SNP X₁ and an environmental factor X₂ by using a binomial distribution with probability of success = 0.4: X₁ ∼Binom(2, 0.4) and X₂ ∼Binom(2, 0.4). This other factor can also be thought of as an environmental exposure with three levels (e.g., for physical activity: never exercise, rarely exercise, or often exercise).

In the FPR setting, the genetic component of the phenotype, Y_G, is set to be equal to the SNP value W. In the power scenario, the genetic component of the phenotype, Y_G, is equal to the product X₁ × X₂. Furthermore, the power to nominate SNPs involved within an interaction were contrasted between mean-based association tests and variance-based association tests. In these simulations, the genetic component is equal to the product X₁ × (X₂ – 1). This is so that X₁’s marginal association with the phenotype is either positive or negative depending on the value of X₂.

We generated final phenotype values by summing the genetic component, Y_G, and random environmental noise, Y_E. Y_E was simulated from a normal distribution or a chi-square distribution with 4 degrees of freedom and scaled appropriately such that Y_G explains Ψ percentage of the variance in the phenotype and Y_E explains 100 – Ψ percent as follows.

Given Ψ, the percent of the variation explained by the environmental component is larger than Ψ by a factor 100- Ψ/ Ψ. After calculating the population variance of the genetic component, V_G, the variance of the environmental noise, V_E, can be calculated as follows:

$$V_E=V_G\times \frac{100-\psi }{\psi }$$ (Equation 2)

In practice, the normally distributed environmental noise can be simulated as Y_E ∼N(0, V_E) for normally distributed phenotypes. Chi-square distributed noise can be simulated as the following for chi-square distributed phenotypes:

$$Y_E=\sqrt{V_E}\times \kappa \left({\chi }^2\left(4\right)\right)$$ (Equation 3)

κ is the function that centers and scales the chi-square input to have mean equal to 0 and variance equal to 1. We created the final phenotypic values by calculating the sum Y_G + Y_E. In all, genotypes and phenotypes were generated for 250,000 individuals.

The association between the SNP and the variance in phenotype was tested via the different variance methods under different phenotype transformations: untransformed, log, reciprocal, and rank inverse normal transformation (RINT). The log and reciprocal transformations were applied after adding the minimum population phenotype value to all individuals’ phenotype values such that all values were greater than 0 prior to transformation. The RINT uses the ranks of phenotype values and inverse transforms the ranks into a normal distribution.

The null hypothesis (no association) was rejected when the nominal p < 0.05. This was repeated across 1,000 simulations with distinct genotypes and phenotypes in each iteration. The power estimates refer to the empirical proportion of simulations where the null hypothesis was rejected in the power scenarios, while we measured FPR by estimating the proportion of simulations where the null hypothesis was rejected in the FPR scenarios. We compared the power of the BF and SVLM methods to the power of the DRM by calculating the null hypothesis rejection rate in simulations where the interaction explained less than or equal to 1% variance in the phenotype (Ψ ≤ 1%). Significance was assessed via a paired t test of whether or not the null hypothesis was rejected across simulations.

Linear regression was used to compare a mean-based approach to a variance-based approach (using the DRM). A contingency table that describes whether the muQTL method rejected the null hypothesis of no association or the vQTL method rejected the null hypothesis of no association was calculated from count data across simulations. We performed a two-sided Fisher’s exact test separately for each percent variance explained value, Ψ, to assess the relationship of a variance test’s power with a mean test’s power.

UK Biobank data

Genome-wide association studies (GWASs) using mean and variance approaches were applied to UK Biobank (UKB).⁴⁶ UKB data was processed previously by the UKB team⁴⁶ and accessed under application ID 47137. The individuals and SNPs used in analysis were limited to those in the Neale lab’s UKB analysis (see Web Resources) because the same quality control criteria were adopted for sample and genotypes in this analysis. By doing so, individuals were removed on the basis of whether they were not used in the UKB team’s principal-component analysis (removing related samples), not of European British ancestry, or had sex chromosome aneuploidy, excess heterozygosity, or outlier genotype missing rates. Genotypes were removed if INFO score < 0.8, MAF < 0.05, or HWE p < 10⁻¹⁰. The full processed and quality-controlled data contained 344,201 individuals and 6,701,215 SNPs. The variants within the analysis are common polymorphisms and were analyzed in a large population (MAF > 0.05 and N > 270,000), protecting against the potential pitfalls of variance tests in unbalanced data.⁴⁷

Analysis was randomly split into two parts. A discovery set, which was used for discovering associations between SNPs and phenotypes, contained 80% of the data, selected randomly from the full dataset. A replication set, which was used for the replication of associations identified in the discovery set, contained the remaining 20% of the data.

GWAS in UKB

A GWAS was performed within the discovery set containing 80% of the data. We removed individuals with BMI levels greater than 5 standard deviations from the mean from analysis to prevent a large influence from outliers, which could be driven by non-modeled factors. BMI levels were adjusted for the following covariates: sex, age, age × sex, age², age² × sex, genotyping array, and principal components 1–20. We performed this by fitting a linear model and calculating the residuals.

Using the residuals, we performed a GWAS by using linear regression (mean effects) and the DRM (variance effects) between a single SNP and adjusted, untransformed BMI. The findings from these analyses were referred to, respectively, as muQTLs and raw vQTLs. We also applied a RINT to the residuals to reduce the correlation between mean and variance effects and proceeded with a GWAS by using the DRM and a dispersion effect test²⁷ (DET). The RINT generally does not remove a mean-variance relationship. The DET aims to find variance effects independent of mean effects, termed “dispersion effects.” We refer to the DRM and DET outcome as RINT vQTLs and dQTLs, respectively.

All genome-wide association analyses were implemented on sets of 5,000 SNPs and performed in parallel. Genome-wide linear regression was performed with PLINK,⁴⁸ and the DRM was performed with the BEDMatrix R package (see Web Resources). We implemented the DET by first using a Python-implemented heteroskedastic linear model²⁷ (see Web Resources), which is based on the DGLM test.⁴⁵ The dispersion effects were then estimated via the additive and log-linear variance effects, as described previously;²⁷ this method is implemented in the “estimate_dispersion_effects.R” file in the linked “hlmm” repository (see Web Resources).

Results from these analyses were compared via correlations. Significance was determined with the criterion p < 5 × 10⁻⁸ for untransformed analyses and p < 1.0 × 10⁻⁵ for RINT results. Significant QTLs were used as the nominated loci for identifying gene-gene (GxG) and GxE interactions. Previous GWAS results were downloaded from the Neale lab webpage (see Web Resources).

Construction of a diet score

We computed a diet score to be used as an interaction factor in GxE analysis by adapting a protocol described previously.^27,49 First, we extracted 18 diet-related variables: “cooked vegetable intake,” “salad/raw vegetable intake,” “fresh fruit intake,” “dried fruit intake,” “bread intake,” “cereal intake,” “tea intake,” “coffee intake,” “water intake,” “oily fish intake,” “non-oily fish intake,” “processed meat intake,” “poultry intake,” “beef intake,” “lamb/mutton intake,” “pork intake,” “cheese intake,” and “salt added to food.” We next fit a linear model by using baseline model covariates plus the 18 diet variables. These baseline model covariates included age, sex, age², age × sex, age² × sex, genotyping array, and principal components 1–20.²⁷ We fit a model to 25% of the UKB discovery set (thus, 20% of the full dataset used in the study) (N = 68,840), and estimate β coefficients for each diet variable. In the remaining 275,361 individuals (which include those from both the discovery and replication sets), we used the estimated $\hat{\mathrm{\beta }}$ coefficients for each diet variable to calculate a diet score:

$$\text{Diet}\text{score}=\hat{\mathrm{\beta }}{X}^T$$ (Equation 4)

Above, $\hat{\mathrm{\beta }}$ is the 1 × 18 vector of coefficient estimates for diet variables and X is a 275,361 × 18 matrix of diet variable values for the 275,361 individuals.

Low diet score values describe a diet predicted to be associated with individuals with low BMI, whereas high diet score values describe a diet predicted to be associated with individuals with high BMI. Potential interactions with genetic polymorphisms may describe a change in the average relationship between diet score and BMI within the general population. This would suggest that the effects of the different diet variables on BMI is synergistically higher or lower than expected.

Making non-diet environmental variables

We created additional environmental variables to use for GxE analysis. We used UKB fields 21022-0.0, 22001-0.0, and 1558-0.0 for age, sex, and alcohol intake frequency. The alcohol intake frequency field was re-coded in the opposite direction such that a higher value indicates a higher alcohol intake frequency. Individuals with missing data or who preferred not to answer were removed. For smoking status, physical activity level (PA), and sedentary behavior level (SB), we generated new variables by using the methods described in Wang et al.²⁸

For smoking status, we used fields 1239-0.0 (“current tobacco smoking”) and 1249-0.0 (“past tobacco smoking”) to create a binary variable. Individuals were only coded as 0 if they do not currently smoke and they answered “I have never smoked” or “just tried once or twice” in regard to their past history. Individuals were classified as 1 if they currently smoke or previously smoked most days or occasionally. Individuals with missing data and who could not fill the criteria were removed.

For PA, we used fields 864-0.0 (“number of days/week walked 10+ minutes”), 874-0.0 (“duration of walks”), 884-0.0 (“number of days/week of moderate physical activity 10+ minutes”), 894-0.0 (“duration of moderate activity”), 904-0.0 (“number of days/week of vigorous physical activity 10+ minutes”), and 914-0.0 (“duration of vigorous activity”), which we labeled DayW, DurW, DayM, DurM, DayV, and DurV, respectively. According to the International Physical Activity Questionnaire analysis guideline (see Web Resources), the total metabolic equivalent minutes (METT) can be approximated as follows:

$$\mathrm{M}\mathrm{E}\mathrm{T}\mathrm{T}=3.3\times \mathrm{D}\mathrm{a}\mathrm{y}\mathrm{W}\times \mathrm{D}\mathrm{u}\mathrm{r}\mathrm{W}+4.0\times \mathrm{D}\mathrm{a}\mathrm{y}\mathrm{M}\times \mathrm{D}\mathrm{u}\mathrm{r}\mathrm{M}+8.0\times \mathrm{D}\mathrm{a}\mathrm{y}\mathrm{V}\times \mathrm{D}\mathrm{u}\mathrm{r}\mathrm{V}.$$ (Equation 5)

Next, PA for each individual was assigned 1, 2, or 3 for low, moderate, or high activity. High PA individuals were classified as having DayV ≥ 3 and METT ≥ 1,500 or DayW + DayM + DayV ≥ 7 and METT ≥ 3,000. Moderate PA individuals were classified as having DayV ≥ 3 and DurV ≥ 20, DayM ≥ 5 and DurM ≥ 30, or DayW ≥ 5 and DurW ≥ 30. Low PA individuals were classified as the remainder (not enough activity recorded to meet the other criteria).

For SB, we used fields 1090-0.0 (“time spent driving”), 1080-0.0 (“time spent using computer”), and 1070-0.0 (“time spent watching television [TV]”). For each variable, “less than an hour a day” (−10) was set equal to 0 and “do not know” or “prefer not to answer” (−1 or −3) answers were imputed with the median of the remaining values. SB was set equal to the sum of the three columns. Outlier individuals, defined as those greater than 5 standard deviations from the mean, were removed.

Sampling random SNPs matched to QTLs

We used random SNPs to calibrate analyses with the genome-wide expectation. We calculated the frequency of homozygous minor genotypes (f_minor), the MAF, and the count of individuals with a non-missing genotype at each SNP (N_miss) to match genome-wide SNPs to QTLs. To identify the underlying null distribution of various statistics in our study, we sampled 10 matched SNPs for each QTL. Each matched SNP had to have an MAF and f_minor that were ±1% margin from the QTL’s MAF and f_minor and an N_miss within 1% of the QTL’s N_miss count and had to be on a different chromosome than the QTL.

Identification of genetic interactions

We tested for genetic interactions associated with untransformed BMI. Pairwise interaction testing was performed between all SNP candidates and with each of the seven environmental factors in the discovery and replication sets separately. For GxE interactions with diet, only 75% of the discovery set (60% of full UKB set) was used for association tests because 25% was used to fit the model for calculating the diet score variable. GxE p values were adjusted with false discovery rate (FDR) and significance determined by FDR < 0.1. For comparison, the GxE interaction analysis was also performed for log-BMI and RINT BMI. p values from a GxG interaction analysis were separately adjusted via FDR, and significance was determined at FDR < 0.1.

GxE discovery rate was compared between the QTL set and the genome-wide matched SNP set. First, the same number of SNPs as the QTL set were sampled from the matched SNP set. Second, the GxE p values from the sampled genome-wide SNPs were adjusted via FDR. Third, the discovery rate within the set was calculated as the proportion of GxE interactions with FDR < 0.1. This was repeated across 10,000 iterations, and the mean discovery rate across the iterations was used as the expected probability in a one-sided binomial test.

Statistical replication of genetic interactions

Genetic interactions discovered in the discovery cohort were tested for replication in the replication set. Given a p value threshold equal to x, all more significant interactions (those with p < x) were identified. Within the replication cohort, an interaction is considered to have been replicated if the direction of effect was the same as in the discovery set and if the p value in the replication set is p < 0.05. The replication rate is the proportion of interactions to have replicated according to these two criteria. We computed the genome-wide replication rate by using the matched and randomly sampled SNPs and testing for GxE interactions within both the 80% and 20% cohorts. The replication rate was calculated at the following p value thresholds: 0.05, 0.01, 2.16 × 10⁻³, 0.005, 5.22 × 10⁻⁴, and 1.80 × 10⁻⁵, where 2.16 × 10⁻³, 5.22 × 10⁻⁴, and 1.80 × 10⁻⁵ are FDR = 0.1, FDR = 0.05, and FDR = 0.01 thresholds, respectively. We calculated these by identifying the maximum GxE p values within the discovery set that pass the respective FDR thresholds. In displays, the gray confidence intervals are derived from a binomial test with rate equal to 0.025, which is the theoretical replication rate under no true association.

The replication rates could be statistically contrasted between two GxE interaction sets (for example, the replication rate of the GxE interactions from the QTLs versus the replication rate of the GxE interactions from the matched SNPs). One set is specified as the background set, and the replication rate within this background set is used as the theoretical success rate in a one-sided exact binomial test. The other parameters in the binomial test are taken from the other GxE set. The number of successes is the number of replicated GxE interactions, and the number of trials is the total number of GxE interactions tested.

Assessing interactions at the FTO locus

We further explored the many interactions found at rs56094641 in the FTO intronic region. A larger model was fitted to untransformed BMI, which contained all FDR < 0.1 interactions and the main effects for each interacting factor. The significance values of the interaction estimates were assessed. Next, we determined whether rs56094641’s variance association was diminished when considering the interactions. We took the residuals from the model and used the DRM to estimate the variance effect. We computed the percent change in DRM effect with the original estimate.

Analyzing the rs12996547 × age interaction

We analyzed a SNP-by-age interaction on BMI levels (FDR < 0.01) further by using GTEx data. The rs12996547 polymorphism in UKB was not used in GTEx consortium analyses.⁵⁰ Leveraging the 1000 Genomes Project⁵¹ and the HaploReg database,⁵² we identified a nearby SNP, rs7575617, in linkage disequilibrium (LD) (D′ = 0.89) that was used in the GTEx analyses and queried the GTEx portal for eQTL associations. Using the GTEx v8 data release, we correlated donor age and TMEM18 expression within visceral adipose tissue samples. In GTEx, donor age is grouped within 10-year bins (e.g., 40–49, 50–59), which we coded as a numerical variable to perform pairwise correlation.

Screening BMI GxE interactions for pleiotropic disease associations

To test whether GxE interactions associated with BMI are also associated with related diseases, three binary disease phenotypes that represent diabetes diagnosis, high blood pressure (HBP) diagnosis, and coronary artery disease (CAD) ascertainment were assembled. Diabetes and HBP was coded with corresponding fields 2443-0.0 and 6150-0.0, which include self-reported questionnaire information. The diabetes phenotype represents a self-reported answer to the question “has a doctor ever told you that you have diabetes?” This would represent a mix of diabetes subtypes, including type 1 and type 2 diabetes. For diabetes, values less than 0 were removed from association testing. For HBP, a value less than 0 represented a control individual and a value equal to 4 represented an affected individual. CAD was specified with criteria from previous research.²⁴ The following individuals were listed as affected individuals: field 20002-0.0 equal to 1075; fields 41203-0.0 or 41205-0.0 equal to 410, 4109, 411, 4119, 412, 4129; fields 41202-0.0 or 41204-0.0 equal to I21, I210, I211, I212, I213, I214, I219, I21X, I22, I220, I221, I228, I229, I23, I230, I231, I232, I233, I234, I235, I236, I241, I252; fields 41200-0.0 or 41210-0.0 equal to K40, K401, K402, K403, K404, K41, K411, K412, K413, K414, K451, K452, K453, K454, K455, K491, K492, K498, K499, K502, K751, K752, K753, K754, K758, K759. All other individuals were listed as the control individuals for CAD.

GxE interactions with FDR < 0.1 and same direction of effect in discovery and replication sets were tested for association with diabetes, HBP, and CAD risk. A p value of less than 0.05 in the replication cohort was not required because the limited sample size in the replication cohort (one quarter the size of the discovery set) may reduce power to identify interaction associations at that level of significance and typically implies that a larger effect needs to be observed within the smaller cohort to reach that level of significance. (We found that only requiring direction of effect will still show statistically significant differences in replication rate between QTLs and random genome-wide SNPs.) Finally, we tested for the GxE interaction with disease by employing logistic regression with identical covariates to the BMI analysis. We repeated this with adjustment for BMI by using BMI as a covariate.

PheWAS enrichment of vQTLs using Open Targets database queries

We tested whether raw vQTLs from our study were enriched for certain phenotype associations compared to SNPs only associated with mean BMI levels, which we term pure muQTLs. First, we performed a phenotype-wide association study (PheWAS) by leveraging the Open Targets database.⁵³ For an input SNP, we identified any phenotypes within the database that have been associated with the SNP during a previous GWAS at p < 0.05. Across a set of queried SNPs, we calculated the proportion that were associated with the phenotype. We repeated this for the set of variance QTLs and the set of pure mean QTLs (no vQTL association). We trimmed the phenotypes list by using the Open Target categories that were relevant to our study (Data S1).

Next, we developed a statistical test to determine whether a given set of SNPs is enriched for association with a phenotype compared to a background set. Given a test set of K SNPs in which m of the K SNPs are associated with the phenotype and a background SNP set in which p is the proportion of SNPs associated with the phenotype, we employ an exact binomial test with m successes, K trials, and p hypothetical probability of success. We test significance under a one-sided alternative hypothesis that the observed success rate, m / K, is improbable (H_A: m / K > p) given an underlying binomial distribution with probability p. The p values from the test were calculated for every phenotype present in the test set. FDR correction was applied, and significance was assessed at FDR < 0.1.

We applied the described PheWAS enrichment test in two settings. First, we evaluated whether the test was robust for use with the real data by randomly sampling 21 pure muQTLs and using the remaining pure muQTLs as the background set. Next, we evaluated whether some associated phenotypes are enriched in the vQTL set compared to in the pure muQTLs by using the pure muQTLs as the background set.

Annotating QTLs with protein-coding genes

All protein-coding genes were downloaded from Ensembl. We queried a QTL in the Open Targets database⁵³ by using the application programming interface (API), and the variant-to-gene (V2G) scores and the Ensembl variant effect predictor (VEP) scores were saved for all Ensembl protein-coding genes. If a queried SNP’s VEP score for a gene was greater than zero in Open Targets (e.g., the variant lies within an intron, exon, or UTR region), then the SNP was annotated with the gene with the greatest VEP score. Otherwise (for intergenic SNPs), the gene with the highest V2G score was used. If no protein-coding genes had a V2G score (because of far proximity), the coding gene with the nearest transcription start site was identified via the Open Targets API. Finally, if the queried SNP was not present in Open Targets, then a SNP in LD was identified as a proxy (Data S2). rs550990127, rs562044398, rs772168224, and rs753789664 are four indels (3 muQTLs, 1 RINT vQTL) that were removed from functional enrichment and PheWAS analyses because of annotation issues.

GeneMania network creation and GO enrichment analysis

GeneMania incorporates multiple biological databases to create a gene network, identify highly interconnected genes, and perform gene ontology (GO) enrichment analysis. We used the browser platform with default settings, except for the addition of the “attributes” databases. We separately queried the list of annotated genes for raw vQTLs and the list of genes for pure muQTLs. We removed major histocompatibility complex (MHC) SNPs from the analysis.

Stratified LD score regression to infer cell type relevance

Stratified LD score regression was performed with gene expression data via the “Multi_tissue_gene_expr” flag and default settings.⁵⁴ Summary statistics were transformed using the “munge_sumstats.py” script. Only non-MHC HapMap3 SNPs were kept for LD score regression analysis. Cell type enrichment p values across the 205 functional annotations were adjusted via the Benjamini-Hochberg method for FDR.⁵⁵ This was applied separately to the genome-wide summary statistics from the muQTL analysis and to the summary statistics from the raw vQTL analysis.

Results

Deviation regression model discovers vQTLs that are due to GxE interactions

To identify genetic variants associated with the variance of quantitative phenotypes, we considered several tests (see Material and methods),^{31,34,35,37, 38, 39, 40, 41} including our approach that we refer to as the DRM. In the DRM, a linear regression is performed on a single SNP and phenotype, where the minor allele count is used as the independent variable and the absolute difference between an individual’s phenotypic value and the phenotype medians within each genotype is used as the dependent variable (after covariate adjustment) (Figure 2A) (see Material and methods). The effect sizes and p values are used to estimate the variance effect of a SNP and assess vQTL significance, similar to a standard GWAS.

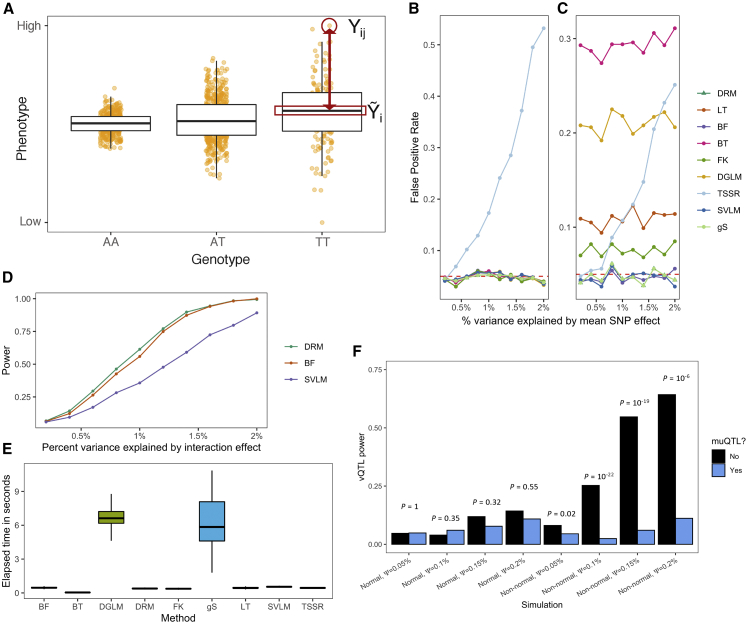
Figure 2.

Assessing a variance test for finding SNPs with interaction effects

(A) The DRM uses the absolute difference between an individual’s phenotype Y_ij (for each genotype i and individual j) (y axis) and the within-genotype phenotype median (Y_i) as a dependent variable. The absolute difference is modeled in a linear regression across genotypes (x axis). Simulated data shown.

(B and C) False positive rates for different variance tests at SNPs with varied mean effects in a (B) normal and (C) non-normal phenotype. Methods tested are as follows: DRM, Levene’s test (LT), Brown-Forsythe test (BF), Bartlett’s test (BT), Fligner-Killeen test (FK), double generalized linear model (DGLM), two-step squared residual approach (TSSR), squared value linear modeling (SVLM), and extended Levene’s test of generalized scale (gS).

(D) Power of the DRM, BF, and SVLM in non-normally distributed phenotypes. The gS method’s power is nearly identical to the DRM and is not displayed.

(E) The elapsed time to perform each method on a single SNP across 1,000 simulations. The data are summarized as boxplots where the middle line is the median, the lower and upper hinges are the first and third quartiles, and the whiskers extend from the hinge with a length of 1.5× the inter-quartile range.

(F) vQTL test power, quantified by the DRM, stratified by whether the SNPs are detected by a muQTL test (linear regression). By using a 2-by-2 contingency table representing the counts of muQTL and vQTL test rejection across 1,000 simulations, Fisher’s exact test assessed whether muQTL power and vQTL power show non-random association. p values are displayed.

We first used simulation to quantify the FPR for the different variance tests. We tested the FPR by using a scenario where a single SNP affects the mean of the phenotype and, thus, a variance effect should not be detected except by random chance. We generated a SNP genotype and a phenotype value for 250,000 individuals. Across 1,000 simulations, we tested for a variance effect, and calculated the FPR as the proportion of simulations where the nominal p < 0.05. We found that the FPR was controlled well by nearly all variance methods when the phenotype was normally distributed (Figure 2B). When the phenotype was non-normal, however, the FPR was substantially elevated for several variance tests, including the FK test⁴¹ or the DGLM,³¹ but not for the DRM, BF test,³⁴ SVLM,³⁹ or the gS³⁷ (Figure 2C). Although we note that the variance of the sample variance is inflated for distributions with excess heteroscedasticity,⁵⁶ our results demonstrate that at least a few tests are robust to a SNP with only a mean effect in a non-normal phenotype. Lastly, we found that transformations created false positives in simulations where SNPs only affect the mean of the phenotype—regardless of the variance test used (FPR = 100%).

We further used simulations to test the ability of vQTLs to reveal SNP-by-factor pairs with an interaction effect on the phenotype. We repeated the previous FPR simulations, except we generated an environmental factor that interacts with the SNP to influence the mean of the phenotype. As the interaction became stronger (percent variance explained by the interaction, Ψ, increases from 0.2% to 2%), the DRM’s power to detect an interaction effect at a SNP increased from less than 10% to nearly 100% (Figure 2D). Additionally, in non-normal traits, we found a 10.1% and 64.1% power increase (p = 6.4 × 10⁻¹⁰ and p = 1.6 × 10⁻¹¹⁰) for the DRM compared to the BF and SVLM, respectively, at polymorphisms with smaller interaction effects (Ψ ≤ 1%) (Figure 2D). The DRM had nearly identical power across interaction effect sizes and trait distributions to the gS (62.800% versus 62.825%; p > 0.05), but the mean time to run the gS was 44.8× longer than the DRM (Figure 2E). Therefore, in our simulated data, vQTLs could identify SNPs with large effect interactions and the DRM had superior power, improved FPR, and better computational efficiency compared to other variance tests (Supplemental Note S1; Figures S1 and S2).

Finally, we contrasted the use of vQTLs for identifying SNPs involved in an interaction with the use of mean-associated loci (muQTLs, as first identified via linear regression). Using a similar testing procedure, we simulated SNP-by-factor interactions where the direction of the SNP effect changes depending on the interacting factor (Material and methods). Across 1,000 simulations, we found that muQTL test power and vQTL test power were not positively correlated. For example, a vQTL test’s power at non-muQTLs in non-normal traits was 54.7% when Ψ = 0.15%, compared to 6.0% at muQTLs (Figure 2F). Our results show that positive and negative effects from a single SNP due to an interaction can remove a muQTL signal (such as shown in Figure 1), yet vQTL methods are robust to this phenomenon, therefore providing a complementary approach to discovering interactions. Finally, although the muQTL approach had increased power to detect the causal SNPs compared to the vQTL approach (Figure S1D), we note that muQTL approaches will pick up variants that directly impact the trait but that are not involved in an interaction (leading to a high FPR). Therefore, our vQTL approach can identify SNPs involved in GxE interactions with higher specificity than using muQTLs.

Performing GWASs in UKB

Hundreds of variants have been associated with BMI, highlighting that diverse pathways, from immune system activation to leptin signaling to the central nervous system, regulate body weight.^32,33 Furthermore, environmental influences and lifestyle choices such as diet, exercise, and gut microbiome composition⁵⁷ also have a major influence on BMI. Therefore, we hypothesized that there may be strong GxE interactions that regulate BMI, and these interactions may appear as a change in the BMI variance at a SNP. In 275,361 unrelated British European individuals from UKB, we searched for genetic variants associated with the means (muQTLs) and variances (vQTLs) in untransformed BMI values (p < 5 × 10⁻⁸) (Figure 3A; Supplemental Note S2).

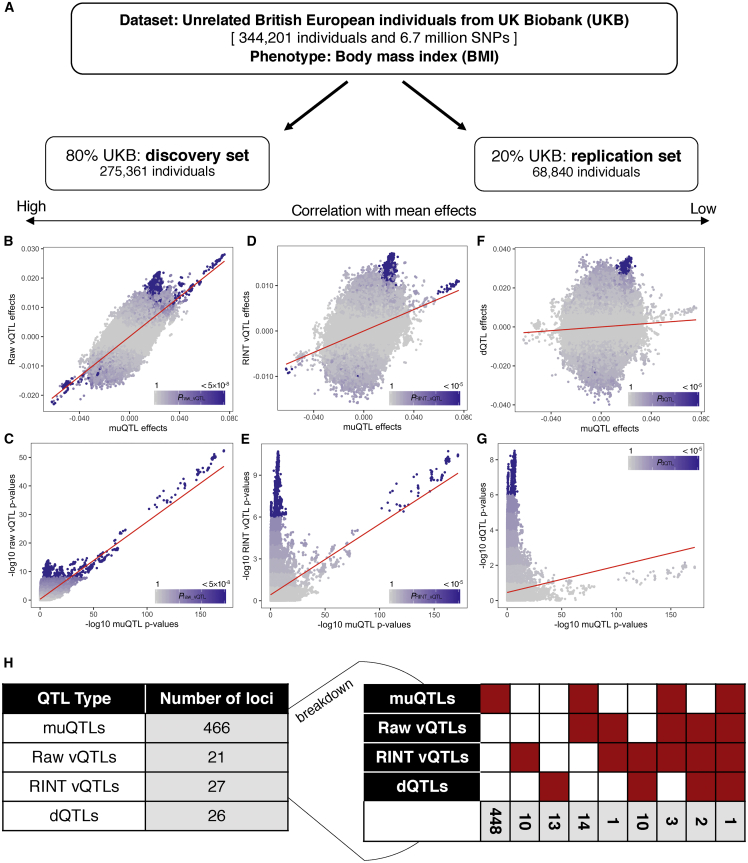
Figure 3.

GWAS of body mass index levels in UK Biobank

(A) Data for imputed genotypes and BMI in unrelated British European individuals were split into a discovery set, representing 80% of the data, and a replication set, representing 20% of the data. Within the discovery set, a GWAS was performed on the means (muQTLs) and variances (raw vQTLs) of untransformed BMI and on the variances (RINT vQTLs) and dispersion (dQTLs) of RINT BMI.

(B–H) Across SNPs, the effect sizes (B) and p values (C) were highly correlated between muQTLs and raw vQTLs. The RINT reduced mean-variance correlation (D) and identified a set of RINT vQTLs with smaller muQTL effects (E). Dispersion effects had the least correlation with mean effects (F), and all dQTLs were not the most significant muQTLs (G). In (B)–(G), the red line represents the line of best fit. Points are colored by the –log₁₀ p value of the y axis analysis, and purple represents significance (p < 5 × 10⁻⁸ with raw BMI, p < 10⁻⁵ with RINT BMI). The GWAS results are summarized in (H), broken down into by the number of QTLs passing the different criteria (indicated by the red coloring and gray counts).

We discovered a strong correlation between mean and variance effects, which we refer to as the “mean-variance relationship” (Figures 3B and 3C). The mean-variance relationship could be explained in a number of ways. Because the sample means and sample variances are correlated in non-normal distributions and BMI is non-normally distributed, variance effects could be a consequence of a SNP’s mean effect and, therefore, any observed associations with phenotypic variance are not indicative of underlying interactions²⁷ (Supplemental Note S3). Alternatively, we hypothesized that a SNP associated with the mean value of a phenotype is also more likely to be involved within interactions, thus creating the correlation we observe. Biologically, SNPs with a main effect (directly impacting the studied trait) may have a greater likelihood of having an interaction effect. Statistically, variance estimates have larger standard errors than mean estimates in a population sample; thus, interactions must have large effect sizes to detect a change in variance (Supplemental Note S4; Figure S3). Consequently, marginal mean SNP effects might be detected as well because of large effect interactions. Therefore, a correlation between mean and variance effects might be due to both real biological and statistical causes.

To disentangle the mean-variance relationship, Young et al. described how analysis of a phenotype with a RINT helps reduce the correlation between mean and variance effects²⁷ and proposed a dispersion effect test to identify differences in variances not driven by the mean effects (known as dispersion effects). We sought to find SNPs associated with both the variance and dispersion of BMI after a RINT. We used the DRM to identify variance effects and Young et al.’s dispersion effect test to discover dispersion effects. We identified SNP associations by using a less-conservative p < 10⁻⁵ threshold to produce an expanded set of SNPs because these analyses resulted in conservative p value distribution (Figures 3D–3G; Figure S4; Supplemental Notes S5 and S6).

We discovered 448 SNPs associated with the mean of untransformed BMI values (which we refer to as “muQTLs”), 21 SNPs associated with the variance of untransformed BMI values (“raw vQTLs”), 27 SNPs associated with the variance of transformed BMI values (“RINT vQTLs”) and 26 SNPs associated with the dispersion of transformed BMI values (“dQTLs”) (Figure 3H). As expected, the correlation with mean effects decreases from raw vQTLs to RINT vQTLs to dQTLs; for example, 18 of 21 raw vQTLs are also muQTLs, 4 of 27 RINT vQTLs are muQTLs, and 3 of 26 dQTLs are muQTLs. We combined the muQTLs, raw vQTLs, RINT vQTLs, and dQTLs into a set of 502 unique QTLs. We next proceeded to the second step of our sequential GxE discovery framework where we searched for pairwise interactions between the 502 unique QTLs and with age, sex, and five environmental factors: smoking status, diet, physical activity, sedentary behavior, and alcohol intake frequency (the details of these factors are described within the Material and methods).

Discovery and replication of GxE interactions

To identify GxE interactions potentially affecting BMI, we used the same set of 275,361 unrelated European individuals. Using the 502 unique QTLs and seven factors (age, sex, smoking status, diet, physical activity, sedentary behavior, and alcohol intake frequency), we tested for 3,514 GxE interactions by applying 3,514 distinct linear models containing a single interaction term. Overall, we identified 78 significant GxE interactions associated with untransformed BMI in the discovery set (FDR < 0.1) (Figure 4A), a 155× greater discovery rate over interaction testing based on a genome-wide-sampled set of SNPs (2.2% versus 0.014%; p = 9.8 × 10⁻¹⁴⁰) with no expected FPR increase (Figures 4B and 4C; Materials and methods; Supplemental Notes S7 and S8; Figures S5A–S5D). In contrast, we failed to identify significant GxG interactions influencing BMI levels (Supplemental Notes S9 and S10; Figure S6).

Figure 4.

Discovery and replication of GxE interactions

(A) Heatmap of all QTLs with an FDR < 0.1 GxE interaction in the discovery set. Each box colored by significance level in the discovery set. Raw vQTL SNPs are highlighted in orange. Smok, smoking status; SB, sedentary behavior level; PA, physical activity level; Alc, alcohol intake frequency.

(B–E) Quantile-quantile plots for all GxE interactions across environmental factors and (B) 5,016 matched genome-wide SNPs, (C) 502 QTLs, (D) 448 muQTLs that are not raw vQTLs, or (E) 21 raw vQTLs. The x axis shows the –log₁₀ p values under the null distribution, and the y axis shows the observed –log₁₀ p values, where each point represents a different GxE interaction. The red line represents the expectation under the null with intercept = 0 and slope = 1.

(F–I) Replication rates of GxE interactions, as quantified by those with the same direction of effect in both discovery and replication sets and p_R < 0.05. Given a threshold x (x axis), the replication rate (y axis) is calculated for all interactions with p_D < x. (F) GxE interactions using 5,016 matched genome-wide SNPs. (G) GxE interactions using all 502 QTL-nominated SNPs. (H) GxE interactions using 448 muQTLs that are not raw vQTLs. (I) GxE interactions using 21 raw vQTLs. In (F)–(I), the confidence interval over replication rates is shown in gray and the expected replication rate under random observations (2.5%) is shown in red. Red points are FDR < 0.1, < 0.05, and < 0.01 cut-offs. In (G) and (I), there are no FDR < 0.1 associations.

We used an independent and randomly selected replication set of 68,840 unrelated British European individuals from UKB to evaluate our findings in the discovery cohort (Figure 3A). We refer to effect size estimates and p values from the discovery set as b_D and p_D and those from the replication set as b_R and p_R. We considered an interaction to be replicated if the direction of effect was the same in both discovery and replication sets [ sign(b_D) = sign(b_R) ] and p_R < 0.05. Overall, 21.1% of significant GxE interactions (FDR < 0.1) replicated, compared to 7.8% of GxE interactions at similar nominal p_D values based on genome-wide SNPs (2.7-fold enrichment, p = 2.2 × 10⁻⁴) (Figures 4F and 4G). The estimated replication rate increased as the significance threshold became stricter: all nine FDR < 0.01 interactions replicated effect direction and four of the nine passed p_R < 0.05 significance. We note that the replication rate is low because of the much smaller sample size in the replication set, which creates difficulty achieving statistical significance at p_R < 0.05. (The rate is 73.7% when requiring only the same direction of effect.) Our data suggest that interactions with the 502 unique QTLs had significantly greater replication rates compared to interactions from genome-wide SNPs, despite similar nominal p_D values (Supplemental Note S11; Figure S5E).

We found that the increased discovery and replication rates are driven by raw variance effects. 14.2% of tested GxE interactions with raw vQTLs were significant (FDR < 0.1), a 10.0-, 8.6-, and 7.7-fold higher GxE discovery rate than muQTLs, RINT vQTLs, and dQTLs, respectively, in the absence of a significant raw vQTL association (1.4%, 1.7%, and 1.9% respective discovery rates, p < 10⁻¹² for each; Figures 4D and 4E; Figures S5E–S5I). Raw vQTLs drove the GxE discovery rate, regardless of transformation to BMI (Supplemental Note S12; Tables S1 and S2). Similarly, the interactions from vQTLs (FDR < 0.1) had a 2.8-fold higher replication rate compared to muQTLs that were not raw vQTLs (38.1% versus 13.5%; p = 4.3 × 10⁻³) (Figures 4H and 4I; Supplemental Note S13). Lastly, we found that the GxE effects correlated best with the raw vQTL effects compared to the muQTL, RINT vQTL, or dQTL effects (Figure S7). Hence, we found that the ability to discover and replicate GxE interactions was primarily driven by a single SNP’s marginal association with untransformed BMI variance.

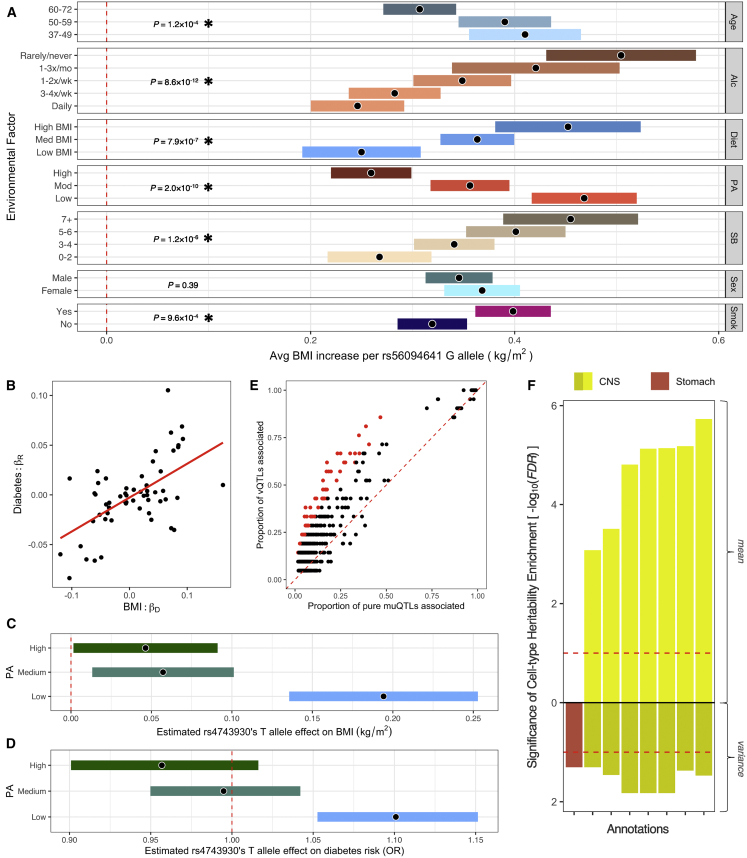
Large GxE interactions influence BMI

The most significant interaction identified with respect to BMI was between the FTO intronic region and alcohol intake frequency (p = 8.6 × 10⁻¹²). The FTO intron region harbors the strongest muQTL (p = 1.3 × 10⁻¹⁷²), raw vQTL (p = 5.4 × 10⁻⁵³), and RINT vQTL (p = 3.7 × 10⁻¹¹) association with BMI (rs56094641), has been functionally implicated as a key obesity regulator in mouse experiments and CRISPR-Cas9 editing of human samples,^58,59 and was recognized as a GxE interaction hotspot in previous studies.⁴⁹ At this locus, we identified additional interactions (FDR < 0.1) with sedentary behavior (p_D = 1.2 × 10⁻⁶), physical activity (p_D = 2.0 × 10⁻¹⁰), diet (p_D = 7.9 × 10⁻⁷), age (p_D = 1.1 × 10⁻⁴), and smoking behavior (p_D = 9.6 × 10⁻⁴) but not with sex (p_D = 0.39) (Table 1; Figure 5A). Using BMI as the response, we fit a model containing each significant interaction with rs56094641 (plus all main effects) and found a significant effect for each GxE term (p < 0.05), suggesting that each interaction is independent (Table S3). Furthermore, modeling the interactions reduced the estimated variance effect by 20.1%.

Table 1.

GxE interactions with FDR < 0.01

SNP	Gene	E	bD	pD	bR	pR	pmean	praw	pRINT	pdisp
rs539515	SEC16B	alc	−0.045	1.1 × 10−5	−0.065	1.6 × 10−3	10−44	10−8	0.26	0.42
rs56094641	FTO	alc	−0.058	8.6 × 10−12	−0.072	2.1 × 10−5	10−172	10−53	10−11	0.01
rs56094641	FTO	SB	0.025	2.5 × 10−6	0.011	0.26	10−172	10−53	10−11	0.01
rs56094641	FTO	PA	−0.103	2.0 × 10−10	−0.077	0.02	10−172	10−53	10−11	0.01
rs56094641	FTO	diet	0.078	9.6 × 10−8	0.091	3.5 × 10−4	10−172	10−53	10−11	0.01
rs58084604	MC4R	diet	0.084	7.2 × 10−7	0.049	0.10	10−73	10−19	10−4	0.21
rs7132908	FAIM2	SB	0.030	8.4 × 10−9	0.008	0.44	10−30	10−11	10−3	0.14
rs12467692	UBE2E3	alc	0.040	6.8 × 10−6	0.031	0.08	10−10	10−3	0.26	0.96
rs12996547	TMEM18	age	−0.007	1.8 × 10−5	−0.006	0.07	10−16	10−7	10−3	0.05

From left to right: the SNP name, annotated gene (based on evidence in the Open Targets database, see Material and methods), environmental factor (Smok = smoking status; SB = sedentary behavior level; PA = physical activity level; Alc = alcohol intake frequency), estimated effect size and p values in the discovery cohort, estimated effect size and p values in the replication cohort, and p values from the four QTL studies: muQTLs, raw vQTLs, RINT vQTLs, and dQTLs. Summary statistics for all available QTLs are available in Data S9.

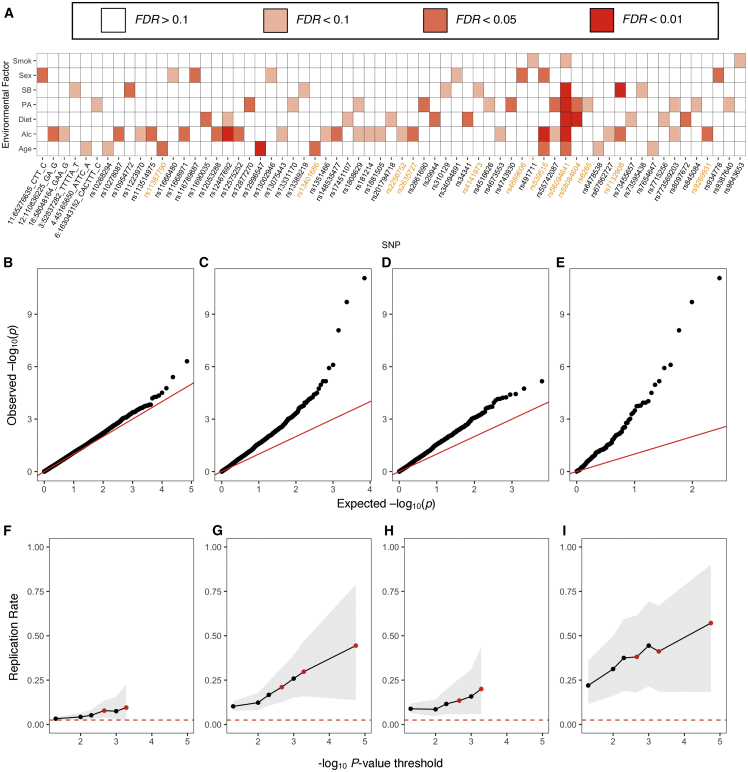
Figure 5.

GxE interactions across environmental factors, human phenotypes, and cell types

(A) The estimated marginal BMI effect of the rs56094641 G allele conditioned on the different environmental co-variates. For visualization, age, sedentary behavior values, and diet (bottom 20%, middle 60%, upper 20%) were grouped and ”rarely” or “never” answers for alcohol intake frequency were combined. Significant GxE interactions are highlighted with an asterisk (FDR < 0.1), and nominal p values are shown.

(B) Estimated GxE effects in BMI within the 80% discovery set (x axis) from linear regression were correlated with estimated GxE effects on diabetes risk within the 20% replication set (y axis) from logistic regression. Each data point represents a different SNP × co-factor interaction. BMI GxE interactions appear predictive of diabetes GxE interactions.

(C and D) The estimated marginal effect of the rs4743930 T allele on (C) BMI and (D) diabetes risk, conditioned on physical activity levels. Estimated diabetes risk effect is in terms of the relative odds ratio (OR). In (A), (C), and (D), the estimate is shown by the black dot, and the bars indicate the 95% confidence intervals. Smok, smoking status; SB, sedentary behavior level; PA, physical activity level; Alc, alcohol intake frequency.

(E) The proportion of pure muQTLs (those with no significant raw vQTL association) associated with a phenotype were compared to the proportion of raw vQTLs that are associated. Each point is a different phenotype that is included in the Open Targets database. Phenotype associations significantly enriched in the raw vQTL set (FDR < 0.1) are highlighted in red.

(F) The −log₁₀(FDR) describe the partitioned enrichment of BMI mean and BMI variance heritability in specifically expressed genes for a given cell type. Only cell-types with FDR < 0.1 in the BMI variance analysis are shown. Dashed red lines drawn at FDR < 0.1.

The most significant GxE interaction identified outside the FTO region was between the rs7132908 variant and sedentary behavior level (p_D = 8.4 × 10⁻⁹). This variant lies in the 3′-UTR of FAIM2, with selective and functional constraint (as estimated by SiPhy⁶⁰ and GERP⁶¹), 30 different bound proteins in ENCODE ChIP-seq experiments,⁶² and a high prevalence of enhancer histone marks and DNase sites across tissue types in the Roadmap Epigenomics Consortium.^52,63 FAIM2 encodes an anti-apoptopic protein and exhibits a brain-specific gene expression pattern across human tissues.⁵⁰ Previously, it has been shown that FAIM2 expression is regulated by dietary exposures⁶⁴ and FAIM2 promotor methylation is regulated by sedentary behavior.⁶⁵ Furthermore, the rs7132908 variant has another significant GxE interaction (FDR < 0.1) with alcohol intake frequency on BMI (p_D = 1.7 × 10⁻⁴).

The four other FDR < 0.01 GxE interactions we discovered were between rs58084604 (near MC4R) and diet (p_D = 7.2 × 10⁻⁷), rs539515 (SEC16B) or rs12467692 (UBE2E3) and alcohol intake frequency (p_D = 1.1 × 10⁻⁵ and p_D = 6.8 × 10⁻⁶, respectively), and rs12996547 (TMEM18) and age (p_D = 1.8 × 10⁻⁵). All nine FDR < 0.01 interactions replicated with the same direction of effect, and four of the nine had p_R < 0.05 (Table 1; Table S4). MC4R gain-of-function mutations protect against obesity risk⁶⁶ and have been functionally validated in obesity in mice,⁶⁷ while Sec16b knockout mice carry decreased cholesterol levels with higher body weight.⁶⁸ We found that age and the rs12996547 haplotype are associated with increased TMEM18 expression in visceral adipose GTEx tissue⁵⁰ (age, r = 0.22, p = 4.4 × 10⁻⁵; SNP, b = 0.155, p = 3 × 10⁻⁴), which may be one mechanism to jointly reduce BMI levels. Previously, Tmem18 germline loss in mice led to increased body weight, whereas overexpression resulted in weight loss by regulating appetite and energy balance.⁶⁹ Our findings in UKB and GTEx lend further evidence to support the role of TMEM18 in BMI.

GxE interactions have pleiotropic effects over BMI and diabetes risk

We aimed to determine whether GxE interactions influencing BMI levels exhibit pleiotropic effects and are shared across human diseases, possibly by jointly influencing BMI and disease risk (Figure S8A). From the set of 78 significant GxE interactions above (FDR < 0.1), we identified a set of 58 GxE interactions associated with the same direction of effect on BMI in both discovery and replication sets. We then screened these GxE interactions against three additional medical diagnoses: CAD, diabetes, and HBP diagnosis (Material and methods).

We found that GxE effects on BMI estimated in the discovery cohort significantly correlated with GxE effects on diabetes risk within the held-out set (r = 0.59, p = 1.3 × 10⁻⁶) (Figure 5B), even after adjusting for BMI as a confounder (r = 0.38, p = 3.3 × 10⁻³) (Figure S8B), indicating that BMI GxE effects are predictive of GxE influences over diabetes risk. Furthermore, we identified one significant disease interaction (FDR < 0.1) where physical activity regulated the association of rs4743930 with diabetes risk (p = 8.7 × 10⁻⁵; FDR = 0.015). In a previous UKB analysis (see “Neale lab GWAS in UK Biobank” in Web Resources), this variant is marginally associated with diabetes risk at p = 0.022 and consequently would not appear as one of the most significant findings in a hypothesis-free GWAS. Within low exercise individuals, the rs4743930 T allele was associated with increased BMI levels (b_D = 0.19 kg/m² per T, p_D = 8.5 × 10⁻¹¹) and increased diabetes risk (OR_D = 1.10, or a 10% risk increase per T, p_D = 2.7 × 10⁻⁵). Within moderate or high exercise individuals, there was a minor association with BMI levels and no significant association with diabetes risk (Figures 5C and 5D). This interaction could be linked to decreased BMI levels and protective diabetes effects in both discovery and replication sets (BMI, b_D = −0.075, b_R = −0.042; diabetes risk, b_D = −0.075, b_R = −0.065), although p_R = 0.25 and p_R = 0.09 for BMI and diabetes risk in the replication set (possibly as a result of lower sample size; Table 1 shows that more than half of the FDR < 0.01 interactions had p_R > 0.05 despite same effect direction). The observed associations remained present after adjusting for BMI as a confounder (b_D = −0.058, p_D = 2.5 × 10⁻³; b_R = −0.066, p_R = 0.09) (Figure S8C).

Leveraging the genomic (transcription start site proximity), transcriptomic (eQTL studies), and epigenomic information (Promoter Capture Hi-C data) found in the Open Targets database,⁵³ we inferred that rs4743930 most likely regulates the BARX1 gene, which is part of the homeobox transcription factor family integral to anatomical development. BARX1 exhibits a noteworthy tissue-specific gene expression pattern across human tissues, with high expression in visceral adipose, esophagus, and stomach tissue and very low expression in other GTEx tissues⁵⁰ (Figure S8D). Previous research has shown that the BARX1 transcription factor protein is a key regulator of stomach cell fate and organogenesis and Barx1^−/− knockout mice have significantly altered stomach morphology as a result of inhibition of the Wnt signaling pathway.^70,71 As the Wnt signaling pathway modulates the formation of adipose tissue and regulates the sensitivity to insulin, it has been proposed that pathway malfunctioning could lead to high co-morbidities of obesity and diabetes.⁷² Here, we provide human genetic evidence of a pathway regulator, BARX1, to support Wnt signaling’s proposed pleiotropy over body weight and diabetes risk.

vQTLs are linked to environmentally influenced pathways and phenotypes

Since SNPs associated with the variance of untransformed BMI acted as hotspots of GxE interactions, we explored whether certain phenotypes and pathways were more likely to be linked to raw vQTLs compared to SNPs only associated with the mean of BMI. These muQTLs, which are not significant vQTLs, are referred to as “pure muQTLs.”

To evaluate this, we used the Open Targets database,⁵³ which contains a large catalog of genotype-phenotype associations. We performed a (mean-based) PheWAS of 21 raw vQTLs and 448 pure muQTLs by querying all phenotypes available in Open Targets. Using a binomial test, we assessed whether the group of raw vQTLs were enriched for an association with a phenotype (nominal p < 0.05) compared to the group of pure muQTLs (nominal p < 0.05) (Material and methods).

Overall, we found vQTLs were enriched for an association with many phenotypes that have a strong environmental influence (whether from diet, exercise, infection, or microbiome). These included several diabetes-, immune-, and hematological-related phenotypes (Table 2; Figure 5E). Permutation analyses of the pure muQTLs showed that the PheWAS-based enrichment test did not have inflation of false positives (Figure S9A).

Table 2.

PheWAS enrichment of raw vQTLs versus pure muQTLs

Phenotypes	muQTL	vQTL	Ratio	p	FDR
Diabetes diagnosed by doctor	0.47	0.86	1.83	2.6 × 10−4	0.017
Diabetes mellitus	0.33	0.67	2.029	1.6 × 10−3	0.047
Diabetic retinopathy	0.05	0.33	6.318	6.85 × 10−5	0.010
Eosinophil counts	0.15	0.43	2.882	1.89 × 10−3	0.055
Hypothyroidism	0.12	0.43	3.647	3.32 × 10−4	0.020
Mean corpuscular haemoglobin	0.23	0.67	2.866	2.87 × 10−5	0.009
Neutrophil percentage	0.23	0.52	2.299	2.98 × 10−3	0.065
Osteoarthritis | non-cancer illness code, self-reported	0.17	0.57	3.310	4.36 × 10−5	0.010
Red blood cell (erythrocyte) distribution width	0.27	0.62	2.305	7.89 × 10−4	0.038
Red blood cell count	0.20	0.57	2.906	1.64 × 10−4	0.014
Reticulocyte fraction of red cells	0.18	0.62	3.536	7.18 × 10−6	0.006
Type 1 diabetes	0.09	0.33	3.861	1.40 × 10−3	0.047
Type 2 diabetes	0.41	0.71	1.762	4.13 × 10−3	0.078
Type 2 diabetes with neurological manifestations	0.06	0.38	6.619	1.24 × 10−5	0.006
Type 2 diabetes with ophthalmic manifestations	0.06	0.33	5.148	2.47 × 10−4	0.017
Ulcerative colitis | non-cancer illness code, self-reported	0.05	0.24	4.513	4.08 × 10−3	0.078

From left to right: the phenotype, the proportion of pure muQTLs and raw vQTLs that are associated with the phenotype, the ratio between the two proportions, the binomial test p value to assess vQTL set enrichment, and the FDR corrected significance. These phenotypes represent a manually curated and incomplete list of all significant findings presented in Data S10.

Next, we mapped non-MHC SNPs to single genes by using genomic proximity and Open Targets’ variant-to-gene pipeline, queried raw vQTL gene sets or pure muQTL gene sets in GeneMania, and performed GO enrichment analysis of the resulting gene network (Material and methods; Supplemental Note S14; Data S3 and S4). We found that the network of raw vQTL genes was enriched for G protein-coupled receptor (GPCR)-related signaling pathways and cell growth processes (Data S5 and S6). In contrast, the pure muQTL network was enriched for developmental processes, particularly in the central nervous system (CNS), with no enrichment in the GPCR-related GOs (Data S7 and S8). GPCRs transduce extracellular signals and activate downstream a cascade of intracellular proteins and pathways, which is essential for how cells interact with the environment.

Polygenic heritability analysis implicates stomach cell types in regulating BMI variability

We evaluated whether the genetic contribution to the variability around the mean of BMI, a potential proxy for GxE interactions, might implicate different cell types in regulating BMI levels compared to studies only on the mean of BMI. In Drosophila, the variability of a phenotype can be heritable.⁷³ Considering this, we performed partitioned LD score regression on mean (muQTL) and variance (raw vQTL) GWAS summary statistics to find cell types enriched for BMI heritability. We used 205 functional annotations from GTEx⁵⁰ and the Franke lab⁷⁴ that describe tissue-specific genes in each cell type.

Overall, we found that estimated cell type enrichment values were similar in both the BMI means and variances analyses (r = 0.81; p = 1.4 × 10⁻⁴⁸) (Figures S9B and S9C). For example, the genetic signals for both were clustered in genes uniquely expressed in the CNS, as described previously.⁵⁴ Notably, we discovered that the heritability of BMI variability was significantly enriched (FDR < 0.1) at genes with the highest expression in stomach cell types (p = 1.2 × 10⁻³; FDR = 0.049), with no significant association in these regions for mean BMI heritability (p = 0.40) (Figure 5F; Supplemental Note S15). This preliminarily suggests that stomach cell types, in addition to CNS cell types, have a critical role over BMI variability and regulating potential GxE interactions and that this would not be discovered in a mean-based analysis.

Discussion

We have identified SNPs associated with the variance of BMI (vQTLs), which are enriched for GxE interactions and for associations with phenotypes under strong environmental influences. When functionally profiling the annotated genes of vQTLs, we found enrichment for GPCR-related signaling pathways, which are key to cells’ responses to the external environment. We also discovered that SNPs clustered near genes highly expressed in stomach cells are enriched for the heritability of BMI variability. This was not revealed in an analysis of the heritability of BMI means.⁵⁴ These findings may suggest a key role for host-gut microbiome interactions within body weight etiology. Future application of our methods across phenotypes has the potential to identify genes, pathways, or cell types that serve as key regulators of the interplay between genetics and environment.

Additionally, we showed how GxE interactions first identified in BMI were predictive of the GxE effects on diabetes risk within a distinct set of individuals. We further discovered a BARX1 regulatory locus that significantly increases BMI and diabetes risk in low exercise individuals but does not have pleiotropic population effects in moderate to high exercise individuals. This framework of screening for SNPs as interaction candidates within quantitative phenotypes to subsequently discover interactions influencing complex disease can be broadly applicable across the range of human phenotypes. Methods to deconvolute case-control disease phenotypes into a quantitative scale that re-captures disease granularity and severity will enable the application of vQTL testing directly to the disease phenotype of interest.

We explored multiple approaches to decouple mean and variance effects, evaluate the relationship between the two, and find GxE interactions. It can be hypothesized that the mean-variance relationship is due to either true underlying interactions or to artifacts of scaling of non-normal distributions. While Young et al.²⁷ introduced a test for identifying SNPs associated with the variance of a phenotype independent of a mean effect (which we referred to as dQTLs), we found that the strongest GxE signal came from the SNPs associated with the variance of BMI prior to statistical transformations (raw vQTLs). Although important to the discovery of interactions, we forewarn that raw vQTLs most likely describe differences in variability, not variance, as the association could be removed by transformation⁷⁵ (only seven of 21 vQTLs on untransformed BMI were also found in the analysis on RINT BMI). Thus, settling whether the mean-variance relationship is a consequence of widespread interactions or of scale phenomena may be difficult through only analysis of observational data. Understanding the underlying causal mechanisms in putative GxE interactions will be required. If raw vQTLs are a robust footprint of interactions and estimated raw vQTL effects correlated strongly with mean-based effects, then this suggests that any SNP directly impacting BMI may be more likely to have its BMI effect modified by another factor.

GWAS type testing is not the only approach to limiting the number of potential interactions to explore. Other previously used approaches for reducing vast genomic data are filtering SNPs on the basis of prior biological information⁷⁶ or combining SNPs into higher-order gene-level data.⁷⁷ A significant drawback of these methods is that they will not be a hypothesis-free genome-wide approach. Prior information is biased to prior knowledge, and gene-level data limit the search space for potential interactions.

Alternatively, new statistical advances (such as LEMMA⁷⁸ or StructLMM⁷⁹) identify broad interactions at single SNPs by simultaneously testing for an interaction with large numbers of environmental variables. LEMMA combines many factors into a single environmental score, whereas StructLMM employs a variance component test to model the environmental similarity between individuals. However, previous application of these multivariate methods to BMI missed key interactions.^78,79 For example, LEMMA did not find the FTO locus where we found six significant interactions (Figure 5A) and StructLMM did not identify the SEC16B locus where we found three significant interactions⁷⁸ (Figure 4A; Figure S10). We found many instances where variants that were not discovered via the multivariate approaches only interacted with a single environmental factor (Figure 4A).^78,79 In cases where a SNP has a unique GxE interaction profile, a simple interaction model may be the more robust model to use. Nonetheless, there now exists a promising opportunity to explore broad interactions between many vQTLs and extensive environmental risk factors within complex traits through combining vQTL tests with multivariate methods.

Although the DRM vQTL approach that was applied in these analyses has advantages in power, any detection of interaction effects will have lower power than tests of main effects. It is anticipated that the increasing sample sizes of GWASs will enable more sensitive detection of significant loci and more precise estimation of their variance effects. This will in turn improve the sensitivity of a variance test in detecting underlying GxE interactions. We note that a limitation of the DRM is that relatedness is not accounted for within a linear mixed model, unlike the Young et al. suite of methods.²⁷ The test statistics could still be adjusted for inflation (due to relatedness) with LD score regression or genomic control,⁸⁰ but how this post-analysis adjustment might compare to a within-analysis adjustment for relatedness (via linear mixed models) in vQTL analysis is unclear. Recent work has also shown that modeling the variance effects can improve the inference of single SNP mean effects.⁸¹

Furthermore, replication of GxE interactions require special attention. Here, we split UKB individuals into two mutually exclusive groups, but this approach is not the same as performing tests on two completely independent population samples. There may be unmeasured confounding factors in the UKB samples that drive spurious associations. Interactions will need to be independently replicated in other cohorts to weed out spurious signals, although any lack of replication could be due to differences in allele frequencies, cultural behavior, and other environmental variables. For our purposes, we used the study design to allow a comparison of replication rates between two sets of GxE interactions.

One future research area is the evaluation of polygenic scores that consider interaction effects. Polygenic scores are currently based on only marginal additive effects, and our research identified strong GxE interactions influencing BMI variability. For example, variants in the FTO intron region (the strongest genetic regulators of obesity) are associated with a nearly double BMI increase in low exercise individuals compared to high exercise individuals (Figure 5A). Interactions can perturb each individual from the expectation given a single genotype, and the ideal individual prediction would accommodate these interaction effects.

Perhaps the most important requisite to improve our understanding of GxE interaction in humans is the collection of accurate, high-quality measurements of relevant environmental variables. Specialized wearable tracking devices and improvements in biomarker data are being explored, and the hope is that these will deliver a quantum improvement in the availability and accuracy of environmental data. In these settings, vQTLs can provide a promising approach to reduce dimensionality of genetic data and increase statistical power to detect GxE interactions. Overall, our work highlights the ability to discover significant environmental influences that modulate the genetic contribution to human phenotypes.

Data and code availability

UK Biobank data was accessed under application number 47137. Code to run a DRM on any genome-wide association study data is available at https://github.com/drewmard/DRM. Computer code to reproduce the analyses is available at https://github.com/drewmard/ukb_vqtl.

Declaration of interests

O.E. is scientific advisor and equity holder in Freenome, Owkin, Volastra Therapeutics, and One Three Biotech. C.V.V.H. is an employee of the Regeneron Genetics Center.

Published: December 15, 2020

Web resources

• BEDMatrix, https://github.com/QuantGen/BEDMatrix

• Deviation regression model, https://github.com/drewmard/DRM

• GeneMania, https://genemania.org/

• GTEx, https://www.gtexportal.org/home/

• HaploReg, https://pubs.broadinstitute.org/mammals/haploreg/haploreg.php

• Heteroscedastic linear mixed model and dispersion effect test, https://github.com/AlexTISYoung/hlmm

• International Physical Activity Questionnaire analysis guideline, https://www.academia.edu/5346814/Guidelines_for_Data_Processing_and_Analysis_of_the_International_Physical_Activity_Questionnaire_IPAQ_Short_and_Long_Forms_Contents

• Linkage Disequilibrium Score Regression, https://github.com/bulik/ldsc

• Neale lab GWAS in UK Biobank, http://www.nealelab.is/uk-biobank

• Open Targets, https://www.opentargets.org/

• Plink, https://www.cog-genomics.org/plink/

• UK Biobank access management system, https://bbams.ndph.ox.ac.uk/ams/

Supplemental information

Document S1

. Figures S1–S10, Tables S1–S4, and Supplemental Notes S1–S15