Abstract
Recent applications of retention modelling in liquid chromatography (2015–2020) are comprehensively reviewed. The fundamentals of the field, which date back much longer, are summarized. Retention modeling is used in retention‐mechanism studies, for determining physical parameters, such as lipophilicity, and for various more‐practical purposes, including method development and optimization, method transfer, and stationary‐phase characterization and comparison. The review focusses on the effects of mobile‐phase composition on retention, but other variables and novel models to describe their effects are also considered. The five most‐common models are addressed in detail, i.e. the log‐linear (linear‐solvent‐strength) model, the quadratic model, the log–log (adsorption) model, the mixed‐mode model, and the Neue–Kuss model. Isocratic and gradient‐elution methods are considered for determining model parameters and the evaluation and validation of fitted models is discussed. Strategies in which retention models are applied for developing and optimizing one‐ and two‐dimensional liquid chromatographic separations are discussed. The review culminates in some overall conclusions and several concrete recommendations.
Keywords: lipophilicity determination, method optimization, method transfer, stationary‐phase characterization, retention mechanisms
Article Related Abbreviations
- ADS
adsorption
- AIC
Akaike information criterion
- ANN
artificial neural network
- GA
genetic algorithm
- HILIC
hydrophilic‐interaction chromatography
- HSM
hydrophobic‐subtraction model
- IEX
ion‐exchange chromatography
- LFER
linear‐free‐energy relationships
- LSS
linear solvent strength
- MM
mixed mode
- NK
Neue–Kuss
- NPLC
normal‐phase liquid chromatography
- PAH
polycyclic aromatic hydrocarbon
- Q
quadratic
1. INTRODUCTION
LC is one of the most essential and pervasive techniques in the toolbox of analytical chemists. Retention modeling serves as a useful technique available for analytical chemists to rapidly develop methods. In LC, an analyte is distributed between a non‐moving stationary phase and a moving mobile phase. The time it takes for the analyte to migrate through the column is referred to as the retention time, , which can be expressed as
| (1) |
where t 0 is the dead time or hold‐up time of the column and k is the analyte retention factor, which is related to the distribution coefficient (K) through
| (2) |
where and are the total mass of analyte in the mobile and the stationary phase, respectively, and are the analyte concentrations in the two phases, and and are the total volumes of each phase in the column. The retention factor is dependent on many different parameters, such as pH, temperature, and mobile‐phase composition (volume fractions of strong solvent, φ). Many equations have been described to relate k to one or more of these parameters and are typically referred to as retention models. Retention modeling is the process of fitting such a model to the experimental data.
LC can be performed in isocratic or gradient mode. In isocratic mode, the mobile‐phase composition is not changed over the course of the run, which means that the total mass of analyte in both phases does not change, with the result of a constant retention factor. This is not the case in gradient mode, where the mobile‐phase strength is increased over the run. This increases the total mass of analyte in the mobile phase and thus decreases the retention factor. To relate k to the solvent strength in gradient elution, the gradient equation has to be used. When a compound elutes before the start of the gradient, the retention time can be calculated through Equation 1, in which k is the retention factor at the initial organic‐modifier concentration. If a compound elutes during the gradient, the retention time can be calculated with the general equation of linear gradients [1].
| (3) |
In this equation, is the retention model (see Section 2.1), describing the relationship between the retention (k) and the organic modifier concentration (φ). The change in φ as a function of time (i.e. the slope of the gradient) is shown with B () and τ is the sum of the dwell time (), the time before the start of the gradient (), and the dead time (t 0). In the case that the analyte elutes after the gradient, the retention time can be calculated by
| (4) |
in which represents the gradient time.
Retention modeling is mostly used to facilitate rapid and efficient method development in many modes of LC and supercritical‐fluid chromatography (SFC). The applications of retention modelling in method development can be divided in several areas. Retention models can be used to characterize newly developed stationary phases and to establish the underlying retention mechanism. In method optimization retention modelling is used to achieve better separations. In method transfer, methods developed or implemented on different systems are harmonized with the aid of retention models. Retention models are used to better understand and more‐accurately describe retention. Additionally, retention modeling is applied outside the field of chromatography, for example in pharmaceutical and environmental science, to determine the octanol–water partition coefficient () of a newly synthesized product or to determine the persistence of a pollutant in the ecosystem [2, 3]. There are different strategies to perform retention modelling, depending on the aim of the study. The general form of a retention model can be described as a relation between a retention parameter and a function combining system and analyte parameters.
In a specific set of models, called linear‐free‐energy relationships (LFER), the function consists the sum of a small number (typically five) of product terms, each consisting of a system parameter () and an analyte parameter ().
| (5) |
Each term is loosely connected with a specific type of interaction between analyte and the stationary phase. Examples are the hydrophobic‐subtraction model of Snyder (HSM) [4, 5] and the model of Abraham [6, 7]. Snyder defined the stationary‐phase parameters in his model as hydrophobicity, steric hindrance, hydrogen‐bond acidity and basicity, and cation‐exchange activity [4, 5]. Abraham identified contributions of molar refraction, solute polarizability, effective hydrogen‐bond acidity and basicity, and the McGowan characteristic volume [6, 7]. In either case, the values of the system parameters depend on the values assigned to a set of reference analytes. The goal of these models is not to predict retention, but to characterize and classify stationary phases. The model does not describe the effect of the mobile‐phase composition. Characterizing analytes is laborious (requiring measurements on different columns), but characterizing systems is easy. Despite the influence of the mobile phase, system parameters are usually interpreted as column or stationary‐phase parameters and values for many stationary phases have been tabulated [8, 9].
A different angle to retention modeling is the use of quantitative structure‐retention relationships (QSRR) that are statistically derived relationships between a number of structural descriptors of an analyte and its retention [10]. Such models, based on large sets of structural parameters and retention data of many compounds, can be used to predict retention of new compounds if their structural parameters can be computed. Similar approaches have been applied to evaluate the pharmacological activity and physicochemical parameters of compounds (quantitative structure‐activity relationships, QSAR, and quantitative structure‐property relationships, QSPR, respectively). The most‐important structural descriptors are identified in the process [11].
A third approach utilizes artificial neural networks (ANNs) to describe retention for (very large) input data sets. An ANN is a computational modeling tool that is inspired by the architecture of the human brain. It consists of an input and an output layer, with one or more hidden layers in between [12], and ANN models are known to require a vast data set [13].
The final approach to retention modeling is based on (semi‐) empirical models that contain abstract parameters to describe retention. Different models have been developed for and applied to many specific modes of LC. Few input data are needed to describe retention and to predict new data through inter‐ or extrapolation. This renders the class of (semi‐) empirical models eminently useful to assist in LC method development [14, 15, 16, 17] and the remainder of this review will focus solely on such models.
Empirical retention models typically feature several parameters that are abstract (i.e. not linked to a specific interaction/mechanism in chromatography), yet which relate analyte‐ and measurement parameters (e.g. volume fraction of organic modifier, salt concentration, pH, etc.) to k. Often the common logarithm or the natural logarithm of the retention factor, i.e. log10 k or is used. Other variables that are not represented by the model (e.g. the stationary phase, temperature) must be kept constant at specified values for the model to remain valid. The model is typically fitted through all data points available.
With increasing computer resources, in silico techniques become much‐more attractive than exhaustive trial‐and‐error experiments for LC method development. In this review, recent developments in and applications of retention modelling will be discussed, with focus on method optimization, method transfer, stationary‐phase characterization, understanding and describing retention, and lipophilicity determination.
2. BACKGROUND THEORY
Several models have been developed and applied for retention modeling. In most cases, the volume fraction of modifier (φ) is the most‐important variable. Only a handful of two‐ or three‐parameter models have been used extensively, viz. the linear‐solvent‐strength model (LSS), the quadratic model (Q), the adsorption model (ADS), the mixed‐mode model (MM), and the Neue‐Kuss model (NK). Optimization programs, such as Drylab [18], PEWS2 [19], and MOREPEAKS [20], rely on one or more of these retention models, which are all based on the volume fraction of the modifier (φ) and are two‐ or three‐parameter models. In the following section, the models and their applications will be briefly discussed. The requirements for input data will also be discussed, such as the elution mode and the number of datapoints.
2.1. Models
2.1.1. Linear solvent strength model
The log‐linear model for RPLC was introduced by Snyder et al. to describe retention as a function of mobile‐phase composition (φ) [21]. It is often referred to as the LSS model (occasionally it is also referred to as the partitioning model). The common form of the model is
| (6) |
where is the natural logarithm of the retention factor at a specific modifier concentration, , often also denoted , refers to the isocratic retention factor of a solute in pure water, φ refers to the volume fraction of the (organic) modifier in the mobile phase, and the slope is related to the interaction of the solute and the (organic) modifier. The LSS model parameters can be calculated from the retention of an analyte in two isocratic runs with different φ. Of the 90 references found for the LSS model in the last six years (2015‐2020), 55% concern 1D RPLC, leaving the rest for other applications such as two‐dimensional liquid chromatography (2DLC), hydrophilic interaction chromatography (HILIC), and supercritical‐fluid chromatography (SFC), shown in Figure 1A.
FIGURE 1.
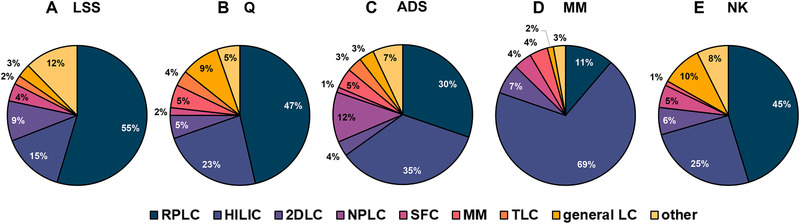
Application to different modes of chromatography for all five models. The data are based on the total number of references published from 2015 to 2020
2.1.2. Quadratic model
Schoenmakers et al. introduced the quadratic model (Q), which can be seen as an extension of the log‐linear model with another parameter. This renders the relation between the and φ convex rather than linear [22].
| (7) |
In this and subsequent retention‐model equations, S 1 and S 2 are empirical coefficients used to describe the influence of the organic modifier on the retention of the analyte. The other parameters in the Q model are identical to those of the LSS model. Of the 45 works reported in literature that use the Q model in the past six years (2015–2020), summarized in Figure 1B, the main application is RPLC (47%). The Q model has also been investigated for describing HILIC retention (23%).
2.1.3. Adsorption model
The adsorption model (ADS) was introduced by multiple researchers during the 1960s and 1970s. Soczewinksi et al. [23], Jandera et al. [24], and Snyder et al. [25] all presented the model in their work on normal‐phase LC (NPLC), and thin‐layer chromatography (TLC). The model, which was designed to account for adsorption, has also been described as the log–log model or the Snyder–Soczewinksi model [23, 24, 25, 26].
| (8) |
In this model, the n parameter is the so‐called solvation number, which represents the ratio of surface areas occupied by adsorbed molecules of the strong eluent component and the analyte. In contrast to the log‐linear LSS model, here is linearly correlated with (log–log model). While the model was initially intended for NPLC (12%), it is now mainly used for retention modeling in HILIC (35%) and RPLC (30%) (Figure 1C).
2.1.4. Mixed‐mode model
The mixed‐mode model (MM) was developed by Jin et al. to describe retention in HILIC. The idea is that it can account for both retention modes of HILIC and RPLC. The model is a combination of the LSS and ADS models [27].
| (9) |
Jin et al. related S 1 to the solute's interaction with the solvents and to the solute's interaction with the stationary phase [27]. The model will be discussed more extensively in Section 3.3.2. The main application of the MM model is for HILIC (69%), as shown in Figure 1D.
2.1.5. Neue–Kuss model
The most recent of the five main models is the three‐parameter Neue–Kuss (NK) model that was based on another model described by Nikitas et al. [28, 29].
| (10) |
where the S 1‐parameter represents the slope and the S 2 ‐parameter represents the curvature of the versus φ plot. When integrating this equation to obtain gradient‐elution retention times an exact solution can be found. Neue [30] suggested that this model could describe the curvature observed in versus φ relationships. Later, Neue and Kuss published the following version of the model in 2010 [31].
| (11) |
Note that the only differences between Equations 10 and 11 are the sign before and the factor 2 in the second term. In Equation 11, the S 1 parameter represents the slope and the S 2 parameter represents the curvature of the versus φ plot. The NK model was developed for gradient RPLC, which is clear from the number of applications (45%). However, it is also often applied to HILIC (25%), as shown in Figure 1E.
2.2. Measurement and use of data
The way in which these empirical models can be used depends on the number and type (isocratic or gradient) of data points that are used to fit the model.
2.2.1. Isocratic or gradient data
All the empirical models covered in this review have been used for optimizing both isocratic and linear‐gradient separations. Isocratic data points would need to be collected at different organic‐modifier concentrations. This can be a tedious task, since not all compounds elute at a reasonable time for every value of φ. Many organic‐modifier concentrations are often required to calculate the model parameters for every compound in a mixture. One way to get around this problem is to use gradient elution. This allows all analytes to be eluted within one run in a reasonable time. To compute the gradient‐elution retention time or the organic‐modifier concentration at the time of elution during or after the gradient, the retention model used must be numerically integrated in the gradient equation (Equations 3 and 4) [20]. Here in Equations 3 and 4 refers to one of the above retention models. To use gradient‐elution experiments (known as scanning gradients) to establish model parameters, this process must be followed in opposite order. It is necessary to vary the effective steepness of the gradient between experiments. The effective steepness (b) is the product of the slope of the ln k versus φ curve (e.g., S LSS), the slope of the gradient (B = Δφ /Δt) and the hold‐up time of the column (t 0)
| (12) |
where V 0 is the hold‐up volume and F is the flow rate. The effective slope can be varied by changing one of three parameters (i) the slope of the gradient (B), (ii) the column volume, or (iii) the flow rate.
The accuracy of prediction is influenced by the selected elution mode. An error‐analysis approach was described by Vivó‐Truyols et al. for translating gradient data to isocratic elution or vice versa [32]. The authors concluded that input data obtained using isocratic experiments yielded the most accurate predictions [32]. Isocratic elution could also be predicted using models constructed based on gradient experiments, but such models were only found accurate across limited ranges of solvent composition [32, 33, 34, 35]. Gradient retention data can be predicted from gradient‐scanning experiments [36, 37, 38], but little research has been performed on the requirements for the experimental data. In a recent paper it was shown that the prediction accuracy of the model depended on many factors, including the proximity of the slope of the predicted gradient to that of the scanning gradients, whether interpolation or extrapolation is applied, and the experimental precision [39].
2.2.2. Number of input datapoints and model evaluation
When calculating the parameters of the empirical models of section 2.1, referred to as retention parameters, there is a limitation as to the minimal number of input datapoints. Generally, the number of parameters determines the number of necessary input runs. Two‐parameter models, such as ADS and LSS, need at least two datapoints for each component, while three‐parameter models, such as MM, NK, and Q, require at least three. Some of these models, for example, NK, have mostly been used with larger numbers of data [31].
Adding more parameters to a model increases the risk that the model will overfit the data. When multiple models are tested on a dataset, the number of parameters may betray the actual quality of the model. To correct for this bias, the Akaike Information Criterion (AIC) can be used, which contains a penalty when more parameters are added [40].
| (13) |
The AIC value is calculated upon fitting the data to the model. The sum‐of‐squares error (SSE) is corrected by the number of parameters (p) and the number of observations (n). A lower (more negative) value represents a better fit, thus aiding in the selection of a correct model [15, 41, 42, 43, 44, 45].
Another way of choosing between two‐ or three‐parameter models is to perform an F‐test of regression to examine whether adding a third term is significant. This test does not evaluate the goodness‐of‐fit, but only the difference between a three‐parameter model and its reduced form. From the five empirical models, the F‐test of regression can be performed on (i) the Q and the LSS models, (ii) the MM and the LSS model, and (iii) the MM and the ADS model. These three combinations have been examined by Roca et al. for modeling the retention of peptides in HILIC [37]. Baczek et al. performed an F‐test on the LSS and Q models in RPLC [46].
3. METHODS
Upon reviewing the literature, we have identified five main domains where retention modelling is applied, and these will be discussed. These five domains and their workflows are summarized in Figure 2. For reference, the lower section of the figure contains a reference to the corresponding paragraphs in the text.
FIGURE 2.
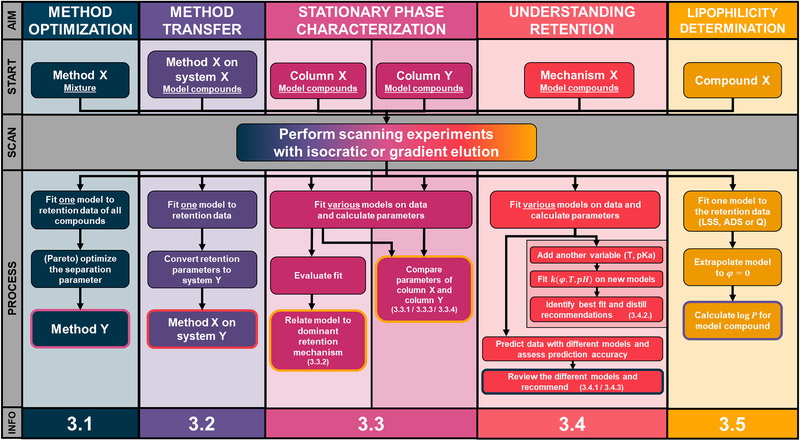
Overview of workflows of the main application domains of retention modelling in recent literature. At the top of the figure, the different aims are shown with the starting point indicated directly below. All domains will require input data which is obtained in the scan step. Next, the different processes are shown in their matching color underneath. The number of models used is indicated in the box and the final goal, whether it is a method, a number or a degree of similarity, is indicated with the colored line around the box. Beneath the workflows, the section number of the corresponding paragraph can be found. The workflows indicated in the figure are generalized and individual works may deviate from it
3.1. Method optimization
In the development and optimization of an LC method, retention modeling can be an important tool. In this section, we review recent literature on method optimization with the aid of retention modeling. The next two sections focus on 1D and 2D methods, whereas a final section addresses elaborate strategies and optimization packages.
3.1.1. Optimization of one‐dimensional separations
After the mobile‐phase components and the stationary phase have been selected, retention modeling can be used to optimize separations. For example, for a separation of a vegetable oil employing a porous‐graphitic‐carbon column, Zhang et al. used the LSS model to optimize the separation with an isopropanol‐toluene gradient [47]. The authors tested the effect of the toluene fraction () on the retention of through the SLSS‐parameter, which was found to be similar for all triacylglycerols, resulting in the same selectivity at all toluene concentrations. Conversely, differences between SLSS‐parameters can indicate to what extent the modifier concentration can be used to optimize selectivity. Fekete et al. reported very large SLSS values for proteins (calculated from two scanning gradients) and a tenfold decrease in retention when the organic‐modifier concentration was increased by 0.8% [48]. Such high SLSS values are one of the reasons why gradient elution is indispensable in RPLC of proteins. Selectivity could be improved by serially coupling columns with increasing retentive capacity and applying multistep gradients [49, 50].
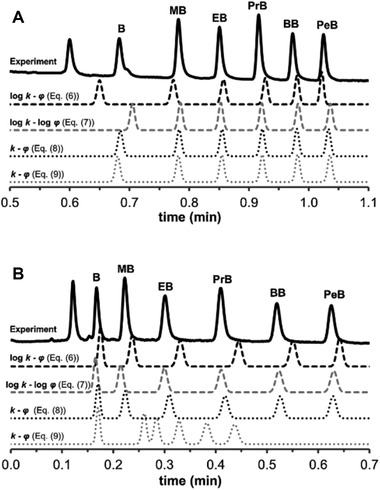
Apart from the mobile‐phase composition, the sample solvent should be considered. A large difference in elution strength between the eluent and the sample solvent may lead to incidents such as breakthrough or peak deformation [51, 52]. Jeong et al. simulated separations to study the effect of an injection with a high‐elution‐strength solvent into a weaker eluent [51]. The LSS and NK models were used for calculating local retention factors. The peak widths were predicted by considering the retention of the analyte in the injection solvent and the in mobile phase. The simulated chromatograms (red) were confirmed with experimental data (black), which is indicated in Figure 3.
FIGURE 3.
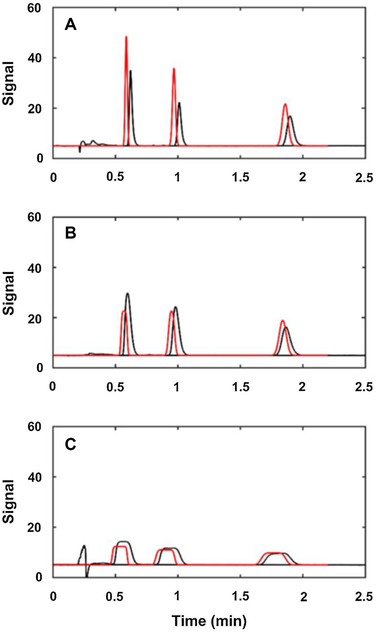
Comparison of the experimental (black) and simulated (red) chromatograms for isocratic separations of alkylbenzenes. Mobile‐phase composition was 30% water and 70% ACN. The injection volume was 100 μL of (A) 50%, (B) 70%, and (C) 90% ACN in water. Reproduced from [51] with permission
Boateng et al. [53] improved a separation of three regioisomers of methoxyphenidine by optimizing the temperature, pH, and organic‐modifier concentration. Retention data were fitted using an ADS model to describe the effects of pH, the LSS or Q model for mobile‐phase composition (φ) or the van ‘t Hoff equation for temperature (T). By varying the three parameters at three different levels, producing a 3 × 3 input data set, an optimized separation was developed with prediction errors lower than 5%. Vaňková et al. investigated the effect of gradient steepness on peak compression using LSS retention models. They determined the mobile‐phase composition at time of elution ( and the corresponding retention factor () [54]. was then related to the peak width. Using this information, the peak compression by the gradient was calculated. A ratio of gradient time to column dead time of 12 was found to give the best kinetic performance for small molecules. Gritti [55] discussed peak compression more extensively and derived a new expression based on the NK model, predicting peak broadening for complex gradient programs. When the peak compression predicted by linear and non‐linear models was compared, no significant difference was observed.
Another objective of method optimization may be to maximize the sensitivity. One way to achieve this is by on‐column focusing, retaining all analytes at the column inlet by decreasing the solvent strength or by changing the temperature [56, 57]. Rerick et al. [57] used an extended form of the NK model that included the effects of temperature. The model was extrapolated to predict retention in case cooling was employed. This model will be further discussed in Section 3.4.2. Chang et al. used the retention parameters of the LSS and ADS model for their peak‐picking algorithm [58]. Clustering based on similarity of retention behavior and isotope ratios was performed. Using this strategy, the authors could rapidly identify 206 precursor ions in a complicated natural extract.
3.1.2. Optimization of two‐dimensional separations
Two‐dimensional liquid chromatography (2DLC) is increasingly applied [59]. Its success can be ascribed to the combination of two different separation mechanisms (i.e. targeting different sample dimensions) and the concurrent increase in peak capacity. However, the combination of two dimensions renders method optimization a more complicated endeavor [60]. When retention modelling is applied in the development of 2D separations, the LSS model is often used to optimize the individual (gradient) dimensions [61, 62, 63, 64]. The SLSS parameter has also been used as a measure for orthogonality (i.e. the degree to which the two dimensions have different selectivities) [65, 66]. S LSS is expected to be similar for compounds of similar molecular weight, but for a given sample it may vary. For that reason, it was decided to use the average S LSS‐parameter of all compounds in the sample of the two separations to calculate the degree of orthogonality ().
| (14) |
It is calculated by multiplying the average S LSS for both dimensions and the organic modifier concentration difference of the gradient of both dimensions ( and ) with the correction factor with respect to the theoretical retention area (γ). This approach was developed by D'Attoma et al. [66] and applied to a RPLC×RPLC separation for peptides of Iguiniz et al. [65], which was able to separate more compounds than the prior 1DLC method. The use of LSS parameters for the degree of orthogonality is novel, although more studies are required to validate the approach.
One of the challenges in coupling two dimensions in 2DLC is the possibility of solvent mismatches, i.e. a weak solvent in one mechanism can be a strong solvent in the other. This has already been discussed to a certain extent in Section 3.1.1. Stoll et al. modelled 2D separations with gradient conditions, specifically a solvent mismatch between the injection solvent (i.e. the 1D eluent) and the 2D mobile phase [67]. The loop volumes were varied (i.e. larger loops) and different loop fillings were employed. To make these simulations, the retention behavior was assumed to be nonlinear following the NK model. Muller et al. tried to model the effect of the dilution factor, which is often applied to reduce the solvent strength of the 1D effluent, when coupling HILIC to RPLC [68]. The NK and the LSS model were used to calculate the retention factor at the time of elution () and the retention factor in the sample solvent (). The effect of several chromatographic parameters of these two retention factors are modelled to find the optimal setup for HILIC×RPLC. It was found that the predictions of and made with LSS and NK are similar.
3.1.3. Optimization programs and strategies
Many tools and software packages have been developed for LC optimization because of growing computing power. These strategies have been developed over the years with increasing knowledge of the parameters influencing retention. An example of this is the development of the Drylab, ChromSword, and PEWS2 method development software [18, 19, 42, 69, 70, 71]. Many of these papers are limited to RPLC, but there are three software packages that can be used for liquid chromatography in general.
Fasoula et al. developed a package of Excel VBA macros for modeling gradient retention data obtained in multilinear gradients [72]. The procedure consists of three steps: first the initial gradient retention data of each compound is fitted to a model and the parameters of that model are calculated. The model is then tested for accurate prediction of different gradients. Lastly, the optimized gradient method is determined. The package comprises ten retention models, of which the two‐parameter models, especially the ADS model, describe simulated and experimental data very well. It was found that implementing more parameters, such as the Q model, increases the accuracy of the prediction, but also consumed more computational resources. The same group published a recent paper on a more elaborate program developed in R [73]. Next to an optimized gradient separation, the software aids in other aspects of the optimization such as peak shapes and base‐line correction, and it is applied to ionized solutes too. The program contains the same 10 retention models as the Excel package of Fasoula et al. to optimize isocratic, gradient, and multigradient separations [72, 73].
Pirok et al. developed an optimization program (PIOTR) for 2DLC separations in MATLAB [20]. With this program both a strong ion‐exchange separation (IEX) and an ion‐pair reversed‐phase separation were optimized. The LSS model was used for optimization in RPLC and the ADS model for optimization in IEX, replacing φ by the salt concentration [c]. The input data for the program is the retention data of two comprehensive liquid chromatography (LC×LC) runs, of which the gradient slopes in both dimensions differ by a factor three. The workflow of the program is shown in Figure 4. The model gave an accurate description of the retention time but could not account for the band broadening. The program also served as a good tool for peptide separation in HILIC, when the NK, the MM, and the Q model were added to the software [15, 37, 74]. Muller et al. reported on a predictive kinetic optimization tool for online HILIC×RPLC that allowed all chromatographic parameters to be optimized simultaneously within experimental restrictions [68]. The method was applied to a phenolic separation, in which the retention was modelled. Another approach was developed by Khalaf et al. for the development of RPLC separations for peptides [75]. The LSS model, the van‘t Hoff equation and an analytical solution for the mass balance on the column were combined, which was successfully applied to the separation of five different peptide mixtures. It is good to note that optimization approaches can also be conducted differently. For example, for RPLC specifically, multiple optimization algorithms have been proposed. Zhang et al. developed a new algorithm to simulate and optimize RPLC data with the aid of genetic algorithms (GA), in which the computation mimics the genetic mechanisms in all live form to adapt to the environment, and multi‐layer perceptron artificial neural networks (MLP‐ANNs) [76]. Alvarez‐Segura et al. compared the use of GAs to that of multiscale optimization (MSO), in which the level of detail in the solution is increased along the search by using subdivision schemes, for the optimization of multi‐linear gradients, simulated by the NK model [77]. The reason for this is that GAs have a hard time fine‐tuning the method. It was found that both methods yielded similar results.
FIGURE 4.
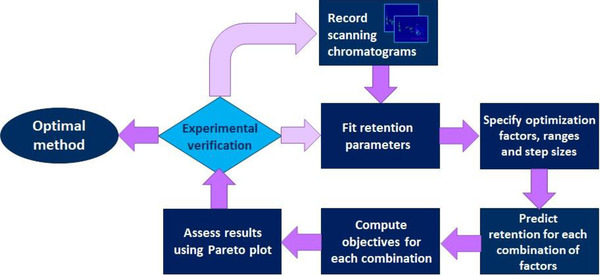
Pareto optimization strategy discussed by Pirok et al. Recorded scanning gradients are used to calculate the retention parameters by fitting the model. By specifying the ranges and step sizes in which the method can be optimized, the program predicts the retention for each component in each combination. The results are assessed in the Pareto plot and the best separation combination is verified through experimental verification. Depending on the verification, more scanning gradients are performed, or the optimal method is chosen. Adapted from [20] with permission
3.2. Method transfer
Retention modeling can also be used to speed up the transfer of methods to different hardware. When gradient methods are transferred, analyst often run into the problem of different dwell volumes and gradient profiles, caused by different mixers, pumps and tubing. Bos et al. developed a response‐function‐based algorithm to determine analyte parameters with a geometry‐induced deformation correction [78]. The LSS parameters for a small set of compounds were determined on different systems with and without a correction of gradient shape, only considering the dwell time. This yielded a decrease of the inter‐system retention prediction error from 9.8 to 2.1% between the first and the second system and 12.2 to 6.5% between the first and the third system. While the study was limited to geometry‐induced deformation, the authors noted that other effects such as those induced by solvent properties, as well as solvatochromic effects still required further study.
Jandera et al. applied four different retention models on the prediction of the retention of a series of standard analytes in short monolithic columns with fast gradients [79]. A prediction error between 0.7 and 1.5% was found for 1 min gradients starting at 100% water for all four models, indicating the validity of the retention models to predict retention in short columns. Next to that, the ADS model provided the most accurate prediction in the fast gradients. The predicted retention of the models is compared to the experimental data in Figure 5.
FIGURE 5.
Comparison of experimental and predicted chromatogram of one‐minute gradients from (A) 0–100% ACN and (B) 50–100% ACN. The four models used are (i) LSS model, (ii) ADS model, (iii) model developed by Jandera et al., and (iv) the NK model. Reproduced from [79] with permission
Gritti studied the transfer of a gradient method between two columns with similar particles but different average pore diameter [80]. He proposed three different gradient transfer methods to maintain the selectivity, based on either the LSS or the NK model. The first method is the “vertical” transfer, in which it was assumed that the LSS model applies for both models and that there is no change in the ‐parameter when changing columns. The retention factor on the two columns would then only vary with the change in column phase ratio (). The second method was referred to as the “horizontal” transfer and assumed that the new retention factor was equal to the old retention factor after shifting the eluent composition from φ to and that the shift in eluent composition () was unique for each compound. These directions refer to the shift in the vs. φ plots. The third method is the in silico approach, in which the best optimal method is found by changing the gradient steepness and the starting concentration of modifier. In Figure 6, the reference chromatogram of the column with a pore diameter of 90 Å is shown with the initial chromatogram in a 450 Å pore diameter column, and the three different transfer methods. The vertical transfer was found to perform worst, while the in‐silico approach performed best. The reason for this was that the linearity of the LSS model is only an approximation.
FIGURE 6.
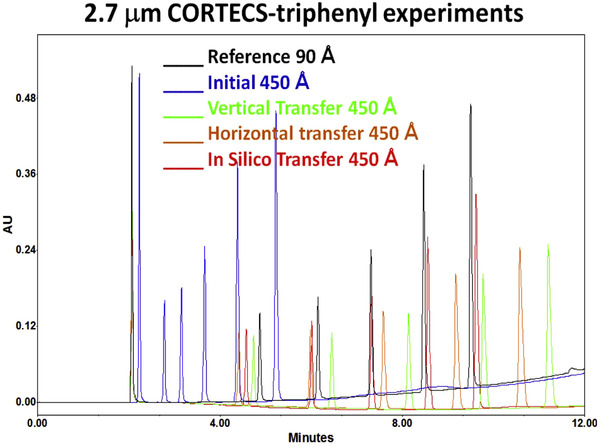
Gradient method transfer between two columns (2.7 μm CORTECS‐triphenyl) with different pore size (90–450 Å). In the figure, the reference gradient chromatogram is shown in black. The direct transfer to a column with a higher pore size is shown in blue. The three different transfer methods are indicated with green (vertical transfer), brown (horizontal transfer) and red (in silico transfer). It is visible that the black line is most similar to the red line, revealing the best gradient method transfer. Reproduced from [80] with permission
3.3. Stationary phase characterization and comparison
Retention modelling is frequently used in the development and characterization of columns and stationary phases. The main part of retention modelling in column characterization is performed with models such as LFER and HSM, leading all the way to enormous column databases [81]. In these methods, the extent of different interactions occurring in a separation and the effect of these interaction on the total retention process are established [7, 82]. The models have been more extensively described in the introduction, but its exclusive application will not further be discussed in this review. Two other approaches to compare columns are classification of stationary phases by performing chromatographic tests or statistical tests and predicting retention behavior with mathematical models, requiring large amounts of data [83, 84]. Since statistical tests yield more than only retention model descriptors [85] and mathematical models often provide information on mechanical and physicochemical properties, which is often not based on any chromatographic retention data [83, 86], these two goals will not be discussed further. The fourth approach for column characterization is the application of semi‐empirical models. In this method, the fit to a model indicates which of the retention mechanisms is dominant, such as mixed‐mode [87], reversed phase [88, 89, 90], normal phase [91], but mostly HILIC [92]. In the past years, HILIC has gained popularity, leading to a better understanding of the mechanism and the influence of several parameters (see Section 3.4), which led to the development of many additional HILIC stationary phases. Stationary phases that can be used in the RPLC and the HILIC mode, depending on the level of organic modifier, have also gained in popularity.
3.3.1. Column comparison
New columns or stationary phase materials are often compared to existing methods by, for example, analyzing the differences in the retention of probe compounds. A C30 bonded silica stationary phase was characterized by Vyňuchalová et al. [93, 94]. The column was compared to other RPLC columns, such as C4, C8, and C18 columns, concerning the retention of homologous non‐polar alkylbenzenes with an extended LSS model. This model included parameters for the methylene group selectivity (α) and the contribution of the end group in the series (β). In Equation 15, the constants a and m increase with the number of repeats (n).
| (15) |
The retention parameters a 0, a 1, m 0, and m 1 were compared between columns, and it was found that the C30 column yielded lower parameters than the standard RPLC columns, indicating lower contributions of methylene groups and end groups and weaker effects of the organic solvent on the decrease of methylene selectivity. Similar stationary phases can be used for different purposes, for example when performing flash purification chromatography. Some manufacturers are producing flash purification stationary phases identical to the analytical stationary phase, only adapting the geometry of the column. Héron et al. compared these with a model based on the LSS model [95], where the change in S is describe with .
| (16) |
| (17) |
where p and q are constant for a binary solvent system. The q‐parameter can then be correlated to the methylene selectivity measured in pure water () and the decrease in selectivity due to an increase of the organic modifier concentration (). As an alternative to C18 bonded phases, graphitic carbon can separate both polar and non‐polar analytes. Lunn et al. [96] compared this phase to other regular RPLC stationary phases regarding its preconcentration capability at the top of the column. The retention parameters were calculated by the NK model from isocratic retention data of small molecules on the different columns. The parameter was used as a marker for its focusing ability, since the extrapolated values predicts retention in 100% water
3.3.2. Classification of new fabricated stationary phases
With the increasing popularity of HILIC and mixed‐mode separations over the last years, there has been a rise in the number of stationary phases developed for these two separation modes. Most of the developments in RPLC, the workhorse of LC, are either developments of the geometrical shape of the column, such as pillar–array separations or channel shape [89, 97] (discussed in Section 3.3.4), or the addition of other separating mechanisms such as ion‐exchange, creating a mixed‐mode separation [88] (discussed in this section). Few new stationary phases for NPLC have been introduced. In 2015, Peristyy et al. investigated the retention behavior of some small molecules on synthetic polycrystalline diamond and fitted the data on the ADS model [91]. Examining the parameters calculated by the model, a higher n‐value (Eq. 8), the parameter that indicates the slope of the versus plot, is found for the more polar compounds than for the polycyclic aromatic hydrocarbons (PAHs). This indicates hydrogen bonding on the surface of the diamond and weak dispersive forces between the PAH molecules and the flat stationary phase.
In the past years, many different stationary phases have been developed for HILIC. To confirm the HILIC retention mechanism, the retention of some probe compounds is often measured at different levels of φ and fitted to the MM model. High regression coefficients indicate a good fit and thus confirm the HILIC mechanism, which is often indicated by a U‐profile retention (i.e. high retention at φ levels close to 0 and 1, but lower retention in between). This retention plot is shown in Figure 7.
FIGURE 7.
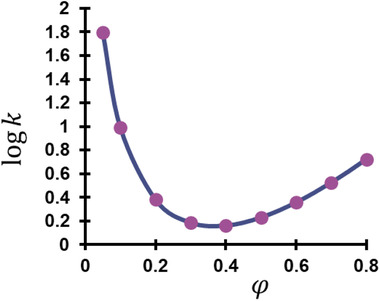
Retention behavior of gallic acid showing higher values at the extreme φ values. Note that φ in this figure concerns the amount of water in the mobile phase, since this is the strong solvent in HILIC. On the right side, gallic acid demonstrates HILIC behaviour and on the right side it exhibits RP behaviour. The model is shown in Equation 18 and the is given by Equation 19. Plot based on the data in ref. [181]
Since the MM model is built by combining both the LSS and the ADS model, the retention data may also be fitted to these two models separately to find the dominant retention mechanism [43, 98, 99, 100]. Many of the developed stationary phases for HILIC are based on a polymeric structure, such as a hyperbranched polyethylenimine stationary phase [101] and a poly(vinyl alcohol)‐cationic cellulose copolymer [102]. Other used polymer functionalized silica stationary phases for HILIC separations are based on polyglycerol [103, 104], polyacrylamide [105], poly(vinyl alcohol) [106], and poly(glycidyl methacrylate‐divinylbenzene) [99].
With the synthesis of new stationary phases, the retention mechanism is often not limited to one specific selectivity, sometimes leading to a mixed‐mode mechanism [87]. For example, this can be based on RPLC with ion repulsion [88, 107], using the LSS model to describe the relation between retention and organic modifier. Another mixed‐mode selectivity was prepared by polymerizing a mixture of glycidyl methacrylate and 2‐dimethylaminoethylmethacrylate, yielding a dual retention mechanism of HILIC and IEX chromatography [108]. The mixed‐mode behavior was confirmed by fitting the retention data to the LSS, ADS, and MM model. It was found that acidic and neutral compounds behaved purely on an adsorption mechanism, while the basic compounds fitted best with the MM model. A perhaps more relevant and contemporary combination of selectivities is the HILIC mechanism with a RP mechanism, dependent on the level of organic modifier in the mobile phase. High levels of organic modifier induce HILIC behavior, whereas high levels of water induce RP behavior, leading to higher retention in both ends of the φ‐scale [90, 109]. The dual retention behavior can be described by the mixed‐mode model of Jin.
| (18) |
Here, a is related to the size of the molecule and to the interaction between analyte and stationary and mobile phase, relates to the interaction between the solutes and the solvents and refers to the direct analyte‐stationary phase interaction [27, 110]. The minimum of the versus plots (), which is shown in Figure 7, can be calculated by the following equation and corresponds to the transition between RPLC and HILIC behavior of analytes. It depends on both the polarity of the sample and the stationary phase [110, 111].
| (19) |
3.3.3. Column comparison between SFC and LC
SFC is experiencing a renaissance in the last years and recently it was compared to LC [83]. Vera et al. published two papers in 2015 on the difference in selectivity of linear polynuclear aromatic hydrocarbons in SFC and LC [112, 113]. In the first paper the retention of the hydrocarbons was modeled with the LSS model [112]. The effect of the organic modifier on the S‐parameter was determined on two different stationary phases. It was found that in SFC using a similar percentage of acetonitrile reduced the retention time by half compared to the use of methanol. This led to the conclusion that retention optimization in SFC is very different from that in HPLC. In the second paper, the same selectivities in HPLC and SFC were compared and it was concluded that PAHs yield different retention between RPLC and RPSFC on the same columns [113].
3.3.4. Comparing different column geometries
Besides optimizing the bonded stationary phase, there also have been improvements in the geometrical fabrication of existing stationary phases. These developments ranged from macrolevel to microlevel, which will be discussed in this order. In 2018, Gilar et al. tested the chromatographic performance of straight and serpentine microfluidic channels [97]. The LSS model was applied for the intrinsic gradient steepness () to model the difference in gradient elution. A negative effect of turns on the efficiency was found, but this was reduced when gradient mode was employed. Gritti et al. evaluated the performance of conically shaped columns to standard cylindrical columns, where the LSS model was used for the retention in gradient elution [114]. The research indicated that, when in gradient mode, a conically shaped column could be advantageous to cylindrical columns, since it reduced peak tailing. Several scientists have devoted their attention to (the simulation of) stationary phase gradients [51, 67, 115, 116]. In one example, the isocratic retention data on the gradient stationary‐phase‐gradient columns was fitted to the NK model, which was then used to predict retention in gradient elution mode [115]. It was stated that the simulated retention fitted very well with the experimental data. This model was then applied to other stationary‐phase gradient geometries and no large differences between using a uniform mixed‐mode or a gradient column were found, but differences were found in the retention depending on the orientation of the stationary‐phase gradient (i.e. the solute retention factor either increases or decreases in the direction of the flowrate) [116].
3.4. Understanding, describing, and predicting retention
One of the objectives of retention modelling is to obtain a better understanding of retention mechanisms. Especially in HILIC, retention modelling can improve the understanding of the mechanism and at the same time reduce the time needed for method optimization. Models that only consider the organic‐modifier concentration, however, cannot describe the retention behavior completely. Other parameters such as buffer concentration, pH and temperature influence the separation efficiency. This section will be subdivided in three parts. The first part will consider the use of the models in section 2.1 to gain a better understanding of retention interactions. The second part focuses on new proposed models to describe more parameters in the separation besides the modifier. The third and final part will cover approaches to perform retention modeling.
3.4.1. Using existing models for understanding retention
Reversed‐phase liquid chromatography
In many cases of retention modelling applied to RP separations the LSS model is applied. While higher‐order models often yield a better description of the data, such as the Q and the NK model, such models also require more input data and risk overfitting the data. Gilar et al. [17] investigated this problem and compared retention prediction by NK and the LSS model. The LSS parameters were calculated in three different ways: looking at the full experimental range, only on experimental data of and a k range from 1 to 30, leading to significantly different parameters. The authors concluded that nonlinear models describe the data best. The authors also recommended that if an LSS model is used it is better to omit data for . Tyteca et al. [117] found a similar deviation from the LSS model for small molecules and peptides and found a better fit for the Q and the NK model. Next to smaller molecules, the retention data of proteins was also investigated, which led to the conclusion that, because of the very steep versus φ curves, nonlinear retention behavior in proteins could not be proven. A recent study on the use of scanning gradients for RPLC optimization found that when a limited number of input experiments was desirable, good fits could be found for the two‐parameter models (LSS and ADS) [39]. However, with increasing number of sampled measurements the fit was best for the ADS model. Next to that, the research showed that the gradient‐slope factor, i.e. the ratio between slopes of the fastest and the slowest scanning gradients, which is often assumed to be at least three, is less important than the proximity of the slope of the predicted gradient to that of the scanning gradients.
For the determination of retention parameters towards the extreme values of φ, Jandera et al. [118] developed a three‐parameter model (ABM model) to allow estimation of retention in pure strong and pure weak solvent (φ = 0 and φ = 1).
| (20) |
where a, b, and m are experimental constants depending on the solute, the stationary phase and the mobile phase [118, 119]. The authors state that in high organic‐modifier concentration, the a‐parameter could be neglected. This model allowed better prediction than the LSS or the ADS model and could also be used for HILIC. One of the drawbacks of the LSS model is that it cannot account for the non‐linearity, making it only applicable to the narrow linear range. Baeza‐Baeza et al. [120] extended the LSS model to include the elution strength changes with the elution degree, g. This parameter was assumed equal to 1 when the solvent strength followed the LSS model. It is larger than 1 when the elution strength decreased along with the organic‐modifier concentration and, reversely, smaller than 1 when it increased with the organic‐modifier concentration. In this way, it affected the linearity of the LSS model. The model could also be applied to other modes of LC.
When performing scanning experiments, it can be advantageous to reduce the time needed for the runs. Baeza‐Baeza et al. combined the accuracy of isocratic data with the speed of gradient experiments by adding solvent concentration pulses in the isocratic runs [121]. The predicted parameters were found to agree with those obtained from isocratic experiments. Gradients have also been investigated in this context, with reports focusing on the fundamental equation of gradient elution [122], non‐linear gradients [123] and pre‐elution of solute in the initial mobile phase [124].
Normal‐phase liquid chromatography
Because of decreased popularity, there has been little development in the field of normal‐phase liquid chromatography (NPLC) with respect to retention modeling. One study compared the slight difference in the ADS model as seen by Snyder and by Soczewinksi [125]. There exist some different perspectives about the n‐term in the ADS model, where Soczewinksi wrote that polar solutes and the polar solvent absorb 1:1 with the absorption sites in the silica [23], whereas Snyder defined n to be the ratio of molecular area of the solute required when adsorbed on the stationary phase versus the molecular area of the strong solvent [25]. Wu et al. applied these models to classic NPLC bonded phases with literature data and to the charge transfer 2,4‐dinitroanilinopropyl (DNAP) column [125]. While the Snyder model predicted better on the classed NPLC phases, the Soczewinski model predicted the charge transfer phase better.
Hydrophilic interaction liquid chromatography
With the potential of HILIC for the separations of highly polar and ionic compounds, the number of applications of HILIC has recently grown [126, 127]. Since the actual retention mechanism of HILIC is not yet completely understood, there have been many published reviews in recent years that attempt to describe the interactions occurring in the column [111, 128, 129, 130].
Recently, papers have focused on the optimization of a complete method, looking at different parameters such as buffers, salts, their concentrations, pH, the organic‐modifier content, temperature, and stationary phase. When optimizing the modifier content, a number of studies used the LSS model [131, 132, 133, 134, 135], the ADS model [100, 131, 132, 133, 134, 135, 136], the Q model [100, 136], and the MM model [131, 133]. Often, more than one model is used to distinguish for example between the partitioning mechanism and the adsorption mechanism [110, 111]. The effect of pH was only found to significantly influence the retention in bare silica columns, since it has a major effect on the charge of the column [100, 134]. There are several other papers that focus on the retention modelling itself. Euerby et al. [14] applied seven existing models to describe the retention as a function of the organic‐modifier concentration and three models to predict the effect of temperature. These models were added to the developed retention‐modelling program, in which the prediction accuracy could be assessed. The importance of the method parameters was ranked for retention and selectivity with statistical approaches and it was found that for retention the observed order of importance was organic‐modifier content > stationary phase > temperature≈pH≈buffer concentration and for selectivity it was stationary phase > pH > buffer concentration > temperature > organic‐modifier content. It was concluded that with gradient results, isocratic experiments could not be predicted. Cesla et al. [46] applied five existing models to the retention of oligosaccharides on different columns for which the magnitude of several mechanisms occurring in the different columns was determined. All five models fitted the retention data to a similar extent. In different studies, the LSS, ADS, Q, MM, and NK model were used by Rácz et al. [137] in Drylab and by Roca et al. [37] in MOREPEAKS. The former study concerned method development for a hallucinogenic mushroom extract on the organic modifier, the pH and the temperature for different columns. The predicted chromatograms by the Q model deviated more from the experimental results than those of the LSS model [137]. In the work of Roca et al., a tryptic digest of bovine‐serum‐albumin was analyzed and retention modelling was used to determine the best combination of column, organic modifier concentration, and additive. To confirm the selection of the model, the F‐test of regression was applied [37]. This retention modeling program was applied by Pirok et al. to separate metabolites with HILIC [15]. The ADS model was found to perform best, only requiring two scanning gradients and yielded acceptable accuracy and linearity. Next to that different stationary‐phase materials were analyzed, where the prediction accuracy in diol columns was found to be better than amide columns.
One aspect that renders the use of gradient data for the retention modeling challenging is the distortion of the gradient shape by the solvent‐delivery system [78]. Therefore, when such data is used to calculate the retention model parameters, such small errors can yield wrong φ values and thus complicate the retention prediction. Wang et al. [138] used a back‐calculation methodology for gradient imperfections and compared their HILIC results to those of RPLC. The authors concluded that column distortion plays a much more important role in HILIC retention projection compared to RPLC.
Mixed‐mode chromatography
When optimizing mixed‐mode separations, scientists often discuss the dual retention mechanism of RPLC and HILIC, depending on the level of organic modifier. This behavior can be described by the U‐profile retention plots, shown in Figure 7, where the minimum describes the φ where the main retention mechanism switches from reversed phase to HILIC (See Eq. 19) [129, 139]. Obradovic et al. investigated the retention of imidazoline and serotonin receptor ligands on a mixed‐mode column and were able to fit the retention data at different mobile phase concentrations to an MM model, thereby confirming the retention mechanism [140]. Balkatzopoulou et al. applied retention modelling to a mixed‐mode reversed‐phase and weak anion‐exchange column. It was found that the retention behavior could be described by a U‐profile plot, i.e., MM model, confirming the RPLC and HILIC behavior of the compounds in lower and higher organic modifier concentration respectively [141].
Other chromatographic modes
Retention modelling has also been applied to more uncommon forms of LC, such as micellar LC, critical chromatography (LCCC), and chiral chromatography. Since other mechanisms play a role in these types of chromatography, it is obvious that the standard retention models are not applicable to these methods. Navarro‐Huerta et al. optimized micellar LC (MLC) by isocratic or gradient elution and applied a wide range of models, some of which are developed for RPLC or specifically for MLC [142]. The most accurate predictions were found from the following model with fixed surfactant concentration:
| (21) |
where c 0, c 1, c 2, c 3, and c 4 are the adjustable fit coefficients of the model. Hegade et al. applied the concept of stationary‐phase optimized selectivity (SOSLC), in which the Q model was applied to the chiral separation of enantiomers [143]. The prediction error of the retention of enantiomers on polysaccharide stationary phases was found to be within 2 and 7% for isocratic and 0 and 12% for gradient elution.
SFC often follows similar retention mechanisms as LC [83]. Vera et al. published two papers on the study of retention of polynuclear aromatic hydrocarbons on phenyl‐type stationary phases [112, 113]. These papers are discussed in Section 3.3.3. Tyteca et al. modeled SFC retention data and applied that in computer assisted method optimization [144]. The MM model, the Q model and the NK model were applied on isocratic and gradient data. The NK and MM model yielded the best retention‐prediction accuracy. The conversion of isocratic to gradient data and vice versa resulted in more difficulties due to pressure differences. De Pauw et al. [145] investigated this pressure‐related problem. Pressure and temperature definition of parameters such as fluidic CO2, volumes, volumetric flow rates, and mobile phase fractions, may differ between systems. The authors found that the retention in SFC could best be described through the mass fraction instead of volume fraction of the organic modifier.
3.4.2. Developing new models for understanding retention
Reversed‐phase liquid chromatography
In many retention models, the elution mode for which the input data is measured should be the same as the preferred elution mode for prediction. For example, when recording isocratic data, the output is more reliable in isocratic mode. The same goes for gradient elution, which has even more restrictions, since the input gradient slopes should be like those predicted [39]. There have been developments to convert such data by defining the retention of analytes in gradient and isocratic elution and transferring this information to the data. This approach is referred to as the iso‐to‐grad approach [32]. Stankov et al. tried to apply this approach to dual‐species eluent (i.e. a combination of two organic modifiers, such as methanol and acetonitrile), and developed and tested four isocratic models with three, four, five, and eight parameters based on the Q model and the LSS model [146]. The authors deemed their prediction better than those of other models, referring to an average root‐mean square error/min of 0.743 for the compounds measured in gradient elution. Claiming a better prediction with increasing number of parameters, the authors stated that the models did not overfit the retention data. The best model was as follows:
| (22) |
where a 0, a 1, a 2, a 3, a 4, a 5, a 6, a 7, and a 8 are regression coefficients for each analyte, solvent and column system. This model requires (at least) nine data points. Tsui et al. [147] developed a three‐parameter‐equilibrium constant stoichiometric displacement retention model for RPLC, which considers the interaction between solute‐sorbent, solute‐ACN (ACN being the mobile phase), and ACN‐sorbent, leading to the following model:
| (23) |
where and are the equilibrium constants of solute‐ACN and ACN‐sorbent, respectively, is the free ACN concentration and x, y, and k 0 are the adjustable parameters. The authors plotted both versus and versus , in which concave upward and concave downward curves were found, respectively. The developed model was able to account for the nonlinearity in the full ACN range. Unfortunately, the work was not compared to conventional retention models, and as such its performance is difficult to assess.
Gritti developed a solvent‐retention model for the description of retention in combined solvent‐ and temperature gradient LC (CST‐GLC) by combining the LSS model with the van‘t Hoff relationship [148]. In this equation, the retention as a factor of the organic modifier concentration and the temperature is written as:
| (24) |
where is the retention factor at the initial φ and temperature, is the S‐parameter from the LSS model, is the isosteric heat of adsorption specific for the analyte, T is the temperature, and R is the ideal gas constant. The author stated that the model described the retention of smaller compounds well over a modified range of temperature from ambient to 90°C. In the work of Wilson et al. temperature‐assisted on‐column solute focusing (TASF) was performed [56]. To model the effect of temperature on the retention, three different models were employed. Two models could be used for a fixed temperature (i.e. 1D model dependent on φ), one based on the LSS model (Equation 25) and one on the NK model (Equation 26), and a third model based on the NK model (Equation 27) included a temperature dependence (i.e. 2D model dependent on φ and T).
| (25) |
| (26) |
| (27) |
In these equations, k 0 and are the retention in pure water, S and describe the solvent strength, a and account for the curvature in the relationship between and φ, and D indicates the effect of temperature. It was found that from the three descriptions of retention, the second equation yielded the most accurate predictions, which was calculated by measuring the retention at an organic modifier fraction of 0.05 at different temperatures. The last model (Eq. 27), which was first published by Neue and Kuss, was also used for the modelling of retention in TASF by Groskreutz et al. [31, 149]. Retention data of parabens and hydroxyphenones was fitted to the model from 12 different solvent compositions and six column temperatures, yielding an R 2‐value of 0.9996. It was claimed that the model could predict retention and shape of the peak under both isocratic and gradient elution conditions. Horner et al. evaluated three temperature‐ and mobile‐phase‐dependent retention models, of which one was Equation 27. The other two models were based on the Pappa‐Louisi partition (Equation 28) and Pappa‐Louisi adsorption (Equation 29) equations.
| (28) |
| (29) |
where both equations have six variable parameters A, B, C, D, E, and F. The model with the best fit, calculated with the AIC value (Section 2.2.2), was Equation 29. It was followed by Equation 28 and the worst fit was found with Equation 27. The authors found that Equation 27 (NK), with the lowest number of parameters, still yielded a decent estimate of the retention.
When the retention of analytes with acid‐base properties is modeled, the retention not only depends on the organic‐modifier concentration, but also on the dissociation constant (K). Andrés et al. developed a simplified model, based on a polarity‐parameter model [150]. This two‐parameter model, which is a simplified form of the LFER by Abraham, was originally developed for neutral compounds in RPLC [151].
| (30) |
In this model, describes the polarity of the mobile phase (related to the volume fraction and the different organic modifiers) and p and q are the fitting parameters. This model was extended to model retention of acid–base compounds for separations with acetonitrile and validated for separations with methanol [150, 152]:
| (31) |
where , p, and q are similar to Equation 30, D describes the ionization degree of the analytes related to the , and f is the ratio between the retention factors of the pure ionized and the pure neutral compound. The model was tested with different types of gradients with methanol (linear, convex, concave, and combinations of those) and at three pH values. In Figure 8 on the left, the predicted retention times for a wide range of acid‐base compounds are plotted against the experimental retention times for the three pH values. On the right, the residuals are shown. From this figure, it can be seen that a higher pH lowers the prediction error [152].
FIGURE 8.
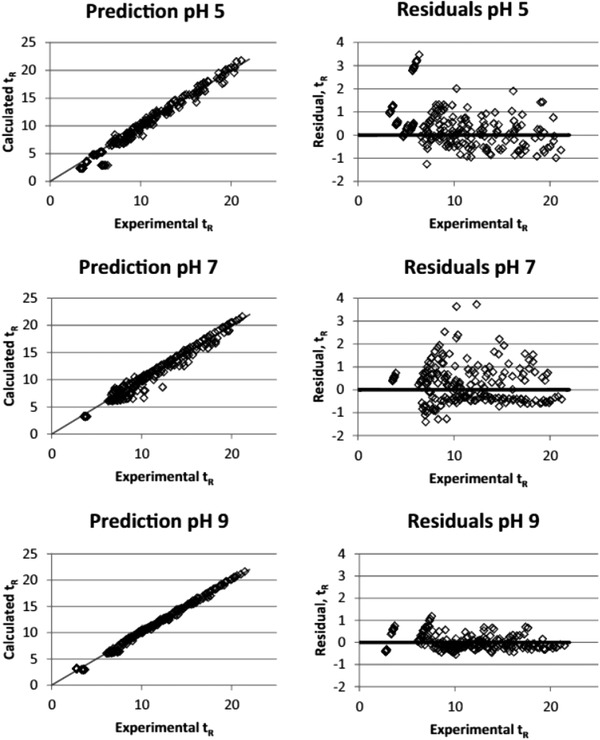
Prediction retention times, calculated with the model in Equation 31, compared to experimental retention times for pH 5, 7, and 9. On the left the two retention times are plotted for each compound and on the right the residuals of the left plot are shown. Retention time is in minutes. Reproduced from [152] with permission
The authors claimed that the model was not size dependent, since it performed as good for small as for complex molecules [152]. Sasaki et al. found that the model of Andrés et al. gave good accuracy, but it could not model compounds that presented multiple‐curved retention behavior, i.e. molecules with multiple values, when changing the pH [153]. In their work, pH‐modifier models were combined in an optimization program to predict the optimal separation in pH and organic modifier, based on the data of 33 runs. While the model of Andrés et al. needed information a priori such as the , the software package of Sasaki et al. could predict retention from the retention input data alone and needed no physiological or chemical information of the target analyte.
Hydrophilic interaction and mixed‐mode chromatography
As could be seen in the section “Hydrophilic interaction liquid chromatography,” HILIC is often described by the MM model. Wang et al. [154] studied the multiple interactions in HILIC further, and described the interactions between the solute, the solvent and the stationary phase into a stoichiometric displacement model for retention (SDM‐R), which is defined as follows:
| (32) |
where , which represents the affinity of 1 mole amount of solute to stationary phase, and Z are both constant, and is the logarithm of the concentration of water in the mobile phase. The model was compared to the LSS and ADS model, and outperformed both models on the retention prediction of proteins in HILIC.
Obradovic et al. developed a novel computational approach to identify the optimal fitting models for dual retention behavior of HILIC and RPLC, typically described with a U‐profile [155]. The considered models were analyzed on their predictive ability of retention and on the accuracy of the turning point (). The research yielded multiple models that outperformed the standard Q and MM model, which were correlated to other parameters that are influencing the separation. These parameters were based on the average retention in HILIC mode, the average retention in RPLC mode and the average retention in the whole range of organic modifier.
3.4.3. Approaches to perform retention modeling
The exact method of conducting retention modelling is not always clear. Tyteca et al. investigated fitting problems encountered when modelling retention [156]. The LSS, ADS, NK, MM, and an extended four‐parameter Neue model, as well as combinations thereof were tested on HILIC and SFC retention data. It was found that adding more scanning experiments and switching to higher‐order models could improve the fitting and modeling of the data. For highly retained compounds, the authors recommended to use very slow gradients (high ) or to start at a higher organic‐modifier concentration. Next to that, modelling retention of less retained compounds benefits from faster gradients. Another problem encountered when fitting HILIC retention data in model is that the retention in HILIC changes as a result of small changes in the mobile phase concentration. For that reason, Tumpa et al. divided the experimental space into different segments with an interpolated polynomial for each part, which is known as spline interpolation [157]. The MM, Q, ADS, and LSS model were tested in this study. The spline interpolation technique was cross validated with the standard retention modeling approach, yielding the new technique with the best values. The prediction error of the retention parameters was below 10% for all compounds.
3.5. Lipophilicity determination
Lipophilicity is an important parameter to describe physicochemical properties and is often used in quantitative structure‐activity relationships (QSARs) for several classes of compounds, such as environmental pollutants, pharmaceuticals, and bioactive compounds. It is generally described as the logarithm of the n‐octanol/water coefficient: . Lipophilicity is a critical parameter in drug discovery, since it plays a crucial role in determining the ADMET (adsorption, distribution, metabolism, excretion, and toxicity) of the potential candidate [158]. For successful drug discovery, drugs are assessed on their pharmacokinetic properties, such as biological half‐life and extent of protein binding, but next to that they are assessed on the delivery to these target sites. After uptake, the drugs must cross several membranes, either passively or actively. These are generally more hydrophobic and thus prefer compounds with higher lipophilicity. In recent years, the average lipophilicity value of potential drugs has increased, exposing its value and influence on the drug industry [158]. Moreover, lipophilicity plays an important role in environmental chemistry, where it is used in the estimation of bioaccumulation in plants and animals, the prediction of adsorption of pollutants in soil and sediments and the assessment of health risks of emerging contaminants [159].
There are various methods, computational and experimental, which can be divided into direct and indirect methods, to calculate lipophilicity, but there are limitations to the direct experimental methods as these (i) cost time, (ii) are labor intensive, (iii) require a lot of sample, and (iv) are often limited by the dynamic range of the detector [160]. For that reason, many indirect methods have been introduced based on separations, of which the most common approach is based on RPLC. When using RPLC as a tool, the descriptor of lipophilicity is the logarithm of the retention parameter (), which can be calculated from the retention time and the dead time (Eq. 1) [2]. At first, isocratic retention factors at specific organic modifier levels were used to correlate the to the , but later the authors opted that the retention factor in 100% water was more demonstrative [161]. This led to the Collander Equation, which is a linear dependence between and [162, 163]:
| (33) |
where a and b are parameters that are characteristic for the non‐polar solvent used in the chromatographic separation. Performing analyses at 100% water, which is thought to lead to major retention loss and to be catastrophic for the column life time [164], leading to large retention times of hydrophobic compounds and to very broad peaks, is omitted. For that reason, often the is estimated from the Snyder–Soczewinski equation (Equation 8). When calculating retention factors from 4 isocratic runs at different organic modifier levels, the can be extrapolated [160]. Liang et al. [165] revised the methodology of lipophilicity determination and argued to use gradients instead of isocratic runs to save time. If gradient runs are performed instead of isocratic runs, the found with three gradient runs agreed better with the determined with isocratic runs than if two gradient runs were used. Next to RPLC, Sobánska argues that TLC can serve as an alternative for lipophilicity determination, since it is inexpensive, fast, and readily available [166].
The extent to which a drug can penetrate biological membranes, such as the blood–brain barrier, cell membranes, and skin, depends heavily on the . A number of groups publish the lipophilicity parameters of many newly synthesized drug candidates [167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177, 178, 179, 180]. In drug discovery research, the LSS model is often used to obtain the , but Hawrył et al. acknowledge the concave structure of the retention plots [169]. For this reason, the Q model was used next to the LSS model to determine the intercept. The Q model gave more accurate results when acetonitrile was used as organic modifier, whereas retention data in methanol fitted better with the LSS model [1, 169]. The same quadratic relation was found by Klose et al. for wide φ ranges [177]. However, other authors found a linear relationship when using acetonitrile [174]. Sztanke et al. [167] compared modifier systems with methanol, acetonitrile, and dioxane and found that methanol systems yield the best experimental lipophilicity indices. However, the research stresses the differences and thus the complexity when performing these scanning gradients.
4. DISCUSSION
In retrospect, the application of retention modelling by means of (semi‐) empirical models has led to a better understanding of general HPLC, specifically RPLC and HILIC. It can be stated that it plays a key‐role in the different fields of application. In the published work on retention modeling, however, a clear distinction between the workflows of the different applications becomes evident, which can be seen in Figures 2 and 9. For method optimization and lipophilicity determination retention modelling is often approached as a black box. Often only one model is applied which is chosen by convention, although there seems to be enough evidence that these models have their inaccuracies. For example, with lipophilicity determination, the is mostly determined by extrapolating the LSS model, while it has often been shown that there is a clear deviation from linearity, especially in the lower φ range [120]. For this reason, lipophilicity determination is ranked with the lowest complexity of the retention modelling, followed by the method optimization (Figure 9). In stationary‐phase characterization, often more models are investigated. Any good performance of a specific model is sometimes used as supporting evidence to conclude that a certain retention mechanism mainly determines the selectivity. In contrast, most work in the domain of method transfer and understanding retention use retention modeling to a much‐sophisticated extent. Researchers also appear to implement increasingly more parameters to conduct retention modeling in these latter domains, attempting to describe each contributing effect.
FIGURE 9.
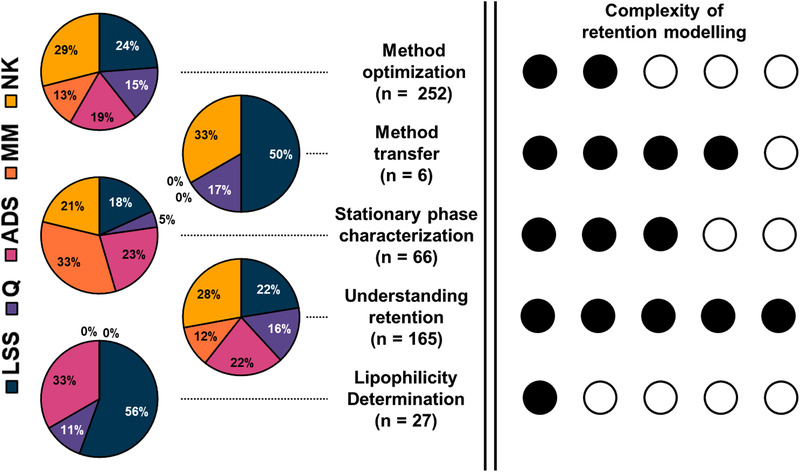
Overview of the different models applied per application. The total number of research papers is found under the title of the application. On the right the degree of complexity is given for the five different application fields
5. CONCLUDING REMARKS
The aim of this review was to provide a comprehensive overview of strategies for and applications of retention modeling. After reviewing the recent literature, we can also make a number of recommendations.
Studies on retention modeling are typically limited to specific purposes, such as method optimization or method transfer. However, from a mathematical point of view, retention modelling is ultimately an exercise in regression statistics and insights obtained in one study should—in principle—be applicable for all purposes.
To our surprise, numerical information on the outcome of retention modeling (e.g. residuals) are rarely reported. Also, in retention‐modeling studies, the experimental (raw) input data and relevant conditions, such as the column dead volume and the dwell volume, are often not reported. It is repeatedly unclear how specific regression results or model parameters were obtained. Unfortunately, all these factors affect the accuracy and precision of the reported retention model parameters [32, 33, 39]. Therefore, it is often not possible to reproduce or critically evaluate published work.
The main application of retention modelling lies in the understanding, description and prediction of retention. There is currently no consensus on the quality of retention models, which frustrates the comparison and evaluation of models. Reported prediction errors range from 0.1 to 10%, but almost all authors speak of “accurate” or “good” models. Some uniformity is badly needed. Given the high efficiency of LC separations, small variations in retention times may result in large variations in resolution. Therefore, retention models for application in method development and optimization require predictions (well) within 1%.
A potentially important application of retention modelling is method transfer. Given the enormous diversity in columns and the continuous innovation in instrumentation, method transfer is increasingly needed. Retention (model) parameters may facilitate a successful transfer of existing methods without a need for renewed method optimization.
If better care is taken of the quality of measurements and reporting, model parameters may eventually be used as system‐independent retention data, which is an attractive proposition.
CONFLICT OF INTEREST
The authors have declared no conflict of interest.
ACKNOWLEDGEMENTS
This work is part of the TooCOLD project carried out within the framework of TTW Open Technology Programme with project number 15506 that is (partly) financed by the Netherlands Organisation for Scientific Research (NWO). Bob Pirok acknowledges the Agilent UR grant #4354. This work was performed in the context of the Chemometrics and Advanced Separations Team (CAST) within the Centre Analytical Sciences Amsterdam (CASA). The valuable contributions of the CAST members are gratefully acknowledged.
den Uijl MJ, Schoenmakers PJ, Pirok BW, van Bommel MR. Recent applications of retention modeling in liquid chromatography. J Sep Sci. 2021;44:88–114. 10.1002/jssc.202000905
REFERENCES
- 1. Schoenmakers PJ, Billiet HAH, Tussen R, De Galan L. Gradient selection in reversed‐phase liquid chromatography. J. Chromatogr. A 1978;149:519–537. [Google Scholar]
- 2. Martel S, Gillerat F, Carosati E, Maiarelli D, Tetko IV, Mannhold R, Carrupt PA. Large, chemically diverse dataset of log P measurements for benchmarking studies. Eur J Pharm Sci. 2013;48:21–9. [DOI] [PubMed] [Google Scholar]
- 3. Xiang Q, Shan G, Wu W, Jin H, Zhu L. Measuring log Kow coefficients of neutral species of perfluoroalkyl carboxylic acids using reversed‐phase high‐performance liquid chromatography. Environ Pollut. 2018;242:1283–90. [DOI] [PubMed] [Google Scholar]
- 4. Marchand DH, Snyder LR, Dolan JW. Characterization and applications of reversed‐phase column selectivity based on the hydrophobic‐subtraction model. J Chromatogr A. 2008;1191:2–20. [DOI] [PubMed] [Google Scholar]
- 5. Snyder LR, Dolan JW, Carr PW. The hydrophobic‐subtraction model of reversed‐phase column selectivity. J Chromatogr A. 2004;1060:77–116. [PubMed] [Google Scholar]
- 6. Abraham MH. Scales of solute hydrogen‐bonding: Their construction and application to physicochemical and biochemical processes. Chem Soc Rev. 1993;22:73–83. [Google Scholar]
- 7. Abraham MH, Rosés M, Poole CF, Poole SK. Hydrogen bonding. 42. Characterization of reversed‐phase high‐performance liquid chromatographic C18 stationary phases. J Phys Org Chem. 1997;10:358–68. [Google Scholar]
- 8. Snyder LR, Dolan JW, Marchand DH, Carr PW. The hydrophobic‐ Subtraction model of reversed‐phase column selectivity. Adv Chromatogr. 2015;50:297–376. [DOI] [PubMed] [Google Scholar]
- 9. Græsbøll R, Nielsen NJ, Christensen JH. Using the hydrophobic subtraction model to choose orthogonal columns for online comprehensive two‐dimensional liquid chromatography. J Chromatogr A. 2014;1326:39–46. [DOI] [PubMed] [Google Scholar]
- 10. Kaliszan R. QSRR: Quantitative structure‐(chromatographic) retention relationships. Chem Rev. 2007;107:3212–46. [DOI] [PubMed] [Google Scholar]
- 11. Kaliszan R, Baczek T, Buciński A, Buszewski B, Sztupecka M. Prediction of gradient retention from the linear solvent strength (LSS) model, quantitative structure‐retention relationships (QSRR), and artificial neural networks (ANN). J Sep Sci. 2003;26:271–82. [Google Scholar]
- 12. Novotná K, Havliš J, Havel J. Optimisation of high performance liquid chromatography separation of neuroprotective peptides: Fractional experimental designs combined with artificial neural networks. J Chromatogr A. 2005;1096:50–7. [DOI] [PubMed] [Google Scholar]
- 13. Barron LP, McEneff GL. Gradient liquid chromatographic retention time prediction for suspect screening applications: A critical assessment of a generalised artificial neural network‐based approach across 10 multi‐residue reversed‐phase analytical methods. Talanta. 2016;147:261–70. [DOI] [PubMed] [Google Scholar]
- 14. Euerby MR, Hulse J, Petersson P, Vazhentsev A, Kassam K. Retention modelling in hydrophilic interaction chromatography. Anal Bioanal Chem. 2015;407:9135–52. [DOI] [PubMed] [Google Scholar]
- 15. Pirok BWJ, Molenaar SRA, van Outersterp RE, Schoenmakers PJ. Applicability of retention modelling in hydrophilic‐interaction liquid chromatography for algorithmic optimization programs with gradient‐scanning techniques. J Chromatogr A. 2017;1530:104–11. [DOI] [PubMed] [Google Scholar]
- 16. Tyteca E, Périat A, Rudaz S, Desmet G, Guillarme D. Retention modeling and method development in hydrophilic interaction chromatography. J Chromatogr A. 2014;1337:116–27. [DOI] [PubMed] [Google Scholar]
- 17. Gilar M, Hill J, McDonald TS, Gritti F. Utility of linear and nonlinear models for retention prediction in liquid chromatography. J Chromatogr A. 2020;1613:460690. [DOI] [PubMed] [Google Scholar]
- 18. Molnar I. Computerized design of separation strategies by reversed‐phase liquid chromatography: Development of DryLab software. J Chromatogr A. 2002;965:175–94. [DOI] [PubMed] [Google Scholar]
- 19. Tyteca E, Liekens A, Clicq D, Fanigliulo A, Debrus B, Rudaz S, Guillarme D, Desmet G. Predictive elution window stretching and shifting as a generic search strategy for automated method development for liquid chromatography. Anal Chem. 2012;84:7823–30. [DOI] [PubMed] [Google Scholar]
- 20. Pirok BWJ, Pous‐Torres S, Ortiz‐Bolsico C, Vivó‐Truyols G, Schoenmakers PJ. Program for the interpretive optimization of two‐dimensional resolution. J Chromatogr A. 2016;1450:29–37. [DOI] [PubMed] [Google Scholar]
- 21. Snyder LR, Dolan JW, Gant JR. Gradient elution in high‐performance liquid chromatography. I. Theoretical basis for reversed‐phase systems. J Chromatogr A. 1979;165:3–30. [Google Scholar]
- 22. Schoenmakers PJ, Billiet HAH, Tijssen R, De Galan L. Gradient selection in reversed‐phase liquid chromatography. J Chromatogr A. 1978;149:519–37. [Google Scholar]
- 23. Soczewinski E. Solvent Composition Effects in Thin‐Layer Chromatography Systems of the Type Silica Gel‐Electron Donor Solvent. Anal Chem. 1969;41:179–82. [Google Scholar]
- 24. Jandera P, Churáček J. Gradient elution in liquid chromatography. I. The influence of the composition of the mobile phase on the capacity ratio (retention volume, band width, and resolution) in isocratic elution ‐ theoretical considerations. J Chromatogr A. 1974;91:207–21. [Google Scholar]
- 25. Snyder LR, Poppe H. Mechanism of solute retention in liquid—solid chromatography and the role of the mobile phase in affecting separation. J Chromatogr A. 1980;184:363–413. [Google Scholar]
- 26. Soczewiński E. Mechanistic molecular model of liquid‐solid chromatography: Retention‐eluent composition relationships. J Chromatogr A. 2002;965:109–16. [DOI] [PubMed] [Google Scholar]
- 27. Jin G, Guo Z, Zhang F, Xue X, Jin Y, Liang X. Study on the retention equation in hydrophilic interaction liquid chromatography. Talanta. 2008;76:522–7. [DOI] [PubMed] [Google Scholar]
- 28. Nikitas P, Pappa‐Louisi A, Agrafiotou P. Effect of the organic modifier concentration on the retention in reversed‐phase liquid chromatography: II. Tests using various simplified models. J Chromatogr A. 2002;946:33–45. [DOI] [PubMed] [Google Scholar]
- 29. Nikitas P, Pappa‐Louisi A, Agrafiotou P. Effect of the organic modifier concentration on the retention in reversed‐phase liquid chromatography: I. General semi‐thermodynamic treatment for adsorption and partition mechanisms. J Chromatogr A. 2002;946:9–32. [DOI] [PubMed] [Google Scholar]
- 30. Neue UD. Chromatographia. Springer; 2006: S45–53. [Google Scholar]
- 31. Neue UD, Kuss HJ. Improved reversed‐phase gradient retention modeling. J Chromatogr A. 2010;1217:3794–803. [DOI] [PubMed] [Google Scholar]
- 32. Vivó‐Truyols G, Torres‐Lapasió JR, García‐Alvarez‐Coque MC. Error analysis and performance of different retention models in the transference of data from/to isocratic/gradient elution. J Chromatogr A. 2003;1018:169–81. [DOI] [PubMed] [Google Scholar]
- 33. Vivó‐Truyols G, Torres‐Lapasió JR, García‐Alvarez‐Coque MC. J. Chromatogr. A 2004: 31–9. [DOI] [PubMed] [Google Scholar]
- 34. Tyteca E, Guillarme D, Desmet G. Use of individual retention modeling for gradient optimization in hydrophilic interaction chromatography: Separation of nucleobases and nucleosides. J Chromatogr A. 2014;1368:125–31. [DOI] [PubMed] [Google Scholar]
- 35. Jandera P, Hájek T, Vyňuchalová K. Retention and bandwidths prediction in fast gradient liquid chromatography. Part 2‐Core‐shell columns. J Chromatogr A. 2014;1337:57–66. [DOI] [PubMed] [Google Scholar]
- 36. Schellinger AP, Carr PW. A practical approach to transferring linear gradient elution methods. J Chromatogr A. 2005;1077:110–9. [DOI] [PubMed] [Google Scholar]
- 37. Roca LS, Schoemaker SE, Pirok BWJ, Gargano AFG, Schoenmakers PJ. Accurate modelling of the retention behaviour of peptides in gradient‐elution hydrophilic interaction liquid chromatography. J Chromatogr A. 2019, 1614, 460650. [DOI] [PubMed] [Google Scholar]
- 38. Nikitas P, Pappa‐Louisi A, Papageorgiou A. Simple algorithms for fitting and optimisation for multilinear gradient elution in reversed‐phase liquid chromatography. J Chromatogr A. 2007;1157:178–86. [DOI] [PubMed] [Google Scholar]
- 39. den Uijl MJ, Schoenmakers PJ, Schulte GK, Stoll DR Bommel MR van, Pirok BWJ. Measuring and using scanning‐gradient data for use in method optimization for liquid‐chromatography. 2020. Manusript submitted for publication. [DOI] [PubMed]
- 40. Akaike H. A New Look at the Statistical Model Identification. IEEE Trans Automat Contr. 1974;19:716–23. [Google Scholar]
- 41. Horner AR, Wilson RE, Groskreutz SR, Murray BE, Weber SG. Evaluation of three temperature‐ and mobile phase‐dependent retention models for reversed‐phase liquid chromatographic retention and apparent retention enthalpy. J Chromatogr A. 2019;1589:73–82. [DOI] [PubMed] [Google Scholar]
- 42. Bos TS, Knol WC, Molenaar SRA, Niezen LE, Schoenmakers PJ, Somsen GW, Pirok BWJ. Recent applications of chemometrics in one‐ and two‐dimensional chromatography. J Sep Sci. 2020;43:1678–1727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Li R, Sun W, Xiao X, Chen B, Wei Y. Retention of stevioside polar compounds on a sulfonic acid‐functionalized stationary phase. J Chromatogr A. 2020. 10.1016/j.chroma.2020.460978. [DOI] [PubMed] [Google Scholar]
- 44. Komendová M, Urban J. Dual‐retention mechanism of dopamine‐related compounds on monolithic stationary phase with zwitterion functionality. J Chromatogr A. 2020;1618 10.1016/j.chroma.2020.460893. [DOI] [PubMed] [Google Scholar]
- 45. Česla P, Vaňková N, Křenková J, Fischer J. Comparison of isocratic retention models for hydrophilic interaction liquid chromatographic separation of native and fluorescently labeled oligosaccharides. J Chromatogr A. 2016;1438:179–88. [DOI] [PubMed] [Google Scholar]
- 46. Baczek T, Markuszewski M Kaliszan R van, Straten MA, Claessens HA. Linear and Quadratic Relationships between Retention and Organic Modifier Content in Eluent in Reversed Phase High‐Performance Liquid Chromatography: A Systematic Comparative Statistical Study. J High Resolut Chromatogr. 2000;23:667–76. [Google Scholar]
- 47. Zhang S‐D, Gong C, Lu Y, Xu X. Separation of Triacylglycerols from Edible Oil Using a Liquid Chromatography‐Mass Spectrometry System with a Porous Graphitic Carbon Column and a Toluene‐Isopropanol Gradient Mobile Phase. J Am Oil Chem Soc. 2018;95:1253–66. [Google Scholar]
- 48. Fekete S, Beck A, Veuthey JL, Guillarme D. Proof of Concept to Achieve Infinite Selectivity for the Chromatographic Separation of Therapeutic Proteins. Anal Chem. 2019;91:12954–61. [DOI] [PubMed] [Google Scholar]
- 49. Fekete S, Ritchie H, Lawhorn J, Veuthey JL, Guillarme D. Improving selectivity and performing online on‐column fractioning in liquid chromatography for the separation of therapeutic biopharmaceutical products. J Chromatogr A. 2020. 10.1016/j.chroma.2020.460901. [DOI] [PubMed] [Google Scholar]
- 50. Alvarez‐Segura T, Camacho‐Molinero C, Torres‐Lapasió JR, García‐Alvarez‐Coque MC. Analysis of amino acids using serially coupled columns. J Sep Sci. 2017;40:2741–51. [DOI] [PubMed] [Google Scholar]
- 51. Jeong LN, Sajulga R, Forte SG, Stoll DR, Rutan SC. Simulation of elution profiles in liquid chromatography—I: Gradient elution conditions, and with mismatched injection and mobile phase solvents. J Chromatogr A. 2016;1457:41–9. [DOI] [PubMed] [Google Scholar]
- 52. Gritti F, Gilar M, Hill J. Mismatch between sample diluent and eluent: Maintaining integrity of gradient peaks using in silico approaches. J Chromatogr A. 2019;1608 10.1016/j.chroma.2019.460414. [DOI] [PubMed] [Google Scholar]
- 53. Boateng BO, Fever M, Edwards D, Petersson P, Euerby MR, Sutcliffe OB. Chromatographic retention behaviour, modelling and optimization of a UHPLC‐UV separation of the regioisomers of the Novel Psychoactive Substance (NPS) methoxphenidine (MXP). J Pharm Biomed Anal. 2018;153:238–47. [DOI] [PubMed] [Google Scholar]
- 54. Vaňková N, De Vos J, Tyteca E, Desmet G, Edge T, Česlová L, Česla P, Eeltink S. Effect of gradient steepness on the kinetic performance limits and peak compression for reversed‐phase gradient separations of small molecules. J Chromatogr A. 2015;1409:152–8. [DOI] [PubMed] [Google Scholar]
- 55. Gritti F. General theory of peak compression in liquid chromatography. J Chromatogr A. 2016;1433:114–22. [DOI] [PubMed] [Google Scholar]
- 56. Wilson RE, Groskreutz SR, Weber SG. Improving the Sensitivity, Resolution, and Peak Capacity of Gradient Elution in Capillary Liquid Chromatography with Large‐Volume Injections by Using Temperature‐Assisted On‐Column Solute Focusing. Anal Chem. 2016;88:5112–21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57. Rerick MT, Groskreutz SR, Weber SG. Multiplicative On‐Column Solute Focusing Using Spatially Dependent Temperature Programming for Capillary HPLC. Anal Chem. 2019;91:2854–60. [DOI] [PubMed] [Google Scholar]
- 58. Chang Q, Shao Y, Yang Y, Yu H, Wang R. Chromatographic retention assisted deconvolution of liquid chromatography‐mass spectrometry chromatogram of natural products. Anal Sci. 2019;35:201–6. [DOI] [PubMed] [Google Scholar]
- 59. Pirok BWJ, Stoll DR, Schoenmakers PJ. Recent Developments in Two‐Dimensional Liquid Chromatography: Fundamental Improvements for Practical Applications. Anal Chem. 2019;91:240–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Pirok BWJ, Gargano AFG, Schoenmakers PJ. Optimizing separations in online comprehensive two‐dimensional liquid chromatography. J Sep Sci. 2018;41:68–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61. Sarrut M, D'Attoma A, Heinisch S. Optimization of conditions in on‐line comprehensive two‐dimensional reversed phase liquid chromatography: Experimental comparison with one‐dimensional reversed phase liquid chromatography for the separation of peptides. J Chromatogr A. 2015;1421:48–59. [DOI] [PubMed] [Google Scholar]
- 62. Sarrut M, Rouvière F, Heinisch S. Theoretical and experimental comparison of one dimensional versus on‐line comprehensive two dimensional liquid chromatography for optimized sub‐hour separations of complex peptide samples. J Chromatogr A. 2017;1498:183–95. [DOI] [PubMed] [Google Scholar]
- 63. Bernardin M, Masle ALe, Bessueille‐Barbier F, Lienemann CP, Heinisch S. Comprehensive two‐dimensional liquid chromatography with inductively coupled plasma mass spectrometry detection for the characterization of sulfur, vanadium and nickel compounds in petroleum products. J Chromatogr A. 2020;1611 10.1016/j.chroma.2019.460605. [DOI] [PubMed] [Google Scholar]
- 64. Sarrut M, Corgier A, Fekete S, Guillarme D, Lascoux D, Janin‐Bussat MC, Beck A, Heinisch S. Analysis of antibody‐drug conjugates by comprehensive on‐line two‐dimensional hydrophobic interaction chromatography x reversed phase liquid chromatography hyphenated to high resolution mass spectrometry. I − Optimization of separation conditions. J Chromatogr B Anal Technol Biomed Life Sci. 2016;1032:103–11. [DOI] [PubMed] [Google Scholar]
- 65. Iguiniz M, Rouvière F, Corbel E, Roques N, Heinisch S. Comprehensive two dimensional liquid chromatography as analytical strategy for pharmaceutical analysis. J Chromatogr A. 2018;1536:195–204. [DOI] [PubMed] [Google Scholar]
- 66. D'Attoma A, Grivel C, Heinisch S. On‐line comprehensive two‐dimensional separations of charged compounds using reversed‐phase high performance liquid chromatography and hydrophilic interaction chromatography. Part I: Orthogonality and practical peak capacity considerations. J Chromatogr A. 2012;1262:148–59. [DOI] [PubMed] [Google Scholar]
- 67. Stoll DR, Sajulga RW, Voigt BN, Larson EJ, Jeong LN, Rutan SC. Simulation of elution profiles in liquid chromatography − II: Investigation of injection volume overload under gradient elution conditions applied to second dimension separations in two‐dimensional liquid chromatography. J Chromatogr A. 2017;1523:162–72. [DOI] [PubMed] [Google Scholar]
- 68. Muller M, Tredoux AGJ, de Villiers A. Predictive kinetic optimisation of hydrophilic interaction chromatography × reversed phase liquid chromatography separations: Experimental verification and application to phenolic analysis. J Chromatogr A. 2018;1571:107–20. [DOI] [PubMed] [Google Scholar]
- 69. Hewitt EF, Lukulay P, Galushko S. Implementation of a rapid and automated high performance liquid chromatography method development strategy for pharmaceutical drug candidates. J Chromatogr A. 2006;1107:79–87. [DOI] [PubMed] [Google Scholar]
- 70. Taheri M, Moazeni‐Pourasil RS, Sheikh‐Olia‐Lavasani M, Karami A, Ghassempour A. Central composite design with the help of multivariate curve resolution in loadability optimization of RP‐HPLC to scale‐up a binary mixture. J Sep Sci. 2016;39:1031–40. [DOI] [PubMed] [Google Scholar]
- 71. Tyteca E, Bieber S, Letzel T, Desmet G. Possibilities and Limitations of Computer‐Assisted Method Development in HILIC: A Case Study. Chromatographia. 2017;80:771–81. [Google Scholar]
- 72. Fasoula S, Zisi C, Gika H, Pappa‐Louisi A, Nikitas P. Retention prediction and separation optimization under multilinear gradient elution in liquid chromatography with Microsoft Excel macros. J Chromatogr A. 2015;1395:109–15. [DOI] [PubMed] [Google Scholar]
- 73. Zisi C, Pappa‐Louisi A, Nikitas P. Separation optimization in HPLC analysis implemented in R programming language. J Chromatogr A. 2020:1617 10.1016/j.chroma.2019.460823. [DOI] [PubMed] [Google Scholar]
- 74. van Schaick G, Pirok BWJ, Haselberg R, Somsen GW, Gargano AFG. Computer‐aided gradient optimization of hydrophilic interaction liquid chromatographic separations of intact proteins and protein glycoforms. J Chromatogr A. 2019;1598:67–76. [DOI] [PubMed] [Google Scholar]
- 75. Khalaf R, Baur D, Pfister D. Optimization of reversed‐phase chromatography methods for peptide analytics. J Chromatogr A. 2015;1425:198–203. [DOI] [PubMed] [Google Scholar]
- 76. Zhang Y. Computer simulation and optimization for reversed‐phase HPLC separation: A novel algorithm simulating and optimizing the non‐linear and non‐ideal separation process in analytical chromatography. Chemom Intell Lab Syst. 2015;149:73–80. [Google Scholar]
- 77. Alvarez‐Segura T, López‐Ureña S, Torres‐Lapasió JR, García‐Alvarez‐Coque MC. Multi‐scale optimisation vs. genetic algorithms in the gradient separation of diuretics by reversed‐phase liquid chromatography. J Chromatogr A. 2020:1609 10.1016/j.chroma.2019.460427. [DOI] [PubMed] [Google Scholar]
- 78. Bos TS, Niezen LE, den Uijl MJ, Molenaar SRA, Lege S, Schoenmakers PJ, Somsen GW, Pirok BWJ. Eliminating the influence of geometry‐induced gradient deformation in liquid chromatographic retention modelling. 2020. Manuscript submitted for publication. [DOI] [PubMed]
- 79. Jandera P, Hájek T. Possibilities of retention prediction in fast gradient liquid chromatography. Part 3: Short silica monolithic columns. J Chromatogr A. 2015;1410:76–89. [DOI] [PubMed] [Google Scholar]
- 80. Gritti F. Gradient method transfer after changing the average pore diameter of the chromatographic stationary phase I – One‐dimensional sample mixture. J Chromatogr A. 2019;1597:119–31. [DOI] [PubMed] [Google Scholar]
- 81.HPLC Columns ‐ HPLC column selectivity measurements of more than 600 reversed phase columns from over 30 manufacturers. http://hplccolumns.org/ (last time accessed: August 19, 2020).
- 82. Abraham MH, Chadha HS, Leo AJ. Hydrogen bonding. XXXV. Relationship between high‐performance liquid chromatography capacity factors and water‐octanol partition coefficients. J Chromatogr A. 1994;685:203–11. [Google Scholar]
- 83. Sykora D, Vozka J, Tesarova E. Chromatographic methods enabling the characterization of stationary phases and retention prediction in high‐performance liquid chromatography and supercritical fluid chromatography. J Sep Sci. 2016;39:115–31. [DOI] [PubMed] [Google Scholar]
- 84. Žuvela P, Skoczylas M, Jay Liu J, Baczek T, Kaliszan R, Wong MW, Buszewski B, Ba̧czek T, Kaliszan R, Wong MW, Buszewski B, Baczek T, Kaliszan R, Wong MW, Buszewski B, Ba̧czek T, Kaliszan R, Wong MW, Buszewski B, Baczek T, Kaliszan R, Wong MW, Buszewski B, Ba̧czek T, Kaliszan R, Wong MW, Buszewski B. Column Characterization and Selection Systems in Reversed‐Phase High‐Performance Liquid Chromatography. Chem Rev. 2019;119:3674–729. [DOI] [PubMed] [Google Scholar]
- 85. Visky D, Vander Heyden Y, Iványi T, Baten P, De Beer J, Kovács Z, Noszál B, Roets E, Massart DL, Hoogmartens J. Characterisation of reversed‐phase liquid chromatographic columns by chromatographic tests. Evaluation of 36 test parameters: Repeatability, reproducibility and correlation. J Chromatogr A. 2002;977:39–58. [DOI] [PubMed] [Google Scholar]
- 86. Galea C, Mangelings D, Vander Heyden Y. Characterization and classification of stationary phases in HPLC and SFC ‐ a review. Anal Chim Acta. 2015;886:1–15. [DOI] [PubMed] [Google Scholar]
- 87. Wang L, Wei W, Xia Z, Jie X, Xia ZZ. Recent advances in materials for stationary phases of mixed‐mode high‐performance liquid chromatography. TrAC ‐ Trends Anal Chem. 2016;80:495–506. [Google Scholar]
- 88. Khalaf R, Forrer N, Buffolino G, Butté A, Morbidelli M. Model‐based description of peptide retention on doped reversed‐phase media. J Chromatogr A. 2015;1407:169–75. [DOI] [PubMed] [Google Scholar]
- 89. Lincoln DR, Lavrik NV, Kravchenko II, Sepaniak MJ. Retention in Porous Layer Pillar Array Planar Separation Platforms. Anal Chem. 2016;88:8741–8. [DOI] [PubMed] [Google Scholar]
- 90. Li Y, Zhu N, Chen T, Wei M, Ma Y. Stationary Phase Based on β‐Cyclodextrin and Poly(N‐isopropylacrylamide) for HILIC and RPLC. Chromatographia. 2016;79:29–36. [Google Scholar]
- 91. Peristyy A, Paull B, Nesterenko PN. Chromatographic performance of synthetic polycrystalline diamond as a stationary phase in normal phase high performance liquid chromatography. J Chromatogr A. 2015;1391:49–59. [DOI] [PubMed] [Google Scholar]
- 92. Qiao L, Shi X, Xu G. Recent advances in development and characterization of stationary phases for hydrophilic interaction chromatography. TrAC ‐ Trends Anal Chem. 2016;81:23–33. [Google Scholar]
- 93. Vyňuchalová K, Jandera P. Comparison of a C30 bonded silica column and columns with shorter bonded ligands in reversedphase LC. Chromatographia. 2015;78:861–71. [Google Scholar]
- 94. Jandera P. Reversed‐phase liquid chromatography of homologous series. A general method for prediction of retention. J Chromatogr A. 1984;314:13–36. [Google Scholar]
- 95. Héron S, Charbonneau D, Albisson P, Estievenart G, Groni S, Tchapla A. A new methodology to determine the isoeluotropic conditions on ultra‐performance flash purification stationary phases from analytical reversed liquid chromatography stationary phase. J Chromatogr A. 2015;1397:59–72. [DOI] [PubMed] [Google Scholar]
- 96. Lunn DB, Yun YJ, Jorgenson JW. Retention and effective diffusion of model metabolites on porous graphitic carbon. J Chromatogr A. 2017;1530:112–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97. Gilar M, McDonald TS, Gritti F, Roman GT, Johnson JS, Bunner B, Michienzi JD, Collamati RA, Murphy JP, Satpute DD, Bannon MP, DellaRovere D, Jencks RA, Dourdeville TA, Fadgen KE, Gerhardt GC. Chromatographic performance of microfluidic liquid chromatography devices: Experimental evaluation of straight versus serpentine packed channels. J Chromatogr A. 2018;1533:127–35. [DOI] [PubMed] [Google Scholar]
- 98. Douša M. 1H‐Tetrazole‐5‐amine Immobilized on Substituted Polymer Gel/Silica as a New Stationary Phase for Hydrophilic Interaction Chromatography. Chromatographia. 2018;81:349–57. [Google Scholar]
- 99. Li S, Li Z, Zhang F, Geng H, Yang B. A polymer‐based zwitterionic stationary phase for hydrophilic interaction chromatography. Talanta. 2020;216 10.1016/j.talanta.2020.120927. [DOI] [PubMed] [Google Scholar]
- 100. Kalíková K, Voborná M, Tesařová E. Chromatographic behavior of new deazapurine ribonucleosides in hydrophilic interaction liquid chromatography. Electrophoresis. 2018;39:2144–51. [DOI] [PubMed] [Google Scholar]
- 101. Peng Y, Hou Y, Zhang F, Shen G, Yang B. A hyperbranched polyethylenimine functionalized stationary phase for hydrophilic interaction liquid chromatography. Anal Bioanal Chem. 2016;408:3633–8. [DOI] [PubMed] [Google Scholar]
- 102. Peng Y, Zhang F, Pan X, Hou Y, Yang B. Poly(vinyl alcohol)‐cationic cellulose copolymer encapsulated SiO2 stationary phase for hydrophilic interaction liquid chromatography. RSC Adv. 2017;7:21336–41. [Google Scholar]
- 103. Li H, Zhang X, Zhang L, Cang H, Kong F, Fan D, Wang W. Hyperbranched polyglycerol functionalized silica stationary phase for hydrophilic interaction liquid chromatography. Anal Sci. 2018;34:433–8. [DOI] [PubMed] [Google Scholar]
- 104. Geng H, Jing J, Zhang F, Zhang F, Yang B. A polar stationary phase obtained by surface‐initiated polymerization of hyperbranched polyglycerol onto silica. Talanta. 2020;209 10.1016/j.talanta.2019.120525. [DOI] [PubMed] [Google Scholar]
- 105. Wang Y, Bu H, Wang L, Wang L, Guo Y, Liang X, Wang S. High efficiency and simple preparation of polyacrylamide coated silica stationary phase for hydrophilic interaction liquid chromatography. J Chromatogr A. 2019;1605 10.1016/j.chroma.2019.07.011. [DOI] [PubMed] [Google Scholar]
- 106. Hou Y, Zhang F, Liang X, Yang B, Liu X, Dasgupta PK. Poly(vinyl alcohol) Modified Porous Graphitic Carbon Stationary Phase for Hydrophilic Interaction Liquid Chromatography. Anal Chem. 2016;88:4676–81. [DOI] [PubMed] [Google Scholar]
- 107. Ding L, Guo Z, Hu Z, Liang X. Mixed‐mode reversed phase/positively charged repulsion chromatography for intact protein separation. J Pharm Biomed Anal. 2017;138:63–9. [DOI] [PubMed] [Google Scholar]
- 108. Wang X, Bo C, Wang C, Wei Y. Controllable preparation of a hydrophilic/ion‐exchange mixed‐mode stationary phase by surface‐initiated atom transfer radical polymerization using a mixture of two functional monomers. J Sep Sci. 2017;40:1861–8. [DOI] [PubMed] [Google Scholar]
- 109. Staňková M, Jandera P. Dual Retention Mechanism in Two‐Dimensional LC Separations of Barbiturates, Sulfonamides, Nucleic Bases and Nucleosides on Polymethacrylate Zwitterionic Monolithic Micro‐Columns. Chromatographia. 2016;79:657–66. [Google Scholar]
- 110. Komendová M, Ribeiro LF, Urban J. Controlling selectivity of polymer‐based monolithic stationary phases. J Sep Sci. 2019;42:952–61. [DOI] [PubMed] [Google Scholar]
- 111. Jandera P, Janás P. Recent advances in stationary phases and understanding of retention in hydrophilic interaction chromatography. A review. Anal Chim Acta. 2017;967:12–32. [DOI] [PubMed] [Google Scholar]
- 112. Vera CM, Shock D, Dennis GR, Samuelsson J, Enmark M, Fornstedt T, Shalliker RA. A preliminary study on the selectivity of linear polynuclear aromatic hydrocarbons in SFC using phenyl‐type stationary phases. Microchem J. 2015;121:136–40. [Google Scholar]
- 113. Vera CM, Shock D, Dennis GR, Samuelsson J, Enmark M, Fornstedt T, Shalliker RA. Contrasting selectivity between HPLC and SFC using phenyl‐type stationary phases: A study on linear polynuclear aromatic hydrocarbons. Microchem J. 2015;119:40–3. [Google Scholar]
- 114. Gritti F, Belanger J, Izzo G, Leveille W. On the performance of conically shaped columns: Theory and practice. J Chromatogr A. 2019;1593:34–46. [DOI] [PubMed] [Google Scholar]
- 115. Jeong LN, Rutan SC. Simulation of elution profiles in liquid chromatography – III. Stationary phase gradients. J Chromatogr A. 2018;1564:128–36. [DOI] [PubMed] [Google Scholar]
- 116. Cain CN, Forzano AV, Rutan SC, Collinson MM. Experimental‐ and simulation‐based investigations of coupling a mobile phase gradient with a continuous stationary phase gradient. J Chromatogr A. 2019;1602:237–45. [DOI] [PubMed] [Google Scholar]
- 117. Tyteca E, De Vos J, Vankova N, Cesla P, Desmet G, Eeltink S. Applicability of linear and nonlinear retention‐time models for reversed‐phase liquid chromatography separations of small molecules, peptides, and intact proteins. J Sep Sci. 2016;39:1249–57. [DOI] [PubMed] [Google Scholar]
- 118. Jandera P, Hájek T, Šromová Z. Mobile phase effects in reversed‐phase and hydrophilic interaction liquid chromatography revisited. J Chromatogr A. 2018;1543:48–57. [DOI] [PubMed] [Google Scholar]
- 119. Jandera P, Kučerová M. Prediction of retention in gradient‐elution normal‐phase high performance liquid chromatography with binary solvent gradients. J Chromatogr A. 1997;759:13–25. [DOI] [PubMed] [Google Scholar]
- 120. Baeza‐Baeza JJ, García‐Alvarez‐Coque MC. Extension of the linear solvent strength retention model including a parameter that describes the elution strength changes in liquid chromatography. J Chromatogr A. 2020;1615 10.1016/j.chroma.2019.460757. [DOI] [PubMed] [Google Scholar]
- 121. Navarro‐Huerta JA, Gisbert‐Alonso A, Torres‐Lapasió JR, García‐Alvarez‐Coque MC. Benefits of solvent concentration pulses in retention time modelling of liquid chromatography. J Chromatogr A. 2019;1597:76–88. [DOI] [PubMed] [Google Scholar]
- 122. Blumberg LM. Migration and elution equations in gradient liquid chromatography. J Chromatogr A. 2019;1599:35–45. [DOI] [PubMed] [Google Scholar]
- 123. De Luca C, Felletti S, Macis M, Cabri W, Lievore G, Chenet T, Pasti L, Morbidelli M, Cavazzini A, Catani M, Ricci A. Modeling the nonlinear behavior of a bioactive peptide in reversed‐phase gradient elution chromatography. J Chromatogr A. 2020;1616 10.1016/j.chroma.2019.460789. [DOI] [PubMed] [Google Scholar]
- 124. Hao W, Wang K, Yue B, Chen Q, Huang Y, Yu J, Li D. Influence of the pre‐elution of solute in initial mobile phase on retention time and peak compression under linear gradient elution. J Chromatogr A. 2020;1618 10.1016/j.chroma.2020.460858. [DOI] [PubMed] [Google Scholar]
- 125. Wu D, Lucy CA. Study of the slope of the linear relationship between retention and mobile phase composition (Snyder‐Soczewiñski model) in normal phase liquid chromatography with bonded and charge‐transfer phases. J Chromatogr A. 2016;1475:31–40. [DOI] [PubMed] [Google Scholar]
- 126. Kartsova LA, Bessonova EA, Somova VD. Hydrophilic Interaction Chromatography. J Anal Chem. 2019;74:415–24. [Google Scholar]
- 127. Guo Y. Recent progress in the fundamental understanding of hydrophilic interaction chromatography (HILIC). Analyst. 2015;140:6452–66. [DOI] [PubMed] [Google Scholar]
- 128. McCalley DV. Understanding and manipulating the separation in hydrophilic interaction liquid chromatography. J Chromatogr A. 2017;1523:49–71. [DOI] [PubMed] [Google Scholar]
- 129. Jandera P, Hájek T. Mobile phase effects on the retention on polar columns with special attention to the dual hydrophilic interaction–reversed‐phase liquid chromatography mechanism, a review. J Sep Sci. 2018;41:145–62. [DOI] [PubMed] [Google Scholar]
- 130. Taraji M, Haddad PR, Amos RIJ, Talebi M, Szucs R, Dolan JW, Pohl CA. Chemometric‐assisted method development in hydrophilic interaction liquid chromatography: A review. Anal Chim Acta. 2018;1000:20–40. [DOI] [PubMed] [Google Scholar]
- 131. Maksić J, Tumpa A, Stajić A, Jovanović M, Rakić T, Jancic‐Stojanovic B. Hydrophilic interaction liquid chromatography in analysis of granisetron HCl and its related substances. Retention mechanisms and method development. J Pharm Biomed Anal. 2016;123:93–103. [DOI] [PubMed] [Google Scholar]
- 132. Douša M, Doubský J. Separation of structurally related primary aliphatic amines using hydrophilic interaction chromatography with fluorescence detection after postcolumn derivatization with o ‐phthaldialdehyde/mercaptoethanol. J Sep Sci. 2017;40:4689–99. [DOI] [PubMed] [Google Scholar]
- 133. Xu X, Gevaert B, Bracke N, Yao H, Wynendaele E, De Spiegeleer B. Hydrophilic interaction liquid chromatography method development and validation for the assay of HEPES zwitterionic buffer. J Pharm Biomed Anal. 2017;135:227–33. [DOI] [PubMed] [Google Scholar]
- 134. Kokotou MG, Thomaidis NS. Characterization of the retention of artificial sweeteners by hydrophilic interaction liquid chromatography. Anal Lett. 2018;51:49–72. [Google Scholar]
- 135. Kasagić‐Vujanović I, Jančić‐Stojanović B, Ivanović D. Investigation of the retention mechanisms of amlodipine besylate, bisoprolol fumarate, and their impurities on three different HILIC columns. J Liq Chromatogr Relat Technol. 2018;41:523–31. [Google Scholar]
- 136. Tircova B, Kozlik P. HILIC‐MS/MS Method for Analysis of Ephedrine in Internet‐available Drugs. Chromatographia. 2017;80:523–8. [Google Scholar]
- 137. Rácz N, Nagy J, Jiang W, Veress T. Modeling Retention Behavior on Analysis of Hallucinogenic Mushrooms Using Hydrophilic Interaction Liquid Chromatography. J Chromatogr Sci. 2019;57:230–7. [DOI] [PubMed] [Google Scholar]
- 138. Wang N, Boswell PG. Accurate prediction of retention in hydrophilic interaction chromatography by back calculation of high pressure liquid chromatography gradient profiles. J Chromatogr A. 2017;1520:75–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139. Jandera P, Hájek T. Utilization of dual retention mechanism on columns with bonded PEG and diol stationary phases for adjusting the separation selectivity of phenolic and flavone natural antioxidants. J Sep Sci. 2009;32:3603–19. [DOI] [PubMed] [Google Scholar]
- 140. Obradović D, Oljačić S, Nikolić K, Agbaba D. Investigation and prediction of retention characteristics of imidazoline and serotonin receptor ligands and their related compounds on mixed‐mode stationary phase. J Chromatogr A. 2019;1585:92–104. [DOI] [PubMed] [Google Scholar]
- 141. Balkatzopoulou P, Fasoula S, Gika H, Nikitas P, Pappa‐Louisi A. Retention prediction of highly polar ionizable solutes under gradient conditions on a mixed‐mode reversed‐phase and weak anion‐exchange stationary phase. J Chromatogr A. 2015;1396:72–6. [DOI] [PubMed] [Google Scholar]
- 142. Navarro‐Huerta JA, Vargas‐García AG, Torres‐Lapasió JR, García‐Alvarez‐Coque MC. Interpretive search of optimal isocratic and gradient separations in micellar liquid chromatography in extended organic solvent domains. J Chromatogr A. 2020;1616 10.1016/j.chroma.2019.460784. [DOI] [PubMed] [Google Scholar]
- 143. Hegade RS, De Beer M, Lynen F. Chiral stationary phase optimized selectivity liquid chromatography: A strategy for the separation of chiral isomers. J Chromatogr A. 2017;1515:109–17. [DOI] [PubMed] [Google Scholar]
- 144. Tyteca E, Desfontaine V, Desmet G, Guillarme D. Possibilities of retention modeling and computer assisted method development in supercritical fluid chromatography. J Chromatogr A. 2015;1381:219–28. [DOI] [PubMed] [Google Scholar]
- 145. De Pauw R, Shoykhet (Choikhet) K, Desmet G, Broeckhoven K. Effect of reference conditions on flow rate, modifier fraction and retention in supercritical fluid chromatography. J Chromatogr A. 2016;1459:129–35. [DOI] [PubMed] [Google Scholar]
- 146. Stankov V, Cvetnić M, Novak Stankov M, Rogošić M, Bolanča T, Ukić Š. Retention Modeling of Gradient Elutions: Application of Iso‐to‐Grad Approach for LC Systems with Dual‐Species Eluent. Chromatographia. 2019;82:749–55. [Google Scholar]
- 147. Tsui HW, Kuo CH, Huang YC. Elucidation of retention behaviors in reversed‐phase liquid chromatography as a function of mobile phase composition. J Chromatogr A. 2019;1595:127–35. [DOI] [PubMed] [Google Scholar]
- 148. Gritti F. Combined solvent‐ and non‐uniform temperature‐programmed gradient liquid chromatography. I – A theoretical investigation. J Chromatogr A. 2016;1473:38–47. [DOI] [PubMed] [Google Scholar]
- 149. Groskreutz SR, Weber SG. Temperature‐assisted solute focusing with sequential trap/release zones in isocratic and gradient capillary liquid chromatography: Simulation and experiment. J Chromatogr A. 2016;1474:95–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150. Andrés A, Téllez A, Rosés M, Bosch E. Chromatographic models to predict the elution of ionizable analytes by organic modifier gradient in reversed phase liquid chromatography. J Chromatogr A. 2012;1247:71–80. [DOI] [PubMed] [Google Scholar]
- 151. Téllez A, Rosés M, Bosch E. Modeling the retention of neutral compounds in gradient elution RP‐HPLC by means of polarity parameter models. Anal Chem. 2009;81:9135–45. [DOI] [PubMed] [Google Scholar]
- 152. Andrés A, Rosés M, Bosch E. Prediction of the chromatographic retention of acid‐base compounds in pH buffered methanol‐water mobile phases in gradient mode by a simplified model. J Chromatogr A. 2015;1385:42–8. [DOI] [PubMed] [Google Scholar]
- 153. Sasaki T, Todoroki K, Toyo'oka T. Simultaneous optimization of pH and binary organic composition by grid form modeling of the retention behavior in reversed‐phase ultra high‐performance liquid chromatography. J Pharm Biomed Anal. 2017;146:251–60. [DOI] [PubMed] [Google Scholar]
- 154. Wang F, Yang F, Tian Y, Liu J, Shen J, Bai Q. Studies on the retention mechanism of solutes in hydrophilic interaction chromatography using stoichiometric displacement theory I. The linear relationship of lgk’ vs. lg[H2O]. Talanta. 2018;176:499–508. [DOI] [PubMed] [Google Scholar]
- 155. Obradović D, Komsta Ł, Agbaba D. Novel computational approaches to retention modeling in dual hydrophilic interactions/reversed phase chromatography. J Chromatogr A. 2020;1619 10.1016/j.chroma.2020.460951. [DOI] [PubMed] [Google Scholar]
- 156. Tyteca E, Desmet G. On the inherent data fitting problems encountered in modelingretention behavior of analytes with dual retention mechanism. J Chromatogr A. 2015;1403:81–95. [DOI] [PubMed] [Google Scholar]
- 157. Tumpa A, Mišković S, Stanimirović Z, Jančić‐Stojanović B, Medenica M. Modeling of HILIC retention behavior with theoretical models and new spline interpolation technique. J Chemom. 2017;31:e2910. [Google Scholar]
- 158. Arnott JA, Planey SL. The influence of lipophilicity in drug discovery and design. Expert Opin Drug Discov. 2012;7:863–75. [DOI] [PubMed] [Google Scholar]
- 159. Chmiel T, Mieszkowska A, Kempińska‐Kupczyk D, Kot‐Wasik A, Namieśnik J, Mazerska Z. The impact of lipophilicity on environmental processes, drug delivery and bioavailability of food components. Microchem J. 2019;146:393–406. [Google Scholar]
- 160. Liang C, Lian H, Recent advances in lipophilicity measurement by reversed‐phase high‐performance liquid chromatography. TrAC ‐ Trends Anal Chem. 2015;68:28–36. [Google Scholar]
- 161. Yamagami C, Yokota M, Takao N. Hydrophobicity Parameters Determined by Reversed‐Phase Liquid Chromatography. IX. Relationship between Capacity Factor and Water‐Octanol Partition Coefficient of Monosubstituted Pyrimidines. Chem Pharm Bull (Tokyo). 1994;42:907–12. [Google Scholar]
- 162. Giaginis C, Tsantili‐Kakoulidou A. Current State of the Art in HPLC Methodology for Lipophilicity Assessment of Basic Drugs. A Review. J Liq Chromatogr Relat Technol. 2007;31:79–96. [Google Scholar]
- 163. Braumann T. Determination of hydrophobic parameters by reversed‐phase liquid chromatography: theory, experimental techniques, and application in studies on quantitative structure‐activity relationships. J Chromatogr A. 1986;373:191–225. [DOI] [PubMed] [Google Scholar]
- 164. Gritti F, Gilar M, Walter TH, Wyndham K. Retention loss of reversed‐phase chromatographic columns using 100% aqueous mobile phases from fundamental insights to best practice. J Chromatogr A. 2020;1612:460662. [DOI] [PubMed] [Google Scholar]
- 165. Liang C, Qiao Jq, Lian Hz. Determination of reversed‐phase high performance liquid chromatography based octanol‐water partition coefficients for neutral and ionizable compounds: Methodology evaluation. J Chromatogr A. 2017;1528:25–34. [DOI] [PubMed] [Google Scholar]
- 166. Sobańska AW. Application of planar chromatographic descriptors to the prediction of physicochemical properties and biological activity of compounds. J Liq Chromatogr Relat Technol. 2018;41:255–71. [Google Scholar]
- 167. Sztanke M, Tuzimski T, Janicka M, Sztanke K. Structure‐retention behaviour of biologically active fused 1,2,4‐triazinones ‐ Correlation with in silico molecular properties. Eur J Pharm Sci. 2015;68:114–26. [DOI] [PubMed] [Google Scholar]
- 168. Hawrył AM, Popiołek ŁP, Hawrył MA, Wieboda RS, Niejedli MA. Chromatographic and calculation methods for analysis of the lipophilicity of newly synthesized thiosemicarbazides and their cyclic analogues 1,2,4‐triazol‐3‐thiones. J Braz Chem Soc. 2015;26:1617–24. [Google Scholar]
- 169. Hawrył A, Kus̈mierz E, Hawrył M, Wieboda R, Wujec M. Determination of lipophilicity of new thiosemicarbazide and 1,2,4‐triazole‐3‐thione derivatives using reversed‐phase HPLC method and theoretical calculations. J Liq Chromatogr Relat Technol. 2015;38:430–7. [Google Scholar]
- 170. Pachuta‐Stec A, Hawrył AM, Wróbel A, Hawrył MA, Pitucha M. Chromatographic Evaluation of the Lipophilic Properties of Some 1,2,4‐Triazole with Potential Antitumour Activity. J Liq Chromatogr Relat Technol. 2015;38:1199–206. [Google Scholar]
- 171. Tosti T, Šegan S, Milić D, Radoičić A, Tešić Ž, Milojković‐Opsenica D. Estimation of Lipophilicity of Some Polyoxygenated Steroids by the Means of Normal‐Phase Thin‐Layer Chromatography. J Liq Chromatogr Relat Technol. 2015;38:1097–103. [Google Scholar]
- 172. Yüksek H, Koca E, Gürsoy‐Kol Ö, Akyildirim O, Çelebier M. Synthesis, in vitro antioxidant activity, and physicochemical properties of novel 4,5‐dihydro‐1H‐1,2,4‐triazol‐5‐one derivatives. J Mol Liq. 2015;206:359–66. [Google Scholar]
- 173. Flieger J, Tatarczak‐Michalewska M, Kowalska A, Rzadkowska M, Szacoń E, Kaczor AA, Matosiuk D. Fragmental method KowWIN as the powerful tool for prediction of chromatographic behavior of novel bioactive urea derivatives. J Braz Chem Soc. 2016;27:2312–21. [Google Scholar]
- 174. Marciniec K, Boryczka S. Chromatographic and Computational Assessment of Lipophilicity of New Anticancer Acetylenequinoline Derivatives. J Chromatogr Sci. 2017;55:934–9. [DOI] [PubMed] [Google Scholar]
- 175. Gonec TT, Malík I, Csöllei J, Jampílek J, Stolaríková J, Solovic I, Miku P, Keltoová S, Kollár P, O'Mahony J, Coffey A. Synthesis and in vitro antimycobacterial activity of novel n‐arylpiperazines containing an ethane‐1,2‐diyl connecting chain. Molecules. 2017;22 10.3390/molecules22122100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176. Milosevic NP, Kojic V, Curcic J, Jakimov D, Milic N, Banjac N, Uscumlic G, Kaliszan R. Evaluation of in silico pharmacokinetic properties and in vitro cytotoxic activity of selected newly synthesized N‐succinimide derivatives. J Pharm Biomed Anal. 2017;137:252–7. [DOI] [PubMed] [Google Scholar]
- 177. Klose MHM, Theiner S, Varbanov HP, Hoefer D, Pichler V, Galanski M, Meier‐Menches SM, Keppler BK. Development and validation of liquid chromatography‐based methods to assess the lipophilicity of cytotoxic platinum(IV) complexes. Inorganics. 2018;6 10.3390/inorganics6040130. [DOI] [Google Scholar]
- 178. Malík I, Csollei J, Solovič I, Pospísilová S, Michnová H, Jampílek J, Čízek A, Kapustíková I, Čurillová J, Pecháčová M, Stolaříková J, Pecher D, Oravec M. Dibasic derivatives of phenylcarbamic acid against mycobacterial strains: Old drugs and new tricks? Molecules. 2018;23 10.3390/molecules23102493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179. Bem M, Radutiu AC, Voicescu M, Caproiu MT, Draghici C, Maganu M, Enache C, Constantinescu T, Balaban AT. 7‐nitrobenzo[c] [1, 2, 5]oxadiazole (nitrobenzofurazan) derivatives with a sulfide group at the 4‐position. synthesis and physical properties. Rev Roum Chim. 2018;63:149–55. [Google Scholar]
- 180. Gomes JC, Cianni L, Ribeiro J, dos Reis Rocho F, da Costa Martins Silva S, Batista PHJ, Moraes CB, Franco CH, Freitas‐Junior LHG, Kenny PW, Leitão A, Burtoloso ACB, de Vita D, Montanari CA. Synthesis and structure‐activity relationship of nitrile‐based cruzain inhibitors incorporating a trifluoroethylamine‐based P2 amide replacement. Bioorganic Med Chem. 2019;27 10.1016/j.bmc.2019.115083. [DOI] [PubMed] [Google Scholar]
- 181. Jandera P, Staňková M, Hájek T. New zwitterionic polymethacrylate monolithic columns for one‐ and two‐dimensional microliquid chromatography. J Sep Sci. 2013;36:2430–40. [DOI] [PubMed] [Google Scholar]


