Abstract
Objectives
To evaluate short-term test-retest repeatability of a deep learning architecture (U-Net) in slice- and lesion-level detection and segmentation of clinically significant prostate cancer (csPCa: Gleason grade group > 1) using diffusion-weighted imaging fitted with monoexponential function, ADCm.
Methods
One hundred twelve patients with prostate cancer (PCa) underwent 2 prostate MRI examinations on the same day. PCa areas were annotated using whole mount prostatectomy sections. Two U-Net-based convolutional neural networks were trained on three different ADCm b value settings for (a) slice- and (b) lesion-level detection and (c) segmentation of csPCa. Short-term test-retest repeatability was estimated using intra-class correlation coefficient (ICC(3,1)), proportionate agreement, and dice similarity coefficient (DSC). A 3-fold cross-validation was performed on training set (N = 78 patients) and evaluated for performance and repeatability on testing data (N = 34 patients).
Results
For the three ADCm b value settings, repeatability of mean ADCm of csPCa lesions was ICC(3,1) = 0.86–0.98. Two CNNs with U-Net-based architecture demonstrated ICC(3,1) in the range of 0.80–0.83, agreement of 66–72%, and DSC of 0.68–0.72 for slice- and lesion-level detection and segmentation of csPCa. Bland-Altman plots suggest that there is no systematic bias in agreement between inter-scan ground truth segmentation repeatability and segmentation repeatability of the networks.
Conclusions
For the three ADCm b value settings, two CNNs with U-Net-based architecture were repeatable for the problem of detection of csPCa at the slice-level. The network repeatability in segmenting csPCa lesions is affected by inter-scan variability and ground truth segmentation repeatability and may thus improve with better inter-scan reproducibility.
Keywords: Test-retest reliability, Neural network models, Prostate cancer, Diffusion MRI
Introduction
In recent years, deep learning (DL)-based convolutional neural networks (CNNs) have gained tremendous attention in medical imaging especially using MRI for various applications such as organ segmentation [1, 2], cancer detection and diagnosis [3–5], and characterization [6, 7]. However, MRI images might be influenced by different sources of noise variations such as scanner acquisition noise [8] and motion artifacts [9]. These variations not only affect the visual quality of an image but may also interfere with downstream analysis of MRI images [10].
Prostate Imaging-Reporting and Data System (PI-RADS) has standardized the diagnosis of PCa using MRI and has shown to be effective in characterizing PCa [11]. However, it has been found that PI-RADS-based scoring has only moderate to good inter- and intra-reader variability [12, 13]. Recently, much attention has been drawn to machine learning (ML) models built using radiomics-derived representations on MRI for PCa detection and characterization [14, 15]. However, the sources of variation in MRI acquisition and reconstruction [16–19] have shown to influence these representations [10]. Therefore, lately, there has been an increasing interest in applying test-retest analysis to rank order radiomics features based on their repeatability and discriminability, and build ML classifiers based on most stable features [20, 21]. In contrast, although several DL approaches have been presented for PCa segmentation [22, 23], detection [24, 25], and characterization [26, 27], to the best of our knowledge, none of them has been explicitly evaluated in the context of test-retest repeatability.
A unique test-retest data of monoexponential fitted prostate apparent diffusion coefficient (ADCm) maps was used in this study. Two MRI scans were taken approximately 15 min apart for each patient. We used only ADCm maps and not bi-parametric MRI (T2W MRI and ADCm) since T2W MRI were not available for two time points. The evaluation of repeatability of DL models trained on ADCm maps taken at such short time span allows us to evaluate stability of DL models against variations with respect to acquisition of images. Additionally, it is also safe to assume that changes in tissue biology are negligible over such a short time span.
Due to increasing popularity of the deep learning architecture, U-Net [26, 28–30] in segmentation, detection, and classification tasks, we use U-Net-based architecture in our study. U-Net [31] is a fully convolutional network designed for semantic segmentation tasks with two components, an encoder and a decoder. The U-Net decoder combines both local information and the contextual information which is required to predict a good segmentation map. Additionally, since there is no dense layer involved in the architecture, images of different sizes can be given as input.
Therefore, in this study, we evaluate test-retest repeatability of convolutional neural networks using a U-Net-based architecture on three different ADCm b value settings for (a) slice-and (b) lesion-level detection and (c) segmentation of clinically significant prostate cancer (csPCa: Gleason grade group (GGG) > 1). A 3-fold cross-validation was performed on training set (N = 78 patients) and evaluated for performance and repeatability on testing data (N = 34 patients).
Materials and methods
MR imaging and data
This retrospective study was compliant with Health Insurance Portability and Accountability Act (HIPAA) and approved by institutional review board. All patients, N = 115, with diagnosed PCa signed informed consent and underwent prostate MRI before robotic-assisted laparoscopic prostatectomy between March 2013 and February 2016 [17, 32]. All patients underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart following repositioning on MR scanner table [19, 32]. The scans were performed using a 3T MR scanner (3 Tesla Philips Ingenuity PET/MR). DWI was performed using a single-shot spin echo–based sequence with monopolar diffusion gradient and an echo-planar read out. Summary acquisition parameters are provided in Table E1 (supplementary), while detailed acquisition protocol was described previously [17]. We evaluated ADCm maps at the voxel level with DWI data for three different b value settings: (a) four b values in the range of 0–900 s/mm2, B4b900 (0, 300, 500, 900 s/mm2) [33], (b) four b value distribution which was previously suggested as being a potentially optimal distribution, B4b2000 (0, 900, 1100, 2000 s/mm2) [16], and (c) two b values in the range of 0–1300 s/mm2, B2b1300 (0 and 1300 s/mm2). The third option was considered to evaluate a setting with minimal number of b values for signal-to-noise-ratio and contrast trade-off in the context of CNN-based classifications [16]. Three patients were excluded due to the presence of severe motion (n = 1) and/or susceptibility artifacts (n = 2). Figure E1 (supplementary) shows the flow chart of inclusion/exclusion criteria of the patients and splitting of the data into training and test sets. The data splits were the same as reported by Merisaari et al [32].
Prostate capsule and lesion segmentation
A radiologist with 9 years of prostate MRI experience in consensus with a board-certified staff urogenital pathologist (10 years of experience in urogenital pathology) delineated the prostate capsule and cancerous regions on DWI with whole mounts prostatectomy sections as ground truth using the Carimas (version 2.9) software. Demographic information (age, PSA), lesion distribution in different zones (peripheral zone, central/transitional zone), GGG categories (1–5), and the distribution of csPCa and non-csPCa (GGG = 1, benign) patches is shown in Table 1.
Table 1.
Demographic and lesion characteristics of N = 112 patients. All patients underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart following repositioning on MR scanner table
| n = patients | 112 | |||
| Age, medium (IQR), years | 64.5 (60–68) | |||
| PSA, medium (IQR), ng/ml | 9.3 (6.6–12.25) | |||
| n = lesions | 170 | |||
| Lesion zones, n (%) | ||||
| Peripheral zone (PZ) | 124 (72.94%) | |||
| Transitional zone (TZ)/central zone (cz) | 46 (27.06%) | |||
| Gleason grade group, n (%) | ||||
| 1 (Gleason score 3 + 3) | 28 (16.47%) | |||
| 2(Gleason score 3 + 4) | 77 (45.29%) | |||
| 3 (Gleason score 4 + 3) | 31 (18.23%) | |||
| 4 (Gleason score 4 + 4.3 + 5.5 + 3 | 17 (10%) | |||
| 5 (Gleason score 4 + 5.5 + 4) | 17 (10%) | |||
| n = 2D axial images, n (%) | SA = 1261 | SB = 1253 | ||
| Atrain = 875 (69.4%) | Atest = 386 (30.6%) | Btrain = 870 (69.4) | Btest = 383 (30.6%) | |
| non-csPCa(GGG = 1, benign) | 594 (47.1%) | 265 (21.0%) | 583 (46.5%) | 262 (20.9%) |
| csPCa (GGG ≤ 1) | 281(22.3%) | 121 (9.6%) | 287 (22.9%) | 121 (9.7%) |
Axial images refer to each 2D axial slice of the whole prostate volume. Each image is considered as positive if a clinically significant prostate cancer (csPCa) lesion exists on the image or is considered as negative
IQR inter-quantile range
U-Net architecture
U-Net [31] is a fully convolutional network designed for semantic segmentation tasks with two components, a descending encoder path and an ascending decoding path. The modified U-Net consists of 5 encoder blocks and 5 decoder blocks. Each of the encoder blocks and decoder blocks consists of two convolutional layers except for the last decoder block with only one convolutional layer accounting for a total of 19 convolutional layers. The decoder and the encoder paths consist of batch normalization layers and drop-out layers in between the convolutional layers, with max pooling in the decoder blocks and up-sampling in the encoder blocks. The model consists of a total of 7,852,002 trainable parameters. Figure E2(b) shows the architectural diagram of U-Net.
U-Net training
The details of data preprocessing and data augmentation are described in the supplementary section (S1). We define the problem of slice-wise detection of clinically significant prostate cancer (csPCa) regions as a classification task. Each slice with prostate voxel was defined either as containing csPCa or non-csPCa (Gleason grade grouping (GGG) = 1/benign). We defined the ground truth labels by considering each extracted patch from ADCm, with the presence of csPCa lesion (GGG > 1) as a positive exemplar, all others were deemed as negative. We used a modified network architecture (U-Netm) for the classification task. The network architecture for U-Netm is shown in Fig. E2(a).
For csPCa lesion detection and segmentation, the manually annotated lesion delineations done with whole mount prostatectomy sections as reference were used as ground truth. A transfer learning strategy was used to initialize the encoder weights of the U-Net by transference of weights from the model U-Netm trained for detection of csPCa at the slice-level. The network architecture of U-Net is shown in Fig. E2(b). We used the segmentation maps outputted by the networks to evaluate lesion detection. We defined a lesion as being detected if ≥ 0.2 DSC overlap existed between the network segmentation map and the ground truth delineation of that corresponding lesion. Figure 1 depicts the training of U-Netm, U-Net. Other related implementation details are provided in the supplementary section (S2). For the source code for the network training and evaluation of repeatability, see https://github.com/amogh3892/Test-retest-repeatability-of-U-Net-in-detecting-segmenting-clinically-significant-prostate-cancer.
Fig. 1.
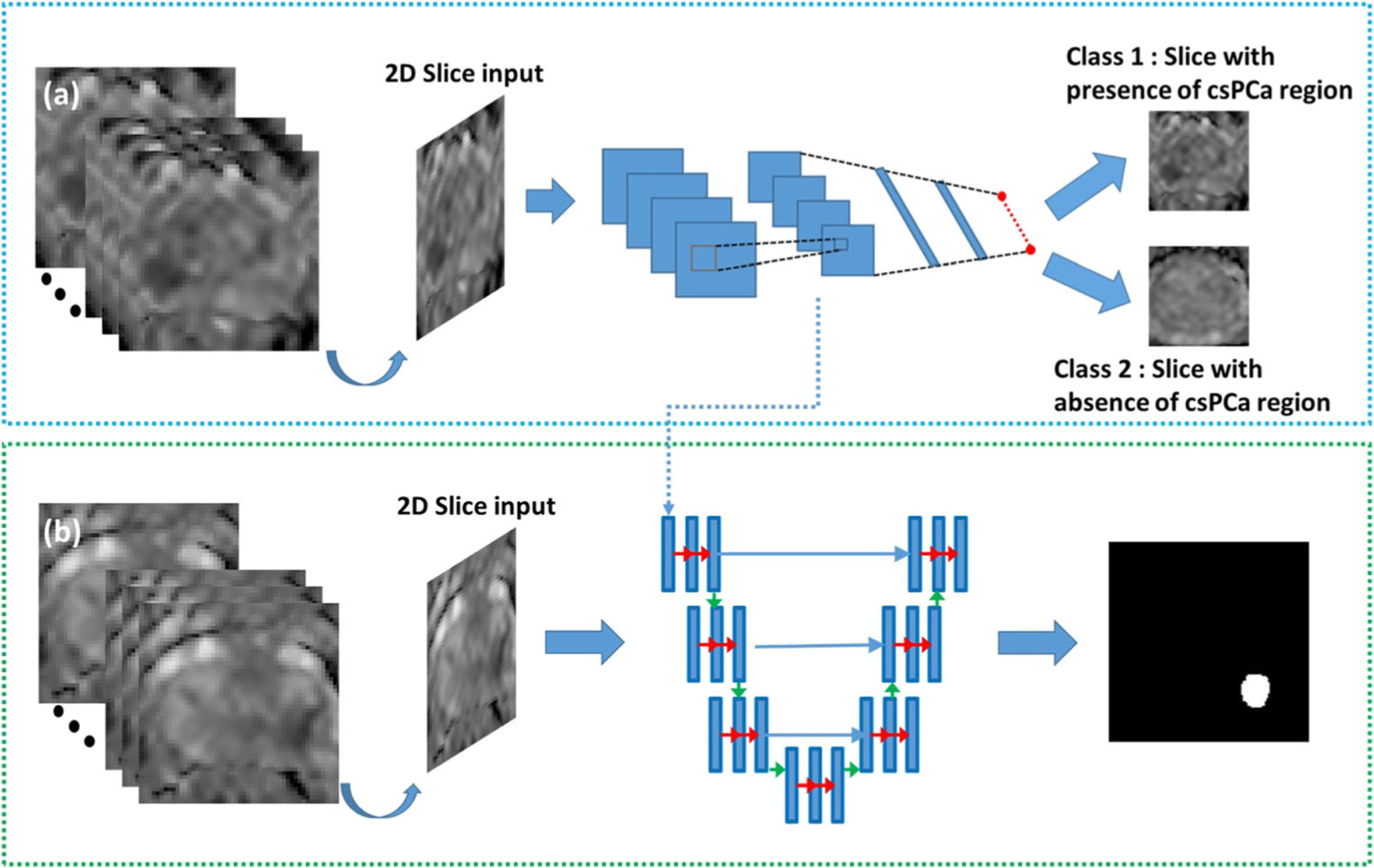
a Training process of a modified U-Net (U-Netm) for detecting 2D patches with presence of clinically significant prostate cancer (csPCa). The input to the network is a 2D patch extracted and cropped to the prostate boundary using the manual segmentation drawn over the prostate capsule. ADCm patches with the presence of csPCa lesion (GGG > 1) were considered as positive samples and others were marked negative. b Training process of U-Net for segmentation of csPCa regions. csPCa regions delineated by an experience radiologist was used as ground truth for lesion segmentation
Evaluation metrics and statistical analysis
Area under the receiver operator characteristic curve (AUCs), sensitivity and positive predictive value (PPV), and dice similarity coefficient (DSC) were used to evaluate the performance of slice- and lesion-level detection and segmentation of csPCa on ADCm respectively. Similarly, intra-class correlation coefficient (ICC(3,1)), proportionate agreement, and DSC were used to evaluate repeatability of the networks for slice- and lesion-level detection and segmentation of csPCa on ADCm respectively. Ninety-five percent confidence intervals were calculated wherever necessary and cross-validation results were reported as mean ± standard deviation. Further details and definitions of the performance metrics are presented in the supplementary section (S3).
Experiment 1: Repeatability of U-Netm in slice-level detection of clinically significant prostate cancer on prostate apparent diffusion coefficient maps
For all three b value settings (B4b900, B4b2000, and B2b1300), U-Netm was trained for slice-level detection of csPCa regions with 3-fold cross-validation setting on the training sets Atrain (networks CA1, CA2, and CA3 trained on the three folds of Atrain) and Btrain (networks CB1, CB2, and CB3 trained on the three folds of Btrain), and was evaluated for performance in terms of AUC. The ensemble of classifiers from 3-fold cross-validation CA (average predictions from CA1, CA2, and CA3) and CB (average predictions from CB1, CB2, and CB3) was used to evaluate the (a) performance in terms of AUCs and (b) repeatability of the network predictions in terms of ICCs on the test set Stest (Atest + Btest). Additionally, other performance metrics such as accuracy, sensitivity, and specificity were reported by calculating the optimal cutoff through Youden index [34]. We combined the test sets Atest and Btest since SA and SB were not co-registered with respect to each other and registration of the scans would lead to additional registration artifacts. Figure 2 shows the overall experimental design for evaluating the repeatability of the network outputs.
Fig. 2.
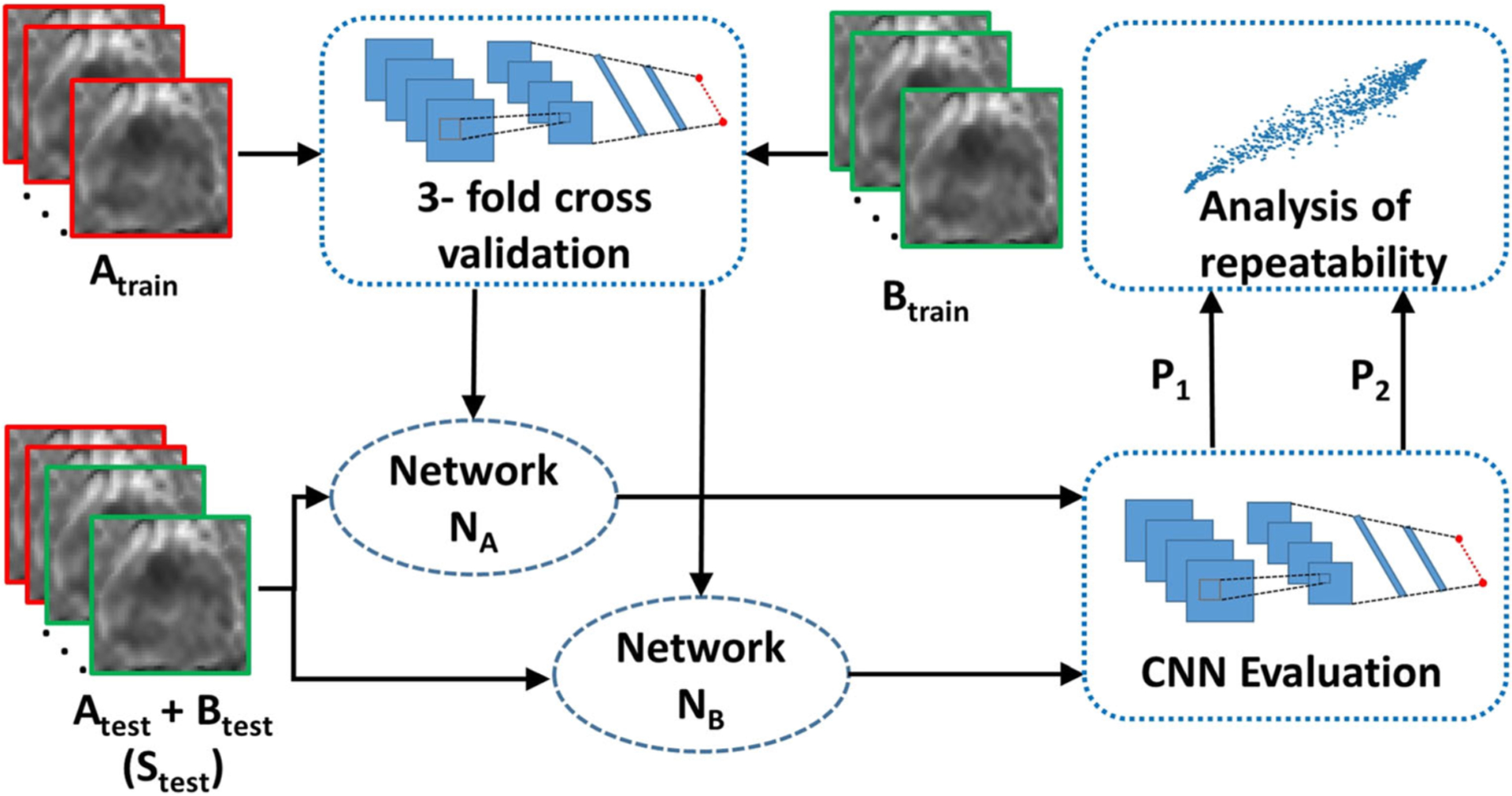
Experimental design for evaluating repeatability of CNNs for (a) slice-level classification of clinically significant prostate cancer (csPCa: Gleason grade group (GGG) > 1) and non-csPCa regions and (b) lesion-level detection and segmentation of csPCa regions. N = 112 patients scheduled for prostatectomy underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart. The scans, SA and SB, were divided into training set (Atrain and Btrain), N = 78, and test set (Atest and Btest) N = 34. Two different instances NA and NB were trained on scans Atrain and Btrain, respectively, and evaluated on a combined test set, Stest (Atest + Btest). The outputs P1 and P2 by NA and NB, respectively, on Stest are used to calculate repeatability of the CNNs
Experiment 2: Repeatability of U-Net in segmentation and detection of clinically significant prostate cancer lesions on prostate apparent diffusion coefficient maps
For all three b value settings (B4b900, B4b2000, and B2b1300), U-Net was trained with a 3-fold cross-validation setting on the training set, Atrain (networks DA1, DA2, and DA3 trained on the three folds of Atrain) and Btrain (networks DB1, DB2, and DB3 trained on the three folds of Btrain) for segmenting csPCa lesions on ADCm maps. The ensemble of segmentation networks from 3-fold cross-validation DA and DB (DA: Logical “OR” of segmentations from DA1, DA2, DA3; and DB: Logical “OR” of segmentations from DB1, DB2, and DB3) was used to obtain final segmentation maps on the test set, Stest. We post-process the output segmentations in order to remove some false positives. The details of post-processing of the lesion segmentations are provided in the supplementary (S4).
We use the output segmentation maps to assess csPCa lesion detection performance by evaluating the sensitivity and positive predictive value of the networks DA and DB. The repeatability of csPCa lesion detection was assessed by evaluating the proportionate agreement between the networks DA and DB.
We further evaluate (a) segmentation performance and (b) repeatability of segmentations in terms of DSC for the detected lesions on Stest. We also assess the repeatability of network segmented volumes and mean ADCm value in the lesion with respect to ICC and compare them with ground truth delineations.
Agreement of inter-scan ground truth segmentation repeatability and U-Net’s segmentation repeatability in segmenting csPCa lesions
We co-registered the scans Atest and Btest and chose only the csPCa lesions that are detected on both Atest and Btest for the analysis. The details of registration are provided in the supplementary section (S5). The agreement between repeatability of ground truth delineations and repeatability of segmentation maps obtained by DA and DB was illustrated using Bland-Altman plots. No systematic bias as a function of the evaluated signal was found to be present in the Bland-Altman plots.
Results
Experiment 1: Repeatability of U-Netm in slice-level detection of clinically significant prostate cancer on prostate apparent diffusion coefficient maps
Table 2 shows the performance metrics of slice-level detection of csPCa on cross-validation and testing cohorts for networks trained on Atrain and Btrain for three different b value settings (B4b900, B4b2000, and B2b1300). For all the b value settings, we can observe that the networks yielded an AUC of 0.81–0.85 for the cross-validation on Atrain and Btrain. The ensemble of classifiers from 3-fold cross-validation, CA and CB, resulted in an AUC of 0.78–0.85 in Stest. A DeLong test [35] between the cross-validation AUCs and AUCs on Stest did not show significant difference between the results obtained (p > 0.11). Figure 3 shows the receiver operator characteristic (ROC) curves of the networks for slice-level detection of csPCa on prostate ADCm maps on B4b900 for cross-validation on Atrain and Btrain and evaluation on Stest.
Table 2.
Cross-validation and hold-out test set performance metrics (AUC, accuracy, sensitivity, specificity) of networks CA (trained on Atrain) and CB (trained on Btrain) in detecting clinically significant prostate cancer slices, evaluated on three different b value settings (a) B4b900 (0, 300, 500, 900 s/mm2), (b) B4b2000 (0, 900, 1100, 2000 s/mm2), and (c) B2b1300 (0 and 1300 s/mm2). N = 112 patients scheduled for prostatectomy underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart. The scans, SA and SB, were divided into training set (Atrain and Btrain), N = 78, and test set (Atest and Btest) N = 34
| b value setting | Cross-validation | AUC (95% CI) | Accuracy | Sensitivity | Specificity | p value (AUC) |
| B4b900 | CA | 0.81 (0.79–0.83) | 74% | 86% | 69% | p = 0.64 |
| CA | 0.82 (0.79–0.84) | 76% | 70% | 79% | ||
| B4b2000 | CA | 0.82 (0.79–0.84) | 78% | 69% | 82% | p = 0.18 |
| CB | 0.80 (0.78–0.83) | 71% | 77% | 69% | ||
| B2b1300 | CA | 0.85 (0.83–0.87) | 78% | 79% | 77% | p = 0.39 |
| CB | 0.84 (0.80–0.86) | 76% | 76% | 76% | ||
| b value setting | Hold-out test set (Stest) | AUC (95% CI) | Accuracy | Sensitivity | Specificity | p value (AUC) |
| B4b900 | CA | 0.78 (0.75–0.81) | 70% | 88% | 69% | p = 0.58 |
| CB | 0.79 (0.76–0.82) | 76% | 75% | 76% | ||
| B4b2000 | CA | 0.80 (0.77–0.84) | 76% | 81% | 74% | p = 0.11 |
| CB | 0.78 (0.75–0.82) | 74% | 74% | 73% | ||
| B2b1300 | CA | 0.84 (0.81–0.87) | 79% | 72% | 82% | p = 0.58 |
| CB | 0.85 (0.83–0.88) | 80% | 77% | 81% |
Fig. 3.
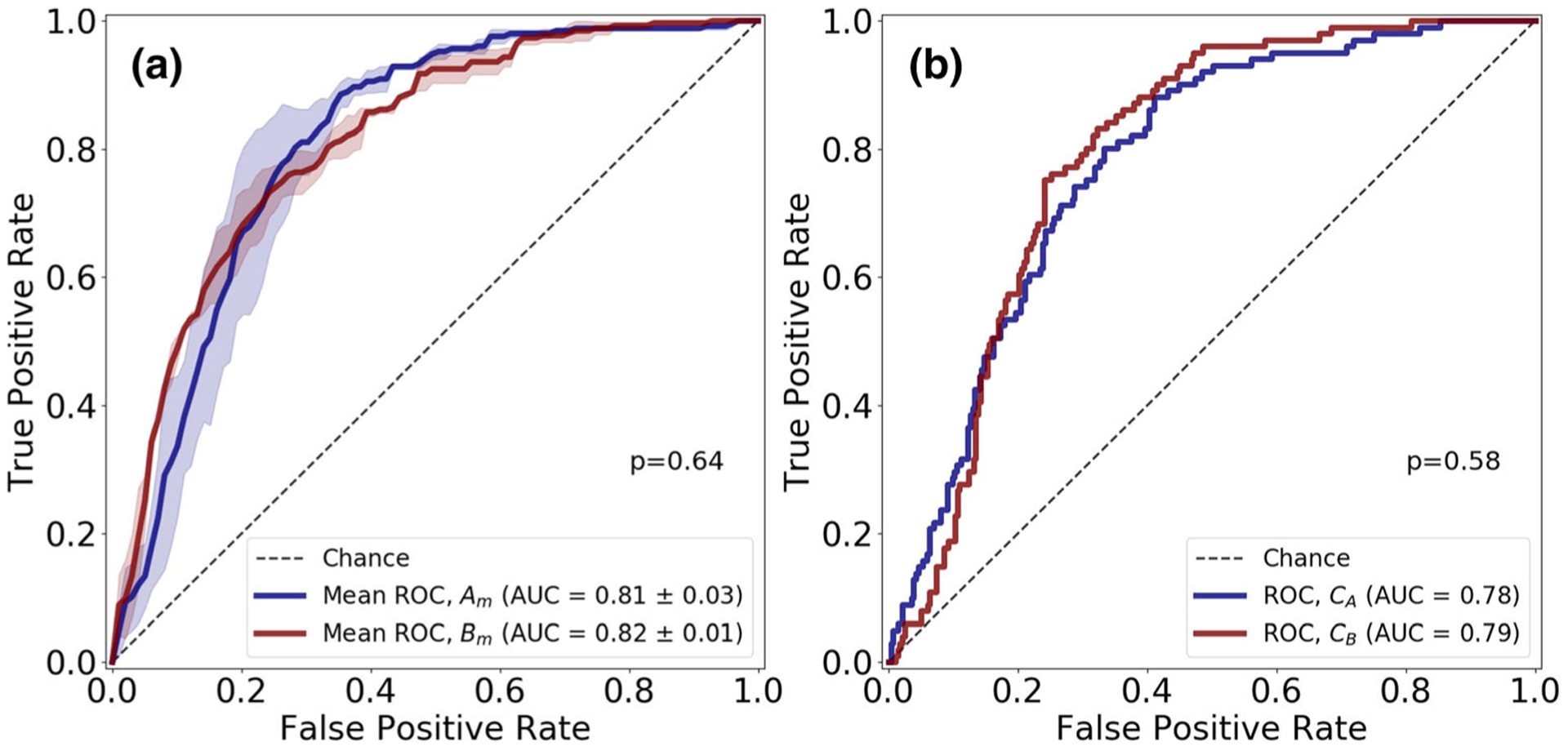
Receiver operating characteristic (ROC) curves for U-Netm in slice-level detection of clinically significant prostate cancer regions on apparent diffusion coefficient ADCm (B4b900: b values (0, 300, 500, 900 s/mm2) maps. The test-retest dataset (SA and SB) of 112 patients were divided into training set (Atrain and Btrain) and test set (Atest and Btest). a 3-fold cross-validation was performed on the training sets Atrain (CA1, CA2, CA3 trained on the three folds of Atrain) and Btrain (CB1, CB2, CB3 trained on the three folds Btrain). a Mean ROC curves, Am and Bm, for 3-fold cross-validation on Atrain and Btrain respectively. b ROC curves for ensemble classifiers CA (average probabilities of CA1, CA2, CA3) and CB (average probabilities of CB1, CB2, CB3) on hold-out test set, Stest (Atest + Btest)
The probability scores of the ensemble classifiers CA and CB are used to evaluate repeatability on Stest. The U-Netm yielded an ICC of 0.83, 95% CI (0.80–0.85); 0.80, 95% CI (0.77–0.83); and 0.83, 95% CI (0.80–0.85) on B4b900, B4b2000, and B2b1300, respectively, in detecting clinically significant prostate cancer regions on ADC maps.
Experiment 2: Repeatability of U-Net in segmentation and detection of clinically significant prostate cancer lesions on prostate apparent diffusion coefficient maps
Table 3 depicts the csPCa lesion detection performance on the cross-validation set and Stest for different b value settings (B4b900, B4b2000, and B2b1300). The networks resulted in a sensitivity of 55–60% and a PPV of 51–53% on the cross-validation set. The networks DA and DB had proportionate agreement of 66–72% in detecting csPCa lesions on Stest and the corresponding sensitivity and PPV was in the range 63–66% and 45–57% respectively.
Table 3.
Cross-validation and hold-out test set performance metrics (true positives, false negatives, false positives, sensitivity, and positive predictive value) of networks DA (trained on Atrain) and DB (trained on Btrain) in detecting clinically significant prostate cancer lesions evaluated on three different b value settings (a) B4b900 (0, 300, 500, 900 s/mm2), (b) B4b2000 (0, 900, 1100, 2000 s/mm2), and (c) B2b1300 (0 and 1300 s/mm2). N = 112 patients scheduled for prostatectomy underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart. The scans, SA and SB, were divided into training set (Atrain and Btrain), N = 78, and test set (Atest and Btest) N = 34
| b value setting | Cross-validation | True positives | False negatives | False positives | Sensitivity | Positive predictive value |
| B4b900 | DA | 64 | 41 | 61 | 61% | 51% |
| DB | 68 | 37 | 63 | 65% | 52% | |
| B4b2000 | DA | 66 | 39 | 60 | 63% | 52% |
| DB | 67 | 38 | 58 | 64% | 54% | |
| B2b1300 | DA | 63 | 42 | 57 | 60% | 53% |
| DB | 58 | 47 | 56 | 55% | 51% | |
| b value setting | Hold-out test set (Stest) | True positives | False negatives | False positives | Sensitivity | Positive predictive value |
| B4b900 | DA | 52 | 27 | 52 | 66% | 50% |
| DB | 51 | 28 | 62 | 65% | 45% | |
| B4b2000 | DA | 50 | 29 | 46 | 63% | 47% |
| DB | 52 | 27 | 56 | 66% | 48% | |
| B2b1300 | DA | 51 | 28 | 39 | 65% | 53% |
| DB | 51 | 28 | 45 | 65% | 53% | |
| b value setting | Repeatability (proportionate agreement) | Agreement (%) | Disagreement (%) | |||
| B4b900 | DA and DB | 90 (66%) | 46 (34%) | |||
| B4b2000 | DA and DB | 83 (72%) | 32 (28%) | |||
| B2b1300 | DA and DB | 79 (69%) | 35 (31%) | |||
Table 4 illustrates the csPCa lesion segmentation performance of the networks on detected csPCa lesions for B4b900, B4b2000, and B2b1300. The networks DA and DB resulted in DSC of 0.47–0.54 on the cross-validation set and 0.58–0.64 on Stest respectively. The DSC between the network segmentations (repeatability) was in the range 0.68–0.72.
Table 4.
Cross-validation and hold-out test set performance of by networks DA (trained on Atrain) and DB (trained on Btrain) in segmenting detected clinically significant prostate cancer lesions evaluated on three different b value settings (a) B4b900 (0, 300, 500, 900 s/mm2), (b) B4b2000 (0, 900, 1100, 2000 s/mm2), and (c) B2b1300 (0 and 1300 s/mm2). N = 112 patients scheduled for prostatectomy underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart. The scans, SA and SB, were divided into training set (Atrain and Btrain), N = 78, and test set (Atest and Btest) N = 34
| Dice similarity coefficient (DSC) | B4b900 | B4b2000 | B2b1300 | |||
|---|---|---|---|---|---|---|
| DA | DB | DA | DB | DA | DB | |
| Cross-validation | 0.47 ± 0.20 | 0.48 ± 0.19 | 0.50 ± 0.21 | 0.54 ± 0.19 | 0.49 ± 0.22 | 0.49 ± 0.20 |
| Hold-out test set (Stest) | 0.61 ± 0.11 | 0.60 ± 0.12 | 0.60 ± 0.18 | 0.64 ± 0.16 | 0.58 ± 0.22 | 0.60 ± 0.22 |
| Repeatability (DSC) DA and DB | 0.68 ± 0.21 | 0.72 ± 0.22 | 0.70 ± 0.20 | |||
Figure 4 shows the overlaid segmentation maps on the ADCm (B4b900) images with DSC reported in 3D. We can observe that, although some of the lesions are poorly segmented by the networks, the repeatability in terms of DSC between the networks is high.
Fig. 4.
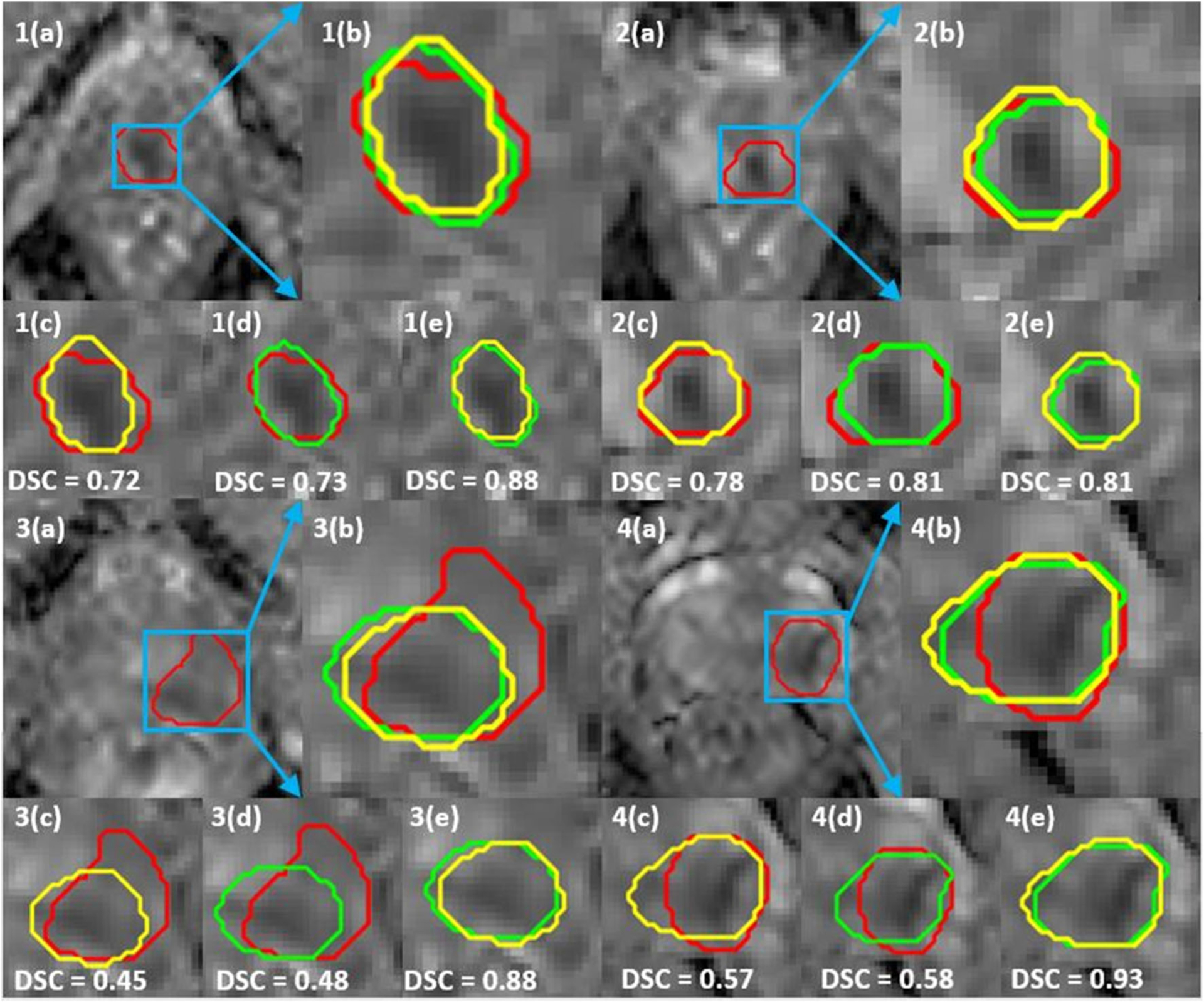
Clinically significant prostate cancer (csPCa) lesion segmentation maps on ADCm (B4b900: b values (0, 300, 500, 900 s/mm2) of networks DA (trained on Atrain) and DB (trained on Btrain). a Full field of view of monoexponential fitted prostate apparent diffusion coefficient (ADCm) maps. b Overlaid ground truth delineation (GT) and segmentation maps of DA and DB. c Dice similarity coefficient (DSC) between GT and DA. d DSC between GT and DB. e DSC between DA and DB. csPCa lesions (1,2) have high DSC overlap both between the ground truth and between the networks. csPCa lesions (3,4) have high DSC overlap between the networks even though they poorly segment the lesions. All DSC reported are evaluated in 3D
Table 5 shows the repeatability of volume measurement and mean ADCm values of ground truth delineations and U-Net-based segmentations on Stest for different b value settings (B4b900, B4b2000, and B2b1300). U-Net obtained an ICC score of 0.89–0.92 and 0.84–0.87 for volume and mean ADCm value, respectively, while compared with ground truth delineations with an ICC score of 0.92 for volume and 0.86–0.98 for mean ADCm.
Table 5.
Repeatability of volume, mean apparent diffusion coefficient (ADC) value of clinically significant prostate cancer (csPCa) lesion in terms of intra-class correlation coefficient (ICC(3,1)) for ground truth delineations, and segmentation maps obtained by U-Net in the hold-out test set (Stest) for ADCm of three different b value settings (a) B4b900 (0, 300, 500, 900 s/mm2), (b) B4b2000 (0, 900, 1100, 2000 s/mm2), and (c) B2b1300 (0 and 1300 s/mm2). N = 112 patients scheduled for prostatectomy underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart. The scans, SA and SB, were divided into training set (Atrain and Btrain), N = 78, and test set (Atest and Btest) N = 34
| Repeatability ICC (95% confidence interval) | B4b900 | B4b2000 | B2b1300 | |||
|---|---|---|---|---|---|---|
| Volume | Mean ADC value | Volume | Mean ADC value | Volume | Mean ADC value | |
| Ground truth delineations | 0.92 (0.86–0.96) | 0.86 (0.77–92) | 0.92 (0.86–0.96) | 0.89 (0.81–0.93) | 0.92 (0.86–0.96) | 0.98 (0.97–0.99) |
| U-Net segmentations (DA and DB) | 0.89 (0.79–0.94) | 0.87 (0.69–0.95) | 0.92 (0.84–0.96) | 0.87 (0.71–0.95) | 0.89 (0.79–0.94) | 0.84 (0.63–0.93) |
Agreement of inter-scan ground truth segmentation repeatability and U-Net’s segmentation repeatability in segmenting csPCa lesions
Figures 5 a and b show the agreement of repeatability of ground truth delineations and network segmentations using a Bland-Altman plot on B4b900. The mean of repeatability between ground truth delineations and network segmentations in terms of DSC are plotted against the difference between ground truth delineations and network segmentation DSC. The plots suggest that the ground truth delineations are in moderate agreement with network-based segmentations in most of the cases, with a few outliers. We can also observe that repeatability of ground truth delineations is slightly better than network-based segmentation repeatability. The Bland-Altman plots for B4b2000 and B2b1300 expressed similar agreement between the ground truth and the network results; these are illustrated in the supplementary figure (Fig. E3).
Fig. 5.
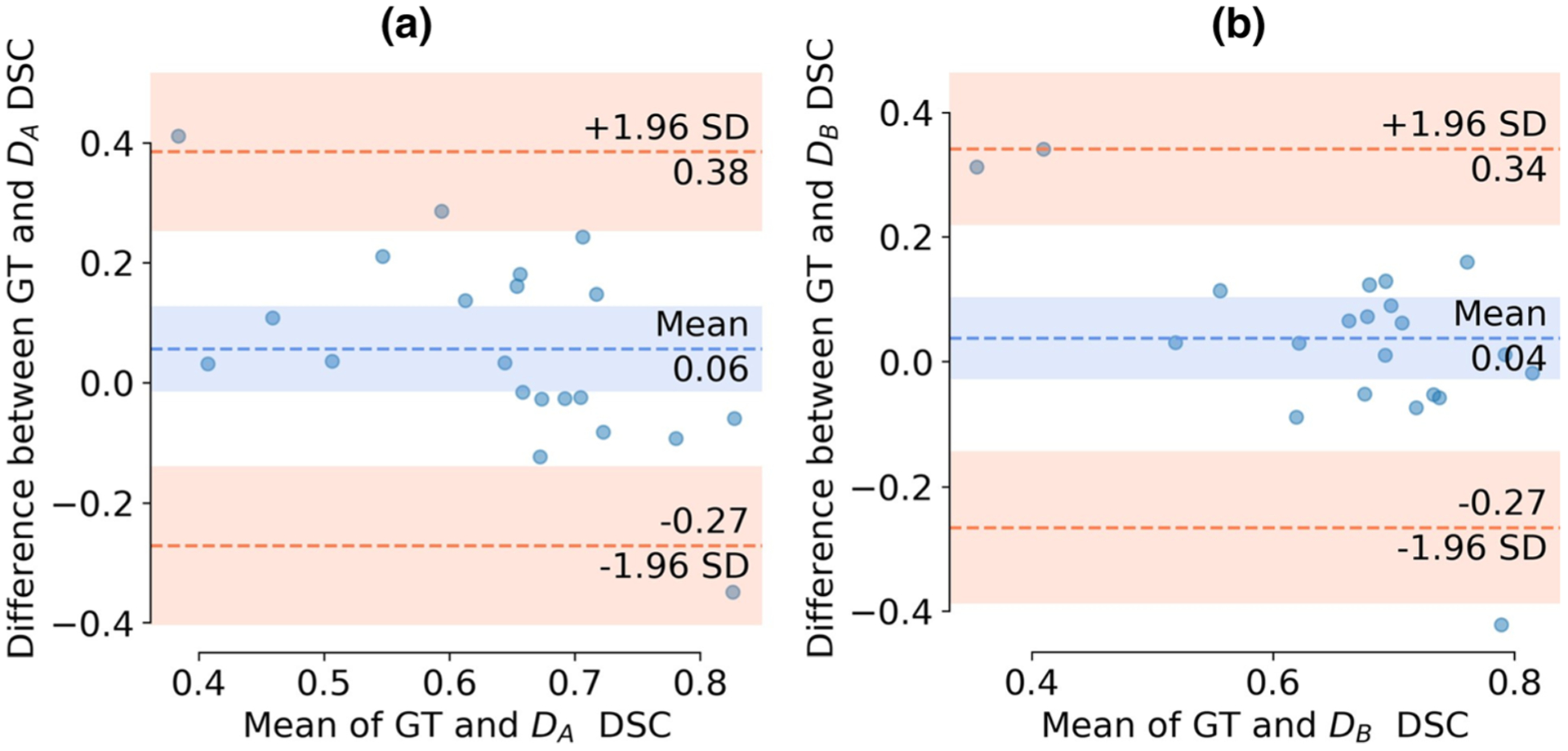
Bland-Altman plots between variation of ground truth delineations (DSC) and variation between network segmentations (DSC) on ADCm (B4b900: b values (0, 300, 500, 900 s/mm2). N = 112 patients scheduled for prostatectomy underwent two prostate MR examinations (SA and SB) performed on the same day approximately 15 min apart. The scans, SA and SB, were divided into training set (Atrain and Btrain), N = 78, and test set (Atest and Btest) N = 34. U-Net architecture-based networks DA and DB trained on Atrain and Btrain respectively. a Bland-Altman plot between ground truth delineations and segmentation maps of DA with Btest co-registered to Atest.. b Bland-Altman plot between ground truth delineations and segmentation maps of DB with Atest co-registered to Btest
Discussion
In this study, we evaluated repeatability of U-Net for (a) slice-and (b) lesion-level detection and (c) segmentation of clinically significant prostate cancer (csPCa: Gleason grade group (GGG) > 1) on prostate apparent diffusion coefficient (ADCm) maps with three different b value settings (B4b900, B4b2000, and B2b1300). The U-Net-based architecture was found to be repeatable (ICC of 0.8–0.83) for slice-level detection of csPCa regions, and moderately repeatable in detecting (proportionate agreement of 66–72%) and segmenting (DSC of 0.68–0.72) csPCa lesions.
High predictive power from single time point with low test-retest repeatability might be misleading. While number of studies have looked at repeatability of radiomics features [32, 36, 37], relatively little work has been done in the context of deep learning (DL), specifically convolutional neural networks (CNNs) [38, 39]. To the best of our knowledge, none of the previous studies has analyzed repeatability of CNNs for detection and segmentation for csPCa. Cole et al [38] analyzed the repeatability of a 3D-CNN in predicting brain age from N = 20 T1-Weighted MRIs and showed that the model was able to predict brain age with high repeatability (ICC 0.9–0.98). Honsy et al [39] showed that their 3D-CNN predictions on CT for lung cancer prognostication had high ICC of 0.91. They analyzed repeatability of a trained network by evaluating the network on test-retest scans. However, in this work, we evaluated test-retest repeatability of a CNN on the testing data by training two separate models on test and retest data. This allowed us to analyze the robustness of parameter learning of the networks.
The patients with csPCa lesions are recommended to undergo treatments such as radiation therapy and surgery [40, 41] while others are recommended an active surveillance strategy. However, invasive biopsies still remain the only standard to determine GGG and identify csPCa. Therefore, in this work, we detected slices with csPCa regions and obtained an AUC of 0.78–0.85 on testing data. Although a few previous studies [42] presented an end-to-end framework to identify csPCa images on multi-parametric MRI, none of these works has analyzed the repeatability of these networks. In our study, the availability of test-retest data enabled us to analyze the robustness of the networks and we showed that the U-Net-based architecture is repeatable in slice-level detection csPCa regions. Additionally, the training of a network for slice-level detection of csPCa regions further helped in initializing the network weights for csPCa lesion segmentation. Figure 6 depicts activation maps of the networks CA and CB calculated using Grad-CAM [43] on four samples, two being csPCa regions and the other two being non-csPCa (GGG = 1/benign) regions on prostate ADCm maps (B2b900). We may observe that the networks CA and CB focus on similar regions to drive decisions.
Fig. 6.
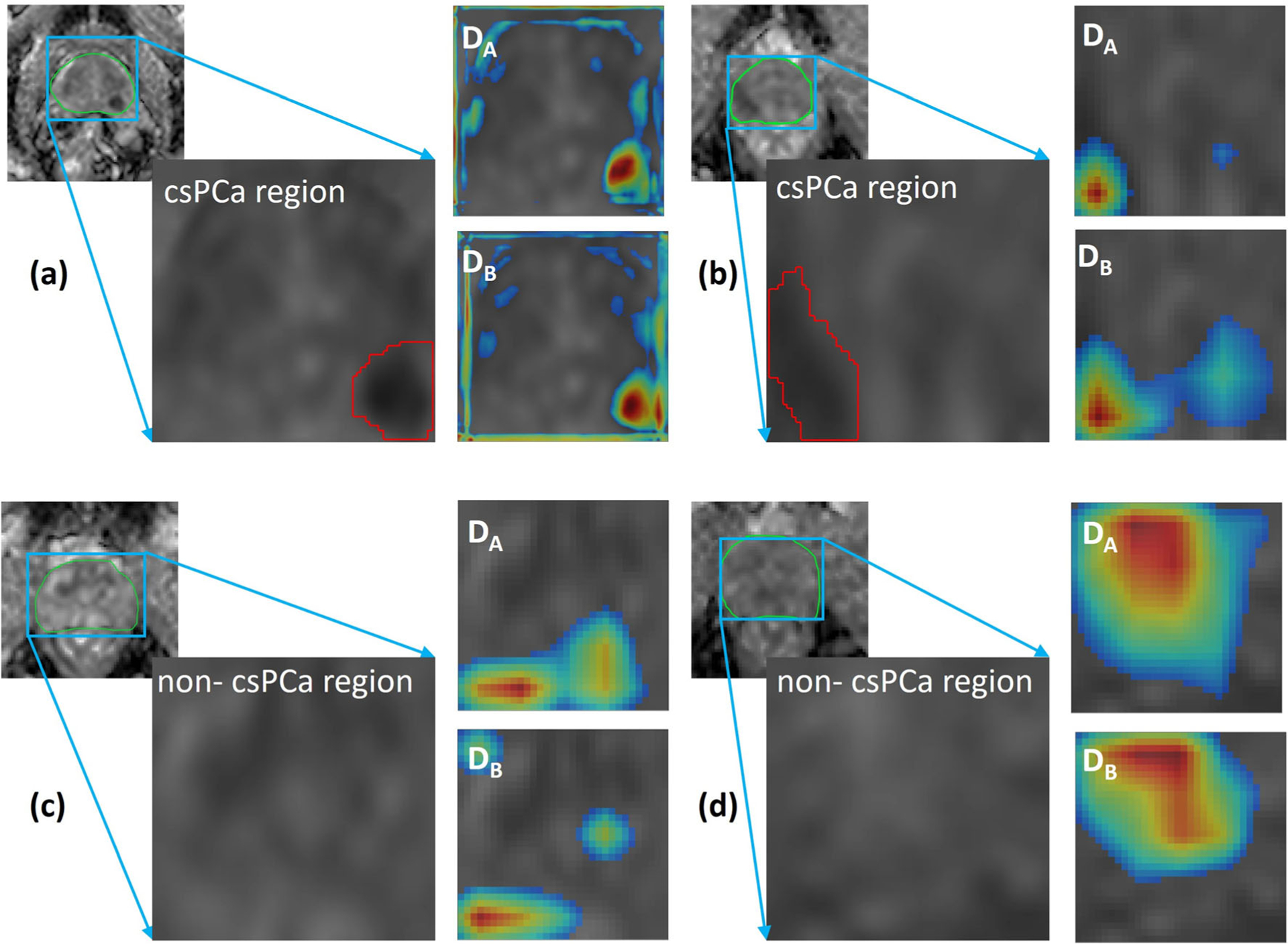
Activation maps of CA and CB on (a, b) clinically significant prostate cancer (csPCa: Gleason grade group (GGG) > 1) regions of ADCm (B4b900: b values (0, 300, 500, 900 s/mm2) maps and (c, d) non-csPCa (GGG = 1/benign) regions. The activation map shows that networks look at a darker ADCm region for csPCa regions compared with non-csPCa regions where the network looks at a brighter area. Additionally, when activations are compared between CA and CB, we may observe that the models focus on similar regions
Detection and segmentation of csPCa regions is vital for performing lesion-wise analysis of PCa and stratifying patients according to different risk categories. Kohl et al [44] used adversarial networks to detect and segment csPCa lesions and obtained a sensitivity of 55% in detecting csPCa lesions and a dice similarity coefficient (DSC) of 0.41 in segmenting csPCa lesions. Our model yielded a sensitivity of 63–65% in detecting csPCa lesions and a DSC of 0.68–0.72 in segmenting csPCa lesions. Additionally, the availability of test-retest scans allowed us to evaluate the repeatability of segmentations and detection of csPCa lesions in terms of DSC and proportionate agreement respectively.
In order to obtain good network reproducibility, it is essential to assess the variability in the test-retest scans themselves. Therefore, we evaluated the repeatability of volume and mean ADCm of the csPCa lesions in terms of ICC and found that they were highly repeatable for all three b value settings (volume: ICC = 0.92; and mean ADCm: ICC = 0.86–0.98). The repeatability of segmentations provided by the networks may also depend on inter-scan ground truth segmentation variability in segmenting lesions and prostate capsule. The Bland-Altman plots suggest that inter-scan ground truth segmentation variability is in moderate agreement with network-based segmentations.
We acknowledge that our study did have its limitations. Our work is limited to only ADCm maps since T2W MRI were not obtained for two time points. However, few previous studies have shown that there are no significant differences between segmentations on T2W and ADC [45]. The number of patients in the study was small and data was obtained from a single institute. Since a single experienced radiologist working in consensus with pathologist delineated the lesions, incorporating multiple reader annotations was considered to be beyond the scope of the current study. However, we have evaluated inter-scan ground truth segmentation variability in segmenting csPCa lesions and its effect on networks’ performance. We have performed detection of csPCa regions and classification of other GGG groups is left for future work. Additionally, future studies are required to evaluate the performance of networks using different functions and/or models for prostate DWI since we have used only one model (diffusion-weighted imaging fitted with monoexponential function). We evaluated repeatability of a single network architecture, and comparison with other network architectures remains to be performed in future studies.
Conclusions
For the three ADCm b value settings, U-Net-based architecture was repeatable in slice-level detection of csPCa regions. The network repeatability in segmenting csPCa lesions is affected by inter-scan variability and ground truth segmentation repeatability and may thus improve with better inter-scan reproducibility.
Supplementary Material
Key Points.
For the three ADCm b value settings, two CNNs with U-Net-based architecture were repeatable for the problem of detection of csPCa at the slice-level.
The network repeatability in segmenting csPCa lesions is affected by inter-scan variability and ground truth segmentation repeatability and may thus improve with better inter-scan reproducibility.
Acknowledgements and funding information
Research reported in this publication was supported by the National Cancer Institute of the National Institutes of Health under award numbers 1U24CA199374-01, R01CA202752-01A1, R01CA208236-01A1, R01 CA216579-01A1, R01 CA220581-01A1, 1U01 CA239055-01, 1U01CA248226-01, National Institute for Biomedical Imaging and Bioengineering 1R43EB028736-01, National Center for Research Resources under award number 1 C06 RR12463-01, VA Merit Review Award IBX004121A from the United States Department of Veterans Affairs Biomedical Laboratory Research and Development Service, The DoD Breast Cancer Research Program Breakthrough Level 1 Award W81XWH-19-1-0668, The DOD Prostate Cancer Idea Development Award (W81XWH-15-1-0558), The DOD Lung Cancer Investigator-Initiated Translational Research Award (W81XWH-18-1-0440), The DOD Peer Reviewed Cancer Research Program (W81XWH-16-1-0329), The Ohio Third Frontier Technology Validation Fund, The Wallace H. Coulter Foundation Program in the Department of Biomedical Engineering and The Clinical and Translational Science Award Program (CTSA) at Case Western Reserve University, DoD Prostate Cancer Research Program Idea Development Award W81XWH-18-1-0524 TYKS-SAPA Research funds (HM, PT, OE, MP, JS, JPB, HA, IJ), Finnish Cancer Society (IJ), Instrumentarium Reseseach Foundation (IJ, HA), Funding from Instrumentarium Science Foundation, Sigrid Jusélius Foundation and Turku University Hospital, TYKS-SAPA research funds were used to cover the cost of MRI examinations. We thank Anitta Entonen (Turku University Hospital, Turku Finland) for her help with patient enrollment and assistance during imaging of PCa patients, and Jaakko Liippo (Turku University Hospital, Turku, Finland) for his help in scanning the histopathological slides. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health, the U.S. Department of Veterans Affairs, the Department of Defense, or the United States Government.
Abbreviations
- ADC
Apparent diffusion coefficient maps
- ADCm
Apparent diffusion coefficient maps obtained using monoexponential fit of DWI signal decay
- AUC
Area under the receiver operating characteristic curve
- CNN
Convolutional neural network
- csPCa
Clinically significant prostate cancer
- DL
Deep learning
- DSC
Dice similarity coefficient
- FN
False negatives
- FP
False positives
- ICC
Intra-class correlation coefficient
- ML
Machine learning
- MRI
Magnetic resonance imaging
- PCa
Prostate cancer
- PI-RADS
Prostate Imaging-Reporting and Data System
- PPV
Positive predictive value
- TP
True positives
Footnotes
Electronic supplementary material The online version of this article (https://doi.org/10.1007/s00330-020-07065-4) contains supplementary material, which is available to authorized users.
Guarantor The scientific guarantor of this publication is Dr. Anant Madabhushi.
Conflict of interest Amogh Hiremath: Philips Research - Former Employment. Dr. Madabhushi is an equity holder in Elucid Bioimaging and in Inspirata Inc. In addition he has served as a scientific advisory board member for Inspirata Inc, Astrazeneca, Bristol Meyers-Squibb and Merck. Currently he serves on the advisory board of Aiforia Inc. He also has sponsored research agreements with Philips, AstraZeneca and Bristol Meyers-Squibb. His technology has been licensed to Elucid Bioimaging. He is also involved in a NIH U24 grant with PathCore Inc, and 3 different R01 grants with Inspirata Inc.. The remaining authors of this manuscript declare no relationships with any companies whose products or services may be related to the subject matter of the article.
Statistics and biometry Dr. Anant Madabhushi, Dr. Rakesh Shiradkar and Dr. Harri Merisaari kindly provided statistical advice for this manuscript.
Informed consent Written informed consent was waived by the Institutional Review Board.
Ethical approval Institutional Review Board approval was obtained.
Study subjects or cohorts overlap The exact study subjects or cohorts have been previously reported in Merisaari et al Magn Reson Med. (2019) which is attached with the manuscript.
- retrospective
- observational/experimental
- performed at one institution
References
- 1.Akkus Z, Galimzianova A, Hoogi A, Rubin DL, Erickson BJ (2017) Deep learning for brain MRI segmentation: state of the art and future directions. J Digit Imaging 30:449–459. 10.1007/s10278-017-9983-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cheng R, Roth HR, Lay N et al. (2017) Automatic magnetic resonance prostate segmentation by deep learning with holistically nested networks. J Med Imaging (Bellingham):4 10.1117/1.JMI.4.4.041302 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Chen Q, Hu S, Long P, Lu F, Shi Y, Li Y (2019) A transfer learning approach for malignant prostate lesion detection on multiparametric MRI. Technol Cancer Res Treat 18:1533033819858363. 10.1177/1533033819858363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sumathipala Y, Lay N, Turkbey B, Smith C, Choyke PL, Summers RM (2018) Prostate cancer detection from multi-institution multiparametric MRIs using deep convolutional neural networks. J Med Imaging (Bellingham) 5:044507 10.1117/1.JMI.5.4.044507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Maicas G, Bradley AP, Nascimento JC, Reid I, Carneiro G (2019) Pre and post-hoc diagnosis and interpretation of malignancy from breast DCE-MRI. Med Image Anal 58:101562 10.1016/j.media.2019.101562 [DOI] [PubMed] [Google Scholar]
- 6.Abraham B, Nair MS (2018) Computer-aided classification of prostate cancer grade groups from MRI images using texture features and stacked sparse autoencoder. Comput Med Imaging Graph 69: 60–68. 10.1016/j.compmedimag.2018.08.006 [DOI] [PubMed] [Google Scholar]
- 7.Pan Y, Huang W, Lin Z et al. (2015) Brain tumor grading based on neural networks and convolutional neural networks. Conf Proc IEEE Eng Med Biol Soc 2015:699–702. 10.1109/EMBC.2015.7318458 [DOI] [PubMed] [Google Scholar]
- 8.Soto ME, Pezoa JE, Torres SN (2011) Thermal noise estimation and removal in MRI: a noise cancellation approach In: San Martin C, Kim S-W (eds) Progress in pattern recognition, image analysis, computer vision, and applications. Springer, Berlin, pp 47–54 [Google Scholar]
- 9.Zaitsev M, Julian M, Herbst M (2015) Motion artefacts in MRI: a complex problem with many partial solutions. J Magn Reson Imaging 42:887–901. 10.1002/jmri.24850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Yang F, Dogan N, Stoyanova R, Ford JC (2018) Evaluation of radiomic texture feature error due to MRI acquisition and reconstruction: a simulation study utilizing ground truth. Phys Med 50:26–36. 10.1016/j.ejmp.2018.05.017 [DOI] [PubMed] [Google Scholar]
- 11.Baruah SK, Das N, Baruah SJ et al. (2019) Combining prostate-specific antigen parameters with prostate imaging reporting and data system score version 2.0 to improve its diagnostic accuracy. World J Oncol 10:218–225. 10.14740/wjon1230 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Schimmöller L, Quentin M, Arsov C et al. (2013) Inter-reader agreement of the ESUR score for prostate MRI using in-bore MRI-guided biopsies as the reference standard. Eur Radiol 23:3185–3190. 10.1007/s00330-013-2922-y [DOI] [PubMed] [Google Scholar]
- 13.Sonn GA, Fan RE, Ghanouni P et al. (2019) Prostate magnetic resonance imaging interpretation varies substantially across radiologists. Eur Urol Focus 5:592–599. 10.1016/j.euf.2017.11.010 [DOI] [PubMed] [Google Scholar]
- 14.Cuocolo R, Stanzione A, Ponsiglione A et al. (2019) Clinically significant prostate cancer detection on MRI: a radiomic shape features study. Eur J Radiol 116:144–149. 10.1016/j.ejrad.2019.05.006 [DOI] [PubMed] [Google Scholar]
- 15.Min X, Li M, Dong D et al. (2019) Multi-parametric MRI-based radiomics signature for discriminating between clinically significant and insignificant prostate cancer: cross-validation of a machine learning method. Eur J Radiol 115:16–21. 10.1016/j.ejrad.2019.03.010 [DOI] [PubMed] [Google Scholar]
- 16.Merisaari H, Jambor I (2015) Optimization of b-value distribution for four mathematical models of prostate cancer diffusion-weighted imaging using b values up to 2000 s/mm(2): simulation and repeatability study. Magn Reson Med 73:1954–1969. 10.1002/mrm.25310 [DOI] [PubMed] [Google Scholar]
- 17.Jambor I, Merisaari H, Taimen P et al. (2015) Evaluation of different mathematical models for diffusion-weighted imaging of normal prostate and prostate cancer using high b-values: a repeatability study. Magn Reson Med 73:1988–1998. 10.1002/mrm.25323 [DOI] [PubMed] [Google Scholar]
- 18.Merisaari H, Movahedi P, Perez IM et al. (2017) Fitting methods for intravoxel incoherent motion imaging of prostate cancer on region of interest level: repeatability and Gleason score prediction. Magn Reson Med 77:1249–1264. 10.1002/mrm.26169 [DOI] [PubMed] [Google Scholar]
- 19.Merisaari H, Toivonen J, Pesola M et al. (2015) Diffusion-weighted imaging of prostate cancer: effect of b-value distribution on repeatability and cancer characterization. Magn Reson Imaging 33:1212–1218. 10.1016/j.mri.2015.07.004 [DOI] [PubMed] [Google Scholar]
- 20.van Timmeren JE, Leijenaar RTH, van Elmpt W et al. (2016) Test–retest data for radiomics feature stability analysis: generalizable or study-specific? Tomography 2:361–365. 10.18383/j.tom.2016.00208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gu J, Zhu J, Qiu Q, Wang Y, Bai T, Yin Y (2019) Prediction of immunohistochemistry of suspected thyroid nodules by use of machine learning-based radiomics. AJR Am J Roentgenol:1–10. 10.2214/AJR.19.21626 [DOI] [PubMed] [Google Scholar]
- 22.Tian Z, Liu L, Zhang Z, Fei B (2018) PSNet: prostate segmentation on MRI based on a convolutional neural network. J Med Imaging (Bellingham) 5:021208 10.1117/1.JMI.5.2.021208 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Tian Z, Liu L, Fei B (2018) Deep convolutional neural network for prostate MR segmentation. Int J Comput Assist Radiol Surg 13: 1687–1696. 10.1007/s11548-018-1841-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Song Y, Zhang Y-D, Yan X et al. (2018) Computer-aided diagnosis of prostate cancer using a deep convolutional neural network from multiparametric MRI. J Magn Reson Imaging 0: 10.1002/jmri.26047 [DOI] [PubMed] [Google Scholar]
- 25.Tsehay YK, Lay NS, Roth HR, et al. (2017) Convolutional neural network based deep-learning architecture for prostate cancer detection on multiparametric magnetic resonance images In: Medical Imaging 2017: Computer-Aided Diagnosis. International Society for Optics and Photonics, p 1013405 [Google Scholar]
- 26.Schelb P, Kohl S, Radtke JP et al. (2019) Classification of cancer at prostate MRI: deep learning versus clinical PI-RADS assessment. Radiology 293:607–617. 10.1148/radiol.2019190938 [DOI] [PubMed] [Google Scholar]
- 27.Abraham B, Nair MS (2019) Automated grading of prostate cancer using convolutional neural network and ordinal class classifier. Inform Med Unlocked 17:100256 10.1016/j.imu.2019.100256 [DOI] [Google Scholar]
- 28.Zabihollahy F, Ukwatta E, Krishna S, Schieda N (2019) Fully automated localization of prostate peripheral zone tumors on apparent diffusion coefficient map MR images using an ensemble learning method. J Magn Reson Imaging. 10.1002/jmri.26913 [DOI] [PubMed] [Google Scholar]
- 29.Cheng R, Lay N, Roth HR et al. (2019) Fully automated prostate whole gland and central gland segmentation on MRI using holistically nested networks with short connections. J Med Imaging (Bellingham) 6:024007 10.1117/1.JMI.6.2.024007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Falk T, Mai D, Bensch R et al. (2019) U-Net: deep learning for cell counting, detection, and morphometry. Nat Methods 16:67–70. 10.1038/s41592-018-0261-2 [DOI] [PubMed] [Google Scholar]
- 31.Ronneberger O, Fischer P, Brox T (2015) U-Net: convolutional networks for biomedical image segmentation In: Navab N, Hornegger J, Wells WM, Frangi AF (eds) Medical image computing and computer-assisted intervention – MICCAI 2015. Springer International Publishing, Cham, pp 234–241 [Google Scholar]
- 32.Merisaari H, Taimen P, Shiradkar R et al. (2019) Repeatability of radiomics and machine learning for DWI: short-term repeatability study of 112 patients with prostate cancer. Magn Reson Med. 10.1002/mrm.28058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Turkbey B, Rosenkrantz AB, Haider MA, et al. (2019) Prostate imaging reporting and data system version 2.1: 2019 update of prostate imaging reporting and data system version 2. Eur Urol 76:340–351. 10.1016/j.eururo.2019.02.033 [DOI] [PubMed] [Google Scholar]
- 34.Youden WJ (1950) Index for rating diagnostic tests. Cancer 3:32–35. [DOI] [PubMed] [Google Scholar]
- 35.DeLong ER, DeLong DM, Clarke-Pearson DL (1988) Comparing the areas under two or more correlated receiver operating characteristic curves: a nonparametric approach. Biometrics 44:837–845 [PubMed] [Google Scholar]
- 36.Schwier M, van Griethuysen J, Vangel MG et al. (2019) Repeatability of multiparametric prostate MRI radiomics features. Sci Rep 9:9441 https://www.nature.com/articles/s41598-019-45766-z. Accessed 18 Sep 2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Varghese BA, Hwang D, Cen SY et al. (2019) Reliability of CT-based texture features: phantom study. J Appl Clin Med Phys 20: 155–163. 10.1002/acm2.12666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Cole JH, Poudel RPK, Tsagkrasoulis D et al. (2017) Predicting brain age with deep learning from raw imaging data results in a reliable and heritable biomarker. Neuroimage 163:115–124. 10.1016/j.neuroimage.2017.07.059 [DOI] [PubMed] [Google Scholar]
- 39.Hosny A, Parmar C, Coroller TP et al. (2018) Deep learning for lung cancer prognostication: a retrospective multi-cohort radiomics study. PLoS Med 15 10.1371/journal.pmed.1002711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Crawford ED, Grubb R, Black A et al. (2011) Comorbidity and mortality results from a randomized prostate cancer screening trial. J Clin Oncol 29:355–361. 10.1200/JCO.2010.30.5979 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Schröder FH, Hugosson J, Roobol MJ, et al. (2009) Screening and prostate-cancer mortality in a randomized European study. N Engl J Med 360(13):1320–1328. https://www.nejm.org/doi/full/10.1056/NEJMoa0810084. Accessed 10 Feb 2020 [DOI] [PubMed] [Google Scholar]
- 42.Wang Z, Liu C, Cheng D, Wang L, Yang X, Cheng K-T (2018) Automated detection of clinically significant prostate cancer in mp-MRI images based on an end-to-end deep neural network. IEEE Trans Med Imaging 37:1127–1139. 10.1109/TMI.2017.2789181 [DOI] [PubMed] [Google Scholar]
- 43.Selvaraju RR, Cogswell M, Das A, Vedantam R, Parikh D, Batra D (2020) Grad-CAM: visual explanations from deep networks via gradient-based localization. Int J Comput Vis 128:336–359. 10.1007/s11263-019-01228-7 [DOI] [Google Scholar]
- 44.Kohl S, Bonekamp D, Schlemmer H-P, et al. (2017) Adversarial networks for the detection of aggressive prostate Cancer. arXiv: 170208014 [cs] [Google Scholar]
- 45.Liechti MR, Muehlematter UJ, Schneider AF et al. (2020) Manual prostate cancer segmentation in MRI: interreader agreement and volumetric correlation with transperineal template core needle biopsy. Eur Radiol. 10.1007/s00330-020-06786-w [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


