Metachronal patterns in artificial cilia for low Reynolds number fluid propulsion

The influence of metachronal patterns on ciliary fluid flow has been studied using a soft robotic cilia array and simulations.

Abstract

Cilia are hair-like organelles, present in arrays that collectively beat to generate flow. Given their small size and consequent low Reynolds numbers, asymmetric motions are necessary to create a net flow. Here, we developed an array of six soft robotic cilia, which are individually addressable, to both mimic nature’s symmetry-breaking mechanisms and control asymmetries to study their influence on fluid propulsion. Our experimental tests are corroborated with fluid dynamics simulations, where we find a good agreement between both and show how the kymographs of the flow are related to the phase shift of the metachronal waves. Compared to synchronous beating, we report a 50% increase of net flow speed when cilia move in an antiplectic wave with phase shift of −π/3 and a decrease for symplectic waves. Furthermore, we observe the formation of traveling vortices in the direction of the wave when metachrony is applied.

INTRODUCTION

Arrays of beating cilia are a biological solution to generate net flow in low Reynolds number flow regimes. Cilia are micrometer-sized hair-like organelles that cover the body of certain microorganisms, such as Paramecium and Opalina, or can project from epithelial cells in carpet-like configurations, like in the lining of the trachea or in the fallopian tubes (1, 2). Although their function can alter from organism to organism (swimming, pumping, and mixing), their fundamental operation remains the same. Because of their small scale, cilia operate at low Reynolds numbers, where nonreciprocal motions are necessary to induce a net flow, as pointed out by Purcell’s scallop theorem (3). At low Reynolds numbers (Re ≪ 1), viscous forces dominate inertial effects, and flow interactions can be described using Stokes equation, which is time reversible. Thus, a swimmer that follows a symmetric pattern of strokes cannot propel itself at low Reynolds numbers. However, cilia display nonreciprocal motions to break the symmetry and generate a net flow. A single cilium beats rhythmically, and its motion can be divided into two phases: the effective and the recovery stroke (4). In cilia, nonreciprocity occurs when the two strokes follow a different trajectory so that the tip of the cilia sweeps an enclosed area in the beating plane. This so-called swept area characterizes the amount of net fluid flow induced in a single beat; the larger this area, the higher the flow rate (5, 6). This type of nonreciprocal motion is also known as spatial asymmetry. In addition to asymmetry on an individual cilium level and when cilia are placed in arrays, the beating of each cilium can be shifted in time with respect to the beating of its neighbors. This coordinated shift induces what biologists call metachronal wave (7). If the wave travels toward the direction of the effective stroke, the wave is defined as symplectic, whereas in the other scenario, the wave is antiplectic. The synchronization mechanism that regulates the metachronal beating is still uncertain; however, it has been shown that metachronal waves can emerge because of hydrodynamical interaction between densely packed cilia (8–11). Furthermore, computational models have identified metachrony to be a major contributing factor for the large fluid flows that are observed in nature (12–15). In contrast to numerical simulations, artificial cilia can be used to experimentally corroborate existing models and gain insights into the effects of nonreciprocal motions on the surrounding viscous fluid to better understand the mechanisms of their biological counterparts (16).

To date, most artificial cilia arrays are magnetically actuated and are manufactured in plate-like (17, 18) or rod-like (19–23) shapes. Both types of magnetic cilia exhibit spatial asymmetry, controlled, for instance, by a rotating magnetic field. However, these arrays of magnetic cilia are collectively controlled by the distant action of a magnet, which makes it challenging to generate controlled metachronal waves. Few manuscripts report on the metachronal motion of magnetic cilia: Hanasoge et al. (24) varied the length of plate-like cilia to induce a phase shift between neighboring cilia, while Marume et al. (25) tuned the orientation of the magnetic chainlike clusters embedded in the cilia structures. Recently, Gu et al. (26) developed a new technique to introduce a phase shift in magnetic cilia. Their cilia carpet is wrapped around a curved support and then magnetized. The curvature of the support defines the metachronal phase shift. Nevertheless, if the metachronal wave is defined in the cilia design, then it is impossible to tune its properties (wavelength and traveling speed) without changing the amplitude or frequency of the driving force, which leads to changing hydrodynamic conditions (Reynolds and Sperm number) (4). Therefore, artificial cilia that can be actuated independently are needed to experimentally corroborate existing computational fluid dynamic (CFD) theories on metachrony. Previous reports have looked into metachronal waves of reciprocal beating pneumatic cilia at high Reynolds numbers (27) or rigid paddle-like robotic arm array with tunable metachronal phase shifts (28, 29), but there is no artificial system that mimics and independently tunes the typical asymmetric ciliary motion at low Reynolds numbers, and, moreover, no experiment where the net flow is related to regular intervals of phase shift angles covering the complete range between 0 and 2π. This work fills this gap and provides an experimental setup where an array of six independent soft inflatable cilia with two degrees of freedom can be controlled independently to study different metachronal waves at low Reynolds numbers. In our system, metachronal waves are actively imposed and do not spontaneously emerge because of hydrodynamic interactions. Furthermore, the collective behavior of the artificial cilia beating in a low Reynolds regime is evaluated through Particle Image Velocimetry (PIV), accurately measuring the induced flow fields. During these experiments, the imposed pressure waves have a fixed amplitude and frequency, leaving phase difference to be the only variable parameter. In this way, we have accurate control over both spatial and metachronal asymmetries of the cilia array. These experiments are compared with CFD simulations to assess the accuracy of the existing theoretical models and to lay a foundation for the experimental observations.

Soft artificial cilia

The experimental setup consists of an array of six equidistant soft robotic cilia, where each cilium consists of two hollow elastomeric cylinders that are combined side by side into a monolithic polydimethylsiloxane (PDMS) structure reported previously (16). By offsetting the inner cavity of the cylinder with respect to its symmetry axis, a large bending deformation upon inflation is accomplished (30). Because these cilia have not one but two inner cavities, the additional degree of freedom can be used to create a swept area and thus spatial asymmetry. This is done by pressurizing each cavity with a dedicated pressure source, where the phase shift between imposed trapezoidal pressure profiles can be used to tune the amount of area that the cilia tip sweeps, as displayed in Fig. 1A (16). The individual cilium exhibits a geometrical symmetry plane, resulting in planar deformations. These cilia are thus mimicking the deformations of planar-beating natural cilia [e.g., respiratory tract cilia (31)], which have been studied in literature using computational and approximate experimental models (6, 13, 15, 32). For the manufacturing and more detailed information on the operational principle and design, we refer to previous publications (16, 30). Where in our previous work we were interested in the hydrodynamic interactions of a single artificial cilium (16), we now focus on the influence of metachrony on fluid flow, in this case, in glycerol. To achieve this, six artificial cilia are aligned to make their beating coplanar, mimicking a simplified cilia array. The imposed amplitudes and frequencies of the pressure signals are maintained fixed, while the phase shift between neighboring cilia is changed to control metachrony. Twelve independent pressure inputs are thus needed to regulate the beating of six artificial cilia. The actuation system consists of 12 electropneumatic valves (SMC Instruments, ITV0050-3MN-Q) controlled through a LabVIEW program to output trapezoidal pneumatic waves. Because of air diffusion through the PDMS (more details in section S1) material of the cilia, we additionally included a pneumatic-hydraulic pressure converter to actuate the cilia with water (fig. S1). The ciliary beat frequency (f) is set to 0.25 Hz, which corresponds to an optimal trade-off between actuation frequency and viscous drag, as described in (16). Because the active cilia length (L) is 14 mm and the viscosity (μ) and density (ρ) of glycerol at 20°C are, respectively, 1.412 Pa · s and 1.260 g · cm⁻³, the Reynolds number ($\mathit{\text{Re}}=\frac{\mathrm{\rho }{L}^{2}f}{\mathrm{\mu }}$) (4) equals 0.04, comparable to what microorganisms experience (33). Computational studies show that the spacing between cilia influences the attained fluid flow, with smaller interciliary distances leading to larger flows, depending on the direction of the traveling wave (14). We set this interciliary distance approximately equal to the cilia length, a ≈ L, which is also the limiting condition for studying the collective behavior of cilia with the envelop model according to Brennen (34). The phase shift between the pressure signals of subsequent cilia directly influences metachrony and will be the main parameter under investigation in this study. Movie S1 shows the ciliary motion in air for changing phase differences (Δφ). Negative phase differences (−π < Δφ < 0) correspond to antiplectic traveling waves, while positive phase differences (0 < Δφ < π) correspond to symplectic. Synchronous (Δφ = 0) and anti-phase (Δφ = π) cilia induce standing waves. Given these parameters, the wavelength of a metachronal wave can be defined as $\mathrm{\lambda }=\frac{2\mathrm{\pi }a}{\mathrm{\Delta }\mathrm{\phi }}$ and the wave speed as $v_m=\frac{2\mathrm{\pi }\mathit{fa}}{\mathrm{\Delta }\mathrm{\phi }}$. Figure 1B displays the artificial cilia motion for antiplectic, symplectic, and synchronous beating patterns.

Fig. 1. Soft artificial cilia.

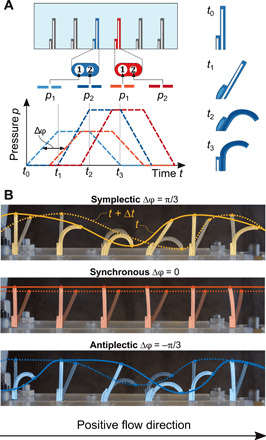
(A) Pressure input functions: Each cilium is actuated with two trapezoidal waves. A metachronal wave is applied by shifting the trapezoidal waves of the neighboring cilium with a constant phase angle. The actuation sequence allows the cilium stroke to be spatially asymmetric. (B) Array of six artificial inflatable cilia independently actuated by 12 fluid pressure inputs. Symplectic and antiplectic waves and synchronous motion can be applied to the array. The superimposed colored lines show the metachronal wave propagation. The solid line represents the initial metachronal wave at the tip of the cilia. The dashed line is the wave at the subsequent frame. The wave travels toward the positive direction for the symplectic wave and the negative for the antiplectic.

RESULTS

To understand the underlying physics of the low Reynolds propulsion of our artificial cilia, we compared the experimental fluid fields with CFD simulations for different values of metachronal phase shifts Δφ. We observed a good agreement in the fluid field structures that provide new insights into the ciliary propulsion mechanisms. This can be seen in Fig. 2, showing simulated and experimental velocity fields of the fluid inside the channel for a synchronous cilia beating pattern. Numerical discrepancies are discussed in the Supplementary Materials and are mainly caused by small variations in the viewing plane (fig. S8) and mismatches between the ideal simulated kinematics and the experimental cilia trajectories (fig. S9). Despite the closed-loop shape of the D channel, we observed no fluid flow in the curved side of the circuit. Given the narrow geometry of the curved channel and the high viscosity of the medium, the fluid propelled by the ciliary beat does not flow to the curved channel but recirculates within the main rectangular channel. We approximated this condition in the simulations by adopting a closed rectangular channel domain. As in (17, 33), artificial cilia beating in a closed channel build up a pressure gradient that drives a backflow at the top half of the channel, in agreement with our experimental observations. Because fluid velocities in the bottom half of the channel are strongly affected by the presence of the artificial cilia, velocities there have higher magnitudes compared to the rest of the channel (Fig. 2). Because of the low Reynolds number regime, the fluid in the immediate vicinity of the cilia moves as fast as the cilia themselves. Therefore, to have a clear analysis on the propulsion effect, we focus on the free-flowing fluid, in the top half of the channel, where backflow occurs (33). Moreover, the analysis of the divergence (fig. S10) shows that the fluid velocities are essentially planar in the free-flowing fluid, while out-of-plane fluid motions occur only between the cilia.

Fig. 2. Fluid velocity fields.

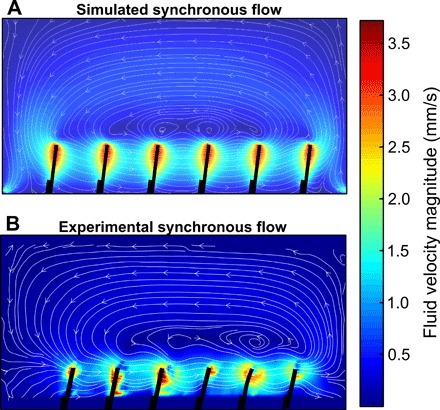
Simulated (panel A) and experimental (panel B) fluid velocity field of the whole channel for synchronous cilia at the beginning of their collective effective stroke. Given the closed-channel boundary conditions, the effective flow induced by cilia is reversed and directed toward the opposite direction, above the cilia. In this study, we analyze how the backflow varies when cilia move with different metachronal waves.

Figure 3A shows how the simulated and experimental backflow velocity varies during a cycle for an antiplectic (−π/3), a symplectic (π/3), and the synchronous motion (no phase shift) at the center of the rectangular face of the channel. The backflow velocity is $\overline{U}=1/\mathrm{\Gamma }{\int }_{\mathrm{\Gamma }}U(y)\mathit{dy}$, where Γ is the free-flowing part of the channel and U(y) is the local horizontal fluid velocity. In the synchronous case, the four cyclic motions of the cilia (inflate void 1, inflate void 2, deflate void 1, and deflate void 2) are clearly distinguishable as four extrema in the speed profile. Because we are looking at the backflow, the first two peaks (effective stroke) are negative as directed toward the negative flow direction (Fig. 1B). Integrating (in the beating plane of the cilia) the local flow velocity over an actuation period and multiplying it with the beating frequency yield a measurement of the averaged flow velocity, $\mathrm{\langle }\overline{U}\mathrm{\rangle }=\frac{1}{T}{\int }_0^T\overline{U}\mathit{dt}$. In ciliary propulsion literature (10), averaged flow is referred to as “net flow” to indicate the difference between the flows induced by the effective and recovery strokes of the cilia at the end of beat cycle. In all three cases, the net backflows are negative, which means that the fluid above the cilia has been propelled toward the negative direction at the end of the cycle. It is important to note that even in the absence of metachrony (Δφ = 0), the presence of the spatial asymmetry alone yields a net flow. To quantitatively compare the contribution of the metachronal shifts to the net backflow for the experiment and the simulation, we normalize the net velocity values of the metachronal patterns with the ones of the synchronous cilia. Figure 3B shows the normalized net backflow velocities (blue circles for the simulation and red squares for the experiments) for the 12 metachronal patterns taken into analysis. The normalized net backflow velocities show a consistent trend both for the simulation and experimental analyses. Therefore, a roughly 50% higher backflow occurs for low antiplectic phase shifts, while the inverse happens for symplectic waves. Higher phase shifts (Δφ > ±2π/3) show a variation of less than 25% on the net backflow.

Fig. 3. Flow measurements.

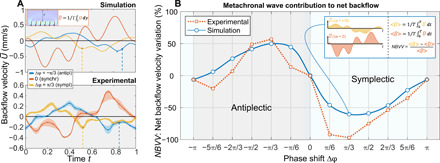
(A) Backflow velocity during one cycle in the synchronous, antiplectic, and symplectic case for experiment and simulation. Dashed lines correspond to the fluid fields depicted in Fig. 4. (B) Net backflow variation for phase shifts between −π and π at fixed π/6 intervals. Values are normalized to the synchronous value of the backflow velocity. Simulation and experiment show the same sinusoidal-like trend where the extrema are at a phase shift of π/3. Negative variation occurs in symplectic waves (positive phase shifts) due to the obstructing mechanism depicted in Fig. 4 and discussed in the section Results.

This analysis can be compared to previous theoretical models by considering the fact that our backflow is related to the effective stroke (therefore, signs are inverted). Despite different cilium kinematics, Gauger et al. (15), Khaderi et al. (14), and Guo et al. (13) predict that low antiplectic phase shift maximizes the net flow because of an obstruction effect. Figure 4 shows that this obstruction mechanism is also captured by our experimental setup. This figure shows the simulated (left) and measured (right) deformations of the cilia and the flow fields at a time where the third cilium from the left (indicated by a red arrow) is in the same upright position for both an antiplectic wave (top) and a symplectic wave (bottom) with a phase shift of Δφ = ± π/3. In the antiplectic configuration, the fourth cilium is also in the effective stroke, therefore not obstructing the fluid flow. In contrast, in the symplectic case, the fourth cilium is about to start again the beat, and its undeformed configuration hinders the fluid flow induced by the third, forming a vortex. The trend displayed in Fig. 3B is in agreement with (13) and (15), whereas Khaderi et al. (14) show that even symplectic metachronous beating patterns outperform synchronous cilia. However, these analogies need to be contextualized. In literature, net flow is defined as the difference of the positive flow in the effective stroke direction and a negative flow in the recovery direction (14). When cilia beat synchronously, the positive flow is induced by the coordinated effective stroke, and the negative flow occurs during the recovery stroke. However, for metachronal cilia, because of the out-of-phase movements, positive and negative flows can appear simultaneously in different sections of the channel-inducing vortices. Because fluid magnitudes and directions are directly related to the cilia kinematics, spatial asymmetry plays a big role in flow generation. A highly spatially asymmetric cilium coupled with the metachronal rhythm of the array causes the emergence of a shielding effect that cancels the negative flow (14). The spatial asymmetry of the cilium in (14) is much higher than ours (16) and other references, where this shielding effect does not occur.

Fig. 4. Ciliary obstruction mechanism.

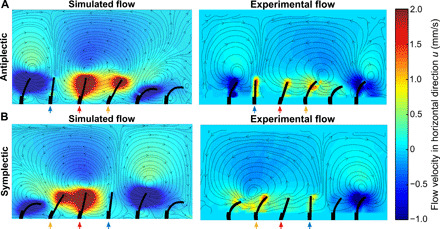
Simulated and experimental horizontal velocity (u) fields for an antiplectic (panel A) and symplectic (panel B) wave of the same phase shift (−π/3), when the third cilium from the left is at the same configuration during the effective stroke. In the symplectic case, the fourth cilium is at the end of the recovery stroke, therefore obstructing the flow induced by the third cilium and inducing a vortex. In the antiplectic case, the configuration of the fourth cilium is more bent to the right and is in the effective stroke, leading to an enhancement of the flow. In the simulation, all cilia have identical kinematics, whereas real cilia exhibit small deviations. The last cilium on the right, for instance, suffers from a pressure drop within the fluidic supply circuit that leads to a lower degree of bending compared to the ideal configuration. However, as the fluid patterns mainly depend on the metachronal waves, the minor differences in the deformed configuration of a single cilium do not pose particular issues.

As discussed above, a notable phenomenon that emerges in our artificial ciliary system is the appearance and propagation of vortices due to the simultaneous presence of effective and recovery flows caused by the phase difference between cilia. While cilia-induced vortices were already predicted in computational models, this is the first time that we can experimentally discern how they are affected with varying metachronies. When a phase difference is imposed, vortex-like structures form in the channel and travel along the cilia array, following the direction of the metachronal wave. Vortices develop on top of a single cilium when switching between effective and recovery strokes (the same phenomenon can be seen in Fig. 4). Thus, the number of vortices depends on the metachronal wave speed. An effective and clear way of visualizing the different metachronal patterns in the fluid fields is to plot the spatiotemporal graphs (kymographs) of the backflow velocities across the channel length, as defined in the inset of Fig. 3A. Kymographs are used in wave physics but are rarely plotted to analyze fluid velocities induced by cilia (35, 36). Figure 5 depicts the experimental and simulated kymographs of the backflow velocity for 12 phase shifts during one period and across the channel length, where color bars indicate the velocity magnitude. The fact that such patterns are clearly distinguishable in the measurements indicates that the experimental hydrodynamic conditions are very well captured by the Stokes flow assumption. Those velocity patterns can be associated to the metachronal kinematics of the cilia, which means that the fluid only moves together with the cilia, without experiencing any inertial effect. In-phase (Δφ = 0) and anti-phase (Δφ = π) pulses in the kymographs are parallel to the spatial direction, because they correspond to standing waves. Pulses in yellow represent positive flow velocities induced by the recovery strokes of the cilia, while pulses in blue to negative flow velocities related to the effective strokes. Thus, it can be assumed that such pulses represent the vortex-like structures. When cilia beat synchronously, we can clearly distinguish the four cyclic motions of the artificial cilia as in the analysis of the backflow (as in Fig. 3A) and observe no traveling vortices. Out-of-phase beatings show pulses that are moving in time, where the slopes in the kymographs measure their traveling speed (Fig. 6A) coinciding with the metachronal wave speed of cilia as previously defined and depicted in Fig. 6B (blue line). For the highest speed traveling waves (Δφ = ± π/6), there are two vortices of opposite sign traveling corresponding to the yellow and blue pulses, due to the limited array size. For larger phase shifts, there are more vortices forming due to the smaller wavelength; therefore, the velocity waves have more pulses, and the kymographs look more scattered. In our artificial cilia setup, the phase shifts are externally imposed, but it is interesting to notice that in some theoretical models of biological cilia where metachronal patterns emerge spontaneously because of local hydrodynamic interactions between cilia, low wave speeds are unstable and tend to stabilize toward high wave speeds (35). Moreover, Osterman and Vilfan (12) defined cilia efficiency as the ratio between the square of the net flow and the cilia mechanical power. As the mechanical power is the same in the 12 configurations that we tested, we can conclude that antiplectic high wave speeds are the most efficient for fluid transport.

Fig. 5. Backflow velocity spatiotemporal graphs.

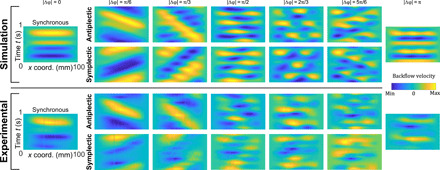
Simulated and experimental kymographs of the backflow during one cycle along the channel length for phase shifts between π and π at fixed π/6 intervals. Yellow corresponds to the positive velocity, and blue corresponds to the negative velocity. Traveling patterns can be distinguished for metachronal waves.

Fig. 6. Metachronal waves speeds.

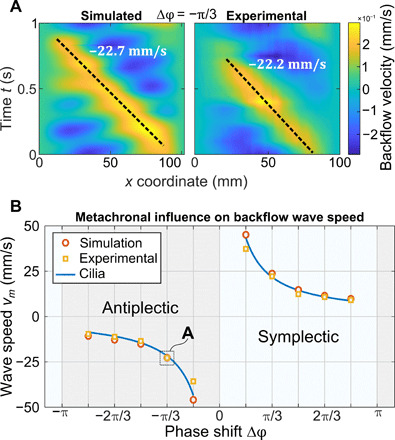
(A) Detailed comparison of kymographs of the same phase shift (−π/3) for simulation and experiment. The slope of the traced line on the direction of the traveling pattern corresponds to the traveling speed of the wave in the fluid. (B) Backflow wave speeds for simulation and experiment in function of the phase shift. Backflow wave speeds match the metachronal wave speed of cilia (blue line), confirming Stokes flow conditions.

DISCUSSION

This paper reports the collective behavior of an array of six soft robotic cilia with 12 degrees of freedom operating in a low Reynolds regime. Each soft robotic cilium is composed of two elastic microactuators that can be addressed individually. These two degrees of freedom allow each artificial cilium to move in a nonreciprocal pattern. In addition, the phase difference between the cilia can be controlled to mimic the metachronal waves observed in biological cilia. Through PIV measurements, we characterize the impact of different metachronal patterns on the fluid transport, corroborating existing theoretical models on ciliary propulsion. Experimental results are compared with fluid dynamics simulations that take into account the soft robotic cilia kinematics and the boundary conditions of our setup. We observed that for small phase difference metachronal waves, antiplectic coordination increases up to 50% of the fluid flow velocity compared to a synchronous beating mode, while symplectic metachrony decreases it. This is caused by an obstruction mechanism between the cilia in the array that hinders the effective flow in case of symplectic waves. In contrast, for slow traveling waves, corresponding to high phase differences, the metachronal effect on flow is less efficient because of the formation of multiple-vortex structures that overall reduce the fluid velocities induced by the cilia. To the best of our knowledge, this is the first experimental system of artificial cilia where nonreciprocal motion and metachronal wavelengths can be tuned independently by individually controlling each cilium. Our work demonstrates experimentally that antiplectic waves with high wavelengths are optimal for fluid transport, which is in accordance with metachronal patterns in biological systems (11).

MATERIALS AND METHODS

Experimental setup

The cilia array is placed along the rectangular side (102 × 20 mm) of a D-shaped channel of 49-mm height (fig. S2). The cilia cover approximately one-third of the channel height, where the remaining space above the cilia is used to characterize the induced fluid flow. The entire setup is made out of black anodized aluminum to reduce unwanted reflections, except for the external front wall and the sides of the rectangular channel that are made out of Plexiglass [poly(methyl methacrylate)] plates. The transparency of these walls allows for observation and laser illumination, respectively, during the PIV analysis. The PIV measurement plane is centered with the cilia tips, 7 mm distant from the inner wall of the channel.

PIV measurements

The velocity of the flow around the cilia and in the main bulk is measured by PIV (37) using fluorescent dye–doped polyethylene microspheres as tracers. These particles have a density of ρ_p = 995 ± 10 kg/m³, a mean diameter of $\overline{D}=49\pm 4$ km, and a Stokes number Stk ≈ 2 · 10⁻¹⁰; therefore, they accurately follow the flow. When the particles are excited by incident laser light, they both scatter light (Mie scattering) and emit light that is redshifted relative to the incident light (Stokes shift). A long-pass filter, with a cutoff wavelength higher than the laser light wavelength, is then used to remove the scattering and only transmit the fluorescent light. The use of fluorescent dye–doped particles as tracers is especially useful when performing PIV in liquids to avoid the contribution of light reflections on the transparent walls and a consequent reduction of the signal-to-noise ratio (S/R). In this experiment, a single-cavity Nd:YAG pulsed laser (λ = 532 nm), synchronized with a complementary metal-oxide semiconductor camera, illuminates the particles. PIV measurement is conducted in time-series mode using an acquisition frequency of 5 Hz for 180 s, capturing a total of 45 cilia beats during one measurement. A schematic of the PIV setup is displayed in fig. S2. Twelve different beating patterns with fixed phase shift have been recorded, changing the phase shifts between recordings equally from −π and π. For each phase shift, 900 PIV images are analyzed via the software DaVis 8.2 (LaVision) using the processing parameters reported in table S1. In this table, the cross-correlation peak ratio is defined as the ratio between the first highest peak of the cross-correlation function divided by the second highest peak. Two passes have been used, both for the initial and the final window size. An example of a cross-correlation map is presented in fig. S4. The seeding density used during the experiment has been computed via image analysis and corresponds to a particle volume fraction (fraction of the particle volume on the fluid volume) pvf = 0.04%. Examples of optical raw images are reported in fig. S3. No particular pre/postprocessing has been conducted. The velocity fields are then averaged over the 45 cilia beats to obtain the 20 mean flow field velocities of a single beat, where the convergence is verified for each flow field (fig. S5). The convergence is obtained by calculating the average error (ε_a) and the SD error (ε_σ) of the fluid velocities for an increasing amount of cycles. Given a fluid velocity u or v at the time $\overline{t}$ of the cycle, the average over N cycles is defined as ${\overline{u}}_N(\overline{t})=\frac{{\Sigma }_{i=1}^N{u}_i(\overline{t})}{N}$ and the SD ${\mathrm{\sigma }}_{\mathrm{uN}}=\sqrt{\frac{{\Sigma }_{i=1}^N{(u_i(\overline{t})-{\overline{u}}_N(\overline{t}))}^2}{N}}$. Therefore, ${\overline{\mathrm{\epsilon }}}_N={\overline{u}}_{N+1}(\overline{t})-{\overline{u}}_N(\overline{t})$ and ε_σN = σ_{uN + 1} − σ_uN.

CFD simulations

To simulate the flow induced by the beating cilia, we have developed a CFD model in which the cilia motion is kinematically described. Because the speed of the beating cilia is low, the drag forces on the cilia remain small so that the cilia do not undergo fluid-induced deformations. The exact geometry of the pneumatic cilia is represented in the CFD model, and their surface is discretized using triangular surface elements (see fig. S6). The centerline motion of the cilia, r^c(s, t), with s being the spatial arc length parameterizing the centerline from its base (0 < s < L) and t being the time (0 < t < T(f⁻¹)), is fitted to the experimental motion for one cilium, using a Fourier series expansion in s and a Taylor series in t. The motion of the cilia surface nodes rⁱ(s, t) is calculated from the cilia centerline motion r^c(s, t). To compute the flow field generated by the ciliary motion, the boundary element method is used. Because of the low Reynolds number (Re = 0.04), we model fluid flow by using the Stokes equation, the solution of which can be written by means of Green’s functions acting in a semi-infinite fluid provided by Blake (38). The drag forces on the cilia surface are treated as a distribution of surface point forces. The velocity u^f(r) at a point in the fluid r due to a point force exerted on the fluid by the cilia at a position r′ on the cilia surface can be obtained as

$${\mathit{u}}^f(\mathit{r})=\mathit{G}(\mathit{r}-{\mathit{r}}^{\prime },h({\mathit{r}}^{\prime }))\mathit{f}(\mathit{r})$$ (1)

with h(r^′)) being the distance of the point force from the substrate and G(r−r^′, h(r′)) The Green’s function for a point force f(r^′) acting in a fluid near a no-slip boundary. These point forces are assumed to be distributed over the surface of the cilia as a traction t(r^′), which is varying linearly over each triangular surface element (39), collectively resulting in the fluid velocity

$${\mathit{u}}^f(\mathit{r})={\displaystyle \underset{j=1}{\overset{\text{nelm}}{\Sigma }}}{\int }_{S_j}\mathit{G}(\mathit{r}-{\mathit{r}}^j,h({\mathit{r}}^j))\mathit{t}({\mathit{r}}^j){\mathit{dS}}_j$$ (2)

with “nelm” being the number of surface elements. As Eq. 2 holds at every point in the fluid, it also holds at every node on the cilium surface u^c(rⁱ). When these equations are assembled in a matrix G, i.e., u^c = Gt, the traction exerted by the cilia on the fluid can be related to its velocity by inverting this relation t = G⁻¹u^c. Once the traction of the cilia surface t is known, we can reuse Eq. 2 to calculate the fluid velocity u^f(r) induced by cilia in the fluid domain through u^f = Gt. Six cilia are accounted for in the fluid domain, represented by a rectangular prism with sides L × W × H = 102 × 20 × 49 mm, in correspondence with the experimental setup (see fig. S7). No-slip boundary conditions are implemented on all channel walls, and the cilia are attached to the bottom wall, coinciding with the semi-infinite no-slip surface defined through Blake’s Green function (38).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/6/49/eabd2508/DC1