Counterfactual simulations underscore the importance of early intervention and aggressive control in combatting COVID-19.
Abstract
Assessing the effects of early nonpharmaceutical interventions on coronavirus disease 2019 (COVID-19) spread is crucial for understanding and planning future control measures to combat the pandemic. We use observations of reported infections and deaths, human mobility data, and a metapopulation transmission model to quantify changes in disease transmission rates in U.S. counties from 15 March to 3 May 2020. We find that marked, asynchronous reductions of the basic reproductive number occurred throughout the United States in association with social distancing and other control measures. Counterfactual simulations indicate that, had these same measures been implemented 1 to 2 weeks earlier, substantial cases and deaths could have been averted and that delayed responses to future increased incidence will facilitate a stronger rebound of infections and death. Our findings underscore the importance of early intervention and aggressive control in combatting the COVID-19 pandemic.
INTRODUCTION
The ongoing coronavirus disease 2019 (COVID-19) pandemic has caused millions of infections and hundreds of thousands of deaths worldwide (1, 2). In the United States, the first imported case of COVID-19 was reported on 20 January 2020 (3). In subsequent weeks, community transmission was established, and the causative pathogen, severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), quickly spread throughout the entire country (2). As of 22 June 2020, more than 2.3 million infections and 120,000 deaths had been confirmed nationwide, making the United States the hardest-hit country in the world to date (4).
In an effort to slow the spread of COVID-19, control measures enforcing social distancing and restricting individual contact were implemented across the United States beginning in mid-March. In other countries, these nonpharmaceutical interventions (NPIs) have successfully limited the spread of COVID-19 (5–12); however, in the United States, the effectiveness of these control measures has been less pronounced. It is therefore important that changes in virus transmissibility within the United States, due to NPIs, be quantified, so that the effects of earlier interventions on cases and deaths can be evaluated.
RESULTS
Inference of COVID-19 transmission dynamics in the United States
In this study, we adapted and applied a dynamic metapopulation model (13, 14) informed by human mobility data (15, 16) (fig. S1) and representing SARS-CoV-2 transmission in 3142 U.S. counties (see Materials and Methods). During the study period, 21 February 2020 to 3 May 2020, measures to control the virus were actively, but heterogeneously, implemented throughout the United States. We explicitly simulated documented and undocumented infections (17), for which separate transmission rates, β and μβ (μ < 1), respectively, are defined. Here, μ is the relative transmissibility of undocumented infections. To reflect heterogeneity in transmission rates across the United States while avoiding a large number of model parameters, we defined a separate βi for counties with greater than 400 cumulative confirmed cases as of 3 May 2020 (n = 311) (fig. S1). The remaining 2831 counties were apportioned among 16 additional transmission rate parameters depending on cumulative case levels and population density (see Materials and Methods). Other parameters in the model include the ascertainment rate, α, which represents the fraction of infections documented as confirmed cases; the average latency period, Z; the average duration of infectiousness, D; and a travel multiplicative factor, θ.
The metapopulation model explicitly simulates intercounty mobility using observed rates of intercounty visits to points of interest (POI) (e.g., restaurants, stores, etc.) on a county-by-county basis. Intracounty mobility is not represented as the relationship between mobility and disease transmission is unknown. Instead, we inferred changing transmission rates within counties using time series records of COVID-19 activity. This parameter estimation was performed using the ensemble adjustment Kalman filter (EAKF) (18) in conjunction with county-level observations of both daily reported cases and deaths in the United States (see Materials and Methods and Supplementary Materials) (19). We focus on the national fitting, as well as major metropolitan areas with large populations and abundant data, for which parameter estimates are well informed. Further, as many states reopened portions of their economies in early May, the study period was limited to 21 February 2020 to 3 May 2020 when active control efforts were in place.
Daily cases and deaths in the United States and the New York metropolitan area are well fit by the transmission model (Fig. 1, A to D). Model estimates for counties with large number of cases and deaths (fig. S2) yield low discrepancy from observations (table S1). The inferred basic reproductive numbers, Rt ≡ βD[α + (1 − α)μ] (17, 20), for six metropolitan areas—New York, New Orleans, Los Angeles, Chicago, Boston, and Miami—on five dates (15 March, 29 March, 12 April, 26 April, and 3 May) are shown in Table 1 (see Materials and Methods). After 15 March, Rt in all six metropolitan areas decreases substantially in association with the implementation of social distancing policies and practices (fig. S3). The estimated effective reproductive numbers, Re ≡ βD[α + (1 − α)μ]S/N, for these six metropolitan areas also decrease after 15 March 2020 (Fig. 1E). In three of the six metropolitan areas, Re is well below 1 as of 3 May 2020. For Chicago, Los Angeles, and Miami, where daily confirmed cases and deaths were still increasing or becoming stable (fig. S1), Re is close to 1. In the New York metropolitan area, Re dropped below 1 on 4 April and continued decreasing since then. The estimated nationwide ascertainment rate declined from 0.20 around 16 March, a time of rapid COVID-19 spread and then stabilized around 0.1 after 5 April (Fig. 1F). Note that this finding indicates that, before 5 April, although testing capacity had increased substantially, daily new infections increased faster, yielding a declining ascertainment rate.
Fig. 1. Model fit and parameter inference.
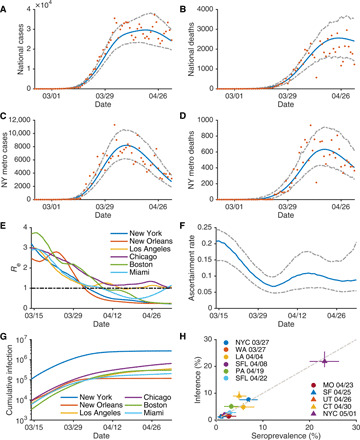
Posterior fitting to daily cases and deaths in the United States (A and B) and the New York metropolitan area (C and D). Orange dots represent observations. Blue and gray lines are the median estimate and 95% CIs, respectively. The estimated effective reproductive number, Re, in six metropolitan areas are shown in (E). The black dotted line indicates Re = 1. (F) The estimated ascertainment rate over time. The blue line and gray dashed lines are the median estimates and 95% CIs, respectively. (G) The estimated cumulative infections (both reported and unreported) in six metropolitan areas. We compare the reported seroprevalence (%) in nine locations on different dates with the inferred percentage cumulative infections on those dates in (H). Whiskers show 95% CIs. Details on the serological survey are provided in Materials and Methods.
Table 1. Estimated basic reproductive numbers.
Estimated basic reproductive numbers (Rt) for the New York, New Orleans, Los Angeles, Chicago, Boston, and Miami metropolitan areas on 15 March, 29 March, 12 April, 26 April, and 3 May. Mean estimate (95% CIs) are presented.
| 15 March | 29 March | 12 April | 26 April | 3 May | |
| New York | 3.10 (2.76, 3.45) | 1.63 (1.41, 1.88) | 0.60 (0.52, 0.66) | 0.38 (0.32, 0.43) | 0.34 (0.30, 0.40) |
| New Orleans | 2.50 (2.11, 2.89) | 1.91 (1.65, 2.27) | 0.44 (0.34, 0.55) | 0.29 (0.22, 0.36) | 0.27 (0.21, 0.34) |
| Los Angeles | 3.12 (2.56, 3.72) | 1.35 (1.06, 1.71) | 1.16 (0.89, 1.38) | 1.17 (0.89, 1.44) | 1.18 (0.91, 1.44) |
| Chicago | 2.84 (2.41, 3.34) | 2.04 (1.74, 2.36) | 1.11 (0.92, 1.29) | 1.39 (1.14, 1.66) | 1.13 (0.92, 1.34) |
| Boston | 3.86 (3.28, 4.47) | 2.19 (1.73, 2.57) | 0.95 (0.77, 1.08) | 0.41 (0.32, 0.54) | 0.33 (0.26,0.40) |
| Miami | 2.96 (2.56, 3.45) | 1.38 (1.12, 1.68) | 0.78 (0.60, 0.96) | 0.76 (0.57, 0.88) | 1.32 (1.07, 1.52) |
Estimated cumulative infections (both reported and unreported) for the New York metropolitan area on 15 March 2020 are one order of magnitude higher than for the other five metropolitan areas (Fig. 1G). Thus, although the estimated Re in New York from 15 March to 3 May 2020 was comparable to or lower than these other areas, the attack rate in New York remains roughly an order of magnitude higher through 3 May 2020. We also overlaid the inferred Rt for the six metropolitan areas with the dates on which local social distancing orders were announced (fig. S3) (21). In general, Rt decreases as more interventions are implemented; however, there are no abrupt changes of Rt associated with the timing of the local interventions, possibly due to a more gradual adjustment of individual human behaviors. The estimated effective reproductive numbers on five dates (15 March, 29 March, 12 April, 26 April, and 3 May) for 311 counties with cumulative cases ≥400 as of 3 May are available online (22). Sensitivity analysis indicates that the inference results are robust to the duration of daytime and nighttime transmission imposed in the model (fig. S4).
Asynchronous transmission reduction in the United States
We observe an asynchronous reduction of Re among counties with 400 or more cases by 3 May, and across all 3142 counties, the estimated effective reproductive numbers exhibit considerable variability (fig. S5). To visualize the speed at which local transmission rates were reduced, we show the first dates when Re dropped below certain threshold values (1.5, 1.25, 1, and 0.75) and stayed below those thresholds until 3 May (Fig. 2). Some metropolitan areas such as San Francisco, New York City, and New Orleans reduced Re below 1 during April and kept it below 1 through 3 May. Less populous counties in the mountain region of the United States also have low effective reproductive numbers, possibly due to lower population density supporting fewer opportunities for sustained transmission. At the same time, a large number of counties still have Re above 1 as of 3 May, indicating that local transmission had not yet been effectively curbed. The asynchronous reduction of transmission rates, partly due to different timelines of local control orders, differing compliance to social distancing rules, and differing starting values of Re, complicates containment and control of COVID-19. Locations with sustained transmission can reintroduce infections to locations where transmission is well suppressed, once control measures are relaxed or lifted, possibly increasing opportunities for local transmission and case growth.
Fig. 2. Asynchronous reduction of effective reproductive numbers.
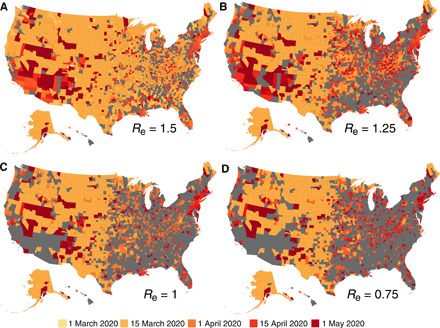
For each county, we show the date when the local effective reproductive number dropped below 1.5 (A), 1.25 (B), 1 (C), and 0.75 (D) and stayed below that threshold until 3 May. Counties in gray are those that either never reached the threshold or failed to remain below the threshold.
The model inference system enables estimation of the evolution of susceptibility in county populations during the pandemic. Nationwide, 95.4% (93.8 to 96.6%) of the U.S. population remained susceptible as of 3 May, with notable differences in key metropolitan areas (fig. S6). Specifically, the estimated susceptible population percentage in the New York metropolitan area was 75.5% (70.5 to 79.4%), which roughly agrees with the 21% seroprevalence reported for New York City on 23 April (23). Further, the estimated cumulative percentage of infected individuals also generally agrees with the reported seroprevalence rates obtained from an independent large-scale serological study (24, 25) for a variety of locations and dates (Fig. 1H). On 3 May, even those counties with a large number of confirmed cases still had high population susceptibility, revealing an absence of herd immunity and continued risk of additional COVID-19 waves. The estimated susceptible population on 3 May in the 100 counties with the most reported cases is available at (22). Additional validations of the estimates of Rt and initial prevalence in the United States against other independent studies are provided in Materials and Methods.
Counterfactual simulations of COVID-19 spread
The inference results indicate that the NPIs varyingly adopted in the United States after 15 March reduced rates of COVID-19 transmission. During the initial growth of a pandemic, infections increase exponentially. As a consequence, early intervention and rapid response are critical for limiting morbidity and mortality. To quantify the effects of earlier interventions on COVID-19 outcomes in the United States, we performed two counterfactual simulations in which the sequence of transmission rates and ascertainment rate inferred for 15 March to 3 May 2020 were shifted back 1 and 2 weeks, i.e., to 8 March and 1 March 2020, respectively. Specifically, we ran the inference from 21 February to 8 or 1 March to constrain the initial model state and then applied the daily posterior parameters, i.e., α and βs, as estimated beginning 15 March. The simulations were generated until 3 May 2020. For the last 1 to 2 weeks without inferred parameters due to the shift in the time window, we applied the final parameter estimates of 3 May 2020, the last day of inference. This approach shifts the asynchronous control timelines for different counties back 1 or 2 weeks, something that a local or aggregate transmission model representing a single geography cannot represent. Further, the metapopulation model construct enables incorporation of the intercounty dynamical interaction of disease transmission, which is crucial for the spatial expansion of COVID-19 during the early stage of the pandemic.
The counterfactual simulations indicate that had observed control measures been adopted 1 week earlier, then the United States would have avoided 601,667 [95% credible interval (CI): 464,381 to 722,880] [52.6% (40.6 to 63.1%)] confirmed cases and 32,335 (23,600 to 40,573) [49.4% (36.1 to 62.0%)] deaths nationwide as of 3 May 2020 (Fig. 3, A and B). In the New York metropolitan area, the epicenter of COVID-19 in the United States at that time, 191,356 (155,726 to 210,593) [72.9% (59.3 to 80.0%)] confirmed cases and 16,950 (14,258 to 18,595) [77.9% (65.5 to 85.5%)] deaths would have been avoided if the same sequence of interventions had been applied one week earlier (Fig. 3, C and D). A more pronounced control effect would have been achieved had the sequence of control measures occurred 2 weeks earlier: A reduction of 1,041,261 (996,933 to 1,076,703) [91.0% (87.1 to 94.0%)] cases and 59,351 (56,238 to 61,789) [90.8% (86.0 to 94.5%)] deaths in the United States (Fig. 3, E and F) and 254,087 (246,134 to 257,738) [96.8% (93.7 to 98.2%)] cases and 21,175 (20,427 to 21,553) [97.3% (93.9 to 99.0%)] deaths in the New York metropolitan area (Fig. 3, G and H). These marked reductions in morbidity and mortality due to more timely deployment of control measures highlight the critical need for aggressive, early response to the COVID-19 pandemic.
Fig. 3. Counterfactual simulations with control interventions beginning in early March, 1 and 2 weeks earlier than implemented.
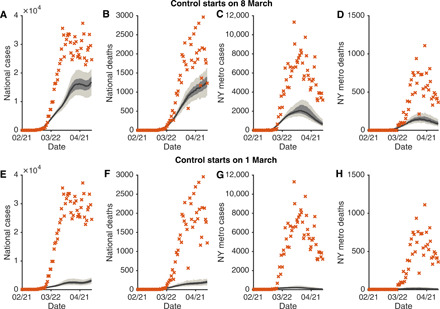
Daily cases and deaths in the United States (A, B, E, and F) and the New York metropolitan area (C, D, G, and H) under early interventions are compared with the observations (orange crosses). The top and bottom rows present counterfactuals with interventions implemented on 8 and 1 March, respectively. The black lines and surrounding bands show the median estimate, interquartile, and 95% CIs.
Simulation of control relaxation and delayed response
Now that COVID-19 is established as a global pandemic, rapid response remains essential to avoid large-scale resurgences of infections and deaths in locations with reopening plans. We quantify the effect of response time on the timing and magnitude of rebound outbreaks in the United States through further simulations. Specifically, we assume that control measures are relaxed beginning 4 May 2020 in all U.S. counties, resulting in a weekly 5% increase in the local transmission rate, β, in each county. If weekly confirmed case numbers increase for 2 or 3 consecutive weeks in a county after relaxation, then a reactive 25% weekly reduction of transmission rates, equivalent to the average transmission rate reduction before 4 May 2020 (fig. S3), is imposed in this county and maintained until local weekly case numbers decline.
For both scenarios, a decline of daily confirmed cases continues for almost 2 weeks after easing of control measures (Fig. 4, A and B). This decreasing trend, caused by the NPIs in place before 4 May 2020, coupled with the lag between infection acquisition and case confirmation, conveys a false signal that the pandemic is well under control. Unfortunately, because of high remaining population susceptibility, a large resurgence of cases follows, peaking in early- and mid-June, despite the resumption of NPI measures. For the 2-week response, increased mortality is less obvious due to a longer lag that disperses deaths over a longer time span (Fig. 4C and fig. S7); however, a 1-week further delay in local response to the resumption of control measures results in a marked resurgence in national deaths (Fig. 4D). Another scenario assuming a one-time 5% increase of transmission rates after control relaxation yielded similar results.
Fig. 4. Effects of response time after control measures are relaxed.
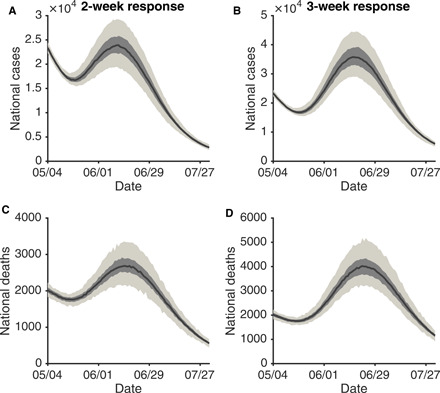
We assume a control relaxation (a weekly 5% increase of the transmission rate) starting on 4 May in all U.S. counties. If the local weekly case number in a county increases for 2 or 3 consecutive weeks, a weekly 25% reduction of the transmission rate is imposed for that county. Daily cases and deaths in the United States for a response time of 2 weeks (A and C) and 3 weeks (B and D) are compared. The black lines and bands show the median estimate, interquartile, and 95% CIs.
Aggregating case and death numbers to national scale could mask marked differences in local transmission. We inspected the relaxation simulations in six counties within the focus metropolitan areas (fig. S8). For counties that have Re well below 1 (viz New York County NY, Orleans Parish LA, and Suffolk County MA), relaxing control measures does not lead to increased cases and deaths, as the increased effective reproductive numbers remain below 1. In contrast, reopenings in counties with Re close to 1 (viz Los Angeles County CA, Cook County IL, and Palm Beach County FL) do produce case growth.
To further highlight the effect of heterogeneous timelines of reopening among different locations, we also ran a simulation in which Florida reopens on 4 May 2020, resulting in a 20% increase in local transmission rates, but control measures in other states remain in place. We examined the daily cases and deaths in the following 30 days in Georgia and Alabama, the two states adjacent to Florida, and compared these outcomes with a baseline scenario in which no state reopens. The results indicate that reopening in Florida leads to increased numbers of cases and deaths in Georgia and Alabama (fig. S9); this increase manifests with a 1-week lag.
DISCUSSION
Unlike a local model describing the transmission dynamics within a single, independent site, the metapopulation model developed here allows study of the effect of asynchronous interventions across different locations. The transmission of SARS-CoV-2 in the United States is a complex dynamical process with rapid spatial progression modulated by local control efforts. In particular, interventions in one location affect transmission in other places by altering the external force of infection via importations. Without spatial structure, the inference system cannot properly capture the dynamical coupling of disease transmission across locations.
The counterfactual experiments presented here (Fig. 3) are based on idealized assumptions. In practice, initiating and implementing interventions earlier during an outbreak are complicated by factors such as general uncertainty, economic concerns, logistics, and the administrative decision process. Public compliance with social distancing rules may also lag due to suboptimal awareness of infection risk. We acknowledge that our counterfactual experiments have simplified these processes; however, we note that by the end of February 2020, a number of other countries, including South Korea and Italy, were already aggressively responding to the virus (26). Our findings indicate that had control measures and reductions of Re in the United States been implemented at a similar time, just 1 to 2 weeks earlier, substantially fewer cases and deaths would have occurred before 3 May. Further, given that more effective control of COVID-19 has been maintained to date in countries such as South Korea, New Zealand, Vietnam, and Iceland, these cases and deaths could have been averted, not merely postponed.
Our model experiments also indicate that rapid detection of increasing case numbers and fast reimplementation of control measures are needed to control rebound outbreaks of COVID-19 (Fig. 4). In these experiments, we assume the ability to reimplement a 25% weekly reduction of transmission rates nationwide. Because of general public fatigue toward NPIs and inconsistent compliance with control measures, this assumed reduction may be overly optimistic.
In this study, we have quantified the sensitivity of COVID-19 cases and deaths to the timing of control measures. Our results demonstrate the marked impact that earlier interventions could have had on the COVID-19 pandemic in the United States. Looking forward, the findings underscore the need for continued vigilance when control measures are relaxed. We recognize the burdens imposed by protracted shutdowns; however, it is vital to balance the dual ambitions of renewing social and economic activity and avoiding a recrudescence.
Countries such as South Korea, Vietnam, New Zealand, and Germany have shown that such a balance may be achievable; the strategies adopted in these countries could be used to guide policies in the United States and elsewhere. Specifically, broader testing and contact tracing capacity (27) are crucial to detect a rebound of COVID-19 before it is well underway (28). Susceptibility to SARS-CoV-2 infection remains high throughout the United States (fig. S6) and can readily support an exponential growth of cases and deaths (29). In addition, potential short-lived immunity against SARS-CoV-2 could replenish the susceptible population (30). Given this situation, economic reopening and loosening of NPI measures would be more safely effected in localities in which Re is well below 1, daily confirmed cases are low, and abundant testing and contact tracing are available to aid isolation and quarantine measures.
Since the initial submission of this paper at the end of May, following a relaxation of intervention measures, the United States has experienced a massive resurgence of infections primarily driven by activity in southern states. In addition, some of the countries that managed to better limit COVID-19 transmission through July 2020 also saw rebounds of infections in August and September. These experiences underscore the necessity of maintaining control measures until sound public health targets are achieved, so that gains in outbreak control are preserved and the cumulative case burden over the entire course of the pandemic is substantially lower than what would result with no NPIs in place.
MATERIALS AND METHODS
The metapopulation model
We use a metapopulation susceptible-exposed-infectious-recovered (SEIR) model to simulate the transmission of COVID-19 among 3142 U.S. counties. In this model, we consider two types of movement: daily work commuting and random movement. Information on county-to-county work commuting is publicly available from the U.S. Census Bureau (15). We further assume that the number of random visitors between two counties is proportional to the average number of commuters between them (13). As the population present in each county is different during daytime and nighttime, we model the transmission dynamics of COVID-19 separately for these two time periods.
We formulate the transmission as a discrete Markov process during both day and night times. Daytime transmission lasts for dt1 days and the nighttime transmission dt2 days (dt1 + dt2 = 1). Here, we assume that daytime transmission lasts for 8 hours, and nighttime transmission lasts for 16 hours, i.e., dt1 = 1/3 day and dt2 = 2/3 day. A model with daytime and nighttime transmission each lasting for 12 hours (dt1 = 1/2 day and dt2 = 1/2 day) yielded similar results (fig. S4). The transmission dynamics are depicted by eqs. S1 to S10 in the Supplementary Materials. In these equations, we define Sij, Eij, , , and Nij as the susceptible, exposed, reported infected, unreported infected, and total population in the subpopulation commuting from county j to county i (i ← j). We also introduce the following model parameters: β is the transmission rate of reported infections, μ is the relative transmissibility of unreported infections, Z is the average latency period (from infection to contagiousness), D is the average duration of contagiousness, α is the fraction of documented infections, and θ is a multiplicative factor adjusting random movement. Note that, in this model, we assume a separate transmission rate, μβ, for undocumented infections, many of whom may experience few or no symptoms. Our previous study in China indicates that the undocumented infections are less contagious than documented infections (17). In addition, we assume a nationwide uniform ascertainment rate α, given that per capita test numbers across different states are generally the same order of magnitude (fig. S7). We integrated eqs. S1 to S10 using a Poisson process to represent the stochasticity of the transmission process.
The transmission model generates daily confirmed cases and deaths for each county. To map infections to deaths, we used an age-stratified infection fatality rate (IFR) and computed the IFR for each county as a weighted average using demographic information on local age structure (31). To account for reporting delays, we mapped simulated documented infections to confirmed cases using a separate observational delay model. In this delay model, we account for the time interval between a person transitioning from latent to contagious (i.e., E → ) and observational confirmation of that individual infection. To estimate this delay period, Td, we examined a U.S. line list data record consisting of 2.67 million confirmed cases (32). Before 3 May 2020, the time-to-event distribution of the interval (in days) from symptom onset to case confirmation is well fit by a gamma distribution (a = 2.6, b = 4.9, mean=12.9 days; fig. S7). Consequently, we adopted a gamma distribution to model Td but added another 2.5 days to the mean periods (ab), as symptom onset is estimated to lag the onset of contagiousness (17). Recent studies on viral dynamics also indicate that presymptomatic infection is common, and infected people can become contagious 2 days before symptom onset (33). As a result, we adopted Td = 15.4 days (a = 2.6, b = 5.9) in this study. On the basis of daily incidence and death data in the United States, the national death curve has a 7-day lag compared with the incidence curve (fig. S7). As a result, we used a gamma distribution with a mean of 22.4 days (a = 2.6, b = 8.6) to represent the delay between a person transitioning from latent to contagious and death.
To represent variability in transmission rates through space and time, we introduced separate estimates for β in the 311 U.S. counties with 400 or more cumulative cases as of 3 May 2020. The remaining counties were classified into 16 groups (evenly distributed into a four-by-four grouping based on cumulative cases and population density), for which separate transmission rates were defined. In total, 327 transmission rates (βi) were estimated in the transmission model. Using the next-generation matrix approach, we derived the local basic reproductive number, Rt = βD[α + (1 − α)μ]. The effective reproductive number in each metropolitan area is the population weighted average of Re in constituent counties.
Data
We used the 2011–2015 5-Year American Commuting Survey (ACS) Commuting Flows data from the U.S. census survey to prescribe the intercounty movement in the transmission model before 15 March 2020 before broad control measures were announced. The county-to-county commuting data are publicly available from the U.S. Census Bureau (15). We visualize the intercounty commuting in fig. S1. After 15 March, the census survey data are no longer representative due to changes of mobility behavior in response to control measures. Therefore, after 15 March 2020, we use estimates of the reduction of intercounty visitors to POI (e.g., restaurants, stores, etc.) to inform the decline of intercounty movement on a county-by-county basis (16). For instance, if the number of intercounty visitors was reduced by 30% in a county on a given day relative to baseline estimates on 15 March 2020, then the size of subpopulations traveling to this county would be reduced by 30% accordingly. These real-time mobility data are available between 1 March 2020 and 7 June 2020. For dates beyond 7 June 2020, we maintained the last known level of intercounty movement.
County-level daily confirmed cases and deaths were compiled by USAFacts (19). Daily cases and deaths in the six metropolitan areas are shown in fig. S1.
Model calibration
To derive an estimate of model parameters, we calibrated the transmission model against county-level incidence data reported from 21 February 2020 to 12 May 2020 and death data reported from 21 February 2020 to 19 May 2020. Specifically, we estimated model parameters using a sequential data assimilation technique. The metapopulation model is a high-dimensional system with 60,232 subpopulations. We therefore applied an efficient data assimilation algorithm—the EAKF (18), which is applicable to high-dimensional model structures, to infer model parameters. The EAKF has been successfully used to infer parameters for seasonal and pandemic influenza and other infectious diseases (34–40).
To improve the identifiability of this high-dimensional model, we further reduced the number of unknown parameters by fixing disease-related parameters (Z, D, and μ) and the mobility factor (θ). These parameters were estimated using the posterior distributions inferred from case data through 13 March 2020 (14). Specifically, we randomly drew these parameters from the posterior ensemble members: Z = 3.59 (95% CI: 3.28 to 3.99), D = 3.56 (3.21 to 3.83), μ = 0.64 (0.56 to 0.70), and θ = 0.15 (0.12 to 0.17).
From 21 February 2020 to 3 May 2020, we performed EAKF inference each day using both case and death data to estimate the ascertainment rate α and transmission rates βi. The prior for the ascertainment rate was drawn from a distribution with a median value α = 0.080 (95% CI: 0.069 to 0.093), estimated in a previous study. The prior transmission rates were scaled on the basis of the local population density using the following relation: Here, PDi is the population density in county i, median(log10(PD)) is the median value of log-transformed population density among all counties, and β is the transmission rate estimated before 13 March 2020 (β0 = 0.95, 95% CI: 0.84 to 1.06). For β shared by multiple counties, population density PDi is averaged over those counties. To account for reporting delays of confirmed cases and deaths, at each daily model update, we integrated the model forward for 14 days using the prior model state and used incidence 10 days ahead and deaths 14 days ahead to constrain current model variables and parameters (i.e., the modes of gamma distributions for delays). Given the large number of parameters in the model, the inference system may not be fully identifiable. To alleviate this issue, we imposed a ±30% limit on the daily change of parameters α and βi. This smoothing constraint is reasonable considering the continuity of human behavioral change. Sensitivity tests obtained similar results with ±25 and ±35% smoothing constraints. A full list of settings for model parameters and variables is presented in Table 2.
Table 2. Setting initial parameters and variables.
The prior transmission rate in each county is scaled by population density using a baseline transmission rate β0 as inferred through 13 March 2020. The relative transmission rate (μ), latency period (Z), infectious period (D), and mobility factor (θ) are fixed at posterior values inferred through 13 March 2020. Values are shown for the median and 95% CIs in the parentheses. The initial numbers of exposed individuals E and unreported infected individuals Iu are drawn from uniform distributions U(0,18C) and U(0,20C) 9 days before the reporting date (T0) of the first case. Here, C is the total number of reported cases between days T0 and T0 + 4.
| Parameter/variable | Values |
| Baseline transmission rate (β0, day−1) | 0.95 (0.84, 1.06) |
| Relative transmission rate (μ) | 0.64 (0.56, 0.70) |
| Latency period (Z, day) | 3.59 (3.28, 3.99) |
| Infectious period (D, day) | 3.56 (3.21, 3.83) |
| Mobility factor (θ) | 0.15 (0.12, 0.17) |
| Reporting rate (α), prior | 0.080 (0.069, 0.093) |
| Initial exposed population (E) | U(0,20C) |
| Initial unreported infected population (Iu) | U(0,18C) |
In total, we performed 20 independent inference runs. The inference results reported in Fig. 1 were obtained from all posterior ensemble members. Implementation details and system initialization are reported in the next section.
We evaluate the goodness of fit at county level using percentage absolute error (PAE) and percentage error (PE). Specifically, we define PAE = Σt∣fitt − obst∣/Σtobst and PE = Σt(fitt − obst)/Σtobst, where fitt is the mean posterior fitting to case or death number and obst is the reported case or death number on day t. The PAE and PE values for cases and deaths in 100 counties are reported in table S1.
System initialization
To initialize the model, we seeded exposed individuals (E) and unreported infections (Iu) in counties with at least one confirmed case before 14 March 2020. Unlike the situation in China, where the outbreak originated from a single city, importation to multiple locations in the United States likely initiated community transmission. To reflect this potential ongoing community transmission before the reporting of the first local infection, for each county with confirmed cases before 14 March, we randomly drew E and Iu from uniform distributions [0,20C] and [0,18C] 9 days before the reporting date (T0) of the first case. Here, C is the total number of reported cases between day T0 and T0 + 4.
The rationale for this seeding strategy is as follows. If an average reporting delay of 9 days is assumed, then we can estimate Ir on day T0 − 9 as , where is the average number of daily cases during the first 5 days with reported cases (T0 to T0 + 4). If we use the upper bound of 5 days for D, then Ir is estimated as C, which is also an upper bound. We assume the mean Iu on day T0 − 9 is 9C, implying a reporting rate of 1/10 = 10%. Drawing Iu from [0,18C] leads to a broader prior range of the reporting rate. As both Ir and Iu were evolved from the exposed population E, we draw E from the range [0,20C]. This crude calculation provides a seeding range for U.S. counties. During inference, this seeding can be adjusted up or down by the filter. The posterior model fittings capture observed outcomes well (table S1).
Metropolitan areas
In this study, we report the transmission dynamics in six metropolitan areas with dense populations and abundant observations: New York, New Orleans, Los Angeles, Chicago, Boston, and Miami. The counties in these metropolitan areas are the following:
-
1)
New York: Kings County NY, Queens County NY, New York County NY, Bronx County NY, Richmond County NY, Westchester County NY, Bergen County NJ, Hudson County NJ, Passaic County NJ, Putnam County NY, and Rockland County NY
-
2)
New Orleans: Jefferson Parish LA, Orleans Parish LA, St. John the Baptist Parish LA, and St. Tammany Parish LA
-
3)
Los Angeles: Los Angeles County CA and Orange County CA
-
4)
Chicago: Cook County IL, DuPage County IL, Kane County IL, McHenry County IL, and Will County IL
-
5)
Boston: Norfolk County MA, Plymouth County MA, and Suffolk County MA
-
6)
Miami: Miami-Dade County FL, Broward County FL, and Palm Beach County FL.
Seroprevalence surveys
The seroprevalence of antibodies to SARS-CoV-2 in several locations in the United States is available from the U.S. Centers for Disease Control and Prevention website (24, 25). Here, we used seroprevalence data available for dates before 3 May 2020. Those sites are as follows: (i) NYC: Manhattan, Bronx, Queens, Kings, and Nassau. (ii) WA: King, Snohomish, Pierce, Kitsap, and Grays Harbor. (iii) LA: state wide. (iv) SFL (south Florida): Miami-Dade, Broward, Palm Beach, and Martin. (v) PA: Bucks, Chester, Cumberland, Delaware, Lancaster, Montgomery, and Philadelphia. (vi) MO: statewide. (vii) SF (San Francisco): Martin, Contra Costa, Alameda, Santa Clara, San Mateo, and San Francisco. (viii) UT: statewide. (ix) CT: statewide.
Further validation of inference results
We compared our inferred Rt values at the state level with estimated Rt values reported at https://rt.live/. The Pearson correlation coefficient is 0.76, indicating a general agreement in trend. A recent study estimated that 108,689 (95% CI: 1023 to 14,182,310) infections occurred in the United States before 12 March 2020 (41). Our inference estimated 236,207 (95% CI: 193,855 to 298,937) total infections in the United States by that date, which is within the CI and in line with the magnitude of the best estimate from that study.
Supplementary Material
Acknowledgments
We thank SafeGraph for sharing the human mobility data and Columbia University Mailman School of Public Health for high-performance computing resources. Funding: This study was supported by funding from the NIH (GM110748) and the NSF (DMS-2027369), as well as a gift from the Morris-Singer Foundation. Author contributions: S.P. and J.S. designed the study. S.P. and S.K. performed the analysis. All authors wrote and reviewed the manuscript. Competing interests: J.S. and Columbia University disclose partial ownership of SK Analytics. J.S. discloses consulting for BNI. All other authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Code and data are available at https://github.com/shaman-lab/Counterfactual. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/sciadv.abd6370/DC1
REFERENCES AND NOTES
- 1.World Health Organization, Coronavirus disease (COVID-2019) situation reports, www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports/ [accessed 22 June 2020].
- 2.Centers for Disease Control and Prevention, www.cdc.gov/coronavirus/2019-ncov/index.html [accessed 22 June 2020].
- 3.Holshue M. L., DeBolt C., Lindquist S., Lofy K. H., Wiesman J., Bruce H., Spitters C., Ericson K., Wilkerson S., Tural A., Diaz G., Cohn A., Fox L. A., Patel A., Gerber S. I., Kim L., Tong S., Lu X., Lindstrom S., Pallansch M. A., Weldon W. C., Biggs H. M., Uyeki T. M., Pillai S. K.; Washington State 2019-nCoV Case Investigation Team , First case of 2019 novel coronavirus in the United States. N. Engl. J. Med. 382, 929–936 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.The New York Times, Coronavirus in the U.S.: Latest Map and Case Count, www.nytimes.com/interactive/2020/us/coronavirus-us-cases.html [accessed 22 June 2020].
- 5.Lai S., Ruktanonchai N. W., Zhou L., Prosper O., Luo W., Floyd J. R., Wesolowski A., Santillana M., Zhang C., Du X., Yu H., Tatem A. J., Effect of non-pharmaceutical interventions to contain COVID-19 in China. Nature 585, 410–413 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chinazzi M., Davis J. T., Ajelli M., Gioannini C., Litvinova M., Merler S., Piontti A. P. Y., Mu K., Rossi L., Sun K., Viboud C., Xiong X., Yu H., Halloran M. E., Longini I. M. Jr., Vespignani A., The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 368, 395–400 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tian H., Liu Y., Li Y., Wu C.-H., Chen B., Kraemer M. U. G., Li B., Cai J., Xu B., Yang Q., Wang B., Yang P., Cui Y., Song Y., Zheng P., Wang Q., Bjornstad O. N., Yang R., Grenfell B. T., Pybus O. G., Dye C., An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science 368, 638–642 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Maier B. F., Brockmann D., Effective containment explains subexponential growth in recent confirmed COVID-19 cases in China. Science 368, 742–746 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang J., Litvinova M., Liang Y., Wang Y., Wang W., Zhao S., Wu Q., Merler S., Viboud C., Vespignani A., Ajelli M., Yu H., Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 368, 1481–1486 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kraemer M. U. G., Yang C.-H., Gutierrez B., Wu C.-H., Klein B., Pigott D. M.; Open COVID- Data Working Group, du Plessis L., Faria N. R., Li R., Hanage W. P., Brownstein J. S., Layan M., Vespignani A., Tian H., Dye C., Pybus O. G., Scarpino S. V., The effect of human mobility and control measures on the COVID-19 epidemic in China. Science 368, 493–497 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dehning J., Zierenberg J., Spitzner F. P., Wibral M., Neto J. P., Wilczek M., Priesemann V., Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 369, eabb9789 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Salje H., Kiem C. T., Lefrancq N., Courtejoie N., Bosetti P., Paireau J., Andronico A., Hozé N., Richet J., Dubost C.-L., Strat Y. L., Lessler J., Levy-Bruhl D., Fontanet A., Opatowski L., Boelle P.-Y., Cauchemez S., Estimating the burden of SARS-CoV-2 in France. Science 369, 208–211 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pei S., Kandula S., Yang W., Shaman J., Forecasting the spatial transmission of influenza in the United States. Proc. Natl. Acad. Sci. U.S.A. 115, 2752–2757 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pei S., Shaman J., Initial Simulation of SARS-CoV2 Spread and Intervention Effects in the Continental US. medRxiv 2020.03.21.20040303 , (2020). [Google Scholar]
- 15.United States Census Bureau. 2011–2015 5-Year ACS Commuting Flows, www.census.gov/data/tables/2015/demo/metro-micro/commuting-flows-2015.html [accessed 3 May 2020].
- 16.SafeGraph, [accessed May 3 2020] www.safegraph.com/.
- 17.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J., Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV-2). Science 368, 489–493 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Anderson J. L., An ensemble adjustment Kalman filter for data assimilation. Mon. Weather Rev. 129, 2884–2903 (2001). [Google Scholar]
- 19.USAFACTS, https://usafacts.org/visualizations/coronavirus-covid-19-spread-map/ [accessed 4 May 2020].
- 20.Diekmann O., Heesterbeek J. A. P., Roberts M. G., The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 7, 873–885 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.The COVID Analysis and Mapping of Policies Project, https://covid-local.org/amp/ [accessed 1 September 2020].
- 22.https://github.com/shaman-lab/Counterfactual.
- 23.J. D. Goodman, M. Rothfeld, 1 in 5 New Yorkers May Have Had Covid-19, Antibody Tests Suggest, www.nytimes.com/2020/04/23/nyregion/coronavirus-antibodies-test-ny.html [accessed 22 June 2020].
- 24.Havers F. P., Reed C., Lim T., Montgomery J. M., Klena J. D., Hall A. J., Fry A. M., Cannon D. L., Chiang C.-F., Gibbons A., Krapiunaya I., Morales-Betoulle M., Roguski K., Rasheed M. A. U., Freeman B., Lester S., Mills L., Carroll D. S., Owen S. M., Johnson J. A., Semenova V., Blackmore C., Blog D., Chai S. J., Dunn A., Hand J., Jain S., Lindquist S., Lynfield R., Pritchard S., Sokol T., Sosa L., Turabelidze G., Watkins S. M., Wiesman J., Williams R. W., Yendell S., Schiffer J., Thornburg N. J., Seroprevalence of Antibodies to SARS-CoV-2 in 10 Sites in the United States, March 23–May 12, 2020. JAMA Intern. Med. 10.1001/jamainternmed.2020.4130 , (2020). [DOI] [PubMed] [Google Scholar]
- 25.Large-scale Geographic Seroprevalence Surveys, [accessed September 1 2020] www.cdc.gov/coronavirus/2019-ncov/cases-updates/geographic-seroprevalence-surveys.html.
- 26.Hsiang S., Allen D., Annan-Phan S., Bell K., Bolliger I., Chong T., Druckenmiller H., Huang L. Y., Hultgren A., Krasovich E., Lau P., Lee J., Rolf E., Tseng J., Wu T., The effect of large-scale anti-contagion policies on the COVID-19 pandemic. Nature 584, 262–267 (2020). [DOI] [PubMed] [Google Scholar]
- 27.Ferretti L., Wymant C., Kendall M., Zhao L., Nurtay A., Abeler-Dörner L., Parker M., Bonsall D., Fraser C., Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science 368, eabb6936 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yamana T., Pei S., Shaman J., Projection of COVID-19 cases and deaths in the US as individual states re-open May 4,2020. medRxiv 2020.05.04.20090670 , (2020). [Google Scholar]
- 29.Baker R. E., Yang W., Vecchi G. A., Metcalf C. J. E., Grenfell B. T., Susceptible supply limits the role of climate in the early SARS-CoV-2 pandemic. Science 369, 315–319 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kissler S. M., Tedijanto C., Goldstein E., Grad Y. H., Lipsitch M., Projecting the transmission dynamics of SARS-CoV-2 through the postpandemic period. Science 368, 860–868 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Verity R., Okell L. C., Dorigatti I., Winskill P., Whittaker C., Imai N., Cuomo-Dannenburg G., Thompson H., Walker P. G. T., Fu H., Dighe A., Griffin J. T., Baguelin M., Bhatia S., Boonyasiri A., Cori A., Cucunubá Z., John R. F., Gaythorpe K., Green W., Hamlet A., Hinsley W., Laydon D., Nedjati-Gilani G., Riley S., van Elsland S., Volz E., Wang H., Wang Y., Xi X., Donnelly C. A., Ghani A. C., Ferguson N. M., Estimates of the severity of coronavirus disease 2019: A model-based analysis. Lancet Infect. Dis. 20, 669–677 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.COVID-19 Case Surveillance Public Use Data, https://data.cdc.gov/Case-Surveillance/COVID-19-Case-Surveillance-Public-Use-Data/vbim-akqf [accessed 28 August 2020].
- 33.He X., Lau E. H. Y., Wu P., Deng X., Wang J., Hao X., Lau Y. C., Wong J. Y., Guan Y., Tan X., Mo X., Chen Y., Liao B., Chen W., Hu F., Zhang Q., Zhong M., Wu Y., Zhao L., Zhang F., Cowling B. J., Li F., Leung G. M., Temporal dynamics in viral shedding and transmissibility of COVID-19. Nat. Med. 26, 672–675 (2020). [DOI] [PubMed] [Google Scholar]
- 34.Yang W., Lipsitch M., Shaman J., Inference of seasonal and pandemic influenza transmission dynamics. Proc. Natl. Acad. Sci. U.S.A. 112, 2723–2728 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pei S., Morone F., Liljeros F., Makse H., Shaman J. L., Inference and control of the nosocomial transmission of methicillin-resistant Staphylococcus aureus. eLife 7, e40977 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Reis J., Shaman J., Retrospective parameter estimation and forecast of respiratory syncytial virus in the United States. PLOS Comput. Biol. 12, e1005133 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Heaney A. K., Alexander K. A., Shaman J., Ensemble forecast and parameter inference of childhood diarrhea in Chobe District, Botswana. Epidemics 30, 100372 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shaman J., Karspeck A., Forecasting seasonal outbreaks of influenza. Proc. Natl. Acad. Sci. U.S.A. 109, 20425–20430 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.DeFelice N. B., Little E., Campbell S. R., Shaman J., Ensemble forecast of human West Nile virus cases and mosquito infection rates. Nat. Commun. 8, 14592 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Pei S., Shaman J., Counteracting structural errors in ensemble forecast of influenza outbreaks. Nat. Commun. 8, 925 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Perkins T. A., Cavany S. M., Moore S. M., Oidtman R. J., Lerch A., Poterek M., Estimating unobserved SARS-CoV-2 infections in the United States. Proc. Natl. Acad. Sci. U.S.A. 117, 22597–22602 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/sciadv.abd6370/DC1


