Unsupervised neural network models of the ventral visual stream

Significance

Primates show remarkable ability to recognize objects. This ability is achieved by their ventral visual stream, multiple hierarchically interconnected brain areas. The best quantitative models of these areas are deep neural networks trained with human annotations. However, they receive more annotations than infants, making them implausible models of the ventral stream development. Here, we report that recent progress in unsupervised learning has largely closed this gap. We find the networks learned with recent unsupervised methods achieve prediction accuracy in the ventral stream that equals or exceeds that of today’s best models. These results illustrate a use of unsupervised learning to model a brain system and present a strong candidate for a biologically plausible computational theory of sensory learning.

Abstract

Deep neural networks currently provide the best quantitative models of the response patterns of neurons throughout the primate ventral visual stream. However, such networks have remained implausible as a model of the development of the ventral stream, in part because they are trained with supervised methods requiring many more labels than are accessible to infants during development. Here, we report that recent rapid progress in unsupervised learning has largely closed this gap. We find that neural network models learned with deep unsupervised contrastive embedding methods achieve neural prediction accuracy in multiple ventral visual cortical areas that equals or exceeds that of models derived using today’s best supervised methods and that the mapping of these neural network models’ hidden layers is neuroanatomically consistent across the ventral stream. Strikingly, we find that these methods produce brain-like representations even when trained solely with real human child developmental data collected from head-mounted cameras, despite the fact that these datasets are noisy and limited. We also find that semisupervised deep contrastive embeddings can leverage small numbers of labeled examples to produce representations with substantially improved error-pattern consistency to human behavior. Taken together, these results illustrate a use of unsupervised learning to provide a quantitative model of a multiarea cortical brain system and present a strong candidate for a biologically plausible computational theory of primate sensory learning.

The remarkable power of primate visual object recognition is supported by a hierarchically organized series of anatomically distinguishable cortical areas, called the ventral visual stream. Early visual areas, such as primary visual cortex (V1), capture low-level features including edges and center-surround patterns (1, 2). Neural population responses in the highest ventral visual area, inferior temporal (IT) cortex, contain linearly separable information about object category that is robust to significant variations present in natural images (3–5). Midlevel visual areas such as V2, V3, and V4 are less well understood, but appear to perform intermediate computations between simple edges and complex objects, correlating with sequentially increasing receptive field size (6–14).

Recently, significant progress has been achieved in approximating the function of the adult primate ventral visual stream through using deep convolutional neural networks (DCNNs), a class of models directly inspired by many of these neurophysiological observations (15, 16). After being trained to learn image categorization tasks from large numbers of hand-labeled images, DCNNs have yielded the most quantitatively accurate predictive models of image-evoked population responses in early, intermediate, and higher cortical areas within the ventral visual stream (17–20). The behavioral error patterns generated by these networks are also more consistent with those of humans and nonhuman primates than alternative models (21). Notably, such networks are not directly optimized to fit neural data, but rather to solve behaviorally relevant tasks such as object recognition. Strong neural and behavioral predictivity just “falls out” of these “goal-driven” neural network models as a consequence of the high-level functional and structural assumptions constraining the networks’ optimization (22). Similar task-based neural network optimization approaches have led to successes in modeling the human auditory cortex (23) and aspects of motor cortex (24). These results suggest that the principle of “goal-driven modeling” may have general utility for modeling sensorimotor systems.

Although this progress at the intersection of deep learning and computational neuroscience is intriguing, there is a fundamental problem confronting the approach: Typical neural network models of the ventral stream are built via supervised training methods involving huge numbers of semantic labels. In particular, today’s best models of visual cortex are trained on ImageNet, a dataset that contains millions of category-labeled images organized into thousands of categories (25, 26). Viewed as a technical tool for machine learning, massive supervision can be acceptable, although it limits the purview of the method to situations with large existing labeled datasets. As a real model of biological development and learning, such supervision is highly implausible, since human infants and nonhuman primates simply do not receive millions of category labels during development (27–29). Put another way, today’s heavily supervised neural-network–based theories of cortical function may effectively proxy aspects of the real behavioral constraints on cortical systems and thus be predictively accurate for adult cortical neural representations, but they cannot provide a correct explanation of how such representations are learned in the first place. Identifying unsupervised learning procedures that achieve good performance on challenging sensory tasks and effective predictions of neural responses in visual cortex would thus fill a major explanatory gap.

Unsupervised Learning Algorithms

Substantial effort has been devoted to unsupervised learning algorithms over several decades, with the goal of learning task-general representations from natural statistics without high-level labeling. We summarize these algorithms in Table 1, while more details can be found in SI Appendix. Early progress came from sparse autoencoding, which, when trained in shallow network architectures on natural images, produces edge-detector–like response patterns resembling some primate V1 neurons (30). However, when applied to deeper networks, such methods have not been shown to produce representations that transfer well to high-level visual tasks or match neural responses in intermediate or higher visual cortex. More recent versions of autoencoders have utilized variational objective functions (31), with improved task transfer performance. Unsupervised learning is also addressed in the predictive coding framework (32), where networks learning to predict temporal or spatial successors to their inputs have achieved better task transfer (33) and improved biological similarity (34).

Table 1.

Short descriptions of optimization goals of unsupervised learning tasks

Method	Description
AutoEncoder	First embed the input images to lower-dimension space and then use the embedding to reconstruct the input
PredNet	Predict the next frame as well some of the network responses to the next frame using previous frames
CPC	Predict the embedding of one image crop using the embeddings of its spatial neighbors
Depth prediction	Predict the per-pixel relative depth image from the corresponding RGB image
Relative position	Predict the relative position of two image crops sampled from a $2\times 2$ image grid
Colorization	Predict the down-sampled color information from the grayscale image
Deep cluster	Embed all images into a lower-dimension space and then use unsupervised clustering results on these embeddings
	as “category” labels to train the networks
CMC	Embed grayscale and color information of one image into two embedding spaces and push together two corresponding
	embeddings while separating them from all of the other embeddings
Instance recognition	Make the embedding of one image unchanged under data augmentations while separating it from the embeddings of
	all of the other images
SimCLR	Aggregate the embeddings of two data-augmented crops from one image while separating them from the embeddings
	of other images in one large batch
Local aggregation	Aggregate the embeddings of one image to its close neighbors in the embedding space while separating them from
	further neighbors

CPC represents contrastive predictive coding (33).

In contrast, self-supervised methods are motivated by the observation that high-level semantic features are implicitly correlated with a wide variety of nonsemantic “proxy” features, many of which are accessible via simple image manipulations. By learning explicitly to predict the proxy feature, the learned representations end up creating representations that implicitly capture higher-level features. For example, the “colorful image colorization” objective (35) trains networks to infer per-pixel colors from grayscale images in which the original color information has been removed. While this objective might seem unrelated to object categorization, to properly color a given pixel, the network must implicitly learn how to distinguish the boundaries and orientations of objects in an image, as well as external scene variables such as lighting environment—building representations that significantly outperform typical autoencoding approaches on categorization transfer. Other self-supervised proxy objectives include image context prediction (36), in-painting (37), and surface-normals/depth estimation (38). Self-supervised methods are intriguingly powerful given their simplicity, but they are also limited by the fact that low-level confounding information can interfere (e.g., texture can often indicate color), hurting the performance of the high-layer representations of these networks in predicting semantic information. Moreover, the specific choice of implicit proxy objective in any given self-supervised method is somewhat ad hoc, and no clear framework is available for generating and selecting improved proxy objectives.

More recently, another family of unsupervised algorithms has emerged with substantially improved transfer performance, approaching that of fully supervised networks (39–44). These contrastive embedding objectives optimize DCNNs to find good embeddings of inputs into a lower-dimensional compact space. The DCNN is treated as a function $f:{\mathbb{R}}^{k\times k}\to S^n$, where ${\mathbb{R}}^{k\times k}$ is the high-dimensional Euclidean space containing $k\times k$ image bitmaps (with $k\sim 10^3$) and $S^n$ is the $n$-dimensional unit sphere ($n=128$). For any input $x\in X$ and any “view” $v\left(x\right)$ of $x$ (typically generated by data augmentations such as image cropping), the goal is to make the embedding $f\left(v\left(x\right)\right)$ “unique”—that is, far away in the embedding space from other stimuli, but close to different views $v\prime$of the original stimulus. Conceptually, this goal can be achieved by optimizing a competitive loss function of the form

$$\mathcal{L}=-\text{log}\frac{\exp \left(f{\left(v\prime \left(x\right)\right)}^{T}f\left(v\left(x\right)\right)/\tau \right)}{{\sum }_i\exp \left(f{\left(v_i\left(x_i\right)\right)}^{T}f\left(v\left(x\right)\right)/\tau \right)},$$ [1]

where $\tau$ is a small positive number and $i$ enumerates over the dataset.

Intuitively, by maximizing embedding distances between unrelated images while maintaining similarity between highly related views, the contrastive objective achieves a form of mutual information maximization (45). Features in higher network layers learn to generically support any natural statistic that reliably distinguishes between sets of inputs that can be computed by the deep network of a given depth (Fig. 1 C and D). By capturing whatever natural correlations are present, the representation is thus more likely to support any specific downstream visual task that implicitly relies on creating distance-based boundaries in that feature space (e.g., object recognition). This genericity represents a significant contrast to the more ad hoc self-supervised methods and underlies the improvement achieved by the contrastive embedding methods.

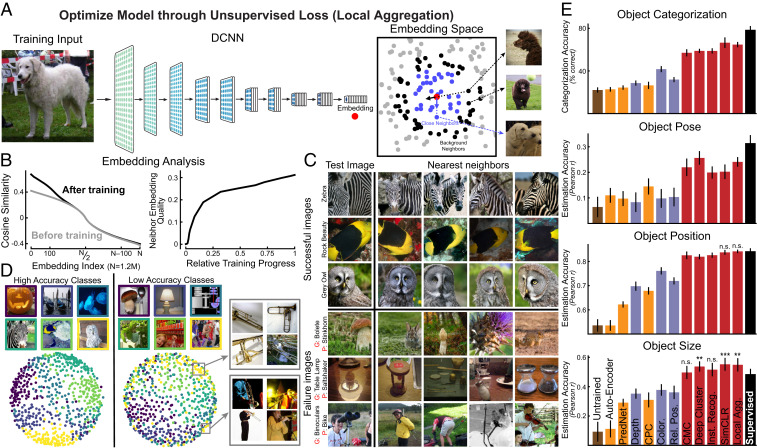
Fig. 1.

Improved representations from unsupervised neural networks based on deep contrastive embeddings. (A) Schematic for one high-performing deep contrastive embedding method, the LA algorithm (41). In LA, all images were embedded into a lower-dimensional space by a DCNN, which was optimized to minimize the distance to close points (blue dots) and to maximize the distance to the “farther” points (black dots) for the current input (red dot). (B) (Left) Change in the embedding distribution before and after training. For each image, cosine similarities to others were computed and ranked; the ranked similarities were then averaged across all images. This metric indicates that the optimization encourages local clustering in the space, without aggregating everything. (Right) Average neighbor-embedding “quality” as training progresses. Neighbor-embedding quality was defined as the fraction of 10 closest neighbors of the same ImageNet class label (not used in training). (C) Top four closest images in the embedding space. Top three rows show the images that were successfully classified using a weighted K-nearest-neighbor (KNN) classifier in the embedding space (K = 100), while Bottom three rows show unsuccessfully classified examples (G means ground truth, P means prediction). Even when uniform distance in the unsupervised embedding does not align with ImageNet class (which itself can be somewhat arbitrary given the complexity of the natural scenes in each image), nearby images in the embedding are nonetheless related in semantically meaningful ways. (D) Visualizations of local aggregation embedding space using the multidimensional scaling (MDS) method. Classes with high validation accuracy are shown at Left and low-accuracy classes are shown at Right. Gray boxes show examples of images from a single class (“trombone”) that have been embedded in two distinct subclusters. (E) Transfer performance of unsupervised networks on four evaluation tasks: object categorization, object pose estimation, object position estimation, and object size estimation. Networks were first trained by unsupervised methods and then assessed on transfer performance with supervised linear readouts from network hidden layers (Materials and Methods). Red bars are contrastive embedding tasks. Blue bars are self-supervised tasks. Orange bars are predictive coding methods and AutoEncoder. Brown bar is the untrained model and black bar is the model supervised on ImageNet category labels. Error bars are standard deviations across three networks with different initializations and four train-validation splits. We used unpaired t tests to measure the statistical significance of the difference between the unsupervised method and the supervised model. Methods without any annotations are significantly worse than the supervised model ($P<0.05$), n.s., insignificant difference; **, significantly better results with $0.001<P<0.01$; and ***, significantly better results with $P<0.001$ (SI Appendix, Fig. S2).

However, computing the denominator of Eq. 1 is intractable for large datasets. Different contrastive methods differ from each other in terms of the approach to resolving this intractability, the definitions of what different views are, and the exact implementations of the contrastive loss form. Such methods include instance recognition (IR) (40), contrastive multiview coding (CMC) (39), momentum contrast (MoCo) (42), simple contrastive learning of representation (SimCLR) (43), and local aggregation (LA) (41). For example, the IR method involves maintaining running averages of embeddings for all inputs (called the “memory bank”) across the training time and replacing $f\left(v^{\prime }\left(x\right)\right)$ and $f\left(v_i\left(x_i\right)\right)$ with the corresponding running-average embeddings $\mathrm{m}\left(x\right)$ and $\mathrm{m}\left(x_i\right)$. A randomly subsampled set of items in the memory bank is then used to approximate the denominator of Eq. 1. The SimCLR algorithm uses another method to make the loss tractable, sampling a large set of inputs (typically 4,096 examples) for every step, and computes the loss treating the sampled set as the whole dataset. The local aggregation method focuses more on improving the loss formulation, encouraging uniqueness by minimizing the distance to “close” embedding points ($\mathrm{C}\left(x\right)\subset X$) and maximizing the distance to “background” points ($\mathrm{B}\left(x\right)\subset X$) for each input (Fig. 1A). This is achieved by minimizing the following loss:

$${\mathcal{L}}_{\mathrm{L}\mathrm{A}}=-\text{log}\frac{\sum _{x_a\in \mathrm{C}\left(x\right)}\exp \left(\mathrm{m}{\left(x_a\right)}^{T}f\left(v\left(x\right)\right)/\tau \right)}{\sum _{x_b\in \mathrm{B}\left(x\right)\cup \mathrm{C}\left(x\right)}\exp \left(\mathrm{m}{\left(x_b\right)}^{T}f\left(v\left(x\right)\right)/\tau \right)}$$ [2]

(See SI Appendix, Methods for more details on how the close and background sets are defined.) After optimization for this objective, the deep embedding forms local clusters (Fig. 1 B, Left). These clusters meaningfully overlap with semantic constructs even though no labels were used to create them (Fig. 1 B, Right and C).

Contrastive Embedding Methods Yield High-Performing Neural Networks

To evaluate these unsupervised learning algorithms, we trained representatives of each method described above, using a standard ResNet18 network architecture (46). Training data were drawn from ImageNet (24), a large-scale database of hand-labeled natural images. We chose this combination of architecture and training set because, when trained in a supervised manner, it has been previously shown to achieve high performance on a variety of visual tasks (46, 47, 48), as well as neural response predictivity (49). In our unsupervised training, the category labels accompanying each ImageNet image were set aside. We found that our unsupervised representations achieved ImageNet test performance in line with previously reported results (SI Appendix, Fig. S1), validating the soundness of our implementations.

We then examined the power of these unsupervised representations for supporting a variety of visual tasks outside the domain of images on which training took place. Using a dataset of images that has previously been used to assess both neural and behavioral consistency of (supervised) deep neural networks (17, 21), we evaluated transfer performance on an object categorization task, as well several object-centric visual tasks independent of object category, including object position localization, size estimation, and pose estimation. As all these tasks have proved to be well supported by neural responses in the ventral visual cortical areas (50), only those computation models that effectively transfer to all these tasks are viable candidates for computational models of the ventral visual pathway.

Transfer performance was assessed by adding a single fully connected linear readout layer on top of any given layer of each pretrained unsupervised representation and then training only the parameters of that readout layer on the desired task. Softmax outputs were used for categorization tasks, while raw regression outputs were used for the continuous estimation tasks. We report cross-validated performance values on held-out images not used during either unsupervised training of the original deep network or the supervised readout layer.

Across all evaluated objective functions, contrastive embedding objectives (red bars in Fig 1E) showed substantially better transfer than other unsupervised methods, including self-supervised objectives (blue bars), predictive coding methods (orange bars), and autoencoders, approaching the performance of the supervised model. In fact, the best of the unsupervised methods (SimCLR and local aggregation) equaled or even outperformed the category-supervised model in several tasks, including object position and size estimation. Unsurprisingly, all unsupervised methods are still somewhat outperformed by the category-supervised model on the object categorization task. (A gap between unsupervised and category-supervised networks existed for the pose estimation task, most likely due to the fact that the ground-truth object pose is actually defined on a category-by-category basis with respect to a category-specific “canonical pose.” See details of the task definitions in SI Appendix.

Because different tasks could in theory be best supported by different layers of the unsupervised networks, we report performance for the best layer (Fig 1E) as well as all network layers (SI Appendix, Fig. S3). However, we found that the higher layers of the trained networks achieved better performance in all of the object-centric tasks compared to the lower layers (SI Appendix, Fig. S3). This finding is consistent with that in Hong et al. (50), where it is shown that decoding performance from neural responses is better in higher ventral visual for both category and category-orthogonal tasks.

Taken together, these results suggest that the deep contrastive embedding methods have achieved a generalized improvement in the quality of the visual representations they create, suggesting their potential as computation models for the ventral visual cortex.

Contrastive Embedding Models Capture Neural Responses throughout Ventral Visual Cortex

To determine whether the improvement of unsupervised methods on task transfer performance translates to better neural predictivity, we compared each unsupervised neural network described in the previous section to neural data from macaque V1, V4, and IT cortex. In this analysis, we used a previously established technique for mapping artificial network responses to real neural response patterns (17, 51). Specifically, we fit a regularized linear regression model from network activations of each unsupervised model to neural responses collected from array electrophysiology experiments in the macaque ventral visual pathway (Fig. 2A). We then report the noise-corrected correlation between model and neural responses across held-out images, for the best-predicting layer for each model (Fig. 2B). Comparison to area V1 was made using neural data collected by Cadena et al. (19), while comparison to areas V4 and IT was made using data collected by Majaj et al. (3, 52). Although these two datasets were collected with different experimental designs, they have both previously been used to evaluate (supervised) deep neural network models, yielding consistent results (17, 19) (see SI Appendix, Methods for more details). The image sets on which V4 and IT neural responses are predicted are quite distinct both in type and content from the training data for the unsupervised networks (ImageNet), representing a strong generalization test for the representations. We also compare the unsupervised networks both to the supervised network, which represents a previously known positive control, and to an untrained model, which represents an objective function-independent architecture-only baseline. Given that network architecture remains fixed across all objective functions, the outcome isolates the impact of choice of objective function on neural predictivity.

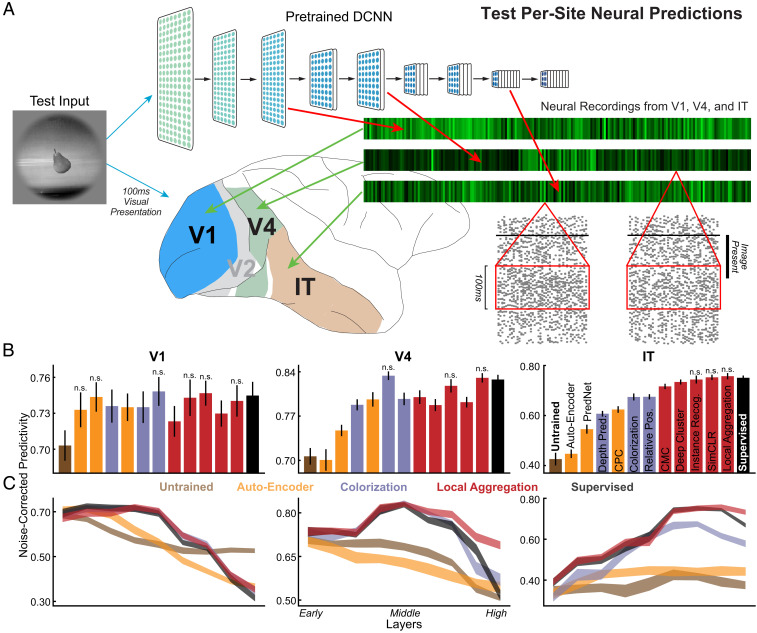
Fig. 2.

Quantifying similarity of unsupervised neural networks to visual cortex data. (A) After being trained with unsupervised objectives, networks were run on all stimuli for which neural responses were collected. Network unit activations from each convolutional layer were then used to predict the V1, V4, and IT neural responses with regularized linear regression (51). For each neuron, the Pearson correlation between the predicted responses and the recorded responses was computed on held-out validation images and then corrected by the noise ceiling of that neuron (Materials and Methods). The median of the noise-corrected correlations across neurons for each of several cortical brain areas was then reported. (B) Neural predictivity of the most-predictive neural network layer. Error bars represent bootstrapped standard errors across neurons and model initializations (Materials and Methods). Predictivity of untrained and supervised categorization networks represents negative and positive controls, respectively. Statistical significance of the difference between each unsupervised method and the supervised model was computed through bootstrapping methods. The methods with comparable neural predictivity are labeled with “n.s.,” and other methods without any annotations are significantly worse than the supervised model ($P<0.05$) (SI Appendix, Fig. S5). (C) Neural predictivity for each brain area from all network layers, for several representative unsupervised networks, including AutoEncoder, colorization, and local aggregation.

Overall, the unsupervised methods that had higher task transfer performance predicted neural responses substantially better than less-performant unsupervised methods. In the first cortical visual area V1, all unsupervised methods were significantly better than the untrained baseline at predicting neural responses, although none were statistically better from the category-supervised model on this metric. In contrast, in intermediate cortical area V4, only a subset of methods achieved parity with the supervised model in predictions of responses. (Interestingly, the deep autoencoder was not better than the untrained model on this metric and both were widely separated from the other trained models.) For IT cortex at the top of the ventral pathway, only the best-performing contrastive embedding methods achieved neural prediction parity with supervised models. Among these methods, the local aggregation model, which has recently been shown to achieve state-of-the-art unsupervised visual recognition transfer performance (41), also achieved the best neural predictivity. In fact, LA exhibits comparable V1, V4, and IT predictivity to its supervised counterpart (P = 0.10, 0.11, and 0.36 correspondingly, computed using bootstrapping methods which repeatedly sampled neurons with replacement for 10,000 times; see SI Appendix, Fig. S4 for details and other significance results). Similarly, good neural predictivity is also achieved by two other contrastive embedding methods, instance recognition and SimCLR. More specifically, IR shows comparable V1, V4, and IT predictivity to the supervised model (P = 0.45, 0.12, and 0.25 correspondingly), although LA surpasses it on both V4 (P = 0.013) and IT (P = 0.021) predictivity, which is consistent with the difference of these two methods in the transfer task performance. Consistent with the result that SimCLR achieves comparable or even better transfer task performance compared to the LA, SimCLR also shows comparable IT predictivity to both the supervised (P = 0.49) and the LA (P = 0.37) models, but its V1 and V4 predictivities are significantly worse than those of the supervised (P = 0.007 and 0.0001) and the LA (P = 0.022 and P < 0.0001) models. This predictivity gap might be due to the fact that SimCLR and LA differ significantly in how the losses are defined (SI Appendix, Methods). To ensure that our results are not specific to the chosen neural network architecture, we also evaluated several alternative architectures and found qualitatively similar results (SI Appendix, Fig. S10).

To further quantify the match between the computational models and brain data, we also investigated which layers of DCNNs best matched cortical brain areas (Fig. 2C and SI Appendix, Fig. S5). Deep contrastive embedding models also show good model-layer-to-brain-area correspondence, with early-layer representations best predicting V1 neural responses, midlayer representations best predicting V4 neural responses, and higher-layer representations best predicting IT neural responses. Although only the local aggregation model is shown in Fig. 2C, other deep contrastive embedding models show similar model–brain correspondence (SI Appendix, Fig. S5). The colorization model, which represents unsupervised models with slightly lower task performance and neural predictivity, shows good model–brain correspondence for both V1 and V4 areas, but its IT neural predictivity starts to drop at an earlier layer compared to the deep contrastive embedding and the supervised models. In contrast, the AutoEncoder model and other unsupervised models with much lower task performance and neural predictivity exhibit even less accurate model–brain correspondence, while the untrained baseline does not show the correct correspondence at all. This conclusion is consistent across multiple quantitative metrics of mapping consistency including optimal layer match (Fig. 2C and SI Appendix, Fig. S5) as well as best predicted layer ratio metric (SI Appendix, Fig. S6).

In addition to the quantitative metrics described above, we also assessed models qualitatively. DCNNs trained with different unsupervised loss functions exhibit first-layer filters with Gabor wavelet-like tuning curves like those observed in V1 data, consistent with their good neural predictivity for V1 neurons (SI Appendix, Fig. S7). The LA model, like the category-supervised model, also exhibited color-opponent center-surround units consistent with empirical observations (53, 54). Additionally, we examined optimal stimuli driving neurons in intermediate and higher model layers using techniques similar to those used in recent model-driven electrophysiology experiments (55). Consistent with qualitative descriptions of receptive fields in the literature on V4 cortex (14), we found that unsupervised models with good quantitative match to V4 data exhibit complex textural patterns as optimal stimuli for their most V4-like layers (SI Appendix, Fig. S8). In contrast, the optimal stimuli driving neurons in the most IT-like model layers appear to contain fragments of semantically identifiable objects and scenes and large-scale organization (SI Appendix, Fig. S9), echoing qualitative neurophysiological findings about IT neurons (56).

Deep Contrastive Learning on First-Person Video Data from Children Yields Competitive Representations

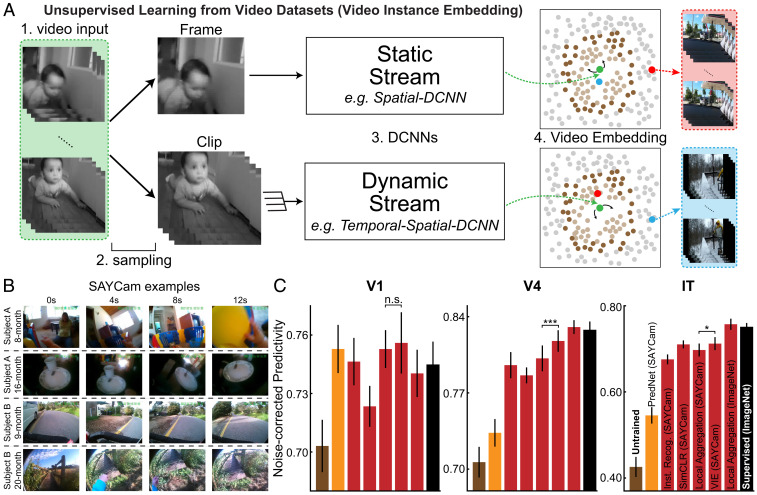
Although we have shown that deep contrastive embedding models learn ventral-stream–like representations without using semantic labels, the underlying set of images used to train these networks—the ImageNet dataset—diverges significantly from real biological datastreams. For example, ImageNet contains single images of a large number of distinct instances of objects in each category, presented cleanly from stereotypical angles. In contrast, real human infants receive images from a much smaller set of object instances than ImageNet, viewed under much noisier conditions (57). Moreover, ImageNet consists of statistically independent static frames, while infants receive a continuous stream of temporally correlated inputs (58). A better proxy of the real infant datastream is represented by the recently released SAYCam (59, 60) dataset, which contains head-mounted video camera data from three children (about 2 h/wk spanning ages 6 to 32 mo) (Fig. 3B).

Fig. 3.

Learning from real-world developmental datastreams. (A) Schematic for VIE method. Frames were sampled into sequences of varying lengths and temporal densities. They were then embedded into lower-dimensional space using static (single image) or dynamic (multiimage) pathways. These pathways were optimized to aggregate the resulting embeddings and their close neighbors (light brown points) and to separate the resulting embeddings and their farther neighbors (dark brown points). (B) Examples from the SAYCam dataset (59), which was collected by head-mounted cameras on infants for 2 h each week between ages 6 and 36 mo. (C) Neural predictivity for models trained on SAYCam and ImageNet. n.s., the difference is not significant ($P>0.05$). *** and *, significant difference (P = 0.0008 for V4 and P = 0.023 for IT). Error bars represent bootstrapped standard errors across neurons and model initializations. Statistical significance of the difference was computed through bootstrapping methods (SI Appendix, Fig. S12).

To test whether deep contrastive unsupervised learning is sufficiently robust to handle real-world developmental videostreams such as SAYCam, we implemented the video instance embedding (VIE) algorithm, a recent extension of LA to video that achieves state-of-the-art results on a variety of dynamic visual tasks, such as action recognition (61) (Fig. 3A). This algorithm extends LA through treating samples from the same temporal scenario (typically a 10-s video) as different views of the input stimuli. VIE also trains a dynamic model to better capture the motion information in a short clip (dynamic stream in Fig. 3A), in addition to a static model for a single frame (static stream in Fig. 3A). These two streams are independently trained with separate network weights and embedding space. Therefore, the same video may be encouraged to cluster with different videos by the two models (Fig. 3 A, Right). Indeed, it has been shown that the static stream better captures object-related information, while the dynamic stream better captures action-related information (61). Moreover, combining both streams yields an even better model on capturing both object- and action-related information.

After training the two stream models on SAYCam, we found that representations learned by VIE are highly robust, approaching the neural predictivity of those trained on ImageNet (Fig. 3C). The temporally aware VIE-trained representation was significantly (although modestly) better than a purely static network trained with LA on SAYCam frames, while both were very substantially better than PredNet, a recent biologically inspired implementation of predictive coding (34). These results show that deep spatiotemporal contrastive learning can take advantage of noisy and limited natural datastreams to achieve primate-level representation learning.

A small but statistically significant gap between the SAYCam-trained and ImageNet-trained networks remains in both neural predictivity and task performance (SI Appendix, Fig. S11), possibly due to limitations either in the dataset (SAYCam was recorded for only 2 h/wk, representing a small fraction of the visual data infants actually receive) or in VIE itself. To investigate how this gap can be bridged, we also tested a VIE model trained on Kinetics-400 (SI Appendix, Fig. S12), a video dataset with short videos collected from YouTube for training action recognition models (62). VIE-Kinetics showed significantly better neural predictivity and task performance compared to VIE-SAYCam and comparable performance to that of the ImageNet-trained models (SI Appendix, Figs. S11 and S12). This finding suggests that a substantial part of the remaining gap is due to limitations in the SAYCam dataset.

Partial Supervision Improves Behavioral Consistency

While infants and nonhuman primates do not receive large numbers of semantic labels during development, it is likely that they do effectively receive at least some labels, either from parental instruction or through environmental reward signals. For human infants, object labels are provided by parents from birth onward, but the earliest evidence for comprehension of any labels is at roughly 6 to 9 mo of age (27), and comprehension of most common object labels is low for many months thereafter (28). However, visual learning begins significantly earlier at, and indeed before, birth (63). This observation suggests that a period of what might be characterized as purely unsupervised early visual learning could be followed by a period of learning partially from labels. To capture this idea, we turned to semisupervised learning, which seeks to leverage small numbers of labeled datapoints in the context of large amounts of unlabeled data.

As with unsupervised learning, the power of semisupervised learning algorithms has developed dramatically in recent years, benefiting from advances in understanding of neural network architectures and loss functions. A state-of-the-art semisupervised learning algorithm, local label propagation (64) (LLP), builds directly on the contrastive embedding methods. Like those methods, LLP embeds datapoints into a compact embedding space and seeks to optimize a particular property of the data distribution across stimuli, but additionally takes into account the embedding properties of sparse labeled data (Fig. 4A). This algorithm first uses a label propagation method to infer the pseudolabels of unlabeled images from those of nearby labeled images. The network is then jointly optimized to predict these inferred pseudolabels while maintaining contrastive differentiation between embeddings with different pseudolabels. As the embedding updates, it leads to more accurate pseudolabels, which in turn further improve the representation. Because pseudolabels can be shared by images that are distant from each other in the embedding space, LLP allows for global aggregation that is unavailable in the purely unsupervised context. (See details of the LLP loss function in SI Appendix.)

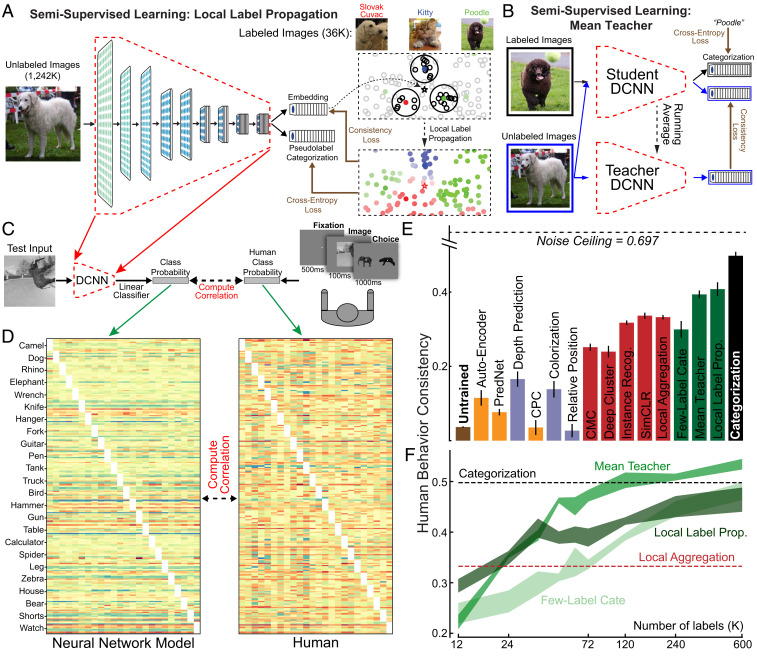
Fig. 4.

Behavioral consistency and semisupervised learning. (A) In the LLP method (64), DCNNs generated an embedding and a category prediction for each example. The embedding ($\star$) of an unlabeled input was used to infer its pseudolabel considering its labeled neighbors (colored points) with voting weights determined by their distances from $\star$ and their local density (the highlighted areas). DCNNs were then optimized with per-example confidence weightings (color brightness) so that its category prediction matched the pseudolabel, while its embedding was attracted toward the embeddings sharing the same pseudolabels and repelled by the others. (B) To measure behavioral consistency, we trained linear classifiers from each model’s penultimate layer on a set of images from 24 classes (21, 49). The resulting image-by-category confusion matrix was compared to data from humans performing the same alternative forced-choice task, where each trial started with a 500-ms fixation point, presented the image for 100 ms, and required the subject to choose from the true and another distractor category shown for 1,000 ms (21, 49). We report the Pearson correlation corrected by the noise ceiling. (C) Example confusion matrices of human subjects and model (LLP model trained with 36,000 labels). Each category had 10 images as the test images for computing the confusion matrices. (D) Behavioral consistency of DCNNs trained by different objectives. Green bars are for semisupervised models trained with 36,000 labels. “Few-Label” represents a ResNet-18 trained on ImageNet with only 36,000 images labeled, the same amount of labels used by MT and LLP models. Error bars are standard variances across three networks with different initializations. (E and F) Behavioral consistency (E) and categorization accuracy in percentage (F) of semisupervised models trained with differing numbers of labels.

Here, we implemented both LLP and an alternative semisupervised learning algorithm, the mean teacher (65) (MT) (SI Appendix, Fig. S14). As precise estimates of the number of object labels available to children and the proportion of these that unambiguously label a specific object do not exist, we trained both semisupervised models on the ImageNet dataset with 1.2 million unlabeled and a range of supervision fractions, corresponding to different estimates of the number of the object speech–vision copresentations infants perceive and comprehend within the first year of life (29). We also implemented a simple few-label control, in which standard supervision was performed using only the labeled datapoints.

For each trained model, we then compared the object recognition error patterns to those in humans and primates, following the methods of Rajalingham et al. (21), who show that category-supervised DCNNs exhibit error patterns with improved consistency to those measured in humans. We first extracted “behavior” from DCNNs by training linear classifiers from the penultimate layer of the neural network model and measured the resulting image-by-category confusion matrix. An analogous confusion matrix was then independently measured from humans in large-scale psychophysical experiments (Fig. 4B). The behavioral consistency between DCNNs and humans is quantified as the noise-corrected correlation between these confusion matrices (SI Appendix, Methods). We evaluated behavioral consistency for semisupervised models as well as the unsupervised models described above. Using just 36,000 labels (corresponding to 3% supervision), both LLP and MT lead to representations that are substantially more behaviorally consistent than purely unsupervised methods, although a gap to the supervised models remains (Fig. 4D; see SI Appendix, Fig. S13 for t-test results). These semisupervised models, especially the LLP model, also achieve slightly better or comparable neural predictivity and task performance results compared to the LA model (SI Appendix, Figs. S11 and S12). Interestingly, although the unsupervised LA algorithm is less consistent than either of the semisupervised methods that feature an interaction between labeled and unlabeled data, it is more consistent than the few-label control. We find broadly similar patterns with different amounts of supervision labels (Fig. 4 E and F). These results suggest that semisupervised learning methods may capture a feature of real visual learning that builds on, but goes beyond, task-independent self-supervision.

Although the best unsupervised model achieves comparable neural predictivity to the supervised model, there is still a significant gap between the human behavior consistency of the unsupervised and the supervised models. One possible explanation of this gap is that categorization behaviors are better supported by a downstream area of IT, rather than area IT itself. Testing this explanation is an intriguing subject for future work.

Discussion

We have shown that deep contrastive unsupervised embedding methods accurately predict image-evoked neural responses in multiple visual cortical areas along the primate ventral visual pathway, equaling the predictive power of supervised models. Moreover, the mapping from the layers of these unsupervised networks to corresponding cortical areas is neuroanatomically consistent and reproduces several qualitative properties of the visual system. We have also shown that when trained on noisy and limited datasets arising from the real developmental experience of children, deep contrastive embeddings learn strong visual representations that achieve good neural predictivity on different areas across the ventral visual stream and show reasonable performance on downstream visual tasks, rivaling those created from clean hand-curated data. These unsupervised models represent a dramatic improvement compared to strong alternative models of biologically plausible learning, like PredNet (34). Moreover, training with a semisupervised learning objective allowing incorporation of small amounts of supervision creates networks with improved behavioral consistency with humans and nonhuman primates. Taken together, these results suggest that an important gap in the promising but incomplete goal-driven neural network theory of visual cortex may be close to resolution.

Contrastive embedding objectives generate image embeddings that remain invariant under certain “viewpoints” while being distinguishable from others. By minimizing these objectives, networks effectively discover nonprespecified high-level image statistics that support reliable and generalizable distinctions (45). This feature distinguishes the deep contrastive embedding approach from earlier unsupervised models such as autoencoders or self-supervised objectives, which optimized low-level or narrowly defined image statistics and, as a result, learned less powerful representations. Because deep contrastive embedding methods are quite generic, and do not require the implementation of strong domain-specific priors (e.g., the presence of visual objects in three-dimensional scenes), the application of similar methods might further the understanding in other sensorimotor cortical domains where supervised neural networks have proved useful as predictors of neural responses (23, 24).

Our results can be taken as a statement about the inductive biases that are needed to build an effective high-performing but biologically plausible visual learning system (66), suggesting that some form of contrastive objective function might be implemented by primates as a key “bias” shaping real learning during development. Given the simplicity of the contrastive loss formula, it is not hard to imagine that it could be implemented by a real neural circuit driving plasticity based on both similarity and differentiation (67). Conceptually, this neural learning circuit would complement the neural system to be learned (e.g., the ventral pathway), computing and relaying errors back to the system as learning occurs, either rapidly in real time (68) or possibly with delayed batching as part of memory consolidation (69). Following up on these possibilities will require the detailed comparison of real-time empirical representation changes during learning (67, 68) to fine-scale model updates during training. Whether such a mechanism is anatomically separate from intermingling with the learning system is also a key question for future investigation.

Although our results help clarify a key problem in the modeling of sensory learning, many major questions remain. The neural predictivity of the best unsupervised method only slightly surpasses that of supervised categorization models. Moreover, the detailed pattern of neural predictivities across units of the best unsupervised models also generally aligns with that of the supervised models (SI Appendix, Fig. S15). One possible explanation for these outcomes is that even if the organism cannot know category labels explicitly, visual categorization might still be a good description of the larger evolutionary constraint that the primate visual system is under. If so, the unsupervised algorithm is best understood as a developmentally accessible proxy for how other inaccessible representational goals might be “implemented” by the organism. A more prosaic alternative explanation is that the neurophysiological data used in this study may simply not have the power to resolve differences between the supervised and best unsupervised models.

A third possibility is that better unsupervised learning methods yet to be discovered will achieve improved neural predictivity results, substantially surpassing that of categorization models. It is important to note that finding such improved models remains necessary: Both for neural response pattern and behavioral consistency metrics, our results show that there remains a substantial gap between all models (supervised and unsupervised) and the noise ceiling of the data: there is reliable neural and behavioral variance that no model correctly predicts. These quantitative gaps may be related to other qualitative inconsistencies between neural network models and human visual behaviors, including the latter’s susceptibility to adversarial and “controversial” examples (70) and their different texture-vs.-shape biases (71).

How can these gaps be bridged? Deep learning systems in neuroscience can be thought of as having several basic components (22, 72): an architecture class capturing neuroanatomical knowledge; an objective function capturing hypotheses about the signals driving learning; a training dataset capturing the environment in which the system learns; and a learning rule for actually converting learning signals into system updates, capturing neural plasticity. Our work addresses only the second and third of these four components—how the visual system might develop postnatally via natural visual experience, replacing an effective but implausible learning signal (heavily supervised categorization in a curated dataset of still images) with one that an organism might more plausibly compute in the real world (unsupervised or semisupervised contrastive embedding loss operating on real developmental videos).

To properly address these very important objective-function and dataset questions in the present work, we limited our investigation to previously validated feedforward network architectures to ensure that any results we obtained could be directly attributable to the loss function rather than architectural changes. However, while feedforward networks might be sufficient to predict temporal averages during the first volley of stimulus-evoked neural responses, they are insufficient to describe the response dynamics of real neurons (73). Recent work has begun to integrate into neural networks analogs of the recurrences and long-range feedbacks that have been ubiquitously observed throughout the visual system, toward better modeling neural dynamics (74, 75). This work has been in the supervised context, so a natural future direction is to connect these architectural improvements with the unsupervised objectives explored here.

As for the learning rule, our work still uses standard backpropagation for optimization (albeit with unsupervised rather than supervised objective functions). Backpropagation has several features that make it unlikely to be implementable in real organisms (76). Historically, the question of biologically plausible unsupervised objective functions (e.g., learning targets) is intertwined with that of biologically plausible learning rules (e.g., the mechanism of error-driven update). Some specific unsupervised objective functions, such as sparse autoencoding, can be optimized with Hebbian learning rules that do not require high-dimensional error feedback (77). However, this intertwining may be problematic, since the more effective objective functions that actually lead to powerful and neurally predictive representations do not obviously lend themselves to simple Hebbian learning. We thus suggest that these two components—optimization target and mechanism—may be decoupled and that such decoupling might be a principle for biologically plausible learning. This hypothesis is consistent with recent work on more biologically plausible local learning rules that effectively implement error feedback (78). It would be of substantial interest to build networks that use these learning rules in conjunction with unsupervised contrastive-embedding objective functions and recurrent convolutional architectures. If successful, this would represent a much more complete goal-driven deep-learning theory of visual cortex.

Better training environments will also be critical. Although SAYCam is more realistic than ImageNet, there are still many important components of real developmental datastreams missing in SAYCam, including (but not limited to) the presence of in utero retinal waves (63), the long period of decreased visual acuity (79), and the lack of nonvisual (e.g., auditory and somatosensory) modalities that are likely to strongly self-supervise (and be self-supervised by) visual representations during development (80). Moreover, real visual learning is likely to be at some level driven by interactive choices on the part of the organism, requiring a training environment more powerful than any static dataset can provide (81, 82).

Ultimately, a theory of visual postnatal development should go beyond just predicting neural responses in adult animals and also provide a model of changes over the time line of postnatal development. The long-term learning dynamics of any model generate trajectories of observables that could in principle be compared to similar observables measured over the course of animal development. The concept of such developmental trajectory comparison is illustrated in SI Appendix, Fig. S16, where we show the trajectories of observables including orientation selectivity, task performance, and an analog of neural maturation rate, over the course of “in silico development.” Treating each distinct unsupervised objective function as a different hypothesis for the learning target of visual development, the comparison of these curves can be seen to successfully distinguish between the various hypotheses, even when the final “adult” state may not easily separate them. To the extent that measurements of these (or other) observables can be made over the course of biological development, it would then be possible to determine which model(s) are closest to the true developmental trajectory or to convincingly falsify all of them. The specific observables that we measure here in silico may not be easily experimentally accessible, as developmental neuroscience remains technically challenging. However, our results suggest a strong motivation for turning a recent panoply of exciting technical neuroscience tools (83, 84) toward the developmental domain. In the context of model-driven experimental designs, such measurements would be of great value not only to provide insights into how visual learning proceeds, but also to inspire better unsupervised or semisupervised learning algorithms.

Materials and Methods

Neural Network Training.

ResNet-18 was used as the network architecture for all results reported in the main text, for all unsupervised objective functions except the PredNet method, as a special architecture is required for PredNet. Three networks with different initializations were trained for each objective function. Most objective functions were trained by adding an additional header upon the visual backbone and then optimizing the whole network with the sum of the objective-specific loss and a weight regularization loss. Table 1 provides short summaries of the objective functions and mathematical details of each can be found in SI Appendix. After training the networks, we fixed the weights of the model and used them only in the downstream task performance, neural predictivity, and human behavior consistency evaluations.

Neural Response Datasets.

The neural responses dataset for the V1 area was collected by Cadena et al. (19) through presenting stimulus to two awake and fixating macaques and recording the neural responses using a linear 32-channel array. The stimulus consisted of 1,450 ImageNet images and texture-like synthesized images matching the outputs of different layers of an ImageNet trained deep neural network toward these ImageNet images. The images were presented for 60 ms each in one trial without blanks and centered on the population receptive field of the neurons. Spike counts between 40 and 100 ms after image presentation were extracted and averaged across trials to get the final responses, as the response latency of these neurons is typically 40 ms. The neural responses dataset for V4 and IT areas was collected by Majaj et al. (3) by presenting stimuli to two fixating macaques, on which three arrays of electrodes were implanted with one array in area V4 and the other two arrays in area IT. The stimuli were constructed by rendering one of 64 three-dimensional objects belonging to eight categories at a randomly chosen position, pose, and size on a randomly chosen naturalistic photograph as background. These images were presented to the primates for 100 ms with 100 ms of gap between images. From the three arrays, the neural responses of 168 IT sites and 88 V4 sites were collected. The averaged responses between 70 and 170 ms after stimuli presentation were used as this window contained most of the object category-related information (17). More details can be found in SI Appendix.

Downstream Task Performance Evaluation.

We sent the stimulus used for the V4 and IT neural response datasets to the pretrained visual backbones as inputs and collected the outputs from all intermediate layers. A principal component analysis-based dimension reduction method was then applied to the outputs of each layer to get a 1,000-dimensional output. For the categorization task, we fitted a linear support vector classifier for each layer to predict the category of the object in the input image. For the other tasks, a linear support vector regression model was fitted instead to predict the corresponding targets. The fitting was done on the train splits and evaluated on the validation splits. The best performance across all layers was reported for each method. The details about how the fitting was done and the meanings of the prediction targets can be found in SI Appendix.

Neural Predictivity Evaluation.

We sent the same stimulus used for the neural response datasets to the pretrained visual backbones as inputs and collected the outputs from all intermediate layers. A linear regression model was fitted from the responses of each layer to predict the neural responses. Following Klindt et al. (51), we reduced the number of regression weights through factorizing the weight matrices into spatial and channel weight matrices. The Pearson correlation was computed between the predicted and the target neural responses. This correlation was further corrected by the noise ceiling of that neuron. The median value of the corrected correlations of all neurons within one cortical area was reported for one layer as its neural predictivity for this area. The best predictivity across all layers was reported for one method. More details can be found in SI Appendix.

Human Behavior Consistency Evaluation.

The stimuli used in this evaluation were generated by putting 24 objects in front of high-variant and independent naturalistic backgrounds (21). For each pretrained network, a linear classifier was trained from the penultimate layer on the training split to predict the category. The resulting confusion matrix on the validation split was compared to that of human subjects, collected by Rajalingham et al. (21). The Pearson correlation between the matrices was computed and then corrected by the noise ceiling. More details can be found in SI Appendix.

Data Availability.

Codes and data have been deposited in GitHub (https://github.com/neuroailab/unsup_vvs).